Planetary Radar—State-of-the-Art Review
Abstract
1. Introduction
2. A Brief History of Planetary Radar
2.1. Planetary Radar Science in the 20th Century
2.2. Planetary Radar Science in the 21st Century
3. Methods Used in Radar Studies
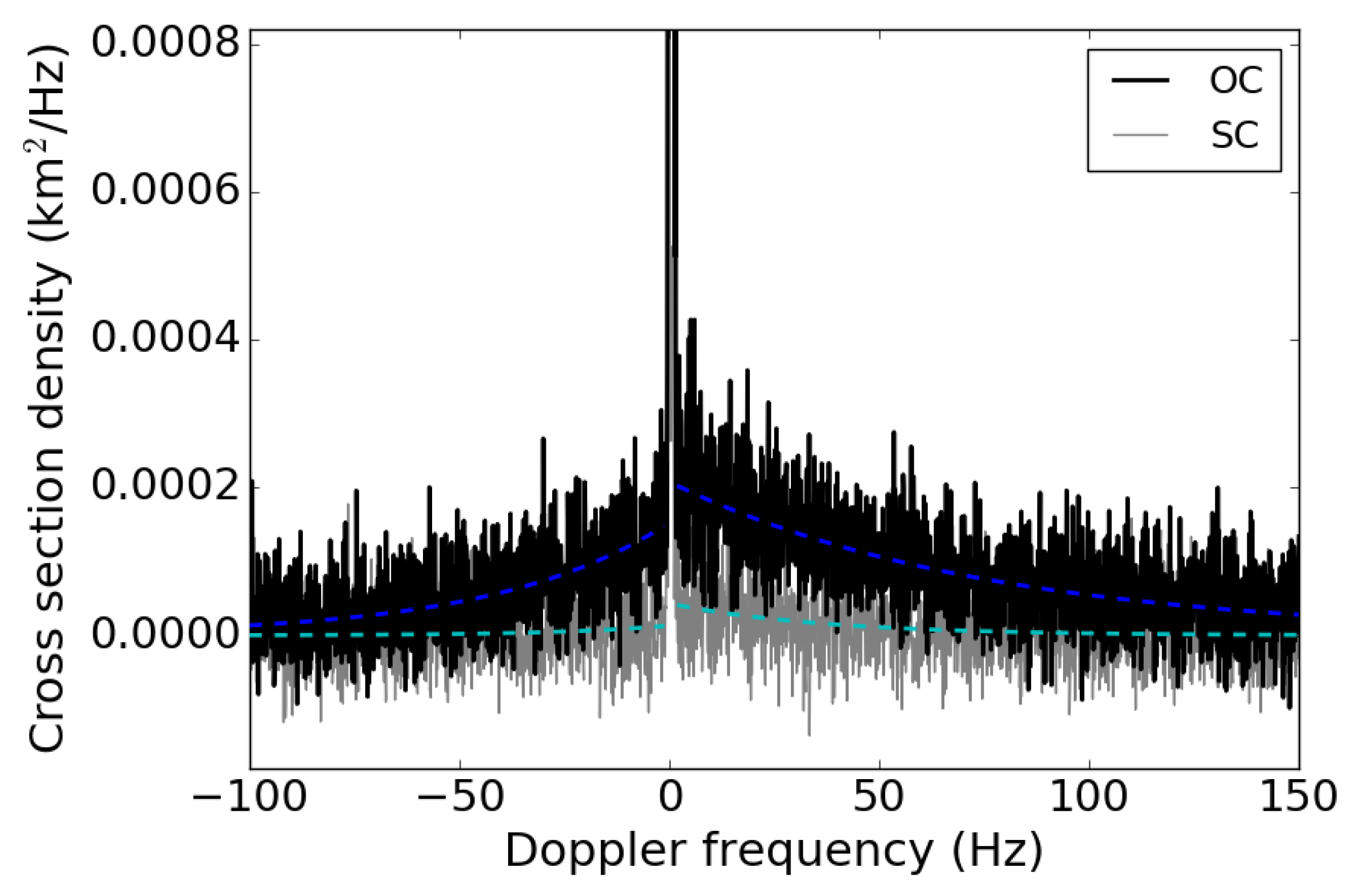
3.1. Echo Power Spectra
3.2. Ranging and Delay–Doppler Imaging
3.3. Synthetic Aperture Radar
3.4. Radar Sounding of Subsurface
3.5. Shape Modeling
3.6. Radar Scattering
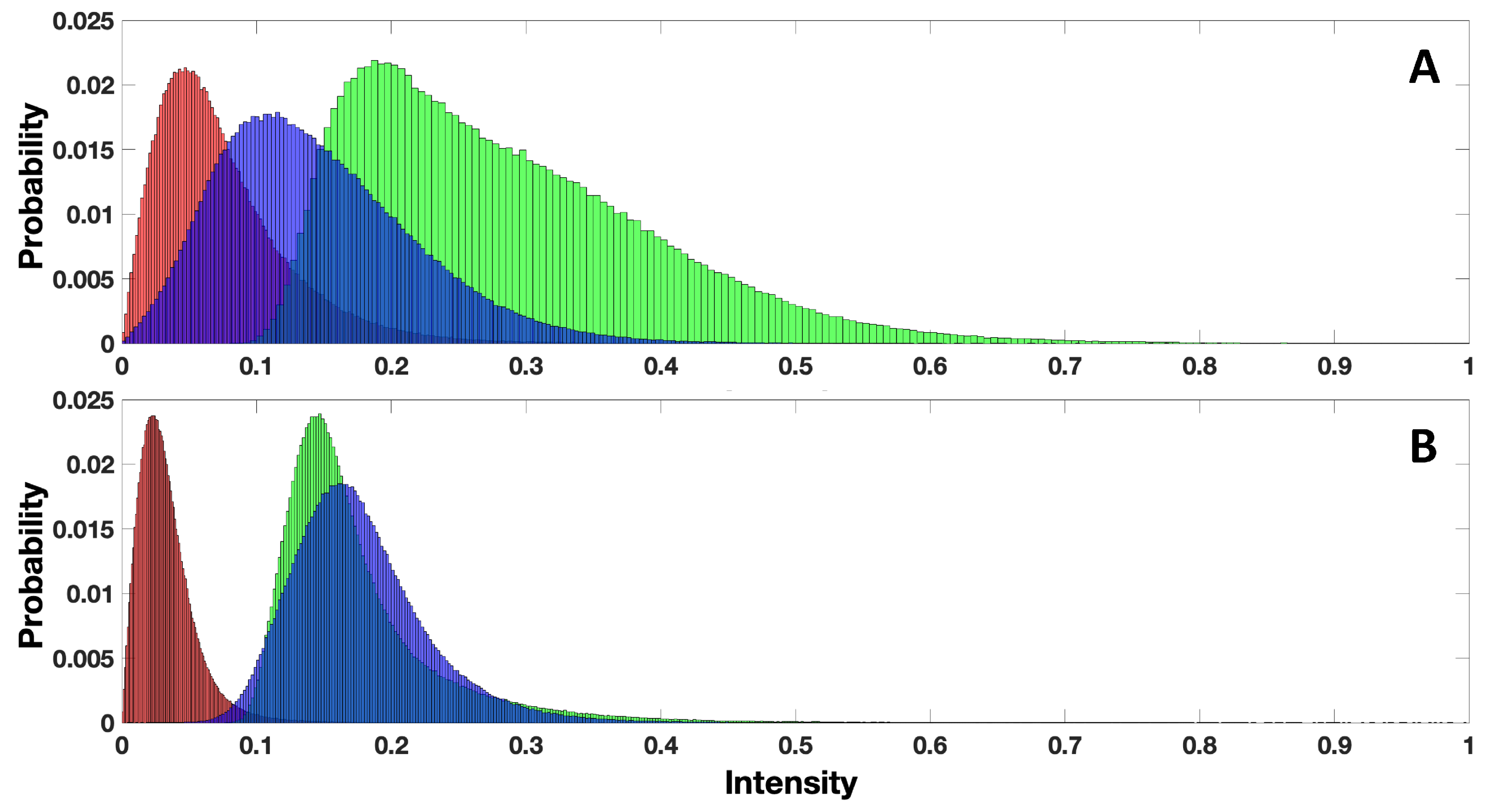
3.6.1. Dual-Polarization Radars
3.6.2. Full/Quad-Polarization Radars
3.6.3. Decomposition
4. Radar Observations of the Moon
4.1. Ground-Based Observations
4.2. Lunar Orbital Radars
5. Radar Observations of the Planets
5.1. Mercury
5.2. Venus
5.3. Mars
5.4. The Galilean Moons
5.5. The Moons and Rings of Saturn
| Object | OC Radar Albedo | SC Radar Albedo | CPR | Wavelength | References |
|---|---|---|---|---|---|
| Mercury | 0.06 | 0.005 | 0.1 | 12.6 cm | [44,192] |
| Venus | 0.11 | 0.01 | 0.1 | 12.6 cm | [44] |
| Moon | 0.07 | 0.007 | 0.1 | 12.6 cm | [44] |
| Mars | 0.08 | 0.02 | 0.3 | 12.6 cm | [44] |
| Europa | 12.6 cm | [193] | |||
| Europa | 3.5 cm | [193] | |||
| Ganymede | 12.6 cm | [193] | |||
| Ganymede | 3.5 cm | [193] | |||
| Callisto | 12.6 cm | [193] | |||
| Callisto | 3.5 cm | [193] | |||
| Enceladus | 12.6 cm | [182] | |||
| Tethys | 12.6 cm | [182] | |||
| Dione | 12.6 cm | [182] | |||
| Rhea | 12.6 cm | [182] | |||
| Titan * | 12.6 cm | [183] | |||
| Iapetus (L *) | 12.6 cm | [181] | |||
| Iapetus (T *) | 12.6 cm | [181] |
5.6. The Radar Scattering Properties of Planets and Moons
6. Radar Observations of Small Solar System Objects
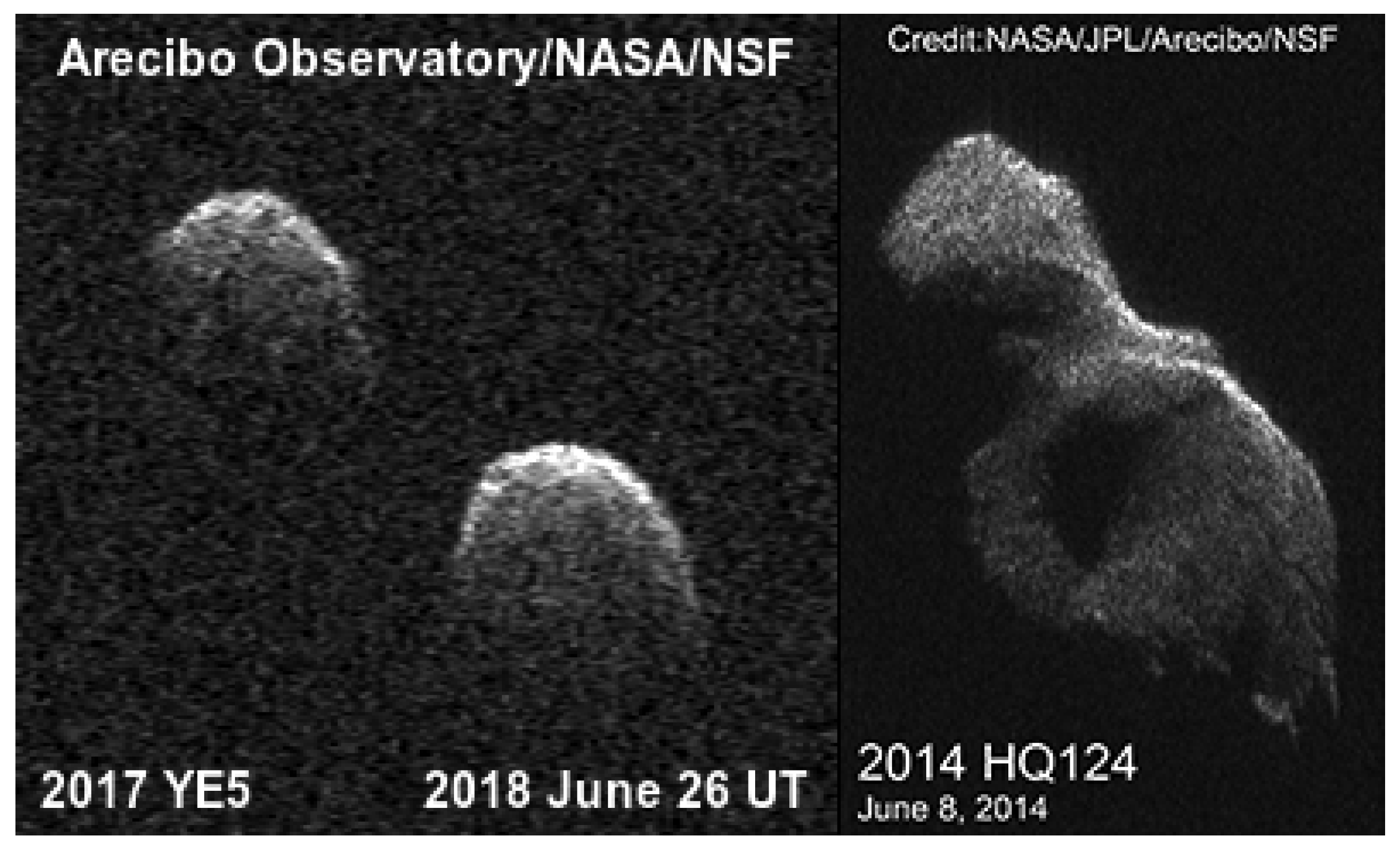
6.1. Asteroids
6.2. Comets
7. The Future of Planetary Radar
7.1. Ground-Based Observations
7.2. Planned Radar Instruments on Future Spacecraft Missions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| BPC | Binary phase coding |
| CONSERT | Comet Nucleus Sounding Experiment by Radiowave Transmission |
| CPR | Circular polarization ratio |
| DART | Double-Asteroid Redirection Test |
| DFSAR | Dual-frequency synthetic aperture radar |
| DSN | Deep space network |
| DSS | Deep space station |
| EISCAT | European Incoherent Scatter Scientific Association |
| ESA | European Space Administration |
| GPR | Ground penetrating radar |
| HF | High frequency |
| ISRO | Indian Space Research Organisation |
| JPL | Jet Propulsion Laboratory |
| JUICE | Jupiter Icy Moons Explorer |
| LCROSS | Lunar Crater Observation and Sensing Satellite |
| LPR | Lunar Penetrating Radar |
| LRO | Lunar Reconnaissance Orbiter |
| LRPR | Lunar Regolith Penetrating Radar |
| LRS | Lunar Radar Sounder |
| MARSIS | Mars Advanced Radar for Subsurface and Ionosphere Sounding |
| MBA | Main-belt asteroid |
| Mini-RF | Miniature Radio Frequency |
| NASA | National Aeronautics and Space Administration |
| NEA | Near-Earth asteroid |
| ngVLA | Next-generation Very Large Array |
| NSF | National Science Foundation |
| OC | Opposite circular |
| PSR | Permanently shadowed region |
| REASON | Radar for Europa Assessment and Sounding: Ocean to Near-surface |
| RGB | Red green blue |
| RIME | Radar for Icy Moons Explorer |
| RIMFAX | Radar Imager for Mars’ subsurface experiment |
| SAR | Synthetic aperture radar |
| SC | Same circular |
| SELENE | Selenological and Engineering Explorer |
| SHARAD | Shallow Radar Sounder |
| SSSO | Small Solar System Object |
| S/N | Signal to noise ratio |
| VenSAR | Venus Synthetic Aperture Radar |
| VERITAS | Venus Emissivity, Radio Science, InSAR, Topography, and Spectroscopy |
| VHF | Very high frequency |
| VISAR | Venus Interferometric Synthetic Aperture Radar |
| VLBA | Very Long Baseline Array |
| VNIR | Visual and near-infrared |
| VOICE | Venus Volcano Imaging and Climate Explorer |
References
- Kastinen, D.; Tveito, T.; Vierinen, J.; Granvik, M. Radar observability of near-Earth objects using EISCAT 3D. Ann. Geophys. 2020, 38, 861–879. [Google Scholar] [CrossRef]
- Vierinen, J.; Tveito, T.; Gustavsson, B.; Kesaraju, S.; Milla, M. Radar images of the Moon at 6-meter wavelength. Icarus 2017, 297, 179–188. [Google Scholar] [CrossRef]
- Price, R.; Green, P.E.J.; Goblick, T.J.J.; Kingston, R.H.; Kraft, L.G.J.; Pettengill, G.H.; Silver, R.; Smith, W.B. Radar Echoes from Venus. Science 1959, 129, 751–753. [Google Scholar] [CrossRef] [PubMed]
- Goldstein, R.M.; Carpenter, R.L. Rotation of Venus: Period Estimated from Radar Measurements. Science 1963, 139, 910–911. [Google Scholar] [CrossRef] [PubMed]
- Dyce, B.R.; Pettengill, G.H.; Shapiro, I.I. Radar determination of the rotations of Venus and Mercury. Astron. J. 1967, 72, 351. [Google Scholar] [CrossRef]
- Shapiro, I.I.; Pettengill, G.H.; Ash, M.E.; Ingalls, R.P.; Campbell, D.B.; Dyce, R.B. Mercury’s Perihelion Advance: Determination by Radar. Phys. Rev. Lett. 1972, 28, 1594–1597. [Google Scholar] [CrossRef]
- Dyce, R.B.; Pettengill, G.H.; Sanchez, A.D. Radar observations of Mars and ’fupiter at 70 CM. Astron. J. 1967, 72, 771. [Google Scholar] [CrossRef]
- Ostro, S.J.; Campbell, D.B.; Pettengill, G.H.; Shapiro, I.I. Radar observations of the icy Galilean satellites. Icarus 1980, 44, 431–440. [Google Scholar] [CrossRef]
- Pettengill, G.H.; Shapiro, I.I.; Ash, M.E.; Ingalls, R.P.; Rainville, L.P.; Smith, W.B.; Stone, M.L. Radar observations of Icarus. Icarus 1969, 10, 432–435. [Google Scholar] [CrossRef]
- Goldstein, R.M. Radar Observations of Icarus. Science 1969, 162, 903–904. [Google Scholar] [CrossRef]
- Kamoun, P.G.; Campbell, D.B.; Ostro, S.J.; Pettengill, G.M.; Shapiro, I.I. Radar Observations of the Nucleus of the Comet P/Encke. Bull. Am. Astron. Soc. 1981, 13, 705. [Google Scholar]
- Greeley, R.; Bender, K.; Thomas, P.E.; Schubert, G.; Limonadi, D.; Weitz, C.M. Wind-related features and processes on Venus: Summary of Magellan results. Icarus 1995, 115, 399–420. [Google Scholar] [CrossRef]
- Slade, M.A.; Butler, B.J.; Muhleman, D.O. Mercury Radar Imaging: Evidence for Polar Ice. Science 1992, 258, 635–640. [Google Scholar] [CrossRef] [PubMed]
- Harmon, J.K.; Slade, M.A. Radar Mapping of Mercury: Full-Disk Images and Polar Anomalies. Science 1992, 258, 640–643. [Google Scholar] [CrossRef]
- Butler, B.J.; Muhleman, D.O.; Slade, M.A. Mercury: Full-disk radar images and the detection and stability of ice at the North Pole. J. Geophys. Res. 1993, 98, 15003–15024. [Google Scholar] [CrossRef]
- Harmon, J.K.; Slade, M.A.; Rice, M.S. Radar imagery of Mercury’s putative polar ice: 1999–2005 Arecibo results. Icarus 2011, 211, 37–50. [Google Scholar] [CrossRef]
- Hapke, B. Coherent backscatter and the radar characteristics of outer planet satellites. Icarus 1990, 88, 407–417. [Google Scholar] [CrossRef]
- Peters, K.J. Coherent-backscatter effect—A vector formulation accounting for polarization and absorption effects and small or large scatterers. Phys. Rev. B 1992, 46, 801–812. [Google Scholar] [CrossRef]
- Giorgini, J.D.; Benner, L.A.; Brozovic, M.; Busch, M.W.; Campbell, D.B.; Chesley, S.R.; Chodas, P.W.; Howell, E.; Margot, J.L.; Milani, A.; et al. Radar Astrometry of Small Bodies: Detection, Characterization, Trajectory Prediction, and Hazard Assessment; Technical Report; Jet Propulsion Laboratory, National Aeronautics and Space Administration: Pasadena, CA, USA, 2009. [Google Scholar]
- Venditti, F.C.F.; Marshall, S.E.; Devogèle, M.; Zambrano-Marin, L.F.; McGilvray, A. The Arecibo Observatory’s legacy and future radar capabilities. Acta Astronaut. 2023, 210, 610–615. [Google Scholar] [CrossRef]
- Giorgini, J.D.; Benner, L.A.M.; Ostro, S.J.; Nolan, M.C.; Busch, M.W. Predicting the Earth encounters of (99942) Apophis. Icarus 2008, 193, 1–19. [Google Scholar] [CrossRef]
- Brozović, M.; Benner, L.A.M.; McMichael, J.G.; Giorgini, J.D.; Pravec, P.; Scheirich, P.; Magri, C.; Busch, M.W.; Jao, J.S.; Lee, C.G.; et al. Goldstone and Arecibo radar observations of (99942) Apophis in 2012–2013. Icarus 2018, 300, 115–128. [Google Scholar] [CrossRef]
- Ostro, S.J.; Benner, L.A.M.; Nolan, M.C.; Magri, C.; Giorgini, J.D.; Scheeres, D.J.; Broschart, S.B.; Kaasalainen, M.; Vokrouhlický, D.; Chesley, S.R.; et al. Radar observations of asteroid 25143 Itokawa (1998 SF36). Meteorit. Planet. Sci. 2004, 39, 407–424. [Google Scholar] [CrossRef]
- Nolan, M.C.; Magri, C.; Howell, E.S.; Benner, L.A.M.; Giorgini, J.D.; Hergenrother, C.W.; Hudson, R.S.; Lauretta, D.S.; Margot, J.L.; Ostro, S.J.; et al. Shape model and surface properties of the OSIRIS-REx target Asteroid (101955) Bennu from radar and lightcurve observations. Icarus 2013, 226, 629–640. [Google Scholar] [CrossRef]
- Shepard, M.K.; Clark, B.E.; Ockert-Bell, M.; Nolan, M.C.; Howell, E.S.; Magri, C.; Giorgini, J.D.; Benner, L.A.M.; Ostro, S.J.; Harris, A.W.; et al. A radar survey of M- and X-class asteroids II. Summary and synthesis. Icarus 2010, 208, 221–237. [Google Scholar] [CrossRef]
- Magri, C.; Consolmagno, G.J.; Ostrch, S.J.; Benner, L.A.; Beeney, B.R. Radar constraints on asteroid regolith properties using 433 Eros as ground truth. Meteorit. Planet. Sci. 2001, 36, 1697–1709. [Google Scholar] [CrossRef]
- Hickson, D.; Boivin, A.; Daly, M.G.; Ghent, R.; Nolan, M.C.; Tait, K.; Cunje, A.; Tsai, C.A. Near surface bulk density estimates of NEAs from radar observations and permittivity measurements of powdered geologic material. Icarus 2018, 306, 16–24. [Google Scholar] [CrossRef]
- Taylor, P.A.; Margot, J.L.; Vokrouhlický, D.; Scheeres, D.J.; Pravec, P.; Lowry, S.C.; Fitzsimmons, A.; Nolan, M.C.; Ostro, S.J.; Benner, L.A.M.; et al. Spin Rate of Asteroid (54509) 2000 PH5 Increasing Due to the YORP Effect. Science 2007, 316, 274. [Google Scholar] [CrossRef]
- Harmon, J.K.; Nolan, M.C.; Husmann, D.I.; Campbell, B.A. Arecibo radar imagery of Mars: The major volcanic provinces. Icarus 2012, 220, 990–1030. [Google Scholar] [CrossRef]
- Campbell, B.A.; Campbell, D.B. Arecibo Radar Maps of Venus from 1988 to 2020. Planet. Sci. J. 2022, 3, 55. [Google Scholar] [CrossRef]
- Rivera-Valentin, E.G.; Meyer, H.M.; Taylor, P.A.; Mazarico, E.; Bhiravarasu, S.S.; Virkki, A.K.; Nolan, M.C.; Chabot, N.L.; Giorgini, J.D. Arecibo S-band Radar Characterization of Local-scale Heterogeneities within Mercury’s North Polar Deposits. Planet. Sci. J. 2022, 3, 62. [Google Scholar] [CrossRef]
- Putzig, N.E.; Phillips, R.J.; Campbell, B.A.; Holt, J.W.; Plaut, J.J.; Carter, L.M.; Egan, A.F.; Bernardini, F.; Safaeinili, A.; Seu, R. Subsurface structure of Planum Boreum from Mars Reconnaissance Orbiter Shallow Radar soundings. Icarus 2009, 204, 443–457. [Google Scholar] [CrossRef]
- Orosei, R.; Lauro, S.E.; Pettinelli, E.; Cicchetti, A.; Coradini, M.; Cosciotti, B.; Di Paolo, F.; Flamini, E.; Mattei, E.; Pajola, M.; et al. Radar evidence of subglacial liquid water on Mars. Science 2018, 361, 490–493. [Google Scholar] [CrossRef] [PubMed]
- Seu, R.; Phillips, R.J.; Biccari, D.; Orosei, R.; Masdea, A.; Picardi, G.; Safaeinili, A.; Campbell, B.A.; Plaut, J.J.; Marinangeli, L.; et al. SHARAD sounding radar on the Mars Reconnaissance Orbiter. J. Geophys. Res. (Planets) 2007, 112, E05S05. [Google Scholar] [CrossRef]
- Plaut, J.J.; Picardi, G.; Safaeinili, A.; Ivanov, A.B.; Milkovich, S.M.; Cicchetti, A.; Kofman, W.; Mouginot, J.; Farrell, W.M.; Phillips, R.J.; et al. Subsurface radar sounding of the south polar layered deposits of Mars. Science 2007, 316, 92–95. [Google Scholar] [CrossRef] [PubMed]
- Stofan, E.R.; Elachi, C.; Lunine, J.I.; Lorenz, R.D.; Stiles, B.; Mitchell, K.L.; Ostro, S.; Soderblom, L.; Wood, C.; Zebker, H.; et al. The lakes of Titan. Nature 2007, 445, 61–64. [Google Scholar] [CrossRef] [PubMed]
- Nozette, S.; Spudis, P.; Bussey, B.; Jensen, R.; Raney, K.; Winters, H.; Lichtenberg, C.L.; Marinelli, W.; Crusan, J.; Gates, M.; et al. The Lunar Reconnaissance Orbiter Miniature Radio Frequency (Mini-RF) Technology Demonstration. Space Sci. Rev. 2010, 150, 285–302. [Google Scholar] [CrossRef]
- Cahill, J.T.S.; Thomson, B.J.; Patterson, G.W.; Bussey, D.B.J.; Neish, C.D.; Lopez, N.R.; Turner, F.S.; Aldridge, T.; McAdam, M.; Meyer, H.M.; et al. The Miniature Radio Frequency instrument’s (Mini-RF) global observations of Earth’s Moon. Icarus 2014, 243, 173–190. [Google Scholar] [CrossRef]
- Bhiravarasu, S.S.; Chakraborty, T.; Putrevu, D.; Pandey, D.K.; Das, A.K.; Ramanujam, V.M.; Mehra, R.; Parasher, P.; Agrawal, K.M.; Gupta, S.; et al. Chandrayaan-2 Dual-frequency Synthetic Aperture Radar (DFSAR): Performance Characterization and Initial Results. Planet. Sci. J. 2021, 2, 134. [Google Scholar] [CrossRef]
- Pupillo, G.; Righini, S.; Orosei, R.; Bortolotti, C.; Maccaferri, G.; Roma, M.; Mastrogiuseppe, M.; Pisanu, T.; Schirru, L.; Cicalò, S.; et al. Testing the potential of the Italian radio telescope for European Radar observations of NEOs. In Proceedings of the 2nd NEO and Debris Detection Conference, Darmstadt, Germany, 24–26 January 2023; p. 41. [Google Scholar]
- Pupillo, G.; Righini, S.; Orosei, R.; Bortolotti, C.; Maccaferri, G.; Roma, M.; Mastrogiuseppe, M.; Pisanu, T.; Schirru, L.; Cicalò, S.; et al. Towards a European Facility for Ground-Based Radar Observations of Near-Earth Objects. Remote Sens. 2023; accepted. [Google Scholar]
- Taylor, P.A.; Wilkinson, S.R.; Paganelli, F.; Samaniego, R.; Shamee, B.; Wallace, A.; Beasley, A. The next generation planetary radar system on the Green Bank Telescope. In Proceedings of the Advanced Maui Optical and Space Surveillance Technologies Conference, Maui, HI, USA, 27–30 September 2022. [Google Scholar]
- Virkki, A.K.; Marshall, S.E.; Venditti, F.C.F.; Zambrano-Marín, L.F.; Hickson, D.C.; McGilvray, A.; Taylor, P.A.; Rivera-Valentín, E.G.; Devogèle, M.; Franco Díaz, E.; et al. Arecibo Planetary Radar Observations of Near-Earth Asteroids: 2017 December–2019 December. Planet. Sci. J. 2022, 3, 222. [Google Scholar] [CrossRef]
- Ostro, S.J. Planetary radar astronomy. Rev. Mod. Phys. 1993, 65, 1235–1295. [Google Scholar] [CrossRef]
- Margot, J.L. A Data-Taking System for Planetary Radar Applications. J. Astron. Instrum. 2021, 10, 2150001. [Google Scholar] [CrossRef]
- Naidu, S.P.; Benner, L.A.M.; Margot, J.L.; Busch, M.W.; Taylor, P.A. Capabilities of Earth-based Radar Facilities for Near-Earth Asteroid Observations. Astron. J. 2016, 152, 99. [Google Scholar] [CrossRef]
- Muhleman, D.O.; Orton, G.S.; Berge, G.L. A model of the Venus atmosphere from radio, radar, and occultation observations. Astrophys. J. 1979, 234, 733–745. [Google Scholar] [CrossRef]
- Campbell, B.A.; Putzig, N.E.; Carter, L.M.; Morgan, G.A.; Phillips, R.J.; Plaut, J.J. Roughness and near-surface density of Mars from SHARAD radar echoes. J. Geophys. Res. Planets 2013, 118, 436–450. [Google Scholar] [CrossRef]
- Skolnik, M.I. Introduction to Radar Systems, 2nd ed.; McGraw-Hill Book Co.: New York, NY, USA, 1980. [Google Scholar]
- Porcello, L.J.; Jordan, R.L.; Zelenka, J.S.; Adams, G.F.; Phillips, R.J.; Brown, W.E.J.; Ward, S.H.; Jackson, P.L. The Apollo lunar sounder radar system. IEEE Proc. 1974, 62, 769–783. [Google Scholar] [CrossRef]
- Picardi, G.; Biccari, D.; Seu, R.; Marinangeli, L.; Johnson, W.T.K.; Jordan, R.L.; Plaut, J.; Safaenili, A.; Gurnett, D.A.; Ori, G.G.; et al. Performance and surface scattering models for the Mars Advanced Radar for Subsurface and Ionosphere Sounding (MARSIS). Planet. Space Sci. 2004, 52, 149–156. [Google Scholar] [CrossRef]
- Ono, T.; Kumamoto, A.; Nakagawa, H.; Yamaguchi, Y.; Oshigami, S.; Yamaji, A.; Kobayashi, T.; Kasahara, Y.; Oya, H. Lunar Radar Sounder Observations of Subsurface Layers Under the Nearside Maria of the Moon. Science 2009, 323, 909. [Google Scholar] [CrossRef]
- Fan, M.; Lyu, P.; Su, Y.; Du, K.; Zhang, Q.; Zhang, Z.; Dai, S.; Hong, T. The Mars Orbiter Subsurface Investigation Radar (MOSIR) on China’s Tianwen-1 Mission. Space Sci. Rev. 2021, 217, 8. [Google Scholar] [CrossRef]
- Kaku, T.; Haruyama, J.; Miyake, W.; Kumamoto, A.; Ishiyama, K.; Nishibori, T.; Yamamoto, K.; Crites, S.T.; Michikami, T.; Yokota, Y.; et al. Detection of Intact Lava Tubes at Marius Hills on the Moon by SELENE (Kaguya) Lunar Radar Sounder. Geophys. Res. Lett. 2017, 44, 10155–10161. [Google Scholar] [CrossRef]
- Perry, M.R.; Putzig, N.E.; Bain, Z.M.; Crown, D.A.; Scheidt, S.P.; Nunes, D.E. Detection and Characterization of Intact Lava Tubes on the Western Flank of Alba Mons in Mars Reconnaissance Orbiter Shallow Radar (SHARAD) Data. In Proceedings of the Ninth International Conference on Mars, Pasadena, CA, USA, 22–26 July 2019; Volume 2089, p. 6405. [Google Scholar]
- Kofman, W.; Herique, A.; Barbin, Y.; Barriot, J.P.; Ciarletti, V.; Clifford, S.; Edenhofer, P.; Elachi, C.; Eyraud, C.; Goutail, J.P.; et al. Properties of the 67P/Churyumov-Gerasimenko interior revealed by CONSERT radar. Science 2015, 349, aab0639. [Google Scholar] [CrossRef]
- Bruzzone, L.; Plaut, J.; Alberti, G.; Blankenship, D.D.; Bovolo, F.; Campbell, B.A.; Castelletti, D.; Gim, Y.; Ilisei, A.M.; Kofman, W.W.; et al. The Radar for Icy Moon Exploration (RIME) on the JUICE Mission. In Proceedings of the AGU Fall Meeting Abstracts, San Francisco, CA, USA, 14–18 December 2015; Volume 2015, p. P53G-01. [Google Scholar]
- Blankenship, D.; Ray, T.; Plaut, J.; Moussessian, A.; Patterson, W.; Romero-Wolf, A.; Grima, C.; Young, D.; Soderlund, K.; Gim, Y.; et al. REASON for Europa. In Proceedings of the 42nd COSPAR Scientific Assembly, Pasadena, CA, USA, 14–22 July 2018; Volume 42, p. B5.3-55-18. [Google Scholar]
- Magri, C.; Nolan, M.C.; Ostro, S.J.; Giorgini, J.D. Radar imaging of asteroid 654 Zelinda. In Proceedings of the Asteroids, Comets, and Meteors: ACM 2002, Berlin, Germany, 29 July–2 August 2002; Volume 500, pp. 485–488. [Google Scholar]
- Viikinkoski, M.; Kaasalainen, M.; Ďurech, J. ADAM: A general method for using various data types in asteroid reconstruction. Astron. Astrophys. 2015, 576, A8. [Google Scholar] [CrossRef]
- Hagfors, T. Backscattering from an undulating surface with applications to radar returns from the Moon. J. Geophys. Res. 1964, 69, 3779–3784. [Google Scholar] [CrossRef]
- Hagfors, T. Remote probing of the moon by infrared and microwave emission and by radar. Radio Sci. 1970, 5, 189–227. [Google Scholar] [CrossRef]
- Thompson, T.W.; Ustinov, E.A.; Heggy, E. Modeling radar scattering from icy lunar regoliths at 13 cm and 4 cm wavelengths. J. Geophys. Res. (Planets) 2011, 116, E01006. [Google Scholar] [CrossRef]
- Mitchell, D.L.; Ostro, S.J.; Hudson, R.S.; Rosema, K.D.; Campbell, D.B.; Velez, R.; Chandler, J.F.; Shapiro, I.I.; Giorgini, J.D.; Yeomans, D.K. Radar Observations of Asteroids 1 Ceres, 2 Pallas, and 4 Vesta. Icarus 1996, 124, 113–133. [Google Scholar] [CrossRef][Green Version]
- Simpson, R.A.; Tyler, G.L. Radar scattering laws for the lunar surface. IEEE Trans. Antennas Propag. 1982, 30, 438–449. [Google Scholar] [CrossRef]
- Shepard, M.K.; Brackett, R.A.; Arvidson, R.E. Self-affine (fractal) topography: Surface parameterization and radar scattering. J. Geophys. Res. Planets 1995, 100, 11709–11718. [Google Scholar] [CrossRef]
- Pettengill, G.H.; Henry, J.C. Enhancement of Radar Reflectivity Associated with the Lunar Crater Tycho. J. Geophys. Res. 1962, 67, 4881–4885. [Google Scholar] [CrossRef]
- Ostro, S.J.; Campbell, D.B.; Shapiro, I.I. Mainbelt asteroids–Dual-polarization radar observations. Science 1985, 229, 442–446. [Google Scholar] [CrossRef]
- Campbell, B.A. High circular polarization ratios in radar scattering from geologic targets. J. Geophys. Res. (Planets) 2012, 117, 6008. [Google Scholar] [CrossRef]
- Virkki, A.; Muinonen, K. Radar scattering by planetary surfaces modeled with laboratory-characterized particles. Icarus 2016, 269, 38–49. [Google Scholar] [CrossRef]
- Virkki, A.K.; Bhiravarasu, S.S. Modeling Radar Albedos of Laboratory-Characterized Particles: Application to the Lunar Surface. J. Geophys. Res. (Planets) 2019, 124, 3025–3040. [Google Scholar] [CrossRef]
- Carter, L.M.; Campbell, D.B.; Campbell, B.A. Impact crater related surficial deposits on Venus: Multipolarization radar observations with Arecibo. J. Geophys. Res. Planets 2004, 109. [Google Scholar] [CrossRef]
- Hickson, D.C. Surface scattering model for dual-polarization planetary radars. Planet. Space Sci. 2022, 221, 105560. [Google Scholar] [CrossRef]
- Raney, R.K.; Spudis, P.D.; Bussey, B.; Crusan, J.; Jensen, J.R.; Marinelli, W.; McKerracher, P.; Neish, C.; Palsetia, M.; Schulze, R.; et al. The Lunar Mini-RF Radars: Hybrid Polarimetric Architecture and Initial Results. Proc. IEEE 2011, 99, 808–823. [Google Scholar] [CrossRef]
- Nord, M.; Ainsworth, T.; Lee, J.S.; Stacy, N. Comparison of Compact Polarimetric Synthetic Aperture Radar Modes. IEEE Trans. Geosci. Remote Sens. 2009, 47, 174–188. [Google Scholar] [CrossRef]
- Lee, J.S.; Pottier, E. Polarimetric Radar Imaging: From Basics to Applications; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar]
- Putrevu, D.; Das, A.; Vachhani, J.; Trivedi, S.; Misra, T. Chandrayaan-2 dual-frequency SAR: Further investigation into lunar water and regolith. Adv. Space Res. 2016, 57, 627–646. [Google Scholar] [CrossRef]
- Zyl, J.J.V.; Zebker, H.A.; Elachi, C. Imaging radar polarization signatures: Theory and observation. Radio Sci. 1987, 22, 529–543. [Google Scholar] [CrossRef]
- Cloude, S.; Pottier, E. A review of target decomposition theorems in radar polarimetry. IEEE Trans. Geosci. Remote Sens. 1996, 34, 498–518. [Google Scholar] [CrossRef]
- Henderson, F.M.; Lewis, A.J. Principles and Applications of Imaging Radar. Manual of Remote Sensing, 3rd ed.; Wiley: New York, NY, USA, 1998; Volume 2. [Google Scholar]
- Cloude, S. Polarisation: Applications in Remote Sensing; Oxford University Press: Oxford, UK, 2009. [Google Scholar] [CrossRef]
- Cloude, S.; Pottier, E. An entropy based classification scheme for land applications of polarimetric SAR. IEEE Trans. Geosci. Remote Sens. 1997, 35, 68–78. [Google Scholar] [CrossRef]
- Campbell, B.A. Radar Remote Sensing of Planetary Surfaces; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Zebker, H.; Lou, Y. Phase calibration of imaging radar polarimeter Stokes matrices. IEEE Trans. Geosci. Remote Sens. 1990, 28, 246–252. [Google Scholar] [CrossRef]
- Raney, R.K.; Cahill, J.T.S.; Patterson, G.W.; Bussey, D.B.J. The m-chi decomposition of hybrid dual-polarimetric radar data with application to lunar craters. J. Geophys. Res. (Planets) 2012, 117, E00H21. [Google Scholar] [CrossRef]
- Hickson, D.C.; Virkki, A.K.; Perillat, P.; Nolan, M.C.; Bhiravarasu, S.S. Polarimetric Decomposition of Near-Earth Asteroids Using Arecibo Radar Observations. Planet. Sci. J. 2021, 2, 30. [Google Scholar] [CrossRef]
- Muhleman, D.O. Radar scattering from Venus and the Moon. Astron. J. 1964, 69, 34–41. [Google Scholar] [CrossRef]
- Campbell, B.A.; Campbell, D.B.; Margot, J.L.; Ghent, R.R.; Nolan, M.C.; Chandler, J.; Carter, L.M.; Stacy, N.J.S. Focused 70-cm wavelength radar mapping of the Moon. IEEE Trans. Geosci. Remote Sens. 2007, 45, 4032–4042. [Google Scholar] [CrossRef]
- Campbell, B.A.; Carter, L.M.; Campbell, D.B.; Nolan, M.; Chandler, J.; Ghent, R.R.; Ray Hawke, B.; Anderson, R.F.; Wells, K. Earth-based 12.6-cm wavelength radar mapping of the Moon: New views of impact melt distribution and mare physical properties. Icarus 2010, 208, 565–573. [Google Scholar] [CrossRef]
- Carter, L.M.; Campbell, B.A.; Hawke, B.R.; Campbell, D.B.; Nolan, M.C. Radar remote sensing of pyroclastic deposits in the southern Mare Serenitatis and Mare Vaporum regions of the Moon. J. Geophys. Res. 2009, 114, E11004. [Google Scholar] [CrossRef]
- Morgan, G.A.; Campbell, B.A.; Campbell, D.B.; Hawke, B.R. Investigating the stratigraphy of Mare Imbrium flow emplacement with Earth-based radar. J. Geophys. Res. Planets 2016, 121, 1498–1513. [Google Scholar] [CrossRef]
- Campbell, B.A.; Hawke, B.R. Radar mapping of lunar cryptomaria east of Orientale basin. J. Geophys. Res. 2005, 110, E09002. [Google Scholar] [CrossRef]
- Campbell, B.A.; Hawke, B.R.; Morgan, G.A.; Carter, L.M.; Campbell, D.B.; Nolan, M. Improved discrimination of volcanic complexes, tectonic features, and regolith properties in Mare Serenitatis from Earth-based radar mapping. J. Geophys. Res. Planets 2014, 119, 313–330. [Google Scholar] [CrossRef]
- Sato, H.; Robinson, M.S.; Lawrence, S.J.; Denevi, B.W.; Hapke, B.; Jolliff, B.L.; Hiesinger, H. Lunar mare TiO2 abundances estimated from UV/Vis reflectance. Icarus 2017, 296, 216–238. [Google Scholar] [CrossRef]
- Watson, K.; Murray, B.C.; Brown, H. The behavior of volatiles on the lunar surface. J. Geophys. Res. 1961, 66, 3033–3045. [Google Scholar] [CrossRef]
- Arnold, J.R. Ice in the lunar polar regions. J. Geophys. Res. 1979, 84, 5659–5668. [Google Scholar] [CrossRef]
- Stacy, N.J.S.; Campbell, D.B.; Ford, P.G. Arecibo Radar Mapping of the Lunar Poles: A Search for Ice Deposits. Science 1997, 276, 1527–1530. [Google Scholar] [CrossRef]
- Nozette, S.; Lichtenberg, C.L.; Spudis, P.; Bonner, R.; Ort, W.; Malaret, E.; Robinson, M.; Shoemaker, E.M. The Clementine Bistatic Radar Experiment. Science 1996, 274, 1495–1498. [Google Scholar] [CrossRef] [PubMed]
- Simpson, R.A.; Tyler, G.L. Reanalysis of C!ementine bistatic radar data from. J. Geophys. Res. 1999, 104, 3845–3862. [Google Scholar] [CrossRef]
- Neish, C.D.; Bussey, D.B.J.; Spudis, P.; Marshall, W.; Thomson, B.J.; Patterson, G.W.; Carter, L.M. The nature of lunar volatiles as revealed by Mini-RF observations of the LCROSS impact site. J. Geophys. Res. 2011, 116, E01005. [Google Scholar] [CrossRef]
- Colaprete, A.; Schultz, P.; Heldmann, J.; Wooden, D.; Shirley, M.; Ennico, K.; Hermalyn, B.; Marshall, W.; Ricco, A.; Elphic, R.C.; et al. Detection of Water in the LCROSS Ejecta Plume. Science 2010, 330, 463–468. [Google Scholar] [CrossRef]
- Spudis, P.D.; Bussey, D.B.J.; Baloga, S.M.; Butler, B.J.; Carl, D.; Carter, L.M.; Chakraborty, M.; Elphic, R.C.; Gillis-Davis, J.J.; Goswami, J.N.; et al. Initial results for the north pole of the Moon from Mini-SAR, Chandrayaan-1 mission. Geophys. Res. Lett. 2010, 37. [Google Scholar] [CrossRef]
- Spudis, P.D.; Bussey, D.B.J.; Baloga, S.M.; Cahill, J.T.S.; Glaze, L.S.; Patterson, G.W.; Raney, R.K.; Thompson, T.W.; Thomson, B.J.; Ustinov, E.A. Evidence for water ice on the moon: Results for anomalous polar craters from the LRO Mini-RF imaging radar. J. Geophys. Res. (Planets) 2013, 118, 2016–2029. [Google Scholar] [CrossRef]
- Elphic, R.C.; Eke, V.R.; Teodoro, L.F.A.; Lawrence, D.J.; Bussey, D.B.J. Models of the distribution and abundance of hydrogen at the lunar south pole. Geophys. Res. Lett. 2005, 34. [Google Scholar] [CrossRef]
- Williams, J.P.; Paige, D.; Greenhagen, B.; Sefton-Nash, E. The global surface temperatures of the moon as measured by the diviner lunar radiometer experiment. Icarus 2017, 283, 300–325. [Google Scholar] [CrossRef]
- Fa, W.; Eke, V.R. Unravelling the Mystery of Lunar Anomalous Craters Using Radar and Infrared Observations. J. Geophys. Res. Planets 2018, 123, 2119–2137. [Google Scholar] [CrossRef]
- Mitchell, J.; Lawrence, S.; Robinson, M.; Speyerer, E.; Denevi, B. Using complementary remote sensing techniques to assess the presence of volatiles at the lunar north pole. Planet. Space Sci. 2018, 162, 133–147. [Google Scholar] [CrossRef]
- Patterson, G.W.; Stickle, A.M.; Turner, F.S.; Jensen, J.R.; Bussey, D.B.J.; Spudis, P.; Espiritu, R.C.; Schulze, R.C.; Yocky, D.A.; Wahl, D.E.; et al. Bistatic radar observations of the Moon using Mini-RF on LRO and the Arecibo Observatory. Icarus 2017, 283, 2–19. [Google Scholar] [CrossRef]
- Feldman, W.C. Fluxes of Fast and Epithermal Neutrons from Lunar Prospector: Evidence for Water Ice at the Lunar Poles. Science 1998, 281, 1496–1500. [Google Scholar] [CrossRef] [PubMed]
- Feldman, W.C.; Maurice, S.; Lawrence, D.J.; Little, R.C.; Lawson, S.L.; Gasnault, O.; Wiens, R.C.; Barraclough, B.L.; Elphic, R.C.; Prettyman, T.H.; et al. Evidence for water ice near the lunar poles. J. Geophys. Res. Planets 2001, 106, 23231–23251. [Google Scholar] [CrossRef]
- Pieters, C.M.; Goswami, J.N.; Clark, R.N.; Annadurai, M.; Boardman, J.; Buratti, B.; Combe, J.P.; Dyar, M.D.; Green, R.; Head, J.W.; et al. Character and Spatial Distribution of OH/H2O on the Surface of the Moon Seen by M3 on Chandrayaan-1. Science 2009, 326, 568–572. [Google Scholar] [CrossRef]
- Paige, D.A.; Siegler, M.A.; Zhang, J.A.; Hayne, P.O.; Foote, E.J.; Bennett, K.A.; Vasavada, A.R.; Greenhagen, B.T.; Schofield, J.T.; McCleese, D.J.; et al. Diviner Lunar Radiometer Observations of Cold Traps in the Moon’s South Polar Region. Science 2010, 330, 479–482. [Google Scholar] [CrossRef]
- Zuber, M.T.; Head, J.W.; Smith, D.E.; Neumann, G.A.; Mazarico, E.; Torrence, M.H.; Aharonson, O.; Tye, A.R.; Fassett, C.I.; Rosenburg, M.A.; et al. Constraints on the volatile distribution within Shackleton crater at the lunar south pole. Nature 2012, 486, 378–381. [Google Scholar] [CrossRef]
- Hayne, P.O.; Hendrix, A.; Sefton-Nash, E.; Siegler, M.A.; Lucey, P.G.; Retherford, K.D.; Williams, J.P.; Greenhagen, B.T.; Paige, D.A. Evidence for exposed water ice in the Moon’s south polar regions from Lunar Reconnaissance Orbiter ultraviolet albedo and temperature measurements. Icarus 2015, 255, 58–69. [Google Scholar] [CrossRef]
- Costello, E.S.; Ghent, R.R.; Hirabayashi, M.; Lucey, P.G. Impact Gardening as a Constraint on the Age, Source, and Evolution of Ice on Mercury and the Moon. J. Geophys. Res. (Planets) 2020, 125, e06172. [Google Scholar] [CrossRef]
- Neish, C.D.; Madden, J.; Carter, L.M.; Hawke, B.R.; Giguere, T.; Bray, V.J.; Osinski, G.R.; Cahill, J.T.S. Global distribution of lunar impact melt flows. Icarus 2014, 239, 105–117. [Google Scholar] [CrossRef]
- Bandfield, J.L.; Cahill, J.T.S.; Carter, L.M.; Neish, C.D.; Patterson, G.W.; Williams, J.P.; Paige, D.A. Distal ejecta from lunar impacts: Extensive regions of rocky deposits. Icarus 2017, 283, 282–299. [Google Scholar] [CrossRef]
- Inderkumar, K.; Maurya, H.; Kumar, A.; Bhiravarasu, S.S.; Das, A.; Putrevu, D.; Pandey, D.K.; Panigrahi, R.K. Retrieval of Lunar Surface Dielectric Constant Using Chandrayaan-2 Full-Polarimetric SAR Data. IEEE Trans. Geosci. Remote Sens. 2022, 60, 4602212. [Google Scholar] [CrossRef]
- Kochar, I.; Chakraborty, T.; Bhiravarasu, S.S.; Das, A.; Putrevu, D.; Panigrahi, R.K. Estimation of lunar surface roughness using Chandrayaan-2 full-polarimetric DFSAR data. Icarus 2023, 406, 115720. [Google Scholar] [CrossRef]
- Bhiravarasu, S.S.; Campbell, B.A.; Tolometti, G.D.; Cahill, J.T.S.; Das, A.; Patterson, G.W.; Chakraborty, T.; Morgan, G.A.; Pandey, D.K.; Thomson, B.J.; et al. New Orbital L-Band Radar Observations of Aristarchus Plateau. In Proceedings of the 53rd Lunar and Planetary Science Conference, Woodlands, TX, USA, 7–11 March 2022; Volume 2678, p. 1773. [Google Scholar]
- Bhiravarasu, S.S.; Stopar, J.D.; Rivera-Valentin, E.G.; Morgan, G.A.; Wolff, G.M.; Neish, C.D.; Cahill, J.T.S.; Chakraborty, T.; Pandey, D.; Das, A.; et al. New L-Band Radar Observations of Ina Feature on the Moon. In Proceedings of the 53rd Lunar and Planetary Science Conference, Woodlands, TX, USA, 7–11 March 2022; Volume 2806, p. 1914. [Google Scholar]
- Campbell, D.B.; Chandler, J.F.; Pettengill, G.H.; Shapiro, I.I. Galilean satellites of Jupiter: 12.6-centimeter radar observations. Science 1977, 196, 650–653. [Google Scholar] [CrossRef]
- Ostro, S.J.; Shoemaker, E.M. The extraordinary radar echoes from Europa, Ganymede, and Callisto: A geological perspective. Icarus 1990, 85, 335–345. [Google Scholar] [CrossRef]
- Muhleman, D.O.; Butler, B.J.; Grossman, A.W.; Slade, M.A. Radar Images of Mars. Science 1991, 253, 1508–1513. [Google Scholar] [CrossRef]
- Harmon, J.K.; Slade, M.A.; Velez, R.A.; Crespo, A.; Dryer, M.J. Radar mapping of Mercury’s polar anomalies. Nature 1994, 369, 213–215. [Google Scholar] [CrossRef]
- Harmon, J.K.; Perillat, P.J.; Slade, M.A. High-Resolution Radar Imaging of Mercury’s North Pole. Icarus 2001, 149, 1–15. [Google Scholar] [CrossRef]
- Paige, D.A.; Wood, S.E.; Vasavada, A.R. The thermal stability of water ice at the poles of Mercury. Science 1992, 258, 643–646. [Google Scholar] [CrossRef] [PubMed]
- Vasavada, A.R.; Paige, D.A.; Wood, S.E. Near-Surface Temperatures on Mercury and the Moon and the Stability of Polar Ice Deposits. Icarus 1999, 141, 179–193. [Google Scholar] [CrossRef]
- Chabot, N.L.; Ernst, C.M.; Denevi, B.W.; Harmon, J.K.; Murchie, S.L.; Blewett, D.T.; Solomon, S.C.; Zhong, E.D. Areas of permanent shadow in Mercury’s south polar region ascertained by MESSENGER orbital imaging. Geophys. Res. Lett. 2012, 39, L09204. [Google Scholar] [CrossRef]
- Deutsch, A.N.; Chabot, N.L.; Mazarico, E.; Ernst, C.M.; Head, J.W.; Neumann, G.A.; Solomon, S.C. Comparison of areas in shadow from imaging and altimetry in the north polar region of Mercury and implications for polar ice deposits. Icarus 2016, 280, 158–171. [Google Scholar] [CrossRef] [PubMed]
- Lawrence, D.J.; Feldman, W.C.; Goldsten, J.O.; Maurice, S.; Peplowski, P.N.; Anderson, B.J.; Bazell, D.; McNutt, R.L.; Nittler, L.R.; Prettyman, T.H.; et al. Evidence for Water Ice Near Mercury’s North Pole from MESSENGER Neutron Spectrometer Measurements. Science 2013, 339, 292. [Google Scholar] [CrossRef] [PubMed]
- Chabot, N.L.; Shread, E.E.; Harmon, J.K. Investigating Mercury’s South Polar Deposits: Arecibo Radar Observations and High-Resolution Determination of Illumination Conditions. J. Geophys. Res. (Planets) 2018, 123, 666–681. [Google Scholar] [CrossRef]
- Neumann, G.A.; Cavanaugh, J.F.; Sun, X.; Mazarico, E.M.; Smith, D.E.; Zuber, M.T.; Mao, D.; Paige, D.A.; Solomon, S.C.; Ernst, C.M.; et al. Bright and Dark Polar Deposits on Mercury: Evidence for Surface Volatiles. Science 2013, 339, 296–300. [Google Scholar] [CrossRef]
- Hamill, C.D.; Chabot, N.L.; Mazarico, E.; Siegler, M.A.; Barker, M.K.; Camacho, J.M.M. New Illumination and Temperature Constraints of Mercury’s Volatile Polar Deposits. Planet. Sci. J. 2020, 1, 57. [Google Scholar] [CrossRef]
- Barker, M.K.; Chabot, N.L.; Mazarico, E.; Siegler, M.A.; Martinez-Camacho, J.M.; Hamill, C.D.; Bertone, S. New Constraints on the Volatile Deposit in Mercury’s North Polar Crater, Prokofiev. Planet. Sci. J. 2022, 3, 188. [Google Scholar] [CrossRef]
- Glantzberg, A.K.; Chabot, N.L.; Barker, M.K.; Mazarico, E.; Siegler, M.A.; Camacho, J.M.M.; Hamill, C.D.; Rivera-Valentín, E.G.; Meyer, H.; Bertone, S.; et al. Investigating the Stability and Distribution of Surface Ice in Mercury’s Northernmost Craters. Planet. Sci. J. 2023, 4, 107. [Google Scholar] [CrossRef]
- Harmon, J.K.; Slade, M.A.; Butler, B.J.; Head, J.W., III; Rice, M.S.; Campbell, D.B. Mercury: Radar images of the equatorial and midlatitude zones. Icarus 2007, 187, 374–405. [Google Scholar] [CrossRef]
- Neish, C.D.; Blewett, D.T.; Harmon, J.K.; Coman, E.I.; Cahill, J.T.S.; Ernst, C.M. A comparison of rayed craters on the Moon and Mercury. J. Geophys. Res. Planets 2013, 118, 2247–2261. [Google Scholar] [CrossRef]
- Hawke, B.; Blewett, D.; Lucey, P.; Smith, G.; Bell, J.; Campbell, B.; Robinson, M. The origin of lunar crater rays. Icarus 2004, 170, 1–16. [Google Scholar] [CrossRef]
- Rivera-Valentin, E.G.; Fassett, C.I.; Denevi, B.W.; Meyer, H.M.; Neish, C.D.; Morgan, G.A.; Stickle, A.M.; Patterson, G.W. Mini-RF S-band radar characterization of a Tycho ray over the lunar south pole. Planet. Sci. J. 2023; Submitted. [Google Scholar]
- Goldstein, R.M.; Rumsey, H.C. A Radar Image of Venus. Icarus 1972, 17, 699–703. [Google Scholar] [CrossRef]
- Masursky, H.; Eliason, E.; Ford, P.G.; McGill, G.E.; Pettengill, G.H.; Schaber, G.G.; Schubert, G. Pioneer Venus radar results—Geology from images and altimetry. J. Geophys. Res. 1980, 85, 8232–8260. [Google Scholar] [CrossRef]
- Saunders, R.S.; Stofan, E.R.; Plaut, J.J.; Senske, D.A. Magellan at Venus: Summary of Science Findings. In Proceedings of the Lunar and Planetary Science Conference, Houston, TX, USA, 15–19 March 1993; p. 1237. [Google Scholar]
- Ford, P.G.; Pettengill, G.H. Venus topography and kilometer-scale slopes. J. Geophys. Res. 1992, 97, 13103–13114. [Google Scholar] [CrossRef]
- Treiman, A.; Harrington, E.; Sharpton, V. Venus’ radar-bright highlands: Different signatures and materials on Ovda Regio and on Maxwell Montes. Icarus 2016, 280, 172–182. [Google Scholar] [CrossRef]
- Crumpler, L. Volcanoes and centers of volcanism on Venus. In Venus II: Geology, Geophysics, Atmosphere, and Solar Wind Environment; Bougher, S.W., Hunten, D.M., Philips, R.J., Eds.; University of Arizona Press: Tucson, AZ, USA, 1997; pp. 697–756. [Google Scholar]
- Campbell, B.A.; Campbell, D.B.; Carter, L.M.; Nolan, M. Long-Term Monitoring of Venus Volcanism Using Earth-Based Radar. In Proceedings of the 43rd Annual Lunar and Planetary Science Conference, Woodlands, TX, USA, 19–23 March 2012; p. 2027. [Google Scholar]
- Herrick, R.R.; Hensley, S. Surface changes observed on a Venusian volcano during the Magellan mission. Science 2023, 379, 1205–1208. [Google Scholar] [CrossRef]
- Campbell, B.A.; Campbell, D.B. Analysis of volcanic surface morphology on Venus from comparison of Arecibo, Magellan, and terrestrial airborne radar data. J. Geophys. Res. 1992, 97, 16293–16314. [Google Scholar] [CrossRef]
- Carter, L.M.; Campbell, D.B.; Campbell, B.A. Volcanic deposits in shield fields and highland regions on Venus: Surface properties from radar polarimetry. J. Geophys. Res. (Planets) 2006, 111, E06005. [Google Scholar] [CrossRef]
- Harmon, J.K. Planetary delay-Doppler radar and the long-code method. IEEE Trans. Geosci. Remote Sens. 2002, 40, 1904–1916. [Google Scholar] [CrossRef]
- Harmon, J.K.; Slade, M.A.; Hudson, R.S. Mars radar scattering: Arecibo/Goldstone results at 12.6- and 3.5-cm wavelengths. Icarus 1992, 98, 240–253. [Google Scholar] [CrossRef]
- Harmon, J.K.; Nolan, M.C. Arecibo radar imagery of Mars: II. Chryse-Xanthe, polar caps, and other regions. Icarus 2017, 281, 162–199. [Google Scholar] [CrossRef]
- Rodriguez Sanchez-Vahamonde, C.; Neish, C. The Surface Texture of Martian Lava Flows as Inferred from Their Decimeter- and Meter-scale Roughness. Planet. Sci. J. 2021, 2, 15. [Google Scholar] [CrossRef]
- Plaut, J.J.; Safaeinili, A.; Holt, J.W.; Phillips, R.J.; Head, J.W.; Seu, R.; Putzig, N.E.; Frigeri, A. Radar evidence for ice in lobate debris aprons in the mid-northern latitudes of Mars. Geophys. Res. Lett. 2009, 36, L02203. [Google Scholar] [CrossRef]
- Watters, T.R.; Campbell, B.; Carter, L.; Leuschen, C.J.; Plaut, J.J.; Picardi, G.; Orosei, R.; Safaeinili, A.; Clifford, S.M.; Farrell, W.M.; et al. Radar Sounding of the Medusae Fossae Formation Mars: Equatorial Ice or Dry, Low-Density Deposits? Science 2007, 318, 1125. [Google Scholar] [CrossRef]
- Phillips, R.J.; Davis, B.J.; Tanaka, K.L.; Byrne, S.; Mellon, M.T.; Putzig, N.E.; Haberle, R.M.; Kahre, M.A.; Campbell, B.A.; Carter, L.M.; et al. Massive CO2 Ice Deposits Sequestered in the South Polar Layered Deposits of Mars. Science 2011, 332, 838. [Google Scholar] [CrossRef]
- Stuurman, C.M.; Osinski, G.R.; Holt, J.W.; Levy, J.S.; Brothers, T.C.; Kerrigan, M.; Campbell, B.A. SHARAD detection and characterization of subsurface water ice deposits in Utopia Planitia, Mars. Geophys. Res. Lett. 2016, 43, 9484–9491. [Google Scholar] [CrossRef]
- Lauro, S.E.; Pettinelli, E.; Caprarelli, G.; Guallini, L.; Rossi, A.P.; Mattei, E.; Cosciotti, B.; Cicchetti, A.; Soldovieri, F.; Cartacci, M.; et al. Multiple subglacial water bodies below the south pole of Mars unveiled by new MARSIS data. Nat. Astron. 2021, 5, 63–70. [Google Scholar] [CrossRef]
- Smith, I.; Lalich, D.; Rezza, C.; Horgan, B.; Whitten, J.; Nerozzi, S.; Holt, J. A solid interpretation of bright radar reflectors under the Mars south polar ice. Geophys. Res. Lett. 2021, 48, e2021GL093618. [Google Scholar] [CrossRef]
- Schroeder, D.M.; Steinbrügge, G. Alternatives to liquid water beneath the south polar ice cap of Mars. Geophys. Res. Lett. 2021, 48, e2021GL095912. [Google Scholar] [CrossRef]
- Cosciotti, B.; Mattei, E.; Brin, A.; Lauro, S.E.; Stillman, D.E.; Cunje, A.; Hickson, D.; Caprarelli, G.; Pettinelli, E. Can clay mimic the high reflectivity of briny water below the Martian SPLD? J. Geophys. Res. Planets 2023, 128, e2022JE007513. [Google Scholar] [CrossRef]
- Lalich, D.; Hayes, A.; Poggiali, V. Explaining bright radar reflections below the south pole of mars without liquid water. Nat. Astron. 2022, 6, 1142–1146. [Google Scholar] [CrossRef]
- Grima, C.; Mouginot, J.; Kofman, W.; Hérique, A.; Beck, P. The basal detectability of an ice-covered Mars by MARSIS. Geophys. Res. Lett. 2022, 49, e2021GL096518. [Google Scholar] [CrossRef]
- Bierson, C.J.; Tulaczyk, S.; Courville, S.W.; Putzig, N.E. Strong MARSIS radar reflections from the base of Martian south polar cap may be due to conductive ice or minerals. Geophys. Res. Lett. 2021, 48, e2021GL093880. [Google Scholar] [CrossRef]
- Mattei, E.; Pettinelli, E.; Lauro, S.E.; Stillman, D.E.; Cosciotti, B.; Marinangeli, L.; Tangari, A.C.; Soldovieri, F.; Orosei, R.; Caprarelli, G. Assessing the role of clay and salts on the origin of MARSIS basal bright reflections. Earth Planet. Sci. Lett. 2022, 579, 117370. [Google Scholar] [CrossRef]
- Orosei, R.; Caprarelli, G.; Lauro, S.; Pettinelli, E.; Cartacci, M.; Cicchetti, A.; Cosciotti, B.; De Lorenzis, A.; De Nunzio, G.; Mattei, E.; et al. Numerical simulations of radar echoes rule out basal CO2 ice deposits at Ultimi Scopuli, Mars. Icarus 2022, 386, 115163. [Google Scholar] [CrossRef]
- Foss, F.J., II; Putzig, N.E.; Campbell, B.A.; Levin, S.A.; Perry, M.R.; Holt, J.W.; Christoffersen, M.S.; Smith, I.B.; Morgan, G.A.; Russell, A.T. Producing 3D radargrams from orbital radar sounding data at Mars: History, results, methods, lessons and plans. Icarus, 2023; in press. [Google Scholar] [CrossRef]
- Putzig, N.E.; Smith, I.B.; Perry, M.R.; Foss, F.J., II; Campbell, B.A.; Phillips, R.J.; Seu, R. Three-dimensional radar imaging of structures and craters in the Martian polar caps. Icarus 2018, 308, 138–147. [Google Scholar] [CrossRef] [PubMed]
- Campbell, D.B.; Chandler, J.F.; Ostro, S.J.; Pettengill, G.H.; Shapiro, I.I. Galilean satellites–1976 radar results. Icarus 1978, 34, 254–267. [Google Scholar] [CrossRef]
- Black, G.J.; Campbell, D.B.; Nicholson, P.D. Icy Galilean Satellites: Modeling Radar Reflectivities as a Coherent Backscatter Effect. Icarus 2001, 151, 167–180. [Google Scholar] [CrossRef]
- Hofgartner, J.D.; Hand, K.P. A continuum of icy satellites’ radar properties explained by the coherent backscatter effect. Nat. Astron. 2023, 7, 534–540. [Google Scholar] [CrossRef]
- Dougherty, M.K.; Grasset, O.; Bunce, E.; Coustenis, A.; Titov, D.V.; Erd, C.; Blanc, M.; Coates, A.J.; Coradini, A.; Drossart, P.; et al. JUICE (JUpiter ICy moon Explorer): A European-led mission to the Jupiter system. In Proceedings of the EPSC-DPS Joint Meeting 2011, Nantes, France, 2–7 October 2011; Volume 2011, p. 1343. [Google Scholar]
- Bruzzone, L.; Plaut, J.J.; Alberti, G.; Blankenship, D.D.; Bovolo, F.; Campbell, B.A.; Ferro, A.; Gim, Y.; Kofman, W.; Komatsu, G.; et al. RIME: Radar for Icy Moon Exploration. In Proceedings of the European Planetary Science Congress, London, UK, 8–13 September 2013; p. EPSC2013-744. [Google Scholar]
- Pappalardo, R.; Lopes, R. The Europa Clipper mission concept. In Proceedings of the 40th COSPAR Scientific Assembly, Moscow, Russia, 2–10 August 2014; Volume 40, p. B0.3-18-14. [Google Scholar]
- Moussessian, A.; Blankenship, D.D.; Plaut, J.J.; Patterson, G.W.; Gim, Y.; Schroeder, D.M.; Soderlund, K.M.; Grima, C.; Young, D.A.; Chapin, E. REASON for Europa. In Proceedings of the AGU Fall Meeting Abstracts, San Francisco, CA, USA, 14–18 December 2015; Volume 2015, p. P13E-05. [Google Scholar]
- Goldstein, R.M.; Morris, G.A. Radar Observations of the rings of Saturn. Icarus 1973, 20, 260–262. [Google Scholar] [CrossRef]
- Ostro, S.J.; Pettengill, G.H.; Campbell, D.B.; Goldstein, R.M. Delay-Doppler radar observations of Saturn’s rings. Icarus 1982, 49, 367–381. [Google Scholar] [CrossRef]
- Nicholson, P.D.; French, R.G.; Campbell, D.B.; Margot, J.L.; Nolan, M.C.; Black, G.J.; Salo, H.J. Radar imaging of Saturn’s rings. Icarus 2005, 177, 32–62. [Google Scholar] [CrossRef]
- Black, G.J.; Campbell, D.B.; Carter, L.M. Ground-based radar observations of Titan: 2000–2008. Icarus 2011, 212, 300–320. [Google Scholar] [CrossRef]
- Black, G.J.; Campbell, D.B.; Carter, L.M.; Ostro, S.J. Radar Detection of Iapetus. Science 2004, 304, 553. [Google Scholar] [CrossRef]
- Black, G.J.; Campbell, D.B.; Carter, L.M. Arecibo radar observations of Rhea, Dione, Tethys, and Enceladus. Icarus 2007, 191, 702–711. [Google Scholar] [CrossRef]
- Campbell, D.B.; Black, G.J.; Carter, L.M.; Ostro, S.J. Radar Evidence for Liquid Surfaces on Titan. Science 2003, 302, 431–434. [Google Scholar] [CrossRef] [PubMed]
- Hofgartner, J.D.; Hayes, A.G.; Campbell, D.B.; Lunine, J.I.; Black, G.J.; MacKenzie, S.M.; Birch, S.P.D.; Elachi, C.; Kirk, R.D.; Le Gall, A.; et al. The root of anomalously specular reflections from solid surfaces on Saturn’s moon Titan. Nat. Commun. 2020, 11, 2829. [Google Scholar] [CrossRef] [PubMed]
- Elachi, C.; Allison, M.D.; Borgarelli, L.; Encrenaz, P.; Im, E.; Janssen, M.A.; Johnson, W.T.K.; Kirk, R.L.; Lorenz, R.D.; Lunine, J.I.; et al. Radar: The Cassini Titan Radar Mapper. In The Cassini-Huygens Mission; Russell, C.T., Ed.; Springer: Dordrecht, The Netherlands, 2004; Volume 115, pp. 71–110. [Google Scholar] [CrossRef]
- Ostro, S.J.; West, R.D.; Janssen, M.A.; Lorenz, R.D.; Zebker, H.A.; Black, G.J.; Lunine, J.I.; Wye, L.C.; Lopes, R.M.; Wall, S.D.; et al. Cassini RADAR observations of Enceladus, Tethys, Dione, Rhea, Iapetus, Hyperion, and Phoebe. Icarus 2006, 183, 479–490. [Google Scholar] [CrossRef]
- Ostro, S.J.; West, R.D.; Wye, L.C.; Zebker, H.A.; Janssen, M.A.; Stiles, B.; Kelleher, K.; Anderson, Y.Z.; Boehmer, R.A.; Callahan, P.; et al. New Cassini RADAR results for Saturn’s icy satellites. Icarus 2010, 206, 498–506. [Google Scholar] [CrossRef]
- Elachi, C.; Wall, S.; Allison, M.; Anderson, Y.; Boehmer, R.; Callahan, P.; Encrenaz, P.; Flamini, E.; Franceschetti, G.; Gim, Y.; et al. Cassini Radar Views the Surface of Titan. Science 2005, 308, 970–974. [Google Scholar] [CrossRef] [PubMed]
- Lorenz, R.D.; Wall, S.; Radebaugh, J.; Boubin, G.; Reffet, E.; Janssen, M.; Stofan, E.; Lopes, R.; Kirk, R.; Elachi, C.; et al. The Sand Seas of Titan: Cassini RADAR Observations of Longitudinal Dunes. Science 2006, 312, 724–727. [Google Scholar] [CrossRef] [PubMed]
- Burr, D.M.; Drummond, S.A.; Cartwright, R.; Black, B.A.; Perron, J.T. Morphology of fluvial networks on Titan: Evidence for structural control. Icarus 2013, 226, 742–759. [Google Scholar] [CrossRef]
- Mastrogiuseppe, M.; Poggiali, V.; Hayes, A.; Lorenz, R.; Lunine, J.; Picardi, G.; Seu, R.; Flamini, E.; Mitri, G.; Notarnicola, C.; et al. The bathymetry of a Titan sea. Geophys. Res. Lett. 2014, 41, 1432–1437. [Google Scholar] [CrossRef]
- Harmon, J.K. Mercury radar studies and lunar comparisons. Adv. Space Res. 1997, 19, 1487–1496. [Google Scholar] [CrossRef]
- Ostro, S.J.; Campbell, D.B.; Simpson, R.A.; Hudson, R.S.; Chandler, J.F.; Rosema, K.D.; Shapiro, I.I.; Standish, E.M.; Winkler, R.; Yeomans, D.K. Europa, Ganymede, and Callisto: New radar results from Arecibo and Goldstone. J. Geophys. Res. 1992, 97, 18227–18244. [Google Scholar] [CrossRef]
- Pravec, P.; Scheirich, P.; Kušnirák, P.; Šarounová, L.; Mottola, S.; Hahn, G.; Brown, P.; Esquerdo, G.; Kaiser, N.; Krzeminski, Z.; et al. Photometric survey of binary near-Earth asteroids. Icarus 2006, 181, 63–93. [Google Scholar] [CrossRef]
- Margot, J.L.; Nolan, M.C.; Benner, L.A.M.; Ostro, S.J.; Jurgens, R.F.; Giorgini, J.D.; Slade, M.A.; Campbell, D.B. Binary Asteroids in the Near-Earth Object Population. Science 2002, 296, 1445–1448. [Google Scholar] [CrossRef] [PubMed]
- Becker, T.M.; Howell, E.S.; Nolan, M.C.; Magri, C.; Pravec, P.; Taylor, P.A.; Oey, J.; Higgins, D.; Világi, J.; Kornoš, L.; et al. Physical modeling of triple near-Earth Asteroid (153591) 2001 SN263 from radar and optical light curve observations. Icarus 2015, 248, 499–515. [Google Scholar] [CrossRef]
- Taylor, P.A.; Warner, B.D.; Magri, C.; Springmann, A.; Nolan, M.C.; Howell, E.S.; Miller, K.J.; Zambrano-Marin, L.F.; Richardson, J.E.; Hannan, M.; et al. The Smallest Binary Asteroid? The Discovery of Equal-Mass Binary 1994 CJ1. In Proceedings of the AAS/Division for Planetary Sciences Meeting Abstracts #46, Tucson, AZ, USA, 9–14 November 2014; Volume 46, p. 409.03. [Google Scholar]
- Taylor, P.A.; Rivera-Valentin, E.G.; Virkki, A.K.; Warner, B.D.; Oey, J.; Venditti, F.C.F.; Marshall, S.E.; Zambrano-Marin, L.F.; Brozovic, M.; Naidu, S.P.; et al. Radar and Optical Observations of Equal-Mass Binary Near-Earth Asteroids (190166) 2005 UP156 and 2017 YE5. In Proceedings of the Lunar and Planetary Science Conference, The Woodlands, TX, USA, 18–22 March 2019; p. 2945. [Google Scholar]
- Tholen, D.J.; Barucci, M.A. Asteroid Taxonomy. In Asteroids II; Binzel, R.P., Gehrels, T., Matthews, M.S., Eds.; University of Arizona Press: Tucson, AZ, USA, 1989; pp. 289–315. [Google Scholar]
- Benner, L.A.M.; Ostro, S.J.; Magri, C.; Nolan, M.C.; Howell, E.S.; Giorgini, J.D.; Jurgens, R.F.; Margot, J.L.; Taylor, P.A.; Busch, M.W.; et al. Near-Earth asteroid surface roughness depends on compositional class. Icarus 2008, 198, 294–304. [Google Scholar] [CrossRef]
- Magri, C.; Ostro, S.J.; Rosema, K.D.; Thomas, M.L.; Mitchell, D.L.; Campbell, D.B.; Chandler, J.F.; Shapiro, I.I.; Giorgini, J.D.; Yeomans, D.K. Mainbelt Asteroids: Results of Arecibo and Goldstone Radar Observations of 37 Objects during 1980–1995. Icarus 1999, 140, 379–407. [Google Scholar] [CrossRef]
- Magri, C.; Nolan, M.C.; Ostro, S.J.; Giorgini, J.D. A radar survey of main-belt asteroids: Arecibo observations of 55 objects during 1999–2003. Icarus 2007, 186, 126–151. [Google Scholar] [CrossRef]
- Harmon, J.K.; Nolan, M.C.; Ostro, S.J.; Campbell, D.B. Radar studies of comet nuclei and grain comae. In Comets II; Festou, M.C., Keller, H.U., Weaver, H.A., Eds.; University of Arizona Press: Tucson, AZ, USA, 2004; pp. 265–279. [Google Scholar]
- Virkki, A.; Zubko, E.; Nolan, M.C.; Howell, E.S.; Benner, L.A.M.; Harmon, J.K. Decimeter-scale particle characterization in the coma of 73P/Schwassmann-Wachmann 3 using dual-wavelength radar observations. Icarus 2019, 325, 94–104. [Google Scholar] [CrossRef]
- Heggy, E.; Palmer, E.M.; Hérique, A.; Kofman, W.; El-Maarry, M.R. Post-rendezvous radar properties of comet 67P/CG from the Rosetta Mission: Understanding future Earth-based radar observations and the dynamical evolution of comets. Mon. Not. R. Astron. Soc. 2019, 489, 1667–1683. [Google Scholar] [CrossRef]
- Lazio, J.; Arnold, B.; Levesque, M.; Berner, J.; Smith, A.; Asmar, S.W.; Lichten, S.; Castaño, R. The Deep Space Network: Enabling Richer Data Sets for Future Solar & Space Physics Missions. Bull. Am. Astron. Soc. 2023, 55, 231. [Google Scholar] [CrossRef]
- Marshall, M.F.; Schnee, S.L.; Cruz-Klueber, V.; Salazar Morales, J.; Nossa, E.; Fagan, T.J.; Crossin, J.J.; Lubar, D.G.; Covert, M.Z.; Hayhurst, M.R.; et al. Cross-Disciplinary Deep Space Radar Needs Study; Technical Report; The Aerospace Corporation: El Segundo, CA, USA, 2023. [Google Scholar]
- Widemann, T.; Grete Straume, A.; Ocampo, A.; Voirin, T.; Carter, L.; Hensley, S.; Bruzzone, L.; Helbert, J.; Carine Vandaele, A.; Marcq, E.; et al. EnVision: A Nominal Science Phase Spanning Six Venus Sidereal Days. In Proceedings of the EGU General Assembly Conference Abstracts, Vienna, Austria, 23–28 April 2023; p. EGU-9889. [Google Scholar] [CrossRef]
- Michel, P.; Küppers, M.; Bagatin, A.C.; Carry, B.; Charnoz, S.; de Leon, J.; Fitzsimmons, A.; Gordo, P.; Green, S.F.; Hérique, A.; et al. The ESA Hera Mission: Detailed Characterization of the DART Impact Outcome and of the Binary Asteroid (65803) Didymos. Planet. Sci. J. 2022, 3, 160. [Google Scholar] [CrossRef]








Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Virkki, A.K.; Neish, C.D.; Rivera-Valentín, E.G.; Bhiravarasu, S.S.; Hickson, D.C.; Nolan, M.C.; Orosei, R. Planetary Radar—State-of-the-Art Review. Remote Sens. 2023, 15, 5605. https://doi.org/10.3390/rs15235605
Virkki AK, Neish CD, Rivera-Valentín EG, Bhiravarasu SS, Hickson DC, Nolan MC, Orosei R. Planetary Radar—State-of-the-Art Review. Remote Sensing. 2023; 15(23):5605. https://doi.org/10.3390/rs15235605
Chicago/Turabian StyleVirkki, Anne K., Catherine D. Neish, Edgard G. Rivera-Valentín, Sriram S. Bhiravarasu, Dylan C. Hickson, Michael C. Nolan, and Roberto Orosei. 2023. "Planetary Radar—State-of-the-Art Review" Remote Sensing 15, no. 23: 5605. https://doi.org/10.3390/rs15235605
APA StyleVirkki, A. K., Neish, C. D., Rivera-Valentín, E. G., Bhiravarasu, S. S., Hickson, D. C., Nolan, M. C., & Orosei, R. (2023). Planetary Radar—State-of-the-Art Review. Remote Sensing, 15(23), 5605. https://doi.org/10.3390/rs15235605






