Study of the Effect of Different Atmospheric Conditions on the Temporal Evolution of the Mixing Layer over Madrid during the Year 2020 by Means of Two Different Methods: Ceilometer Signals and the ECMWF-IFS Meteorological Model

Abstract

Atmospheric aerosols are one of the main factors that contribute to poor air quality. These aerosols are mostly concentrated within the atmospheric boundary layer (ABL) and mixing layer (ML). The ABL extends from ground level to the lowest level of the troposphere directly affected by surface temperature, solar irradiance, the orography and its proximity to coastal areas, causing turbulence in a daily cycle. This turbulence controls the vertical mixing of aerosols and pollutants and their dispersion in the ML. Therefore, proper characterization of these layers is of crucial importance in numerical weather forecasting and climate models; however, their estimation nowadays presents some spatial and temporal limitations. In order to deal with these limitations and to assess the influence of different meteorological conditions on the temporal evolution of the aforementioned layers, the evolution of the ML over Madrid (Spain) has been studied for the year 2020 by means of ceilometer profiles fed into the STRATfinder algorithm. This algorithm is able to give reliable estimates of the height of the ABL (ABLH) and ML (MLH). The results are compared with the ECMWF-IFS model predictions, which is able to compute the MLH under any meteorological condition. Then, the influence of the meteorology in the estimation of MLHs was established by classifying data based on the season and six different prevalent synoptic meteorological situations defined using ground-level pressure fields, as well as by splitting the days into four periods (morning, daytime, evening and nighttime). Our results show that both datasets, the STRATfinder values and the ECMWF-IFS model computations, are very sensitive to the meteorological conditions that play a main role in the MLH temporal evolution. For instance, high solar irradiance and ground radiation cause high turbulence and convection that lead to a well-developed ML. In cases in which the ML is well developed, both methods show similar results, and there are therefore better correlations between them. On the contrary, the results presented here show that the presence of high relative humidity and low temperatures hamper the growth of the ML, causing different errors in both MLH estimations and poor correlations between them. Furthermore, the ECMWF-IFS model has shown a sharp decrease, identified as an artificial behavior from 16:00 UTC, because of the influence of low solar zenith angles and the temporal interpolation. The STRATfinder algorithm also shows a sharp decrease just before the sunset because of the way the algorithm distinguishes between the ML and the residual layer. Thus, this study concludes that the MLH temporal evolution still needs to be characterized using complementary tools, since the methods presented here are strongly affected by the meteorological conditions and do not show enough reliability to work individually. However, ceilometer measurements offer great potential as a correction tool for ABL heights derived from models involved in air pollution dispersion assessments.

1. Introduction

It is well known that aerosols are one of the main factors that contribute to poor air quality, constituting a public health risk, and therefore, their characterization is a priority [1]. However, this characterization is hampered by the fact that aerosols present a heterogeneous distribution in the atmosphere, being mostly concentrated within the atmospheric boundary layer (ABL) [2]. Therefore, the understanding of the ABL processes is a key factor in air quality and future climate scenarios, since it has the potential to improve the forecasting of pollutants’ dispersion and cloud dynamics [3]. This layer regulates the exchange of energy and moisture between the surface and the atmosphere and plays a critical role in greenhouse gas concentration budgets, limiting the vertical mixing of air pollutants emitted near the surface [4,5]. The ABL extends from ground level up to a variable height that usually coincides with the presence of a temperature inversion and also depends on the orography, which causes different behaviors in mountainous terrains, urban or rural flat environments or in proximity to coastal areas [6]. Furthermore, the ABL, which is affected by the radiation emitted by Earth’s surface and its variability throughout the day [7], presents a marked daily cycle in clear-sky situations, starting with the increase in the land surface temperature after sunrise, which intensifies convection, causing, in turn, the ascension of warm air masses and the downward displacement of colder ones. Then, the convective processes and turbulence become weaker because of the gradual reduction in solar irradiance during the early evening. It is worth noting the importance of the surface albedo, since different surfaces respond differently to solar heating [8]. The ABL is composed of different sublayers, such as the residual layer (RL), the nocturnal boundary layer (NBL) and the mixing layer (ML) [9,10]. The latter is formed during the first part of the ABL’s cycle and is defined as the lowest atmospheric layer in which aerosols and moisture are dispersed via vertical mixing processes generated by the ascending air parcels [11,12,13]. While the NBL and RL are a consequence of the second part of the cycle, the weakening of turbulence produces the transition of the ML into a stable stratified boundary layer close to the surface, the NBL, and a remnant of the daytime ML just above the NBL, the RL [14]. The limit between the ABL and the free troposphere above, which can be defined as the ABL height (ABLH), is marked during the day by a strong aerosol gradient caused by vertical turbulent mixing processes. During the nighttime or in the absence of solar radiation, the strongest aerosol gradient sometimes corresponds to the top of the RL or other layers growing within the ABL, hampering the estimation of the ABLH and yielding inaccurate results [15]. It is worth noting that during the daytime period, when the ML is well developed, the ABLH can be considered equal to the ML height (MLH) because the distribution of aerosols is strongly influenced by turbulent mixing [14].

A proper representation of these processes’ evolution is required from air quality forecast systems in order to accurately estimate pollutant concentrations, normally driven by many factors including surface heat flux, weather patterns, surface roughness, etc. [16]. In most numerical meteorological models included in air quality modelling systems, the height of the ABL is usually calculated using the potential temperature profile or Richardson number, but uncertainties in meteorological fields can produce more than 50% uncertainty in shallow boundary layers and 20% in deeper boundary layers [17]. Traditionally, the spatial and temporal resolution of meteorological models were not able to accurately estimate turbulent fluxes within the ABL. Recent advances in computational power have improved forecasts, but uncertainties in meteorological fields and different definitions of the ABL still affect the numerical predictions of the ABL height and, consequently, the concentration of chemical species in cases of a shallow ABL can lead to severe air pollution episodes. The present numerical weather models produce a high spatial and temporal resolution of ABL heights; however, they still show limitations in accurately simulating the ML creation and daily evolution, and thus, validation is required using observational data.

Nowadays, the ABLH is mostly monitored by means of radiosounding in the frame of the World Meteorological Organization Radiosounding Global Network [18]; however, these are taken only twice per day (00:00 and 12:00 UTC) and mainly at airports. The analysis of long time series of MLH data obtained with fixed-hour radiosonde soundings has yielded remarkable results, especially in relation to their influence on the levels of atmospheric pollutants. Salvador et al. [19] evaluated the impact of variations in the MLH at midday on air pollutant concentrations and health in Madrid during the period of 2011–2014. The decrease in the MLH was very well correlated to a linear increase in the daily number of exceedances of the European Union’s NO₂ hourly limit value (200 μg/m³) at hotspot urban traffic monitoring stations. A statistically significant relationship between the reductions in the MLH with an increase in all-natural-cause daily mortality was also found. Nevertheless, reliable ABLH data with a higher temporal resolution would allow for more in-depth studies of the processes that drive the temporal changes throughout the day.

Therefore, in order to improve the spatial and temporal coverage of ABLH monitoring, new approaches based on vertically resolved data from optical remote-sensing instruments are currently being studied. These instruments, which are able to operate continuously and in the framework of different networks, aid in capturing the ABL diurnal cycle and drive short-term model predictions of aerosol dispersion [20,21]. Among these optical remote-sensing instruments, aerosol lidars are a powerful tool to retrieve the ABLH or MLH through aerosol vertical profiles [22]. Ceilometers, single-wavelength micro-lidars intended for cloud base height detection, are one of the most frequently used lidar systems in atmospheric observation. Currently, some ceilometers present an emission wavelength centered at 1064 nm, making them highly proficient for the detection of atmospheric aerosols. Their main advantages are their high-quality attenuated backscatter profiles provided as a result of recent advances in measurement technology and algorithm development [23,24], and their suitability for unmanned/unattended continuous operation. Furthermore, ceilometers usually operate in two main dense networks as the EUMETNET E-PROFILE [25] and the ICENET (Iberian Ceilometer Network, [2]). Despite this, two assumptions are needed to use these kind of instruments for estimating the ABLH: (1) aerosols emitted at the surface are well mixed within the ABL and show a marked gradient with the free troposphere [26], and (2) at the top of the ABL, there is an interface of contact with the free troposphere where there are fluctuations in aerosol concentrations due to air masses moving downwards from the free troposphere and moving upwards from the ABL. As a result of these fluctuations, the backscattering profiles present a greater variance at the interface than in the ABL or the free troposphere [27]. For conditions of low solar irradiance that cause stratification, in which ABLHs are lower than the previous day’s ABLH, and a diffuse gradient between the ABL and the free troposphere is observed, this high variance is useful to detect the MLH in the backscattering profiles [14].

Based on the assumptions above, by means of these attenuated backscatter profiles, some advanced methods, named “second-generation” algorithms, are able to compute the MLH [3,28]. One of these advanced methods is the STRAT-2D, described by Haeffelin et al. [20], which computes the temporal and vertical structure of the ABL in order to ensure the temporal consistency of ABLH estimates. It is also worth mentioning the Pathfinder algorithm that was developed by de Bruine et al. [29] and uses the graph theory to track the diurnal evolution of the layer. Both methods are the basis of STRATfinder, widely described by Kotthaus et al. [15], which is able to estimate high-quality products from ceilometer signals at different scales and has been shown to provide reliable results when compared to thermodynamic layer heights derived from temperature profiles.

However, ceilometers and aerosol lidars are not exempt from problems, presenting two main issues that can directly affect the observation of the MLH. First of all, ceilometers present a blind zone in the near range due to the incomplete overlap between the laser beam and the telescope field of view, thus increasing the uncertainties related to the detection of layers developed at low heights [30]. The second issue is related to the signal-to-noise ratio (SNR), which is strongly influenced, because of its reliance, by the amount of atmospheric aerosols or moisture that can swiftly extinguish the emitted light and the solar irradiance that increases the presence of artifacts in the received signal [31]. These problems are exacerbated when the system itself presents inherently low power. Therefore, in order to solve these issues, including the impossibility to deploy the instrument in a particular location of interest, the use of models to compute atmospheric layer heights appears as a new approach. Also, it must be taken into account that, presently, the maximum skill of regional numerical weather prediction models can be realized thanks to a spatiotemporal sampling of the lower atmosphere, comparable to the model’s effective resolution [32].

Thus, the aim of the present work is to provide an assessment of the effect of different meteorological conditions on the estimation of the temporal evolution of MLHs during the whole of 2020 in Madrid. Section 2 describes the ceilometer instrument that provides the profiles for the STRATfinder algorithm, the meteorological model employed for comparison (ECMWF-IFS) and the methodology followed. Section 3 summarizes the main results obtained when the datasets are analyzed by season and also when compared for six different synoptic meteorological patterns (SMPs) defined by Salvador et al. [33] for the Iberian Peninsula. Section 4 concludes the main findings of the work.

2. Materials and Methods

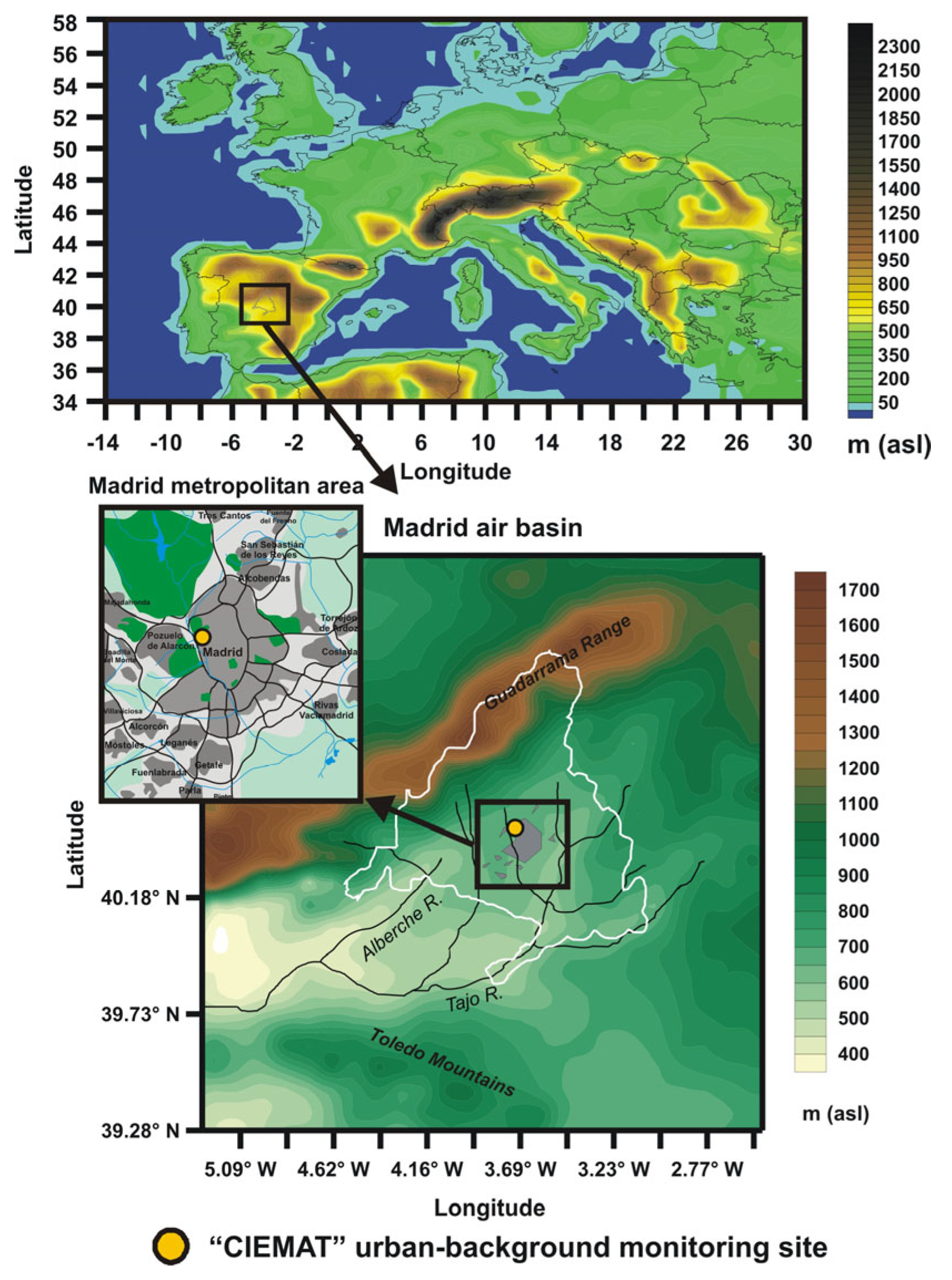
2.1. Experimental Site: Madrid

The city of Madrid and its metropolitan area, located in the center of Spain, have a population of nearly 7 million inhabitants, being one of the most populated regions in the Iberian Peninsula (Figure 1).

The pollution plume over Madrid is mostly fed by residential heating and traffic emissions, while the industrial activity, composed mainly of light factories, does not represent an important pollution source [34]. Its climate, considered as continental–Mediterranean, presenting hot, dry summers and cold winters, both dominated by clear-sky conditions [35], is governed by the presence of the Azores high-pressure system, leading to periods of high stability, poor ventilation and increases in air pollution.

In the northwest outskirts of the city of Madrid is located the Department of Environment of the CIEMAT (40.45 N; 3.72 W; 669 m above sea level), where, since December 2019, a ceilometer, the Lufft CHM15k-Nimbus [2,30], is deployed, next to the MDR-CIEMAT ACTRIS station [36], and, since 2020, the ceilometer has been a part of ICENET. The instrument presents an Nd:YAG laser, which emits a 1064 nm wavelength at a repetition frequency, according to the manufacturer, ranging between 5 and 7 kHz. The overlap between the telescope (mounted next to the laser, biaxial configuration) and the laser beam is 90% complete between 555 and 855 m above ground level, according to the instrument datasheet, but Heese et al. [30] found that the complete overlap is located at 1500 m a.g.l. In light of this, the application of a correction function to reduce the incomplete overlap is necessary, thus producing a useful signal from 232 m up to 15.36 km a.g.l. The overlap function applied to the data in this study is the one calculated and applied by the instrument itself automatically, which has been successfully tested in previous works [2,14]. All of these characteristics facilitate the study of atmospheric aerosols and clouds by means of the backscattered signal. The atmospheric vertical profiles are obtained from the backscattered signals with a temporal resolution of 15 s and a spatial resolution of 15 m, and are finally stored in the database as daily files. All of the available ceilometer profiles—a total of 332 days in the year 2020, stored in the Madrid database, covering different synoptic meteorological situations, which give rise to different air pollution episodes and clean atmospheric conditions—are used in the present research.

Furthermore, the surface meteorological parameters, temperature and relative humidity, used in this research are obtained from an automated meteorological station (U3-NRC, Onset HOBO) located next to the MDR-CIEMAT ACTRIS station. Concretely, this station measures the temperature and relative humidity at 4 m a.g.l. and records data every 10 min, thus obtaining 47,808 sets of 10 min averaged data from the 332 days stored in the Madrid database.

2.2. Ceilometer Profiles and PBLH Estimation Algorithm (STRATfinder)

MLHs are obtained for a total of 332 days in 2020 by means of the STRATfinder algorithm, fed with the ceilometer CHM15K data. The 28 days lost during 2020 are due to some instrument failures that occurred on 28–29 January, 5–14 April, 21–26 May, 10–14 and 17 September, 29–31 October and 30 November. Since the ceilometer data are filtered for low clouds and rain, and only days with more than 13 h are considered to be part of the analysis, a total of 201 days remain in the database after filtering. Then, in order to estimate MLHs, ceilometer daily files were processed by means of one of the robust algorithms to automatically detect the mixed layer height, the STRATfinder algorithm (GNU General Public License v3.0, [15]). Succinctly, STRATfinder is an algorithm specifically designed for the estimation of ABLHs together with MLHs from ceilometer data, thanks to the Dijkstra algorithm [37]. STRATfinder estimates the MLH and ABLH forwards in time, while an ancillary layer height (XLH) is estimated backwards in time (from midnight to noon) to assist the detection of the ABLH during the final hours of the day, when the ML begins to decay. Then, the Dijkstra algorithm is applied to track the MLH, ABLH and XLH that is merged into a preliminary ABLH to determine, by connecting individual paths, the MLH and ABLH for the whole daily file. The temporal resolution of the outputs of STRATfinder is one minute, although the results have been averaged to one hour because of computational requirements. The Haar wavelet transform employed within the algorithm allows for the calculation of uncertainty in the retrieved values, based on the comparison of the transient local minima and the final retrieved MLH. By tuning the Haar wavelet transform parameters, it is possible to determine the standard deviations, obtaining ranges in the order of tenths of meters (<80 m), depending on the temporal averaging.

2.3. Meteorological Model ECMWF-IFS

The ECMWF-IFS is a global meteorological model that resolves the dynamics of the atmosphere, including the physical processes affecting surface energy fluxes, weather or the evolution of the atmospheric layers, among others. According to the documentation (https://confluence.ecmwf.int/display/FUG/2+The+ECMWF+Integrated+Forecasting+System+-+IFS (accessed on 4 September 2023)), the ECMWF-IFS is composed of various coupled modules: an atmospheric model, an ocean wave model (ECWAM), an ocean model (NEMO), a land surface model (HTESSEL) and a data analysis system (4D-VAR). The atmospheric model can be used in three main configurations, according to the length of the forecast: HRES for detailed 10-day forecasts, ensemble (ENS) to study uncertainty in the 15-day forecasts and extended ENS, and seasonal runs to estimate the probabilities of general conditions over longer time scales. In addition to the forecasting resolution, the configuration based on HRES has additional advantages over the ENS configuration, such as greater orographic detail, 1 h of temporal resolution, 9 km of horizontal resolution and 137 vertical levels. For these reasons, HRES is the configuration chosen for the present study. It is worthwhile to note that, for operational reasons, the meteorological variables were downloaded from the ECMWF MARS archive (access provided by AEMET, the Spanish Meteorological Agency), with a temporal resolution of 3 h, and subsequently interpolated to 1 h in order to be consistent with the temporal resolution set for the STRATfinder outputs. The ECMWF-IFS is updated periodically to improve the forecasts. With relevance to the period of the present study (the year 2020), the model was updated on 30 June 2020; thus, the version of the model for the first half of the year was Cycle 46r1, while in the second half of the year, the version was Cycle 47r1.

In general, the structure of the ECMWF-IFS is the same in each of the model configurations and is based on two main formulations: (1) a diagnostic that describes the static relationship between pressure, density, temperature and height, and (2) a prognostic that describes the time evolution of the horizontal wind components, the surface pressure, the temperature and the water vapor content of the model atmosphere. Furthermore, the ECMWF-IFS model presents additional features, which are essential for the present research, to describe processes of radiation, gravity wave drag, vertical turbulence, convection, clouds and surface interactions. More specifically, in this model, the ML is represented by two schemes: a turbulence scheme [38] and a moist convection scheme [39]. The latter comprises a mass flux scheme for moist shallow and deep cumulus convection and is switched off in cases with stratocumulus-topped boundary layers. The turbulence scheme comprises a turbulent eddy diffusion and mass flux scheme, which represents clear and stratocumulus-topped boundary layers. This scheme is treated differently in the surface layer (defined by the American Meteorological Society as the lowest 10% or so of the atmospheric boundary layer) and above. At the surface, where the mechanical generation of turbulence exceeds buoyant generation, the turbulence fluxes are calculated by means of a first order K-diffusion closure based on the Monin–Obukhov similarity theory [40]. Above the surface layer, a K-diffusion turbulence closure is used everywhere except for the case of unstable (convective) boundary layers, for which an eddy diffusivity mass-flux framework is applied to represent the non-local boundary layer eddy fluxes [38].

In order to estimate the turbulent and convective mixing in the boundary layer, the ECMWF-IFS takes the following considerations: in a stratocumulus-topped boundary layer, the turbulent mixing is due to surface and cloud top-driven eddies, while in a dry boundary layer, the mixing is caused by surface-driven eddies. Thus, the convective boundary layer height is determined as the uppermost level where the updraft vertical velocity is greater than 0 and the local Richardson number is lower than 50. In the case of stable boundary layers, the boundary layer height is diagnosed as the height where the bulk Richardson number becomes superior to 0.25. The ECMWF set these limits for the Richardson number following the work of Seidel et al. [41], who identified a non-negative height in all cases without being strongly dependent on the radiosounding vertical resolution. Therefore, the MLH is equal to the boundary layer’s height in cloud-clear boundary layer and stratocumulus-topped boundary layer cases, where the boundary layer is located near the cloud top because more turbulent mixing is required, while for cumulus-topped boundary layers, the MLH is equal to the cloud base.

2.4. Methodology for Classification of Days Based on Meteorological Fields

A classification of the most frequent synoptic meteorological patterns (SMPs) that happened over the Iberian Peninsula over the period of 2001–2019 has already been performed [33]. With the aim to improve upon the analysis, in this study, the classification process has been extended to the year 2020. Each day of this year was thus assigned to a specific SMP for the subsequent analysis of the estimation of the ABLH using different methods.

The technique employed for classifying daily datasets of sea level pressure (SLP) at 12 UTC into similar groups was the non-hierarchical k-means cluster analysis. It comprises 6 stages (Salvador et al. [33] and references therein) that assures the physical meaning of the SMP:

Firstly, the reanalysis global fields of SLP for each day at 12 UTC were downloaded from the NCEP/NCAR (NOAA/OAR/ESRL PSD, Broadway Boulder, CO, USA) reanalysis dataset open access repository [42]. Then, a selection of k SLP fields was taken to be used as initial conditions in the classification procedure, based on results concerning typical SMPs occurring in the western Mediterranean basin, which were obtained in previous studies. The Euclidean distance from each SLP data field to each k-cluster center was calculated for the value of every grid point and summed. Once every SLP data field was grouped into a specific cluster, new cluster centers were calculated as the arithmetic mean of all their members, grid point by grid point. This procedure was repeated iteratively until each SLP field remained in its cluster. Then, composite maps representing the SMPs were obtained by averaging all the SLP fields grouped into each cluster. The final number of clusters (k) was selected using variance plots.

In this study, an additional validation procedure was performed on the resulting clusters. A complete dataset of parameters, which characterize the daily meteorological situation at the surface level in the central region of the Iberian Peninsula, was analyzed for assuring the physical meaning of the SMPs. Measurements of meteorological variables performed in an instrumented tower, atmospheric stability parameters from numerical models and radiosondes were obtained and analyzed for this purpose.

As a result, six different and realistic SMPs over the Iberian Peninsula were determined with this circulation classification methodology.

2.5. Statistical Analysis

In order to classify days based on the synoptic pattern, a statistical analysis for each day was performed, obtaining the mean absolute error (MAE), mean square error (MSE), root mean square error (RMSE), mean absolute percentage error (MAPE) and R squared (R²) for each days. However, only the MAPE and R² are shown here because of their very intuitive interpretation. These statistics are related to the distance between both heights estimated at every point and the evolution of the shape of both MLs throughout the day, respectively. Concretely, the MAPE is estimated as the difference between the actual (STRATfinder results) and the forecasted (ECMWF-IFS computations) data. For its part, the R² is estimated from the variance of the observed and simulated values and describes the temporal relationship between both methods. The total of 201 days (4824 h) available in the dataset is distributed as follows: 870 h correspond to spring (MAM: 92—56 cases), 1636 h to summer (JJA: 92—24 cases), 1077 h to winter (DJF: 91—46 cases) and finally, 1241 h correspond to autumn (SON: 91—39 cases), where the season was considered for complete months.

The MAPE can be interpreted as the inverse of the agreement between the datasets, or more specifically, as the average percentage difference between predictions and observations. Based on our experience, it can be inferred that for this type of study, values below 60% indicate a low but acceptable accuracy of the model, while values lower than 50% can be considered as reasonably good accuracy. One of the advantages that presents the use of this statistical parameter is its lower sensitivity to outliers than the RMSE. The only limitation comes from the normalization when the values are close to zero due to the division by small values, but the low altitude limit of the ceilometer data (232 m) prevents this problem. For its part, the R² value measures how much of the dependent variable variation is explained by the independent variable in the model. Values between 0.75 and 1 indicate that a significant amount of variance is explained, while values between 0.5 and 0.75 are considered reasonable, according to our experience.

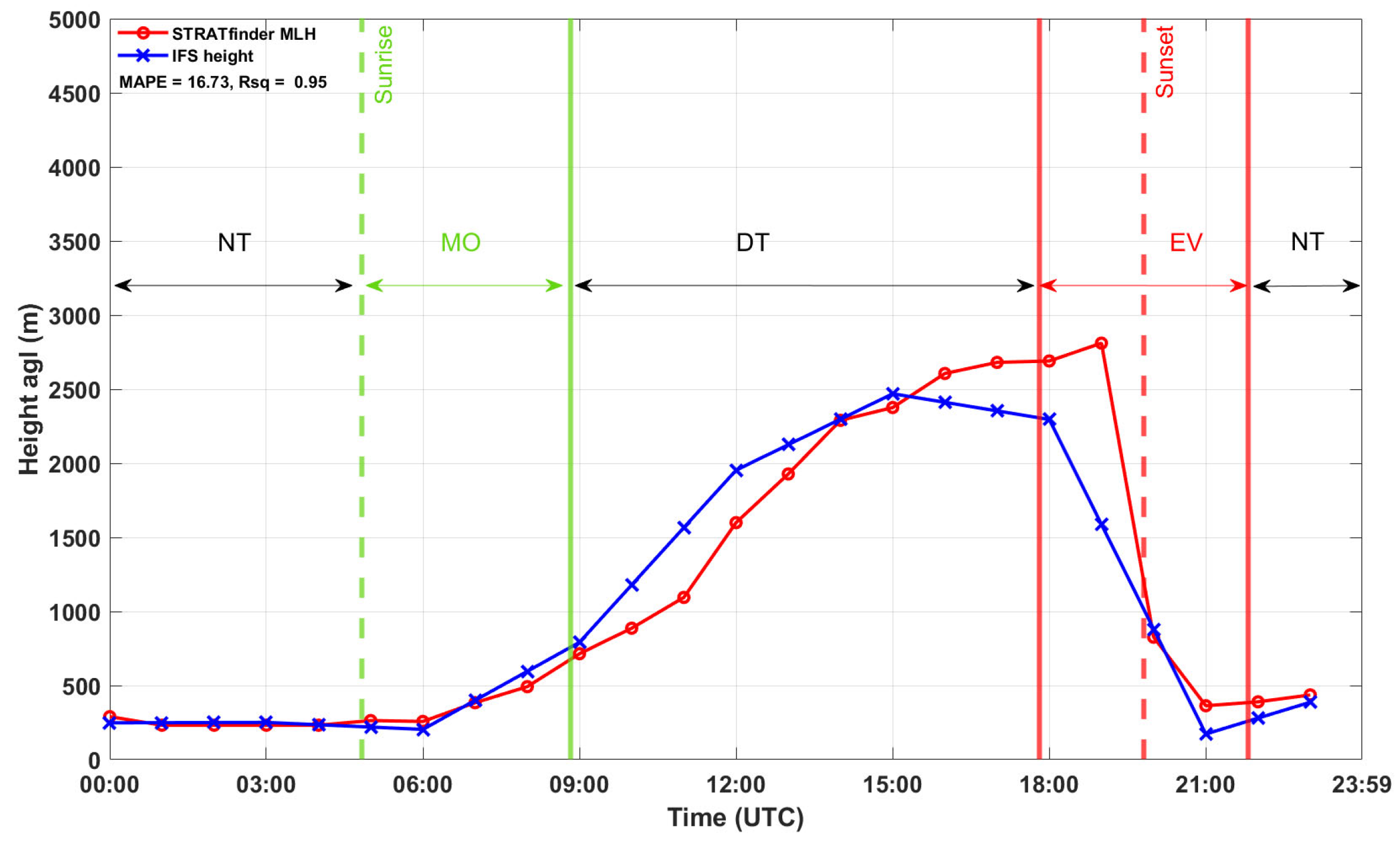
The determination of the MLH is more difficult at transition periods of the day, such as the morning transition from the sunrise until the time when the nocturnal layer is eroded and the mixing layer begins to grow rapidly, or the evening transition after sunset, when turbulent mixing weakens. During these periods, there is high uncertainty and inaccuracy in the results. In order to take this into account, in Section 3.3, each day has been divided into four periods with different characteristics during the diurnal course of the ML development: nighttime, (NT: sunset + 2 h to sunrise), morning (MO: sunrise to sunrise +4 h), daytime (DT: sunrise +4 h to sunset −2 h) and evening (EV: sunset −2 h until sunset +2 h), following the details of Kotthaus and Grimmond [23] (see Figure 2). Statistics were calculated for each one of these periods.

As a summary of the procedure, Figure 2 shows an example of the temporal evolution of the MLH obtained using STRATfinder (red circles) and computed with the ECMWF-IFS (blue crosses) model on 4 July 2020, both with one hour of temporal resolution. The purpose of this figure, which takes advantage of a clear sky day with a clear evolution of the ML, is to illustrate the way the data will be analyzed and introduce different parameters and statistical variables used in the analysis. In this day, the MAPE shows a low value, 16.73, which means that the MLH computed with the model is very similar throughout the day to the MLH estimated using STRATfinder. In general, the MLH estimates of both methods are very similar, except at the beginning and at the end of the DT, when the model shows deviations that increase the MAPE slightly, as will be explained next. The R² presents a value of about 0.95, meaning that, on this particular day, both methods are highly positively correlated. This result also points out that when the MLH estimated with STRATfinder changes its tendency, the MLH predicted via the model changes in the same way. Thus, in this case, the R² is only reduced slightly from 1 because the predicted MLH starts to decrease at 16:00, while the MLH from STRATfinder continues to grow until 19:00, followed by a sudden decrease; after that, both methods are well correlated again.

Taking a look into the parts of the day, the MLH obtained via STRATfinder and computed using the ECMWF-IFS during NT begins with a height of about 250 m and continues to range between minimum values until the start of MO, when, because of the convection that begins with sunrise at 4:59, the ML grows. Then, between 09:00 and 16:00, during the DT period, the ML obtained via STRATfinder and computed with the ECMWF-IFS grows quickly by 1891 and 1619 m, respectively, because of the heating of the air by sunlight. It is worthwhile to note that between 10:00 and 13:00, the ECMWF-IFS overestimates the ML (by around 292, 471, 354 and 197 m) in respect of STRATfinder, most likely influenced by a combination of small solar zenith angles and the interpolation to 1 h of temporal resolution. After solar noon, at 13:15, the solar radiation that reaches the atmosphere decreases, reducing the convection and, therefore the growth of the ML. This behavior becomes clear between 16:00 and 19:00, during EV, when the STRATfinder ML grows by only 200 m, from 2606 to 2811 m. However, in the same time period, the MLHs computed with the ECMWF-IFS decrease by around 881 m, which confirms the idea of the dependence of this model on the solar zenith angle. In addition, as mentioned before, this decrease is also caused by the interpolation from 3 h to 1 h of temporal resolution, leading both to an artificial behavior. Finally, at 20:00, both MLH estimates agree again due to a rapid sinking of the STRATfinder values, related to the way in which this algorithm computes the MLH during NT; after sunset, the ML is considered extinct, leaving behind the residual layer only. Because of this consideration, the STRATfinder values also show a sharp artificial decrease. The behavior of the ECMWF-IFS estimates is a relevant feature that may be related to a slight dependence of this model on solar radiation and the interpolation from three hours to one hour of temporal resolution; thus, this model does not show enough flexibility to be adapted to different atmospheric situations over short periods of time.

3. Results and Discussion

3.1. Seasonal Analysis

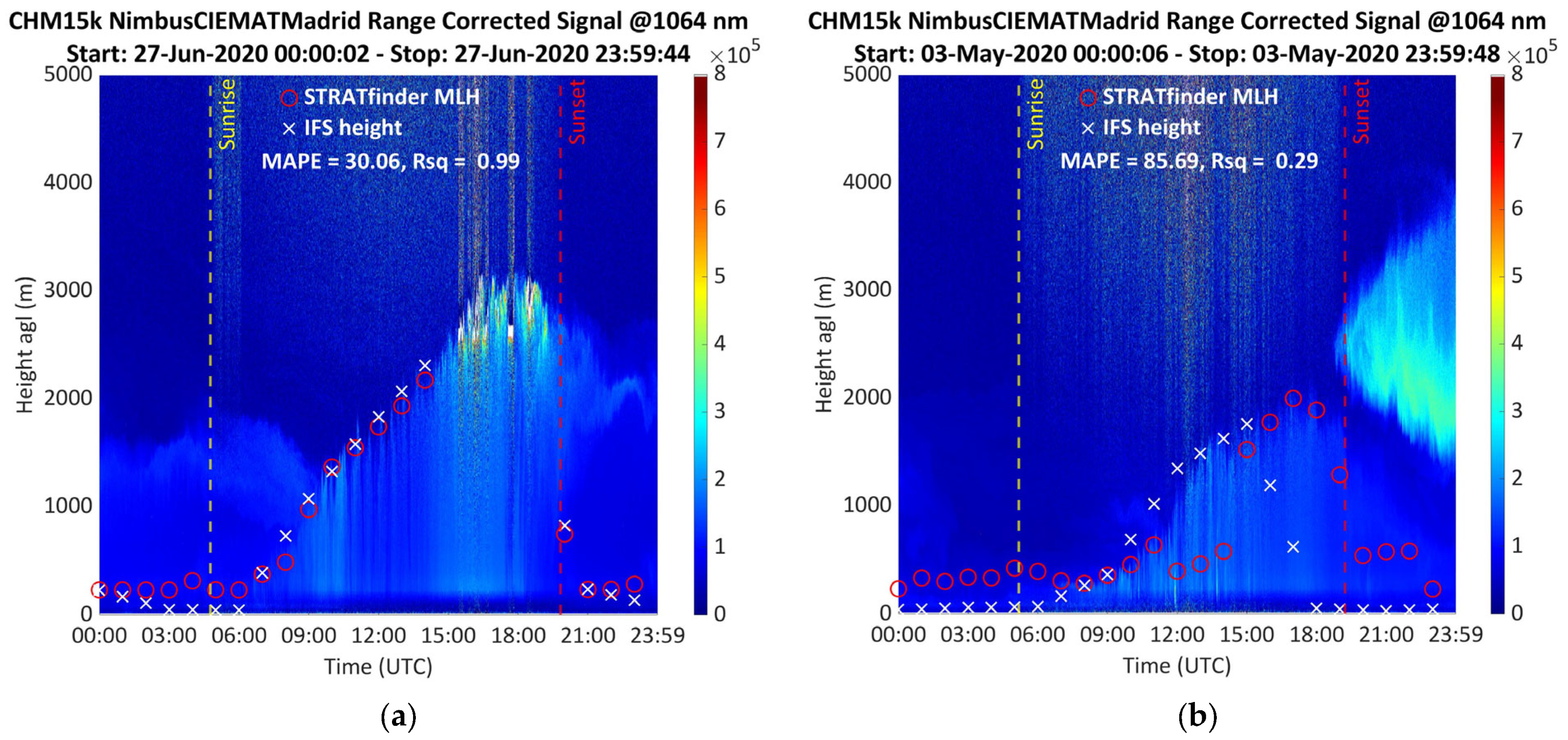
In Figure 3, some illustrative examples of the features frequently found during the seasonal analysis are presented. Figure 3a corresponds to 27 June, with an exceptionally good correlation between the datasets. It is worthwhile to note that the convection became evident between 6:00 and 9:00 as vertical lines in the blue area below the ML line, which indicates the movement of the air masses. Low clouds appeared on top of the ML when it reached its highest development at the end of the day (15:00–19:00 UTC), so those points were filtered out. The agreement between the STRATfinder ceilometer-derived results and the ECMWF-IFS prediction was better during the day (12:00–18:00) than at nighttime (00:00–06:00). This is generally the case due to the limitation of the ceilometer at low altitudes caused by the effect of the partial overlap, as described above. A lowest limit of 232 m was applied to the STRATfinder algorithm after the ceilometer signals were partially corrected using overlap synthetic estimation [2,30]. This day showed a high R² value (0.99) thanks to the good agreement between both datasets, and the MAPE was 30.06, one of the lowest values of this study. Completely different results were obtained for the analysis of 3 May, shown in Figure 3b. The discrepancy during the nighttime hours was larger, and the model predicted a faster decay of the MLH after 15:00 UTC than was observed experimentally. In addition, the presence of some spikes in the ceilometer signal (below 500 m between 10:00 and 14:00), possibly due to low clouds, not detected by the automated algorithm included in the instrument, led to STRATfinder switching between different layers in the high-frequency data, with the result of an erroneous 1 h average value. This gave a very low R² value (0.29) and high MAPE (85.69). Thus, this type of behavior was found in 6.01% of the cases. 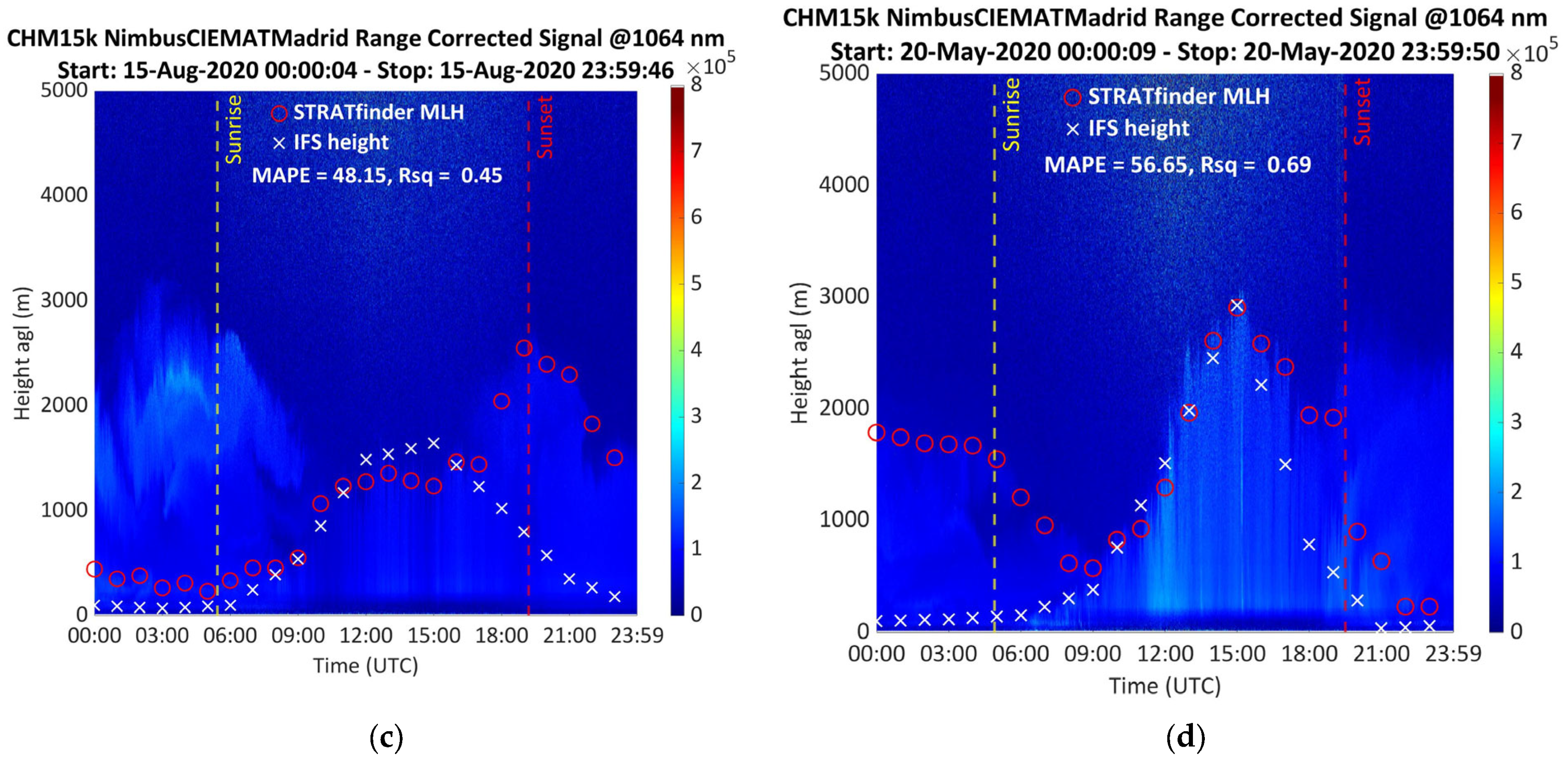Figure 3c shows the evolution on 15 August, with reasonably good agreement until the late afternoon, when the STRATfinder algorithm failed to identify the mixing layer and followed the aerosol layer, with values as high as 2.5 km at sunset (19:00 UTC). This discrepancy reduced the R² down to 0.45 and increased the MAPE up to 48.15, still a reasonable value due to the good agreement between 00:00 and 15:00. This type of problem was found in 8.20% of the days and is linked to a homogenous aerosol layer during nighttime. Figure 3b,d do not show this behavior in spite of the presence of a nocturnal aerosol layer; however, the ceilometer signal could identify different aerosol structures, favoring the STRATfinder algorithm to obtain the MLH. In the case of Figure 3c, the aerosol layer detected during nighttime is fairly homogeneous, hindering the estimation of the MLH. A similar situation is observed in Figure 3d, corresponding to 20 May. In this case, the estimation of the STRATfinder failed in the early morning (00:00–09:00), selecting the top of the aerosol layer, in clear discrepancy with the model prediction because the aerosol layer was pretty homogeneous and well mixed with the ML. The reasonably good agreement for the rest of the day produced an R² of 0.69 and an MAPE of 56.65. This situation was found in 10.93% of the days and is directly related, again, to the presence of a homogeneous aerosol layer in the atmosphere during the morning. In these cases, STRATfinder is not able to distinguish the MLH from the residual layer due to a lack of large differences between those layers in the ceilometer signal. The cases shown in Figure 3a,c have a noticeable aerosol layer at 1500 and 2000 m, respectively, in the early morning; however, in these cases, STRATfinder was able to distinguish between the ML and the aerosol layer thanks to a slight decoupling of both layers. Then, it is worthwhile to note that the use of one single algorithm to estimate the MLH is still risky, and the correct identification of the source of the issues is mandatory.

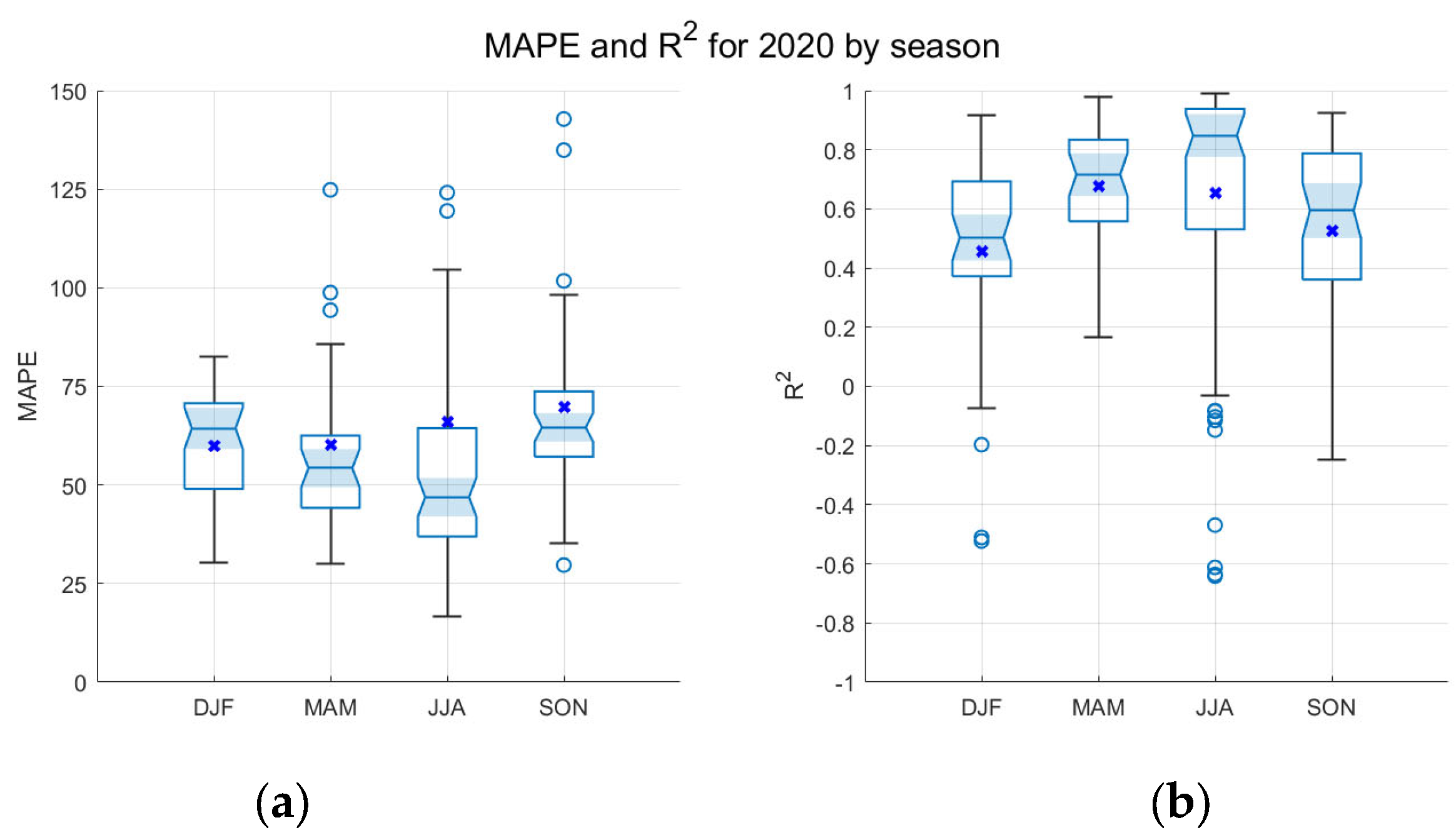
In order to study the reasons for the good and bad agreements between the estimates, boxplots for the values of the MAPE and R² for each season in the year 2020 are plotted in Figure 4a and Figure 4b, respectively. The best agreement is obtained in summer (JJA), with median (± standard deviation) MAPE values equal to 46.92 ± 16.73 and an R² of about 0.84 ± 0.43. The worst results are obtained for autumn (SON, MAPE: 64.61 ± 28.88, R²: 0.59 ± 0.32) and winter (DJF, MAPE: 64.36 ± 14.62, R²: 0.50 ± 0.34). Thus, if the MAPE is considered as an indicator of the distance, in height, between both ECMWF-IFS and STRATfinder values, Figure 4a suggests that there is a statistically significant difference between the discrepancy in MLH estimations during cold seasons and warm seasons. However, a Wilcoxon test shows that the difference between spring and winter is not statistically significant (p = 0.06). This result is related to Figure 4b, which suggests that the correlations in the summer months are significantly higher than those in the spring months. The higher correlation for the summer months coincides with the low relative humidity measured at the meteorological station (35.21 ± 9.96%), with regard to the values of spring (62.83 ± 15.48%), autumn (63.57 ± 19.85%) and winter (75.60 ± 16.64). This result confirms that the similar temporal evolution or shape of both MLH estimates is a consequence of the meteorological conditions, namely high temperatures and solar radiation levels and low relative humidity values.

3.2. Influence of Synoptic Meteorological Patterns on the MLH

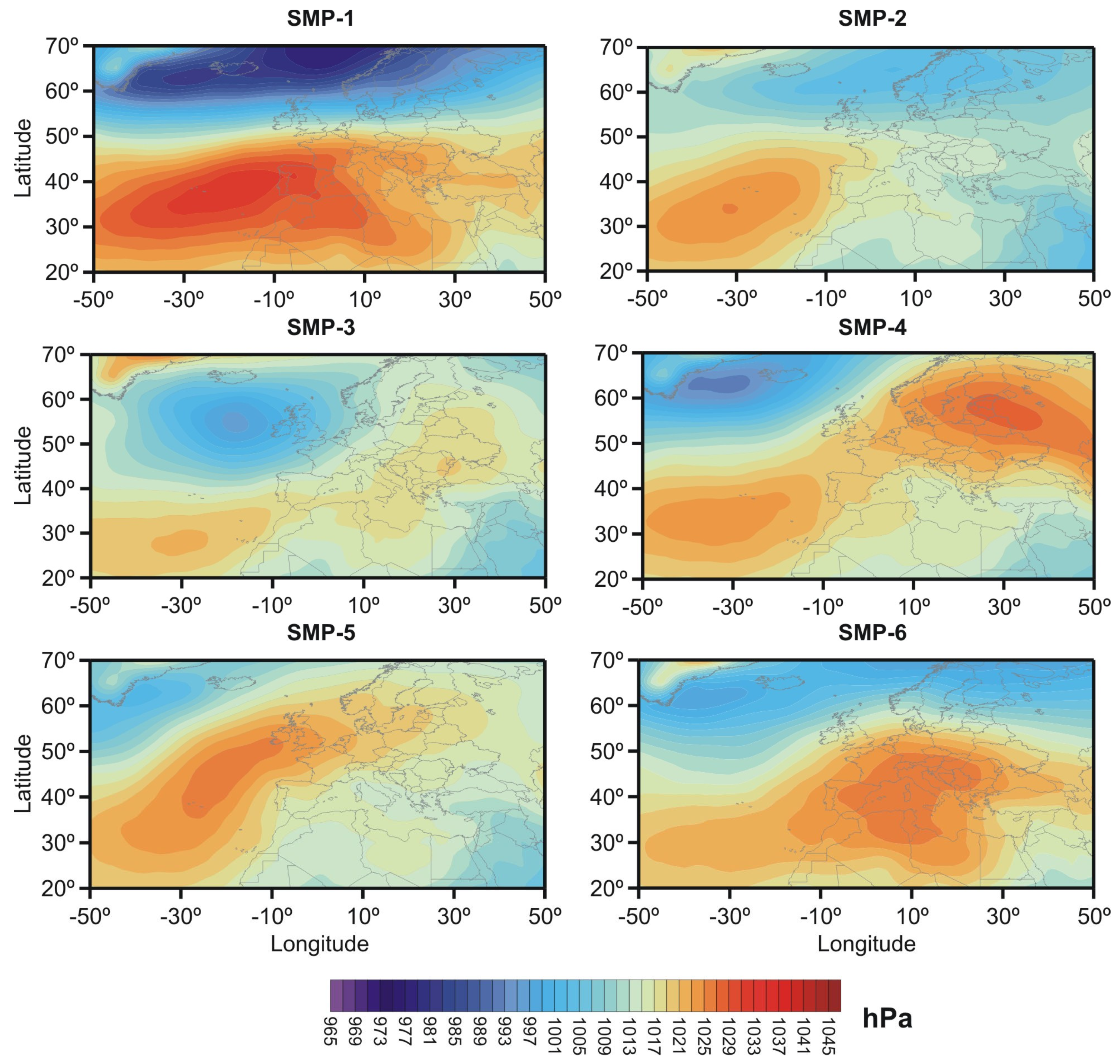
A brief description of the SMPs is provided as follows: SMP-1 is characterized by the presence of high pressures over the Iberian Peninsula, leading to high atmospheric stability and a blockage of the entrance of air masses from marine or continental regions outside. It represents 4% of all days in the period of 2001–2019 and 8% of the days in 2020, mainly in winter, and explains 7.7% of the total cluster variance. SMP-2 is characterized by an anticyclone centered on the Azores Islands and a low-pressure center situated between the United Kingdom and the Scandinavian countries. The pressure gradient is low over Western Europe. The location of the main pressure center suggests the predominant occurrence of smooth air flows entering from the Atlantic Ocean (NW) into the Iberian Peninsula. It occurred on 32% of all days of the period 2001–2019 and 31% of the days in 2020, mainly in the summer season, and explains 22.50% of the total cluster variance. SMP-3 presents a strong pressure gradient between the Azores Islands’ high-pressure center, which is displaced southwards from its usual position and the low-pressure center that is shifted to the west of the United Kingdom. It generates western air mass flows with high wind speeds over the Iberian Peninsula. This SMP occurred on 15% of all days of the period 2001–2019 and 14% of the days in 2020, mainly in the autumn and spring seasons, explaining 19.30% of the total cluster variance. SMP-4 is characterized by two high-pressure systems, one over Eastern Europe and the other over the Azores Islands, and a low-pressure center located to the west of Iceland. It generated moderate western and northwestern air mass flows over the Iberian Peninsula and occurred on 16% of the days of the period 2001–2019 and 13% of the days in 2020, mainly in autumn and spring. SMP-4 explains 19.40% of the total cluster variance. SMP-5 is characterized by the presence of high pressures displaced to the northwest of the Iberian Peninsula, blocking the entry of northern air mass flows but allowing the advection of air masses from continental Europe and the Mediterranean Sea over the Iberian Peninsula. This SMP occurred on 21% of all days during the period of 2001–2019 and 20% of the days in 2020, mainly in spring and summer, explaining 18.00% of the total cluster variance. Finally, SMP-6 has high pressures extending along the western and central Mediterranean basin and can trigger the transport of African dust towards regions of the Iberian Peninsula and the Balearic Islands. It represents 12% of all days of the period 2001–2019, and 14% of the days in 2020, mainly in winter, and also, this SMP explains 13.20% of the total cluster variance. Each of these SMPs are shown in Figure 5.

Since the SMP classification was performed at a daily time resolution, it is assumed here that the 24 h of a day are represented by the same SMP. Finally, two main remarks are needed about the SMPs: (1) SMP-1 and SMP-6 are the only clusters that are not present in every season—concretely, they are not present in summer—and (2) the clusters are distributed differently between the seasons; see

Table 1. Distribution of the analyzed hours by SMP and season.

	All	SMP-1	SMP-2	SMP-3	SMP-4	SMP-5	SMP-6
Winter	1077	387	92	209	92	35	262
Spring	870	22	427	98	67	208	48
Summer	1636	0	1101	91	93	351	0
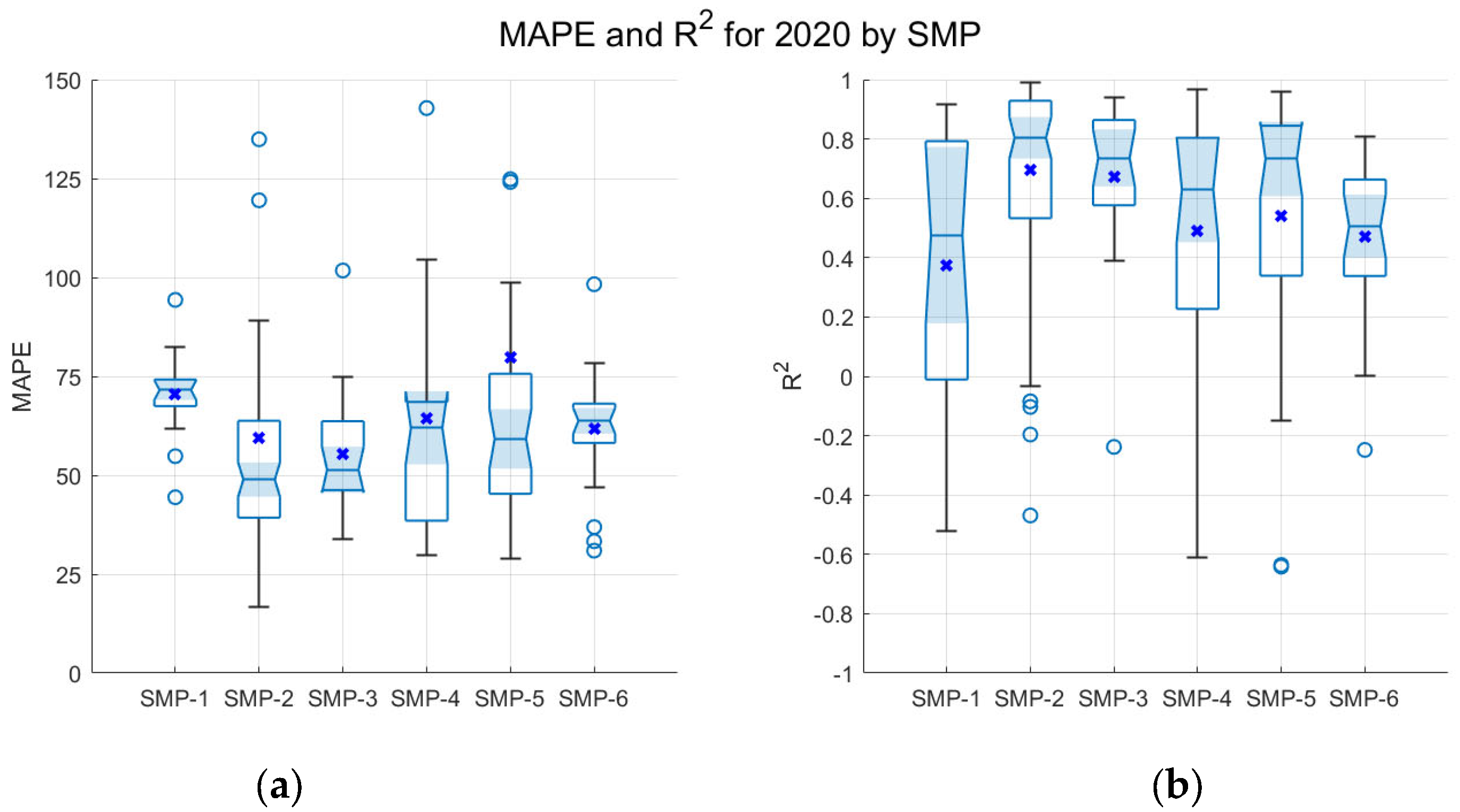
Autumn	1241	48	150	158	321	282	282

. Furthermore, the statistical scores obtained for 2020, separated by SMP, are shown in Figure 6. In summary, the largest number of good agreements is obtained for SMP-2, and the worst agreements are obtained for SMP-1 and SMP-6.

Both SMP-1 and SMP-6 have the lowest mean values of solar irradiance, 93.26 ± 47.11 and 95.42 ± 59.85 W/m², respectively, representing 38.23% and 39.12% of the mean solar irradiance measured for SMP-2, the cluster with the highest value of this parameter (243.89 ± 71.55 W/m²). The lack of solar irradiance clearly restricts the growth of the ML, leading to a detection error in STRATfinder. In most cases, the algorithm identifies the residual layer as the ML, resulting in bad agreements between STRATfinder and the EMCWF-IFS model. This misidentification gives a low median R² and high median MAPE values. Concretely, SMP-1 and SMP-6 show median R² values of about 0.48 ± 0.46 and 0.51 ± 0.25, and median MAPE values of 71.53 ± 10.47 and 63.75 ± 14.64, as shown Figure 6, respectively. Otherwise, it is worth noting that, as Molero et al. [14] found, the relative humidity is inversely correlated with the MLH, and they also remarked that values greater than 60% are related to poorly developed MLs. Thus, both SMP-1 and SMP-6 present mean values of relative humidity greater than 60%; more specifically, the mean relative humidity values found during 2020 for both SMPs are about 74.38 ± 17.36% and 74.76 ± 17.13%, respectively, confirming the poor relationship between poorly developed MLs and bad agreements between the methods. Figure 6a shows the small variation in MAPE values for both SMPs, indicating that the poor agreements between both MLH datasets are quite constant over the 81 days affected by these two SMPs. However, the values of R² (Figure 6b) show a different behavior, since, because of the high deviation aforementioned and according to a Wilcoxon test, only SMP-2 (p = 0.01, p = 1.02 × 10⁻⁴) and SMP-3 (p = 0.03, p = 4 × 10⁻³) are significantly different to SMP-1 and SMP-6. This high variation, which disrupts the differences between SMPs, is caused by the meteorological conditions that, in turn, cause different shapes of the MLH measured via the ceilometer and computed using the model.

SMP-2 and SMP-5 have the first and second highest mean solar irradiance, 243.89 ± 71.55 and 189.04 ± 88.33 W/m², and the lowest mean relative humidity, 44.91 ± 17.83% and 54.48 ± 18.32%, respectively. This combination of high solar irradiance and low relative humidity results in a well-developed ML and clear-sky days, aiding the identification of the MLH via STRATfinder from the ceilometer signals and confirming the better agreement with the ECMWF-IFS model estimates during warmer seasons. The largest number of good agreements is obtained for SMP-2, as shown through the median MAPE (48.91 ± 44.93) and R² (0.80 ± 0.31) values. However, SMP-5 has a similar median R² value (0.73 ± 0.42) but an 18% larger MAPE (59.19 ± 75.34) with an exceptionally large variability. This difference in the MAPE is due to the large amount of autumnal and wintry hours of this cluster, resulting in 36.84% of days being partly cloudy, while these days represent just 16.82% for SMP-2. During cloudy days, the measured mean solar irradiance decreased for SMP-5, around 33%, with regard to the mean solar irradiance obtained for the rest of the days classified as SMP-5. Thus, as Figure 6 shows, this large proportion of partly cloudy days leads to an unexpected result linked with the meteorological conditions. Thereby, non-statistically significant differences were expected between SMP-2 and SMP-5 but, on the contrary, these non-statistically significant differences were found between SMP-5 and SMP-6 in terms of the MAPE and, between SMP-5 and both SMP-1 and SMP-6, in terms of the R². Hence, this behavior of SMP-5 confirms the aforementioned observation that solar irradiance is a limiting factor for estimating the MLH using the STRATfinder algorithm, because it can lead the algorithm to experience detection errors.

SMP-3 is characterized by a high relative humidity (73.30 ± 17.74%) and low solar irradiance (108.37 ± 82.55 W/m²), similar to SMP-1 and SMP-6. However, in spite of these characteristics, SMP-3 has the second lowest median MAPE (51.39 ± 15.24) and the second highest R² (0.74 ± 0.27). These statistical parameters suggest an agreement between STRATfinder and the model that is even better than the one found for SMP-5, which is not expected according to the atmospheric characteristics of SMP-3. In this way, these results can be explained by the fact that, after the data filtering, from a total of 53 days identified as SMP-3, only 23 days were not filtered out. Before filtering, spring and summer represented 26.41% of the hours of this cluster, whereas after filtering, these seasons represented 34% of the remaining hours. Furthermore, for the summer data, only 5 h was filtered out. Hence, the influence of warmer days, which show better results in terms of their MAPE and R², is larger percentage-wise than before data filtering, thus explaining the statistical performance of SMP-3.

For its part, SMP-4 is mainly autumnal, with 56.02% of its data belonging to this season. This SMP presents a mean relative humidity of 58.43 ± 19.82% and a mean solar irradiance of 159.25 ± 93.12 W/m². Furthermore, its median values of MAPE and R² are 61.98 ± 37.71 and 0.63 ± 0.41, respectively. The statistical parameters indicate a good agreement between the STRATfinder results and the EMCWF-IFS model, but slightly worsen due to the effect of the high relative humidity, close to 60%, which cannot be compensated for by solar irradiance as in the case of SMP-5. Therefore, it can be affirmed that the atmospheric variables and, as a consequence, the statistical performance of this cluster lies between two different groups, formed of SMP-2 on the one hand and SMP-1 and SMP-6 on the other.

Therefore, Figure 6a and the Wilcoxon test identify statistically significant differences between SMP-1 and the other five SMPs because of its high mean relative humidity and low mean solar radiation values, which leads to high MAPE values with a low variability. Figure 6b also shows statistically significant differences between SMP-1 and SMP-6 on the one hand and SMP-2 on the other, further demonstrating that this analysis, based on synoptic atmospheric situations, shows that the best performance in MLH comparisons are always linked to atmospheric scenarios or meteorological conditions that favor well-developed MLs.

3.3. Parts of the Day

In order to further identify the aforementioned behaviors, each day was divided into four parts, following the details of Kotthaus and Grimmond [23], as is shown in Figure 2. Since only four hours of data are included in some of the four parts (NT, MO, DT and EV), as is the case of MO in Figure 2 where none were filtered out, no day-by-day statistical analysis is possible with this approach. Instead, the whole year of STRATfinder data for each part has been compared with the equivalent estimations of the model.

Table 2. Distribution of the times in the day analyzed by season.

	All	NT	MO	DT	EV
Winter	1077	564	160	154	199
Spring	870	318	151	244	157
Summer	1636	539	304	566	227
Autumn	1241	600	196	235	210

and

Table 3. Distribution of the times in the day analyzed by SMP.

	All	NT	MO	DT	EV
SMP-1	457	240	64	70	83
SMP-2	1770	636	319	558	257
SMP-3	556	262	81	114	99
SMP-4	573	240	93	137	103
SMP-5	876	357	163	222	134
SMP-6	592	286	91	98	117

show the data distribution by season and SMP, respectively, with reasonable distribution for all cases, validating the statistical analysis distributed based on the time of day and season.

The largest amount of hours analyzed correspond to summer, while, contrary to what may be expected, the smallest number correspond to spring instead of winter. This oddity is a result of the data filtering, since 60.59% of the spring days were filtered out, whereas winter and autumn only lost 50.68% and 43.17% of the days, respectively. Furthermore, it is worthwhile to note that all the seasons present the largest number of available hours in the NT period, except for summer, to which DT contributes the most.

The analysis reveals reasonable correlations for DT (0.70) and EV (0.62); however, these two periods have high MAPE values (60.67 and 71.06, respectively), which are a consequence of the temporal interpolation need of the EMCWF-IFS model data. As Figure 3b,d show, at 16:00, the ML estimated via the model decreases sharply, while STRATfinder still detects an increase in the ML or a very smooth decrease until 18:00 or 19:00. Although the model and the algorithm show a similar tendency during both parts of the day, there are noticeable differences during the transition of DT to EV that increase the MAPE.

The annual correlations for NT and MO are very low (0.10 and 0.06, respectively), indicating a problem with low values of the MLH that must be considered in future works. These parts of the day are therefore discarded from the following analyses. However, some analyses can still be drawn. From an initial analysis based on the data shown in

Table 4. Annual MAPE and R² values obtained for the four parts of the day.

	MAPE	R2
NT	71.77	0.10
MO	53.17	0.06
DT	60.67	0.70
EV	71.06	0.62

, it can be seen that the annual MAPE obtained for NT is around 18.29% and 1.00% higher than the MAPEs obtained for DT and EV, respectively. They are even lower in the case of MO than those found for DT and EV (14.11% and 33.65%, respectively), indicating that both methods do not show excessively different estimated MLH values. During NT, it is usual to find a very stable layer, with its upper limit at a low altitude, showing very small and rapid variations which, as it is shown in Figure 2 (now Figure 3), the STRATfinder algorithm can detect. This algorithm, as indicated in the body of the text, can work with a temporal resolution of 1 min, so the averaging performed (1 h) is able to continue showing some of these oscillations. However, the ECMWF-IFS model, with an initial temporal resolution of 3 h, shows a very flat estimate of the ML due to interpolation to 1 h, thus failing to detect these oscillations and consequently lowering the value of the R².

The MO period is a similar case in which there is a first part of about two hours that repeats the pattern identified at NT, and then a sudden change with a rapid rise in the ML. Again, the datasets are faced with variations that are too fast for the model, causing another collapse in the R² values. For example, during DT, when the ascent and subsequent stabilization of the MLH mask the small oscillations, the correlation between both methods is much better.

Looking at

Table 5. Annual MAPE and R² values obtained for the six SMPs in the four parts of the day.

	NT		MO		DT		EV
	MAPE	R2	MAPE	R2	MAPE	R2	MAPE	R2
SMP-1	83.64	0.11	62.32	0.16	28.06	0.61	63.86	0.50
SMP-2	65.44	0.08	52.96	0.04	55.42	0.68	66.04	0.67
SMP-3	73.47	0.48	55.14	0.44	29.40	0.82	61.37	0.33
SMP-4	74.89	0.07	49.28	0.02	60.08	0.69	82.83	0.54
SMP-5	71.42	0.03	56.55	0.08	108.25	0.39	91.41	0.35
SMP-6	72.16	0.10	43.61	0.19	43.23	0.64	61.70	0.33

, it can be seen that by classifying the periods of the day into the different SMPs, the annual MAPE values show a very similar behavior to that observed for the values in Table 4. However, regarding the annual R² values, SMP-3 shows R² values for NT (0.48) and MO (0.44) that are much higher than those in Table 4 and higher than those of the other SMPs for these two parts of the day. This behavior can be explained thanks to one of the characteristics of this SMP compared to the others: its low AOD values. The AOD of SMP-3 is, on average, about 17%, 32%, 22.3%, 46% and 24% lower than the AODs of SMP-1, -2, -4, -5, and -6, respectively. When the AOD is low, the ceilometer has difficulties detecting the upper limit of the ML, decreasing its ability to detect the small and rapid oscillations of the ML’s upper limit. Therefore, with a low AOD, STRATfinder shows a more flat temporal evolution of the ML, similar to that shown via the model.

Since the annual values are highly affected by some issues in the estimations of the MLH, and in order to give light to the behavior of the ML during the DT and EV periods, the dataset has also been divided based on SMPs, as shown in Table 5. Taking a closer look at the MAPE and R² values, some interesting results need to be analyzed. For instance, reasonable correlations for DT with a median value of about 0.66 ± 0.14 are found, while the EV, for its part, presents a lower median value of R², which is about 0.43 ± 0.14. In the case of the MAPE, DT again shows a reasonable median value (49.33 ± 29.58), while in the EV period, this value is slightly greater (64.95 ± 12.74). One can observe that the temporal interpolation applied to the ECMWF-IFS data influences these results, so in order to give light to this hint, the cases of SMP-1 and SMP-6 are analyzed next.

Then, for the DT period, SMP-1 and SMP-6 present low annual MAPE values, 28.06 and 43.23, respectively, pointing out that the SMPs with meteorological conditions for the poorest development of the ML now present the best agreement between the datasets, contrary to the previous observations. It is worthwhile to note that these annual MAPE values for SMP-1 and SMP-6 are about 56.05% and 29.93% lower than the values found during the EV (63.86 and 61.70, respectively). This behavior reinforces the idea of the influence of the temporal interpolation on the ECMWF-IFS model results. Since these SMPs are principally composed of autumnal and wintry days, the DT periods during these SMPs are short; therefore, only a couple of actual (without interpolation) computations of the ECMWF-IFS model are included in this period. Then, the model estimates the decrease in the RL height prematurely, just in the beginning of the EV period. However, the STRATfinder results that present a better temporal resolution can fluctuate in their detection of the last moments of the ML during the early hours of the EV, explaining in that way the large increase in the MAPE values. The annual values of R² for SMP-1 and SMP-6 act in the same way, with the DT (0.61 and 0.64, respectively) being about 18.42% and 48.45% greater than during EV (0.50 and 0.33, respectively), confirming the effect of the interpolation.

As shown in Table 5, SMP-5 presents the highest annual MAPE values in both DT (108.25) and EV (91.41) because of the effect of its large amount of partly cloudy days, commented on above, that leads to errors in the STRATfinder values. However, this SMP is the only one with a lower value during EV, concretely showing a decrease of about 18.43%. This behavior is a consequence of the low MLHs estimated via STRATfinder at the end of the DT and the beginning of the EV periods. It is worth mentioning the case of SMP-2 that presents smaller differences between periods, that is, a 16.08% larger MAPE and a 2.11% lower R² value. The small difference in the R² points out that the sharp decrease in both datasets is found at the same time or with an hour of difference, as in the case of Figure 2 and Figure 3a,d. Nonetheless, the differences in the MAPE suggest that, in spite of the fact that the model works better during the warmer seasons (62.20% of the analyzed hours during SMP-2 were in the summer), the STRATfinder MLH values are normally larger at the beginning of the EV period.

4. Conclusions

In this study, the effect of different meteorological conditions (seasons, synoptic patterns and parts of the day) on the temporal evolution of the MLH has been analyzed by means of the STRATfinder algorithm fed with ceilometer profiles. The results were compared with EMCWF-IFS model computations. Thus, our results show that the MLHs computed using the ECMWF-IFS model are in good agreement with the heights estimated using STRATfinder during the summer months because of the good conditions for the development of the ML in terms of solar radiation and relative humidity during these months. The low surface temperatures detected at the weather station during winter and autumn, as well as the more frequent presence of clouds together with the low solar irradiance and the high relative humidity measured (above 60%) during these seasons, lead to a poorly developed ML, causing, in turn, the worst correlation between both STRATfinder and the ECMWF-IFS model.

The analysis of the evolution of the MLH under different synoptic meteorological situations reinforces the fact of the high sensitivity of the algorithm and the model to meteorological conditions. Thus, SMP-2, which presents the greatest agreement between the two datasets, is the cluster with the highest temperature and solar irradiance, as well as the lowest relative humidity, providing ideal conditions for well-developed MLs. On the contrary, SMP-1 and SMP-6, with higher relative humidity and lower temperature and solar irradiance than SMP-2, correspond to days with a poorly developed ML and, therefore, poor agreement between the two datasets. The results obtained for SMP-5 highlight the importance of solar irradiance as a limiting factor for obtaining MLHs with STRATfinder because it can lead the algorithm to experience detection errors. Therefore, it can be concluded from this part that it is necessary to forecast the SMP so that the model can be parameterized based on atmospheric conditions.

The results of the analysis based on periods of the day show that the values obtained for the NT and MO periods, because of the poor temporal resolution of the model, cannot be analyzed properly. Concerning the DT and EV, these periods present good agreement between both datasets when taking a look only at the annual R², which presents values of around 0.70 and 0.62, respectively. However, the annual MAPE values are higher than might be expected according to the annual R² values found. These high MAPE values are a consequence of the effect of the faster decrease in the MLHs estimated using the EMCWF-IFS model from 16:00 UTC, which seems to be an artifact resulting from the temporal interpolation and the model parameterization. This idea is reinforced when splitting the periods of the day based on SMPs, when SMP-1 and SMP-6, the periods with the shortest DT, show high differences between DT and EV because of the decrease in the MLH to the height of the RL, observed in the ECMWF-IFS model computations just at the beginning of the EV. On the contrary, the STRATfinder values are able to detect the MLH during the early hours of the EV, made easier by its better temporal resolution, causing a strong difference in the tendency of both shapes, leading to low correlations or bad agreements between them.

Therefore, although both datasets have been shown to be very sensitive to meteorological patterns, the computation of the MLH using the EMCWF-IFS model appears to be more accurate than STRATfinder to detect the ML in cases where it is coupled homogeneously to the residual layer, and because of the limitations of the ceilometer signals described above, such as the presence of low clouds or the overlap height. However, the model, which seems to be optimized for the warmest seasons, is affected by the aforementioned artificial behavior in the growing phase but especially after 16:00 UTC, when the computed MLHs start to decrease independently of the evolution of the aerosol layer because of the temporal interpolation of the data. For their part, the STRATfinder results also present an artifact that is related to how the algorithm discriminates between the ML and the RL, but in this case, the artifact is found closer to sunset. So, it can be affirmed that the STRATfinder values are more reliable than the computations of the ECMWF-IFS model during NT, MO, the final hours of the DT and the early hours of the EV periods. Atmospheric conditions, such as temperature, relative humidity and solar irradiance, are directly related to the development of the ML, influencing, in turn, the MLH estimates. Cases with low temperature or solar irradiance values, low relative humidity or a combination of these factors that lead to a poorly developed ML highlight the aforementioned artificial performance of the model and the ceilometer detection issues when low clouds or homogeneous aerosol layers appear.

It can be concluded that, for a complete description of the temporal evolution of the ABL, strongly conditioned by the meteorological conditions that take place in each case, in addition to ceilometer signals, the use of other complementary methods is necessary, while the temporal resolution of the ECMWF-IFS model continues to not be improved. The STRATfinder algorithm has demonstrated in this study that a temporal resolution of one hour is sufficient to detect variations in the MLH that can be critical, for example, during the NT and MO periods, when the air quality worsens under stable conditions or inversions. Therefore, the model needs to be improved to achieve an actual temporal resolution of at least one hour. For that purpose, it is crucial to provide more detailed information of the ABL height for the evaluation of predictions provided via high-resolution numerical models. The recent implementation of ceilometer networks will allow for a better characterization of the complexity of ABL dynamics at larger scales, offering great potential as a correction tool for ABL heights derived from models. This study has also highlighted the need for the use of datasets longer than one year, which can absorb drastic atmospheric changes, thus reducing the significant uncertainties observed (see Figure 4 and Figure 6) during the comparison of both datasets. Future research should focus on developing methodologies that use ceilometer profiles as input data for models involved in air pollution dispersion assessments.