Abstract
Recently, light use efficiency (LUE) models driven by remote sensing data have been widely employed to estimate the gross primary productivity (GPP) of different terrestrial ecosystems at global or regional scales. Furthermore, the two-leaf light use efficiency (TL-LUE) model has been reported to improve the accuracy of GPP estimation, relative to the big-leaf MOD17 model, by separating the entire canopy into sunlit and shaded leaves through the use of constant clumping index estimation (Ω). However, ignoring obvious seasonal changes in the vegetation clumping index (CI) most likely results in GPP estimation errors since the CI tends to present seasonal changes, especially with respect to the obvious presence or absence of leaves within the canopy of deciduous vegetation. Here, we propose a TL-CLUE model that considers the seasonal difference in the CI based on the TL-LUE model to characterize general changes in canopy seasonality. This method composites monthly CI values into two or three Ω values to capture the general seasonal changes in CI while attempting to reduce the potential uncertainty caused during CI inversion. In theory, CI seasonality plays an essential role in the distribution of photosynthetically active radiation absorbed by the canopy (APAR). Specifically, the seasonal difference in CI values mainly considers the state of leaf growth, which is determined by the MODIS land surface phenology (LSP) product (MCD12Q2). Therefore, the one-year cycle (OYC) of leaf life is divided into two (leaf-off and leaf-on) or three seasons (leaf-off, leaf-scattering, and leaf-gathering) according to this MODIS LSP product, and the mean CI of each corresponding season for each vegetation class is computed to smoothen the uncertainties within each seasonal section. With these two or three seasonal Ω values as inputs, the TL-CLUE model by which the seasonal differences in CI are incorporated into the TL-LUE model is run and evaluated based on observations from 84 eddy covariance (EC) tower sites across North America. The results of the analysis reveal that the TL-LUE model widely overestimates GPP for most vegetation types during the leaf-on season, particularly during the growth peak. Although the TL-LUE model shows that the temporal characteristics of GPP agree with the EC observations in terms of general trends, the TL-CLUE model further improves the accuracy of GPP estimation by considering the seasonal changes in the CI. The result of GPP estimation from the TL-CLUE model shows a lower error (RMSE = 2.46 g C m−2 d−1) than the TL-LUE model (RMSE = 2.75 g C m−2 d−1) and somewhat decreases the eight-day GPP overestimation in the TL-LUE model with a constant Ω by approximately 9.76 and 8.970% when adapting three and two Ωs from different seasons, respectively. The study demonstrates that the uncertainty of seasonal disturbance in the CI, quantified by a standard deviation of approximately 0.071 relative to the mean CI of 0.746, is diminished through simple averaging. The seasonal difference in CI should be considered in GPP estimation of terrestrial ecosystems, particularly for vegetation with obvious canopy changes, where leaves go through the complete physiological processes of germination, stretching, maturity, and falling within a year. This study demonstrates the potential of the MODIS CI application in developing ecosystem and hydrological models.
1. Introduction
Gross primary productivity (GPP) is the amount of carbon dioxide (CO2) uptake via photosynthesis by vegetation per unit of time [1]. GPP is a key parameter for understanding global carbon exchange and effectively mitigating climate change [2], and is even viewed as an important basis for measuring ecological services and products such as fiber, wood, and food [3,4]. However, annual and interannual GPP estimations have greater uncertainties in different regions and ecosystem types [5] than the uncertainties at a global scale [6,7].
GPP estimation models are generally classified as data-driven, process-based, and remote-sensing models [8,9,10,11]. Furthermore, remote-sensing models are divided into light use efficiency (LUE) models [12,13] and vegetation index models, which are both favored by numerous researchers due to their relatively simple theories, practical applications, and easily accessible model driving data at the global scale [14,15]. LUE models based on LUE and photosynthetically active radiation absorbed by the vegetation canopy (APAR), such as the MOD17 GPP model [16], are easy to implement and have great potential for exploring the temporal and spatial dynamics of global or regional GPP [17,18,19,20]. Therefore, LUE models are suitable for the study of continuous spatiotemporal changes in GPP [21]. LUE models have been used for widespread estimation of GPP [9,22,23,24,25], of which the classical fundamental theory is as follows [8,26]:
where PAR is the incoming photosynthetically active radiation (MJ m−2), FPAR is the fraction of PAR absorbed by the vegetation canopy, Ɛmax is theoretically the maximum LUE (g C MJ−1), and σ represents the scale of environmental stress factors such as soil water and air temperature on Ɛmax, ranging from 0 to 1.
Recently, various LUE models have shown major differences in the constraint of Ɛmax from environmental stress factors and APAR calculations [4]. Most models assume that the canopy is a large leaf that equally utilizes direct and diffuse radiation and that GPP increases linearly with APAR [27]. Nevertheless, there is a difference between the LUE values of sunlit and shaded leaves in that they are restricted by the maximum carboxylation rate and maximum electron transport rate, respectively [28,29,30]. Compared to sunlit leaves, shaded leaves absorb only diffuse radiation, resulting in low APAR [31] values due to the direct radiation limitation of sunlit leaves. Consequently, neglecting the distinct difference in APAR values between sunlit and shaded leaves will lead to errors in GPP estimation [4]. An accurate estimation of canopy-level GPP must separate the canopy into sunlit and shaded leaves [27,30]. The MOD17 GPP model underestimates the GPP in dense vegetation regions due to its insufficient consideration of shaded leaves [32,33], indicating that the GPP estimation is affected by the canopy structure of vegetation, such as sunlit and shaded leaves, in LUE models [34,35,36]. The two-leaf light use efficiency (TL-LUE) model [4] separates the canopy into sunlit and shaded leaves by the method proposed in the Boreal Ecosystem Productivity Simulator (BEPS) [29], which performed well in 298 site-year validation data from the FLUNNET2015 dataset and outperformed the MOD17 GPP model in various ecosystems [36]. Hence, the TL-LUE model has received attention in the study of remote sensing of vegetation.
In the TL-LUE model, the vegetation canopy is divided into sunlit and shaded leaves based on the foliage clumping index (CI), which qualifies the degree of leaf gathering relative to a random distribution within the specific canopy structure [37] and is a core variable for describing the canopy structure of vegetation [38] and retrieving the leaf area index (LAI), one of the key parameters in LUE models. The CI affects the distribution and interception of canopy inner radiation, further controlling carbon uptake and the transformation of energy and evapotranspiration. In addition, the CI is crucial for the estimation and explication of vegetation evapotranspiration and photosynthesis [39] and plays a vital role in ecological and methodological models [40]. Ignoring the CI would lead to at least 12% overestimation of global GPP [39]. The contribution of shaded leaves to the total GPP is 56, 40, and 39% in EBF, ENF, and shrubs, respectively [41]. Additionally, the CI has a large influence on the estimation of the canopy level, which may be due to its effect on the ratio of sunlit leaves to shaded leaves (e.g., the TL-LUE model) or changes in the PAR interception area [39].
Currently, only a constant CI estimation (Ω) in a one-year cycle (OYC) is applied in the TL-LUE model, but CI differences can be observed in different seasons, although the uncertainty of seasonal disturbances in the CI is obvious in most cases, with a lower CI value in the leaf-on season and a higher CI value in the leaf-off season, particularly in deciduous broadleaf forests and mixed forests [42]. Furthermore, CI has been able to detect seasonal changes in some vegetation structures, especially in deciduous broadleaf forests and shrubs [43]. Therefore, the TL-LUE model using the Ω constant undoubtedly leads to uncertainty in GPP estimation in theory since the seasonal difference in vegetation CI leads to a change in the APAR values between sunlit and shaded leaves, which would affect the accuracy of GPP estimation in the TL-LUE model.
In addition to having ample carbon cycle observation data, such as crop yield inventory, SIF, atmospheric OCS, and particularly flux data measured by eddy covariance towers, North America also spans a wide range of latitudes and has a wide variety of vegetation types. As a result, it is a reasonable and suitable place to research the carbon cycle in terrestrial ecosystems. The study intends to improve the GPP estimation in the TL-LUE model by considering the seasonal changes in CI (TL-CLUE). The OYC for leaf life is divided into two or three seasons based on the MODIS land surface phenology products (MCD12Q2), and the corresponding values of Ω to the seasons are estimated. We simulate the eight-day GPP of North America during 2002~2020 by the TL-CLUE model driven by meteorological and vegetation data. This study provides an alternative way to improve GPP estimation and provides insights into the carbon cycle for different vegetation types across North America.
2. Data
2.1. Flux Site Data
Flux data originating from FLUXNET2015 (https://fluxnet.org/data/fluxnet2015-dataset/, accessed on 17 May 2023) and AmeriFlux (https://AmeriFlux.lbl.gov/, accessed on 17 May 2023) have the standard format of eddy covariance (EC) flux data, with better processing and quality control [44], covering different global regions. The time series of the FLUXNET2015 data (ranging from 2001 to 2014) is shorter than that of the AmeriFlux data (from 2000 to 2022). The FLUXNET dataset recently published by AmeriFlux has high quality that is assured through outlier filtering, gap filling, and uncertainty estimation. GPP could be obtained from the difference between net ecosystem exchange (NEE) and respiration based on light-response curves [45]. The quality label is due to the proportion of great data, including observation and excellent filling, and the study uses data whose quality label is over 0.8 and contains at least 90% metrological and flux data. Additionally, we removed data with GPP values of less than 0, out-of-order temporal characteristics, and unrealistic patterns of vegetation growth. The vegetation type of the site was determined by combining the site description and Moderate Resolution Imaging Spectroradiometer (MODIS) Land Cover Version 6.1 (MCD12Q1.061) product. The study aggregated half-hour data of more than 5 days into an eight-day dataset to coincide with the temporal resolution of the remote sensing data, of which the following variables were selected for the study: GPP, solar shortwave radiation (SWRad), vapor pressure deficit (VPD), and minimum air temperature (Tamin). The study used data from a total of 84 EC sites across North America from 2002 to 2020 for different vegetation types (Table 1): DBF (14), ENF (24), MF (3), CRO (15), WSA (2), OSH (11), SAV (3), and GRA (12) (Figure 1).

Table 1.
Parameters required for the TL-LUE model for different vegetation types.
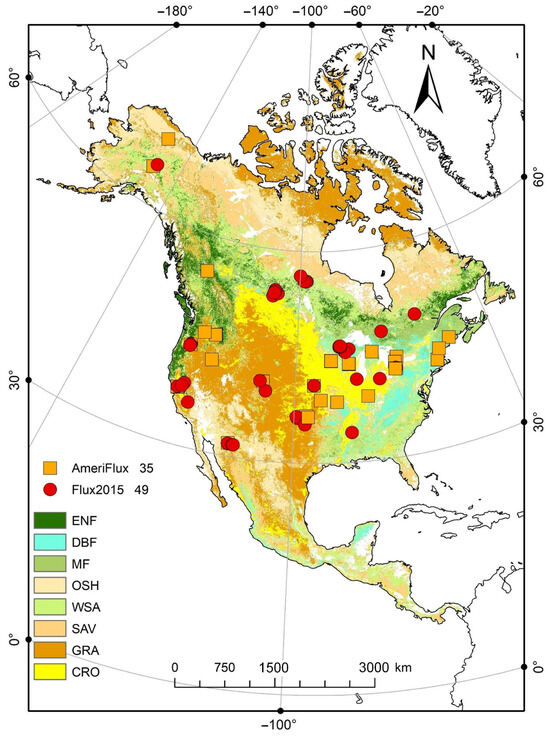
Figure 1.
Site distribution of GPP measurement eddy covariance towers across North America in different vegetation types obtained from the MODIS Year Land Cover Version 061 (MCD12Q1.061) product. There are 35 sites from the AmeriFlux dataset indicated by orange rectangles, and 49− sites from the FLUXNET2015 dataset represented by red circles.
2.2. MODIS CI
The MODIS CI dataset was inverted from the MODIS bidirectional reflectance distribution function (BRDF) by the adjusted kernel-driven BRDF model [47,48]. The CI has spatiotemporal differences that are greater in herbaceous vegetation such as grass, shrub, crop, and savanna than in forests [42] and shows strong seasonal changes, particularly in deciduous needleleaf forests [43]. The Savitzky–Golay logistic [49] method was utilized to eliminate the CI uncertainties resulting from clouds, fog, snow, ice, atmospheric dust, etc. The measurement extent of the eddy covariance flux towers is approximately 20~100 times the tower height, ranging from tens of meters to tens of kilometers [39,50]. Therefore, the flux sites in CRO, GRA, SWA, OSH, and SAV with 10 m of vegetation should adopt the LAI of a cell (2 × 2) with a 1 × 1 km area, and the flux sites in ENF, DBF, and MF with over 10 m of vegetation should use the average LAI of cells (6 × 6) with a 3 × 3 km area.
Additionally, the estimation of the CI of different seasons for every vegetation type is given by the synthesis inference combining the MODIS CI data and some published literature on the CI [32,42,43,51,52], which was used for optimizing the only constant Ω parameter of the TL-LUE model.
2.3. MODIS Land Cover and LAI
Land cover (LC) data from the NASA Earth Observing System Data and Information System (EOSDIS) with a spatial resolution of 500 m during 2001~2021 were generated by the integrated decision tree algorithm [53] and classified into 17 types of land cover depending on the vegetation classification scheme of the International Geosphere Biosphere Program (IGBP), which is followed by the EC flux site.
The LAI is defined as half of the total area of all leaves per unit area on the ground [54], which is a key parameter indicating the structure and function of vegetation and has an important role in the balance of the ecosystem, carbon cycle, and vegetation growth. The MODIS LAI product (MOD15A2H.061) provides eight-day LAI data from 2002 to 2020 with a spatial resolution of 500 m, which is highly appropriate for analyzing the carbon cycle and vegetation growth. In addition, the MODIS LAI is the common LAI resource of LUE models.
2.4. Meteorological Data
Modern Era Retrospective Analysis for Research and Application, Version 2 (MERRA-2), developed by the updated Goddard Earth Observing System Version 5 (GEOS-5) from the Global Modeling and Assimilation Office (GMAO) National Aeronautical and Space Administration (NASA), provides hourly and daily data with a spatial resolution of 0.5 × 0.625° from 1980~2023 and passes verification using field-observed data; thus, it is widely used for the estimation of GPP [55,56]. Variables selected from MERRA-2 for the study included Tamin, dew point temperature (Td), average air temperature (Ta), and surface incoming shortwave flux (SSF). Then, these variables were aggregated to an eight-day scale and interpolated to a spatial resolution of 0.05 × 0.05° by the modified cosine function [57], which was effective in eliminating abrupt changes from one side to the other [58]. The VPD (hPa) was calculated based on Td (°C) and Ta (°C):
where SVP is saturated vapor pressure (hPa) and RH is relative humidity [12].
3. Model and Methods
3.1. Two-Leaf Light Use Efficiency Model
The TL-LUE model [4], which is based on the MOD17 GPP model, separates the entire canopy APAR into the APAR of sunlit and shaded leaves using the BEPS model [29], and the estimation of GPP in the model is as follows:
where εmsu and εmsh are the maximum LUE of sunlit and shaded leaves, respectively; APARsu and APARsh are the APAR (MJ m−2 d−1) of sunlit and shaded leaves, respectively; and σ is the scale of environmental stress factors such as air temperature and vapor pressure deficit to the maximum LUE. These parameters are calculated as follows:
where α is the canopy albedo for each vegetation type (Table 1); β is the sun-leaf angle (usually 60°) of the spherical canopy; θ is the solar zenith angle; PARdif, PARdir, and PARdif,u are the PAR of diffuse, direct, and scattering PAR under a canopy, respectively [29]; C represents multiple scattering PAR inside the canopy; LAIsh and LAIsu are the LAI of sunlit and shaded leaves [29], respectively, and the calculation of these parameters is as follows:
where Ω is the estimation of the vegetation CI.
The calculation of σ in Equation (5) is as follows:
where Tamin and VPD are the lowest daily air temperature and vapor pressure deficit, respectively; Tamin_min and VPDmin (Table 1) are the smallest air temperature and vapor pressure deficit, respectively, when photosynthesis decreases to 0; and Tamin_max and VPDmax (Table 1) are the highest air temperature and vapor pressure deficit, respectively, when photosynthesis reaches the strongest level. VPDmax, VPDmin, Tamin_min, and Tamin_max are closely related to vegetation type [36]. In various biomes, f(VPD) and g(Tamin) are the scales of the vapor pressure deficit and the minimum air temperature, respectively, to the maximum LUE, ranging from 0 to 1. The calculation and verification of relative parameters in the TL-LUE model have already been established using observed data from the global flux network [36,59].
3.2. Sensitivity Analysis by SIMLAB
In the LUE models, the accuracy of GPP estimation is affected by the structure of the canopy. The CI is a key parameter for the description of the canopy structure. With the availability of improved global long-term CI products, it is feasible to incorporate the temporal variation in the CI in remote sensing and land surface modeling research in the future [60]. Hence, the seasonal variation in the CI would lead to changes in GPP to some extent. The accuracy of GPP estimation partly depends on the CI, which is why it is important to classify the canopy of vegetation into sunlit and shaded leaves in the TL-LUE model. In this study, due to the mutual influence between various input parameters, the total sensitivity of GPP to the CI was evaluated by the extended Fourier amplitude sensitivity test (EFAST) [61] formed by combining Fourier amplitude sensitivity analysis (FAST) [62] and Sobol [63], and the sensitivity was measured by the variance of GPP outputted from the TL-LUE model caused by the changes in the CI. This sensitivity analysis can be implemented by SIMLab 4.0 software [64]. SIMLAB is a comprehensive stand-alone software for performing the total sensitivity analysis based on Monte Carlo and sampling-based methods. The Joint Research Centre (JRC) of the European Commission has provided financial assistance for the design and enhancements to SIMLAB since its first version was released in 1999. SIMLAB is available for any individual or organization from the website: https://ec.europa.eu/jrc/en/samo/simlab, accessed on 28 May 2023. The sensitivity of the anisotropic flattening index to vegetation parameters in the double canopy reflectance model is analyzed by the EFAST method [65].
3.3. Description of the TL-CLUE Model
The purpose of the study is to improve the accuracy of GPP estimation by considering seasonal differences in the CI (Figure 2), and includes four parts: (1) analysis of seasonal variation in the CI and the total sensitivity of GPP to CI changes based on the TL-LUE model; (2) division of the OYC into different seasons and estimation of the CI in each season; (3) description of seasonal canopy changes depending on the different Ωs of different seasons (TL-CLUE); and (4) evaluation of the performance of the TL-CLUE model at site and spatial scales and exploration of the spatial and temporal pattern of GPP simulation by the TL-CLUE model across North America during 2002~2020.
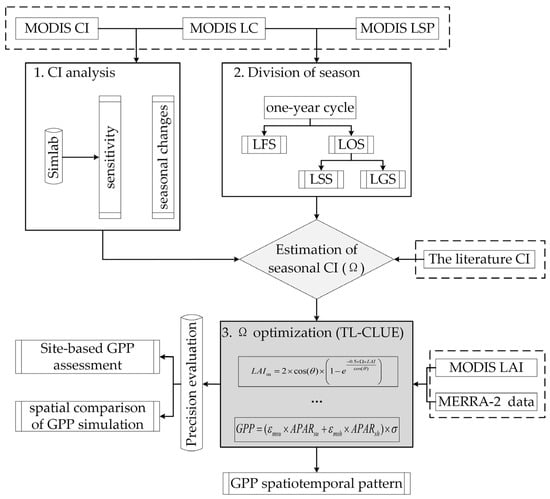
Figure 2.
Flow chart of the improvement of GPP estimation by considering seasonal differences in the CI (TL-CLUE). The total sensitivity of GPP to the CI is explored by the EFAST method. The OYC for leaf growth is divided into LFS and LSS, consisting of LOS and LGS, labeled according to MODIS LC (land cover) data (MCD12Q1.061) and MODIS LSP (land surface phenology) data (MCD12Q2 V061). Then, the corresponding average CI (Ω) of each season for each vegetation type is estimated based on MODIS CI data and published literature.
There is potential for the seasonal differences in the CI to reflect the changes in the vegetation status [32,43,52]. When ignoring the seasonal variability and interannual variation in the CI, the use of only a constant CI over time will lead to larger uncertainties in modeling studies [43]. In this study, it was expected that the uncertainties of GPP estimation would be reduced by replacing the constant Ω currently used in the TL-LUE model with separate Ωs for different seasons (TL-CLUE). The key to the TL-CLUE model is to acquire an appropriate CI value (i.e., Ωi) that not only represents the basic trend of the foliage clumping state within a canopy in different seasons but also reduces the potential uncertainty that is probably caused by the upper-level data products (i.e., MODIS/BRDF) and model inversion. In theory, the constant Ω currently adopted in the TL-LUE model is not consistent with the fact that the CI varies in different seasons. Therefore, it is appropriate to improve the estimation of GPP in the TL-LUE model by updating Equation (8) with different Ωs from different seasons instead of a constant Ω as follows:
where Ωi is the Ω in the ith season (Table 2), and i represents different seasons, including the leaf-on season, leaf-off season, leaf-scattering season, and leaf-gathering season.

Table 2.
The OYC of leaf growth is divided into the LFS and LOS, consisting of the LGS and LSS for different vegetation types, labeled according to the MODIS Land Surface Phenology product (MCD12Q2 V061).
The CI of remote sensing data with a high temporal resolution, such as the daily and eight-day data, currently remains a large uncertainty in the intra-annual changes caused by surrounding and background reflectance changes resulting from various environmental factors, such as brief rainstorms and windstorms. Additionally, although the use of monthly CI data reduces some effects originating from low quality and ephemeral background reflectance, it will make the model complicated to run. Relatively, there are apparent seasonal differences in the CI, with higher values during the dormancy period and lower values during the growing season [42], and the lowest values of the CI occur at the peak of the growing season because the mature dense canopy likely leads to a strong aggregation effect [43]. Therefore, there is a great advantage to using the seasonal Ω values with obvious seasonal differences to improve GPP estimation in the TL-LUE model.
Global land surface phenology (LSP) with a spatial resolution of 500 m from 2001 to 2021 is provided annually by the Terra and Aqua combined Moderate Resolution Imaging Spectroradiometer (MODIS) Land Cover Dynamics (MCD12Q2 V061) Version 6.1 data product. The MODIS LSP product is derived from the time series of the two-band Enhanced Vegetation Index (EVI2) calculated from MODIS Nadir Bidirectional Reflectance Distribution Function (BRDF)-Adjusted Reflectance (NBAR). EVI2 with no blue band was developed in 2008 [66] and is less susceptible to atmospheric interference, such as aerosols and clouds than some other vegetation indices. Previous studies confirmed that the MODIS LSP product has an excellent performance in monitoring land surface phenology [67,68], so has been widely used for various direct or indirect studies relative to phenology. In addition, the MODIS LSP phenology has the same spatial resolution as the MOIS CI, which is useful for matching spatial characteristics. Therefore, the OYC was divided into a leaf-off season (before Greenup and after Dormancy), leaf-on season (from Greenup to Dormancy), leaf-scattering season (from Greenup to MidGreenup and from MidGreendown to Dormancy), and leaf-gathering season (from MidGreenup to MidGreendown (Table 2) according to these four threshold dates from the MODIS LSP data.
Then, the Ωs values of these different seasons for each vegetation type were determined by synthesizing the MODIS CI and some of the published literature on the CI [32,42,43,51,52] (Table 3). These Ωs in the different seasons for different vegetation types were consistent with those of previous studies and realities.

Table 3.
CI estimation of the different seasons in Table 2 for each vegetation type. Ω is excessively higher in the LFS than in the LOS, and the lowest Ω occurs in the LGS, which is slightly lower than that in the LSS.
To explore seasonal changes (g C m−2 d−1) and annual spatial characteristics (g C m−2 yr−1) of GPP across the North American continent, the eight-day GPP from 2002 to 2020 was simulated by the TL-CLUE model.
3.4. Model Evaluation Metrics
The accuracy of the eight-day GPP estimation was assessed against 84 EC flux sites in the OYC, LOS, LSS, LGS, and LFS. The difference in GPP simulation between the TL-CLUE model and the TL-LUE model was explored in terms of spatial heterogeneity and seasonal change. Additionally, the accuracy of GPP estimation in the TL-LUE and TL-CLUE models was evaluated by root mean square error (RMSE) (Equation (14)), Bias (Equation (15)), relative to the mean predictive Bias (Rbias) (Equation (16)), and coefficient of determination (R2) (Equation (17)) as follows:
where vo, vm, i, and n are the observed value, estimated value, value ordinal number, and sample size, respectively.
4. Results
4.1. Changes in GPP and CI in Different Vegetation Types
4.1.1. Eight-Day Changes in GPP
GPP exhibited seasonal changes for each vegetation type (Figure 3). The beginning date of the apparent increase in GPP was approximately on the 73rd~97th day for DBF, MF, OSH, CRO, GRA, and SAV, the 65th day for ENF, and the 33rd day for WSA. In contrast, the end date of the visible decrease in GPP was on the 281st~305th day for DBF, ENF, MF, OSH, CRO, and GRA, the 321st day for WSA, and the 249th day for SAV (Figure 3). The GPP of most vegetation was near 0 in the leaf-off season (Figure 3). The GPP showed a yearly trend of increasing to decreasing, and the peak GPP that occurred around July (Figure 3) was 11.93 for DBF, 7.01 for ENF, 8.85 for MF, 3.13 for OSH, 9.77 for CRO, 3.73 for GRA, 4.48 for WSA, and 11.62 g C m−2 d−1 for SVA. In the leaf-on season, the TL-LUE model widely overestimated GPP (Figure 3), particularly in the leaf-gathering season, of which the average overestimation of GPP was 1.72 for DBF, 3.41 for ENF, 5.70 for MF, 2.37 for OSH, 3.78 for CRO, 1.67 for GRA, 1.33 for WSA, and 2.31 g C m−2 d−1 for SAV.
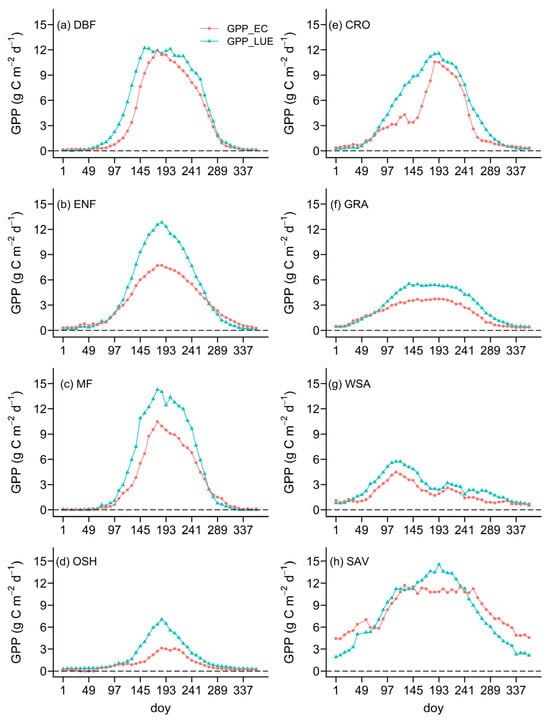
Figure 3.
Comparison of the eight-day change in GPP (red point line) observed at the EC site with GPP (deep green point line) estimated by the TL-LUE model for DBF (a): deciduous broadleaf forest, ENF (b): evergreen needleleaf forest, MF (c): mixed forest, OSH (d): open shrublands, CRO (e): croplands, GRA (f): grasslands, WSA (g): woody savannas, SAV (h): savannas during 2002~2020, respectively. There is an evident overestimation of GPP in the TL-LUE model, particularly in the growing peak, by approximately 5.70 for MF, 3.78 for OSH, and 2.37 g C m−2 d−1 for CRO.
4.1.2. Sensitivity of GPP to CI of Different Vegetation Types
CI presented similar seasonal variation characteristics in that its value was widely lower in the LOS than in the leaf-off season, but its uncertainty (measured by SD) should not be ignored (Figure 4). The highest CI values that occurred in the leaf-off season were approximately 0.72~0.78 for DBF, MF, and OSH, 0.63 for ENF, and 0.82~0.86 for CRO, GRA, WSA, and SAV. In the leaf-off season, the CI uncertainty quantified by SD was approximately 0.055~0.077 for CRO, DBF, GRA, OSH, and WSA, 0.02~0.03 for MF and SAV, and 0.078 for ENF (Figure 4). In the leaf-off season, the lowest CI of 0.63 with a response uncertainty of 0.078 occurred in ENF, but the highest CI of 0.86 occurred in CRO (Figure 3). The constant Ω that is currently used in the TL-LUE model was near the CI in the leaf-off season but significantly higher than that in the leaf-on season, which led to GPP overestimation in the leaf-on season. The CI decreased from the end of the leaf-off season until it was reduced to the lowest CI around the leaf-gathering season (Figure 4), and the lowest CI and its uncertainty represented by SD were 0.64 (0.084) for DBF, 0.53 (0.087) for ENF, 0.57 (0.084) for MF, 0.68 (0.066) for OSH, 0.76 (0.071) for CRO, 0.73 (0.074) for GRA, 0.72 (0.072) for WSA and 0.68 (0.056) for SAV (Figure 4). The large uncertainty of the CI, as measured by SD, led to a wide fluctuation of the eight-day GPP estimation in the leaf-on season. For the OYC, the greatest difference in the CI between the LFS and LOS ranged from approximately 0.068 to 0.12 in CRO, DBF, ENF, GRA, and WSA, and the uncertainty denoted by SD ranged from approximately 0.065 to 0.082 (Figure 4), which implied that the temporal variation features of the eight-day CI were likely disturbed by the large uncertainty measured by SD.
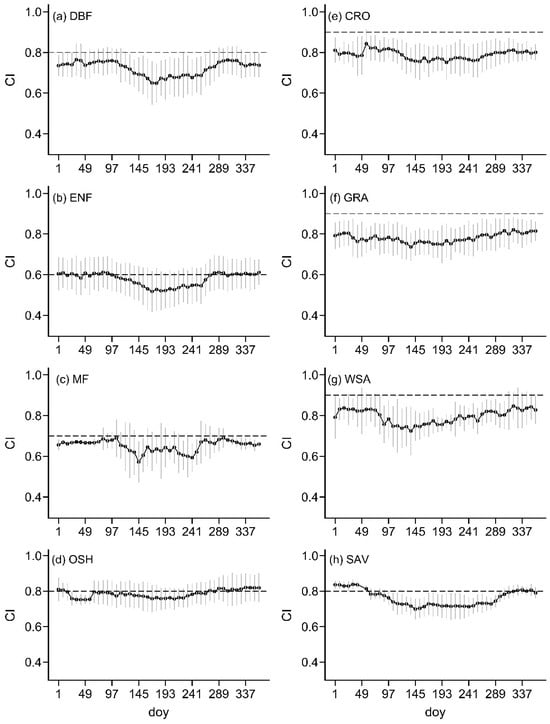
Figure 4.
Eight-day changes in the mean CI (black point line) for different vegetation types during 2002~2020. The gray solid vertical line represents the uncertainty of the CI, as measured by the standard deviation (SD), the black dashed line is the default of Ω currently used in the TL-LUE model, and the black dots are eight-day CI mean in each vegetation type by averaging CI values from 2002 to 2020 in all sites extracted from the MODIS CI. This figure shows that although the eight-day average CIs capture general seasonal trends for some vegetation classes, some large uncertainties exist due to the changes in the background and ambient reflectivity, abnormal land surface shadows, insufficient BRDF information, and even some systematic vibrations that cannot be well understood in some classes, e.g., approximately from 0.016 to 0.161 for MF, from 0.032 to 0.132 for WSA, and from 0.048 to 0.093 for GRA.
The total sensitivity of GPP to CI was quantified by the variance of the GPP estimation from the TL-LUE model caused by the changes in CI, and this sensitivity could be implemented by the SIMLAB software. There was an obvious sensitivity of the GPP estimated by the TL-LUE model to the CI (>0.7) (Figure 5). The total sensitivity of GPP to CI was 0.85~0.88 for DBF, MF, CRO, and OSH and 0.73~0.80 for WSA, SAV, GRA, and ENF (Figure 5), of which the largest sensitivity (0.88) was in DBF and the smallest was in WSA (0.73). The analysis of the sensitivity of GPP to the CI revealed that CI played an important role in the estimation of GPP from the TL-LUE model.
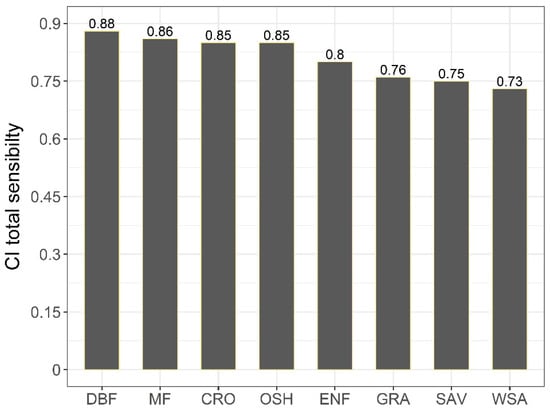
Figure 5.
The total sensitivity of the eight-day GPP to the CI in different vegetation types. This total sensitivity is more than 0.72 for various vegetation types in the figure, which indicates that changes in the CI would affect the magnitude of GPP to some extent.
4.2. Evaluation of GPP Estimated by the TL-CLUE Model
4.2.1. Verification of GPP Estimation against Sites
The result of GPP estimated by the TL-CLUE model (Bias = 1.04, RMSE = 2.26 g C m−2 d−1) was better than that (Bias = 1.31, RMSE = 2.53 g C m−2 d−1) estimated by the TL-LUE model (Table 4). Compared to the RMSE of the TL-LUE model, the RMSE of the TL-CLUE model decreased by 6.75~15.25% in different vegetation types (Table 4), particularly in the WSA (15.17%). The Bias values of the TL-LUE model were 1.11~1.14 for DBF and OSH, 1.30 for CRO, ENF, MF, and SVA, and 0.75~0.91 g C m−2 d−1 for WSA and GRA (Table 4), indicating that GPP was generally overestimated by the TL-LUE model. Relatively, the Bias value of the TL-CLUE model was 0.80~0.96 for DBF and OSH, 0.65~1.95 for CRO, ENF, MF, and SVA, and 0.56~0.65 g C m−2 d−1 for WSA and GRA (Table 4). These results illustrate that the uncertainty of GPP estimation in the TL-CLUE model was approximately 12% lower than this uncertainty in the TL-LUE model.

Table 4.
Accuracy of eight-day GPP estimated by the TL-CLUE and TL-LUE models for different vegetation types. The uncertainty of the eight-day GPP estimation quantified by RMSE (g C m−2 d−1) and Bias (g C m−2 d−1) in the TL-CLUE model is lower than that in the TL-LUE model. In terms of overall vegetation, the accuracy of the eight-day GPP estimation is increased by approximately 9.76% by considering the seasonal difference in the CI in the TL-CLUE model.
The consistency of the observed GPP with the GPP estimated by the TL-CLUE model (a) and TL-LUE model (b) was shown in the leaf-on season (Figure 6a1,b1), leaf-scattering season (Figure 6a3,b3), leaf-gathering season (Figure 6a2,b2), leaf-off season (Figure 6a4,b4), and OYC (Figure 6a5,b5). Regardless of the period, the regression line of the TL-CLUE model was closer to the 1:1 theory line than the line of the TL-LUE model. The consistency between the estimated GPP and the observed GPP was best in the OYC (Figure 6a5,b5), followed by the LSS (Figure 6a3,b3), and it was worst in the leaf-off season (Figure 6a4,b4). The RMSE of the TL-CLUE model was lower than that of the TL-LUE model by 10.75, 11.9, 8, 1.08, and 10.55% in the leaf-on season, leaf-gathering season, leaf-scattering season, leaf-off season, and OYC, respectively. The uncertainty of GPP estimation from the TL-CLUE model was lower than the uncertainty of the TL-LUE model. The RMSE relying on the TL-CLUE model was reduced by approximately 12, 8, and 10.7% for the leaf-gathering season, leaf-scattering season, and leaf-on season, respectively (Figure 6). The difference in Bias between the TL-CLUE model and TL-LUE model was approximately −0.68, −0.26, and −0.49 g C m−2 d−1 for the leaf-gathering season, leaf-scattering season, and leaf-on season, respectively (Figure 6). The improvement of GPP estimation in the TL-CLUE model in the leaf-on season was higher than that in the leaf-gathering season, but lower than that in the leaf-scattering season. The error of GPP estimation from the TL-CLUE model in the OYC (Bias = 0.83 g C m−2 d−1) was higher than that in the leaf-off season (Bias = −0.16 g C m−2 d−1) but lower than the error in the leaf-on season (Bias = 1.37 g C m−2 d−1), revealing that the uncertainty of GPP estimation in the whole year was mainly due to that in the leaf-on season. The Bias difference between the TL-CLUE model and TL-LUE model was 0.49 and 0.31 g C m−2 d−1 in the leaf-on season and OYC, respectively, which indicated that the TL-CLUE model reduced the error of GPP estimations. Overall, the TL-CLUE model improved the accuracy of GPP estimation to some extent, particularly in the leaf-on season, which is critical for the improvement of GPP estimation on the annual scale.
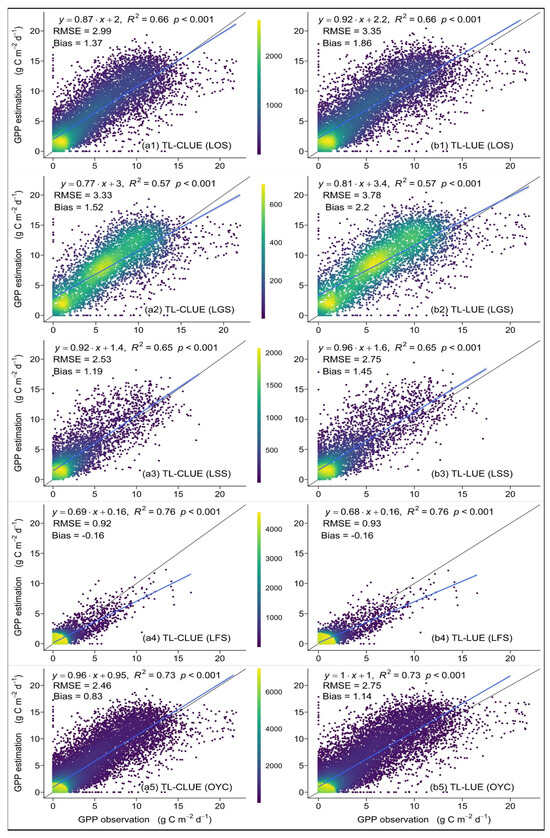
Figure 6.
Comparison of the consistency of the observed GPP with GPP estimated by the TL-CLUE (a1–a5) and TL-LUE (b1–b5) models in the LOS (a1,b1), LGS (a2,b2), LSS (a3,b3), LFS (a4,b4), and OYC (a5,b5), respectively. The 1:1 theory line is shown by the black dashed line, and the regression line is displayed by the blue dashed line.
4.2.2. Accuracy of GPP Estimation under Three and Two Estimations of CI
The TL-CLUE model can decrease the relative bias of GPP estimation. When the TL-CLUE model used three Ωs, the relative bias of GPP estimation was approximately 1.71 for SAV, 7.09 for EBF, 7.70 for MF, 9.47 for ENF, 10.50 for WSA, 12.66 for GRA, 13.77 for CRO, and 15.18% for OSH (Figure 7). Throughout all vegetation types, three and two Ωs reduced the relative bias of GPP estimation by approximately 9.76 and 8.97%, respectively (Figure 7), indicating that the improvement in GPP estimation in the TL-CLUE model relying on two Ωs was nearly as good as the improvement depending on three Ωs. Therefore, we recommend using two Ωs from the leaf-on and leaf-off seasons to optimize the constant Ω that is currently used in the TL-LUE model.
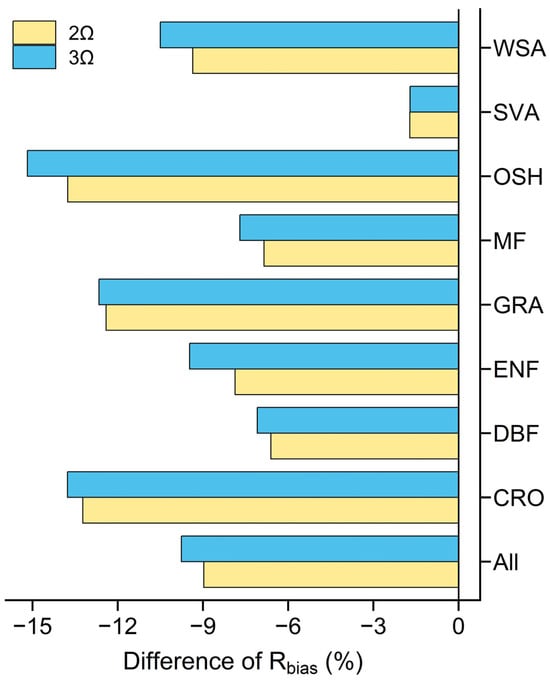
Figure 7.
Rbias difference of eight-day GPP estimation between the TL-CLUE model and the TL-LUE model. The TL-CLUE model adopts 2 (yellow par) and 3 (light blue par) Ωs from different seasons.
4.3. Spatial and Temporal Patterns of GPP across North America
4.3.1. GPP Difference between the TL-CLUE and TL-LUE Models
In the leaf-on season, the difference in GPP simulation between the TL-CLUE model and the TL-LUE model was less than 0 on the entire North American continent (Figure 8a), indicating that the TL-CLUE model can decrease GPP overestimation. The difference was approximately −50~0 g C m−2 yr−1 in the Rocky Mountains and in high latitude regions north of 55°N (Figure 8a). With decreasing latitude and elevation, the difference increased to −100~−50 g C m−2 yr−1 in the central and eastern regions between 30 and 50°N. The difference was only −200 g C m−2 yr−1 less than that in coastal areas south of 30°N (Figure 8a). The spatial difference in GPP simulation showed that the reduction in the error of GPP simulation from the TL-CLUE model exhibited definite spatial heterogeneity in the leaf-on season.
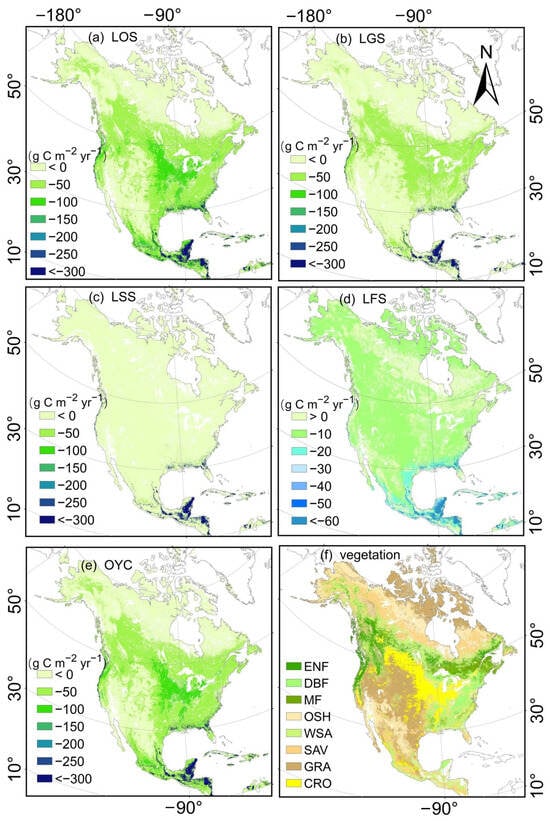
Figure 8.
The spatial difference in GPP simulation between the TL-CLUE and TL-LUE models in the leaf-on season (a), leaf-gathering season (b), leaf-scattering season (c), leaf-off season (d), and one-year cycle (e) in different vegetation types (f) obtained from the MODIS Year Land Cover (MCD12Q1.061) across North America during 2002~2020. The magnitude and spatial characteristics of the difference in GPP simulation between the TL-CLUE and TL-LUE models in the leaf-on season are similar to those in the OYC for most areas of North America. The difference is less than 0, approximately from −100 to 0 g C m−2 yr−1, in the leaf-on season and OYC across North America.
In the leaf-gathering and leaf-scattering seasons, the differences in GPP simulation between the TL-CLUE model and the TL-LUE model were less than those in the leaf-on season. Even this difference ranged from −50 to 0 g C m−2 yr−1 across most of North America in the leaf-scattering season (Figure 8c). In the leaf-gathering season, this difference could be roughly classified into two areas in North America: ranging from −50 to 0 g C m−2 yr−1 in the Rocky Mountains and the north of 52°N regions and ranging from −100 to −50 g C m−2 yr−1 in the others (Figure 8b). These results indicate that the spatial heterogeneity of GPP simulation in the TL-CLUE model is similar to that in the TL-LUE model in the leaf-gathering and leaf-scattering seasons, particularly with the term of the leaf-scattering season.
In the leaf-off season, the above difference values were 10 g C m−2 yr−1 within most of North America (Figure 8d). The difference was only greater than 0 for SAV, MF, and other special regions (Figure 8d,f), which is attributed to the fact that the real CI is higher than the default CI currently used in the TL-LUE model in these regions. The difference was −10~0 g C m−2 yr−1 in the majority of areas other than SAV and lower than that in the eastern coastal belt south of 35°N (Figure 8d).
For the OYC, the difference in the yearly GPP simulation between the TL-CLUE model and the TL-LUE model showed great spatial heterogeneity. The difference was approximately −150~−100 g C m−2 yr−1 in the central regions from 30~50°N (Figure 8e) and −100~−50 g C m−2 yr−1 in low-latitude and low-elevation regions, mainly including the eastern and central regions and some northwestern areas north of 50°N (Figure 8e). The difference was approximately −30 g C m−2 yr−1 in the Rocky Mountains, on the Labrador Plateau, and the high-latitude regions north of 55°N and less than −200 g C m−2 yr−1 only on the east coast south of 35°N (Figure 8e). The difference was approximately −100~0 g C m−2 yr−1 and exhibited obvious latitudinal zonality in most of North America.
4.3.2. Spatial Characteristics of Seasonal GPP Simulation in the TL-CLUE Model
Across North America, GPP showed obvious spatial heterogeneity and seasonal differences (Figure 9a). In the leaf-on season, GPP was approximately 0 north of 60°N, increasing to 800~1200 g C m−2 yr−1 at 40~50°N, and increasing to the largest value of 1600~2400 g C m−2 yr−1 south of 40°N. This result indicates that GPP increases with decreasing latitude. GPP was less than 800 g C m−2 yr−1 west of 100°W, 800~2400 g C m−2 yr−1 east of 100°W, and below 400 g C m−2 yr−1 in the Rocky Mountains and on the Labrador Plateau east of Hudson Bay (Figure 9a). However, values of 800~2400 g C m−2 yr−1 appeared in the middle and eastern regions, which are mainly composed of plains and mountains. While the spatial patterns of GPP during the leaf-gathering season were comparable to those during the leaf-on season, the magnitude was significantly lower, especially in the eastern coastal regions south of 50°N with a range of 800 to 1200 g C m−2 yr−1 (Figure 9c). However, during the leaf-scattering season, GPP ranged from 0 to 400 g C m−2 yr−1 over most of North America, and only in the eastern coastal regions south of 40°N did it rise to approximately 700 g C m−2 yr−1 (Figure 9d). These findings suggest that the contribution of the leaf-gathering season to GPP is more than that of the leaf-scattering season. In summary, the spatial characteristics of GPP across North America were largely determined by latitude, longitude, and terrain. In the leaf-off season, GPP was approximately 0 in the main areas across North America (Figure 9b) and 400~900 g C m−2 yr−1 only in coastal areas south of 35°N.
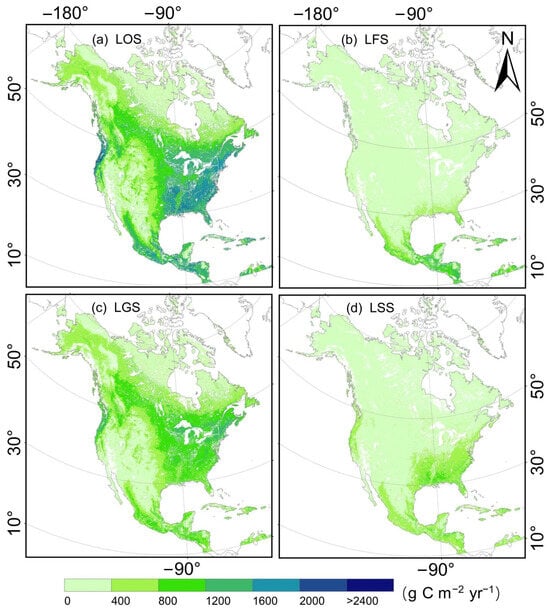
Figure 9.
The spatial characteristics of GPP simulated by the TL-CLUE model in the leaf-on season (a), leaf-gathering season (b), leaf-scattering season (c), and leaf-off season (d) across North America during 2002~2020. GPP in the leaf-on season shows obvious spatial heterogeneity; the lowest value, ranging from approximately 0 to 400 g C m−2 yr−1, occurs in the high elevation areas of the Rocky Mountains and high latitude areas north of 52°N, and the highest value, ranging from approximately 1800 to 2200 g C m−2 yr−1, occurs on the east coast south of 48°N. GPP is near 0 in the leaf-off season for most areas of North America.
Throughout the year, the spatial pattern of GPP was similar to this pattern in the leaf-on season (Figure 10). GPP was less than 700 g C m−2 yr−1 on the Labrador Plateau, the Rocky Mountains, and north of 60°N, 700~2000 g C m−2 yr−1 at 45~60°N, and 2000~3200 g C m−2 yr−1 in the middle and eastern areas and coastal areas at lower latitudes (Figure 10), which reveals that latitude and elevation are the key factors for the spatial pattern of GPP across North America.
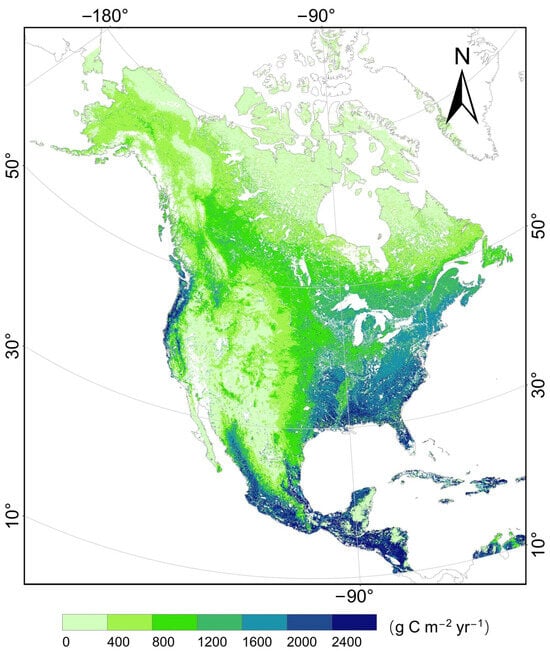
Figure 10.
The annual spatial pattern of GPP simulated by the TL-CLUE model across North America during 2002~2020. The magnitude and spatial patterns of the annual GPP are close to those of the leaf-on season shown in Figure 9a, which could be attributed to the fact that GPP is mainly generated by vegetation in the leaf-on season.
5. Discussion
Recently, the majority of land surface models (LSM) have adopted the different photosynthesis rates of sunlit and shaded leaves to improve GPP estimation [69,70,71]. Previous studies have reported that there is an obvious seasonal difference in CI, with higher values during the leaf-off season and lower values during the leaf-on season, particularly for DBF and MF [42]. The seasonal changes in CI have the potential to reflect the variation of the vegetation canopy [32,43,52]. Unfortunately, numerous LSMs only use the simple climatology CI [72,73], which most likely leads to uncertainties in GPP modeling. With the improvement of long-term global CI products, it is feasible to incorporate the temporal variation of CI into the study of remote sensing and land surface simulation [60].
The MODIS LSP product is widely used for the studies of the seasonal patterns and interannual variations of global land surface [68], and contains seven vegetation phenology metrics determined by the EVI2, of which the Greenup, MidGreenup, MidGreenup, and Dormancy are used for dividing the one-year cycle of leaf growth into two or three seasons in the study. The Enhanced Vegetation Index 2 (EVI2) is a vegetation index derived from remote sensing data, often satellite imagery, used to monitor and assess the health and growth of vegetation, particularly with respect to phenological events. In the MODIS LSP product, Greenup is the Date when EVI2 first crossed 15% of the segment EVI2 amplitude, meaning vegetation begins to turn green and leaves begin to grow. Therefore, it is rational that Greenup acted as the start date of the leaf-on season in this study. However, vegetation indices retrieved from remote sensing data do not always directly reflect the physiological processes of vegetation [74], and variations of vegetation structures are not immediately detected by relative vegetation indices. Therefore, it was a clever strategy to select MidGreenup from the MODIS LSP product as the start date of the leaf-gathering season instead of Maturity in this study. Previous studies have revealed that leaves generally reach the clumping state first, but the leaf greenness, represented by chlorophyll concentration, gradually increases [75,76]. The corresponding Ωs in different seasons are estimated based on the MODIS CI with the long temporal resolution by averaging. Compared to the CI with shorter temporal resolutions such as daily and eight-day, CI with the longer temporal resolution decreases to some extent the influences of low-quality data and fugacious changes in ambient reflectance such as rainstorms by averaging, which offers relatively reasonable CI to zonal and global simulation of ecology and meteorology CI [42], even though some useful information may be lost along with noise in the process of CI averaging.
Numerous factors affect the seasonal patterns of the CI. For instance, snow cover decreases the accuracy of CI retrievals by the main algorithm, resulting in a noticeably higher CI in snow-covered areas than in snow-free areas, with an average CI bias of ~0.13 for needleleaf forests and ~0.32 for the other vegetation types [77]. Therefore, it is suggested that CI values determined through quality screening and averaging should be used to more accurately characterize the seasonal change in surface CI, even though the consistency of C6 CI data retrieved from MODIS BRDF (MCD43 V006) (R2 = 0.89, RMSE = 0.05, bias = 0.02) with field measurement is better than that of C5 CI data retrieved from MODIS BRDF (MCD43 V005) (R2 = 0.80, RMSE = 0.07, bias = 0.03) [42].
Although the MODIS CI applied in the study is extremely improved, with very little extreme outlier value relative to other CI products, by the hotspot-adjusted model and a backup algorithm [47], the CI data retrieved from remote sensing directional observations tend to remain highly uncertain. First, the use of BRDF information, particularly reconstructed BRDF information, is insufficient in the inversion of key land surface parameters of the carbon cycle and energy balance due to an incomplete viewing angle, which poses a large challenge for the precise retrieval of CI based on the linear relationship between the CI and NDHD. Furthermore, CI data with a vast spatial range retrieved from remote sensing are more susceptible to changes in ambient and background reflectivity in theory [32]. For example, high soil moisture leads to diminished soil reflectance in the red band, and vegetation growth below the forest further reduces the total background reflectance of the red band just after the start of the rainy season in sparse sites [78]. The daily CI in the ENF and MF shows a short increase during August and September in southeastern North America. These short-term fluctuations could be attributed to the local tropical storm that affected the retrieval values of the main algorithm by destroying the canopy and disturbing the background reflectance [79,80]. Another source of uncertainty is the abnormal land surface shadow caused by landscape relief [81,82]. Additionally, there is a difference in scattering characteristics and distribution structures for heterogeneous cells with different land cover types, which would introduce some uncertainties to the linear extension of BRDF in space [83,84]. To better understand the structure and temporal variation in global vegetation [43], further studies are required to reduce the retrieval uncertainties of the eight-day CI, especially from the trajectory of daily BRDF.
The results of the sensitivity analysis demonstrate that there is an obvious influence of the CI on the estimation of GPP. In this study, eight-day GPP overestimation could be reduced by 8.97 and 9.76% in the TL-CLUE model depending on two and three Ωs from different seasons, which may be attributed to the fact that the estimation of seasonal CI would smooth the fluctuation resulting from the low-quality data and short-term variations in background reflectance by quality screening and averaging. It can therefore be suggested that the seasonal Ω can provide relatively credible information on the CI seasonal changes for ecological and meteorological modeling at global or regional scales. Additionally, the CI is a vital parameter to estimate LAI, of which seasonal change is a key factor in controlling the GPP of vegetation [85]. The study found that the TL-LUE model generally overestimated the GPP for each vegetation type, which might be explained by the fact that the Ω that is presently used in the TL-LUE model is far greater than the actual CI of the vegetation, which leads to a much higher GPP estimation of sunlit leaves with a higher CI than the GPP estimation of shaded leaves with a lower CI, particularly during peak vegetation growth. When other conditions remain unchanged, the higher the Ω is, the more scattering leaves will lead to the absorption of more radiation and a larger LUE [86]; thus, vegetation can transfer more solar energy to generate more GPP.
There is an apparent seasonal difference in CI, with lower values in the leaf-on season than in the leaf-off season, which is in agreement with previous studies of field measurements [87,88,89] and remote sensing estimations at regional scales [32,90]. This study is in accord with previous research that found a larger CI in the growing season and a smaller CI in the dormancy season. Moreover, the seasonal difference in CI is also caused by canopy cover and arrangement, vegetation under the trees, and background reflectance [32,42,43]. Among all vegetation types, ENF has the lowest CI, with 0.63 in the leaf-off season and 0.52 in the leaf-on season, which is consistent with a previous study that reported that needleleaf forests have an extremely gathered canopy (0.5 < Ω < 0.7) [91]. Seasonal differences in CI can reflect changes in the canopy structure of deciduous vegetation types [42,43]. An interesting finding is that the improvement of the estimated GPP depending on two Ωs (8.97%) of the leaf-on season and the leaf-off season is nearly as high as the estimated GPP that relies on 3 Ωs (9.76%) of the leaf-scattering, leaf-gathering, and leaf-off seasons, which may be explained by the small difference in the CI between the leaf-gathering and leaf-scattering seasons. The appearance of a canopy has already been formed in the early stage of vegetation growth due to the rapid leaf growth. Therefore, the CI only exhibits slight changes in most of the leaf-on season after the completion of leaf growth.
The error of GPP estimation at a certain degree is decreased by two or three Ωs from different seasons instead of by only Ω in the TL-LUE model. The current MODIS CI values retrieved from the MODIS BRDF product (MCD43 V006) released in 2016 with a higher temporal resolution, such as the eight-day dataset, exhibits a large uncertainty, as measured by SD, in intra-annual variation (Figure 4), which likely contributes to uncertainties in GPP estimation. The accuracy of GPP estimation improved by the eight-day CI in the TL-LUE model is limited, and even less than that is improved by the Ωs in different seasons, although this result is not presented in the study due to space constraints. Hence, to better understand the structure and temporal variation in global vegetation [43], further studies are required to reduce the retrieval uncertainties of the eight-day CI, especially from the trajectory of daily BRDF. In addition, further research is needed to explore the effects of other significant parameters, such as vegetation albedo and LUE, on the estimation of GPP. The LUE, including Ɛmax, Ɛmsu, and Ɛmsh, is variable with diffuse PAR rather than the constant used in the TL-LUE model [92]. The photochemical reflectance index (PRI), solar-induced chlorophyll fluorescence (SIF), and near-infrared reflectance of terrestrial vegetation (NIRv) that appeared in recent decades have great potential to advance LUE models and improve GPP estimation. For example, the combination of PRI and SIF has been able to enhance the accuracy of GPP estimation [93]. Additionally, considering other key environmental stress factors, especially plant available water, would decrease the uncertainty of GPP estimation for LUE models. Several recently published studies explored the influence of various environmental stress factors on GPP estimation in LUE models. For instance, a previous study reported that soil temperature and soil water are the main control factors for vegetation GPP in cold and dry regions, respectively [86]. Another study found that a complex adjustment mechanism results in a nonlinear response of vegetation to VPD [86]. A published study improved the accuracy of global GPP estimation by considering the fertilization of CO2 in an LUE model [12]. Integrating multiple environmental stress factors is expected to improve the estimation of GPP. Although EC flux data are widely used as benchmark data, GPP is influenced by various systematic and random errors, such as instrument failure, the subpar filter method, and the split GPP approach lacking sufficient accuracy from NEE. Therefore, further improvement of the quality of EC flux data is necessary to more precisely estimate GPP.
6. Conclusions
In this study, we attempted to decrease the uncertainty of the GPP estimation of the TL-LUE model by considering the seasonal differences in CI (TL-CLUE). The TL-CLUE model depends on different Ωs values from different seasons to adjust the distribution of APAR between sunlit leaves and shaded leaves among different seasons. Although the GPP estimations from the TL-LUE and TL-CLUE models are both in line with the observed GPP at EC flux sites, the regression analysis shows that the fluctuation in GPP estimation from the TL-CLUE model (RMSE = 2.46 g C m−2 d−1) is lower than that from the TL-LUE model (RMSE = 2.75 g C m−2 d−1). When three and two Ωs from different seasons are used in the TL-CLUE model, the eight-day GPP overestimation could be reduced by approximately 9.76 and 8.97%, respectively, of which two Ωs from the leaf-off and leaf-on seasons are recommended to optimize the TL-LUE model out of consideration for shrinking computing costs and simplifying the model. We anticipate that the proposed method will be incorporated into the MODIS GPP algorithms to improve GPP estimation in the future. The result of the GPP simulation shows that GPP has an obvious seasonal difference, with much larger GPP in the leaf-on season than in the leaf-off season, and spatial heterogeneity, with GPP increases with decreasing latitude and elevation across North America. Greater efforts and challenges are needed to enhance the quality of the CI, particularly at higher temporal scales such as weekly and daily relative to monthly. Future research is required to better understand the role that other key parameters of the TL-LUE model, such as the maximum LUE, play in the estimation of GPP.
Author Contributions
Conceptualization, Z.L. and Z.J.; Data curation, Z.L., C.W. and J.G.; Formal analysis, Z.L. and G.G.; Funding acquisition, Z.J.; Methodology, Z.L., Z.J. and C.W.; Software, Z.L.; Supervision, Y.T. and S.C.; Validation, Z.L. and S.Y.; Visualization, Z.L. and Z.T.; Writing—original draft, Z.L.; Writing—review & editing, Z.J., C.W. and J.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Major Program of the Natural Science Foundation of China (42090013) and the General Program of the Natural Science Foundation of China (41971288).
Data Availability Statement
The FLUXNET2015 dataset and AmeriFlux dataset can be downloaded from https://fluxnet.org/data/download-data/, accessed on 17 May 2023 and https://AmeriFlux.lbl.gov/data/download-data/, accessed on 17 May 2023, respectively. Both MODIS Year Land Cover, land surface phenology, and eight-day leaf area index with 500 m of the spatial resolution can be downloaded from https://lpdaac.usgs.gov/product_search/?view=cards&sort=title, accessed on 20 May 2023. Meteorological data from NASA MERRA-2 can be downloaded from https://disc.gsfc.nasa.gov/, accessed on 20 May 2023.
Acknowledgments
The analysis data for this study includes FLUXNET2015 and AmeriFlux datasets, MODIS products, and NASA MERRA-2 data. We Sincerely appreciate contributors to these data. We thank Xiang Zhao for generously sharing this MERRA-2 data. We are grateful for the insight criticism and suggestions from all anonymous reviewers and the editor.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Chapin, F.S.; Matson, P.A.; Mooney, H.A.; Vitousek, P.M. Principles of Terrestrial Ecosystem Ecology; Springer: New York, NY, USA, 2002; pp. 3–22. ISBN 978-971-4419-9504-4419. [Google Scholar]
- Friedlingstein, P.; Jones, M.W.; O’sullivan, M.; Andrew, R.M.; Hauck, J.; Peters, G.P.; Peters, W.; Pongratz, J.; Sitch, S.; Le Quéré, C. Global carbon budget 2019. Earth Syst. Sci. Data 2019, 11, 1783–1838. [Google Scholar] [CrossRef]
- Beer, C.; Reichstein, M.; Tomelleri, E.; Ciais, P.; Jung, M.; Carvalhais, N.; Rödenbeck, C.; Arain, M.A.; Baldocchi, D.; Bonan, G.B. Terrestrial gross carbon dioxide uptake: Global distribution and covariation with climate. Science 2010, 329, 834–838. [Google Scholar] [CrossRef]
- He, M.; Ju, W.; Zhou, Y.; Chen, J.; He, H.; Wang, S.; Wang, H.; Guan, D.; Yan, J.; Li, Y. Development of a two-leaf light use efficiency model for improving the calculation of terrestrial gross primary productivity. Agric. For. Meteorol. 2013, 173, 28–39. [Google Scholar] [CrossRef]
- Hilton, T.W.; Whelan, M.E.; Zumkehr, A.; Kulkarni, S.; Berry, J.A.; Baker, I.T.; Montzka, S.A.; Sweeney, C.; Miller, B.R.; Elliott Campbell, J. Peak growing season gross uptake of carbon in North America is largest in the Midwest USA. Nat. Clim. Chang. 2017, 7, 450–454. [Google Scholar] [CrossRef]
- Chang, J.; Ciais, P.; Wang, X.; Piao, S.; Asrar, G.; Betts, R.; Chevallier, F.; Dury, M.; François, L.; Frieler, K. Benchmarking carbon fluxes of the ISIMIP2a biome models. Environ. Res. Lett. 2017, 12, 045002. [Google Scholar] [CrossRef]
- Ito, A.; Nishina, K.; Reyer, C.P.; François, L.; Henrot, A.-J.; Munhoven, G.; Jacquemin, I.; Tian, H.; Yang, J.; Pan, S. Photosynthetic productivity and its efficiencies in ISIMIP2a biome models: Benchmarking for impact assessment studies. Environ. Res. Lett. 2017, 12, 085001. [Google Scholar] [CrossRef]
- Monteith, J.L. Solar radiation and productivity in tropical ecosystems. J. Appl. Ecol. 1972, 9, 747–766. [Google Scholar] [CrossRef]
- Potter, C.S.; Randerson, J.T.; Field, C.B.; Matson, P.A.; Vitousek, P.M.; Mooney, H.A.; Klooster, S.A. Terrestrial ecosystem production: A process model based on global satellite and surface data. Glob. Biogeochem. Cycles 1993, 7, 811–841. [Google Scholar] [CrossRef]
- Xiao, X.; Hollinger, D.; Aber, J.; Goltz, M.; Davidson, E.A.; Zhang, Q.; Moore III, B. Satellite-based modeling of gross primary production in an evergreen needleleaf forest. Remote Sens. Environ. 2004, 89, 519–534. [Google Scholar] [CrossRef]
- Guan, X.; Chen, J.M.; Shen, H.; Xie, X. A modified two-leaf light use efficiency model for improving the simulation of GPP using a radiation scalar. Agric. For. Meteorol. 2021, 307, 108546. [Google Scholar] [CrossRef]
- Zheng, Y.; Shen, R.; Wang, Y.; Li, X.; Liu, S.; Liang, S.; Chen, J.M.; Ju, W.; Zhang, L.; Yuan, W. Improved estimate of global gross primary production for reproducing its long-term variation, 1982–2017. Earth Syst. Sci. Data 2020, 12, 2725–2746. [Google Scholar] [CrossRef]
- Marshall, M.; Tu, K.; Brown, J. Optimizing a remote sensing production efficiency model for macro-scale GPP and yield estimation in agroecosystems. Remote Sens. Environ. 2018, 217, 258–271. [Google Scholar] [CrossRef]
- Guan, X.; Shen, H.; Li, X.; Gan, W.; Zhang, L. A long-term and comprehensive assessment of the urbanization-induced impacts on vegetation net primary productivity. Sci. Total Environ. 2019, 669, 342–352. [Google Scholar] [CrossRef]
- Zhang, Y.; Xiao, X.; Wu, X.; Zhou, S.; Zhang, G.; Qin, Y.; Dong, J. A global moderate resolution dataset of gross primary production of vegetation for 2000–2016. Sci. Data 2017, 4, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Running, S.W.; Nemani, R.; Glassy, J.M.; Thornton, P.E. MODIS Daily Photosynthesis (PSN) and Annual Net Primary Production (NPP) Product (MOD17) Algorithm Theoretical Basis Document; NASA Goddard Space Flight Cent.: Greenbelt, MD, USA, 1999.
- Dong, J.; Xiao, X.; Wagle, P.; Zhang, G.; Zhou, Y.; Jin, C.; Torn, M.S.; Meyers, T.P.; Suyker, A.E.; Wang, J. Comparison of four EVI-based models for estimating gross primary production of maize and soybean croplands and tallgrass prairie under severe drought. Remote Sens. Environ. 2015, 162, 154–168. [Google Scholar] [CrossRef]
- Yuan, W.; Zheng, Y.; Piao, S.; Ciais, P.; Lombardozzi, D.; Wang, Y.; Ryu, Y.; Chen, G.; Dong, W.; Hu, Z. Increased atmospheric vapor pressure deficit reduces global vegetation growth. Sci. Adv. 2019, 5, eaax1396. [Google Scholar] [CrossRef] [PubMed]
- Zhao, M.; Running, S.W. Drought-induced reduction in global terrestrial net primary production from 2000 through 2009. Science 2010, 329, 940–943. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Song, C.; Sun, G.; Band, L.E.; Noormets, A.; Zhang, Q. Understanding moisture stress on light use efficiency across terrestrial ecosystems based on global flux and remote-sensing data. J. Geophys. Res. Biogeosci. 2015, 120, 2053–2066. [Google Scholar] [CrossRef]
- Sun, Z.; Wang, X.; Zhang, X.; Tani, H.; Guo, E.; Yin, S.; Zhang, T. Evaluating and comparing remote sensing terrestrial GPP models for their response to climate variability and CO2 trends. Sci. Total Environ. 2019, 668, 696–713. [Google Scholar] [CrossRef]
- Mäkelä, A.; Pulkkinen, M.; Kolari, P.; Lagergren, F.; Berbigier, P.; Lindroth, A.; Loustau, D.; Nikinmaa, E.; Vesala, T.; Hari, P. Developing an empirical model of stand GPP with the LUE approach: Analysis of eddy covariance data at five contrasting conifer sites in Europe. Glob. Chang. Biol. 2008, 14, 92–108. [Google Scholar] [CrossRef]
- Yu, R. An improved estimation of net primary productivity of grassland in the Qinghai-Tibet region using light use efficiency with vegetation photosynthesis model. Ecol. Modell. 2020, 431, 109121. [Google Scholar] [CrossRef]
- Wang, H.; Jia, G.; Fu, C.; Feng, J.; Zhao, T.; Ma, Z. Deriving maximal light use efficiency from coordinated flux measurements and satellite data for regional gross primary production modeling. Remote Sens. Environ. 2010, 114, 2248–2258. [Google Scholar] [CrossRef]
- Yuan, W.; Liu, S.; Zhou, G.; Zhou, G.; Tieszen, L.L.; Baldocchi, D.; Bernhofer, C.; Gholz, H.; Goldstein, A.H.; Goulden, M.L. Deriving a light use efficiency model from eddy covariance flux data for predicting daily gross primary production across biomes. Agric. For. Meteorol. 2007, 143, 189–207. [Google Scholar] [CrossRef]
- Monteith, J.L. Climate and the efficiency of crop production in Britain. Phil. Trans. R. Soc. Lond. B 1977, 281, 277–294. [Google Scholar] [CrossRef]
- Wang, Y.-P.; Leuning, R. A two-leaf model for canopy conductance, photosynthesis and partitioning of available energy I:: Model description and comparison with a multi-layered model. Agric. For. Meteorol. 1998, 91, 89–111. [Google Scholar] [CrossRef]
- Propastin, P.; Ibrom, A.; Knohl, A.; Erasmi, S. Effects of canopy photosynthesis saturation on the estimation of gross primary productivity from MODIS data in a tropical forest. Remote Sens. Environ. 2012, 121, 252–260. [Google Scholar] [CrossRef]
- Chen, J.; Liu, J.; Cihlar, J.; Goulden, M. Daily canopy photosynthesis model through temporal and spatial scaling for remote sensing applications. Ecol. Modell. 1999, 124, 99–119. [Google Scholar] [CrossRef]
- De Pury, D.; Farquhar, G. Simple scaling of photosynthesis from leaves to canopies without the errors of big-leaf models. Plant Cell Environ. 1997, 20, 537–557. [Google Scholar] [CrossRef]
- Rap, A.; Scott, C.; Reddington, C.; Mercado, L.; Ellis, R.; Garraway, S.; Evans, M.; Beerling, D.; MacKenzie, A.; Hewitt, C. Enhanced global primary production by biogenic aerosol via diffuse radiation fertilization. Nat. Geosci. 2018, 11, 640–644. [Google Scholar] [CrossRef]
- He, L.; Liu, J.; Chen, J.M.; Croft, H.; Wang, R.; Sprintsin, M.; Zheng, T.; Ryu, Y.; Pisek, J.; Gonsamo, A. Inter-and intra-annual variations of clumping index derived from the MODIS BRDF product. Int. J. Appl. Earth Obs. Geoinf. 2016, 44, 53–60. [Google Scholar] [CrossRef]
- Chen, B.; Arain, M.A.; Chen, J.M.; Wang, S.; Fang, H.; Liu, Z.; Mo, G.; Liu, J. Importance of shaded leaf contribution to the total GPP of Canadian terrestrial ecosystems: Evaluation of MODIS GPP. J. Geophys. Res. Biogeosci. 2020, 125, e2020JG005917. [Google Scholar] [CrossRef]
- Cheng, S.J.; Bohrer, G.; Steiner, A.L.; Hollinger, D.Y.; Suyker, A.; Phillips, R.P.; Nadelhoffer, K.J. Variations in the influence of diffuse light on gross primary productivity in temperate ecosystems. Agric. For. Meteorol. 2015, 201, 98–110. [Google Scholar] [CrossRef]
- Zhang, M.; Yu, G.-R.; Zhuang, J.; Gentry, R.; Fu, Y.-L.; Sun, X.-M.; Zhang, L.-M.; Wen, X.-F.; Wang, Q.-F.; Han, S.-J. Effects of cloudiness change on net ecosystem exchange, light use efficiency, and water use efficiency in typical ecosystems of China. Agric. For. Meteorol. 2011, 151, 803–816. [Google Scholar] [CrossRef]
- Zhou, Y.; Wu, X.; Ju, W.; Chen, J.M.; Wang, S.; Wang, H.; Yuan, W.; Andrew Black, T.; Jassal, R.; Ibrom, A. Global parameterization and validation of a two-leaf light use efficiency model for predicting gross primary production across FLUXNET sites. Geophys. Res. Biogeosci. 2016, 121, 1045–1072. [Google Scholar] [CrossRef]
- Nilson, T. A theoretical analysis of the frequency of gaps in plant stands. Agric. Meteorol. 1971, 8, 25–38. [Google Scholar] [CrossRef]
- Govind, A.; Guyon, D.; Roujean, J.-L.; Yauschew-Raguenes, N.; Kumari, J.; Pisek, J.; Wigneron, J.-P. Effects of canopy architectural parameterizations on the modeling of radiative transfer mechanism. Ecol. Model. 2013, 251, 114–126. [Google Scholar] [CrossRef]
- Chen, B.; Coops, N.C.; Fu, D.; Margolis, H.A.; Amiro, B.D.; Black, T.A.; Arain, M.A.; Barr, A.G.; Bourque, C.P.-A.; Flanagan, L.B. Characterizing spatial representativeness of flux tower eddy-covariance measurements across the Canadian Carbon Program Network using remote sensing and footprint analysis. Remote Sens. Environ. 2012, 124, 742–755. [Google Scholar] [CrossRef]
- Chen, H.; Niu, Z.; Huang, W.; Feng, J. Predicting leaf area index in wheat using an improved empirical model. J. Appl. Remote Sens. 2013, 7, 073577. [Google Scholar] [CrossRef]
- Mercado, L.; Lloyd, J.; Carswell, F.; Malhi, Y.; Meir, P.; Nobre, A.D. Modelling Amazonian forest eddy covariance data: A comparison of big leaf versus sun/shade models for the C-14 tower at Manaus I. Canopy photosynthesis. Acta Amaz. 2006, 36, 69–82. [Google Scholar] [CrossRef]
- Yin, S.; Jiao, Z.; Dong, Y.; Zhang, X.; Cui, L.; Xie, R.; Guo, J.; Li, S.; Zhu, Z.; Tong, Y. Evaluation of the Consistency of the Vegetation Clumping Index Retrieved from Updated MODIS BRDF Data. Remote Sens. 2022, 14, 3997. [Google Scholar] [CrossRef]
- Wei, S.; Fang, H.; Schaaf, C.B.; He, L.; Chen, J.M. Global 500 m clumping index product derived from MODIS BRDF data (2001–2017). Remote Sens. Environ. 2019, 232, 111296. [Google Scholar] [CrossRef]
- Pastorello, G.; Trotta, C.; Canfora, E.; Chu, H.; Christianson, D.; Cheah, Y.-W.; Poindexter, C.; Chen, J.; Elbashandy, A.; Humphrey, M. The FLUXNET2015 dataset and the ONEFlux processing pipeline for eddy covariance data. Sci. Data 2020, 7, 225. [Google Scholar] [CrossRef] [PubMed]
- Reichstein, M.; Falge, E.; Baldocchi, D.; Papale, D.; Aubinet, M.; Berbigier, P.; Bernhofer, C.; Buchmann, N.; Gilmanov, T.; Granier, A. On the separation of net ecosystem exchange into assimilation and ecosystem respiration: Review and improved algorithm. Glob. Chang. Biol. 2005, 11, 1424–1439. [Google Scholar] [CrossRef]
- Tang, S.; Chen, J.; Zhu, Q.; Li, X.; Chen, M.; Sun, R.; Zhou, Y.; Deng, F.; Xie, D. LAI inversion algorithm based on directional reflectance kernels. J. Environ. Manag. 2007, 85, 638–648. [Google Scholar] [CrossRef] [PubMed]
- Jiao, Z.; Dong, Y.; Schaaf, C.B.; Chen, J.M.; Román, M.; Wang, Z.; Zhang, H.; Ding, A.; Erb, A.; Hill, M.J. An algorithm for the retrieval of the clumping index (CI) from the MODIS BRDF product using an adjusted version of the kernel-driven BRDF model. Remote Sens. Environ. 2018, 209, 594–611. [Google Scholar] [CrossRef]
- Jiao, Z.; Schaaf, C.B.; Dong, Y.; Román, M.; Hill, M.J.; Chen, J.M.; Wang, Z.; Zhang, H.; Saenz, E.; Poudyal, R. A method for improving hotspot directional signatures in BRDF models used for MODIS. Remote Sens. Environ. 2016, 186, 135–151. [Google Scholar] [CrossRef]
- Savitzky, A.; Golay, M.J. Smoothing and differentiation of data by simplified least squares procedures. Anal. Chem. 1964, 36, 1627–1639. [Google Scholar] [CrossRef]
- Schmid, H. Experimental design for flux measurements: Matching scales of observations and fluxes. Agric. For. Meteorol. 1997, 87, 179–200. [Google Scholar] [CrossRef]
- Li, F.; Hao, D.; Zhu, Q.; Yuan, K.; Braghiere, R.K.; He, L.; Luo, X.; Wei, S.; Riley, W.J.; Zeng, Y. Vegetation clumping modulates global photosynthesis through adjusting canopy light environment. Glob. Chang. Biol. 2023, 29, 731–746. [Google Scholar] [CrossRef]
- Pisek, J.; Govind, A.; Arndt, S.K.; Hocking, D.; Wardlaw, T.J.; Fang, H.; Matteucci, G.; Longdoz, B. Intercomparison of clumping index estimates from POLDER, MODIS, and MISR satellite data over reference sites. ISPRS J. Photogramm. Remote Sens. 2015, 101, 47–56. [Google Scholar] [CrossRef]
- Friedl, M.A.; Sulla-Menashe, D.; Tan, B.; Schneider, A.; Ramankutty, N.; Sibley, A.; Huang, X. MODIS Collection 5 global land cover: Algorithm refinements and characterization of new datasets. Remote Sens. Environ. 2010, 114, 168–182. [Google Scholar] [CrossRef]
- Chen, J.M.; Black, T. Defining leaf area index for non-flat leaves. Plant Cell Environ. 1992, 15, 421–429. [Google Scholar] [CrossRef]
- Wang, L.; Zhu, H.; Lin, A.; Zou, L.; Qin, W.; Du, Q. Evaluation of the latest MODIS GPP products across multiple biomes using global eddy covariance flux data. Remote Sens. 2017, 9, 418. [Google Scholar] [CrossRef]
- Wu, C.; Munger, J.W.; Niu, Z.; Kuang, D. Comparison of multiple models for estimating gross primary production using MODIS and eddy covariance data in Harvard Forest. Remote Sens. Environ. 2010, 114, 2925–2939. [Google Scholar] [CrossRef]
- Zhao, M.; Running, S.W.; Nemani, R.R. Sensitivity of Moderate Resolution Imaging Spectroradiometer (MODIS) terrestrial primary production to the accuracy of meteorological reanalyses. J. Geophys. Res. Biogeosci. 2006, 111, G01002. [Google Scholar] [CrossRef]
- Mu, Q.; Zhao, M.; Running, S.W. Improvements to a MODIS global terrestrial evapotranspiration algorithm. Remote Sens. Environ. 2011, 115, 1781–1800. [Google Scholar] [CrossRef]
- Wu, X.; Ju, W.; Zhou, Y.; He, M.; Law, B.E.; Black, T.A.; Margolis, H.A.; Cescatti, A.; Gu, L.; Montagnani, L. Performance of linear and nonlinear two-leaf light use efficiency models at different temporal scales. Remote Sens. 2015, 7, 2238–2278. [Google Scholar] [CrossRef]
- Fang, H. Canopy clumping index (CI): A review of methods, characteristics, and applications. Agric. For. Meteorol. 2021, 303, 108374. [Google Scholar] [CrossRef]
- Saltelli, A.; Tarantola, S.; Chan, K.-S. A quantitative model-independent method for global sensitivity analysis of model output. Technometrics 1999, 41, 39–56. [Google Scholar] [CrossRef]
- Cukier, R.; Fortuin, C.; Shuler, K.E.; Petschek, A.; Schaibly, J.H. Study of the sensitivity of coupled reaction systems to uncertainties in rate coefficients. I Theory. J. Chem. Phys. 1973, 59, 3873–3878. [Google Scholar] [CrossRef]
- Sobol, I.M. Sensitivity analysis for non-linear mathematical models. Math. Model. Comput. Exp. 1993, 1, 407–414. [Google Scholar]
- Tarantola, S.; Becker, W. SIMLAB software for uncertainty and sensitivity analysis. In Handbook of Uncertainty Quantification; Springer: Cham, Swizterland, 2017; pp. 1979–1999. ISBN 1978-1973-1319-11259-11256. [Google Scholar]
- Bai, D.; Jiao, Z.; Dong, Y.; Zhang, X.; Li, Y.; He, D. Analysis of the sensitivity of the anisotropic flat index to vegetation parameters based on the two-layer canopy reflectance model. J. Remote Sens. 2017, 21, 1–11. [Google Scholar] [CrossRef]
- Jiang, Z.; Huete, A.R.; Didan, K.; Miura, T. Development of a two-band enhanced vegetation index without a blue band. Remote Sens. Environ. 2008, 112, 3833–3845. [Google Scholar] [CrossRef]
- Zhang, X.; Friedl, M.A.; Schaaf, C.B.; Strahler, A.H.; Hodges, J.C.; Gao, F.; Reed, B.C.; Huete, A. Monitoring vegetation phenology using MODIS. Remote Sens. Environ. 2003, 84, 471–475. [Google Scholar] [CrossRef]
- Xiao, W.; Sun, Z.; Wang, Q.; Yang, Y. Evaluating MODIS phenology product for rotating croplands through ground observations. J. Appl. Remote Sens. 2013, 7, 073562. [Google Scholar] [CrossRef]
- Carrer, D.; Roujean, J.L.; Lafont, S.; Calvet, J.C.; Boone, A.; Decharme, B.; Delire, C.; Gastellu-Etchegorry, J.P. A canopy radiative transfer scheme with explicit FAPAR for the interactive vegetation model ISBA-A-gs: Impact on carbon fluxes. J. Geophys. Res. Biogeosci. 2013, 118, 888–903. [Google Scholar] [CrossRef]
- Chen, J.M.; Mo, G.; Pisek, J.; Liu, J.; Deng, F.; Ishizawa, M.; Chan, D. Effects of foliage clumping on the estimation of global terrestrial gross primary productivity. Glob. Biogeochem. Cycles 2012, 26, GB1019. [Google Scholar] [CrossRef]
- Sprintsin, M.; Chen, J.M.; Desai, A.; Gough, C.M. Evaluation of leaf-to-canopy upscaling methodologies against carbon flux data in North America. J. Geophys. Res. Biogeosci. 2012, 117, G01023. [Google Scholar] [CrossRef]
- Braghiere, R.K.; Quaife, T.; Black, E.; He, L.; Chen, J. Underestimation of global photosynthesis in Earth system models due to representation of vegetation structure. Glob. Biogeochem. Cycles 2019, 33, 1358–1369. [Google Scholar] [CrossRef]
- Li, C.; Lu, H.; Leung, L.R.; Yang, K.; Li, H.; Wang, W.; Han, M.; Chen, Y. Improving land surface temperature simulation in CoLM over the Tibetan Plateau through fractional vegetation cover derived from a remotely sensed clumping index and model-simulated leaf area index. J. Geophys. Res. Atmos. 2019, 124, 2620–2642. [Google Scholar] [CrossRef]
- Zeng, L.; Wardlow, B.D.; Xiang, D.; Hu, S.; Li, D. A review of vegetation phenological metrics extraction using time-series, multispectral satellite data. Remote Sens. Environ. 2020, 237, 111511. [Google Scholar] [CrossRef]
- Croft, H.; Chen, J.M.; Zhang, Y. Temporal disparity in leaf chlorophyll content and leaf area index across a growing season in a temperate deciduous forest. Int. J. Appl. Earth Obs. Geoinf. 2014, 33, 312–320. [Google Scholar] [CrossRef]
- Li, J.; Lu, X.; Ju, W.; Li, J.; Zhu, S.; Zhou, Y. Seasonal changes of leaf chlorophyll content as a proxy of photosynthetic capacity in winter wheat and paddy rice. Ecol. Indic. 2022, 140, 109018. [Google Scholar] [CrossRef]
- Dong, Y.; Jiao, Z.; Yin, S.; Zhang, H.; Zhang, X.; Cui, L.; He, D.; Ding, A.; Chang, Y.; Yang, S. Influence of snow on the magnitude and seasonal variation of the clumping index retrieved from MODIS BRDF products. Remote Sens. 2018, 10, 1194. [Google Scholar] [CrossRef]
- Ryu, Y.; Baldocchi, D.D.; Verfaillie, J.; Ma, S.; Falk, M.; Ruiz-Mercado, I.; Hehn, T.; Sonnentag, O. Testing the performance of a novel spectral reflectance sensor, built with light emitting diodes (LEDs), to monitor ecosystem metabolism, structure and function. Agric. For. Meteorol. 2010, 150, 1597–1606. [Google Scholar] [CrossRef]
- Gao, Y.; Wang, W.; Liu, X.; Zhang, L.; Dend, F.; Yang, C.; Sun, Q. Evaluation of carbon sequestration of forest ecosystem in Xiamen city. Res. Environ. Sci. 2019, 32, 2001–2007. [Google Scholar] [CrossRef]
- Van Stan, J.T.; Coenders-Gerrits, M.; Dibble, M.; Bogeholz, P.; Norman, Z. Effects of phenology and meteorological disturbance on litter rainfall interception for a Pinus elliottii stand in the Southeastern United States. Hydrol. Process. 2017, 31, 3719–3728. [Google Scholar] [CrossRef]
- Pisek, J.; Chen, J.M.; Lacaze, R.; Sonnentag, O.; Alikas, K. Expanding global mapping of the foliage clumping index with multi-angular POLDER three measurements: Evaluation and topographic compensation. ISPRS J. Photogramm. Remote Sens. 2010, 65, 341–346. [Google Scholar] [CrossRef]
- Zhu, G.; Ju, W.; Chen, J.M.; Gong, P.; Xing, B.; Zhu, J. Foliage clumping index over China’s landmass retrieved from the MODIS BRDF parameters product. IEEE Trans. Geosci. Electron. 2011, 50, 2122–2137. [Google Scholar] [CrossRef]
- Román, M.O.; Gatebe, C.K.; Schaaf, C.B.; Poudyal, R.; Wang, Z.; King, M.D. Variability in surface BRDF at different spatial scales (30 m–500 m) over a mixed agricultural landscape as retrieved from airborne and satellite spectral measurements. Remote Sens. Environ. 2011, 115, 2184–2203. [Google Scholar] [CrossRef]
- Walthall, C.; Roujean, J.L.; Morisette, J. Field and landscape BRDF optical wavelength measurements: Experience, techniques and the future. Remote Sens. Rev. 2000, 18, 503–531. [Google Scholar] [CrossRef]
- Asaadi, A.; Arora, V.K.; Melton, J.R.; Bartlett, P. An improved parameterization of leaf area index (LAI) seasonality in the Canadian Land Surface Scheme (CLASS) and Canadian Terrestrial Ecosystem Model (CTEM) modelling framework. Biogeosciences 2018, 15, 6885–6907. [Google Scholar] [CrossRef]
- Bao, S.; Wutzler, T.; Koirala, S.; Cuntz, M.; Ibrom, A.; Besnard, S.; Walther, S.; Šigut, L.; Moreno, A.; Weber, U. Environment-sensitivity functions for gross primary productivity in light use efficiency models. Agric. For. Meteorol. 2022, 312, 108708. [Google Scholar] [CrossRef]
- Chen, J.M. Optically-based methods for measuring seasonal variation of leaf area index in boreal conifer stands. Agric. For. Meteorol. 1996, 80, 135–163. [Google Scholar] [CrossRef]
- Sprintsin, M.; Cohen, S.; Maseyk, K.; Rotenberg, E.; Grünzweig, J.; Karnieli, A.; Berliner, P.; Yakir, D. Long term and seasonal courses of leaf area index in a semi-arid forest plantation. Agric. For. Meteorol. 2011, 151, 565–574. [Google Scholar] [CrossRef]
- Fang, H.; Liu, W.; Li, W.; Wei, S. Estimation of the directional and whole apparent clumping index (ACI) from indirect optical measurements. ISPRS J. Photogramm. Remote Sens. 2018, 144, 1–13. [Google Scholar] [CrossRef]
- Pisek, J.; Ryu, Y.; Sprintsin, M.; He, L.; Oliphant, A.J.; Korhonen, L.; Kuusk, J.; Kuusk, A.; Bergstrom, R.; Verrelst, J. Retrieving vegetation clumping index from Multi-angle Imaging SpectroRadiometer (MISR) data at 275 m resolution. Remote Sens. Environ. 2013, 138, 126–133. [Google Scholar] [CrossRef]
- Chen, J.M.; Rich, P.M.; Gower, S.T.; Norman, J.M.; Plummer, S. Leaf area index of boreal forests: Theory, techniques, and measurements. J. Geophys. Res. Atmos. 1997, 102, 29429–29443. [Google Scholar] [CrossRef]
- Li, X.; Liang, H.; Cheng, W. Evaluation and comparison of light use efficiency models for their sensitivity to the diffuse PAR fraction and aerosol loading in China. Int. J. Appl. Earth Obs. Geoinf. 2021, 95, 102269. [Google Scholar] [CrossRef]
- Wang, X.; Chen, J.M.; Ju, W. Photochemical reflectance index (PRI) can be used to improve the relationship between gross primary productivity (GPP) and sun-induced chlorophyll fluorescence (SIF). Remote Sens. Environ. 2020, 246, 111888. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).