1. Introduction
Remote sensing image change detection (CD), as an important branch of the remote sensing field, aims to utilize multi-temporal image data acquired by satellites, aircraft, and other remote sensing sensors to monitor the spatial and temporal changes of objects such as the Earth’s surface, cities, forests, farmlands, and natural environments. CD refers to the quantitative analysis of the characteristics and processes of surface changes from co-registered remote sensing images acquired at different time periods [
1]. The definition of change varies depending on the specific application task and can range from simple binary coarse changes to detailed multi-class semantic changes. CD techniques based on remote sensing images are widely applied in various fields, including environmental change monitoring [
2,
3], land resource management [
4], urban expansion [
5], and disaster monitoring [
6,
7].
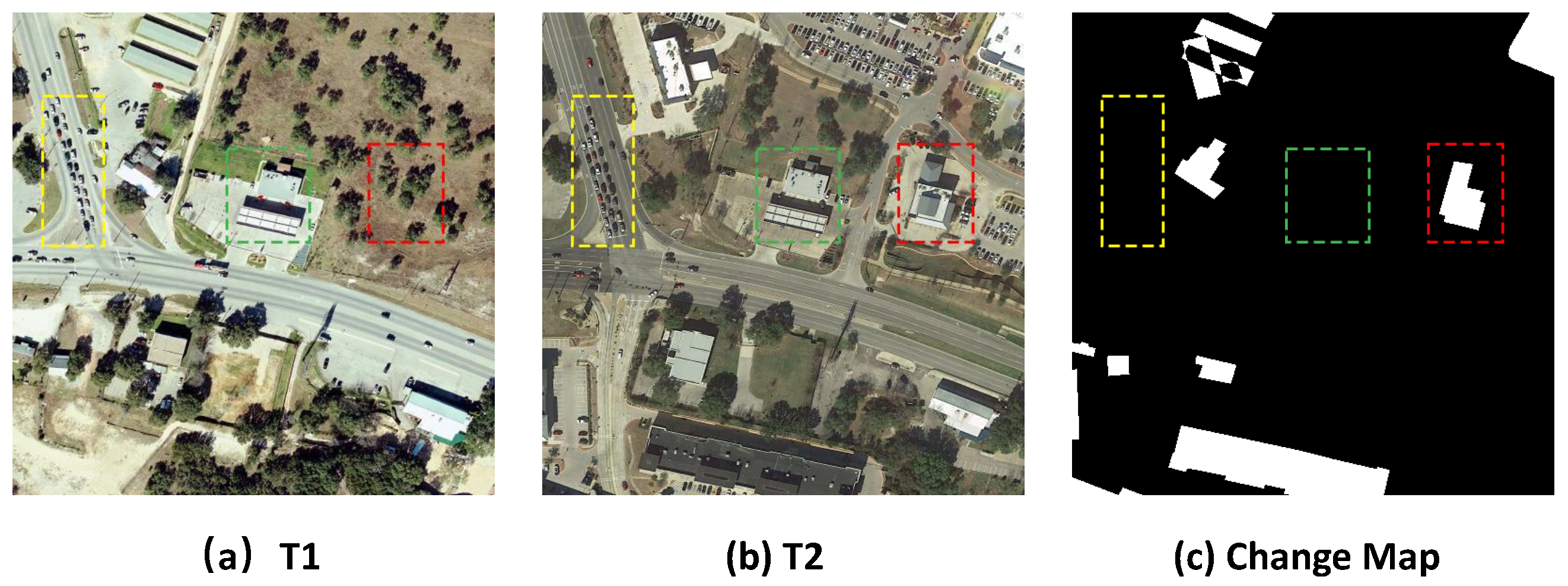
CD faces a series of challenges, as shown in
Figure 1. The core task of CD is to track the changes that users want to highlight, such as new buildings (red box), while ignoring changes caused by external factors (green box), such as environmental changes, lighting conditions, fog, or seasonal variations. It also involves filtering out uninteresting targets, such as traffic flow (yellow box). The difficulty of the task lies in the fact that the same feature target presents different spectral features at different time points as well as spatial locations due to environmental factors such as lighting conditions, shooting angle, and atmospheric conditions. Therefore, an excellent CD needs to identify and localize the feature target of interest, and at the same time be able to distinguish between real changes and pseudo-changes caused by environmental noise, which requires powerful feature extraction, spatial–temporal modeling, and change discrimination capabilities. The combination of these capabilities enables the model to accurately capture changes at points of interest in complex scenes and ensure reliable CD results.
By rethinking the task of CD in remote sensing imagery, we find that it is closely related to the remote sensing image semantic segmentation task. This is because in essence, the CD task can be viewed as an intensive change pixel segmentation task. The difference is that this task requires remote sensing images that have been bi-temporal and co-registered as two inputs , to the model. In this case, the determination of positive and negative samples is based on whether they have different semantics within different temporal phases at the same geographic location. This means assessing whether the change map label Y corresponds with the model output. Under the optimization objective of minimizing the empirical loss, these two tasks can be formulated as and . However, the temporal information between bi-temporal phases is wasted if CD is only used as an ordinary semantic segmentation task, so the interactive fusion between bi-temporal feature information also needs to be considered by the model .
Traditional CD methods heavily rely on the results of difference maps. If a significant amount of information is lost during the generation of difference maps, it can lead to unstable accuracy in detection results. Deep learning has been proven to be an effective means of feature learning, capable of automatically extracting abstract features of complex objects in a multi-level manner. The end-to-end structure of deep learning enables us to directly obtain CD results from multi-temporal remote sensing images. We summarize the processing workflow of the CD task into three stages: (1) extraction of bi-temporal features, (2) interaction and fusion of bi-temporal features, (3) discriminative feature generation for the final change map. With the continuous development of high-resolution remote sensing, both ConvNet-based [
8,
9,
10,
11] and Transformer-based [
12,
13,
14] methods, driven by a large amount of remote sensing data [
8,
9,
15,
16,
17,
18,
19], have shown excellent performance.
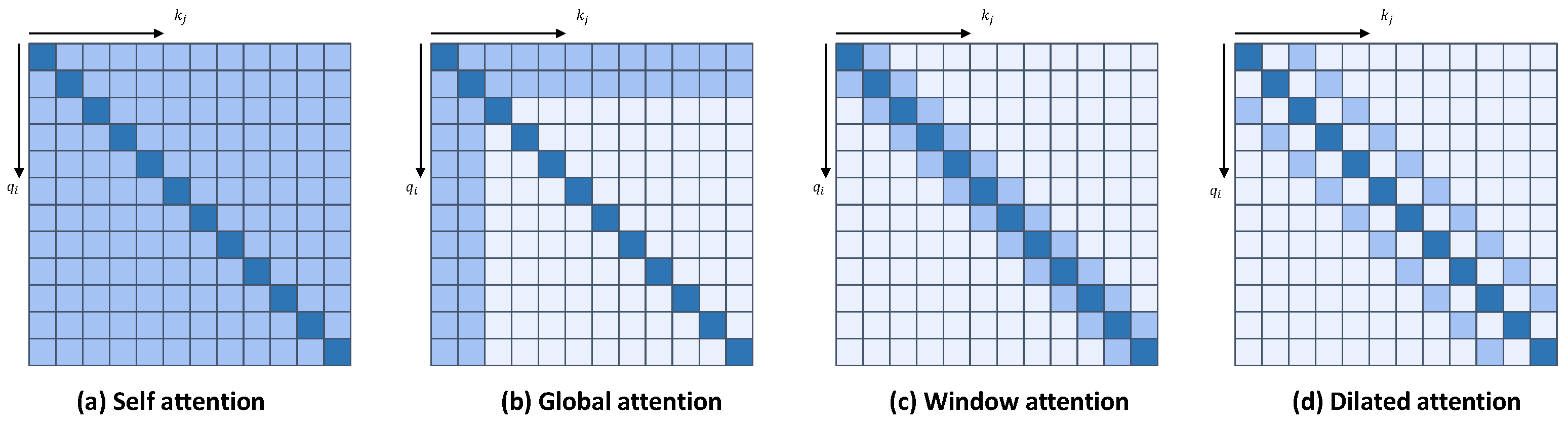
Most approaches consider the CD task as a task of dense pixel segmentation [
20,
21,
22], which aligns with the view that these tasks are closely related to semantic segmentation tasks. Therefore, these methods attempt to obtain a larger receptive field in the bi-temporal feature extraction stage. Methods based on ConvNet, limited by the receptive field of convolutional kernels, often seek to expand the receptive field as much as possible through mechanisms such as dilated convolution [
23], channel attention [
24], spatial attention [
25], and mixed attention of channel and spatial [
26]. Methods based on Transformer use self-attention with a full receptive field to capture global relationships in spatial–temporal features. However, traditional self-attention is still hindered by quadratic computational complexity with respect to the number of pixels. Therefore, most Transformer-based methods aim to reduce the number of pixels to reduce computational cost.
In the feature interaction and fusion stage, the model integrates the results from the feature extraction part and extracts change information from the bi-temporal data. Therefore, it may be necessary to consider the processing of feature information at multiple stages and scales. During these processes, the model needs to organically fuse features at the same scale from the two temporal phases, which can be achieved through various operations such as subtraction, concatenation, summation, and so on. Effective interaction fusion helps preserve the essential features of land changes and distinguish them from invariant features. Therefore, at this stage, most methods attempt to introduce attention blocks to help the model focus on change-related features. In the final discrimination stage of the change map, there are two approaches. The first is based on pixel classification, which is similar to how semantic segmentation tasks are approached. In this method, the processed change features are projected onto a multi-channel classification map to obtain the final classification result for change pixels. The second approach is based on metric learning [
27], which posits that changes can be discerned by measuring the distances between features. Consequently, a contrastive loss is employed to increase the distance between feature vectors that represent changing regions during the optimization process, while reducing the distance between feature vectors representing unchanged regions. Ultimately, a simple threshold is used to obtain the final change map, such as [
8,
9].
It is well-known that CNNs enhance the translational invariance and local inductive bias of the network through locally shared convolutional kernels, while Transformer is initialized with dot product self-attention which is by definition a global one-dimensional operation, resulting in the same weight of attention assigned to all pixel features, which implies that some of the inductive biases in the Transformer-based model have to be learned either through a large amount of data or by introducing effective task experience [
28]. Therefore, we try to summarize some inductive biases for the CD task and introduce them into our model, and design a new encoder as well as a feature interaction fusion module to achieve better CD results in remote sensing images. On the one hand, the CD task, as an intensive segmentation task, requires both a global receptive field for the change classification task and local information for accurate edge segmentation of the change graph. Therefore, in the extraction stage of bi-temporal features, we would like to obtain a global receptive field that approximates self-attention without incurring such an expensive cost as on the self-attention side. At the same time, localization is introduced in the change information interaction fusion stage to accomplish better change map segmentation. On the other hand, the CD task needs to consider how to capture and establish the correlation between bi-temporal co-registered images on top of the dense segmentation task. However, most methods rely only on simple operations such as differencing and splicing between bi-temporal features to integrate the bi-temporal features, and this direct feature fusion strategy makes it difficult to extract change feature information effectively.
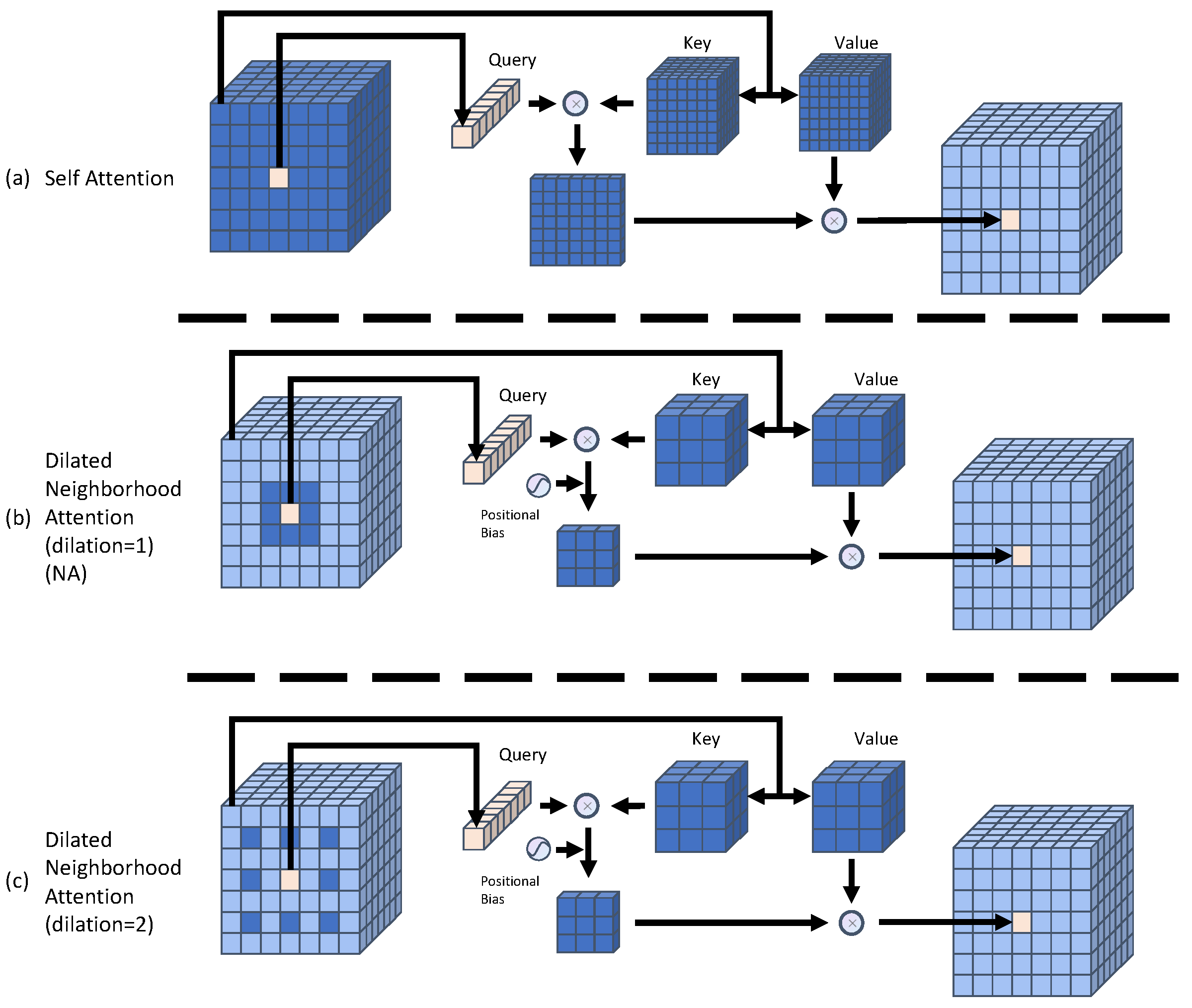
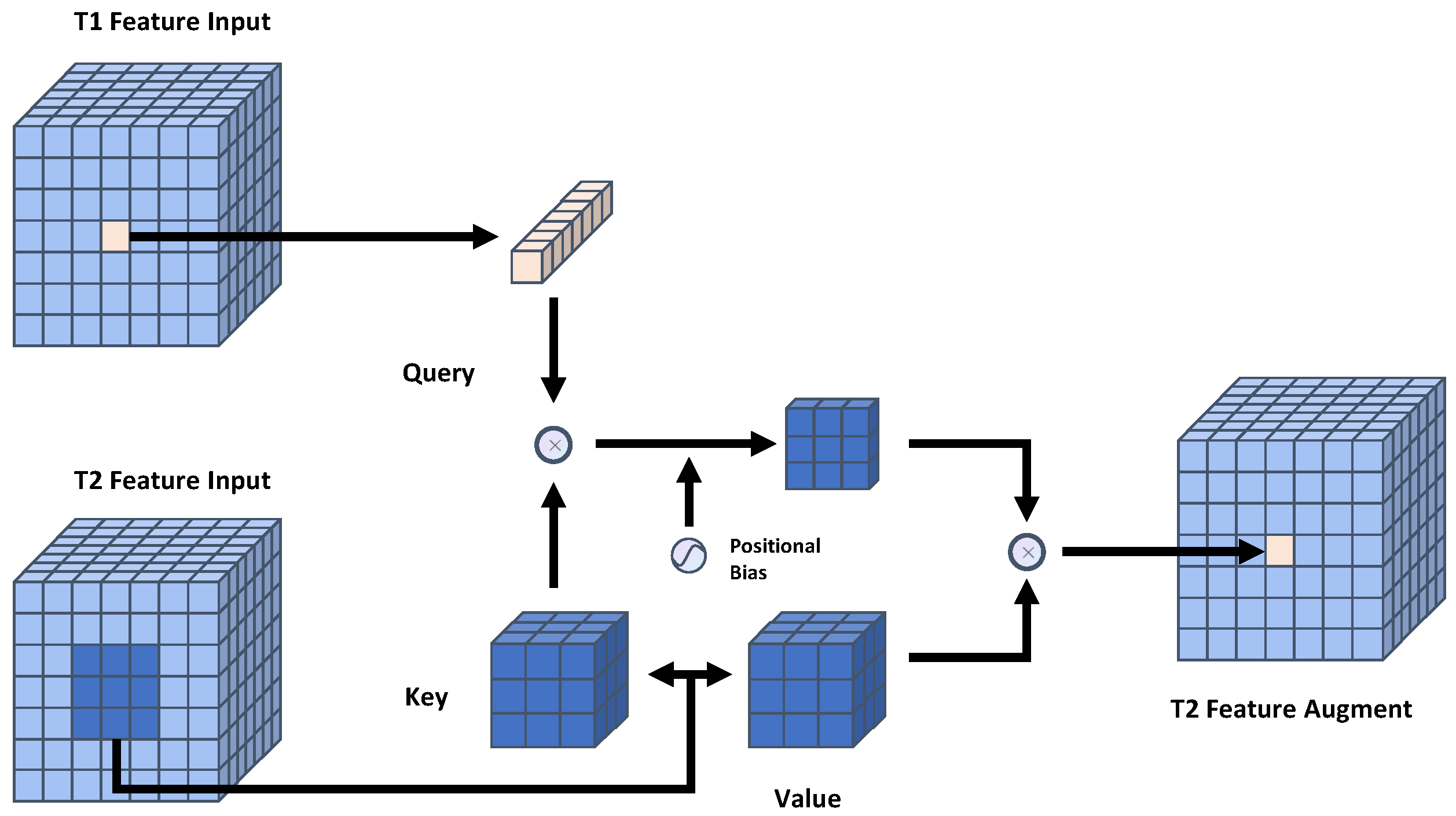
Our study aims to optimize the remote sensing image CD process by exploring the essentials of the CD task by introducing certain inductive biases, especially in Transformer-based models. The CD task requires the model to be able to capture global contextual information, but also needs to preserve local detailed features. We would like to pursue balancing the global perceptual field with the local information to improve the global contextual perceptual field while reducing the computational complexity, so as to capture the temporal change features of feature targets more efficiently. We introduce a simple, flexible, and powerful dilated neighborhood attention module (DiNA) into the whole process of CD. Based on DiNA, we constructed DiNAT for embedding into the Transformer structure. By stacking DiNAT modules with different expansion rates, we construct an encoder structure for temporal feature extraction, which allows the sense field to grow exponentially in the feature extraction phase and captures the context at a farther range without any additional computational cost, and augment the change feature while filtering the pseudo-change noise in the interaction phase of the bi-temporal change features by acquiring the inductive bias of the local neighborhoods by means of it, further capturing the temporal-phase semantic change features of the CD task. In addition, we improved DINA and obtained Cross-NA, and constructed the Temporal Neighborhood Cross Differ Module based on Cross-NA to improve the interaction of temporal information to help the model better capture the change information between bi-temporal features, thus obtaining better results.
The contributions of our work can be summarized as follows:
We proposed a Transformer-based Siamese network structure called BTNIFormer for addressing CD tasks in remote sensing images. By considering the key aspects of CD from the perspective of semantic segmentation, we employ a sparse sliding-window attention mechanism named DiNA that localizes the attention scope of each pixel to its nearest neighborhood. This introduces inductive bias into the CD task, leading to improved results.
By stacking DiNAT with different dilation rates, we construct an Encoder structure that achieves a global receptive field close to self-attention without incurring quadratic computational costs.
The Temporal Neighborhood Cross Differ Module, which is composed of the Cross-NA module, is used at each scale stage of the bi-temporal feature map to realize more effective extraction of spatial–temporal variation information and filtering of variation noise.
We conducted extensive experiments on two publicly available CD datasets to validate the effectiveness of our approach. Through quantitative and qualitative experimental analysis, our network demonstrated fewer misclassifications and more precise change result edge segmentation effects.
The remaining sections of this paper are organized as follows. The related work is introduced in
Section 2.
Section 3 provides the conceptual background and implementation details of our proposed method. Experimental results are presented and analyzed in
Section 4. The conclusion and future prospects are discussed in
Section 5.