Super Resolution of Satellite-Derived Sea Surface Temperature Using a Transformer-Based Model
Abstract
:1. Introduction
2. Materials and Methods
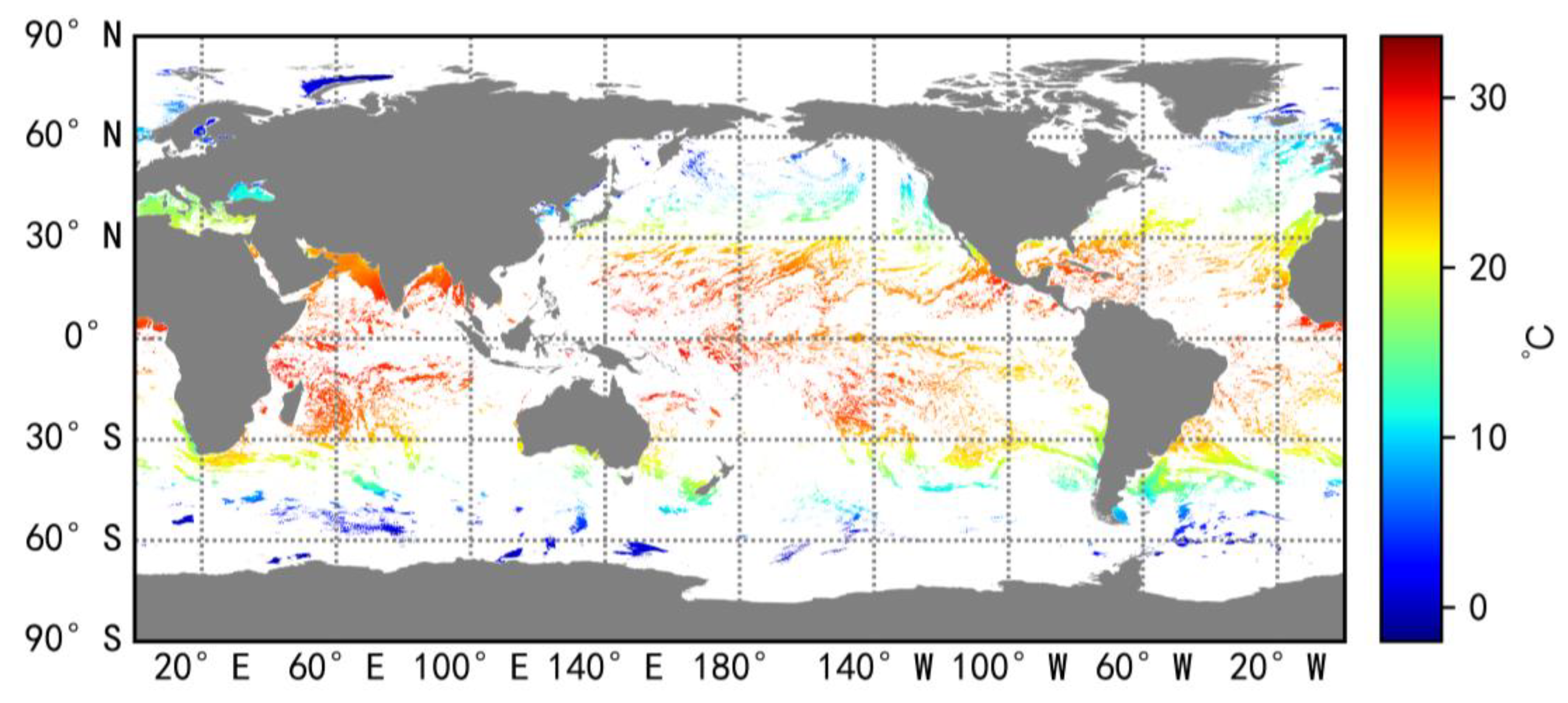
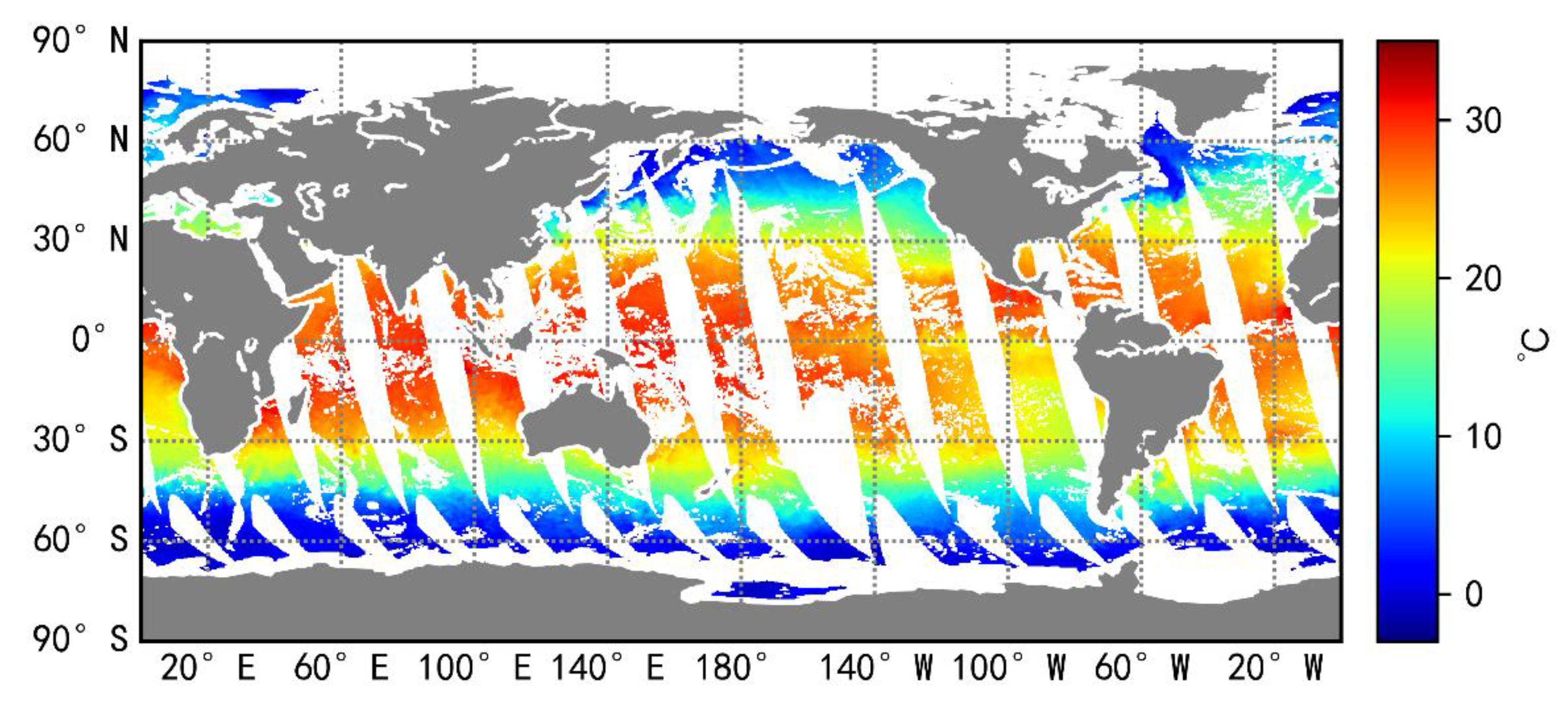
2.1. Training Data
2.2. Methods
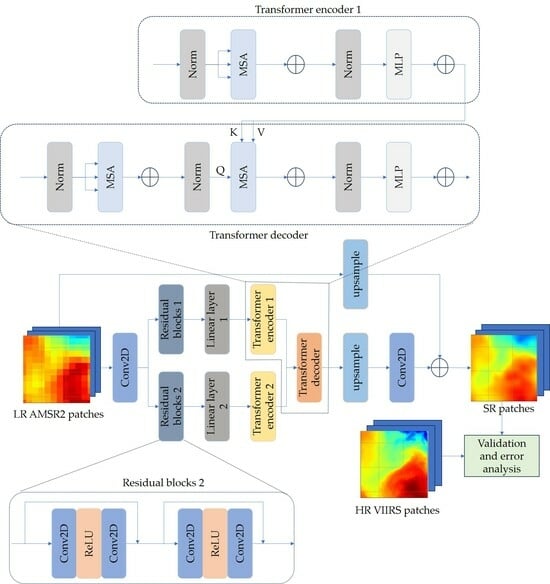
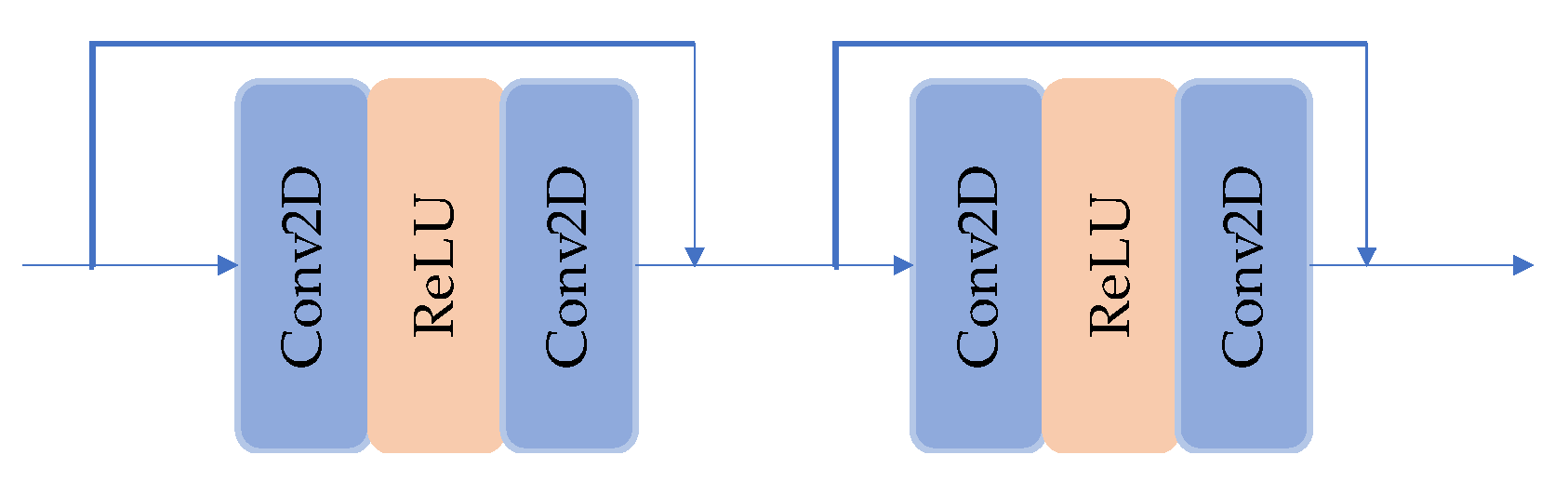
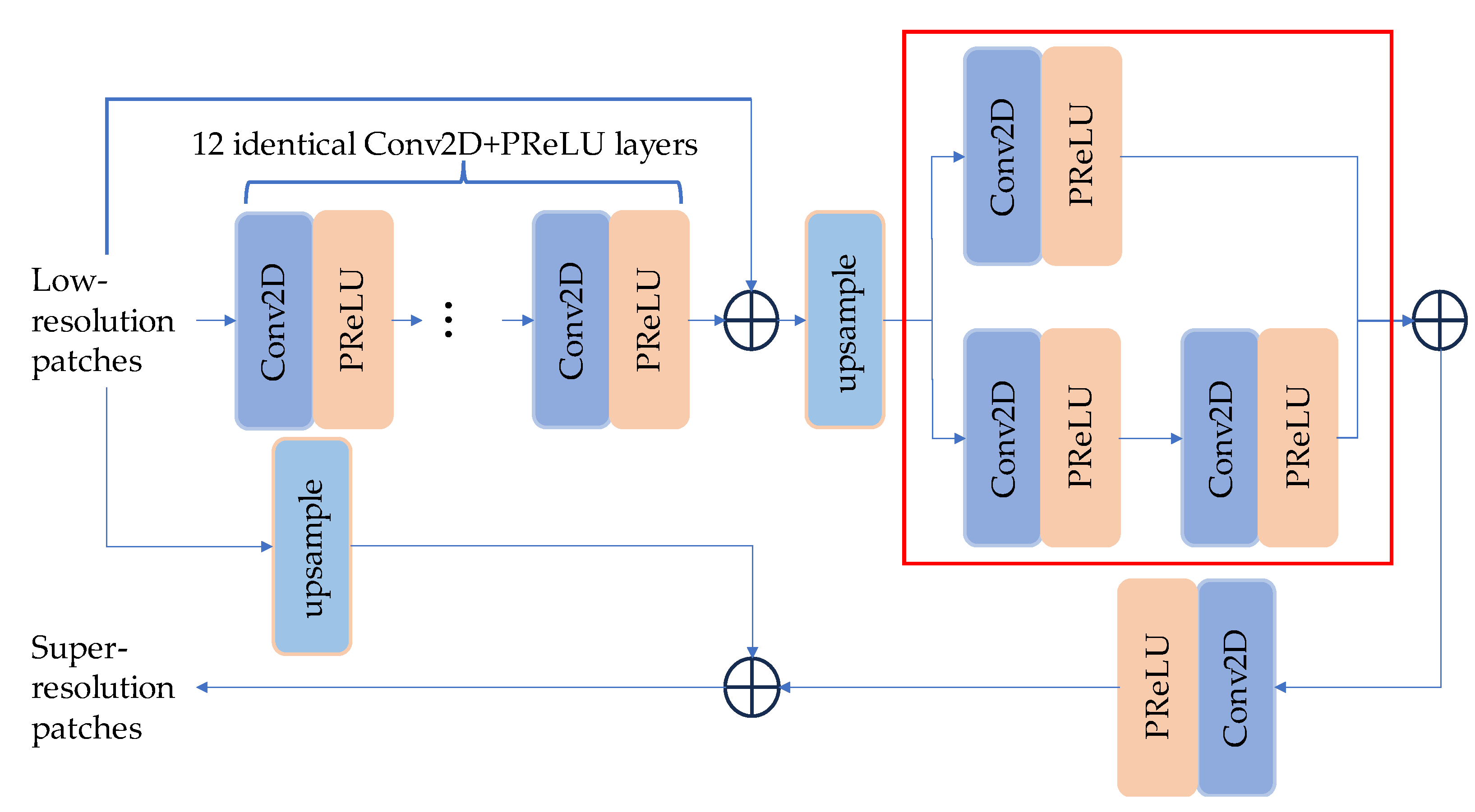
2.2.1. The Proposed Model
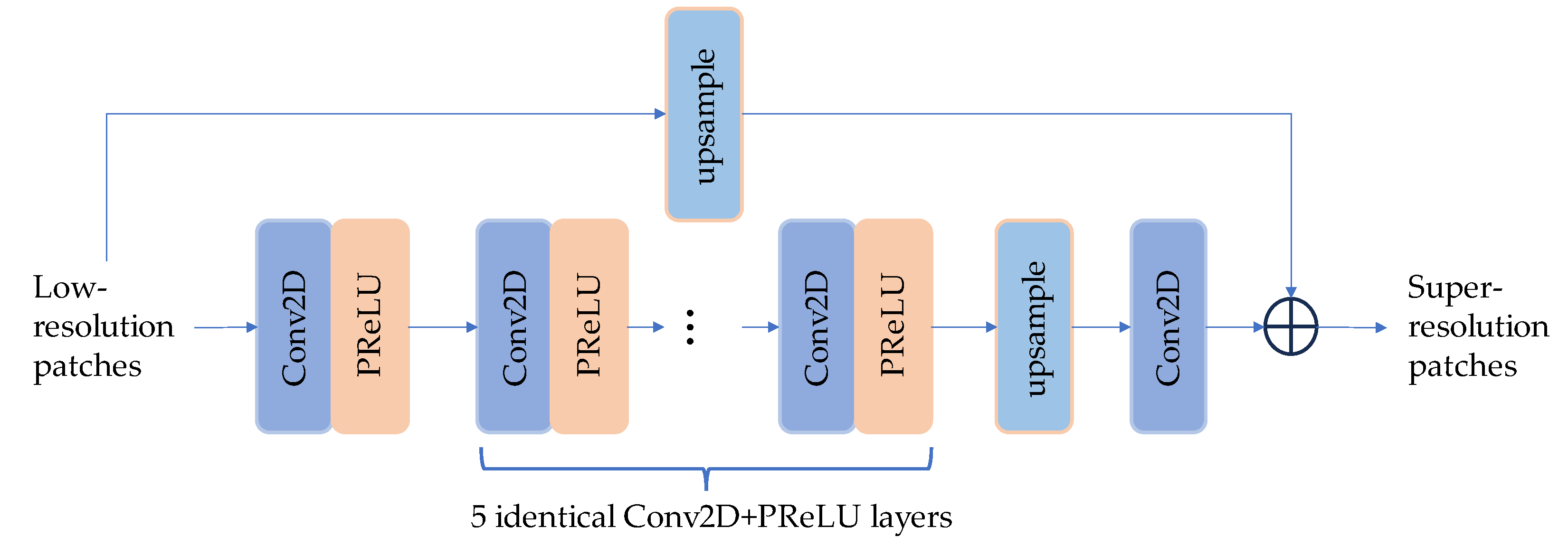
2.2.2. Other SR Models
2.2.3. Loss Function and Implementation Details
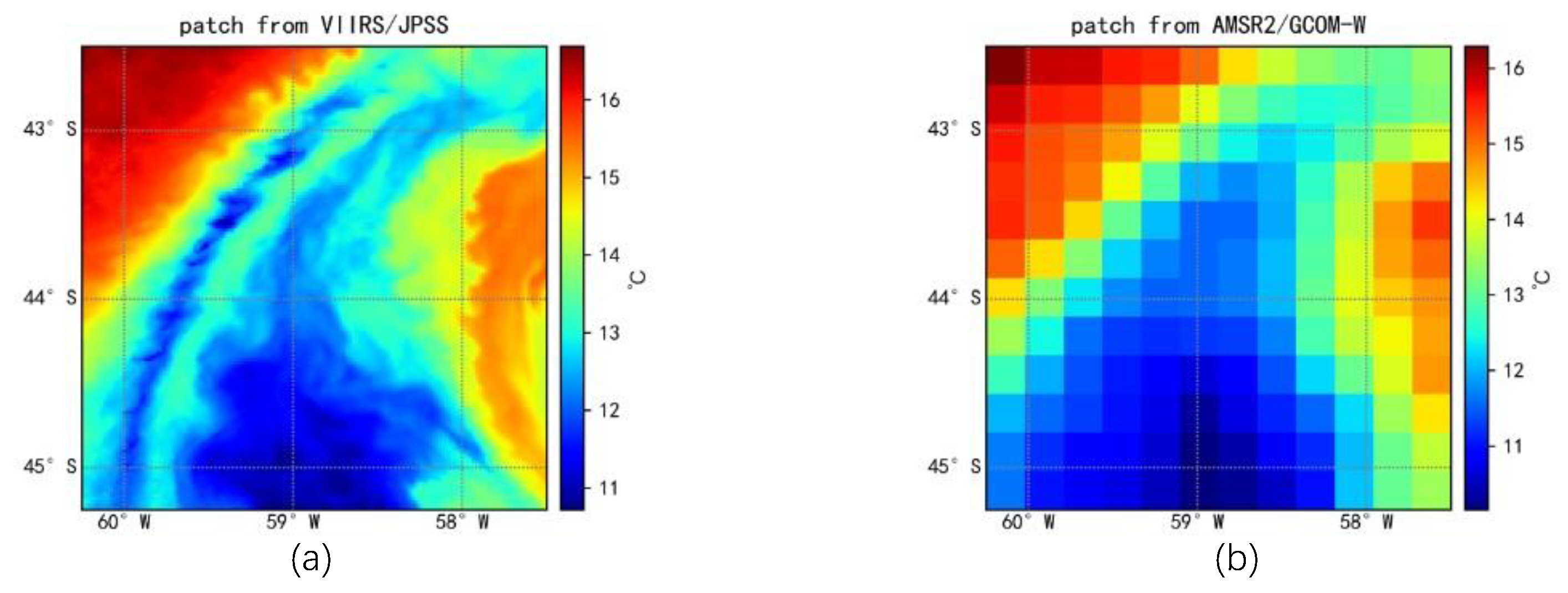
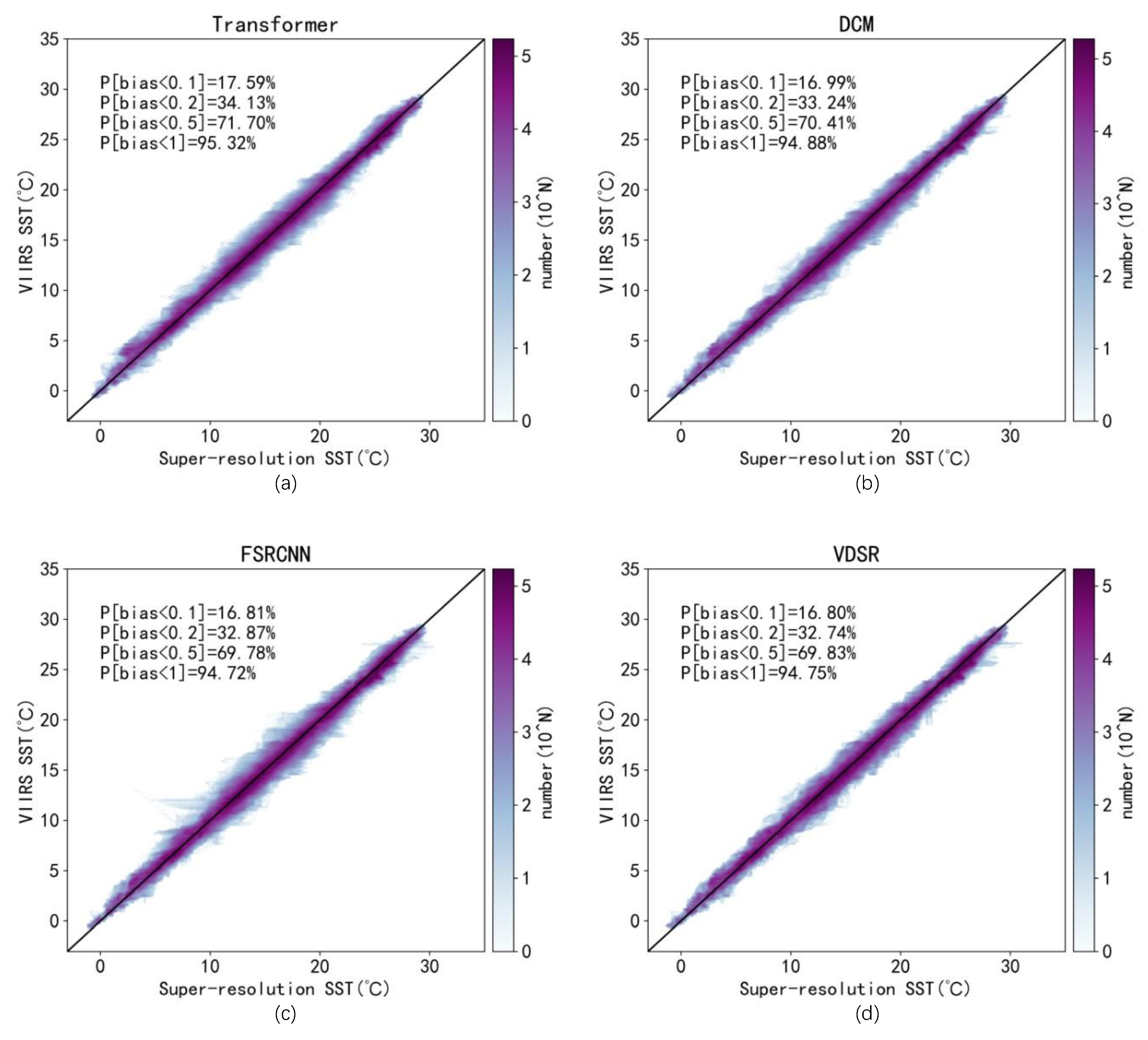
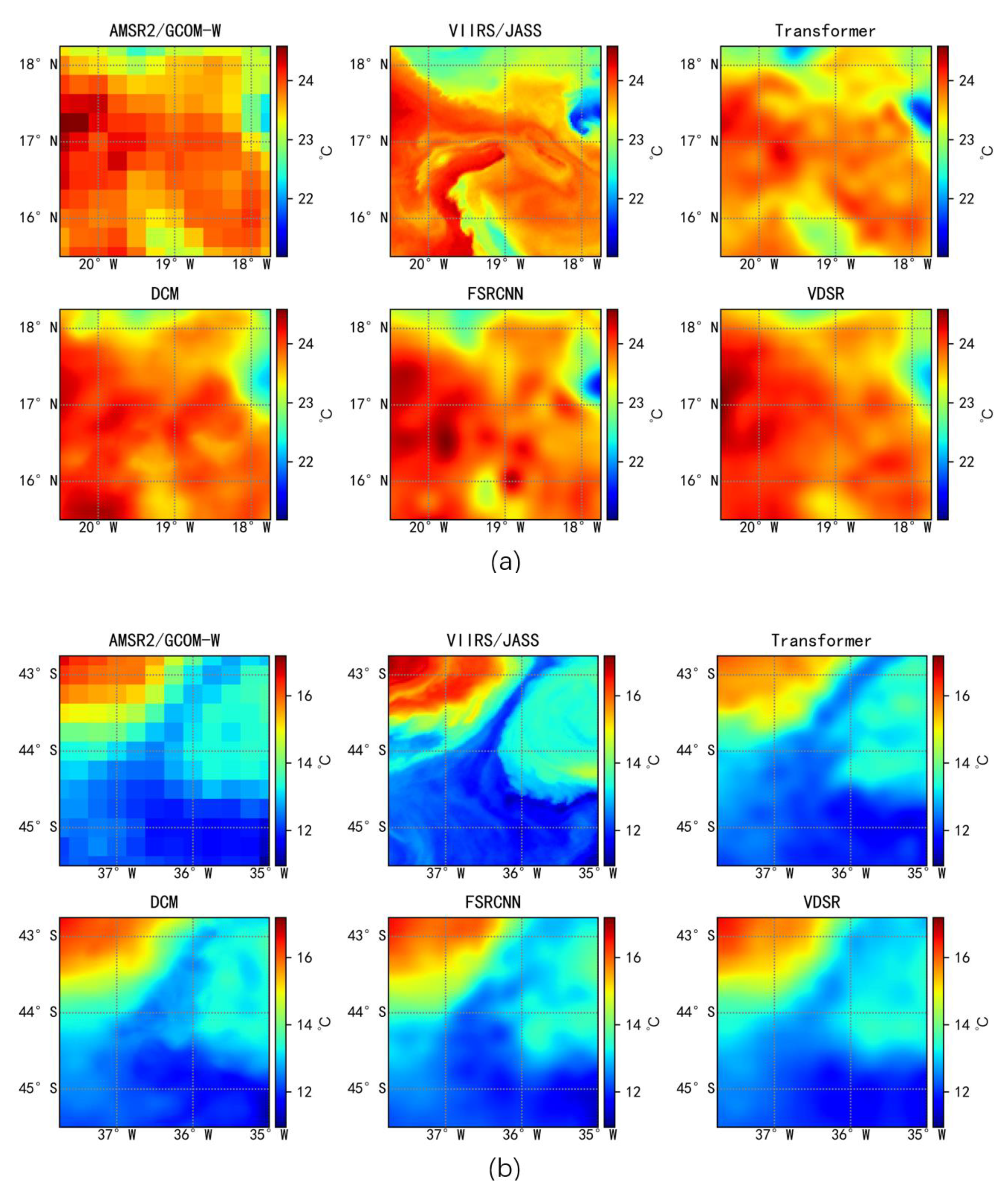
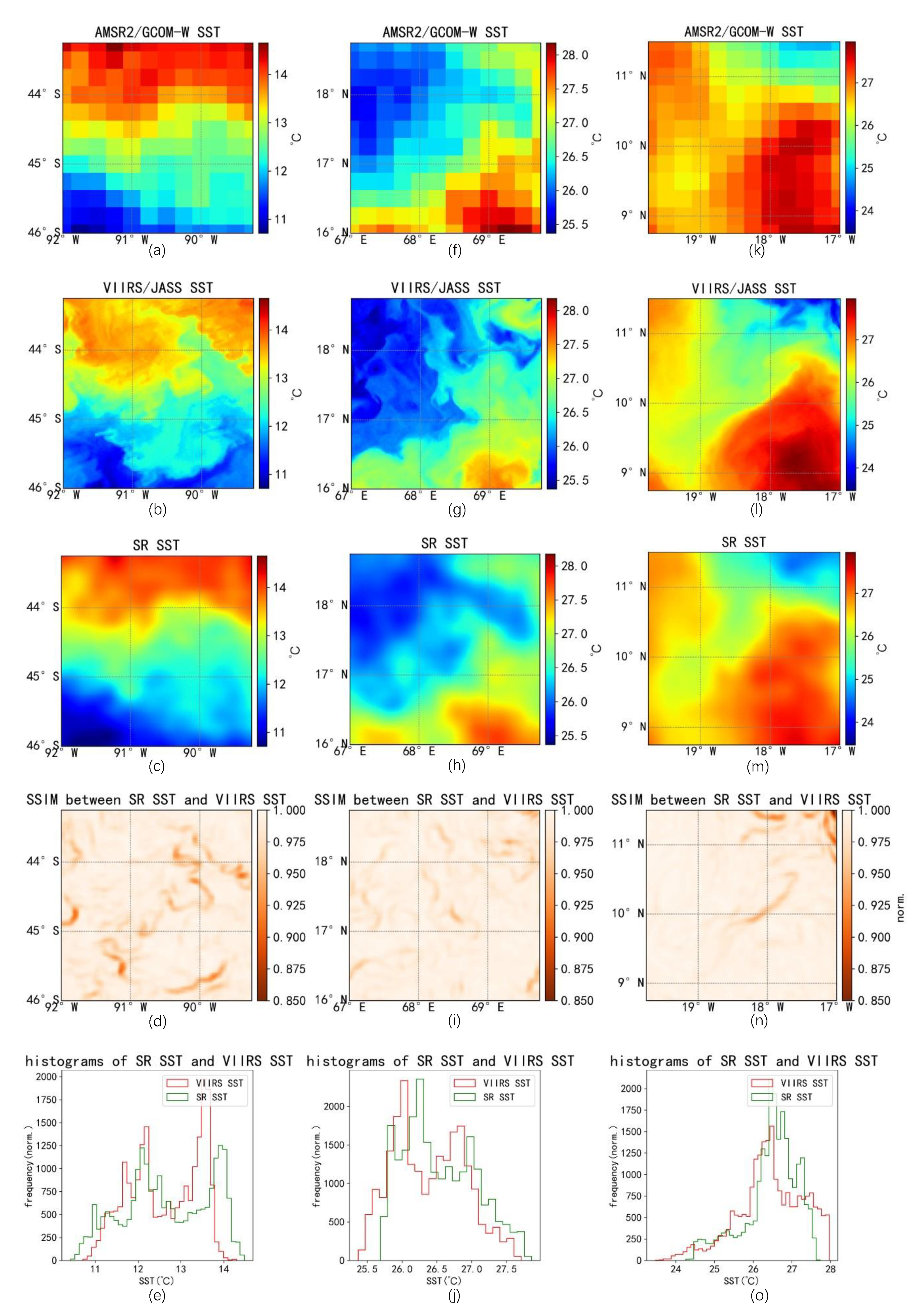
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yang, C.; Leonelli, F.E.; Marullo, S.; Artale, V.; Beggs, H.; Nardelli, B.B.; Chin, T.M.; De Toma, V.; Good, S.; Huang, B.; et al. Sea Surface Temperature Intercomparison in the Framework of the Copernicus Climate Change Service (C3S). J. Clim. 2021, 34, 5257–5283. [Google Scholar] [CrossRef]
- Tandeo, P.; Chapron, B.; Ba, S.; Autret, E.; Fablet, R. Segmentation of Mesoscale Ocean Surface Dynamics Using Satellite SST and SSH Observations. IEEE Trans. Geosci. Remote Sens. 2014, 52, 4227–4235. [Google Scholar] [CrossRef]
- Carroll, A.G.; Armstrong, E.M.; Beggs, H.M.; Bouali, M.; Casey, K.S.; Corlett, G.K.; Dash, P.; Donlon, C.J.; Gentemann, C.L.; Høyer, J.L.; et al. Observational Needs of Sea Surface Temperature. Front. Mar. Sci. 2019, 6, 420. [Google Scholar] [CrossRef]
- Chin, T.M.; Vazquez-Cuervo, J.; Armstrong, E.M. A multi-scale high-resolution analysis of global sea surface temperature. Remote Sens. Env. 2017, 200, 154–169. [Google Scholar] [CrossRef]
- Ping, B.; Su, F.; Han, X.; Meng, Y. Applications of Deep Learning-Based Super-Resolution for Sea Surface Temperature Reconstruction. IEEE J. Stars 2021, 14, 887–896. [Google Scholar] [CrossRef]
- Martin, S. An Introduction to Ocean Remote Sensing; Cambridge University Press: Cambridge, UK, 2014; pp. 86–89. ISBN 978-1-107-01938-6. [Google Scholar]
- Sato, H.; Fujimoto, S.; Tomizawa, N.; Inage, H.; Yokota, T.; Kudo, H.; Fan, R.; Kawamoto, K.; Honda, Y.; Kobayashi, T.; et al. Impact of a Deep Learning-based Super-resolution Image Reconstruction Technique on High-contrast Computed Tomography: A Phantom Study. Acad. Radiol. 2023, 30, 2657–2665. [Google Scholar] [CrossRef] [PubMed]
- Dong, C.; Loy, C.C.; He, K.; Tang, X. Image Super-Resolution Using Deep Convolutional Networks. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 38, 295–307. [Google Scholar] [CrossRef] [PubMed]
- Dong, C.; Loy, C.C.; Tang, X. Accelerating the Super-Resolution Convolutional Neural Network. In Proceedings of the Computer Vision–ECCV 2016: 14th European Conference, Amsterdam, The Netherlands, 11–14 October 2016; Leibe, B., Matas, J., Sebe, N., Welling, M., Eds.; Springer International Publishing: Cham, Switzerland, 2016; pp. 391–407. [Google Scholar] [CrossRef]
- Kim, J.; Lee, J.K.; Lee, K.M. Accurate Image Super-Resolution Using Very Deep Convolutional Networks. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 1646–1654. [Google Scholar]
- Haut, J.M.; Paoletti, M.E.; Fernandez-Beltran, R.; Plaza, J.; Plaza, A.; Li, J. Remote Sensing Single-Image Superreso-lution Based on a Deep Compendium Model. IEEE Geosci. Remote Sens. Lett. 2019, 16, 1432–1436. [Google Scholar] [CrossRef]
- Ducournau, A.; Fablet, R. Deep Learning for Ocean Remote Sensing: An Application of Convolutional Neural Networks for Super-Resolution on Satellite-Derived SST Data. In Proceedings of the 2016 9th Iapr Workshop On Pattern Recognition in Remote Sensing (Prrs), Cancun, Mexico, 4 December 2016. [Google Scholar] [CrossRef]
- Khoo, J.J.D.; Lim, K.H.; Pang, P.K. Deep Learning Super Resolution of Sea Surface Temperature on South China Sea. In Proceedings of the 2022 International Conference on Green Energy, Computing and Sustainable Technology (GECOST), Miri Sarawak, Malaysia, 26–28 October 2022; pp. 176–180. [Google Scholar] [CrossRef]
- Lloyd, D.T.; Abela, A.; Farrugia, R.A.; Galea, A.; Valentino, G. Optically Enhanced Super-Resolution of Sea Surface Temperature Using Deep Learning. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–14. [Google Scholar] [CrossRef]
- Izumi, T.; Amagasaki, M.; Ishida, K.; Kiyama, M. Super-resolution of sea surface temperature with convolutional neural network and generative adversarial network-based methods. J. Water Clim. Chang. 2022, 13, 1673–1683. [Google Scholar] [CrossRef]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An Image is Worth 16 × 16 Words: Transformers for Image Recognition at Scale. arXiv 2020, arXiv:2010.11929. [Google Scholar] [CrossRef]
- Lei, S.; Shi, Z.; Mo, W. Transformer-Based Multistage Enhancement for Remote Sensing Image Super-Resolution. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–11. [Google Scholar] [CrossRef]
- Jonasson, O.; Gladkova, I.; Ignatov, A.; Kihai, Y. Algorithmic Improvements and Consistency Checks of the NOAA Global Gridded Super-Collated SSTs from Low Earth Orbiting Satellites (L3S-LEO). In Proceedings of the Ocean Sensing and Monitoring XIII, Online. 12–16 April 2021; Volume 11752. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, A.; Polosukhin, I. Attention is all you need. arXiv 2017, arXiv:1706.03762. [Google Scholar] [CrossRef]
- Ba, J.L.; Kiros, J.R.; Hinton, G.E. Layer normalization. arXiv 2016, arXiv:1607.06450. [Google Scholar] [CrossRef]
- Hendrycks, D.; Gimpel, K. Gaussian error linear units (gelus). arXiv 2016, arXiv:1606.08415. [Google Scholar] [CrossRef]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L.; et al. PyTorch: An Imperative Style, High-Performance Deep Learning Library. arXiv 2019, arXiv:1912.01703. [Google Scholar] [CrossRef]
- Xu, B.; Wang, N.; Chen, T.; Li, M. Empirical evaluation of rectified activations in convolutional network. arXiv 2015, arXiv:1505.00853. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam. A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar] [CrossRef]
- Huang, J.; Mumford, D. Statistics of natural images and models. In Proceedings of the 1999 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (Cat. No PR00149), Fort Collins, CO, USA, 23–25 June 1999; pp. 541–547. [Google Scholar] [CrossRef]
- Jost, L. Entropy and diversity. Oikos 2006, 113, 363–365. [Google Scholar] [CrossRef]




| Model | Mean Bias (°C) | RSD (°C) | RMS (°C) | N |
|---|---|---|---|---|
| Transformer | 0.10 | 0.35 | 0.48 | 213,052,500 |
| DCM | 0.12 | 0.37 | 0.50 | 213,052,500 |
| FSRCNN | 0.13 | 0.36 | 0.49 | 213,052,500 |
| VDSR | 0.15 | 0.35 | 0.49 | 213,052,500 |
| Bilinear | 0.21 | 0.43 | 0.55 | 213,052,500 |
| Cubic | 0.18 | 0.41 | 0.53 | 213,052,500 |
| Transformer | DCM | FSRCNN | VDSR | AMSR2 | VIIRS | Bilinear | Cubic | |
|---|---|---|---|---|---|---|---|---|
| Entropy | 4.20 | 4.19 | 4.19 | 4.18 | 4.12 | 4.24 | 4.18 | 4.22 |
| Definition | 75.46 | 57.69 | 57.40 | 50.10 | 3.99 | 128.08 | 48.85 | 52.80 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zou, R.; Wei, L.; Guan, L. Super Resolution of Satellite-Derived Sea Surface Temperature Using a Transformer-Based Model. Remote Sens. 2023, 15, 5376. https://doi.org/10.3390/rs15225376
Zou R, Wei L, Guan L. Super Resolution of Satellite-Derived Sea Surface Temperature Using a Transformer-Based Model. Remote Sensing. 2023; 15(22):5376. https://doi.org/10.3390/rs15225376
Chicago/Turabian StyleZou, Runtai, Li Wei, and Lei Guan. 2023. "Super Resolution of Satellite-Derived Sea Surface Temperature Using a Transformer-Based Model" Remote Sensing 15, no. 22: 5376. https://doi.org/10.3390/rs15225376
APA StyleZou, R., Wei, L., & Guan, L. (2023). Super Resolution of Satellite-Derived Sea Surface Temperature Using a Transformer-Based Model. Remote Sensing, 15(22), 5376. https://doi.org/10.3390/rs15225376