Sea Clutter Suppression Using Smoothed Pseudo-Wigner–Ville Distribution–Singular Value Decomposition during Sea Spikes
Abstract
1. Introduction
2. Preliminaries
2.1. SVD Algorithm
2.2. SPWVD Algorithm
- Pseudo-Wigner–Ville distribution (PWVD);The most fundamental improvement made to the WVD is the application of a window function to the parameter in the time domain.where * denotes a one-dimensional convolution in terms of frequency f.
- Smoothed Wigner–Ville distribution (SWVD);Smoothing the WVD directly yields the following:where ** represents a two-dimensional convolution, the parameters involved are time t and frequency f, and denotes a smoothing filter.
- Smoothed pseudo-Wigner–Ville distribution (SPWVD).In simultaneously applying the window functions and to the parameters t and , while guaranteeing that , we obtain the following:
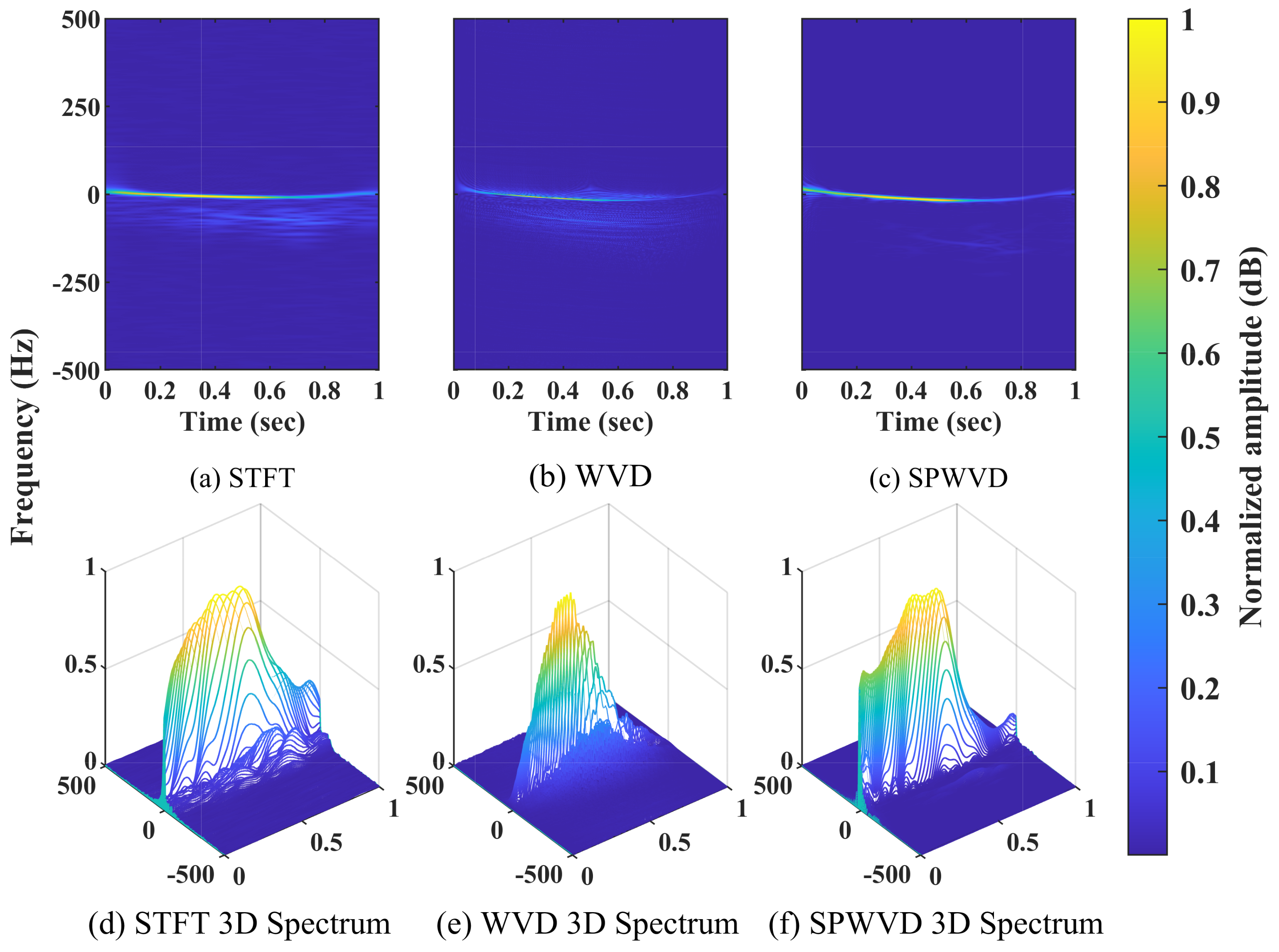
2.3. Time–Frequency Transforms of Radar Echoes
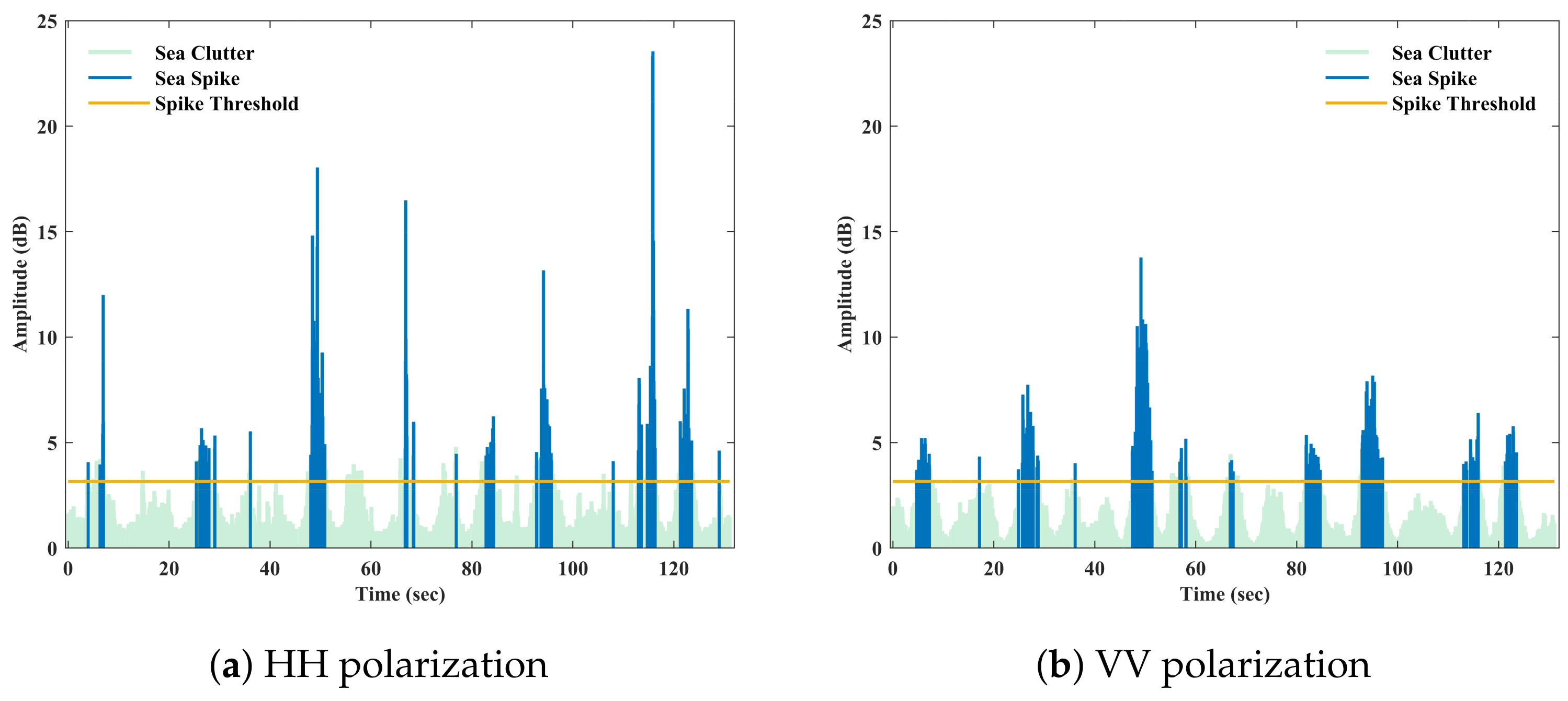
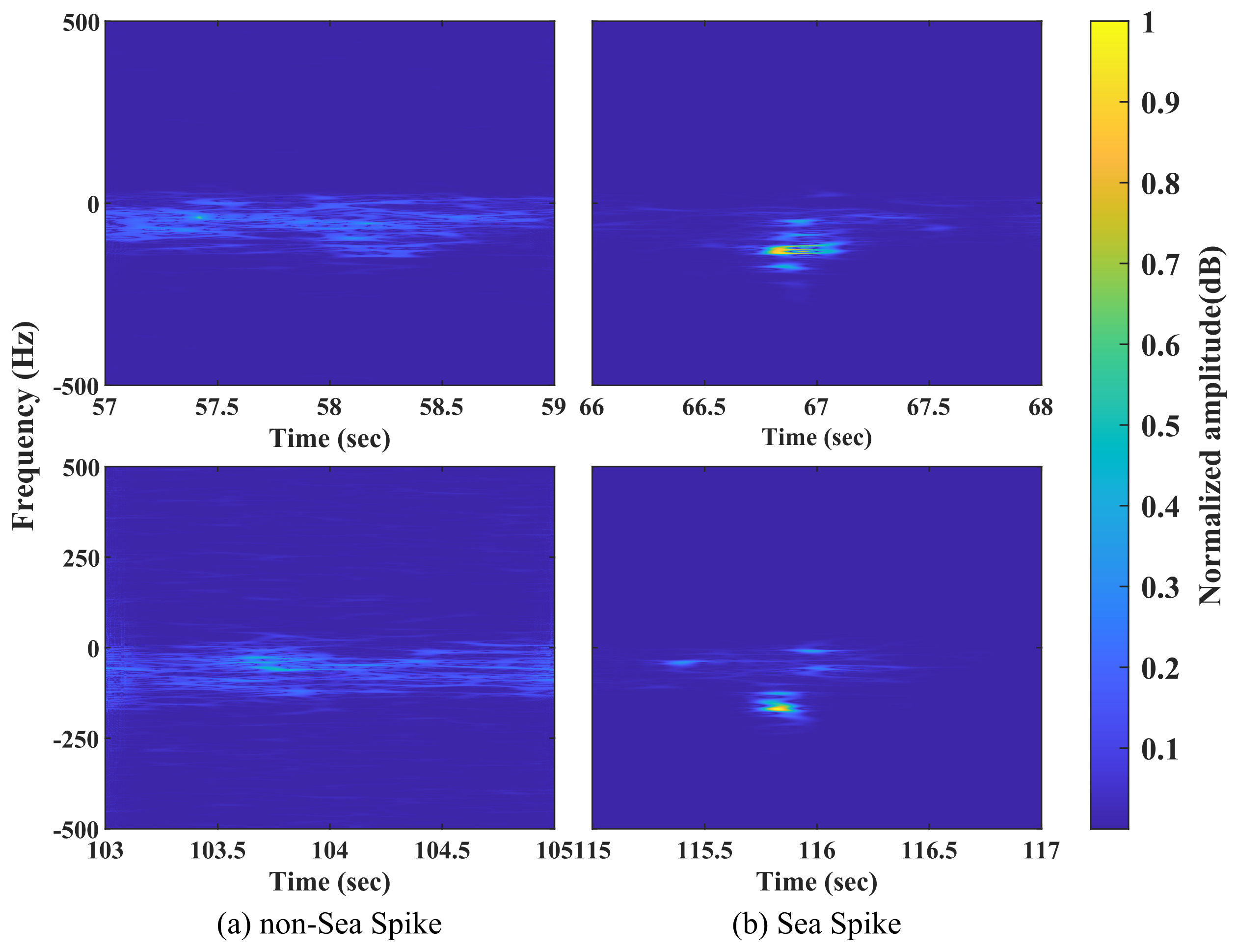
2.4. Sea Spike Determination
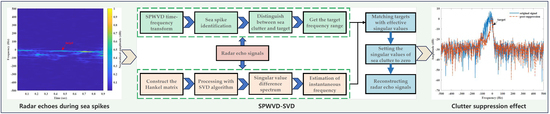
3. SPWVD-SVD Sea Clutter Suppression Algorithm
| Algorithm 1: Pseudo-code of the SPWVD-SVD algorithm. |
 |
3.1. Target and Sea Spike Determination
3.2. Singular Value Difference Spectrum
3.3. Estimating Target Frequency
4. Experiments and Discussion
4.1. IPIX Data Sources
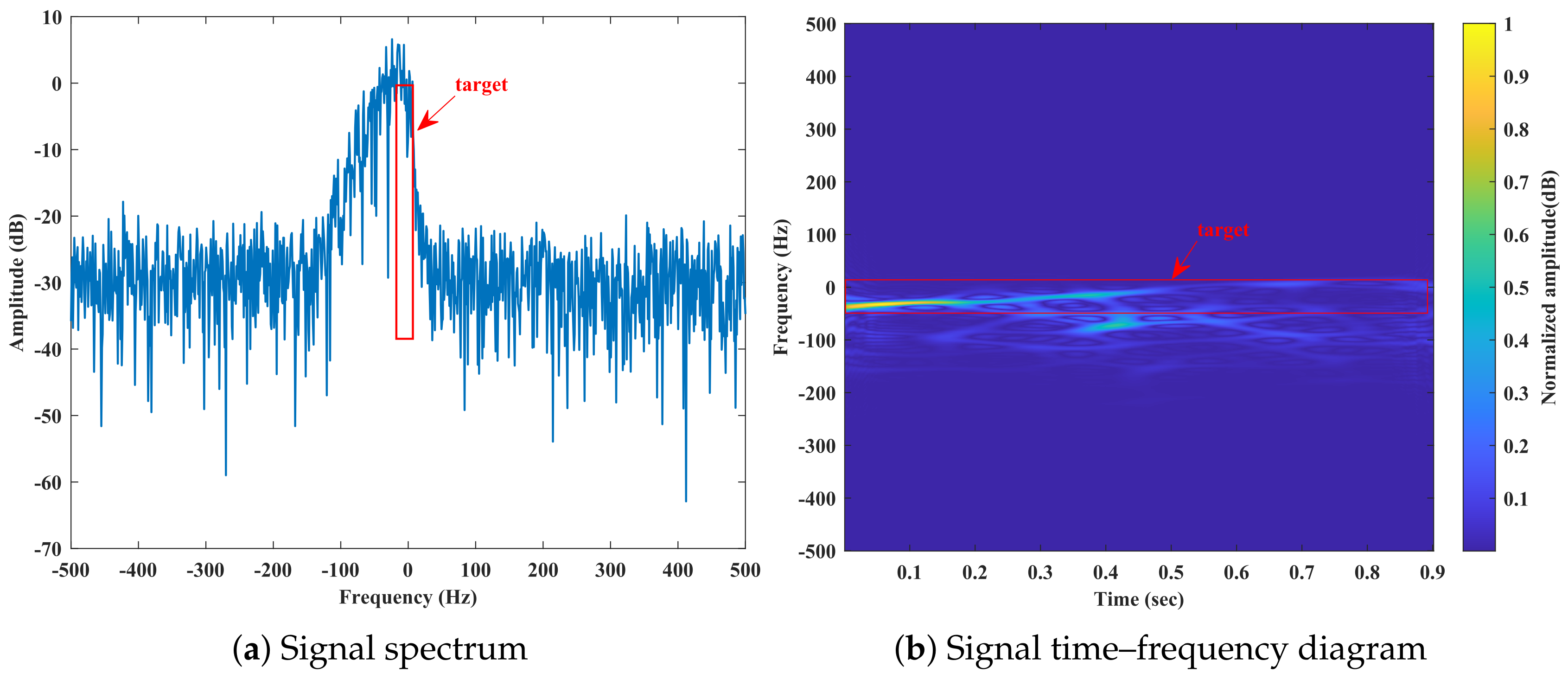
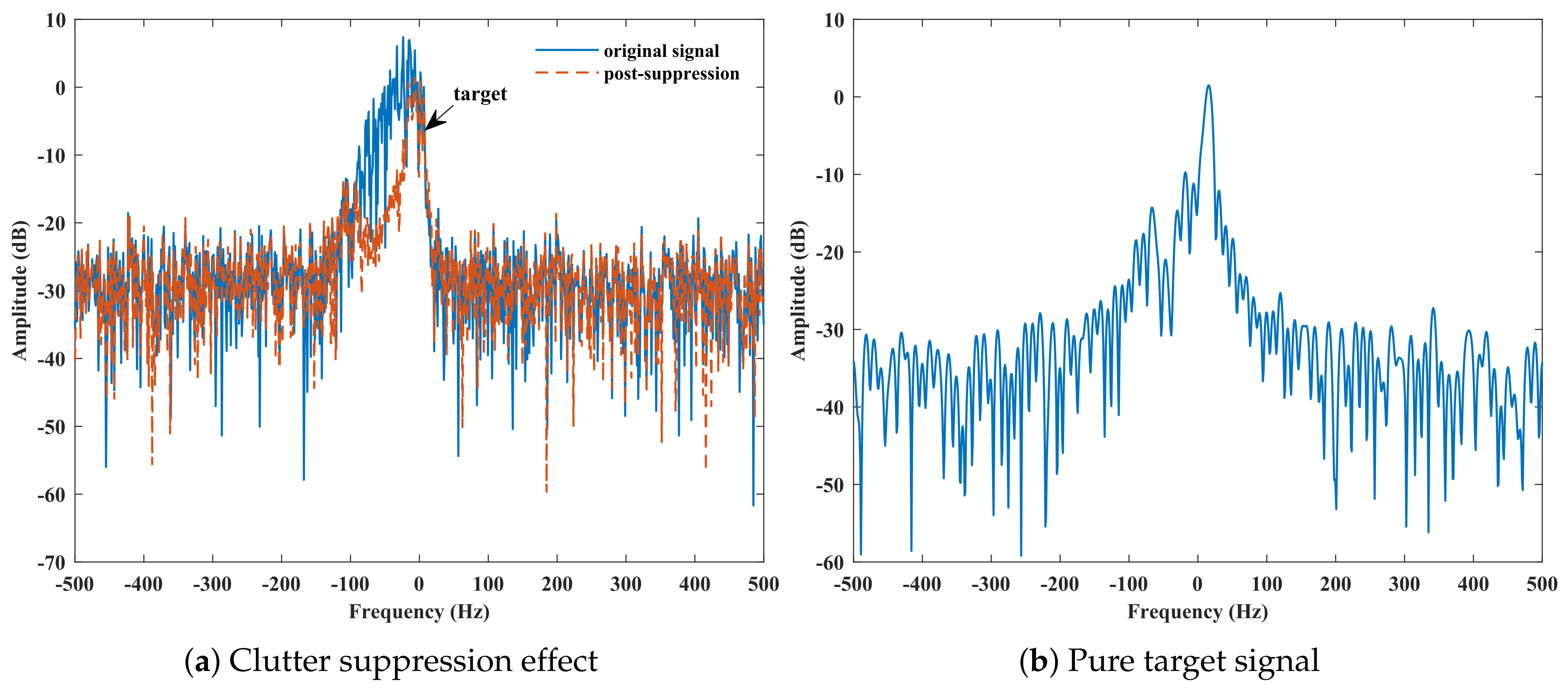
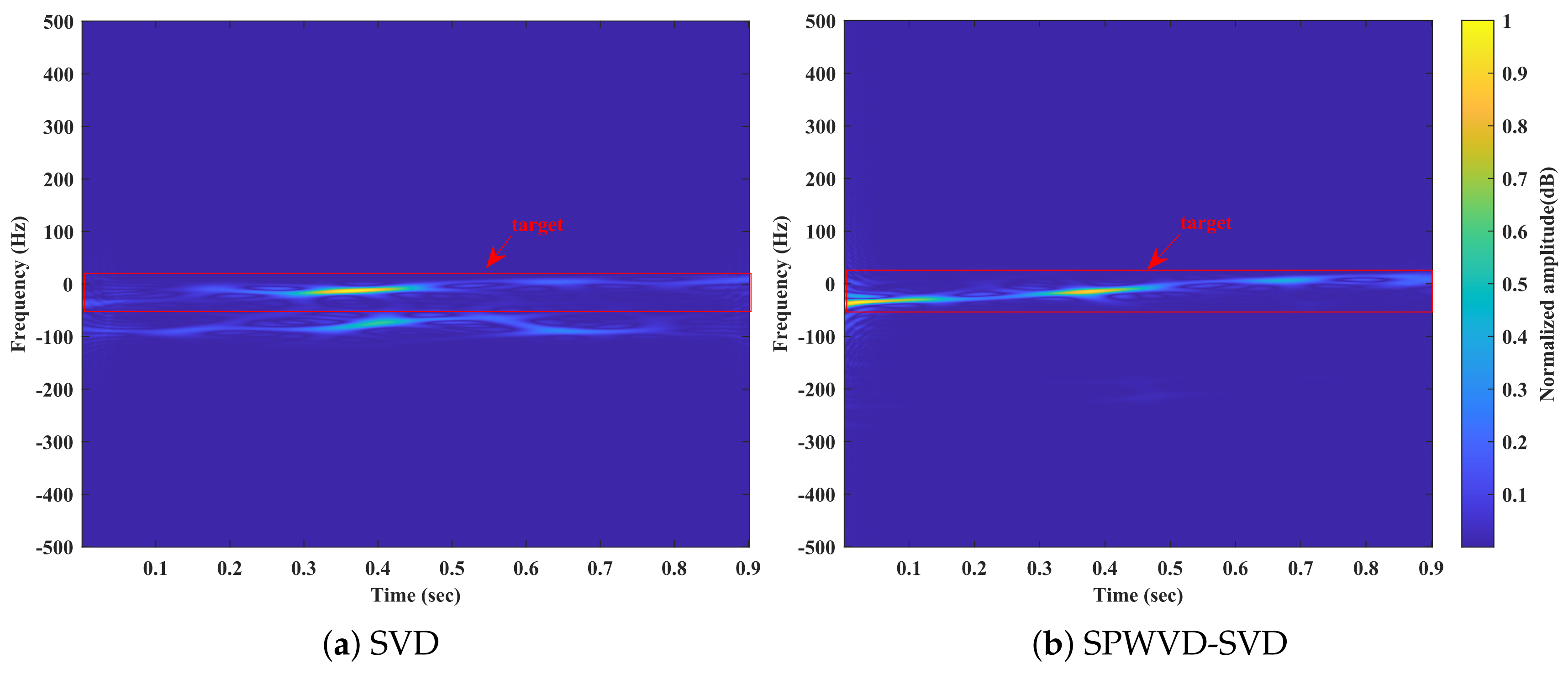
4.2. Verification of the SPWVD-SVD Suppression Algorithm
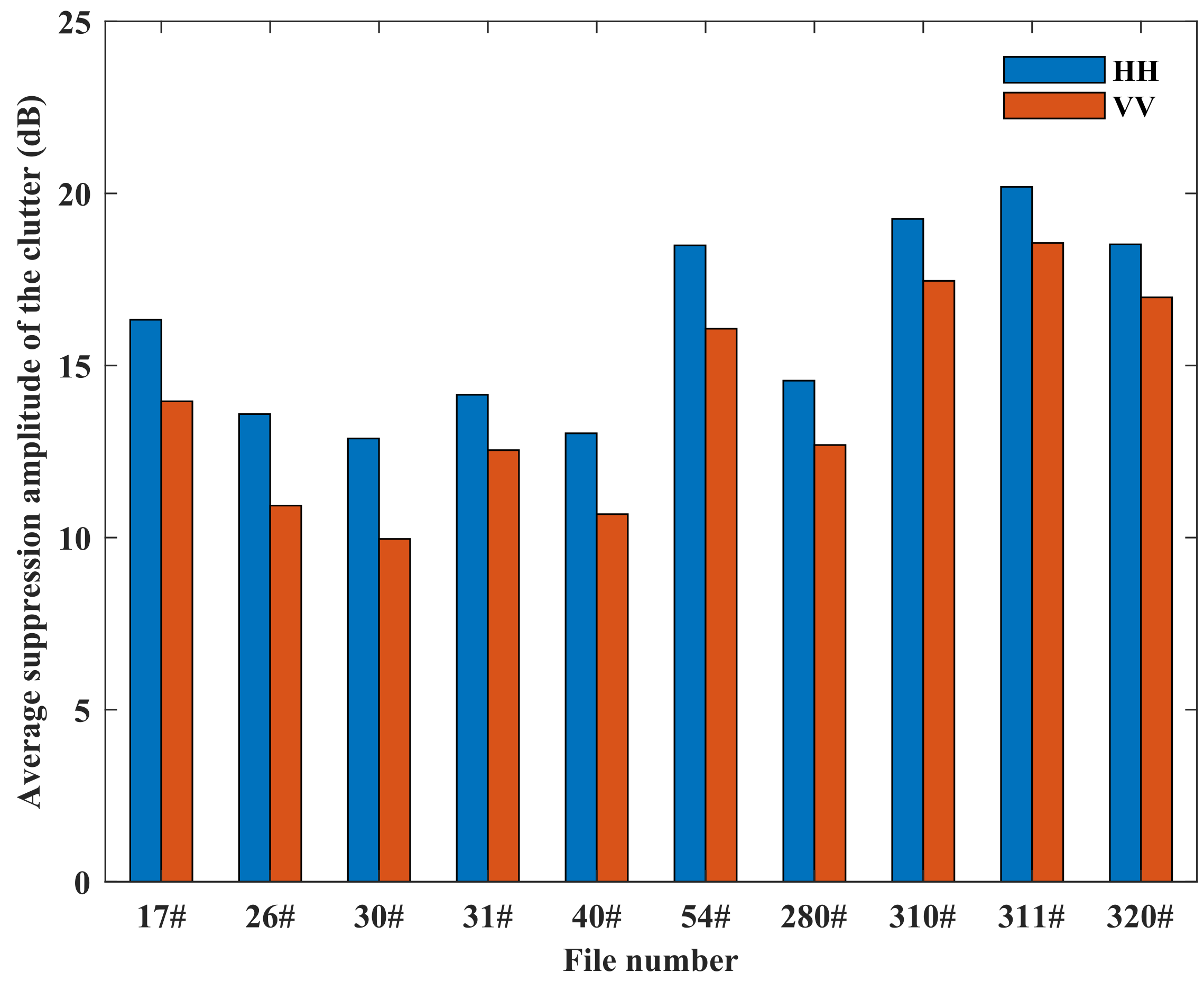
4.3. Suppression Effects under Different Sea Conditions
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shuwen, X.; Xiaohui, B.; Zixun, G.; Penglang, S. Status and prospects of feature-based detection methods for floating targets on the sea surface. J. Radars 2020, 9, 684–714. [Google Scholar]
- You, H.; Yong, H.; Jian, G.; Xiaolong, C. An overview on radar target detection in sea clutter. Mod. Radar 2014, 36, 1–9. [Google Scholar]
- Wang, H.; Kirlin, R.L. Improvement of high frequency ocean surveillance radar using subspace methods based on sea clutter suppression. In Proceedings of the Sensor Array and Multichannel Signal Processing Workshop, Rosslyn, VA, USA, 6 August 2002; pp. 557–560. [Google Scholar]
- Khan, R.; Power, D.; Walsh, J. Ocean clutter suppression for an HF ground wave radar. In Proceedings of the CCECE’97. Canadian Conference on Electrical and Computer Engineering. Engineering Innovation: Voyage of Discovery. Conference Proceedings, St. John’s, NL, Canada, 25–28 May 1997; Volume 2, pp. 512–515. [Google Scholar]
- Lu, K.; Liu, X.; Liu, Y. Ionospheric decontamination and sea clutter suppression for HF skywave radars. IEEE J. Ocean. Eng. 2005, 30, 455–462. [Google Scholar] [CrossRef]
- Lu, X.; Sun, R. A study on clutter cancellation method based on modified Hankel matrix singular value decomposition. Mod. Radar 2012, 34, 19–26. [Google Scholar]
- Chen, Z.; He, C.; Zhao, C.; Xie, F. Using SVD-FRFT filtering to suppress first-order sea clutter in HFSWR. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1076–1080. [Google Scholar] [CrossRef]
- Yan, Y.; Wu, G.; Dong, Y.; Bai, Y. Floating small target detection in sea clutter based on the singular value decomposition of low rank perturbed random matrices. In Proceedings of the 2021 IEEE 5th Advanced Information Technology, Electronic and Automation Control Conference (IAEAC), Chongqing, China, 12–14 March 2021; pp. 527–531. [Google Scholar]
- Stankovic, L.; Thayaparan, T.; Dakovic, M. Signal decomposition by using the S-method with application to the analysis of HF radar signals in sea-clutter. IEEE Trans. Signal Process. 2006, 54, 4332–4342. [Google Scholar] [CrossRef]
- Zuo, L.; Li, M.; Zhang, X.; Wang, Y.; Wu, Y. An efficient method for detecting slow-moving weak targets in sea clutter based on time–frequency iteration decomposition. IEEE Trans. Geosci. Remote Sens. 2012, 51, 3659–3672. [Google Scholar] [CrossRef]
- Zhang, X.W.; Yang, D.D.; Guo, J.X.; Zuo, L. Weak moving target detection based on short-time fourier transform in sea clutter. In Proceedings of the 2019 IEEE 4th International Conference on Signal and Image Processing (ICSIP), Wuxi, China, 19–21 July 2019; pp. 415–419. [Google Scholar]
- Li, Z.; Ye, H.; Liu, Z.; Sun, Z.; An, H.; Wu, J.; Yang, J. Bistatic SAR clutter-ridge matched STAP method for nonstationary clutter suppression. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–14. [Google Scholar] [CrossRef]
- Hu, J.; Tung, W.W.; Gao, J. Detection of low observable targets within sea clutter by structure function based multifractal analysis. IEEE Trans. Antennas Propag. 2006, 54, 136–143. [Google Scholar] [CrossRef]
- Guan, J.; Liu, N.B.; Huang, Y.; He, Y. Fractal characteristic in frequency domain for target detection within sea clutter. IET Radar Sonar Navig. 2012, 6, 293–306. [Google Scholar] [CrossRef]
- Metcalf, J.; Blunt, S.D.; Himed, B. A machine learning approach to cognitive radar detection. In Proceedings of the 2015 IEEE Radar Conference (RadarCon), Arlington, VA, USA, 10–15 May 2015; pp. 1405–1411. [Google Scholar]
- Callaghan, D.; Burger, J.; Mishra, A.K. A machine learning approach to radar sea clutter suppression. In Proceedings of the 2017 IEEE Radar Conference (RadarConf), Seattle, WA, USA, 8–12 May 2017; pp. 1222–1227. [Google Scholar]
- Yan, Y.; Xing, H. Small floating target detection method based on chaotic long short-term memory network. J. Mar. Sci. Eng. 2021, 9, 651. [Google Scholar] [CrossRef]
- Djebbari, A.; Reguig, F.B. Short-time Fourier transform analysis of the phonocardiogram signal. In Proceedings of the ICECS 2000. 7th IEEE International Conference on Electronics, Circuits and Systems (Cat. No. 00EX445), Jounieh, Lebanon, 17–20 December 2000; Volume 2, pp. 844–847. [Google Scholar]
- Barbarossa, S.; Zanalda, A. A combined Wigner-Ville and Hough transform for cross-terms suppression and optimal detection and parameter estimation. In Proceedings of the ICASSP-92: 1992 IEEE International Conference on Acoustics, Speech, and Signal Processing, San Francisco, CA, USA, 23–26 March 1992; Volume 5, pp. 173–176. [Google Scholar]
- Rosenberg, L. Sea-spike detection in high grazing angle X-band sea-clutter. IEEE Trans. Geosci. Remote Sens. 2013, 51, 4556–4562. [Google Scholar] [CrossRef]
- Posner, F.L. Spiky sea clutter at high range resolutions and very low grazing angles. IEEE Trans. Aerosp. Electron. Syst. 2002, 38, 58–73. [Google Scholar] [CrossRef]
- Greco, M.; Stinco, P.; Gini, F. Identification and analysis of sea radar clutter spikes. IET Radar Sonar Navig. 2010, 4, 239–250. [Google Scholar] [CrossRef]
- Poon, M.W.; Khan, R.H.; Le-Ngoc, S. A singular value decomposition (SVD) based method for suppressing ocean clutter in high frequency radar. IEEE Trans. Signal Process. 1993, 41, 1421–1425. [Google Scholar] [CrossRef] [PubMed]
- Lv, M.; Zhou, C. Study on sea clutter suppression methods based on a realistic radar dataset. Remote Sens. 2019, 11, 2721. [Google Scholar] [CrossRef]
- Zuo, L.; Chan, X.; Lu, X.; Li, M. Decomposing sea echoes in the time-frequency domain and detecting a slow-moving weak target in the sea clutter. J. Xidian Univ. 2019, 46, 84–90. [Google Scholar]
- Zhao, X.; Ye, B. Selection of effective singular values using difference spectrum and its application to fault diagnosis of headstock. Mech. Syst. Signal Process. 2011, 25, 1617–1631. [Google Scholar] [CrossRef]
- Zhao, H.; Wu, H.; Li, J.; Zhang, H.; Wang, X. Dtree2vec: A High-Accuracy and Dynamic Scheme for Real-Time Book Recommendation by Serialized Chapters and Local Fine-Grained Partitioning. IEEE Access 2020, 8, 23197–23208. [Google Scholar] [CrossRef]


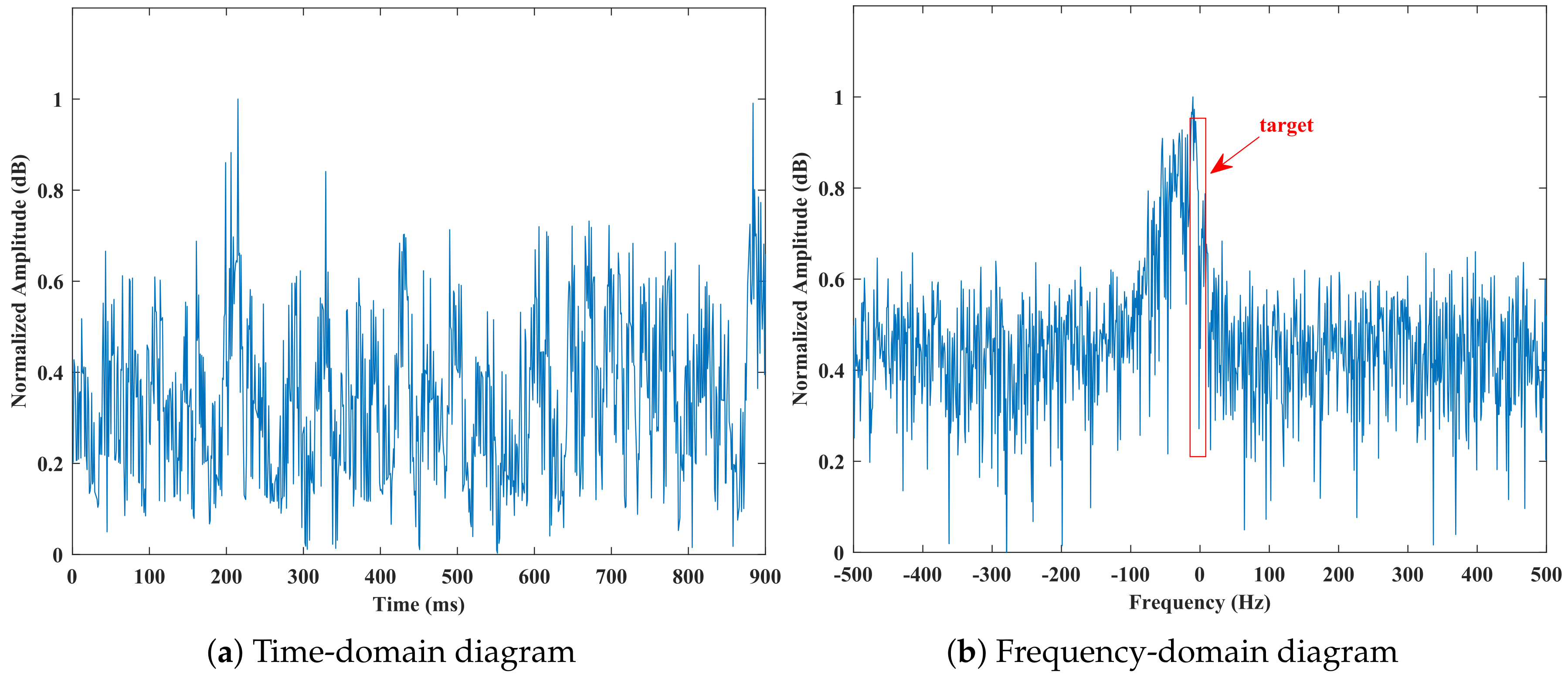
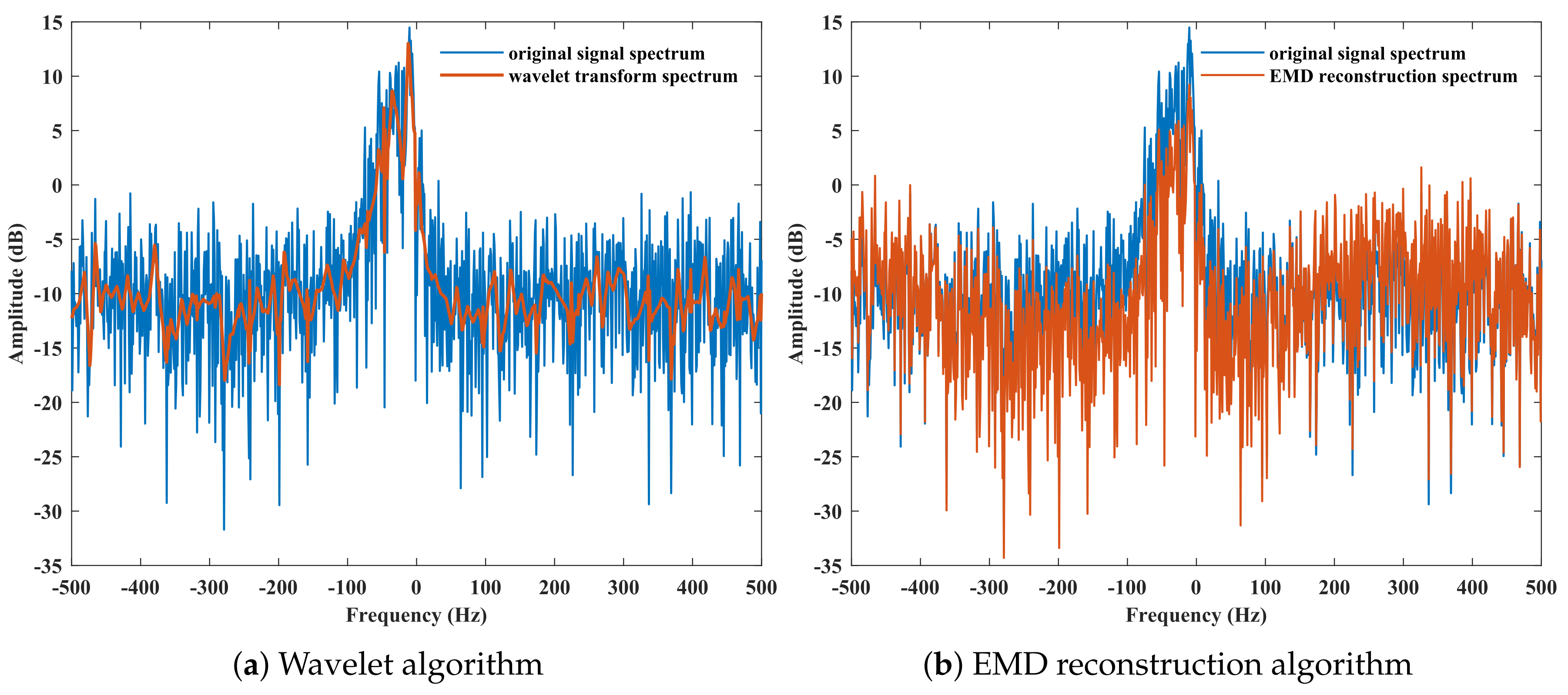


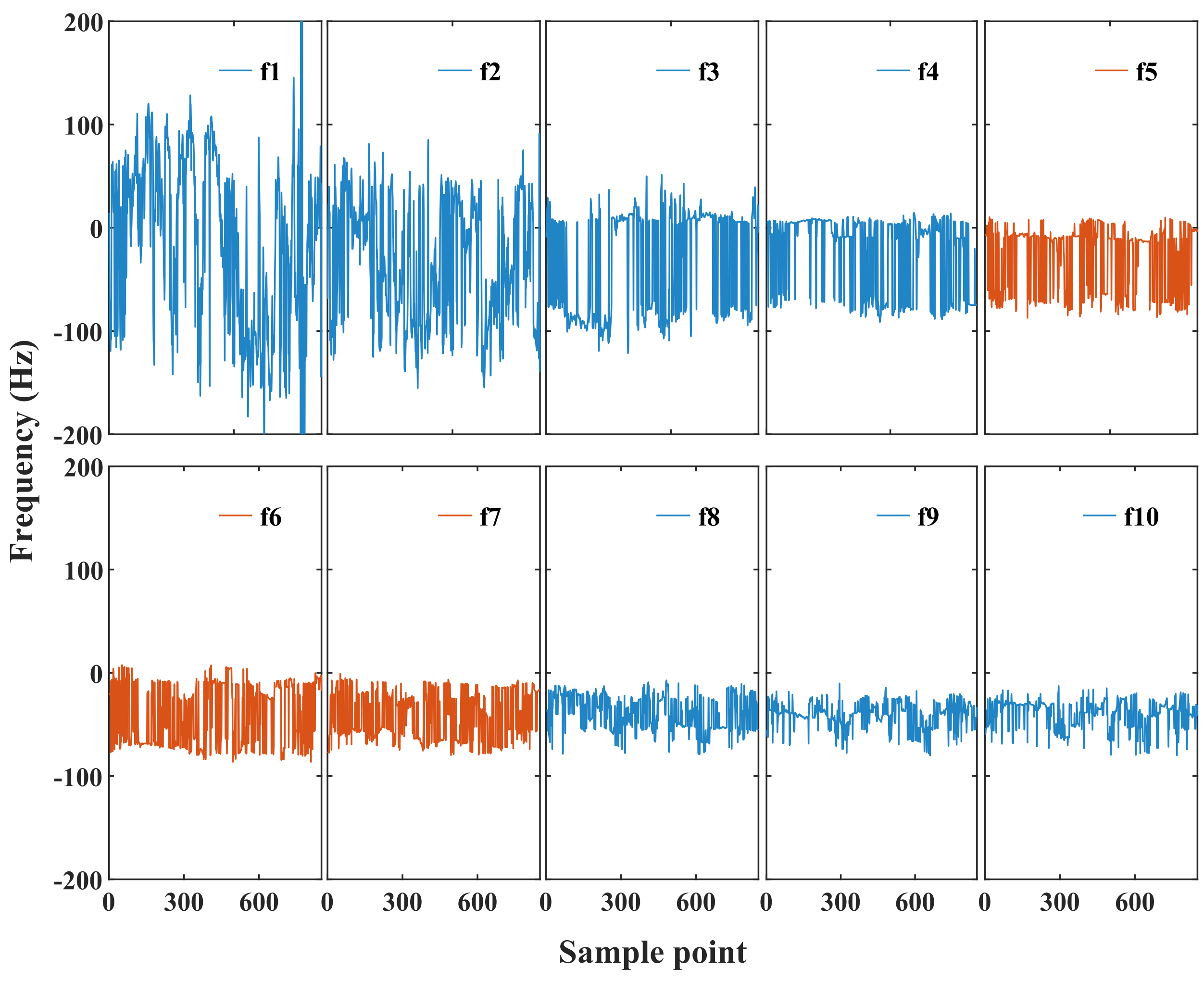


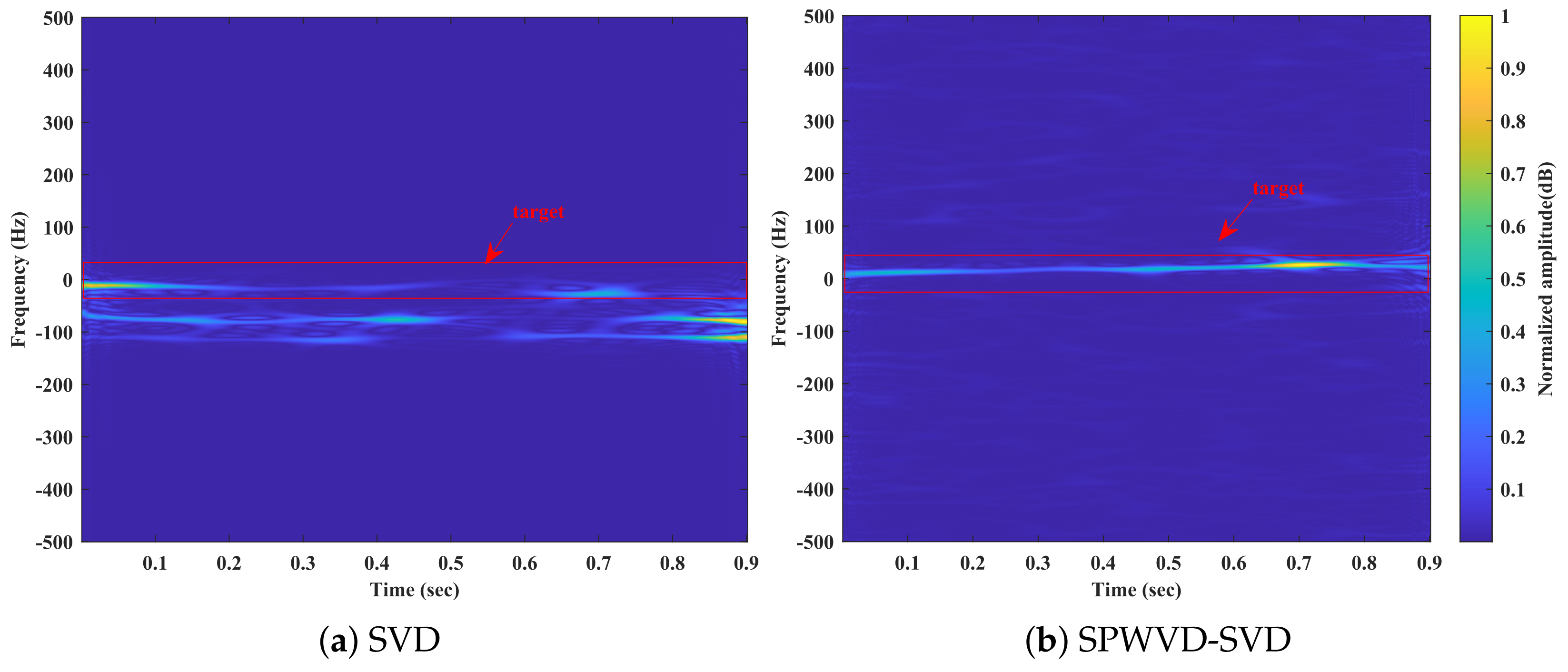
| Data Name | Wave Height (m) | Wind Speed (km/h) | Primary Bin | Secondary Bin |
|---|---|---|---|---|
| #17 | 2.2 | 9 | 9 | 8, 10, 11 |
| #26 | 1.1 | 9 | 7 | 6, 8 |
| #30 | 0.9 | 19 | 7 | 6, 8 |
| #31 | 0.9 | 19 | 7 | 6, 8, 9 |
| #40 | 1.0 | 9 | 7 | 5, 6, 8 |
| #54 | 0.7 | 20 | 8 | 7, 9, 10 |
| #280 | 1.6 | 10 | 8 | 7, 9, 10 |
| #310 | 0.9 | 33 | 7 | 6, 8, 9 |
| #311 | 0.9 | 33 | 7 | 6, 8, 9 |
| #320 | 0.9 | 28 | 7 | 6, 8, 9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, G.; Zhang, H.; Gao, Y.; Ma, B. Sea Clutter Suppression Using Smoothed Pseudo-Wigner–Ville Distribution–Singular Value Decomposition during Sea Spikes. Remote Sens. 2023, 15, 5360. https://doi.org/10.3390/rs15225360
Li G, Zhang H, Gao Y, Ma B. Sea Clutter Suppression Using Smoothed Pseudo-Wigner–Ville Distribution–Singular Value Decomposition during Sea Spikes. Remote Sensing. 2023; 15(22):5360. https://doi.org/10.3390/rs15225360
Chicago/Turabian StyleLi, Guigeng, Hao Zhang, Yong Gao, and Bingyan Ma. 2023. "Sea Clutter Suppression Using Smoothed Pseudo-Wigner–Ville Distribution–Singular Value Decomposition during Sea Spikes" Remote Sensing 15, no. 22: 5360. https://doi.org/10.3390/rs15225360
APA StyleLi, G., Zhang, H., Gao, Y., & Ma, B. (2023). Sea Clutter Suppression Using Smoothed Pseudo-Wigner–Ville Distribution–Singular Value Decomposition during Sea Spikes. Remote Sensing, 15(22), 5360. https://doi.org/10.3390/rs15225360