Deep Unfolding Sparse Bayesian Learning Network for Off-Grid DOA Estimation with Nested Array
Abstract
:1. Introduction
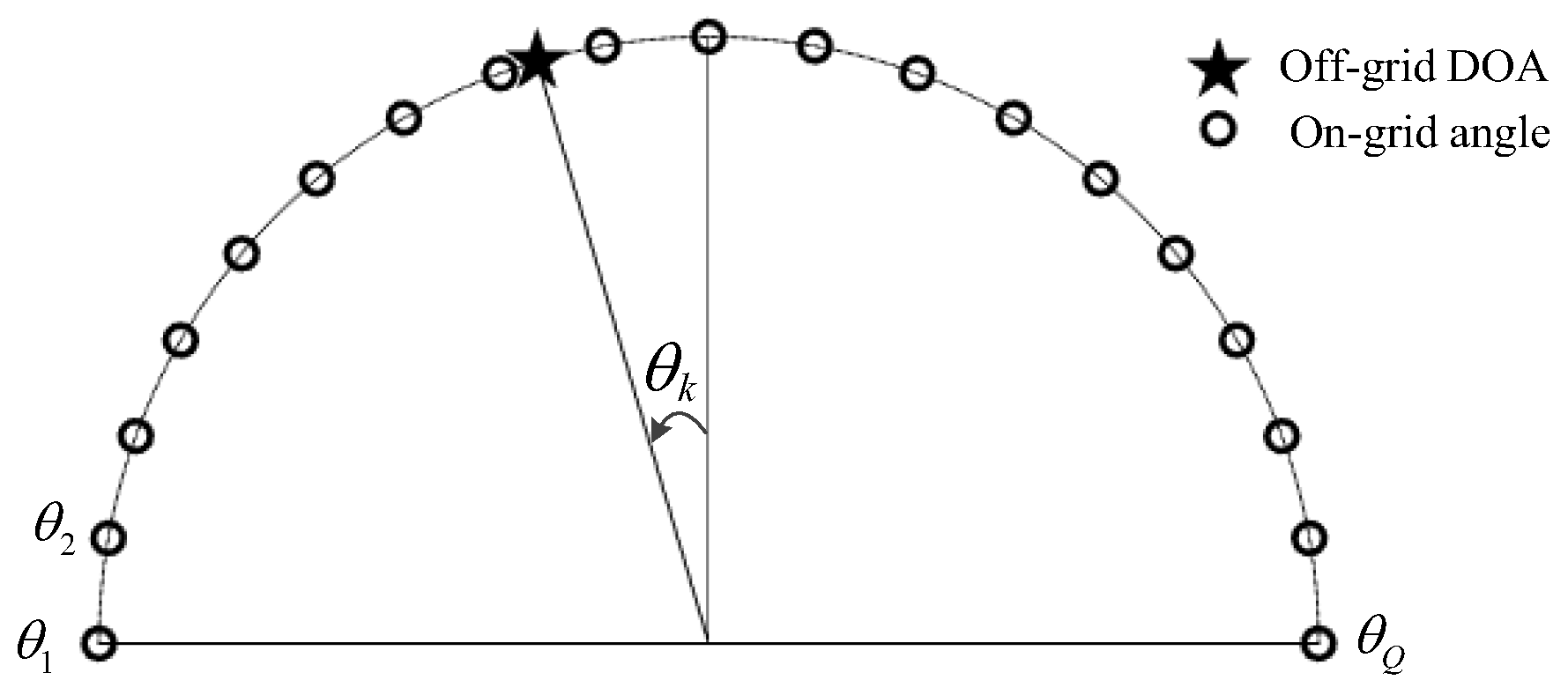
2. Signal Model for Off-Grid DOA with NA
3. Proposed Algorithm
3.1. Transformation of the Array Output to the Real Domain
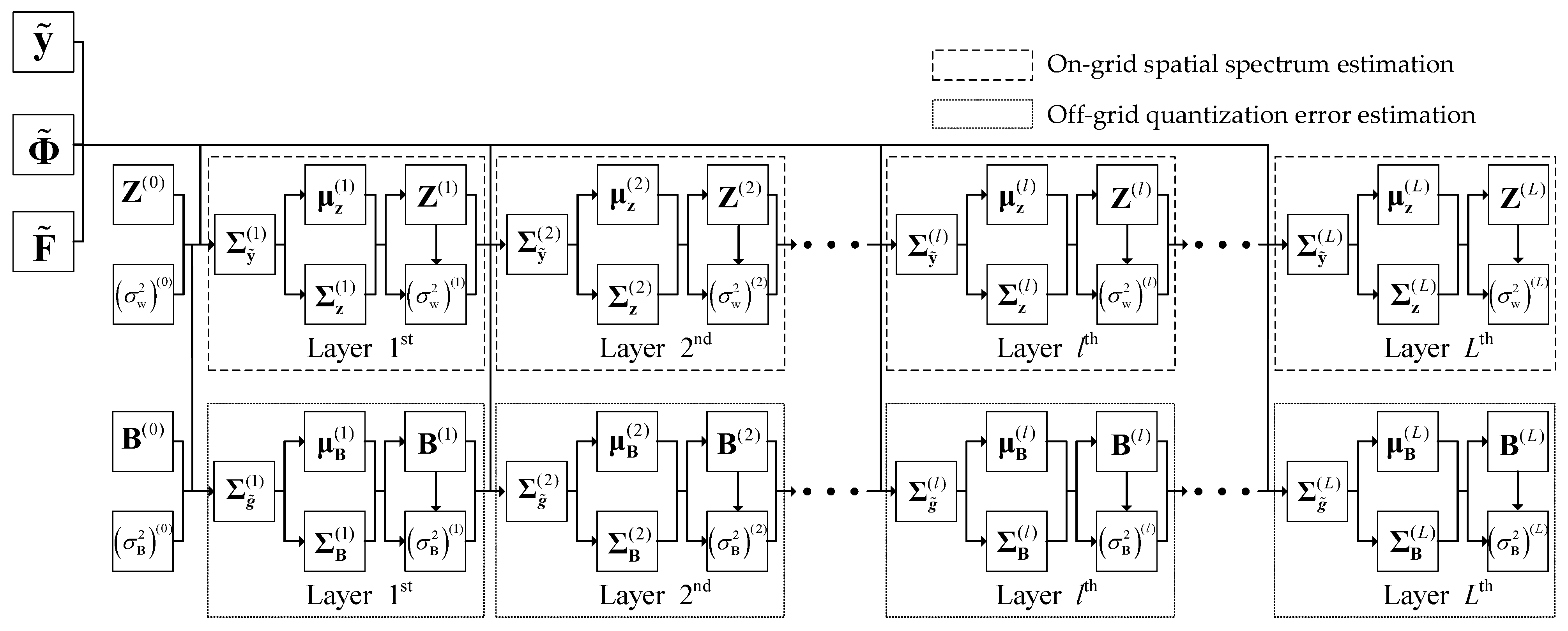
3.2. Deep Unfolding Sparse Bayesian Learning Network
3.3. Network Implementation of Proposed Method
| Algorithm 1 DSBL Network for Off-Grid DOA Estimation with NA | |
| 1: | Calculate the covariance matrix using Equation (4). |
| 2: | Apply the vector form of covariance matrix in Equation (5). |
| 3: | Combine real and imaginary parts in Equation (12) as the input of the DSBL network. |
| 4: | Perform the trained DSBL network to acquire spatial spectrum and off-grid quantization error. |
| 5: | Obtain off-grid DOA from the peaks of the spatial spectrum and the corresponding off-grid quantization error in Equation (3). |
4. Computer Simulation Experiments
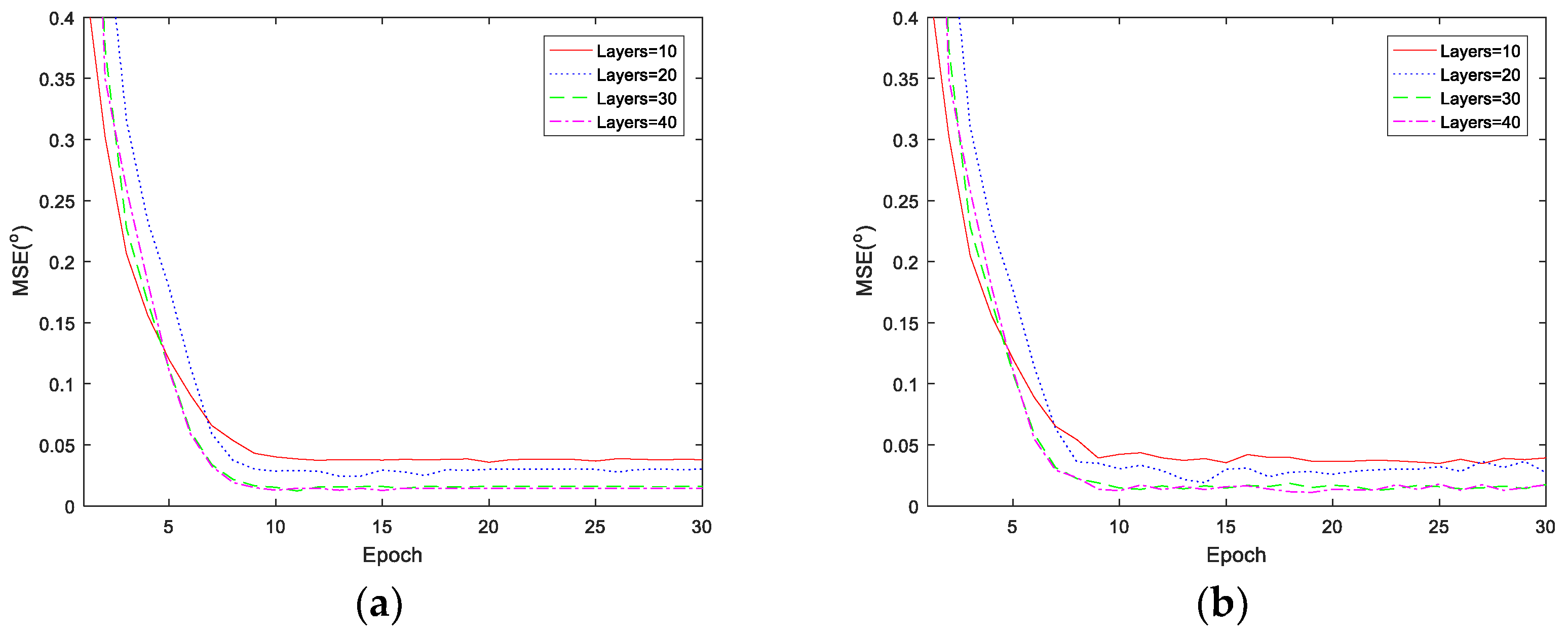
4.1. Layer Number Determination
4.2. Comparison of Convergence Performance
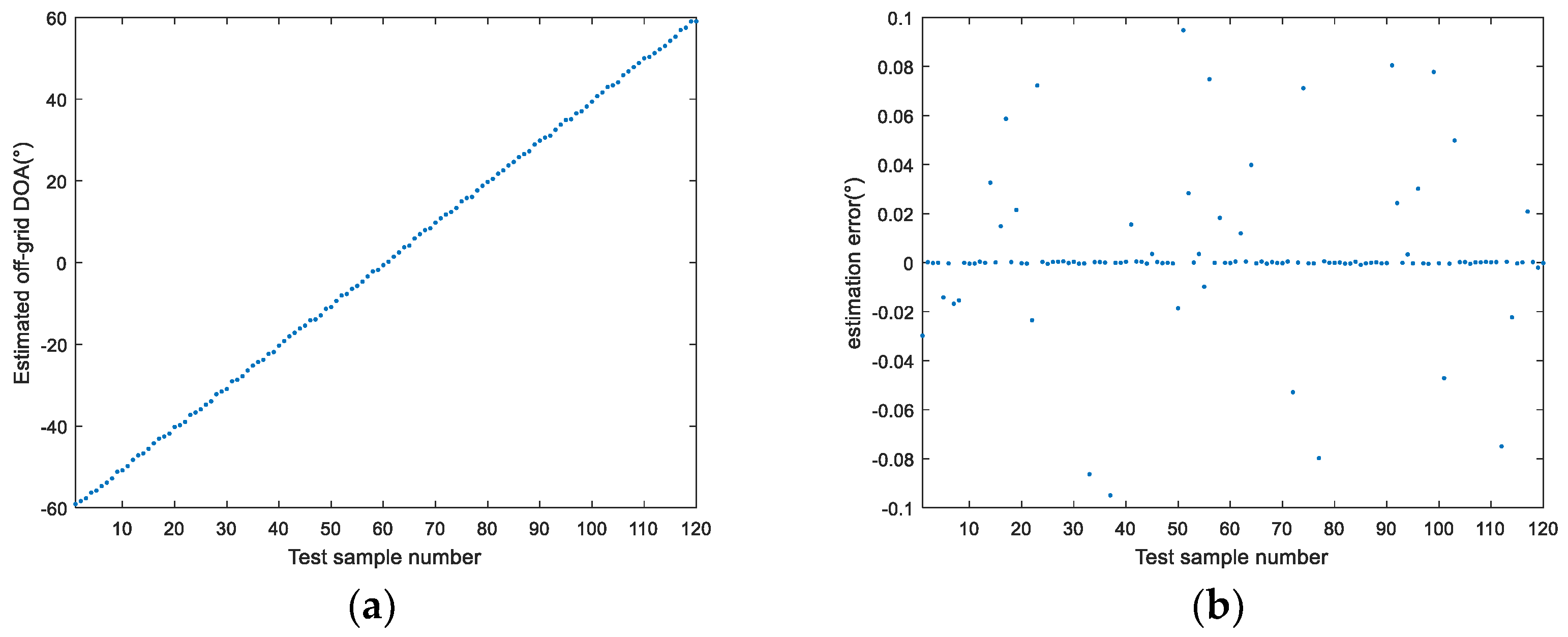
4.3. Generalization Ability for Off-Grid DOA Estimation
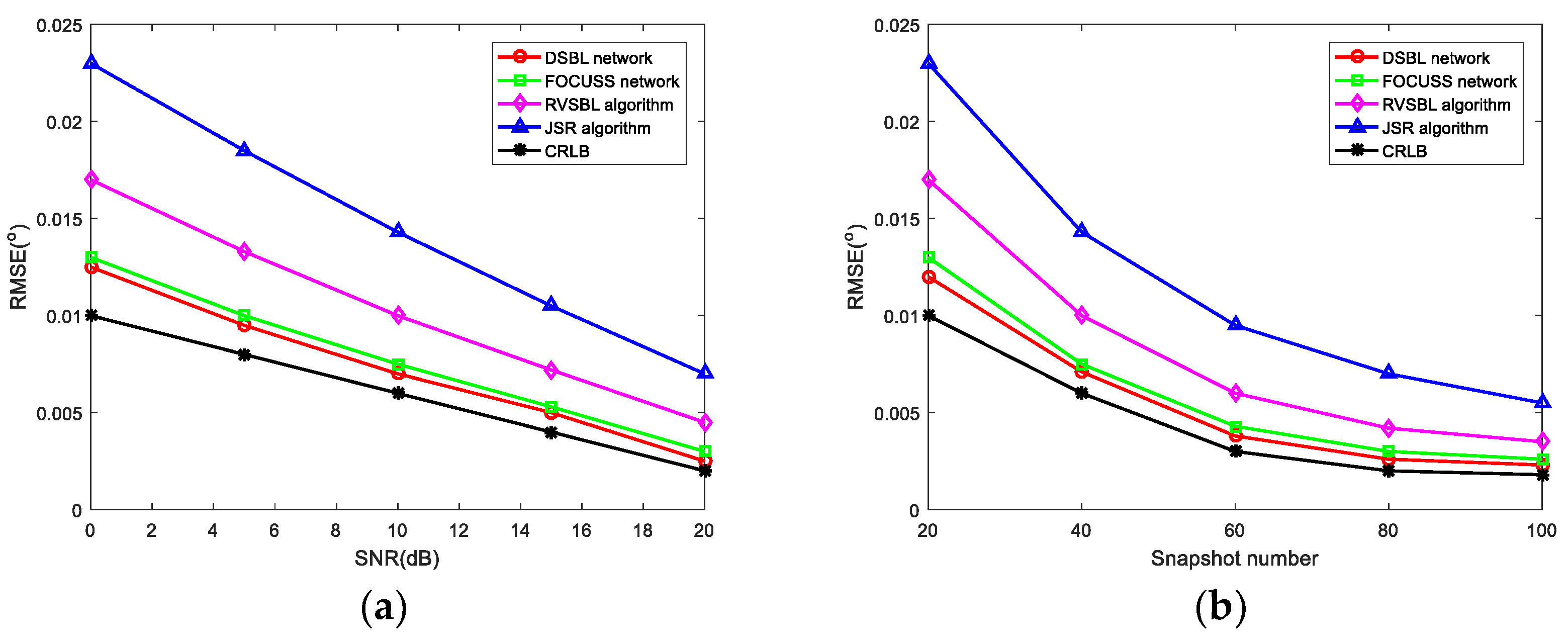
4.4. RMSE Comparison of DOA Estimation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, H.; Yan, J.; Liu, W.; Zhang, Q. Array Scheduling with Power and Bandwidth Allocation for Simultaneous Multibeam Tracking Low-Angle Targets in a VHF-MIMO Radar. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 5714–5730. [Google Scholar] [CrossRef]
- Zhang, Z.; Wen, F.; Shi, J. 2D-DOA estimation for coherent signals via a polarized uniform rectangular array. IEEE Signal Process. Lett. 2023, 30, 893–897. [Google Scholar] [CrossRef]
- Wang, X.; Guo, Y.; Wen, F. EMVS-MIMO radar with sparse Rx geometry: Tensor modeling and 2D direction finding. IEEE Trans. Aerosp. Electron. Syst. 2023. [Google Scholar] [CrossRef]
- Moffet, A. Minimum-Redundancy Linear Arrays. IEEE Trans. Antennas Propag. 1968, 16, 172–175. [Google Scholar] [CrossRef]
- Pal, P.; Vaidyanathan, P.P. Nested Arrays: A Novel Approach to Array Processing with Enhanced Degrees of Freedom. IEEE Trans. Signal Process. 2010, 58, 4167–4181. [Google Scholar] [CrossRef]
- Vaidyanathan, P.P.; Pal, P. Sparse Sensing with Co-Prime Samplers and Arrays. IEEE Trans. Signal Process. 2011, 59, 573–586. [Google Scholar] [CrossRef]
- Qin, S.; Zhang, Y.D.; Amin, M.G. Generalized Coprime Array Configurations for Direction-of-Arrival Estimation. IEEE Trans. Signal Process. 2015, 63, 1377–1390. [Google Scholar] [CrossRef]
- Sellone, F.; Serra, A. A novel online mutual coupling compensation algorithm for uniform and linear arrays. IEEE Trans. Signal Process. 2007, 55, 560–573. [Google Scholar] [CrossRef]
- BouDaher, E.; Ahmad, F.; Amin, M.G.; Hoorfar, A. Mutual coupling effect and compensation in non-uniform arrays for direction-of-arrival estimation. Digit. Signal Process. 2017, 61, 3–14. [Google Scholar] [CrossRef]
- Chen, P.; Cao, Z.; Chen, Z.; Wang, X. Off-Grid DOA Estimation Using Sparse Bayesian Learning in MIMO Radar with Unknown Mutual Coupling. IEEE Trans. Signal Process. 2019, 67, 208–220. [Google Scholar] [CrossRef]
- Donoho, D.L. Compressed Sensing. IEEE Trans. Inf. Theory 2006, 52, 1289–1306. [Google Scholar] [CrossRef]
- Candes, E.J.; Tao, T. Near-Optimal Signal Recovery from Random Projections: Universal Encoding Strategies. IEEE Trans. Inf. Theory 2006, 52, 5406–5425. [Google Scholar] [CrossRef]
- Liu, Q.; So, H.C.; Gu, Y. Off-Grid DOA Estimation with Nonconvex Regularization via Joint Sparse Representation. Signal Process. 2017, 140, 171–176. [Google Scholar] [CrossRef]
- Zhang, X.; Jiang, T.; Li, Y.; Liu, X. An Off-Grid DOA Estimation Method Using Proximal Splitting and Successive Nonconvex Sparsity Approximation. IEEE Access 2019, 7, 66764–66773. [Google Scholar] [CrossRef]
- Das, A. Theoretical and Experimental Comparison of Off-Grid Sparse Bayesian Direction-of-Arrival Estimation Algorithms. IEEE Access 2017, 5, 18075–18087. [Google Scholar] [CrossRef]
- Yang, J.; Yang, Y. A Correlation-Aware Sparse Bayesian Perspective for DOA Estimation with Off-Grid Sources. IEEE Trans. Antennas Propag. 2019, 67, 7661–7666. [Google Scholar] [CrossRef]
- Chen, F.; Dai, J.; Hu, N.; Ye, Z. Sparse Bayesian Learning for Off-Grid DOA Estimation with Nested Arrays. Digit. Signal Process. 2018, 82, 187–193. [Google Scholar] [CrossRef]
- Yang, Z.; Zhang, C.; Xie, L. Robustly Stable Signal Recovery in Compressed Sensing with Structured Matrix Perturbation. IEEE Trans. Signal Process. 2012, 60, 4658–4671. [Google Scholar] [CrossRef]
- Zhu, H.; Leus, G.; Giannakis, G.B. Sparsity-Cognizant Total Least-Squares for Perturbed Compressive Sampling. IEEE Trans. Signal Process. 2011, 59, 2002–2016. [Google Scholar] [CrossRef]
- Jagannath, R.; Hari KV, S. Block Sparse Estimator for Grid Matching in Single Snapshot DoA Estimation. IEEE Signal Process. Lett. 2013, 20, 1038–1041. [Google Scholar] [CrossRef]
- Yang, Z.; Xie, L.; Zhang, C. Off-Grid Direction of Arrival Estimation Using Sparse Bayesian Inference. IEEE Trans. Signal Process. 2013, 61, 38–43. [Google Scholar] [CrossRef]
- Tan, Z.; Yang, P.; Nehorai, A. Joint Sparse Recovery Method for Compressed Sensing with Structured Dictionary Mismatches. IEEE Trans. Signal Process. 2014, 62, 4997–5008. [Google Scholar] [CrossRef]
- Wu, X.; Zhu, W.; Yan, J. Direction of Arrival Estimation for Off-Grid Signals Based on Sparse Bayesian Learning. IEEE Sens. J. 2016, 16, 2004–2016. [Google Scholar] [CrossRef]
- Li, Y.; Tofighi, M.; Monga, V.; Eldar, Y.C. An Algorithm Unrolling Approach to Deep Image Deblurring. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Brighton, UK, 12–17 May 2019; pp. 7675–7679. [Google Scholar]
- Borgerding, M.; Schniter, P.; Rangan, S. AMP-Inspired Deep Networks for Sparse Linear Inverse Problems. IEEE Trans. Signal Process. 2017, 65, 4293–4308. [Google Scholar] [CrossRef]
- Sun, J.; Li, H.; Xu, Z. Deep ADMM-Net for Compressive Sensing MRI. In Proceedings of the Advanced Neural Information Processing Systems (NIPS), Barcelona, Spain, 5–10 December 2016; pp. 10–18. [Google Scholar]
- Yang, Y.; Sun, J.; Li, H.; Xu, Z. ADMM-CSNet: A Deep Learning Approach for Image Compressive Sensing. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 42, 521–538. [Google Scholar] [CrossRef]
- Zheng, S.; Jayasumana, S.; Romera-Paredes, B.; Vineet, V.; Su, Z.; Du, D.; Huang, C.; Torr, P.H. Conditional Random Fields as Recurrent Neural Networks. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 7–13 December 2015; pp. 1529–1537. [Google Scholar]
- Hosseini, S.A.; Yaman, B.; Moeller, S.; Hong, M.; Akçakaya, M. Dense Recurrent Neural Networks for Accelerated MRI: History-Cognizant Unrolling of Optimization Algorithms. IEEE J. Sel. Top. Signal Process. 2020, 14, 1280–1291. [Google Scholar] [CrossRef]
- Li, R.; Zhang, S.; Zhang, C.; Liu, Y.; Li, X. Deep Learning Approach for Sparse Aperture ISAR Imaging and Autofocusing Based on Complex-Valued ADMM-Net. IEEE Sens. J. 2021, 21, 3437–3451. [Google Scholar] [CrossRef]
- Li, R.; Zhang, S.; Zhang, C.; Liu, Y.; Li, X. A Computational Efficient 2-D Block-Sparse ISAR Imaging Method Based on PCSBL-GAMP-Net. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–14. [Google Scholar] [CrossRef]
- Wipf, D.P.; Rao, B.D. An empirical Bayesian strategy for solving the simultaneous sparse approximation problem. IEEE Trans. Signal Process. 2007, 55, 3704–3716. [Google Scholar] [CrossRef]
- Liu, Z.; Huang, Z.; Zhou, Y. An efficient maximum likelihood method for direction-of-arrival estimation via sparse Bayesian learning. IEEE Trans. Wirel. Commun. 2012, 11, 1–11. [Google Scholar] [CrossRef]
- Dempster, A.P.; Laird, N.M.; Rubin, D.B. Maximum likelihood from incomplete data via the EM algorithm. J. R. Stat. Society. Ser. B Methodol. 1977, 39, 1–38. [Google Scholar] [CrossRef]
- Su, X.; Liu, Z.; Shi, J.; Hu, P.; Liu, T.; Li, X. Real-Valued Deep Unfolded Networks for Off-Grid DOA Estimation via Nested Array. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 4049–4062. [Google Scholar] [CrossRef]
- Das, A. Real-valued sparse Bayesian learning for off-grid direction-of-arrival (DOA) estimation in ocean acoustics. IEEE J. Ocean. Eng. 2021, 46, 172–182. [Google Scholar] [CrossRef]
- Stoica, P.; Larsson, E.G.; Gershman, A.B. The stochastic CRB for array processing: A textbook derivation. IEEE Signal Process. Lett. 2001, 8, 148–150. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gong, Z.; Su, X.; Hu, P.; Liu, S.; Liu, Z. Deep Unfolding Sparse Bayesian Learning Network for Off-Grid DOA Estimation with Nested Array. Remote Sens. 2023, 15, 5320. https://doi.org/10.3390/rs15225320
Gong Z, Su X, Hu P, Liu S, Liu Z. Deep Unfolding Sparse Bayesian Learning Network for Off-Grid DOA Estimation with Nested Array. Remote Sensing. 2023; 15(22):5320. https://doi.org/10.3390/rs15225320
Chicago/Turabian StyleGong, Zhenghui, Xiaolong Su, Panhe Hu, Shuowei Liu, and Zhen Liu. 2023. "Deep Unfolding Sparse Bayesian Learning Network for Off-Grid DOA Estimation with Nested Array" Remote Sensing 15, no. 22: 5320. https://doi.org/10.3390/rs15225320
APA StyleGong, Z., Su, X., Hu, P., Liu, S., & Liu, Z. (2023). Deep Unfolding Sparse Bayesian Learning Network for Off-Grid DOA Estimation with Nested Array. Remote Sensing, 15(22), 5320. https://doi.org/10.3390/rs15225320





