1. Introduction
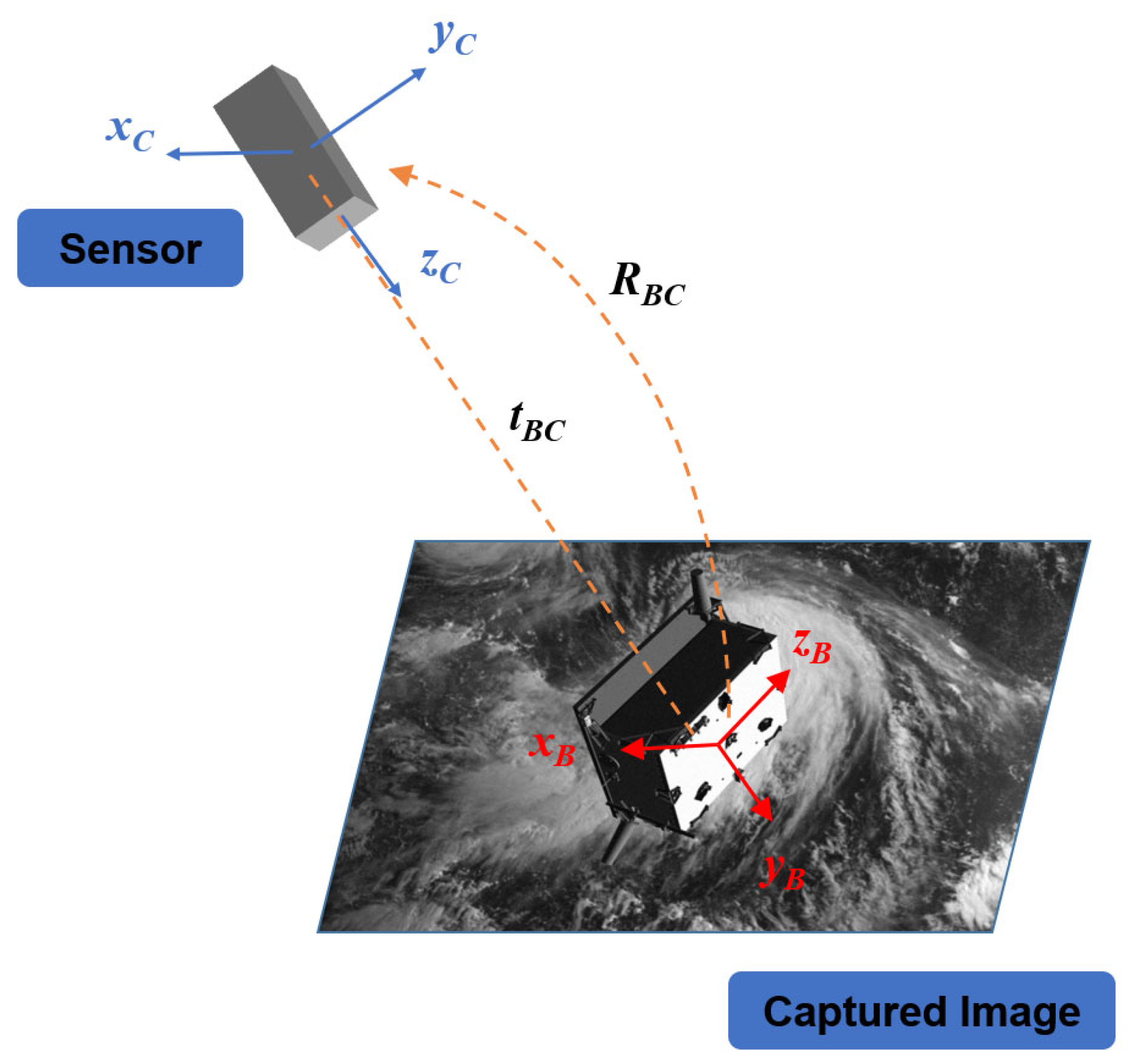
Non-cooperative space object pose estimation is an urgent problem to be solved in the space field; it has very important application value in relative navigation, rendezvous and docking, active debris removal (ADR) on-orbit servicing (OOS), etc. [
1,
2,
3,
4,
5,
6]. For the special environment of on-orbit work, the pose estimation [
7,
8] algorithm based on a low-quality, low-power monocular sensor provides a feasible scheme for space application, and it has received extensive attention from scientific research institutions and researchers. Some institutions [
9,
10,
11,
12] have carried out relevant studies and semi-physical simulation experiments on the pose estimation of non-cooperative space objects by using monocular vision cameras. Compared with monocular sensors, light detection and ranging (LIDAR) and depth cameras have a smaller scope, larger size, and higher power consumption, and they are more constrained by complex space environments. Therefore, the data obtained using the monocular sensor are more consistent with the pose estimation of the non-cooperative space objects. ESA and Stanford University held the Satellite Pose Estimation Challenge competition in 2019 (SPEC2019), using a monocular sensor to photograph scale models like the Tango satellite to create the Spacecraft Pose Estimation Dataset (SPEED) [
13], which was collected through semi-physical simulation experiments and the simulated space environment. The results indicate a new direction for non-cooperative space object pose estimation based on monocular vision. The positional relationship between the sensor and the satellite to be measured is shown in
Figure 1.
Considering the specific mission scenario, the task of pose determination poses theoretical and technical challenges. It necessitates the discovery of optimal algorithmic solutions and sensor architectures. For non-cooperative space object pose estimation, common measurement methods include monocular sensors [
14], binocular cameras [
15], time-of-flight (TOF) cameras [
16], LIDAR [
17] sensors, laser range sensors [
18], etc. Different sensors can be chosen based on the type of object, spatial environment, and satellite performance. Due to varying data output from different sensors, different processing methods can be employed. Considering factors such as on-board environment and cost, a low-power, lightweight, and cost-effective monocular sensor is more suitable. Similarly, monocular sensors are used in other pose estimation tasks, such as 2D hand pose estimation [
19], camera pose estimation [
20], head pose estimation [
21], etc.
Over the past few decades, vision-based non-cooperative space object pose estimation has relied on manually designed features [
2,
22,
23] that are described using feature descriptors and detected using feature detectors. These features are then detected in a 2D image, and their corresponding 3D counterparts are used to determine the relative attitude. These features include keypoints, corners, edges, etc. However, feature-based methods have defects in their generalization ability, robustness, and identification efficiency when ranging from the complex spatial environment to tens of thousands of non-cooperative space object species. With the rapid development of computing power and algorithms, the use of deep learning technology to extract features from tremendous data has been gradually applied to the field of non-cooperative space objects detection, and its powerful feature extraction as well as generalization ability can effectively solve the disadvantages of traditional methods.
Deep learning is widely used in satellite pose estimation [
24,
25], and it can be divided into a direct method and an indirect method. The direct method of estimating satellite pose information directly through the model has the advantages of simple process and fast estimating speed. The indirect method, however, is to deduce satellite pose information through multi-process and multi-task means. It is widely used to promote estimating precision and clarify processes. Its general processing flow [
26] is as follows:
Satellite localization network (SLN): Using object detection networks to train satellite object detectors in order to achieve precise satellite localization results.
Landmark regression network (LRN): Input the object detected by SLN into the landmark regression network for training.
Pose solver: The detected satellite landmarks are solved for satellite poses using PnP solver.
The UniAdelaide team [
26] used the MMDetection network for object detection, then clipped out the object area and provided it to the HRNet [
27] for landmark regression, and finally used PnP solver to calculate the pose information about satellite. Reference [
28] used similar methods to detect satellite landmarks, whose processing was similar to the above methods, and different deep learning models were used in satellite localization network and landmark regression network. In reference [
28], the transformer model was used, but it was only used in traditional landmark regression tasks. This method indicates that the model estimating process was divided into four steps, and the total processing stage took 212.1 ms. The pose estimation of non-cooperative space objects based on key point detection can detect their pose information with high accuracy, but there are problems such as being very time-consuming, having a complicated detection process [
26,
28,
29], etc. It requires multiple steps and models to detect relevant information and requires obvious key points of non-cooperative space objects; otherwise, it is difficult to measure the CAD model and key points.
As end-to-end methods based on deep learning are widely used in industry, especially in pose estimation tasks of six degrees of freedom, deep learning models [
30,
31,
32] based on convolutional neural networks are applied to pose estimation problems. However, convolutional neural networks have a strong feature extraction ability [
33,
34], but their remote modeling ability is poor, and only focusing on the feature pixels around the current pixel has limitations. Since the use of the transformer model in speech recognition in 2017, it has received extensive attention from industry and academia, and the model has achieved great success in timing information features such as natural language processing and speech recognition. Its core component, a self-attention mechanism, has powerful feature extraction and temporal correlation ability; that is, it highlights the advantages of convolutional neural network and recurrent neural network. Subsequently, transformer models led by vision transformer [
35,
36] and detection transformer (DETR) [
37] have achieved excellent results in the field of computer vision, especially in image recognition and object detection. In reference [
28], the transformer model is applied to satellite pose estimation, but this work only uses the transformer model for satellite landmark regression, whose function is consistent with the key point detection of the DETR model, and it fails to directly output the satellite pose information through an end-to-end learning structure. Combined with the advantages of the transformer model, this paper needs to explore an end-to-end pose estimation method based on the transformer model.
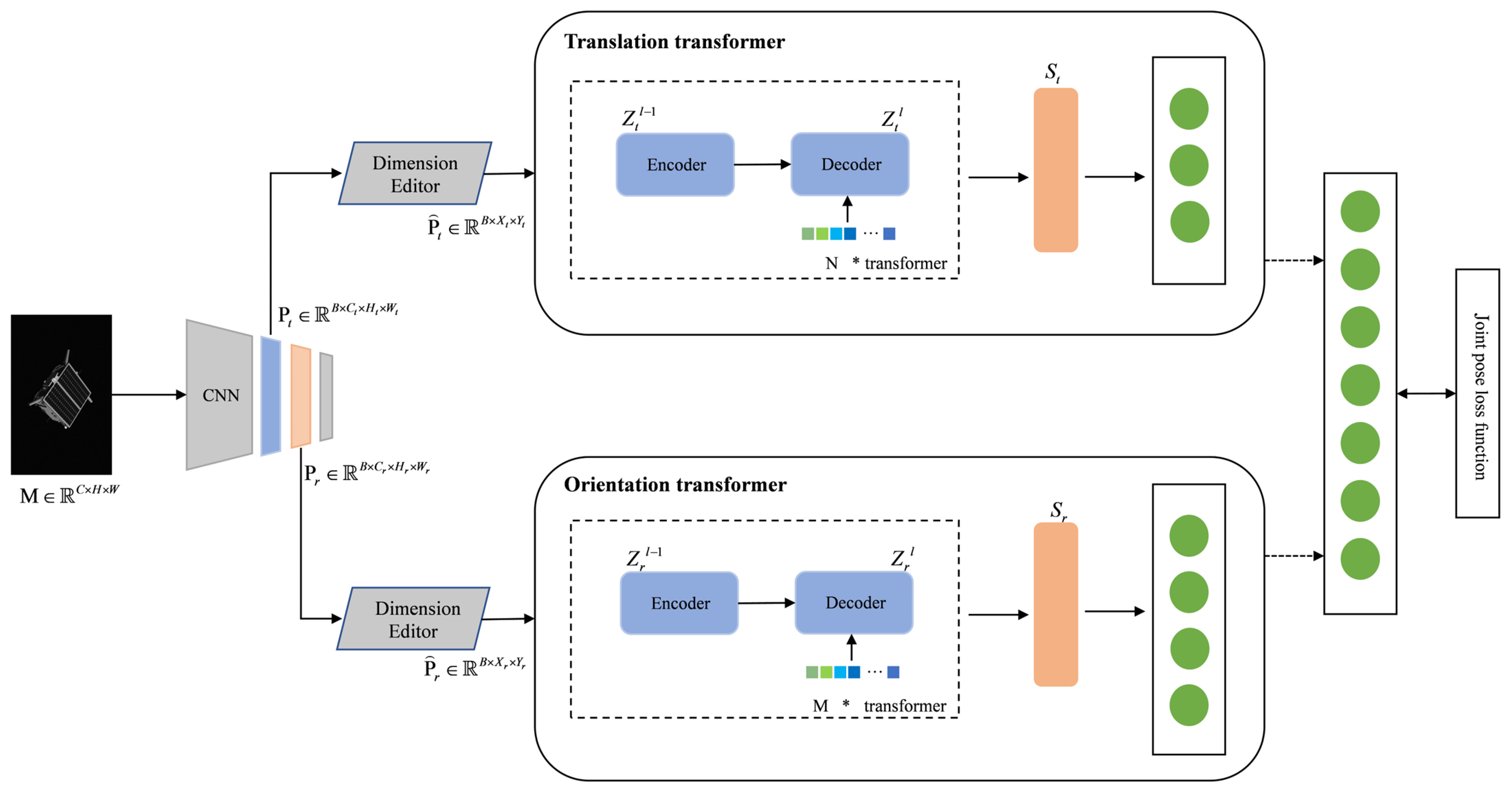
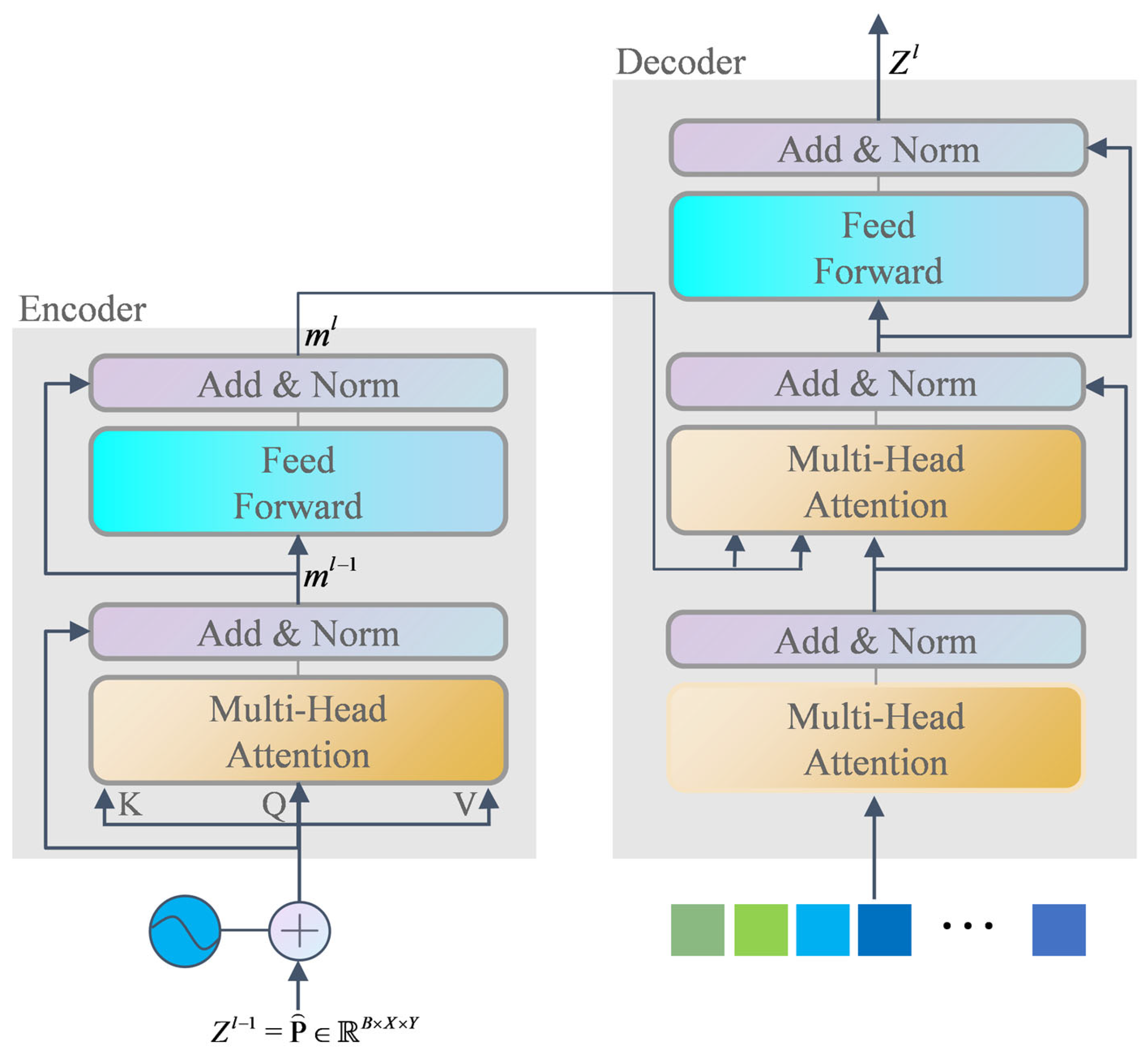
Aiming to solve the problems of the complex detection process, prior knowledge, and long detection time in existing non-cooperative space object pose estimation, this paper explores the application of the transformer model in the pose estimation of non-cooperative space objects and designs an efficient pose estimation algorithm of non-cooperative space objects based on dual-channel transformer. In this method, the pose information of non-cooperative space targets is directly output through end-to-end learning; that is, the image taken by the monocular sensor is input into the model, and the model can directly output the pose information of non-cooperative space targets without using the CAD model of the object. The algorithm uses EfficientNet as the backbone network for feature extraction and randomly selects two feature layers to input into the two pose estimation subnetworks of translation transformer and orientation transformer. The dual-channel network is used to learn translation information and orientation information, respectively, which effectively avoids the interaction between the two kinds of information. According to the characteristics of orientation information, a quaternion SoftMax-like activation function is designed to improve the accuracy of the satellite orientation information. Finally, experiments are performed on SPEED provided by ESA. The experimental results show that the proposed algorithm can successfully predict the satellite pose information, and the recognition efficiency is significantly improved compared with other methods. The main contributions of this paper are as follows:
An end-to-end learning non-cooperative space object pose estimation network is proposed to input the images taken with a monocular sensor into the model. The model directly outputs the pose information of the non-cooperative space objects, which can simplify the estimating process of pose information.
A dual-channel transformer non-cooperative space object pose estimation network is designed to innovatively apply transformer to the end-to-end learning satellite pose estimation task. The dual-channel network design successfully decouples the spatial translation information and orientation information of satellites.
A new quaternion SoftMax-like activation function is designed to make the model output according to the quaternion constraint so as to effectively improve the precision of orientation prediction.
The paper is structured as follows:
Section 2 presents our proposed dual-channel transformer model with a quaternion activation function. We provide a detailed description of the model architecture, including the design of the dual-channel mechanism and the quaternion activation function.
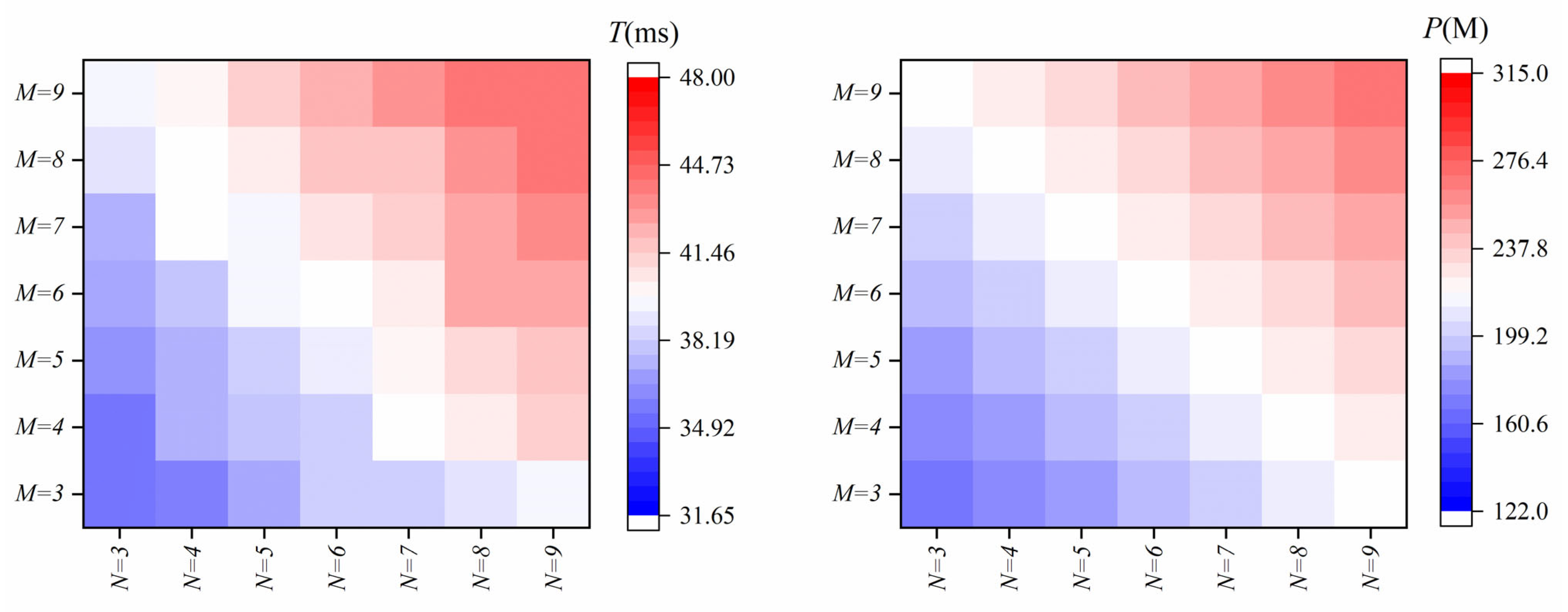
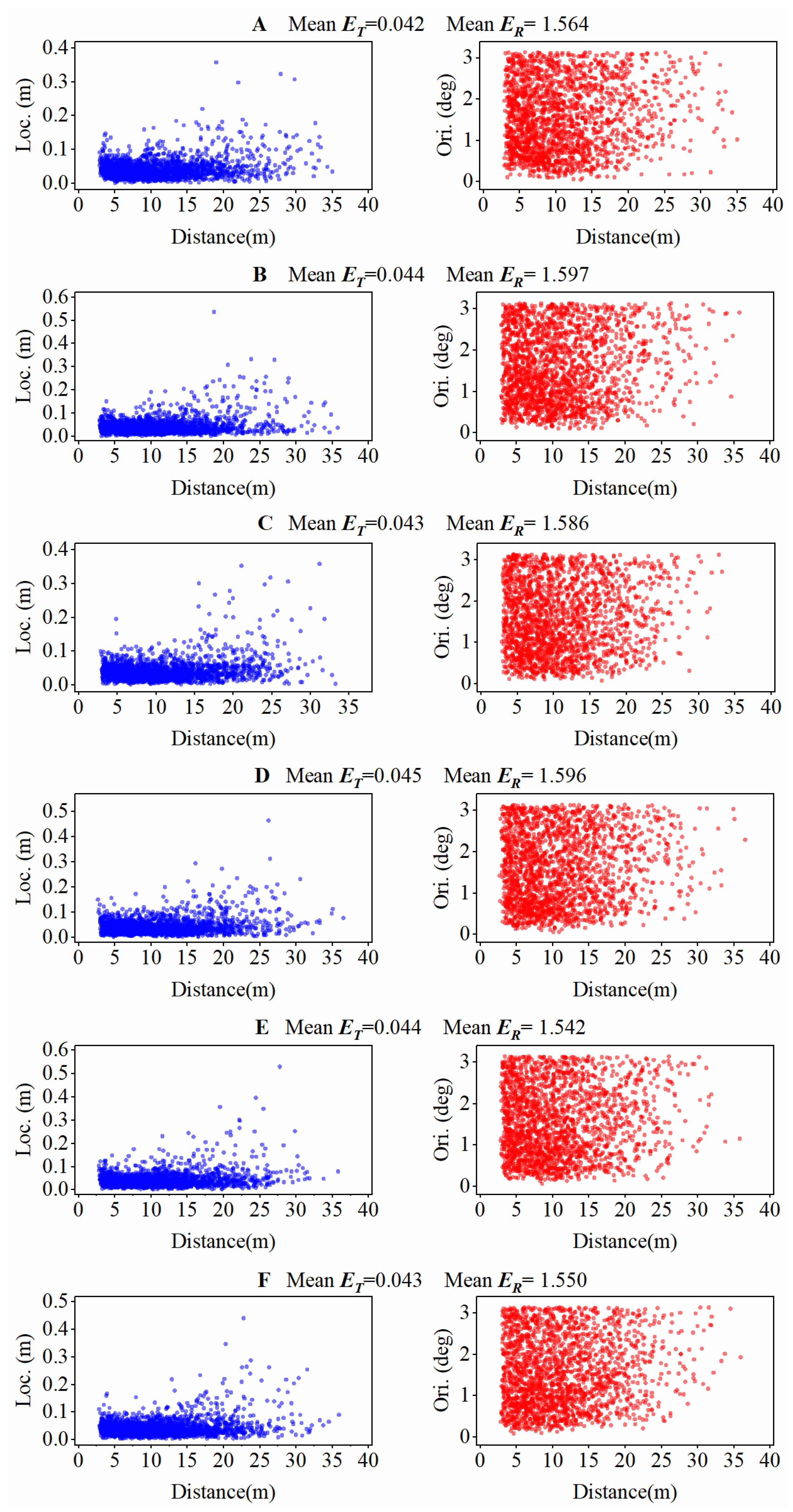
Section 3 focuses on the experimental setup and results analysis. First, we analyze the data used in our experiments, including their characteristics and sources. Then, we introduce the evaluation metrics employed to assess the performance of the dual-channel transformer model. Finally, we present the results of the multiple ablation experiments conducted. Furthermore, we compare the performance of our model with that of other existing models.
Section 4 focuses on drawing conclusions while summarizing the innovations and beneficial effects of our work.