MuA-SAR Fast Imaging Based on UCFFBP Algorithm with Multi-Level Regional Attention Strategy
Abstract
:1. Introduction
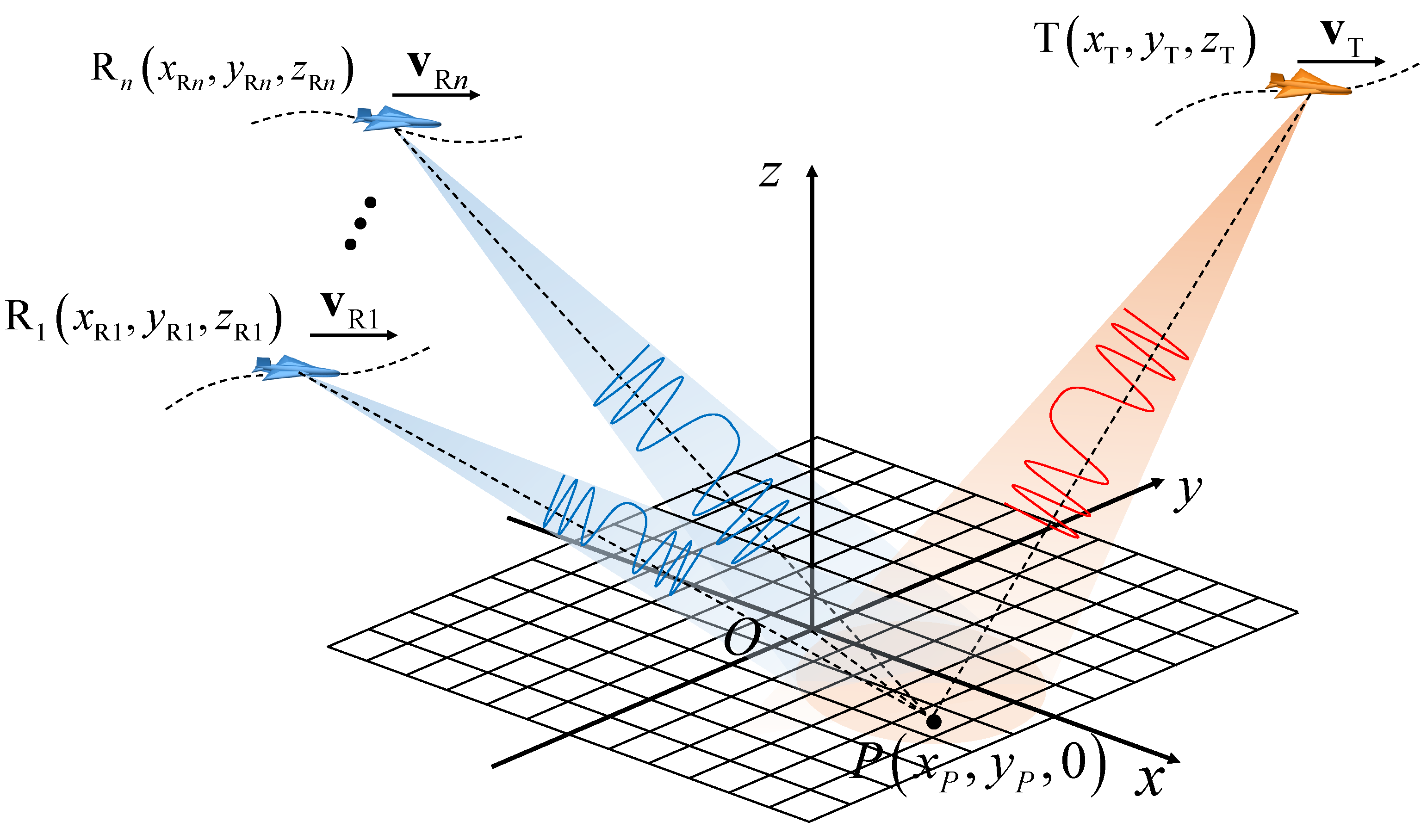
2. Echo Signal Model of MuA-SAR System
3. WS Analysis for MuA-SAR Imaging
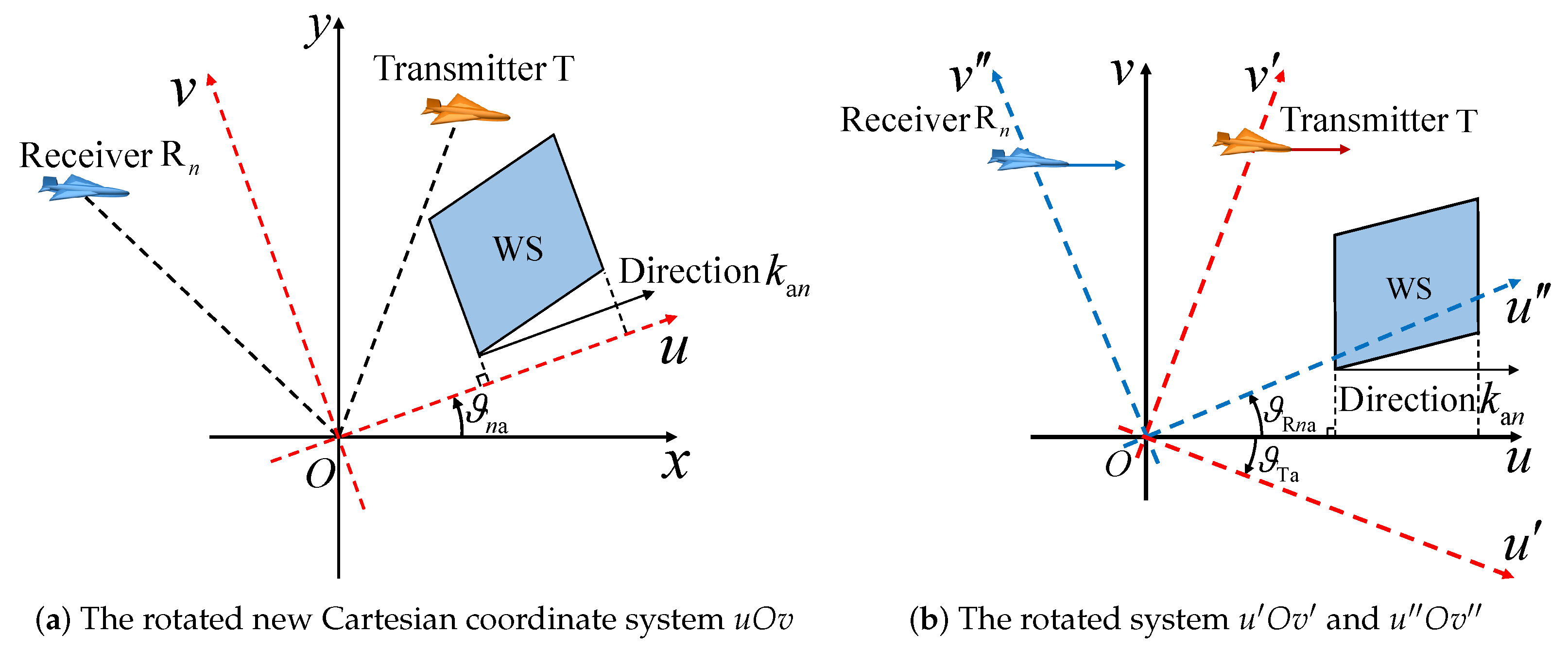
3.1. The Distribution Principles of WS
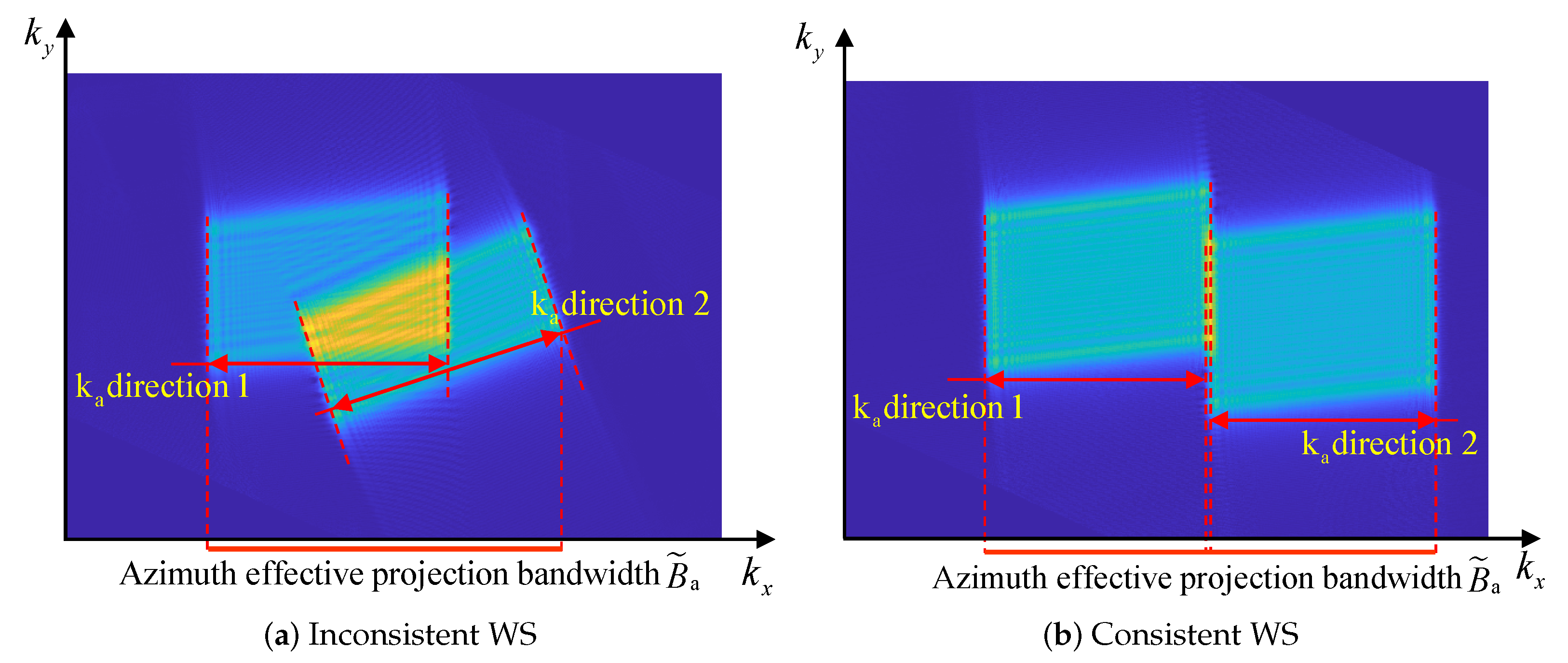
3.2. Influence of Consistency of WS Distribution on Imaging
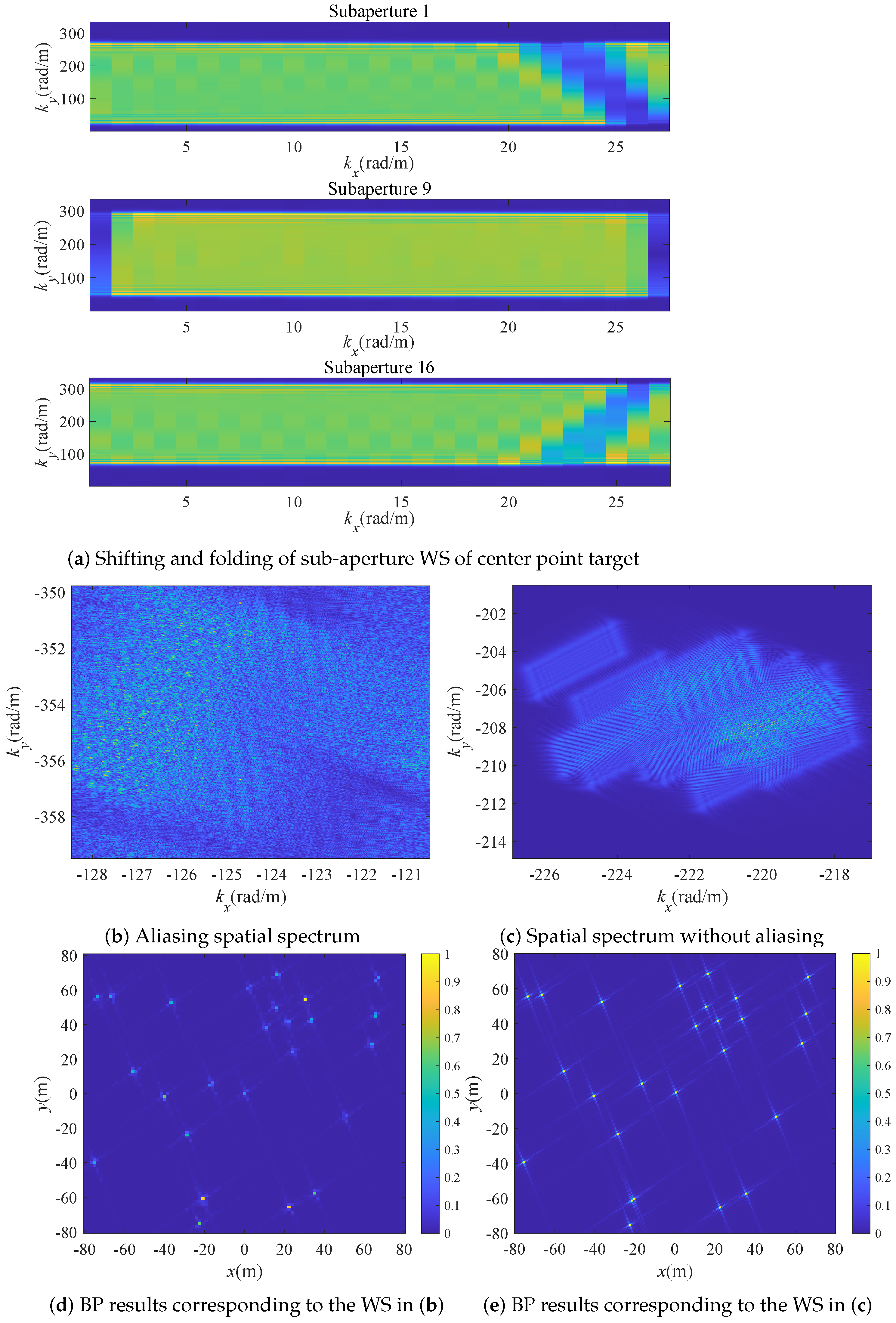
3.3. Analysis of Aliasing Phenomenon of WS
4. Proposed Algorithm
4.1. Description of the Proposed Algorithm
4.2. Computational Complexity Analysis
- (a)
- BP imaging process at the initial level.
- (b)
- The upsampling operation in coherent fusion process from level 0th to the level .
- (c)
- The image segmentation process based on MSER from level 0 to level.
5. Simulation Experiments
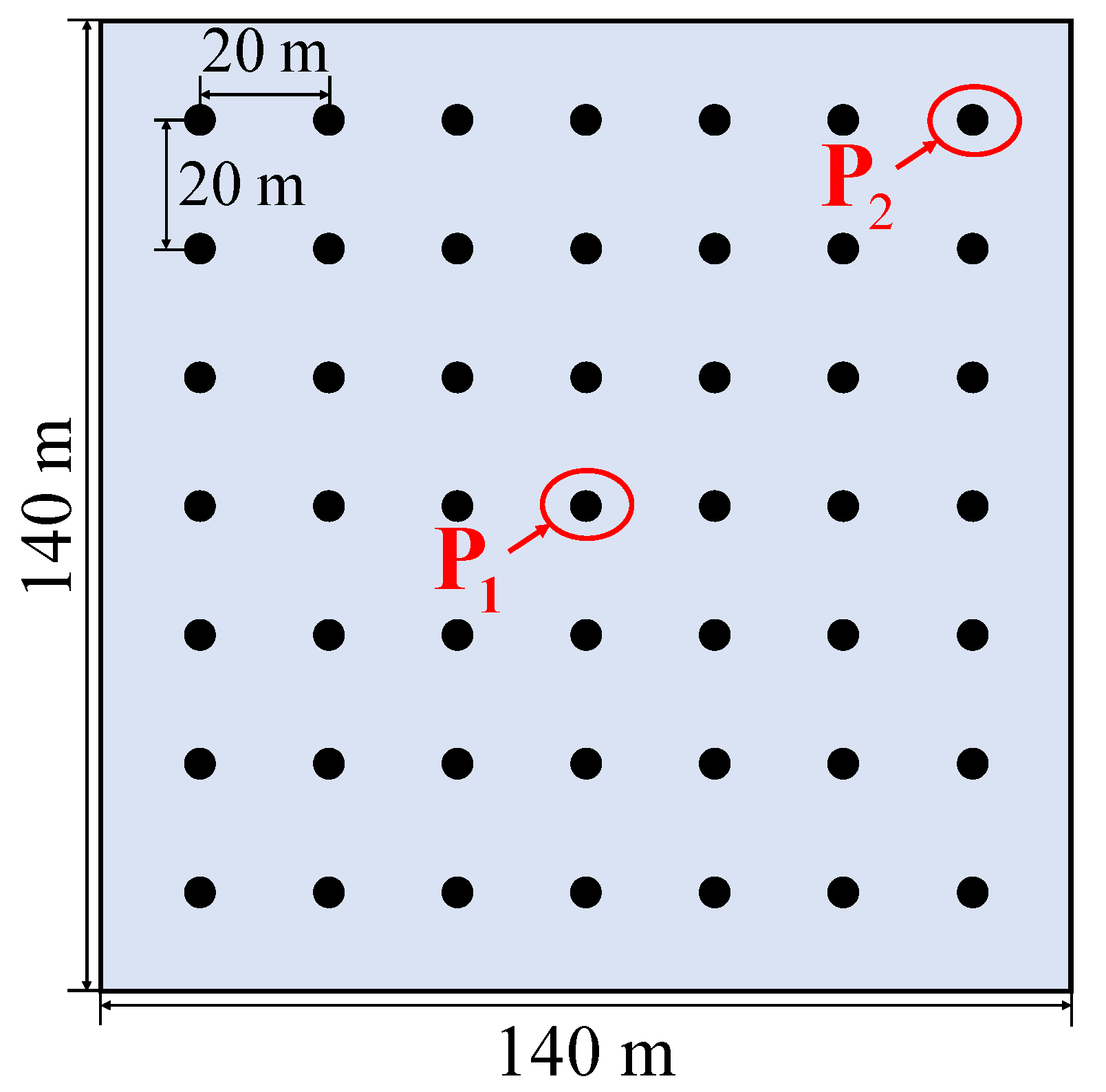
5.1. Point Target Simulation
5.2. 2D Surface Target Simulation
6. Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| MuA-SAR | multistatic airborne SAR |
| UCFFBP | unified Cartesian fast factorized back projection |
| GCCS | global Cartesian coordinate system |
| UPC | unified polar coordinate |
| AFBP | accelerated fast backprojection |
| WFBP | wavenumber domain fast backprojection |
| MFT | matrix Fourier transform |
| WS | wavenumber spectrum |
| MSER | maximally stable extremal regions |
References
- Gao, F.; Yang, Y.; Wang, J.; Sun, J.; Yang, E.; Zhou, H. A deep convolutional generative adversarial networks (DCGANs)-based semi-supervised method for object recognition in synthetic aperture radar (SAR) images. Remote Sens. 2018, 10, 846. [Google Scholar] [CrossRef]
- Zhou, F.; Tian, T.; Zhao, B.; Bai, X.; Fan, W. Deception against near-field synthetic aperture radar using networked jammers. IEEE Trans. Aerosp. Electron. Syst. 2019, 55, 3365–3377. [Google Scholar] [CrossRef]
- Fei, G.; Aidong, L.; Kai, L.; Erfu, Y.; Hussain, A. A novel visual attention method for target detection from SAR images. Chin. J. Aeronaut. 2019, 32, 1946–1958. [Google Scholar]
- Baraha, S.; Sahoo, A.K. Synthetic Aperture Radar Image and its Despeckling using Variational Methods: A Review of Recent Trends. Signal Process. 2023, 212, 109156. [Google Scholar] [CrossRef]
- Cumming, I.G.; Wong, F.H. Digital processing of synthetic aperture radar data. Artech House 2005, 1, 108–110. [Google Scholar]
- Long, T.; Zeng, T.; Hu, C.; Dong, X.; Chen, L.; Liu, Q.; Xie, Y.; Ding, Z.; Li, Y.; Wang, Y.; et al. High resolution radar real-time signal and information processing. China Commun. 2019, 16, 105–133. [Google Scholar]
- Lu, J.; Zhang, L.; Huang, Y.; Cao, Y. High-resolution forward-looking multichannel SAR imagery with array deviation angle calibration. IEEE Trans. Geosci. Remote Sens. 2020, 58, 6914–6928. [Google Scholar] [CrossRef]
- Wu, J.; Yang, J.; Huang, Y.; Yang, H.; Wang, H. Bistatic forward-looking SAR: Theory and challenges. In Proceedings of the 2009 IEEE Radar Conference, Pasadena, CA, USA, 4–8 May 2009; pp. 1–4. [Google Scholar]
- Chen, R.; Li, W.; Li, K.; Zhang, Y.; Yang, J. A Super-Resolution Scheme for Multichannel Radar Forward-Looking Imaging Considering Failure Channels and Motion Error. IEEE Geosci. Remote Sens. Lett. 2023, 20, 1–5. [Google Scholar] [CrossRef]
- Mao, D.; Zhang, Y.; Pei, J.; Huo, W.; Zhang, Y.; Huang, Y.; Yang, J. Forward-looking geometric configuration optimization design for spaceborne-airborne multistatic synthetic aperture radar. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 8033–8047. [Google Scholar] [CrossRef]
- Santi, F.; Antoniou, M.; Pastina, D. Point spread function analysis for GNSS-based multistatic SAR. IEEE Geosci. Remote Sens. Lett. 2014, 12, 304–308. [Google Scholar] [CrossRef]
- Krieger, G.; Moreira, A. Spaceborne bi-and multistatic SAR: Potential and challenges. IEE Proc.-Radar Sonar Navig. 2006, 153, 184–198. [Google Scholar] [CrossRef]
- Krieger, G.; Zonno, M.; Rodriguez-Cassola, M.; Lopez-Dekker, P.; Mittermayer, J.; Younis, M.; Huber, S.; Villano, M.; De Almeida, F.Q.; Prats-Iraola, P.; et al. MirrorSAR: A fractionated space radar for bistatic, multistatic and high-resolution wide-swath SAR imaging. In Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017; pp. 149–152. [Google Scholar]
- Moccia, A.; Renga, A. Spatial resolution of bistatic synthetic aperture radar: Impact of acquisition geometry on imaging performance. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3487–3503. [Google Scholar] [CrossRef]
- Xu, F.; Zhang, Y.; Wang, R.; Mi, C.; Zhang, Y.; Huang, Y.; Yang, J. Heuristic path planning method for multistatic UAV-borne SAR imaging system. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 8522–8536. [Google Scholar] [CrossRef]
- Smith, A. A new approach to range-Doppler SAR processing. Int. J. Remote Sens. 1991, 12, 235–251. [Google Scholar] [CrossRef]
- Hughes, W.; Gault, K.; Princz, G. A comparison of the Range-Doppler and Chirp Scaling algorithms with reference to RADARSAT. In Proceedings of the IGARSS’96, 1996 International Geoscience and Remote Sensing Symposium, Lincoln, NE, USA, 31 May 1996; Volume 2, pp. 1221–1223. [Google Scholar]
- Li, C.; Zhang, H.; Deng, Y.; Wang, R.; Liu, K.; Liu, D.; Jin, G.; Zhang, Y. Focusing the L-band spaceborne bistatic SAR mission data using a modified RD algorithm. IEEE Trans. Geosci. Remote Sens. 2019, 58, 294–306. [Google Scholar] [CrossRef]
- Rigling, B.D.; Moses, R.L. Polar format algorithm for bistatic SAR. IEEE Trans. Aerosp. Electron. Syst. 2004, 40, 1147–1159. [Google Scholar] [CrossRef]
- Sun, J.; Mao, S.; Wang, G.; Hong, W. Polar Format Algorithm for Spotlight Bistatic Sar with Arbitrary Geometry Configuration. Prog. Electromagn. Res. 2010, 103, 323–338. [Google Scholar] [CrossRef]
- Cumming, I.G.; Neo, Y.L.; Wong, F.H. Interpretations of the omega-K algorithm and comparisons with other algorithms. In Proceedings of the IGARSS 2003 IEEE International Geoscience and Remote Sensing Symposium (IEEE Cat. No. 03CH37477), Toulouse, France, 21–25 July 2003; Volume 3, pp. 1455–1458. [Google Scholar]
- Liu, B.; Wang, T.; Wu, Q.; Bao, Z. Bistatic SAR data focusing using an omega-K algorithm based on method of series reversion. IEEE Trans. Geosci. Remote Sens. 2009, 47, 2899–2912. [Google Scholar]
- Zhu, R.; Zhou, J.; Tang, L.; Kan, Y.; Fu, Q. Frequency-domain imaging algorithm for single-input–multiple-output array. IEEE Geosci. Remote Sens. Lett. 2016, 13, 1747–1751. [Google Scholar] [CrossRef]
- Gaibel, A.; Boag, A. Back-projection SAR imaging using FFT. In Proceedings of the 2016 European Radar Conference (EuRAD), London, UK, 5–7 October 2016; pp. 69–72. [Google Scholar]
- Zeng, D.; Zeng, T.; Hu, C.; Long, T. Back-projection algorithm characteristic analysis in forward-looking bistatic SAR. In Proceedings of the 2006 CIE International Conference on Radar, Shanghai, China, 16–19 October 2006; pp. 1–4. [Google Scholar]
- McCorkle. Focusing of synthetic aperture ultra wideband data. In Proceedings of the IEEE 1991 International Conference on Systems Engineering, Dayton, OH, USA, 1–3 August 1991; pp. 1–5. [Google Scholar]
- Yang, Y.; Pi, Y.; Li, R. Back projection algorithm for spotlight bistatic SAR imaging. In Proceedings of the 2006 CIE International Conference on Radar, Shanghai, China, 16–19 October 2006; pp. 1–4. [Google Scholar]
- Feng, D.; An, D.; Huang, X. An extended fast factorized back projection algorithm for missile-borne bistatic forward-looking SAR imaging. IEEE Trans. Aerosp. Electron. Syst. 2018, 54, 2724–2734. [Google Scholar] [CrossRef]
- Xiao, S.; Munson, D.C.; Basu, S.; Bresler, Y. An N 2 logN back-projection algorithm for SAR image formation. In Proceedings of the Thirty-Fourth Asilomar Conference on Signals, Systems and Computers (Cat. No. 00CH37154), Pacific Grove, CA, USA, 29 October–1 November 2000; Volume 1, pp. 3–7. [Google Scholar]
- McCorkle, J.W.; Rofheart, M. Order N^2 log (N) backprojector algorithm for focusing wide-angle wide-bandwidth arbitrary-motion synthetic aperture radar. In Proceedings of the Radar Sensor Technology, Orlando, FL, USA, 8–9 April 1996; Volume 2747, pp. 25–36. [Google Scholar]
- Yegulalp, A.F. Fast backprojection algorithm for synthetic aperture radar. In Proceedings of the 1999 IEEE Radar Conference, Radar into the Next Millennium (Cat. No. 99CH36249), Waltham, MA, USA, 22 April 1999; pp. 60–65. [Google Scholar]
- Ding, Y.; Munson, D.J. A fast back-projection algorithm for bistatic SAR imaging. In Proceedings of the International Conference on Image Processing, Rochester, NY, USA, 22–25 September 2002; Volume 2, p. 2. [Google Scholar]
- Ulander, L.M.; Hellsten, H.; Stenstrom, G. Synthetic-aperture radar processing using fast factorized back-projection. IEEE Trans. Aerosp. Electron. Syst. 2003, 39, 760–776. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, Q.; Hu, J.; Shi, S.; Li, C.; Cheng, W.; Fang, G. An Efficient Algorithm Based on Frequency Scaling for THz Stepped-Frequency SAR Imaging. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–15. [Google Scholar] [CrossRef]
- Ulander, L.M.; Froelind, P.O.; Gustavsson, A.; Murdin, D.; Stenstroem, G. Fast factorized back-projection for bistatic SAR processing. In Proceedings of the 8th European Conference on Synthetic Aperture Radar, VDE, Aachen, Germany, 7–10 June 2010; pp. 1–4. [Google Scholar]
- Zhou, S.; Yang, L.; Zhao, L.; Wang, Y.; Zhou, H.; Chen, L.; Xing, M. A new fast factorized back projection algorithm for bistatic forward-looking SAR imaging based on orthogonal elliptical polar coordinate. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 1508–1520. [Google Scholar] [CrossRef]
- Zhang, L.; Li, H.L.; Qiao, Z.J.; Xu, Z.W. A fast BP algorithm with wavenumber spectrum fusion for high-resolution spotlight SAR imaging. IEEE Geosci. Remote Sens. Lett. 2014, 11, 1460–1464. [Google Scholar] [CrossRef]
- Sun, H.; Sun, Z.; Chen, T.; Miao, Y.; Wu, J.; Yang, J. An Efficient Backprojection Algorithm Based on Wavenumber-Domain Spectral Splicing for Monostatic and Bistatic SAR Configurations. Remote Sens. 2022, 14, 1885. [Google Scholar] [CrossRef]
- Guo, Y.; Suo, Z.; Jiang, P.; Li, H. A Fast Back-Projection SAR Imaging Algorithm Based on Wavenumber Spectrum Fusion for High Maneuvering Platforms. Remote Sens. 2021, 13, 1649. [Google Scholar] [CrossRef]
- Dong, Q.; Yang, Z.; Sun, G.; Xing, M. Cartesian factorized backprojection algorithm for synthetic aperture radar. In Proceedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 1074–1077. [Google Scholar]
- Dong, Q.; Sun, G.C.; Yang, Z.; Guo, L.; Xing, M. Cartesian factorized backprojection algorithm for high-resolution spotlight SAR imaging. IEEE Sens. J. 2017, 18, 1160–1168. [Google Scholar] [CrossRef]
- Li, Y.; Xu, G.; Zhou, S.; Xing, M.; Song, X. A novel CFFBP algorithm with noninterpolation image merging for bistatic forward-looking SAR focusing. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–16. [Google Scholar] [CrossRef]
- Xu, F.; Wang, R.; Frey, O.; Huang, Y.; Mi, C.; Mao, D.; Yang, J. Spatial Configuration Design for Multistatic Airborne SAR Based on Multiple Objective Particle Swarm Optimization . IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–16. [Google Scholar]
- Zeng, T.; Cherniakov, M.; Long, T. Generalized approach to resolution analysis in BSAR. IEEE Trans. Aerosp. Electron. Syst. 2005, 41, 461–474. [Google Scholar] [CrossRef]
- Dower, W.; Yeary, M. Bistatic SAR: Forecasting spatial resolution. IEEE Trans. Aerosp. Electron. Syst. 2018, 55, 1584–1595. [Google Scholar] [CrossRef]
- Matas, J.; Chum, O.; Urban, M.; Pajdla, T. Robust wide-baseline stereo from maximally stable extremal regions. Image Vis. Comput. 2004, 22, 761–767. [Google Scholar] [CrossRef]
- Donoser, M.; Bischof, H. Efficient maximally stable extremal region (MSER) tracking. In Proceedings of the 2006 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’06), New York, NY, USA, 17–22 June 2006; Volume 1, pp. 553–560. [Google Scholar]
- Wang, R.; Xu, F.; Pei, J.; Wang, C.; Huang, Y.; Yang, J.; Wu, J. An improved faster R-CNN based on MSER decision criterion for SAR image ship detection in harbor. In Proceedings of the IGARSS 2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July–2 August 2019; pp. 1322–1325. [Google Scholar]
- Pu, W.; Wu, J.; Huang, Y.; Li, W.; Sun, Z.; Yang, J.; Yang, H. Motion errors and compensation for bistatic forward-looking SAR with cubic-order processing. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6940–6957. [Google Scholar] [CrossRef]
- Wang, W.Q. GPS-based time & phase synchronization processing for distributed SAR. IEEE Trans. Aerosp. Electron. Syst. 2009, 45, 1040–1051. [Google Scholar]
- Krieger, G.; Younis, M. Impact of oscillator noise in bistatic and multistatic SAR. IEEE Geosci. Remote Sens. Lett. 2006, 3, 424–428. [Google Scholar] [CrossRef]
- Potter, L.C.; Moses, R.L. Attributed scattering centers for SAR ATR. IEEE Trans. Image Process. 1997, 6, 79–91. [Google Scholar] [CrossRef]




| Algorithm | Advantage | Disadvantage |
|---|---|---|
| RDA/CSA | Uniformly process the spatial variability, High efficiency | Complicated space-variant problems for multiple platforms |
| PFA | Minimize processing load | Approximate calculation, Not applicable to wide swath scenes and multiple platforms |
| Omega-K | Accurately calculate geometric relationships | Requires specific configuration and straight trajectory |
| BP | Accurate, Suitable for any configuration and trajectory | High computational complexity |
| FFBP | High efficiency | Interpolation leads to error accumulation for multiple platforms |
| CFFBP | Noninterpolation, High efficiency | Not suitable for multiple platforms |
| Radar Signal Parameters | Geometric Configuration Parameters | ||
|---|---|---|---|
| Parameters | Value | Parameters | Value |
| Carrier frequency | 9.6 GHz | Initial position of T | (7.32, 13.32, 5.00) km |
| Bandwidth | 200 MHz | Velocity vector of T | (24.85, −147.93, 0.00) m/s |
| Sampling rate | 220 MHz | Initial position of R1 | (2.50, 15.00, 5.00) km |
| Pulse repetition frequency | 1024 Hz | Velocity vector of R1 | (0.00, −150.00, 0.00) m/s |
| Pulse time width | 4 μs | Initial position of R2 | (2.67, 14.99, 4.73) km |
| Synthetic aperture time | 4 s | Velocity vector of R2 | (−4.03, −149.95, 0.00) m/s |
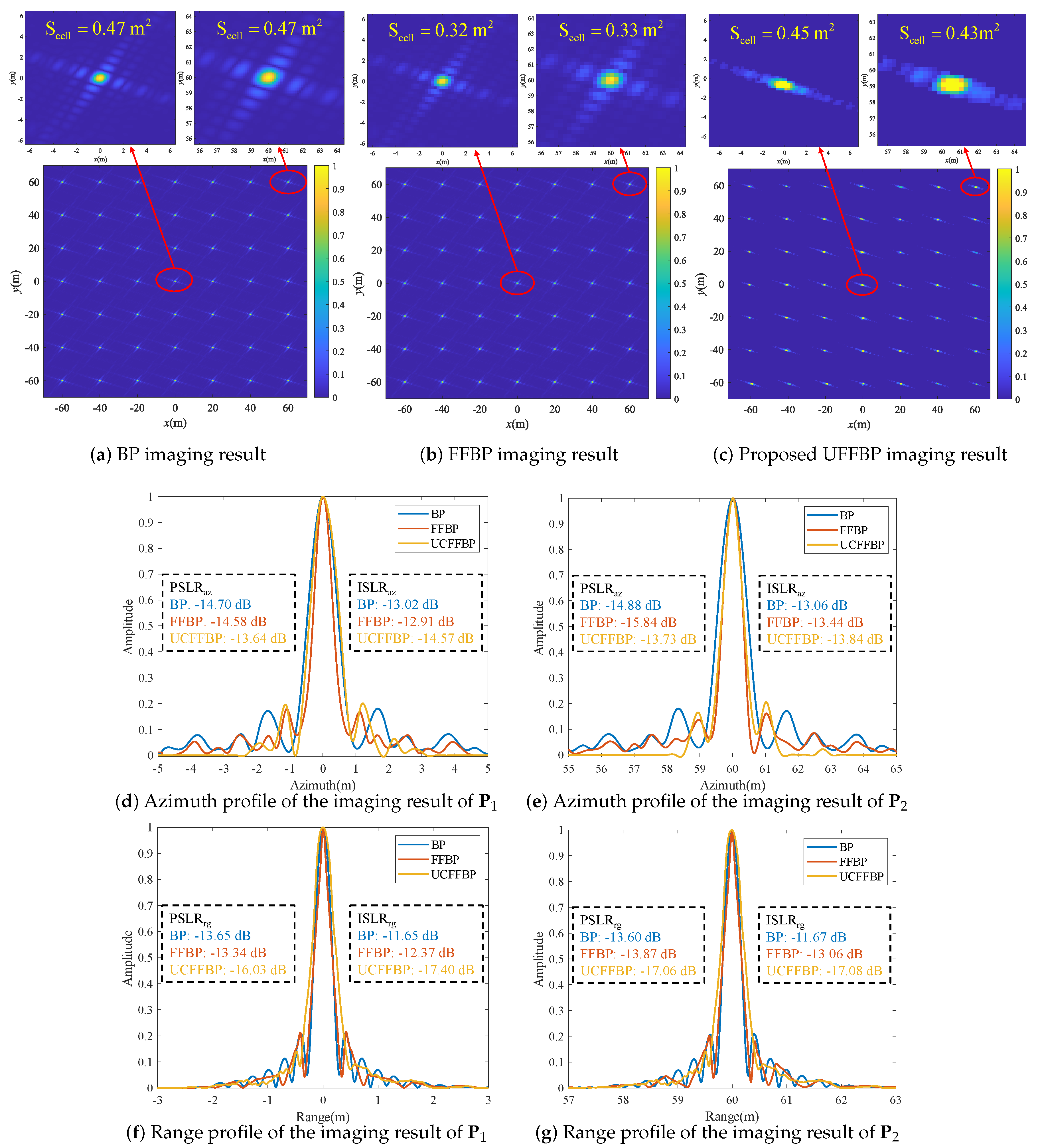
| Algorithm | Measured Parameters | Point Target P1 | Point Target P2 |
|---|---|---|---|
| Scell (m2) | 0.47 | 0.47 | |
| BP algorithm | PSLRaz/PSLRrg (dB) | −14.70/−13.65 | −14.88/−13.60 |
| ISLRaz/ISLRrg (dB) | −13.02/−11.65 | −13.06/−11.67 | |
| Scell (m2) | 0.32 | 0.33 | |
| FFBP | PSLRaz/PSLRrg (dB) | −14.58/−13.34 | −15.84/−13.87 |
| ISLRaz/ISLRrg (dB) | −12.91/−12.37 | −13.44/−13.06 | |
| Scell (m2) | 0.45 | 0.43 | |
| Proposed algorithm | PSLRaz/PSLRrg (dB) | −13.64/−16.03 | −13.73/−17.06 |
| ISLRaz/ISLRrg (dB) | −14.57/−17.40 | −13.84/−17.08 |
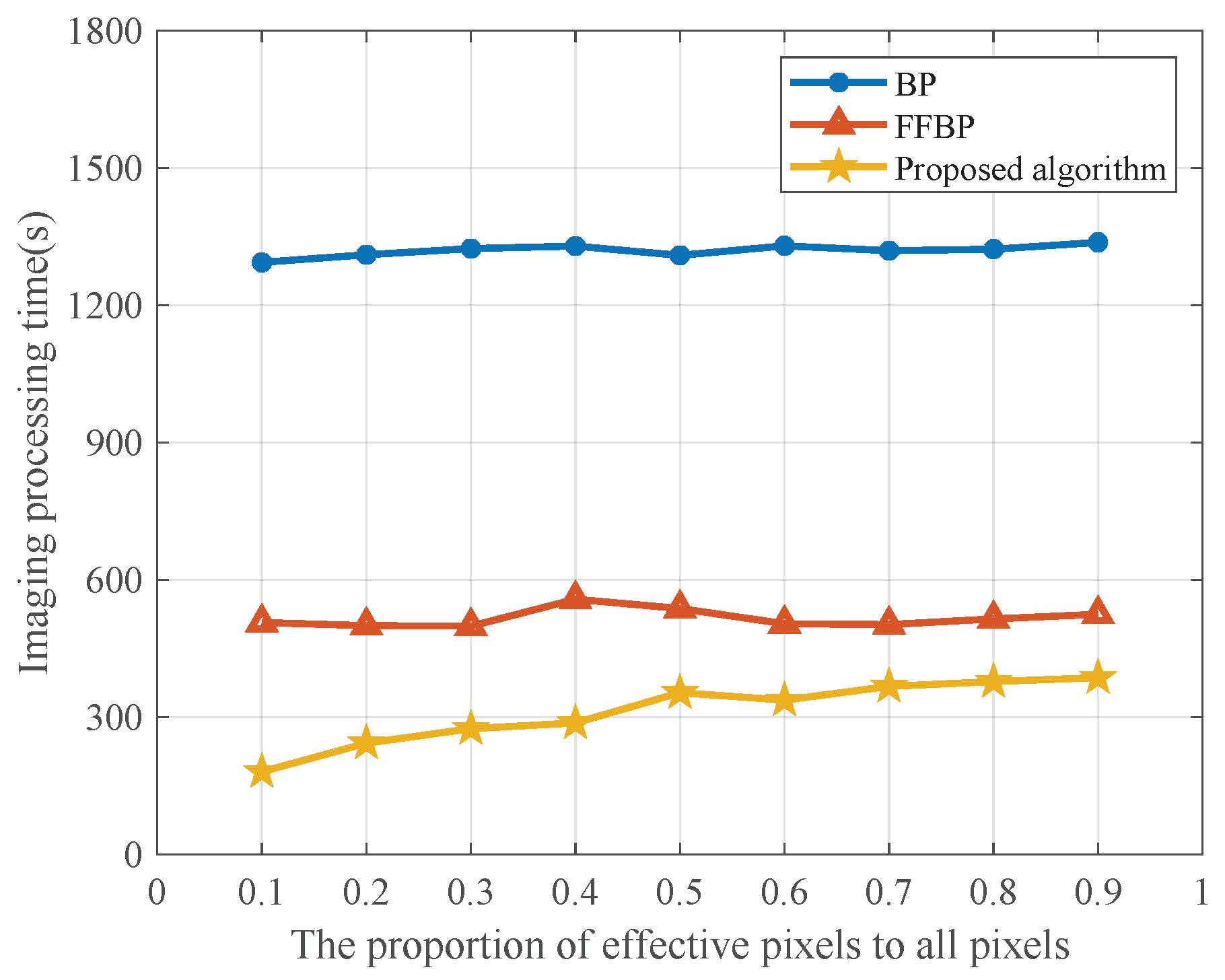
| Group | BP Algorithm | FFBP Algorithm | Proposed Algorithm |
|---|---|---|---|
| 1 | 51.5 | 38.3 | 23.4 |
| 2 | 50.8 | 37.9 | 22.9 |
| 3 | 52.9 | 38.2 | 22.3 |
| 4 | 54.5 | 37.8 | 22.6 |
| 5 | 52.1 | 38.7 | 22.4 |
| 6 | 53.2 | 37.6 | 23.0 |
| Average Value | 52.5 | 38.1 | 22.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, F.; Wang, R.; Huang, Y.; Mao, D.; Yang, J.; Zhang, Y.; Zhang, Y. MuA-SAR Fast Imaging Based on UCFFBP Algorithm with Multi-Level Regional Attention Strategy. Remote Sens. 2023, 15, 5183. https://doi.org/10.3390/rs15215183
Xu F, Wang R, Huang Y, Mao D, Yang J, Zhang Y, Zhang Y. MuA-SAR Fast Imaging Based on UCFFBP Algorithm with Multi-Level Regional Attention Strategy. Remote Sensing. 2023; 15(21):5183. https://doi.org/10.3390/rs15215183
Chicago/Turabian StyleXu, Fanyun, Rufei Wang, Yulin Huang, Deqing Mao, Jianyu Yang, Yongchao Zhang, and Yin Zhang. 2023. "MuA-SAR Fast Imaging Based on UCFFBP Algorithm with Multi-Level Regional Attention Strategy" Remote Sensing 15, no. 21: 5183. https://doi.org/10.3390/rs15215183
APA StyleXu, F., Wang, R., Huang, Y., Mao, D., Yang, J., Zhang, Y., & Zhang, Y. (2023). MuA-SAR Fast Imaging Based on UCFFBP Algorithm with Multi-Level Regional Attention Strategy. Remote Sensing, 15(21), 5183. https://doi.org/10.3390/rs15215183









