Improving the Accuracy of Urban Waterlogging Simulation: A Novel Computer Vision-Based Digital Elevation Model Refinement Approach for Roads and Densely Built-Up Areas

Abstract

Urban waterlogging is a natural disaster that occurs in developed cities globally and has inevitably become severe due to urbanization, densification, and climate change. The digital elevation model (DEM) is an important component of urban waterlogging risk prediction. However, previous studies generally focused on optimizing hydrological models, and there is a potential improvement in DEM by fusing remote sensing data and hydrological data. To improve the DEM accuracy of urban roads and densely built-up areas, a multisource data fusion approach (MDF-UNet) was proposed. Firstly, Fuzhou city was taken as an example, and the satellite remote sensing images, drainage network, land use, and DEM data of the study area were collected. Secondly, the U-Net model was used to identify buildings using remote sensing images. Subsequently, a multisource data fusion (MDF) method was adopted to reconstruct DEM by fusing the buildings identification results, land use, and drainage network data. Then, a coupled one-dimensional (1D) conduit drainage and two-dimensional (2D) hydrodynamic model was constructed and validated. Finally, the simulation results of the MDF-UNet approach were compared with the raw DEM data, inverse distance weighting (IDW), and MDF. The results indicated that the proposed approach greatly improved the simulation accuracy of waterlogging points by 29%, 53%, and 12% compared with the raw DEM, IDW, and MDF. Moreover, the MDF-UNet method had the smallest median value error of 0.08 m in the inundation depth simulation. The proposed method demonstrates that the credibility of the waterlogging model and simulation accuracy in roads and densely built-up areas is significantly improved, providing a reliable basis for urban waterlogging prevention and management.

1. Introduction

Urban waterlogging is an environmental disaster that has become more frequent in recent times as a consequence of global climate change, rapid urbanization, and densification. It severely impacts urban infrastructure, the economy, and public safety [1], highlighting the importance and necessity of urban waterlogging forecasting [2,3]. In urban waterlogging simulations, terrain plays a vital role in determining the direction, velocity, intensity, and depth of rainwater flow [4,5]. The accuracy of the digital elevation model (DEM) is an important part of the prediction model that directly affects the prediction accuracy of urban waterlogging [6]. Therefore, DEM must be fully considered and evaluated in the process of urban waterlogging prediction [7,8].

Currently, commonly used DEM data sources are remote sensing, digitized maps, precision measurement, and numerical simulation. Remote sensing data are mainly obtained by remote sensing technology such as satellites and LiDAR, and have the advantages of large scale and high spatial resolution [9,10,11]. However, the accuracy and quality of the data is easily affected by many factors, such as cloud coverage and feature occlusion [12,13,14]. A digitized map is used to generate the elevation data by extrapolation based on the existing digital two-dimensional (2D) map [15]. This method has been widely used for DEM production in different regions and at different scales due to its automated production process and relatively low cost. However, it has low accuracy and resolution and, hence, is inapplicable to scenarios with high DEM requirements. Precision measurement is the measurement and recording of the ground elevation using measuring instruments such as the global positioning system (GPS) [16,17] and a total station [18]. The former uses GPS receivers to track data and differential technology, with the advantages of relatively low measurement costs and precise local area elevation [19]; however, it is affected by GPS signal errors and accuracy limitations. Although the latter is of high accuracy, it is costly and requires specialized equipment and technicians, and therefore, the measurement accuracy can be reduced under poor field conditions. Numerical simulation derives the elevation data based on physical and geomorphological models, etc. [20,21]. High-resolution DEM data can be produced on demand and used to explore the changes and responses of geographic systems under different elevation and topographic conditions. However, this method requires complex numerical calculations and model building, demanding simulation software and computer hardware performance. Having taken into account the strengths and weaknesses of the above methods, a majority of researchers have opted for the freely available satellite-based global DEM [22,23,24], which is released by some agencies and organizations, such as the Shuttle Radar Topography Mission of the US National Aeronautics and Space Administration (NASA SRTM) [25]. However, various factors can reduce the reliability of urban waterlogging models. The spurious artifacts generated by the digital surface model due to the reflection of radar and light signals from building artifacts can block or alter the rainwater flow path over the ground, leading to anomalous results. Moreover, a lot of building artifacts can affect the accuracy of terrain elevation in the city, thereby decreasing the reliability of prediction results [5]. For example, inundation in building areas is often simulated, and road waterlogging in densely built-up areas cannot be, which is not consistent with the actual situation in rainstorm events. The high-precision requirement of publicly acceptable, low-cost urban waterlogging simulation is not supported by the accuracy of raw DEM data directly obtained through different technologies.

Given the limitations of those technologies, it is necessary to combine multiple data sources and various data processing methods to improve the accuracy of raw DEM data in practical applications where data fusion and calibration methods are commonly used [7]. Data fusion is the integration of multiple data sources to improve the DEM data accuracy, including merging the DEMs produced by different technologies, enhancing the DEMs with available auxiliary data from other DEMs, and fusing the InSAR images with different acquisition geometries [26,27]. For example, three DEM images, the Advanced Land Observing Satellite (ALOS), SRTM, and Advanced Spaceborne Thermal Emission and Reflection Radiometer (ASTER), from open-source databases were processed by three different methods, namely Gram–Schmidt pan sharpening (GS), weighted fusion, and feature-point-embedding fusion [28]. Three-dimensional coordinate information, RGB data, and the normalized coordinate information of airborne point cloud data were regarded as multi-information to improve the accuracy of DEM construction [29,30]. Besides, the remotely sensed Cartosat-1 stereo image pairs and surveyed ground truth points were integrated to develop DEM [31]. Calibration methods improve DEM data accuracy by eliminating systematic errors and calibrating raw data, whose methods include mean calibration, median calibration, regression calibration, interpolation, polynomial fitting, and so on [32]. The calibrating data are composed of global vegetation [33], stereoscopic satellite imagery [34], and interferometric synthetic aperture radar data [35,36]. Data fusion and calibration are effective methods to improve DEM accuracy compared to other accuracy-improving methods with low cost. However, most of the existing studies are about DEM data enhancement by fusing multi-source data at the macro level, such as the ASTER Global Digital Elevation Model generated for almost the whole globe [37], and global STDM30 [38]. And several scholars have researched improving DEM accuracy for specific terrains, such as the fault scarps [39], steep terrain [40], bare slope [41], large-scale seafloor topography [42], mine [43], and so on. The urban features of the DEM accuracy improvement in those areas have been seldom considered, which is crucial for urban waterlogging prediction and management. Urban waterlogging simulation is significantly influenced by the DEM accuracy of roads and buildings, the two land use types that make up the majority of the city [44]. According to the actual records of urban waterlogging, roads experience most of the inundation due to their poor permeability and low terrain compared with other land use types [45]. Road inundation causes serious consequences during rainstorm events, as they are the main passages in the city crowded with pedestrians and vehicles [46,47]. However, the building artifact locations are less likely to be waterlogged due to the presence of vertical abruptness and a higher elevation than roads. Due to the nature of these inundation locations, it is vital to precisely identify roads and buildings and contrapuntally enhance the DEM accuracy of these locations for waterlogging simulation. A great deal of research has been conducted on adjusting the elevation of areas with densely packed buildings or vegetation [48]. For example, machine learning methods have been used to remove building and forest parts [49]; simple and progressive morphological filters have been applied to remove building artifacts [50]; building complexes have been added and unphysical representations of bridges have been removed by a proposed geographic information system (GIS)-based correction method [51]. Cities have high building density, and the entire densely built-up area is easily identified as a building type; however, the roads and the gaps between buildings are often ignored, resulting in a significant inundation bias that inevitably causes an erroneous result that is difficult to correct later. Although satellite night-time lights, global population density, and OpenStreetMap buildings were combined to obtain a more accurate range of buildings, it is difficult to acquire comprehensive, up-to-date data on cities [52].

To address the above-mentioned issues, in this study, we focused on improving the accuracy of urban terrain based on the U-Net image segmentation model and simulating waterlogging in the Fengban River basin in Fuzhou City, China. The primary objectives of this work were (1) to accurately identify building areas through the U-Net image segmentation model; (2) to reconstruct urban terrain by fusing multiple sources of data such as buildings, roads, and drainage networks; and (3) to evaluate the differences in waterlogging risk under different terrain reconstruction methods. The novelty of this study was to propose a multisource data fusion (MDF) method for terrain reconstruction, thereby enhancing the accuracy of the waterlogging simulation by considering the segmentation and the gap between urban buildings. This study helps increase the accuracy of the analysis of urban waterlogging risk, serves as a reference for resilient cities, and may also provide an effective research methodology for other scholars.

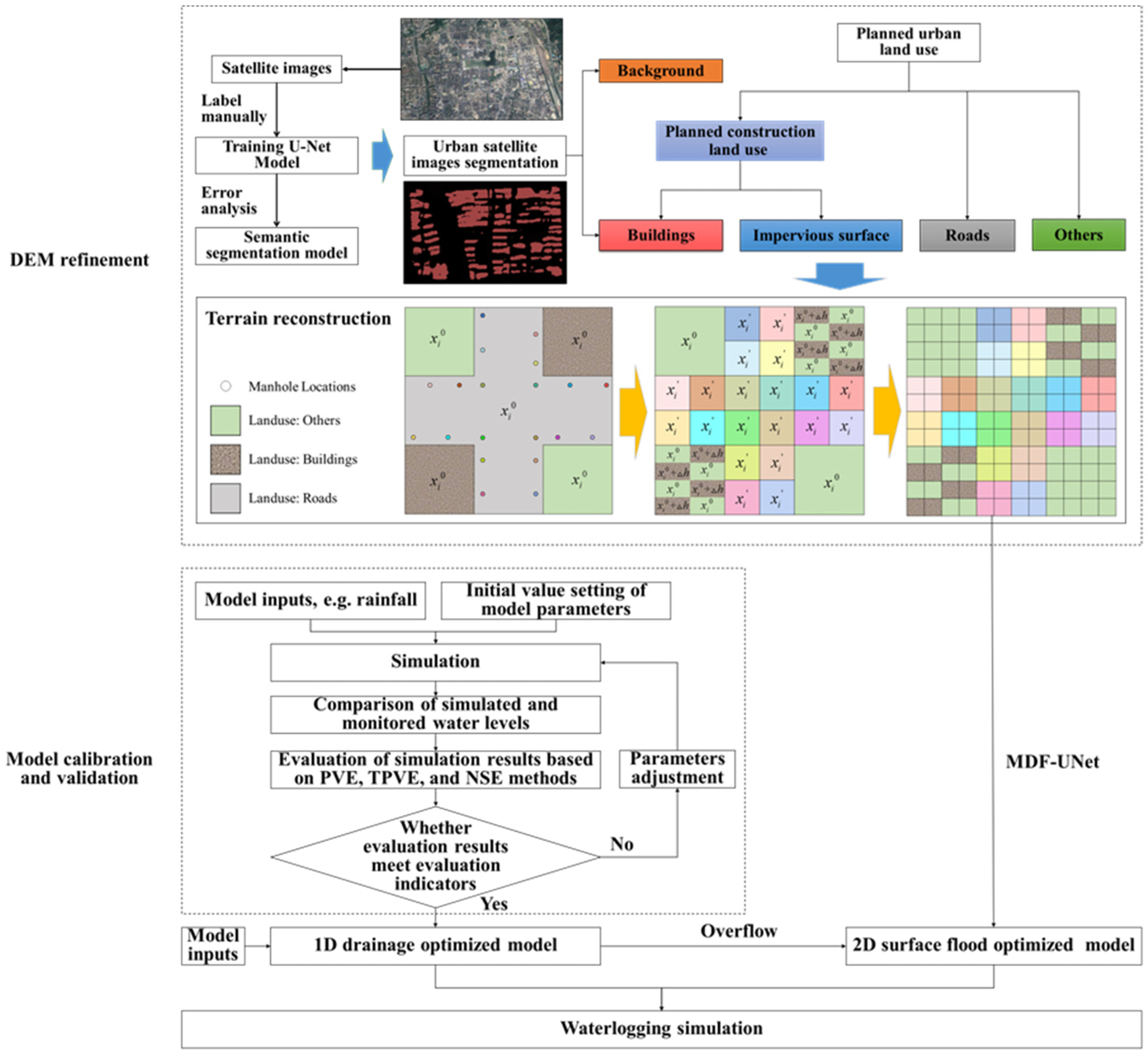
2. Methodology

The building areas were segmented based on the satellite image data by binarizing buildings and other regions in the city with a U-Net image segmentation model. Firstly, the study area was divided into slices of the same size as the test set of the deep learning model. The areas under similar environmental conditions were taken as the training and validation sets to identify the building areas in the whole study area. Secondly, the urban terrain was reconstructed by combining the results of building area identification with the data on roads and drainage networks. Finally, the modified DEM data were used for two-dimensional (2D) modeling, coupled with a one-dimensional (1D) conduit drainage pipe model to simulate urban waterlogging. The framework of this study is shown in Figure 1.

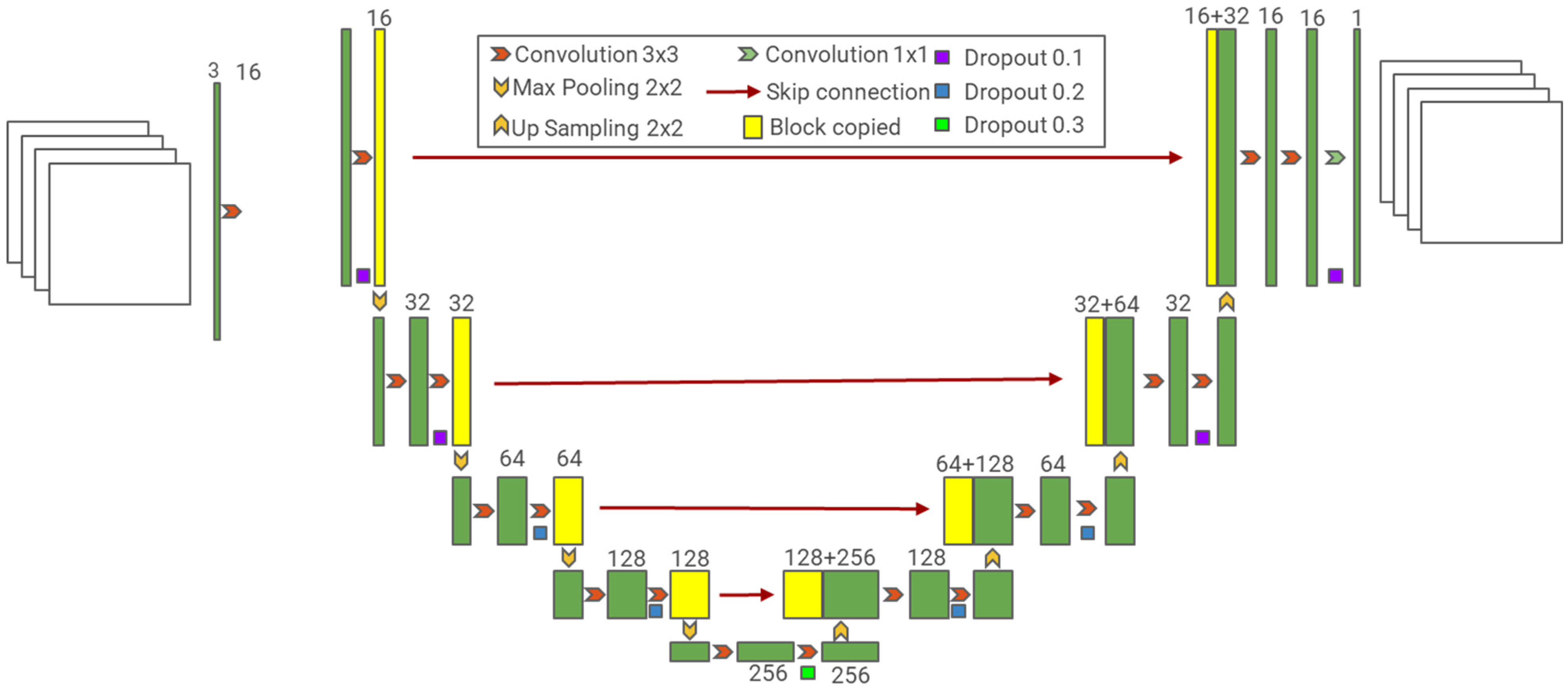
2.1. U-Net Model for Segmentation

Image segmentation is one of the most important challenges in computer vision, and its main task is to classify objects in the image at the pixel level according to requirements [53,54]. The image segmentation methods are divided into two categories based on different principles. One is the traditional method of image segmentation based on digital image processing, topology, mathematics, and other pixel analyses, including the pixel-threshold method, region-based and edge-detection-based methods (such as Sobel, Roberts, and Canny operators), etc. [55,56]. The advantages of this method are its interpretability and operation efficiency; however, its effect is not ideal for complex images. The second method involves deep learning (DL)-based methods, such as fully convolutional networks (FCN) [57], U-Net [58], etc. The segmentation results for complex images are confirmed using DL models, despite the high model complexity and computational costs. In this study, U-Net was used as the segmentation model for the buildings, considering that the research object was the satellite remote sensing image.

The structure of the U-Net model is symmetrical, which is a variant of FCN (Figure 2). The U-Net was initially used for medical image segmentation and has been proven to have high accuracy even with a small amount of labeled data [59]. It consists of an encoder–decoder structure, where the encoder is responsible for feature extraction, and the decoder is used to restore the original image resolution. To construct a U-Net model for building segmentation, firstly, the scope of the buildings in the satellite image was labeled manually. Secondly, the labeled images were trained by the U-Net model. Finally, the validation images were predicted using the trained model, and the effectiveness of building area segmentation was evaluated.

2.2. Topographic Reconstruction Model

Inverse distance weighting (IDW) is a spatial interpolation technique that is used to estimate the value of an unknown variable at a known location [60]. The IDW value is determined by calculating the weighted average estimate value of the surrounding data points [61,62]. As the data point is further away from the unknown location, the less weight it has, the less influence it will have on the estimated value.

The point to be inserted is assumed as $y$, the $n$ known point is denoted as $y_1\sim y_n$, and the distance between $y_1\sim y_n$ is denoted as $d_1\sim d_n$ and $y$, respectively. Then, the sum of the inverse of the distances is given by Equation (1).

$$D={\displaystyle \sum _{i=1}^n\frac{1}{d_i}}$$

(1)

The weights of the point $y$ to be inserted corresponding to each known point $y_i$ are calculated as follows (Equation (2)).

$$w_i=\frac{1}{D}\cdot \frac{1}{d_i}$$

(2)

Therefore, the estimated value of the point to be inserted can be calculated according to Equation (3).

$$Z(y)={\displaystyle \sum _{i=1}^n{w}_{i}Z(y_i)}$$

(3)

where $z\left(y\right)$ and $z\left(y_i\right)$ denote the point $y$ to be interpolated and the known point $y_i$ value, respectively, and $i=1,2,\dots ,n$.

One advantage of the IDW approach is that it is implemented using basic mathematical formulas instead of complex statistical models or algorithms, making it relatively simple and easy to understand. Meanwhile, it provides flexibility using continuous and categorical data [63]. However, it is sensitive to the choice of the weighting function. The IDW function used in the IDW may lead to the over- or under-estimation of values near the edges of the dataset or in regions with few data points [64]. In addition, this method assumes a uniform spatial structure of data, which may not always be the case in real-world scenarios. It may produce biased results if the data points are not evenly distributed or if there are large gaps in the data.

The MDF method was introduced in response to the problem of low accuracy and isolated distribution due to the insufficient density of the original DEM data. The discrete elevation points in road areas and the building heights were measured manually, considering the characteristics of urban surface elevation (e.g., vertical abruptness) [65]. Then, the fusion of multiple sources of data was interpolated into the original DEM to improve its accuracy.

Urban DEMs were classified into three types based on the land use layers: roads, buildings, and others. The elevation values of point $i$ of the road, building, and other types of ranges are assumed to be $R\left(x_i\right)$, $B\left(x_i\right)$, and $O\left(x_i\right)$ obtained by interpolation using this method, respectively. The elevation value ${x_i}^0$ corresponds to the raw DEM at the elevation point $i$, while ${x_i}^{\prime }$ is the elevation interpolation between the top elevation value of the nearest inspection well and the original DEM data at the point $i$ within the road. The elevation value $R\left(x_i\right)$ within the road range is assigned to the exact elevation point measured manually by nearest matching. $B\left(x_i\right)$ is the sum of the raw DEM data and a fixed value (∆h), which is an increased value from the raw DEM value within the building areas to reflect the fact that buildings are at a higher elevation than the other types of land use around it and avoid waterlogging at building areas, such as 10 m, or 30 m. $O\left(x_i\right)$ is equal to the corresponding elevation value of the raw DEM. The elevation of every point $i$ in the merged raster location can be calculated using Equations (4)–(6).

$$R\left(x_i\right)={x_i}^{\prime }$$

(4)

$$B(x_i)={x_i}^0+△h$$

(5)

$$O(x_i)={x_i}^0$$

(6)

Then, the raster points were constructed in steps $d$, and each point was interpolated using the point $i$ in the merged raster data. Thus, for each point $i$, the corresponding elevation was calculated by Equation (7).

$$Z(x)={\displaystyle \sum _{j=1}^n\epsilon Z\left(x_j\right)}$$

(7)

where $n$ denotes the number of reference points that need to satisfy the condition that the distance between the point to be interpolated and the reference point is less than $2d$. The elevation value of the reference point in the merged raster data is $Z(x)$, and $\epsilon$ is the corresponding weight coefficient calculated in the selected interpolation method, such as IDW.

2.3. Hydrological and Hydrodynamic Model

A distributed hydrological model is used to simulate rainfall–runoff relationships. There are several ways to simulate the infiltration of precipitation into unsaturated soil, such as the Horton equation, Green–Ampt model, and runoff curve method. The Horton equation is widely used because of applicability in urban areas and the small number of parameters. In this study, the Horton equation is used for infiltration calculation. The calculation of a 1D conduit drainage pipe model was achieved by solving a system of 1D Saint Venant equations [66].

$$\frac{\partial A}{\partial t}+\frac{\partial Q}{\partial x}=0$$

(8)

$$\frac{\partial Q}{\partial t}+gA\frac{\partial h}{\partial x}+gA{S}_0+\frac{\partial (Q^2/A)}{\partial x}=0$$

(9)

where $A$ is pipe section area (m²); $t$ is time (s); $Q$ is the flow rate (m³/s); $x$ is the length of pipe along the direction of water flow (m); $g$ is the acceleration of gravity (m/s²); $h$ is water depth (m); $S_0$ is the slope of the pipe bottom; and $K$ is the flow resistance coefficient.

The 2D hydrodynamic model includes the DEM construction and the creation of a two-dimensional grid on the ground surface. After dividing the grid based on topographic data, setting relevant parameters, and initial conditions (e.g., initial water level, etc.), the surface inundation can be calculated and simulated. In the 2D hydrodynamic model, the small variation in the terrain of the urban area was taken into account, assuming that the flow extended mainly in the horizontal direction and ignoring the variation in flow velocity in the vertical direction. The shallow water equation, namely the Navier–Stokes equation in mean depth form, was used to mathematically describe the 2D flow regime [67]. The calculation formula is as follows:

$$\frac{\partial h}{dt}+\frac{\partial (hu)}{dx}+\frac{\partial (hv)}{dy}=0$$

(10)

$$\frac{\partial (hu)}{\partial t}+\frac{\partial }{\partial x}(h{u}^2+\frac{1}{2}g{h}^2)+\frac{\partial (huv)}{\partial y}=gh\left(S_{0,x}-S_{f,x}\right)$$

(11)

$$\frac{\partial (hu)}{\partial t}+\frac{\partial }{\partial y}(h{v}^2+\frac{1}{2}g{h}^2)+\frac{\partial (huv)}{\partial x}=gh\left(S_{0,y}-S_{f,y}\right)$$

(12)

where $h$ is the water depth (m); $u$ and $v$ are the velocity components in the $x$ and $y$ directions (m/s); $S_{0,x}$ and $S_{0,y}$ are the bottom slope components in the $x$ and $y$ directions, respectively; $S_{f,x}$ and $S_{f,y}$ are the friction components in the $x$ and $y$ directions, respectively.

The 1D and 2D coupling model can fully reflect the relationship between the underground drainage network and the ground surface for water exchange, which is connected through the nodes (e.g., inspection wells, rainwater wells, etc.) in the drainage network model. When the pipeline is overloaded, the node water level will rise, and the water will overflow from the coupling node to the ground surface, and the water flow is exchanged through the node to complete the 1D model to the 2D model. When the pipeline drainage capacity is restored and the pipeline is not in a full state, the water flow in the ground surface will flow back to the drainage system through the nodes.

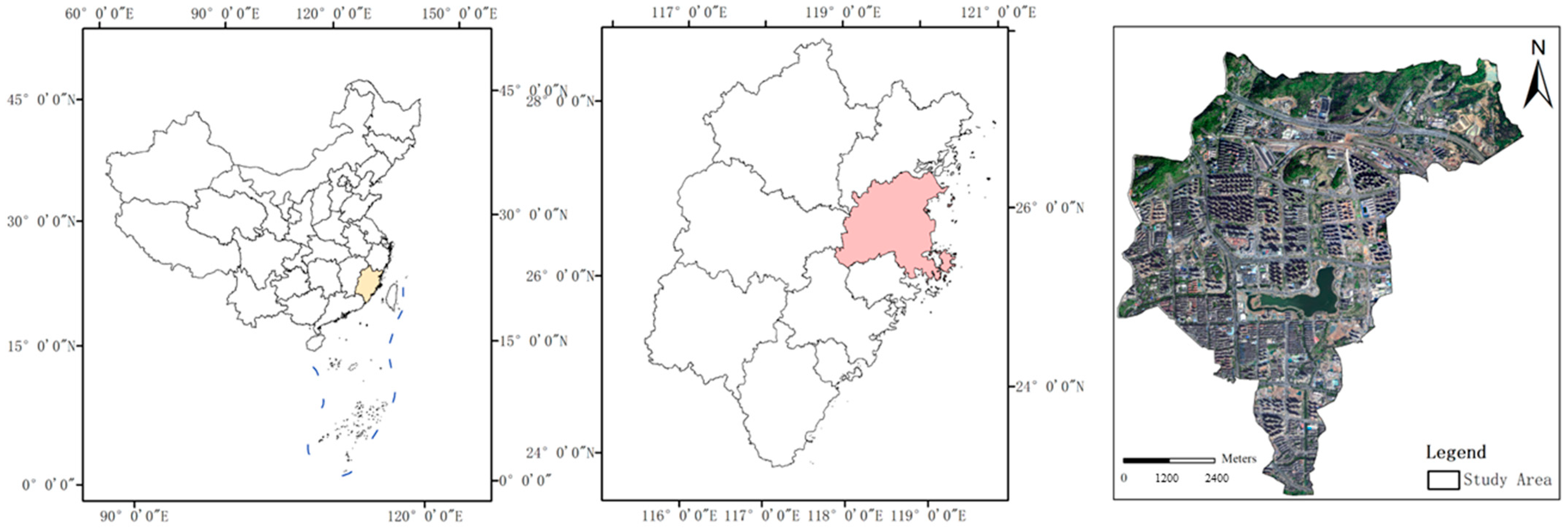
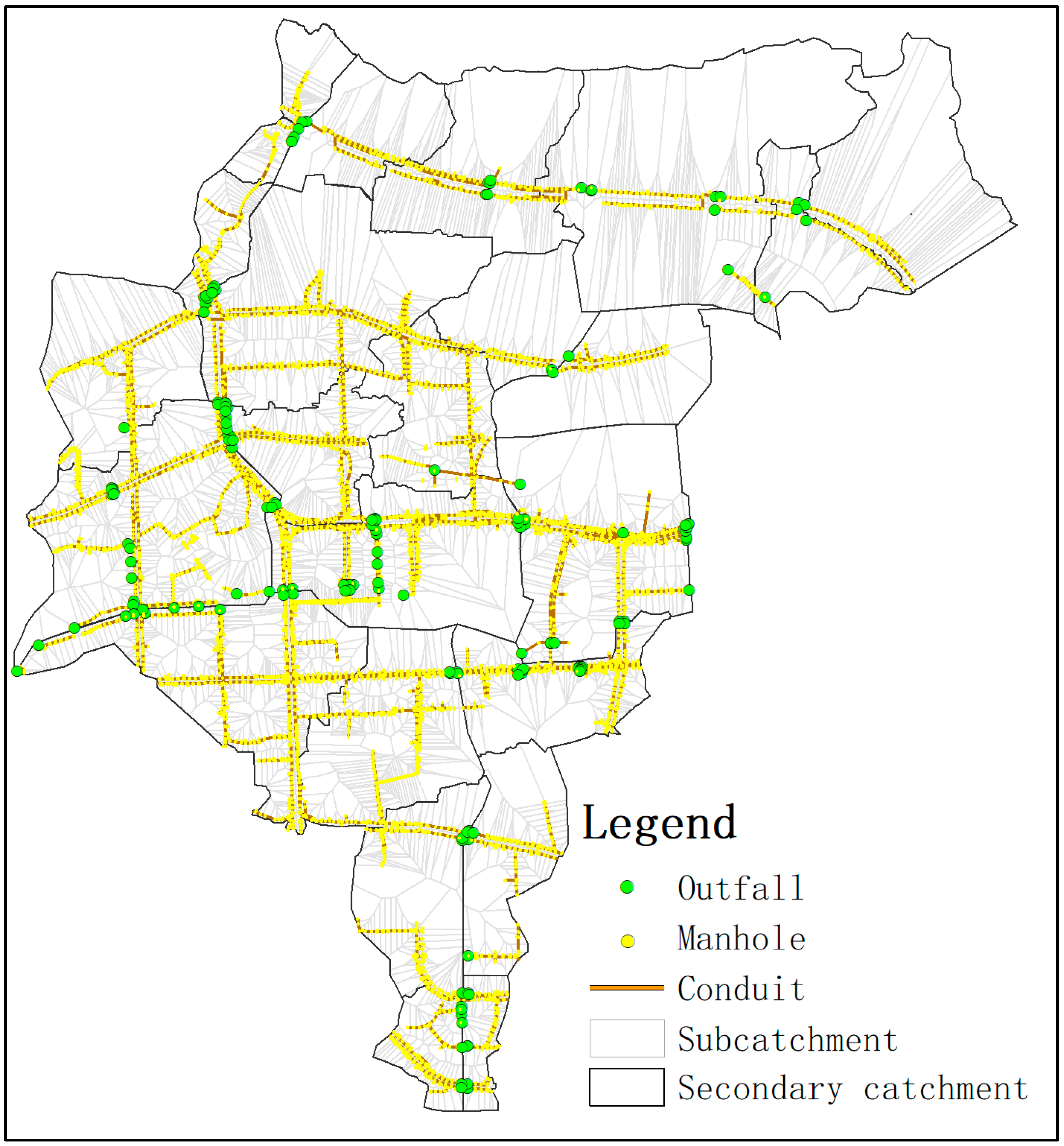
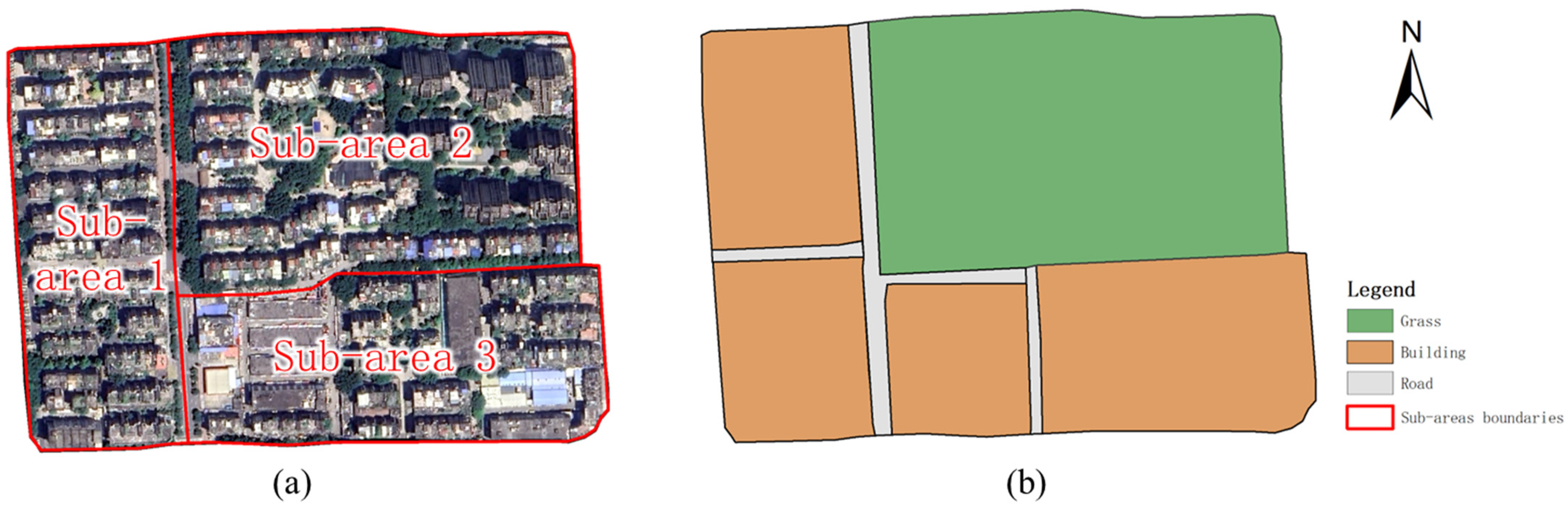
3. Study Area and Data Source

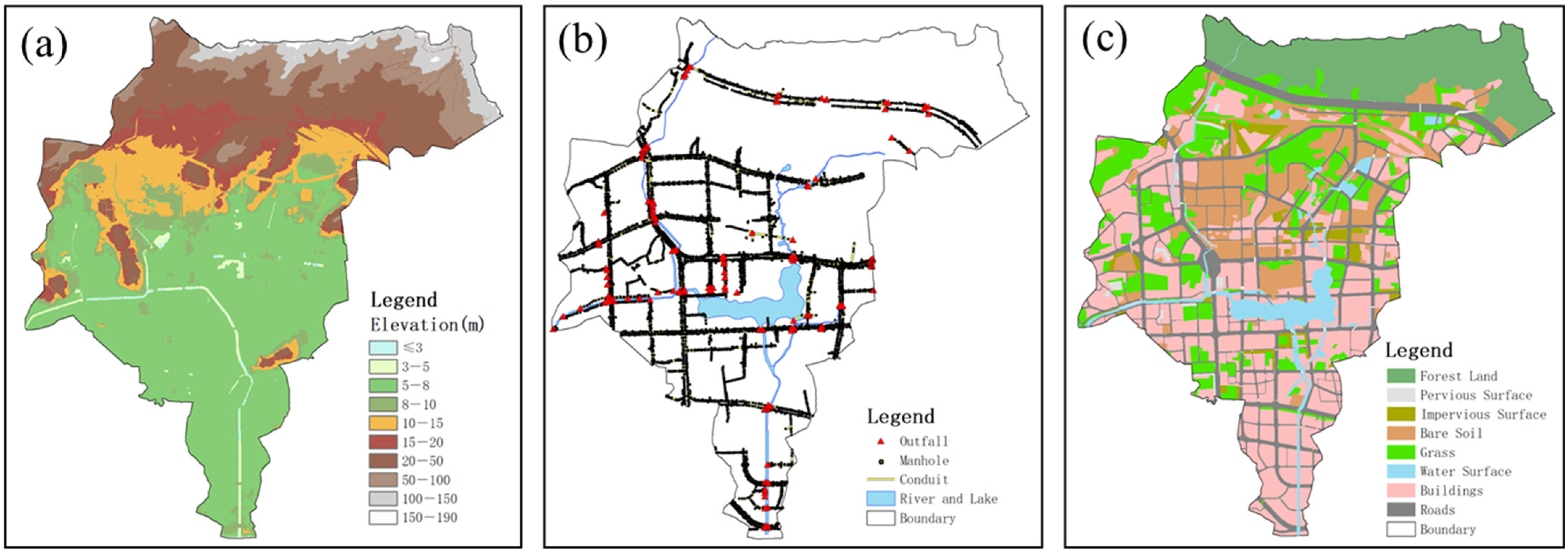
3.1. Data

In this study, the Fengban River basin, with an area of 15.06 km² in Fuzhou City, Fujian Province, China, was selected as the study area, and the location is shown in Figure 3.

The remote sensing images in Figure 3 were obtained from the Sentinel-2 satellite. It carries a multispectral imager (MSI) at an altitude of 786 km, covering 13 spectral bands with a width of up to 290 km and a ground resolution of 10 m, 20 m, and 60 m, respectively. Moreover, with different spatial resolutions from the visible and the near infrared (NIR) to the short-wave infrared (SWIR), the Sentinel-2 data are the only ones among the optical data that contain three bands in the red-edge range which is very effective for different surface identification. In addition, one Sentinel-2 satellite has a revisit period of 10 days, and the two complement each other with a revisit period of 5 days, which is advantageous for later renewal of land use identification under rapid urbanization. The collected data for terrain reconstruction were the DEM, satellite remote sensing image, drainage network data, and land use layer of the study area (Figure 4).

DEM data with a resolution of 2 m × 2 m obtained from the Fuzhou City Survey Institute have higher accuracy than the publicly available DEM data, usually 90 m × 90 m or 30 m × 30 m. The obtained data show the topographic changes; for example, the surface elevation is higher in the mountainous area in the north (mostly above 50 m) and lower in the developed urban area in the south, which is full of buildings. Furthermore, most of the river distributions can be seen because of their lower elevation compared to the surrounding area. However, this accuracy of DEM data is insufficient for a precise urban waterlogging simulation and can negatively influence the inundation, including the location, ranges, and depth of waterlogging.

The drainage network data include the vector distribution and related parameters, such as areas, diameters, and elevations of drainage network elements, namely manholes, outfalls, and conduits. These data are mainly used for the construction of a 1D conduit drainage pipe model, while the ground elevation data of manholes are vital for terrain reconstruction. There are 8179 nodes collected, with a large span of ground elevations, in which the lowest is 0.87 m, the highest is 56.31 m, and the average is 11.02 m. Almost all nodes with a ground elevation greater than 15 m are located in the northern part of the study area, and the south and central parts are relatively flat, where the ground elevation is between 5 and 10 m. The average ground elevation of nodes is lower than the average elevation of DEM in the same area, with a smaller mean square deviation since nodes are mainly located on roads and rarely on mountains or grasslands.

The land use layer includes eight different types of land uses, namely grass, water surface, shrub, bare soil, permeable square, impermeable square, building, and road. Buildings, grass, and roads make up the top three areas, with respective area percentages of 29.13%, 21.77%, and 15.13%. The northern mountainous area with higher terrain has shrubs as the underlying surface type, and the north-central area has more bare soil surface types, while the south is a developed area and the south-central area is dominated by buildings.

Furthermore, the monitored data during rainfall, such as rainfall intensity, the water level of the river and manhole, inundated ranges, and depth, were used in the model simulation and analysis process, which were obtained from the monitoring system of the government management agency. All monitoring data are recorded at 10 min intervals.

3.2. Building Area Segmentation Using U-Net Model

The remote sensing images with a range of 10 km × 10 km of Fuzhou city were obtained and segmented into sub-images of 200 m × 200 m, and finally 2500 image datasets were obtained. A total of 1742 sub-images outside the study area were selected as the training set for building area segmentation, 400 as the validation set, and 448 sub-images including the study area were used as the test set. Building areas in the training set were labeled manually and trained using the U-Net model. After a number of training and parameter adjustments, the final model network parameters were set as follows: the initial learning rate was 0.00001, the number of iterations was 100, and regularization was used to prevent model overfitting. Mean intersection over union (MIOU) and mean pixel accuracy (MPA) were used as evaluation indicators for segmentation results.

$$MIOU=\frac{1}{k+1}{\displaystyle {\sum }_{i=0}^k\frac{p_{ii}}{{\displaystyle {\sum }_{j=0}^k{p}_{ij}}+{\displaystyle {\sum }_{j=0}^k{p}_{ji}-p_{ii}}}}$$

(13)

$$MPA=\frac{SUM(P_i)}{k}$$

(14)

where $k$ is the number of categories, $p_{ij}$ and $p_{ji}$ are the number of pixels which have been wrongly classified as from classes $i$ to $j$ and $j$ to $i$, respectively. $p_{ii}$ is the number of correctly classified $i$, and $SUM(P_i)$ is the accuracy of $i$.

The results indicate that $MIOU$ and $MPA$ for building area segmentation are 0.84 and 0.91, respectively. The U-Net used in this study has proved to be accurate in building area segmentation.

3.3. Model Construction

In this study, a 1D conduit drainage pipe model and a 2D hydrodynamic model were constructed based on the processed data, which included 2592 manholes, 93 outfalls, and 2499 conduits with a total length of 60.14 km. Firstly, six primary catchment areas were manually divided according to the distribution of rivers, and then the secondary catchments were delineated using the D8 algorithm based on the revised DEM data of high accuracy [68,69]. Thirdly, the secondary catchments were divided as drainage network catchment units based on high-precision road locations and manually adjusted according to the correspondence between manholes and outfalls. Finally, 2759 sub-catchments were obtained with a total area of 15.06 km², and the model is shown in Figure 5.

The accuracy of simulation results was evaluated using the Nash–Sutcliffe Efficiency coefficient (NSE), which is often used to verify the goodness of the hydrological model simulation results [70]. Its calculation formula is as follows:

$$NSE=1-\frac{{\displaystyle {\sum }_{t=1}^n(y_t-{y^{\prime }}_t}{)}^2}{{\displaystyle {\sum }_{t=1}^n(y_t-\overline{y_t}}{)}^2}$$

(15)

where $n$ is the number of observed and simulated values during the simulation time; $y_t$ and ${y^{\prime }}_t$ are the observed and simulated values at moment $t$, while $\overline{y_t}$ is the mean of the observed values.

The NSE value ranges from negative infinity to 1. If the NSE value is close to 1, it indicates the model is of good quality and credible, and the overall results are reliable. If it is close to 0, it suggests the process simulation errors are large, and the simulation results are close to the mean level of the observed values. The model is unreliable if NSE is significantly below 0 [71].

Peak value error (PVE) is the ratio of the absolute error of peak values. This ratio is calculated between the monitored and simulated manhole water levels and the actual monitored peak one and multiplied by 100% in a specific period. The model simulation effect on the peak value of the water level is credible if the PVE is less than 25%. The time of peak value error (TPVE) refers to the time error between the peak values in the monitored and simulated manhole water levels. A TPVE of less than 10 min indicates accurate simulation in terms of peak present time, while a TPVE of more than 30 min indicates low accuracy.

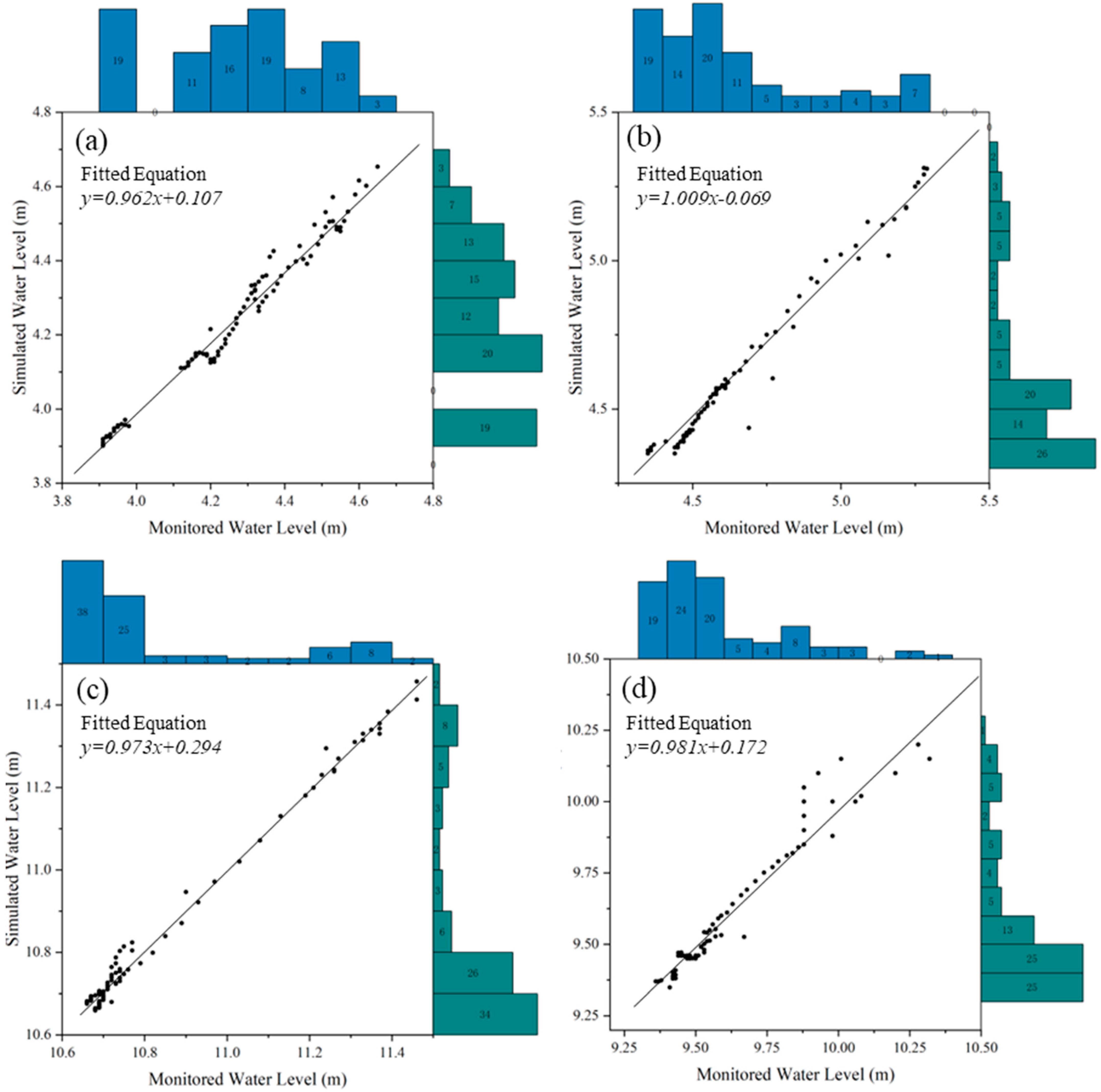
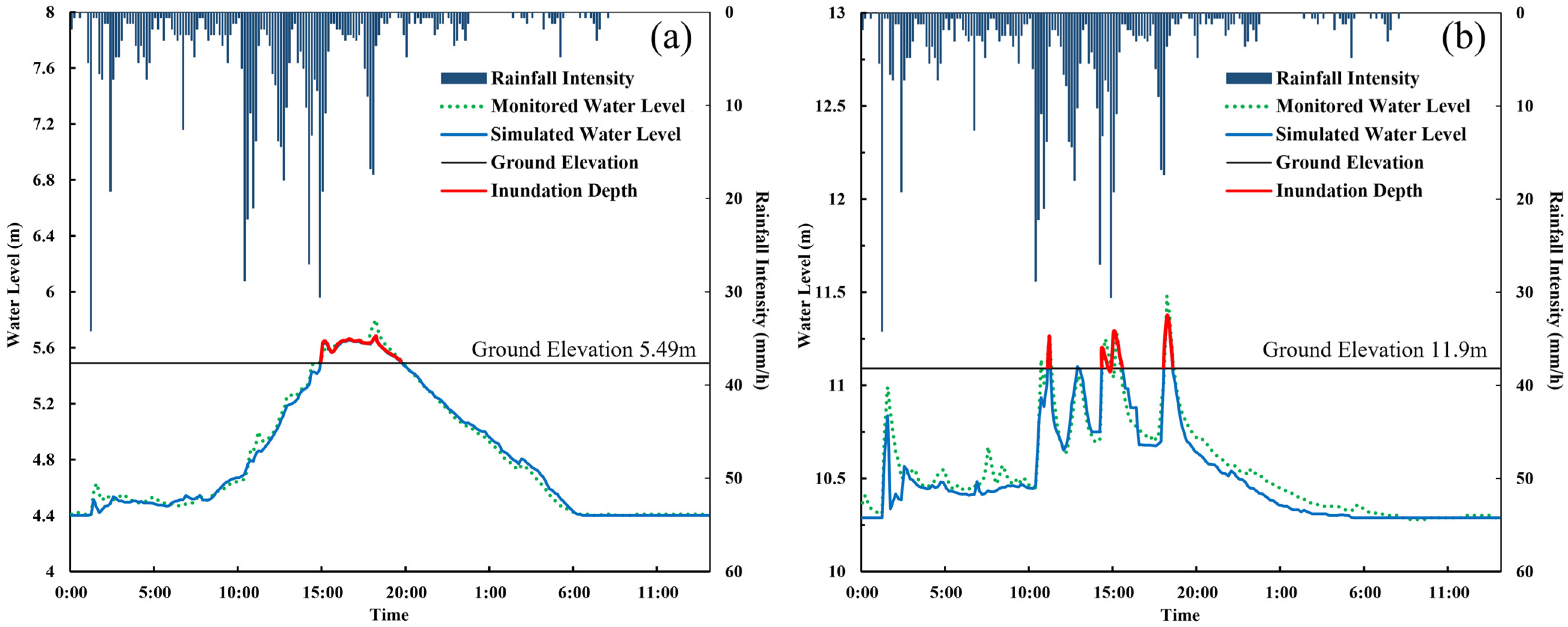
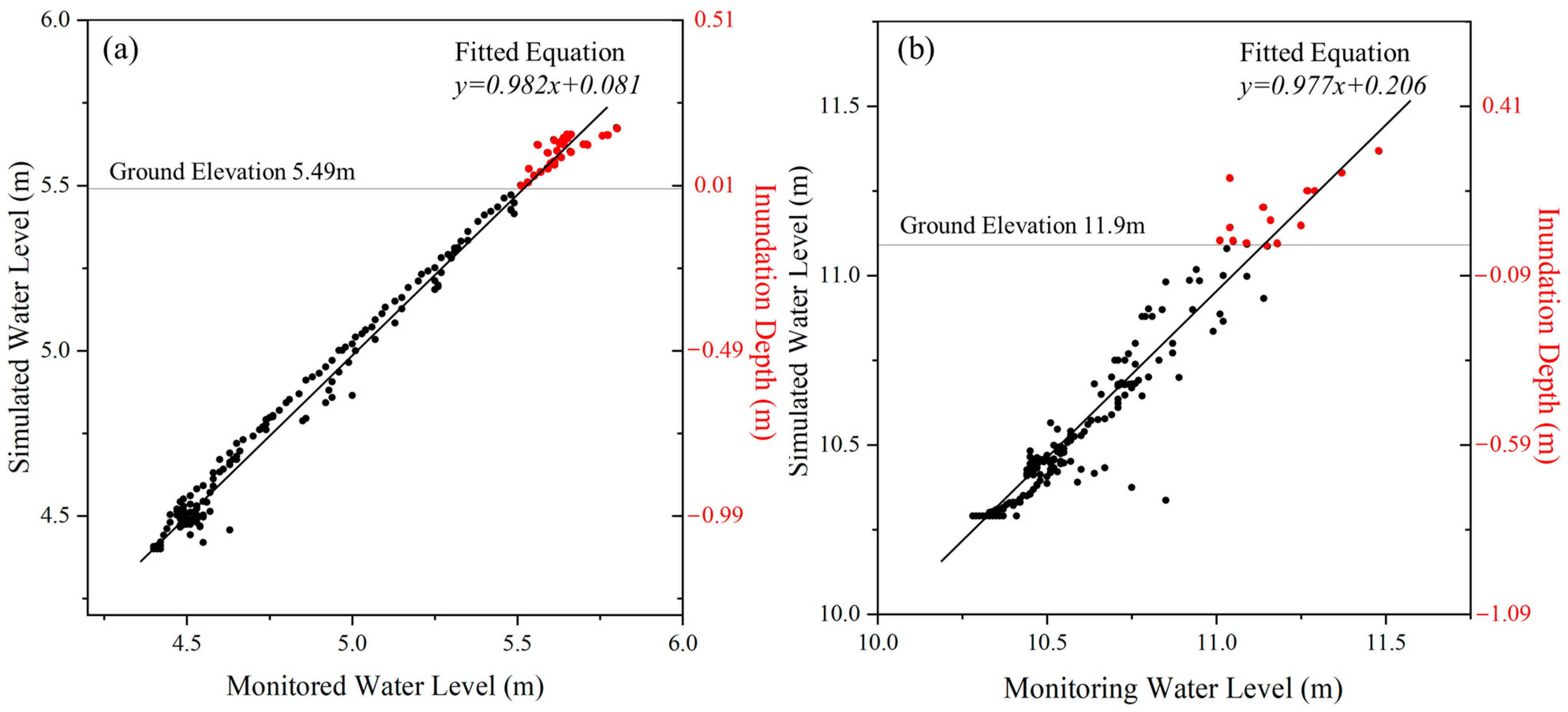
3.4. Model Calibration and Evaluation

The parameters of the catchment and the drainage were optimized by comparing the simulated and monitored water levels during the rainfall period based on the monitored data (rainfall intensity, manhole water level, and river water level at outlets of the drainage network), and the optimized parameters are shown in

Table 1. The key parameters and the optimized values.

Module	Parameter	Value Range	Optimized Value
Subcatchment	N-Imperv	0.011~0.025	0.023
	N-Perv	0.060~0.300	0.096
	Dstore-Imperv (mm)	2.00~4.00	2.75
	Dstore-Perv (mm)	2.50~10.00	4.81
Infiltration	Max. Infil. Rate (mm/h)	30.00~90.00	75.32
	Min. Infil. Rate (mm/h)	0.10~10.00	4.53
	Decay Constant	2.00~7.00	4.79
Drainage	Roughness	0.010~0.030	0.016

below.

This optimization eliminates the negative influence of the inaccurate simulation results on the waterlogging model. Four manholes, numbered M1 to M4, were selected to demonstrate the calibration and evaluation of model accuracy. The accuracy of the optimized model was analyzed by scatter plots, which represent the simulated and monitored water levels (Figure 6).

As can be seen from the fitted equation in Figure 6, the slope and intercept are 0.962, 1.009, 0.973, 0.981 and 0.107, −0.069, 0.294, 0.172, respectively, indicating that the optimized model can reliably predict a small difference between the data of the two groups with high accuracy and confidence. Consequently, the trend of changes in manhole water levels can be simulated accurately. The scatter points in the upper right of the figures represent the high-water-level data, where the maximum point represents the peak value. The peak values of M1, M2, and M3, as shown in Figure 6a,b,c, respectively, are closely distributed around, even on the function y = x, demonstrating that the model performs well in terms of the peak value.

Meanwhile, the evaluation indicators PVE, TPVE, and NSE were used to evaluate the optimized model, whose statistics are shown in

Table 2. Statistics of evaluation results.

NO.	WL	PV (m)	TPV	PVE (m)	TPVE (min)	NSE
M1	MWL	4.65	13:10	0.01	0	0.87
	SWL	4.66	13:20
M2	MWL	8.28	14:00	0.05	10	0.88
	SWL	8.33	13:50
M3	MWL	11.46	13:20	0.03	10	0.91
	SWL	11.43	13:10
M4	MWL	10.32	13:30	0.11	20	0.79
	SWL	10.21	13:10

below.

The PVE and TPVE values of M1, M2, M3, and M4 are 0.01 m, 0.05 m, 0.03 m, 0.11 m, and 0 min, 10 min, 10 min, and 20 min, respectively, satisfying the requirements of model calibration. The NSE values obtained are 0.87, 0.88, 0.91, and 0.79, indicating that the model is of good quality and reliable, which is consistent with the conclusions of the previous analyses.

4. Results and Discussions

Based on the rate-determined 1D drainage pipe network model, the surveyed, unprocessed raw DEM data and the processed DEM data by IDW, MDF, and MDF-UNet methods were used to construct 1D and 2D coupled models, respectively.

4.1. Overall Inundation Analysis

The differences in simulation results between different DEM data processing methods were compared using the rainfall data monitored on a rainy day in the study area and the different waterlogging scenarios simulated based on the four different DEM-made coupled models under the same boundary conditions. The simulation results are shown in Figure 7.

Figure 7 shows the distribution of inundated areas, where the green triangles indicate the waterlogging locations recorded during the rainfall event. According to the figure, 10 locations were simulated by raw DEM data, six by the IDW method, and 13 and 15 by the MDF and MDF-UNet methods, respectively. The MDF-UNet method improved the accuracy of simulating waterlogging locations, namely from the raw data of 58.8% to the proposed approach of 88.2%. Two inundated areas located in the building area were simulated by the MDF-UNet method but not by the MDF method. This situation will be discussed in detail in the subsequent section. In addition, two areas among the 17 recorded were not simulated by the MDF-UNet method. The waterlogging in these two areas was caused by the blocked rainwater grates and was therefore not considered in our proposed models. In addition, it is impossible to overlook that the raw DEM data and IDW method also record inundated areas at numerous sites where waterlogging is unlikely and does not occur.

Two inundated areas, represented by manhole 5 (M5) and manhole 6 (M6) as nodes with heavy waterlogging, were selected to demonstrate the accuracy of manhole water levels and waterlogging depths under the MDF method. The location M5, as shown in Figure 8a, is in the southern area where buildings are densely distributed, the bottom elevation is 4.40 m, and the ground is 6.02 m. It is close to the outlets and belongs downstream of the drainage network. The location M6 (Figure 8b) is situated upstream in the northern region, where there are several hills, and it has a bottom elevation of 10.29 m and a ground elevation of 11.43 m.

The simulated water level generated using the coupled model was compared with the monitored water level and is shown in Figure 9. The solid black lines represent the ground elevation of manholes, the curve below the black line indicates the water level of the underground manhole, and the curve above the black line indicates rainwater overflows from manholes that cause ground waterlogging. The depth at which waterlogging occurs is calculated by subtracting the data value from the ground elevation of the manhole.

The M5 location had a relatively long waterlogging duration, namely inundating at 15:00 and receding at 19:40, while intermittent waterlogging appeared at the location of M6 with inundated periods of 11:00–11:10, 14:20–14:50, and 18:00–18:30 (Figure 9). This is because M5 is located downstream of the drainage network. In M5, the rainwater flow time of upstream manholes is not similar because of the different catchment areas and the eventual flow of the rainwater to M5. The water level of M6, located upstream of the drainage network, is very sensitive to rainfall intensity; therefore, waterlogging appears with an increase in rainfall intensity.

The simulated and monitored water levels were characterized by the scatter points, as shown in Figure 10. The points above the solid line indicate that the water level exceeds the ground elevation of manholes, and waterlogging is generated.

The inundated data of M5, namely the red points above ground elevation, fit well with the fitted equation, showing that the simulated and the monitored are close to each other and that the inundated depth simulation is accurate. In Figure 10b, the distribution of the red points representing the inundated depth is a little scattered. However, the slope of the fitted equation indicates that the trend of the inundated depth simulation of M6 is good, but there is a small deviation in the specific values. The reason is that M6 is located in the northern mountainous region, and the catchment and land use parameters are more difficult to determine compared to the developed urban areas with a large number of impermeable underlying surfaces.

4.2. Inundated Areas Distribution on Roads

The statistical analysis of inundated depth on roads (Table 1 and Figure 11) found that the waterlogging areas of raw DEM are significantly larger, and the depths are smaller compared to other methods. This is due to its inaccurate description of the elevation of buildings around roads, resulting in waterlogging in the location of buildings. Figure 11 illustrates that the result of the simulated interpolation method is more accurate than the raw DEM data in Area 1.

At the same time, the decrease in the inundated area led to an increase in the inundated depth under the same rainfall scenario (Figure 12). In order to accurately describe the waterlogging process in non-building locations, especially on roads, the MDF and MDF-UNet methods took into account building heights by correcting raw elevation, thereby guaranteeing that waterlogging occurred in non-building locations.

The inundated depths on the roads in Area 1 are in descending order: MDF > MDF-UNet > IDW > the raw DEM data. The difference in inundated depths between the first three is relatively smaller, while the raw DEM is larger, justifying the previous analysis (Figure 12a). Furthermore, the inundation depth error of the raw DEM data simulation is the largest, with a maximum error of 0.4 m (Figure 12b). The errors of the other three methods are within 0.2 m. The inundation depth error of the MDF-UNet method, with the smallest error median value, is less than 0.1 m, indicating that the proposed method improves the accuracy of the inundated depth simulation.

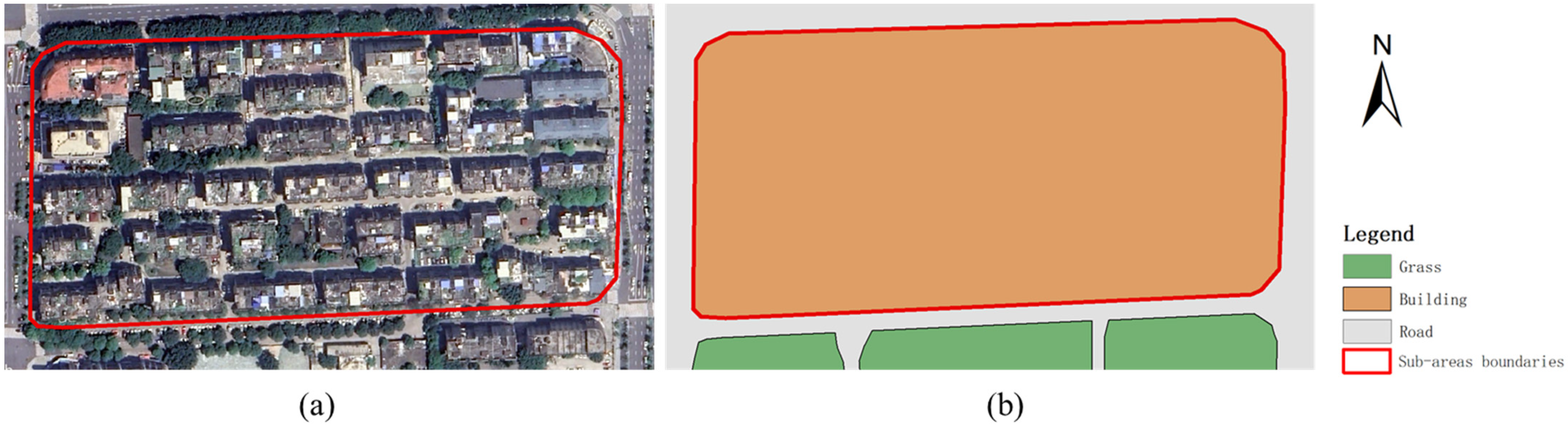
4.3. Inundated Areas Distribution in Densely Built-Up Areas

An apartment complex occupying the largest number of buildings in the city consists of a number of adjacent residential buildings and is usually surrounded by the main roads of the city. In many developed cities with large populations, buildings are densely distributed in apartment complexes and are very close to each other. As a result, the whole apartment complex is usually divided into a building area during the creation of land use layers ignoring non-building parts such as the lawn, garden, and play areas between the residential buildings in the apartment complex. Although most land use application scenarios can function without non-building components, waterlogging simulation demands data accuracy. Therefore, it is impossible to simulate waterlogging in realistic scenarios within apartment complexes using the above-mentioned division approach. In this study, the inundated areas in two apartment complexes were considered representatives of densely built-up areas and were analyzed and discussed.

Area 2 is an apartment complex in the study area in which the buildings are densely distributed and horizontally arranged (Figure 13a). From its satellite image, we can see that most of the buildings in Area 2 are residential buildings, except for a building with a pink roof in the upper left corner, which is a senior citizen activity center (Figure 13a). Area 2 has trails with vegetation on either side and between buildings to facilitate the movement of the inhabitants around the area. Figure 13b shows a whole building area as the land use layer, ignoring the trails and other non-building areas.

Figure 14a–d show the ground-inundated areas in Area 2 simulated by the raw DEM, IDW, MDF, and MDF-UNet methods, respectively, at the same time.

According to the raw DEM, a large amount of waterlogging occurred at the local nadir. It did not consider the sites where waterlogging often occurs and where it is unlikely to occur in realistic situations; instead, it depended entirely on the accuracy of the DEM data (Figure 14a). The IDW method interpolates adjacent spatial data based on raw DEM data, but it is not applicable to urban built-up areas due to its limitations, which was confirmed by simulation results that differ significantly from reality (Figure 14b). The MDF method relied entirely on the land use layer, and all the components were shown as buildings and were set to non-inundated sites. Consequently, Figure 14c did not show waterlogging at any location in Area 2. The MDF method is suitable for scenarios where the accuracy of the land use layer is very high and precisely describes the exact location of the buildings; however, it is not well suited to situations where the accuracy is low. Figure 14d shows the waterlogging simulation results based on the MDF-UNet method proposed in this paper. Waterlogging also occurred in Area 2, even though the land use was designated as a building, because, in this method, buildings were identified based on image segmentation rather than the land use layer. Instead of being located where the actual buildings stand, the specific sites susceptible to waterlogging were the internal pathways between the buildings within the apartment complex. These areas are often not accurately represented in the raw DEM data.

Among these simulation results, the raw DEM has the largest inundated area, but the least maximum inundated depth, while the MDF-UNet method is the opposite (Table 2). The maximum inundated depth of the former is 0.12 m, with all below 0.15 m, which is a normal and safe condition for residents during heavy rainfall. The latter model sets the actual building location without waterlogging, reducing the area and increasing the depth relative to the raw DEM, where the maximum depth is 0.56 m. The inundated area and maximum inundated depth determined by the IDW method are 3025 m² and 0.14 m, respectively. Notably, the MDF method is excluded from this discussion given the characteristics that building areas are set as unsubmerged areas during the DEM processing. A comparison of the ground-inundated area and depth simulated by different methods is shown in

Table 3. Comparison of the inundated area and depth of Area 2.

	Raw DEM	IDW	MDF-UNet	MDF
Inundated Area (m2)	32,722	3025	9562	/
Maximum Inundated Depth (m)	0.12	0.14	0.56	/

.

In previous sections, a case where whole densely built-up areas are identified as buildings in the land use layer has been discussed using the example of Area 2. In the following sections, another case where the whole area with a scattered distribution of buildings is identified as other land use types are discussed, except for buildings.

Area 3 is a densely built-up area and is divided into three sub-areas, as shown in Figure 15a. Sub-area 1 has the highest building distribution density, and all are residential buildings. The second highest density of building distribution is found in Sub-area 3, most of whose buildings are assembly factories with larger individual footprints and gaps between factory buildings than residential buildings. Sub-area 2 is partly occupied by residential buildings and partly by office buildings, with high building heights, broad building spacing, and a high proportion of greenery. As a result, in the land use layer, Sub-areas 1 and 3 are identified as buildings, while Sub-area 2 is a grassland (Figure 15b). This pattern of land use identification is a challenge for the simulation of waterlogging in this area; for example, it is possible to simulate waterlogging at building locations.

The simulation results of ground waterlogging in Area 3 are illustrated in Figure 16, which shows that different DEM processing methods are used when making models.

The calculated inundated area and depth of Sub-area 2 using four different DEM simulation results are shown in

Table 4. Comparison of the inundated area and depth of Area 3.

	Raw DEM	IDW	MDF	MDF-UNet
Inundated Area (m2)	30,589	32,518	16,527	20,126
Maximum Inundated Depth (m)	0.42	0.28	0.83	0.74

.

The ground-inundated areas and maximum inundated depths based on raw DEM (Figure 16a) and MDF methods (Figure 16c) in Area 3 are 30,589 m² and 0.42 m, and 16,527 m² and 0.83 m, respectively. The simulated inundated locations in non-building areas are very similar due to the fact that the MDF method is based on the raw DEM data when processing DEM, focusing on the elevation of building locations. Under both methods, waterlogging exists in building areas of Sub-area 2, indicating that waterlogging may occur in the simulation results owing to the categorization of building locations as non-buildings. The IDW method has the smallest standard deviation among the four methods, with a maximum inundated depth of 0.28 m, ignoring the location of buildings. Although the building areas in sub-area 2 are labeled as grasslands in the land use layer, the MDF-UNet method accurately simulated waterlogging, because of the precise identification of building locations.

4.4. Limitations and Recommendations

This study introduced an MDF-UNet approach to reconstruct DEM based on satellite remote sensing image segmentation, and then improved the accuracy of waterlogging simulation. The results confirmed that the proposed approach has many advantages over other methods, with the universality that can be applied to other areas, especially those without high accuracy DEM. Another advantage of this approach is that it can fully use the existing and available data, including remote sensing images, drainage network, and land use to obtain high-quality DEM data at low cost. However, it has the following limitations: (1) This method is introduced to reconstruct the DEM based on accurate data, and does not provide an accuracy validation on multisource data. A data accuracy evaluation method will be further studied to fully improve the DEM accuracy improvement framework. (2) Although the U-Net image segmentation model used in this study improves the recognition accuracy of building areas, different colors and shapes may cause recognition errors. In future research, it is necessary to develop an advanced image segmentation model combining media information data to improve building area recognition.

5. Conclusions

Waterlogging simulation is greatly important to the prediction of increasing inundation risk, whose accuracy is largely influenced by DEM data, especially on roads and built-up areas. The MDF-UNet approach proposed in this study can effectively solve the problem of low accuracy of available DEM by fusing existing multisource data with remote sensing images. The U-Net image segmentation model based on remote sensing image data was employed to identify the building areas, and then the identified results were combined with land use and drainage data to reconstruct terrain. The main conclusions of this study are as follows:

(1)

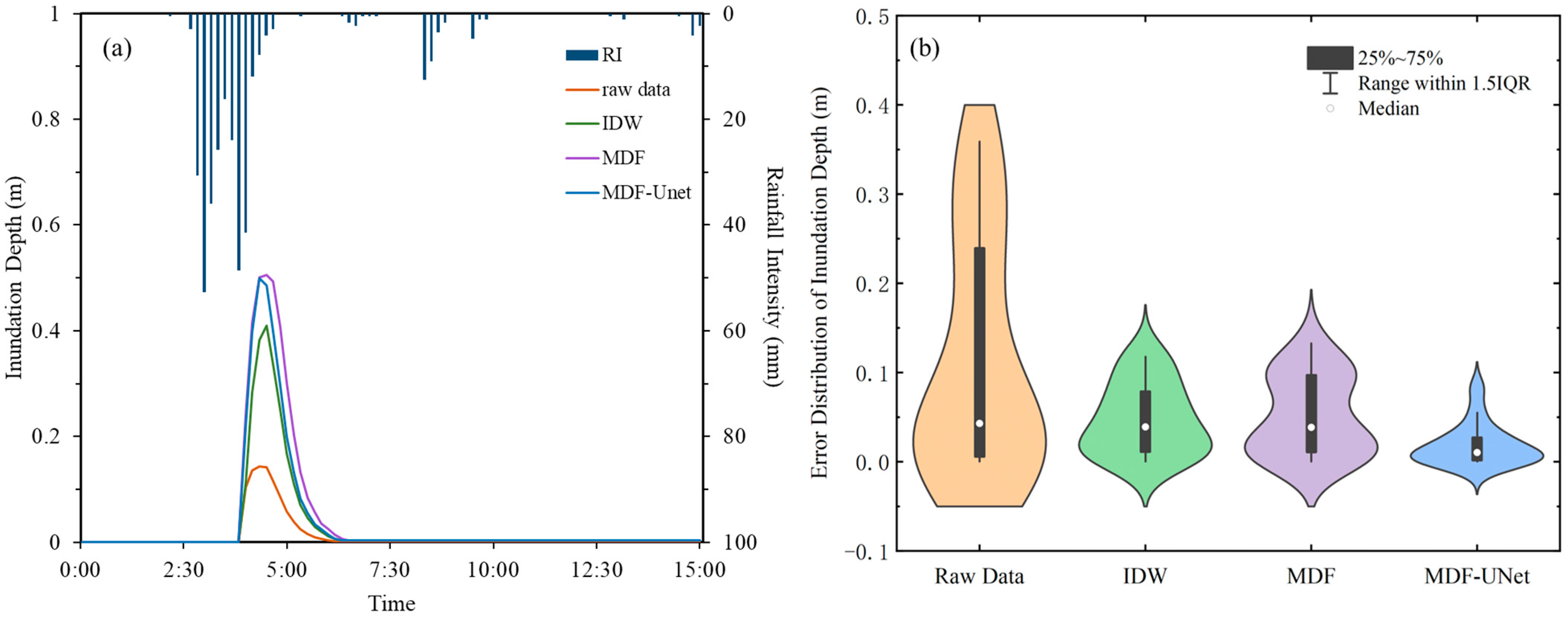
The MDF-UNet method improved the simulation accuracy of urban waterlogging locations compared to the raw DEM data and the data from the IDW and MDF methods. Among the 17 historically recorded waterlogging points in the study area, 10 were simulated, while the number was 15 using the proposed method. The accuracy improved from 58.8% to 88.2%.

(2)

The difference between the IDW, MDF, and MDF-UNet methods in the road waterlogging range simulation was small, without including the inundated depth. The ranking of maximum inundated depth obtained from different methods was MDF > MDF-UNet > IDW > raw DEM, and the median value errors of the first three methods are within 0.2 m compared with the raw DEM data of 0.4 m. This was due to the fact that the latter was not processed; hence, the accuracy could not meet the high data quality requirements for waterlogging simulation.

(3)

The waterlogging model based on the MDF-UNet method was more compatible with the actual situation, especially in building locations, both in terms of inundated ranges and depths. The inundation ranges simulated by the raw DEM data, IDW and MDF-UNet methods were 32,722 m², 3025 m², and 9562 m² in densely built-up Area 2, and the maximum inundated depths simulated by the same set of methods were 0.42 m, 0.28 m, 0.83 m, and 0.74 m in Area 3, respectively.

The simulation results demonstrated that the proposed MDF-UNet approach had a significant positive effect on urban waterlogging simulation, and greatly improved the ability to accurately predict inundation risk, especially on roads and building areas. In future work, we will continue to focus on the intelligent identification methods of inundation ranges and depths, as well as the segmentation technique of building areas, to reduce the errors of urban waterlogging simulation.