Colocation in Time and Space of High-Precision Two-Way Optical and Microwave Observations for Calibration of a Microwave Ranging Link—The ACES Mission Case
Abstract
:1. Motivation
Background
2. Simulation
2.1. Simulation Software
2.2. Clock and Time Distribution
2.3. Orbit Propagation
2.4. Atmosphere
2.4.1. Ray-Tracing Technique
2.4.2. Turbulence
2.4.3. Dispersive Effects
2.5. Data Set
3. Calibration Strategy
3.1. Basic Workflow
3.2. Optimum Approach
4. Assessment of Parameter Estimation
4.1. Data Set
4.2. A Priori Errors of the LSA Process
4.3. “Best Possible” Test—Orbit
4.4. “Best Possible” Test—Troposphere
5. Results and Discussion
5.1. Optimum Approach
5.2. Residual Analysis
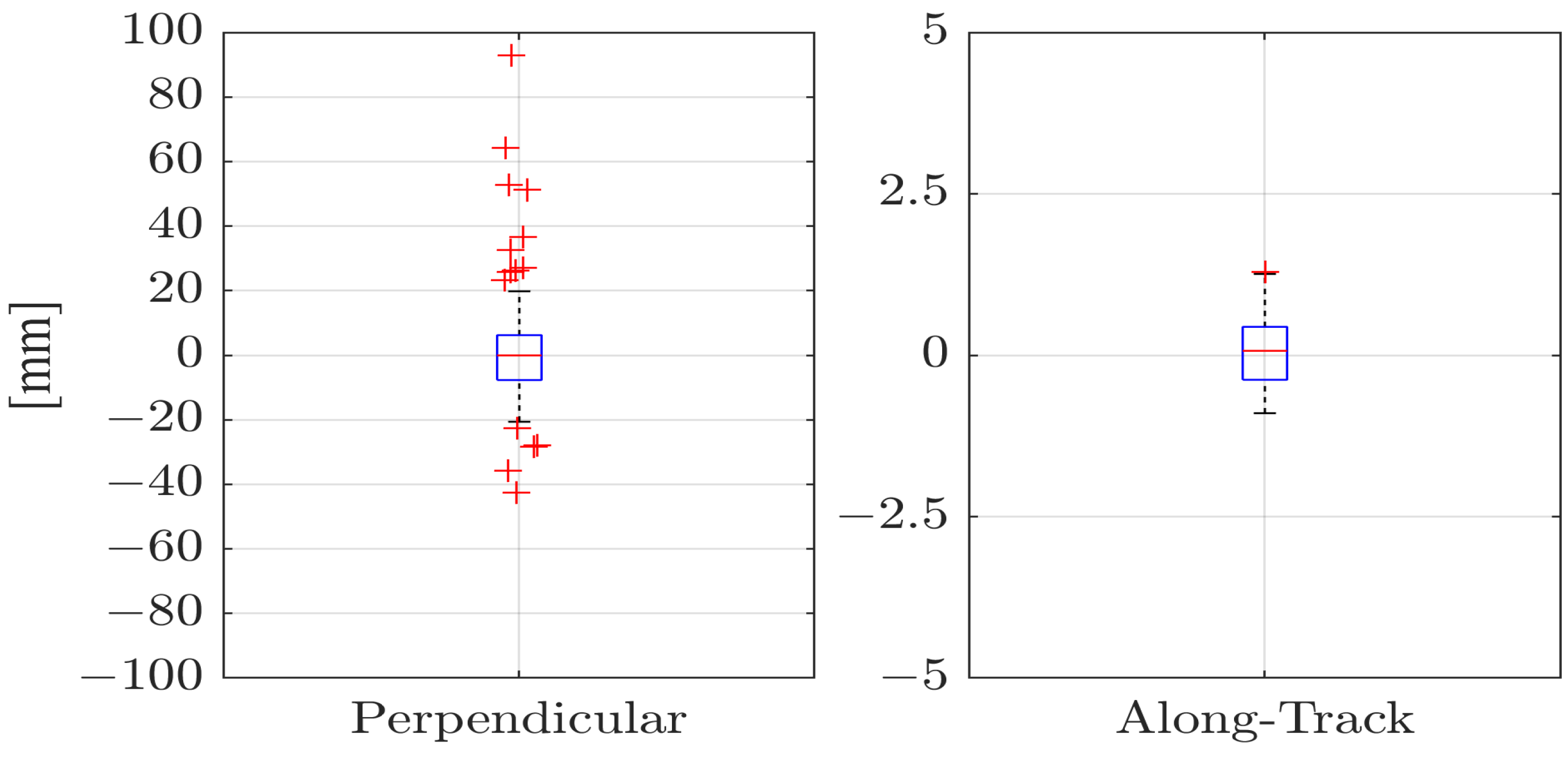
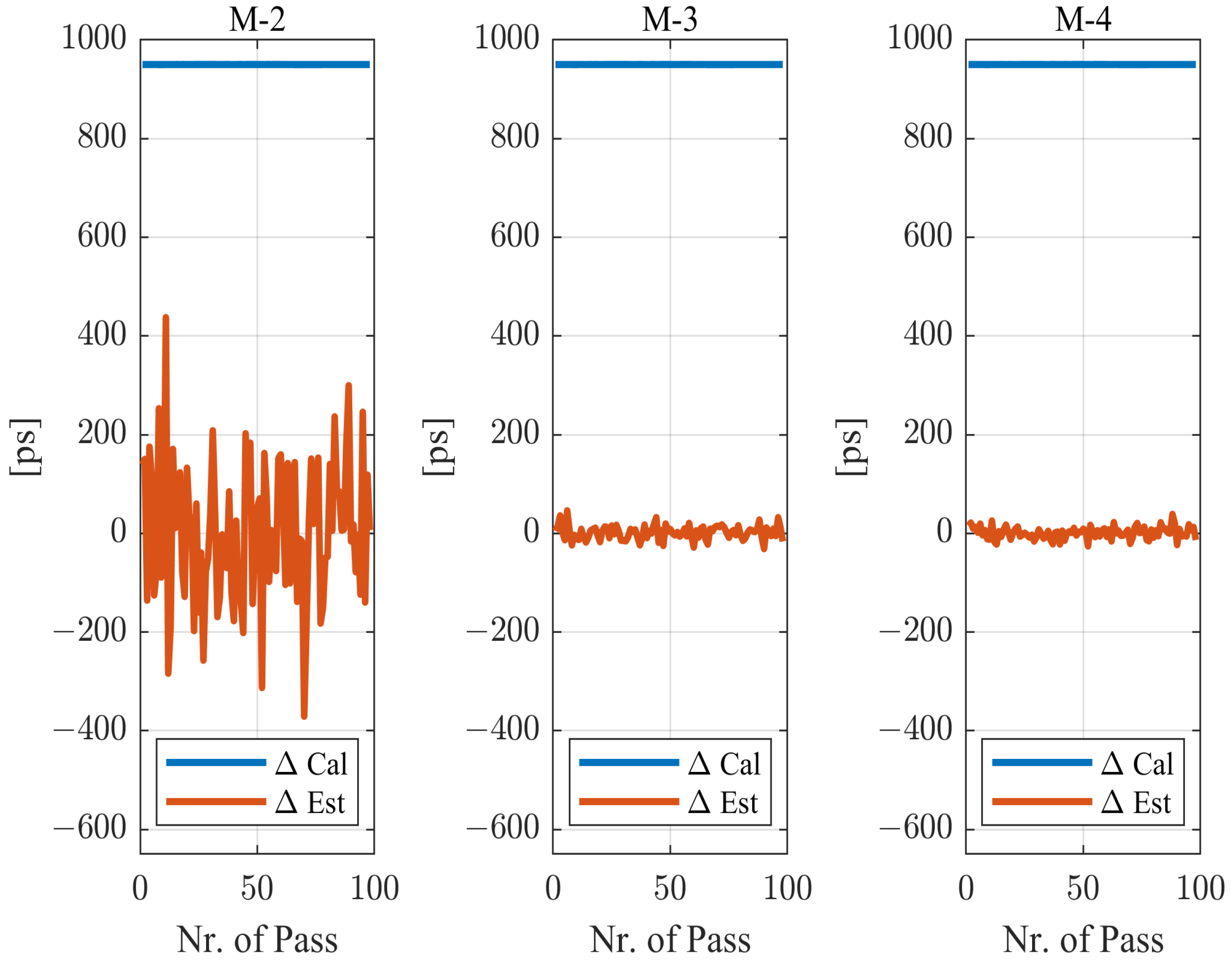
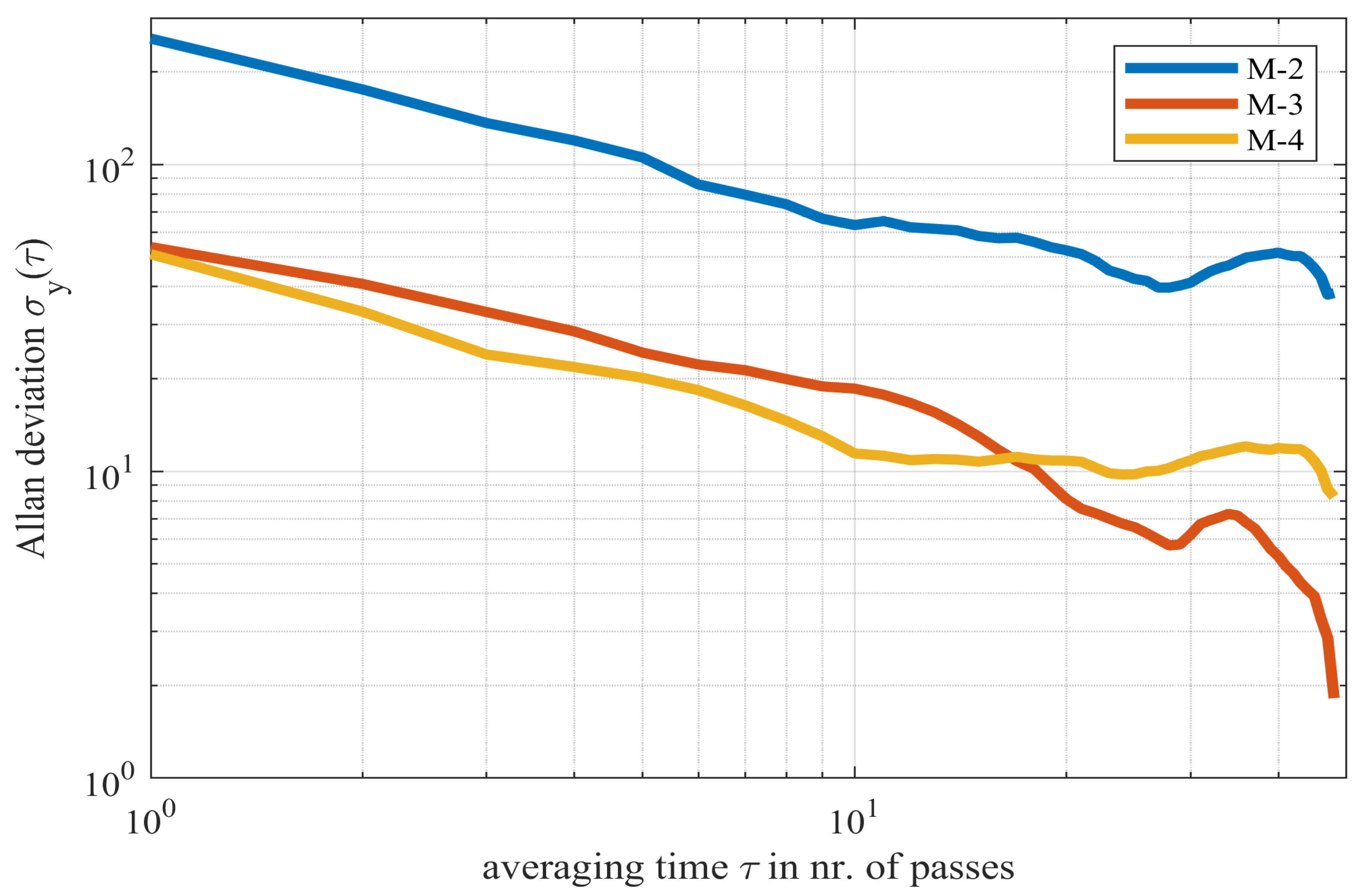
5.3. Time Synchronization Analysis
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| ACES | Atomic Clock Ensemble in Space |
| AHM | Active Hydrogen Maser |
| CNES | Centre national d’études spatiales |
| ECMWF | European Centre for Medium-Range Weather Forecasts |
| ELT | European Laser Timing |
| ERA | ECMWF’s new atmospheric reanalysis |
| ESA | European Space Agency |
| GGOS | Global Geodetic Observing System |
| IAG | International Association of Geodesy |
| IERS | International Earth Rotation and Reference Systems Service |
| ISS | International Space Station |
| ITU-R | International Telecommunication Union—Radiocommunication Sector |
| LNE-SYRTE | Laboratoire national de métrologie et d’essais—Système de Références Temps-Espace |
| LSA | Least-Squares Adjustment |
| MWL | Microwave Link System |
| NOAA | National Oceanic and Atmospheric Administration |
| NWM | Numerical Weather Model |
| OD | Orbit Determination |
| OmC | Observed minus Computed |
| SLR | Satellite Laser Ranging |
| SHM | Space Hydrogen Maser |
| STEC | Slant Total Electron Content |
| TDS | Timing Distribution System |
| TEC | Total Electron Content |
| TLE | Two-Line Elements |
| VMFo | Vienna Mapping Function 3—Optical |
| VMF3 | Vienna Mapping Function 3 |
References
- Gross, R.; Beutler, G.; Plag, H.-P. Integrated scientific and societal user requirements and functional specifications for the GGOS. In Global Geodetic Observing System: Meeting the Requirements of a Global Society on a Changing Planet in 2020; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Montenbruck, O.; Hauschild, A.; Steigenberger, P. Differential Code Bias Estimation using Multi-GNSS Observations and Global Ionosphere Maps. NAVIGATION J. Inst. Navig. 2014, 61, 191–201. [Google Scholar] [CrossRef]
- Wang, N.; Li, Z.; Duan, B.; Hugentobler, U.; Wang, L. GPS and GLONASS observable-specific code bias estimation: Comparison of solutions from the IGS and MGEX networks. J. Geod. 2020, 94, 74. [Google Scholar] [CrossRef]
- Cacciapuoti, L.; Salomon, C. Space clocks and fundamental tests: The ACES experiment. Eur. Phys. J. Spec. Top. 2009, 172, 57–68. [Google Scholar] [CrossRef]
- Nasca, R. Challenging Einstein on the ISS: ACES Takes a Step Ahead. Available online: https://www.esa.int/Enabling_Support/Space_Engineering_Technology/Challenging_Einstein_on_the_ISS_ACES_takes_a_step_ahead (accessed on 23 February 2023).
- ACES Workshop 2022. Available online: https://aces2022.sciencesconf.org/ (accessed on 25 October 2022).
- Salomon, C.; Cacciapuoti, L.; Dimarq, N. Atomic Clock Ensemble In Space: An Update. Int. J. Mod. Phys. 2007, 16, 2511–2523. [Google Scholar] [CrossRef]
- Salomon, C.; Dimarcq, N.; Abgrall, M.; Clairon, A.; Laurent, P.; Lemonde, P.; Santarelli, G.; Uhrich, P.; Bernier, L.G.; Busca, G.; et al. Cold atoms in space and atomic clocks: ACES. Comptes Rendus Acad. Sci. Paris 2001, 2, 1313–1330. [Google Scholar] [CrossRef]
- Schreiber, U.; Prochazka, I.; Lauber, P.; Hugentobler, U.; Schafer, W.; Cacciapuoti, L.; Nasca, R. The European laser timing (ELT) experiment on-board ACES. In Proceedings of the 2009 IEEE International Frequency Control Symposium Joint with the 22nd European Frequency and Time Forum, Besancon, France, 20–24 April 2009; pp. 594–599. [Google Scholar]
- Atomic Clock Ensemble in Space. Available online: http://wsn.spaceflight.esa.int/docs/Factsheets/20%20ACES%20LR.pdf (accessed on 23 February 2023).
- Lilley, M.; Savalle, E.; Angonin, M.C.; Delva, P.; Guerlin, C.; Le Poncin-Lafitte, C.; Meynadier, F.; Wolf, P. ACES/PHARAO: High-performance space-to-ground and ground-to-ground clock comparison for fundamental physics. GPS Solut. 2021, 25, 34. [Google Scholar] [CrossRef]
- Kodet, J.; Schreiber, K.U.; Eckl, J.; Ploetz, C.; Maehler, S.; Schueler, T.; Kluegel, T.; Riepl, S. Co-location of space geodetic techniques carried out at the Geodetic Observatory Wettzell using a closure in time and a multi-technique reference target. J. Geodt. 2018, 92, 1097–1112. [Google Scholar] [CrossRef]
- Prochazka, I. SLR station biases. In Proceedings of the ILRS Technical Workshop, Matera, Italy, 26–30 October 2015. [Google Scholar]
- Prochazka, I.; Kodet, J.; Blazej, J.; Kirchner, G.; Koidl, F.; Wang, P. Identification and calibration of one-way delays in satellite laser ranging systems. Adv. Space Res. 2017, 59, 2466–2472. [Google Scholar] [CrossRef]
- Thaller, D.; Dach, R.; Seitz, M.; Beutler, G.; Mareyen, M.; Richter, B. Combination of GNSS and SLR observations using satellite co-locations. J. Geod. 2011, 85, 257–272. [Google Scholar] [CrossRef]
- Belli, A.; Exertier, P.; Pavlis, E.C.; Lemoine, F.G. Time bias of laser ranging observations. In Proceedings of the 2017 ILRS Technical Workshop, Riga, Latvia, 2–5 October 2017. [Google Scholar]
- Meng, W.; Zhang, H.; Huang, P.; Wang, J.; Zhang, Z.; Liao, Y.; Ye, Y.; Hu, W.; Wang, Y.; Chen, W.; et al. Design and experiment of onboard laser time transfer in Chinese Beidou navigation satellites. Adv. Space Res. 2013, 51, 951–958. [Google Scholar] [CrossRef]
- Schreiber, U.; Kodet, J.; Eckl, J.; Herold, G.; Kronschnabl, G.; Plötz, C.; Neidhardt, A. All optical time and frequency distribution for space geodesy. In Proceedings of the 2015 ILRS Technical Workshop, Matera, Italy, 26–30 October 2015. [Google Scholar]
- Dominguez, P.N.; Schmidt, T.; Boland, R.; Zeltner, R.; Holzwarth, R.; Klugel, T.; Kodet, J.; Schreiber, U. Pulsed optical timing distribution system with sub-ps accuracy for applications in geodesy. In Proceedings of the ION 2022 Precise Time and Time Interval Systems and Applications Meeting, Long Beach, CA, USA, 25–27 January 2022. [Google Scholar]
- NOAA Global Forecast System (GFS). Available online: https://registry.opendata.aws/noaa-gfs-bdp-pds (accessed on 7 March 2023).
- Aragon-Angel, A.; Rovira-Garcia, A.; Arcediano-Garrido, E.; Ibáñez-Segura, D. Galileo Ionospheric Correction Algorithm Integration into the Open-Source GNSS Laboratory Tool Suite (gLAB). Remote Sens. 2021, 13, 191. [Google Scholar] [CrossRef]
- Kluegel, T.; Maehler, S.; Schade, C. Local ties at the geodetic observatory Wettzell. In Proceedings of the International Workshop on Laser Ranging, Bad Koetzting, Germany, 16–20 May 2011. [Google Scholar]
- Blanchet, L.; Salomon, C.; Teyssandier, P.; Wolf, P. Relativistic theory for time and frequency transfer to order c−3. Astron. Astrophys. 2001, 370, 320–329. [Google Scholar] [CrossRef]
- Marz, S.; Schlicht, A.; Bamann, C. Relativistic corrections in the European Laser Timing (ELT) experiment. In Proceedings of the 20th International Workshop on Laser Ranging, Potsdam, Germany, 9–14 October 2016. [Google Scholar]
- Vollmair, P.; Schlicht, A.; Marz, S.; Hugentobler, U. Combination of microwave and optical observations for minimizing atmospheric induced variations in parameter estimation. In Proceedings of the International Workshop on Laser Ranging, Yebes, Spain, 7–11 November 2022. [Google Scholar]
- Kasdin, N.J.; Walter, T. Discrete simulation of power law noise (for oscillator stability evaluation). In Proceedings of the 1992 IEEE Frequency Control Symposium, Hershey, PA, USA, 27–29 May 1992; pp. 274–283. [Google Scholar]
- Kasdin, N.J. Discrete simulation of colored noise and stochastic processes and 1/f/sup /spl alpha// power law noise generation. Proc. IEEE 1995, 83, 802–827. [Google Scholar] [CrossRef]
- CS Systèmes d’Information. OREKIT. 2018. Available online: https://www.orekit.org/site-orekit-9.2/index.html (accessed on 7 March 2023).
- Kelso, T.S. CelesTrak. 2022. Available online: https://celestrak.org/ (accessed on 7 March 2023).
- Hairer, E.; Wanner, G.; Nørsett, S.P. Nonstiff problems. In Solving Ordinary Differential Equations I; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Holmes, S.A.; Featherstone, W.E. A unified approach to the Clenshaw summation and the recursive computation of very high degree and order normalised associated Legendre functions. J. Geod. 2002, 76, 279–299. [Google Scholar] [CrossRef]
- Montenbruck, O.; Gill, E. Satellite Orbits: Models, Methods and Applications; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Saastamoinen, J. Atmospheric Correction for the Troposphere and Stratosphere in Radio Ranging of Satellites. Geophy. Monog. Ser. 1972, 15, 247–251. [Google Scholar]
- Boisits, J.; Landskron, D.; Boehm, J. VMF3o: The Vienna Mapping Functions for Optical Frequencies. J. Geod. 2020, 94, 57. [Google Scholar] [CrossRef]
- Niell, A.E. Global mapping functions for the atmosphere delay at 310 radio wavelengths. J. Geophys. Res. 1996, 101, 3227–3246. [Google Scholar] [CrossRef]
- Boehm, J.; Schuh, H. Vienna mapping functions. In Proceedings of the 16th EVGA Working Meeting, Leipzig, Germany, 9–10 May 2003. [Google Scholar]
- Boehm, J.; Niell, A.; Tregoning, P.; Schuh, H. Global Mapping Function (GMF): A new empirical mapping function based on numerical weather model data. J. Geophys. Res. 2006, 33. [Google Scholar] [CrossRef]
- Ionospheric Correction Algorithm for Galileo Single Frequency Users. Available online: https://www.gsc-europa.eu/sites/default/files/sites/all/files/Galileo_Ionospheric_Model.pdf (accessed on 7 March 2023).
- Petit, G.; Luzum, B. IERS Conventions 2010; IERS Technical Note 36; Verlag des Bundesamts für Kartographie und Geodäsie: Frankfurt am Main, Germany, 2010; p. 137. [Google Scholar]
- NCEI Geomagnetic Modeling Team and British Geological Survey. World Magnetic Model 2020; NOAA National Centers for Environmental Information; NOAA: Asheville, NC, USA, 2019. Available online: https://www.ncei.noaa.gov/products/world-magnetic-model (accessed on 7 March 2023).
- Chulliat, A.; Brown, W.; Alken, P.; Beggan, C.; Nair, M.; Cox, G.; Woods, A.; Macmillan, S.; Meyer, B.; Paniccia, M. The US/UK World Magnetic Model for 2020–2025: Technical Report; National Centers for Environmental Information; NOAA: Asheville, NC, USA, 2020.
- Hofmeister, A.; Boehm, J. Application of ray-traced tropospheric slant delays to geodetic VLBI analysis. J. Geod. 2017, 91, 945–964. [Google Scholar] [CrossRef]
- Kačmařík, M.; Douša, J.; Dick, G.; Zus, F.; Brenot, H.; Moller, G.; Pottiaux, E.; Kapłon, J.; Hordyniec, P.; Václavovic, P.; et al. Inter-technique validation of tropospheric slant total delays. Atmos. Meas. Tech. 2017, 10, 2183–2208. [Google Scholar] [CrossRef]
- Keihm, S.J. Water Vapor Radiometer Measurements of the Tropospheric Delay Fluctuations at Goldstone Over a Full Year. Telecommun. Data Acquis. Prog. Rep. 1995, 122, 1–11. [Google Scholar]
- Nilsson, T.; Gradinarsky, L.; Elgered, G. Correlations between slant wet delays measured by microwave radiometry. IEEE Trans. Geosci. Remote Sens. 2005, 43, 1028–1035. [Google Scholar] [CrossRef]
- Nilsson, T.; Elgered, G.; Gradinarsky, L. Characterizing atmospheric turbulence and instrumental noise using two simultaneously operating microwave radiometers. In Proceedings of the 2006 IEEE Microrad Proceedings 9th Specialist Meeting on Microwave Radiometry and Remote Sensing Applications: Microrad’06, San Juan, Puerto Rico, 28 February–3 March 2006; pp. 270–275. [Google Scholar]
- Nilsson, T.; Haas, R.; Elgered, G. Simulations of atmospheric path delays using turbulence models. In Proceedings of the 18th European VLBI for Geodesy and Astrometry Work Meeting, Vienna, Austria, 12–13 April 2017. [Google Scholar]
- Boehm, J.; Wresnik, J.; Pany, A. Simulation of Wet Zenith Delays and Clocks. Available online: https://ivscc.gsfc.nasa.gov/publications/memos/ivs-2006-013v03.pdf (accessed on 7 March 2023).
- Treuhaft, R.N.; Lany, G.E. The effect of the dynamic wet troposphere on radio interferometric measurements. Radio Sci. 1987, 22, 251–265. [Google Scholar] [CrossRef]
- Prochazka, I.; Kral, L.; Blazej, J. Picosecond laser pulse distortion by propagation through a turbulent atmosphere. In Coherence and Ultrashort Pulse Laser Emission; Duarte, F.J., Ed.; IntechOpen: Rijeka, Croatia, 2010; Chapter 19. [Google Scholar]
- Gardner, C.S. Effects of random path fluctuations on the accuracy of laser ranging systems. Appl. Opt. 1976, 15, 2539. [Google Scholar] [CrossRef] [PubMed]
- Andrews, L.C.; Phillips, R.L. Laser satellite communication systems. In Laser Beam Propagation through Random Media; SPIE Press: Bellingham, WA, USA, 2005; p. 481. [Google Scholar]
- Hobiger, T.; Piester, D.; Baron, P. A correction model of dispersive troposphere delays for the ACES microwave link. Radio Sci. 2013, 48, 131–141. [Google Scholar] [CrossRef]
- Liebe, H.J. An atmospheric millimeter-wave propagationmodel. Int. J. Infrared Millim. Waves 2013, 10, 631–650. [Google Scholar] [CrossRef]
- Liebe, H.J.; Hufford, G.A.; Cotton, M.G. Propagation modeling of the moist air and suspended water/ice particles at frequencies below 1000 GHz. In Proceedings of the AGARD 52 Meeting, Palma de Mallorca, Spain, 17–21 May 1993. [Google Scholar]
- ITU-R Attenuation by Atmospheric Gases and Related Effects Recommendation ITU-R P.676-8. 2009. Available online: https://www.itu.int/dms_pubrec/itu-r/rec/p/R-REC-P.676-8-200910-S!!PDF-E.pdf (accessed on 7 March 2023).
- Prochazka, I.; Kodet, J.; Blazei, J.; Koidl, F.; Kirchner, G. SPAD detector package for European Laser Time transfer in space. In Proceedings of the Single Photon Workshop, Boulder, CO, USA, 3–6 November 2009. [Google Scholar]
- Chen, G.; Herring, T.A. Effects of atmospheric azimuthal asymmetry on the analysis of space geodetic data. J. Geophys. Res. Solid Earth 1997, 102, 20489–20502. [Google Scholar] [CrossRef]
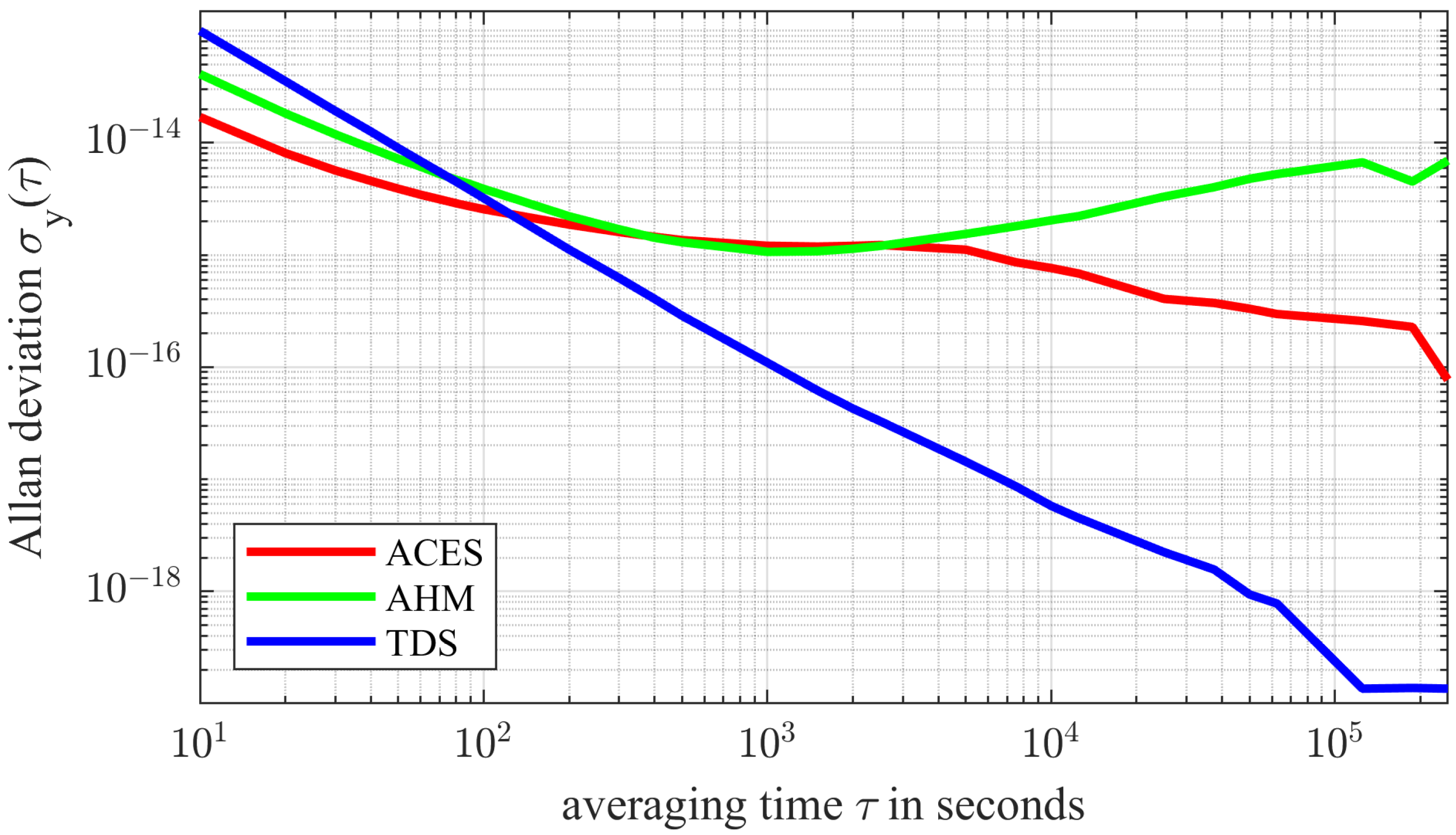
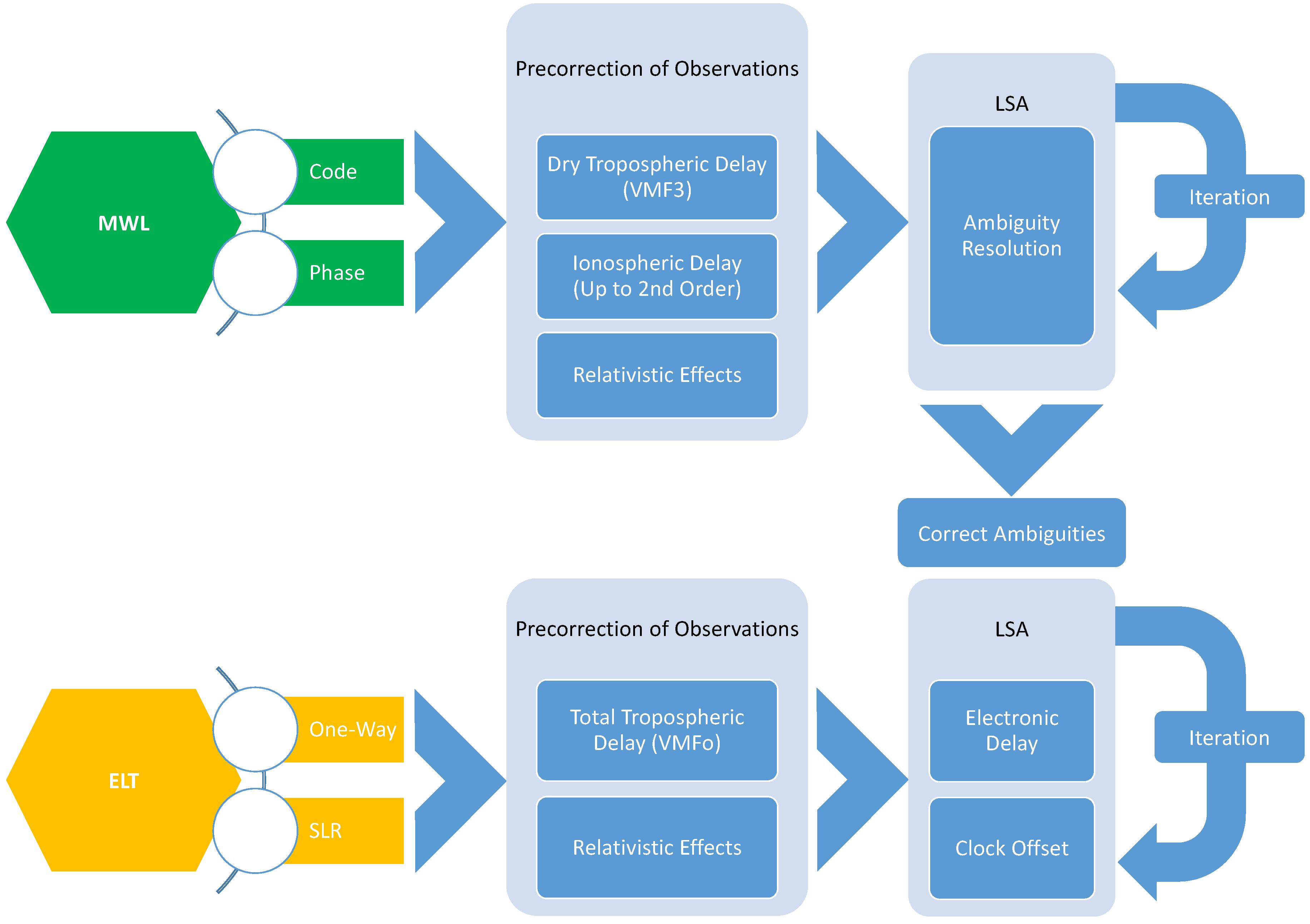
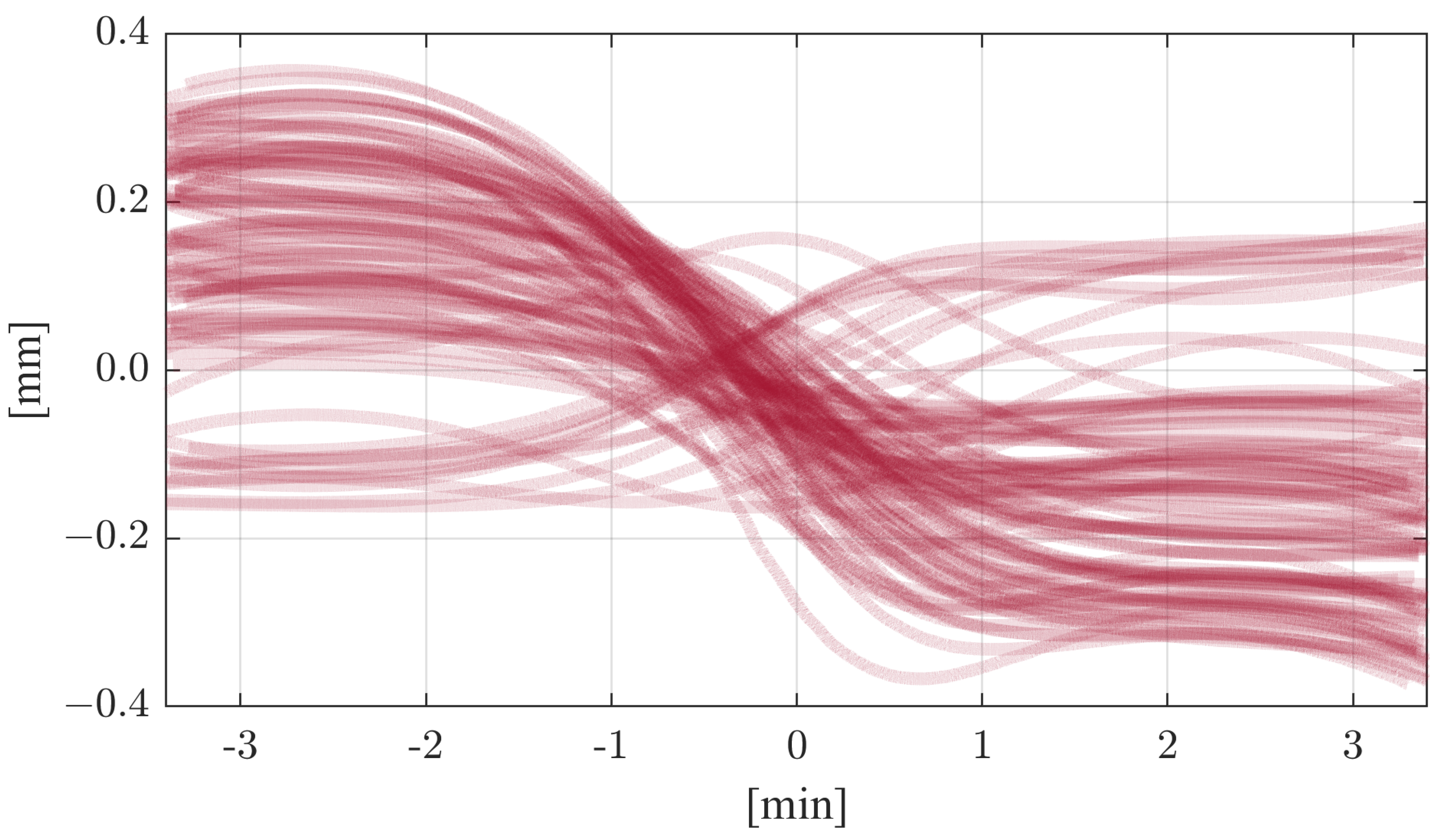
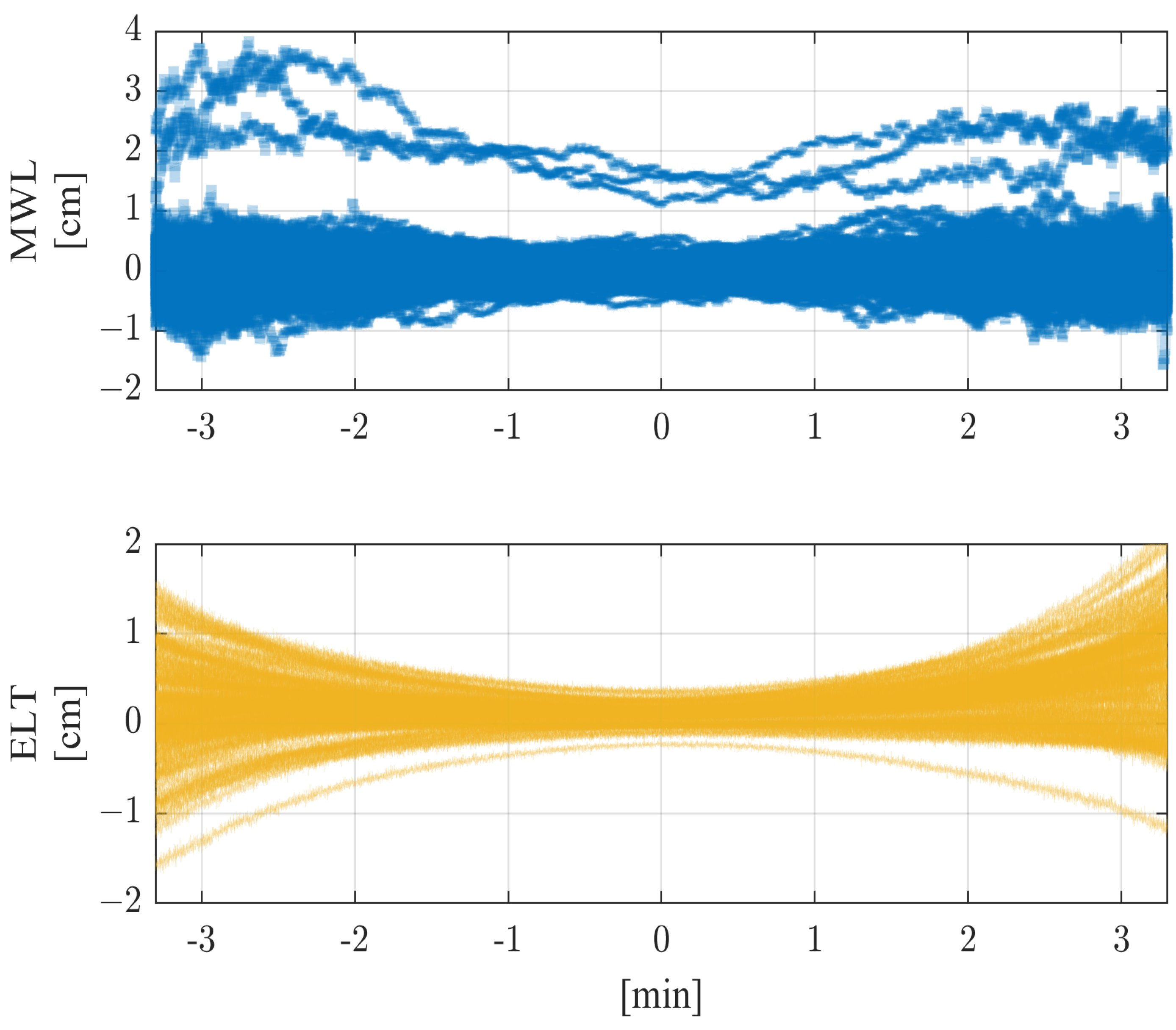

| Parameter | Model | MWL | ELT |
|---|---|---|---|
| Troposphere | GFS [20] | X | X |
| Orbit | TLE | X | X |
| Ionosphere | NeQuickG [21] | X | - |
| Clocks | Colored-Noise | X | X |
| TDS Offset | Intertechnique Offset | - | X |
| TDS Noise | Intertechnique Colored Noise | - | X |
| Local Ties | Height Offset | - | X |
| Sagnac | 1st & 2nd Order | X | X 1 |
| Shapiro | - | X | X |
| Measurement Noise | White Noise | X | X |
| Electronic Delay | Static | X | - |
| Noise Type | ACES | Ground | TDS |
|---|---|---|---|
| White Phase | - | - | |
| Flicker Phase | |||
| White Frequency 1 | - | ||
| Flicker Frequency | - | - | |
| Random Walk Frequency | - | - |
| Parameter | Description | LSA | Model |
|---|---|---|---|
| Troposphere 1 | VMF3 and VMFo | X | X |
| Orbit | Common short arc | X | - |
| Ionosphere | Corrected via STEC | - | X |
| Clocks | Offset | X | - |
| Sagnac | Based on initial orbit | - | X |
| Shapiro | Based on initial orbit | - | X |
| Electronic delays | Parameters of interest | X | - |
| Method | MWL | ELT One-Way | ELT Two-Way | Wet-Gradient 1 |
|---|---|---|---|---|
| 1 | X | - | - | - |
| 2 | X | X | - | - |
| 3 | X | X | X | - |
| 4 | X | X | X | X |
| Parameter | 25th Percentile | Median | 75th Percentile | RMS |
|---|---|---|---|---|
| Radial | 1.05 | 4.83 | 8.32 | 7.97 |
| Along-Track | 6.24 | 16.93 | 26.37 | 20.58 |
| Cross-Track | −3.39 | 2.43 | 3.95 | 3.85 |
| Range | −14.23 | −1.48 | 13.70 | 17.46 |
| Trp-ELT | 0.06 | 0.19 | 0.37 | 0.42 |
| Trp-MWL | 1.01 | 2.93 | 6.03 | 6.58 |
| Ion-Down | −0.001 | −0.00006 | 0.001 | 0.002 |
| Ion-Up | −0.002 | 0.00009 | 0.002 | 0.002 |
| Range | 25th Percentile | Median | 75th Percentile | RMS |
|---|---|---|---|---|
| a priori | −14.235 | −1.475 | 13.703 | 17.461 |
| a posteriori | −0.014 | −0.003 | 0.012 | 0.017 |
| Troposphere | 25th Percentile | Median | 75th Percentile | RMS |
|---|---|---|---|---|
| a priori | 1.01 | 2.93 | 6.03 | 6.58 |
| a posteriori | −0.18 | 0.02 | 0.23 | 0.49 |
| Mean | Mean Formal Errors | Standard Deviation | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Parameter | M-1 | M-2 | M-3 | M-4 | M-1 | M-2 | M-3 | M-4 | M-1 | M-2 | M-3 | M-4 |
| Downlink | - | 4.7 | 3.9 | 1.3 | - | 7.1 | 2.0 | 2.0 | - | 249 | 55 | 49 |
| Uplink | - | 0.7 | 0.8 | −0.6 | - | 2.0 | 1.7 | 1.5 | - | 48 | 29 | 27 |
| Clock | 950 | 2.1 | 1.6 | 1.1 | 0.08 | 4.2 | 1.7 | 1.5 | 0.01 | 143 | 14 | 12 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vollmair, P.; Schlicht, A.; Hugentobler, U. Colocation in Time and Space of High-Precision Two-Way Optical and Microwave Observations for Calibration of a Microwave Ranging Link—The ACES Mission Case. Remote Sens. 2023, 15, 4897. https://doi.org/10.3390/rs15204897
Vollmair P, Schlicht A, Hugentobler U. Colocation in Time and Space of High-Precision Two-Way Optical and Microwave Observations for Calibration of a Microwave Ranging Link—The ACES Mission Case. Remote Sensing. 2023; 15(20):4897. https://doi.org/10.3390/rs15204897
Chicago/Turabian StyleVollmair, Peter, Anja Schlicht, and Urs Hugentobler. 2023. "Colocation in Time and Space of High-Precision Two-Way Optical and Microwave Observations for Calibration of a Microwave Ranging Link—The ACES Mission Case" Remote Sensing 15, no. 20: 4897. https://doi.org/10.3390/rs15204897
APA StyleVollmair, P., Schlicht, A., & Hugentobler, U. (2023). Colocation in Time and Space of High-Precision Two-Way Optical and Microwave Observations for Calibration of a Microwave Ranging Link—The ACES Mission Case. Remote Sensing, 15(20), 4897. https://doi.org/10.3390/rs15204897








