Combined GRACE and GPS to Analyze the Seasonal Variation of Surface Vertical Deformation in Greenland and Its Influence
Abstract
1. Introduction
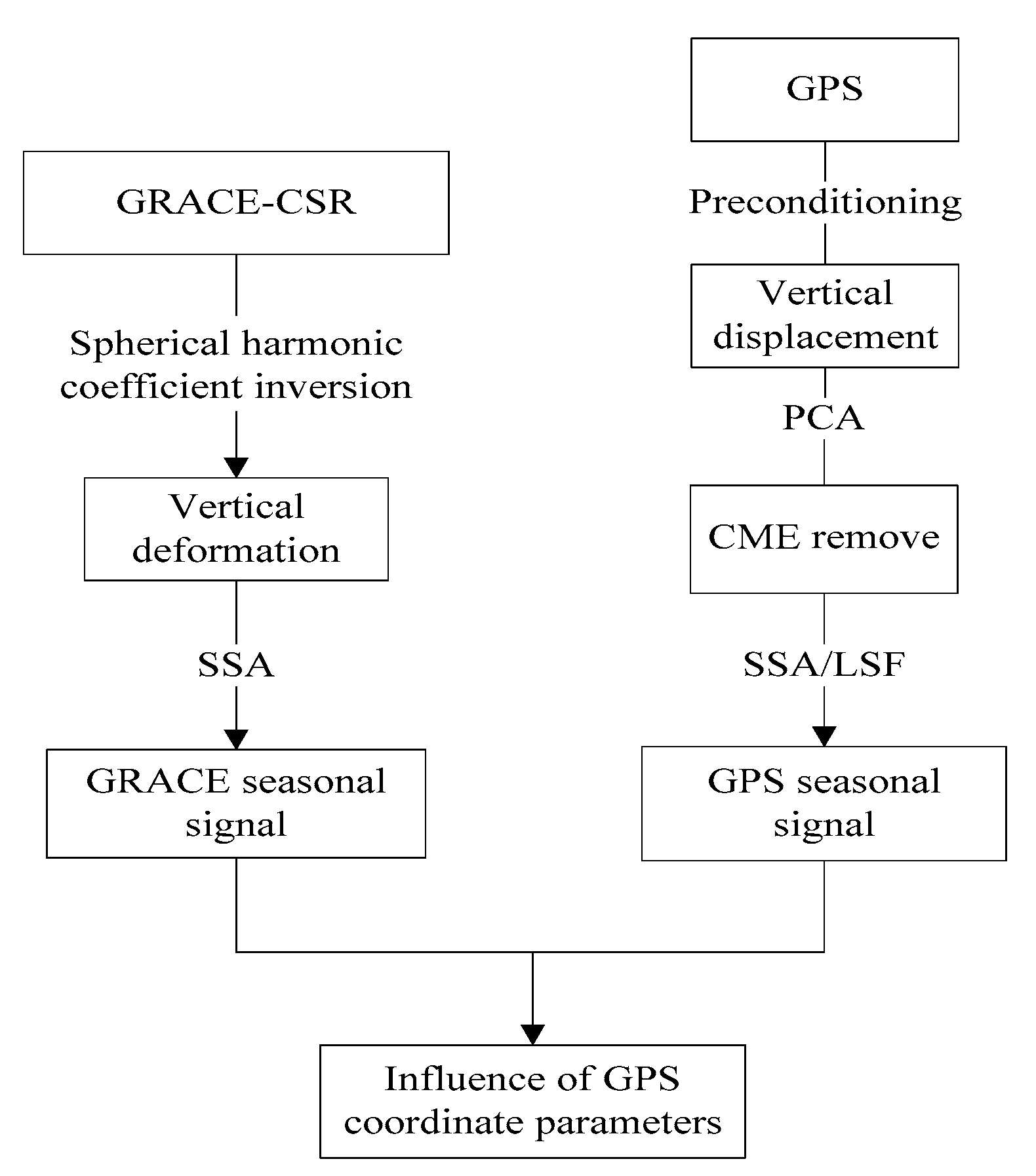
2. Materials and Methods
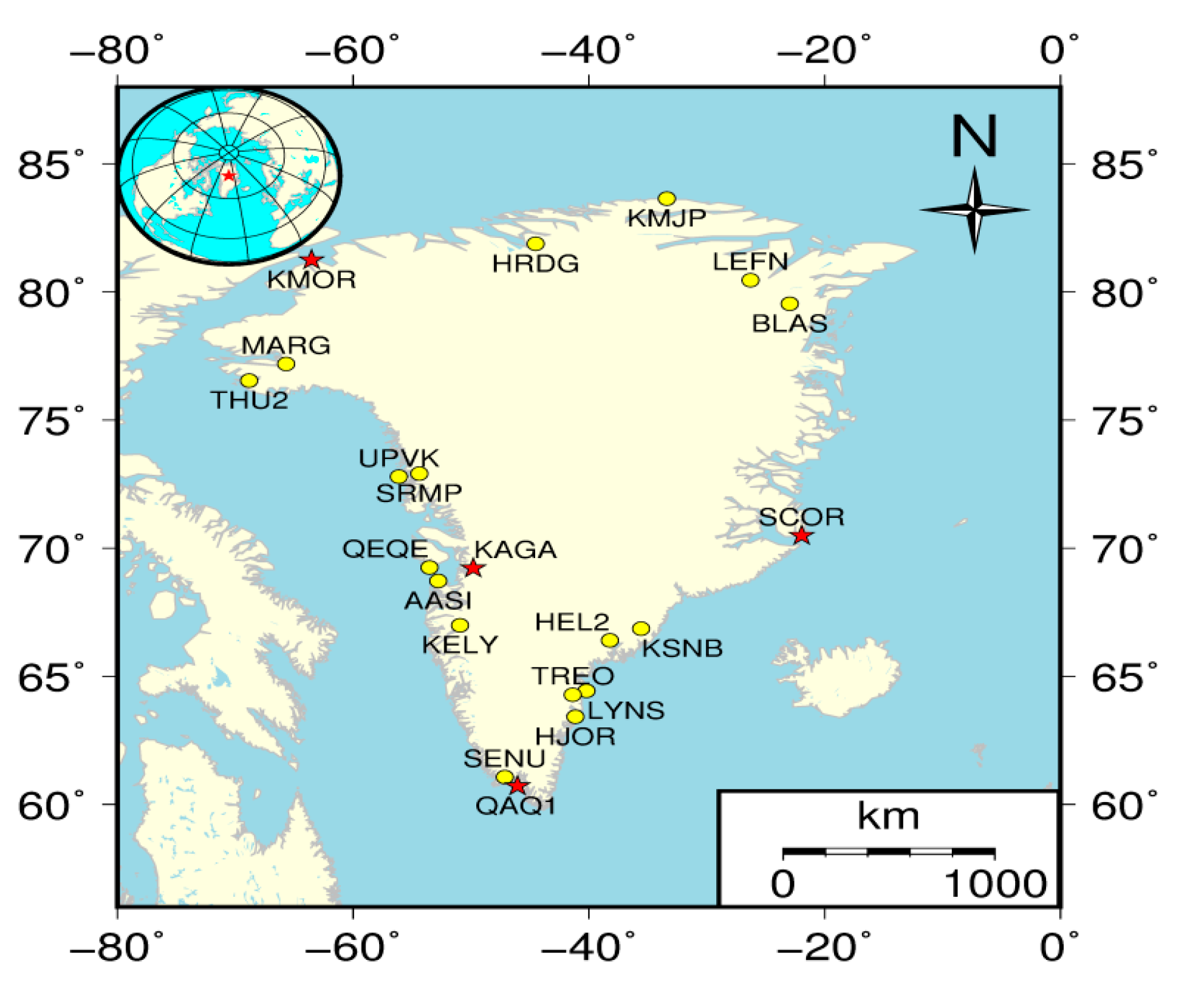
2.1. GPS Data
2.2. GRACE Data
2.3. Singular Spectrum Analysis
2.4. Evaluation Indices
2.4.1. Weighted Root Mean Square (WRMS)
2.4.2. Optimal Noise Model
2.4.3. Amplitude Contribution
3. Results and Discussions
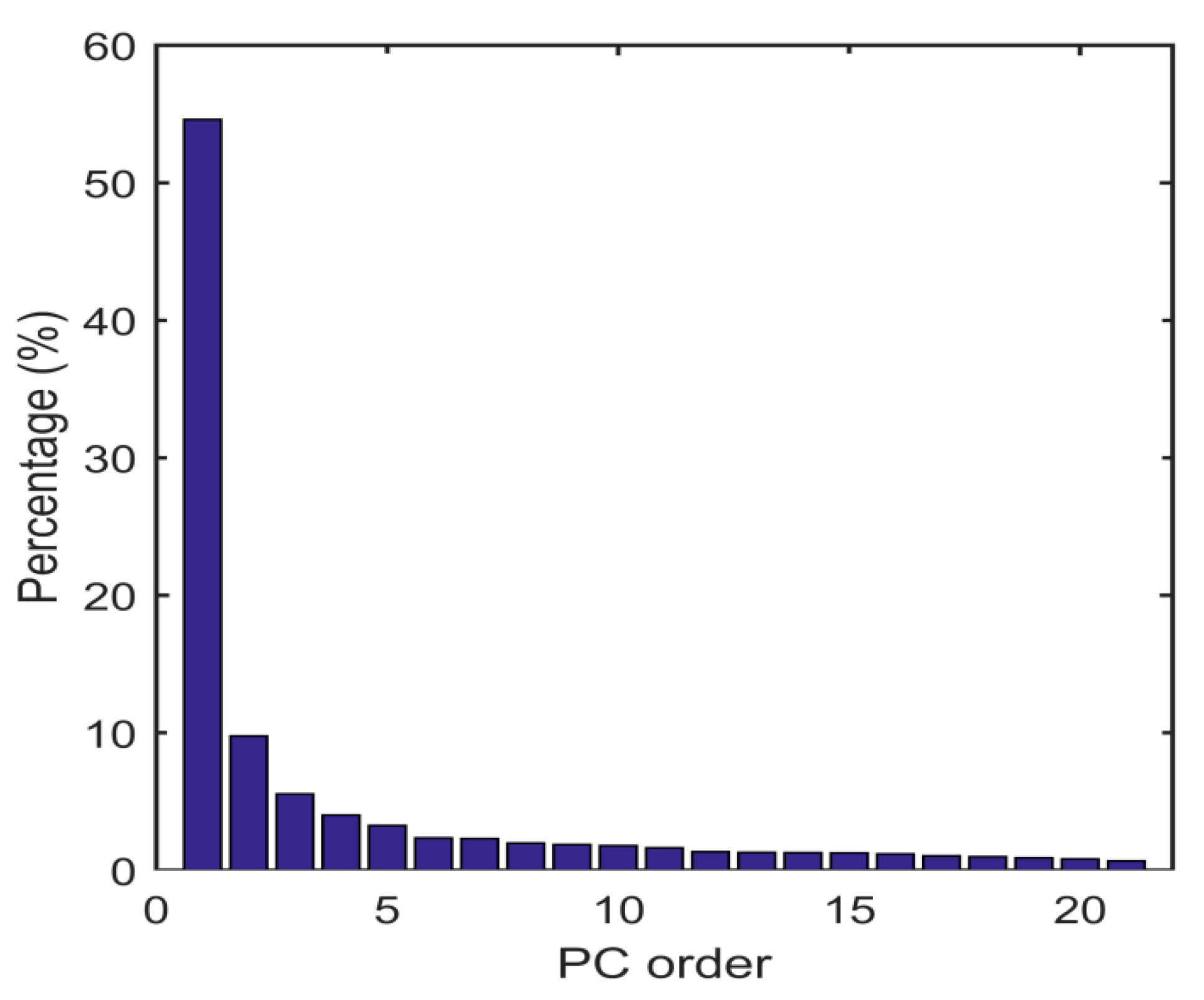
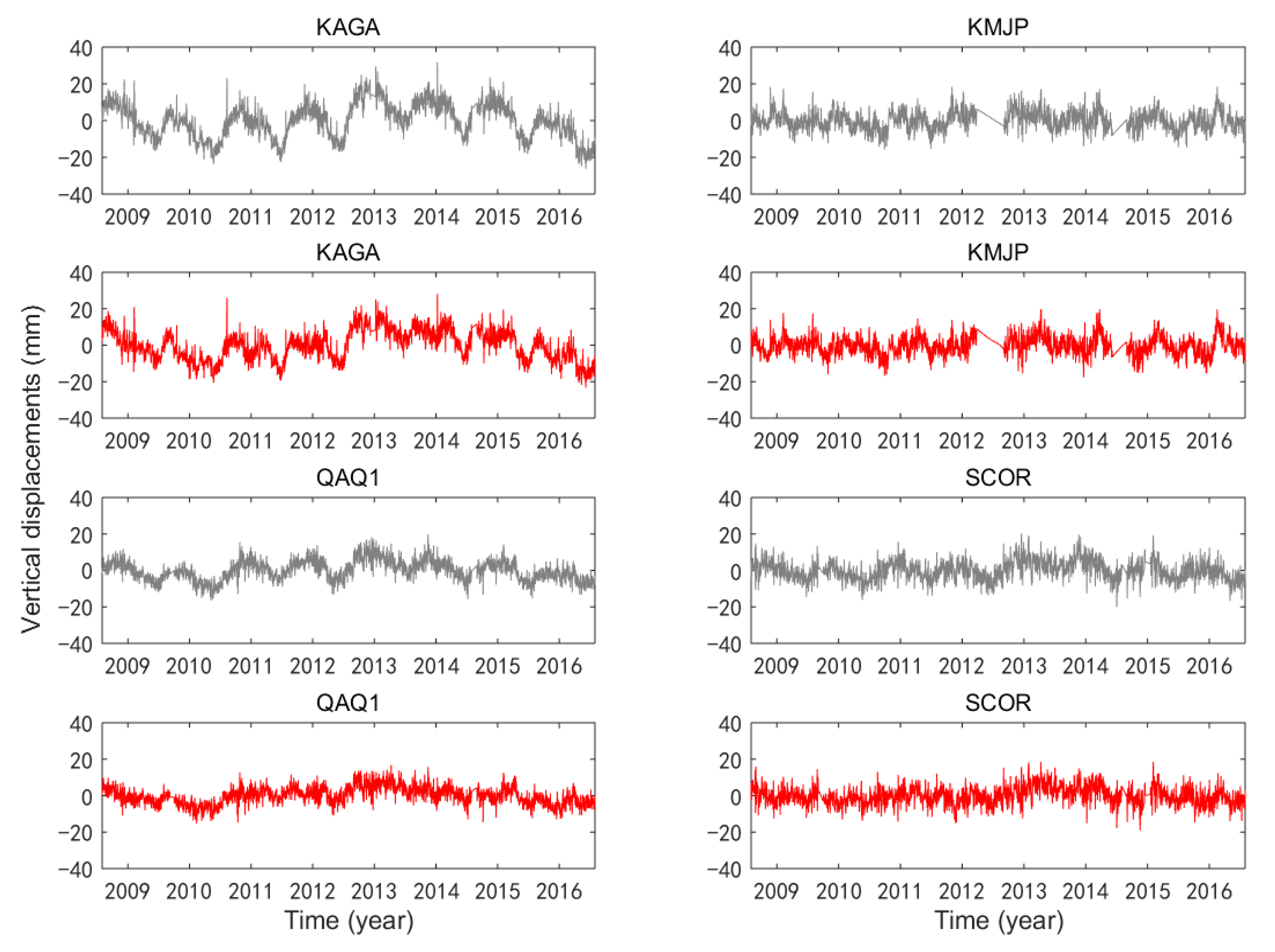
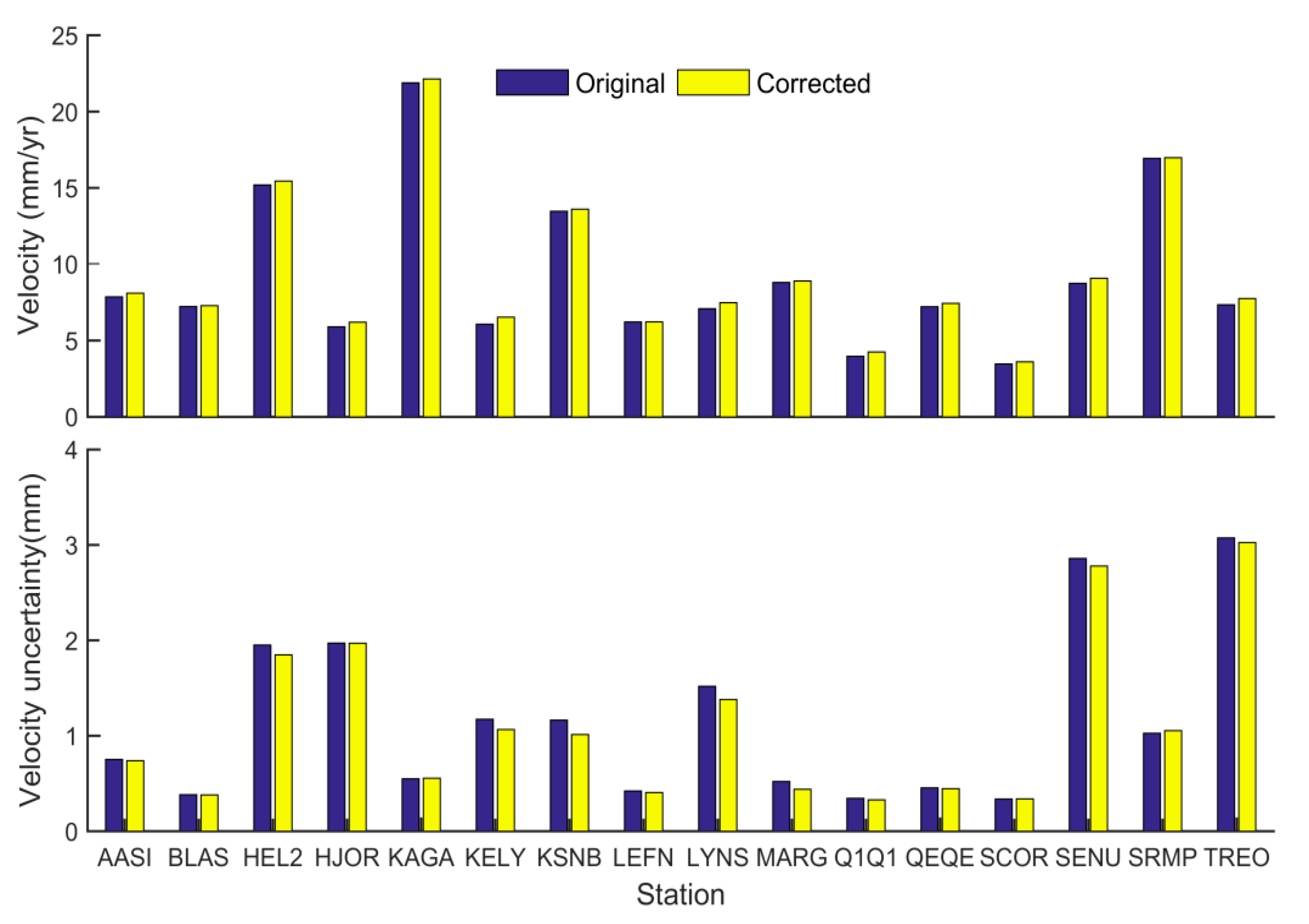
3.1. Common Model Error Analysis of GPS Station Coordinates
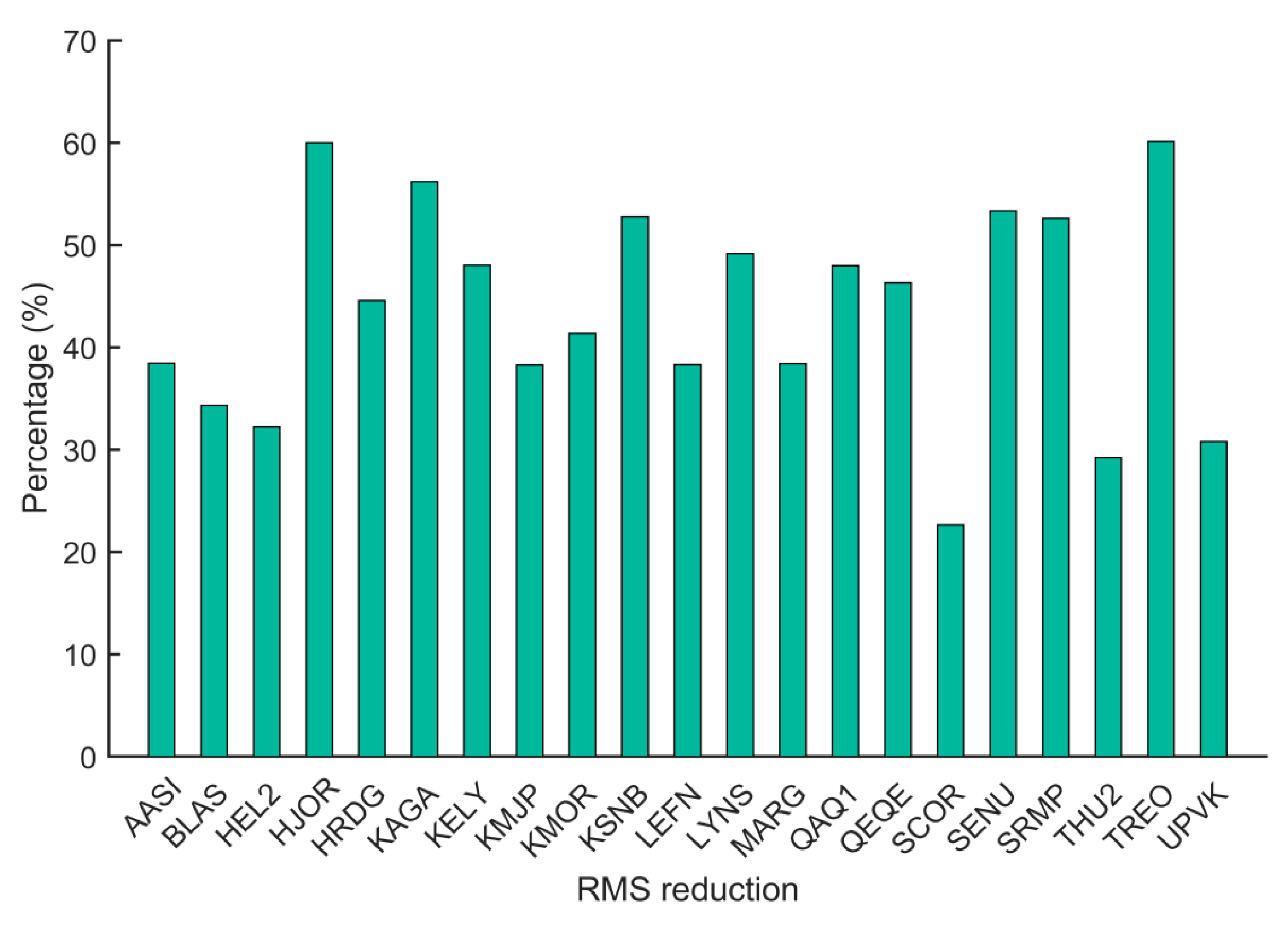
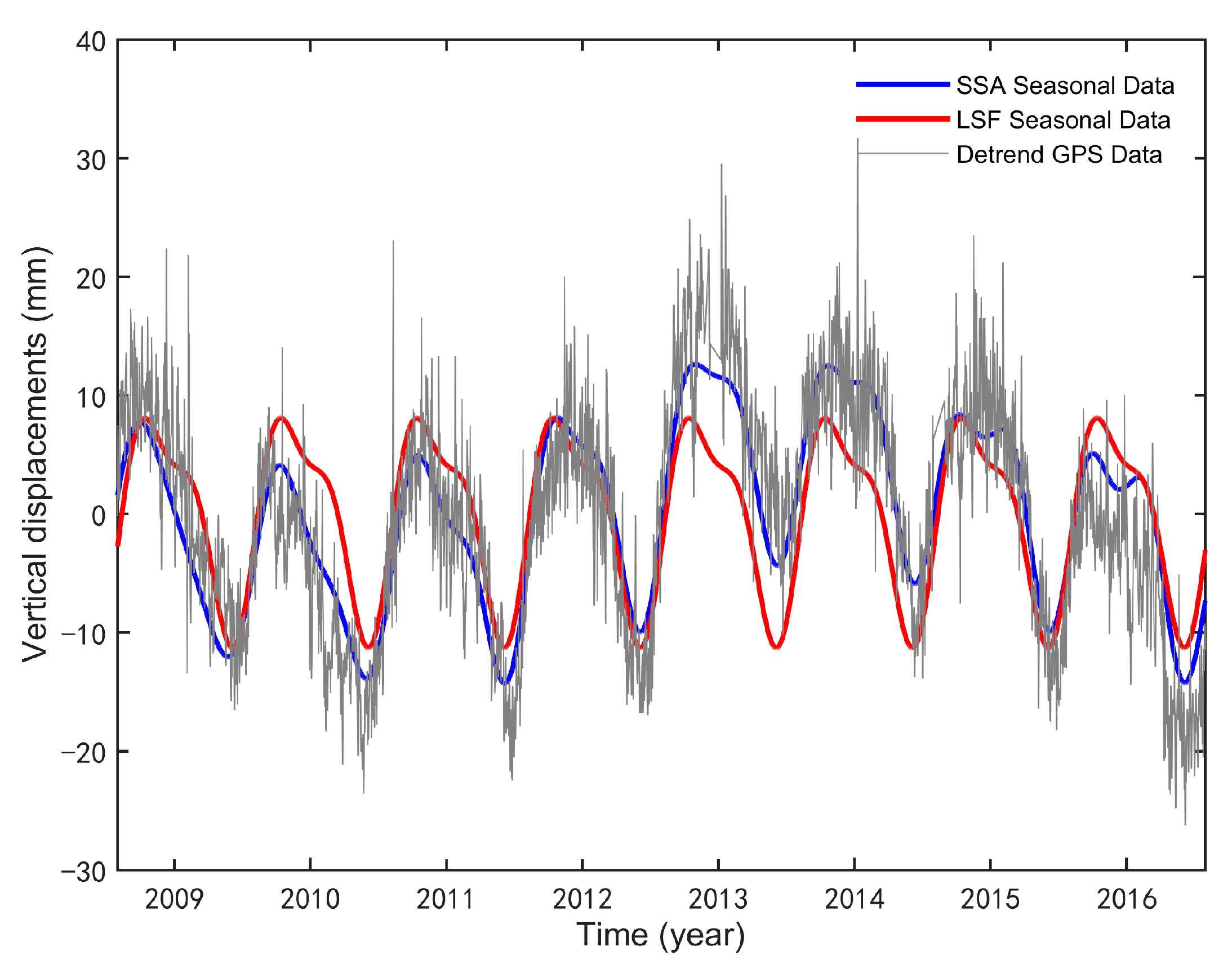
3.2. Seasonal Signal Extraction of GPS Station Coordinates
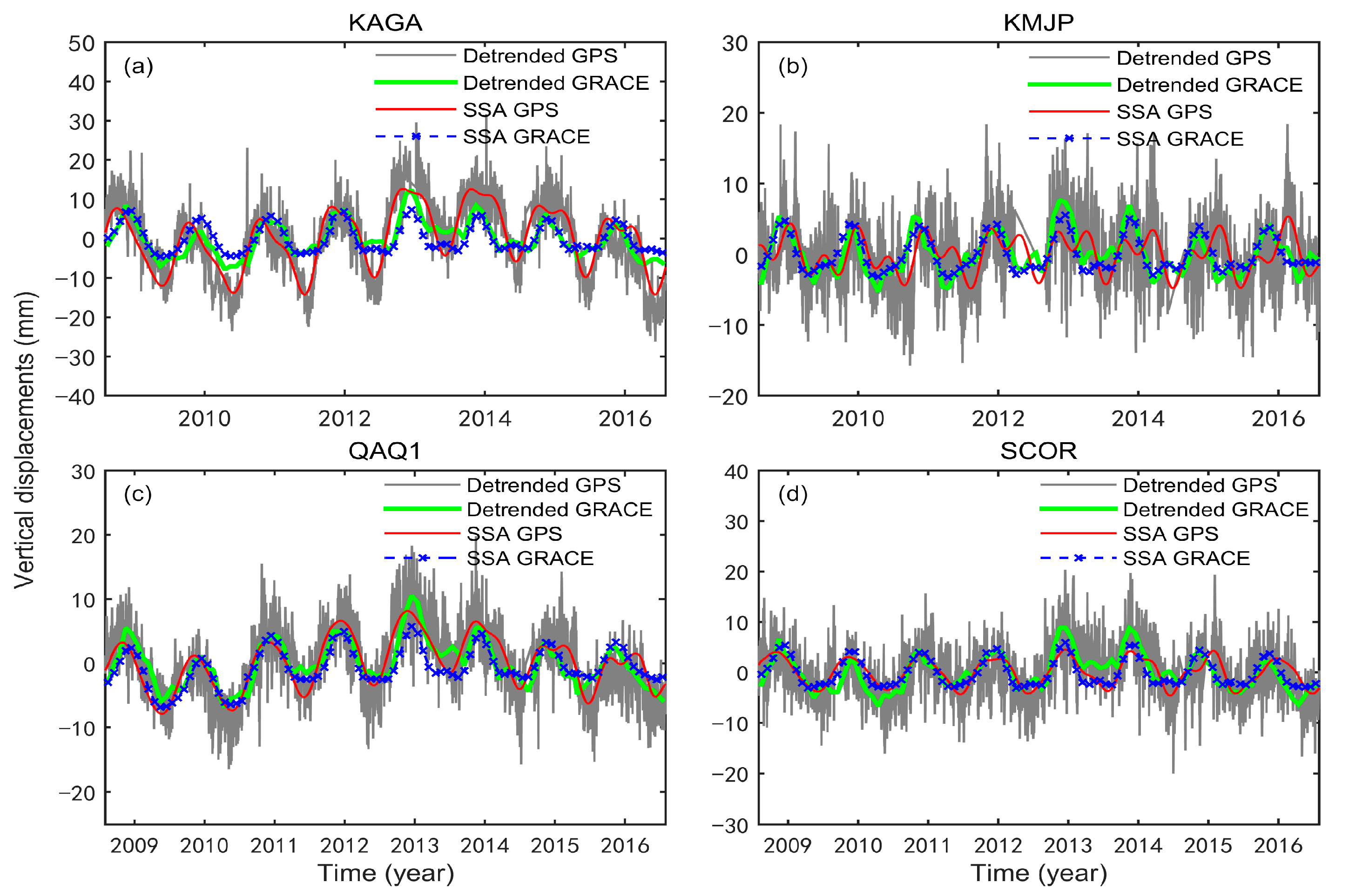
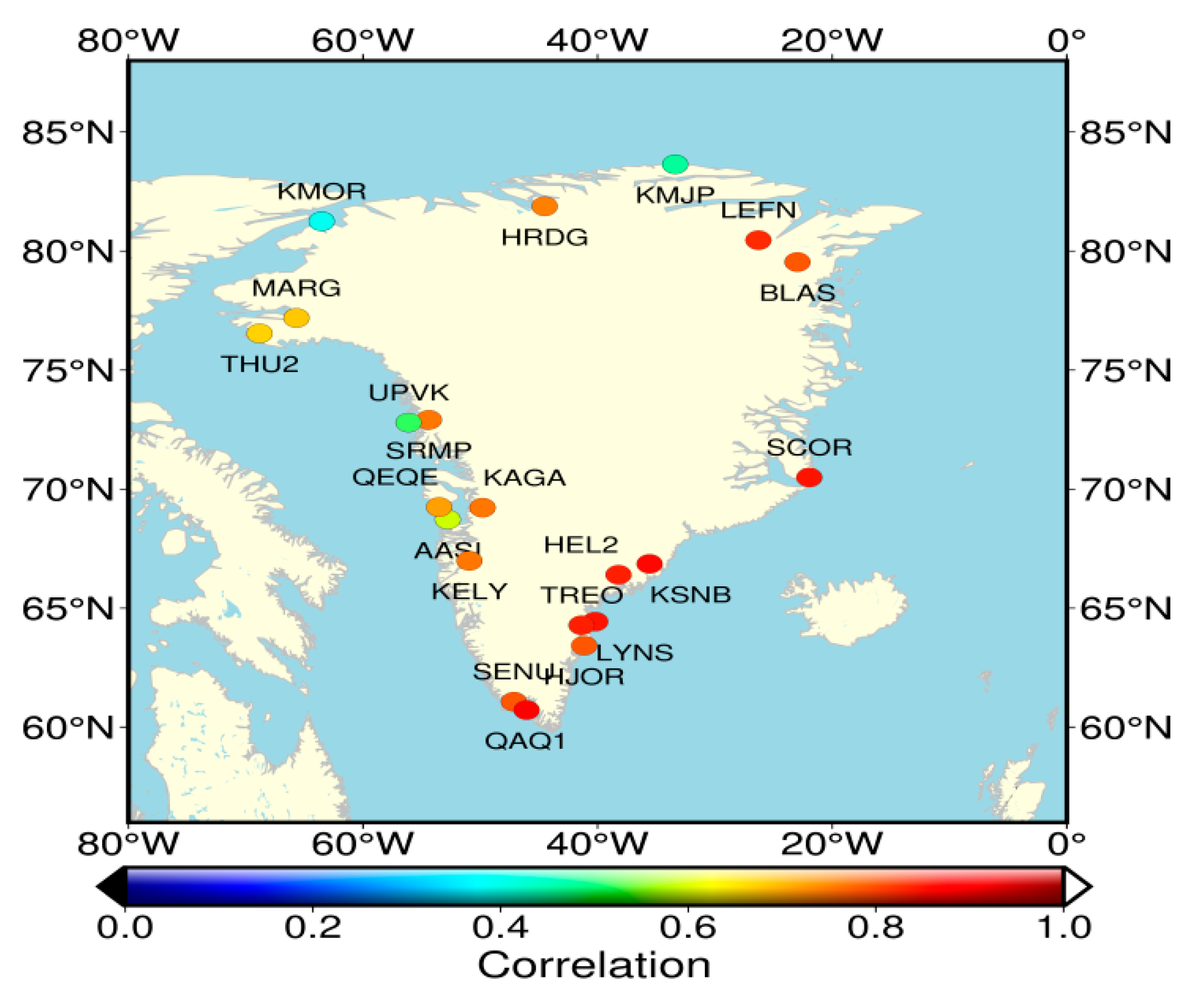
3.3. Comparative Analysis of GRACE and GPS Seasonal Vertical Deformation
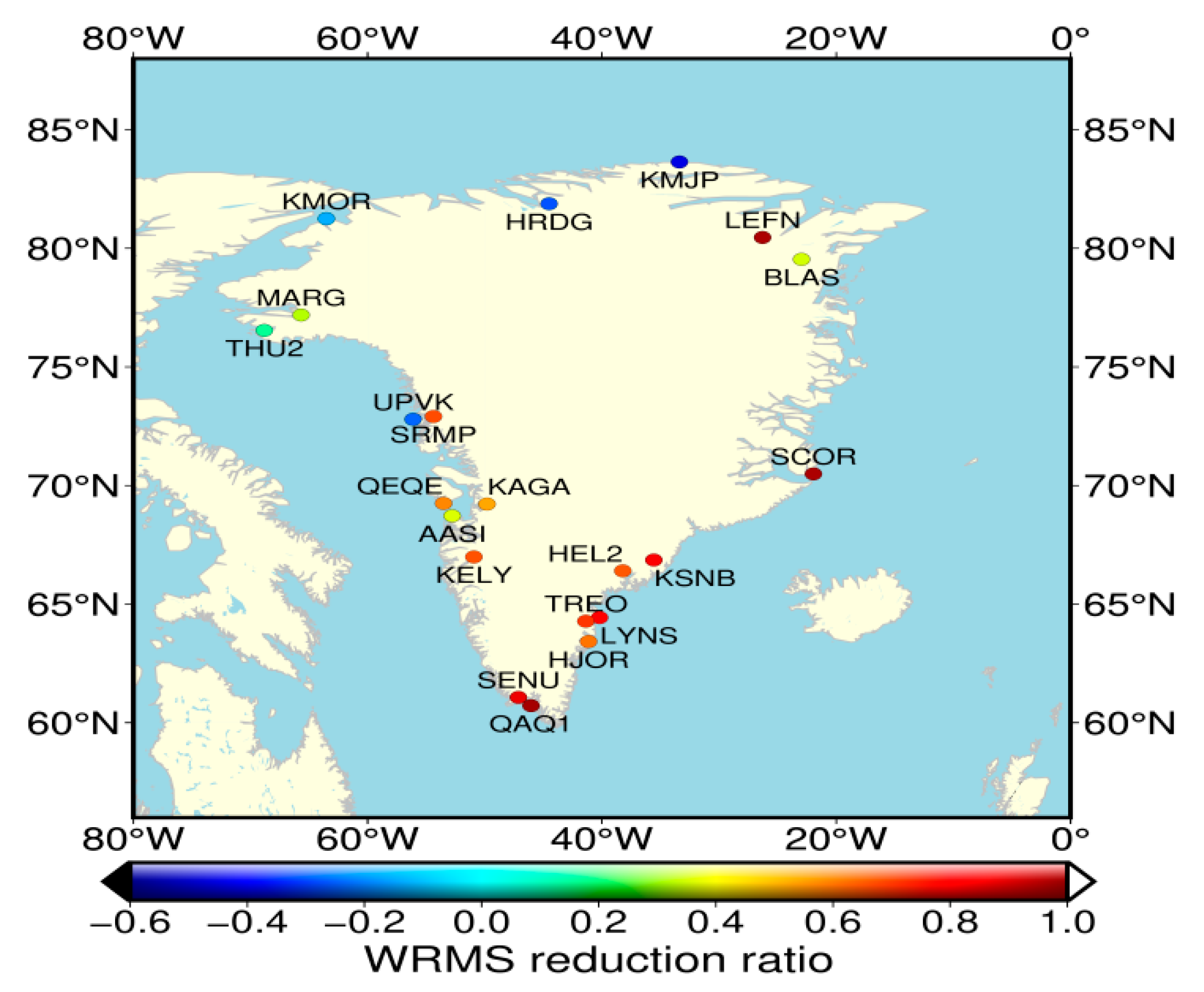
3.4. Influence of GRACE Seasonal Load Deformation on GPS Station Coordinates
4. Discussions
4.1. Cause for Vertical Seasonal Changes Affecting Differences
4.2. Cause for Coordinate Parameters Affecting Differences
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dong, D.; Herring, T.A.; King, R.W. Estimating regional deformation from a combination of space and terrestrial geodetic data. J. Geod. 1998, 72, 200–214. [Google Scholar] [CrossRef]
- Wang, M.; Zhang, Z.S.; Xu, M.Y.; Zhou, W.; Li, P.; You, X.Q. Data processing and accuracy analysis of national 2000′ GPS geodetic control network. Chin. J. Geophys. 2005, 48, 817–823. (In Chinese) [Google Scholar] [CrossRef]
- Jiang, W.P.; Xia, C.Y.; Li, Z.; Guo, Q.Y.; Zhang, S.Q. Analysis of environmental loading effects on regional GPS coordinate time series. Acta Geod. Cartogr. Sin. 2014, 43, 1217–1223. [Google Scholar]
- Deng, L.S. Research on effects of unmodeled errors and environmental loading on GPS coordinate time series. Acta Geod. Cartogr. Sin. 2018, 47, 1560. [Google Scholar]
- Pan, Y.; Chen, R.Z.; Ding, H.; Xu, X.Y.; Gang, Z.; Shen, W.B.; Xiao, Y.X.; Li, S.Y. Common Mode Component and Its Potential Effect on GPS-Inferred Three-Dimensional Crustal Deformations in the Eastern Tibetan Plateau. Remote Sens. 2019, 11, 1975. [Google Scholar] [CrossRef]
- Zhan, W.; Tian, Y.F.; Zhang, Z.W.; Zhu, C.D.; Wang, Y. Seasonal patterns of 3D crustal motions across the seismically active southeastern Tibetan Plateau. J. Asian Earth Sci. 2020, 192, 104274. [Google Scholar] [CrossRef]
- Hu, S.Q.; Wang, T.; Guan, Y.H.; Yang, Z.Y. Analyzing the seasonal fluctuation and vertical deformation in Yunnan province based on GPS measurement and hydrological loading model. Chin. J. Geophys 2021, 64, 2613–2630. (In Chinese). [Google Scholar]
- Swenson, S.; Wahr, J. Methods for inferring regional surface-mass anomalies from Gravity Recovery and Climate Experiment (GRACE) measurements of time-variable gravity. J. Geophys. Res. Solid Earth 2002, 107, ETG 3-1−ETG 3-13. [Google Scholar] [CrossRef]
- Davis, J.L.; Elósegui, P.; Mitrovica, J.X.; Tamisiea, M.E. Climate-driven deformation of the solid Earth from GRACE and GPS. Geophys. Res. Lett. 2004, 31, L24605. [Google Scholar] [CrossRef]
- Moreira, D.M.; Calmant, S.; Perosanz, F.; Xavier, L.; Rotunno Filho, O.C.; Seyler, F.; Monteiro, A.C. Comparisons of observed and modeled elastic responses to hydrological loading in the Amazon basin. Geophys. Res. Lett. 2016, 43, 9604–9610. [Google Scholar] [CrossRef]
- Van Dam, T.; Wahr, J.; Lavallée, D. A comparison of annual vertical crustal displacements from GPS and Gravity Recovery and Climate Experiment (GRACE) over Europe. J. Geophys. Res. Solid Earth 2007, 112, B03404. [Google Scholar] [CrossRef]
- Chanard, K.; Avouac, J.P.; Ramillien, G.; Genrich, J. Modeling deformation induced by seasonal variations of continental water in the Himalaya region: Sensitivity to Earth elastic structure. J. Geophys. Res. Solid Earth 2014, 119, 5097–5113. [Google Scholar] [CrossRef]
- Bevis, M.; Wahr, J.; Khan, S.A.; Madsen, F.B.; Brown, A.; Willis, M.; Kendrick, E.; Knudsen, P.; Box, J.E.; Francis, O.; et al. Bedrock displacements in Greenland manifest ice mass variations, climate cycles and climate change. Proc. Natl. Acad. Sci. USA 2012, 109, 11944–11948. [Google Scholar] [CrossRef] [PubMed]
- Ding, Y.H.; Huang, D.F.; Shi, Y.L.; Jiang, Z.S.; Chen, T. Determination of vertical surface displacements in Sichuan using GPS and GRACE measurements. Chin. J. Geophys. 2018, 61, 4777–4788. (In Chinese). [Google Scholar]
- Zhan, W.; Li, F.; Hao, W.F.; Yan, J.G. Regional characteristics and influencing factors of seasonal vertical crustal motions in Yunnan, China. Geophys. J. Int. 2017, 210, 1295–1304. [Google Scholar] [CrossRef]
- Hao, M.; Freymueller, J.T.; Wang, Q.; Cui, D.X.; Qin, S.L. Vertical crustal movement around the southeastern Tibetan Plateau constrained by GPS and GRACE data. Earth Planet. Sci. Lett. 2016, 437, 1–8. [Google Scholar] [CrossRef]
- Chen, C.; Zou, R.; Liu, R.L. Vertical deformation of seasonal hydrological loading in the southern Tibet detected by joint analysis of GPS and GRACE. Geomat. Inf. Sci. Wuhan Univ. 2018, 43, 30–36. [Google Scholar]
- Nagale, D.S.; Kannaujiya, S.; Gautam, P.K.; Taloor, A.K.; Sarkar, T. Impact assessment of the seasonal hydrological loading on geodetic movement and seismicity in Nepal Himalaya using GRACE and GNSS measurements. Geod. Geodyn. 2022, 13, 445–455. [Google Scholar] [CrossRef]
- Jiang, W.P.; Li, Z.; Van Dam, T.; Ding, W.W. Comparative analysis of different environmental loading methods and their impacts on the GPS height time series. J. Geod. 2013, 87, 687–703. [Google Scholar] [CrossRef]
- Fang, J.; He, M.L.; Luan, W.; Jiao, J.H. Crustal vertical deformation of Amazon Basin derived from GPS and GRACE/GFO data over past two decades. Geod. Geody. 2021, 12, 441–450. [Google Scholar] [CrossRef]
- Liu, B.; Ma, X.J.; Xing, X.M.; Tan, J.B.; Peng, W.; Zhang, L.Q. Quantitative Evaluation of Environmental Loading Products and Thermal Expansion Effect for Correcting GNSS Vertical Coordinate Time Series in Taiwan. Remote Sens. 2022, 14, 4480. [Google Scholar] [CrossRef]
- Jiang, W.P.; Deng, L.S.; Li, Z.; Zhou, X.H.; Liu, H.F. Effects on noise properties of GPS time series caused by higher-order ionospheric corrections. Adv. Space Res. 2014, 53, 1035–1046. [Google Scholar] [CrossRef]
- Bian, Y.; Yue, J.P.; Ferreira, V.G.; Cong, K.L.; Cai, D.J. Common Mode Component and Its Potential Effect on GPS-Inferred Crustal Deformations in Greenland. Pure Appl. Geophys. 2021, 178, 1805–1823. [Google Scholar] [CrossRef]
- Li, F.; Ma, C.; Zhang, S.K.; Lei, J.T.; Hao, W.F.; Zhang, Q.C.; Li, W.H. Noise analysis of the coordinate time series of the continuous GPS station and the deformation patterns in the Antarctic Peninsula. Chin. J. Geophys 2016, 59, 2402–2412. (In Chinese). [Google Scholar]
- He, X.; Bos, M.S.; Montillet, J.P.; Fernandes, R.M.S. Investigation of the noise properties at low frequencies in long GNSS time series. J. Geod. 2019, 93, 1271–1282. [Google Scholar] [CrossRef]
- He, X.X.; Yu, K.G.; Montillet, J.P.; Xiong, C.L.; Lu, T.D.; Zhou, S.J.; Ma, X.P.; Cui, H.C.; Ming, F. GNSS-TS-NRS: An Open-Source MATLAB-Based GNSS Time Series Noise Reduction Software. Remote Sens. 2020, 12, 3532. [Google Scholar] [CrossRef]
- Li, Z. Research on Seasonal Variations and Noise of GNSS Coordinate Time Series. Ph.D. Thesis, Hohai University, Nanjing, China, 2020. [Google Scholar]
- Blewitt, G.; Lavallée, D. Effect of annual signals on geodetic velocity. J. Geophys. Res. Solid Earth 2002, 107, 9–11. [Google Scholar] [CrossRef]
- Nikolaidis, R. Observation of Geodetic and Seismic Deformation with the Global Positioning System. Ph.D. Thesis, University of California, San Diego, CA, USA, 2002. [Google Scholar]
- Wang, M.R. Study of Time-Frequency Analysis of GPS Coordinate Time Series in Antarctica. Ph.D. Thesis, North China University of Science and Technology, Tangshan, China, 2016. [Google Scholar]
- Li, Z.; Jiang, W.P.; Liu, H.F.; Qu, X.C. Noise Model Establishment of IGS Reference Station Time Series inside China and its Analysis. Acta Geod. Cartogr. Sin. 2012, 41, 496–503. [Google Scholar]
- Farrell, W.E. Deformation of the Earth by surface loads. Rev. Geophys. 1972, 10, 761–797. [Google Scholar] [CrossRef]
- Sun, Y.; Riva, R.; Ditmar, P. Optimizing estimates of annual variations and trends in geocenter motion and J2 from a combination of GRACE data and geophysical models. J. Geophys. Res. Solid Earth 2016, 121, 8352–8370. [Google Scholar] [CrossRef]
- Loomis, B.D.; Rachlin, K.E.; Luthcke, S.B. Improved Earth oblateness rate reveals increased ice sheet losses and mass-driven sea level rise. Geophys. Res. Lett. 2019, 46, 6910–6917. [Google Scholar] [CrossRef]
- Swenson, S.; Wahr, J. Post-processing removal of correlated errors in GRACE data. Geophys. Res. Lett. 2006, 33, L08402. [Google Scholar] [CrossRef]
- Han, S.C.; Shum, C.K.; Jekeli, C.; Kuo, C.Y.; Wilson, C.; Seo, K.W. Non-isotropic filtering of GRACE temporal gravity for geophysical signal enhancement. Geophys. J. Int. 2010, 163, 18–25. [Google Scholar] [CrossRef]
- Jin, S.; Zou, F. Re-estimation of glacier mass loss in Greenland from GRACE with correction of land-ocean leakage effects. Glob. Planet. Chang. 2015, 135, 170–178. [Google Scholar] [CrossRef]
- Geruo, A.; Wahr, J.; Zhong, S. Computations of the viscoelastic response of a 3-D compressible Earth to surface loading: An application to Glacial Isostatic Adjustment in Antarctica and Canada. Geophys. J. Int. 2013, 192, 557–572. [Google Scholar]
- Vautard, R.; Ghil, M. Singular spectrum analysis in nonlinear dynamics, with applications to paleoclimatic time series. Phys. D 1989, 35, 395–424. [Google Scholar] [CrossRef]
- Jiang, Z.H.; Ding, Y.G. Generality and Applied Features for Singular Spectrum Analysis. Acta Meteorol. Sin. 1998, 56, 736–745. [Google Scholar]
- Vautard, R.; Yiou, P.; Ghil, M. Singular-spectrum analysis: A toolkit forshort, noisy chaotic signals. Phys. D 1992, 58, 95–126. [Google Scholar] [CrossRef]
- Plaut, G.; Vautard, R. Spells of low-frequency oscillations and weather regimesin the northern hemisphere. J. Atmos. Sci. 1994, 51, 210–236. [Google Scholar] [CrossRef]
- Schwarz, G. Estimating the dimension of a model. Ann. Stat. 1978, 6, 461–464. [Google Scholar] [CrossRef]
- Dong, D.; Fang, P.; Bock, Y.; Webb, F.; Prawirodirdjo, L.; Kedar, S.; Jamason, P. Spatiotemporal filtering using principal component analysis and Karhunen-Loeve expansion approaches for regional GPS network analysis. J. Geophys. Res. Solid Earth 2006, 111, B03405. [Google Scholar] [CrossRef]
- Ma, C.; Li, F.; Zhang, S.K.; Lei, J.T.; Dong-Chen, E.; Hao, W.F.; Zhang, Q.C. The coordinate time series analysis of continuous GPS stations in the Antarctic Peninsula with consideration of common mode error. J. Geophys. 2016, 59, 2783–2795. (In Chinese) [Google Scholar]
- Chen, Q.; Van Dam, T.; Sneeuw, N.; Collilieux, X.; Weigelt, M.; Rebischung, P. Singular spectrum analysis for modeling seasonal signals from GPS time series. J. Geodyn. 2013, 72, 25–35. [Google Scholar] [CrossRef]
- Li, Z.; Yue, J.P.; Li, W.; Lu, D.K. Investigating mass loading contributes of annual GPS observations for the Eurasian plate. J. Geodyn. 2017, 111, 43–49. [Google Scholar] [CrossRef]
- Feng, T.F.; Shen, Y.Z.; Chen, Q.J.; Wang, F.W. Seasonal driving sources and hydrological-induced secular trend of the vertical displacement in North China. J. Hydrol. Reg. Stud. 2022, 41, 101091. [Google Scholar] [CrossRef]
- Jiang, W.P.; Li, Z.; Liu, H.F.; Zhao, Q. Cause analysis of the non-linear variation of the IGS reference station coordinate time series inside China. J. Geophys. 2013, 56, 2228–2237. (In Chinese) [Google Scholar]
- He, X.; Bos, M.S.; Montillet, J.P.; Fernandes, R.M.S. Spatial variations of stochastic noise properties in GPS time series. Remote Sens. 2021, 13, 4534. [Google Scholar] [CrossRef]
- Bian, Y.K.; Yue, J.P.; Gao, W.; Li, Z.; Lu, D.K.; Xiang, Y.F.; Chen, J. Analysis of the spatiotemporal changes of ice sheet mass and driving factors in Greenland. Remote Sens. 2019, 11, 862. [Google Scholar] [CrossRef]
- Zhang, B.; Liu, L.; Khan, S.A.; Van Dam, T.; Bjørk, A.A.; Peings, Y.; Zhang, E.Z.; Bevis, M.; Yao, Y.B.; Noël, B. Geodetic and model data reveal different spatio-temporal patterns of transient mass changes over Greenland from 2007 to 2017. Earth Planet Sci. Lett. 2019, 515, 154–163. [Google Scholar] [CrossRef]
- Zou, F.; Tenzer, R.; Fok, H.S.; Nichol, J.E. Recent Climate Change Feedbacks to Greenland Ice Sheet Mass Changes from GRACE. Remote Sens. 2020, 12, 3250. [Google Scholar] [CrossRef]
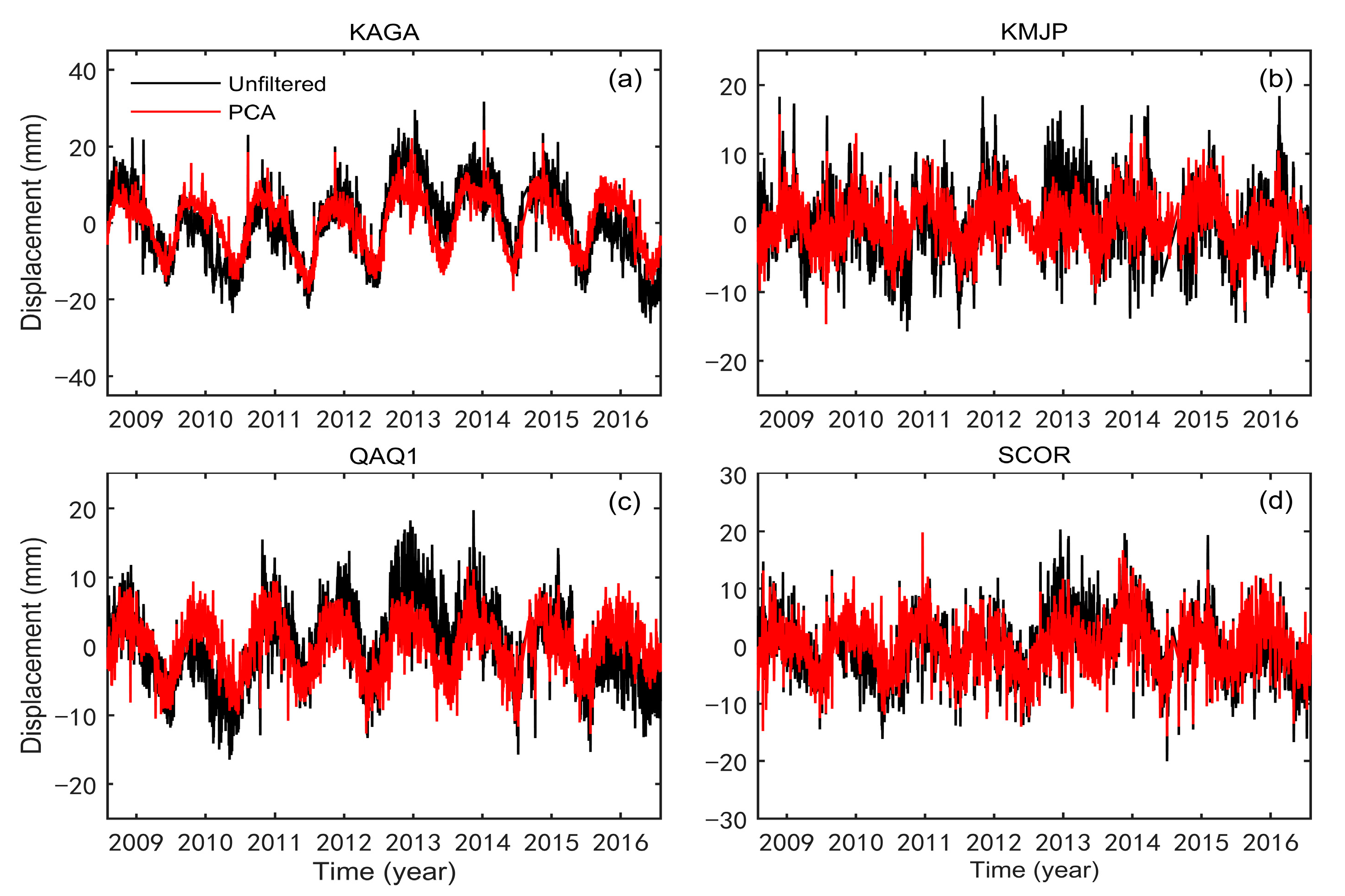
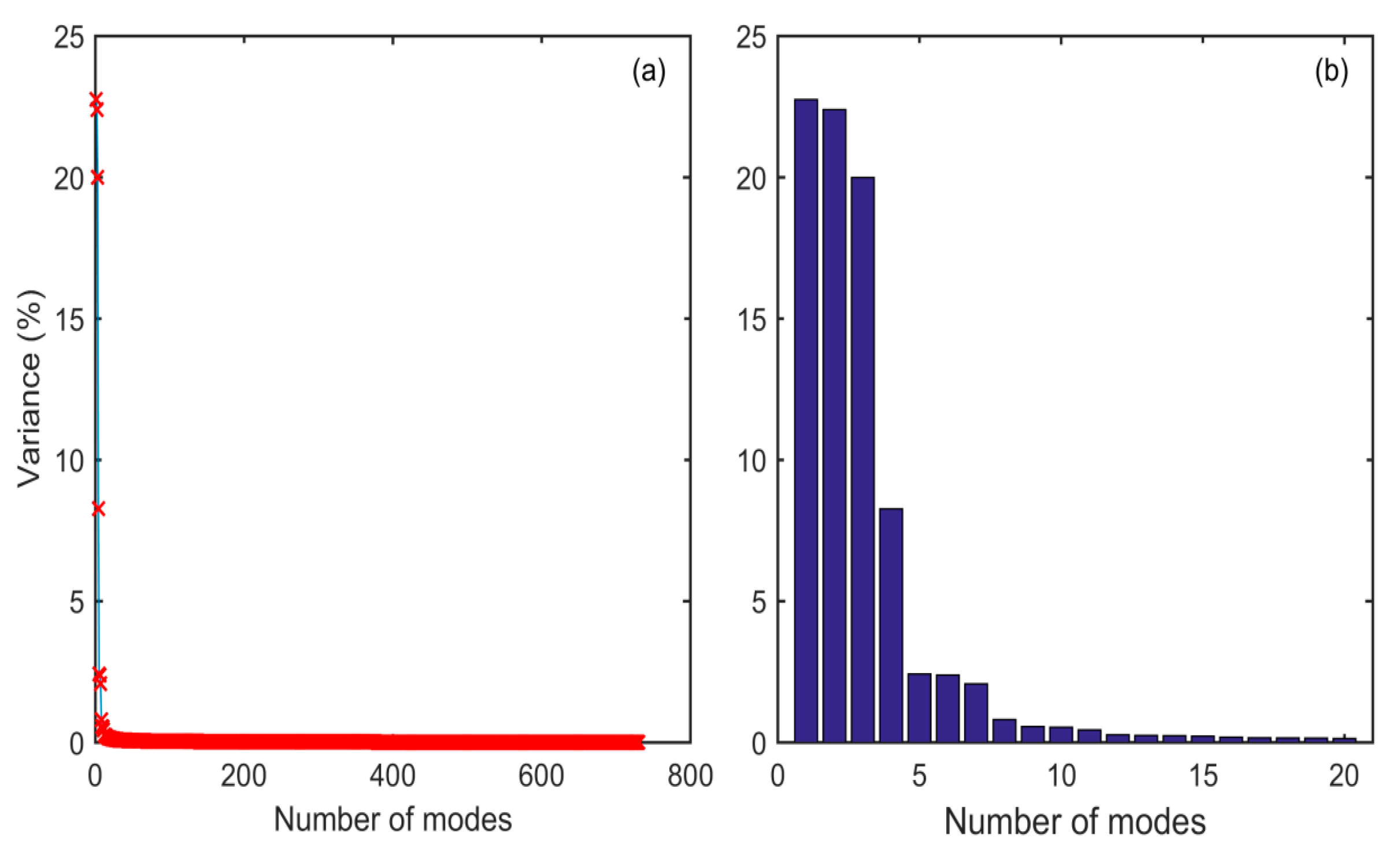
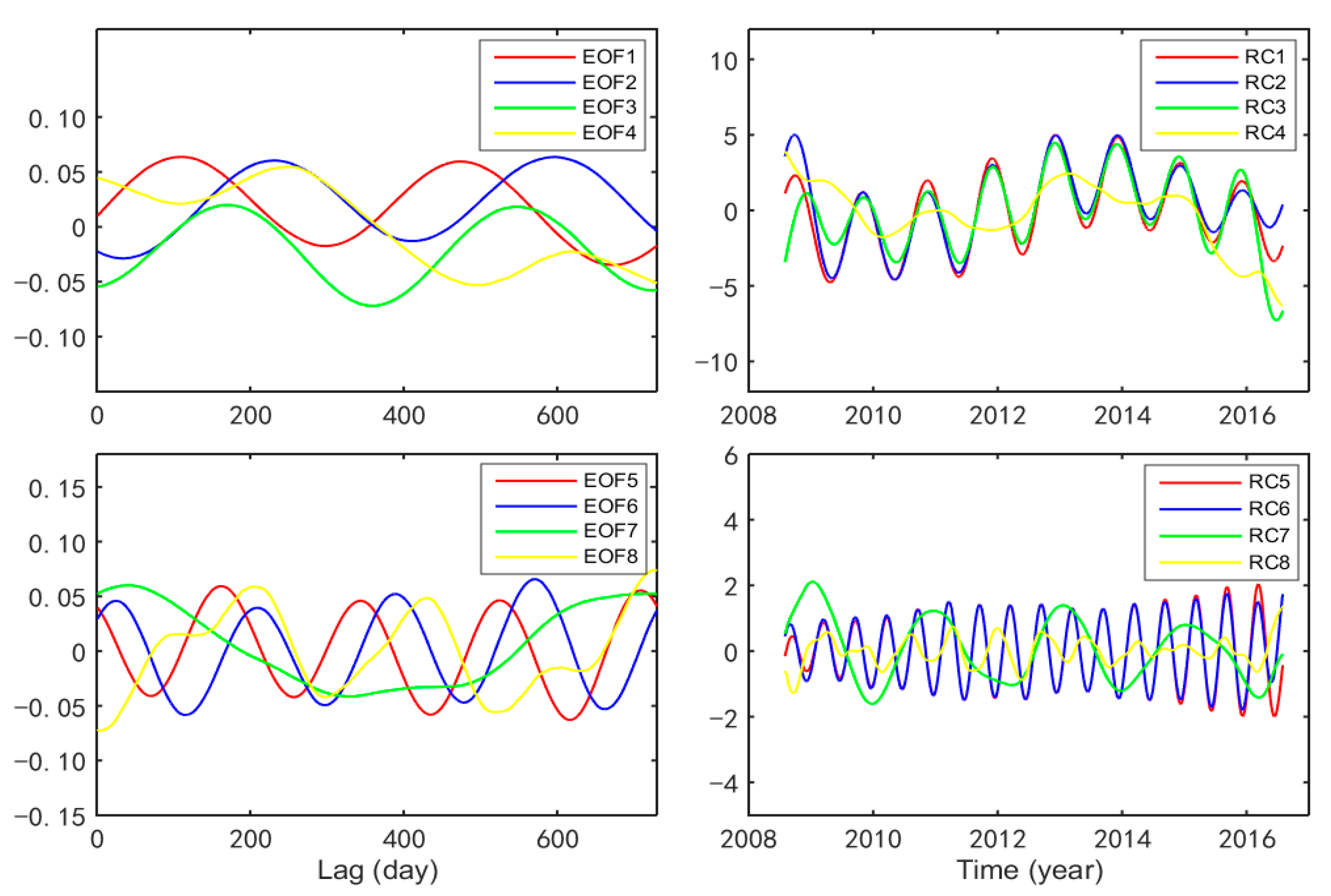
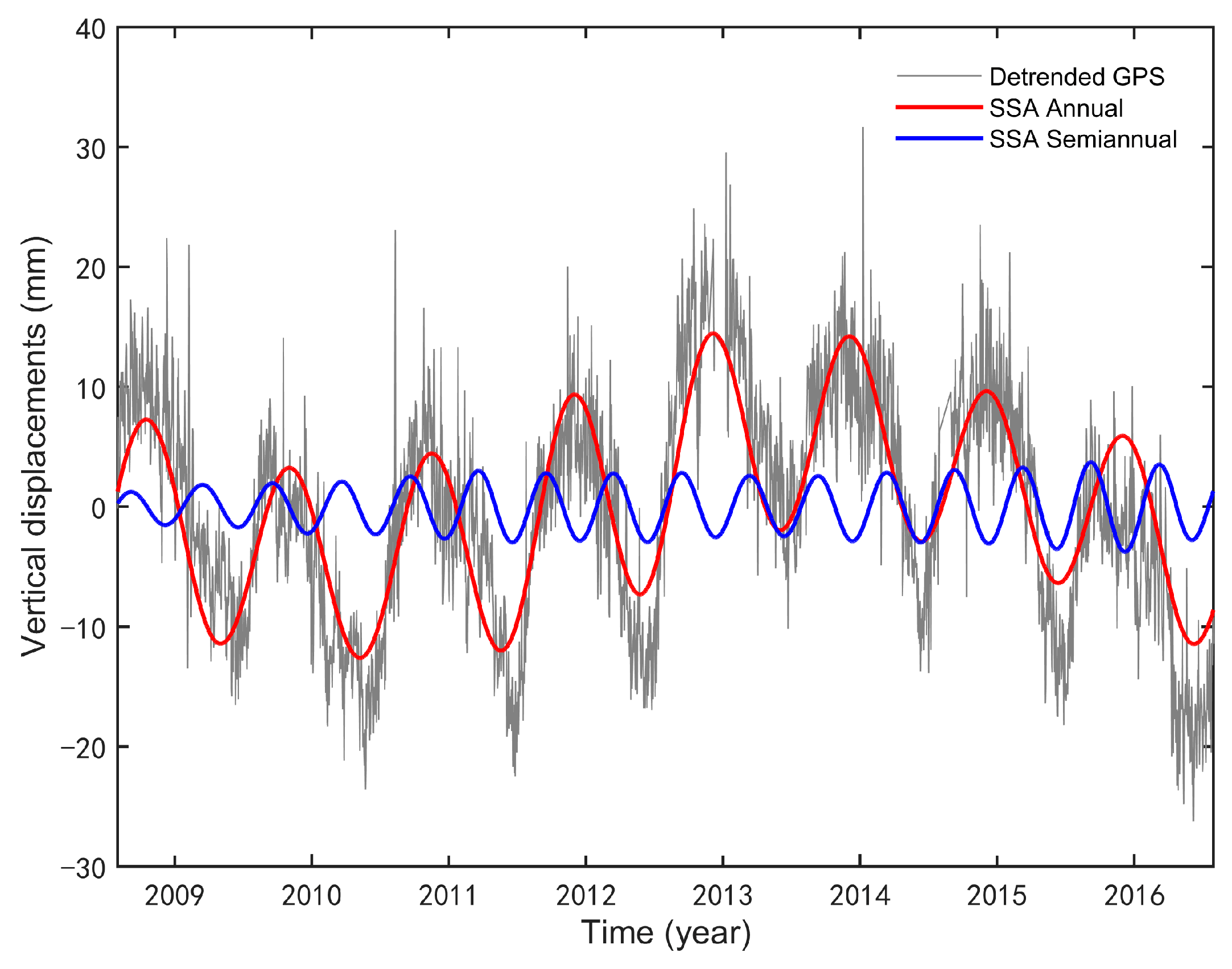

| Station | PCA | Station | PCA | ||||||
|---|---|---|---|---|---|---|---|---|---|
| U1 | U2 | U3 | U4 | U1 | U2 | U3 | U4 | ||
| AASI | 0.58 | 0.37 | 1.00 | 1.00 | LYNS | 0.72 | 0.54 | 0.56 | 0.06 |
| BLAS | 0.42 | 0.60 | 0.33 | 0.26 | MARG | 0.42 | 0.71 | 0.36 | 0.13 |
| HEL2 | 0.56 | 0.31 | 0.51 | 0.00 | QAQ1 | 0.56 | 0.23 | 0.12 | 0.10 |
| HJOR | 0.72 | 0.54 | 0.43 | 0.09 | QEQE | 0.61 | 0.01 | 0.57 | 0.03 |
| HRDG | 0.37 | 0.93 | 0.31 | 0.06 | SCOR | 0.42 | 0.22 | 0.14 | 0.31 |
| KAGA | 0.83 | 0.06 | 0.86 | 0.51 | SENU | 0.79 | 0.75 | 0.09 | 0.25 |
| KELY | 0.65 | 0.09 | 0.53 | 0.23 | SRMP | 0.60 | 0.14 | 0.17 | 0.03 |
| KMJP | 0.33 | 0.90 | 0.38 | 0.00 | THU2 | 0.35 | 0.69 | 0.16 | 0.23 |
| KMOR | 0.49 | 0.95 | 0.25 | 0.04 | TREO | 1.00 | 1.00 | 0.62 | 0.52 |
| KSNB | 0.70 | 0.16 | 0.40 | 0.32 | UPVK | 0.42 | 0.37 | 0.13 | 0.21 |
| LEFN | 0.43 | 0.77 | 0.20 | 0.16 | |||||
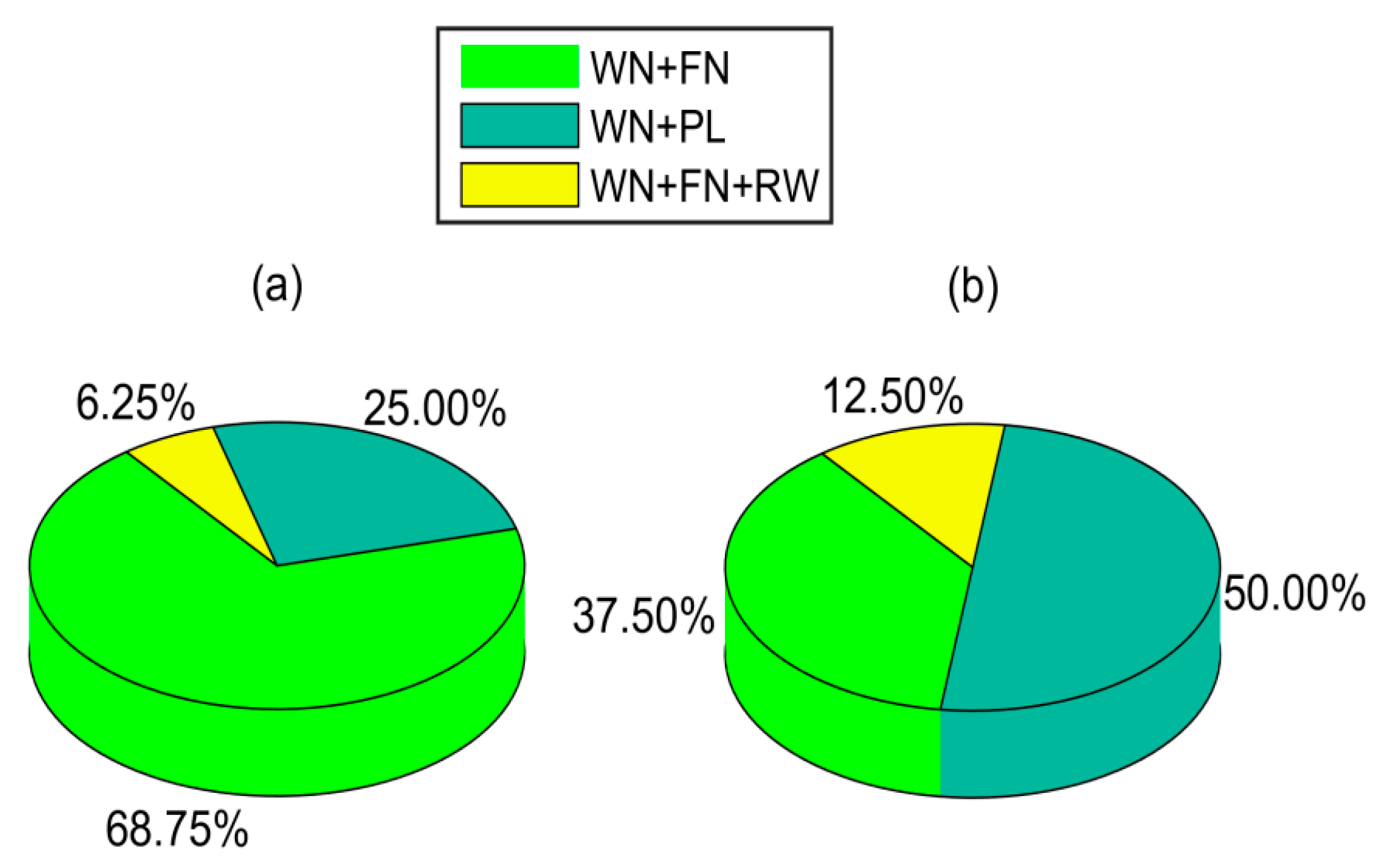
| Station | Unfiltered | Filtered | ||
|---|---|---|---|---|
| AIC | BIC | AIC | BIC | |
| AASI | WN + PL | WN + PL | WN + FN | WN + FN |
| BLAS | WN + FN | WN + FN | WN + FN | WN + FN |
| HEL2 | WN + FN | WN + FN | WN + PL | WN + PL |
| HJOR | WN + FN | WN + FN | WN + PL | WN + PL |
| KAGA | WN + FN + RW | WN + FN | WN + FN | WN + FN |
| KELY | WN + PL | WN + PL | WN + PL | WN + PL |
| KSNB | WN + FN | WN + FN | WN + PL | WN + PL |
| LEFN | WN + FN | WN + FN | WN + FN | WN + FN |
| LYNS | WN + PL | WN + PL | WN + PL | WN + PL |
| MARG | WN + FN | WN + FN | WN + FN | WN + FN |
| QAQ1 | WN + FN | WN + FN | WN + PL | WN + PL |
| QEQE | WN + FN | WN + FN | WN + PL | WN + PL |
| SCOR | WN + PL | WN + PL | WN + FN + RW | WN + FN + RW |
| SENU | WN + FN + RW | WN + FN | WN + PL | WN + PL |
| SRMP | WN + FN | WN + FN | WN + PL | WN + PL |
| TREO | WN + FN + RW | WN + FN + RW | WN + FN + RW | WN + FN + RW |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bian, Y.; Li, Z.; Huang, Z.; He, B.; Shi, L.; Miao, S. Combined GRACE and GPS to Analyze the Seasonal Variation of Surface Vertical Deformation in Greenland and Its Influence. Remote Sens. 2023, 15, 511. https://doi.org/10.3390/rs15020511
Bian Y, Li Z, Huang Z, He B, Shi L, Miao S. Combined GRACE and GPS to Analyze the Seasonal Variation of Surface Vertical Deformation in Greenland and Its Influence. Remote Sensing. 2023; 15(2):511. https://doi.org/10.3390/rs15020511
Chicago/Turabian StyleBian, Yankai, Zhen Li, Zhiquan Huang, Bing He, Liangliang Shi, and Song Miao. 2023. "Combined GRACE and GPS to Analyze the Seasonal Variation of Surface Vertical Deformation in Greenland and Its Influence" Remote Sensing 15, no. 2: 511. https://doi.org/10.3390/rs15020511
APA StyleBian, Y., Li, Z., Huang, Z., He, B., Shi, L., & Miao, S. (2023). Combined GRACE and GPS to Analyze the Seasonal Variation of Surface Vertical Deformation in Greenland and Its Influence. Remote Sensing, 15(2), 511. https://doi.org/10.3390/rs15020511





