1. Introduction
Estimating the bearing angle of an uncooperative underwater target is vitally important in underwater acoustic engineering [
1,
2,
3,
4]. Considering that the unknown underwater environment sometimes causes uncertain measurement noise that will degrade the estimation accuracy of the interested target’s bearing angle, the robust bearing angle estimating technique is necessary and has attracted a number of researchers’ attention [
5,
6,
7,
8]. In addition, the techniques of passive bearing angle estimation can be based on two different ways, namely the DOA estimation and the DOA tracking methods. The DOA estimation merely depends on the measurements from a certain period. Besides the measurements, the DOA tracking techniques also utilize the prior motion information of an interested target. Although the DOA estimation has already made many milestones in various bearing angle estimation missions [
9,
10,
11], its ignorance of the target’s kinematics makes the DOA estimation techniques always have superior estimating results when the target is nearly static and the environment is stable. When the target is maneuvering or the measurement noise shifts because the underwater environment is uncertain, the DOA estimation methods can hardly have satisfied results. In addition, in order to make reliable and accurate estimations of an uncooperative underwater target’s bearing angle, the DOA estimation techniques usually need a wide observation window, which will lead to heavy on-board computational load and which will occupy a lot of on-board limited storage.
Considering the advantages and drawbacks of the DOA estimation methods, DOA tracking techniques have been proposed. Instead of merely utilizing the measurement information, DOA tracking methods take both the target’s motion model and the current measurements into consideration. Based on the Bayesian estimation principle, the DOA tracking techniques can reach higher estimating accuracy and can occupy less on-board computing or storage resources, especially when the underwater target is maneuvering [
12,
13,
14,
15]. In addition, the unpredicted moving objects or environmental changes in the ocean can sometimes make the measurements uncertain, which will degrade the bearing angle estimation accuracy or even make the estimating procedure diverge. Under this circumstance, the robust DOA tracking technique is necessary to guarantee the precision of the whole estimation process. Among all the robust DOA tracking techniques, two categories can be divided depending on the basic mathematical principles, namely the data-inspiring robust tracking techniques [
16] and the Bayesian inferring techniques [
17,
18]. These two categories of robust DOA tracking techniques are both derived based on the widely used Kalman filter technique [
19,
20,
21]. The former one utilizes good estimations from a long tracking period to adjust the weight of the bad measurements when the measurement noise becomes uncertain. As a result, the weights of the poor measurements can become very small to make the current bearing angle estimations mainly depend on the historical good estimations. These kinds of data-inspiring robust DOA tracking techniques have proven their efficiency in a number of research studies [
22,
23,
24,
25,
26] nevertheless, their convergence is still an open question. When the hyper-parameters of the inspired robust DOA tracking are set inappropriately, the estimations usually have poor accuracy and sometimes diverge.
To overcome the drawbacks of the data-inspiring robust tracking techniques, the Bayesian inferring techniques, or the so-called variational Bayesian (VB) robust tracking techniques, are proposed and have been utilized in a various of research studies [
27,
28,
29]. Unlike the data-inspiring robust tracking methods, the VB robust tracking techniques are strictly derived mathematically. By assuming the prior probability density functions (PDFs) of the tracking parameters and the interested time-varying parameters (i.e., covariance matrix of the uncertain measurements noise) along with optimizing the Kullback–Leibler Divergence (KLD) among the posterior PDFs, the VB technique can analytically estimate the tracking parameters and other interested parameters simultaneously. Different from the data-inspiring robust tracking methods, the VB robust tracking techniques have strict mathematical foundations and can guarantee convergence and accuracy if the prior PDFs are set properly. Under this circumstance, the VB robust tracking techniques do not need good estimations from a long period to output reliable results when measurements become uncertain, and they are more theoretically complete.
In addition, the error between the guess of the initial state and its real value will influence the final DOA tracking accuracy since the DOA tracking system has high nonlinearities. If the error is large enough, the tracking results will even be diverged [
30]. Under this circumstance, before operating a DOA tracking algorithm, the initial MSEM should be set properly. However, in the real DOA tracking scenario, it is almost impossible to obtain an accurate error covariance matrix since the real initial states cannot be accurately obtained. In addition, the uncertain underwater environment always affects the state estimating results and makes the initial MSEM much harder to accurately predetermine. To deal with this problem, some researchers suggested utilizing a large guess of the initial MSEM to make the tracking system have fast converging speed and to deal with the large error between the initial guesses of the states and their real values. However, since the underwater target DOA tracking system has high nonlinearities, setting a large guess of the initial MSEM sometimes makes the whole tracking procedure become unstable or even diverge. As a consequence, how to set a proper guess of the initial MSEM with respect to the error of the initial guess of the state and its real value is still an open question. Usually, the initial MSEM is set by engineering experience, which is similar to an expert system that tries to have common solutions. Although some adaptive tracking techniques have been designed to weaken the influences by the initial error [
31], the unproperly set initial MSEM still affects the overall tracking performance. Under these circumstances, a robust and accurate technique for properly setting the guess of the initial MSEM is necessary. Usually, the traditional Bayesian estimating techniques rely heavily on the mathematical model of the systems or parameters to be estimated, but the guess of the initial MSEM does not have a determined and accurate mathematical model with respect to the system state, which makes the traditional methods fail. However, the value of the guess of the initial MSEM has a relationship with the theoretical measurements calculated by the state by the measurement model, initial guess of the state, and its real value. Under this circumstance, the data characteristics other than the mathematical characteristics of the guess of the initial MSEM can be analyzed and utilized. As a result, although the traditional techniques have few general solutions for the problem of properly setting the guess of the initial MSEM, the latest data-driven AI techniques allow the problem discussed above to be solved.
Except for depending heavily on the mathematical derivations, the AI techniques can only rely on the statistical characteristics to infer the inner nonlinear relationship between the inputs and the outputs from a certain system. As a result, the AI techniques are more suitable for the problems that are hard to be mathematically or analytically depicted but have plenty of data resources. After the back propagated (BP) training method was proposed by Rumelhart et al. [
32] and after the deep learning scheme that brought the deep artificial neural network (DANN) into light by Hinton et al. [
33], the DANN has shown its powerful abilities in many fields, such as automation, parameter estimation, target tracking, etc. Among all of the DANNs, the deep convolutional neural networks (DCNNs) and the variations of the DCNNs (i.e., Resnet [
34], Senet [
35]) are the most notable ones, with robust and accurate performances, especially for regression and classification problems that are hard to be analytically modeled. By adopting the convolutional and pooling ideas into one DANN, the DCNN can be modeled much deeper and can easily be trained. Based on the DCNN technique, Lecun et al. [
36] proposed a DCNN named Lennet-5 to deal with the digital image classification task. Ref. [
37] considered the training efficiency and the gradient vanishing problem caused by the DCNNs and proposed the shortcut concept to make the DCNNs have a much deeper structure so that the DCNNs can deal with more complicated classification and regression issues. Ref. [
38] considered that the different features may have different weights during the training process of the designed DCNNs and proposed an attention-based scheme to make the designed DCNNs more robust and accurate. Besides the principle developments of the DCNNs, the applications of them have also attracted a number of researchers from various fields, especially from the field of underwater target localization, detection, classification, and tracking [
37,
38,
39,
40,
41,
42,
43]. Niu et al. [
37,
38,
39,
40] have published a series of research studies to make the underwater target localization task more accurate and robust to the uncertain underwater environment. Wang et al. [
41,
42] utilized the DCNNs technique in estimating the unknown parameters in the underwater acoustical channel. Based on the DCNNs technique, Ref. [
40] developed intelligent target classification algorithms that can obtain higher accuracy and classification speed than the traditional methods. Ref. [
43] proposed a DCNN-based seabed parameters inversion method. However, to the best of the authors’ knowledge, very few research studies have considered using the advanced DCNN technique for the underwater target DOA tracking problem. As a result, the potential and strength of the DCNNs in the underwater target DOA tracking scenario, especially in dealing with the proper setting of the guess of the initial MSEM, have not been proven yet.
Based on the above analysis, an AI-aided variational Bayesian extended Kalman filter (AI-VBEKF)-based robust direction-of-arrival (DOA) technique is proposed to make reliable estimations of the bearing angle of an uncooperative underwater target with uncertain environment noise. The main contributions of this study are summarized as follows.
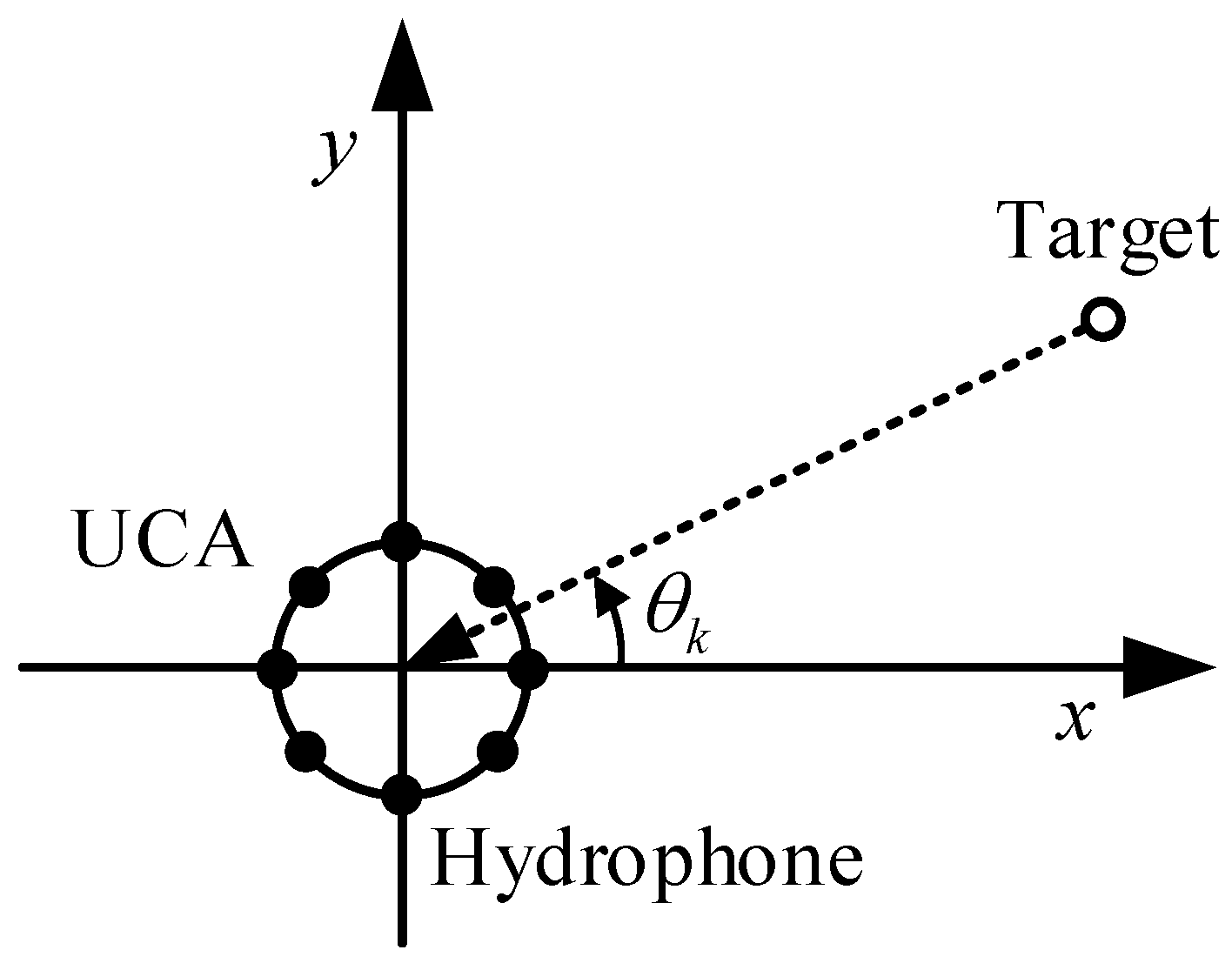
Firstly, a uniform circular array (UCA) is considered to provide measurements of the underwater target. By adopting the UCA as the measurement system, the port and starboard ambiguity problem is overcome. In addition, the uniform aperture at all bearing angles is processed.
Secondly, considering the effects caused by the unproperly set guess of the initial MSEM, an attention-based DCNN is designed to make reliable initial guesses of it and to make the later DOA tracking process steady and accurate.
Thirdly, considering that the unknown underwater disturbance can sometimes make the measurement noise uncertain, the AI-VBEKF is designed to robustly estimate the bearing angle of the underwater target with a shifting covariance matrix of the uncertain measurement noise.
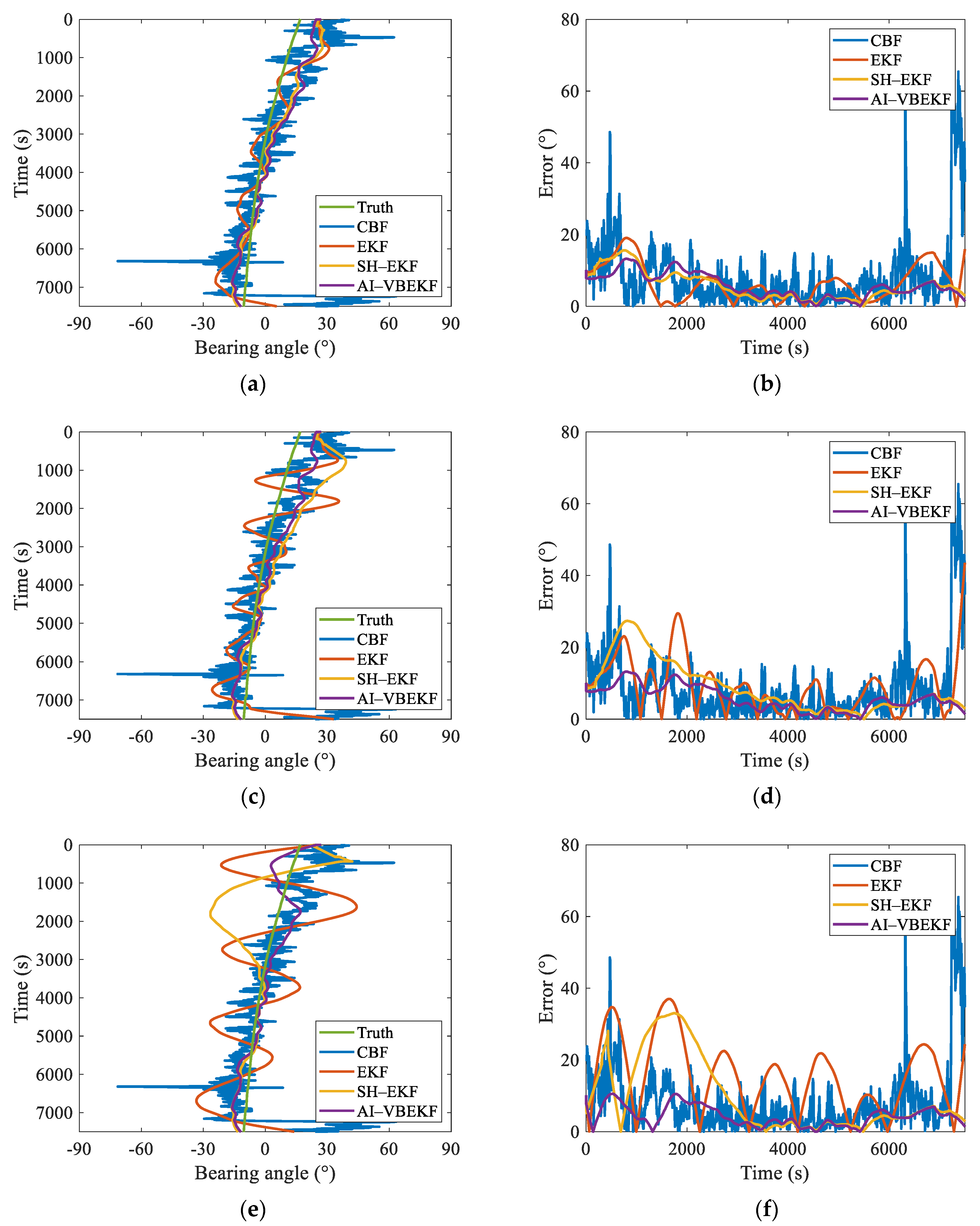
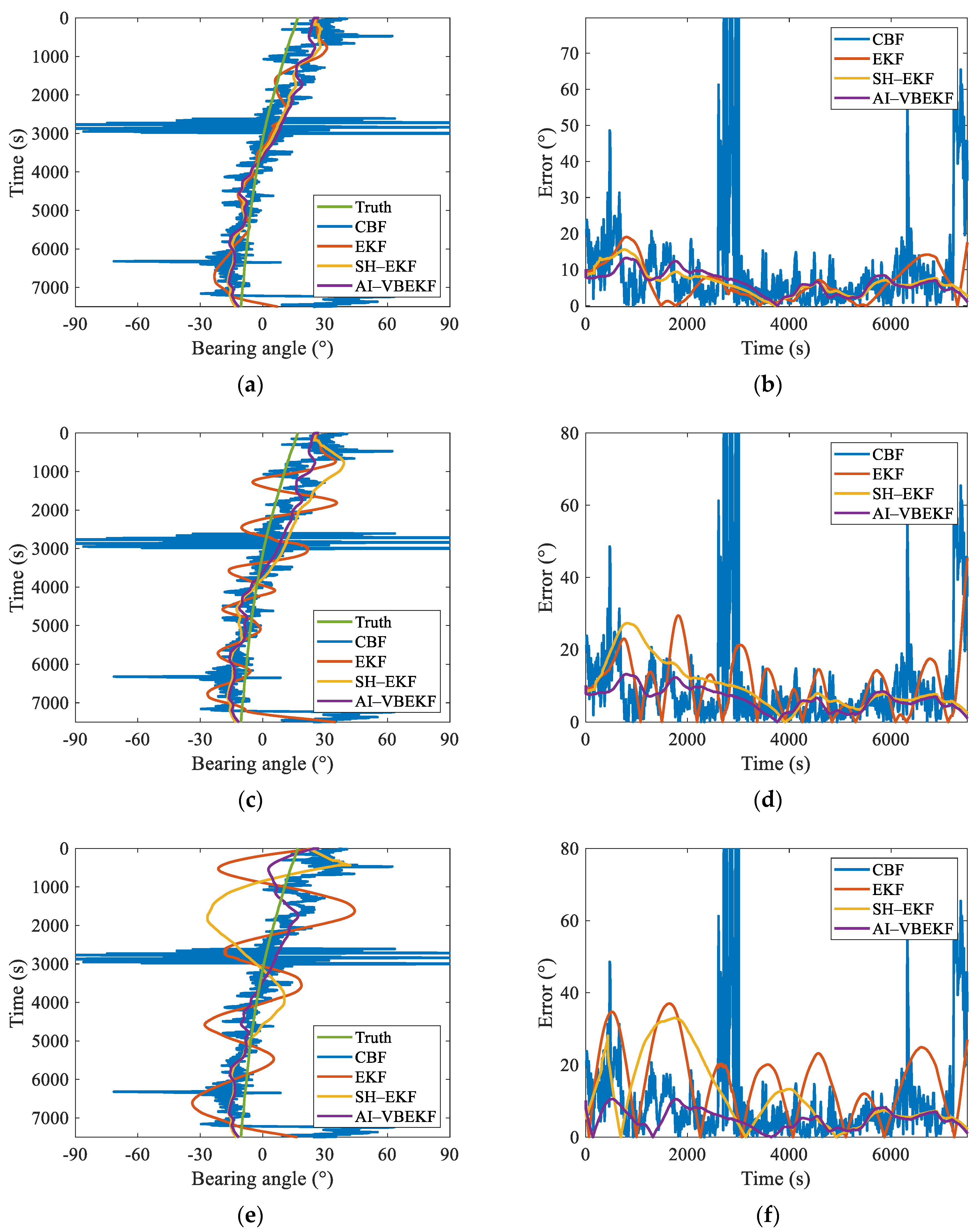
Finally, based on the sea trail data from the South China Sea in July 2021, the proposed AI-VBEKF is verified. The robust and accurate estimation results proved the superior characteristics of the proposed DOA tracking method.
The remainder of this paper is organized as follows:
Section 2 shows the kinematic model and the measurement model of the DOA tracking problem. In
Section 3, the VB-EKF using a UCA is derived first. In addition, the attention-based DCNN is proposed to make a good estimation of the guess of the initial MSEM. Then, based on the VB-KEF and proposed DCNN, the whole frame of the AI-VBKEF is proposed. In
Section 4, the simulation and experiment verification results are shown. Finally, the conclusions are drawn in
Section 5.
3. Methods
3.1. EKF for DOA Tracking
Since the measurement model depicted by Equation (9) has high nonlinearities, the extended Kalman filter (EKF) scheme is used to derived a DOA tracking algorithm in this section.
From Equation (1), the one-step prediction of the state estimate
is depicted as:
where
is the state transition matrix given by Equation (2), and
is the state estimate at tracking step
k − 1. The one-step prediction of the MSEM
is expressed as:
where
is the MSEM at step
k − 1,
is the noise driving matrix given by Equation (3), and
is the covariance matrix of the process noise.
Then, considering the UCA-based measurement model given in Equation (9), the Kalman filter gain
is expressed as:
where
is the first order Taylor expansion of the nonlinear measurement model.
is the MNCM. According to Equation (9),
can be calculated as:
The elements of the matrix
(
,
) are given by [
44]:
where
denotes the estimate of the target signal, which is given by [
45]:
where
is the predicted bearing angle, i.e., the first term of
,
is obtained by using Equations Equations (5) and (8)
and
denote the conjugate transposition and the Hilbert transform, respectively.
The state estimate
at tracking step
k is expressed as:
where
is the measurement of the UCA at step
k. The one-step prediction of MSEM
is modified by
, i.e.,
where
denotes the MSEM at tracking step
k. From Equations (10)–(17), the current bearing angle estimation can be calculated by the inputs of
and
.
From the above analysis, the DOA tracking process not only depends on the measurements but also utilizes the target’s prior motion information. Therefore, the DOA tracking techniques can be robust to the target’s motion; especially, the kinematic model of the target is accurate. However, from Equation (12), it is obvious that the measurement noise will affect the Kalman gain, which will hugely influence the final tracking precision. In addition, from Equation (10), it is obvious that the initial values of the state and MSEM will influence the final tracking accuracy. As a result, in the scenario of accurate and robust underwater DOA tracking, both the uncertain measurement noise and proper setting of the and need to be considered.
3.2. VB-EKF for Robust DOA Tracking
Regarding the measurement model with high nonlinearity depicted by Equation (7), the extended Kalman filter (EKF) technique is used for DOA tracking in this section. Furthermore, considering the fluctuations of the MNCM caused by the unknown underwater environment, the variational Bayesian approach is utilized to improve the tracking performance by estimating the MNCM. Thus, the VB-EKF for DOA tracking using the UCA is proposed, and the details are given as follows.
3.2.1. Choice of Prior Distribution
In the framework of the standard EKF [
5], the one-step predicted probability density distribution (PDF)
and the likelihood PDF
are assumed to be subject to Gaussian distributions as follows:
where
denotes the PDF of the Gaussian distribution with mean
μ and covariance matrix
Σ, and
is the nonlinear measurement function given by Equation (7).
and
denote the one-step prediction of state and MSEM, respectively, which are given by Equations (10) and (11).
In order to infer
along with
, a conjugate prior distribution needs to be selected for the fluctuant MNCM
since a conjugate distribution can guarantee the same functional forms of the prior distribution and the posterior distribution. In the Bayesian theory, inverse Wishart distribution is usually used as the conjugate prior to the covariance matrix of a Gaussian distribution with known mean [
6]. Since
is the covariance matrix of Gaussian distribution, the prior distribution
is selected as an inverse Wishart distribution given by:
where
denotes the PDF of the inverse Wishart distribution with degree of freedom (dof)
λ and inverse scale matrix
Ψ [
3],
and
are the dof and the inverse scale matrix of
, respectively.
The posterior distribution
is also subject to an inverse Wishart distribution as follows:
To guarantee that
is the inverse Wishart distribution given by Equation (20), the previous approximate posteriors is spread through a forgetting factor
, which indicates the extent of the time-fluctuations of the MNCM. Then, the prior dof
and the prior inverse scale matrix
are given as follows:
where n denotes the order of the MNCM
.
3.2.2. Variational Approximations of Posterior PDFs
According to the variational Bayesian approximation, the joint posterior PDF of the state
and the MNCM
is approximated to
where
and
are the approximate posterior PDF of
and
, respectively. The variational Bayesian approximation is formed by minimizing the Kullback–Leibler divergence (KLD) between the true joint distribution
and the approximate distribution
, i.e.,
where
denotes the KLD between
and
, and
The optimal solution of Equation (25) satisfies the following Equations [
4]:
where
and
denote the expectation with regard to
and
, respectively, and
and
denote the constants with respect to
and
, respectively. Since the variational parameters of
and
are coupled, a fix-point iteration process is applied to solve Equations (27) and (28), i.e., the approximate posterior PFD
is updated to
at the
-th iteration using the posterior PDF
, and
is updated to
using the posterior
.
According to Equations (18)–(20), the joint PDF is expressed as
The posterior
is updated according to Equations (12), (16) and (17) as:
where the mean vector
and the covariance matrix
are given as follows:
where
denotes the Jacobian matrix of the measurement function.
is obtained by substituting
into
given by Equation (13).
Based on the new estimated state
and MSEM
, a more accurate approximation of
can be obtain by performing linearization with
[
6], i.e.,
The estimate of the signal
is also used instead of the real one to calculate the measurement function
by using Equation (7). Thus, Equation (32) is upgraded to
According to Equations (18)–(20),
is given by
where
Similar to Equation (34),
is linearized as
where
denotes the Jacobian matrix of the measurement function
at
, and
is obtained by substituting
into Equation (13). Substituting Equation (38) into Equation (37), we obtain:
From Equation (36),
is updated as
where the dof
and the inverse scale matrix
are given as follows:
Then, according to Equation (29),
is given by:
where
is given by:
The modified one step predicted PDF
at the I + 1th iteration is defined as:
where the modified MNCM
are formulated as:
Finally, after
N fixed-point iterations, the variational approximations of the posterior PDFs are given as follows:
Combining the EKF depicted by Equations (10)–(17) and the VB estimating technique, the state can be robustly estimated under uncertain measurement noise.
3.3. AI-VBEKF for Robust DOA Tracking
Considering the high nonlinearities of the measurement model by Equation (7), the initial values will affect the tracking results. Since the EKF is based on the Taylor series expansion to linearize the nonlinear system model, the truncation error will become unacceptable if the error between the initial guess of the state and its real value is quite large. In addition, if the initial MSEM cannot be set properly, the DOA tracking results will be in low accuracy or even diverged. In the real underwater DOA tracking scenario, the initial DOA of the target can be obtained by traditional DOA estimation methods (i.e., CBF, MVDR, MUSIC, et.al.), but the initial MSEM cannot be determined since the initial error between the real state and the estimated one is unknown. If the initial MSEM is set too small, the DOA tracking algorithm will converge very slowly or cannot converge at all. On the contrary, if the initial MSEM is set too large, the DOA tracking process will be soon diverged since the Kalman gain will become uncontrolled during the measurement update steps for nonlinear tracking systems. As a result, a proper preset initial MSEM not only affects the final DOA tracking accuracy but also determines the convergence of the total tracking procedure. However, in the real DOA tracking scenario, the initial MSEM can only be set by engineering experience. To solve this problem and deal with the uncertain measurement noise, an AI-aided robust DOA tracking algorithm is proposed in this subsection.
In order to minimalize the final DOA tracking error caused by the inaccurate initial guess of the MSEM, an AI-aided robust DOA tracking algorithm is proposed by this subsection. Firstly, considering that the different initial state guesses will lead to different theoretical measurement calculations by the measurement model, the error between the real measurements and the theoretical ones contains the information of the error of the initial guess of the MSEM between its true value. Thus, based on the difference between the theoretical measurement calculations and the real measurements, the initial MSEM can be estimated via deep learning techniques. By utilizing the covariance matrix of the difference between the theoretical measurement calculations and the real measurements from all bearing angles with different initial errors as inputs, an attention-based deep convolutional neural network is proposed by this subsection to output reliable initial MSEM. Then, utilizing the estimated MSEM as the input of the VB-EKF, the AI-VBEKF for a robust DOA tracking algorithm is finally carried out in this subsection.
3.3.1. Input Data Processing
Supposing the initial state is selected as:
Using the measurement model depicted by Equation (9), the error between the theoretical measurement and the real measurement can be presented as:
Using Equation (50), the quadratic form of the error between the theoretical measurement and the real measurement can be presented as:
where
is a matrix with the dimension of
.
From Equation (7), it can be found that the real measurement has a strong relationship with the real DOA angle of the target and its angular velocity. When the value of the real state changes, the measurement will also change. In addition, the estimated state influences the value of the theoretical measurement computed by the measurement model. Thus, the computed has the information of the difference of the real values of the state and its estimated values. From the view of data-driven techniques, can be utilized to output this error and can make good estimation of the guess of the initial MSEM.
In addition, from Equation (51), it is obvious that the size of depends on the number of the snapshots in one measurement time interval. In order to make reliable DOA estimations and DOA tracking, the value of M is usually set high during one measurement updating step (i.e., the same as the sampling rate of the sonar system). As a result, the size of is usually large, and the nonlinear relationship between the real guess of the initial MSEM and its real values is hard to be dug out by shallow BP neural networks. In order to make sufficient utilization of the data resources obtained by the sonar system and make reliable estimations of the guess of the initial MSEM, an attention-based DCNN is proposed in the following subsection.
3.3.2. Attention-Based Deep Convolutional Neural Network
As mentioned in
Section 3.3.1, since the traditional BP neural networks have limited ability in dealing with a large matrix and the computed
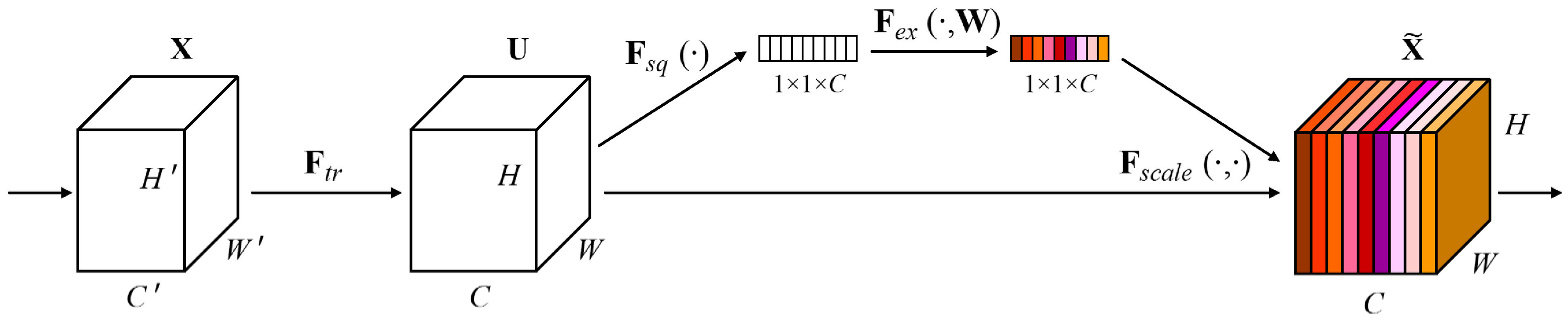
has the form of a symmetric matrix such as an image, an attention-based DCNN is proposed by this subsection. Among the latest DCNNs, the attention-based DCNN is the most popular one and has been utilized in a number of target classification, localization, and tracking missions. Unlike the basic DCNN that cannot be developed very deep and the Resnet that cannot give different features different weights, which make the overall performance degrade, the attention-based DCNN not only utilizes the advantages of the Resnet to make the DCNN much deeper than the traditional ones, but also develops the attention scheme that values different features with different weights to make the DCNN have better tracking performance. The basic structure of the attention-based DCNN is shown in
Figure 2 [
35].
From
Figure 2 [
35], the main difference between the attention-based DCNN and the other DCNNs is the “squeeze and excitation” block. For any given data with the dimension
, firstly a transformation mapping
is operated to generate the feature maps U, which can be depicted as:
From Equation (52), it is obvious that the operation has no difference with other DCNNS (i.e., is the traditional DCNN or Resnet). As a result, the attention-based DCNNs can be fitted into any existing DCNNs to enhance their performance.
After the
mapping operation, the “squeeze and excitation” block can operate. Firstly, the feature maps U is operated via a squeeze process that aims to compress the information of the feature maps into a one-dimensional vector. By operating in this way, the compressed feature of every channel of the feature maps U is generated. The squeeze operation can be depicted as the following equation:
where
is the
-th channel of the feature maps U, and
is the squeeze operation.
From Equation (53), it can be found that the squeeze operation operates on every feature map with the dimension of
. After the squeeze operation, every feature map of U turns to a real number so that the information is maximally compressed. Then, the excitation operation is processed to calculate the weights of every feature map. The excitation operation aims to fully capture the channel-wise dependencies of the input feature maps U. By utilizing full connection layers and the ReLU activation function, the nonlinear mapping process made by the excitation operation can be depicted as:
where
is the output of the excitation operation,
is the excitation operation,
is the first fully connected (FC) layer that can be regarded as a nonlinear operation to extract the inner information of the input
,
is the ReLU activating function,
is the second FC layer, and
is a typical activating function that can be selected as a sigmoid function in general.
From Equation (54), after the excitation operation, the inner relationships between every feature map in U can be represented by
. Thus,
is the core of the attention-based DCNN, for it depicts the weights of every feature inside the whole feature maps U shown by Equation (52). As long as
is obtained, the weights vector of every feature map is known. As a result, the final output of the attention-based DCNN can be represented as:
where
is the final scaling operation that refers to the channel-wise multiplication between the
-th element of the output of the excitation operation and the
-th feature map of U. It is obvious from Equation (52) and Equation (55) that the original feature maps U is weighted by the “squeeze and excitation” block. This weighting mechanism is similar to paying attention to different features such that the whole deep learning technique is called the attention-based DCNN.
From Equation (52) and the above statements, the first mapping operation
can be any type of DCNN technique. As the Resnet has proven its superior performance in underwater target localization missions [
38], the
is selected as the residual model [
38] and the attention-based DCNN blocks combined with the residual model can be shown as the following block as shown in
Figure 3:
Equations (52)–(55) represent the whole theoretical derivations of the attention-based DCNN. In addition, since this DCNN is mainly based on the “squeeze and excitation” block, the mentioned attention-based DCNN is also called the Senet. Here, substitute Equation (51) into Equation (52), and change the initial input to . The Senet can then be directly utilized to analyze the inner nonlinear relationship between the real values of the state and its estimated values.
3.3.3. Design of the AI-VBEKF
From Equation (9), if the measurement noise varies for the same initial error between the initial guess of the state and its real value,
computed by Equation (51) will change by different
. Supposing the number of varying covariance matrix of
is
and the measurement
has snapshots with the number of M,
will have the dimensions of
. Then, substituting Equation (51) into Equation (52) and changing the initial input
to
with
covariance matrix of the measurement noise and M snapshots, Equation (52) can be represented as:
In addition, if the transformation mapping
is chosen as the residual model, and the following steps are the same as the aforementioned ones (Equations (53)–(55)), the attention-based DCNN combined with the residual model can be proposed. By using
with different
as inputs and the differences between the initial guess of the state and its real value as outputs, the attention-based DCNN for the initial guess of the error of the covariance matrix of the states can be proposed as in
Table 1.
Then, by combining the proposed attention-based DCNN, the EKF DOA tracking scheme and the VB robust estimating technique, the AI-VBEKF, which has the abilities of estimating the guess of the initial MSEM and performing robust DOA tracking, can be depicted as Algorithm 1.
| Algorithm 1: AI-VBEKF |
Input.
Calculate as Equation (50).
Calculate as Equation (51).
Initial MSEM estimation by attention-based DCNN.
Inputs: , , , , , , ρ, N.
Time update
.
.
,.
Iteration measurement update
Initialization: , .
For
Update
is calculated by Equation (7), is calculated by Equation (13).
,
,
.
Update
is calculated by Equation (7), is calculated by Equation (13).
,
, ,
.
End for
, , , .
Outputs: , , , . |
3.3.4. Performance Metrics
In the underwater target DOA tracking scenario, the angular velocity of the target is quite small, for the target usually moves at a relatively far distance from the observer. To obtain the accurate initial MNCM of the target, only the difference between the real initial angle and its estimation will be determined by the attention-based DCNN. According to the goal of the estimation of the initial guess of the error of the covariance matrix of the states, the metrics for quantifying the performance of the proposed attention-based DCNN can be described as:
where
is the estimated initial guess of the DOA angle, and
is the real initial values of the DOA angle and its angular velocity.
is the total number of the training data.