Observation of Near-Inertial Internal Gravity Waves in the Southern South China Sea
Abstract
1. Introduction
2. Data and Methods
2.1. Data
2.2. Band-Pass Filtering
2.3. Modal Decomposition
3. Results
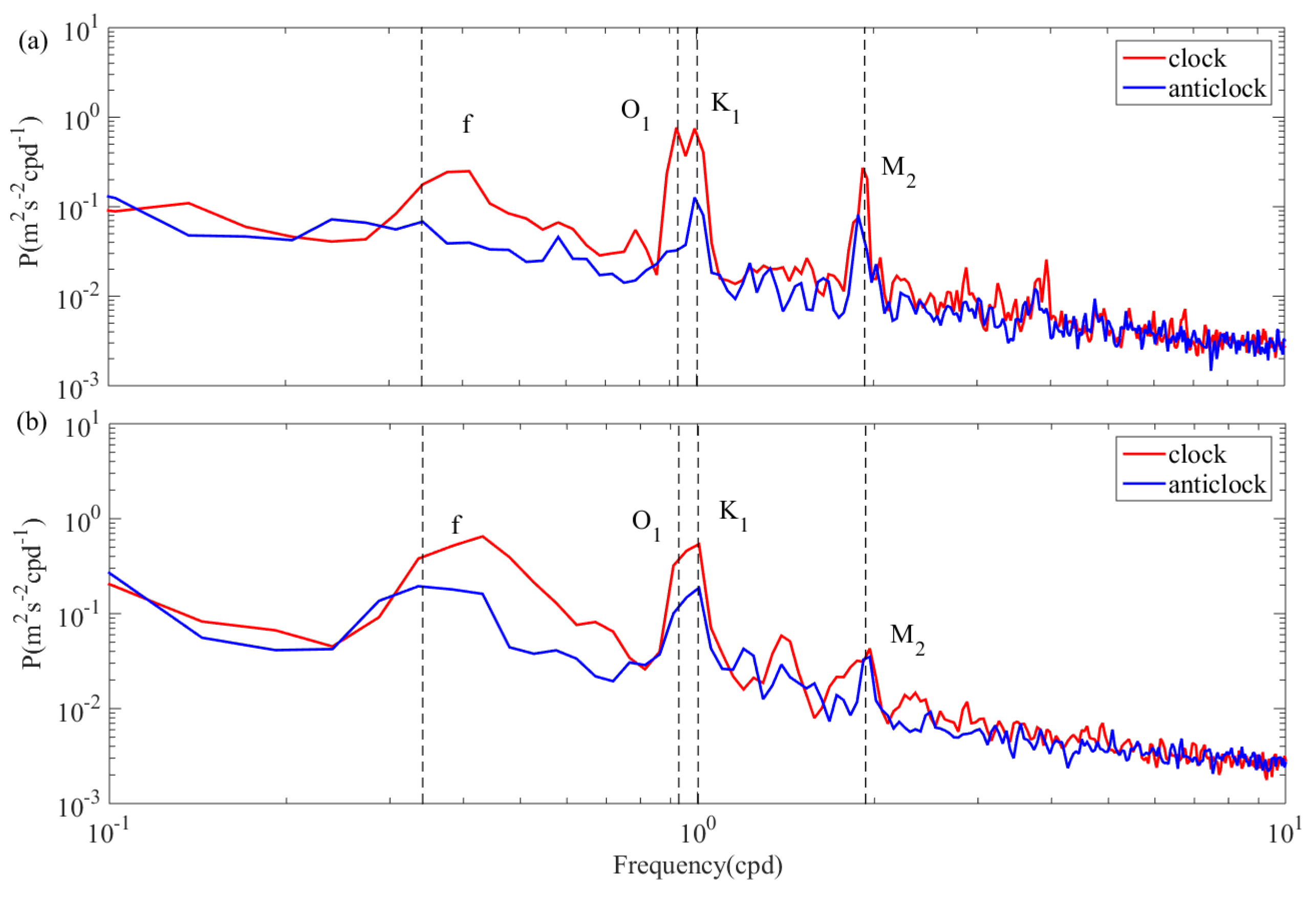
3.1. Current Spectra
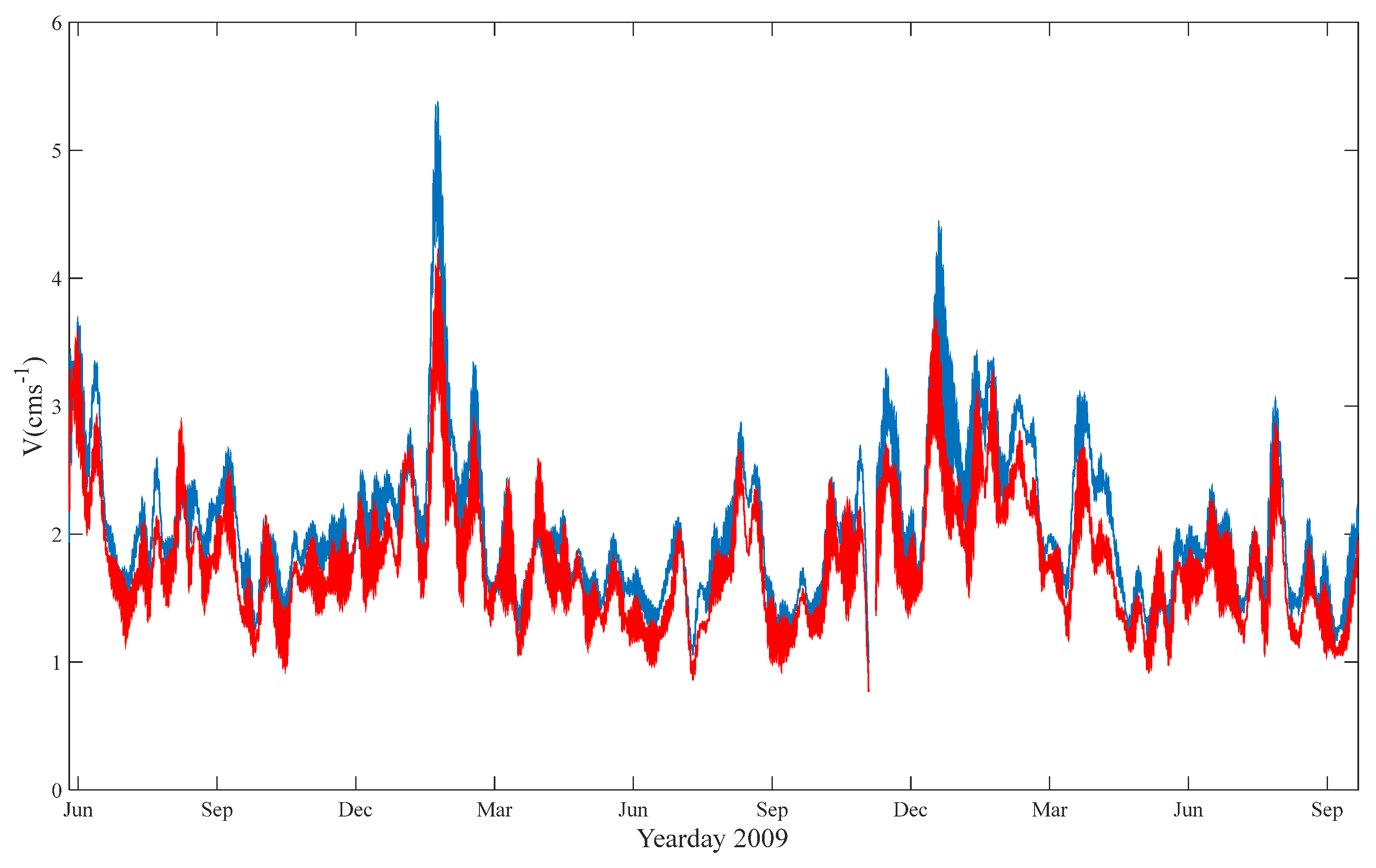
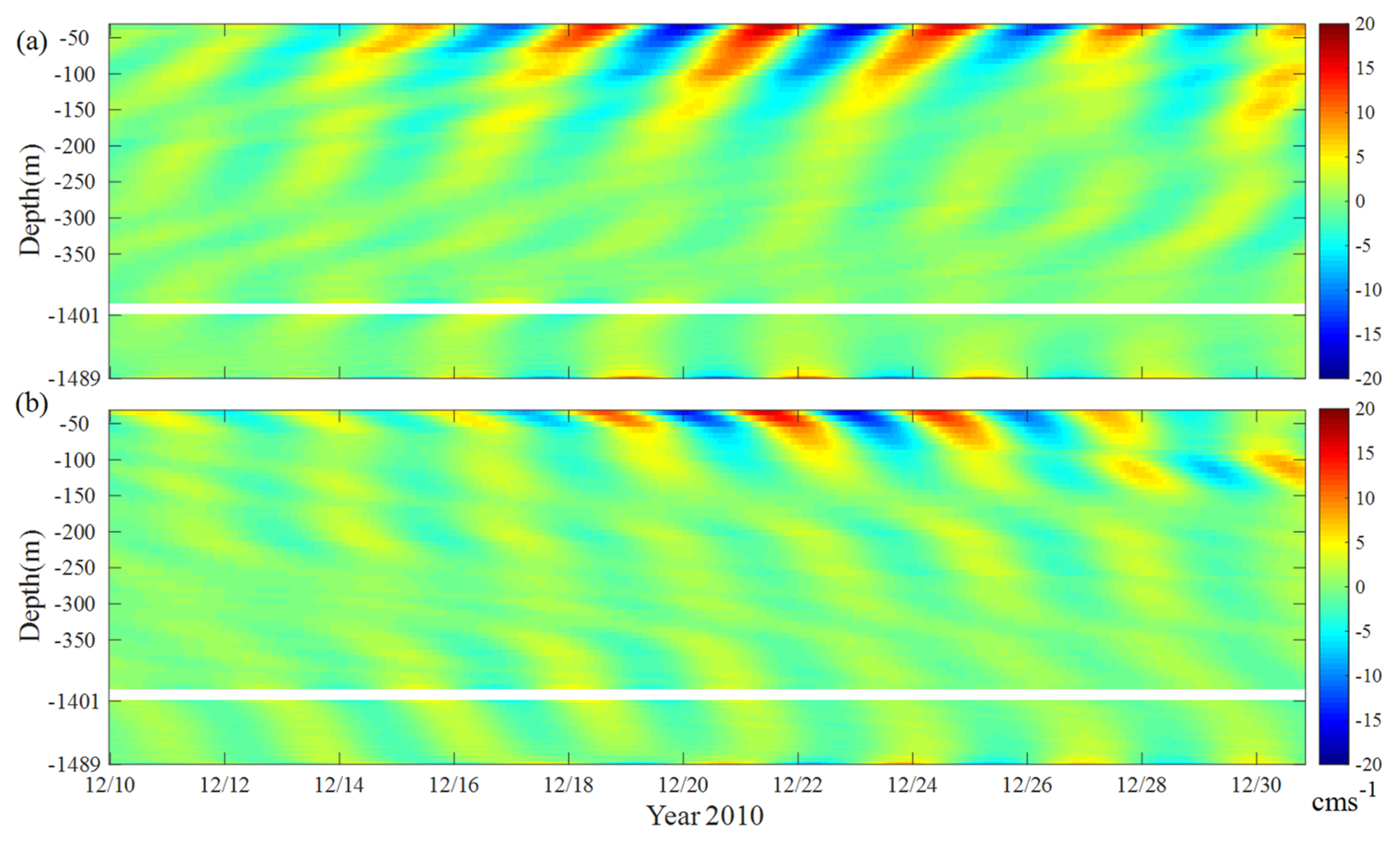
3.2. Characteristics of NIWs
3.3. Modal Contents of NIWs
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Alford, M.H.; Gregg, M.C. Near-inertial mixing: Modulation of shear, strain and microstructure at low latitude. J. Geophys. Res. Ocean. 2001, 106, 16947–16968. [Google Scholar] [CrossRef]
- Ferrari, R.; Wunsch, C. Ocean Circulation Kinetic Energy: Reservoirs, Sources, and Sinks. Annu. Rev. Fluid Mech. 2009, 41, 253–282. [Google Scholar] [CrossRef]
- Xie, X.; Liu, Q.; Shang, X.; Chen, G.; Wang, D. Poleward propagation of parametric subharmonic instability-induced inertial waves. J. Geophys. Res. Ocean. 2016, 121, 1881–1895. [Google Scholar] [CrossRef]
- Xie, X.-H.; Shang, X.-D.; Chen, G.-Y.; Sun, L. Variations of diurnal and inertial spectral peaks near the bi-diurnal critical latitude. Geophys. Res. Lett. 2009, 36, 02606. [Google Scholar] [CrossRef]
- Nikurashin, M.; Ferrari, R. Radiation and dissipation of internal waves generated by geostrophic gotions impinging on small-scale topography: Application to the Southern Ocean. J. Phys. Oceanogr. 2010, 40, 2025–2042. [Google Scholar] [CrossRef]
- Alford, M.H.; Cronin, M.; Klymak, J. Annual Cycle and Depth Penetration of Wind-Generated Near-Inertial Internal Waves at Ocean Station Papa in the Northeast Pacific. J. Phys. Oceanogr. 2012, 42, 889–909. [Google Scholar] [CrossRef]
- Liang, X.; Thurnherr, A. Eddy-Modulated Internal Waves and Mixing on a Midocean Ridge. J. Phys. Oceanogr. 2012, 42, 1242–1248. [Google Scholar] [CrossRef]
- Xu, Z.; Yin, B.; Hou, Y.; Xu, Y. Variability of internal tides and near-inertial waves on the continental slope of the northwestern South China Sea. J. Geophys. Res. Ocean. 2013, 118, 197–211. [Google Scholar] [CrossRef]
- Le Boyer, A.; Alford, M.H.; Pinkel, R.; Hennon, T.D.; Yang, Y.J.; Ko, D.; Nash, J. Frequency Shift of Near-Inertial Waves in the South China Sea. J. Phys. Oceanogr. 2020, 50, 1121–1135. [Google Scholar] [CrossRef]
- Wang, S.; Cao, A.; Chen, X.; Li, Q.; Song, J. On the resonant triad interaction over mid-ocean ridges. Ocean Model. 2021, 158, 101734. [Google Scholar] [CrossRef]
- Pollard, R.T.; Millard, R.C., Jr. Comparison between observed and simulated wind-generated inertial oscillations. Deep. Sea Res. Oceanogr. Abstr. 1970, 17, 153–175. [Google Scholar] [CrossRef]
- Jiang, J.; Lu, Y.; Perrie, W. Estimating the energy flux form the wind to ocean inertial motions: The sensitivity to surface wind fields. Geophys. Res. Lett. 2005, 32, L15610. [Google Scholar] [CrossRef]
- Furuichi, N.; Hibiya, T.; Niwa, Y. Model-predicted distribution of wind-induced internal wave energy in the world’s oceans. J. Geophys. Res. Atmos. 2008, 113, C09034. [Google Scholar] [CrossRef]
- Rimac, A.; von Storch, J.-S.; Eden, C.; Haak, H. The influence of high-resolution wind stress field on the power input to near-inertial motions in the ocean. Geophys. Res. Lett. 2013, 40, 4882–4886. [Google Scholar] [CrossRef]
- Wunsch, C. The Work Done by the Wind on the Oceanic General Circulation. J. Phys. Oceanogr. 1998, 28, 2332–2340. [Google Scholar] [CrossRef]
- Alford, M.H.; MacKinnon, J.A.; Simmons, H.L.; Nash, J.D. Near-Inertial Internal Gravity Waves in the Ocean. Annu. Rev. Mar. Sci. 2016, 8, 95–123. [Google Scholar] [CrossRef]
- Moehlis, J.; Smith, S.L. Radiation of Mixed Layer Near-Inertial Oscillations into the Ocean Interior. J. Phys. Oceanogr. 2001, 31, 1550–1560. [Google Scholar] [CrossRef]
- Simmons, H.; Alford, M. Simulating the Long-Range Swell of Internal Waves Generated by Ocean Storms. Oceanography 2012, 25, 30–41. [Google Scholar] [CrossRef]
- Jochum, M.; Briegleb, B.P.; Danabasoglu, G.; Large, W.G.; Norton, N.J.; Jayne, S.R.; Alford, M.H.; Bryan, F.O. The Impact of Oceanic Near-Inertial Waves on Climate. J. Clim. 2013, 26, 2833–2844. [Google Scholar] [CrossRef]
- Alford, M.H.; Peacock, T.; MacKinnon, J.A.; Nash, J.D.; Buijsman, M.C.; Centurioni, L.R.; Chao, S.-Y.; Chang, M.-H.; Farmer, D.M.; Fringer, O.B.; et al. The formation and fate of internal waves in the South China Sea. Nature 2015, 521, 65–69. [Google Scholar] [CrossRef]
- Gao, J.; Ma, X.; Dong, G.; Chen, H.; Liu, Q.; Zang, J. Investigation on the effects of Bragg reflection on harbor oscillations. Coast. Eng. 2021, 170, 103977. [Google Scholar] [CrossRef]
- Garrett, C. What is the “near-inertial” band and why is it different from the rest of the internal wave spectrum? J. Phys. Oceanogr. 2001, 31, 962–971. [Google Scholar] [CrossRef]
- Alford, M.H. Improved global maps and 54-year history of wind-work on ocean inertial motions. Geophys. Res. Lett. 2003, 30, 1424. [Google Scholar] [CrossRef]
- Mayer, D.A.; Mofjeld, H.O.; Leaman, K.D. Near-Inertial Internal Waves Observed on the Outer Shelf in the Middle Atlantic Bight in the Wake of Hurricane Belle. J. Phys. Oceanogr. 1981, 11, 87–106. [Google Scholar] [CrossRef]
- D’Asaro, E.A. The Energy Flux from the Wind to Near-Inertial Motions in the Surface Mixed Layer. J. Phys. Oceanogr. 1985, 15, 1043–1059. [Google Scholar] [CrossRef]
- Cuypers, Y.; Le Vaillant, X.; Bouruet-Aubertot, P.; Vialard, J.; McPhaden, M.J. Tropical storm-induced near-inertial internal waves during the Cirene experiment: Energy fluxes and impact on vertical mixing. J. Geophys. Res. Ocean. 2013, 118, 358–380. [Google Scholar] [CrossRef]
- Cao, A.; Guo, Z.; Song, J.; Lv, X.; He, H.; Fan, W. Near-Inertial Waves and Their Underlying Mechanisms Based on the South China Sea Internal Wave Experiment (2010–2011). J. Geophys. Res. Ocean. 2018, 123, 5026–5040. [Google Scholar] [CrossRef]
- Wang, G.H.; Su, J.L.; Ding, Y.H.; Chen, D. Tropical cyclone genesis over the south China sea. J. Mar. Syst. J. Eur. Assoc. Mar. Sci. Tech. 2007, 68, 318–326. [Google Scholar] [CrossRef]
- Sun, L.; Zheng, Q.A.; Wang, D.X.; Hu, J.; Tai, C.K.; Sun, Z. A case study of near-inertial oscillation in the South China Sea using mooring obser-vations and satellite altimeter data. J. Oceanogr. 2011, 67, 677–687. [Google Scholar] [CrossRef]
- Yang, B.; Hou, Y. Near-inertial waves in the wake of 2011 Typhoon Nesat in the northern South China Sea. Acta Oceanol. Sin. 2014, 33, 102–111. [Google Scholar] [CrossRef]
- Ma, Y.; Zhang, S.; Qi, Y.; Jing, Z. Upper ocean near-inertial response to the passage of two sequential typhoons in the northwestern South China Sea. Sci. China Earth Sci. 2019, 62, 863–871. [Google Scholar] [CrossRef]
- He, H.; Cao, A.; Wang, Y.; Song, J. Evolution of oceanic near-inertial waves induced by typhoon Sarika (2016) in the South China Sea. Dyn. Atmos. Ocean. 2022, 100, 101332. [Google Scholar] [CrossRef]
- Gao, J.; Ma, X.; Zang, J.; Dong, G.; Ma, X.; Zhu, Y.; Zhou, L. Numerical investigation of harbor oscillations induced by focused transient wave groups. Coast. Eng. 2020, 158, 103670. [Google Scholar] [CrossRef]
- Guan, S.; Zhao, W.; Huthnance, J.; Tian, J.; Wang, J. Observed upper ocean response to typhoon Megi (2010) in the Northern South China Sea. J. Geophys. Res. Ocean. 2014, 119, 3134–3157. [Google Scholar] [CrossRef]
- Yang, B.; Hou, Y.J.; Hu, P.; Liu, Z.; Liu, Y. Shallow Ocean response to tropical cyclones observed on the continental shelf of the north-western South China Sea. J. Geophys. Res. Ocean. 2015, 120, 3817–3836. [Google Scholar] [CrossRef]
- Shang, X.; Liu, Q.; Xie, X.; Chen, G.; Chen, R. Characteristics and seasonal variability of internal tides in the southern South China Sea. Deep. Sea Res. Part I Oceanogr. Res. Pap. 2015, 98, 43–52. [Google Scholar] [CrossRef]
- Liu, Q.; Xie, X.; Shang, X.; Chen, G. Coherent and incoherent internal tides in the southern South China Sea. Chin. J. Oceanol. Limnol. 2016, 34, 1374–1382. [Google Scholar] [CrossRef]
- Liu, J.; He, Y.; Li, J.; Cai, S.; Wang, D.; Huang, Y. Cases Study of Nonlinear Interaction Between Near-Inertial Waves Induced by Typhoon and Diurnal Tides Near the Xisha Islands. J. Geophys. Res. Ocean. 2018, 123, 2768–2784. [Google Scholar] [CrossRef]
- Xu, J.; Huang, Y.; Chen, Z.; Liu, J.; Liu, T.; Li, J.; Cai, S.; Ning, D. Horizontal variations of typhoon-forced near-inertial oscillations in the south China sea simulated by a numerical model. Cont. Shelf Res. 2019, 180, 24–34. [Google Scholar] [CrossRef]
- Li, R.X.; Chen, C.S.; Dong, W.J.; Beardsley, R.C.; Wu, Z.; Gong, W.; Liu, Y.; Liu, T.; Xu, D. Slope-intensified storm-induced near-inertial oscillations in the South China Sea. J. Geophys. Res. Ocean. 2021, 126, e2020JC016713. [Google Scholar] [CrossRef]
- Liu, Q.; Shang, X.D.; Xie, X. Observations of semidiurnal M2 internal tidal parametric subharmonic instability in the north-eastern South China Sea. J. Oceanol. Limnol. 2021, 39, 8. [Google Scholar]
- Chen, G.; Xue, H.; Wang, D.; Xie, Q. Observed near-inertial kinetic energy in the northwestern South China Sea. J. Geophys. Res. Ocean. 2013, 118, 4965–4977. [Google Scholar] [CrossRef]
- Ma, Y.; Wang, D.; Shu, Y.; Chen, J.; He, Y.; Xie, Q. Bottom-reached near-inertial waves induced by the tropical cyclones, Conson and Mindulle, in the South China Sea. J. Geophys. Res. Ocean. 2022, 127, e2021JC018162. [Google Scholar] [CrossRef]
- Cao, A.; Guo, Z.; Pan, Y.; Song, J.; He, H.; Li, P. Near-Inertial Waves Induced by Typhoon Megi (2010) in the South China Sea. J. Mar. Sci. Eng. 2021, 9, 440. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 Global Reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Gill, A.E. Atmosphere-Ocean Dynamics; Academic Press: New York, NY, USA, 1982. [Google Scholar]
- Nash, J.; Alford, M.H.; Kunze, E. Estimating Internal Wave Energy Fluxes in the Ocean. J. Atmos. Ocean. Technol. 2005, 22, 1551–1570. [Google Scholar] [CrossRef]
- Zhao, Z.; Alford, M.H.; Mackinnon, J.A.; Pinkel, R. Long-Range Propagation of the Semidiurnal Internal Tide from the Ha-waiian Ridge. J. Phys. Oceanogr. 2010, 40, 713–736. [Google Scholar] [CrossRef]
- Leaman, K.D.; Sanford, T.B. Vertical energy propagation of inertial waves: A vector spectral analysis of velocity pro-files. J. Geophys. Res. 1975, 80, 1975–1978. [Google Scholar] [CrossRef]
- Gonella, J. A rotary-component method for analyzing meteorological and oceanographic vector time series. Deep Sea Res. Oceanogr. Abstr. 1972, 19, 833–846. [Google Scholar] [CrossRef]
- Gill, A.E. On the Behavior of Internal Waves in the Wakes of Storms. J. Phys. Oceanogr. 1984, 14, 1129–1151. [Google Scholar] [CrossRef]
- Fu, L.-L. Observations and models of inertial waves in the deep ocean. Rev. Geophys. Space Phys. 1981, 19, 141–170. [Google Scholar] [CrossRef]
- Shen, J.; Fang, W.; Zhang, S.; Qiu, Y.; Zhang, J.; Xie, X. Observed Internal Tides and Near-Inertial Waves in the Northern South China Sea: Intensified f-Band Energy Induced by Parametric Subharmonic Instability. J. Geophys. Res. Ocean. 2020, 125, e2020JC016324. [Google Scholar] [CrossRef]
- Park, J.J.; Kim, K.; Schmitt, R.W. Global distribution of the decay timescale of mixed layer inertial motions observed by satellite-tracked drifters. J. Geophys. Res. Atmos. 2009, 114, C11010. [Google Scholar] [CrossRef]
- Dunphy, M.; Lamb, K.G. Focusing and vertical mode scattering of the first mode internal tide by mesoscale eddy interaction. J. Geophys. Res. Ocean. 2014, 119, 523–536. [Google Scholar] [CrossRef]
- Asselin, O.; Thomas, L.; Young, W.; Rainville, L. Refraction and straining of wind-generated near-inertial waves by barotropic eddies. J. Phys. Oceanogr. 2020, 50, 3439–3454. [Google Scholar] [CrossRef]
- Kunze, E. Near-Inertial Wave Propagation in Geostrophic Shear. J. Phys. Oceanogr. 1985, 15, 544–565. [Google Scholar] [CrossRef]












| Mooring | Effective Depths (m) | Sampling Time (h) | Sampling Interval (m) | |
|---|---|---|---|---|
| First Mooring | WHLS75K ADCP | 14~390 | 1 | 8 |
| WHS150K ADCP | 1377~1445 | 0.5 | 4 | |
| Second Mooring | WHLS75K ADCP | 31~415 | 1 | 8 |
| WHS150K ADCP | 1401~1489 | 0.5 | 4 | |
| Kinetic Energy (KJ/m2) | Mode 1 | Mode 2 | Mode 3 | Mode 4 | Sum |
|---|---|---|---|---|---|
| Spring | 0.018 | 0.032 | 0.036 | 0.021 | 0.107 |
| Summer | 0.027 | 0.029 | 0.036 | 0.023 | 0.115 |
| Autumn | 0.015 | 0.043 | 0.037 | 0.025 | 0.120 |
| Winter | 0.083 | 0.085 | 0.089 | 0.067 | 0.324 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Q.; Cui, J.; Shang, X.; Xie, X.; Wu, X.; Gao, J.; Mei, H. Observation of Near-Inertial Internal Gravity Waves in the Southern South China Sea. Remote Sens. 2023, 15, 368. https://doi.org/10.3390/rs15020368
Liu Q, Cui J, Shang X, Xie X, Wu X, Gao J, Mei H. Observation of Near-Inertial Internal Gravity Waves in the Southern South China Sea. Remote Sensing. 2023; 15(2):368. https://doi.org/10.3390/rs15020368
Chicago/Turabian StyleLiu, Qian, Jian Cui, Xiaodong Shang, Xiaohui Xie, Xiangbai Wu, Junliang Gao, and Huan Mei. 2023. "Observation of Near-Inertial Internal Gravity Waves in the Southern South China Sea" Remote Sensing 15, no. 2: 368. https://doi.org/10.3390/rs15020368
APA StyleLiu, Q., Cui, J., Shang, X., Xie, X., Wu, X., Gao, J., & Mei, H. (2023). Observation of Near-Inertial Internal Gravity Waves in the Southern South China Sea. Remote Sensing, 15(2), 368. https://doi.org/10.3390/rs15020368








