Abstract
Soil moisture (SM) has significant impacts on the Earth’s energy and water cycle system. Remote sensing, such as the Soil Moisture Active Passive (SMAP) mission, has delivered valuable estimations of global surface soil moisture. However, it has a 2~3 days revisit time leading to gaps between SMAP areas. To achieve accurate and comprehensive real-time forecast of SM, we propose a spatial–temporal deep learning model based on the Convolutional Gated Recursive Units with Data Integration (DI_ConvGRU) to capture the spatial and temporal variation in SM simultaneously by modeling the influence of adjacent SM values in space and time. Experiments show that the DI_ConvGRU outperforms the ConvGRU with Linear Interpolation (interp_ConvGRU) and the Long Short-Term Memory with Data Integration (DI_LSTM). The best performance (Bias = 0.0132 m3/m3, ubRMSE = 0.022 m3/m3, R = 0.977) has been achieved through the use of spatial–temporal deep learning model and Data Integration term. In comparison with interp_ConvGRU and DI_LSTM, DI_ConvGRU has improved the model performance in 74.88% and 68.99% of the regions according to RMSE, respectively. The predictability of SM depends highly on SM memory characteristics. DI_ConvGRU can provide accurate spatial–temporal forecast for SM with missing data, making them potentially useful for applications such as filling observational gaps in satellite data.
1. Introduction
Soil moisture (SM), as an essential ground diagnostic variable in the Earth system, plays a vital role in energy, water, and carbon cycles between the atmosphere and land surface [1]. SM was identified as one of the Essential Climate Variables by the Global Climate Observing System [2]. Therefore, accurate forecast of SM is important for many critical applications, such as numerical weather forecasts [3], disaster monitoring of drought [4], the carbon cycle modelling [5], agriculture yield assessment [6], and many other scientifically and socially important applications.
Microwave remote sensing has a significant association with the soil dielectric constant, and satellite data can be utilized to provide SM from regional to global scales with daily or hourly temporal resolution [7], providing SM datasets with high information content, large observation range, high speed, and relatively high accuracy. The Soil Moisture Active Passive (SMAP) mission [1,8,9] was launched in 2015 and received the highest ranking of mission priorities from the National Research Council [10]. The mission seeks to provide SM retrieval for the top 5 cm of the soil column using L-band microwaves with a spatial resolution of 40 km. Because the L-band has a greater capacity to penetrate vegetation than the C- or X-bands, it has been deemed the most appropriate band for SM in high-density vegetative zones. It is also committed to producing long-term and global SM products with an accuracy requirement of 0.04 cm3/cm3 volumetric SM with the unbiased root mean square error [1]. Furthermore, the employment of anti-interference hardware and kurtosis-based algorithms contributes to the reduction of radio frequency interference (RFI) produced by human activity [11]. Thus, SMAP products have attracted a lot of attention and have substantially increased the measurement capability of SM. However, it has a revisit time of 2–3 days, which causes gaps between SMAP areas. Thus, these temporal and spatial gaps can limit their applications.
Many researchers [12,13,14,15,16,17] used deep learning (DL) models to forecast SM because of their ability to learn nonlinear mappings, automatically extract features, and build dynamic systems. DL models can be divided into three categories: spatial models [18], temporal models [19,20], and spatial–temporal models [21]. Spatial models, such as the Convolutional Neural Network (CNN), were proposed by LeCun and Bengio (1995) [18]. CNNs typically comprise a convolutional layer, a pooling layer, and a fully connected layer, with the convolutional and pooling layers alternated. Convolutional layers can extract spatial characteristics. As a result, the grid of SM and meteorological time series data can be taken as CNN-processed images. For example, Wang et al. [22] used CNN to predict SM content using near infrared spectroscopy. Hegazi et al. [23] used Sentinel-1 images to train a CNN-based algorithm to estimate SM content over agricultural areas. Temporal models include the long short-term memory (LSTM) and the gated recurrent unit (GRU). LSTM and GRU can successfully correlate contextual information when processing serial data and are frequently employed in Earth system research for time series data prediction. For example, Fang et al. [12,13] employed LSTM to predict surface SM based on climate forcing and soil texture. In addition, Filipovi et al. [24] forecasted the second layer SM using LSTM. Spatial–temporal models, such as the convolutional LSTM (ConvLSTM) [21], substituted matrix multiplication with a convolution operation of each gate in an LSTM cell. The model can capture and use both spatial and temporal correlations, making it an effective tool for forecasting spatial–temporal variables. For example, Li et al. [15] showed that ConvLSTM outperformed independent CNN or LSTM in terms of SM forecast accuracy. A et al. [25] utilized ConvLSTM to assess the root zone SM. Li et al. [16] suggested a ConvLSTM based on attention-mechanisms for SM prediction and demonstrated the relevance of temporal and spatial correlation on model performance. It is well known that the state of each pixel’s SM at each time step depends not only on its own historical observation, but also on the state of its neighboring pixels at the current time. It may also be directly influenced by the historical state of neighboring pixels, as well as by the time series data of meteorological forcing variables and static geographical attributes. For spatial models, spatial features are extracted by convolutional layers, however, “flattening” loses spatial autocorrelation and its inter-grid order, and its forecasting in the time dimension cannot introduce long-term memory structure. The time series model is used to build mapping relationships between time series of variables at a particular point, although there are significant issues such missing spatial information. As a result, the spatial–temporal models have the advantage of concurrently capturing spatial and temporal changes for SM forecast.
In addition, both LSTM and GRU retain important features through various gate functions, which ensures that the vital information for SM prediction will not be lost in long-term propagation. GRU has one less gate function than LSTM, so there are fewer parameters of GRU and it is faster than LSTM, but the accuracy is similar. ConvGRU is based on the combination of GRU and CNN; by superimposing convolutional operations on different regions, it can obtain temporal relationships and spatial features to better predict their future change patterns based on information mining.
All the aforementioned SM prediction methods based on deep learning have some drawbacks, including the inability to handle large amounts of missing remote sensing data. The key to forecast SM is SM memory characteristics. Thus, using lagged SM in DL models is a common practice, but this is challenging to perform with remotely sensed data because of missing data. Previously, Fang et al. [14] proposed the LSTM with an adaptive data integration kernel (called DI_LSTM) model for training SMAP L3 SM with missing spatial coverage at a time step. That is, the lagged SM is added as an input variable to the input data. When lagged SM data is missing, the predicted value from the previous moment is added as an input variable to the input data. However, LSTM-based models are trained in a point-to-point manner, which allows them to completely understand SM temporal correlation but ignores the impact of SM’s spatial distribution on SM forecast.
Therefore, to address the challenges mentioned above, we propose a Convolutional Gated Recursive Units with Data Integration (DI_ConvGRU) model for SM forecast. The SMAP L3 SM was used as the training target of the model, and the daily lagged SM from the SMAP L3 remote sensing data set and meteorological time series and static characteristics were used as predictors. The contributions of this paper are fourfold: (1) Given the spatial–temporal complexity of SM and the gap caused by the revisit time of remote sensing data, we developed a spatial–temporal DL model (DI_ConvGRU) for real-time SM forecast; (2) We validated the model’s prediction performance and compared it with other models in two ways: spatial–temporal model versus time series model (DI_LSTM) and DI term versus linear interpolation (interp_ConvGRU, that is ConvGRU with Linear Interpolation); (3) Evaluating the computational performance of DI_ConvGRU by comparing it with other DL models (ConvGRU, LSTM, DI_LSTM, and interp_ConvGRU); (4) We intuitively display and analyze the performance of the prediction models for various climatic zones and input factors. We expect this to help researchers improve the predictive performance for SM intentionally and strategically.
2. Data Sources
The domain of this study was restricted to China (18°–54°N, 73°–135°E). We used SMAP version 8, Level 3 passive radiometer SM product [26] as the target to training and forecast SM by using the DL models. The SMAP L3 SM product is a composite product released daily that contains SM observations from descending orbit (6:00 AM) and ascending orbit (6:00 PM). It has a spatial resolution of about 36 km and a revisit time of 2–3 days. Revisit time is the time when a satellite observation from a point can return to that point again, and satellite scan gaps can result in a large number of SMAP pixels with missing values; vegetation water content, urban areas, and water bodies can all also result in SMAP pixels with missing values. The average values of descending and ascending directions were determined as the day’s SM data in order to increase the spatial coverage of the data. Chan and Zhang et al. [27,28] showed that the performance of the ascending and descending orbit SM products was similar. Like Koster et al. [29], we did not screen the SM data according to its quality control information to allow greater spatial and temporal coverage. The SMAP L3 SM product used in this study over the 3-year period (1 April 2015–31 March 2018) is freely available from the National Snow and Ice Data Center (NSIDC) (https://nsidc.org/data/SPL3SMP, last accessed on 15 November 2022).
The spatial and temporal variation of SM is controlled by a variety of factors, and this work selected lagged SM, meteorological forcing variables and static physiographic attributes that have been commonly used in DL studies in recent years [12,13,14,15,16]. The lagged climatic forcing was extracted from the land component of the fifth generation of European Reanalysis (ERA5-Land) [30], and included precipitation, temperature, radiation, humidity, and wind speed (the lagged time is 1 day). Physiographic attributes contain soil properties extracted from the China soil dataset for land surface modeling (CSDL) [31], including sand, silt, clay content, bulk density, and land cover type extracted from the United States Geological Survey [32] as well as the digital elevation model (DEM) [33]. All data were resampled to SMAP L3 grid with a resolution of 36 km and the time series data were aggregated to a daily time scale.
3. Methods
3.1. Components of the Model
3.1.1. ConvGRU Model
ConvGRU is modified according to ConvLSTM [21], converting LSTM to GRU [34] for calculation. The GRU neural network is an adaptation of the LSTM that optimizes the cell structure on the basis of the LSTM neural network to decrease the parameters and speed up the training while maintaining similar accuracy. The main concept of ConvGRU is to combine matrix operations with convolutional operations in order to extract spatial characteristics using convolutional computation and retrieve temporal features using GRU. As shown in Figure 1, all the linear layers in GRU are transformed into Conv layers, and the input variables of two-dimensional variables in GRU are transformed into three-dimensional variables in ConvGRU. Then, the convolution filter is applied to the input-to-state and state-to-state transitions of a passenger flow grid cell.

Figure 1.
Inner structure of ConvGRU. X is the input and H is the hidden layer.
For each time step t, the update gate Zt and reset gate Rt of ConvGRU are formulated as follows (for further detail, refer to [21]):
Input data
Updata Gate
Reset Gate
New Memory
Hidden Memory
where represents the t-th step of inputs time steps. The term is the inputs, is the SM data, forcing and static attributes, respectively. is the hidden state. The operator denotes the convolution operator and denotes the Hadamard product. is the sigmoid function, represents the hyperbolic tangent function, and is 2D Conv kernels for spatial dimension. Update gate and reset gate are both four-dimensional tensors, where the four dimensions denote time, feature, and the rows and columns of spatial data.
3.1.2. Data Integration (DI)
Data Integration (DI) was used to process SMAP L3 data with a huge number of missing values in response to neural networks’ inability to handle missing values [14]. In this method, the observed values at time t are used when SM data are available, while the predicted values at time t − 1 are used when there are no SM data at time t. Therefore, during the model run, the most recent observations or forecasts are added as injection terms to the model input data. Although initial model training will result in inaccurate data filling and poor forecasts, the forecast network can enhance its capacity to fill the missing values and converge in the training process as the iteration goes on.
3.2. Structure of DI_ConvGRU Model
To better capture the spatial interactions and temporal evolution of surrounding SM simultaneously, we proposed a ConvGRU model with Data Integration (DI_ConvGRU) for SM forecast. As shown in Figure 2, the model consists of an input layer, three ConvGRU layers, and an output layer.
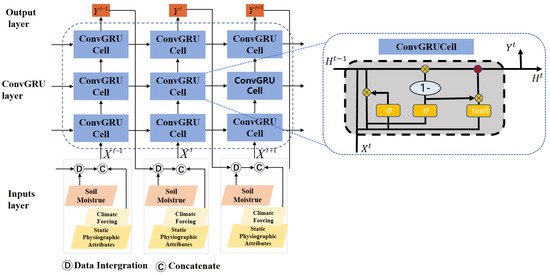
Figure 2.
The network structure of DI_ConvGRU. X is the input, H is the hidden layer, and Y is the output.
For the input layer, we first checked to see if there were any SM observations when the time step was 0 (i.e., t = 0). We filled missing values with zero values when there were no SM observations; it was verified with experiments that using zero values or average values had similar effect on the prediction results. After filling the SM image completely, lagged SM were combined with other variables as inputs to the first ConvGRU cell for training to obtain the forecast of for the first day. We repeated the procedure at t = 0 when the time step was 1 (i.e., t = 1). The difference was that when the SM observation is missing, we substituted the first day’s forecast , which results in the next day’s forecast, . The operation was repeated for the time t = 1 when the time step was 2 (i.e., t = 2). Because of inaccurate initial value filling in this setup, the network produced poor predicted values during the first few training epochs. However, as the prediction network improved during training, it also improved at filling in the gaps, thus the training would eventually converge. For DI_ConvGRU, to the ConvGRU cell is expressed as:
where is the value of a pixel in the SM grid data on time step t, and is the predicted value of pixel on time step t − 1.
At each time step, the loss function was calculated for the pixels with SMAP observations as [14]:
where N is the length of the time series, and are the SMAP SM observations and the model’s predicted value at time t, respectively.
3.3. Experiment Setup and Model Setting
In this work, DI_ConvGRU was compared with four other DL models, namely ConvGRU, LSTM, DI_LSTM, and interp_ConvGRU. For brevity, we mainly show the comparison of DI_ConvGRU, DI_LSTM, and interp_ConvGRU in the results section. DI_LSTM combines DI with LSTM instead of ConvGRU compared with DI_ConvGRU, while interp_ConvGRU uses linear interpolation to fulfill the missing values of SM images. All codes are available at https://github.com/YeZhang929/DI_ConvGRU (last accessed on 15 November 2022). The codes of LSTM and DI_LSTM were modified from Fang et al. [14] (https://github.com/mhpi/hydroDL, last accessed on 15 November 2022).
The whole data set was divided into three parts following a chronological order for training, validating, and testing with the ratio of 60%, 10%, and 30%, respectively. We processed the input data as 5-D tensors (the five dimensions are the samples, timesteps, width, height, and features) required by the network. All the variables were normalized using the min-max method, since normalization can make the data more focused and helps to improve the prediction accuracy and fitting speed of the model.
For the spatial–temporal models (i.e., ConvGRU, DI_ConvGRU and interp_ConvGRU), the input feature map size is 50 × 50, the number of ConvGRU layers is 3, and the number of filters in each ConvGRU layer is 64, 64, and 1, respectively. The default hyperbolic tangent “tanh” activation function is utilized, and each layer kernel is 3 × 3. The network layers were joined by stacking. The size of feature maps (50 × 50) was kept constant with the input SM by using the same padding technique. The number of filters in the LSTM layers was set to 128 for DI_LSTM, and all other parameter values were made in accordance with Fang et al. [14].
We used the early stop method during the model training to improve generalization performance and prevent overfitting. The model training was stopped when the validation set loss was not decreased for 20 consecutive training cycles. Empirically, 100 iterations and 16 batches were chosen as the parameters. The Adam optimizer was used to train the model, and the time step was set at 16. In addition, a timer was put up in the code to keep track of the training time, serving as a benchmark for assessing the model fitting efficiency.
We performed the experiments on a server with a CPU: AMD Ryzen 7 5800X 8-Core Processor 3.80 GHz, GPU: RTX2080Ti and RAM: 11 GB running Pycharm. The Anaconda platform was used as the base platform for DL training, pytorch 1.10.2 was the backend, and CUDA technology was used to implement the computation. The Python version is 3.9.
To explore the sensitivity of predictions to different inputs, we designed four experiments to test the prediction performance of the DL models based on different input data for 1-, 2-, and 3-day forecasts. Experiment I served as the baseline, in which the model was built using ConvGRU and using only climate forcing as inputs. In Experiment II, Interp_ConvGRU was built using climate forcing and lagged SM as input, which was used to show the effect of adding lagged SM gap filled by linearly interpolation compared with Experiment I. It is not suitable to build a ConvGRU with lagged SM but without gap filling because of the frequent gaps in the original SMAP SM. As a result, we did not build ConvGRU with climate forcing and lagged SM. In Experiment III, DI_ConvGRU was built using climate forcing and lagged SM, which was used to show the effect of DI instead of the linear interpolation in Experiment II. In Experiment IV, DI_ConvGRU was built using climate forcing, lagged SM, and static physiographic attributes, which were used to show the effect of static data compared with Experiment III.
3.4. Performance Evaluation Measures
This work used the several indicators to evaluate the predictive performance of the DL model, including the Bias, Root Mean Square Error (RMSE), the unbiased RMSE (ubRMSE), and Pearson’s Correlation Coefficient (R) and Kling-Gupta efficiency (KGE). These criteria are calculated as follows:
where and are the corresponding mean and standard deviation of the predicted values and the observed values for i-th test value. is the number of timesteps. KGE [35] is a composite indicator reflecting the agreement between observed and predicted values. KGE varies between and 1, and values close to 1 indicate that model forecasts are accurate.
The performance of the DL models was evaluated for both the whole China and eight climate regions. The former was used to evaluate the overall performance of models, while the latter was used to reveal why the model performed differently in different regions as well as the possible reasons that soil moisture has different behavior and influencing factors in different climates [1].
4. Results
4.1. Overall Performance of DI_ConvGRU, interp_ConvGRU and DI_LSTM
We first show the prediction performance of the DI_ConvGRU, interp_ConvGRU, and DI_LSTM models for SM using SMAP L3 SM as the training target. For the 1-day, 2-day, and 3-day forecasts of the test period, the density scatter plot of the predicted and SMAP L3 SM by DI_ConvGRU, interp_ConvGRU, and DI_LSTM is shown in Figure 3. Compared with interp_ConvGRU and DI_LSTM, DI_ConvGRU had the highest R value in the range of 0.975 to 0.977 and the lowest ubRMSE in the range of 0.022 m3/m3 to 0.023 m3/m3, making it the best DL model for SMAP SM prediction. Additionally, the two spatial–temporal DL models’ regression lines were more closely aligned with the ideal line (y = x) than the time series model (DI_LSTM), which had worse metrics and a diverging scatter plot distribution. This indicates that the spatial–temporal DL models, which extracted the spatial aspects of SM using the convolution operator, were more appropriate for SM forecasting than the time series model. The DI_ConvGRU outperformed the interp_ConvGRU, proving that the DI term is better suited for spatial–temporal SM prediction than the linear interpolation.
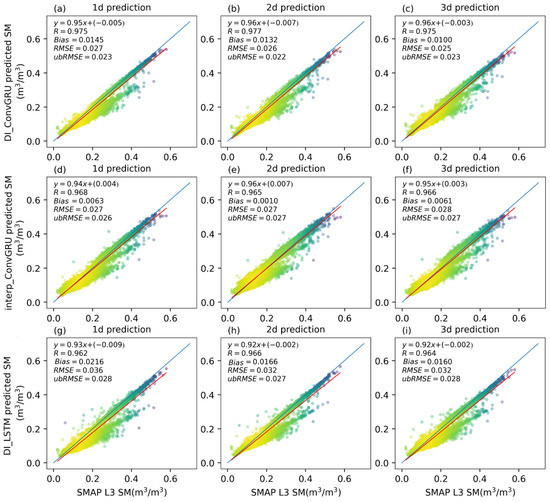
Figure 3.
The density scatter plot of the predicted SM and SMAP L3 SM by DI_ConvGRU (a–c), interp_ConvGRU (d–f) and DI_LSTM (g–i) for 1-day, 2-day, and 3-day forecasts. The blue line is the 1:1 line and the red line is the regression line. Yellow indicates high density and purple indicates low density.
Figure 4 displays the performance maps of DI_ConvGRU during the test period, taking into account bias, RMSE, and R. The average bias between the predicted SM and the SMAP L3 SM for the 1-day forecast, as shown in Figure 4a, was 0.0013 m3/m3, suggesting a positive deviation between the predicted SM and the SMAP L3 SM. In the majority of China (Figure 4b), the RMSE was lower than the design measurement accuracy (0.04 m3/m3) of the original SMAP, but a small number of pixels with high RMSE existed in the northeastern and coastal regions of China, which may be because of the high annual precipitation and high variability in humidity in these areas. Furthermore, with an average R of 0.673 (Figure 4c), the magnitude of R values differed significantly between geographical areas. Lower R values appeared in central and northern China, which may be a result of either increased vegetation moisture content or subpar SMAP data quality. For SM forecasting in the majority of China, particularly in the western, southeastern, and northwestern regions, the model had high accuracy (high R, low RMSE). However, the forecasting ability was generally inferior in the northern and northeastern regions (i.e., relatively low R and large RMSE). The patterns of the model’s bias, RMSE, and R for the 2- and 3-day forecasts were consistent with those for the 1-day forecasts, with a slight decline in forecast performance.
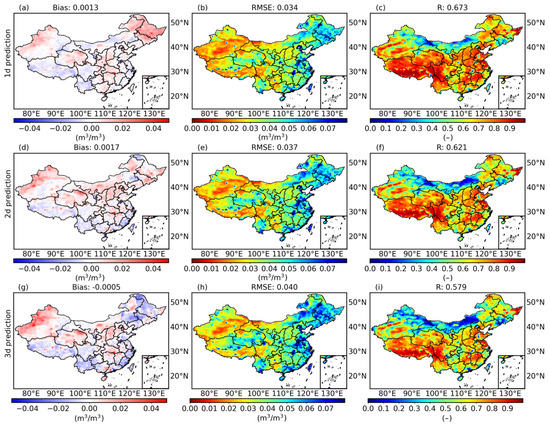
Figure 4.
Performance of ConvGRU model with data integration (DI_ConvGRU) during the test period from 1 April 2017 to 31 March 2018 in China. Shown are the Bias (a,d,g) for 1-, 2-, and 3-day forecasts, respectively, RMSE (b,e,h) and R (c,f,i).
The spatial patterns of the various metrics of the three models, i.e., DI_ConvGRU, interp_ConvGRU, and DI LSTM, were similar, as shown in Figure 4, Figures S1 and S2. For 1-day, 2-day, and 3-day forecasts, DI_ConvGRU (Figure 4) performed better than interp_ConvGRU (Figure S1) and DI_LSTM (Figure S2) in terms of average metric. Taking 1-day forecast as an example, the averaged bias, RMSE and R of DI_ConvGRU were 0.0013 m3/m3, 0.034 m3/m3, 0.673, respectively, while those of interp_ConvGRU were −0.0002 m3/m3, 0.036 m3/m3, 0.650 and those of DI_LSTM were 0.0065 m3/m3, 0.037 m3/m3, 0.666. The best spatial performance for bias, which was very close to 0, was provided by DI_ConvGRU. The interp_ConvGRU (Figure S1) had a significant positive bias in the northern region of China and a significant negative bias in the southern region, while the DI_LSTM (Figure S2) had a significant positive bias throughout the entire study area, particularly in the area of the Kunlun Mountains in Qinghai Province, which had a relatively large positive bias, and its RMSE and R were both poorly performed. Therefore, DI_ConvGRU can not only better capture the spatial–temporal characteristics of SM but can also handle the irregular observations of SMAP SM more effectively than DI_LSTM and interp_ConvGRU.
4.2. Comparison of Model Training Efficiency
As shown in Figure 5, we examined the training times of five different DL models to compare the performance of the DL model. Each model was trained using the early stop method as described in Section 3.3. The training time of each epoch of DI_ConvGRU, interp_ConvGRU, ConvGRU, LSTM, and DI_LSTM were 115 s, 143 s, 245 s, 866 s, and 2873 s, respectively. That is, DI_ConvGRU had the lowest training time while DI_ LSTM had the highest, nearly 25 times as much as DI_ConvGRU. In contrast to LSTM and DI_LSTM, which trained 100 epochs by randomly selecting one pixel from each 2 × 2 pixel, ConvGRU, interp_ConvGRU, and DI_ConvGRU trained 100 epochs for 50 × 50 images. As a result, LSTM, DI_LSTM training took a much longer time than that of ConvGRU, interp_ConvGRU, and DI_ConvGRU. It should be noted that the model’s lengthy training period will have an impact on how timely real-time forecasting is.
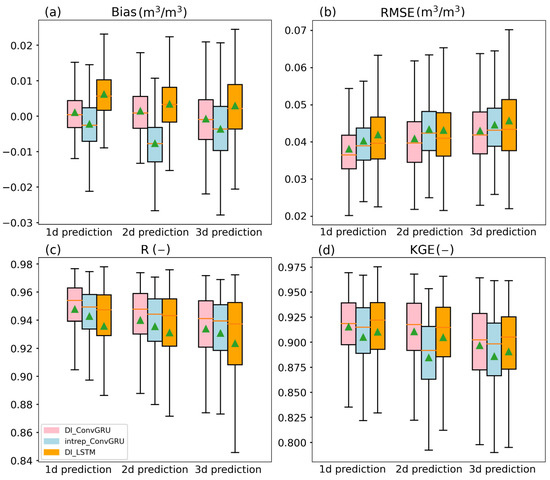
Figure 5.
Box plots of the Bias (a), RMSE (b), R (c) and KGE (d) of comparison between SMAP L3 SM and predicted values of DI_ConvGRU, interp_ConvGRU and DI_LSTM. The green triangles represents the mean of the corresponding box plot.
4.3. Improvements of Model Performance by DI_ConvGRU
Figure 5 displays the Bias, RMSE, R, and KGE box plots of the DI_ConvGRU, interp_ConvGRU, and DI_LSTM models, calculated for each day of the test period. According to this figure, DI_ConvGRU was the most effective DL model for SMAP SM prediction since it had a Bias near zero, the highest mean R ranging from 0.933 to 0.948, and the lowest mean RMSE ranging from 0.038 to 0.043 for the 1-, 2-, and 3-day forecasts. The RMSE of DI_ConvGRU at different prediction days was lowered by roughly 3.59~5.99% compared with interp_ConvGRU, while it was decreased by 5.34~9.07% compared with DI_LSTM. According to the Bias in Figure 5a, interp_ConvGRU had significant underestimation, while DI_LSTM had significant overestimation compared with DI_ConvGRU. The above results reinforced the conclusion in Section 4.1 that the replacement of LSTM with ConvGRU had a greater effect on the model performance than the replacement of linear interpolation by DI term. However, according to KGE, interp_ConvGRU had the worst performance, indicating that the model’s performance was negatively impacted by the direct interpolation of SMAP SM, which can be effectively fixed by DI.
Figure 6 demonstrates the spatial distribution of improvement provided by DI_ConvGRU over China compared with interp_ConvGRU and DI_LSTM. Compared with interp_ConvGRU, DI_ConvGRU improved the model performance over 74.88% of all regions according to RMSE. The improvement in RMSE (with an average of 5.75%) was higher than that in R (with an average of 3.5%). It was worth noting that DI_ConvGRU improved RMSE by more than 10% in most regions, such as Xinjiang, Southwest, and East China. R improved most significantly in Xinjiang, by more than 20%. Compared with DI_LSTM, DI_ConvGRU improved its performance over 68.99% of regions according to RMSE. The improvement in RMSE (with an average of 7.6%) was much higher than that in R (with an average of 0.88%). According to RMSE, DI_ConvGRU improved significantly by more than 20% in most areas of China, except in the northeast. In contrast, according to R, DI_ConvGRU improved in the south, the Qinghai–Tibet Plateau, south of Xingjiang, and parts of the northeast, but it degenerated significantly in the northeast and northern regions, which led to a value near to zero for the average improvement in R. Overall, DI_ConvGRU outperformed interp_ConvGRU and DI_LSTM in most regions according to R and RMSE, though it underperformed DI_LSTM in the northeast and northern regions of China according to R.
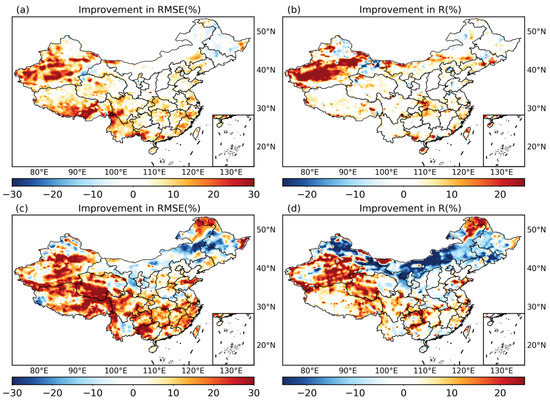
Figure 6.
Improvements from interp_ConvGRU (or DI_LSTM) to DI_ConvGRU. RMSE improvements (a,c) were calculated as , and R improvements (b,d) were calculated as.
4.4. The Model Performance in Different Climate Regions
Assessment of SM based on climate zone can accurately depict climate change and its possible effects on terrestrial ecosystems and the environment [36]. Therefore, based on the Köppen–Geiger climate zone [37], we studied the predicting performance of SM over several climate zones in China. The mean values of the various metrics for the eight climate zones are summarized in Table 1. The polar tundra climate zone, which locates on the Qinghai–Tibet Plateau and makes up 15.96% of the study area, had the best forecast performance among the eight climatic zones, while the tropical climate zone had the worst. The high performance for polar tundra climate zone may be led by the strong soil moisture memory reflected by the high lagged R (0.801). Lagged SM can be viewed as an SM memory trait; specifically, the soil has the ability to “remember” wet or dry anomalies long after the atmospheric conditions that generated them have been forgotten. The predictability of SM is strongly influenced by SM memory properties, as demonstrated by Pan et al. [38]. The poor performance for the tropical climate zone may be led by the small fraction of samples (less than 0.4%) and low lagged R (0.541), and a similar situation also happened to the cold no dry season climate zone. The Arid desert climate zone has the second largest area (20.91%) among the eight climate zones and is mainly found in areas with low SM values and low precipitation. The poor performance of the model prediction performance (mean R: 0.544) may be due to the low lagged R and the high coefficient of variation (0.404). In general, low SM data lagged R and large SM data dispersion are detrimental to model prediction, and the lagged R of SM has a significant correlation with model prediction performance, which has a correlation of 0.793 with the mean R.

Table 1.
Mean value of different metric of different climate regions, including soil moisture (SM, m3/m3), Coefficient of Variation (CV) and the lagged correlation of SM (lagged R), the Bias (m3/m3), root-mean-square error (RMSE, m3/m3) and Pearson’s Correlation Coefficient (R) of the DI_ConvGRU, and number of pixels.
Figure 7 shows the SM time series of 6 pixels, which were randomly selected from climate regions with a relatively high number of pixels. The prediction of all DL models was for the period of test data set (from 1 April 2017 to 31 March 2018). Figure 7 indicates that DI_ConvGRU can capture peaks and valleys with greater accuracy and that provide predictions with quite similar trend to the original SMAP SM. However, DI_LSTM appeared to have more unrealistic extreme values and underestimate (e.g., pixel A, C) or overestimate (e.g., pixel E, F) in some cases, probably because the DI_LSTM model was trained point-to-point, thus ignoring the capture of neighboring pixel information, i.e., the capture of spatial features. For pixel A, interp_ConvGRU had a persistent underestimation after 150 days; this was probably caused by to the accumulated error from the interpolation of SM. Throughout the time series of pixel D, while the predictions of these three DL models were generally consistent with the original SMAP SM values, interp_ConvGRU appeared to be consistently overestimated. When the original SMAP SM values are not known, interp_ConvGRU (e.g., pixels A, B, and F) was readily exaggerated the SM values. In summary, DI_ConvGRU tended to provide predictions close to the observational time series than interp_ConvGRU and DI_LSTM.
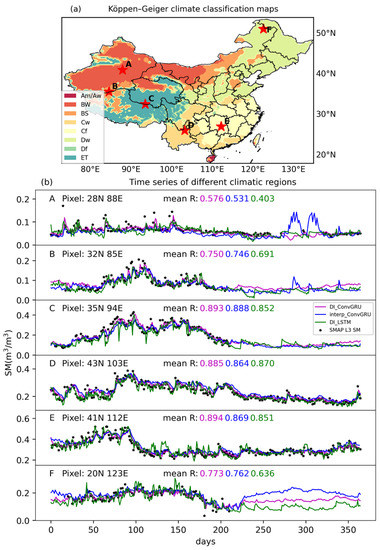
Figure 7.
(a) Randomly selected pixel locations in the Köppen–Geiger climate region map of China and (b) Forecast of SM time series in different climatic regions by different models (from 1 April 2017 to 31 March 2018).
4.5. Influence of Different Input on Forecast Models
Figure 8 shows the box plots of the test results of the DL models trained on different datasets. ConvGRU in Experiment I performed the worst with an RMSE value of 0.067 m3/m3, an R value of 0.868, and a KGE value of 0.778 for the 1-day forecast. Compared with Experiment I, the mean RMSE value of interp_ConvGRU in Experiment II was reduced by 39.55%, the mean R value was increased by 8.64%, and the KGE value was increased by 16.32% when the linearly interpolated lagged SM was added to Experiment I. This shows that even the linearly interpolated lagged SM significantly improved the prediction performance of the model. Consistent with previous studies [16,38], this occurred mainly because SM has significant persistent properties. Experiment III demonstrated improvements in all metrics compared with Experiment II, including a 5.22% decrease in RMSE and a 0.53% increase in R. This shows that the real-time update of DI terms also improved the performance of the model. DI_ConvGRU had the best performance in Experiment IV, where lagged SM, meteorological forcing variables, and static geographic attributes were taken into account. The RMSE value dropped by 0.79%, the average R value rose by 0.11%, and the KGE value rose by 0.76%. In general, the lagged SM had the most significant impact on the model performance, followed by the DI term and the static data. Similar to the above results of the 1-day forecast, the same conclusion can be drawn based on the results of 2- and 3-day forecasts, though the models’ performance became worse as the forecasting time increased. It should be noted that the forecasting performance was increasingly influenced by static geographical attributes when forecasting for 2 and 3 day.
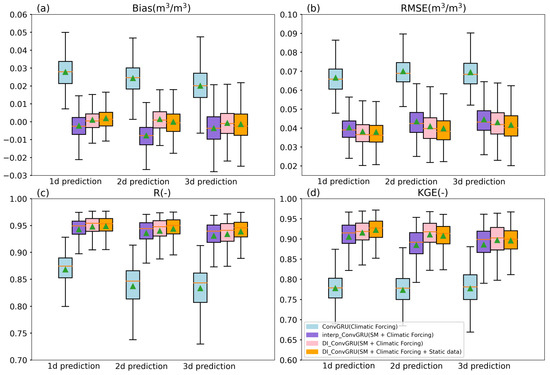
Figure 8.
Box plots of the Bias, RMSE, R and KGE of models trained with different datasets during the tested period. Those four models were trained using (a) ConvGRU with Climatic Forcing data (blue; including the lagged precipitation, temperature, radiation, humidity, and wind speed, where the lagged time is 1 day). (b) interp_ConvGRU with SM (lagged SMAP L3 SM gap filled by linearly interpolation) and Climatic Forcing data (purple); (c) DI_ConvGRU with SM (lagged SMAP L3 SM) and Climatic Forcing data (pink); and (d) DI_ConvGRU with SM (lagged SMAP L3 SM), Climatic Forcing and Static data (blue; including sand, silt, clay content, bulk density, land cover type and DEM).
5. Discussion
The DL model has been used in hydrology, particularly in prediction tasks like streamflow [39], pan evaporation [40], and floods [41], demonstrating its robustness and generality. We consider that the current state of each pixel of the SM depends not only on its own historical observations, but also on the state of its surrounding pixels. In addition, it may be directly influenced by meteorological forcing and static geographic attributes of neighboring pixels. Further complicating the forecast of SM are the gaps in the SMAP L3 remote sensing data. Therefore, we proposed DI_ConvGRU to predict the SM, allowing for the capture of the spatial–temporal features and to handle the missing data.
We compared the prediction performance of DI_ConvGRU with interp_ConvGRU and DI_LSTM in terms of temporal analysis and spatial analysis (Figure 3, Figure 4, Figure 5 and Figure 6, Figures S1 and S2), and found that DI_ConvGRU can not only capture the spatial–temporal characteristics of SM better, but it can also effectively handle the missing data in SMAP SM. From the spatial–temporal statistical scatter plot (Figure 3 and Figure 5), DI_ConvGRU was the best DL model used for SMAP SM prediction, which had the highest R, very close to 1, compared with interp_ConvGRU and DI_LSTM. This indicated that predictions of DI_ConvGRU were very close to SMAP SM observations. However, the spatial analysis results are not very satisfactory. In Eastern China (Figure 4b,e,h, Figure S1b,e,h, Figure S2b,e,h), we found that the RMSE values of DL models were generally large at some pixel points, especially in the case of predicted 2- and 3-day forecasts. The reason may come from the standard deviation of SMAP SM (Figure S3a), where we found a significant correlation between the value of RMSE and the standard deviation of SMAP SM. However, for different models, we found that the correlation of RMSE with the standard deviation of SMAP SM was different. For example, in the eastern part of Heilongjiang province, this correlation was not significant for DI_ConvGRU, but it was larger for interp_ConvGRU and DI_LSTM. It can be seen from Figure 4c and Figure S3b that the mapping of R was consistent with the mapping of lagged R, and that the lagged R of SM memory had a significant positive correlation (0.793) with the R of DI_ConvGRU (Figure S3c). The stronger the SM memory, the better the prediction performance of DI_ConvGRU. This is consistent with previous studies [35].
The overall improvement of DI_ConvGRU compared with DI_LSTM was larger than that compared with interp_ConvGRU (Figure 6), but the improvement over different regions was not even; sometimes it even degenerated (Figure 7). For example, the R values of DI_LSTM were higher than DI_ConvGRU by more than 10% in northern Xinjiang as well as the Inner Mongolia region. This indicated that DI_LSTM may be more suitable for the prediction in these areas. We also found that the improvement in RMSE of DI_ConvGRU (Figure 5c) was consistent with the trend of lagged correlation of SM (Figure S3b). This indicated that DI_ConvGRU can capture the SM memory characteristic better than the other two DL models, especially DI_LSTM.
We also investigated the impact of missing SMAP SM data (Figure S4) on the prediction performance of the model. Figure S4a,b show the percentage of missing SMAP SM data per day and per pixel in the test phase, respectively. As shown in Figure S4a, the winter between 2017 and 2018 had the highest rate of missing SM values of SMAP, over 70%. This was followed by spring and autumn, while summer had the lowest rate of missing data (40%). As can be seen from Figures S5 and S6, the prediction performance of the DL models, especially DI_ConvGRU, was affected by the missing rate of SMAP data in different seasons. However, interp_ConvGRU was subject to larger errors that were caused by the interpolation (blue box plot), and there was an accumulation of errors. That is, the large amount of missing data in winter had little impact on the performance in winter but a large impact on the second spring. Therefore, the DI term can effectively prevent the accumulation of errors. Figure S4b shows that there are more missing data in the western part of China than in the eastern part. However, the performance of DL models (Figure 4, Figures S1 and S2) had good performance in most areas of China, except the northern part. The above results indicate that the missing data rate in different locations did not affect the model performance much, but the missing data in different seasons did affect it to some extent.
It is expected that the DI_ConvGRU proposed in this work can be applied on remote sensing data of soil moisture other than SAMP. Furthermore, it has the potential to be applied on predictions of remote sensing variables with gaps other than soil moisture, which needs further study to verify its suitability. As this work shows that the performance of the DI_ConvGRU depends heavily on soil moisture memory effects that are represented by the lagged SM, there are questions to be answered about whether this method can be useful for gap-filling of other variables, such as leaf area index, and the quality of its performance in that type of usage.
6. Conclusions
SM is a key physical parameter in land surface processes and is involved in key processes such as hydrological processes, surface runoff, and land-atmosphere interactions. It also provides the basis for meteorological services such as drought and flood warnings. In this study, we proposed a convolutional gated recursive unit with a data integration (DI_ConvGRU) model for accurate and real-time SM prediction using SMAP L3 SM data. The model can capture the spatial and temporal correlations of time series SM and adapt to the irregular observations of SMAP SM for prediction. Comparisons were made with interp_ConvGRU (for verifying the role of DI terms) and DI_LSTM (for verifying whether the spatial–temporal model improves the prediction accuracy of SM), and DI_ConvGRU has improved the model performance in 74.88% and 68.99% of the regions according to RMSE comparison with interp_ConvGRU and DI_LSTM, respectively. We analyzed and discussed three aspects of the model performance: the overall performance of the model, the model performance in different climatic regions, and the influence of different factors. The conclusions are as follows:
- (1)
- DI_ConvGRU can not only better capture the spatial–temporal characteristics of SM, but also effectively handle the missing data in SMAP SM. In terms of prediction accuracy and convergence speed, the DI_ConvGRU model outperformed the other DL models (ConvGRU, LSTM, DI_LSTM and interp_ConvGRU), and it achieved good performance with a bias of 0.0132 m3/m3, an ubRMSE of 0.022 m3/m3 and an R of 0.977. Using ConvGRU instead of LSTM had a greater impact on the model performance than linear interpolation with DI terms.
- (2)
- Among the eight climate zones, the polar regions had the best prediction performance, and the tropical regions had the worst performance. We find that the prediction performance of the model is strongly related to the lagged R of the SM and the coefficient of variation of the SM. The spatial–temporal model’s image-to-image training strategy collected not only information on the time series but also the spatial information of surrounding pixels, whereas the DI term-based model better captured the peaks.
- (3)
- The lagged SM has the most significant impact on the model performance, followed by the DI term and static data. Error buildup may result from the linear interpolation-based DL model, while the DI-based model can successfully avoid it. Additionally, while the missing data rate for various places had little impact on the model’s performance, the missing data rate in different seasons had some effects.
In general, the research results presented in this work can provide some reference value for the improvement of prediction models for other meteorological variables. However, the work has some limitations, and further research can be carried out in the following aspects in the future. First, the use of linear interpolation for meteorological forcing variables as well as geographically static attribute data may produce errors and reduce the predictive performance of the model. Second, the quality of SMAP SM data and severe data deficiencies can affect the prediction results of the model, and the deep learning model can be optimized by using high-quality data (for data quality control) and by combining multiple data. Third, because of GPU memory restrictions and the relatively low performance of GPU (RTX 2080Ti) we employed in our study, we were forced to divide the study area into 50 × 50 images. Therefore, utilizing a more powerful GPU could further shorten the training time of DI_ConvGRU and enhance prediction performance. Fourth, our evaluation of the model prediction performance was incomplete because it only considers cases where SMAP SM observations had values. We can evaluate the predicted values using site data instead of the missing pixel points of SMAP SM values. Finally, the DI_ConvGRU model will be useful for long-term SM hindcasts or forecasts as well as weather modeling; the model can also be employed as a spatial–temporal gap filling strategy for remote sensing data reconstruction.
Supplementary Materials
The following are available online at https://www.mdpi.com/article/10.3390/rs15020366/s1, Figure S1: Performance of ConvGRU with Linear Interpolation (interp_ConvGRU) during the test period from 1 April 2017 to 31 March 2018 in China. Shown are the Bias (a, d, g), RMSE (b, e, h) and R (c, f, i) R for 1-, 2-, and 3-day forecasts, respectively, Figure S2: Same as Figure S1 but for DI_LSTM, Figure S3: (a) Standard deviation of SMAP L3 SM; (b) Lagged R of SMAP L3 SM; (c) Relationship between lagged R of SM and R of DI_ConvGRU, Figure S4: Percentage of SMAP SM data missing for (a) each day and (b) each pixel, Figure S5: Box plot of RMSE (a) and R (b) of DI_ConvGRU, interp_ConvGRU and DI_LSTM for different season.
Author Contributions
Conceptualization, W.S.; methodology, Y.Z. (Ye Zhang) and W.S.; validation, Y.Z. (Ye Zhang) and W.S.; formal analysis, W.S. and Y.Z. (Ye Zhang); investigation, W.S., Q.L. and Y.Z. (Ye Zhang); writing—original draft preparation, Y.Z. (Ye Zhang); writing—review and editing, W.S., Y.Z. (Ye Zhang) and F.H.; visualization, Y.Z. (Ye Zhang), L.L. and Y.Z. (Yongkun Zhang); supervision, W.S.; project administration, W.S.; funding acquisition, W.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China under Grants 42088101, 41975122, U1811464, 42105144, 4227515, and 42205149, the National Key R&D Program of China under Grant 2017YFA0604300, Guangdong Basic and Applied Basic Research Foundation 2021B0301030007, the Innovation Group Project of Southern Marine Science and Engineering Guangdong Laboratory (Zhuhai) (311020008), and the Fundamental Research Funds for the Central Universities, Sun Yat-Sen University.
Data Availability Statement
SMAP data can be downloaded from the website of the National Snow and Ice Data Center (NSIDC, https://nsidc.org/data/SPL3SMP, last accessed on 15 November 2022). The ERA5-Land dataset is available at https://cds.climate.copernicus.eu/cdsapp#!/dataset/reanalysis-era5-land?tab=form (last accessed on 15 November 2022). The Chinese soil properties dataset can be obtained at http://globalchange.bnu.edu.cn (last accessed on 15 November 2022). The land cover type data is available at http://edcwww.cr.usgs.gov/landdaac/glcc/glcc.html (last accessed on 15 November 2022). The Digital Elevation Model data can be obtained from the website of Multi-Error-Removed Improved-Terrain DEM (http://hydro.iis.u-tokyo.ac.jp/~yamadai/MERIT_DEM/, last accessed on 15 November 2022).
Acknowledgments
The authors thank the anonymous reviewers for providing such valuable comments.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Seneviratne, S.I.; Corti, T.; Davin, E.L.; Hirschi, M.; Jaeger, E.B.; Lehner, I.; Orlowsky, B.; Teuling, A.J. Investigating Soil Moisture–Climate Interactions in a Changing Climate: A Review. Earth-Sci. Rev. 2010, 99, 125–161. [Google Scholar] [CrossRef]
- World Meteorological Organization. The Global Observing System for Climate: Implementation Needs; World Meteorological Organization: Geneva, Switzerland, 2016; Volume 200, p. 316. [Google Scholar]
- Dirmeyer, P.A.; Halder, S. Sensitivity of Numerical Weather Forecasts to Initial Soil Moisture Variations in CFSv2. Weather Forecast. 2016, 31, 1973–1983. [Google Scholar] [CrossRef]
- Marengo, J.A.; Galdos, M.V.; Challinor, A.; Cunha, A.P.; Marin, F.R.; Vianna, M.d.S.; Alvala, R.C.S.; Alves, L.M.; Moraes, O.L.; Bender, F. Drought in Northeast Brazil: A Review of Agricultural and Policy Adaptation Options for Food Security. Clim. Resil. Sustain. 2022, 1, e17. [Google Scholar] [CrossRef]
- Green, J.K.; Seneviratne, S.I.; Berg, A.M.; Findell, K.L.; Hagemann, S.; Lawrence, D.M.; Gentine, P. Large Influence of Soil Moisture on Long-Term Terrestrial Carbon Uptake. Nature 2019, 565, 476–479. [Google Scholar] [CrossRef] [PubMed]
- Baik, J.; Zohaib, M.; Kim, U.; Aadil, M.; Choi, M. Agricultural Drought Assessment Based on Multiple Soil Moisture Products. J. Arid Environ. 2019, 167, 43–55. [Google Scholar] [CrossRef]
- Laachrate, H.; Fadil, A.; Ghafiri, A. Soil Moisture Retrieval Using Microwave Remote Sensing: Review of Techniques and Applications. In Geospatial Technology; Advances in Science, Technology & Innovation; Jarar Oulidi, H., Fadil, A., Semane, N.E., Eds.; Springer International Publishing: Cham, Switzerland, 2019; pp. 31–50. [Google Scholar] [CrossRef]
- Zeng, J.; Chen, K.-S.; Bi, H.; Chen, Q. A Preliminary Evaluation of the SMAP Radiometer Soil Moisture Product Over United States and Europe Using Ground-Based Measurements. IEEE Trans. Geosci. Remote Sens. 2016, 54, 4929–4940. [Google Scholar] [CrossRef]
- Colliander, A.; Jackson, T.J.; Bindlish, R.; Chan, S.; Das, N.; Kim, S.B.; Cosh, M.H.; Dunbar, R.S.; Dang, L.; Pashaian, L.; et al. Validation of SMAP Surface Soil Moisture Products with Core Validation Sites. Remote Sens. Environ. 2017, 191, 215–231. [Google Scholar] [CrossRef]
- Board, S.S.; Council, N.R. Earth Science and Applications from Space: National Imperatives for the Next Decade and Beyond; National Academies Press: Washington, DC, USA, 2007. [Google Scholar]
- Piepmeier, J.R.; Johnson, J.T.; Mohammed, P.N.; Bradley, D.; Ruf, C.; Aksoy, M.; Garcia, R.; Hudson, D.; Miles, L.; Wong, M. Radio-Frequency Interference Mitigation for the Soil Moisture Active Passive Microwave Radiometer. IEEE Trans. Geosci. Remote Sens. 2013, 52, 761–775. [Google Scholar] [CrossRef]
- Fang, K.; Shen, C.; Kifer, D.; Yang, X. Prolongation of SMAP to Spatiotemporally Seamless Coverage of Continental U.S. Using a Deep Learning Neural Network. Geophys. Res. Lett. 2017, 44, 11030–11039. [Google Scholar] [CrossRef]
- Fang, K.; Pan, M.; Shen, C. The Value of SMAP for Long-Term Soil Moisture Estimation with the Help of Deep Learning. IEEE Trans. Geosci. Remote Sens. 2018, 57, 2221–2233. [Google Scholar] [CrossRef]
- Fang, K.; Shen, C. Near-Real-Time Forecast of Satellite-Based Soil Moisture Using Long Short-Term Memory with an Adaptive Data Integration Kernel. J. Hydrometeorol. 2020, 21, 399–413. [Google Scholar] [CrossRef]
- Li, Q.; Wang, Z.; Shangguan, W.; Li, L.; Yao, Y.; Yu, F. Improved Daily SMAP Satellite Soil Moisture Prediction over China Using Deep Learning Model with Transfer Learning. J. Hydrol. 2021, 600, 126698. [Google Scholar] [CrossRef]
- Li, Q.; Zhu, Y.; Shangguan, W.; Wang, X.; Li, L.; Yu, F. An Attention-Aware LSTM Model for Soil Moisture and Soil Temperature Prediction. Geoderma 2022, 409, 115651. [Google Scholar] [CrossRef]
- Li, L.; Dai, Y.; Shangguan, W.; Wei, N.; Wei, Z.; Gupta, S. Multistep Forecasting of Soil Moisture Using Spatiotemporal Deep Encoder–Decoder Networks. J. Hydrometeorol. 2022, 23, 337–350. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y. Convolutional Networks for Images, Speech, and Time Series. In The Handbook of Brain Theory and Neural Networks; MIT Press: Cambridge, MA, USA, 1995; Volume 3361. [Google Scholar]
- Elman, J.L. Finding Structure in Time. Cogn. Sci. 1990, 14, 179–211. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Shi, X.; Chen, Z.; Wang, H.; Yeung, D.-Y.; Wong, W.; Woo, W. Convolutional LSTM Network: A Machine Learning Approach for Precipitation Nowcasting. arXiv 2015, arXiv:1506.04214. [Google Scholar]
- Wang, C.; Wu, X.H.; Li, L.Q.; Wang, Y.S.; Li, Z.W. Convolutional Neural Network Application in Prediction of Soil Moisture Content. Spectrosc. Spect. Anal. 2018, 38, 36–41. [Google Scholar]
- Hegazi, E.H.; Yang, L.; Huang, J. A Convolutional Neural Network Algorithm for Soil Moisture Prediction from Sentinel-1 SAR Images. Remote Sens. 2021, 13, 4964. [Google Scholar] [CrossRef]
- Filipović, N.; Brdar, S.; Mimić, G.; Marko, O.; Crnojević, V. Regional Soil Moisture Prediction System Based on Long Short-Term Memory Network. Biosyst. Eng. 2022, 213, 30–38. [Google Scholar] [CrossRef]
- Yinglan, A.; Wang, G.; Hu, P.; Lai, X.; Xue, B.; Fang, Q. Root-Zone Soil Moisture Estimation Based on Remote Sensing Data and Deep Learning. Environ. Res. 2022, 212, 113278. [Google Scholar] [CrossRef]
- O’Neill, P.E.; Chan, S.; Njoku, E.G.; Jackson, T.; Bindlish, R.; Chaubell, J. SMAP L3 Radiometer Global Daily 36 km EASE-Grid Soil Moisture, Version 8; NASA National Snow and Ice Data Center Distributed Active Archive Center: Boulder, CO, USA, 2021. Available online: https://nsidc.org/data/spl3smp/versions/8 (accessed on 23 June 2022). [CrossRef]
- Zhang, R.; Kim, S.; Sharma, A. A Comprehensive Validation of the SMAP Enhanced Level-3 Soil Moisture Product Using Ground Measurements over Varied Climates and Landscapes. Remote Sens. Environ. 2019, 223, 82–94. [Google Scholar] [CrossRef]
- Chan, S.K.; Bindlish, R.; O’Neill, P.; Jackson, T.; Njoku, E.; Dunbar, S.; Chaubell, J.; Piepmeier, J.; Yueh, S.; Entekhabi, D.; et al. Development and Assessment of the SMAP Enhanced Passive Soil Moisture Product. Remote Sens. Environ. 2018, 204, 931–941. [Google Scholar] [CrossRef]
- Koster, R.D.; Reichle, R.H.; Mahanama, S.P.P. A Data-Driven Approach for Daily Real-Time Estimates and Forecasts of Near-Surface Soil Moisture. J. Hydrometeorol. 2017, 18, 837–843. [Google Scholar] [CrossRef]
- Sabater, J.M. ERA5-Land Hourly Data from 1981 to Present, Copernicus Climate Change Service (C3S) Climate Data Store (CDS) [Data Set]; Copernicus Climate Data Store: Brussels, Belgium, 2019. [Google Scholar]
- Shangguan, W.; Dai, Y.; Liu, B.; Zhu, A.; Duan, Q.; Wu, L.; Ji, D.; Ye, A.; Yuan, H.; Zhang, Q.; et al. A China Data Set of Soil Properties for Land Surface Modeling. J. Adv. Model. Earth Syst. 2013, 5, 212–224. [Google Scholar] [CrossRef]
- Loveland, T.R.; Reed, B.C.; Brown, J.F.; Ohlen, D.O.; Zhu, Z.; Yang, L.; Merchant, J.W. Development of a Global Land Cover Characteristics Database and IGBP DISCover from 1 Km AVHRR Data. Int. J. Remote Sens. 2000, 21, 1303–1330. [Google Scholar] [CrossRef]
- Balenović, I. Quality Assessment of High Density Digital Surface Model over Different Land Cover Classes. Period. Biol. 2016, 117, 459–470. [Google Scholar] [CrossRef]
- Chung, J.; Gulcehre, C.; Cho, K.; Bengio, Y. Empirical Evaluation of Gated Recurrent Neural Networks on Sequence Modeling. arXiv 2014, arXiv:1412.3555. [Google Scholar]
- Gupta, H.V.; Kling, H.; Yilmaz, K.K.; Martinez, G.F. Decomposition of the Mean Squared Error and NSE Performance Criteria: Implications for Improving Hydrological Modelling. J. Hydrol. 2009, 377, 80–91. [Google Scholar] [CrossRef]
- Li, M.; Wu, P.; Sexton, D.M.H.; Ma, Z. Potential Shifts in Climate Zones under a Future Global Warming Scenario Using Soil Moisture Classification. Clim. Dyn. 2021, 56, 2071–2092. [Google Scholar] [CrossRef]
- Beck, H.E.; Zimmermann, N.E.; McVicar, T.R.; Vergopolan, N.; Berg, A.; Wood, E.F. Present and Future Köppen-Geiger Climate Classification Maps at 1-Km Resolution. Sci. Data 2018, 5, 180214. [Google Scholar] [CrossRef]
- Pan, J.; Shangguan, W.; Li, L.; Yuan, H.; Zhang, S.; Lu, X.; Wei, N.; Dai, Y. Using Data-driven Methods to Explore the Predictability of Surface Soil Moisture with FLUXNET Site Data. Hydrol. Process. 2019, 33, 2978–2996. [Google Scholar] [CrossRef]
- Crow, W.T.; Chen, F.; Reichle, R.H.; Xia, Y. Diagnosing Bias in Modeled Soil Moisture/Runoff Coefficient Correlation Using the SMAP Level 4 Soil Moisture Product. Water Resour. Res. 2019, 55, 7010–7026. [Google Scholar] [CrossRef]
- Abed, M.; Imteaz, M.A.; Ahmed, A.N.; Huang, Y.F. Modelling Monthly Pan Evaporation Utilising Random Forest and Deep Learning Algorithms. Sci. Rep. 2022, 12, 13132. [Google Scholar] [CrossRef] [PubMed]
- Nayak, M.; Das, S.; Senapati, M.R. Improving Flood Prediction with Deep Learning Methods. J. Inst. Eng. India Ser. B 2022, 103, 1189–1205. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).