Forcing Mechanisms of the Interannual Sea Level Variability in the Midlatitude South Pacific during 2004–2020
Abstract
1. Introduction
2. Data and Models
2.1. Altimetric Sea Level Data
2.2. Atmospheric Reanalyses and Climate Indices
2.3. Argo-Based Steric Sea Level Estimates
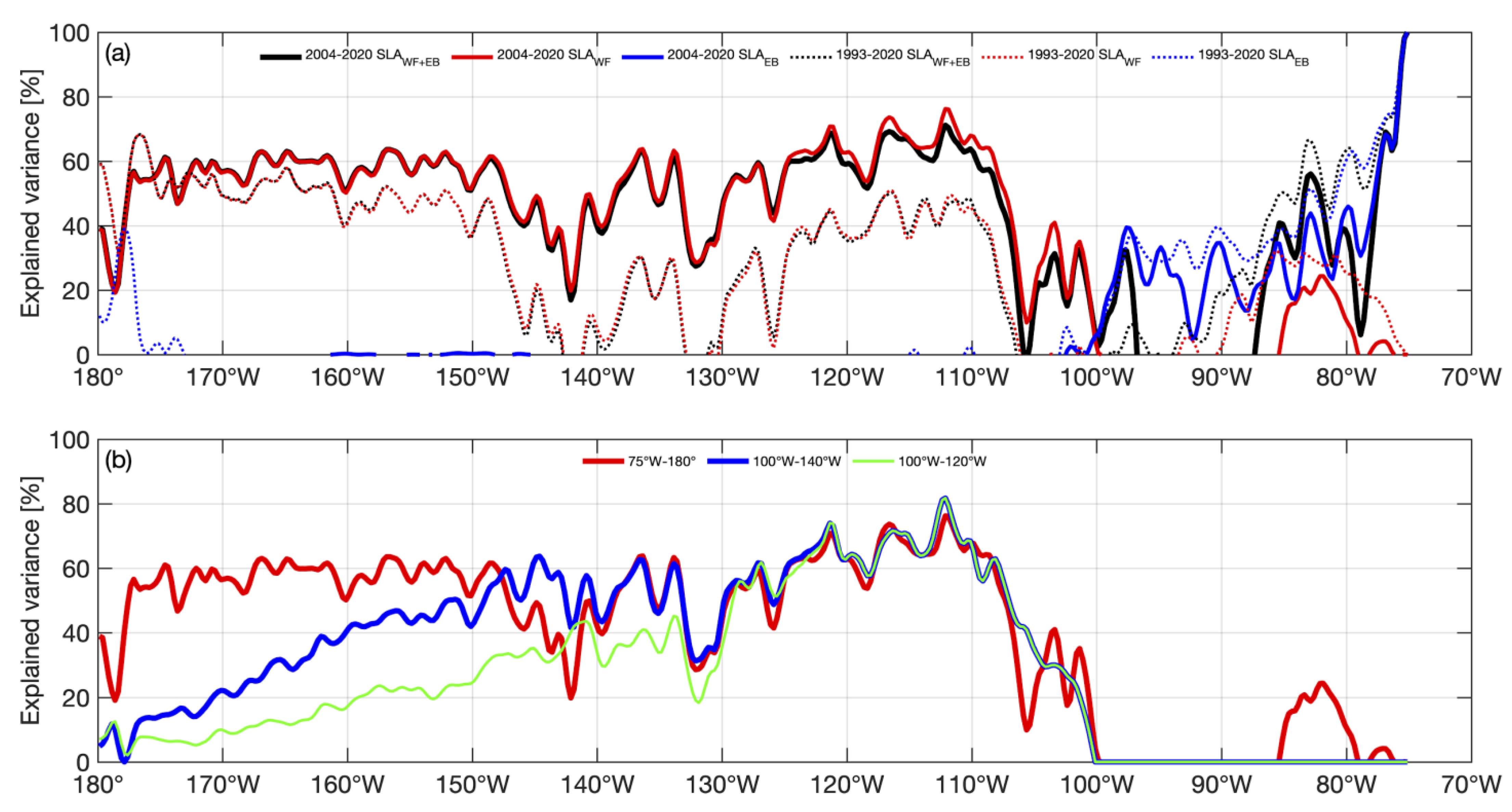
2.4. 1.5 Layer Reduced-Gravity Model
3. Results and Discussion
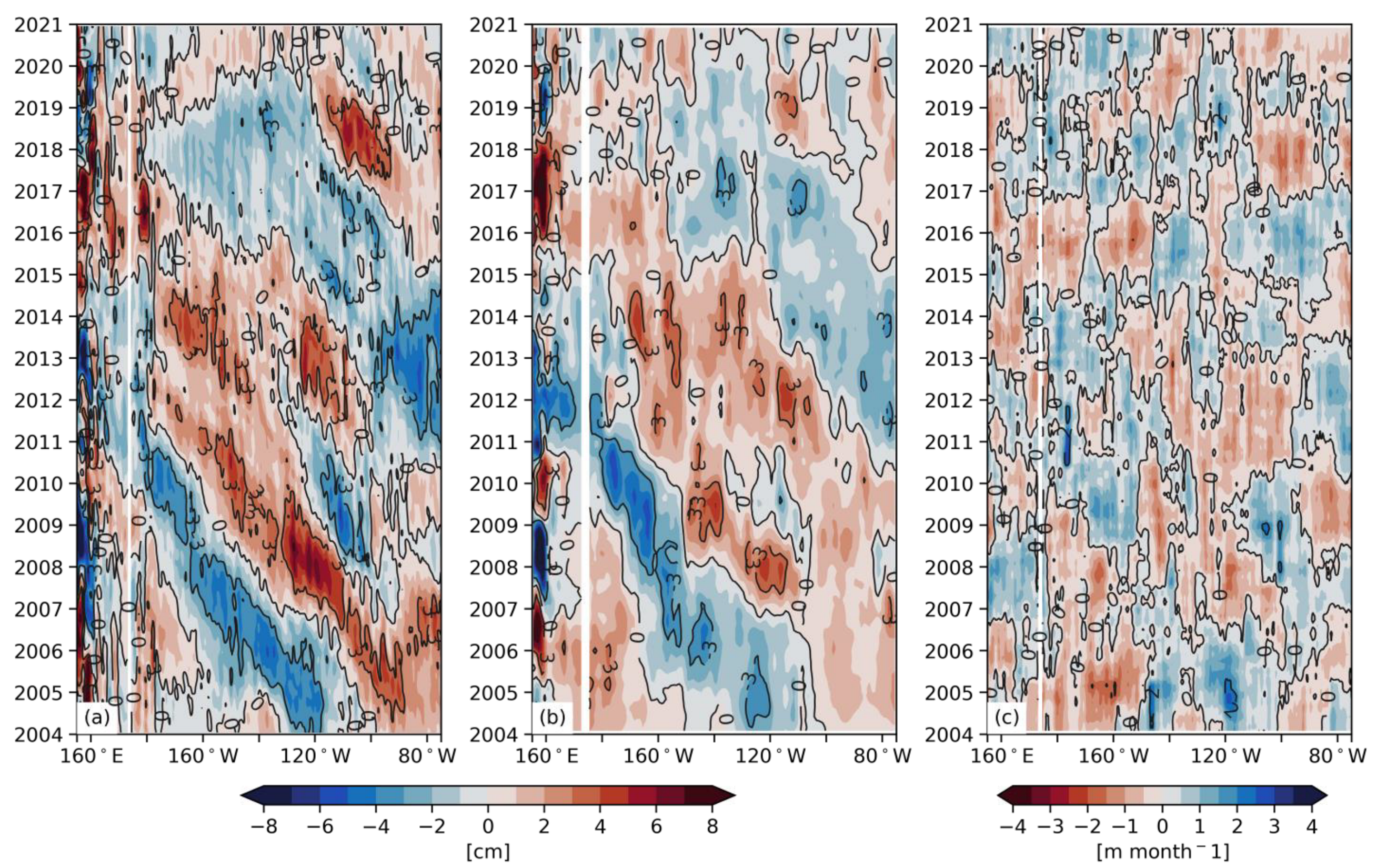
3.1. Basin-Scale Sea Level Changes and Local Wind Forcing in 2015–2020
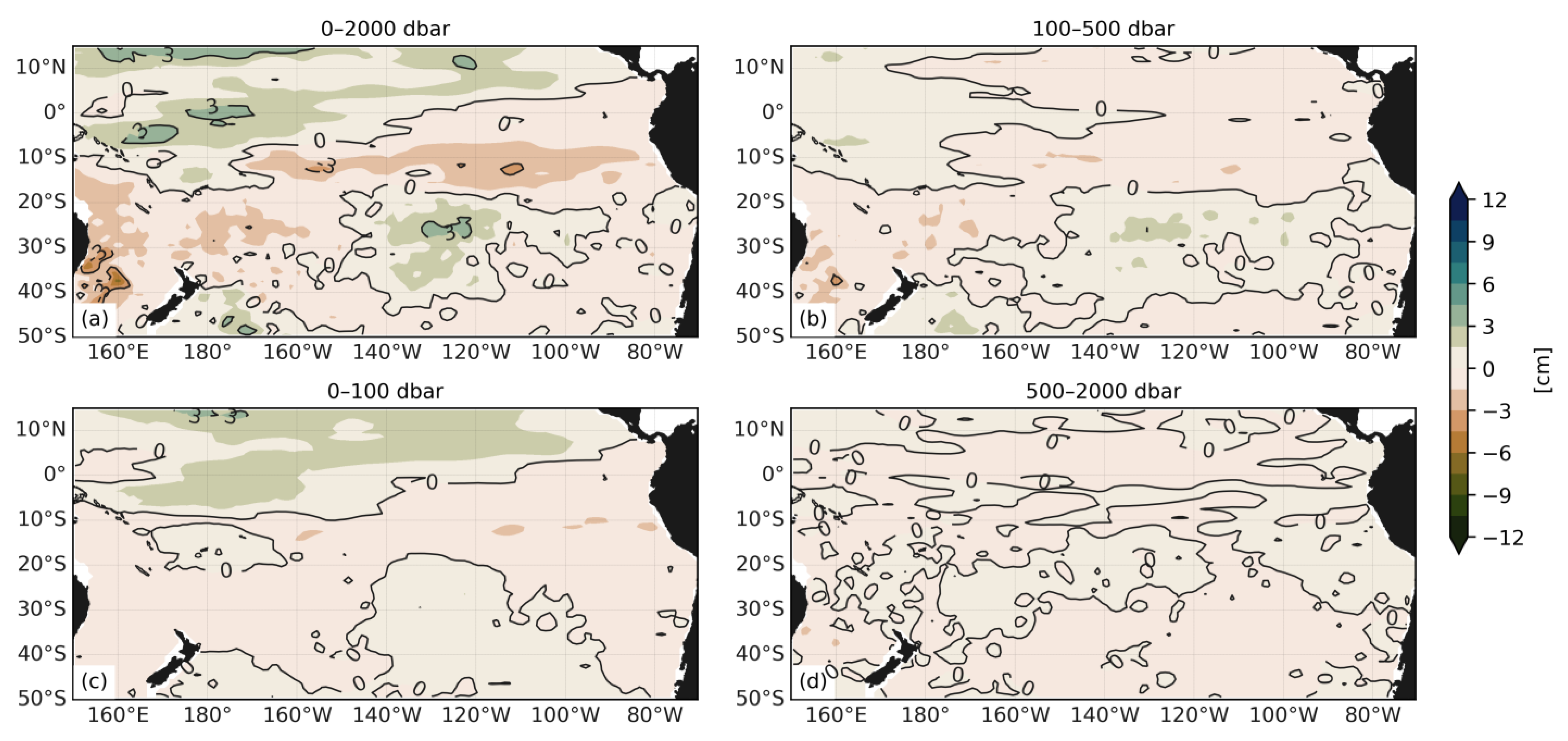
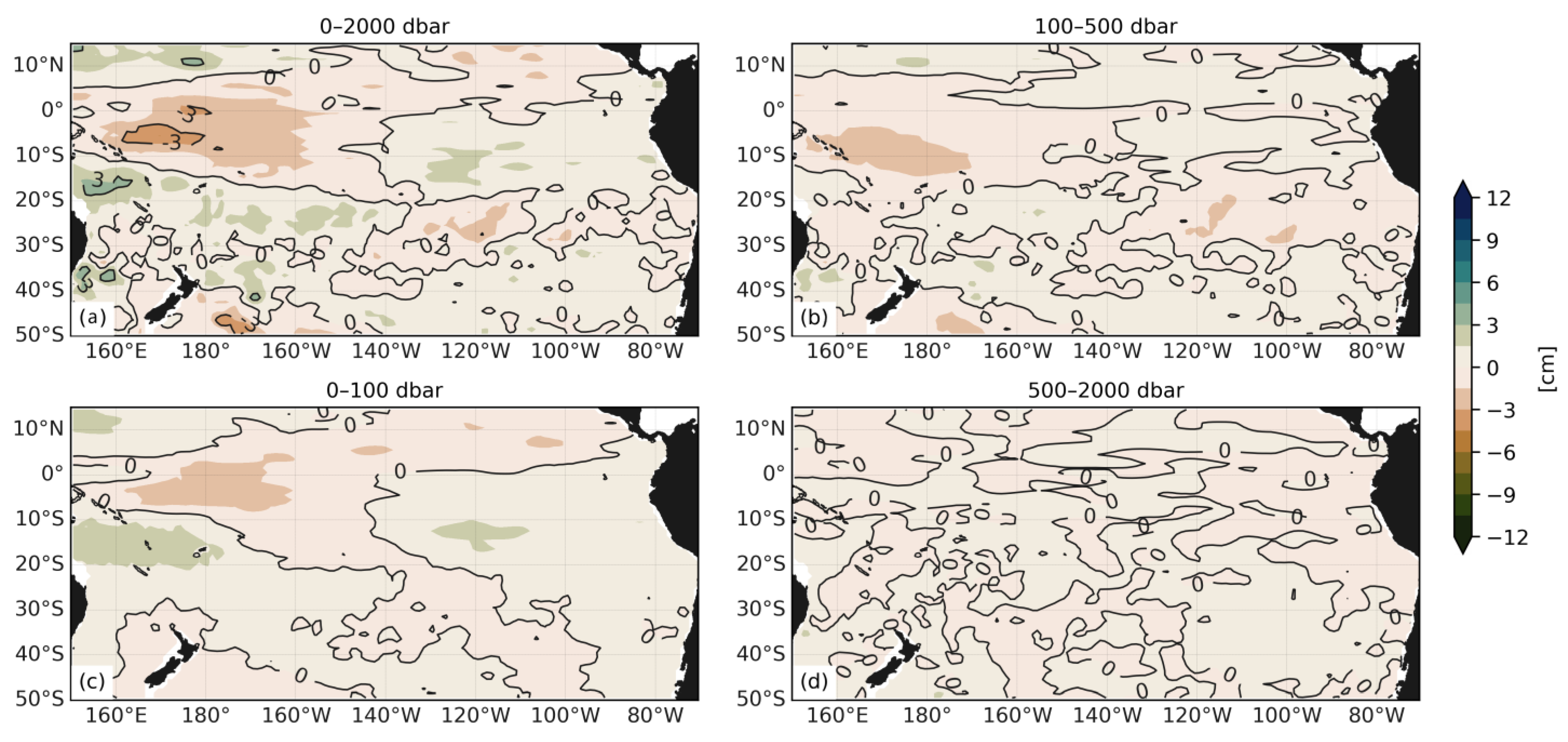
3.2. Basin-Scale Thermosteric and Halosteric Sea Level Changes in 2015–2020
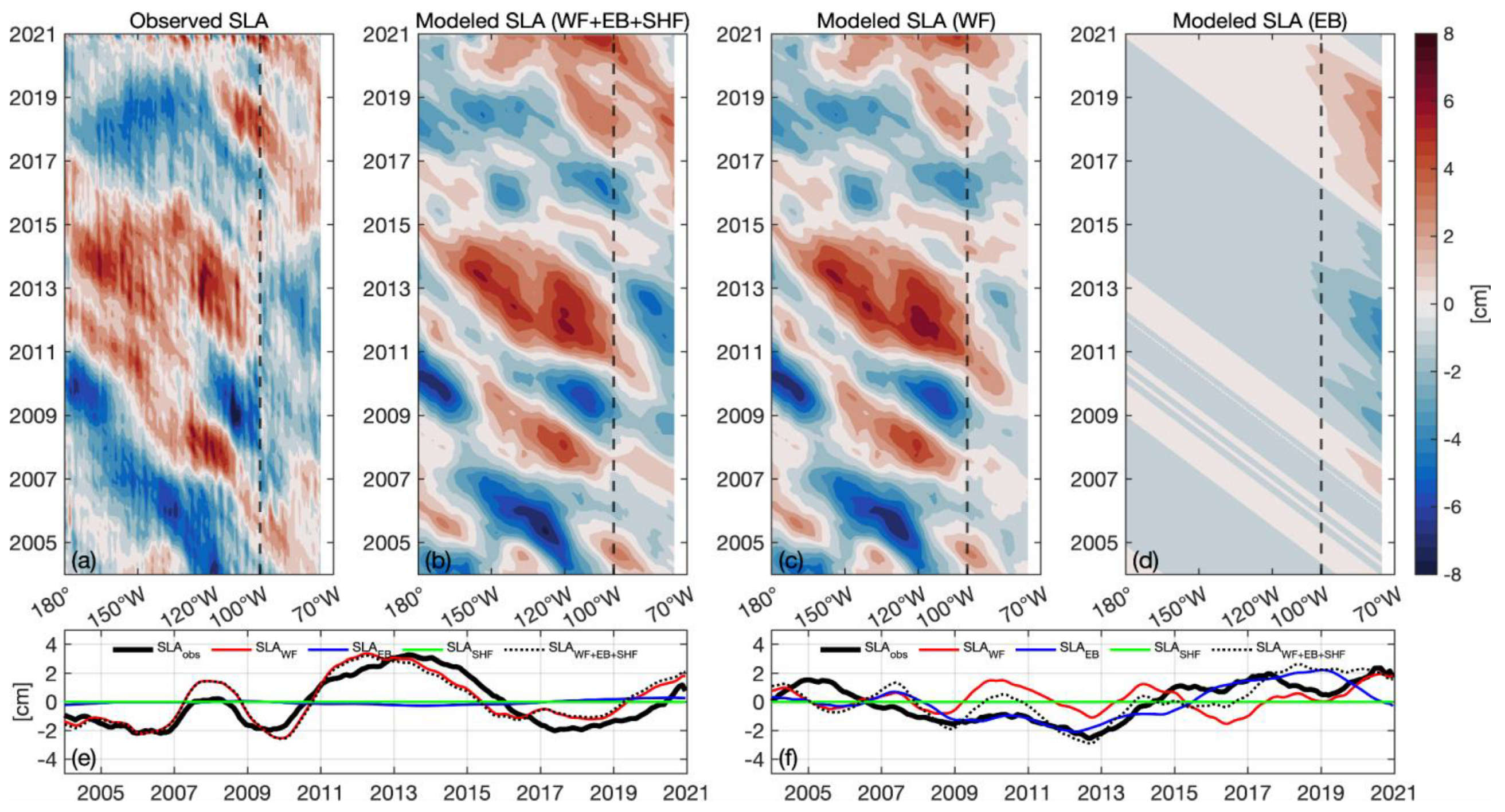
3.3. Wind-Driven Rossby Waves and Surface Heat Flux Forcing
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ablain, M.; Meyssignac, B.; Zawadzki, L.; Jugier, R.; Ribes, A.; Spada, G.; Benveniste, J.; Cazenave, A.; Picot, N. Uncertainty in satellite estimates of global mean sea-level changes, trend and acceleration. Earth Syst. Sci. Data 2019, 11, 1189–1202. [Google Scholar] [CrossRef]
- Chen, X.; Zhang, X.; Church, J.A.; Watson, C.S.; King, M.A.; Monselesan, D.; Legresy, B.; Harig, C. The increasing rate of global mean sea-level rise during 1993–2014. Nat. Clim. Change 2017, 7, 492–495. [Google Scholar] [CrossRef]
- Von Schuckmann, K.; Palmer, M.D.; Trenberth, K.E.; Cazenave, A.; Chambers, D.; Champollion, N.; Hansen, J.; Josey, S.A.; Loeb, N.; Mathieu, P.P.; et al. An imperative to monitor Earth’s energy imbalance. Nat. Clim. Change 2016, 6, 138–144. [Google Scholar] [CrossRef]
- Von Schuckmann, K.; Cheng, L.; Palmer, M.D.; Hansen, J.; Tassone, C.; Aich, V.; Adusumilli, S.; Beltrami, H.; Boyer, T.; Cuesta-Valero, F.J.; et al. Heat stored in the Earth system: Where does the energy go? Earth Syst. Sci. Data 2020, 12, 2013–2041. [Google Scholar] [CrossRef]
- Hakuba, M.Z.; Frederikse, T.; Landerer, F.W. Earth’s Energy Imbalance From the Ocean Perspective (2005–2019). Geophys. Res. Lett. 2021, 48, e2021GL093624. [Google Scholar] [CrossRef]
- Loeb, N.G.; Lyman, J.M.; Johnson, G.C.; Allan, R.; Doelling, D.R.; Wong, T.; Soden, B.; Stephens, G.L. Observed changes in top-of-the-atmosphere radiation and upper-ocean heating consistent within uncertainty. Nat. Geosci. 2012, 5, 110–113. [Google Scholar] [CrossRef]
- Oppenheimer, M.; Glavovic, B.; Hinkel, J.; van de Wal, R.; Magnan, A.K.; Abd-Elgawad, A.; Cai, R.; Cifuentes-Jara, M.; Deconto, R.M.; Ghosh, T.; et al. Sea Level Rise and Implications for Low-Lying Islands, Coasts and Communities. In IPCC Special Report on the Ocean and Cryosphere in a Changing Climate; Po, H.-O., Roberts, D., Masson-Delmotte, V., Zhai, P., Tignor, M., Poloczanska, E., Mintenbeck, K., Alegri, A., Nicolai, M., Okem, A., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2019; pp. 321–445. [Google Scholar] [CrossRef]
- Chen, J.L.; Wilson, C.R.; Tapley, B.D. Contribution of ice sheet and mountain glacier melt to recent sea level rise. Nat. Geosci. 2013, 6, 549–552. [Google Scholar] [CrossRef]
- Becker, M.; Meyssignac, B.; Letetrel, C.; Llovel, W.; Cazenave, A.; Delcroix, T. Sea level variations at tropical Pacific islands since 1950. Glob. Planet. Change 2012, 80–81, 85–98. [Google Scholar] [CrossRef]
- Kumar, V.; Melet, A.; Meyssignac, B.; Ganachaud, A.; Kessler, W.S.; Singh, A.; Aucan, J. Reconstruction of Local Sea Levels at South West Pacific Islands-A Multiple Linear Regression Approach (1988–2014). J. Geophys. Res. Oceans 2018, 123, 1502–1518. [Google Scholar] [CrossRef]
- Nicholls, R.J.; Cazenave, A. Sea-Level Rise and Its Impact on Coastal Zones. Science 2010, 328, 1517–1520. [Google Scholar] [CrossRef]
- Carret, A.; Llovel, W.; Penduff, T.; Molines, J. Atmospherically Forced and Chaotic Interannual Variability of Regional Sea Level and Its Components Over 1993–2015. J. Geophys. Res. Oceans 2021, 126, e2020JC017123. [Google Scholar] [CrossRef]
- Forget, G.; Ponte, R.M. The partition of regional sea level variability. Prog. Oceanogr. 2015, 137, 173–195. [Google Scholar] [CrossRef]
- Köhl, A. Detecting Processes Contributing to Interannual Halosteric and Thermosteric Sea Level Variability. J. Clim. 2014, 27, 2417–2426. [Google Scholar] [CrossRef]
- Meyssignac, B.; Piecuch, C.G.; Merchant, C.J.; Racault, M.F.; Palanisamy, H.; MacIntosh, C.; Sathyendranath, S.; Brewin, R. Causes of the regional variability in observed sea level, sea surface temperature and ocean colour over the period 1993–2011. In Integrative Study of the Mean Sea Level and Its Components; Springer: Cham, Switzerland, 2017; pp. 191–219. [Google Scholar]
- Griffies, S.M.; Yin, J.; Durack, P.J.; Goddard, P.; Bates, S.C.; Behrens, E.; Bentsen, M.; Bi, D.; Biastoch, A.; Böning, C.W.; et al. An assessment of global and regional sea level for years 1993–2007 in a suite of interannual CORE-II simulations. Ocean Model. 2014, 78, 35–89. [Google Scholar] [CrossRef]
- Llovel, W.; Lee, T. Importance and origin of halosteric contribution to sea level change in the southeast Indian Ocean during 2005–2013. Geophys. Res. Lett. 2015, 42, 1148–1157. [Google Scholar] [CrossRef]
- Lu, Y.; Li, Y.; Duan, J.; Lin, P.; Wang, F. Multidecadal Sea Level Rise in the Southeast Indian Ocean: The Role of Ocean Salinity Change. J. Clim. 2022, 35, 1479–1496. [Google Scholar] [CrossRef]
- Palmer, M.D.; Durack, P.J.; Chidichimo, M.P.; Church, J.A.; Cravatte, S.; Hill, K.; Johannessen, J.A.; Karstensen, J.; Lee, T.; Legler, D.; et al. Adequacy of the ocean observation system for quantifying regional heat and freshwater storage and change. Front. Mar. Sci. 2019, 6, 416. [Google Scholar] [CrossRef]
- Sprintall, J.; Cravatte, S.; Dewitte, B.; Du, Y.; Gupta, A.S. ENSO Oceanic Teleconnections. In El Niño Southern Oscillation in a Changing Climate; McPhaden, M., Santoso, A., Cai, W., Eds.; John Wiley & Sons: Hoboken, NJ, USA, 2020. [Google Scholar] [CrossRef]
- Thompson, D.W.; Wallace, J.M. Annular modes in the extratropical circulation. Part I: Month-to-month variability. J. Clim. 2000, 13, 1000–1016. [Google Scholar] [CrossRef]
- Qu, T.; Fukumori, I.; Fine, R.A. Spin-up of the southern hemisphere super gyre. J. Geophys. Res. Ocean. 2019, 124, 154–170. [Google Scholar] [CrossRef]
- Zilberman, N.V.; Roemmich, D.H.; Gille, S.T. Meridional volume transport in the South Pacific: Mean and SAM-related variability. J. Geophys. Res. Oceans 2014, 119, 2658–2678. [Google Scholar] [CrossRef]
- Llovel, W.; Kolodziejczyk, N.; Close, S.; Penduff, T.; Molines, J.-M.; Terray, L. Imprint of intrinsic ocean variability on decadal trends of regional sea level and ocean heat content using synthetic profiles. Environ. Res. Lett. 2022, 17, 044063. [Google Scholar] [CrossRef]
- Cravatte, S.; Serazin, G.; Penduff, T.; Menkes, C. Imprint of chaotic ocean variability on transports in the southwestern Pacific at interannual timescales. Ocean Sci. 2021, 17, 487–507. [Google Scholar] [CrossRef]
- Sun, J.; Zhang, L.; Hu, D. Decadal and Long-Term Variability of Sea Level in the Southwestern Pacific During 1948–2018. Geophys. Res. Lett. 2022, 49, e2022GL098747. [Google Scholar] [CrossRef]
- LloveL, W.; Terray, L. Observed southern upper-ocean warming over 2005–2014 and associated mechanisms. Environ. Res. Lett. 2016, 11, 124023. [Google Scholar] [CrossRef]
- Roemmich, D.; Church, J.; Gilson, J.; Monselesan, D.; Sutton, P.; Wijffels, S. Unabated planetary warming and its ocean structure since 2006. Nat. Clim. Change 2015, 5, 240–245. [Google Scholar] [CrossRef]
- Roemmich, D.; Gilson, J.; Sutton, P.; Zilberman, N. Multidecadal Change of the South Pacific Gyre Circulation. J. Phys. Oceanogr. 2016, 46, 1871–1883. [Google Scholar] [CrossRef]
- Volkov, D.L.; Lee, S.K.; Landerer, F.W.; Lumpkin, R. Decade-long deep ocean warming detected in the subtropical South Pacific. Geophys. Res. Lett. 2017, 44, 927–936. [Google Scholar] [CrossRef]
- Qiu, B.; Chen, S. Decadal Variability in the Large-Scale Sea Surface Height Field of the South Pacific Ocean: Observations and Causes. J. Phys. Oceanogr. 2006, 36, 1751–1762. [Google Scholar] [CrossRef]
- McPhaden, M.J. Playing hide and seek with El Niño. Nat. Clim. Change 2015, 5, 791–795. [Google Scholar] [CrossRef]
- Zhang, C.; Luo, J.J.; Li, S. Impacts of tropical Indian and Atlantic Ocean warming on the occurrence of the 2017/2018 La Niña. Geophys. Res. Lett. 2019, 46, 3435–3445. [Google Scholar] [CrossRef]
- Holbrook, N.J.; Goodwin, I.D.; McGregor, S.; Molina, E.; Power, S.B. ENSO to multi-decadal time scale changes in East Australian Current transports and Fort Denison sea level: Oceanic Rossby waves as the connecting mechanism. Deep. Sea Res. Part II Top. Stud. Oceanogr. 2011, 58, 547–558. [Google Scholar] [CrossRef]
- Kessler, W.S.; Cravatte, S. ENSO and Short-Term Variability of the South Equatorial Current Entering the Coral Sea. J. Phys. Oceanogr. 2013, 43, 956–969. [Google Scholar] [CrossRef]
- Kersalé, M.; Volkov, D.L.; Pujiana, K.; Zhang, H. Interannual variability of sea level in the southern Indian Ocean: Local vs. remote forcing mechanisms. Ocean Sci. 2022, 18, 193–212. [Google Scholar] [CrossRef]
- Nagura, M.; McPhaden, M.J. Interannual Variability in Sea Surface Height at Southern Midlatitudes of the Indian Ocean. J. Phys. Oceanogr. 2021, 51, 1595–1609. [Google Scholar] [CrossRef]
- Volkov, D.L.; Lee, S.-K.; Gordon, A.L.; Rudko, M. Unprecedented reduction and quick recovery of the South Indian Ocean heat content and sea level in 2014–2018. Sci. Adv. 2020, 6, eabc1151. [Google Scholar] [CrossRef] [PubMed]
- Bowen, M.M.; Sutton, P.J.H.; Roemmich, D. Wind-driven and steric fluctuations of sea surface height in the southwest Pacific. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef]
- Taburet, G.; Sanchez-Roman, A.; Ballarotta, M.; Pujol, M.-I.; Legeais, J.-F.; Fournier, F.; Faugere, Y.; Dibarboure, G. DUACS DT2018: 25 years of reprocessed sea level altimetry products. Ocean Sci. 2019, 15, 1207–1224. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Kalnay, E.; Kanamitsu, M.; Kistler, R.; Collins, W.; Deaven, D.; Gandin, L.; Iredell, M.; Saha, S.; White, G.; Woollen, J.; et al. The NCEP/NCAR 40-year reanalysis project. Bull. Am. Meteorol. Soc. 1996, 77, 437–472. [Google Scholar] [CrossRef]
- Kobayashi, S.; Ota, Y.; Harada, Y.; Ebita, A.; Moriya, M.; Onoda, H.; Onogi, K.; Kamahori, H.; Kobayashi, C.; Endo, H.; et al. The JRA-55 Reanalysis: General Specifications and Basic Characteristics. J. Meteorol. Soc. Jpn. Ser. II 2015, 93, 5–48. [Google Scholar] [CrossRef]
- Yu, L. Global Air–Sea Fluxes of Heat, Fresh Water, and Momentum: Energy Budget Closure and Unanswered Questions. Annu. Rev. Mar. Sci. 2019, 11, 227–248. [Google Scholar] [CrossRef] [PubMed]
- Roemmich, D.; Gilson, J. The 2004–2008 mean and annual cycle of temperature, salinity, and steric height in the global ocean from the Argo Program. Prog. Oceanogr. 2009, 82, 81–100. [Google Scholar] [CrossRef]
- Roemmich, D.; Alford, M.H.; Claustre, H.; Johnson, K.; King, B.; Moum, J.; Oke, P.; Owens, W.B.; Pouliquen, S.; Purkey, S.; et al. On the Future of Argo: A Global, Full-Depth, Multi-Disciplinary Array. Front. Mar. Sci. 2019, 6, 439. [Google Scholar] [CrossRef]
- Wong, A.P.S.; Wijffels, S.E.; Riser, S.C.; Pouliquen, S.; Hosoda, S.; Roemmich, D.; Gilson, J.; Johnson, G.C.; Martini, K.; Murphy, D.J.; et al. Argo Data 1999–2019: Two Million Temperature-Salinity Profiles and Subsurface Velocity Observations From a Global Array of Profiling Floats. Front. Mar. Sci. 2020, 7, 700. [Google Scholar] [CrossRef]
- Barnoud, A.; Pfeffer, J.; Guérou, A.; Frery, M.; Siméon, M.; Cazenave, A.; Chen, J.; Llovel, W.; Thierry, V.; Legeais, J.; et al. Contributions of Altimetry and Argo to Non-Closure of the Global Mean Sea Level Budget Since 2016. Geophys. Res. Lett. 2021, 48, e2021GL092824. [Google Scholar] [CrossRef]
- Gaillard, F.; Reynaud, T.; Thierry, V.; Kolodziejczyk, N.; Von Schuckmann, K. In Situ–Based Reanalysis of the Global Ocean Temperature and Salinity with ISAS: Variability of the Heat Content and Steric Height. J. Clim. 2016, 29, 1305–1323. [Google Scholar] [CrossRef]
- Qiu, B. Large-scale variability in the midlatitude subtropical and subpolar North Pacific Ocean: Observations and causes. J. Phys. Oceanogr. 2002, 32, 353–375. [Google Scholar] [CrossRef]
- Chelton, D.B.; DeSzoeke, R.A.; Schlax, M.G.; El Naggar, K.; Siwertz, N. Geographical variability of the first baroclinic Rossby radius of deformation. J. Phys. Oceanogr. 1998, 28, 433–460. [Google Scholar] [CrossRef]
- Duan, J.; Li, Y.; Wang, F.; Hu, A.; Han, W.; Zhang, L.; Lin, P.; Rosenbloom, N.; Meehl, G.A. Rapid Sea-Level Rise in the Southern-Hemisphere Subtropical Oceans. J. Clim. 2021, 34, 9401–9423. [Google Scholar] [CrossRef]
- Zhang, X.; Church, J.A. Sea level trends, interannual and decadal variability in the Pacific Ocean. Geophys. Res. Lett. 2012, 39. [Google Scholar] [CrossRef]
- Hill, K.L.; Rintoul, S.R.; Ridgway, K.R.; Oke, P.R. Decadal changes in the South Pacific western boundary current system revealed in observations and ocean state estimates. J. Geophys. Res. Atmos. 2011, 116. [Google Scholar] [CrossRef]
- Alory, G.; Delcroix, T. Interannual sea level changes and associated mass transports in the tropical Pacific from TOPEX/Poseidon data and linear model results (1964–1999). J. Geophys. Res. Atmos. 2002, 107, 17-1–17-22. [Google Scholar] [CrossRef]
- Cheng, L.; Trenberth, K.E.; Fasullo, J.T.; Mayer, M.; Balmaseda, M.; Zhu, J. Evolution of Ocean Heat Content Related to ENSO. J. Clim. 2019, 32, 3529–3556. [Google Scholar] [CrossRef]
- L’Heureux, M.L.; Thompson, D.W.J. Observed Relationships between the El Niño–Southern Oscillation and the Extratropical Zonal-Mean Circulation. J. Clim. 2006, 19, 276–287. [Google Scholar] [CrossRef]
- Pohl, B.; Fauchereau, N.; Reason, C.J.C.; Rouault, M. Relationships between the Antarctic Oscillation, the Madden–Julian Oscillation, and ENSO, and Consequences for Rainfall Analysis. J. Clim. 2010, 23, 238–254. [Google Scholar] [CrossRef]
- Gasparin, F.; Roemmich, D. The strong freshwater anomaly during the onset of the 2015/2016 El Niño. Geophys. Res. Lett. 2016, 43, 6452–6460. [Google Scholar] [CrossRef]
- Rykova, T.; Oke, P.R. Recent freshening of the East Australian Current and its eddies. Geophys. Res. Lett. 2015, 42, 9369–9378. [Google Scholar] [CrossRef]
- Johnson, G.C.; Purkey, S.G.; Zilberman, N.V.; Roemmich, D. Deep Argo Quantifies Bottom Water Warming Rates in the Southwest Pacific Basin. Geophys. Res. Lett. 2019, 46, 2662–2669. [Google Scholar] [CrossRef]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Germineaud, C.; Volkov, D.L.; Cravatte, S.; Llovel, W. Forcing Mechanisms of the Interannual Sea Level Variability in the Midlatitude South Pacific during 2004–2020. Remote Sens. 2023, 15, 352. https://doi.org/10.3390/rs15020352
Germineaud C, Volkov DL, Cravatte S, Llovel W. Forcing Mechanisms of the Interannual Sea Level Variability in the Midlatitude South Pacific during 2004–2020. Remote Sensing. 2023; 15(2):352. https://doi.org/10.3390/rs15020352
Chicago/Turabian StyleGermineaud, C., D. L. Volkov, S. Cravatte, and W. Llovel. 2023. "Forcing Mechanisms of the Interannual Sea Level Variability in the Midlatitude South Pacific during 2004–2020" Remote Sensing 15, no. 2: 352. https://doi.org/10.3390/rs15020352
APA StyleGermineaud, C., Volkov, D. L., Cravatte, S., & Llovel, W. (2023). Forcing Mechanisms of the Interannual Sea Level Variability in the Midlatitude South Pacific during 2004–2020. Remote Sensing, 15(2), 352. https://doi.org/10.3390/rs15020352







