Estimating Nighttime PM2.5 Concentration in Beijing Based on NPP/VIIRS Day/Night Band
Abstract
1. Introduction
2. Study Area and Data
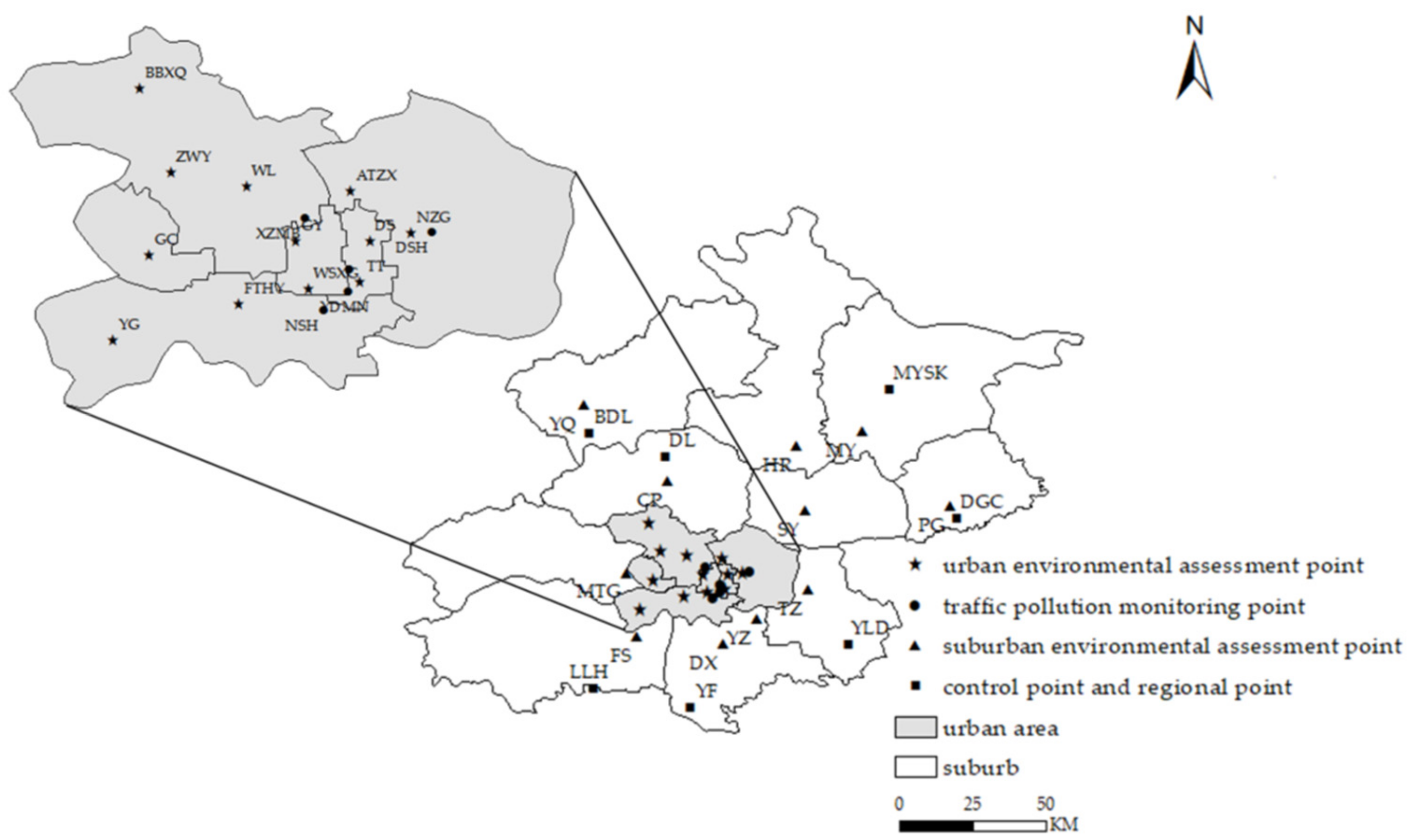
2.1. Study Area
2.2. Data
2.2.1. Ground PM2.5 Measurements
2.2.2. Remote Sensing Data
- VIIRS
- 2.
- MODIS
2.2.3. Meteorological Data
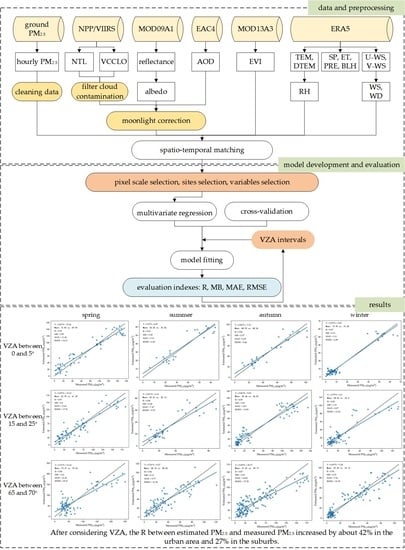
3. Method
3.1. Data Preprocessing
3.1.1. Selection of Observations by Cloud Mask
3.1.2. Moonlight Correction
3.1.3. Data Integration
3.2. Model Development
3.2.1. Pixel Scale Selection
3.2.2. Sites Selection
3.2.3. Variables Selection
3.2.4. Multivariate Regression Model Building
3.3. Model Validation
4. Results and Discussion
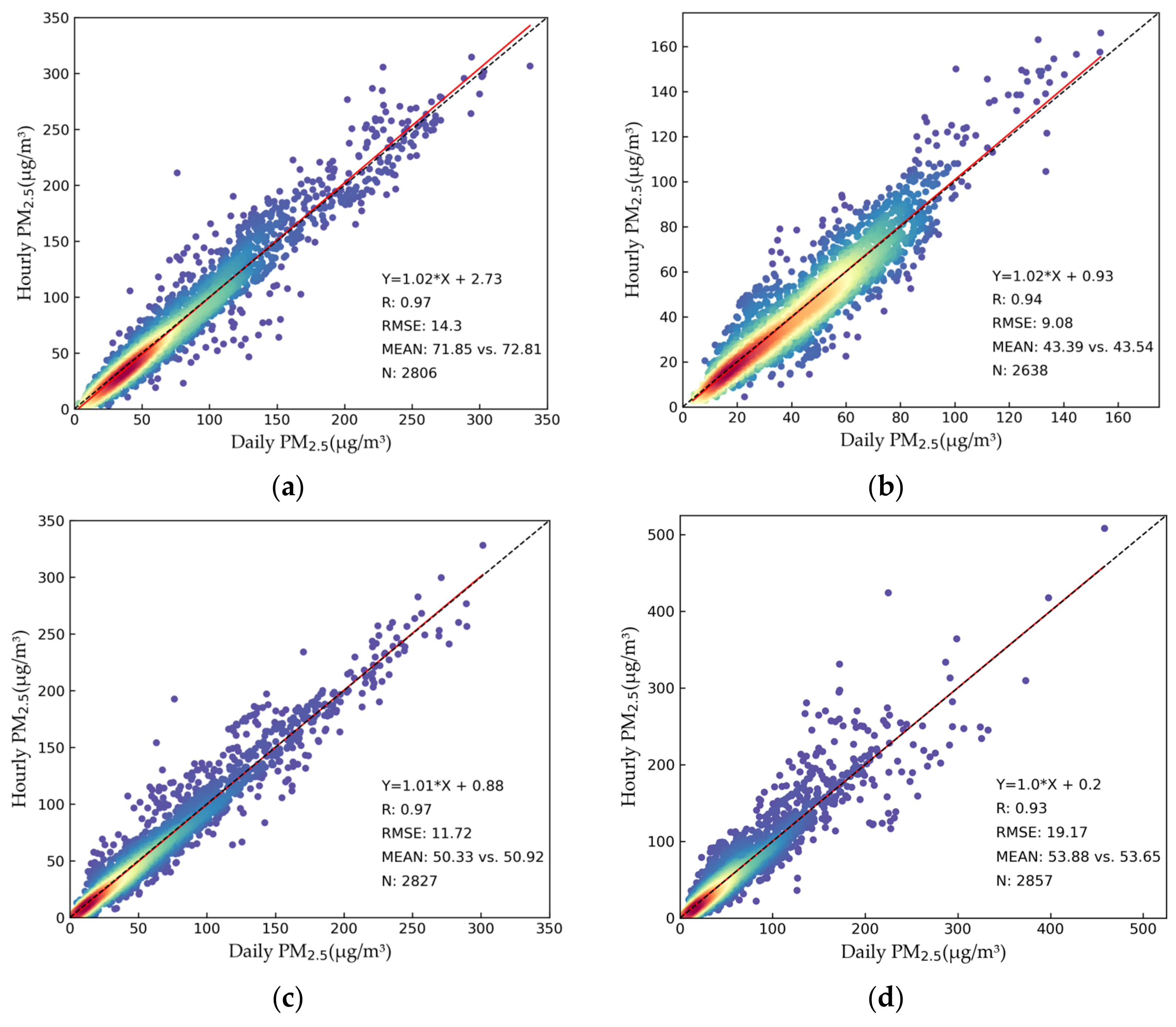
4.1. Collaboration between Nighttime PM2.5 and Daytime PM2.5
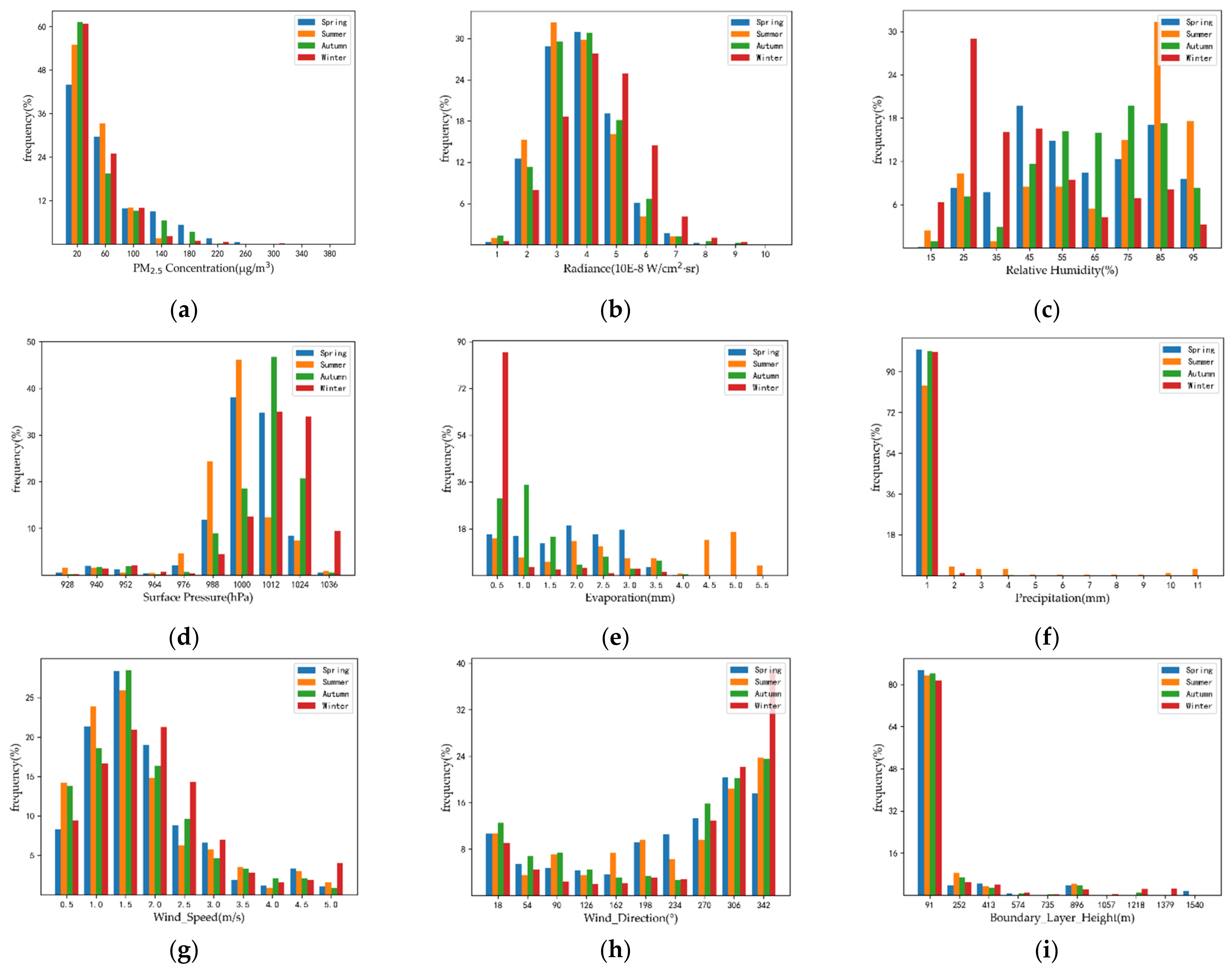
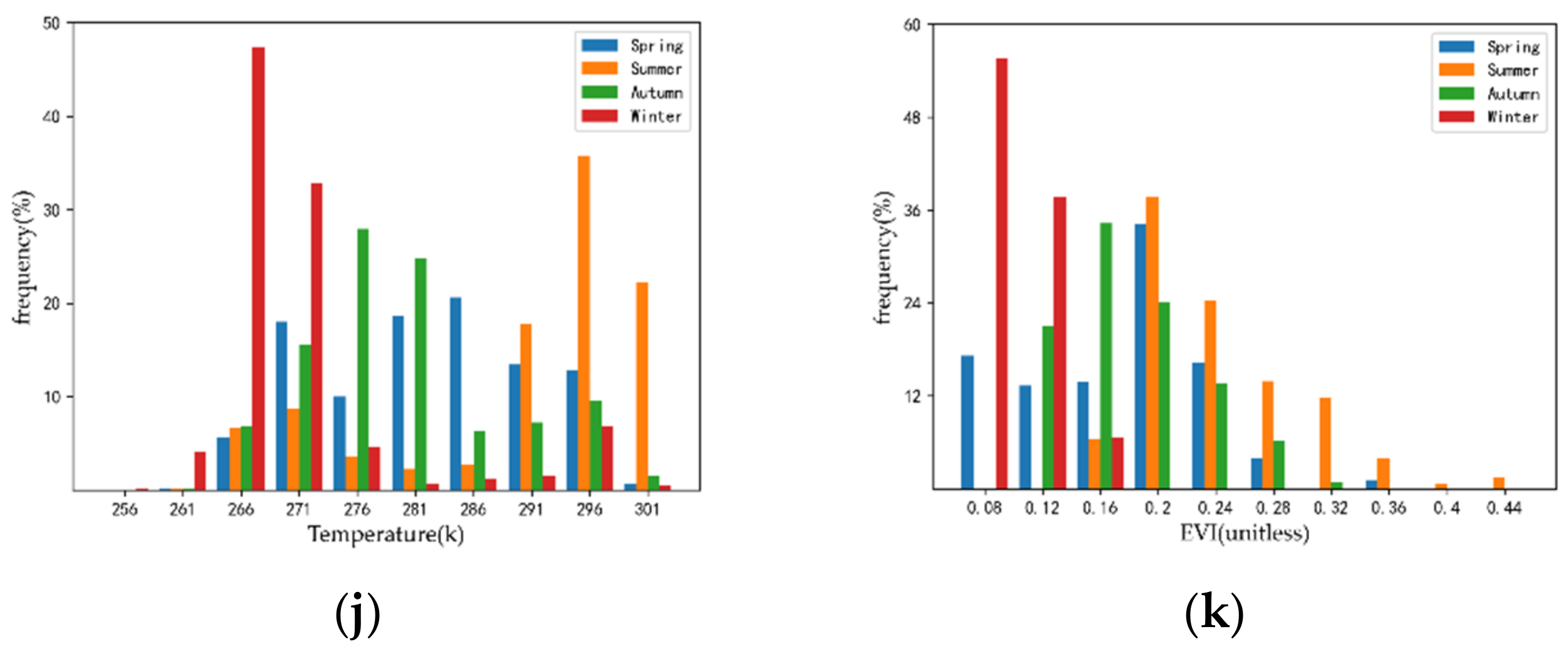
4.2. Descriptive Statistics
4.3. The Result of Correcting Moonlight
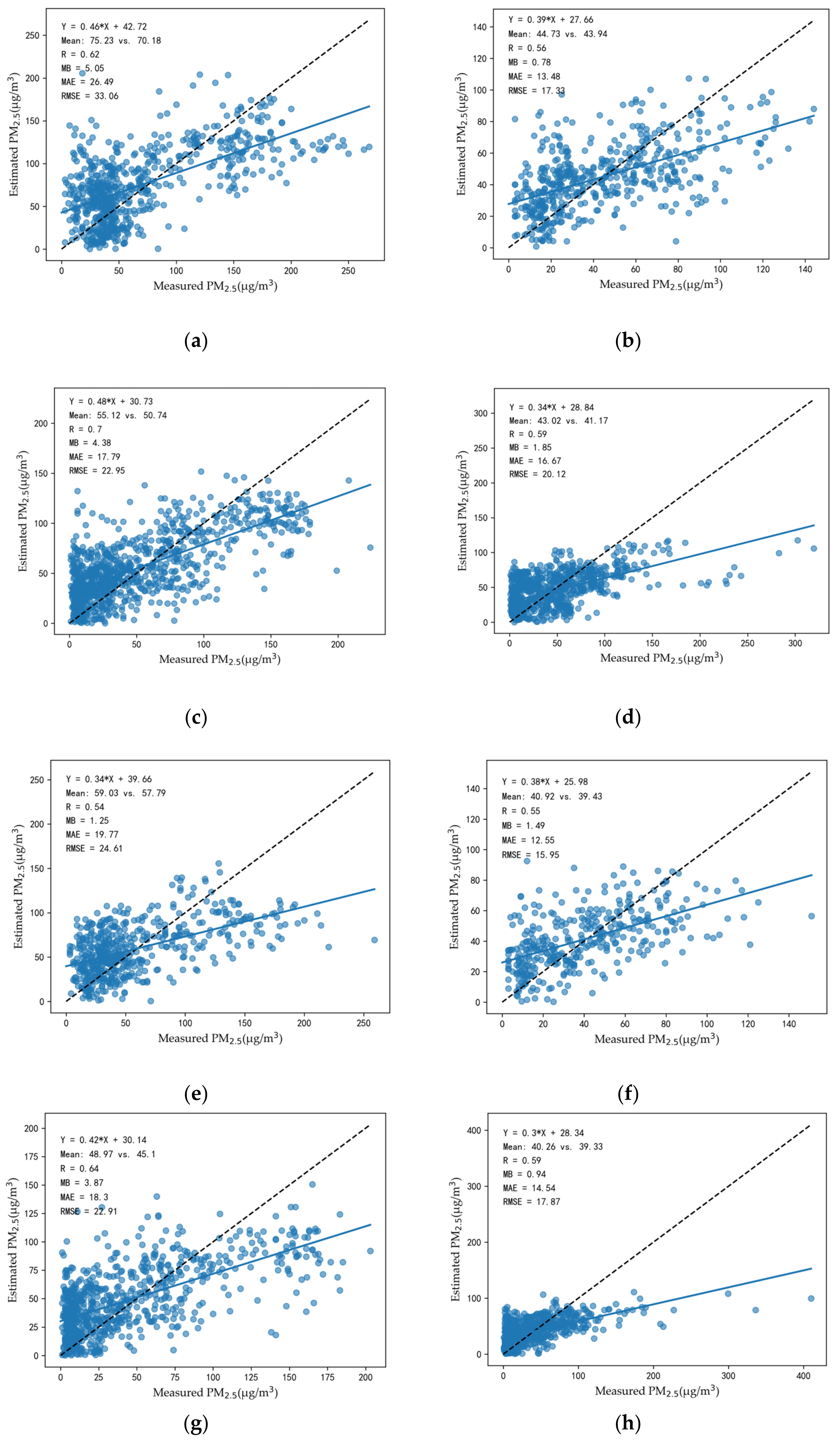
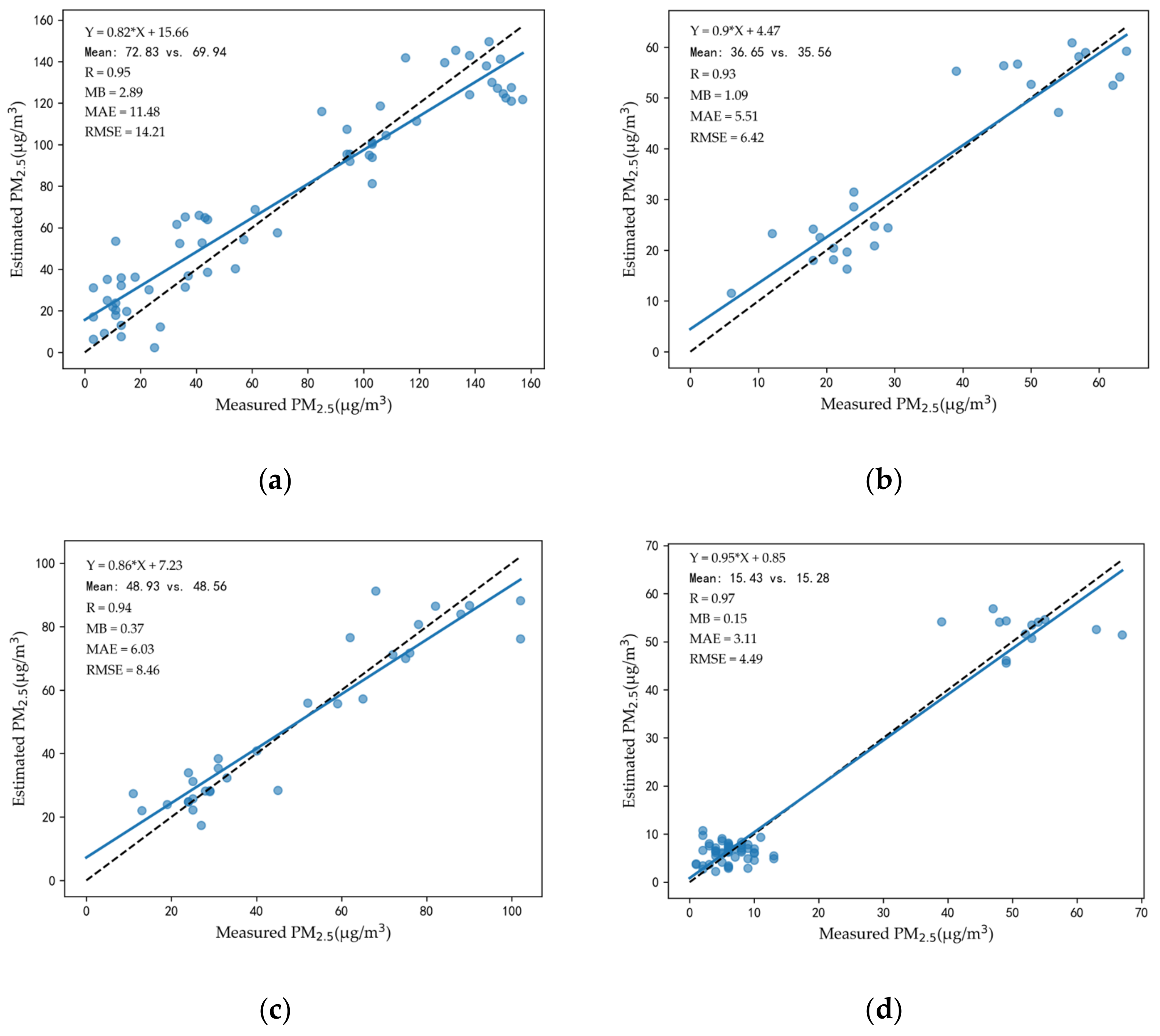
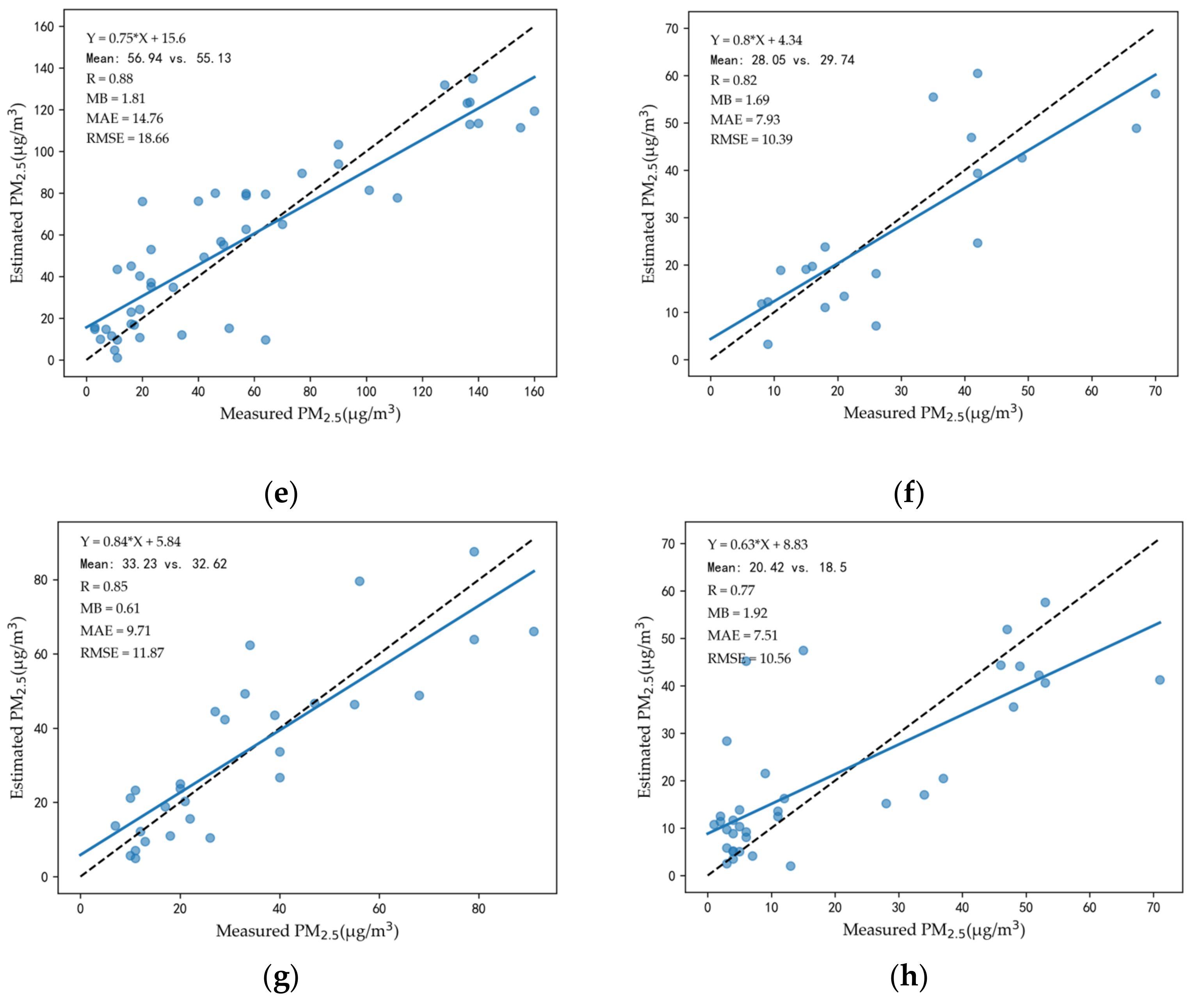
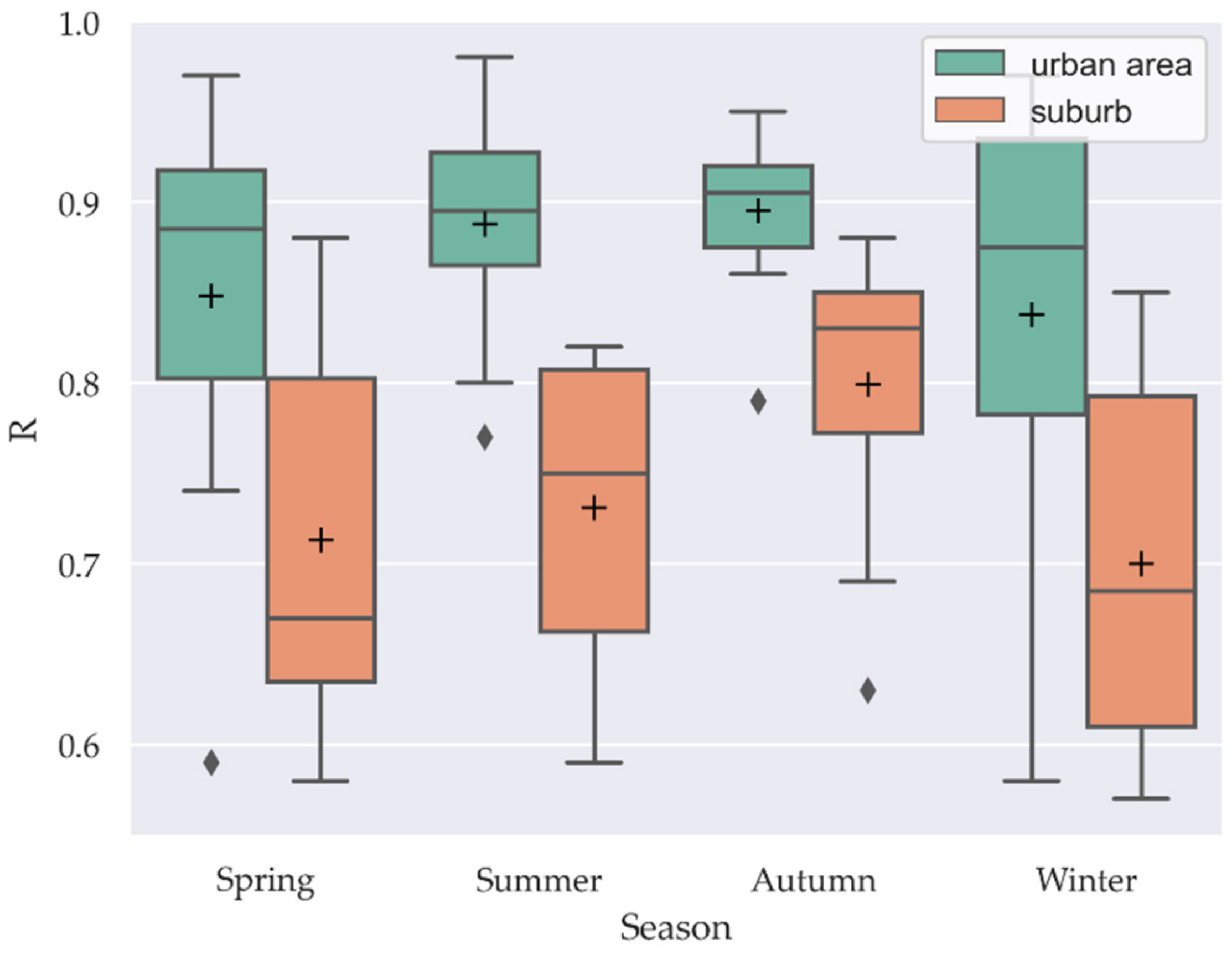
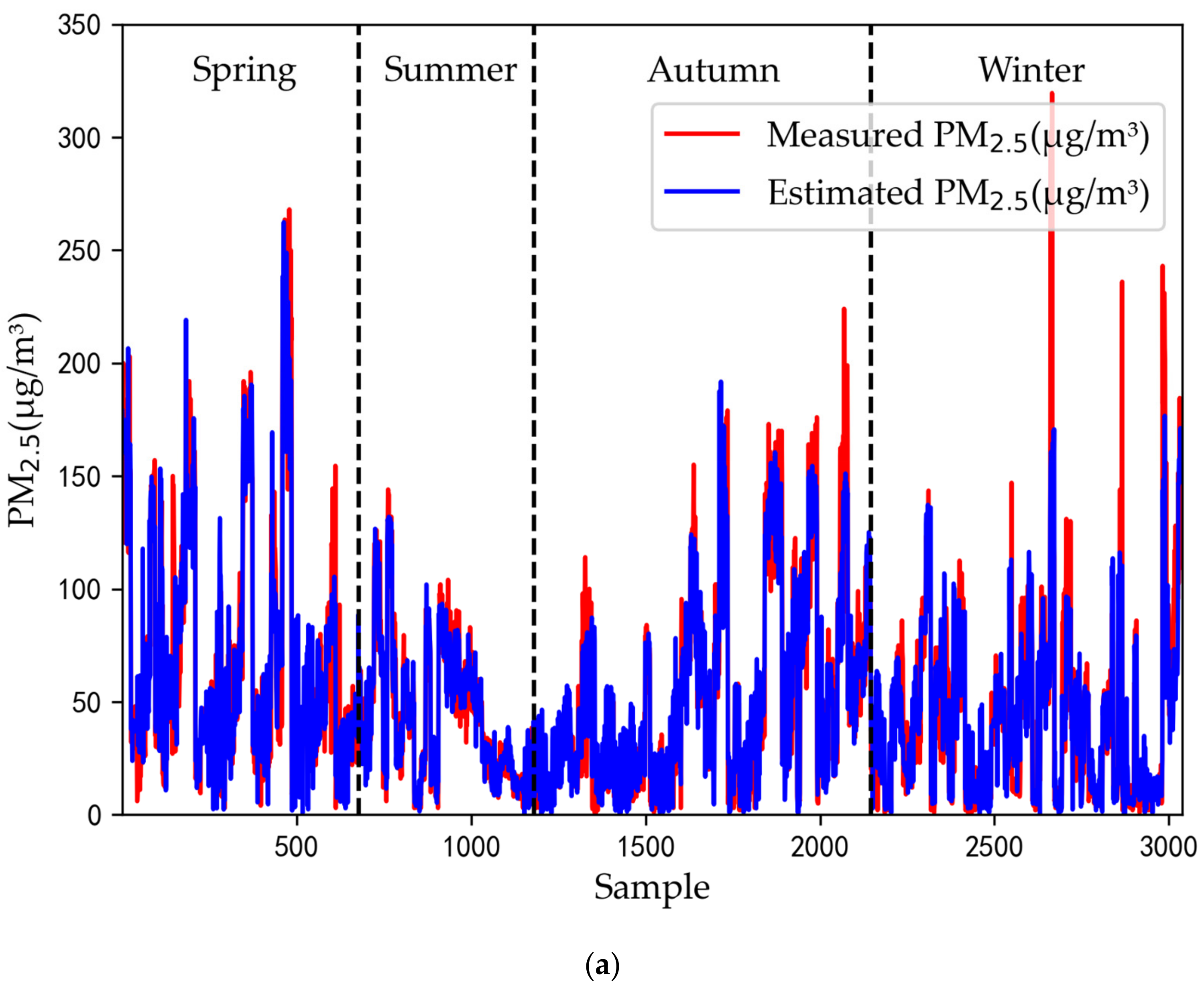
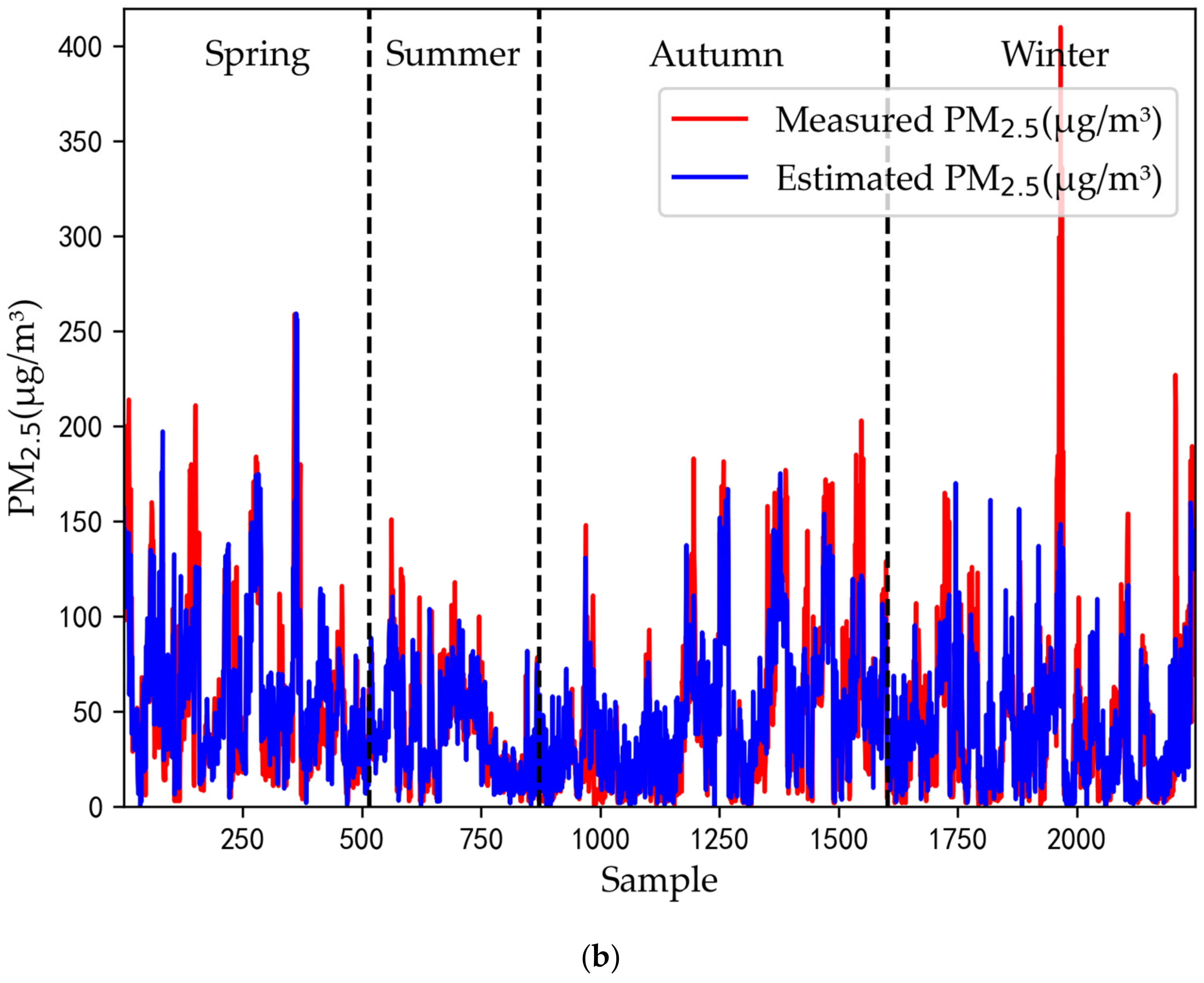
4.4. Model Performance
5. Conclusions
- Estimating PM2.5 at night can cooperate with estimated PM2.5 in the daytime, then reasonably evaluate the concentration of PM2.5. Taking NPP (2:00 CST) and Terra (11:00 CST) as examples, the correlation coefficient between the mean of PM2.5 at transit time and daily PM2.5 was as high as 0.95.
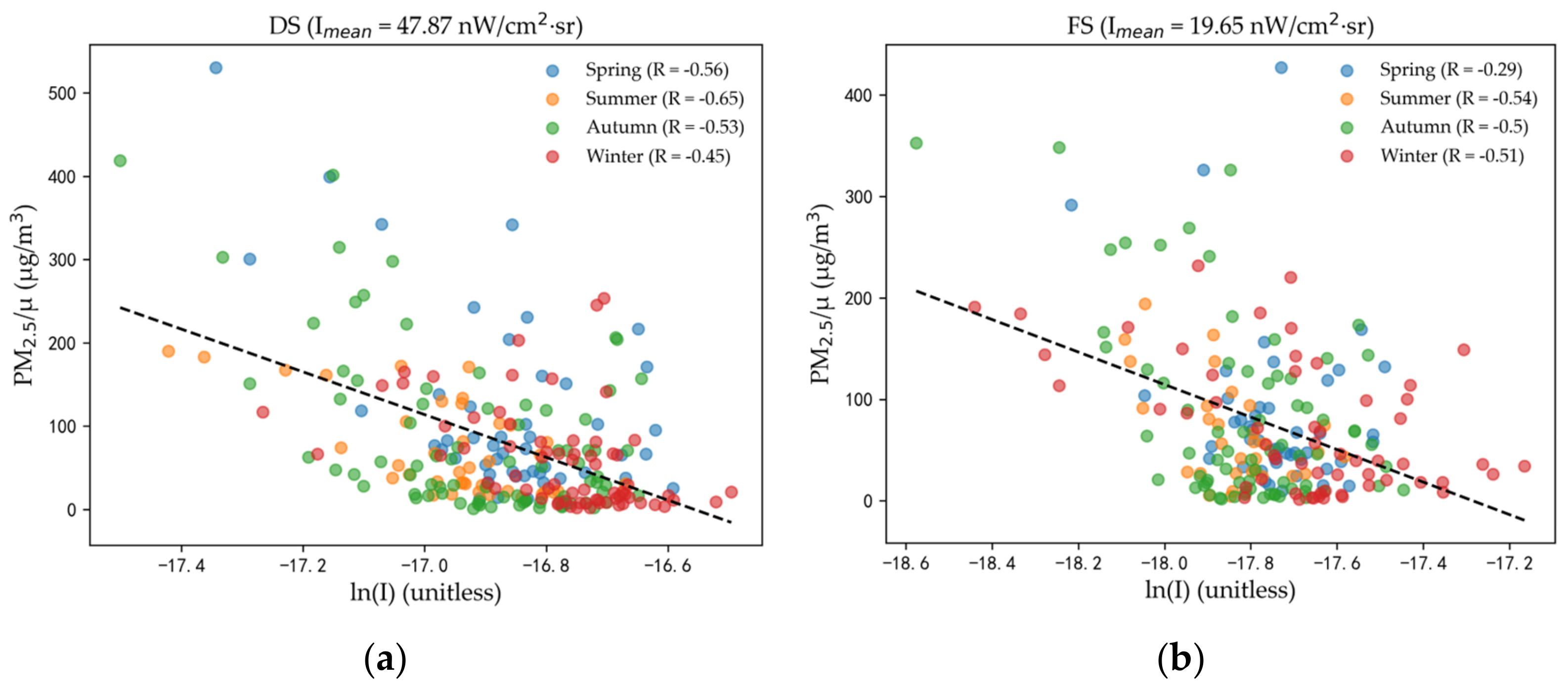
- In urban and suburban areas with high artificial light background at night (annual radiance above 14 nW/cm2·sr), moonlight represents only a small fraction of the light flux received by the satellite. The impact of moonlight can be ignored in estimating nighttime PM2.5. However, moonlight must be corrected in low light areas such as control points and regional points.
- The impact factors of estimating PM2.5 in urban and suburban areas are diverse each season, predominantly in meteorological changes. These factors significantly affecting the estimation are radiance, annual radiance, relative humidity, and evaporation.
- It is essential to consider light anisotropy when utilizing NTL to estimate PM2.5. In this study, coefficients between estimated PM2.5 and measured PM2.5 boosted greatly after introducing the satellite viewing zenith angle. Specifically, in four seasons it increased from 0.62, 0.56, 0.7, and 0.59 to 0.85, 0.89, 0.9, and 0.84 in the urban area, and from 0.54, 0.55, 0.64, and 0.59 to 0.71, 0.73, 0.8, and 0.7 in the suburbs.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Silver, B.; Reddington, C.; Arnold, S.; Spracklen, D. Substantial changes in air pollution across China during 2015–2017. Environ. Res. Lett. 2018, 13, 114012. [Google Scholar] [CrossRef]
- Reddy, V.; Yedavalli, P.; Mohanty, S.; Nakhat, U. Deep air: Forecasting air pollution in Beijing, China. Environ. Sci. 2018. [Google Scholar]
- Linares, C.; Diaz, J. Impact of particulate matter with diameter of less than 2.5 microns [PM2. 5] on daily hospital admissions in 0-10-year-olds in Madrid. Spain [2003–2005]. Gac. Sanit. 2009, 23, 192–197. [Google Scholar] [CrossRef] [PubMed]
- Hansen, J.; Sato, M.; Ruedy, R. Radiative forcing and climate response. J. Geophys. Res. Atmos. 1997, 102, 6831–6864. [Google Scholar] [CrossRef]
- Pui, D.Y.; Chen, S.-C.; Zuo, Z. PM2.5 in China: Measurements, sources, visibility and health effects, and mitigation. Particuology 2014, 13, 1–26. [Google Scholar] [CrossRef]
- Cohen, A.J.; Brauer, M.; Burnett, R.; Anderson, H.R.; Frostad, J.; Estep, K.; Balakrishnan, K.; Brunekreef, B.; Dandona, L.; Dandona, R. Estimates and 25-year trends of the global burden of disease attributable to ambient air pollution: An analysis of data from the Global Burden of Diseases Study 2015. Lancet 2017, 389, 1907–1918. [Google Scholar] [CrossRef]
- Hu, F.; Guo, Y. Health impacts of air pollution in China. Front. Environ. Sci. Eng. 2021, 15, 1–18. [Google Scholar] [CrossRef]
- Li, J.; Carlson, B.E.; Lacis, A.A. How well do satellite AOD observations represent the spatial and temporal variability of PM2. 5 concentration for the United States? Atmos. Environ. 2015, 102, 260–273. [Google Scholar] [CrossRef]
- Marsha, A.; Larkin, N.K. A statistical model for predicting PM2.5 for the western United States. J. Air Waste Manag. Assoc. 2019, 69, 1215–1229. [Google Scholar] [CrossRef]
- Zhai, S.; Jacob, D.J.; Wang, X.; Shen, L.; Li, K.; Zhang, Y.; Gui, K.; Zhao, T.; Liao, H. Fine particulate matter (PM2.5) trends in China, 2013–2018: Separating contributions from anthropogenic emissions and meteorology. Atmos. Chem. Phys. 2019, 19, 11031–11041. [Google Scholar] [CrossRef]
- You, W.; Zang, Z.; Zhang, L.; Li, Y.; Wang, W. Estimating national-scale ground-level PM2.5 concentration in China using geographically weighted regression based on MODIS and MISR AOD. Environ. Sci. Pollut. Res. 2016, 23, 8327–8338. [Google Scholar] [CrossRef] [PubMed]
- Zou, B.; Chen, J.; Zhai, L.; Fang, X.; Zheng, Z. Satellite based mapping of ground PM2.5 concentration using generalized additive modeling. Remote Sens. 2017, 9, 1. [Google Scholar] [CrossRef]
- Zhang, X.; Hu, H. Improving satellite-driven PM2.5 models with VIIRS nighttime light data in the Beijing–Tianjin–Hebei region, China. Remote Sens. 2017, 9, 908. [Google Scholar] [CrossRef]
- Unnithan, S.K.; Gnanappazham, L. Spatiotemporal mixed effects modeling for the estimation of PM2.5 from MODIS AOD over the Indian subcontinent. GIScience Remote Sens. 2020, 57, 159–173. [Google Scholar] [CrossRef]
- Wu, J.; Yao, F.; Li, W.; Si, M. VIIRS-based remote sensing estimation of ground-level PM2.5 concentrations in Beijing–Tianjin–Hebei: A spatiotemporal statistical model. Remote Sens. Environ. 2016, 184, 316–328. [Google Scholar] [CrossRef]
- Geng, G.; Zhang, Q.; Martin, R.V.; van Donkelaar, A.; Huo, H.; Che, H.; Lin, J.; He, K. Estimating long-term PM2.5 concentrations in China using satellite-based aerosol optical depth and a chemical transport model. Remote Sens. Environ. 2015, 166, 262–270. [Google Scholar] [CrossRef]
- Goldberg, D.L.; Gupta, P.; Wang, K.; Jena, C.; Zhang, Y.; Lu, Z.; Streets, D.G. Using gap-filled MAIAC AOD and WRF-Chem to estimate daily PM2.5 concentrations at 1 km resolution in the Eastern United States. Atmos. Environ. 2019, 199, 443–452. [Google Scholar] [CrossRef]
- Wei, J.; Huang, W.; Li, Z.; Xue, W.; Peng, Y.; Sun, L.; Cribb, M. Estimating 1-km-resolution PM2.5 concentrations across China using the space-time random forest approach. Remote Sens. Environ. 2019, 231, 111221. [Google Scholar] [CrossRef]
- Just, A.C.; Arfer, K.B.; Rush, J.; Dorman, M.; Shtein, A.; Lyapustin, A.; Kloog, I. Advancing methodologies for applying machine learning and evaluating spatiotemporal models of fine particulate matter (PM2.5) using satellite data over large regions. Atmos. Environ. 2020, 239, 117649. [Google Scholar] [CrossRef]
- Yang, N.; Shi, H.; Tang, H.; Yang, X. Geographical and temporal encoding for improving the estimation of PM2.5 concentrations in China using end-to-end gradient boosting. Remote Sens. Environ. 2022, 269, 112828. [Google Scholar] [CrossRef]
- Zeng, Q.; Xie, T.; Zhu, S.; Fan, M.; Chen, L.; Tian, Y. Estimating the Near-Ground PM2.5 Concentration over China Based on the CapsNet Model during 2018–2020. Remote Sens. 2022, 14, 623. [Google Scholar] [CrossRef]
- Li, R.; Liu, X.; Li, X. Estimation of the PM2.5 pollution levels in Beijing based on nighttime light data from the defense meteorological satellite program-operational linescan system. Atmosphere 2015, 6, 607–622. [Google Scholar] [CrossRef]
- Wang, J.; Aegerter, C.; Xu, X.; Szykman, J.J. Potential application of VIIRS Day/Night Band for monitoring nighttime surface PM2.5 air quality from space. Atmos. Environ. 2016, 124, 55–63. [Google Scholar] [CrossRef]
- Zhao, X.; Shi, H.; Yu, H.; Yang, P. Inversion of nighttime PM2.5 mass concentration in Beijing based on the VIIRS day-night band. Atmosphere 2016, 7, 136. [Google Scholar] [CrossRef]
- Zhao, X.; Shi, H.; Yang, P.; Zhang, L.; Fang, X.; Liang, K. Inversion algorithm of PM2.5 air quality based on nighttime light data from NPP-VIIRS. J. Remote Sens. 2017, 21, 291–299. [Google Scholar]
- Ke, L.; Chaoshun, L.; Penglong, J. Estimation of nighttime PM2.5 concentration in Shanghai based on NPP/VIIRS Day Night Band data. Acta Sci. Circumstantiae 2019, 39, 1913–1922. [Google Scholar]
- Fu, D.; Xia, X.; Duan, M.; Zhang, X.; Li, X.; Wang, J.; Liu, J. Mapping nighttime PM2.5 from VIIRS DNB using a linear mixed-effect model. Atmos. Environ. 2018, 178, 214–222. [Google Scholar] [CrossRef]
- Wang, M.; Wang, Y.; Teng, F.; Li, S.; Lin, Y.; Cai, H. Estimation and Analysis of PM2.5 Concentrations with NPP-VIIRS Nighttime Light Images: A Case Study in the Chang-Zhu-Tan Urban Agglomeration of China. Int. J. Environ. Res. Public Health 2022, 19, 4306. [Google Scholar] [CrossRef]
- Chen, H.; Xu, Y.; Mo, Y.; Zhang, Y.; Yang, Z. Estimating nighttime PM2.5 concentrations in Huai’an based on NPP/VIIRS nighttime light data. Acta Sci. Circumstantiae 2022, 42. [Google Scholar]
- Li, X.; Zhang, C.; Li, W.; Liu, K. Evaluating the use of DMSP/OLS nighttime light imagery in predicting PM2.5 concentrations in the northeastern United States. Remote Sens. 2017, 9, 620. [Google Scholar] [CrossRef]
- McHardy, T.; Zhang, J.; Reid, J.; Miller, S.; Hyer, E.; Kuehn, R. An improved method for retrieving nighttime aerosol optical thickness from the VIIRS Day/Night Band. Atmos. Meas. Tech. 2015, 8, 4773–4783. [Google Scholar] [CrossRef]
- Zhang, G.; Shi, Y.; Xu, M. Evaluation of LJ1-01 nighttime light imagery for estimating monthly PM2.5 concentration: A comparison with NPP-VIIRS nighttime light data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 3618–3632. [Google Scholar] [CrossRef]
- Johnson, R.S.; Zhang, J.; Hyer, E.J.; Miller, S.D.; Reid, J.S. Preliminary investigations toward nighttime aerosol optical depth retrievals from the VIIRS Day/Night Band. Atmos. Meas. Tech. 2013, 6, 1245–1255. [Google Scholar] [CrossRef]
- Román, M.O.; Wang, Z.; Sun, Q.; Kalb, V.; Miller, S.D.; Molthan, A.; Schultz, L.; Bell, J.; Stokes, E.C.; Pandey, B. NASA’s Black Marble nighttime lights product suite. Remote Sens. Environ. 2018, 210, 113–143. [Google Scholar] [CrossRef]
- Kyba, C.C.; Aubé, M.; Bará, S.; Bertolo, A.; Bouroussis, C.A.; Cavazzani, S.; Espey, B.R.; Falchi, F.; Gyuk, G.; Jechow, A. Multiple angle observations would benefit visible band remote sensing using night lights. J. Geophys. Res. Atmos. 2022, 127, e2021JD036382. [Google Scholar] [CrossRef]
- Lee, S.; Chiang, K.; Xiong, X.; Sun, C.; Anderson, S. The S-NPP VIIRS day-night band on-orbit calibration/characterization and current state of SDR products. Remote Sens. 2014, 6, 12427–12446. [Google Scholar] [CrossRef]
- Deng, Y.; Liu, J.; Liu, Y.; Xu, S. Spatial distribution estimation of PM2.5 concentration in Beijing by applying Bayesian geographic weighted regression model. Sci. Surv. Mapp. 2018, 43, 39–45. [Google Scholar]
- Rohde, R.A.; Muller, R.A. Air pollution in China: Mapping of concentrations and sources. PLoS ONE 2015, 10, e0135749. [Google Scholar] [CrossRef]
- Liao, L.; Weiss, S.; Mills, S.; Hauss, B. Suomi NPP VIIRS day-night band on-orbit performance. J. Geophys. Res. Atmos. 2013, 118, 12705–712718. [Google Scholar] [CrossRef]
- Qiu, S.; Shao, X.; Cao, C.Y.; Uprety, S.; Wang, W.H. Assessment of straylight correction performance for the VIIRS Day/Night Band using Dome-C and Greenland under lunar illumination. Int. J. Remote Sens. 2017, 38, 5880–5898. [Google Scholar] [CrossRef]
- Baker, N. Joint Polar Satellite System (JPSS) VIIRS Cloud Cover/Layers Algorithm Theoretical Basis Document (ATBD). NASA Goddard Space Flight Cent. Tech. Rep. 2011. [Google Scholar]
- Liang, W.G.; Zhao, Y.S. A new method of surface albedo inverse model based on energy transmission. Remote Sens. Land Resour. 2007, 19, 53–56. [Google Scholar]
- Miller, S.D.; Turner, R.E. A Dynamic Lunar Spectral Irradiance Data Set for NPOESS/VIIRS Day/Night Band Nighttime Environmental Applications. IEEE Trans. Geosci. Remote Sens. 2009, 47, 2316–2329. [Google Scholar] [CrossRef]
- Li, X.; Ma, R.; Zhang, Q.; Li, D.; Liu, S.; He, T.; Zhao, L. Anisotropic characteristic of artificial light at night – Systematic investigation with VIIRS DNB multi-temporal observations. Remote Sens. Environ. 2019, 233, 111357. [Google Scholar] [CrossRef]
- Kocifaj, M.; Bará, S. Aerosol characterization using satellite remote sensing of light pollution sources at night. Mon. Not. R. Astron. Soc. Lett. 2020, 495, L76–L80. [Google Scholar] [CrossRef]
- Kocifaj, M.; Bará, S. Diffuse light around cities: New perspectives in satellite remote sensing of nighttime aerosols. Atmos. Res. 2022, 266, 105969. [Google Scholar] [CrossRef]

| Source | Abbreviation | Content | Unit | Spatial Resolution | Temporal Resolution |
|---|---|---|---|---|---|
| BJMEMC 1 | PM2.5 | PM2.5 | μg/m3 | - | Hourly |
| VIIRS/SDR | NTL | Nighttime light | W/cm2·sr | 750 m × 750 m | Daily |
| VIIRS/EDR | VCCLO | Cloud cover layers | - | 6 km × 6 km | Daily |
| MOD09A1 | Reflectance | Surface reflectance | - | 500 m × 500 m | 8-Day |
| MOD13A3 | EVI | Enhanced Vegetation Index | - | 1 km × 1 km | Monthly |
| EAC4 | AOD | Total AOD at 550 nm | - | 0.75° × 0.75° | 3-h |
| ERA5 | TEM | 2 m temperature | K | 0.1° × 0.1° | Hourly |
| DTEM | 2 m dew point temperature | K | 0.1° × 0.1° | Hourly | |
| SP | Surface pressure | Pa | 0.1° × 0.1° | Hourly | |
| ET | Evaporation | m | 0.1° × 0.1° | Hourly | |
| PRE | Precipitation | m | 0.1° × 0.1° | Hourly | |
| U-WS | 10 m u-component of wind | m/s | 0.1° × 0.1° | Hourly | |
| V-WS | 10 m v-component of wind | m/s | 0.1° × 0.1° | Hourly | |
| BLH | Boundary layer height | m | 0.25° × 0.25° | Hourly |
| Site | 1 × 1 Pixel | 3 × 3 Pixels | 5 × 5 Pixels |
|---|---|---|---|
| DS | −0.03 | −0.52 | −0.55 |
| TT | 0.11 | −0.08 | −0.41 |
| GY | −0.44 | −0.63 | −0.65 |
| WSXG | −0.03 | −0.35 | −0.45 |
| ATZX | −0.23 | −0.54 | −0.61 |
| NZG | −0.12 | −0.51 | −0.63 |
| WL | −0.3 | −0.54 | −0.51 |
| BBXQ | −0.09 | 0.05 | 0.07 |
| FTHY | −0.5 | −0.42 | −0.29 |
| YG | −0.3 | −0.41 | −0.37 |
| GC | −0.32 | −0.69 | −0.63 |
| QM | −0.37 | −0.62 | −0.59 |
| YDMN | 0 | −0.13 | −0.29 |
| XZMB | −0.13 | −0.31 | −0.62 |
| NSH | −0.38 | −0.53 | −0.51 |
| DSH | −0.21 | −0.38 | −0.38 |
| FS | −0.62 | −0.64 | −0.46 |
| DX | −0.11 | −0.06 | 0.03 |
| YZ | −0.57 | −0.56 | −0.54 |
| TZ | −0.55 | −0.57 | −0.59 |
| SY | −0.38 | −0.57 | −0.53 |
| CP | −0.55 | −0.7 | −0.63 |
| MTG | −0.27 | −0.6 | −0.66 |
| PG | −0.67 | −0.72 | −0.7 |
| HR | −0.5 | −0.54 | −0.56 |
| MY | −0.32 | −0.56 | −0.6 |
| YQ | −0.38 | −0.64 | −0.64 |
| DL | 0.16 | 0.18 | 0.18 |
| BDL | 0.18 | 0.14 | 0.2 |
| MYSK | 0.21 | 0.22 | 0.23 |
| DGC | 0.2 | 0.05 | −0.07 |
| YLD | −0.36 | −0.1 | 0.01 |
| YF | 0.12 | 0.25 | 0.2 |
| LLH | 0.07 | −0.01 | 0.04 |
| Mean | −0.23 | −0.35 | −0.37 |
| Site | Spring | Summer | Autumn | Winter | Imean |
|---|---|---|---|---|---|
| DS | −0.56 | −0.65 | −0.53 | −0.45 | 47.87 |
| TT | −0.53 | −0.46 | −0.36 | −0.27 | 44.77 |
| GY | −0.65 | −0.81 | −0.62 | −0.52 | 40.61 |
| WSXG | −0.41 | −0.46 | −0.5 | −0.41 | 42.26 |
| ATZX | −0.58 | −0.79 | −0.55 | −0.52 | 48.47 |
| NZG | −0.65 | −0.73 | −0.65 | −0.47 | 43.85 |
| WL | −0.52 | −0.61 | −0.47 | −0.42 | 27.95 |
| BBXQ 1 | 0.11 | 0.13 | 0.05 | 0 | 11.6 |
| FTHY | −0.26 | −0.3 | −0.23 | −0.37 | 35.22 |
| YG | −0.27 | −0.44 | −0.42 | −0.34 | 12.66 |
| GC | −0.61 | −0.74 | −0.54 | −0.62 | 35.45 |
| QM | −0.64 | −0.71 | −0.58 | −0.43 | 60.15 |
| YDMN | −0.29 | −0.28 | −0.32 | −0.26 | 35.87 |
| XZMB | −0.58 | −0.74 | −0.58 | −0.58 | 36.68 |
| NSH | −0.5 | −0.54 | −0.45 | −0.53 | 44.55 |
| DSH | −0.46 | −0.3 | −0.35 | −0.41 | 32.84 |
| FS | −0.29 | −0.54 | −0.5 | −0.51 | 19.65 |
| DX 1 | 0.35 | 0.26 | −0.2 | −0.27 | 13.98 |
| YZ | −0.45 | −0.7 | −0.61 | −0.4 | 32.04 |
| TZ | −0.61 | −0.61 | −0.63 | −0.51 | 38.48 |
| SY | −0.38 | −0.69 | −0.53 | −0.51 | 30.31 |
| CP | −0.62 | −0.75 | −0.66 | −0.5 | 26.25 |
| MTG | −0.63 | −0.81 | −0.57 | −0.62 | 26.38 |
| PG | −0.66 | −0.87 | −0.62 | −0.64 | 20.43 |
| HR | −0.53 | −0.54 | −0.52 | −0.65 | 22.49 |
| MY | −0.62 | −0.72 | −0.57 | −0.47 | 27.72 |
| YQ | −0.6 | −0.75 | −0.6 | −0.59 | 21.63 |
| DL 1 | 0.36 | 0.37 | 0.06 | −0.08 | 2.23 |
| BDL 1 | 0.24 | 0.39 | 0.02 | 0.14 | 2.79 |
| MYSK 1 | 0.39 | 0.6 | 0.14 | −0.2 | 1.42 |
| DGC 1 | 0.06 | 0.2 | −0.26 | −0.28 | 6.33 |
| YLD 1 | 0.14 | 0.28 | −0.21 | −0.19 | 4.39 |
| YF 1 | 0.39 | 0.53 | 0.1 | −0.23 | 6.96 |
| LLH1 | 0.38 | 0.3 | −0.26 | −0.24 | 4.58 |
| Variable | Urban Area | Suburb | ||||||
|---|---|---|---|---|---|---|---|---|
| Spring | Summer | Autumn | Winter | Spring | Summer | Autumn | Winter | |
| ln(I) | √ | √ | √ | √ | √ | √ | √ | √ |
| Mean ln(I) | √ | √ | √ | √ | √ | √ | √ | √ |
| RH/μ | √ | √ | √ | √ | √ | √ | √ | √ |
| SP | √ | √ | √ | √ | √ | |||
| ET | √ | √ | √ | √ | √ | √ | √ | √ |
| PRE | √ | √ | √ | √ | √ | |||
| WS | √ | √ | √ | √ | √ | √ | ||
| WD | √ | √ | √ | √ | ||||
| BLH | √ | √ | √ | √ | √ | √ | ||
| TEM | √ | √ | √ | |||||
| EVI | √ | √ | √ | √ | √ | |||
| Time | Spring | Summer | Autumn | Winter | Mean |
|---|---|---|---|---|---|
| 2:00 CST | 0.84 | 0.79 | 0.83 | 0.8 | 0.82 |
| 11:00 CST | 0.92 | 0.9 | 0.94 | 0.84 | 0.9 |
| 14:00 CST | 0.93 | 0.85 | 0.94 | 0.83 | 0.89 |
| Variable | Min | Max | Mean | Midian | Std |
|---|---|---|---|---|---|
| PM2.5 (μg/m3) | 1.00 | 410.00 | 46.82 | 33.00 | 45.16 |
| Radiance (W/cm2·sr) | 5.36 × 10−9 | 9.25 × 10−8 | 3.45 × 10−8 | 3.38 × 10−8 | 1.27 × 10−8 |
| Relative humidity (%) | 9.84 | 101.4 | 58.88 | 58.85 | 23.21 |
| Surface pressure (hPa) | 923.77 | 1041.45 | 1006.32 | 1009.22 | 17.44 |
| Evaporation (mm) | 0.00 | 5.24 | 1.19 | 0.84 | 1.26 |
| Precipitation (mm) | 0.00 | 10.93 | 0.16 | 0.00 | 0.95 |
| Wind speed (m/s) | 0.03 | 5.10 | 1.56 | 1.35 | 1.01 |
| Wind direction (°) | 0.01 | 359.95 | 232.62 | 280.61 | 114.54 |
| Boundary layer height (m) | 11.38 | 1614.31 | 140.59 | 41.37 | 263.69 |
| Temperature (K) | 253.77 | 302.18 | 278.96 | 276.54 | 11.05 |
| EVI (unitless) | 0.05 | 0.41 | 0.15 | 0.15 | 0.07 |
| Site | ln(I) | ln(I′) |
|---|---|---|
| DS | −0.55 | −0.55 |
| TT | −0.4 | −0.4 |
| GY | −0.65 | −0.65 |
| WSXG | −0.44 | −0.44 |
| ATZX | −0.61 | −0.61 |
| NZG | −0.62 | −0.62 |
| WL | −0.5 | −0.5 |
| BBXQ | 0.07 | 0.11 |
| FTHY | −0.29 | −0.28 |
| YG | −0.37 | −0.35 |
| GC | −0.63 | −0.62 |
| QM | −0.59 | −0.59 |
| YDMN | −0.29 | −0.27 |
| XZMB | −0.62 | −0.62 |
| NSH | −0.5 | −0.5 |
| DSH | −0.38 | −0.37 |
| FS | −0.46 | −0.44 |
| DX | 0.03 | 0.08 |
| YZ | −0.54 | −0.53 |
| TZ | −0.59 | −0.58 |
| SY | −0.53 | −0.52 |
| CP | −0.63 | −0.63 |
| MTG | −0.66 | −0.65 |
| PG | −0.7 | −0.7 |
| HR | −0.56 | −0.55 |
| MY | −0.6 | −0.58 |
| YQ | −0.64 | −0.64 |
| DL | 0.18 | 0.27 |
| BDL | 0.2 | 0.3 |
| MYSK | 0.23 | 0.3 |
| DGC | −0.07 | 0 |
| YLD | 0.01 | 0.08 |
| YF | 0.2 | 0.23 |
| LLH | 0.04 | 0.09 |
| (5, 15] | (15, 25] | (25, 35] | (35, 45] | (45, 50] | (50, 55] | (55, 60] | (60, 65] | (65, 70] | ||
|---|---|---|---|---|---|---|---|---|---|---|
| urban area | ||||||||||
| Spring | R | 0.79 | 0.91 | 0.74 | 0.97 | 0.89 | 0.88 | 0.59 | 0.92 | 0.84 |
| MB (μg/m3) | 0.1 | 0.8 | 0.18 | 1.69 | 0.31 | 0.42 | 2.22 | 0.91 | 1.61 | |
| MAE (μg/m3) | 6.48 | 13.61 | 19.11 | 12.54 | 19.35 | 6.71 | 9.69 | 16.94 | 21.42 | |
| RMSE (μg/m3) | 8.03 | 17.91 | 24.06 | 16.2 | 28.57 | 9.11 | 11.5 | 22.96 | 28.17 | |
| Mean (μg/m3) | 40.21 | 62.29 | 79.95 | 82.92 | 71.52 | 48.06 | 164.75 | 59.42 | 72.27 | |
| Summer | R | 0.8 | 0.88 | 0.98 | 0.92 | 0.95 | 0.89 | 0.9 | 0.77 | 0.86 |
| MB (μg/m3) | 1.29 | 0.48 | 0.18 | 0.16 | 0.65 | 0.06 | 0.27 | 0.25 | 0.12 | |
| MAE (μg/m3) | 6.2 | 7.47 | 7.01 | 4.92 | 8.45 | 6.12 | 3.09 | 7.18 | 9.77 | |
| RMSE (μg/m3) | 7.46 | 9.78 | 8.83 | 6.45 | 11.43 | 7.85 | 3.66 | 8.98 | 12.38 | |
| Mean (μg/m3) | 75.52 | 30.61 | 67.71 | 31.08 | 48.65 | 57.71 | 21.18 | 61.29 | 38.76 | |
| Autumn | R | 0.91 | 0.95 | 0.86 | 0.79 | 0.92 | 0.9 | 0.92 | 0.89 | 0.87 |
| MB (μg/m3) | 5.0 | 2.59 | 0.03 | 1.03 | 3.53 | 1.9 | 0.59 | 2.34 | 2.03 | |
| MAE (μg/m3) | 15.21 | 10.9 | 7.45 | 13.57 | 16.72 | 14.44 | 13.63 | 16.05 | 14.82 | |
| RMSE (μg/m3) | 20.88 | 13.85 | 10.1 | 17.74 | 21.15 | 18.49 | 17.19 | 20.56 | 17.59 | |
| Mean (μg/m3) | 45.21 | 49.46 | 38.7 | 43.65 | 65.69 | 60.81 | 70.22 | 55.55 | 51.81 | |
| Winter | R | 0.94 | 0.88 | 0.76 | 0.85 | 0.87 | 0.64 | 0.97 | 0.58 | 0.92 |
| MB (μg/m3) | 0.15 | 1.15 | 4.56 | 0.81 | 0.93 | 0.84 | 0.19 | 2.36 | 0.31 | |
| MAE (μg/m3) | 4.89 | 8.97 | 21.7 | 21.96 | 10.28 | 10.38 | 5.11 | 12.9 | 7.81 | |
| RMSE (μg/m3) | 6.57 | 13.36 | 26.18 | 28.93 | 13.04 | 12.5 | 6.69 | 16.07 | 10.39 | |
| Mean (μg/m3) | 24.32 | 28.05 | 68.16 | 64.28 | 45.55 | 39.56 | 40.2 | 46.71 | 33.43 | |
| suburbs | ||||||||||
| Spring | R | 0.61 | 0.69 | 0.58 | 0.87 | 0.82 | 0.63 | 0.75 | 0.65 | 0.65 |
| MB (μg/m3) | 0.21 | 2.56 | 0.93 | 9.8 | 1.62 | 0.95 | 0.31 | 0.59 | 2.67 | |
| MAE (μg/m3) | 7.06 | 17.87 | 16.2 | 18.07 | 22.92 | 12.02 | 12.1 | 14.63 | 24.1 | |
| RMSE (μg/m3) | 8.58 | 21.98 | 20.64 | 22.47 | 33.06 | 14.66 | 16.38 | 18.23 | 31.48 | |
| Mean (μg/m3) | 33.77 | 62.02 | 66.47 | 84.91 | 59 | 47.02 | 134.95 | 41.54 | 64.15 | |
| Summer | R | 0.66 | 0.64 | 0.79 | 0.8 | 0.82 | 0.59 | 0.71 | 0.67 | 0.81 |
| MB (μg/m3) | 0.13 | 0.62 | 0.25 | 0.17 | 0.81 | 1.02 | 0.45 | 0.86 | 1.14 | |
| MAE (μg/m3) | 10.82 | 8.14 | 13.51 | 7 | 13.7 | 12.03 | 5.72 | 13.45 | 9.97 | |
| RMSE (μg/m3) | 12.42 | 10.27 | 16.47 | 8.81 | 17.17 | 14.17 | 6.94 | 15.97 | 12.53 | |
| Mean (μg/m3) | 68.98 | 22.65 | 48.62 | 25.84 | 46.43 | 58.26 | 21.65 | 53.48 | 36.58 | |
| Autumn | R | 0.85 | 0.81 | 0.69 | 0.63 | 0.86 | 0.81 | 0.85 | 0.76 | 0.88 |
| MB (μg/m3) | 6.32 | 5.97 | 0.35 | 1.82 | 5.48 | 3.84 | 0.81 | 4.0 | 3.0 | |
| MAE (μg/m3) | 15.66 | 14.32 | 11.63 | 14.22 | 22.55 | 14.41 | 16.31 | 18.75 | 14.34 | |
| RMSE (μg/m3) | 20.42 | 17.4 | 14.37 | 17.29 | 26.45 | 18.61 | 20.52 | 23.66 | 17.67 | |
| Mean (μg/m3) | 41 | 48.82 | 35.85 | 39.83 | 69.6 | 53.93 | 62.17 | 50.6 | 47.59 | |
| Winter | R | 0.57 | 0.61 | 0.57 | 0.8 | 0.75 | 0.62 | 0.85 | 0.61 | 0.85 |
| MB (μg/m3) | 10.29 | 1.19 | 5.53 | 2.09 | 1.13 | 0.2 | 0.3 | 0.04 | 0.24 | |
| MAE (μg/m3) | 29.06 | 9.24 | 21.34 | 20.85 | 13.72 | 8.43 | 11.05 | 13.69 | 9.67 | |
| RMSE (μg/m3) | 35.34 | 11.97 | 27.06 | 27.75 | 16.84 | 11.17 | 14.17 | 16.21 | 12.58 | |
| Mean (μg/m3) | 61.93 | 25.94 | 66.98 | 54.47 | 52 | 25.85 | 41.3 | 33.37 | 31.54 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deng, J.; Qiu, S.; Zhang, Y.; Cui, H.; Li, K.; Cheng, H.; Liu, Z.; Dou, X.; Qian, Y. Estimating Nighttime PM2.5 Concentration in Beijing Based on NPP/VIIRS Day/Night Band. Remote Sens. 2023, 15, 349. https://doi.org/10.3390/rs15020349
Deng J, Qiu S, Zhang Y, Cui H, Li K, Cheng H, Liu Z, Dou X, Qian Y. Estimating Nighttime PM2.5 Concentration in Beijing Based on NPP/VIIRS Day/Night Band. Remote Sensing. 2023; 15(2):349. https://doi.org/10.3390/rs15020349
Chicago/Turabian StyleDeng, Jianqiong, Shi Qiu, Yu Zhang, Haodong Cui, Kun Li, Hongjia Cheng, Zhaoyan Liu, Xianhui Dou, and Yonggang Qian. 2023. "Estimating Nighttime PM2.5 Concentration in Beijing Based on NPP/VIIRS Day/Night Band" Remote Sensing 15, no. 2: 349. https://doi.org/10.3390/rs15020349
APA StyleDeng, J., Qiu, S., Zhang, Y., Cui, H., Li, K., Cheng, H., Liu, Z., Dou, X., & Qian, Y. (2023). Estimating Nighttime PM2.5 Concentration in Beijing Based on NPP/VIIRS Day/Night Band. Remote Sensing, 15(2), 349. https://doi.org/10.3390/rs15020349