LiDAR-Based Local Path Planning Method for Reactive Navigation in Underground Mines

Abstract

Reactive navigation is the most researched navigation technique for underground vehicles. Local path planning is one of the main research difficulties in reactive navigation. At present, no technique can perfectly solve the problem of local path planning for the reactive navigation of underground vehicles. Aiming to address this problem, this paper proposes a new method for local path planning based on 2D LiDAR. First, we convert the LiDAR data into a binary image, and we then extract the skeleton of the binary image through a thinning algorithm. Finally, we extract the centerline of the current laneway from these skeletons and smooth the obtained roadway centerline as the current planned local path. Experiments show that the proposed method has high robustness and good performance. Additionally, the method can also be used for the global path planning of underground maps.

1. Introduction

The first generation of autonomous guided vehicles for underground mines was developed in the early 1960s, 1970s, and 1980s [1,2]. These vehicles primarily assist navigation by drawing lines on the floor or lights on the roof. A CCD camera was used to detect the relative position of the straight line directly above or ahead of the vehicle. With the development of technology, vehicle navigation techniques have been mainly divided into two categories. The first category is absolute navigation. The vehicle knows its real-time position in a fixed co-ordinate system. A path is planned in this fixed co-ordinate system, and the vehicle follows this path. Absolute navigation is widely used in indoor and outdoor mobile robots, and simultaneous localization and mapping (SLAM) is the most popular technique in absolute navigation [3,4]. The second category is reactive navigation. The vehicle does not need to know its position on the entire map, it should only know its relative position in the current visible environment, assisting vehicle navigation based on this relative position. In the past few decades, a large amount of software for autonomous driving in mines has been developed, such as AutoMine, MINEGEM, and the Scooptram automation system, and numerous experiments and applications have been carried out in many mines [5]. To date, reactive navigation is the most widely used technique in mines [1,6,7,8], and LiDAR has become the most widely used type of sensor in the underground environment [9].

However, there are still some key issues to be overcome in the application of reactive navigation in mines. Path planning is a critical technique in reactive navigation research. Thus far, there are several different types of mature path planning algorithms [10,11,12], for example, Dijkstra’s algorithm [13], the A* algorithm [14], the potential field method (PFM) [15], the probabilistic roadmap method (PRM) [16], and Rapidly-exploring Random Trees (RRT) [17]. The above algorithms are widely used in different scenarios. Generally speaking, the path planning algorithm needs a starting point and a target point. In reactive navigation in a mine, it is difficult to determine the exact starting point and ending point. Therefore, the above algorithms are difficult to directly apply to the path planning of reactive navigation.

Fortunately, the underground laneway environment has a unique geometry. In the field of mobile robots, the environments in which robots work are divided into indoor and outdoor environments. Indoor refers to an environment where the ground is flat and the space is closed, such as offices and production rooms. An outdoor environment refers to an environment where the ground is uneven and the space is open, such as urban roads and the wild. The underground laneway environment is not the same as the standard indoor and outdoor environment. The underground laneway has the property of a closed structure in the indoor environment and the property of uneven ground in the outdoor environment. Since the underground laneway has floors, ceilings, and walls, it is closer to the indoor environment [1]. Compared with an environment such as an office, the underground environment is simpler, and this structure is called a corridor-like structure.

Aiming at the corridor-like structure of an underground laneway, authors [18] engaged in research in the field of mining have proposed the classic follow-the-wall technology for reactive navigation. The neural network method is an effective means to realize the technology of following the wall. Pomerleau [19] describes how to use a neural network to enable the vehicle to learn to drive, and Dubrawski [20] uses a neural network to allow a vehicle to learn by trial and error online. However, the neural network method requires further research and has not been popularized or applied in mining applications. Due to the unique structure of the underground laneway, some authors take the centerline of the laneway as the planned path. For example, Larsson [21,22] proposed a method based on the Hough transform by detecting two parallel lines in the LiDAR data, considering the center line of these two parallel straight lines as the local planned path of reactive navigation. However, this method can only be applied to the local path planning of a vehicle moving straight, and the method fails when the vehicle turns.

To solve the local path planning problem of the reactive navigation of underground vehicles, we propose a new method of local path planning based on 2D LiDAR. The proposed method can be applied to environments with corridor-like structures, in addition to downhole environments. The main innovations of this research are as follows. (1) A new concept of path planning based on 2D LiDAR is proposed. The idea of extracting the centerline of the laneway using the thinning algorithm is demonstrated by graphing the 2D LiDAR data. (2) A search tree building algorithm to search useful information from images is proposed. (3) The proposed method has high efficiency and good robustness, and it can not only be used for the local path planning of the reactive navigation of underground vehicles but can also be used for the path planning of underground vehicles based on the global map. The structure of the remaining sections of this paper is as follows. Section 2 presents the environment for our experiments and the data used for algorithm validation. Section 3 describes in detail our proposed method and the method used to verify the algorithm. Section 4 verifies the performance of the proposed method on two datasets. Section 5 discusses the impact and outlook of key parameters on the proposed method. Section 6 provides the conclusion.

2. Study Materials

In this study, the load haul dump (LHD) is used as the research object of reactive navigation. As shown in Figure 1, a 2D LiDAR is installed on the front body and the rear body of the LHD. The scanning frequency of the LiDAR is 50 Hz, the angular resolution is 0.5°, and the scanning angle is 270°. The length of the LHD is approximately 10.7 m, the width is approximately 2.7 m, and the height is approximately 2.5 m. The LiDAR data are transmitted to the intelligent controller through the vehicle network, and then the data collected by the intelligent controller are transmitted to the terminal computer through Wi-Fi. When conducting experiments, we record and save LiDAR data through a rosbag file at the remote terminal.

Experiments were carried out at the following two mines, where experimental data were recorded in a rosbag file.

A map of the experiment in Mine A is shown in Figure 2. Mine A mainly adopts the filling mining method. The width of the laneway is around 4.5 m, A-B-D-E-F-G is the main transportation laneway, and the length of the laneway is around 130 m. Point C is the orepass, and the length of the laneway in section BC is approximately 30 m. There are two chambers of the same size near point A, among which the fire chamber is shown in Figure 2c. During the experiment, the driving path of the LHD is A-B-C-B-A-B-D-E-F-G. During this process, the driving mode of the LHD includes straight movement, left turns, and right turns. The travel time is around 290 s. A total of 14,454 frames of LiDAR data are recorded, which we define as dataset 1. In dataset 1, there are 10,847 frames with the straight driving mode, 1109 frames with left turns, and 2498 frames with right turns.

A map of the experiment in Mine B is shown in Figure 3. Mine B mainly adopts the natural caving mining method. The width of the laneway is approximately 4.1 m, A-B is the main transportation laneway, the total length of the laneway is approximately 200 m, and there are 27 mining entrances. During the experiment, the LHD drove straight from point A to point B, and the travel time was around 235 s. During this process, the LHD only traveled straight. A total of 11,705 frames of LiDAR data were recorded, which we define as dataset 2.

The maps of the above two mines were obtained using the corresponding datasets through Cartographer [23]. This paper evaluates the effectiveness and robustness of our proposed method on these two datasets.

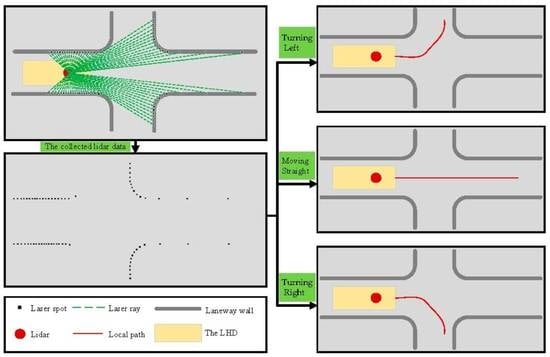
3. Methodology

The main idea of our algorithm is to convert each frame of LiDAR data into a binary map, use a thinning algorithm to extract the skeleton of the map, and select a suitable polyline in the skeleton as the local planning path of the current frame. The flowchart of the proposed algorithm is shown in Figure 4.

3.1. Binary Map

In this section, we convert each frame of data collected by LiDAR into a binary map. The original range data obtained by LiDAR contain invalid points and noise. We need to extract the laser spots on the tunnel wall scanned by the LiDAR. We set a valid distance according to LiDAR attributes and LiDAR installation position. In this work, the SICK LMS151 LiDAR is used, and the scanning range is 0.5 m to 50 m. When the reflectivity is 10%, the scanning range is 18 m. As shown in Figure 1, the LiDAR is installed on the axle of the LHD with a width of 2.7 m. Therefore, the valid range of the distance set in this work is $[1.35 \mathrm{m},20 \mathrm{m}]$. By setting a valid range, the influence of the interference points on our subsequent algorithm can be avoided.

The range data of one frame received by the LiDAR are $R=\{r_1,r_2,\cdots r_i,\cdots r_n\}$. $n$ is the number of laser points. According to the scanning range of the LiDAR, the angle data $A=\{{\theta }_{1,}{\theta }_2,\cdots {\theta }_i,\cdots {\theta }_n\}$ corresponding to each laser point can be obtained by linear interpolation. We select valid laser points according to Equation (1).

$$R^{\prime }={\left\{minLim<r_i<maxLim,r_i\in R\right\}}_{i=1}^n,$$

(1)

$minLim,maxLim$ is the minimum and maximum value of the valid range, respectively. Then, we convert the valid laser point $R^{\prime }$ from polar coordinates to Cartesian coordinates according to Equation (2).

$$\begin{array}{l}\left\{\begin{array}{l}{x}_i=r_i\cos ({\theta }_i),r_i\in R^{\prime },{\theta }_i\in A\\ y_i=r_i\sin ({\theta }_i),r_i\in R^{\prime },{\theta }_i\in A\end{array}\right.\\ Pc={\left\{\left(x_i,y_i\right)\right\}}_{i=0}^{n^{\prime }}\end{array}$$

(2)

where $Pc$ is a two-dimensional point cloud in the Cartesian coordinate system (Figure 4b), and $n^{\prime }$ is the number of laser points in $R^{\prime }$. $x_i,y_i$ is the value of the $i$th laser point in $R^{\prime }$ in the Cartesian coordinate system, and ${\theta }_i$ is the angle value corresponding to the $i$th laser point in $R^{\prime }$.

According to the principle of LiDAR scanning, $Pc$ is an orderly cluster of points. In the Cartesian coordinate system, the points in set $Pc$ are sequentially connected into a closed envelope (Figure 4c). To convert this into a binary map, gridding is required. A certain range containing the envelope is gridded, and the grid size is defined as the resolution of the map. We set the mesh color inside the envelope to black, and the mesh color outside the envelope to white. We calculate the Cartesian coordinates of the grid center point according to Equation (3).

$$\begin{array}{l}\left\{\begin{array}{l}{h}_{ij}=xmin+(j-0.5)\ast resolution\\ l_{ij}=ymin+(rn-i+0.5)\ast resolution\end{array}\right.\\ Po={\left\{\left(h_{ij},l_{ij}\right)\right\}}_{i=1,j=1}^{rn,cn}\end{array}$$

(3)

$h_{ij},l_{ij}$ are the coordinates of the grid center in row $i$ and column $j$, $xmin,ymin$ are the minimum values of the $x,y$ coordinates of the grid area. $rn$ is the number of lines, and $cn$ is the number of lines. $resolution$ is the map resolution. Then, the binary map (Figure 4d) can be obtained according to Equation (4).

$$BM(i,j)=\left\{\begin{array}{l}0,(h_{ij},l_{ij})\in I\\ 1,(h_{ij},l_{ij})\notin I\end{array}\right.$$

(4)

$BM$ represents a binary map, and $I$ represents the interior point set of the envelope.

There are many methods used to determine whether a point is inside the polygon [24], for example, area summation, angle summation, and ray casting. This study adopts the ray casting approach, which is implemented in detail as follows [25,26]: We shoot a ray from the centroid of a grid and count the intersections with the envelope; if the number is odd, the point is inside the envelope; if it is even, the point is outside.

3.2. Thinning Algorithm

There are many methods for road centerline extraction [27,28,29]. Considering the efficiency of the algorithm, we adopt the skeletonization algorithm. The skeletonization algorithm is widely used in the image field. Cornea [30] summarizes the skeletonization algorithm in detail, and it is mainly divided into the following categories: (1) thinning and boundary propagation; (2) distance field-based, (3) geometric, and (4) general-field functions.

The above algorithms operate either on discrete voxelized datasets or on continuous polygonal representations of 3D objects. In this work, only the skeleton of the 2D binary map needs to be extracted. For the skeletonization of two-dimensional binary graphs, Zhang [31] proposed a fast parallel thinning algorithm called the Zhang–Suen thinning algorithm. This algorithm is very effective in processing binary images, so we choose this algorithm. Algorithm 1 describes the process of the Zhang–Suen thinning algorithm.

Algorithm 1 Thinning algorithm

Input: Binary map $BM(rn,cn)$, where 1 is background and 0 is foreground Output: Refined map $RM(rn\times cn)$ 1: while Ture do 2:    Define an empty matrix $S1,S2$ with 2 columns 3:    for $i=1 \mathrm{to} rn \mathbf{do}$ 4:       for $j=1 \mathrm{to} cn \mathbf{do}$ 5:          if $BM(i,j)>0 \mathbf{then} \mathrm{Continue} \mathbf{end\; if}$ 6:          Count the number $n \mathrm{of} 0 \mathrm{to} 1$ occurrences of two adjacent pixels in eight pixels near $BM(i,j)$ from $BM(i-1,j)$ clockwise around $BM(i,j)$ 7:          if $n\ne 1 \mathbf{then} \mathrm{Continue} \mathbf{end\; if}$ 8:       Count the number $n^{\prime } \mathrm{of} \mathrm{pixels} \mathrm{whose} 8 \mathrm{pixels} \mathrm{near} BM(i,j) \mathrm{are} \mathrm{foreground}$ 9:          if $n^{\prime }>2 \mathrm{or} n^{\prime }>6 \mathbf{then} \mathrm{Continue} \mathbf{end\; if}$ 10:         if $BM(i-1,j)\ast BM(i,j+1)\ast BM(i+1,j)\ne 0 \mathbf{then} \mathrm{Continue} \mathbf{end\; if}$ 11:         if $BM(i,j+1)\ast BM(i+1,j)\ast BM(i,j-1)\ne 0 \mathbf{then} \mathrm{Continue} \mathbf{end\; if}$ 12:         Append $[i,j] \mathrm{after} \mathrm{the} \mathrm{last} \mathrm{line} \mathrm{of} S1$ 13:      end for 14:    end for 15:    if $S1 \mathrm{is} \mathrm{not} \mathrm{empty} \mathbf{then}$ 16:       The pixel value of $BM(S1) \mathrm{is} \mathrm{assigned} \mathrm{the} \mathrm{background} \mathrm{value} 0$ 17:    else 18:       Break 19:    end if 20:    Repeat lines 3–19, changing $S1 \mathrm{to} S2 \mathrm{and} \mathrm{lines} 10\text{–}11 \mathrm{to} \mathrm{lines} 21\text{–}22$ 21:    if $BM(i-1,j)\ast BM(i,j+1)\ast BM(i,j-1)\ne 0 \mathbf{then} \mathrm{Continue} \mathbf{end\; if}$ 22:    if $BM(i,j+1)\ast BM(i+1,j)\ast BM(i,j-1)\ne 0 \mathbf{then} \mathrm{Continue} \mathbf{end\; if}$ 23 end while 24: Output the refined map $RM=BM$

3.3. Centerline Extraction

After obtaining the skeleton map (Figure 4e) of the binary map, it is necessary to select a laneway centerline in the skeleton map. First, we select the pixel closest to the coordinate origin as the search start point $s$. From the starting point, we search for unsearched pixels along the right, upper right, lower right, upper, lower, upper left, lower left, and left directions, and we establish a search tree to store pixels. Algorithm 2 describes the building process of the search tree in detail.

Algorithm 2 Search tree algorithm

$$\begin{gathered} \mathbf{Input}: \mathrm{Binary} \mathrm{map} RM(rn\times cn); \mathrm{Start} \mathrm{point} s \\ \mathbf{Output}: \mathrm{Search} \mathrm{tree} Tree(p\times 11) \\ 1: \mathrm{Initialize} \mathrm{an} \mathrm{array} \mathrm{of} 2\mathrm{D} \mathrm{search} \mathrm{trees} Tree(1\times 11),Tree(1,1:2)=s, Tree(1,3)=NAN,Tree(1,4:11)=0, \mathrm{and} \mathrm{use} F\mathrm{lag}(rn\times cn) \mathrm{to} \mathrm{indicate} \mathrm{whether} \mathrm{the} \mathrm{points} \mathrm{have} \mathrm{been} \mathrm{searched},Flag=zeros(rn,cn) \\ 2: \mathrm{Use} current \mathrm{to} \mathrm{represent} \mathrm{the} \mathrm{current} \mathrm{node}, \mathrm{and} number \mathrm{to} \mathrm{represent} \mathrm{the} \mathrm{size} \mathrm{of} \mathrm{the} Tree \\ 3: \mathbf{while} current\le number \mathrm{do} \\ 4: a=Tree(current,1) \mathrm{and} a=Tree(current,2) \\ 5: \mathbf{if} b<cn \mathrm{then} \\ 6: \mathbf{if} RM(a,b+1)=1 \mathrm{and} Flag(a,b+1)=0 \mathbf{then} \\ 7: number=number+1,Tree(current,4)=number, \\ Tree=[Tree;zeros(1,11)],Tree(number,1:2)=[a,b+1], \\ Tree(number,3)=current,Flag(a,b+1)=1 \\ 8: \mathbf{end} \mathbf{if} \\ 9: \mathbf{end} \mathbf{if} \\ 10: \mathrm{Like} \mathrm{lines} 5\text{–}9, \mathrm{search} \mathrm{for} \mathrm{the} \mathrm{pixels} \mathrm{in} \mathrm{the} \mathrm{upper} \mathrm{right}, \mathrm{lower} \mathrm{right}, \mathrm{upper}, \mathrm{lower}, \mathrm{left}, \mathrm{lower} \mathrm{left}, \mathrm{and} \mathrm{left} \mathrm{direction} \mathrm{of} (a,b) \mathrm{in} \mathrm{turn} \\ 11: current=current+1 \\ 12: \mathbf{end} \mathbf{while} \end{gathered}$$

After generating the search tree, we search from the leaf node of the search tree to the parent node layer by layer until the root node of the search tree is found; see Algorithm 3. We can find all paths in this skeleton map.

Algorithm 3 Get all paths from the search tree

$$\begin{gathered} \mathbf{Input}: \mathrm{Search} \mathrm{tree} Tree(p\times 11) \\ \mathbf{Output}: \mathrm{All} \mathrm{path} paths(k\times 1) \\ 1: \mathbf{for} i=1 \mathrm{to} p \mathbf{do} \\ 2: \mathbf{if} Tree(i,4:11)=0 \\ 3: ki=i \\ 4: \mathbf{while} Tree(ki,3) \mathrm{is} \mathrm{not} NAN \mathbf{do} \\ 5: ki=Tree(ki,3) \\ 6: paths=[paths;Tree(ki,1:2)] \\ 7: \mathbf{end} \mathbf{while} \\ 8: \mathbf{end} \mathbf{if} \\ 9: \mathbf{end} \mathbf{for} \end{gathered}$$

Next, we select the most appropriate path among all paths according to the current vehicle driving mode. According to Equation (5), the driving mode of the vehicle is divided into three modes: forward, left, and right.

$$run\_mode=\left\{\begin{array}{l}1,\mathrm{turn} \mathrm{left}\\ 0,\mathrm{straight}\\ -1,\mathrm{turn} \mathrm{right}\end{array}\right.$$

(5)

In the formula, $run\_mode$ represents the current operation mode of the LHD. We calculate the direction of each path according to Equation (6).

$$\overrightarrow{paths(k)}=paths(k).end-s$$

(6)

$\overrightarrow{paths(k)}$ represents the direction of the $k$th path, which is a three-dimensional vector. $paths(k).end$ represents the last point of the $k$th path. $\overrightarrow{X}=(1,0,0)$ indicates the direction of the positive X axis. According to Equations (7)–(9), we calculate the angles of all paths to the positive X axis, respectively.

$$\overrightarrow{C}=\overrightarrow{paths(k)}\times \overrightarrow{X}=\left|\overrightarrow{paths(k)}\right|\left|\overrightarrow{X}\right|\sin <\overrightarrow{paths(k)},\overrightarrow{X}>$$

(7)

where $| |$ represents the module of the vector, and $<>$ represents the included angle of the vector. The vector $\overrightarrow{C}$ represents the vector product of $\overrightarrow{paths(k)}$ and $\overrightarrow{X}$.

$$\alpha =\mathrm{acos}(\frac{\overrightarrow{paths(k)}•\overrightarrow{X}}{\left|\overrightarrow{paths(k)}\right|\left|\overrightarrow{X}\right|})$$

(8)

$\alpha$ is the included angle between $\overrightarrow{paths(k)}$ and $\overrightarrow{X}$. We calculate the angle ${\phi }_k$ between the $k$th path and the positive direction of X axis using Equation (9).

$${\phi }_k=\left\{\begin{array}{l}\alpha ,\overrightarrow{C}(3)\ge 0\\ -\alpha ,\overrightarrow{C}(3)<0\end{array}\right.$$

(9)

$\overrightarrow{C}(3)$ represents the component of vector $\overrightarrow{C}$ in the Z-axis direction. We calculate the included angle between all paths and the positive direction of the X axis to form a set $\Phi =\left\{{\phi }_1,{\phi }_2,\cdots ,{\phi }_{n^{″}}\right\}$. $n^{″}$ is the number of paths. The angle ${\phi }_k$ is defined as follows: the angle from the positive direction of the X axis rotating counterclockwise to the direction of the target path is positive; otherwise, the angle from the positive direction of the X axis rotating clockwise to the direction of the target path is negative, and the value range of the angle is $\left[-\pi ,\pi \right]$. The path is selected according to Equation (10).

$$select\_path=\left\{\begin{array}{l}paths(\left[\min (\left|\Phi \right|)\right]), run\_mode=0\\ paths(\left[\max (\Phi )\right]), run\_mode=1 \\ paths(\left[\min (\Phi )\right]), run\_mode=-1 \end{array}\right.$$

(10)

where $[ ]$ represents the corresponding index, and $select\_path$ is the optimal path selected. To generate a locally planned path, the current LiDAR origin is added to the beginning of the selected path to form an initial locally planned path.

3.4. Smoothing Method

To enable the vehicle to run more smoothly, the raw local planning path needs to be smoothed [32]. In particular, if the current driving mode is straight, we wish to avoid the influence of the intersection in the laneway. We first use the following method for smoothing. The start and end points of the raw local planning path form a straight line. We calculate the distances from the other $n-1$ points to the line except for these two points. If the distance of the point is greater than $dlim$, we delete this point; otherwise, we keep this point. In Figure 5, A and B are the endpoints of the initial local planning path. The distance between the gray point in the figure and the straight line AB is greater than $dlim$, which needs to be deleted, and other points are reserved. In this paper, $dlim$ is taken as 0.3 m.

After filtering out the outliers on the point path, we use the Bezier curve to fit $path$. The general expression of the Bezier curve is shown in Equation (11).

$$\begin{array}{l}S(t)={\displaystyle \sum _{i=0}^n{B}_i^n(t)P_i},t\in [0,1]\\ B_i^n(t)=t^i{(1-t)}^{n-i}\end{array},$$

(11)

$P_i$ is the $i$th control point, and $n$ is the degree of the Bezier curve. In this paper, $n$ is taken as 3. $S$ is the Bezier curve. We find the optimal control point of the Bezier curve according to the least square method (4)–(12) [33].

$$\underset{P_i}{\mathrm{argmin} }{\displaystyle \sum _{j=1}^m{\left(pat{h}_j-{\displaystyle \sum _{i=0}^n{B}_i^n(t)P_i}\right)}^2}$$

(12)

$pat{h}_j$ is the $j$th point in the $path$, and $m$ is the number of points in the $path$. We substitute the optimal control point $P_i$ into (4)–(11) to obtain the path of local planning (red line in Figure 4f).

3.5. Method Comparison and Robustness Evaluation

There are few studies on the local path planning method for the reactive navigation of underground vehicles. At present, the method based on the Hough transform [34,35] is the most up-to-date. This method was proposed by Larsson [21] in 2008. The main idea is to detect whether two parallel lines satisfy certain constraints by performing the Hough transform on LiDAR data. If it exists, we solve the centerline of the two straight lines as the local planning path. If it does not exist, the path cannot be planned. The method is robust when the vehicle does not turn. However, this method cannot be used while turning. Therefore, we only compare this method with the method proposed in this paper in the straight-line mode.

In this paper, the offset and direction error are used to quantitatively describe the accuracy of the algorithm. As shown in Figure 6, to calculate the error, we choose a point on the axle as a reference point. Here, we choose a point with a distance of 0.5 m along the LiDAR scan direction as the reference point. When the vehicle is moving forward, we use the front LiDAR, and when the vehicle is moving backward, we use the rear LiDAR. The distance from the reference point to the local planned path is the offset error. When the reference point is on the left side of the local planning path, the offset error is positive; otherwise, when the reference point is on the right side of the local planning path, the offset error is negative. The positive direction of the current X axis is used as the reference direction, and the difference between the direction of the local planned path and the reference direction is used as the direction error. The positive and negative direction error are consistent with the angle definition given in Section 3.3.

To systematically evaluate the robustness of the algorithm proposed in this paper, we refer to the evaluation method proposed by Larsson [21]. We consider two different ways of corrupting the data: adding noise to the scan of the dataset and using a lower data rate. In the present research, first, 10%, 20%, 33%, and 50% of noise is added to the original data, respectively. Second, we reduce the amount of data by 1/2, 3/4, 5/6, and 8/9 of the original data, respectively.

4. Results

To verify the validity of the proposed method, two data sets are tested in this section. The two datasets come from two different mines, described in Section 2.

4.1. Dataset 1

There are three different driving modes of LHD in dataset 1, including straight movement, left turning, and right turning. Firstly, the accuracy of the proposed method is analyzed for the three different driving modes. Finally, the experimental results of the whole dataset 1 are summarized.

4.1.1. In the Case of Moving Straight

Figure 7 shows the local path planning of the proposed method and the method of the Hough transform in the straight-moving case in dataset 1. The LiDAR data collection positions of (a–f) correspond to the vicinity of points A, C, B, E, F, and G in Figure 2d, respectively. It can be seen that (1) in different situations, whether in the normal situation (Figure 7b), under the interference of the chamber (Figure 7a), or under the interference of the intersection (Figure 7c–f), the proposed method can accurately find the centerline of the current laneway. (2) The proposed method is consistent with the local path planning of the Hough transform. (3) The local path of the proposed method is a curve, which is consistent with the changing trend of the laneway, while the local path of the Hough transform method is a straight line.

Figure 8 shows a quantitative evaluation of the results of Figure 7—that is, the evaluation of the offset and direction error of the two methods. The mean absolute offset error of the proposed method is 0.1542 m, and the mean absolute direction error is 0.0775 rad. The average absolute offset error of the Hough transform method is 0.2040 m, and the absolute direction error is 0.0509 rad. To summarize, it can be concluded that in the case of straight travel, the proposed method’s accuracy is comparable to the local path planning accuracy of the Hough transform method, and the errors are all within the allowable range.

4.1.2. In the Case of Turning Left

Figure 9 shows the local path planning of the proposed method in the case of a left turn in dataset 1. The LiDAR data collection locations in Figure 9a–c correspond to the turning paths of C-B-A in Figure 2. It can be seen that as the visible curve area of the LiDAR increases, the local path planning becomes closer to the road centerline. The local path planning errors in Figure 9a–c are shown in

Table 1. The corresponding error in Figure 9.

Figure 8	Offset Error (m)	Direction Error (Rad)
(a)	−0.1154	−0.0102
(b)	0.1300	0.0771
(c)	−0.2812	−0.6213

. It can be seen that the offset and direction error in Figure 9c are large, but the local path is on the road centerline. This shows that during the experiment, the vehicle did not drive along the optimal laneway centerline at the position shown in Figure 9c. With the exception of Figure 9c, the absolute mean offset error of the local path planning in Figure 9a,b is 0.1227 m and the absolute mean direction error is 0.0437 rad.

4.1.3. In the Case of Turning Right

Figure 10 shows the local path planning of the proposed method in the case of the right turn in dataset 1. The LiDAR data collection position of Figure 10a–c corresponds to the turning path of A-B-C in Figure 2, and the LiDAR data collection position of Figure 10d,e corresponds to the vicinity of point D in Figure 2. Looking at Figure 10a–e, as in the case of a left turn, it can be seen that as the LiDAR’s visible curve area increases, and the local path planning moves closer to the road centerline. The local path planning errors in Figure 10a–e are shown in

Table 2. The corresponding error in Figure 10.

Figure 10	Offset Error (m)	Direction Error (Rad)
(a)	0.0143	−0.1461
(b)	−0.4274	−0.3398
(c)	−0.1696	0.0069
(d)	0.1871	0.1028
(e)	0.1477	−0.0920

. The absolute average offset error of the local path planning for the proposed method is 0.1892 m, and the absolute average direction error is 0.1395 rad.

4.1.4. Summary

Dataset 1 has 14,454 frames of LiDAR data. The previous section evaluated the effectiveness and accuracy of the proposed method for some feature frames in different situations. The following is a statistical analysis of the accuracy and efficiency of the proposed method after dataset 1 is processed.

To better illustrate the superiority of the proposed method, we used the Hough transform method for comparison. Figure 11 shows the statistical results of the proposed method and the Hough transform method after processing dataset 1, respectively. It can be seen that (1) the absolute average offset error of the proposed method is smaller than the corresponding value of the Hough transform method, and the offset error of the proposed method has a small degree of fluctuation, while the offset error of the Hough transform method has more discrete points (Figure 11a). (2) The absolute average direction error of the proposed method is slightly larger than the corresponding value for the Hough transform method, but the number of discrete points of the direction error of the Hough transform method is greater (Figure 11b). (3) The number of rejected frames for the Hough transform method is 938 frames, while the number of rejected frames for the proposed method is 0 (Figure 11c). This is because the Hough transform method cannot be applied to turning intersections, so 938 frames are rejected. Alternatively, it shows that the proposed method can be applied in both straight and turning situations.

In addition to this, we perform statistics on the processing time of dataset 1 between the proposed method and the Hough transform method, as shown in

Table 3. The time consumption of the proposed method and the Hough transform method for dataset 1.

Method	Total Time (s)	Average Time (s)
Hough transform	5295.17	0.366
Proposed	409.83	0.028

. The codes all run in MATLAB, the CPU is an Intel (R) Core (TM) i9-9900K, and the main frequency is 3.60 Hz. It can be obtained that the speed of the proposed method for processing dataset 1 is around 13 times that of the Hough transform method.

Then, we add different levels of noise to each frame of LiDAR data in dataset 1, and the statistical results of error are shown in Figure 12. It can be seen that (1) adding different levels of noise does not affect the absolute average offset error, but when adding 33% and 50% of horizontal noise, it has a greater impact on the outliers of the offset error, and as the noise level increases, the outliers are increasingly scattered (Figure 12). (2) Adding different levels of noise has a greater impact on the absolute average direction error (Figure 12b). In addition to this, the number of rejected frames increases to 117 frames when 50% noise is added (Figure 12c). (3) Adding different levels of noise has little effect on the number of discrete points of offset error and direction error (Figure 12a,b). From the perspective of adding different levels of noise, the proposed method has better robustness.

Below, we randomly reduce different levels of data for each frame of LiDAR data in dataset 1. Figure 13 shows the statistical result of the error. It can be seen that (1) the law of reducing data at different levels is essentially the same as the law of adding noise at different levels, and the direction error is more sensitive than the offset error. (2) When removing 3/4 of the original LiDAR data—that is, the number of LiDAR data points per frame is 135—the number of rejected frames gradually increases (Figure 13c).

Generally, the above experiments that involved adding different levels of noise and reducing different levels of data in dataset 1 show that the proposed method is robust and can perform local path planning for the reactive navigation of underground vehicles.

4.2. Dataset 2

Dataset 2 only refers to the straight driving mode, but there are more and more complex intersections than dataset 1. We adopt a map resolution of 0.5. Below, we extract nine feature frames from dataset 2 (Figure 14). The LiDAR data collection positions in Figure 14a–i correspond to points a-i in Figure 3c. It can be seen that the proposed method is essentially the same as the local path plan using the Hough transform method, and both can find the centerline of the current driving laneway.

Figure 15 shows a quantitative evaluation of the results of Figure 14—that is, the evaluation of the offset and direction error of the two methods. The mean absolute offset error of the proposed method is 0.2093 m and the mean absolute direction error is 0.0466 rad. The average absolute offset error of the Hough transform method is 0.1271 m, and the absolute direction error is 0.0543 rad. To summarize, it can be concluded that the proposed method’s accuracy is comparable to the local path planning accuracy of the Hough transform method, and the errors are all within the allowable range.

Dataset 2 has 11,705 frames of LiDAR data. The following is a statistical analysis of the accuracy and efficiency of dataset 2 after processing by the proposed method. Figure 16 shows the statistical results of the proposed method and the Hough transform method after processing dataset 2, respectively. The number of rejected frames for both methods is 0. It can be seen that the fluctuation degree of the offset error of the proposed method is smaller than that of the Hough transform method, and the difference in the absolute average offset error is small (Figure 16a). (2) The fluctuation degree of the direction error of the proposed method is smaller than that of the Hough transform method, but its absolute average direction error is larger (Figure 16b).

Table 4. The time consumption of the proposed method and the Hough transform method for dataset 2.

Method	Total Time (s)	Average Time (s)
Hough transform	4251.26	0.363
Proposed	730.43	0.062

shows the processing time of the proposed method and the method of Hough transform for dataset 2. It can be obtained that the speed of the proposed method in processing dataset 1 is around 6 times that of the Hough transform method.

As with dataset 1, the robustness of the proposed method is evaluated by adding different levels of noise to dataset 2 and reducing thedata by the different levels. Figure 17 shows the error statistics of the proposed method and the Hough transform method when adding different levels of noise to dataset 2. Consistent with the basic results of dataset 1, the influence of noise on the direction error is greater than that on the offset error, but the influence of noise on the error is within the allowable range (Figure 17a,b). Since there are no turns in dataset 2, the number of rejected frames is three until the added noise level is 50% (Figure 17c). Figure 18 shows the reduction of the data at different levels for dataset 2. The error statistics of the proposed method and the Hough transform method are consistent with those obtained when adding different levels of noise.

Generally, the testing of the proposed method through datasets 1 and 2 shows that the proposed method is comparable in accuracy to the Hough transform method, has good robustness, runs faster, and solves the problems of the Hough transform method, which cannot be used for the problem of local path planning at turning intersections.

5. Discussion

Firstly, the influence of the map resolution on the proposed method is analyzed by testing the error of the proposed method under different map resolutions. Then, the application scope of the proposed method is extended.

5.1. Sensitivity Analysis of Map Resolution

In this section, we discuss the performance of the proposed method under different map accuracies through datasets 1 and 2. Figure 19 shows the results of the proposed method after processing dataset 1 at different map resolutions. It can be seen that (1) with the increase in the map resolution, the absolute average offset error and the direction error both show a decreasing trend, and the fluctuation degree of the error is slightly smaller, but a few outlier errors increase (Figure 19a,b). (2) When the map resolution is 0.5 m, rejected frames begin to appear, and when the map resolution is 1 m, the number of rejected frames reaches 3590 frames, which is approximately 25% of the total number of frames in dataset 1 (Figure 19c).

Table 5. The time consumption of the proposed method for dataset 1 under different map resolutions.

Resolution (m)	Total Time (s)	Average Time (s)
0.1	3533.86	0.244
0.3	409.83	0.028
0.5	164.25	0.011
1	53.1	0.004

shows the processing time of the proposed method on dataset 1 at different map resolutions. It can be seen that as the map resolution increases, the time consumed decreases exponentially. Under the premise of ensuring that the number of frames rejected using the proposed method when processing dataset 1 is zero, and considering the error and efficiency comprehensively, the optimal map resolution of dataset 1 is 0.3 m.

Moreover, we analyze dataset 2 in the same way. Figure 20 shows the results of the proposed method after processing dataset 2 under different map resolutions, which is essentially consistent with the law obtained from dataset 1. However, the difference is that with the increase in the map resolution, there is no increase in the error of a few outliers. We refer to this phenomenon as phenomenon 1.

Table 6. The time consumption of the proposed method for dataset 2 under different map resolutions.

Resolution (m)	Total Time (s)	Average Time (s)
0.1	6548.62	0.559
0.3	730.43	0.062
0.5	284	0.024
1	84.18	0.007

shows the processing time of the proposed method on dataset 2 at different map resolutions. The same rule as in Table 5 can be obtained. However, in the process of comparing Table 5 and Table 6, we find another phenomenon: under the same map resolution, the processing of dataset 2 is more time-consuming than processing dataset 1. We call this phenomenon 2. On the premise of ensuring that the number of frames rejected using the proposed method when processing dataset 2 is 0, considering the error and efficiency comprehensively, the optimal map resolution of dataset 2 is 0.5 m.

The following is the analysis and explanation of phenomenon 1. Firstly, why is the error of the proposed method smaller as the map resolution increases? Figure 21 is a binary map under different map resolutions. It can be seen that with the increase in the map resolution, the skeleton of the binary map becomes simpler—that is, the centerline of the laneway becomes rougher. The smaller the map resolution, the finer the generated laneway centerline, and the more sensitive the generated laneway centerline to the shape of the laneway walls (Figure 21a). Conversely, the greater the map resolution, the rougher the generated laneway centerline, and the less sensitive the resulting laneway centerline is to the shape of the two walls of the laneway (Figure 21d). To ensure the smooth running of the vehicle in the laneway, the smoother the driving path, the better. Generally speaking, the two walls of the laneway are uneven (Figure 3b), or there is chamber interference (Figure 2c). To reduce the influence of the shape of the two walls of the laneway on the centerline, the map resolution should be larger. The smaller the influence of the two walls of the laneway on the generation of the center line, the smaller the error. Since the driving mode corresponding to 75% of the LiDAR data in dataset 1 is straight, and the driving mode corresponding to all LiDAR data in dataset 2 is straight, it is the same as the situation in Figure 21. Thus, the greater the resolution of the map, the smaller the mean error for dataset 1 and dataset 2.

Secondly, as the resolution of the map increases, dataset 1 has a small number of outlier errors, while dataset 2 has no such situation. Figure 22 is a binary map and its skeleton of the LiDAR data corresponds to Figure 10b under different map resolutions, and the corresponding driving mode is a right turn. It can be seen that as the map resolution increases, the path to the right becomes shorter and shorter until it disappears completely, and the error corresponding to Figure 22d is the largest. Therefore, in turn mode, the greater the map resolution, the greater the error. Since the LiDAR data in the turning mode of dataset 1 have 3607 frames, as the map resolution increases, their corresponding error will increase, and there will be few outlier errors in the dataset. Meanwhile, dataset 2 has no LiDAR data in turn mode, so this does not occur.

From phenomenon 1, we can conclude that in the straight mode, we should choose a value with a larger map resolution, and in the turning mode, we should choose a value with a smaller map resolution.

The following is an analysis and explanation of phenomenon 2. Firstly, why is the time consumption different between for the proposed method when processing dataset 1 and dataset 2 under the same map resolution? By observing the LiDAR data in Figure 7 corresponding to dataset 1 and Figure 14 corresponding to dataset 2, it can be found that the LiDAR data in Figure 14 have a larger range. In other words, each frame of LiDAR data in dataset 2 has a wider range than that in dataset 1, so the binary map generated under the same map resolution is larger and has more grids. This shows that the efficiency of the proposed method is proportional to the number of grids in the binary map.

5.2. Prospect

The underground laneway is a corridor-type structure, and the centerline of the laneway can be used as the driving path of the vehicle. The proposed method belongs to the image-based path planning methods; therefore, the proposed method can be used for global path planning for underground mines. Figure 23a,b show the global paths extracted using the proposed method in the maps corresponding to dataset 1 (Figure 2d) and dataset 2 (Figure 3a), respectively. The resolution of the maps is 0.2 m. The red line in the figure is the centerline of the main laneway extracted using the proposed method.

The proposed method is well suited for corridor-like structured environments, especially underground mines, and can be used to plan both local and global paths. With the continuous advance of mining, the stability of rock mass is getting worse and worse [36,37], and the unmanned driving technology of mining vehicles will gradually be promoted.

6. Conclusions

The method proposed in this paper solves the problem of local path planning for the reactive navigation of underground vehicles. The proposed method is superior to the Hough transform method and can be used not only for local path planning in the case of straight driving but also for local path planning in the case of turning. In addition to the downhole environment, the proposed method can be used in an environment with corridor-like structures. The effectiveness and robustness of the proposed method are verified through two real datasets. The experimental results show that (1) in the vehicle straight mode, the proposed method has the same accuracy as the Hough transform method, and both can accurately obtain the centerline of the current laneway. (2) In the vehicle turning mode, the problem whereby the Hough transform method cannot plan a local path is solved, and the proposed method can still provide a more accurate driving direction for the vehicle. (3) By adding different levels of noise to the original data and removing different levels of data, we show that the proposed method has strong robustness and stability. (4) The efficiency of the proposed method is much higher than that of the Hough transform method, which can greatly reduce the time for the vehicle control program. Additionally, the proposed method can also be used for the global path planning of underground maps and can be used as a path planning method for the absolute navigation of underground vehicles.

In future work, we intend to integrate the proposed method with the control method to realize the reactive navigation of underground vehicles. The first step in future work is to simulate the underground environment on the simulation platform [38] and realize the reactive navigation of underground vehicles in the simulation environment through integrated technology. The second step is to apply the integrated technology to real underground vehicles.