Detecting Deforestation Using Logistic Analysis and Sentinel-1 Multitemporal Backscatter Data

Abstract

This paper presents a new approach for detecting deforestation using Sentinel-1 C-band backscattering data. It is based on the temporal analysis of the backscatter intensity and its correlation with the scattering behavior of deforested plots. The backscatter intensity temporal variability is modeled with a logistic function, whose lower and upper boundaries are, respectively, set based on the representative backscatter values for forest and deforested plots. The approach also enables the identification of the date of each deforestation event, corresponding to the inflection point of the logistic curve that best fits the backscatter intensity time series. The methodology was applied to two forest biomes, a tropical forest at Iguazu National Park in Argentina and a temperate forest in the Brăila region in Romania. The optimal flattening parameter was 0.12 for both sites, with an F1-score of 0.93 and 0.71 for the tropical and temperate forests, respectively. The temporal accuracy shows a bias on the estimated date, with a slight delay of 2 months. The results reveal that the Sentinel C-band data can be successfully used for deforestation detection over tropical forests; however, the accuracy for temperate forests might be 20 pp lower, depending on the environmental conditions, such as rainfall, snow and management after logging.

1. Introduction

Forests are essential to life, supporting wild species and providing countless goods and vital ecosystem services, such as clean water and carbon storage [1]. In recent decades, the world’s forests have been under increasing threat from climate warming and direct or indirect human intervention [2,3]. Wildfires and severe storms are two of the natural phenomena that have the greatest impact on forest disturbance [4,5]. Illegal logging is also identified as a threat to forests, resulting in a noticeable disturbance to forest biodiversity and soil [6]. Illegal logging activities occur mainly in tropical areas in remote regions that are difficult to access and, therefore, difficult to control on the ground [7,8]. To effectively manage a forest and act against illegal deforestation, a near-real-time deforestation monitoring system is required [9].

Forest change detection, through remote sensing, has predominantly relied on optical data since they are easier to process and interpret, as well as long imagery time series of medium spatial resolution (30 m) over more than forty years, which are freely available. Several approaches for multispectral satellite image time-series change detection have been developed [10,11]. However, multispectral data are only suitable for change detection when long data sets of continuous images are available, being ineffective when their availability is limited by the presence of near-permanent cloud cover generating large time series gaps, which occurs in tropical and northern regions.

Space-borne synthetic aperture radar (SAR) data have the advantage of providing cloud-free observations, but due to the relative complexity of processing and interpretation, they have been underutilized in operational programs. Multitemporal SAR data have demonstrated their potential for reliable change detection, resulting from the complete or partial removal of the tree cover in forest areas at any time, day and night, under all weather conditions [12,13]. With the European Space Agency (ESA) Sentinel-1 mission, a long and regular SAR imagery time series, with a temporal resolution of at least 12 days, is available for tropical regions. Despite Sentinel-1′s wavelength (C-band) not being the optimal frequency for forest monitoring, its high temporal and spatial resolution enables the development of new algorithms for deforestation detection [14,15]. In fact, increasing the temporal resolution improves the change detection capability and decreases the delay in detecting deforestation [16].

Mapping approaches are based on image classification (supervised or unsupervised) [17,18] or automated change analysis [19,20,21,22] applied to a calibrated SAR backscatter time series. Zhao et al. [18] proposed an approach based on a convolutional neural network, U-net [23], and Sentinel-1 SAR data to produce monthly maps of forest logging showing accuracies (F1-score) of around 70%. Maretto et al. [24] have proposed two spatio-temporal variations of the U-net architecture, incorporating both the spatial and temporal contexts. The authors concluded that the new approach to the method outperforms the U-net architecture, reaching an accuracy of approximately 95%. Other authors have evaluated the potential of SAR interferometric coherence for deforestation detection [25,26]. Akbari and Solberg [25] combined multitemporal InSAR and backscatter intensity for forest clear-cut detection, concluding that tough coherence was the strongest predictor; there was an added value in using both types of data.

SAR and multispectral fusion have also proved to be of added value in increasing deforestation detection accuracy. Reiche et al. [27,28] proposed a pixel-based multi-sensor time series correlation and fusion approach based on the Landsat NDVI and ALOS PALSAR backscattering time series. The synergies between both data improved the temporal and spatial accuracies of historical deforestation detection (with an overall accuracy of 88%), in comparison to the use of Landsat or SAR PALSAR data alone, by overcoming the missing data in the Landsat time series.

Many of the above-mentioned algorithms rely on some form of reference data on the location of clear-cut plots. This is critical for remote or inaccessible regions of the world where the acquisition of reference data is not possible. This is the case for tropical forests, where the process of collecting reference data is expensive and time-consuming due to their remote locations, weather conditions, and/or insecure access to the region. Moreover, the reference data must be timely acquired before some vegetation has regrown [22]. To avoid or reduce the dependence on reference data to train deforestation detection algorithms, we propose a new algorithm that does not depend explicitly on training data.

This paper proposes a new approach based on the temporal analysis of the backscattering intensity and logistic regression analysis to detect deforestation areas in tropical and European-type forests. The evergreen forest is characterized by a stable and relatively high backscattering intensity over time due to volume scattering [29]. It is expected that a change in the forest, such as partial harvesting or clear-cut, would change the backscattering behavior from predominantly volume scattering to surface scattering. The consequence is the reduction of the backscattering intensity. In the proposed approach, the temporal behavior of the backscatter intensity is modeled by a logistic function, whose upper and lower limits are defined by the forest and the deforested backscatter intensity, respectively. The deforestation’s date corresponds to the inflection point of the logistic curve that best fits, in the least squares estimation, the backscatter data time series. Although the method does not require reference data, the availability of referenced data should improve the detection of deforestation. In this case, the forest and non-forest areas can be locally characterized in terms of backscattering intensity. The proposed methodology is applied to two Sentinel-1 (C-band) time series: one for the Iguazu National Park in Argentina and another for the Brăila region in Romania.

The structure of this paper is as follows: Section 2 is devoted to describing the data and the test areas. The methodology is described in Section 3. In the next two sections, Section 4 and Section 5, the results are presented and discussed. Finally, in Section 6, some conclusions are drawn.

2. Test Sites and Data

2.1. Test Sites

In order to assess the performance of the developed methodology, two different evergreen forest areas: a tropical forest in the Iguazu National Park, Argentina, and a north-European conifer forest in Brăila, Romania, were selected.

Located in Misiones Province in the Northeastern tip of Argentina and bordering the Brazilian state of Parana to the north, Iguazu National Park (S25 34 38.485 W54 17 9.863) is one of the most stunning natural sites due to its massive waterfalls. It was inscribed on the World Heritage List in 1984. The waterfall permanently spreads large amounts of water into the surrounding forests, creating an extremely humid micro-climate favoring lush and dense subtropical vegetation harboring diverse fauna. Today, the park is mostly surrounded by a landscape that has been strongly altered due to heavy logging, both historically and into the present. The Iguazu Falls experience a humid subtropical climate with abundant precipitation and high temperatures year-round. The period with the greatest volume of water flowing over the falls is usually December to February, coinciding with one of the periods of greatest rainfall. Deforestation in the area is mainly caused by selective logging and agricultural expansion, resulting in visible clear-cut plots (Figure 1a).

Brăila is in the southeastern part of Romania (Figure 1b). Brăila is characterized by a predominantly continental climate, with long winters lasting from September to March-April. The annual precipitation is 350–400 mm per year. This area is characterized by agricultural land practice and forest land cover clusters across the Danube River. Nevertheless, most of the area contains shrubs predominantly but also flooded and dampened wetlands, marshes, and other types of steppe vegetation, or vegetation characteristic of the plain areas.

2.2. Forest Mask and Reference Data

In order to validate the developed deforestation detection methodology, reference data were acquired for the monitoring period under evaluation. Although there are several global datasets with reference data on forest degradation and clear-cuts (e.g., GlobalForestWatch, Hansen et al., 2013) updated annually, their use is unsuitable when evaluating the clear-cuts occurring within time series with different time gaps, for which a finer temporal resolution is required. Furthermore, as far as we know, there is no forest cover, nor forest cover change map, available for both test sites. Therefore, reference data were generated by the manual digitalization of identified polygons, by visual interpretation, as the deforested areas in the Sentinel-2 images. For that, the Sentinel Playground web platform was used.

First, a forest mask representing the situation at the beginning of the monitoring period was generated in January 2019 and March 2020 for Iguazu and Brăila, respectively, by excluding agricultural areas, water bodies, and artificial areas. Stable forest areas are characterized by pixels whose spectral signatures are stable in time. Secondly, all the deforested plots identified during the monitoring period were manually digitized, and an attribute corresponding to the date when the deforestation event occurred was added to each plot (Figure 2). As some Sentinel-2 images were not available due to the cloud cover conditions, the deforestation date might not correspond to the exact deforestation event date but to the date of the first cloud-free image available. Deforestation was considered whenever an abrupt decay in the pixels’ spectral signature was observed, particularly in the infrared wavelengths.

For the period under analysis, the Iguazu site accounts for 840 km² of forested area, including all the deforestation plots that correspond to about 9% of the total initial forest area (76 km²), whilst the Brăila site accounts for 11 km² of forested area, including all the deforestation plots that correspond to about 4% of the total initial forest area (0.46 km²). The mean area of the deforestation plots is 441 ha and 19 ha for Iguazu and Brăila, respectively.

2.3. Sentinel-1 SAR Data and Preprocessing

The Sentinel-1 C-band images, made available by the European Space Agency (ESA), were used to detect deforestation in both test sites. The images were downloaded from the Alaska SAR Facility (https://asf.alaska.edu/, accessed on 2 May 2022). The images were acquired in interferometric wide (IW)-swath mode, descending orbit and were provided as single-look complex (SLC) products. In total, 53 dual-polarized images were retrieved for the Iguazu test site from January 2019 to December 2021. For the Brăila test site, 24 dual-polarized images, which were acquired from March to September 2020, were downloaded. Initially, the algorithm was applied to a 1-year time series, but because of the long-lasting snow during the long winters, the results were greatly affected. As a consequence, only the results of the spring–summer seasons were analyzed.

The SAR images were preprocessed using the workflow proposed by [30]: apply the orbit file; radiometric calibration; speckle filtering; multilooking; and range-Doppler terrain correction. The terrain correction uses the Copernicus Global DEM with 30 m of spatial resolution. The individual VV and VH terrain-corrected backscatter images were further collocated, and the multitemporal SAR filtering was applied [31] to the time series stack. The multitemporal filter avoids the spatial resolution reduction of common spatial filters. For each test site, the final data set is a stack of geocoded gamma-naught backscatter images in both polarizations (VV/VH) with 10 m of spatial resolution.

3. Methods

For forest stands, the C-band radar backscatter is mostly due to the branch-layer volume scattering in all polarizations [32]. At this frequency, the incident field cannot penetrate the canopy beyond the branch layer, and hence, the radar measurements are not directly sensitive to the surface parameters. On the other hand, the dominant scattering mechanism observed for the deforested plots (p.e. at clear-cuts) is surface scattering in all polarizations. In fact, after harvesting, the scattering mechanism is expected to change from volume to surface scattering, resulting in a significant decrease in the cross-polarized (VH) backscattering. However, this behavior is only observed if the forest residues are removed after clear-cutting; otherwise, there will be a significant increase in surface roughness that inhibits that behavior. Previous studies have shown that the VH backscatter is more sensitive to differences between stable forest and deforested areas, exhibiting abrupter decays after tree felling than the ones observed for the co-polarized (VV) backscatter [18,20]. In this study, we propose a pixel-based approach to detect the transition from volume to surface scattering and to estimate the deforestation event date. The approach assumes that the soil roughness and moisture are constant for a relatively short period and that the backscatter variation is a function of pixel scattering mechanisms. The temporal period should be relatively short, such that the vegetation does not change.

The developed method follows the next three steps [33]: (1) preprocessing and multitemporal filtering (already mentioned in Section 2); (2) analyzing the pixels’ intensity temporal variability; (3) fitting a sigmoid curve to the data (logistic analysis) and estimating the sigmoid parameters.

3.1. Analysis of Pixels Intensity Temporal Variability

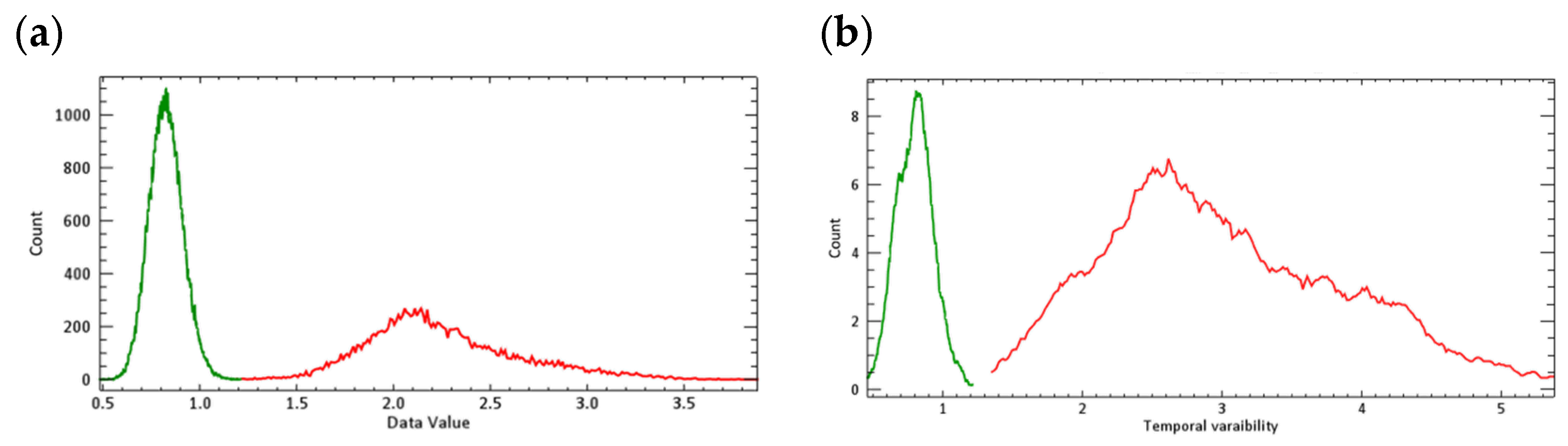
The stable forest is characterized by a relatively high backscatter intensity and low temporal variability, while a deforested area is characterized by a high temporal variability within a short period or a high backscatter intensity amplitude over the time series. The analysis of the pixel backscatter temporal variability can be used to discriminate between stable and non-stable forest pixels in the time series.

The temporal variability of the backscattering intensity $\left(\mathsf{\sigma }\right)$ has been estimated as in Equation (1):

$$\mathsf{\sigma }\left(\mathrm{x},\mathrm{y}\right)=\sqrt{\frac{1}{\mathrm{M}}{\displaystyle \sum }_{\mathrm{i}=1}^{\mathrm{M}}{\left({\mathrm{J}}_{\mathrm{i}}-\overline{\mathrm{J}}\right)}^2}$$

(1)

where $\overline{\mathrm{J}}$ is the temporal average of the backscattering intensities at the pixel (x,y) given in decibels, J_i is the backscatter intensity in image i, and M is the number of images. This estimator expresses a low temporal variability for forests and a high temporal variability for deforested areas, as shown in Figure 3. High temporal variability is also observed in agricultural areas, at the dam, and in the river margins due to the water level change. Forest pixels and non-forest pixels are perfectly separated using the standard deviation. Since this metric allows the discrimination of stable forest pixels from the remaining pixels, it is possible to reduce the number of pixels to be included in the logistic analysis. Therefore, pixels with a standard deviation lower than a given threshold (set as 1.2 db, in this case) corresponding to the stable forests are excluded from further analysis. The remaining pixels are selected as candidates for further logistic regression analysis. It is worth noting that, as the number of selected pixels depends on the defined threshold, a relaxed threshold is preferred.

Assuming that the deforested areas exhibit significantly higher standard deviation values and correspond to a small percentage of the total forest area, the temporal variability threshold can be empirically determined by computing a certain percentile value from the temporal standard deviation values. Based on a preliminary assessment, the value corresponding to the 85th percentile is proposed as the threshold value. However, this value can be fine-tuned using ancillary data and by evaluating its impact on the accuracy of the estimation of the deforested areas. It is important to point out that the pixels’ candidates are not yet the final deforested pixels but a subset of the total number of the initial pixels in each image that will be analyzed in the next step.

3.2. Logistic Analysis

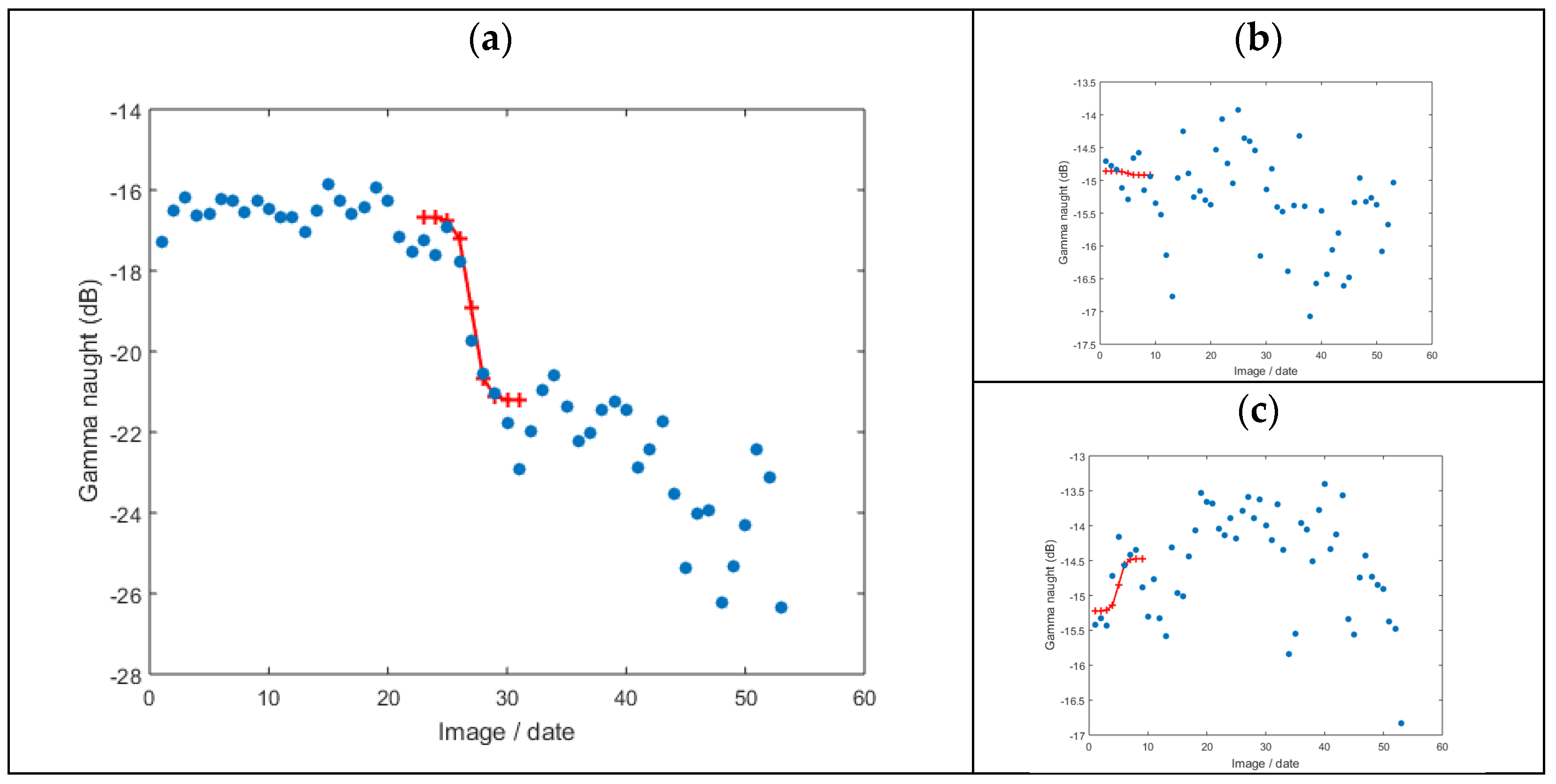
The logistic analysis aims to identify the forest pixels that were disturbed along the time series and to estimate the date of the change event based on the temporal behavior of the backscattering intensities. Figure 4a shows a typical temporal variation of the backscatter intensity for a deforestation event. In the first half of the time series, the pixel intensity is relatively stable, around −16 db, but then there is an abrupt decay of the backscattering intensity to values of around −22 db. Thus, a deforested pixel (clear-cut) is identified when a sudden drop is observed in the backscatter time series. Different behavior is expected for the stable forest and non-forest pixels, and the estimated logistic function may be a flat logistic function (Figure 4b) or an inverted logistic function (Figure 4c).

We have assumed that the backscatter intensity decay is modeled using the generalized logistic function (Equation (2)):

$${\mathsf{\gamma }}_{\mathrm{i}}\left(\mathrm{x},\mathrm{y}\right)=\frac{\mathrm{k}}{1+{\mathrm{e}}^{-\mathrm{a}\left({\mathrm{t}}_{\mathrm{i}}-{\mathrm{t}}_0\right)}}+\mathrm{LowLim}\mathrm{i}=1,\dots ,\mathrm{M}$$

(2)

where ${\mathsf{\gamma }}_{\mathrm{i}}$ is the corresponding backscattering intensity for each pixel at (x,y); M is the number of SAR images; k is the maximum backscatter intensity; a is the growth parameter, which describes the steepness of the curve (if a has negative values, the curve decreases, while if a has positive values, the curve increases); t_i is the inflection point, corresponding to the date of the deforestation event in a reference time frame t₀; and LowLim is the lowest backscatter intensity value of the curve. The inflection point of the logistic curve is the point where the second derivative is zero, meaning that it is a turning point in the backscatter intensity (corresponding to a clear-cut or any other type of change).

The number of parameters to be estimated can be reduced by previously defining the values for k, LowLim, and a. The k and the LowLim parameters can be computed as the maximum and minimum backscatter intensity values of the pixel time series, respectively. In order to account for outliers in the backscatter time series, the percentile 95% and 5% values were computed instead, respectively. The growth parameter, a, can be defined as a function of the expected steepness of the backscatter decay. The steepness of the curve is related to the temporal resolution of the SAR mission. For fast detection, the growth parameter must be in the range [−2, −5] approximating the logistic curve to the Heaviside function [34]. A steepness value of −2 was considered in this study, meaning that a deforested pixel is detected within a two-images interval, as it is represented in Figure 4 (the plus symbols in red). The inflection point date is slightly delayed relative to the first signal of intensity decay. This delay is positively correlated with the temporal resolution of the SAR images and the steepness of the curve (parameter a). Assuming that deforestation began at 10% of backscattering intensity decay, the delay relative to the inflection point (t₀) would be computed as log(1/0.9 − 1)/a, corresponding to 1.1 images, for a = −2. This means a bias of at least a 1.1 image time delay is expected. Both the number of images (M) and the temporal resolution of the time series are factors that contribute to the accuracy of the estimated date of the pixel intensity decay.

Additionally, the deforestation date (t_i) is determined through a search in the solution space by minimizing the following error function (Equation (3)):

$${\mathrm{E}}_{\mathrm{i}}={\displaystyle \sum }_{\mathrm{j}=\mathrm{N}}^{\mathrm{M}-\mathrm{N}}{\left({\mathsf{\gamma }}_{\mathrm{j}}\left(\mathrm{x},\mathrm{y}\right)-\frac{\mathrm{k}\left(\mathrm{x},\mathrm{y}\right)}{1+{\mathrm{e}}^{-\mathrm{a}\left({\mathrm{t}}_{\mathrm{i}}-{\mathrm{t}}_0\right)}}+\mathrm{LowLim}\left(\mathrm{x},\mathrm{y}\right)\right)}^2\mathrm{i}=1\dots \mathrm{M}$$

(3)

A sliding window in time, with dimension N, was adopted for the error function evaluation. In such a way, for each date t_i, only the N before and after images are considered for the error estimation. Consequently, small disturbing meteorological events, such as rainfall, wind, or snow, before or after the main event are excluded from the local analysis. This approach was adopted to estimate the deforestation date of all the candidate pixels and also to compute the fitting error of the logistic function. Regardless of the temporal behavior of the pixel backscatter intensities, a date for the inflection point of the logistic function is always computed. It should be noted that the pixels that do not show a significant temporal decay of the backscatter intensity, such as the stable forest, may have a relatively low misfit (Figure 4b).

As a consequence, a further criterion is required to identify pixels whose best-fitted logistic function significantly differs from the typical S-shape of the logistic function. For that, we propose the use of a flattening parameter to discriminate pixels characterized by an S-shape profile from pixels characterized by an approximately linear profile (Figure 4b) or inverted logistic function (Figure 4c). This flattening parameter is based on the fact that the second derivative of the logistic function is characterized by two peaks of opposite signs, which are located symmetrically around the estimated date. This means that the backscatter intensity is clustered into two groups, one with high intensities and the other with low intensities, at opposite sides of the estimated date. The flattening parameter is defined in Equation (4):

$$flat=\frac{{\gamma }_{max}-{\gamma }_{min}}{\left|{\gamma }_{max}\right|}$$

(4)

where ${\gamma }_{max}$ and ${\gamma }_{min}$ are, respectively, the maximum and minimum bounds of the logistic function computed for the best-fit date t_i. The flattening parameter is used to identify the pixels with a significantly high inflection in the backscatter intensities. Based on the gamma-naught values (in dB) for a typical stable forest, a flattening parameter in the range [0.1, 0.2] identifies pixels with a significant backscattering decay to be considered a non-stable forest or a deforested pixel. This parameter can be fine-tuned with a small sample of reference data for the study area. It is worth noting that the flat parameter is not dependent on the stable forest backscatter intensities but rather on their relative changes.

3.3. Results Accuracy Assessment

Two metrics were used to assess the accuracy of the deforestation map: spatial and temporal accuracy. The spatial accuracy was assessed by computing the precision, recall and F1-score of the binary deforestation map, independent of the time of the change event. The temporal accuracy was assessed by computing the mean delay of the deforestation detection (or the root mean square error of the time of the change event).

In order to estimate the temporal accuracy, the mean time lag between the reference date and the estimated date was calculated. For this comparison, the estimated deforestation date for each plot was computed as the median value of all the pixels’ dates inside the plot. The reference data, obtained by a visual interpretation of the Sentinel-2 data, are dependent on the availability of cloud-free images; thus, the “reference” data might be shifted for one or more months. Thus, the temporal accuracy is, in this case, a rough approximation of the temporal accuracy.

The spatial accuracy is computed from the entries of a confusion matrix, i.e., the number of True Positives (TP), False Positives (FP), and False Negatives (FN). The True Positive (TP) values correspond to pixels that were correctly identified as deforested areas by the algorithm (pixels inside the training samples); the False Negative (FN) values correspond to pixels identified as deforested that were misclassified by the algorithm as forest pixels (missing pixels inside the training samples); and the False Positive (FP) values correspond to the pixels identified as forests that were misclassified by the algorithm as deforested pixels (pixels identified outside the training samples). The True Negative (TN) values were not computed for the current study.

The spatial accuracy metrics that were computed from the confusion matrix are: (1) the recall, which is the percentage of the deforested pixels correctly predicted by the algorithm; (2) the precision, which is the percentage of pixels predicted by the algorithm as deforested, that really corresponds to the deforested pixels; and (3) the F1-score, which is the weighted average of the precision and recall.

As the overall accuracy is biased by the dominant stable forest, it is not a suitable metric to assess the accuracy of the method. In this case, the F1-score is preferred.

4. Results

In this section, we summarize the results obtained in the two test sites: Iguazu (Argentina) and Brăila (Romania). As a first step, the SAR images were preprocessed according to the workflow described in Section 2 and collocated and ordered in terms of the acquisition date. The temporal variability of each pixel was computed using the temporal standard deviation (Section 3), being the candidate pixels selected among those with a standard deviation value higher than the 85th percentile. The candidate pixels were further analyzed using the logistic function for the detection of deforested pixels and the estimation of the deforestation date. A flattening value of 0.14 and a time window of 5 images/dates were used for deforestation detection.

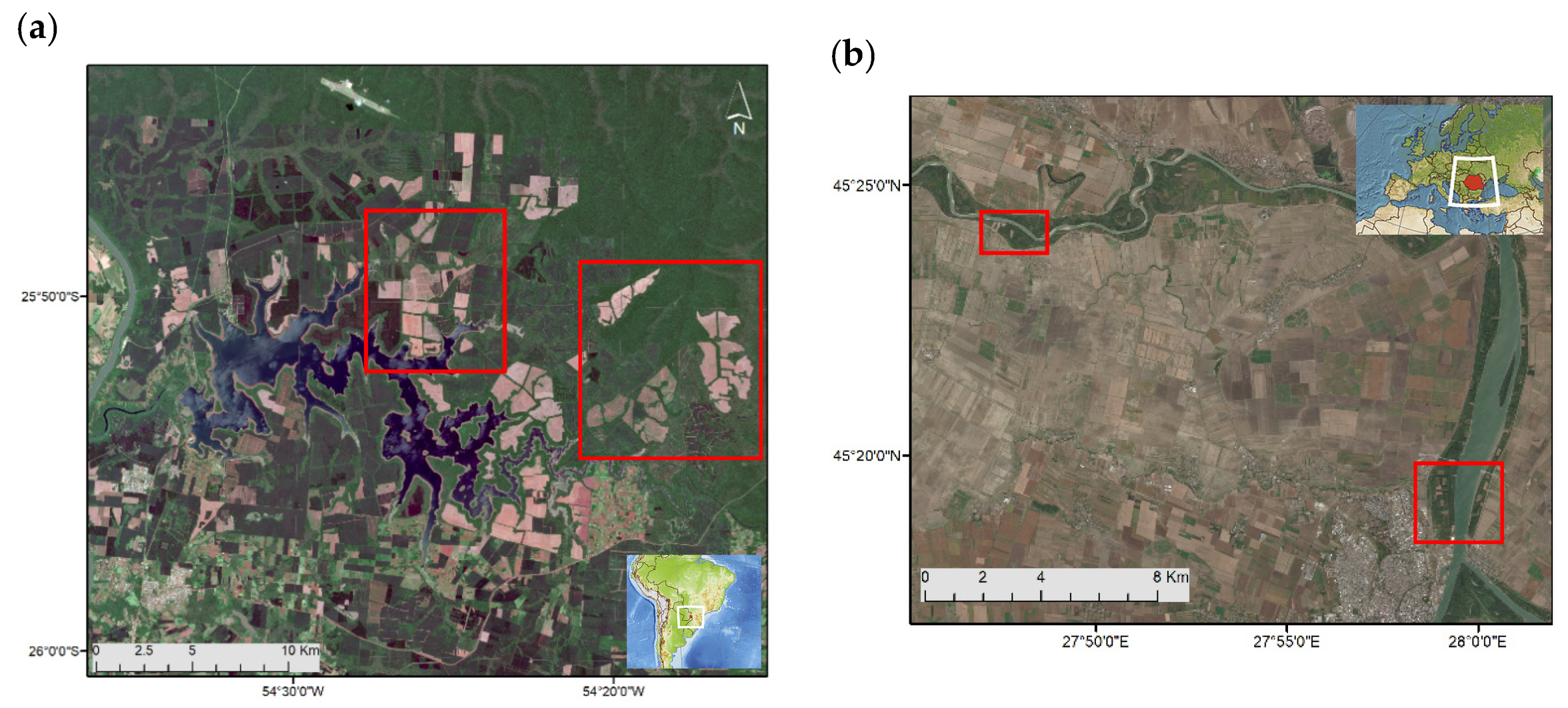
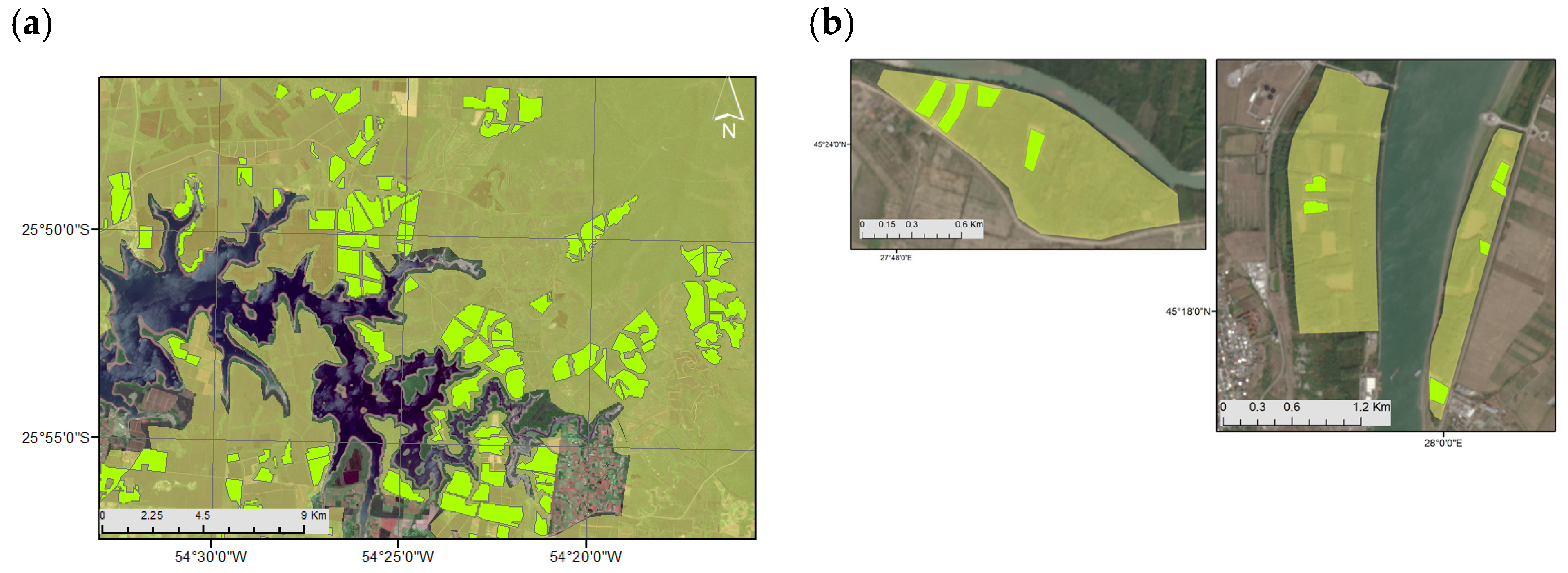
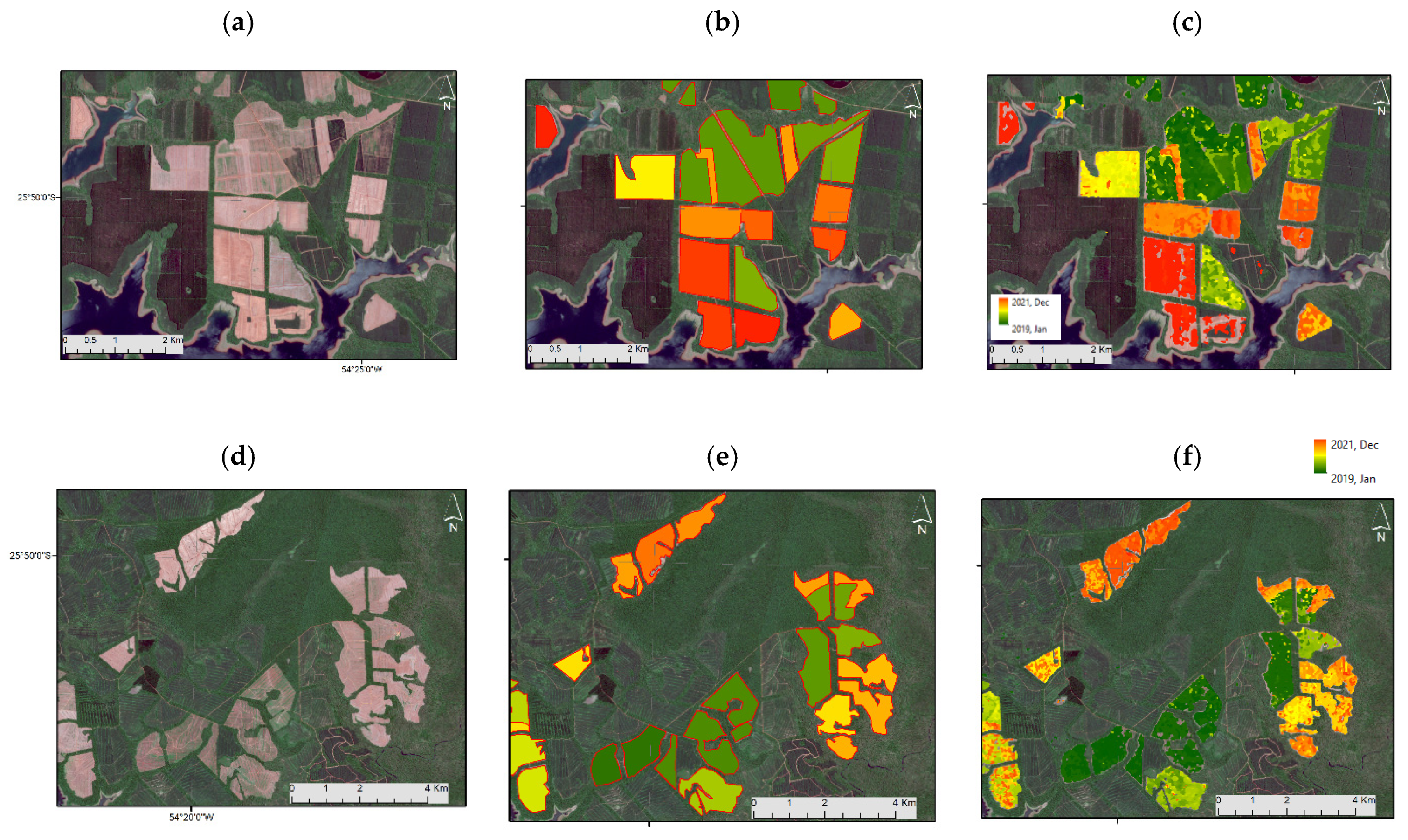
Figure 5 shows the deforestation map for the two selected areas in the Iguazu test site, highlighted as red rectangles in Figure 1. The maps exhibit the estimated deforestation event date for each plot by using a graduated color scale ranging from dark green (January 2019) to dark red (December 2021). The comparison of the deforested map with the reference plots reveals that the vast majority of the deforested areas have been correctly identified, both in terms of spatial location and completeness (Figure 5c). However, some limitations are evident in the resulting change maps.

First, we can observe that some reference plots are incompletely filled (the southern area in Figure 5c), meaning that a forest change was not detected. This effect is more pronounced at the latest dates (dark red color) and can be due to the border effects. With a time window of five images, the first and last five dates of the time series are out of the estimation domain. However, there are still other incompletely filled plots, most likely due to the speckle noise or incomplete deforestation.

Second, we also found that deforestation was falsely detected in some areas (the northwest area in Figure 5c). Some of these areas were deforested in the past, while others correspond to areas recently transformed into agricultural areas. For instance, a plot in the northwest area was incorrectly identified as a deforested area when deforestation occurred in the past. At some point along the time series, the backscatter intensity values for that plot suddenly decreased, misleading the algorithm. This phenomenon may occur after a period with an increase in soil moisture or the presence of snow.

Third, the predictions are generally noisy inside a plot. The noise may be specifically due to an incorrect estimation of the deforestation date within each plot, resulting in different colors. As the estimated deforestation date is related to the logistic function best fit to the backscatter time series, it is expected that neighboring pixels should have the same estimated deforestation date, as observed in most plots. The most likely reason for this apparent incorrect predicted date might be the presence of some deforestation residues still in the ground that were only removed later. Looking into more detail, we observe that, in some of these plots, some rows of small bushes remain within the ground after deforestation. In some plots, deforestation occurred in two steps: first, harvesting and timber removal, and second, soil preparation for a new forest plantation. This means that the algorithm can detect fine details, in time and space, during forest interventions, revealing its suitability for the development of an almost real-time forest monitoring system.

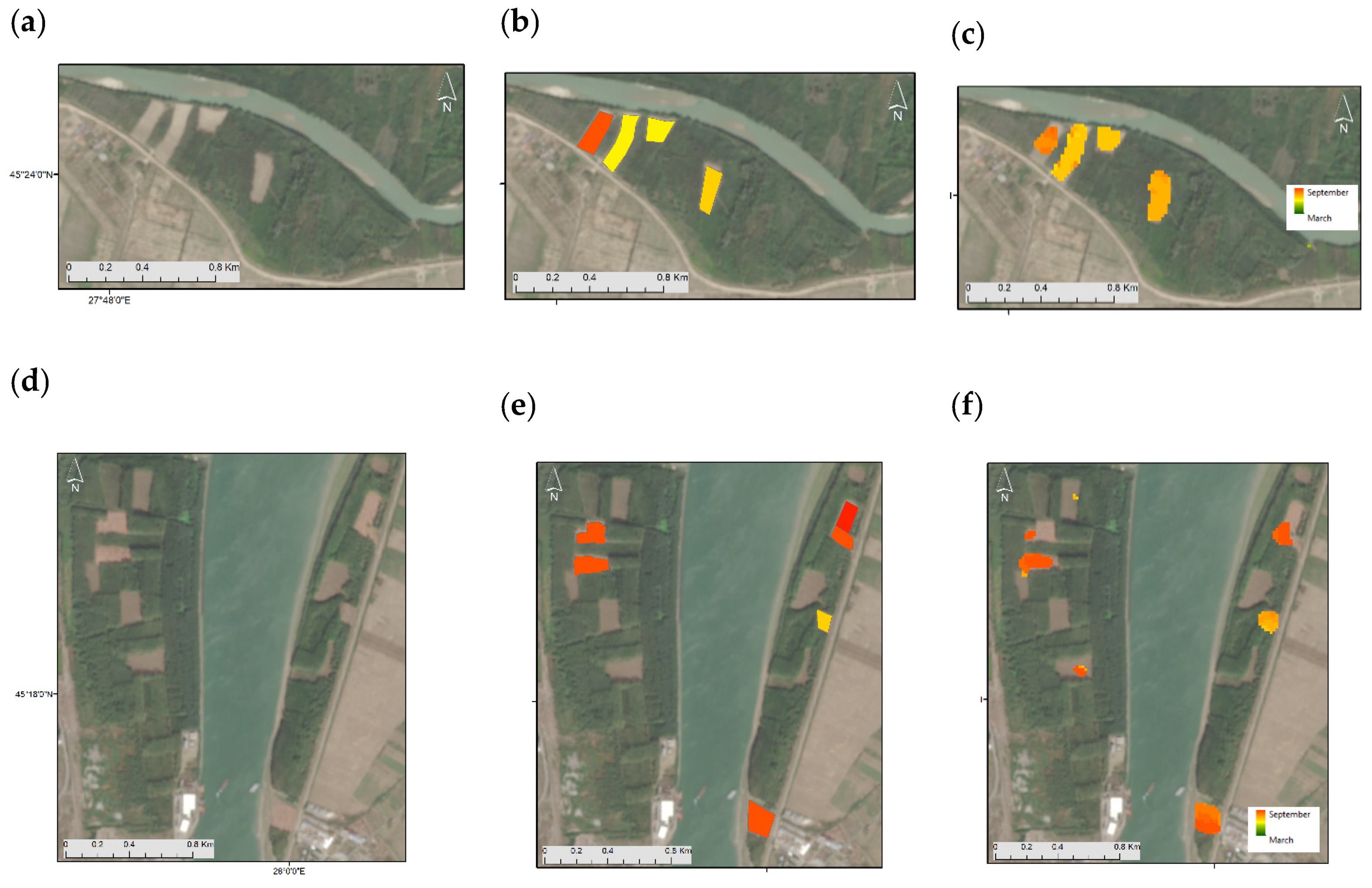
Figure 6 shows the results of the deforestation detection algorithm for the two selected areas in the Brăila test site, highlighted as red rectangles in Figure 1, for a time series between March and September 2020. In this test site, the broad-leaved forest patches are situated along the Danube River on the eastern side of the Brăila municipality. It is clear from Figure 6 that the dimension and number of plots for the Brăila test site are considerably smaller than for the Iguazu test site. Additionally, the time series is shorter, with just 6 months, but with a higher temporal resolution of 6 days. However, the results are quite similar to those obtained for the Iguazu test site, in what concerns incompletely filled plots and false detections, mostly in areas where deforestation occurred in the recent past. The main difference was that the results for the estimated deforestation date were less noisy than for Iguazu. This could be due to different logging practices and an increase in the temporal resolution of the time series. It was observed that, in this area, deforestation corresponds to the clear-cuts completed in a short period. In this case, an optimal fit is achieved between the logistic function and the backscatter time series. Additionally, the high temporal resolution improves the estimation of the sigmoid curve inflection point.

In Brăila, all the reference plots were detected, although not completely filled. On the other hand, some small deforestation areas were incorrectly detected without any correspondence with the plots in the reference map (Figure 6f). This commission error seems to be more pronounced in Brăila than in Iguazu. For some phenomena, the backscatter signal has higher values at the beginning of the time series, and the sudden decrease in the backscatter intensities may induce the algorithm in error, resulting in the detection of a false deforestation event. The presence of snow or a soil moisture increase in the deforested plots may also lead to an increase in the backscatter signal.

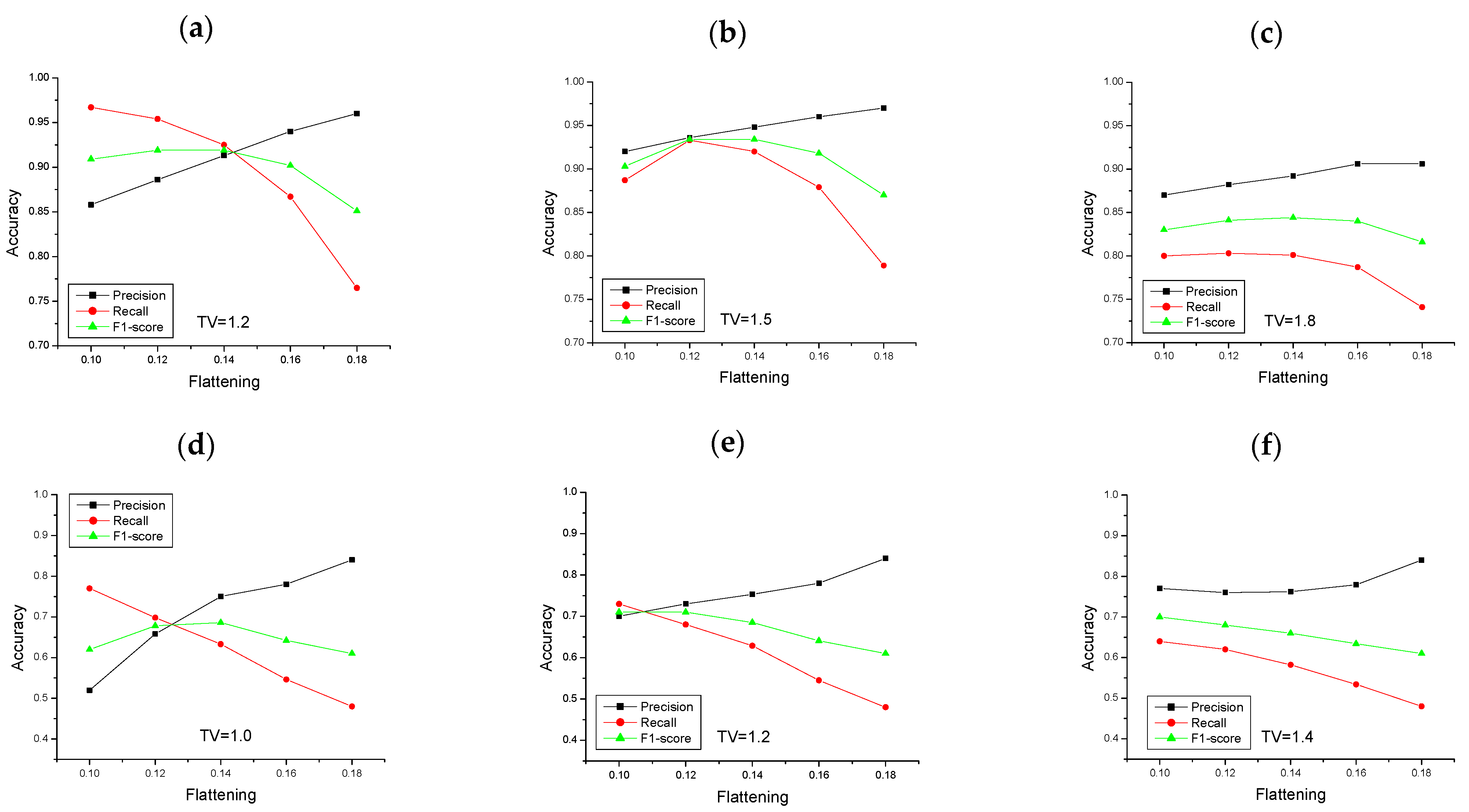
The developed approach implies the setting of two threshold values: one for the temporal variability and another for the logistic function flattening. The first is determined as the 85th percentile of the temporal standard deviation (Equation (1)). The second is an empirical parameter determined by the experimental data analysis that retrieved a value between 0.10 and 0.18. The algorithm sensitivity to both the temporal variability and flattening threshold was assessed. For that purpose, 12 deforestation maps were computed for both test sites, using all the possible combinations among three different temporal variability thresholds and four flattening thresholds, and were then compared with the reference data. We have evaluated the following temporal variability values: 1.8 dB, 1.5 dB and 1.2 dB for Iguazu and 1.4 dB, 1.2 dB and 1.0 dB for Brăila, corresponding to the 90th, 85th and 80th percentiles, respectively.

The best results are obtained with temporal variability thresholds of 1.5 dB and 1.2 dB for the Iguazu and Brăila test sites, respectively. As expected, a decrease in the number of candidate pixels is observed when the temporal variability threshold increases. As an example, for the Iguazu test site, varying the temporal variability threshold from 1.2 dB to 1.8 dB reduces the number of candidate pixels by about 50%, from 501,953 to 245,045 pixels. Consequently, an increase in the temporal variability threshold may under-sample the deforested area, leading to an omission error increase. It is important to notice that the temporal variability is computed only for those pixels inside the forest mask.

The accuracy metrics for both test sites are presented in Figure 7. The accuracy values are slightly different for the two sites. The results for Iguazu outperformed the ones for Brăila by more than 20 pp (percentage points) for all the metrics. The highest F1-score for Brăila is 0.71, while for Iguazu, it is 0.93. In general, the behavior of the three metrics is similar for both sites, with a positive relationship between flattening and precision. An increase in the flattening threshold is associated with a more well-pronounced decay in the backscattering values, resulting in higher confidence for the forest change detection and, consequently, an increase in precision. Contrarily, a negative relationship is observed for the recall, meaning that lower flattening values are related to higher recall values at the cost of lower precision. However, the F1-score seems to be less sensitive to flattening than the other two metrics. In general, the algorithm produces few false positives.

It is also evident that precision and recall are more sensitive to flattening than to a temporal variability threshold. However, it was verified that for a given value of flattening, both precision and recall decrease with an increase in the temporal variability threshold. This result seems to suggest that it would be better to select a lower temporal variability threshold since the accuracy is more influenced by flattening rather than by temporal variability. The challenge is to select the smallest number of candidate pixels that do not compromise the accuracy of the deforestation maps. According to the accuracy assessment, the optimal flattening threshold is 1.2 for both sites, whilst the temporal variability is site dependent and was set as 1.5 dB and 1.2 dB for the Iguazu and Brăila sites, respectively, as mentioned above.

The temporal accuracy was computed for the reference plots identified at both test sites. The deforestation date was determined with a mean time delay of −0.45 and −1.18 months and a standard deviation relative to the mean time delay of 2.0 and 2.1 months for Iguazu and Brăila, respectively. Results point out a bias on the deforestation date estimation, corresponding to a slight delay of 2 months maximum. In our opinion, this metric represents a rough approximation for temporal accuracy due to a less accurate determination of the exact deforestation date from the Sentinel-2 images. If better reference data, such as data on the exact day of the deforestation event, were available, the observed delay might have been reduced. This is particularly evident for the Iguazu test site, where, due to the large area of the plots, logging must have lasted for more than one month. It must be noted that the accuracy of the estimated deforestation date is related to the SAR images’ temporal resolution. In addition, it is expected that time series have a regular sampling over time, which is not the case for the Iguazu test site.

This study was developed using a desktop computer with an Intel Core i7-10700k processor and 32 GB of RAM. It took 22 min to process the Iguazu time series with 350,798 candidate pixels and 30 s to process the Brăila image with 30,376 candidate pixels, both subsets obtained after applying the threshold value corresponding to the 85th percentile. It is important to notice that, although the two test sites have similar dimensions, both in azimuth and range, the use of a temporal variability threshold reduces differently the number of candidate pixels in each site for logistic fitting.

5. Discussion

We have developed a method for deforestation detection that relies on a logistic function fitting to backscattering time series. Based on the goodness of the fit and the logistic function flattening, a pixel is classified as either a stable forest or not. The transition from a stable forest area to a deforested area is determined by the flattening of the sigmoid curve. A flattening above a given threshold is classified as a sudden change in forest behavior. The duration of the deforestation event, estimated from the generalized logistic regression, is related to the growth rate of the logistic curve (a parameter in Equation (2)). The lower growth rate values ($\left|a\right|<2$) are related to longer deforestation events, while higher growth rate values ($\left|a\right|>2$) are related to shorter deforestation events.

The deforestation results obtained for both test sites (Iguazu, in Argentina, and Brăila, in Romania) show that the proposed method demonstrates a robust performance for the detection of deforested areas and also for the estimation of the deforestation date. More importantly, the method does not require training data. However, the threshold value might be optimized even with the use of a small number of reference samples for forest and deforested areas. The use of the logistic function and its flattening and inflection point parameters proved to be effective for deforestation detection, retrieving a small false negative rate. We have observed that recall (true positive rate) is negatively related to the flattening parameter. On the other side, precision (positive predicted value) is positively related to the flattening parameter.

The deforestation maps produced in this study are generally similar to those reported by other authors [21,22,25] but were obtained using a simpler methodology. The methodologies used by those authors either require ground data for image classification [18,24], bi-temporal SAR data [20], or multitemporal SAR data [21,22,25]. Most of the multitemporal SAR data approaches are based on the use of a statistical test within a moving window for forest change detection, requiring ground truth for the parametrization of the statistical test [22]. In their study, the authors define a similarity criterion for forest (the reference), and whenever that criterion is not verified, pixels are identified as non-forest pixels. Similarly, in our study, the reference for forest corresponds to the maximum backscatter intensity (the k parameter in the logistic function), and the decay is defined by the flattening parameter. However, our approach does not require training samples for stable forests and non-forest areas characterization once the change detection criterion is defined by the relative mean flattening of the logistic function. Moreover, another difference is that the size of the pixel domain is reduced to a set of pixels with backscattering values higher than the 85th percentile. This criterion may also be applied to the method proposed by Hansen and Mitchard [22] for a considerable processing time reduction.

The introduction of a temporal variability threshold aims to create a subset of pixels that have experienced some type of change during the analyzed period to reduce the computational cost. The 85th percentile is only an indicative value and must be fine-tuned by the user as a function of the test area; in areas of high forest disturbance, a lower value must be used (e.g., 80th). This allows the identification of a subset of candidate pixels to be analyzed by the logistic function by eliminating stable pixels from the analysis. The impact of the temporal variability threshold on the results was analyzed and presented in Figure 7. The main conclusion is that an increase in the percentile will lead to an increase in omission errors that can be avoided with the use of lower threshold values (the 80th or 75th). This step may be omitted from the methodology flowchart, and consequently, all pixels will be analyzed; however, in this case, the computational cost would be very high (it could take hours depending on the computer processing capacity and the number of images in the time series). In order to overcome these computational issues, the algorithm can be easily implemented in the Google Earth Engine or in the Google Colab platform with the advantage of not requiring the download of images and the use of high-performance computational resources.

The proposed approach is based on the backscatter intensity decrease, which results from the backscatter mechanism change from volume to surface scattering. In the case of clear-cutting, the scattering mechanism change from volume to surface scattering is expected to considerably reduce the backscattering intensity. This change in land cover is efficiently detected by the proposed method. However, in the case of forest degradation (canopy defoliation or dead trees), backscattering intensities exhibit only a slight decrease, which may be assumed as a seasonal backscatter variation when using short time series. In such cases, longer SAR backscattering intensities time series are required for forest monitoring to identify a declining trend. This is not specific to the method but rather a limitation of the SAR C-band. The L-band or future P-band ESA Biomass satellites would be more suitable for forest monitoring. Nevertheless, the method can be defined as an almost near real-time detection method within the temporal resolution of the satellite images. For example, for the Sentinel-1 images with a temporal resolution of 12 days, 48 days are enough to detect a change in the forest.

The main limitations of the proposed method are due to the backscattered signal changes resulting from meteorological events, such as rain or snow. Rain has the effect of increasing soil moisture and, consequently, the intensity of the backscattered signals, which may mask out the deforested areas, particularly in cases of persistent rainfall events. Snow has a similar effect on recently deforested areas, with bare soil areas (recently deforested areas) covered with snow during the winter, having a signature equivalent to a stable forest. When the snow melts at the end of winter, this results in a significant change detection with the same characteristics as deforestation. In these cases, there is an increase in the commission error. In our approach, to avoid these types of errors, an asymmetric logistic function can be defined with a larger time window, e.g., three months before the deforestation event. The presence of snow and soil moisture changes during spring was the main source of error observed in the Brăila test site. It is worth mentioning that these limitations are mainly dependent on the backscattering signal characteristics than on the method itself.

The developed approach may equally be applied to the interferometric coherence time series or to a time series with both types of data to evaluate their synergies. However, interferometric coherence is affected by temporal decorrelation, and an increase in the coherence expected after a deforestation event may be hidden or mitigated by this temporal decorrelation. The temporal decorrelation increases with time, which is expected to occur in the C-band within one month.

6. Conclusions

In this study, a new method was developed for deforestation detection. The method is based on the temporal variability of the backscatter intensities and its correlation with the forest and deforested areas’ spectral signatures. The method relies on a logistic function fitting to backscatter intensity time series. The date of the deforestation has been estimated by minimizing a cost function, and the logistic function flattening has been proposed to filter out false deforested pixels. The proposed method does not require ground truth data, although the flattening parameter may be fine-tuned, and the results improved if reference data were available. Compared to the other approaches reported in the literature, its main advantage is that not only does it require no ground truth (reference data) but also no further user supervision. The algorithm was evaluated in two test sites using Sentinel-1 SAR data. The achieved accuracy is similar to those obtained with similar approaches, reaching an F1-Score of 0.71 at the Brăila test site (conifer forest) and an F1-Score of 0.93 at the Iguazu test site (tropical forest). The results show the potential of the Sentinel-1 C-band data for successful deforestation detection over tropical forests, even though the results’ accuracy over coniferous forests may be reduced to about 20 pp, depending on the environmental conditions, such as rainfall, snow and management after logging. This methodology may contribute to the development of an operational near-real-time monitoring system for vast forest areas, especially in regions with frequent cloud cover, enabling the detection of selective or illegal logging.