The Retrieval of Forest and Grass Fractional Vegetation Coverage in Mountain Regions Based on Spatio-Temporal Transfer Learning
Abstract
:1. Introduction
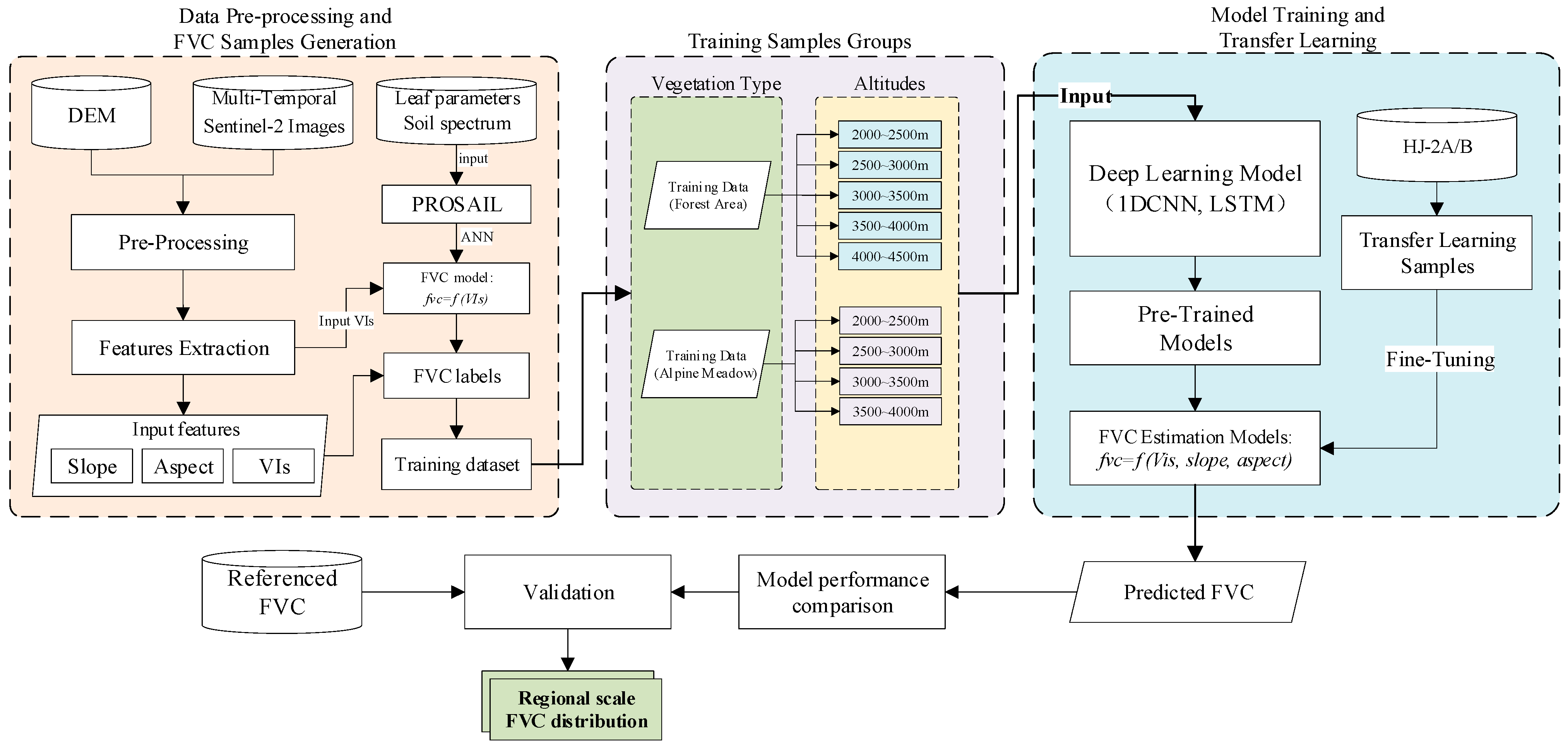
2. Materials and Methods
2.1. Study Area
2.2. Data Sources
2.2.1. Remote Sensing Image Data and Preprocessing
2.2.2. Site FVC
2.2.3. Vegetation Cover Classification
2.3. FVC Training Samples of Mountain Area
2.4. Features Extraction
2.5. Deep Transfer Learning Method
2.5.1. 1D-CNN Neural Network Model
2.5.2. LSTM Neural Network Model
2.5.3. Pre-Training Samples and Valid Samples
2.5.4. Pre-Training Samples and Valid Samples
2.6. Validation
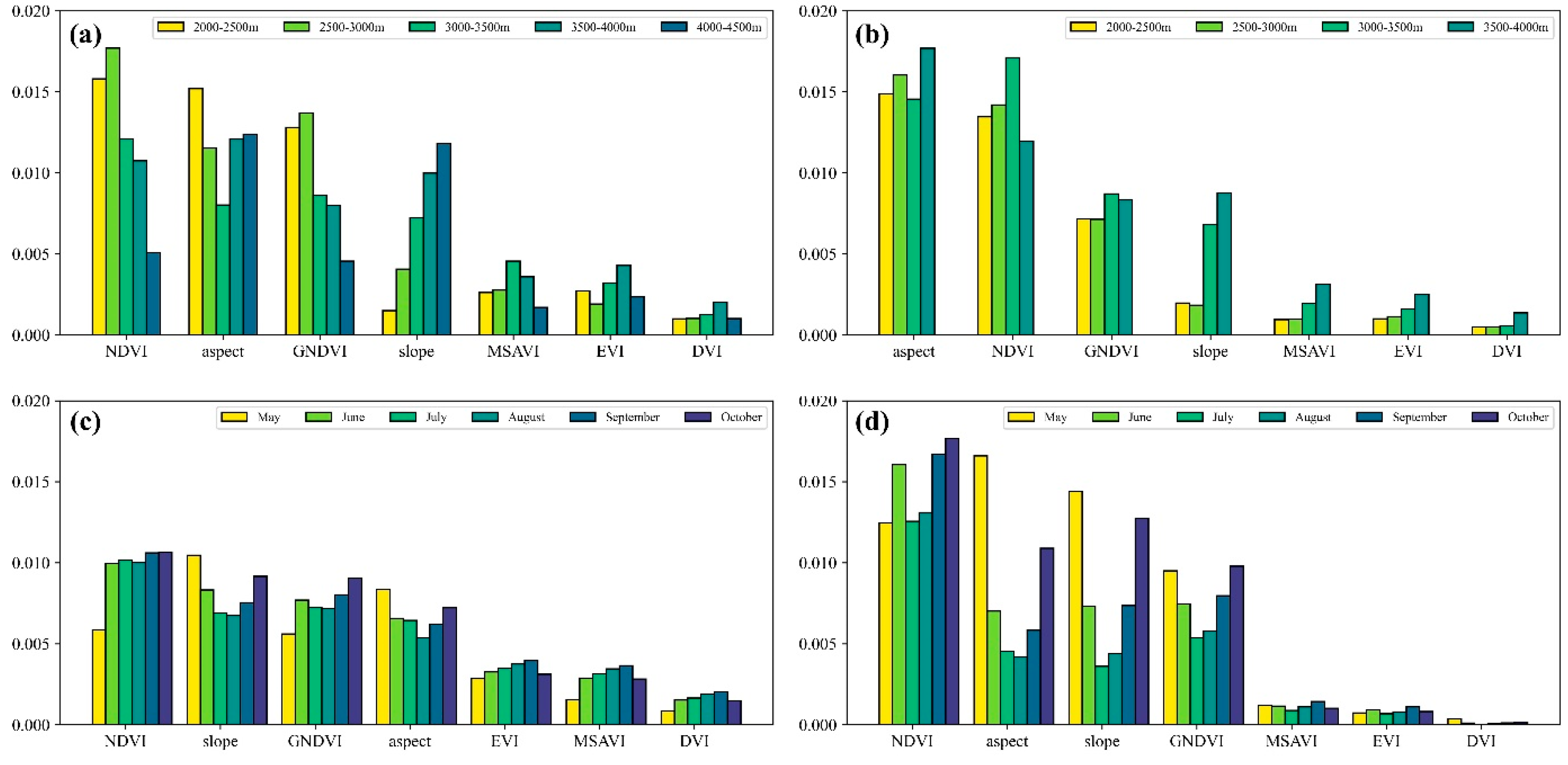
2.7. Feature Importance
3. Results
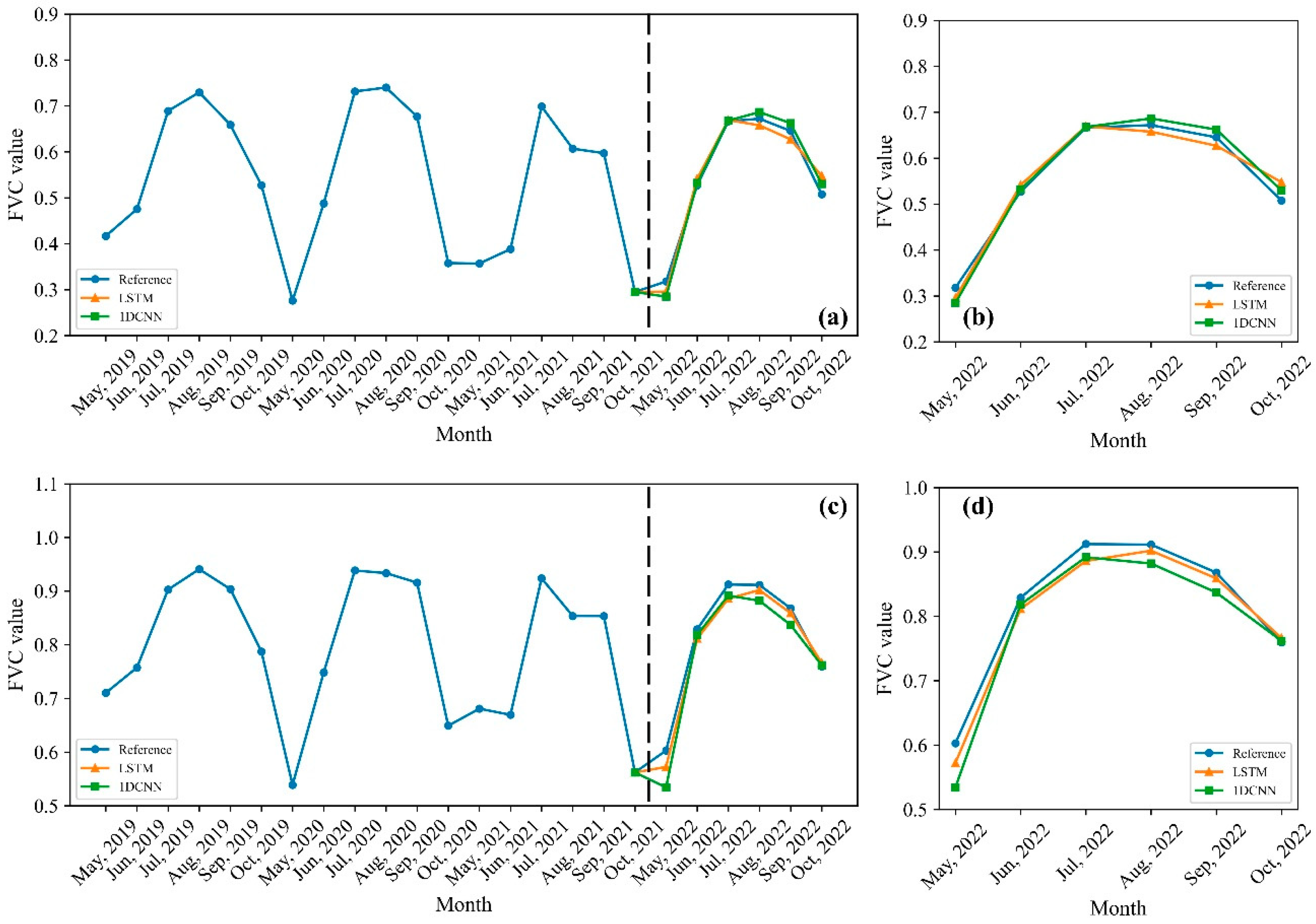
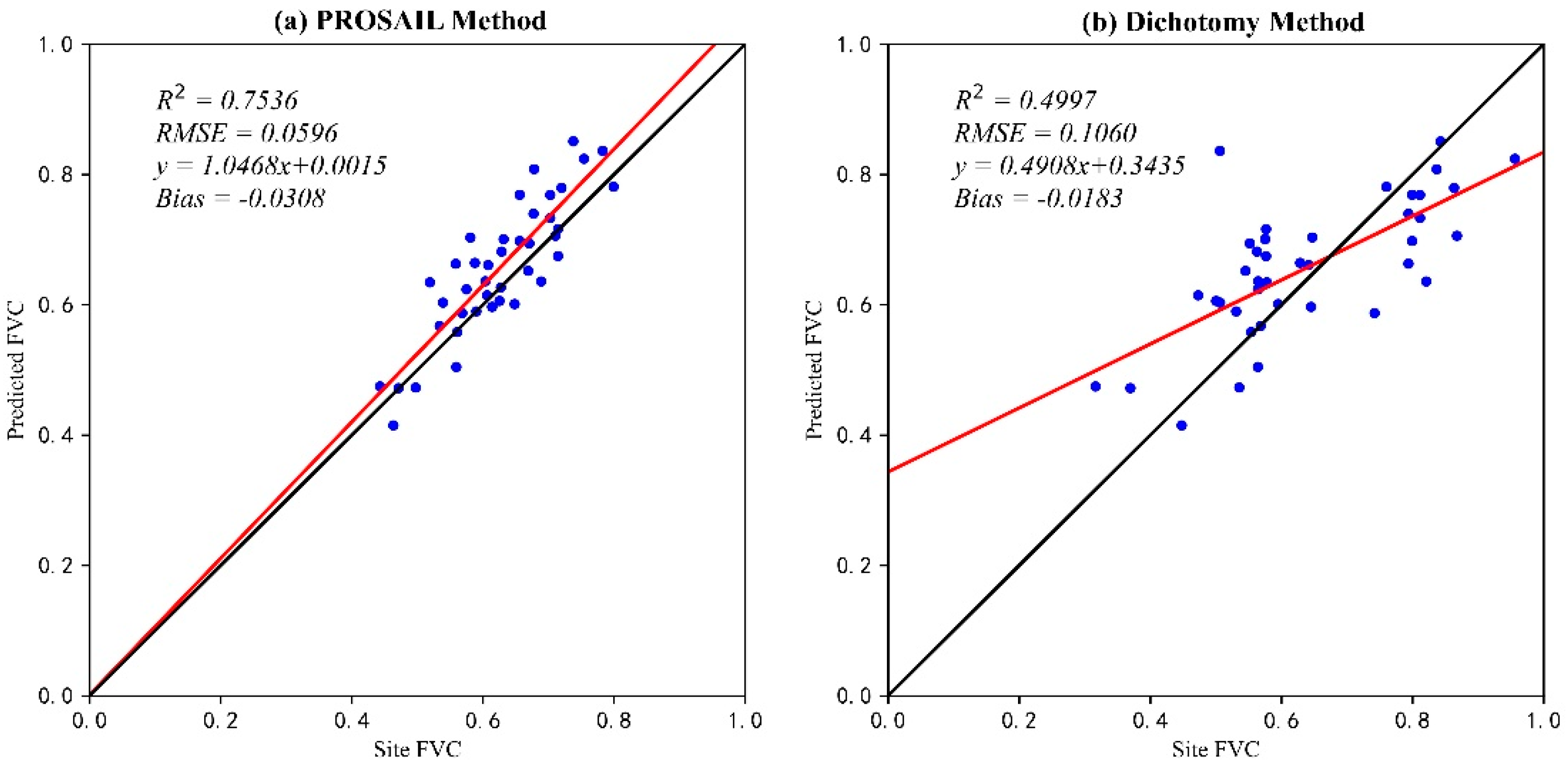
3.1. Result of FVC Retrieval
3.2. Importance Ranking of Features on FVC Retrieval
4. Discussion
4.1. Model Performance
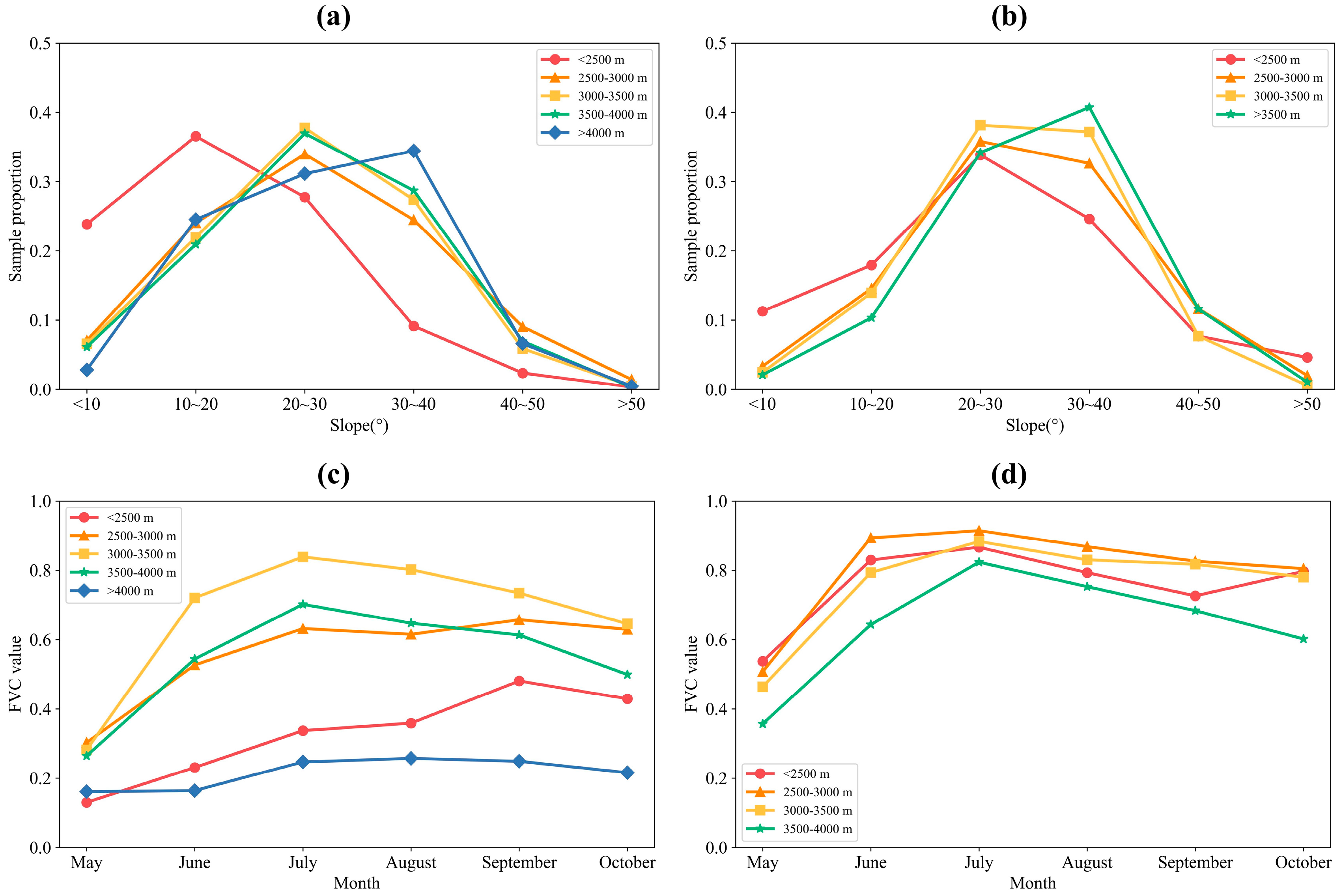
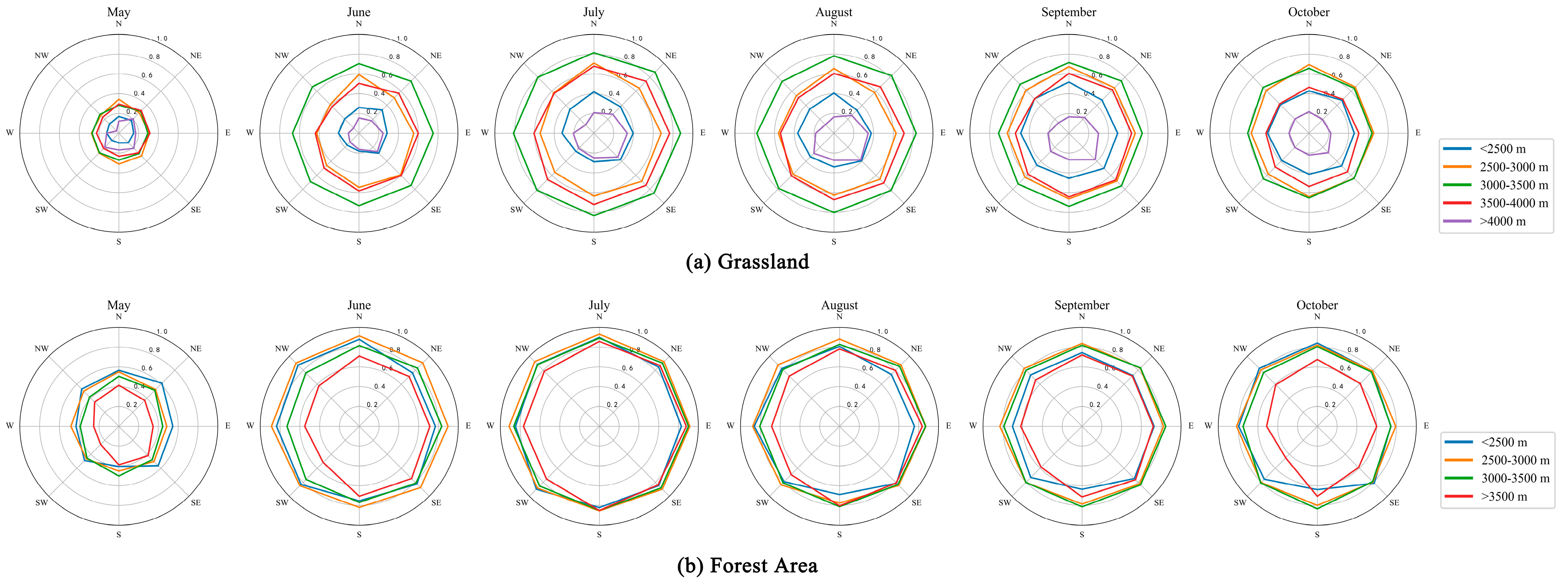
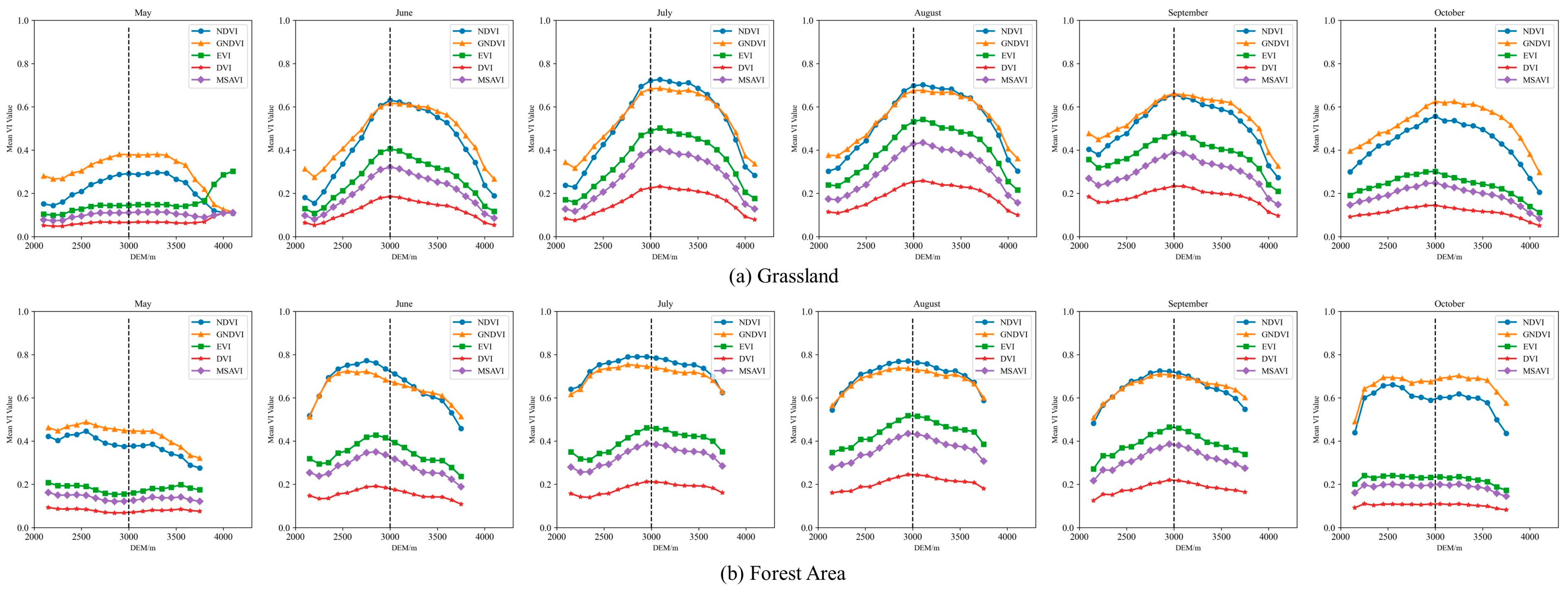
4.2. Influence of Topographic Features on FVC Retrieval
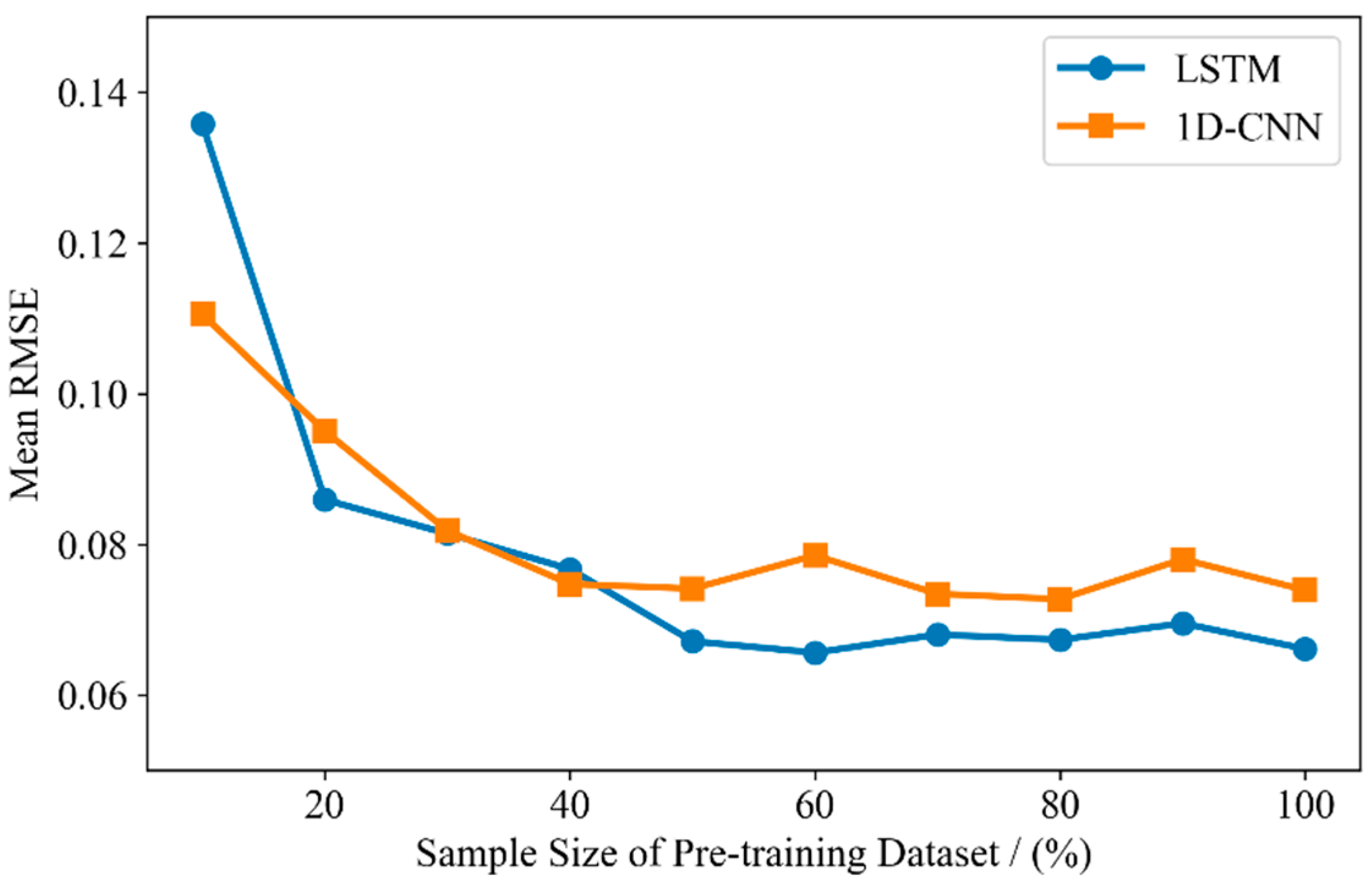
4.3. Influence of Pre-Training Sample Size
4.4. Implications and Limitations
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Grêt-Regamey, A.; Brunner, S.H.; Kienast, F. Mountain Ecosystem Services: Who Cares? Mt. Res. Dev. 2012, 32, S23–S34. [Google Scholar]
- Berger, F.; Rey, F. Mountain Protection Forests against Natural Hazards and Risks: New French Developments by Integrating Forests in Risk Zoning. Nat. Hazards 2004, 33, 395–404. [Google Scholar] [CrossRef]
- Messerli, B.; Ives, J.D. Mountains of the World: A Global Priority; Parthenon Publishing: Nashville, TN, USA, 1997. [Google Scholar]
- Carlson, T.N.; Ripley, D.A. On the Relation between NDVI, Fractional Vegetation Cover, and Leaf Area Index. Remote Sens. Environ. 1997, 62, 241–252. [Google Scholar]
- Gao, L.; Wang, X.; Johnson, B.A.; Tian, Q.; Wang, Y.; Verrelst, J.; Mu, X.; Gu, X. Remote Sensing Algorithms for Estimation of Fractional Vegetation Cover Using Pure Vegetation Index Values: A Review. ISPRS J. Photogramm. Remote Sens. 2020, 14, 364–377. [Google Scholar]
- Verger, A.; Baret, F.; Weiss, M. GEOV2/VGT: Near real time estimation of global biophysical variables from VEGETATION-P data. In Proceedings of the MultiTemp 2013: 7th International Workshop on the Analysis of Multi-temporal Remote Sensing Images, Banff, AB, Canada, 25–27 June 2013; pp. 1–4. [Google Scholar]
- Baret, F.; Weiss, M.; Verger, A.; Smets, B. ATBD for LAI, FAPAR and FCOVER from PROBA-V Products at 300 m Resolution (GEOV3). 2016. Available online: http://www.fp7-imagines.eu/media/Documents/ImagineS_RP2.1_ATBD-LAI300m_I1.73.pdf (accessed on 1 October 2023).
- Jia, K.; Liang, S.; Liu, S.; Li, Y.; Xiao, Z.; Yao, Y.; Jiang, B.; Zhao, X.; Wang, X.; Xu, S. Global Land Surface Fractional Vegetation Cover Estimation Using General Regression Neural Networks from MODIS Surface Reflectance. IEEE Trans. Geosci. Remote Sens. 2015, 53, 4787–4796. [Google Scholar]
- Wang, Y.; Tan, L.; Wang, G.; Sun, X.; Xu, Y. Study on the Impact of Spatial Resolution on Fractional Vegetation Cover Extraction with Single-Scene and Time-Series Remote Sensing Data. Remote Sens. 2022, 14, 4165. [Google Scholar] [CrossRef]
- Mu, X.; Zhao, T.; Ruan, G.; Song, J.; Wang, J.; Yan, G.; Mcvicar, T.R.; Yan, K.; Gao, Z.; Liu, Y.; et al. High Spatial Resolution and High Temporal Frequency (30-m/15-Day) Fractional Vegetation Cover Estimation over China Using Multiple Remote Sensing Datasets: Method Development and Validation. J. Meteorol. Res. 2021, 35, 128–147. [Google Scholar] [CrossRef]
- Mu, X.; Huang, S.; Ren, H.; Yan, G.; Song, W.; Ruan, G. Validating GEOV1 Fractional Vegetation Cover Derived From Coarse-Resolution Remote Sensing Images Over Croplands. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 439–446. [Google Scholar] [CrossRef]
- Liu, D.; Jia, K.; Wei, X.; Xia, M.; Zhang, X.; Yao, Y.; Zhang, X.; Wang, B. Spatiotemporal Comparison and Validation of Three Global-Scale Fractional Vegetation Cover Products. Remote Sens. 2019, 11, 2524. [Google Scholar] [CrossRef]
- Florinsky, I.V.; Kuryakova, G.A. Influence of Topography on Some Vegetation Cover Properties. CATENA 1996, 27, 123–141. [Google Scholar] [CrossRef]
- Song, W.; Yan, K.; Mu, X.; Yan, G. Estimation and Uncertainty Analyses of Fractional Vegetation Cover (FVC) over Mountain Area. In Proceedings of the AGU Fall Meeting Abstracts, San Francisco, CA, USA, 12–16 December 2016; Volume 2016, p. B31E-0515. [Google Scholar]
- Adhikari, H.; Heiskanen, J.; Maeda, E.E.; Pellikka, P.K.E. The Effect of Topographic Normalization on Fractional Tree Cover Mapping in Tropical Mountains: An Assessment Based on Seasonal Landsat Time Series. Int. J. Appl. Earth Obs. Geoinf. 2016, 52, 20–31. [Google Scholar] [CrossRef]
- Gemmell, F. An Investigation of Terrain Effects on the Inversion of a Forest Reflectance Model. Remote Sens. Environ. 1998, 65, 155–169. [Google Scholar] [CrossRef]
- Soenen, S.A.; Peddle, D.R.; Coburn, C.A. SCS+C: A Modified Sun-Canopy-Sensor Topographic Correction in Forested Terrain. IEEE Trans. Geosci. Remote Sens. 2005, 43, 2148–2159. [Google Scholar] [CrossRef]
- Duguay, C.R.; LeDrew, E.F. Estimating Surface Reflectance and Albedo from Landsat-5 Thematic Mapper over Rugged Terrain. Photogramm. Eng. Remote Sens. 1992, 58, 551–558. [Google Scholar]
- Baret, F.; Clevers, J.G.P.W.; Steven, M.D. The Robustness of Canopy Gap Fraction Estimates from Red and Near-Infrared Reflectances: A Comparison of Approaches. Remote Sens. Environ. 1995, 54, 141–151. [Google Scholar] [CrossRef]
- Wittich, K.P.; Hansing, O. Area-Averaged Vegetative Cover Fraction Estimated from Satellite Data. Int. J. Biometeorol. 1995, 38, 209–215. [Google Scholar]
- Zhao, J.; Li, J.; Liu, Q.; Zhang, Z.; Dong, Y. Comparative Study of Fractional Vegetation Cover Estimation Methods Based on Fine Spatial Resolution Images for Three Vegetation Types. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar]
- Montandon, L.; Small, E. The Impact of Soil Reflectance on the Quantification of the Green Vegetation Fraction from NDVI. Remote Sens. Environ. 2008, 112, 1835–1845. [Google Scholar] [CrossRef]
- Huang, R.; Chen, J.; Feng, Z.; Yang, Y.; You, H.; Han, X. Fitness for Purpose of Several Fractional Vegetation Cover Products on Monitoring Vegetation Cover Dynamic Change—A Case Study of an Alpine Grassland Ecosystem. Remote Sens. 2023, 15, 1312. [Google Scholar] [CrossRef]
- Maurya, A.K.; Nadeem, M.; Singh, D.; Singh, K.P.; Rajput, N.S. Critical Analysis of Machine Learning Approaches for Vegetation Fractional Cover Estimation Using Drone and Sentinel-2 Data. In Proceedings of the 2021 IEEE International Geoscience and Remote Sensing Symposium IGARSS, Brussels, Belgium, 11–16 July 2021; pp. 343–346. [Google Scholar]
- Song, D.-X.; Wang, Z.; He, T.; Wang, H.; Liang, S. Estimation and Validation of 30 m Fractional Vegetation Cover over China through Integrated Use of Landsat 8 and Gaofen 2 Data. Sci. Remote Sens. 2022, 6, 100058. [Google Scholar] [CrossRef]
- Chen, J.; Yi, S.; Qin, Y.; Wang, X. Improving Estimates of Fractional Vegetation Cover Based on UAV in Alpine Grassland on the Qinghai–Tibetan Plateau. Int. J. Remote Sens. 2016, 37, 1922–1936. [Google Scholar]
- Weiss, K.; Khoshgoftaar, T.M.; Wang, D. A Survey of Transfer Learning. J. Big Data 2016, 3, 9. [Google Scholar] [CrossRef]
- Pan, S.J.; Yang, Q. A Survey on Transfer Learning. IEEE Trans. Knowl. Data Eng. 2010, 22, 1345–1359. [Google Scholar] [CrossRef]
- Shin, H.-C.; Roth, H.R.; Gao, M.; Lu, L.; Xu, Z.; Nogues, I.; Yao, J.; Mollura, D.; Summers, R.M. Deep Convolutional Neural Networks for Computer-Aided Detection: CNN Architectures, Dataset Characteristics and Transfer Learning. IEEE Trans. Med. Imaging 2016, 35, 1285–1298. [Google Scholar]
- Wan, L.; Zhou, W.; He, Y.; Wanger, T.C.; Cen, H. Combining Transfer Learning and Hyperspectral Reflectance Analysis to Assess Leaf Nitrogen Concentration across Different Plant Species Datasets. Remote Sens. Environ. 2022, 269, 112826. [Google Scholar] [CrossRef]
- Khaki, S.; Pham, H.; Wang, L. Simultaneous Corn and Soybean Yield Prediction from Remote Sensing Data Using Deep Transfer Learning. Sci. Rep. 2021, 11, 11132. [Google Scholar]
- Yli-Heikkila, M.; Wittke, S.; Luotamo, M.; Puttonen, E.; Sulkava, M.; Pellikka, P.; Heiskanen, J.; Klami, A. Scalable Crop Yield Prediction with Sentinel-2 Time Series and Temporal Convolutional Network. Remote Sens. 2022, 14, 4193. [Google Scholar] [CrossRef]
- Wang, A.X.; Tran, C.; Desai, N.; Lobell, D.; Ermon, S. Deep Transfer Learning for Crop Yield Prediction with Remote Sensing Data. In Proceedings of the 1st ACM SIGCAS Conference on Computing and Sustainable Societies, San Jose, CA, USA, 20–22 June 2018; ACM: Menlo Park, CA, USA; San Jose, CA, USA, 2018; pp. 1–5. [Google Scholar]
- Astola, H.; Seitsonen, L.; Halme, E.; Molinier, M.; Lönnqvist, A. Deep Neural Networks with Transfer Learning for Forest Variable Estimation Using Sentinel-2 Imagery in Boreal Forest. Remote Sens. 2021, 13, 2392. [Google Scholar] [CrossRef]
- Yu, R.; Li, S.; Zhang, B.; Zhang, H. A Deep Transfer Learning Method for Estimating Fractional Vegetation Cover of Sentinel-2 Multispectral Images. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Holben, B.N. Characteristics of Maximum-Value Composite Images from Temporal AVHRR Data. Int. J. Remote Sens. 1986, 7, 1417–1434. [Google Scholar] [CrossRef]
- Marcial-Pablo, M.D.J.; Gonzalez-Sanchez, A.; Jimenez-Jimenez, S.I.; Ontiveros-Capurata, R.E.; Ojeda-Bustamante, W. Estimation of Vegetation Fraction Using RGB and Multispectral Images from UAV. Int. J. Remote Sens. 2019, 40, 420–438. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, L.; Chen, X.; Gao, Y.; Xie, S.; Mi, J. GLC_FCS30: Global Land-Cover Product with Fine Classification System at 30 m Using Time-Series Landsat Imagery. Earth Syst. Sci. Data 2021, 13, 2753–2776. [Google Scholar] [CrossRef]
- Anderson, K.; Fawcett, D.; Cugulliere, A.; Benford, S.; Jones, D.; Leng, R. Vegetation Expansion in the Subnival Hindu Kush Himalaya. Glob. Chang. Biol. 2020, 26, 1608–1625. [Google Scholar] [CrossRef]
- Jacquemoud, S.; Verhoef, W.; Baret, F.; Bacour, C.; Zarco-Tejada, P.J.; Asner, G.P.; François, C.; Ustin, S.L. PROSPECT+SAIL Models: A Review of Use for Vegetation Characterization. Remote Sens. Environ. 2009, 113, S56–S66. [Google Scholar] [CrossRef]
- Rosema, A.; Verhoef, W.; Noorbergen, H.; Borgesius, J.J. A New Forest Light Interaction Model in Support of Forest Monitoring. Remote Sens. Environ. 1992, 42, 23–41. [Google Scholar]
- Gastellu-Etchegorry, J.-P.; Demarez, V.; Pinel, V.; Zagolski, F. Modeling Radiative Transfer in Heterogeneous 3-D Vegetation Canopies. Remote Sens. Environ. 1996, 58, 131–156. [Google Scholar] [CrossRef]
- Rouse, J.W.; Haas, R.H.; Schell, J.A.; Deering, D.W. Monitoring Vegetation Systems in the Great Plains with ERTS. NASA Spec. Publ. 1974, 351, 309. [Google Scholar]
- Gitelson, A.A.; Kaufman, Y.J.; Merzlyak, M.N. Use of a Green Channel in Remote Sensing of Global Vegetation from EOS-MODIS. Remote Sens. Environ. 1996, 58, 289–298. [Google Scholar]
- Huete, A.; Didan, K.; Miura, T.; Rodriguez, E.P.; Gao, X.; Ferreira, L.G. Overview of the Radiometric and Biophysical Performance of the MODIS Vegetation Indices. Remote Sens. Environ. 2002, 83, 195–213. [Google Scholar] [CrossRef]
- Richardson, A.J.; Wiegand, C.L. Distinguishing Vegetation from Soil Background Information. Photogramm. Eng. Remote Sens. 1977, 43, 1541–1552. [Google Scholar]
- Qi, J.; Chehbouni, A.; Huete, A.R.; Kerr, Y.H.; Sorooshian, S. A Modified Soil Adjusted Vegetation Index. Remote Sens. Environ. 1994, 48, 119–126. [Google Scholar] [CrossRef]
- Mazza, A.; Gargiulo, M.; Scarpa, G.; Gaetano, R. Estimating the NDVI from SAR by Convolutional Neural Networks. In Proceedings of the IGARSS 2018—2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 1954–1957. [Google Scholar]
- Kattenborn, T.; Leitloff, J.; Schiefer, F.; Hinz, S. Review on Convolutional Neural Networks (CNN) in Vegetation Remote Sensing. ISPRS J. Photogramm. Remote Sens. 2021, 173, 24–49. [Google Scholar] [CrossRef]
- Kiranyaz, S.; Ince, T.; Gabbouj, M. Real-Time Patient-Specific ECG Classification by 1-D Convolutional Neural Networks. IEEE Trans. Biomed. Eng. 2016, 63, 664–675. [Google Scholar] [CrossRef] [PubMed]
- Rußwurm, M.; Körner, M. Multi-Temporal Land Cover Classification with Long Short-Term Memory Neural Networks. The International Archives of the Photogrammetry. Remote Sens. Spat. Inf. Sci. 2017, 42, 551–558. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Gers, F.A.; Schraudolph, N.N.; Schmidhuber, J. Learning Precise Timing with LSTM Recurrent Networks. J. Mach. Learn. Res. 2003, 3, 115–143. [Google Scholar]
- Hüsken, M.; Stagge, P. Recurrent Neural Networks for Time Series Classification. Neurocomputing 2003, 50, 223–235. [Google Scholar] [CrossRef]
- Cao, J.; Zhang, Z.; Luo, Y.; Zhang, L.; Zhang, J.; Li, Z.; Tao, F. Wheat Yield Predictions at a County and Field Scale with Deep Learning, Machine Learning, and Google Earth Engine. Eur. J. Agron. 2021, 123, 126204. [Google Scholar] [CrossRef]
- Lundberg, S.M.; Lee, S.-I. A Unified Approach to Interpreting Model Predictions. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; Volume 30. [Google Scholar]
- Lundberg, S.M.; Erion, G.; Chen, H.; DeGrave, A.; Prutkin, J.M.; Nair, B.; Katz, R.; Himmelfarb, J.; Bansal, N.; Lee, S.-I. From Local Explanations to Global Understanding with Explainable AI for Trees. Nat. Mach. Intell. 2020, 2, 56–67. [Google Scholar] [CrossRef]
- Ali, A.M.; Darvishzadeh, R.; Skidmore, A.; Gara, T.W.; Heurich, M. Machine Learning Methods’ Performance in Radiative Transfer Model Inversion to Retrieve Plant Traits from Sentinel-2 Data of a Mixed Mountain Forest. Int. J. Digit. Earth 2021, 14, 106–120. [Google Scholar] [CrossRef]
- Allen, R.B.; Peet, R.K. Gradient Analysis of Forests of the Sangre de Cristo Range, Colorado. Can. J. Bot. 1990, 68, 193–201. [Google Scholar] [CrossRef]
- Busing, R.T.; White, P.S.; MacKenzie, M.D. Gradient Analysis of Old Spruce—Fir Forests of the Great Smoky Mountains circa 1935. Can. J. Bot. 1993, 71, 951–958. [Google Scholar] [CrossRef]
- Ojoyi, M.; Mutanga, O.; Odindi, J.; Abdel-Rahman, E.M. Application of Topo-Edaphic Factors and Remotely Sensed Vegetation Indices to Enhance Biomass Estimation in a Heterogeneous Landscape in the Eastern Arc Mountains of Tanzania. Geocarto Int. 2016, 31, 1–21. [Google Scholar] [CrossRef]
- Liu, B.; Biswas, S.R.; Yang, J.; Liu, Z.; He, H.S.; Liang, Y.; Lau, M.K.; Fang, Y.; Han, S. Strong Influences of Stand Age and Topography on Post-Fire Understory Recovery in a Chinese Boreal Forest. For. Ecol. Manag. 2020, 473, 118307. [Google Scholar] [CrossRef]
- Shen, B.; Ding, L.; Ma, L.; Li, Z.; Pulatov, A.; Kulenbekov, Z.; Chen, J.; Mambetova, S.; Hou, L.; Xu, D.; et al. Modeling the Leaf Area Index of Inner Mongolia Grassland Based on Machine Learning Regression Algorithms Incorporating Empirical Knowledge. Remote Sens. 2022, 14, 4196. [Google Scholar] [CrossRef]
- De Castilho, C.V.; Magnusson, W.E.; De Araújo, R.N.O.; Luizão, R.C.C.; Luizão, F.J.; Lima, A.P.; Higuchi, N. Variation in Aboveground Tree Live Biomass in a Central Amazonian Forest: Effects of Soil and Topography. For. Ecol. Manag. 2006, 234, 85–96. [Google Scholar] [CrossRef]
- Warren, R.J. Mechanisms Driving Understory Evergreen Herb Distributions across Slope Aspects: As Derived from Landscape Position. Plant Ecol. 2008, 198, 297–308. [Google Scholar] [CrossRef]
- Mokarram, M.; Sathyamoorthy, D. Modeling the Relationship between Elevation, Aspect and Spatial Distribution of Vegetation in the Darab Mountain, Iran Using Remote Sensing Data. Model. Earth Syst. Environ. 2015, 1, 30. [Google Scholar] [CrossRef]
- Jin, X.; Zhang, Y.; Schaepman, M.E.; Clevers, J.; Su, Z.; Cheng, J.; Jiang, J.; van Genderen, J. Impact of elevation and aspect on the spatial distribution of vegetation in the Qilian mountain area with remote sensing data. In Proceedings of the XXI Congress: Silk Road for Information from Imagery and Remote Sensing (ISPRS 2008), Beijing, China, 3–11 July 2008; The International Society for Photogrammetry: Hannover, Germany, 2008; pp. 1385–1390. [Google Scholar]
- Kumar, P.; Chen, H.Y.H.; Thomas, S.C.; Shahi, C. Linking Resource Availability and Heterogeneity to Understorey Species Diversity through Succession in Boreal Forest of Canada. J. Ecol. 2018, 106, 1266–1276. [Google Scholar] [CrossRef]
- Grime, J.P. Competitive Exclusion in Herbaceous Vegetation. Nature 1973, 242, 344–347. [Google Scholar]
- Purevdorj, T.S.; Tateishi, R.; Ishiyama, T.; Honda, Y. Relationships between Percent Vegetation Cover and Vegetation Indices. Int. J. Remote Sens. 1998, 19, 3519–3535. [Google Scholar] [CrossRef]
- An, S.; Zhang, X.; Chen, X.; Yan, D.; Henebry, G. An Exploration of Terrain Effects on Land Surface Phenology across the Qinghai–Tibet Plateau Using Landsat ETM+ and OLI Data. Remote Sens. 2018, 10, 1069. [Google Scholar] [CrossRef]
- Ma, X.; Lu, L.; Ding, J.; Zhang, F.; He, B. Estimating Fractional Vegetation Cover of Row Crops from High Spatial Resolution Image. Remote Sens. 2021, 13, 3874. [Google Scholar] [CrossRef]


| Model | Parameters | Variables Name | Range | Step |
|---|---|---|---|---|
| PROSAIL | Chlorophyll a + b concentration (μg/cm2) | 20–80 | 10 | |
| Dry matter content (g/cm2) | 0.005–0.015 | 0.005 | ||
| Carotenoid content (g/cm2) | 0 | - | ||
| Equivalent water thickness (cm) | 0.005–0.015 | 0.005 | ||
| Brown pigment content | 0–1.5 | 0.5 | ||
| SAIL | Leaf structure parameter | 1–2 | 0.5 | |
| Leaf area index (m2/m2) | 0–7 | 0.5 | ||
| ) | 30–70 | 10 | ||
| Hot spot parameter | 0.1 | - | ||
| ) | 25–65 | 10 |
| Elevation(m) | Sample Points | |
|---|---|---|
| Grassland | Forest Area | |
| <2500 | 1684 | 2271 |
| 2500~3000 | 14,484 | 38,203 |
| 3000~3500 | 25,631 | 35,949 |
| 3500~4000 | 33,717 | 15,731 |
| >4000 | 2942 | — |
| Month | Grassland | Forest Area | ||||||
|---|---|---|---|---|---|---|---|---|
| LSTM | 1DCNN | LSTM | 1DCNN | |||||
| R2 | RMSE | R2 | RMSE | R2 | RMSE | R2 | RMSE | |
| May | 0.7498 | 0.1022 | 0.6149 | 0.1306 | 0.8675 | 0.0625 | 0.7620 | 0.0993 |
| June | 0.9678 | 0.0544 | 0.9546 | 0.0579 | 0.936 | 0.0448 | 0.9003 | 0.0475 |
| July | 0.9632 | 0.0562 | 0.9440 | 0.0691 | 0.8857 | 0.0408 | 0.8662 | 0.0410 |
| August | 0.9703 | 0.0596 | 0.9456 | 0.0717 | 0.9226 | 0.0599 | 0.8983 | 0.0613 |
| September | 0.9371 | 0.0824 | 0.9215 | 0.0789 | 0.8844 | 0.0771 | 0.8830 | 0.0736 |
| October | 0.8766 | 0.0733 | 0.8524 | 0.0753 | 0.7891 | 0.0632 | 0.7721 | 0.0673 |
| Average | 0.9108 | 0.0714 | 0.8722 | 0.0806 | 0.8809 | 0.0581 | 0.8470 | 0.0650 |
| Slope | Aspect | ||
|---|---|---|---|
| Class | Range (°) | Direction | Range (°) |
| 1 | <10 | N | 337.5~22.5 |
| 2 | 10~20 | NE | 22.5~67.5 |
| 3 | 20~30 | E | 67.5~112.5 |
| 4 | 30~40 | SE | 112.5~157.5 |
| 5 | 40~50 | S | 157.5~202.5 |
| 6 | >50 | SW | 202.5~247.5 |
| W | 247.5~292.5 | ||
| NW | 292.5~337.5 | ||
| Sample Size | All Vegetations | Grassland | Forest Area | |||
|---|---|---|---|---|---|---|
| LSTM | 1DCNN | LSTM | 1DCNN | LSTM | 1DCNN | |
| 10% | 0.1358 | 0.1105 | 0.1601 | 0.1165 | 0.1005 | 0.1004 |
| 20% | 0.0859 | 0.0950 | 0.0834 | 0.0869 | 0.0882 | 0.1009 |
| 30% | 0.0814 | 0.0818 | 0.0779 | 0.0813 | 0.0845 | 0.0810 |
| 40% | 0.0767 | 0.0747 | 0.0811 | 0.0843 | 0.0716 | 0.0634 |
| 50% | 0.0671 | 0.0741 | 0.0743 | 0.0728 | 0.0581 | 0.0739 |
| 60% | 0.0656 | 0.0785 | 0.0706 | 0.0814 | 0.0596 | 0.0782 |
| 70% | 0.0680 | 0.0734 | 0.0713 | 0.0781 | 0.0638 | 0.0639 |
| 80% | 0.0673 | 0.0727 | 0.0793 | 0.0812 | 0.0591 | 0.0633 |
| 90% | 0.0695 | 0.0780 | 0.0709 | 0.0771 | 0.0675 | 0.0780 |
| 100% | 0.0653 | 0.0735 | 0.0714 | 0.0806 | 0.0581 | 0.0650 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, Y.; Zhou, X.; Lv, T.; Tao, Z.; Zhang, H.; Li, R.; Zhai, M.; Liang, H. The Retrieval of Forest and Grass Fractional Vegetation Coverage in Mountain Regions Based on Spatio-Temporal Transfer Learning. Remote Sens. 2023, 15, 4857. https://doi.org/10.3390/rs15194857
Huang Y, Zhou X, Lv T, Tao Z, Zhang H, Li R, Zhai M, Liang H. The Retrieval of Forest and Grass Fractional Vegetation Coverage in Mountain Regions Based on Spatio-Temporal Transfer Learning. Remote Sensing. 2023; 15(19):4857. https://doi.org/10.3390/rs15194857
Chicago/Turabian StyleHuang, Yuxuan, Xiang Zhou, Tingting Lv, Zui Tao, Hongming Zhang, Ruoxi Li, Mingjian Zhai, and Houyu Liang. 2023. "The Retrieval of Forest and Grass Fractional Vegetation Coverage in Mountain Regions Based on Spatio-Temporal Transfer Learning" Remote Sensing 15, no. 19: 4857. https://doi.org/10.3390/rs15194857
APA StyleHuang, Y., Zhou, X., Lv, T., Tao, Z., Zhang, H., Li, R., Zhai, M., & Liang, H. (2023). The Retrieval of Forest and Grass Fractional Vegetation Coverage in Mountain Regions Based on Spatio-Temporal Transfer Learning. Remote Sensing, 15(19), 4857. https://doi.org/10.3390/rs15194857









