Using the Commercial GNSS RO Spire Data in the Neutral Atmosphere for Climate and Weather Prediction Studies
Abstract
:1. Introduction
- (1)
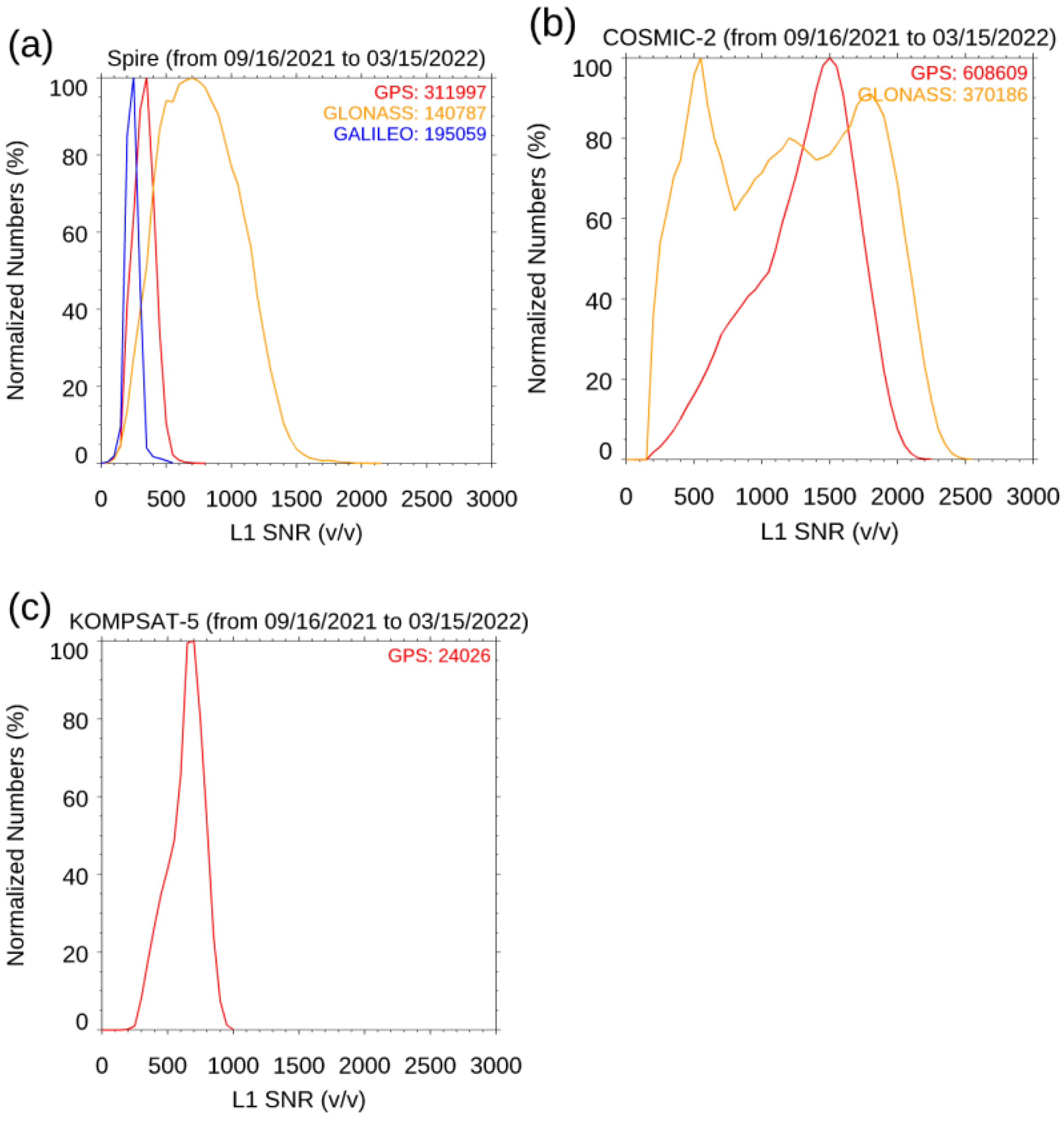
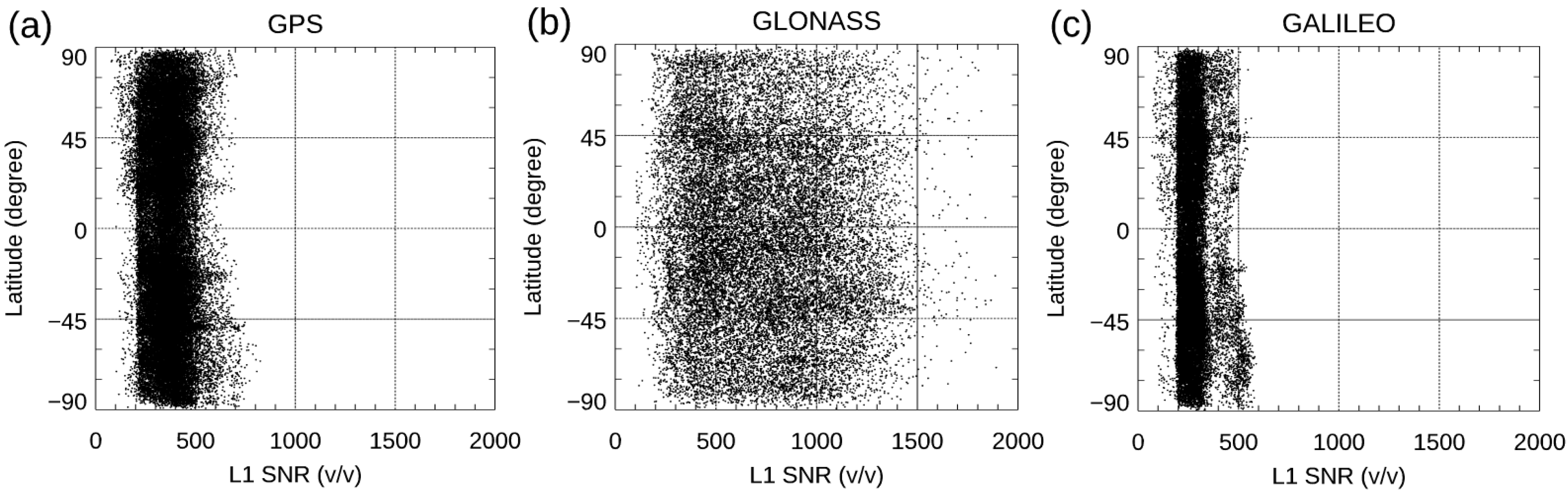
- Does lower signal-noise ratio (SNR) commercial CubeSat RO data lead to lower precision and more significant observation errors? The SNR is defined as the magnitude of the RO signals divided by the noise level from the receiver in the voltage-to-voltage unit (v/v). The SNR of the RO signal is one of the critical parameters that indicates the quality of RO measurements (i.e., time delay and excess phases) and Level 2 (L2) data products (i.e., bending angle (BA), refractivity, temperature, and moisture profiles). When RO signals are stronger or the noise level is smaller, the magnitude of the SNR will be larger, which may indicate an improved observation quality. While COSMIC-1 and COSMIC-2 used an antenna of two feet, the antenna from CubeSat is only one foot. Figure 1 depicts the SNR histograms of Spire, COSMIC-2, and KOMPSAT-5 for different GNSS RO emitters. The sample numbers are normalized to the maximum number of the SNR bin. With the TGRS receiver, COSMIC-2 has a larger mean SNR than that of Spire and KOMPSAT-5. The mean COSMIC-2 L1 SNR ranges from 250 to 2500 v/v [31,32], while the L1 SNR for Spire ranges from 200 v/v to 1500 v/v, lower than that from COSMIC-2 (Figure 1). The mean L1 SNR for KOMPAST-5 is 570 v/v. With a higher SNR than that of other RO missions, COSMIC-2 is expected to penetrate deeper into the lower troposphere [30,31,32,33].
- (2)
- Does lower-SNR Spire RO data lead to less accurate retrieval results? Whether the RO data products derived from lower SNR signals obtained from commercial CubeSats are as accurate as those from high SNR signals is a significant concern for the RO community and climate and atmospheric scientists. The causes of retrieval uncertainty may include receiver quality, antenna geometry, the accuracy of the Precise Orbit Determination (POD) estimation, L0 to L1a processing, L1a-L1b (excess phase) processing, and L1b-L2 (bending angle and refractivity profiles) processing [33].
- (3)
- How do we optimize the Spire RO data in the NWP data assimilation (DA) system? As mentioned above, because the RO bending angle and refractivity uncertainty, especially in the lower troposphere, are highly related to the atmospheric condition, we must carefully examine the observation uncertainty for each RO mission to use the RO data optimally in NWP DA algorithms.
2. Data and Methodology
2.1. Spatial and Local Time Distribution of Spire and Other RO Missions
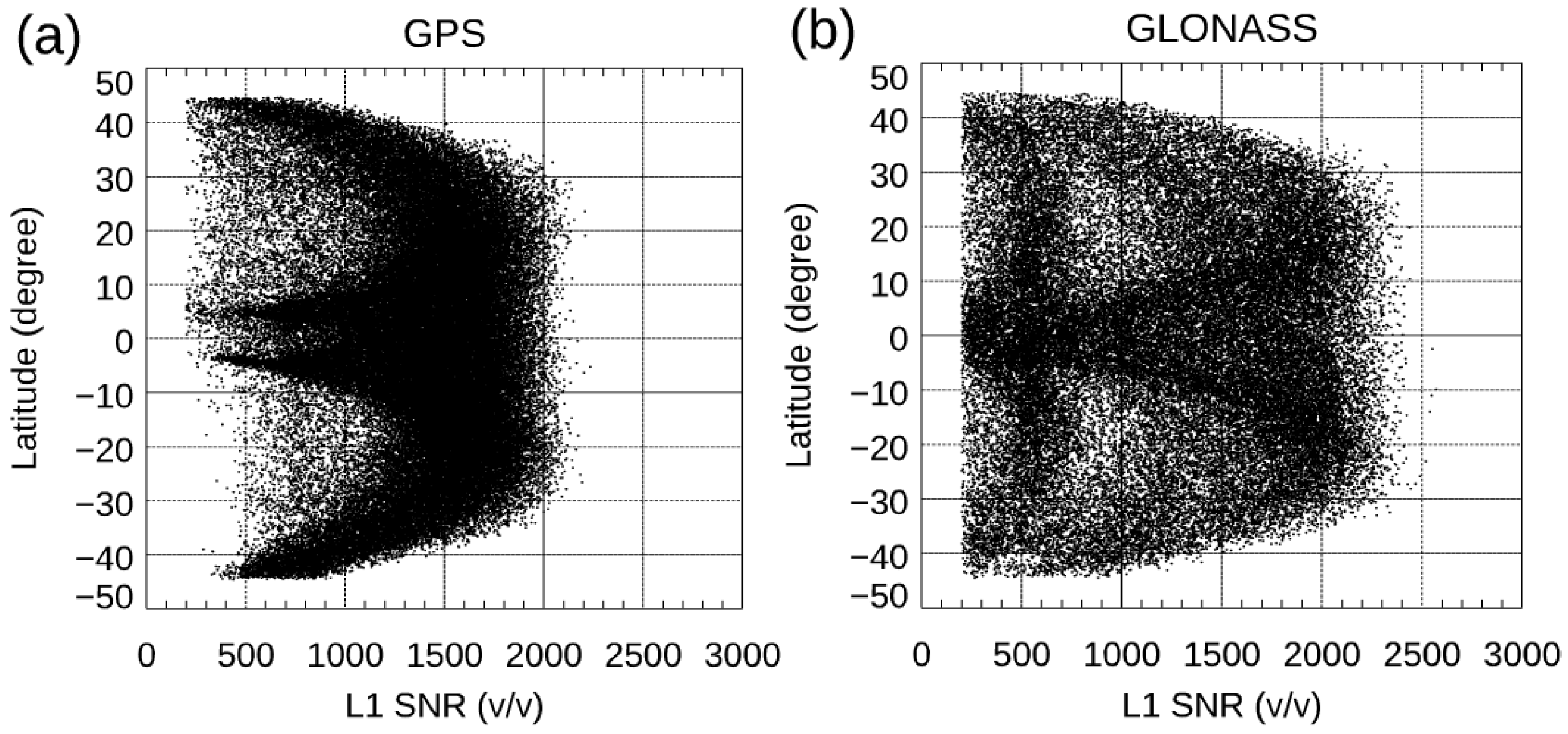
2.2. Spire Signal-to-Noise (SNR) Latitudinal Distribution
2.3. UCAR RO Data, STAR-Processed Spire Data, Global Radiosonde Data, and Reanalysis Data
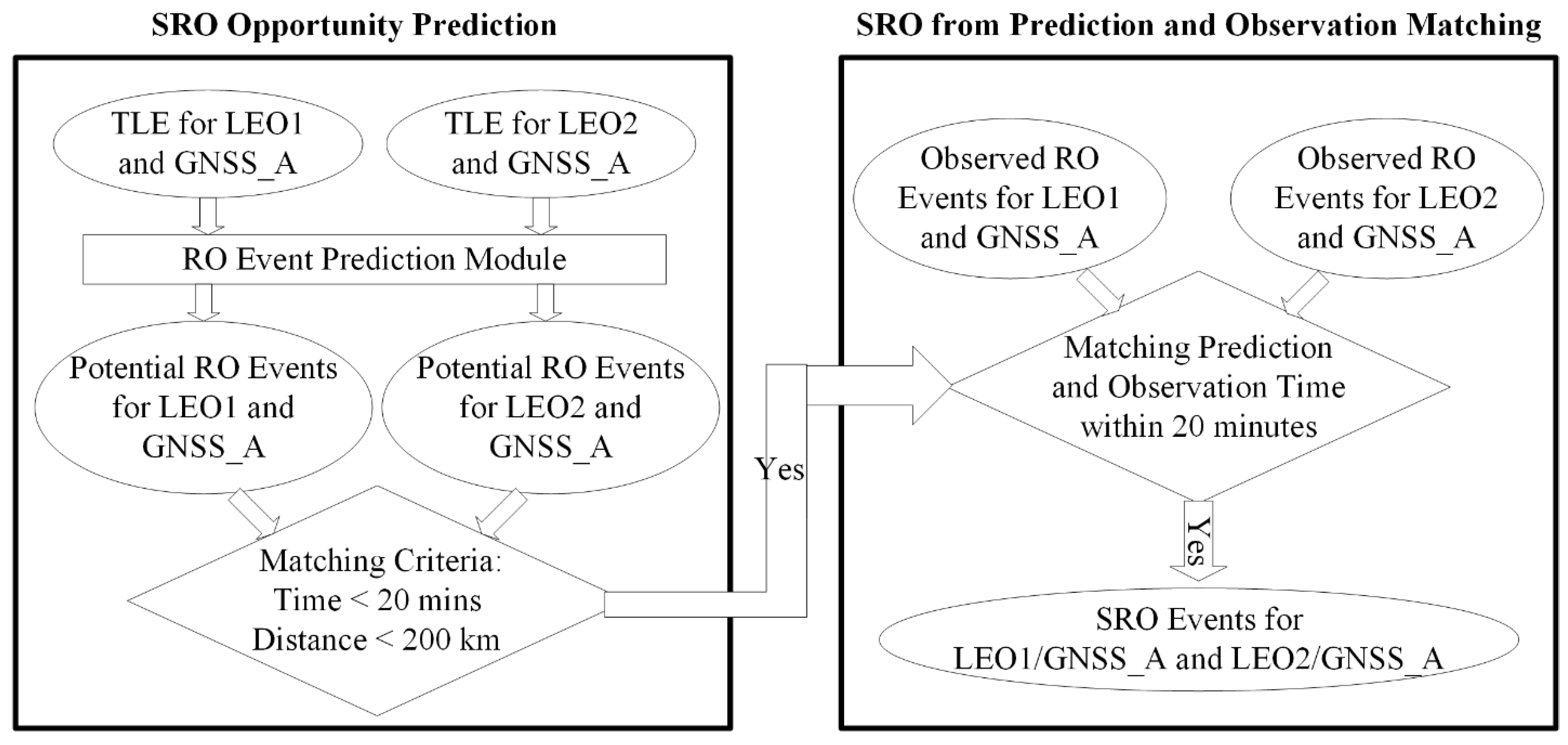
2.4. SRO Methodology and Approaches to Collecting Coplanar Spire–RO Data
3. Assessment of Spire Data Characteristics
3.1. The Lowest Penetration Height
3.2. Precision
3.3. Stability
4. Quantify the Spire Retrieval Accuracy and Uncertainty
4.1. Initial Comparison of UCAR Spire Products with STAR Spire Retrievals
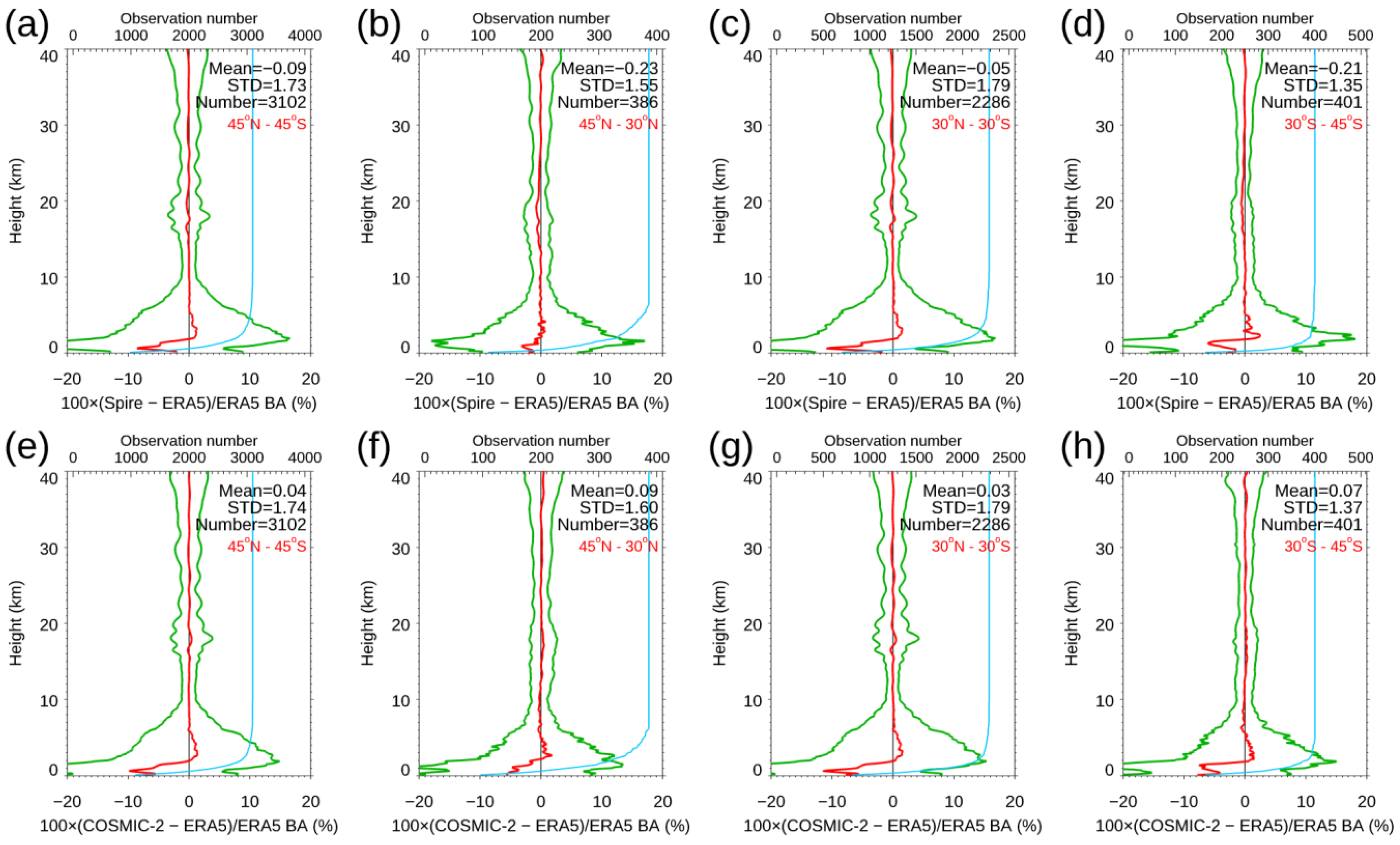
4.2. Assessment of the Spire Bending Angle Accuracy by Comparing with ERA5
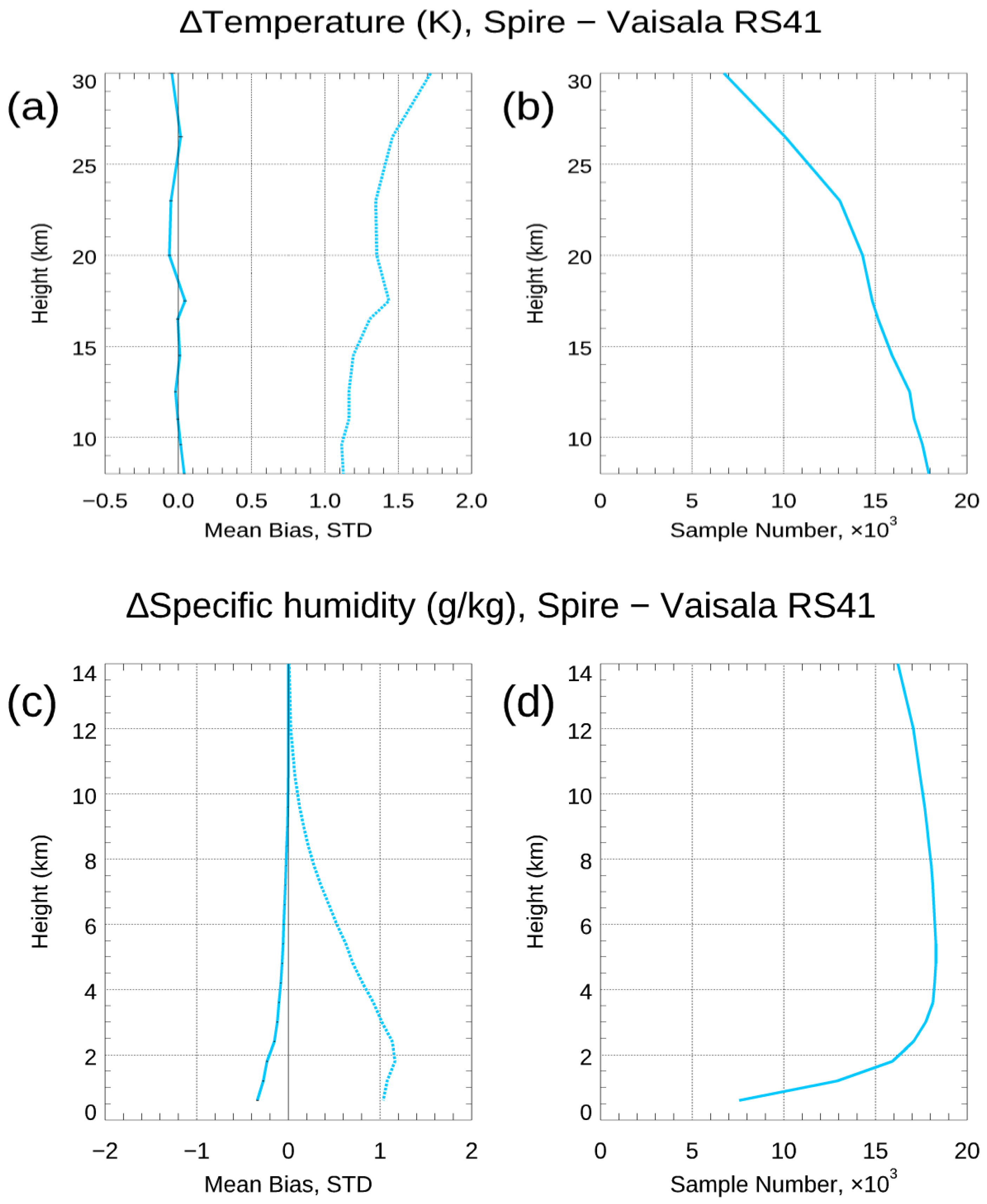
4.3. Assessment of Spire Temperature and Water Vapor Accuracy by Comparing to RS41 Radiosonde Observation
5. Estimates of the Error Covariance Matrix for NWP Data Assimilation
6. Discussion
7. Conclusions and Future Work
- (1)
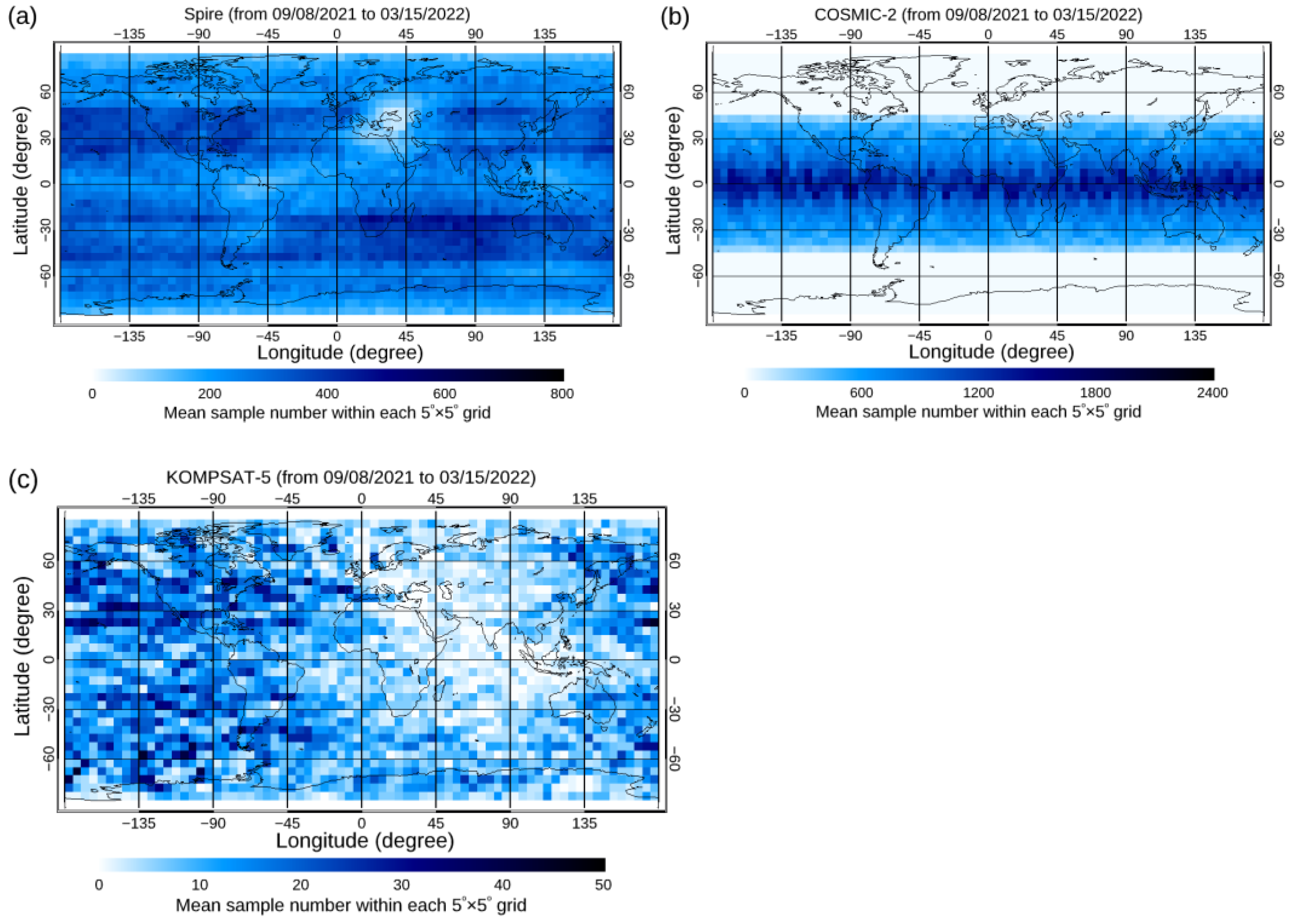
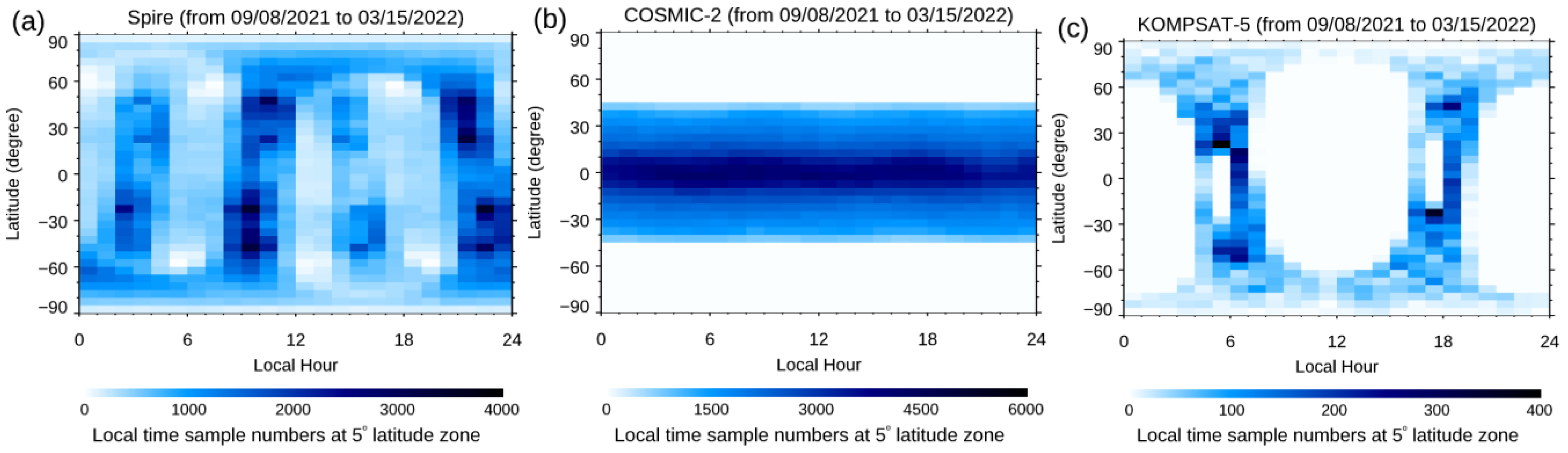
- The spatial and temporal coverage. Spire had close to 30 satellites at LEO orbits during DO3 and DO4. Although the complete global Spire RO occultation was around 20 K per day during the performance periods, the CWDP purchased about 3000 Spire occultation profiles per day during DO3 and 5500 Spire occultation profiles per day in DO4. While COSMIC-2 has an inclination angle of 24°, Spire is in the Sun-synchronized orbits. While Spire data cover the globe and are distributed relatively evenly across all latitudes, COSMIC-2 observations can cover all latitudes within [45°N, 45°S]. Spire has observations peaking local time ranges in 2–3, 9–10, 14–15, and 21–22, while the KOMPSAT5 observation peaking local times are located at 6 and 18, and COSMIC-2 observations cover all local times.
- (2)
- The effect of the SNR on Spire data penetration. The lowest penetration height is an essential indicator of RO data quality. The lowest penetration height of RO tracking is usually related to the data’s SNR and the atmosphere’s dryness. Although with a lower SNR in general, the pattern of the lowest penetration height for Spire was similar to that for COSMIC-2. The Spire and COSMIC-2 penetration heights were from around a 0.6 to 0.8 km altitude over tropical oceans. We also compared the lowest penetration height of 80% of the total data for different RO missions in different latitudinal zones. GeoOptics and Spire had lower penetration heights (for 80% of the total data) than COSMIC-2 in the latitudinal zones of [30°S, 45°S] and [45°N, 30°N]. This may be owed to COSMIC-2’s SNR being lower in the latitudinal zones of [30°S, 45°S] and [45°N, 30°N].
- (3)
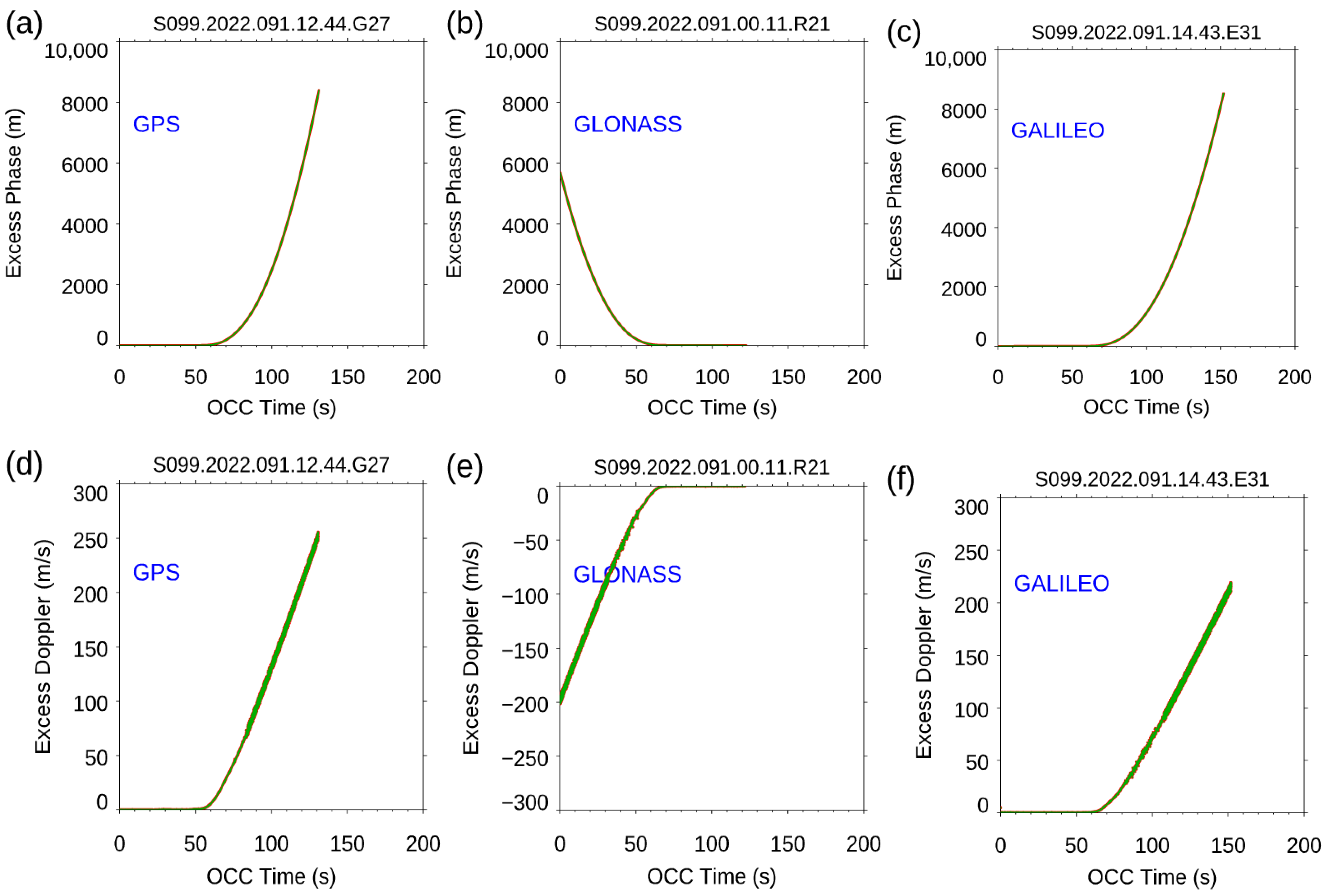
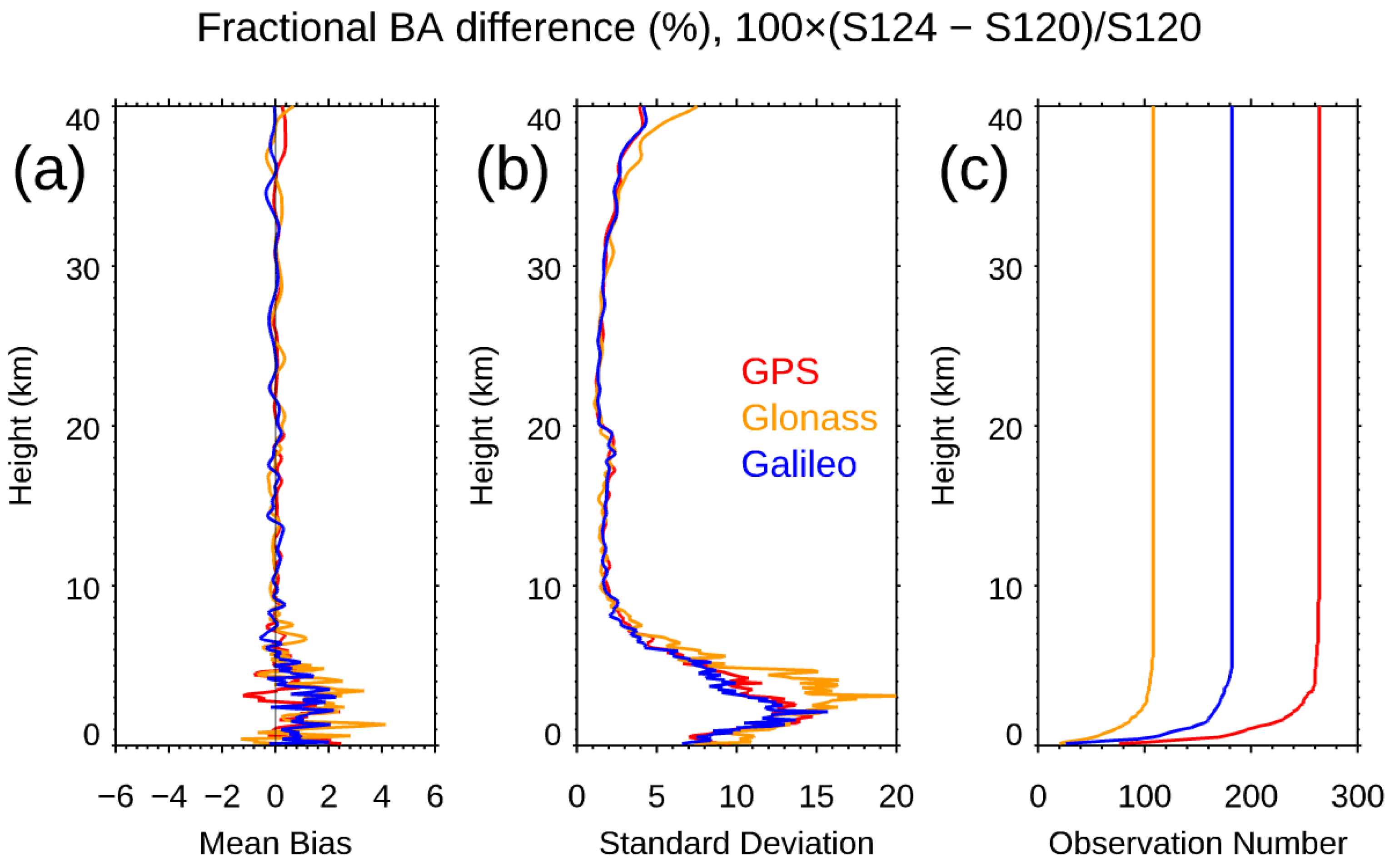
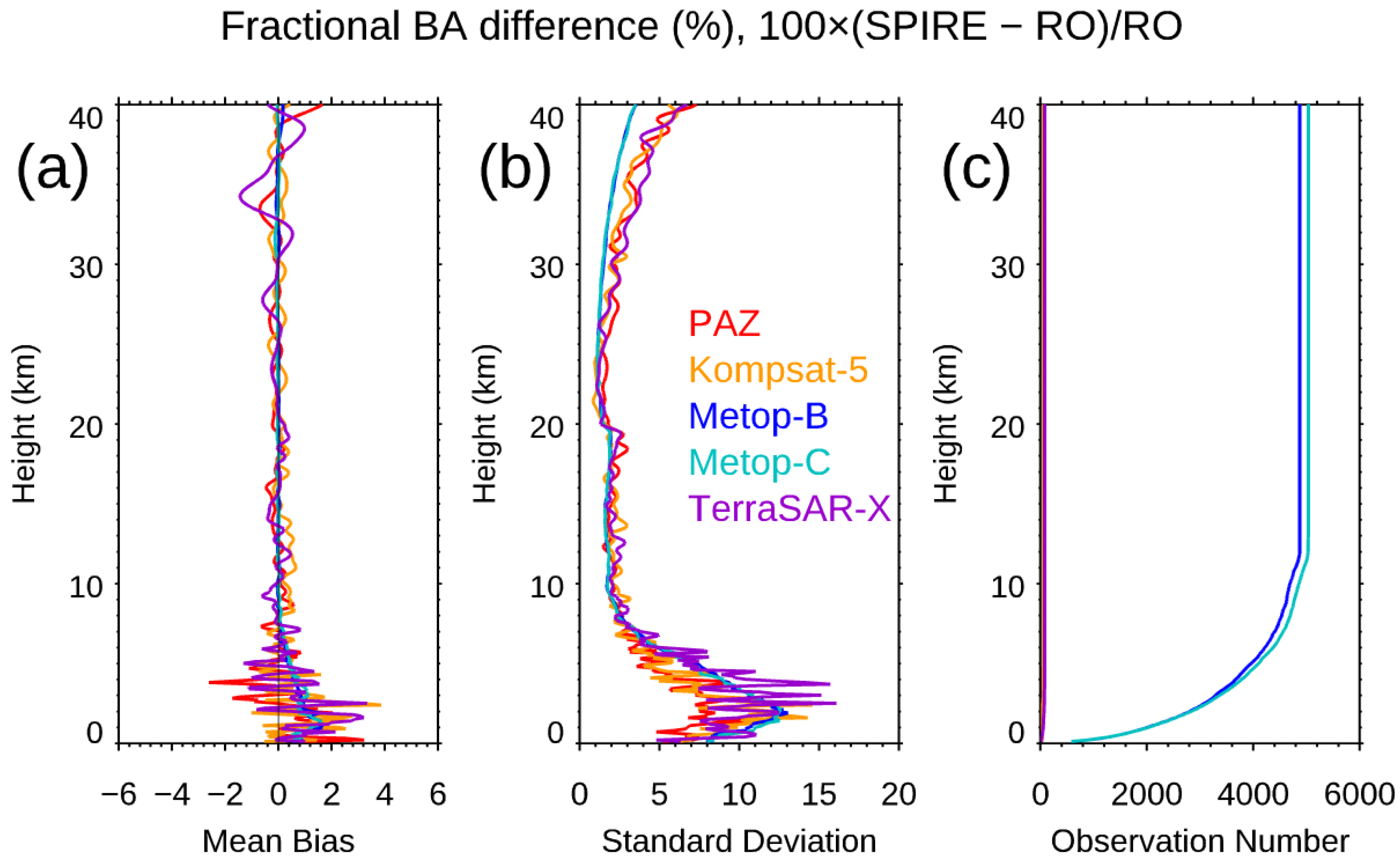
- The Spire data precision and stability. We used the Spire–Spire SRO pairs to quantify the Spire precision for the bending angle, dry temperature, and water vapor mixing ratio. The results showed that the mean differences were very close to zero from the surface to a 40 km altitude for all three physical quantities. The standard deviations from the bending angle, dry temperature, and water vapor mixing ratio were similar to those from other RO missions, such as COSMIC-2 and COSMIC-1. We also compared the fractional mean BA difference for Spire S124 and S120 from the surface to a 40 km altitude, but separated with GPS, GLONASS, and GALILEO, respectively. Although the SNR ranges from different emitters were different, the mean differences for GPS, GLONASS, and GALILEO were all close to zero with STDs of 1.81, 1.78, and 1.78, respectively. We also compared the precision of COSMIC-1 (SRO pairs collected from 2006) and COSMIC-2 (SRO pairs collected from 2021) with those from Spire (SRO pairs collected from 2022). All the comparisons were within [45°N,45°S]. We found that the COSMIC-2 STDs over mid-latitudes were slightly more significant than those from Spire, which may be owed to their lower SNR over the same regions. Although it was not shown in this paper, the receiver quality for different flight modules is very close. Although using slightly different receivers, the precision of Spire STRATOS receivers is of the same quality as those of COSMIC-2 TGRS receivers.
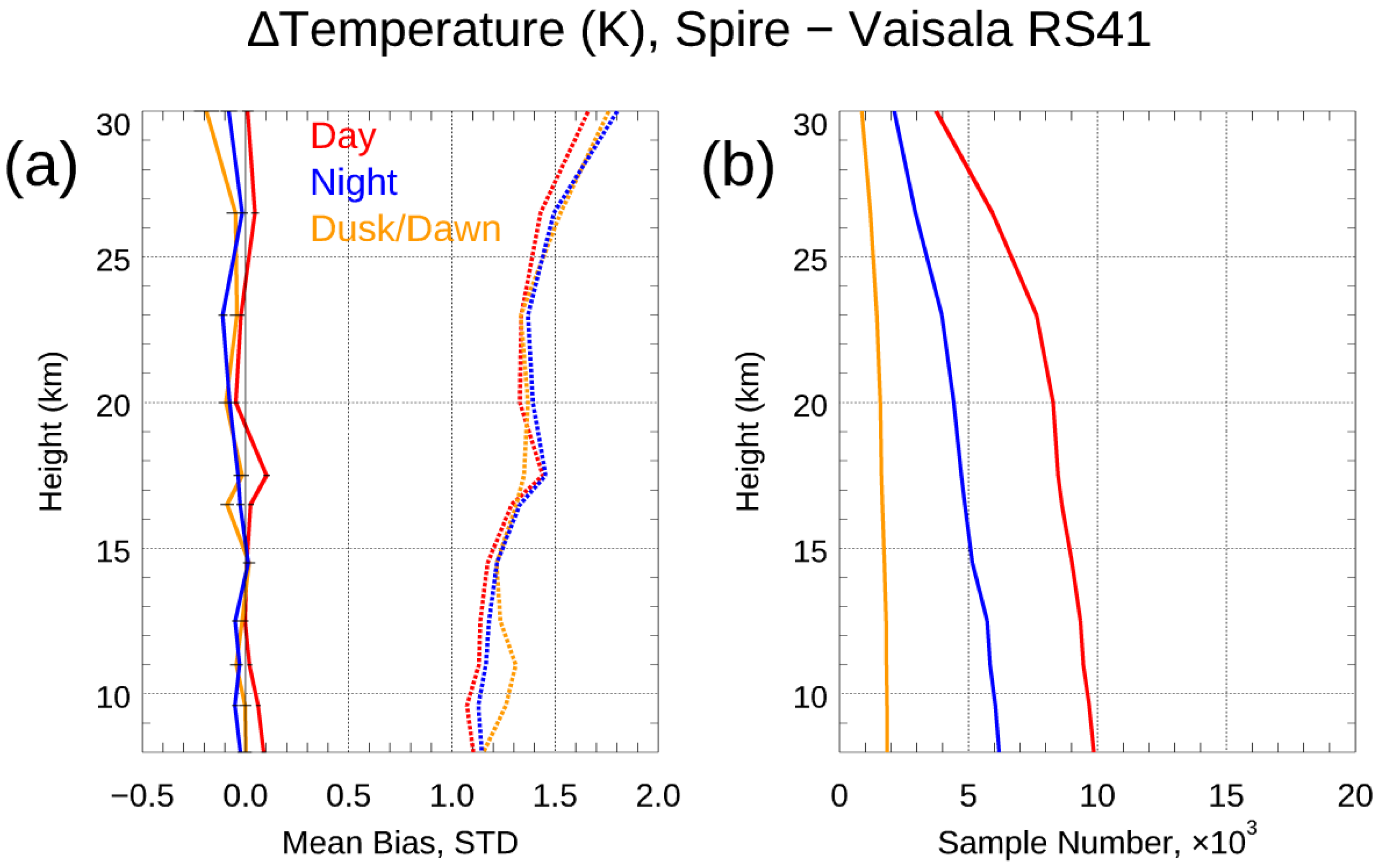
- (4)
- The effect of the SNR on the Spire retrieval accuracy. The UCAR Spire retrievals were consistent with those from the STAR-independent derived BA retrievals. The independent statistical analysis and validation from ERA5 and the direct bending angle profile comparison from these SRO cases above 35 km suggested: (i) the RO bending angle profiles retrieved from the GPS satellites were, in general, better than those from the GLONASS satellites; (ii) significant uncertainty existed for the RO bending angle profiles from GLONASS, which may indicate a potential RO phase issue related to the clock, residual ionospheric effects, receiver noise, and orbit determination errors for GLONASS. We validated the Spire temperature and water vapor profiles by comparing them with collocated radiosonde in situ data. Generally, over the height region between 8 km and 16.5 km, the RS41 RAOB matched the Spire temperature profiles very well, with temperature biases of <0.02 K. Over the height range from 17.8 to 26.4 km, the temperature biases were ~−0.034 K, with RS41 RAOB being warmer.
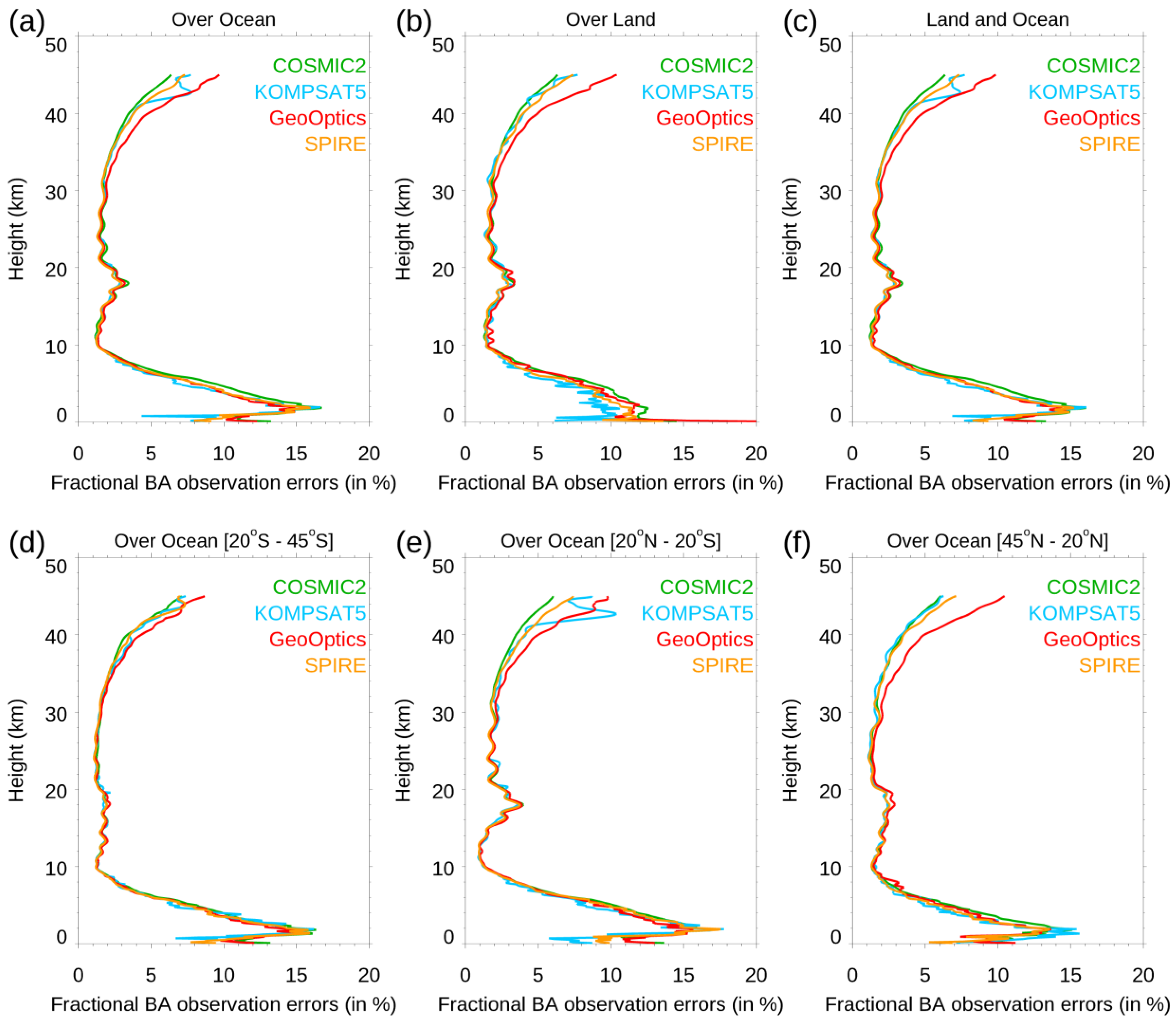
- (5)
- Estimates of the error covariance matrix for NWP. Below 9 km, the RO observation errors increased with a decreasing height and peaked at around 2 km. The magnitude of the relative BA errors in the troposphere for Spire was very close to that from COSMIC-2, KOMPSAT-5, and GeoOptics missions (also see [55]). In the lower troposphere, their peak values at a 2 km altitude over oceans (~15%) were more significant than those over land (~12%). These significant errors in the lower troposphere may have resulted from a greater RO retrieval uncertainty relative to the middle and upper troposphere, due to multipath propagation and a smaller SNR over mid-latitudes for COSMIC-2. The COSMIC-2 retrieval uncertainty was slightly more significant over oceans at mid-latitudes (45°N–30°N and 30°S–45°S), which may also be owed to COSMIC-2’s SNR being lower in those latitudinal zones.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. STAR Spire Data Products

References
- Anthes, R.A.; Bernhardt, P.A.; Chen, Y.; Cucurull, L.; Dymond, K.F.; Ector, D.; Healy, S.B.; Ho, S.-P.; Hunt, D.C.; Kuo, Y.; et al. The COSMIC/FORMOSAT-3 Mission: Early Results. Bull. Am. Meteorol. Soc. 2008, 89, 313–334. [Google Scholar] [CrossRef]
- Ho, S.-P.; Anthes, R.A.; Ao, C.O.; Healy, S.; Horanyi, A.; Hunt, D.; Mannucci, A.J.; Pedatella, N.; Randel, W.J.; Simmons, A. The COSMIC/FORMOSAT-3 Radio Occultation Mission after 12 Years: Accomplishments, Remaining Challenges, and Potential Impacts of COSMIC-2. Bull. Am. Meteorol. Soc. 2020, 101, E1107–E1136. [Google Scholar] [CrossRef]
- Bean, B.R.; Dutton, E.J. Radio Meteorology. National Bureau of Standards Monogr., No. 92; U.S. Government Printing Office: Washington, DC, USA, 1966; p. 435. [Google Scholar]
- Ho, S.-P.; Goldberg, M.; Kuo, Y.-H.; Zou, C.-Z.; Shiau, W. Calibration of Temperature in the Lower Stratosphere from Microwave Measurements Using COSMIC Radio Occultation Data: Preliminary Results. Terr. Atmos. Ocean. Sci. 2009, 20, 87. [Google Scholar] [CrossRef]
- Ho, S.-P.; Zhou, X.; Kuo, Y.-H.; Hunt, D.; Wang, J.-H. Global Evaluation of Radiosonde Water Vapor Systematic Biases using GPS Radio Occultation from COSMIC and ECMWF Analysis. Remote Sens. 2010, 2, 1320–1330. [Google Scholar] [CrossRef]
- Alexander, S.P.; Tsuda, T.; Kawatani, Y. COSMIC GPS Observations of Northern Hemisphere winter stratospheric gravity waves and comparisons with an atmospheric general circulation model. Geophys. Res. Lett. 2008, 35. [Google Scholar] [CrossRef]
- Alexander, S.P.; Tsuda, T.; Kawatani, Y.; Takahashi, M. Global distribution of atmospheric waves in the equatorial upper troposphere and lower stratosphere: COSMIC observations of wave mean flow interactions. J. Geophys. Res. Atmos. 2008, 113, D24115. [Google Scholar] [CrossRef]
- Luna, D.; Alexander, P.; De La Torre, A. Evaluation of uncertainty in gravity wave potential energy calculations through GPS radio occultation measurements. Adv. Space Res. 2013, 52, 879–882. [Google Scholar] [CrossRef]
- Nath, D.; Chen, W.; Guharay, A. Climatology of stratospheric gravity waves and their interaction with zonal mean wind over the tropics using GPS RO and ground-based measurements in the two phases of QBO. Theor. Appl. Clim. 2014, 119, 757–769. [Google Scholar] [CrossRef]
- Healy, S. Forecast impact experiment with a constellation of GPS radio occultation receivers. Atmos. Sci. Lett. 2008, 9, 111–118. [Google Scholar] [CrossRef]
- Healy, S. Surface pressure information retrieved from GPS radio occultation measurements. Q. J. R. Meteorol. Soc. 2013, 139, 2108–2118. [Google Scholar] [CrossRef]
- Aparicio, J.M.; Deblonde, G.; Aparicio, J.M. Impact of the Assimilation of CHAMP Refractivity Profiles on Environment Canada Global Forecasts. Mon. Weather Rev. 2008, 136, 257–275. [Google Scholar] [CrossRef]
- Poli, P.; Moll, P.; Puech, D.; Rabier, F.; Healy, S.B. Quality Control, Error Analysis, and Impact Assessment of FORMOSAT-3/COSMIC in Numerical Weather Prediction. Terr. Atmos. Ocean. Sci. 2009, 20, 101–113. [Google Scholar] [CrossRef]
- Melbourne, W.G.; Davis, E.S.; Duncan, C.B.; Hajj, G.A.; Hardy, K.R.; Kursinski, E.R.; Meehan, T.K.; Young, L.E.; Yunck, T.P. The Application of Spaceborne GPS to Atmospheric Limb Sounding and Global Change Monitoring; NASA Jet Propulsion Laboratory: Pasadena, CA, USA, 1994. Available online: https://ntrs.nasa.gov/archive/nasa/casi.ntrs.nasa.gov/19960008694.pdf (accessed on 1 June 2023).
- Yunck, T.P.; Liu, C.-H.; Ware, R. A History of GPS Sounding. Terr. Atmos. Ocean. Sci. 2000, 11, 001. [Google Scholar] [CrossRef]
- Smith, E.; Weintraub, S. The constants in the equation for atmospheric refractive index at radio frequencies. J. Res. Natl. Inst. Stand. Technol. 1953, 50, 39. [Google Scholar] [CrossRef]
- Neiman, P.J.; Ralph, F.M.; Wick, G.A.; Kuo, Y.-H.; Wee, T.-K.; Ma, Z.; Taylor, G.H.; Dettinger, M.D. Diagnosis of an Intense Atmospheric River Impacting the Pacific Northwest: Storm Summary and Offshore Vertical Structure Observed with COSMIC Satellite Retrievals. Mon. Weather Rev. 2008, 136, 4398–4420. [Google Scholar] [CrossRef]
- Wee, T.-K. A variational regularization of Abel transform for GPS radio occultation. Atmos. Meas. Tech. 2018, 1947–1969. [Google Scholar] [CrossRef]
- Xie, F.; Syndergaard, S.; Kursinski, E.R.; Herman, B.M. An Approach for Retrieving Marine Boundary Layer Refractivity from GPS Occultation Data in the Presence of Superrefraction. J. Atmos. Ocean. Technol. 2006, 23, 1629–1644. [Google Scholar] [CrossRef]
- Ho, S.-P.; Kuo, Y.-H.; Schreiner, W.; Zhou, X. Using SI-traceable global positioning system radio occultation measurements for climate monitoring in “State of the Climate in 2009”. Bull. Am. Meteorol. Soc. 2010, 91, S36–S37. [Google Scholar]
- Ho, S.P.; Yue, X.; Zeng, Z.; Ao, C.O.; Huang, C.Y.; Kursinski, E.R.; Kuo, Y.H. Applications of COSMIC radio occultation data from the troposphere to ionosphere and potential impacts of COSMIC-2 data. Bull. Am. Meteorol. Soc. 2014, 95, ES18–ES22. [Google Scholar] [CrossRef]
- Ho, S.-P.; Peng, L.; Anthes, R.A.; Kuo, Y.-H.; Lin, H.-C. Marine Boundary Layer Heights and Their Longitudinal, Diurnal, and Interseasonal Variability in the Southeastern Pacific Using COSMIC, CALIOP, and Radiosonde Data. J. Clim. 2015, 28, 2856–2872. [Google Scholar] [CrossRef]
- Ho, S.-P.; Kirchengast, G.; Leroy, S.; Wickert, J.; Mannucci, A.J.; Steiner, A.; Hunt, D.; Schreiner, W.; Sokolovskiy, S.; Ao, C.; et al. Estimating the uncertainty of using GPS radio occultation data for climate monitoring: Intercomparison of CHAMP refractivity climate records from 2002 to 2006 from different data centers. J. Geophys. Res. Earth Surf. 2009, 114, D23107. [Google Scholar] [CrossRef]
- Ho, S.-P.; Hunt, D.; Steiner, A.; Mannucci, A.J.; Kirchengast, G.; Gleisner, H.; Heise, S.; Von Engeln, A.; Marquardt, C.; Sokolovskiy, S.; et al. Reproducibility of GPS radio occultation data for climate monitoring: Profile-to-profile inter-comparison of CHAMP climate records 2002 to 2008 from six data centers. J. Geophys. Res. Earth Surf. 2012, 117, D18111. [Google Scholar] [CrossRef]
- Steiner, A.K.; Ladstädter, F.; Ao, C.O.; Gleisner, H.; Ho, S.-P.; Hunt, D.; Schmidt, T.; Foelsche, U.; Kirchengast, G.; Kuo, Y.-H.; et al. Consistency and structural uncertainty of multi-mission GPS radio occultation records. Atmos. Meas. Tech. 2020, 13, 2547–2575. [Google Scholar] [CrossRef]
- Ho, S.-P.; Peng, L.; Vömel, H. Characterization of the long-term radiosonde temperature biases in the upper troposphere and lower stratosphere using COSMIC and Metop-A/GRAS data from 2006 to 2014. Atmos. Chem. Phys. 2017, 17, 4493–4511. [Google Scholar] [CrossRef]
- Ho, S.-P.; Peng, L. Global water vapor estimates from measurements from active GPS RO sensors and passive infrared and microwave sounders. In Green Chemistry Applications; IntechOpen: London, UK, 2018. [Google Scholar] [CrossRef]
- Lin, C.C.; Yang, S.C.; Ho, S.P.; Pedatella, N.M. Exploring the terrestrial and space weather using an operational radio occultation satellite constellation—A FORMOSAT-7/COSMIC-2 Special Issue after 1-year on orbit. Terr. Atmos. Ocean. Sci. 2022, 32, 1–3. [Google Scholar] [CrossRef]
- Cucurull, L.; Derber, J.C.; Purser, R.J. A bending angle forward operator for global positioning system radio occultation measurements. J. Geophys. Res. Atmos. 2013, 118, 14–28. [Google Scholar] [CrossRef]
- Ho, S.-P.; Pedatella, N.; Foelsche, U.; Healy, S.; Weiss, J.P.; Ullman, R. Using Radio Occultation Data for Atmospheric Numerical Weather Prediction, Climate Sciences, and Ionospheric Studies and Initial Results from COSMIC-2, Commercial RO Data, and Recent RO Missions. Bull. Am. Meteorol. Soc. 2022, 103, E2506–E2512. [Google Scholar] [CrossRef]
- Ho, S.-P.; Zhou, X.; Shao, X.; Zhang, B.; Adhikari, L.; Kireev, S.; He, Y.; Yoe, J.; Xia-Serafino, W.; Lynch, E. Initial Assessment of the COSMIC-2/FORMOSAT-7 Neutral Atmosphere Data Quality in NESDIS/STAR Using In Situ and Satellite Data. Remote Sens. 2020, 12, 4099. [Google Scholar] [CrossRef]
- Chen, Y.; Shao, X.; Cao, C.-Y.; Ho, S.-P. Simultaneous Radio Occultation Predictions for Inter-Satellite Comparison of Bending Angle Profiles from COSMIC-2 and GeoOptics. Remote Sens. 2021, 13, 3644. [Google Scholar] [CrossRef]
- Zhang, B.; Ho, S.-P.; Cao, C.; Shao, X.; Dong, D.; Chen, Y. Verification and Validation of the COSMIC-2 Excess Phase and Bending Angle Algorithms for Data Quality Assurance at STAR. Remote Sens. 2022, 14, 3288. [Google Scholar] [CrossRef]
- Jing, X.; Ho, S.-P.; Shao, X.; Liu, T.-C.; Chen, Y.; Zhou, X.-J. Spire RO Thermal Profiles for Climate Studies: Initial Comparisons of the Measurements from Spire, NOAA-20 ATMS, Radiosonde, and COSMIC-2. Remote Sens. 2023, 15, 3710. [Google Scholar] [CrossRef]
- Irisov, V.; Masters, D.; Gorbunov, M.; Nguyen, V.; Sikarin, R.; Bloom, A.; Rocken, C. Comparison of Spire RO profiles processed by UCAR and Spire. In Proceedings of the 8th International Radio Occultation Working Group Meeting—IROWG-8, Virtual, 7–13 April 2021. [Google Scholar]
- McCarty, W.; Todling, R.; Privé, N.; Chattopadhyay, M.; Partyka, G.; Gelaro, R. Assessment of New Radio Occultation Measure- ments at the Global Modeling and Assimilation Office. In Proceedings of the 8th International Radio Occultation Working Group Meeting—IROWG-8, Virtual, 7–13 April 2021. [Google Scholar]
- Murphy, M.J.; Haase, J.S. Evaluation of GNSS Radio Occultation Profiles in the Vicinity of Atmospheric Rivers. Atmosphere 2022, 13, 1495. [Google Scholar] [CrossRef]
- Angling, M.J.; Nogués-Correig, O.; Nguyen, V.; Vetra-Carvalho, S.; Bocquet, F.-X.; Nordstrom, K.; Melville, S.E.; Savastano, G.; Mohanty, S.; Masters, D. Sensing the ionosphere with the Spire radio occultation constellation. J. Space Weather Space Clim. 2021, 11, 56. [Google Scholar] [CrossRef]
- Bosch, G. GNSS Radio Occultation in Advanced Numerical Weather Prediction Models. GEOmedia 2019, 23, 34–37. [Google Scholar]
- Forsythe, V.V.; Duly, T.; Hampton, D.; Nguyen, V. Validation of Ionospheric Electron Density Measurements Derived from Spire CubeSat Constellation. Radio Sci. 2020, 55, e2019RS006953. [Google Scholar] [CrossRef]
- Zeng, Z.; Schreiner, W.S.; Weiss, J. Evaluation of Spire GNSS RO data for global tropopause and PBL detections. AGU Fall Meet. Abstr. 2020, 2020, IN029-02. [Google Scholar]
- Alessandro, P. SPIRE/STRATOS (GNSS-RO) Quality Assessment Summary; Telespazio: Rome, Italy, 2020. [Google Scholar]
- Adhikari, L.; Ho, S.-P.; Zhou, X. Inverting COSMIC-2 Phase Data to Bending Angle and Refractivity Profiles Using the Full Spectrum Inversion Method. Remote Sens. 2021, 13, 1793. [Google Scholar] [CrossRef]
- Chen, Y.; Cao, C.; Shao, X.; Ho, S.-P. Assessment of the Consistency and Stability of CrIS Infrared Observations Using COSMIC-2 Radio Occultation Data over Ocean. Remote Sens. 2022, 14, 2721. [Google Scholar] [CrossRef]
- Ho, S.-p.; Kireev, S.; Shao, X.; Zhou, X.; Jing, X. Processing and Validation of the STAR COSMIC-2 Temperature and Water Vapor Profiles in the Neural Atmosphere. Remote Sens. 2022, 14, 5588. [Google Scholar] [CrossRef]
- Jing, X.; Shao, X.; Liu, T.-C.; Zhang, B. Comparison of GRUAN RS92 and RS41 Radiosonde Temperature Biases. Atmosphere 2021, 12, 857. [Google Scholar] [CrossRef]
- Miller, W.J.; Chen, Y.; Ho, S.-P.; Shao, X. Evaluating the impacts of COSMIC-2 GNSS RO bending angle assimilation on Atlantic hurricane forecasts using the HWRF model. Mon. Weather Rev. 2023, 151, 1821–1847. [Google Scholar] [CrossRef]
- Shao, X.; Ho, S.-P.; Zhang, B.; Cao, C.; Chen, Y. Consistency and Stability of SNPP ATMS Microwave Observations and COSMIC-2 Radio Occultation over Oceans. Remote Sens. 2021, 13, 3754. [Google Scholar] [CrossRef]
- Shao, X.; Ho, S.-P.; Zhang, B.; Zhou, X.; Kireev, S.; Chen, Y.; Cao, C. Comparison of COSMIC-2 radio occultation retrievals with RS41 and RS92 radiosonde humidity and temperature measurements. Terr. Atmos. Ocean. Sci. 2021, 32, 1015–1032. [Google Scholar] [CrossRef]
- Cao, C.; Wang, W.; Lynch, E.; Bai, Y.; Ho, S.-P.; Zhang, B. Simultaneous Radio Occultation for intersatellite comparison of bending angle toward more accurate atmospheric sounding. J. Atmos. Ocean. Technol. 2020, 37, 2307–2320. [Google Scholar] [CrossRef]
- Dallas Masters, Seizing Opportunity: Spire’s CubeSat Constellation of GNSS, AIS, and ADS-B Sensors, Stanford PNT Symposium, 2018-11-08. Available online: http://web.stanford.edu/group/scpnt/pnt/PNT18/presentation_files/I07-Masters-Spire_GNSS_AIS_ADS-B.pdf (accessed on 1 June 2023).
- Kursinski, E.R.; Gebhardt, T. A method to deconvolve errors in GPS RO-derived water vapor histograms. J. Atmos. Ocean. Technol. 2014, 31, 2606–2628. [Google Scholar] [CrossRef]
- Kuo, Y.-H.; Wee, T.-K.; Sokolovskiy, S.; Rocken, C.; Schreiner, W.; Hunt, D.; Anthes, R.A. Inversion and error estimation of GPS radio occultation data. J. Meteorol. Soc. Jpn. 2004, 82, 507–531. [Google Scholar] [CrossRef]
- Parrish, D.F.; Derber, J.C. The National Meteorological Center’s Spectral Statistical-Interpolation Analysis System. Mon. Weather Rev. 1992, 120, 1747–1763. [Google Scholar] [CrossRef]
- Anthes, R.; Sjoberg, J.; Feng, X.L.; Syndergaard, S. Comparison of COSMIC and COSMIC-2 Radio Occultation Refractivity and Bending Angle Uncertainties in August 2006 and 2021. Atmosphere 2022, 13, 790. [Google Scholar] [CrossRef]
- Culverwell, I.D.; Lewis, H.W.; Offiler, D.; Marquardt, C.; Burrows, C.P. The Radio Occultation Processing Package, ROPP. Atmos. Meas. Tech. 2015, 8, 1887–1899. [Google Scholar] [CrossRef]
- Schreiner, W.; Rocken, C.; Sokolovskiy, S.; Hunt, D. Quality assessment of COSMIC/FORMOSAT-3 GPS radio occultation data derived from single- and double-difference atmospheric excess phase processing. GPS Solut. 2009, 14, 13–22. [Google Scholar] [CrossRef]






| 10°N–10°S | 30°N–10°N | 10°S–30°S | 45°N–30°N | 30°S–45°S | 60°N–45°N | 45°S–60°S | 90°N–60°N | 60°S–90°S | |
|---|---|---|---|---|---|---|---|---|---|
| COSMIC-2 | 0.85 km | 0.90 km | 0.75 km | 1.35 km | 1.10 km | ||||
| Spire | 0.90 km | 0.90 km | 0.75 km | 0.80 km | 0.55 km | 0.45 km | 0.25 km | 0.45 km | 0.20 km |
| KOMPSAT-5 | 1.85 km | 1.50 km | 1.15 km | 0.40 km | 0.95 km | 0.35 km | 0.40 km | 0.25 km | 0.20 km |
| PAZ | 2.65 km | 1.85 km | 2.05 km | 0.90 km | 1.30 km | 0.45 km | 0.45 km | 0.35 km | 0.35 km |
| Mean Difference | Standard Deviation | |
|---|---|---|
| Spire–PAZ | 0.01% | 3.25% |
| Spire–KOMSAT-5 | 0.18% | 3.20% |
| Spire–Metop-B GRAS | 0.12% | 1.94% |
| Spire–Metop-C GRAS | 0.06% | 2.89% |
| Spire–TerraSAR-X | −0.13% | 3.35% |
| Mean | Standard Deviation | Sample Number at 10 km Altitude | |
|---|---|---|---|
| 0–500 v/v | 0.12% | 4.15% | 364 |
| 500–1000 v/v | 0.10% | 4.14% | 1727 |
| 1000–1500 v/v | 0.24% | 3.97% | 2559 |
| 1500–2000 v/v | 0.16% | 3.87% | 2325 |
| >2000 v/v | 0.19% | 4.07% | 332 |
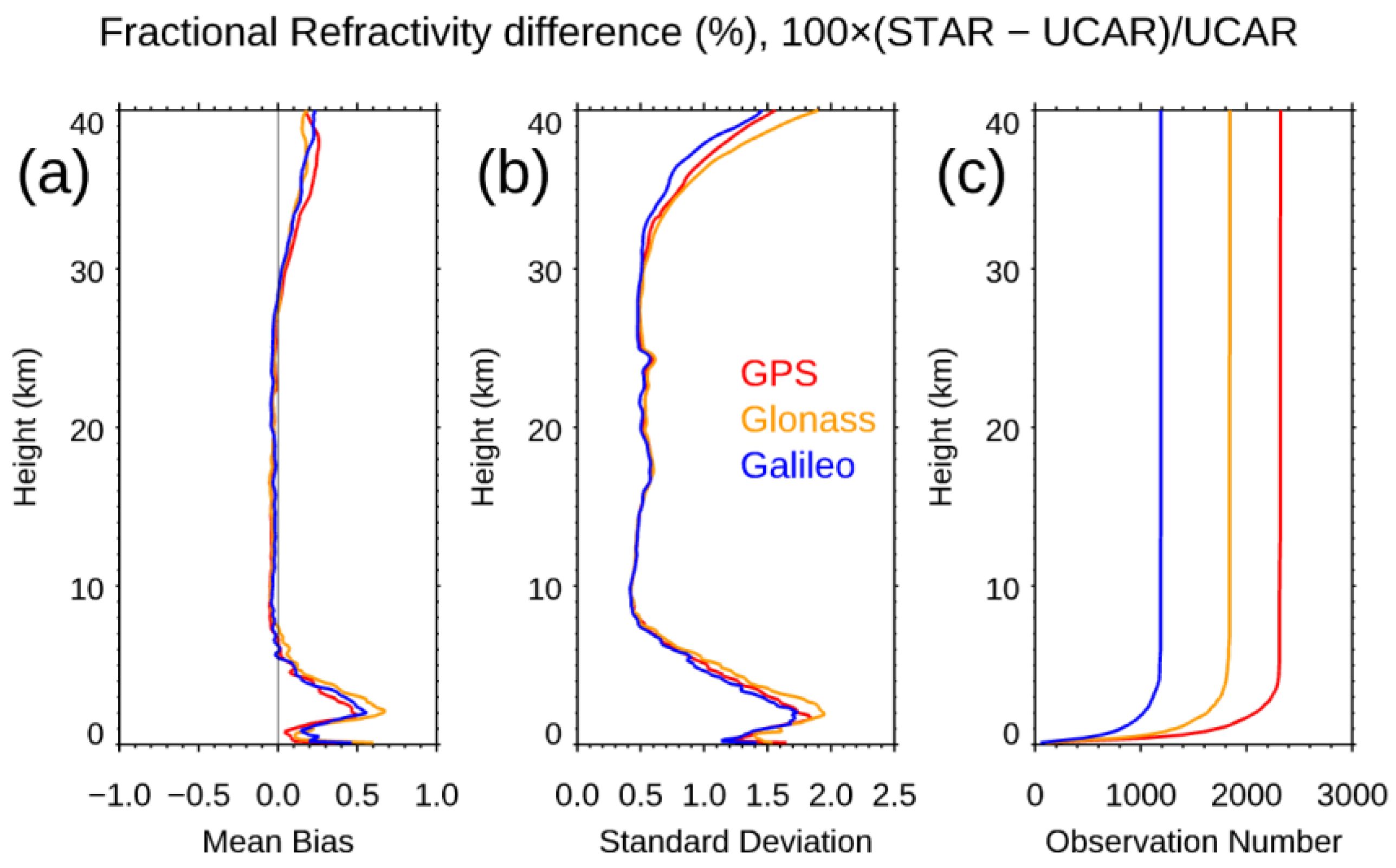
| Mean | Standard Deviation | |
|---|---|---|
| GPS | 0.06% | 0.73% |
| GLONASS | 0.06% | 0.78% |
| GALILEO | 0.06% | 0.69% |
| Spire Retrieval | µ(ΔT) (σ(ΔT)) (K) (8–11 km) | µ(ΔT) (σ(ΔT)) (K) (12.5–16.5 km) | µ(ΔT) (σ(ΔT)) (K) (17.8–26.4 km) | µ(ΔH) (σ(ΔH)) (g/kg) (below 4.2 km) | µ(ΔH) (σ(ΔH)) (g/kg) (4.8–8.4 km) |
|---|---|---|---|---|---|
| UCAR wetPf2 | 0.02(1.13) | 0.00(1.22) | −0.01(1.40) | −0.19(1.02) | −0.04(0.45) |
| Height Range | Day | Night | Dusk/Dawn |
|---|---|---|---|
| 8–11 km | 0.06 (1.10) | −0.04 (1.15) | −0.01 (1.21) |
| 12.5–16.5 km | 0.01 (1.20) | −0.02 (1.25) | −0.02 (1.25) |
| 17.8–26.4 km | 0.02 (1.38) | −0.05 (1.46) | −0.06 (1.35) |
| Height Range | Day | Night | Dusk/Dawn |
|---|---|---|---|
| Below 4.2 km | −0.17 (1.03) | −0.23 (1.07) | −0.15 (0.89) |
| 4.8–8.4 km | −0.04 (0.45) | −0.06 (0.49) | −0.02 (0.39) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ho, S.-p.; Zhou, X.; Shao, X.; Chen, Y.; Jing, X.; Miller, W. Using the Commercial GNSS RO Spire Data in the Neutral Atmosphere for Climate and Weather Prediction Studies. Remote Sens. 2023, 15, 4836. https://doi.org/10.3390/rs15194836
Ho S-p, Zhou X, Shao X, Chen Y, Jing X, Miller W. Using the Commercial GNSS RO Spire Data in the Neutral Atmosphere for Climate and Weather Prediction Studies. Remote Sensing. 2023; 15(19):4836. https://doi.org/10.3390/rs15194836
Chicago/Turabian StyleHo, Shu-peng, Xinjia Zhou, Xi Shao, Yong Chen, Xin Jing, and William Miller. 2023. "Using the Commercial GNSS RO Spire Data in the Neutral Atmosphere for Climate and Weather Prediction Studies" Remote Sensing 15, no. 19: 4836. https://doi.org/10.3390/rs15194836
APA StyleHo, S.-p., Zhou, X., Shao, X., Chen, Y., Jing, X., & Miller, W. (2023). Using the Commercial GNSS RO Spire Data in the Neutral Atmosphere for Climate and Weather Prediction Studies. Remote Sensing, 15(19), 4836. https://doi.org/10.3390/rs15194836








