Regional-to-Local Point-Voxel Transformer for Large-Scale Indoor 3D Point Cloud Semantic Segmentation

Abstract

Semantic segmentation of large-scale indoor 3D point cloud scenes is crucial for scene understanding but faces challenges in effectively modeling long-range dependencies and multi-scale features. In this paper, we present RegionPVT, a novel Regional-to-Local Point-Voxel Transformer that synergistically integrates voxel-based regional self-attention and window-based point-voxel self-attention for concurrent coarse-grained and fine-grained feature learning. The voxel-based regional branch focuses on capturing regional context and facilitating inter-window communication. The window-based point-voxel branch concentrates on local feature learning while integrating voxel-level information within each window. This unique design enables the model to jointly extract local details and regional structures efficiently and provides an effective and efficient solution for multi-scale feature fusion and a comprehensive understanding of 3D point clouds. Extensive experiments on S3DIS and ScanNet v2 datasets demonstrate that our RegionPVT achieves competitive or superior performance compared with state-of-the-art approaches, attaining mIoUs of 71.0% and 73.9% respectively, with significantly lower memory footprint.

1. Introduction

Semantic segmentation of large-scale point cloud scenes is a crucial task in 3D computer vision, serving as the core capability for machines to comprehend the 3D world. It has found extensive applications in autonomous driving [1,2], robotics [3,4], and augmented reality [5,6]. In particular, deep learning has made striking breakthroughs in computer vision over the past few years. Enabling reliable semantic parsing of point cloud data using deep neural networks has become an emerging hot research direction and attracted wide interest [7]. Unlike 2D images, 3D point clouds are intrinsically sparse and irregularly scattered in a continuous 3D space. They are unstructured in nature and often at a massive scale. These unique properties impose difficulties in directly adopting convolution operations, which have been the mainstay for 2D image analysis [8,9]. In recent years, convolutional networks (CNNs) [10,11,12] and Transformer [13,14,15] architectures have led to striking advances in semantic parsing of 2D visual data. However, efficiently learning discriminative representations from disordered 3D point sets using deep neural networks, especially at large-scale indoor scenes, remains a challenging open problem.

Abundant methods have explored the comprehension of 3D point clouds and obtained decent performance. In order to leverage convolutional neural networks (CNNs) for point cloud analysis, one category of approaches [16,17,18,19] first transforms the 3D points into discrete representations such as voxels, before applying CNN models to extract high-dimensional features. Another line of work [9,20,21,22,23], pioneered by PointNet [8], directly processes points in the native continuous space. Through alternating steps of grouping and aggregation, PointNet-style models are able to capture multi-scale contextual information from unordered 3D point sets. However, most of these existing methods concentrate on aggregating local feature representations but do not explicitly model long-range dependencies, which have been shown to be vital for capturing contextual information from distant spatial locations [24].

Transformers [25] based on self-attention come naturally with the ability to model long-range dependencies, and the permutation and cardinality invariance of self-attention in Transformers make them inherently suitable for point cloud processing. Recently, inspired by the transformer’s remarkable success [13,14,15,26,27,28] in the 2D image domain, a number of studies [29,30,31,32] have investigated adapting Transformer architectures to process unstructured 3D point sets. Engel et al. [29] proposed a kind of point transformer algorithm, which incorporates standard self-attention to extract global features for capturing point relationships and shape information in the 3D space. Guo et al. [31] presented offset-attention that computes the offset difference between self-attention features and input features in an element-wise manner. Concurrently, a spectrum of scholars have explored embedding self-attention modules in diverse point cloud tasks, witnessing noteworthy successes as showcased in works like [30,33]. Despite the promising advancements in point cloud transformers, a clear limitation persists. These models need to generate expansive attention maps due to the use of conventional self-attention mechanisms, placing a high computational complexity (quadratic) and consuming a huge number of GPU memory. This methodology, while rigorous, becomes implausible when scaling up to expansive 3D point cloud datasets, thereby hindering large-scale modeling pursuits.

Furthermore, in an effort to aggregate localized neighborhood information from point clouds, Zhao et al. [30] introduced another kind of point transformer algorithm, which establishes local vector attention within neighboring point sets. Guo et al. [31] proposed the use of neighbor embedding strategies to enhance point embedding. The PointSwin, as presented by Jiang et al. [34], employs self-attention based on a sliding window to capture local details from point clouds. While the two point transformers, PCT and the PointSwin, have achieved significant advancements, certain challenges continue to hinder their efficiency and performance. These methods fall short of establishing attention across features of different scales, which is crucial for 3D visual tasks [35]. For instance, a large indoor scene often encompasses both smaller instances (such as chairs and lamps) and larger objects (like tables). Recognizing and understanding the relationships between these entities necessitates a multi-scale attention mechanism. Moreover, when delving into large-scale scene point clouds, an optimal blend of both coarse-grained and fine-grained features becomes pivotal [36]. Coarse-grained features present a bird’s eye view, providing a general overview of the scene, whereas fine-grained ones are key in identifying and interpreting small details. Integrating both these feature dimensions can significantly amplify the potential and accuracy of point cloud semantic segmentation, particularly in heterogeneous and complex scenarios.

In addressing the challenges discussed previously, we present a novel dual-branch block named the Regional-to-Local Point-Voxel Transformer Block (R2L Point-Voxel Transformer Block), specifically engineered for the semantic segmentation of large-scale indoor point cloud scenes. This block is designed to effectively capture both coarse-grained regional and fine-grained local features within large-scale indoor point cloud senses with linear computational complexity. Our method has two key components, including a voxel-based regional self-attention for coarse-grained features modeling and a window-based point-voxel self-attention for fine-grained features learning and multi-scale feature fusion. More specifically, we first spatially partition the raw point clouds into non-overlapping cubes, termed “windows”, following the concept similar to that of the Swin Transformer [14]. Then, we voxelize the point clouds using a window size unit and establish a hash table [37] between the points and voxels. Voxel-based regional self-attention is subsequently applied among the nearest neighboring voxels to obtain coarse-grained features. Finally, the aggregated voxels serving as special “points” participate in the window-based point-voxel self-attention with their corresponding points to obtain fine-grained features. The voxel-based regional self-attention achieves information interaction between different windows while aggregating voxel features. Meanwhile, the window-based point-voxel self-attention not only focuses on learning fine-grained local features, but also captures high-level voxel information, enabling multi-scale feature fusion by treating voxels as specialized points.

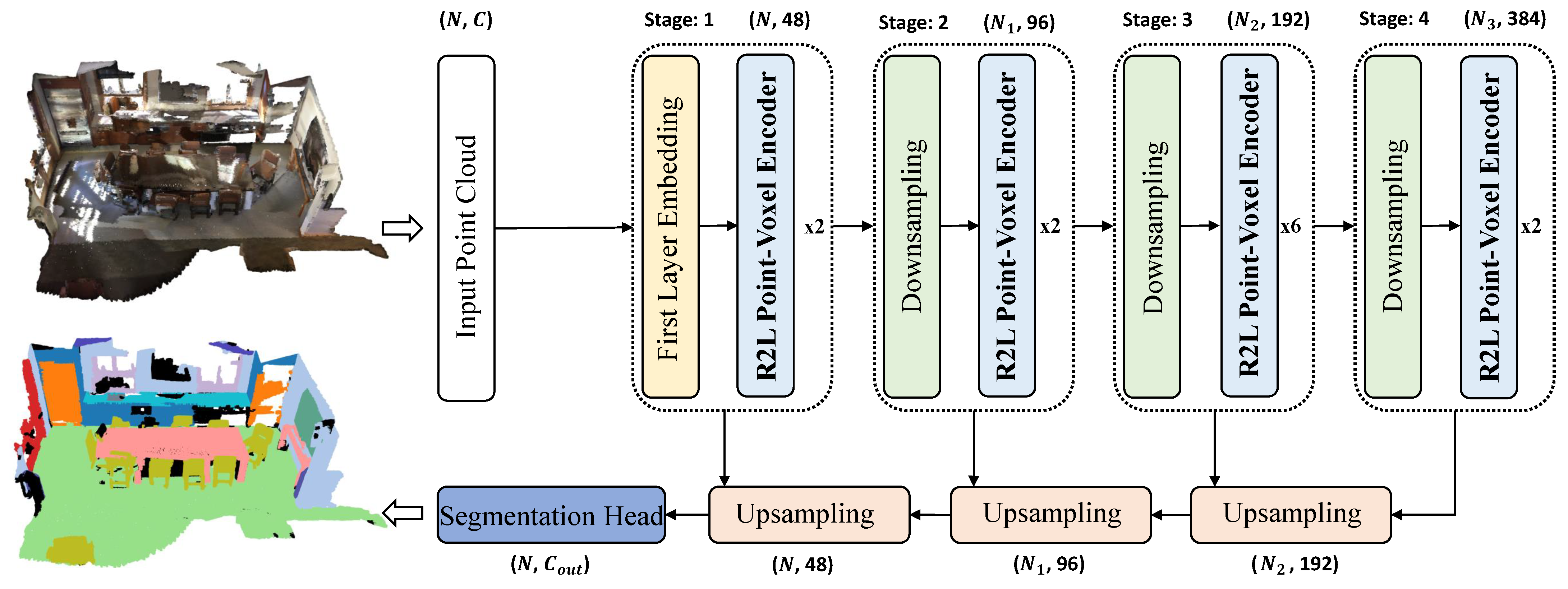
Building upon the R2L Point-Voxel Transformer Block, we propose a network for large-scale indoor point cloud semantic segmentation, named RegionPVT (Regional-to-Local Point-Voxel Transformer), as depicted in Figure 1. We conducted experiments on two publicly available large-scale indoor point cloud scene datasets, S3DIS [38] and ScanNet v2 [39]. Our results are not only competitive with but also surpass state-of-the-art benchmarks, achieving mIoUs of 71.0% and 73.6% respectively. Compared to our baseline, Swin3d (without shifted window) [40], there is a 1.6 percentage point enhancement of mIoU on the S3DIS dataset. Additionally, in comparison to voxel-based approaches (Fast Point Transformer [32], MinkowskiNet [19]), we observed mIoU improvements of 0.9 and 5.6 percentage points, respectively. In the subsequent sections, we delve deeper into the details of our proposed large-scale indoor point cloud semantic segmentation network.

2. Related Work

Our work for 3D semantic segmentation is a Transformer-based point-voxel fusion network architecture that is inspired by Vision Transformers. Therefore, in this section, we first present mainstream approaches in point cloud semantic segmentation in Section 2.1. Then, we introduce the relevant Vision Transformer works associated with our model in Section 2.2, and finally, we discuss related work on Transformers for point cloud analysis in Section 2.3.

2.1. Semantic Segmentation on Point Clouds

In the realm of 3D semantic segmentation on point clouds, methods can be divided into three predominant paradigms: voxel-based approaches [18,19,32], point-based techniques [8,9,20,41,42,43], and hybrid methodologies [44,45,46,47]. Voxel-based strategies strive to transform the inherently irregular structure of point clouds into a structured 3D voxel grid, leveraging the computational strengths of 3D CNNs. To enhance voxel efficiency, notable frameworks such as OctNet [16], O-CNN [17], and kd-Net [48] shift their focus to tree structures for non-empty voxels. Meanwhile, SparseConvNet [18] and MinkowskiNet [19] promote the use of discrete sparse tensors, making it easier to create efficient, fully sparse convolutional networks designed for fast voxel processing. However, the granularity of voxel-based methods, constricted by resolution constraints, occasionally sacrifices minute geometric details during the voxelization phase. On the other hand, point-based methods aim to create advanced neural networks that can process raw point clouds. Leading the way in this field, PointNet [8] pioneered the approach of using raw point clouds as clean inputs for neural networks. This was followed by a series of creative efforts [9,20,41,43] that focused on using hierarchical local structures and incorporating valuable semantic features through complex feature combination methods. While these techniques are excellent at capturing detailed local structures and avoiding issues related to quantization, they come with significant computational costs, especially for large-scale situations. Connecting the two approaches, hybrid techniques cleverly combine both point-based and voxel-based features. By combining the advantages of both approaches, they use the precise details provided by point clouds and the broader context provided by voxel structures. For instance, frameworks like PVCNN [44] and DeepFusionNet [46] smoothly blend layers from both approaches, cleverly avoiding any potential issues that could arise from voxelization. Our proposed methodology aligns with this hybrid spectrum but distinguishes itself by adeptly facilitating concurrent learning of both regional and local features within its hybrid architecture.

2.2. Vision Transformers

Recently, the Transformer architecture, initially designed for natural language processing, has established itself as a significant player in the computer vision field, demonstrating compelling results. The groundbreaking Vision Transformer (ViT) [26] is proof that using a transformer encoder for image classification can work, competing with traditional Convolutional Neural Networks (CNNs) in terms of performance, especially when provided with plenty of data. Inspired by ViT’s discoveries, a series of innovations [13,14,15,26,27,28] began journeys to improve and enhance vision transformer designs. For example, when dealing with the subtle difficulties of tasks like semantic segmentation and object detection that require detailed predictions, Pyramid Vision Transformer (PVT) [13] uses a pyramid structure, aiming to extract hierarchical features while also including spatial reduction attention, which helps reduce the computational load. Battling the inherent quadratic complexity characterizing global attention’s computation and memory footprints, the Swin Transformer [14] introduces a partitioned, non-overlapping window-based local attention, further bolstered by a shifted window strategy, fostering inter-window feature exchanges. Expanding the range of perception, the Focal Transformer [15] introduces “focal attention”, a skillful mechanism skilled at blending detailed local features with broader global interactions. Adding another layer of sophistication, RegionViT [49] infuses global insights directly into localized tokens via a regional-to-local attention mechanism. Our contribution to this evolving narrative is a unique extension that adapts conventional self-attention and window-based self-attention to accommodate 3D point clouds. By innovating a multi-scale feature learning and fusion strategy, we accentuate both precision and operational efficiency.

2.3. Transformer on Point Cloud Analysis

In recent years, the Transformer approach has made a lasting impact on a wide range of point cloud analysis tasks, demonstrating its strength in tasks like semantic segmentation [30,31,32,40], object detection [36,50,51], and registration [52]. In the domain of 3D semantic segmentation, the Point Transformer [30] extends the original PointNet architecture [8]. It cleverly divides point cloud data into smaller groups and performs vector attention computations within these groups. On the other hand, the Fast Point Transformer [32] provides an efficient self-attention mechanism that can incorporate 3D voxel information while reducing computational complexity. On a similar trajectory, the Stratified Transformer [40] computes self-attention within small cubic areas, utilizing a layered key-sampling technique along with a modified window framework. However, even though they have made significant progress in understanding point clouds, these Transformer-based approaches struggle with the inherent computational challenges of self-attention, which grows quadratically. This computational bottleneck often confines their explorations to localized interactions with circumscribed receptive fields, thus leading to an unintended neglect of complex scene structures and the important details of multi-scale features. Our proposed method, while anchoring itself within the Transformer universe, diverges by judiciously learning both macroscopic regional patterns and microscopic local intricacies. Notably, it accomplishes this under a linear computational footprint, adeptly integrating features across both regional and local spectrums.

3. Material and Methods

In this section, we first briefly introduce the datasets used for the evaluation of our proposed model in Section 3.1. Then, we present the detailed network architecture of our model in Section 3.2. Subsequently, we describe the baselines and evaluation metrics employed in our experiments in Section 3.3. Finally, we present the implementation details of our approach in Section 3.4.

3.1. Datasets

We conducted experiments and evaluations of our proposed method on two publicly available indoor point cloud datasets: S3DIS [38] and ScanNet v2 [39]. Both datasets are large-scale because they occupy a large 3D space and include a large number of sample points.

S3DIS. The S3DIS dataset [38], commonly used for point cloud semantic segmentation, consists of 271 room scans across 6 areas from 3 buildings, covering approximately 6020 square meters in total. The spaces exhibit varying functionalities, architectures, and interior designs, primarily including offices, corridors, and restrooms. Each room contains 0.5–2.5 million points. The points are annotated with semantic labels from 13 categories (

Table 1. S3DIS data set statistics table.

Ceiling	Floor	Wall	Beam	Column	Window	Door	Table	Chair	Sofa	Bookcase	Board	Clutter
24.0%	23.8%	18.4%	1.8%	1.5%	1.3%	4.0%	3.8%	4.6%	0.5%	4.5%	0.7%	11.1%

) and have 3D coordinates and color attributes. Following previous works [22,30,41,43], we used Areas 1, 2, 3, 4, and 6 for training, and Area 5 for evaluation. Our method was tested on Area 5.

ScanNet V2. We used the second official version of ScanNet [39], comprising 1513 room scans. Some rooms were captured by different sensors, resulting in point clouds with per-point semantic labels from 20 categories (

Table 2. ScanNet v2 test data set statistics table.

Wall	Floor	Cabinet	Bed	Chair	Sofa	Table	Door	Window	Bookshelf
38.8%	35.7%	2.4%	2.0%	3.8%	2.5%	3.3%	2.2%	0.4%	1.6%
Picture	Counter	Desk	Curtain	Refrigerator	Shower curtain	Toilet	Sink	Bathtub	Other furniture
0.2%	0.6%	1.7%	0.7%	0.3%	0.04%	0.2%	0.2%	0.2%	2.9%

). Following common practices [20,22,41,53], our model employed per-point coordinate and RGB color as input features for this 20-class 3D semantic segmentation task. We used 1201 samples to train our model and set aside 312 samples to validate its performance. The prediction results for the official test set, which had a sample size of 100 with all semantic labels publicly unavailable, were obtained from the model that performed the best on the validation set and were ultimately submitted to the officials for the test results due to the strict submission of ScanNet online test benchmark, where each method can be only tested once.

3.2. Methods

The 3D indoor scene semantic segmentation network we propose, titled Regional-to-Local Point-Voxel Transformer (RegionPVT), fundamentally adopts a pyramid U-Net architecture comprising an encoder and a decoder, as depicted in Figure 1. This architecture encompasses an initial point embedding layer, a Regional-to-Local Point-Voxel Transformer Encoder Block (R2L Point-Voxel Transformer Encoder Block), a tokenization module for both points and voxels and modules for both downsampling and upsampling. Specifically, for the initial point embedding, we employ KPConv [41] to extract the local spatial features of the points. Within the point and voxel tokenization module, we first partition the point cloud scene spatially into non-overlapping cubic regions. Each cube is treated as a window, with every point within it regarded as a local token for the window-based point-voxel self-attention computation. For voxel tokenization, each window is considered as a voxel, and points within are voxelized. As network depth increases, to balance the computational consumption and achieve feature maps at varied resolutions, we incorporate a downsampling procedure. Before progressing to the subsequent stage, the channel dimensions on local tokens (akin to CNNs) are doubled, while the spatial resolution is quartered. For upsampling, we resort to common trilinear interpolation techniques used in point cloud analysis. Each layer of the encoder communicates with its corresponding decoder via skip connections. The Regional-to-Local Point-Voxel Transformer Encoder consists of two primary components: a window-based point-voxel attention layer based on local points within the same window and its corresponding regional token and a voxel-based regional attention layer based on local regional voxels. Given its pyramid structure, our RegionPVT can generate multi-scale features for point clouds, making it easily adaptable for broader visual applications like object detection, point cloud classification, part segmentation, and more, not just limited to indoor point cloud semantic segmentation.

In the following sections, we delve into the detailed composition of RegionPVT’s encoder and decoder modules. Section 3.2.1 introduces the proposed Voxel-based Regional Self-Attention mechanism. Section 3.2.2 presents the Window-based Point-Voxel Self-Attention mechanism. Section 3.2.3 describes the complete Regional-to-Local Point-Voxel Transformer Encoder. Finally, Section 3.2.4 explains the downsampling and upsampling layers employed in our model’s encoder–decoder architecture.

3.2.1. Voxel-Based Regional Self-Attention

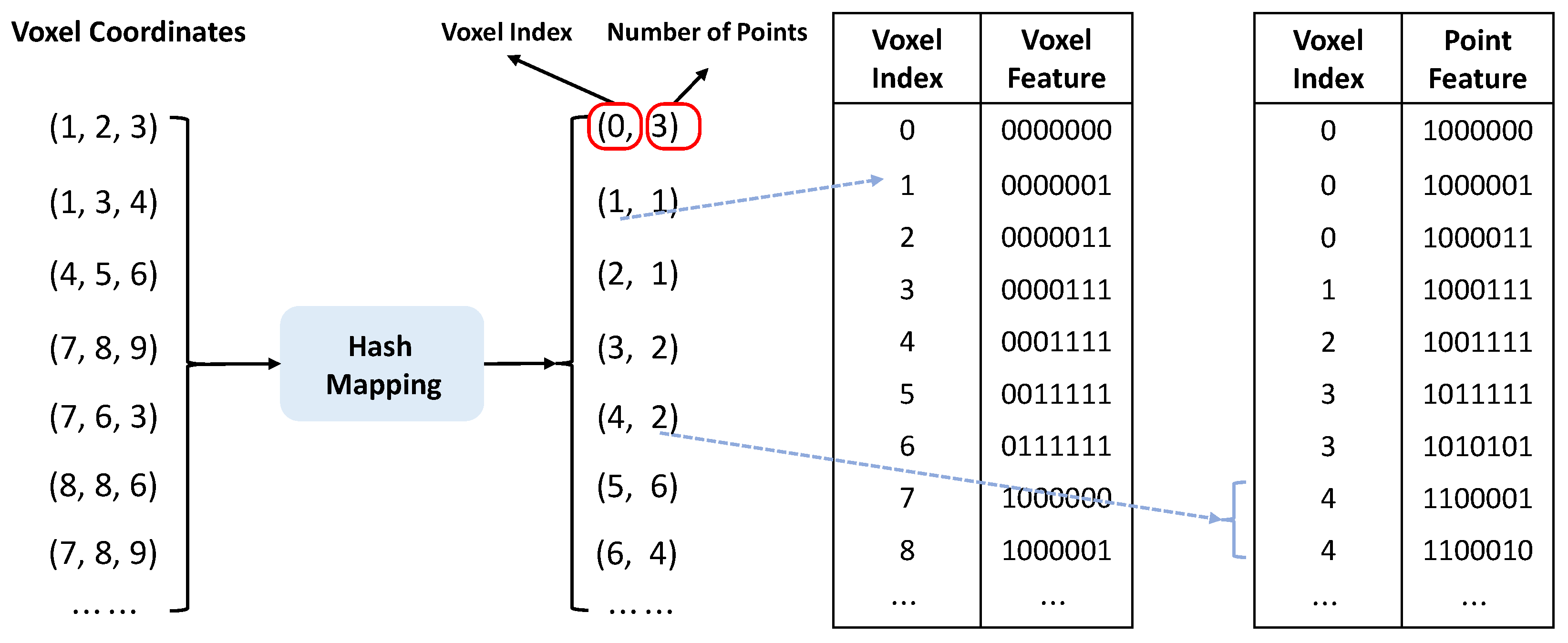
In the framework of point-based local window multi-head self-attention, point clouds are divided into non-overlapping windows based on their spatial coordinates. For every individual window, self-attention computations are performed for its contained points, enabling the capture of local feature relationships within the 3D point cloud. Conversely, with our voxel-based regional self-attention approach, point clouds are voxelized in accordance with the window sizes. Subsequently, a hash mapping is established between the voxels and their associated point cloud segments within the respective windows as shown in Figure 2. Then, the regional self-attention is carefully calculated for every voxel, incorporating insights from its k-nearest neighboring voxels, which highlights the regional feature interplay on a voxel level within the 3D point clouds. It is worth mentioning that the advanced hash mapping method speeds up the process of finding neighboring voxels, doing so with an $O\left(N\right)$ complexity. Meanwhile, the point-based methods [8,30,43] require constructing neighbors using a search for the k-nearest neighbors [54], a process with a complexity of $O(Nlog(N\left)\right)$, which can be quite slow when working with large sets of point clouds. Moreover, a crucial feature of our voxel splitting method is its accuracy; it only focuses on valid voxels, ensuring that each voxel contains at least one point from the point clouds.

Specifically, for the voxel-based regional self-attention mechanism, the input point cloud is denoted as $\mathcal{P}={\left\{\left(p_n,f_n\right)\right\}}_{n=1}^N$. Here, $p_n$ represents the spatial coordinates of the nth point, while $f_n$ encapsulates the inherent features of $p_n$, such as color, normal vectors, and so forth. In alignment with methodologies presented in [32,55], the point cloud is voxelized via the ensuing process:

Initially, we employ an encoding layer ${\delta }_{\mathrm{enc}}:{\mathbb{R}}^3\mapsto {\mathbb{R}}^{D_{\mathrm{enc}}}$ to positionally encode the point cloud coordinates, encoding them into a high-dimensional space ${\mathbb{R}}^{D_{\mathrm{enc}}}$. This encoding aims to mitigate information loss during the voxelization process. We denote this as:

$${\mathbf{e}}_n={\delta }_{\mathrm{enc}}\left({\mathbf{p}}_n-\frac{1}{k_i}\sum _{n\in k_i}{\mathbf{p}}_n\right),$$

(1)

where $k_i$ represents the set of point indices within the ith voxel. Subsequently, our voxel feature can be defined as follows ${\mathbf{f}}_i\in {\mathbb{R}}^{D_{\mathrm{enc}}}$:

$${\mathbf{f}}_i={\mathsf{\Omega }}_{n\in k_i}\left({\mathbf{f}}_n\oplus {\mathbf{e}}_n\right),$$

(2)

where ⊕ represents the concatenation operation of a vector, $\mathsf{\Omega }$ is an operator with permutation-invariant properties, such as taking the $average(·),sum(·),max(·)$. In our experiment setting, we employ the $average(·)$ operation.

We formally represent the voxelization of the input point cloud, denoted as $\mathcal{P}$, by the tuple $\mathcal{V}={\left\{\left({\mathbf{v}}_i,{\mathbf{f}}_i,{\mathbf{c}}_i\right)\right\}}_{i=1}^M$. In this context, M is the number of voxels, ${\mathbf{v}}_i$ specifies the spatial coordinate of the ith voxel. The feature associated with this voxel is given by ${\mathbf{f}}_i$. Additionally, ${\mathbf{c}}_i$, which represents the centroid of the ith voxel, is computed as an average of the points within it: ${\mathbf{c}}_i=\frac{1}{{\mathbf{k}}_i}{\sum }_{n\in {\mathbf{k}}_i}{\mathbf{p}}_n$.

In our approach, the voxel-based regional self-attention mechanism ingests the input $\mathcal{V}={\left\{\left({\mathbf{v}}_i,{\mathbf{f}}_i,{\mathbf{c}}_i\right)\right\}}_{i=1}^M$ and efficiently employs a hash table, which aids in identifying the k-nearest neighbors for each voxel. Here, the regional neighbor indices for ${\mathbf{c}}_i$ are represented as $\mathcal{N}\left(i\right)$. Given this setup, the self-attention calculation at the voxel level, focusing on ${\mathbf{c}}_i$, is elegantly captured by equation

$${\mathbf{f}}_i^{\prime }=\sum _{j\in \mathcal{N}\left(i\right)}softmax\left(\phi {\left({\mathbf{f}}_i\right)}^T\psi \left({\mathbf{f}}_j\right)+\delta ({\mathbf{c}}_i,{\mathbf{c}}_j)\right)\alpha \left({\mathbf{f}}_j\right).$$

(3)

In the context of this equation, ${\mathbf{f}}_i^{\prime }$ denotes the resultant feature. The functions $\phi ,\psi ,$ and $\alpha$ stand for linear projection layers of the input feature. Lastly, $\delta ({\mathbf{c}}_i,{\mathbf{c}}_j)$ acts as a position encoding function, introducing spatial contextual awareness into the self-attention mechanism.

Complexity Analysis. To conclude, let us delve into the computational complexity associated with our voxel-based regional self-attention mechanism. Considering that the number of neighbor indices denoted by $\mathcal{N}\left(i\right)$ in Equation (3) stands at k, and post voxelization, the voxel count totals to M, the computational overhead for our voxel-based regional self-attention becomes $O(M·k^2)$. Given that k is invariant, the overall complexity scales linearly. Such a linear scaling greatly alleviates the computational demands typically associated with the Transformer’s self-attention operation, making our approach both efficient and resource conservative.

3.2.2. Window-Based Point-Voxel Self-Attention

A traditional Transformer block is fundamentally composed of a multi-head attention module complemented by a feed-forward network (FFN). The global self-attention mechanism in such a setup poses a computational challenge as its complexity grows quadratically with the increment in the number of input tokens. When processing point clouds with tens of thousands of points used as direct input, this results in a memory overhead of $O\left(N^2\right)$ (N being the total count of input points), making it practically unworkable. In alignment with the methodologies outlined in [34,40], we adopt local window-based multi-head self-attention to learn fine-grained point representations while maintaining cross-scale information exchange.

To effectively leverage the inherent structure of 3D spatial data, we spatially segment the 3D space into distinct, non-overlapping cubic regions, termed “windows”. Every point within the 3D point cloud landscape is associated with a specific window, determined by its spatial coordinates. Within each of these windows, multi-head self-attention operates in isolation. As a result, when computing the attention map for a given query point, only the neighboring points within its designated window and the associated voxel token (which can be thought of as a unique “point token”) are considered. This contrasts with global self-attention, which typically involves all input points. Such window-centric partitioning markedly streamlines computational demands. Importantly, our method does not merely zone in on high-resolution local features. It also weaves in voxel-level insights, ensuring a rich interplay of features across multiple scales. Given the inherent sparsity and irregular distribution of point clouds, the points each window houses can fluctuate. For the tth window, let us represent the count of its encapsulated points as $k_t$. Defining the number of attention heads as $N_h$ and the dimension of each head as $N_d$, we can infer that the dimension $N_c=N_h\times N_d$ is associated with the points in the tth window and its corresponding voxel token, or, more precisely, $\mathbf{X}\in {\mathbb{R}}^{k_t\times (N_h\times N_d)}$ and $\mathbf{V}\in {\mathbb{R}}^{N_h\times N_d}$. For our window-based point-voxel self-attention scheme, the input can be succinctly denoted as ${\mathbf{X}}^{\prime }=\left[\mathbf{X}\right|\left|\mathbf{V}\right]\in {\mathbb{R}}^{(k_t+1)\times (N_h\times N_d)}$. To elucidate further, the application of the point-voxel multi-head self-attention mechanism on the tth window is formulated as follows:

$$\mathbf{Q}={Linear}_q\left({\mathbf{X}}^{\prime }\right),\mathbf{K}={Linear}_k\left({\mathbf{X}}^{\prime }\right),\mathbf{V}={Linear}_v\left({\mathbf{X}}^{\prime }\right),$$

(4)

$${\mathbf{Attn}}_{i,j,h}={\mathbf{Q}}_{i,h}·{\mathbf{K}}_{j,h},$$

(5)

$${\mathbf{Attn}}_{i,.,h}^{\prime }=softmax\left({\mathbf{Attn}}_{i,.,h}\right),$$

(6)

$${\mathbf{Y}}_{i,h}=\sum _{j=1}^{k_t}{\mathbf{Attn}}_{i,j,h}^{\prime }\times {\mathbf{V}}_{j,h},$$

(7)

$$\widehat{\mathbf{Z}}=Linear\left(\mathbf{Y}\right).$$

(8)

The matrices $\mathbf{Q},\mathbf{K},$ and $\mathbf{V}$ of dimensions ${\mathbb{R}}^{(k_t+1)\times N_h\times N_d}$ are derived from the input features ${\mathbf{X}}^{\prime }$ using three separate linear transformations. Here, · symbolizes the dot product operation between vectors ${\mathbf{Q}}_{i,h}$ and ${\mathbf{K}}_{j,h}$. The attention score matrix, represented as $\mathbf{Attn}$, has dimensions of ${\mathbb{R}}^{(k_t+1)\times (k_t+1)\times N_h}$. From this, the aggregated feature matrix $\mathbf{Y}$ with dimensions ${\mathbb{R}}^{(k_t+1)\times N_h\times N_d}$ is obtained. These features are then linearly transformed to yield the output feature matrix $\widehat{\mathbf{Z}}$, which is of size ${\mathbb{R}}^{(k_t+1)\times (N_h\times N_d)}$.

In Vision Transformers (ViT) tailored for 2D imagery, empirical studies have continually emphasized the indispensable role of positional encodings within the Transformer’s architecture. When transposed to 3D Transformers, though the spatial coordinates of the point cloud are inherently woven into the feature learning process, there is a risk that nuanced positional cues could be masked or even jettisoned as the network delves deeper. It is worth noting that, unlike the uniformly arrayed pixels in 2D imagery, 3D points exist within a vastly more intricate, continuous spatial configuration. This innate complexity amplifies the challenges when capitalizing on the $xyz$ positional coordinates of these point clouds. To more astutely harness this spatial information within our 3D Transformer, we integrated the contextual relative position encoding strategy delineated in the stratified transformer—refer to [40] for a comprehensive exploration.

Complexity Analysis. To wrap things up, let us distill the computational complexity inherent to the window-based point-voxel multi-head self-attention mechanism. The expressions from (4) through (8) detail the multi-head self-attention operations pertinent to a singular window. Given an average point cloud count of m within each window, the computational intricacy of this window-based approach is presented as $O\left(\frac{N}{m}\times {(m+1)}^2\right)\approx O\left(N\times m\right)$, with m being substantially smaller than N. In a comparative light, this is a marked decline from the $O\left(N^2\right)$ complexity endemic to a global multi-head self-attention, effectuating a considerable attenuation in the computational demands of the Transformer block.

3.2.3. Regional-to-Local Point-Voxel Transformer Encoder

Our proposed Region-to-Local (R2L) Point-Voxel Transformer Encoder, as illustrated in Figure 3, consists of an R2L point-voxel attention and a feed-forward network (FFN). Specifically, in the R2L point-voxel attention domain, the Voxel-based Regional Self-Attention (RSA) first conducts self-attention computation on all regional tokens, effectively learning regional information at the voxel level. Subsequently, the Local Window-based Point-Voxel Self-Attention (LSA) employs local tokens associated with regional tokens to grasp local characteristics. The participation of the corresponding regional tokens in the LSA computation infuses more extensive regional insights, enabling interaction across different windows and thereby broadening the receptive field. Within the R2L point-voxel encoder, both RSA and LSA utilize Multihead Self-Attention (MSA) tailored for distinct input tokens. Ultimately, an FFN layer is incorporated for feature enhancement. Furthermore, we integrate layer normalization (LN) and residual connections within the conventional Transformer encoder. Given the input of the network’s dth layer, consisting of regional tokens (voxels) ${\mathcal{V}}_r^{d-1}$ and local tokens (points) ${\mathcal{X}}_l^{d-1}$, the R2L Point-Voxel Transformer Encoder can be articulated as

$$\begin{array}{cc}\hfill {\mathcal{Y}}_r^d& ={\mathcal{V}}_r^{d-1}+\mathbf{RSA}\left(\mathbf{LN}\left({\mathcal{V}}_r^{d-1}\right)\right),{\mathcal{X}}_t^{d-1}=\left[{\mathcal{Y}}_{r_t}^d\parallel {\left\{{\mathcal{X}}_{l_{t,i}}^{d-1}\right\}}_{i\in k_t}\right],\hfill \\ \hfill {\mathcal{Z}}_t^d& ={\mathcal{X}}_t^{d-1}+\mathbf{LSA}\left(\mathbf{LN}\left({\mathcal{X}}_t^{d-1}\right)\right),{\mathcal{X}}_t^d={\mathcal{Z}}_t^d+\mathbf{FFN}\left(\mathbf{LN}\left({\mathcal{Z}}_t^d\right)\right),\hfill \end{array}$$

(9)

where $t\in \{1,\dots ,M\}$ denotes the spatial index associated with a regional token, i serves as the local token index within the tth window. The variable $k_t$ represents the number of local tokens present in that window. The input to the LSA, ${\mathcal{X}}_t^{d-1}$, incorporates both a regional token and its associated local tokens, facilitating the exchange of information between the regional and local tokens. On the other hand, the outputs ${\mathcal{X}}_{l_t}^d$ and ${\mathcal{V}}_{r_t}^d$ can be extracted from ${\mathcal{X}}_t^d$, similarly to the top right expression in Equation (9).

The RSA facilitates the exchange of information across local regional tokens, encompassing the voxel level coarse-grained context of the point cloud scene. On the other hand, the LSA integrates features among tokens within a spatial region (i.e., points within a window and their corresponding voxels), encompassing both regional tokens (voxel tokens) and local tokens (point tokens). Since the regions are divided by non-overlapping windows, the RSA is also designed to exchange information among these regions where the LSA takes one regional token and then combines with it the local tokens in the same region. In this setup, all local tokens are still capable of obtaining broader regional information while maintaining focus on their local neighbors. With these two attentions, the R2L can effectively and efficiently exchange information among all regional and local tokens. The self-attention mechanism of regional tokens aims to extract higher-level details, serving as a bridge for local token information to transition between regions. Conversely, the R2L point-voxel attention focuses on local contextual information with one regional token.

Complexity Analysis. Given a point cloud input encompassing N points, where each window, on average, contains m points, and the voxel-based regional self-attention engages with k neighboring entities, the computational intricacy for this self-attention can be outlined as $O\left(\frac{N}{m}\times k^2\right)$. Meanwhile, the complexity for the window-based point-voxel self-attention stands at $O\left(\frac{N}{m}\times {(m+1)}^2\right)$. Therefore, the collective computational complexity for the R2L Point-Voxel Transformer encoder can be delineated as $O\left(\frac{N}{m}\times (k^2+{(m+1)}^2)\right)$. Notably, given that $k\ll m\ll N$, the overall complexity simplifies to $O(N\times m)$. This figure is substantially more favorable compared to the $O\left(N^2\right)$ complexity found with global self-attention in some existing methods [29,56]. Furthermore, the proposed R2L Point-Voxel Transformer encoder enables capturing both fine-grained local and larger regional details. By prioritizing local feature learning, it significantly reduces computational complexity, enhances efficiency, and is highly memory efficient.

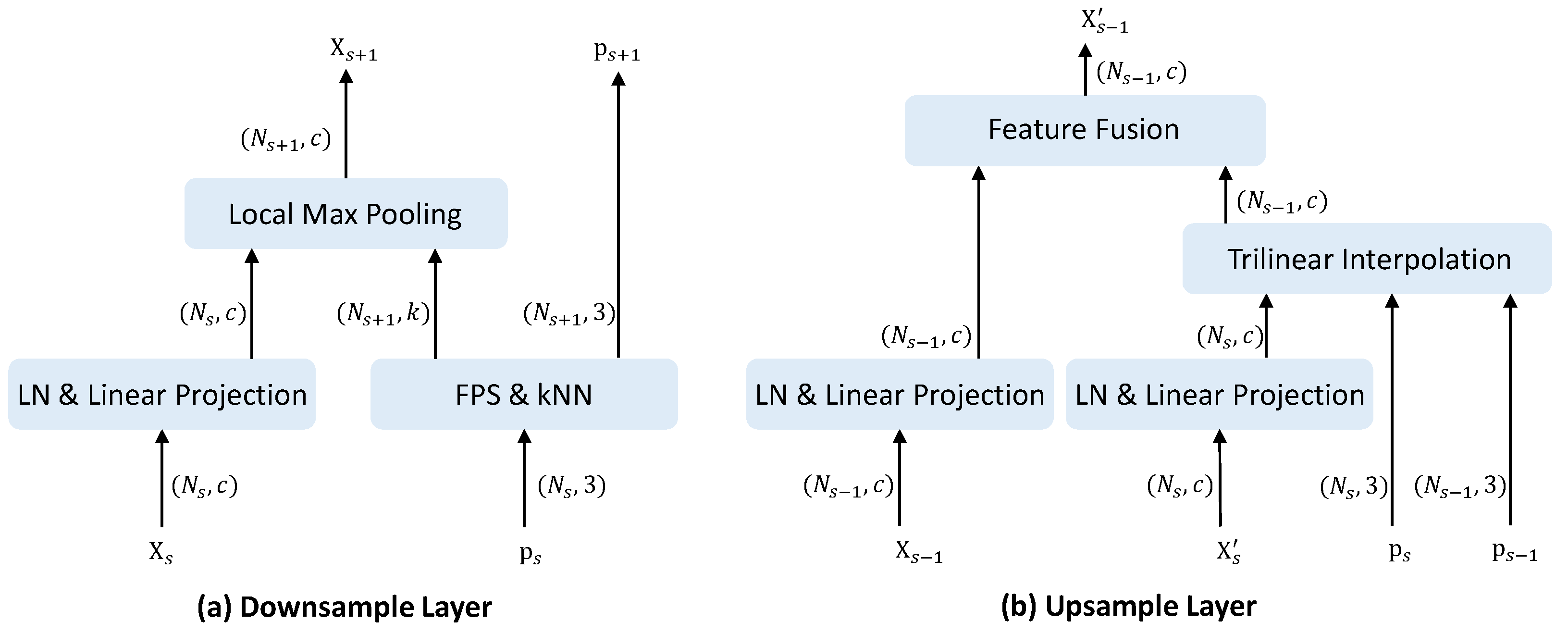
3.2.4. Downsampling and Upsampling Layer

Following previous methods [8,9,22,30], the downsampling layer depicted in Figure 4a operates as follows: The input coordinates ${\mathbf{p}}_s$ are first passed to the FPS and kNN module for sampling and grouping. The farthest point sampling (FPS) is applied to obtain the centroid points ${\mathbf{p}}_{s+1}$. Next, the kNN search is performed on the original points to acquire the grouping indices ${\mathbf{idx}}_{\mathrm{group}}\in {\mathbb{R}}^{N_{s+1}\times k}$. The number of centroids after downsampling is a quarter of the original, i.e., $N_{s+1}=⌈\frac{1}{4}{N}_s⌉$. In parallel, the input features ${\mathbf{x}}_s$ are fed into a layer normalization and linear projection layer. Finally, local max-pooling is conducted over the groups to aggregate the projected features, outputting the downsampled features ${\mathbf{x}}_{s+1}$.

Figure 4b shows the upsampling layer. The decoder features ${\mathbf{x}}_s^{\prime }$ are first projected with layer normalization and a linear layer. Interpolation is then performed between the current coordinates ${\mathbf{p}}_s$ and prior ${\mathbf{p}}_{s-1}$. The encoder features ${\mathbf{x}}_{s-1}$ from the previous stage undergo layer normalization and linear transformation. These features are summed by the feature fusion module to produce the decoded output ${\mathbf{x}}_{s-1}^{\prime }$.

3.3. Baseline and Evaluation Metrics

In our evaluation, we rigorously compared our network model against an array of state-of-the-art methods across two datasets. For the S3DIS dataset, we selected a range of methods to compare with our network model, including PointNet [8], SegCloud [57], PointCNN [20], SPGraph [58], PAT [59], PointWeb [42], GACNet [60], SegGCN [61], MinkowskiNet [19], PAConv [43], KPConv [41], PatchFormer [35], CBL [62], FastPointTransformer [32], PointTransformer [30], PointNeXt-XL [22], and Swin3d [40].

Meanwhile, for the ScanNet v2 dataset, our comparisons were made against PointNet++ [9], 3DMV [63], PanopticFusion [64], PointCNN [20], PointConv [53], JointPointBased [65], PointASNL [56], SegGCN [61], RandLA-Net [21], KPConv [41], JSENet [66], FusionNet [46], SparseConvNet [18], MinkowskiNet [19], PointTransformer [30], PointNeXt-XL [22], and FastPointTransformer [32].

Our comparative analysis was comprehensive, encompassing a wide range of methodologies: point-based techniques (e.g., PointTransformer [30] and PointNeXt-XL [22]), voxel-based approaches (such as MinkowskiNet [19] and FastPointTransformer [32]), and hybrid strategies that seamlessly integrate voxels and points (like PatchFormer [35]). An in-depth discussion on the evaluations and consequential results is elaborated in the subsequent Section 4.1.

In assessing the efficacy of our advanced network, we resort to three vital metrics, each capturing a distinct aspect of the model’s predictive prowess: Mean Classwise Intersection over Union (mIoU), Mean of Classwise Accuracy (mAcc), and Overall Pointwise Accuracy (OA). These metrics collectively provide a robust evaluation, ensuring a comprehensive assessment of our proposed model against ground truths.

3.4. Implementation Details

In Figure 1, we present the central architecture of our 3D semantic segmentation network. Inputs to our model included both the $xyz$ coordinates and the $rgb$ color values. We initialized the feature dimension at 48, with the number of attention heads set to 3. Notably, both these parameters were doubled with every subsequent downsampling layer. For the S3DIS dataset, we constructed a network comprising four stages, delineated by block depths of $[2,2,6,2]$. Meanwhile, for the ScanNet v2 dataset, the architecture encompassed five stages characterized by block depths of $[3,3,9,3,3]$.

In our experimental setup for both the S3DIS and ScanNet v2 datasets, we utilized a server powered by an Intel(R) Xeon(R) E5-2650 v4 @ 2.20GHz × 40 CPU, accompanied by 4 Tesla V100 16G GPUs, 200 GB RAM, CUDA 10.2, and cuDNN v7. Specifically for the S3DIS dataset, the model was trained for 76,500 iterations using the AdamW [67] optimizer. The initial learning rate was determined at 0.006, with a batch size of 8, and we employed the cross-entropy loss as the optimization metric. Following common practice [30,43], the raw input point clouds were grid-sampled at an initial size of 0.04 m. The training phase saw the input point count restricted to 80,000, while the testing phase employed the entire raw point cloud. Notably, the starting window size was 0.16 m, doubling after each downsampling layer. Data augmentation for S3DIS encompassed z-axis rotation, scaling, jittering, and color dropout.

When transitioning to the ScanNet v2 experiments, our model was trained across 600 epochs, with weight decay, batch size, and grid sampling configured to 0.1, 8, and 0.02m, respectively. The training phase retained a ceiling of 120,000 input points and an initial window size of 0.1 m. Data augmentation, beyond random jitter, mirrored the S3DIS approach. To streamline the training process and conserve GPU memory across both datasets, we leveraged PyTorch’s native Automatic Mixed Precision (AMP). Furthermore, any other training parameters remained consistent between both datasets.

4. Results and Discussion

In this section, we first exhibit the detailed results on S3DIS and ScanNet v2, with comparisons to other state-of-the-art methods in Section 4.1. Subsequently, we provide ablation experiments to analyze the efficacy of the key components within our proposed model design in Section 4.2. Finally, we discuss the computational requirements that our model needed in Section 4.3.

4.1. Evaluation

We conduct a rigorous comparison of our innovative approach with contemporary cutting-edge semantic segmentation techniques. In accordance with previous study [8,9,20,21,22,30,41,43,53], we report the OA, mAcc, and mIoU on Area 5 of S3DIS dataset, while for the ScanNet v2 dataset, we report the validation set mIoU (Val mIoU) and the online test set mIoU (Test mIoU) for a fair comparison. Results related to various evaluation metrics for the S3DIS and ScanNet v2 datasets are clearly laid out in

Table 3. Results on Area 5 of S3DIS dataset for semantic segmentation.

Method	Input	OA (%)	mAcc (%)	mIoU (%)
SegCloud [57]	voxel	-	57.4	48.9
MinkowskiNet [19]	voxel	-	71.7	65.4
FastPointTransformer [32]	voxel	-	77.3	70.1
PointNet [8]	point	-	49.0	41.1
TangentConv [68]	point	-	62.2	52.6
PointCNN [20]	point	85.9	63.9	57.3
SPGraph [58]	point	86.4	66.5	58.0
ParamConv [69]	point	-	67.0	58.3
PAT [59]	point	-	70.8	60.1
PointWeb [42]	point	87.0	66.6	60.3
HPEIN [70]	point	87.2	68.3	61.9
GACNet [60]	point	87.8	-	62.9
SegGCN [61]	point	88.2	70.4	63.6
PAConv [43]	point	-	-	66.6
KPConv [41]	point	-	72.8	67.1
CBL [62]	point	90.6	75.2	69.4
Swin3d(w/o shifted) [40]	point	-	-	69.4
Swin3d(w shifted) [40]	point	-	-	70.1
PointTransformer [30]	point	90.8	76.5	70.4
PointNeXt-XL [22]	point	90.6	-	70.5
PVCNN [44]	hybrid	87.1	-	59.0
DeepFusion [46]	hybrid	-	72.3	67.2
PatchFormer [35]	hybrid	-	-	68.1
PVT [47]	hybrid	-	-	68.2
Ours	hybrid	91.0	77.3	71.0

and

Table 4. Results on ScanNet v2 dataset for semantic segmentation.

Method	Input	Val mIoU (%)	Test mIoU (%)
SparseConvNet [18]	voxel	69.3	72.5
FastPointTransformer [32]	voxel	72.1	-
MinkowskiNet [19]	voxel	72.2	73.6
PointNet++ [9]	point	53.5	55.7
3DMV[63]	point	-	48.4
PanopticFusion [64]	point	-	52.9
PointCNN [20]	point	-	45.8
PointConv [53]	point	61.0	66.6
JointPointBased [65]	point	69.2	63.4
PointASNL [56]	point	63.5	66.6
SegGCN [61]	point	-	58.9
RandLA-Net [21]	point	-	64.5
KPConv [41]	point	69.2	68.6
JSENet [66]	point	-	69.9
PointTransformer [30]	point	70.6	-
PointNeXt-XL [22]	point	71.5	71.2
DeepFusion [46]	hybrid	-	68.8
Ours	hybrid	73.6	73.9

. For a deeper dive into class-specific performances, one can refer to

Table 5. Detailed results on S3DIS Area 5 for semantic segmentation. MinkUNet: MinkowskiNet, FPT: FastPointTransformer, Point Trans.: PointTransformer.

Method	Input	OA	mAcc	mIoU	Ceiling	Floor	Wall	Beam	Column	Window	Door	Table	Chair	Sofa	Bookcase	Board	Clutter
MinkUNet [19]	voxel	-	71.7	65.4	91.8	98.7	86.2	0.0	34.1	48.9	62.4	81.6	89.8	47.2	74.9	74.4	58.6
FPT [32]	voxel	-	77.3	70.1	94.2	98.0	86.0	0.2	53.8	61.2	77.3	81.3	89.4	60.1	72.8	80.4	58.9
PointNet [8]	point	-	49.0	41.1	88.8	97.3	69.8	0.0	3.9	46.3	10.8	59.0	52.6	5.9	40.3	26.4	33.2
SegCloud [57]	point	-	57.4	48.9	90.1	96.1	69.9	0.0	18.4	38.4	23.1	70.4	75.9	40.9	58.4	13.0	41.6
TangentConv [68]	point	-	62.2	52.6	90.5	97.7	74.0	0.0	20.7	39.0	31.3	77.5	69.4	57.3	38.5	48.8	39.8
PointCNN [20]	point	85.9	63.9	57.3	92.3	98.2	79.4	0.0	17.6	22.8	62.1	74.4	80.6	31.7	66.7	62.1	56.7
PointWeb [42]	point	87.0	66.6	60.3	92.0	98.5	79.4	0.0	21.l	59.7	34.8	76.3	88.3	46.9	69.3	64.9	52.5
HPEIN [70]	point	87.2	68.3	61.9	91.5	98.2	81.4	0.0	23.3	65.3	40.0	75.5	87.7	58.5	67.8	65.6	49.4
GACNet [60]	point	87.8	-	62.9	92.3	98.3	81.9	0.0	20.4	59.1	40.9	85.8	78.5	70.8	61.7	74.7	52.8
PAT [59]	point	-	70.8	60.1	93.0	98.5	72.3	1.0	41.5	85.l	38.2	57.7	83.6	48.1	67.0	61.3	33.6
ParamConv [69]	point	-	67.0	58.3	92.3	96.2	75.9	0.3	6.0	69.5	63.5	66.9	65.6	47.3	68.9	59.1	46.2
SPGraph [58]	point	86.4	66.5	58.0	89.4	96.9	78.1	0.0	42.8	48.9	61.6	84.7	75.4	69.8	52.6	2.1	52.2
SegGcN [61]	point	88.2	70.4	63.6	93.7	98.6	80.6	0.0	28.5	42.6	74.5	88.7	80.9	71.3	69.0	44.4	54.3
PAConv [43]	point	-	73.0	66.6	94.6	98.6	82.4	0.0	26.4	58.0	60.0	89.7	80.4	74.3	69.8	73.5	57.7
KPConv [41]	point	-	72.8	67.1	92.8	97.3	82.4	0.0	23.9	58.0	69.0	91.0	81.5	75.3	75.4	66.7	58.9
CBL [62]	point	90.6	75.2	69.4	93.9	98.4	84.2	0.0	37.0	57.7	71.9	91.7	81.8	77.8	75.6	69.1	62.9
Point Trans. [30]	point	90.8	76.5	70.4	94.0	98.5	86.3	0.0	38.0	63.4	74.3	89.1	82.4	74.3	80.2	76.0	59.3
PVT	hybrid	-	-	68.2	91.2	98.8	86.2	0.3	34.2	49.9	61.5	81.6	89.9	48.2	80.0	76.5	54.7
Ours	hybrid	91.0	77.3	71.0	95.1	98.4	85.5	0.0	35.8	65.1	72.3	91.4	81.9	75.5	82.8	75.9	62.8

and

Table 6. Detailed results on ScanNet v2 for semantic segmentation. SpaConvNet: SparseConvNet, MinkUNet: MinkowskiNet, PaFusion: PanopticFusion.

Method	Input	Val	Test	Bath	Bed	Bksf	Cab	Chair	Cntr	Curt	Desk	Door	Floor	Othr	Pic	Ref	Show	Sink	Sofa	Tab	Toil	Wall	Wind
SpaConvNet [18]	voxel	69.3	72.5	64.7	82.1	84.6	72.1	86.9	53.3	75.4	60.3	61.4	95.5	57.2	32.5	71.0	87.0	72.4	82.3	62.8	93.4	86.5	68.3
MinkUNet [19]	voxel	72.2	73.6	85.9	81.8	83.2	70.9	84.0	52.1	85.3	66.0	64.3	95.1	54.4	28.6	73.1	89.3	67.5	77.2	68.3	87.4	85.2	72.7
PointNet++ [9]	point	53.5	55.7	73.5	66.1	68.6	49.1	74.4	39.2	53.9	45.1	37.5	94.6	37.6	20.5	40.3	35.6	55.3	64.3	49.7	82.4	75.6	51.5
3DMV [63]	point	-	48.4	48.4	53.8	64.3	42.4	60.6	31.0	57.4	43.3	37.8	79.6	30.1	21.4	53.7	20.8	47.2	50.7	41.3	69.3	60.2	53.9
PanFusion [64]	point	-	52.9	49.1	68.8	60.4	38.6	63.2	22.5	70.5	43.4	29.3	81.5	34.8	24.1	49.9	66.9	50.7	64.9	44.2	79.6	60.2	56.1
PointCNN [20]	point	-	45.8	57.7	61.1	35.6	32.1	71.5	29.9	37.6	32.8	31.9	94.4	28.5	16.4	21.6	22.9	48.4	54.5	45.7	75.5	70.9	47.5
PointConv [53]	point	61.0	66.6	78.1	75.9	69.9	64.4	82.2	47.5	77.9	56.4	50.4	95.3	42.8	20.3	58.6	75.4	66.1	75.3	58.8	90.2	81.3	64.2
JointPoint [71]	point	69.2	63.4	61.4	77.8	66.7	63.3	82.5	42.0	80.4	46.7	56.1	95.1	49.4	29.1	56.6	45.8	57.9	76.4	55.9	83.8	81.4	59.8
PointASNL [56]	point	63.5	66.6	70.3	78.1	75.1	65.5	83.0	47.1	76.9	47.4	53.7	95.1	47.5	27.9	63.5	69.8	67.5	75.1	55.3	81.6	80.6	70.3
SegGCN [61]	point	-	58.9	83.3	73.1	53.9	51.4	78.9	44.8	46.7	57.3	48.4	93.6	39.6	6.1	50.1	50.7	59.4	70.0	56.3	87.4	77.1	49.3
RandLA-Net [21]	point	-	64.5	77.8	73.1	69.9	57.7	82.9	44.6	73.6	47.7	52.3	94.5	45.4	26.9	48.4	74.9	61.8	73.8	59.9	82.7	79.2	62.1
KPConv [41]	point	-	68.4	84.7	75.8	78.4	64.7	81.4	47.3	77.2	60.5	59.4	93.5	45.0	18.1	58.7	80.5	69.0	78.5	61.4	88.2	81.9	63.2
JSENet [66]	point	-	69.9	88.1	76.2	82.1	66.7	80.0	52.2	79.2	61.3	60.7	93.5	49.2	20.5	57.6	85.3	69.1	75.8	65.2	87.2	82.8	64.9
DeepFusion [46]	hybrid	-	68.8	70.4	74.1	75.4	65.6	82.9	50.1	74.1	60.9	54.8	95.0	52.2	37.1	63.3	75.6	71.5	77.1	62.3	86.1	81.4	65.8
Ours	hybrid	73.6	73.9	86.3	81.3	78.4	65.4	89.7	66.9	78.1	68.6	65.2	94.9	56.4	28.4	63.8	67.1	66.3	84.2	74.6	94.4	84.9	69.0

. It is noteworthy that our approach achieves top-tier performance on both of these challenging large-scale 3D indoor point cloud datasets.

On the S3DIS dataset, the performance of our proposed method significantly surpasses that of other approaches. It exceeds our baseline—Swin3d without shift (69.4% mIoU)—by 1.6 percentage points in mIoU. When compared with the shifted version of Swin3d (70.1% mIoU), our model still demonstrates a 0.9 percentage point improvement in mIoU. Furthermore, relative to other methods, our approach achieves state-of-the-art levels for both OA and mAcc. Specifically, our method outperforms voxel-based methods like MinkowskiNet and Fast Point Transformer by 5.6 and 0.9 percentage points in mIoU, respectively. When compared to point-based methods like PointTransformer and PointNeXt-XL, we observe improvements of 0.6 and 0.5 percentage points in mIoU, respectively. This improvement is attributed to the introduction of our voxel branch with self-attention. Features from the voxel level offer a broader receptive field for point-based self-attention, bolstering information exchange between different windows and consequently enhancing dense point prediction accuracy.

Regarding the ScanNet v2 dataset, our method’s validation of mIoU again surpasses that of voxel-based methods like MinkowskiNet and Fast Point Transformer, with improvements of 1.0 and 1.1 percentage points in mIoU, respectively. When set against point-based techniques, namely PointTransformer and PointNeXt-XL, we observe advantages of 2.6 and 1.7 percentage points in mIoU. Contrary to the performance uplift of MinkowskiNet on the S3DIS dataset, the improvement of our method on the Scannet v2 dataset is not as pronounced. This difference relates to the dataset sparsity levels. As the ScanNet v2 dataset is sparser than S3DIS, there is less information loss during voxelization. For denser data, the voxelization process inevitably incurs a higher loss of information, which allows excelling of voxel-based methods like MinkowskiNet on sparser datasets. However, our approach consistently achieves outstanding results on both datasets due to our fusion of voxel and point multi-scale information, coupled with our region-to-local encoder module.

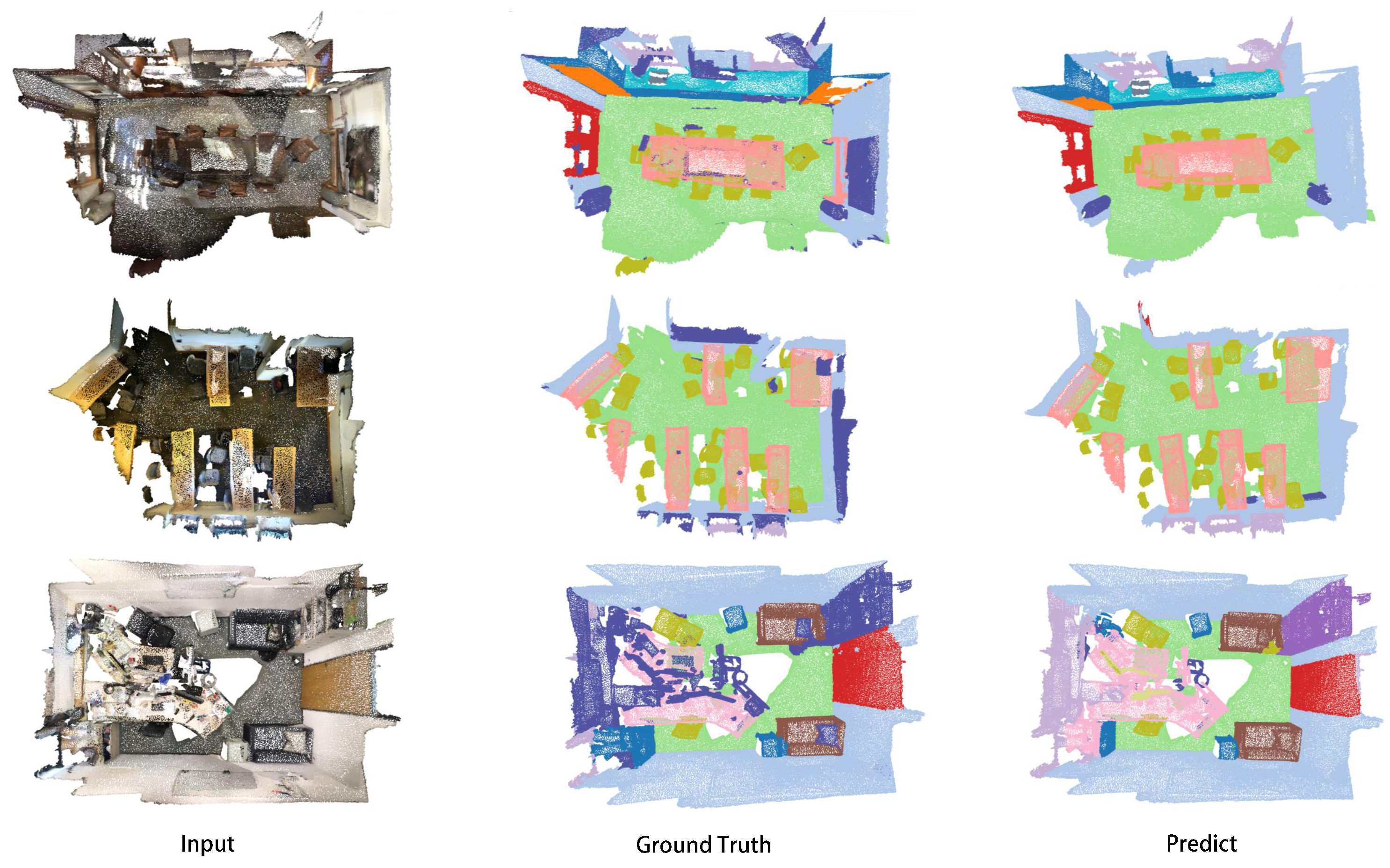
Qualitative visualization results on the test datasets can be seen in Figure 5 and Figure 6. The left column showcases the network’s input point cloud, the central column represents the actual input labels, and the right column depicts predictions from our network. As the figures illustrate, our network can adeptly predict every point cloud, aligning well with the Ground Truth, whether on dense datasets like S3DIS or sparser ones like ScanNet v2.

4.2. Ablation Study

To thoroughly validate the efficacy of each main component in our proposed RegionPVT model, we conducted extensive ablation experiments focused on two main aspects—the main components of our model and the skip connections within the voxel branch. The ablation study was performed on S3DIS to enable fair comparison, strengthen result credibility, and improve experimental efficiency.

4.2.1. Model Design

To underscore the individual and combined significance of each main component in our proposed RegionPVT model, we meticulously performed ablation studies.

Table 7. Ablation study on the proposed RegionPVT on S3DIS.

Exp	LSA	CRPE	RSA	VPE	mIoU (%)
I	✓				67.4
II	✓	✓			68.5
III	✓	✓	✓		70.5
IV	✓	✓	✓	✓	71.0

furnishes a detailed breakdown of these experiments. Spanning from Exp.I through IV, we progressively enhanced the model, initiating with the foundational Local Window-based Point-Voxel Self-Attention (LSA), subsequently integrating the Contextual Relative Position Encoding (CRPE), followed by the inclusion of Voxel-based Regional Self-Attention (RSA), culminating with the integration of Voxel Position Encoding (VPE).

The results demonstrate consistent mIoU improvement as more components were added, validating the efficacy of each module. Introducing CRPE and VPE in Exp.II and Exp.IV lead to gains of 1.1 and 0.5 percentage points, respectively, showing the importance of positional encoding for the large-scale point cloud semantic segmentation task. The largest jump emerged from adding RSA, improving mIoU by two percentage points in Exp. III. This highlighted the pivotal role of RSA in semantic understanding, enabled by the coarse-grained regional features it provides. The RSA module not only incorporated a broader context, but also enhanced information interaction among different windows. Overall, the local window-based self-attention, voxel positional encoding, and particularly the voxel-based regional self-attention each contributed collectively to the performance, demonstrating that the proposed components are well-designed and integrate synergistically within the RegionPVT framework for point cloud segmentation.

4.2.2. Skip Connections in Voxel Branch

In

Table 8. Ablation study of the skipped connection in the voxel branch of our proposed RegionPVT.

Method	OA (%)	mAcc (%)	mIoU (%)
RegionPVT (w voxel skip connection)	90.6	75.5	68.9
RegionPVT (w/o voxel skip connection)	91.0	77.3	71.0

, we investigated the influence of integrating skip connections within the voxel branch. In this configuration, regional tokens passed to the subsequent stage are derived from the preceding stage’s regional tokens which were processed via the R2L Point-Voxel Transformer encoder and then voxel-downsampled. This approach contrasts with the method of receiving tokens from the local tokens of the previous stage, which are first downsampled, followed by voxelization. The results showcased in Table 8 reveal that the performance of RegionPVT equipped with voxel-branch skip connections trails that of the RegionPVT variant devoid of such connections. We theorize this discrepancy arises because our voxel resolution is rather compact, where a single window epitomizes one voxel. With the expansive dimensions of our regional windows across four stages—namely [0.16 m, 0.32 m, 0.64 m, 1.28 m]—further voxel downsampling intensifies their sparsity, engendering pronounced feature attrition. Some windows in ensuing stages find themselves devoid of corresponding regional tokens, which curtails effective information exchange, culminating in a performance decline. To counteract this, we gravitate towards solely downsampling the points, ensuring that the subsequent stage’s regional tokens stem from the voxelized points.

4.3. Computational Requirements Analysis

As depicted in

Table 9. Comparison of FLOPs, Params, and Memory consumption on the S3DIS dataset.

Method	mIoU ↑ (%)	FLOPs ↓ (G)	Params ↓ (M)	Memory ↓ (GB)
KPConv [41]	67.1	2.0	25.6	2.9
PosPool [72]	66.7	2.0	18.4	5.1
PAConv [43]	66.6	1.3	11.8	3.3
PointTransformer [30]	70.4	0.8	7.8	2.5
Ours	71.0	1.8	9.5	1.7

, we offer a comprehensive comparison of Floating Point Operations (FLOPs), model parameters (Params), and Memory consumption against several state-of-the-art (SOTA) methods. Our evaluation criteria strictly adhere to the methodology proposed by PAConv [43], basing our measurements on an input of 4096 points and a batch size of one within the S3DIS dataset.

Amongst the compared methods, our model achieved the highest performance, registering a mIoU of 71.0%. This underscores the superiority of our approach. Notably, even as our approach concurrently learns both coarse-grained regional and fine-grained local features, it remains computationally efficient. With 1.8 G FLOPs, our model’s computational complexity is slightly higher compared to PointTransformer [30], yet substantially lower than KPConv [41] and PosPool [72]. This suggests that our model is capable of delivering exceptional performance without a huge increase in computational overhead. In terms of model parameters, our approach utilizes 9.5 M parameters, making it more compact than KPConv and PosPool, even though it is slightly larger than PointTransformer. Nonetheless, given the improvement in performance, this trade-off is considered reasonable. Most importantly, our model excels in memory efficiency. With a consumption of just 1.7 GB, our model stands out as the most memory efficient amongst all listed, highlighting its potential value in memory-constrained deployment scenarios.

In summary, our method strikes a harmonious balance between high performance and computational efficiency. It ensures the economical use of memory and parameters while setting new benchmarks for the large-scale indoor point cloud semantic segmentation task.

5. Conclusions

In this work, we introduced a novel Regional-to-Local Point-Voxel Transformer (RegionPVT), which captures both regional and local features within indoor 3D point cloud scenes effectively for the semantic segmentation task. The proposed method tackles computational and memory consumption challenges of multi-scale feature learning in large-scale indoor point cloud scenes by facilitating a voxel-based regional self-attention and a window-based voxel-point self-attention. The former efficiently captures broad, coarse-grained regional features, and the latter delves deep, enabling the extraction of fine-grained local details. The combined effect of these modules not only helps with multi-scale feature fusion, but also strengthens information exchange across different windows. By embedding a regional token within each window, our window-based self-attention concurrently facilitates the breadth of regional insights and the depth of local features, thus achieving a harmonious blend of scale and detail.

More importantly, our RegionPVT stands out by finding just the right balance between the performance and computational requirements. It adeptly learns both regional and local features while maintaining computational and memory efficiency—a balance often sought but seldom achieved in the domain. Our extensive empirical evaluations on S3DIS and ScanNet v2 datasets underscore RegionPVT’s prowess. Not only does it outperform hybrid and voxel-based methods, but it also shows competitive results compared with point-based counterparts, all the while using much less memory.

Also, our method has some limitations. Although we achieved satisfying results in terms of performance, computational complexity, and memory consumption, the training process of our approach is relatively slower compared to that of previous methods. Moreover, we only verified our method on two indoor scene datasets, leaving its applicability to larger-scale outdoor scene datasets yet to be further explored. In the future, we will attempt to optimize our model using advanced CUDA operators to enhance inference speed, while also testing its performance on a more diverse range of large-scale point cloud scene datasets. Furthermore, global structural information is crucial for feature point localization and overall understanding in 3D scene comprehension tasks. Efficient learning of global information will be a worthy area of exploration.