Ecosystem Evapotranspiration Partitioning and Its Spatial–Temporal Variation Based on Eddy Covariance Observation and Machine Learning Method
Abstract
:1. Introduction
2. Materials and Methods
2.1. Data
2.1.1. FLUXNET2015 Dataset
2.1.2. Remote Sensing Data
2.1.3. Soil Moisture Data
2.2. Methods
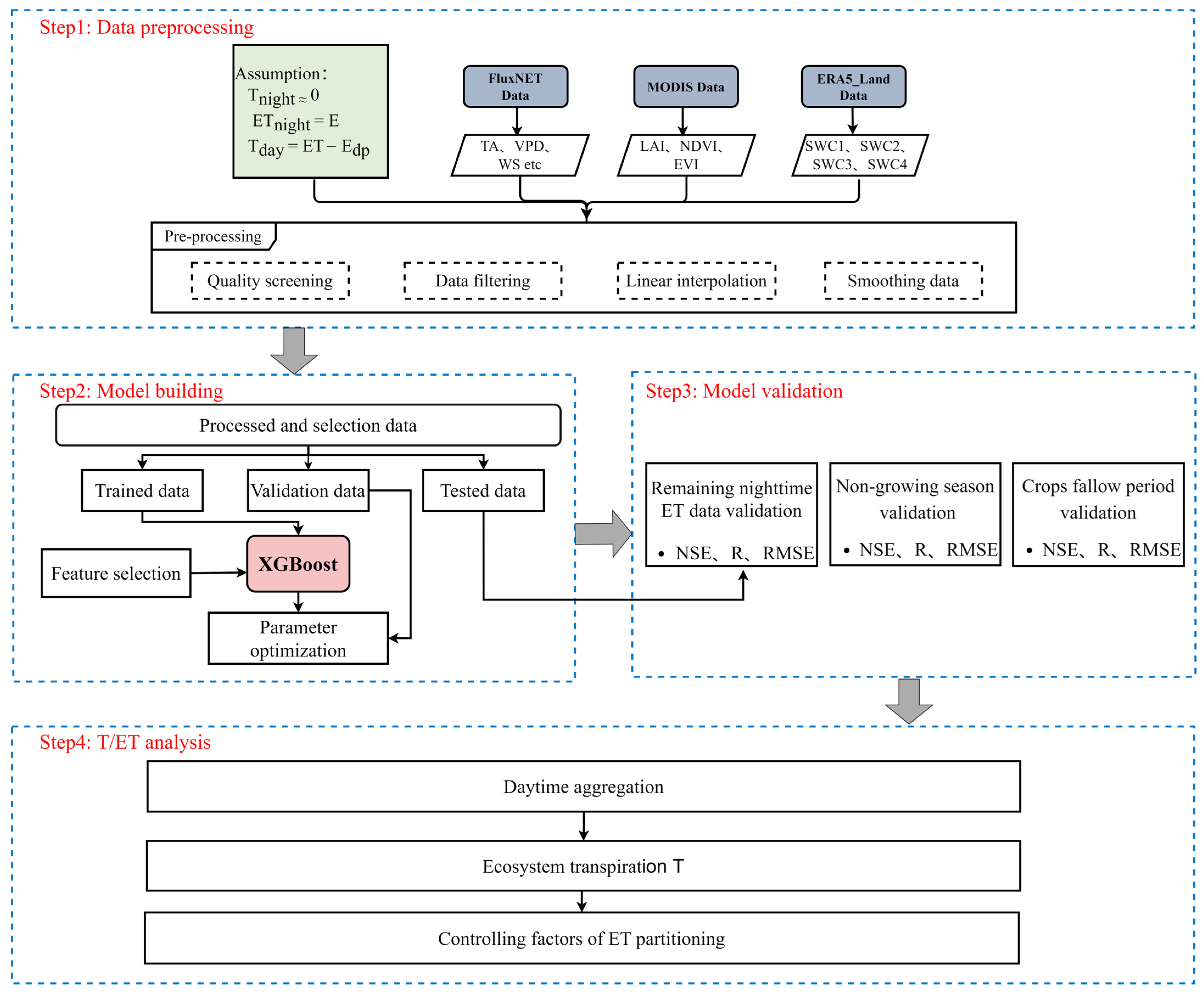
2.2.1. Overview of the ET Partitioning Method
2.2.2. Extreme Gradient Boosting
2.2.3. Feature Selection
2.2.4. Parameter Optimization
2.3. Model Evaluation
2.3.1. Data Set Split
2.3.2. Model Evaluation
2.3.3. Validation of Results
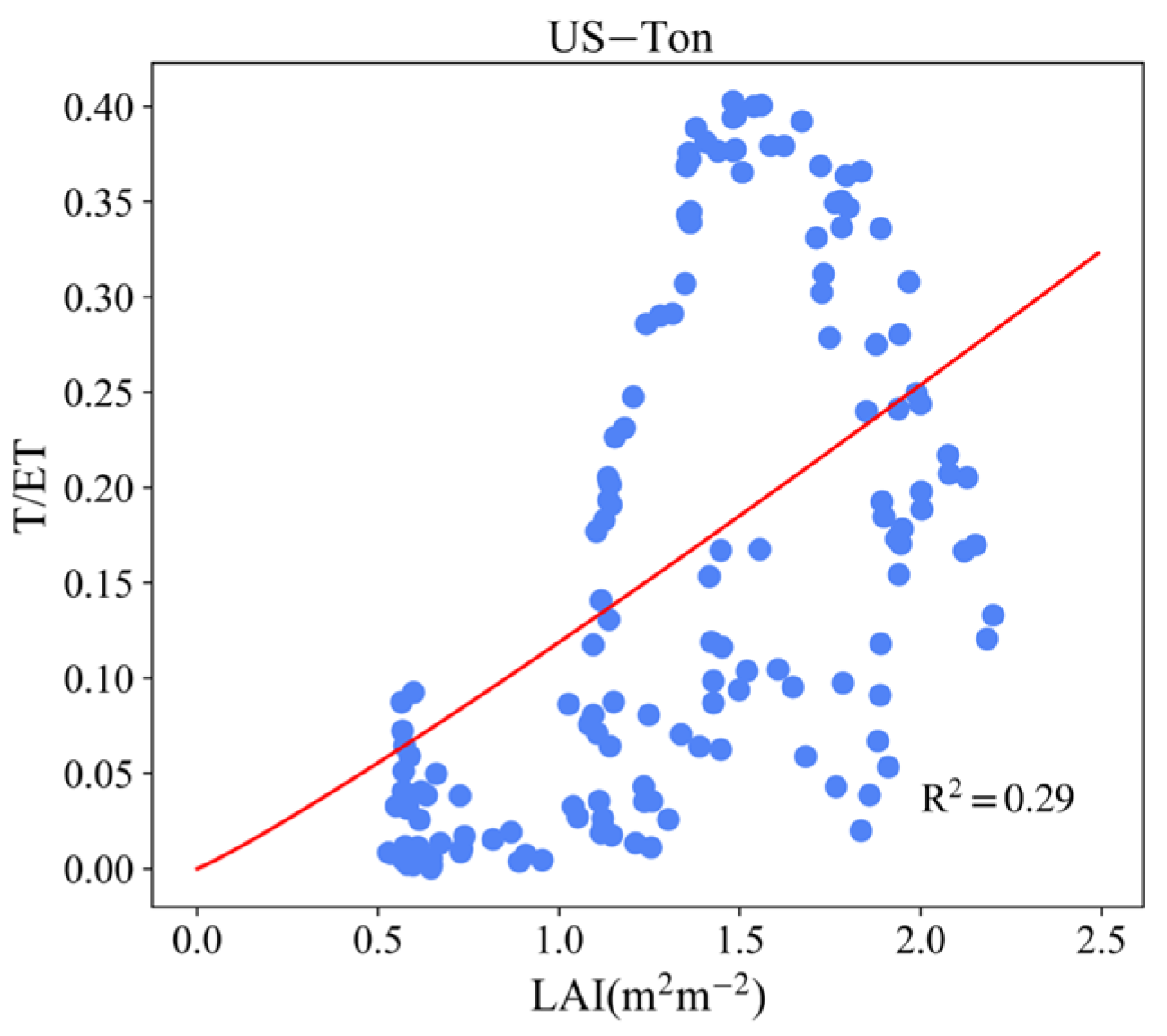
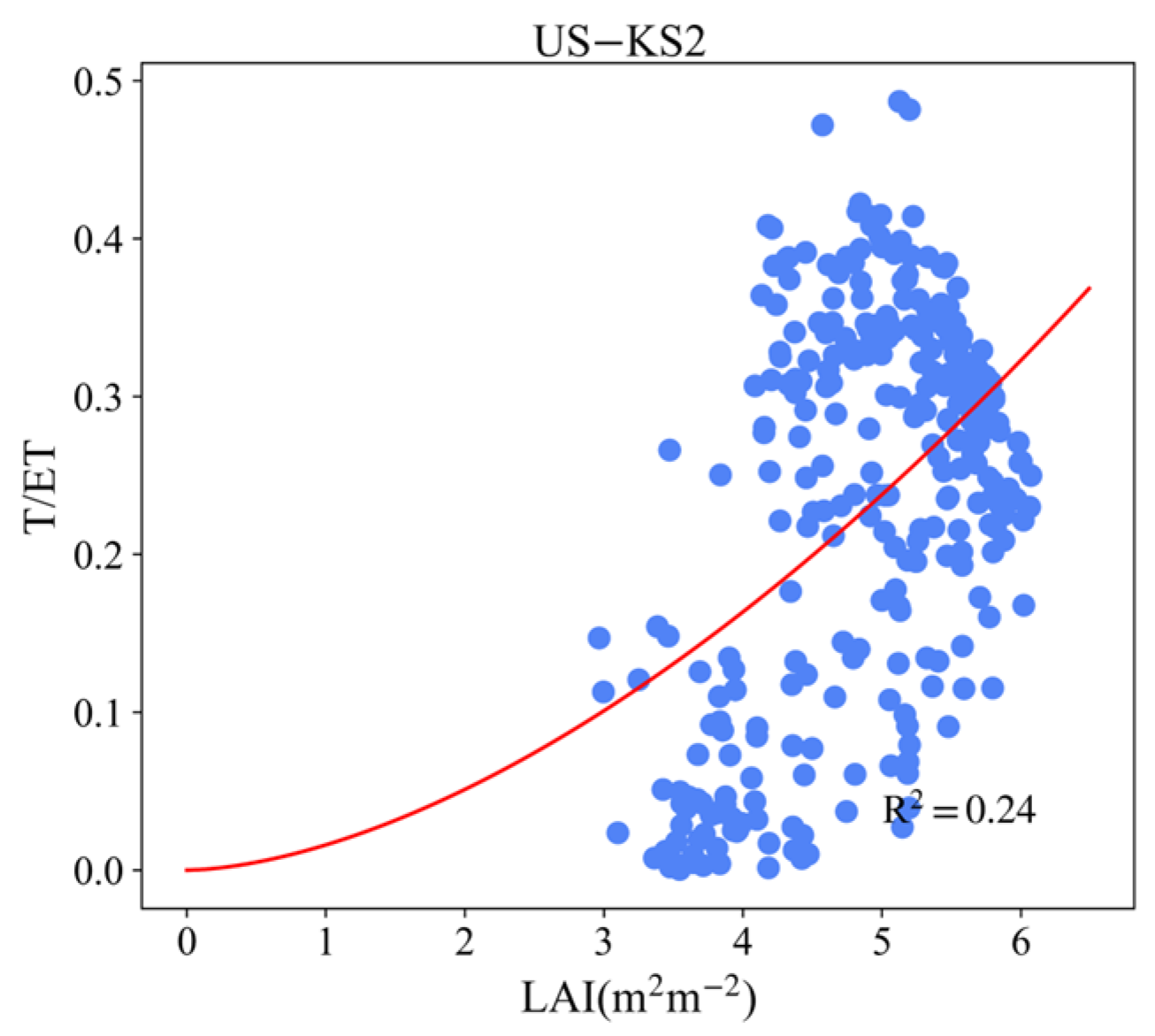
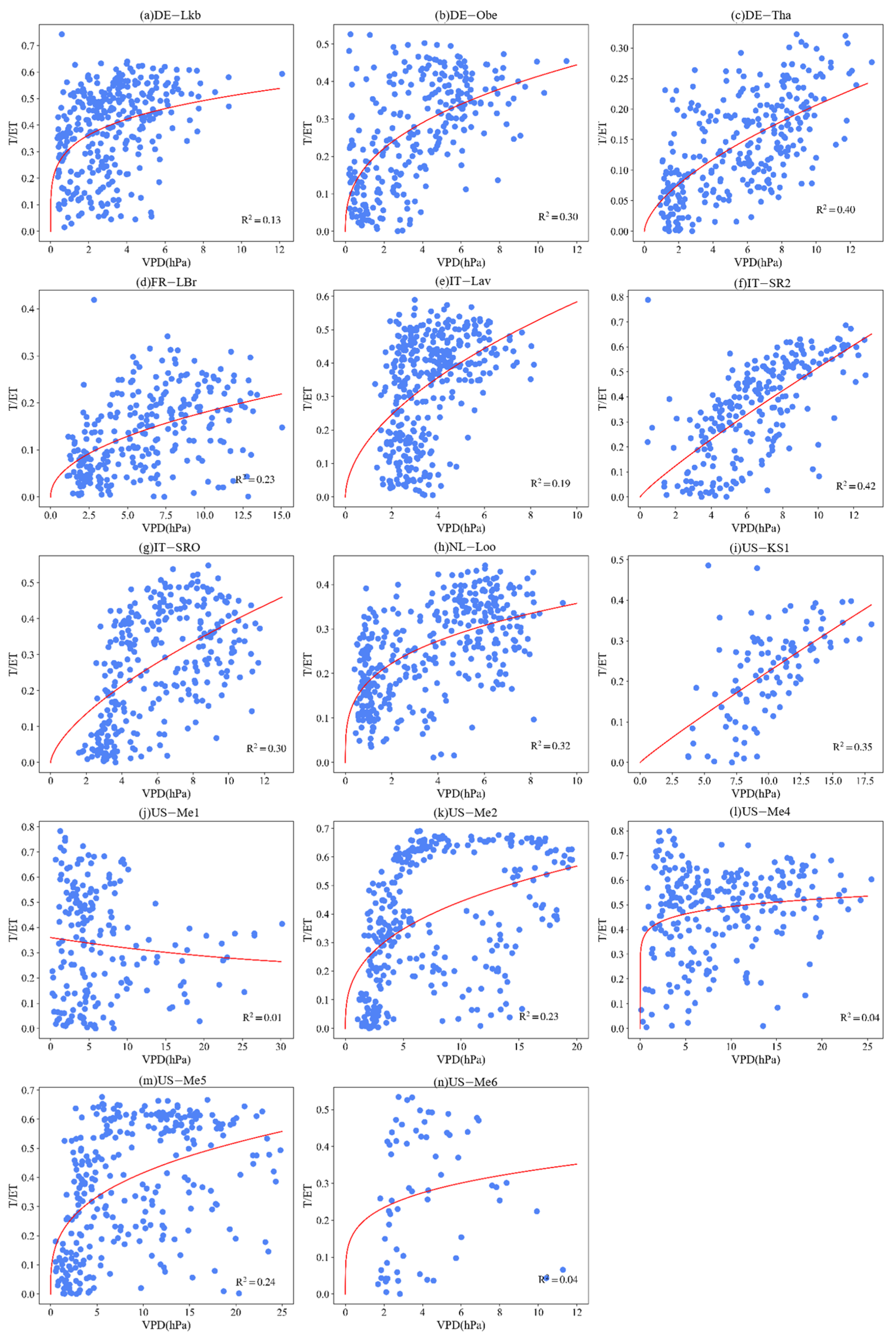
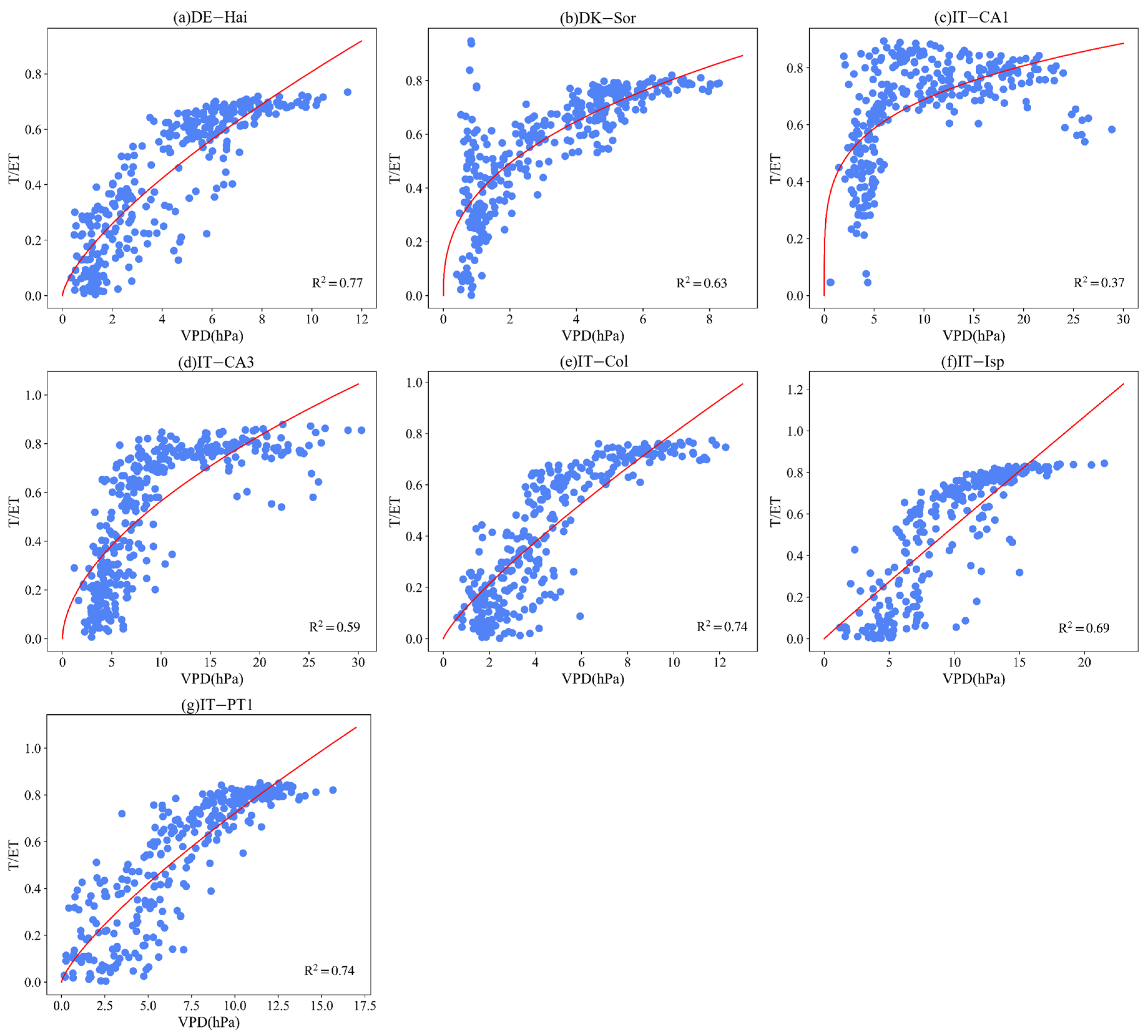
2.4. The Impacts of LAI and VPD on the Temporal Variations in T/ET
3. Results
3.1. Feature Selection
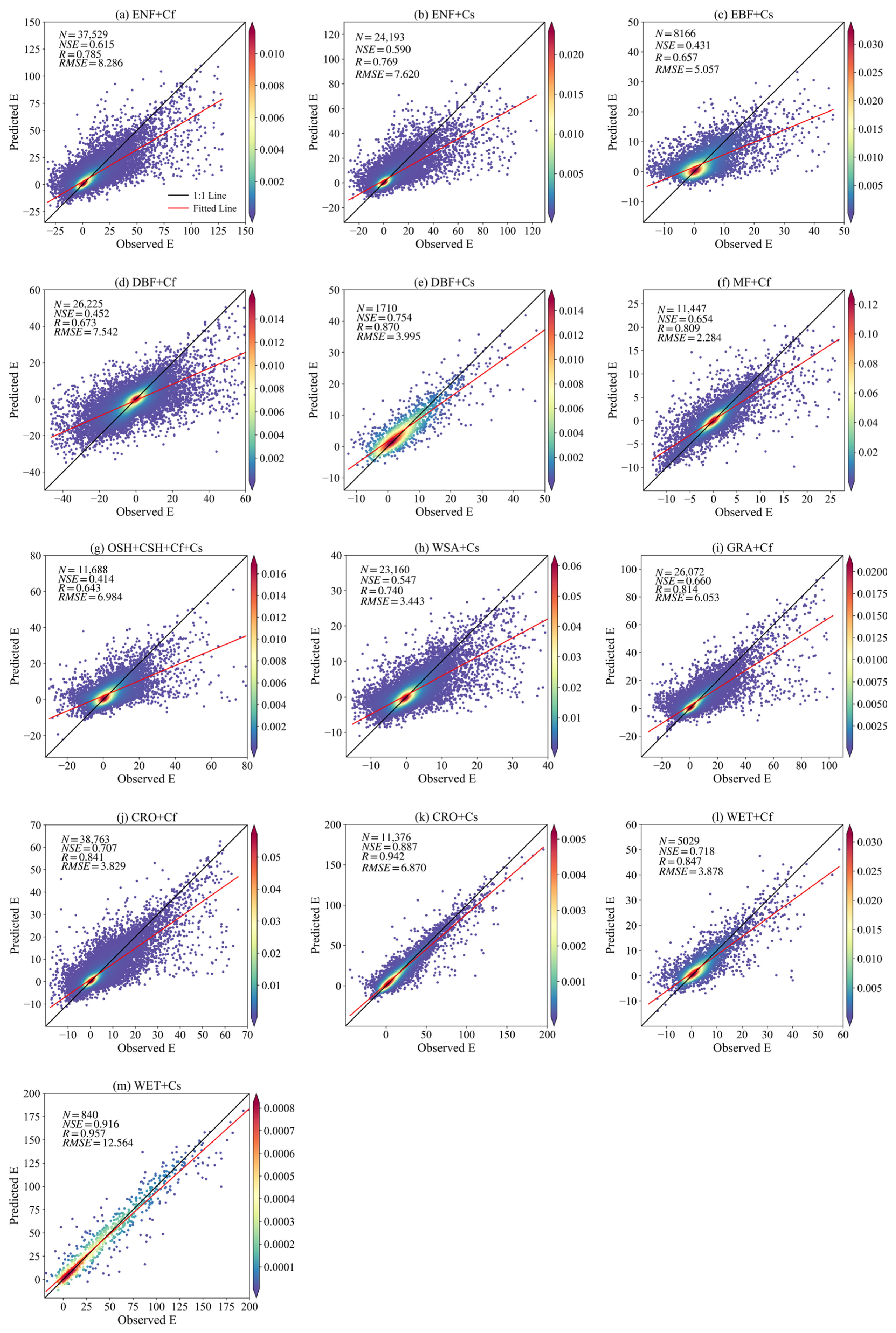
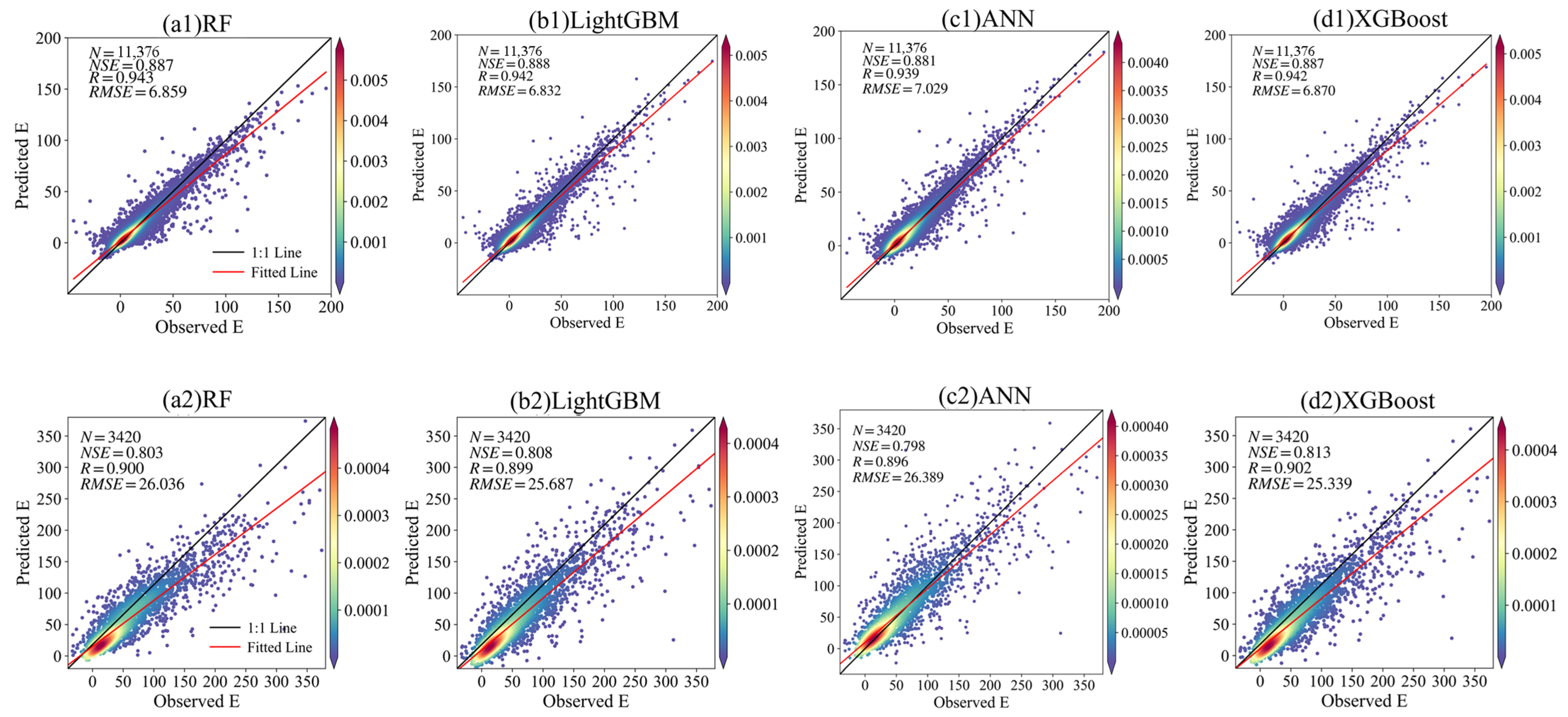
3.2. Model Results and Validation
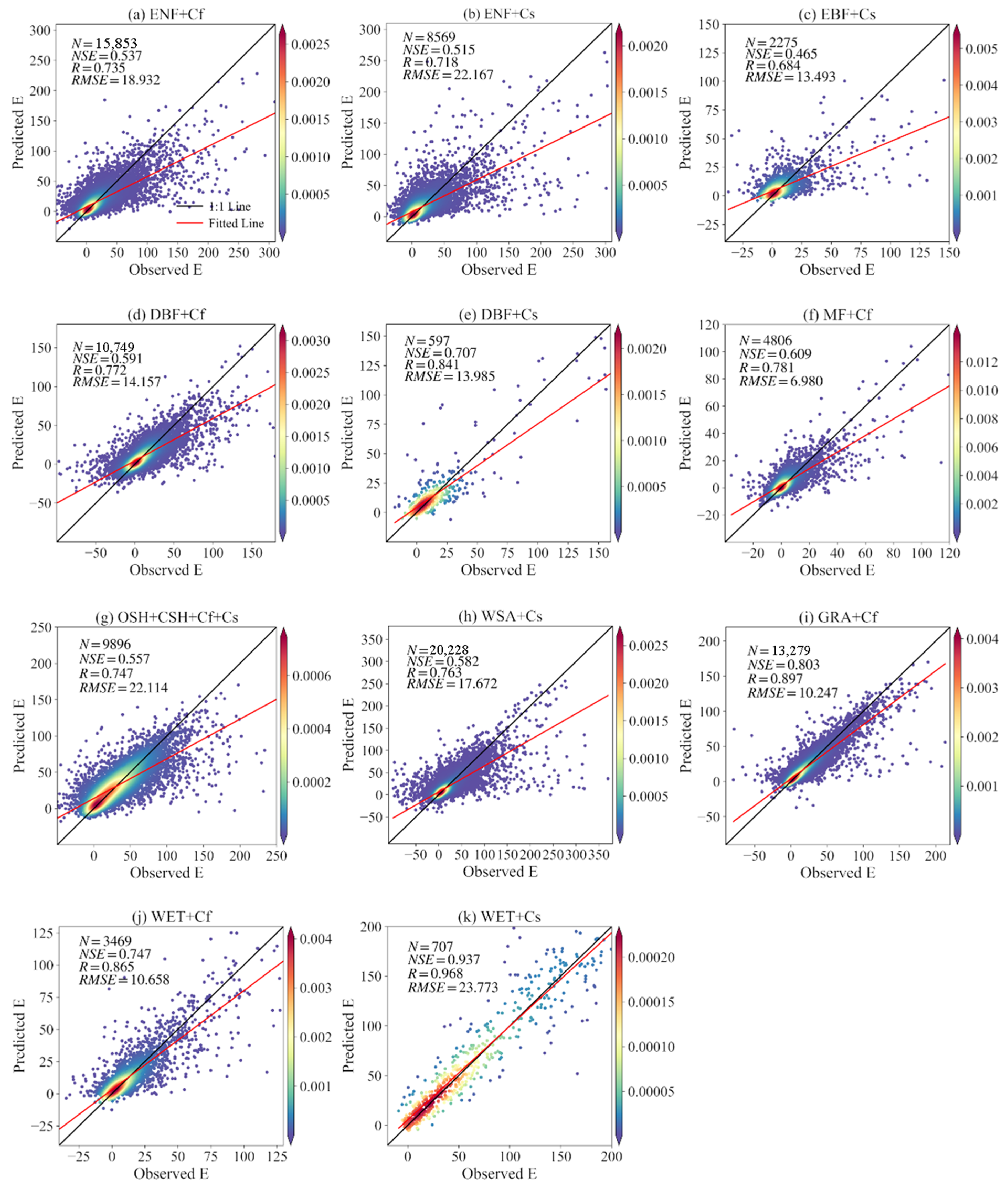
3.2.1. Model Performance on the Remaining Night-Time Data
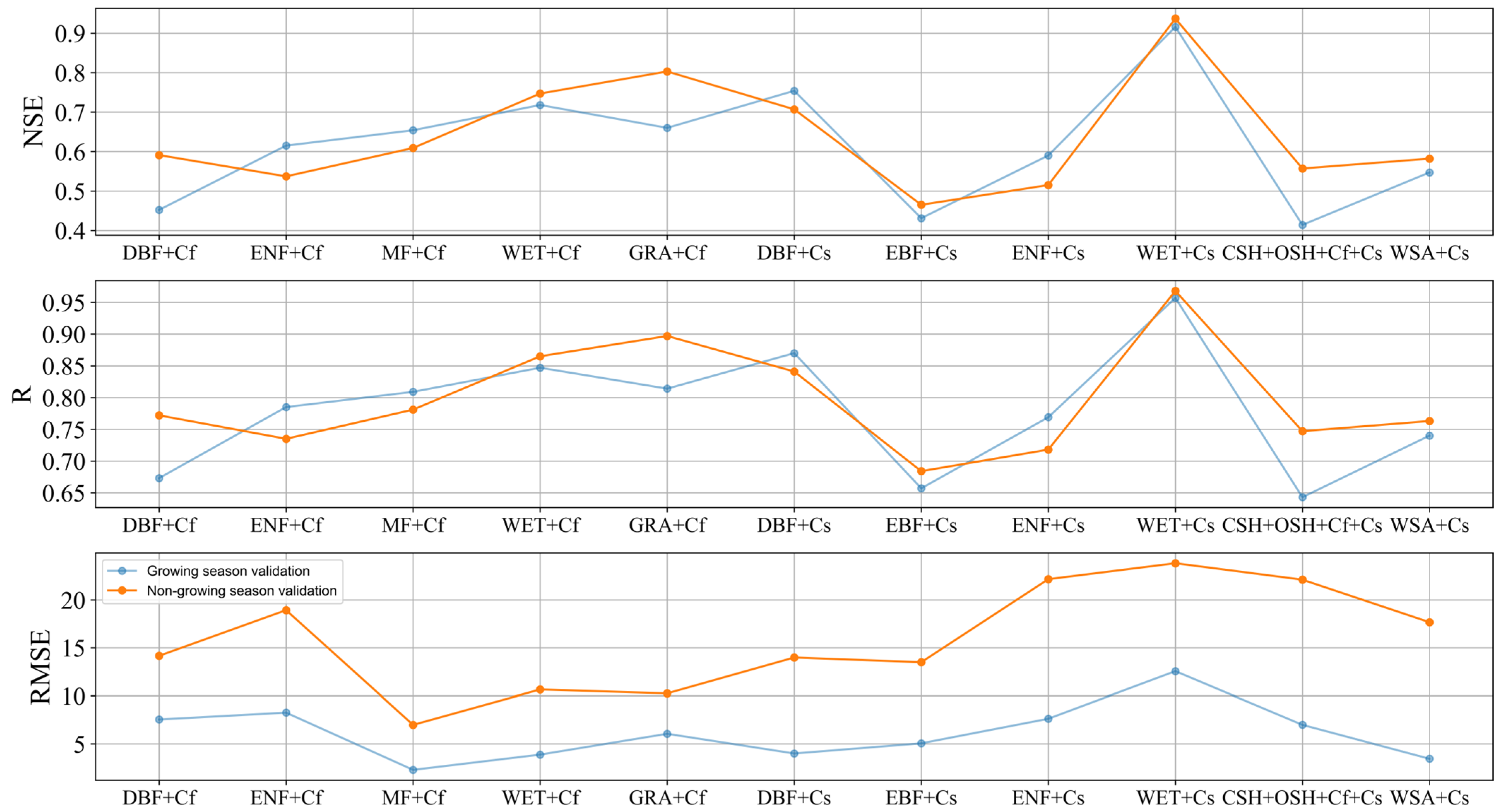
3.2.2. Validation during the Non-Growing Season
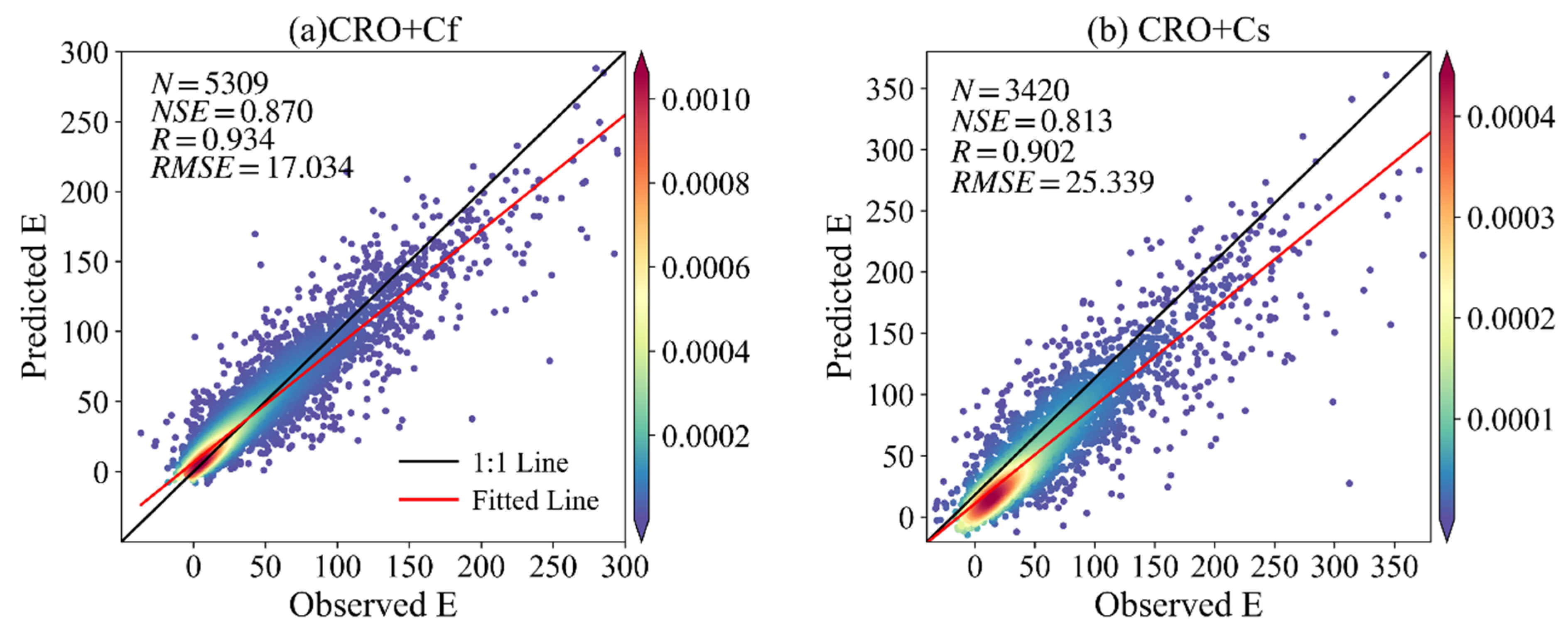
3.2.3. Validation during the Crop Fallow Period
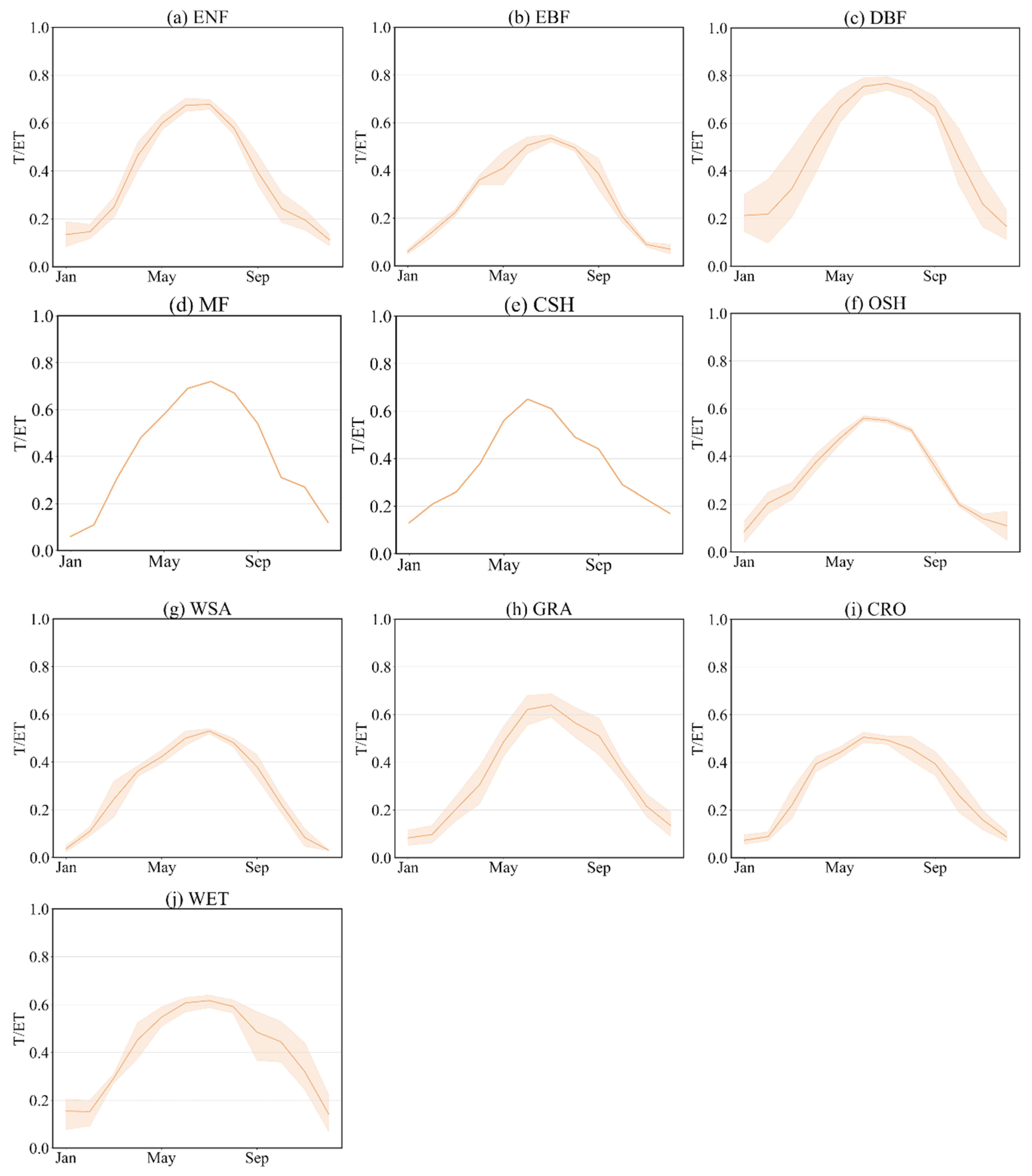
3.3. Variations in ET Partitioning in Different Ecosystems
3.4. Effect of LAI and VPD on T/ET
4. Discussion
4.1. Model Performances in Different Ecosystems
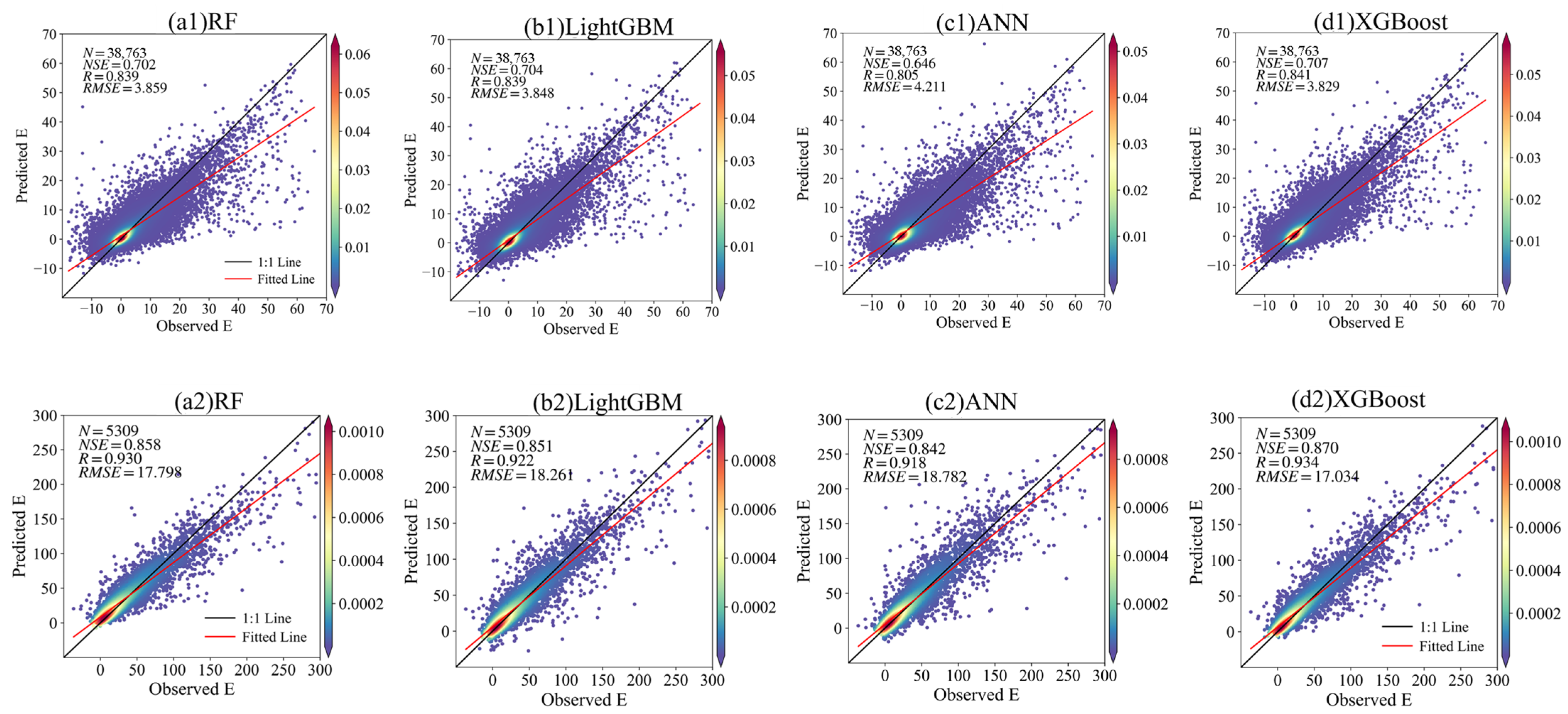
4.2. The Impact of Different Machine Learning Algorithms on ET Partitioning in the CRO Ecosystem
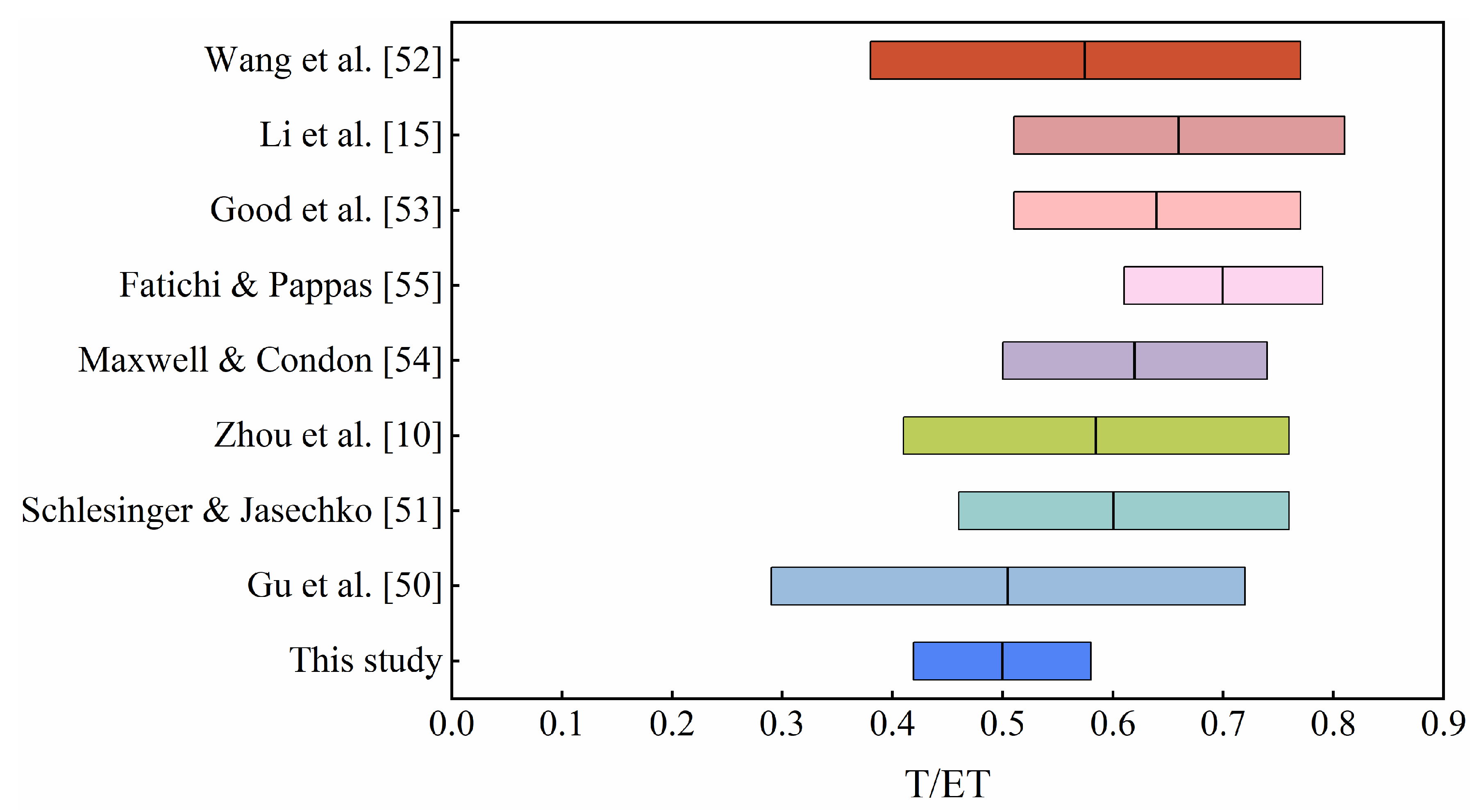
4.3. Comparison with Other ET Partitioning Methods
4.4. Controlling Factors of ET Partitioning
4.5. Implications and Limitations
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A

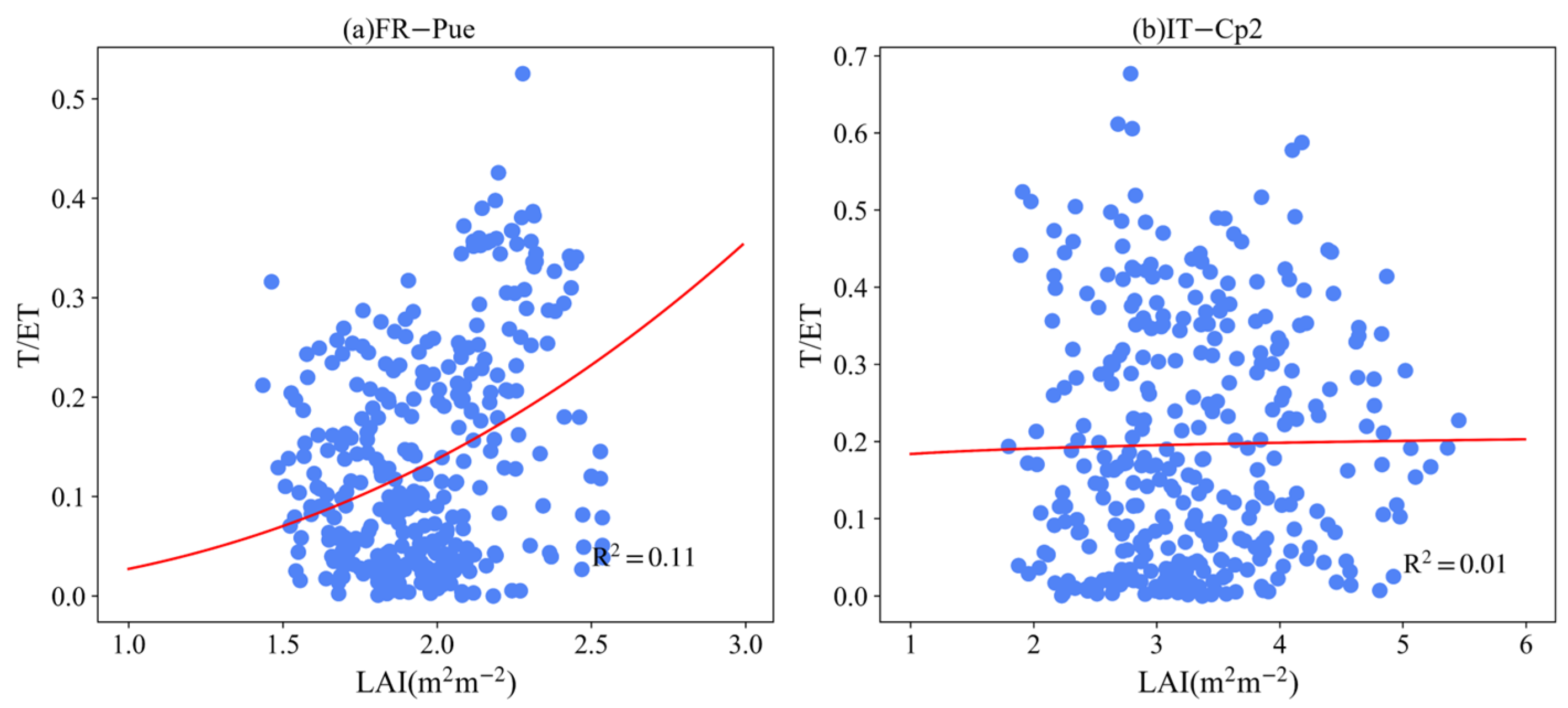
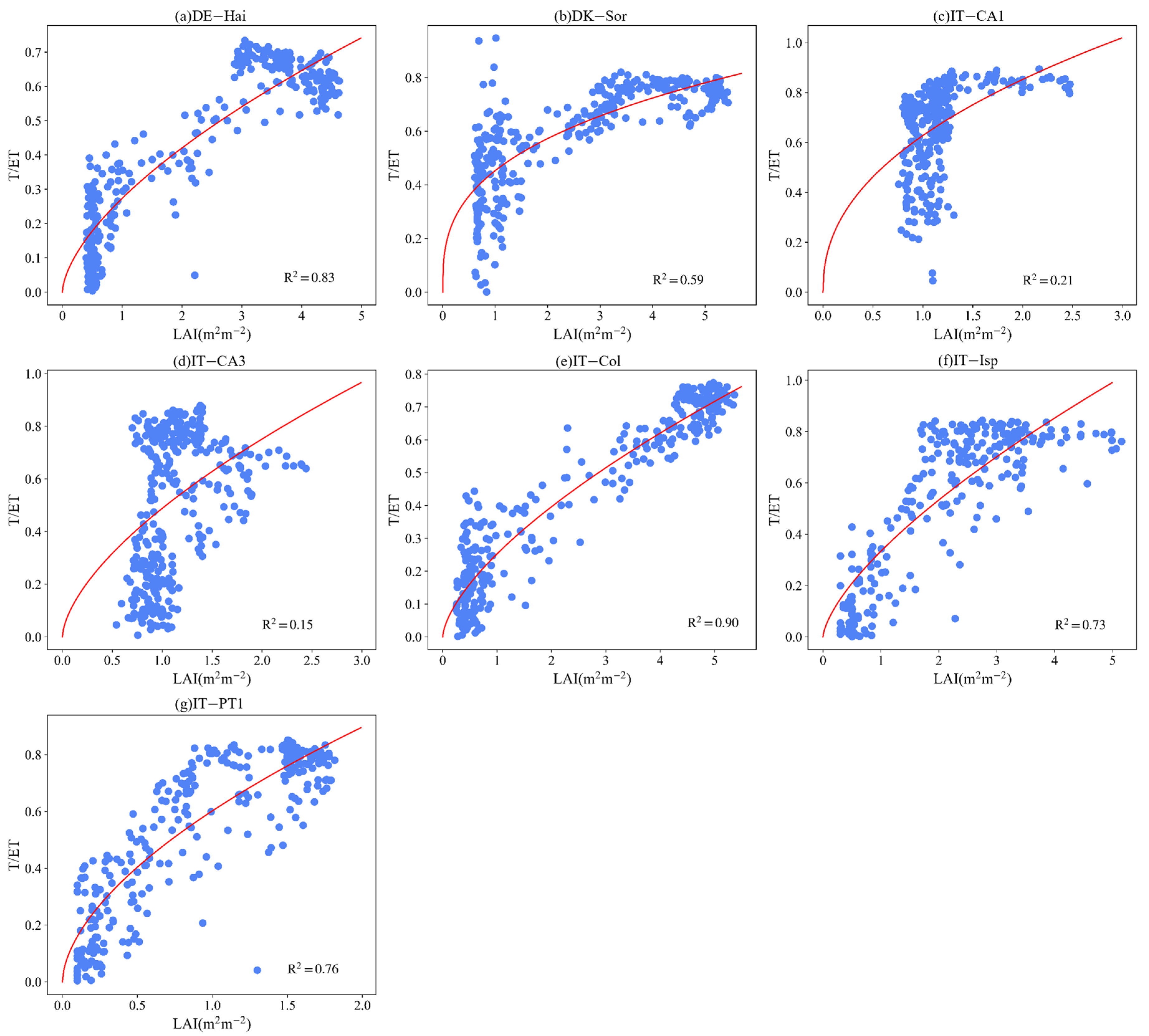

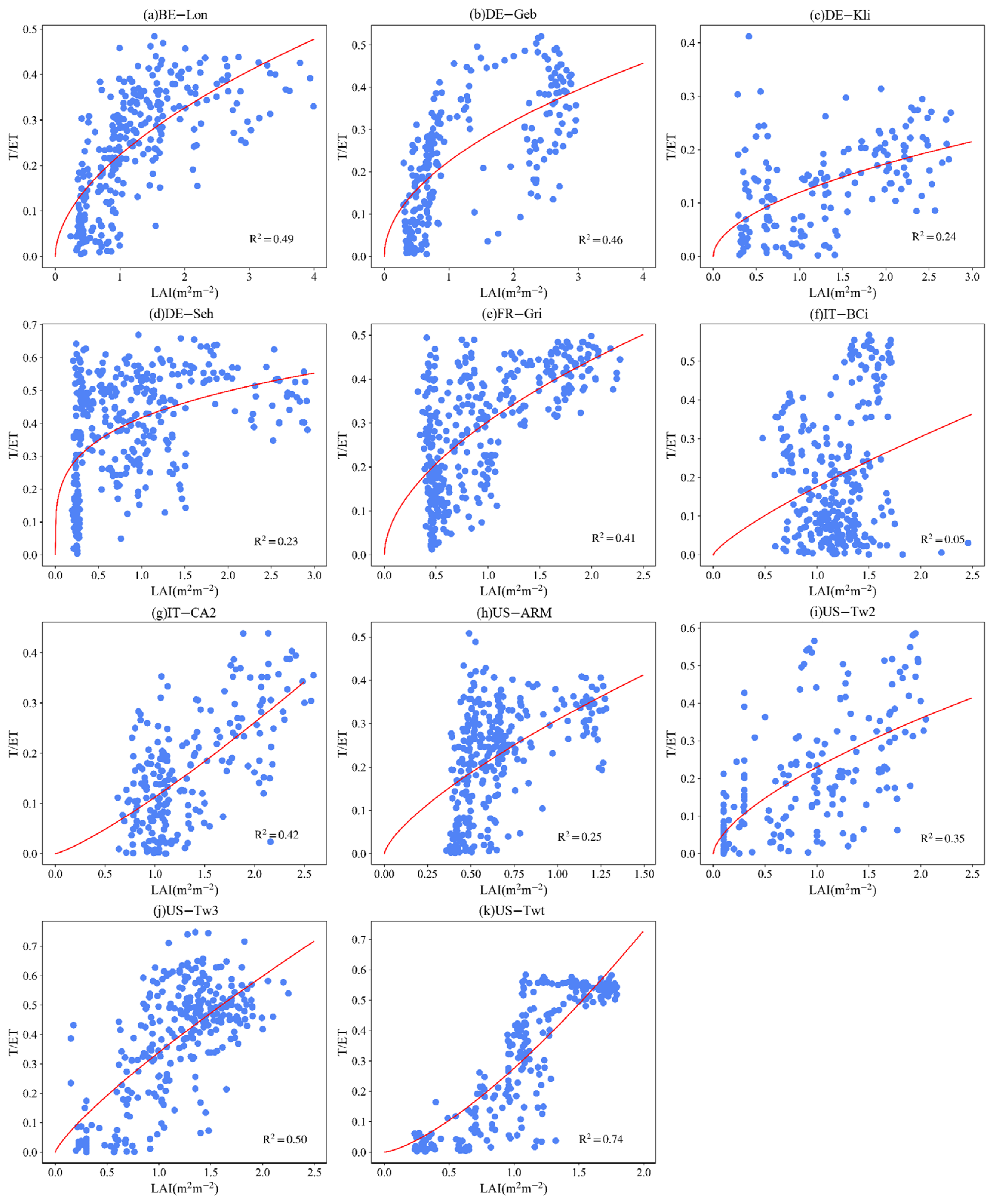

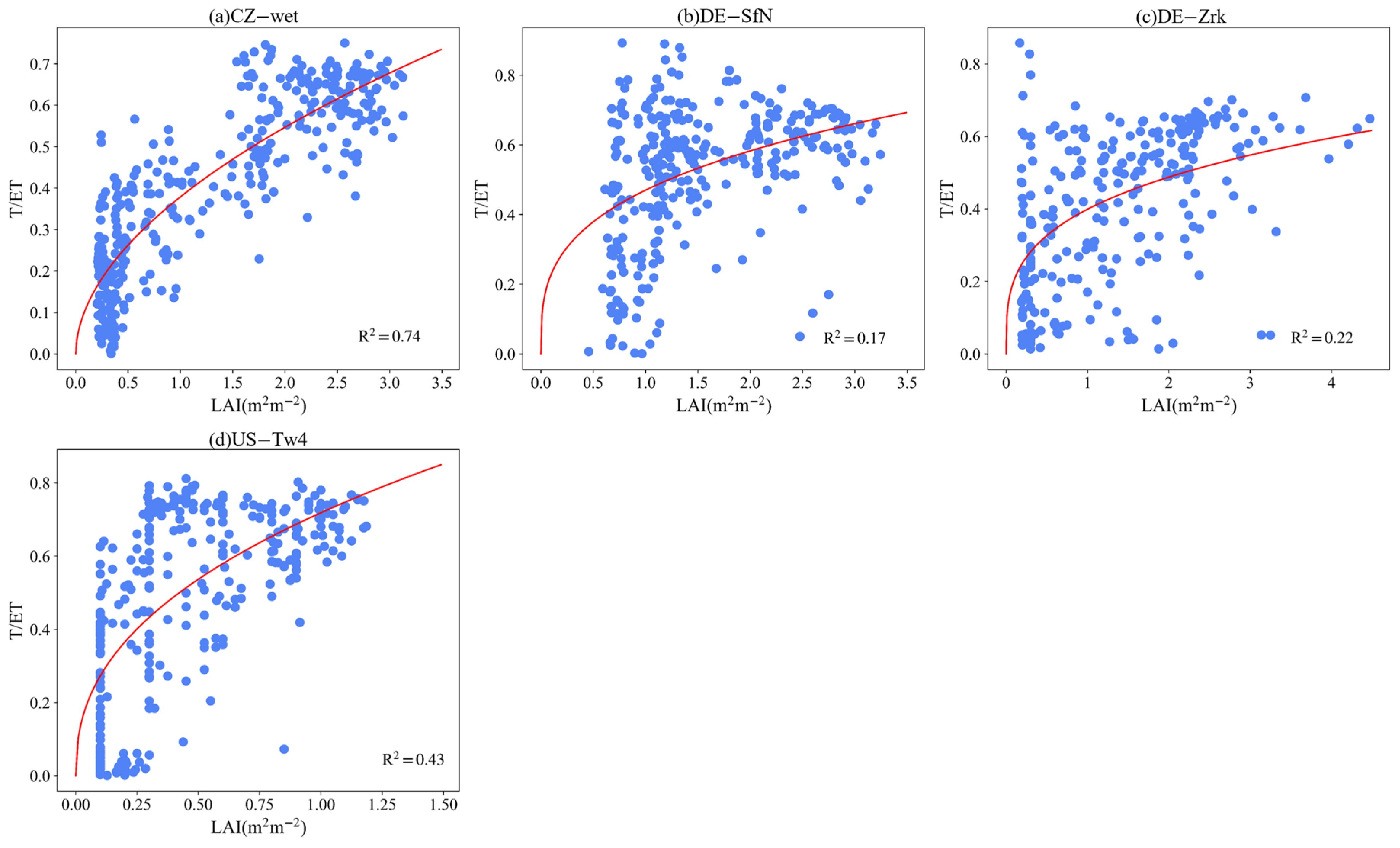



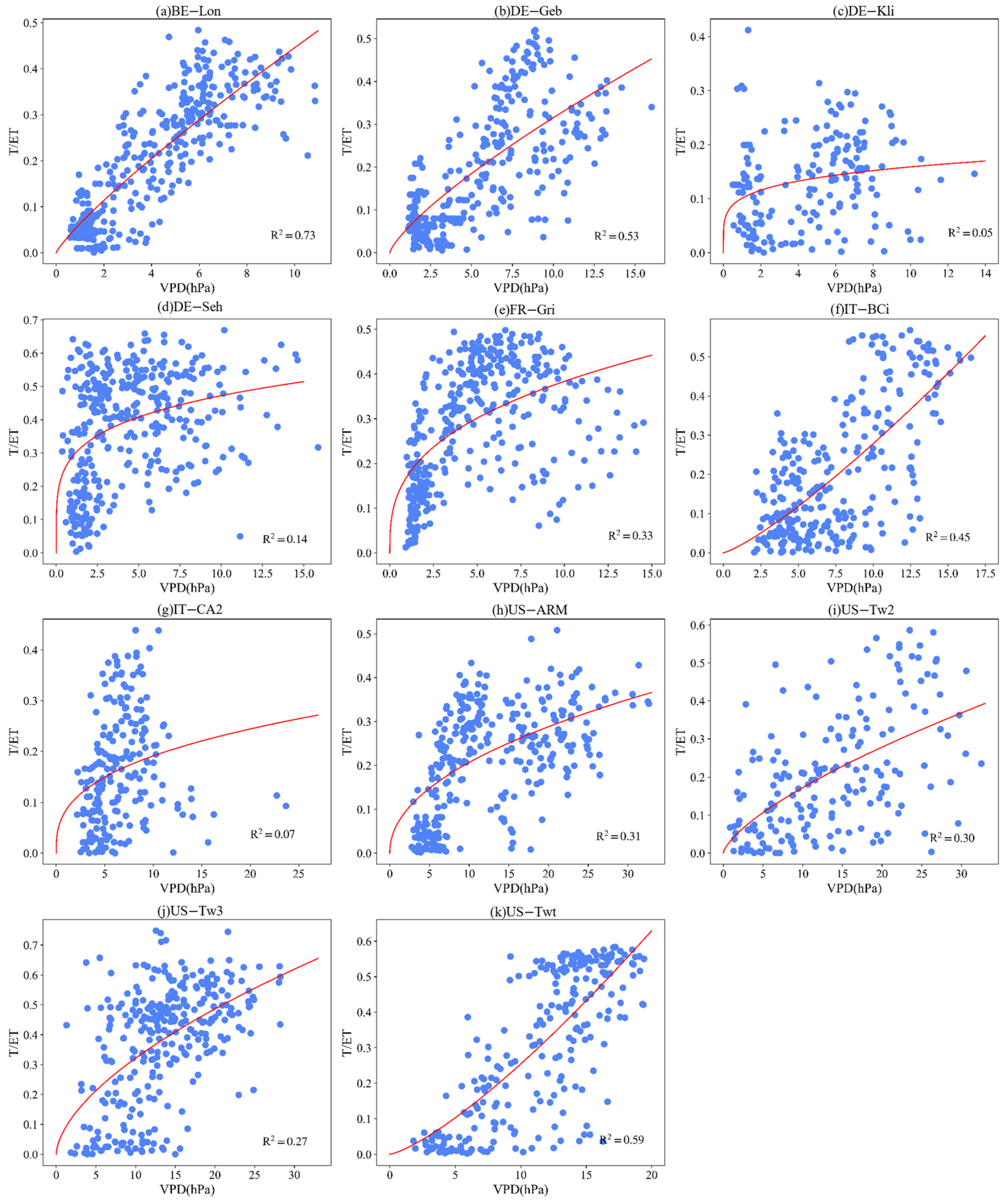
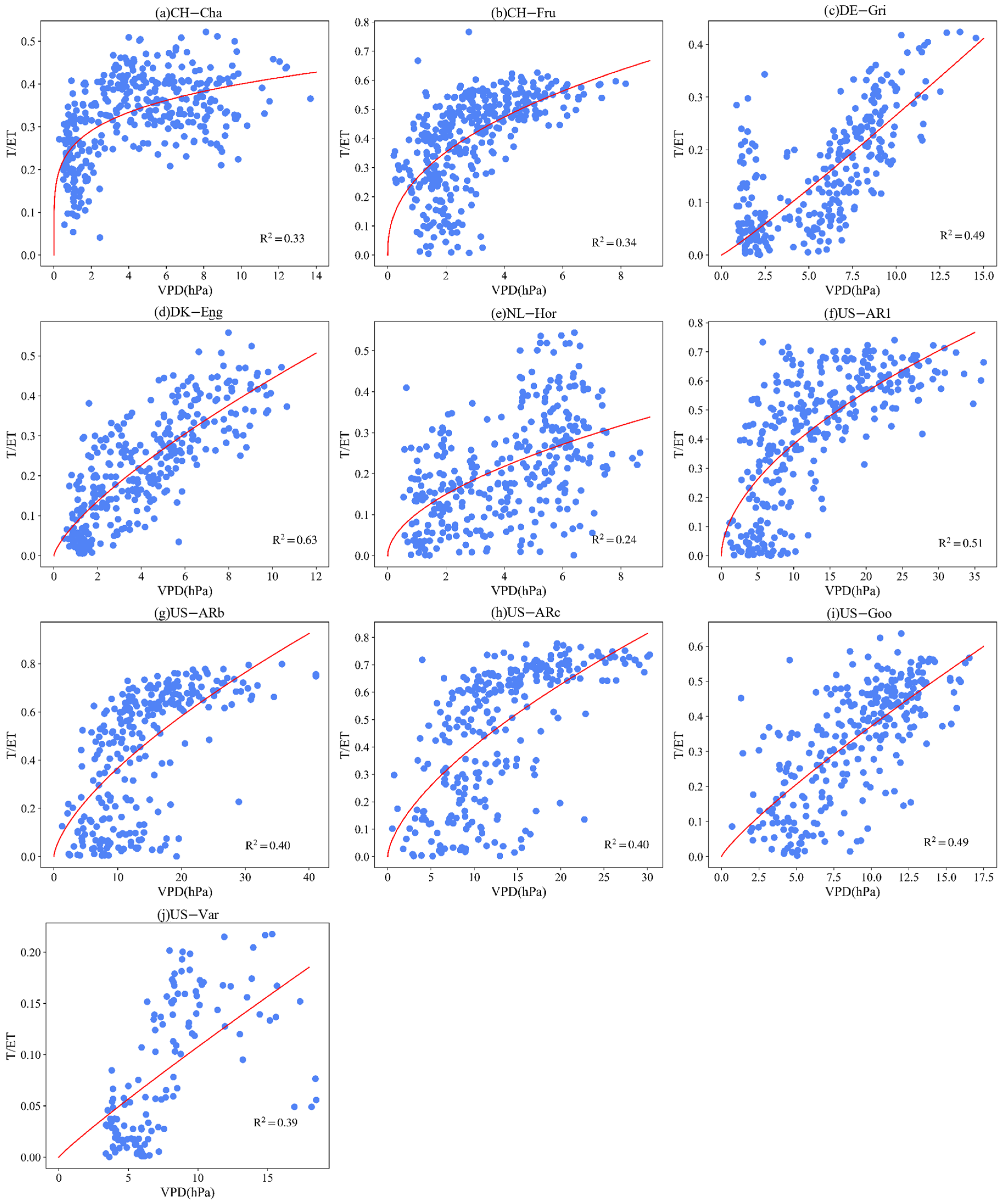

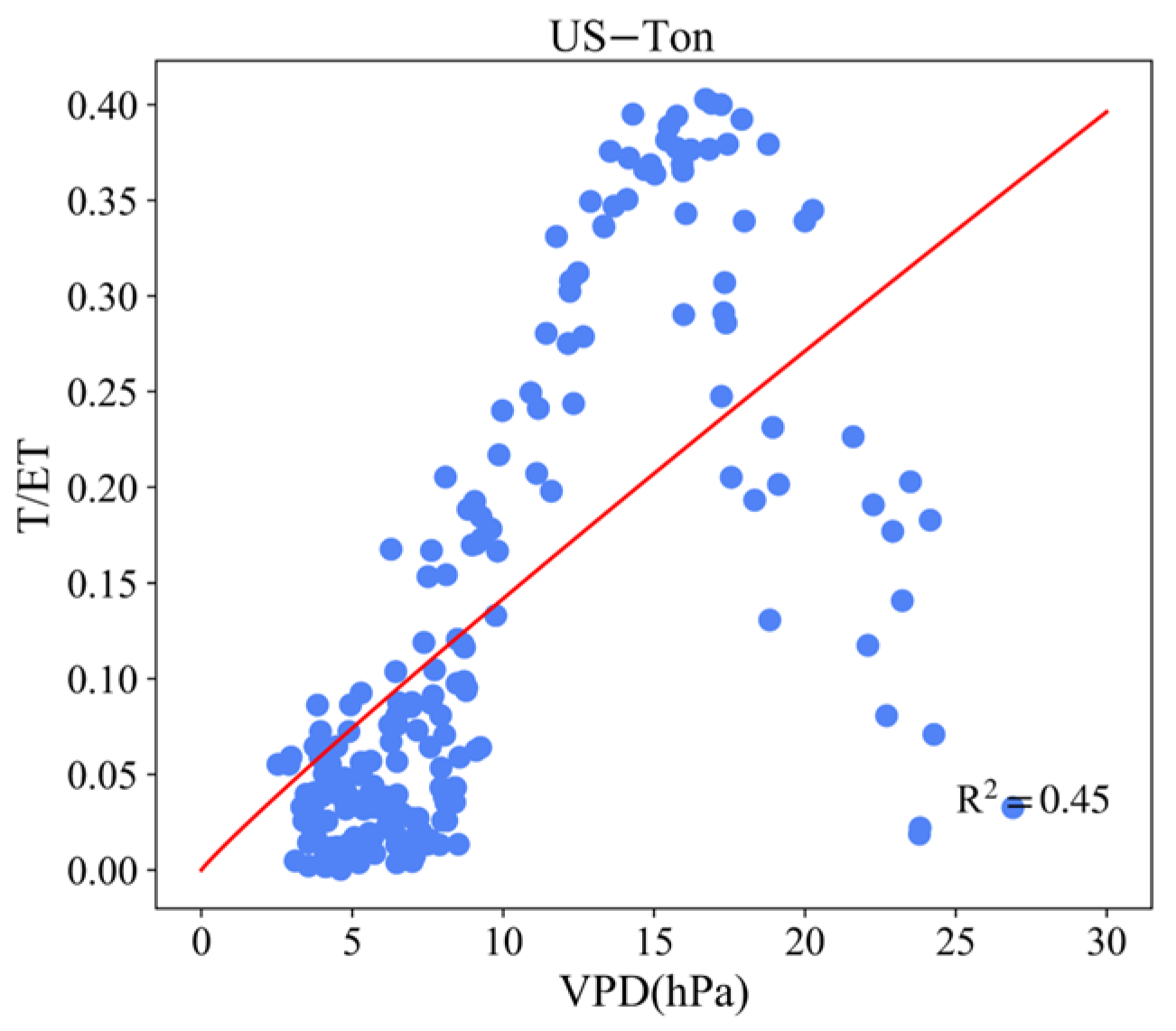

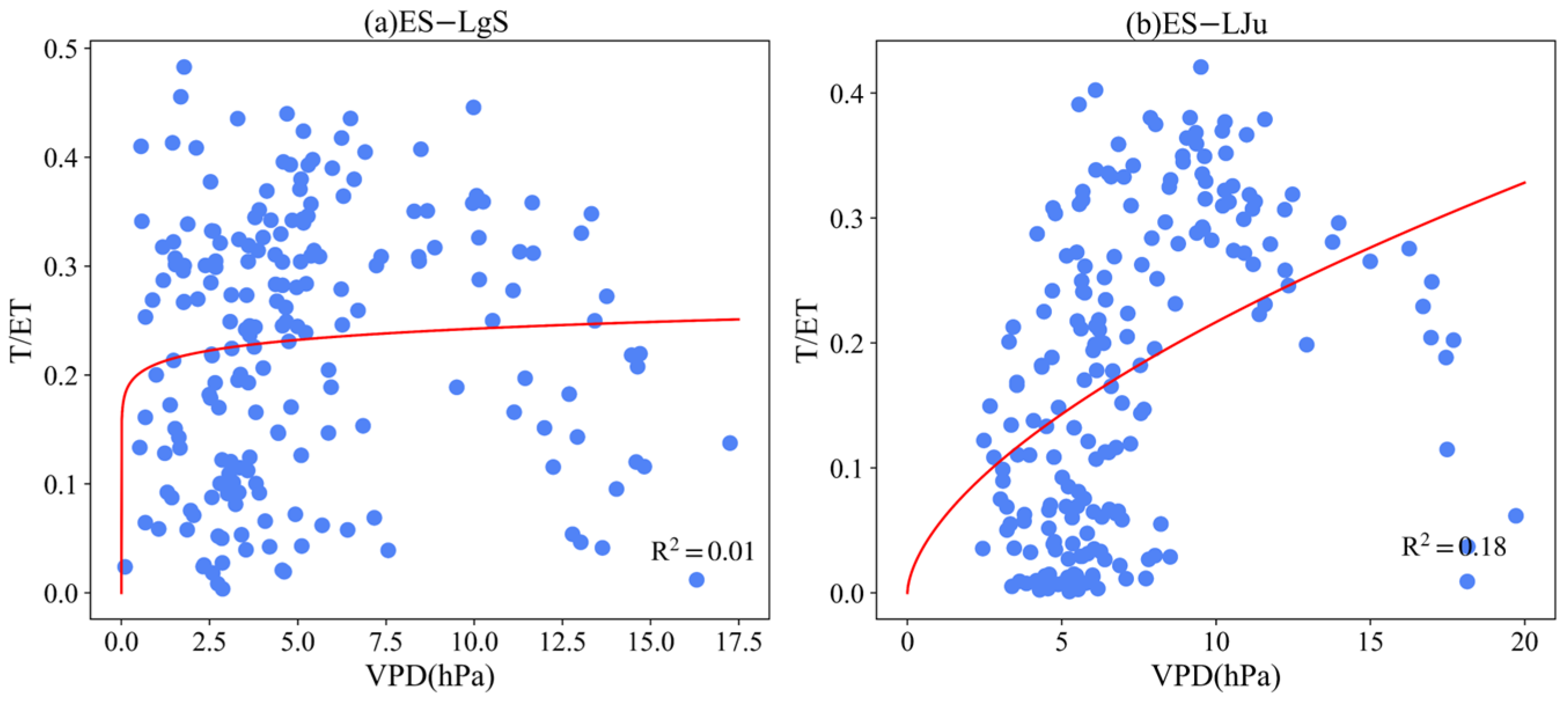
Appendix B
| Site ID | Latitude | Longitude | Ecosystem | Koppen Climate Classification | Years | Average T/ET |
|---|---|---|---|---|---|---|
| BE-Lon | 50.55 | 4.74 | CRO | Cf | 2004–2014 | 0.35 |
| DE-Geb | 51.1 | 10.91 | CRO | Cf | 2001–2014 | 0.44 |
| DE-Kli | 50.89 | 13.52 | CRO | Cf | 2004–2014 | 0.32 |
| DE-Seh | 50.87 | 6.45 | CRO | Cf | 2007–2010 | 0.43 |
| DK-Fou | 56.48 | 9.59 | CRO | Cf | 2005 | 0.49 |
| FR-Gri | 48.84 | 1.95 | CRO | Cf | 2004–2014 | 0.38 |
| US-ARM | 36.61 | −97.49 | CRO | Cf | 2003–2012 | 0.31 |
| ES-LgS | 37.1 | −2.97 | OSH | Cs | 2007–2009 | 0.39 |
| ES-LJu | 36.93 | −2.75 | OSH | Cs | 2004–2013 | 0.44 |
| US-KS2 | 28.61 | −80.67 | CSH | Cf | 2003–2006 | 0.50 |
| DE-Hai | 51.08 | 10.45 | DBF | Cf | 2000–2009 | 0.53 |
| DK-Sor | 55.49 | 11.65 | DBF | Cf | 2001–2009 | 0.63 |
| IT-Col | 41.85 | 13.59 | DBF | Cf | 2000–2014 | 0.60 |
| IT-Isp | 45.81 | 8.63 | DBF | Cf | 2013–2014 | 0.68 |
| IT-PT1 | 45.20 | 9.06 | DBF | Cf | 2002–2004 | 0.44 |
| DE-Lkb | 49.10 | 13.30 | ENF | Cf | 2009–2013 | 0.48 |
| DE-Obe | 50.79 | 13.72 | ENF | Cf | 2008–2014 | 0.43 |
| DE-Tha | 50.96 | 13.57 | ENF | Cf | 2000–2014 | 0.46 |
| FR-LBr | 44.72 | −0.77 | ENF | Cf | 2000–2008 | 0.49 |
| IT-Lav | 45.96 | 11.28 | ENF | Cf | 2003–2014 | 0.52 |
| NL-Loo | 52.17 | 5.74 | ENF | Cf | 2000–2014 | 0.46 |
| US-KS1 | 28.46 | −80.67 | ENF | Cf | 2002 | 0.54 |
| CH-Cha | 47.21 | 8.41 | GRA | Cf | 2005–2014 | 0.46 |
| CH-Fru | 47.12 | 8.54 | GRA | Cf | 2005–2014 | 0.50 |
| CN-HaM | 37.37 | 101.18 | GRA | Cf | 2002–2004 | 0.43 |
| DE-Gri | 50.95 | 13.51 | GRA | Cf | 2004–2014 | 0.53 |
| DK-Eng | 55.69 | 12.19 | GRA | Cf | 2005–2008 | 0.43 |
| NL-Hor | 52.24 | 5.07 | GRA | Cf | 2004–2011 | 0.48 |
| US-AR1 | 36.43 | −99.42 | GRA | Cf | 2009–2012 | 0.39 |
| US-ARb | 35.55 | −98.04 | GRA | Cf | 2005–2006 | 0.58 |
| US-ARc | 35.5465 | −98.04 | GRA | Cf | 2005–2006 | 0.65 |
| US-Goo | 34.25 | −89.87 | GRA | Cf | 2002–2006 | 0.49 |
| BE-Vie | 50.31 | 5.998 | MF | Cf | 2000–2014 | 0.59 |
| CZ-wet | 49.02 | 14.77 | WET | Cf | 2009–2014 | 0.47 |
| DE-SfN | 47.81 | 11.33 | WET | Cf | 2012–2014 | 0.52 |
| DE-Zrk | 53.88 | 12.89 | WET | Cf | 2013–2014 | 0.50 |
| IT-BCi | 40.52 | 14.96 | CRO | Cs | 2007–2012 | 0.40 |
| IT-CA2 | 42.38 | 12.03 | CRO | Cs | 2011–2014 | 0.41 |
| US-Tw2 | 38.10 | −121.64 | CRO | Cs | 2012–2013 | 0.40 |
| US-Tw3 | 38.12 | −121.65 | CRO | Cs | 2013–2014 | 0.50 |
| US-Twt | 38.11 | −121.65 | CRO | Cs | 2009–2014 | 0.33 |
| US-Ton | 38.43 | −120.97 | WSA | Cs | 2001–2014 | 0.35 |
| US-Var | 38.41 | −120.95 | WSA | Cs | 2000–2014 | 0.50 |
| IT-CA1 | 42.38 | 12.03 | DBF | Cs | 2011–2014 | 0.73 |
| IT-CA3 | 42.38 | 12.02 | DBF | Cs | 2011–2014 | 0.72 |
| FR-Pue | 43.74 | 3.60 | EBF | Cs | 2002–2014 | 0.41 |
| IT-Cp2 | 41.70 | 12.36 | EBF | Cs | 2012–2014 | 0.49 |
| IT-SR2 | 43.73 | 10.29 | ENF | Cs | 2013–2014 | 0.61 |
| IT-SRo | 43.73 | 10.28 | ENF | Cs | 2000–2010 | 0.56 |
| US-Me1 | 44.58 | −121.5 | ENF | Cs | 2004–2005 | 0.40 |
| US-Me2 | 44.45 | −121.56 | ENF | Cs | 2002–2014 | 0.48 |
| US-Me4 | 44.50 | −121.62 | ENF | Cs | 2000 | 0.57 |
| US-Me5 | 44.44 | −121.57 | ENF | Cs | 2000–2002 | 0.53 |
| US-Me6 | 44.32 | −121.61 | ENF | Cs | 2012–2014 | 0.37 |
| US-Tw4 | 38.10 | −121.64 | WET | Cs | 2013–2014 | 0.45 |
| Site ID | Crop Fallow Period |
|---|---|
| BE-Lon | 29 September 2004–12 November 2004, 3 August 2005–11 August 2005, 15 September 2006–21 September 2006, 5 August 2007–25 August 2007, 4 November 2008–12 January 2009, 7 August 2009–2 September 2009, 2 December 2009–9 December 2009, 5 September 2010–14 September 2010, 16 August 2011–24 August 2011, 13 October 2012–24 October 2012, 12 August 2013–23 August 2013, 15 November 2013–23 November 2013, 22 August 2014–13 September 2014 |
| DE-Geb | 16 January 2001–22 January 2001, 1 September 2001–18 October 2001, 12 August 2003–3 September 2003, 10 September 2004–20 September 2004, 23 August 2005–29 August 2005, 22 November 2005–7 December 2005, 20 April 2006–3 May 2006, 1 November 2006–16 November 2006, 29 August 2007–16 September 2007, 20 August 2008–11 September 2008, 15 October 2008–12 December 2008, 27 August 2009–1 September 2009, 24 September 2009–20 October 2009, 24 August 2010–10 September 2010, 15 November 2012–24 November 2012, 8 October 2013–15 October 2013, 19 August 2014–23 August 2014 |
| DK-Kli | 30 August 2005–27 September 2005, 24 October 2006–29 October 2006, 6 March 2007–12 March 2007, 26 April 2007–2 May 2007, 12 February 2008–29 April 2008, 25 August 2009–12 October 2010, 26 March 2012–2 May 2013, 25 September 2013–11 October 2013 |
| DK-Fou | 12 May 2005–24 May 2005 |
| FR-Gri | 31 December 2004–1 January 2005, 2 May 2005–9 May 2005, 28 September 2005–4 October 2005, 15 July 2006–17 July 2006, 29 June 2007–2 July 2007, 10 September 2008–21 September 2008, 30 July 2009–2 August 2009, 19 July 2010–23 July 2010, 3 August 2012–15 August 2012, 6 August 2013–9 August 2013, 5 August 2014–9 August 2014 |
| US-ARM | 25 July 2003–29 July 2003, 28 September 2003–1 October 2003, 19 May 2004–23 May 2004, 26 October 2005–30 October 2005, 21 June 2006–3 July 2006, 10 November 2006–14 November 2006, 25 September 2008–27 September 2008, 18 June 2009–20 June 2009, 26 September 2009–30 September 2009, 28 September 2010–30 September 2010, 15 June 2011–18 June 2011, 25 October 2011–29 October 2011, 21 May 2012–9 June 2012, 10 October 2012–15 October 2012 |
| IT-BCi | 2 December 2007–13 February 2008, 2 August 2008–7 September 2008, 18 November 2008–31 December 2008, 8 January 2009–18 February 2009, 2 August 2009–13 September 2009, 21 November 2009–23 December 2009, 1 January 2010–31 January 2010, 6 February 2010–18 February 2010, 2 August 2010–13 August 2010, 21 August 2010–1 September 2010, 14 September 2010–30 September 2010, 1 November 2010–9 November 2010, 11 December 2010–30 January 2011, 21 June 2011–2 August 2011, 15 October 2011–3 November 2011, 4 January 2012–11 February 2012, 1 November 2012–23 November 2012 |
| IT-CA2 | 22 October 2012–9 November 2012 |
| US-Twt | 4 April 2009–19 May 2009, 9 September 2009–21 September 2009, 4 October 2009–31 October 2009, 9 November 2009–26 November 2009, 1 January 2010–12 February 2010, 12 April 2010–7 May 2010, 21 October 2010–23 November 2010, 3 January 2011–24 February 2011, 20 April 2011–3 May 2011, 1 November 2011–30 December 2011, 15 March 2012–27 March 2012, 19 June 2012–30 June 2012, 3 November 2012–30 December 2012, 2 January 2013–16 February 2013, 5 February 2014–19 February 2014, 9 November 2014–31 December 2014 |
| Influencing Factors | Relative Contribution (%) | R2 |
|---|---|---|
| LAI | 22% | 27% |
| VPD | 5% |
References
- Jung, M.; Reichstein, M.; Ciais, P.; Seneviratne, S.I.; Sheffield, J.; Goulden, M.L.; Bonan, G.; Cescatti, A.; Chen, J.; De Jeu, R.; et al. Recent decline in the global land evapotranspiration trend due to limited moisture supply. Nature 2010, 467, 951–954. [Google Scholar] [CrossRef]
- Dorigo, W.; Dietrich, S.; Aires, F.; Brocca, L.; Carter, S.; Cretaux, J.F.; Dunkerley, D.; Enomoto, H.; Forsberg, R.; Güntner, A.; et al. Closing the water cycle from observations across scales: Where do we stand? Bull. Am. Meteorol. Soc. 2021, 102, E1897–E1935. [Google Scholar] [CrossRef]
- Trenberth, K.E.; Fasullo, J.T.; Kiehl, J. Earth’s global energy budget. Bull. Am. Meteorol. Soc. 2009, 90, 311–324. [Google Scholar] [CrossRef]
- Lian, X.; Piao, S.; Huntingford, C.; Li, Y.; Zeng, Z.; Wang, X.; Ciais, P.; McVicar, T.R.; Peng, S.; Ottlé, C.; et al. Partitioning global land evapotranspiration using CMIP5 models constrained by observations. Nat. Clim. Chang. 2018, 8, 640–646. [Google Scholar] [CrossRef]
- Baldocchi, D.D.; Ryu, Y. A Synthesis of Forest Evaporation Fluxes—From Days to Years—As Measured with Eddy Covariance. In Forest Hydrology and Biogeochemistry; Ecological Studies; Springer: Dordrecht, The Netherlands, 2011; pp. 101–116. [Google Scholar]
- Wen, X.; Yang, B.; Sun, X.; Lee, X. Evapotranspiration partitioning through in-situ oxygen isotope measurements in an oasis cropland. Agric. For. Meteorol. 2016, 230–231, 89–96. [Google Scholar] [CrossRef]
- Lu, X.; Liang, L.L.; Wang, L.; Jenerette, G.D.; McCabe, M.F.; Grantz, D.A. Partitioning of evapotranspiration using a stable isotope technique in an arid and high temperature agricultural production system. Agric. Water Manag. 2017, 179, 103–109. [Google Scholar] [CrossRef]
- Cammalleri, C.; Rallo, G.; Agnese, C.; Ciraolo, G.; Minacapilli, M.; Provenzano, G. Combined use of eddy covariance and sap flow techniques for partition of ET fluxes and water stress assessment in an irrigated olive orchard. Agric. Water Manag. 2013, 120, 89–97. [Google Scholar] [CrossRef]
- Scanlon, T.M.; Kustas, W.P. Partitioning carbon dioxide and water vapor fluxes using correlation analysis. Agric. For. Meteorol. 2010, 150, 89–99. [Google Scholar] [CrossRef]
- Zhou, S.; Yu, B.; Zhang, Y.; Huang, Y.; Wang, G. Partitioning evapotranspiration based on the concept of underlying water use efficiency. Water Resour. Res. 2016, 52, 1160–1175. [Google Scholar] [CrossRef]
- Niu, Z.; He, H.; Zhu, G.; Ren, X.; Zhang, L.; Zhang, K.; Yu, G.; Ge, R.; Li, P.; Zeng, N.; et al. An increasing trend in the ratio of transpiration to total terrestrial evapotranspiration in China from 1982 to 2015 caused by greening and warming. Agric. For. Meteorol. 2019, 279, 107701. [Google Scholar] [CrossRef]
- Cao, R.; Hu, Z.; Jiang, Z.; Yang, Y.; Zhao, W.; Wu, G.; Feng, X.; Chen, R.; Hao, G. Shifts in ecosystem water use efficiency on china’s loess plateau caused by the interaction of climatic and biotic factors over 1985–2015. Agric. For. Meteorol. 2020, 291, 108100. [Google Scholar] [CrossRef]
- Zhang, Y.; Kong, D.; Gan, R.; Chiew, F.H.S.; McVicar, T.R.; Zhang, Q.; Yang, Y. Coupled estimation of 500 m and 8-day resolution global evapotranspiration and gross primary production in 2002–2017. Remote Sens. Environ. 2019, 222, 165–182. [Google Scholar] [CrossRef]
- Zhou, K.; Zhang, Q.; Xiong, L.; Gentine, P. Estimating evapotranspiration using remotely sensed solar-induced fluorescence measurements. Agric. For. Meteorol. 2022, 314, 108800. [Google Scholar] [CrossRef]
- Li, X.; Gentine, P.; Lin, C.; Zhou, S.; Sun, Z.; Zheng, Y.; Liu, J.; Zheng, C. A simple and objective method to partition evapotranspiration into transpiration and evaporation at eddy-covariance sites. Agric. For. Meteorol. 2019, 265, 171–182. [Google Scholar] [CrossRef]
- Nelson, J.A.; Carvalhais, N.; Cuntz, M.; Delpierre, N.; Knauer, J.; Ogée, J.; Migliavacca, M.; Reichstein, M.; Jung, M. Coupling Water and Carbon Fluxes to Constrain Estimates of Transpiration: The TEA Algorithm. J. Geophys. Res. Biogeosci. 2018, 123, 3617–3632. [Google Scholar] [CrossRef]
- Liuyang, Y. Evapotranspiration Partitioning Based on Leaf and Ecosystem Water Use Efficiency. Agric. For. Meteorol. 2014, 184, 56–70. [Google Scholar] [CrossRef]
- Jung, M.; Reichstein, M.; Margolis, H.A.; Cescatti, A.; Richardson, A.D.; Arain, M.A.; Arneth, A.; Bernhofer, C.; Bonal, D.; Chen, J.; et al. Global patterns of land-atmosphere fluxes of carbon dioxide, latent heat, and sensible heat derived from eddy covariance, satellite, and meteorological observations. J. Geophys. Res. 2011, 116, G00J07. [Google Scholar] [CrossRef]
- Irvin, J.; Zhou, S.; McNicol, G.; Lu, F.; Liu, V.; Fluet-Chouinard, E.; Ouyang, Z.; Knox, S.H.; Lucas-Moffat, A.; Trotta, C.; et al. Gap-filling eddy covariance methane fluxes: Comparison of machine learning model predictions and uncertainties at FLUXNET-CH4 wetlands. Agric. For. Meteorol. 2021, 308–309, 108528. [Google Scholar] [CrossRef]
- Kim, Y.; Johnson, M.S.; Knox, S.H.; Black, T.A.; Dalmagro, H.J.; Kang, M.; Kim, J.; Baldocchi, D. Gap-filling approaches for eddy covariance methane fluxes: A comparison of three machine learning algorithms and a traditional method with principal component analysis. Glob. Chang. Biol. 2020, 26, 1499–1518. [Google Scholar] [CrossRef]
- Zhao, W.L.; Gentine, P.; Reichstein, M.; Zhang, Y.; Zhou, S.; Wen, Y.; Lin, C.; Li, X.; Qiu, G.Y. Physics-Constrained Machine Learning of Evapotranspiration. Geophys. Res. Lett. 2019, 46, 14496–14507. [Google Scholar] [CrossRef]
- Papale, D.; Valentini, R. A new assessment of European forests carbon exchanges by eddy fluxes and artificial neural network spatialization. Glob. Chang. Biol. 2003, 9, 525–535. [Google Scholar] [CrossRef]
- Tramontana, G.; Migliavacca, M.; Jung, M.; Reichstein, M.; Keenan, T.F.; Camps-Valls, G.; Ogee, J.; Verrelst, J.; Papale, D. Partitioning net carbon dioxide fluxes into photosynthesis and respiration using neural networks. Glob. Chang. Biol. 2020, 26, 5235–5253. [Google Scholar] [CrossRef]
- Eichelmann, E.; Mantoani, M.C.; Chamberlain, S.D.; Hemes, K.S.; Oikawa, P.Y.; Szutu, D.; Valach, A.; Verfaillie, J.; Baldocchi, D.D. A novel approach to partitioning evapotranspiration into evaporation and transpiration in flooded ecosystems. Glob. Chang. Biol. 2022, 28, 990–1007. [Google Scholar] [CrossRef]
- Whitley, R.; Medlyn, B.; Zeppel, M.; Macinnis-Ng, C.; Eamus, D. Comparing the Penman–Monteith equation and a modified Jarvis–Stewart model with an artificial neural network to estimate stand-scale transpiration and canopy conductance. J. Hydrol. 2009, 373, 256–266. [Google Scholar] [CrossRef]
- Xu, S.; Yu, Z.; Ji, X.; Sudicky, E.A. Comparing three models to estimate transpiration of desert shrubs. J. Hydrol. 2017, 550, 603–615. [Google Scholar] [CrossRef]
- Fan, J.; Zheng, J.; Wu, L.; Zhang, F. Estimation of daily maize transpiration using support vector machines, extreme gradient boosting, artificial and deep neural networks models. Agric. Water Manag. 2021, 245, 106547. [Google Scholar] [CrossRef]
- Pastorello, G.; Trotta, C.; Canfora, E.; Chu, H.; Christianson, D.; Cheah, Y.W.; Poindexter, C.; Chen, J.; Elbashandy, A.; Humphrey, M.; et al. Author Correction: The FLUXNET2015 dataset and the ONEFlux processing pipeline for eddy covariance data. Sci. Data 2021, 8, 72. [Google Scholar] [CrossRef]
- Knauer, J.; Zaehle, S.; Medlyn, B.E.; Reichstein, M.; Williams, C.A.; Migliavacca, M.; De Kauwe, M.G.; Werner, C.; Keitel, C.; Kolari, P.; et al. Towards physiologically meaningful water-use efficiency estimates from eddy covariance data. Glob. Chang. Biol. 2017, 24, 694–710. [Google Scholar] [CrossRef]
- Medlyn, B.E.; De Kauwe, M.G.; Lin, Y.S.; Knauer, J.; Duursma, R.A.; Williams, C.A.; Arneth, A.; Clement, R.; Isaac, P.; Limousin, J.M.; et al. How do leaf and ecosystem measures of water-use efficiency compare? New Phytol. 2017, 216, 758–770. [Google Scholar] [CrossRef]
- Chen, B.; Wang, P.; Wang, S.; Ju, W.; Liu, Z.; Zhang, Y. Simulating canopy carbonyl sulfide uptake of two forest stands through an improved ecosystem model and parameter optimization using an ensemble Kalman filter. Ecol. Model. 2023, 475, 110212. [Google Scholar] [CrossRef]
- Muñoz-Sabater, J.; Dutra, E.; Agustí-Panareda, A.; Albergel, C.; Arduini, G.; Balsamo, G.; Boussetta, S.; Choulga, M.; Harrigan, S.; Hersbach, H.; et al. ERA5-Land: A state-of-the-art global reanalysis dataset for land applications. Earth Syst. Sci. Data 2021, 13, 4349–4383. [Google Scholar] [CrossRef]
- Yang, S.; Zhang, J.; Zhang, S.; Wang, J.; Bai, Y.; Yao, F.; Guo, H. The potential of remote sensing-based models on global water-use efficiency estimation: An evaluation and intercomparison of an ecosystem model (BESS) and algorithm (MODIS) using site level and upscaled eddy covariance data. Agric. For. Meteorol. 2020, 287, 107959. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. Xgboost: A scalable tree boosting system. In Proceedings of the 22nd Acm Sigkdd International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Shin, H. XGBoost Regression of the Most Significant Photoplethysmogram Features for Assessing Vascular Aging. IEEE J. Biomed. Health Inf. 2022, 26, 3354–3361. [Google Scholar] [CrossRef]
- Liashchynskyi, P.; Liashchynskyi, P. Grid search, random search, genetic algorithm: A big comparison for NAS. arXiv 2019, arXiv:1912.06059. [Google Scholar]
- Fan, J.; Yue, W.; Wu, L.; Zhang, F.; Cai, H.; Wang, X.; Lu, X.; Xiang, Y. Evaluation of SVM, ELM and four tree-based ensemble models for predicting daily reference evapotranspiration using limited meteorological data in different climates of China. Agric. For. Meteorol. 2018, 263, 225–241. [Google Scholar] [CrossRef]
- Krause, P.; Boyle, D.; Bäse, F. Comparison of different efficiency criteria for hydrological model assessment. Adv. Geosci. 2005, 5, 89–97. [Google Scholar] [CrossRef]
- Yu, H.; Wen, X.; Li, B.; Yang, Z.; Wu, M.; Ma, Y. Uncertainty analysis of artificial intelligence modeling daily reference evapotranspiration in the northwest end of China. Comput. Electron. Agric. 2020, 176, 105653. [Google Scholar] [CrossRef]
- Stoy, P.C.; El-Madany, T.; Fisher, J.B.; Gentine, P.; Gerken, T.; Good, S.P.; Liu, S.; Miralles, D.G.; Perez-Priego, O.; Skaggs, T.H.; et al. Reviews and syntheses: Turning the challenges of partitioning ecosystem evaporation and transpiration into opportunities. Biogeosciences 2019, 16, 3747–3775. [Google Scholar] [CrossRef]
- Li, H.; Wu, Y.; Liu, S.; Xiao, J.; Meteorology, F. Regional contributions to interannual variability of net primary production and climatic attributions. Agric. For. Meteorol. 2021, 303, 108384. [Google Scholar] [CrossRef]
- Ding, Y.; Gong, X.; Xing, Z.; Cai, H.; Zhou, Z.; Zhang, D.; Sun, P.; Shi, H. Attribution of meteorological, hydrological and agricultural drought propagation in different climatic regions of China. Agric. Water Manag. 2021, 255, 106996. [Google Scholar] [CrossRef]
- Yao, Y.; Wang, X.; Li, Y.; Wang, T.; Shen, M.; Du, M.; He, H.; Li, Y.; Luo, W.; Ma, M.; et al. Spatiotemporal pattern of gross primary productivity and its covariation with climate in China over the last thirty years. Glob. Chang. Biol. 2018, 24, 184–196. [Google Scholar] [CrossRef]
- Fernández-Martínez, M.; Vicca, S.; Janssens, I.A.; Sardans, J.; Luyssaert, S.; Campioli, M.; Chapin, F.S., III; Ciais, P.; Malhi, Y.; Obersteiner, M.; et al. Nutrient availability as the key regulator of global forest carbon balance. Nat. Clim. Chang. 2014, 4, 471–476. [Google Scholar] [CrossRef]
- Cui, N.; Mei, X.; Gong, D.; Feng, Y. Estimation of maize evapotranspiration using extreme learning machine and generalized regression neural network on the China Loess Plateau. Hydrol. Res. 2017, 48, 1156–1168. [Google Scholar] [CrossRef]
- Tang, D.; Feng, Y.; Gong, D.; Hao, W.; Cui, N. Evaluation of artificial intelligence models for actual crop evapotranspiration modeling in mulched and non-mulched maize croplands. Comput. Electron. Agric. 2018, 152, 375–384. [Google Scholar] [CrossRef]
- Tu, J.; Wei, X.; Huang, B.; Fan, H.; Jian, M.; Li, W. Improvement of sap flow estimation by including phenological index and time-lag effect in back-propagation neural network models. Agric. For. Meteorol. 2019, 276–277, 107608. [Google Scholar] [CrossRef]
- Montesinos López, O.A.; Montesinos López, A.; Crossa, J. Overfitting, Model Tuning, and Evaluation of Prediction Performance. In Multivariate Statistical Machine Learning Methods for Genomic Prediction; Springer: Cham, Switzerland, 2022; pp. 109–139. [Google Scholar]
- Dokeroglu, T.; Deniz, A.; Kiziloz, H.E. A comprehensive survey on recent metaheuristics for feature selection. Neurocomputing 2022, 494, 269–296. [Google Scholar] [CrossRef]
- Gu, C.; Ma, J.; Zhu, G.; Yang, H.; Zhang, K.; Wang, Y.; Gu, C. Partitioning evapotranspiration using an optimized satellite-based ET model across biomes. Agric. For. Meteorol. 2018, 259, 355–363. [Google Scholar] [CrossRef]
- Schlesinger, W.H.; Jasechko, S. Transpiration in the global water cycle. Agric. For. Meteorol. 2014, 189–190, 115–117. [Google Scholar] [CrossRef]
- Wang, L.; Good, S.P.; Caylor, K.K. Global synthesis of vegetation control on evapotranspiration partitioning. Geophys. Res. Lett. 2014, 41, 6753–6757. [Google Scholar] [CrossRef]
- Good, S.P.; Noone, D.; Bowen, G. Hydrologic connectivity constrains partitioning of global terrestrial water fluxes. Science 2015, 349, 175–177. [Google Scholar] [CrossRef]
- Maxwell, R.M.; Condon, L.E. Connections between groundwater flow and transpiration partitioning. Science 2016, 353, 377–380. [Google Scholar] [CrossRef]
- Fatichi, S.; Pappas, C. Constrained variability of modeled T: ET ratio across biomes. Geophys. Res. Lett. 2017, 44, 6795–6803. [Google Scholar] [CrossRef]
- Chen, H.; Huang, J.J.; McBean, E. Partitioning of daily evapotranspiration using a modified shuttleworth-wallace model, random Forest and support vector regression, for a cabbage farmland. Agric. Water Manag. 2020, 228, 105923. [Google Scholar] [CrossRef]
- Moran, M.; Scott, R.; Keefer, T.; Emmerich, W.; Hernandez, M.; Nearing, G.; Paige, G.; Cosh, M.; O’Neill, P.E. Partitioning evapotranspiration in semiarid grassland and shrubland ecosystems using time series of soil surface temperature. Agric. For. Meteorol. 2009, 149, 59–72. [Google Scholar] [CrossRef]
- Raz-Yaseef, N.; Yakir, D.; Schiller, G.; Cohen, S. Dynamics of evapotranspiration partitioning in a semi-arid forest as affected by temporal rainfall patterns. Agric. For. Meteorol. 2012, 157, 77–85. [Google Scholar] [CrossRef]
- Hu, Z.; Yu, G.; Fu, Y.; Sun, X.; Li, Y.; Shi, P.; Wang, Y.; Zheng, Z. Effects of vegetation control on ecosystem water use efficiency within and among four grassland ecosystems in China. Glob. Chang. Biol. 2008, 14, 1609–1619. [Google Scholar] [CrossRef]
- Sun, X.; Wilcox, B.P.; Zou, C.B. Evapotranspiration partitioning in dryland ecosystems: A global meta-analysis of in situ studies. J. Hydrol. 2019, 576, 123–136. [Google Scholar] [CrossRef]
- Wei, Z.; Lee, X.; Wen, X.; Xiao, W.J.A.; Meteorology, F. Evapotranspiration partitioning for three agro-ecosystems with contrasting moisture conditions: A comparison of an isotope method and a two-source model calculation. Agric. For. Meteorol. 2018, 252, 296–310. [Google Scholar] [CrossRef]
- Cao, R.; Huang, H.; Wu, G.; Han, D.; Jiang, Z.; Di, K.; Hu, Z. Spatiotemporal variations in the ratio of transpiration to evapotranspiration and its controlling factors across terrestrial biomes. Agric. For. Meteorol. 2022, 321, 108984. [Google Scholar] [CrossRef]
- Schwärzel, K.; Zhang, L.; Montanarella, L.; Wang, Y.; Sun, G. How afforestation affects the water cycle in drylands: A process-based comparative analysis. Glob. Chang. Biol. 2020, 26, 944–959. [Google Scholar] [CrossRef]
- Beer, C.; Ciais, P.; Reichstein, M.; Baldocchi, D.; Law, B.E.; Papale, D.; Soussana, J.F.; Ammann, C.; Buchmann, N.; Frank, D.; et al. Temporal and among-site variability of inherent water use efficiency at the ecosystem level. Glob. Biogeochem. Cycles 2009, 23, 3233. [Google Scholar] [CrossRef]
- Nelson, J.A.; Pérez-Priego, O.; Zhou, S.; Poyatos, R.; Zhang, Y.; Blanken, P.D.; Gimeno, T.E.; Wohlfahrt, G.; Desai, A.R.; Gioli, B.; et al. Ecosystem transpiration and evaporation: Insights from three water flux partitioning methods across FLUXNET sites. Glob. Chang. Biol. 2020, 26, 6916–6930. [Google Scholar] [CrossRef]
- Scott, R.L.; Biederman, J.A. Partitioning evapotranspiration using long-term carbon dioxide and water vapor fluxes. Geophys. Res. Lett. 2017, 44, 6833–6840. [Google Scholar] [CrossRef]
- Stoy, P.C.; Mauder, M.; Foken, T.; Marcolla, B.; Boegh, E.; Ibrom, A.; Arain, M.A.; Arneth, A.; Aurela, M.; Bernhofer, C.; et al. A data-driven analysis of energy balance closure across FLUXNET research sites: The role of landscape scale heterogeneity. Agric. For. Meteorol. 2013, 171, 137–152. [Google Scholar] [CrossRef]

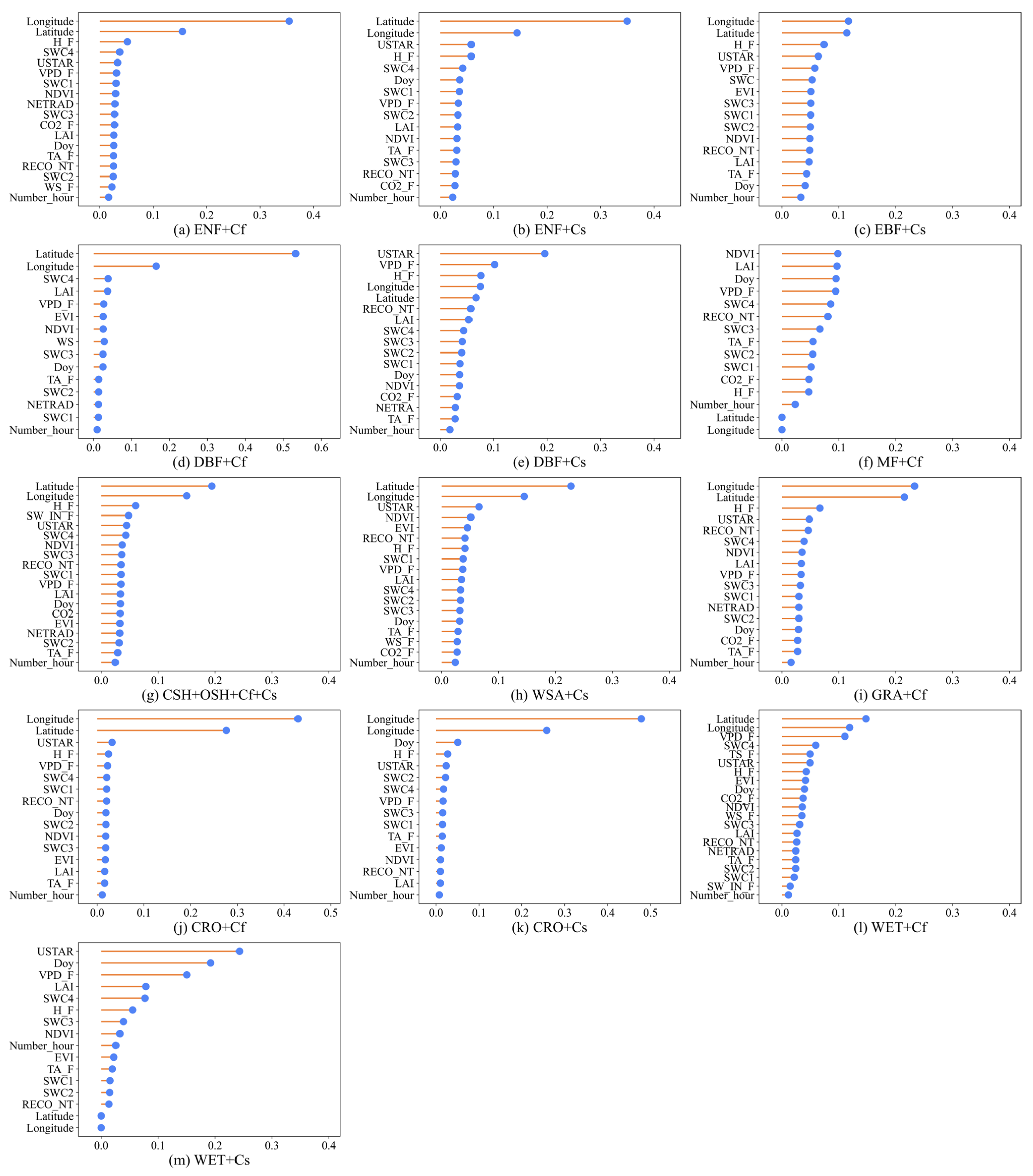


| Ecosystems | Climatic Type | n_estimators | max_depth | Subsample | min_child_weight |
|---|---|---|---|---|---|
| ENF | Cf | 490 | 120 | 0.5 | 9 |
| Cs | 430 | 130 | 0.7 | 7 | |
| EBF | Cs | 500 | 167 | 0.3 | 3 |
| DBF | Cf | 225 | 100 | 0.5 | 9 |
| Cs | 261 | 127 | 0.9 | 4 | |
| MF | Cf | 720 | 10 | 0.7 | 4 |
| CSH + OSH | Cf + Cs | 685 | 65 | 0.5 | 9 |
| WSA | Cs | 969 | 301 | 0.5 | 9 |
| GRA | Cf | 766 | 40 | 0.6 | 9 |
| CRO | Cf | 439 | 31 | 0.4 | 5 |
| Cs | 989 | 85 | 0.6 | 6 | |
| WET | Cf | 935 | 10 | 0.7 | 5 |
| Cs | 943 | 12 | 0.6 | 6 |
| Ecosystems | Climatic Type | Combination of Variables |
|---|---|---|
| ENF | Cf | Longitude, Latitude, H, SWC4, USTAR, VPD, SWC1, NDVI, NETRAD, SWC3, CO2, LAI, Doy, TA, RECO_NT, SWC2, WS, Number_hour |
| Cs | Longitude, Latitude, USTAR, H, SWC4, Doy, SWC1, VPD, SWC2, LAI, NDVI, TA, SWC3, RECO_NT, CO2, Number_hour | |
| EBF | Cs | Longitude, Latitude, H, USTAR, VPD, SWC4, EVI, SWC3, SWC1, SWC2, NDVI, RECO_NT, LAI, TA, Doy, Number_hour |
| DBF | Cf | Longitude, Latitude, SWC4, WS_F, VPD, EVI, NDVI, LAI, SWC3, Doy, TA, SWC2, NETRAD, SWC1, Number_hour |
| Cs | USTAR, VPD, H, Longitude, Latitude, RECO_NT, LAI, SWC4, SWC3, SWC2, SWC1, Doy, NDVI, CO2, NETRAD, TA, Number_hour | |
| MF | Cf | NDVI, VPD, Doy, TA, SWC4, RECO_NT, SWC3, LAI, SWC2, SWC1, CO2, H, Number_hour, Longitude, Latitude |
| CSH + OSH | Cf + Cs | Latitude, Longitude, H, SW_IN, USTAR, SWC4, NDVI, SWC3, RECO_NT, SWC1, VPD, LAI, Doy, CO2, EVI, NETRAD, SWC2, TA, Number_hour |
| WSA | Cs | Latitude, Longitude, USTAR, NDVI, EVI, RECO_NT, H, SWC1, VPD, LAI, SWC4, SWC2, SWC3, Doy, TA, WS, CO2, Number_hour |
| GRA | Cf | Latitude, Longitude, H, USTAR, RECO, SWC4, NDVI, VPD, LAI, SWC3, SWC1, NETRAD, SWC2, Doy, CO2, TA, Number_hour |
| CRO | Cf | Longitude, Latitude, USTAR, H, VPD, SWC4, SWC1, RECO_NT, Doy, SWC2, NDVI, SWC3, EVI, LAI, TA, Number_hour |
| Cs | Longitude, Latitude, Doy, H, USTAR, SWC2, SWC4, VPD, SWC3, SWC1, TA, EVI, NDVI, RECO_NT, LAI, Number_hour | |
| WET | Cf | Latitude, Longitude, VPD, SWC4, TS, USTAR, H, EVI, Doy, CO2, NDVI, WS, SWC3, LAI, RECO_NT, NETRAD, TA, SWC2, SWC1, SW_IN, Number_hour |
| Cs | USTAR, Doy, VPD, H, SWC4, LAI, SWC3, NDVI, Number_hour, EVI, TA, SWC1, SWC2, RECO_NT, Latitude, Longitude |
| Ecosystems | Climatic Type | Training | Validation | Testing | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| NSE | R | RMSE | NSE | R | RMSE | NSE | R | RMSE | ||
| CRO | Cf | 0.970 | 0.986 | 1.235 | 0.694 | 0.822 | 4.039 | 0.707 | 0.841 | 3.829 |
| Cs | 0.990 | 0.994 | 0.240 | 0.834 | 0.912 | 7.854 | 0.887 | 0.942 | 6.870 | |
| DBF | Cf | 0.807 | 0.923 | 4.448 | 0.434 | 0.618 | 7.743 | 0.452 | 0.673 | 7.542 |
| Cs | 0.991 | 0.994 | 0.783 | 0.703 | 0.826 | 4.263 | 0.754 | 0.870 | 3.995 | |
| ENF | Cf | 0.953 | 0.976 | 3.059 | 0.583 | 0.739 | 8.637 | 0.615 | 0.785 | 8.286 |
| Cs | 0.972 | 0.983 | 2.544 | 0.558 | 0.742 | 7.852 | 0.590 | 0.769 | 7.620 | |
| MF | Cf | 0.925 | 0.964 | 1.105 | 0.624 | 0.776 | 2.414 | 0.654 | 0.809 | 2.284 |
| WET | Cf | 0.976 | 0.994 | 1.164 | 0.682 | 0.816 | 3.981 | 0.718 | 0.847 | 3.878 |
| Cs | 0.990 | 0.993 | 1.263 | 0.902 | 0.939 | 12.713 | 0.916 | 0.957 | 12.564 | |
| GRA | Cf | 0.947 | 0.982 | 2.397 | 0.643 | 0.801 | 6.211 | 0.660 | 0.814 | 6.053 |
| EBF | Cs | 0.862 | 0.946 | 2.541 | 0.403 | 0.634 | 5.368 | 0.431 | 0.657 | 5.057 |
| CSH + OSH | Cf + Cs | 0.894 | 0.963 | 3.029 | 0.401 | 0.627 | 7.304 | 0.414 | 0.643 | 6.984 |
| WSA | Cs | 0.961 | 0.980 | 0.991 | 0.532 | 0.718 | 3.551 | 0.547 | 0.740 | 3.443 |
| Ecosystem | Climatic Type | Growing Season Validation | Fallow Period Validation | ||||
|---|---|---|---|---|---|---|---|
| NSE | R | RMSE | NSE | R | RMSE | ||
| CRO | Cf | 0.707 | 0.841 | 3.829 | 0.870 | 0.934 | 17.034 |
| CRO | Cs | 0.887 | 0.942 | 6.870 | 0.813 | 0.902 | 25.339 |
| Ecosystem | This Study | Published Studies |
|---|---|---|
| ENF | 0.53 ± 0.08 | Zhou et al. [10] (0.59 ± 0.06) |
| Schlesinger and Jasechko et al. [51] (0.55 ± 0.15) | ||
| DBF | 0.68 ± 0.11 | Schlesinger and Jasechko et al. [51] (0.67 ± 0.14) |
| GRA | 0.50 ± 0.10 | Zhou et al. [10] (0.56 ± 0.05) |
| Schlesinger and Jasechko et al. [51] (0.57 ± 0.19) | ||
| CRO | 0.40 ± 0.08 | Zhou et al. [10] (0.53–0.75) |
| Li et al. [15] (0.62 ± 0.16) | ||
| Gu et al. [50] reported a mean value of 0.39 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, L.; Zhang, D.; Zhang, J.; Zhang, J.; Zhang, S.; Bai, Y.; Yang, S. Ecosystem Evapotranspiration Partitioning and Its Spatial–Temporal Variation Based on Eddy Covariance Observation and Machine Learning Method. Remote Sens. 2023, 15, 4831. https://doi.org/10.3390/rs15194831
Lu L, Zhang D, Zhang J, Zhang J, Zhang S, Bai Y, Yang S. Ecosystem Evapotranspiration Partitioning and Its Spatial–Temporal Variation Based on Eddy Covariance Observation and Machine Learning Method. Remote Sensing. 2023; 15(19):4831. https://doi.org/10.3390/rs15194831
Chicago/Turabian StyleLu, Linjun, Danwen Zhang, Jie Zhang, Jiahua Zhang, Sha Zhang, Yun Bai, and Shanshan Yang. 2023. "Ecosystem Evapotranspiration Partitioning and Its Spatial–Temporal Variation Based on Eddy Covariance Observation and Machine Learning Method" Remote Sensing 15, no. 19: 4831. https://doi.org/10.3390/rs15194831
APA StyleLu, L., Zhang, D., Zhang, J., Zhang, J., Zhang, S., Bai, Y., & Yang, S. (2023). Ecosystem Evapotranspiration Partitioning and Its Spatial–Temporal Variation Based on Eddy Covariance Observation and Machine Learning Method. Remote Sensing, 15(19), 4831. https://doi.org/10.3390/rs15194831







