Abstract
As rainfall exhibits high spatiotemporal variability, accurate and real-time rainfall monitoring is vitally important in fields such as hydrometeorological research, agriculture and disaster prevention and control. Nevertheless, the current dedicated rain sensors cannot fulfill the requirement for comprehensive precipitation observation, owing to their respective limitations. Within the last two decades, the utilization of commercial microwave links (CMLs) for rainfall estimation, as an opportunistic sensing method, has generated considerable attention. Relying on CML networks deployed and maintained by mobile network operators can provide near-surface precipitation information over large areas at a low cost. Although scholars have developed several algorithms for obtaining rainfall estimates from CML data, the rainfall estimation technique based on CMLs remains challenging due to the complex effect in the microwave radiation transmission process. In this paper, we provide a comprehensive review of the technical principles, developments and workflows for this technology, alongside its application in environmental monitoring and hydrological modeling. Furthermore, this paper outlines the current challenges and future research directions, which will hopefully draw the attention of researchers and provide valuable guidance.
1. Introduction
1.1. Background
Precipitation, as one of the most significant links in the Earth’s water cycle, is intimately associated with people’s lives. The spatial and temporal heterogeneity of precipitation development is the main cause of natural disasters such as droughts, floods and mudslides [1]. Accurate monitoring of precipitation has significant implications in fields such as agriculture, hydrometeorological research and water resource management.
Currently, meteorological operations mainly rely on rain gauges, weather radar and meteorological satellites to measure precipitation. However, due to the inherent limitations of these dedicated rain sensors, quantitative precipitation products still cannot satisfy the requirements of comprehensive meteorological observations, especially as global warming may lead to more extreme precipitation events [2]. Rain gauges, which are believed to provide point measurements of surface rainfall, are unsuitable for constructing a monitoring network due to their low spatial representativeness. In addition, wind and splash effects introduce uncertainties in its measurement [3]. Contrary to rain gauges, based on the statistical power–law relationship between the radar reflectivity Z and the rain rate R, weather radar allows for quantitative precipitation estimation (QPE) over large areas. However, the parameters of the Z–R relationship are highly sensitive to the raindrop size distribution (DSD) associated with precipitation types, geographical locations and climatic characteristics, which may cause large systematic biases [4]. Other uncertainty sources include ground clutter, beam blockage, bright bands and the vertical variability of the precipitation system [5]. As meteorological satellite technology matures, satellites can measure precipitation almost globally, which is especially important in areas where radar and rain gauges are not available [6]. However, subject to low spatial and temporal resolution, satellite products are not available for small-scale hydrological applications, such as catchment modeling in urban and mountainous areas. Moreover, although several satellite-based rainfall inversion algorithms have been developed [7,8], the accuracy of their estimates still needs to be improved [9].
Consequently, the concept of opportunistic rainfall measurement methods emerged, and the potential of devices such as commercial microwave links (CMLs) [10], personal weather stations [11], vehicle windscreen wipers [12] and street cameras [13] has been successively explored. These methods can provide additional precipitation information and promise to improve dedicated precipitation products, with CMLs being one that has the most prospective application. Based on existing CML networks built and maintained by mobile network operators, it can provide alternative precipitation observations in a cost-effective manner in areas lacking rain sensors [14] or additional precipitation information in areas with existing rainfall observations to enhance the spatial and temporal resolution as well as the accuracy of precipitation products [15,16].
1.2. The Principle and Development of Rainfall Estimation by CMLs
CMLs typically provide line-of-sight wireless backhaul connectivity for cellular communication networks, as well as serving as infrastructure for services such as smart cities. As shown in Figure 1, CMLs transmit microwave signals which carry data information between two cell towers to achieve message communication at two locations. Currently, the operating frequencies of CMLs mainly range from 15 to 40 GHz and are extending to the E-band due to the demand for higher bandwidth. In these frequencies, where the wavelengths are comparable to the size of the raindrop particles, the microwave signals are significantly attenuated by scattering and absorption. Considering the rainfall at location x on the path, the specific rain-induced attenuation γ(x) (dB·km−1) at that location can be calculated as:
where Qext(D, f, T) (m2) is the extinction cross section of a raindrop particle of size D (mm), which is related to the signal frequency f (GHz) and raindrop temperature T (K). Nx(D) (m−3·mm−1), i.e., the DSD function, is the number concentration of raindrop particles of size D at location x. Meanwhile, according to the definition of rain rate, the rain rate R(x) (mm·h−1) at this location can be expressed as:
where V(D) (m·s−1) is the falling velocity of a raindrop of size D. Since both γ(x) and R(x) are functions of Nx(D), the relationship between the two can be deduced. The theoretical calculation results show that the relationship between γ and R approximates a power–law form [17]:
where a (mm−b·hb·dB·km−1) and b (dimensionless) are the power–law parameters, which are associated with frequency, polarization and, to a lesser extent, with DSD [18,19] (compared to the Z–R relationship). The total attenuation A (dB) of a CML of length L (km) due to rainfall on the path can be obtained by integrating γ(x) over the path:
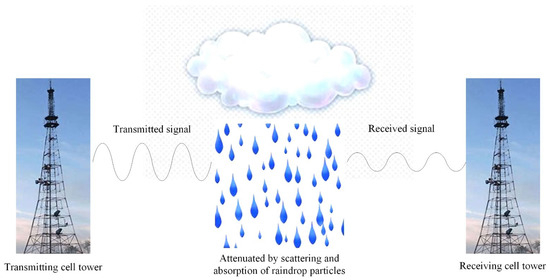
Figure 1.
The basic principle of estimating rainfall using CMLs. CMLs typically connect two cell towers and carry information via microwave signals to enable data exchange between the two locations. When rainfall occurs on the CML path, the received signal is significantly attenuated due to scattering and absorption of the wave by raindrop particles. The path-averaged rain rate can be retrieved based on the power–law relationship between rain rate and rain-induced attenuation.
Then, the specific rain-induced attenuation over the entire CML path can be expressed as:
Substitute Equation (3) into (5) to obtain an estimate of the path-averaged rain rate, with the real path-averaged rain rate shown by Equation (7):
Figure 2 presents the scatter plot of CML rainfall estimates versus real rain rates at different frequencies and rainfall types. It can be seen that the deviation between the CML rain rate and the real rain rate is much larger for frequencies outside of 22 to 38 GHz. Comparing the path-averaged rain rate, , with , it is straightforward to realize that the two are equal only if b approximates unity or R(x) is nearly constant. This means that taking into account the spatial variability of rainfall, only CMLs operating within 20 to 40 GHz are suitable for rainfall estimation. However, in the last century, the low frequency of prevalent CMLs was not applicable for monitoring rainfall. This is reflected in the insensitivity of the microwave signal to rainfall on the one hand, and due to the inherent error between the rainfall estimate and the path-averaged rain rate on the other. In addition, it is too expensive to deploy a dedicated microwave link rainfall monitoring network compared to radar-based regional measurements. As a result, studies 20 years ago were mainly limited to dedicated experimental microwave links. Based on a multi-band dual-polarized microwave link of the Tropical Rainfall Measuring Mission (TRMM), Rincon et al. [20] demonstrated the validity of the power–law relationship for rainfall estimation; subsequently, scientists further found that estimating rain rate using dual-frequency differential attenuation has a higher stability than single-frequency does [21,22,23,24].
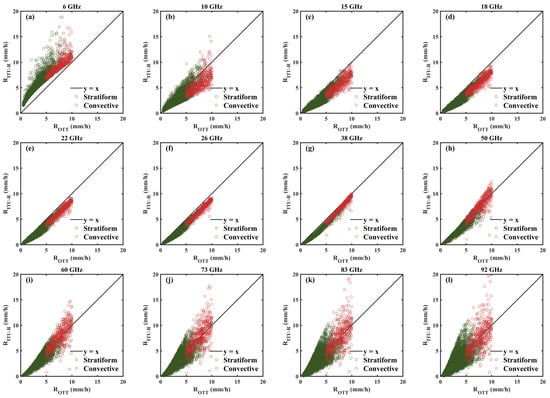
Figure 2.
Two-dimensional scatter plots obtained from real rain rates and rain rates inverted by the γ–R relation at frequencies (a) 6 GHz, (b) 10 GHz, (c) 15 GHz, (d) 18 GHz, (e) 22 GHz, (f) 26 GHz, (g) 38 GHz, (h) 50 GHz, (i) 60 GHz, (j) 73 GHz, (k) 83 GHz and (l) 92 GHz. It is worth noting that the real rain rates are obtained from an OTT Parsivel disdrometer deployed in Nanjing, whereas the CML-based rain rates are simulatively calculated using the T-matrix algorithm based on the γ–R relationship and the DSD data recorded by the disdrometer. The rainfall types are identified using the disdrometer data according to the classification criteria proposed in [25]. (Reprinted with permission from Pu et al., 2023. Copyright 2023 IEEE).
The landmark breakthrough in this technology occurred around 2006. As we enter the 21st century, the growing demand for wireless network terminals, such as cellphones, has led to a dramatic increase in the number of CMLs with operating frequencies ranging from 20 to 40 GHz. The mobile network operators who installed and maintained these CMLs have established an adequate infrastructure for monitoring rainfall using CMLs. As a result, the large quantity of CMLs that are otherwise used for communications can be used as opportunistic sensors, and the signal impairments that are undesirable to telecommunication engineers instead become an additional source of rainfall information.
In Israel, Messer et al. [10] used CMLs to estimate rainfall for the first time and compared them with rain gauges and radar, demonstrating the potential of CMLs. Almost simultaneously, a rainfall inversion experiment in the Netherlands [26] also suggested that CMLs could be an effective complement to radar QPE. Later, experimental studies on the estimation of rainfall using CMLs have successively been carried out in France [27], Germany [28], Switzerland [29,30], the Czech Republic [31], Italy [32], Brazil [33], China [34,35], Sri Lanka [36], some countries in Africa [37,38,39], etc., as shown in Figure 3.
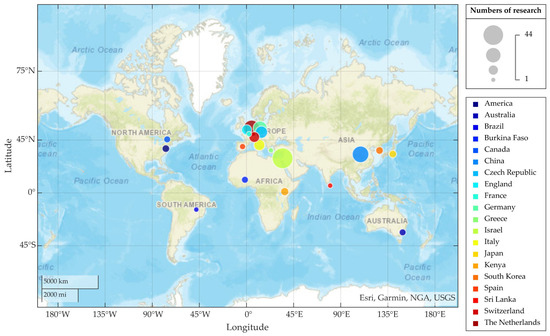
Figure 3.
World map with the main countries that have researched rainfall measurement techniques based on CMLs. Notably, Antarctica and the Arctic have been omitted from the figure. In addition, the number of research is based on the references in this paper, which may not fully encompass all published studies but can reflect the approximate distribution.
This paper provides a detailed overview of the techniques for rainfall estimation based on CMLs, in contrast to previous review articles [40,41,42,43], with the aim of providing a comprehensive introduction to readers new to the field and offering researchers our view of current challenges and future research directions for the technique. The rest of this paper is organized as follows: Section 2 details the processes involved in obtaining rainfall estimates from the attenuation information of the CMLs. Other applications of CMLs as opportunistic sensors are discussed in Section 3. Section 4 summarizes the current challenges. In Section 5 we present possible future directions. Section 6 provides a conclusion and outlook.
2. Procedures in Deriving Rainfall Maps from Attenuation
When the path of CMLs is exposed to rainfall, additional attenuation of the microwave signal occurs accordingly. However, these attenuation increments are not entirely due to scattering and absorption by raindrop particles. Phenomena such as electronic component drift, changes in water vapor, multipath effects, and wet antenna effects can also lead to changes in signal quality. Deriving rainfall estimates from CML attenuation is, therefore, a sophisticated process, which is described in detail in this section.
2.1. Classification of Dry and Wet Periods
As mentioned above, phenomena other than or triggered by rainfall may also cause signal impairment. Therefore, when we obtain attenuation data for CMLs, typically the transmitted signal level (TSL) minus the received signal level (RSL), the first critical issue is to determine at each timestamp whether the CMLs are affected by rainfall. More simply, the CML data need to be classified into dry (rain free) and wet (rainy) periods. In order to accomplish the classification of dry and wet periods, scholars have developed a variety of methods, which can be broadly divided into three categories.
The first category is based on the analysis of attenuation sequences to determine whether rainfall exists on the path of CMLs. The simplest way to distinguish between dry and wet periods is based on a global threshold for attenuation, with periods above the threshold being treated as wet [44]. Rahimi et al. [23] found that RSL sequences of dual-frequency microwave links are highly correlated during wet periods and suggested setting correlation thresholds to distinguish between dry and wet periods. Further, Overeem et al. [45] extended the spatial correlation of rainfall from individual CMLs to all CMLs within a certain range and proposed the so-called nearby link approach (NLA). They considered a time period as wet if the RSLs of at least half of the CMLs in the range decreased simultaneously during that time period. In addition, Schleiss et al. [27] found significant differences in the local variability of signal attenuation between dry and wet periods and proposed the use of a rolling window to calculate the standard deviation of the attenuation sequence to identify dry and wet periods based on a predetermined threshold. Recently, Graf et al. [46] proposed an improved version of this algorithm, arguing that the threshold can depend on the fluctuating trend of individual CMLs rather than only on climatology. Based on the short-time Fourier transform of the RSL sequence, Chwala et al. [28] found that the normalized amplitude difference between low and high frequencies of the power spectrum can be used to determine the dry and wet periods.
The second category of classification methods relies on dedicated rainfall observations in the vicinity of CMLs. As near-surface rainfall measurement instruments, rain gauges are widely used to achieve dry/wet period classification for CMLs [47,48]. In the literature [49], considering the elevation angle of the radar, if the path-averaged rain rate of the radar QPE is greater than 0.1 mm/h, the current and subsequent time steps are regarded as wet periods. Kumah et al. [50,51] utilized Meteosat Second Generation satellites to check for the presence of rain areas in the path of CMLs.
The last category is data-driven approaches based on machine learning. Thanks to the massive data, they can derive hidden feature information to explore patterns of signal fluctuations and apply them to dry and wet period classification. Reller et al. [52] demonstrated the applicability of a factor graph-based quasi-periodic signal model for dry and wet period classification. The literature [53,54] reported cases where Markov models were employed to determine dry and wet periods. In addition, dry/wet classification based on the multifamily likelihood ratio test [55] and the kernel Fisher discriminant analysis [56] have been attempted. Subsequently, time-delay neural networks [57], long short-term memory neural networks (LSTM) [58,59], support vector machines (SVM) [60] and convolutional neural networks (CNN) [61] are also used for dry and wet period identification for CMLs. In [62], the dry and wet period classification performance of several machine learning models was compared and the ensemble machine learning classifier was recommended as the preferred one. Additional information on existing dry and wet period classification algorithms can be found in Table 1.

Table 1.
Existing techniques for dry and wet period classification.
2.2. Determination of Baseline
After the classification of dry and wet periods, the wet period attenuation cannot be used directly for rainfall inversion; instead, the baseline attenuation (also known as the zero-level attenuation), which consists mainly of free-space losses and gas attenuation, needs to be removed from the wet period attenuation. Considering the generally short duration of rainfall, a common assumption is that factors affecting baseline attenuation may differ little between the wet period and the preceding dry period. Thus, the baseline can be set as the most recent dry period attenuation prior to rainfall [23] or the average dry period attenuation over a period of time before and after the rainfall event [64] and kept constant during the wet period. However, a constant baseline during the wet period may be impractical. To reflect the variability of the baseline during the wet period, Upton et al. [48] linearly interpolated the dry period attenuation at both ends of the rainfall event to determine the baseline. Fenicia et al. [65] compared a single-parameter baseline model based on a low-pass linear filter with a constant baseline model and found the former to have superior performance. Based on the temporal distribution of rainfall, the baseline can also be estimated as the median of all dry period attenuation over a long period prior to the wet period [45].
Furthermore, some baseline estimation algorithms have been developed that do not require dry and wet period classification. Assuming that the rain rate is a random process, Ostrometzky et al. [66] demonstrated that information about the baseline is hidden in the minimum attenuation and suggested using a sliding window to estimate the baseline. For the median attenuation method described above, the baseline can be estimated as the median of all attenuations by utilizing a sufficiently large window without the need for dry/wet classification because the window can contain more dry-period samples [45,47].
2.3. Wet Antenna Attenuation (WAA) Correction
Rainfall not only scatters and absorbs microwaves, but other phenomena associated with it, such as increased water vapor, decreased temperature and antenna wetting, can lead to additional attenuation that cannot be eliminated by the baseline. Considering that attenuation due to temperature and water vapor variations is typically one to two orders of magnitude smaller than rain-induced attenuation (with the possible exception of the water vapor absorption band around 22 GHz), these can generally be ignored. However, the water film covering antennas can change the antenna’s directivity, efficiency and reflectivity [67], introducing additional attenuation up to a few dB. The lack of correction for wet antenna attenuation (WAA) has been shown to lead to a significant overestimation of rainfall estimates based on CMLs [26].
In order to eliminate the effect of WAA, an exponential model related to the measured attenuation was proposed by Kharadly et al. [68]. Later, based on the fact that measured attenuation consists of path attenuation and WAA, the literature [69] extended the exponential WAA model to link it to path attenuation. Leijnse et al. [70] assumed a power–law relationship between the water film thickness and the rain rate and calculated the WAA based on the water film thickness and electromagnetic scattering theory. Some studies [71] also treated WAA directly as a function of rain rate. Overeem et al. [49] suggested ignoring the process of antenna wetting and drying and treating WAA as constant. On the contrary, long antenna drying and wetting processes have also been observed, and time-dependent dynamic WAA models have been proposed [29,72]. Pastorek et al. [73] compared the above empirical models and found that the WAA model, which is directly related to the rain rate, performs better, and that because the parameters of the model are independent of the CML frequency and path length, it is portable to CMLs with similar antenna characteristics. In the absence of rainfall observations, Fencl et al. [74] suggest that WAA can be quantified by using short CMLs, or, if short CMLs are not available, by statistics from CMLs and rainfall climatology. On the basis of the analysis of WAA time series, the LSTM algorithm [75] has also been applied to WAA estimation. In addition, since WAA is mainly related to antenna reflectivity, Moroder et al. [76] have developed a microwave measurement system that can measure attenuation and WAA simultaneously, which may present opportunities for WAA correction.
2.4. Calibration of the γ–R Relationship and Rainfall Estimation
For the coefficients a and b in the relationship between specific rain-induced attenuation and rain rate, the International Telecommunication Union Recommendations (ITU-R) [77] provide a reliable reference in the absence of microphysical information for rainfall. However, the ITU-R model, as a statistical model fitted from global data, has been found to potentially perform sub-optimally in localized areas in several reports [78,79,80,81,82]. As shown in Figure 4, for the Nanjing area, the ITU-R model would significantly overestimate rainfall under high rain rate conditions compared to the local γ–R relationship. Therefore, based on T-matrix or the Mie scattering theory, some scholars have also utilized DSD data to fit power–law parameters appropriate to the local climate. Using data from the disdrometer deployed in Nanjing, China, Song et al. [83] estimated rainfall using the improved γ–R relationship. The study concluded that the results are more accurate than the ITU-R model and highlighted the significance of establishing the local γ–R relationship. Han et al. [84] then fit the power–law relationship for stratiform and convective rainfall separately, demonstrating superior performance over the ITU–R relationship.
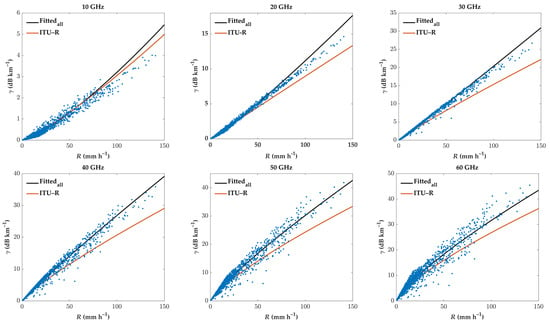
Figure 4.
Scatter plots of specific rain-induced attenuation and rain rates at different frequencies. It is worth noting that the rain rates are obtained from an OTT Parsivel disdrometer deployed in Nanjing, whereas the specific rain-induced attenuations are simulated using the T-matrix algorithm based on the DSD data recorded by the disdrometer.
After calibration of the power–law relationship, the path-averaged rain rate can be estimated based on Equations (4) and (6):
2.5. Rainfall Mapping
Although line-integrated rainfall observations are certainly valuable for many hydrometeorological studies and applications, the need to provide the spatial distribution of rainfall, i.e., generate rainfall maps from the estimations of CMLs, is more necessary. The simplest approach is to treat the CMLs as virtual rain gauges located at their midpoint location [45]. However, such an assumption is not reasonable given the heterogeneity of rainfall over the path of long-distance CMLs. Therefore, Goldshtein et al. [85] proposed an iterative algorithm to represent CML measurements using multiple data points along the path. Several studies [86,87] compared the two strategies and found that the dominance of the latter is positively correlated with the spatial variability of rainfall. Then, spatial interpolation techniques such as inverse distance weighting (IDW) and ordinary kriging (OK) can be employed to reconstruct sparse rainfall estimates to continuous spatial distribution. Eshel et al. [88] quantitatively analyzed the performance of different interpolation algorithms. The results showed the OK algorithm, which uses more priori information, performs slightly better than IDW. More sophisticated algorithms that consider rainfall inhomogeneity over the paths of CMLs include tomographic analysis techniques [32,89,90], the block kriging type approach [91], stochastic reconstruction algorithms [92,93] and the compressed sensing theory [94,95,96,97]. Furthermore, the literature [98] reported that CMLs can provide information on the spatial structure of rainfall fields and that the error in the estimation of the spatial autocorrelation function is only 5%.
3. Other Applications
3.1. Environmental Monitoring Other Than Rainfall Estimation
Due to the interaction of microwaves with the atmosphere during transmission, the signals of CMLs carry atmospheric environmental information. On the basis of electromagnetic theory, considering the absorption bands of different atmospheric variables separately, CMLs can theoretically invert atmospheric variables for the purpose of environmental monitoring.
3.1.1. Monitoring Phenomena Related to Water Vapor
The method of monitoring water vapor using CMLs that are operating at the water vapor absorption band around 22 GHz was first proposed by David et al. [99], whereas Chwala et al. [100] and Montomoli et al. [101] also suggested the use of phase delay and normalized differential spectral attenuation to measure absolute humidity, respectively. Subsequently, Alpert et al. [102] generated daily moisture fields in Israel, and the results were in better agreement with ground-based observations than the current weather prediction product. With the expansion of microwave frequencies, the potential of E-band CMLs to monitor near-surface water vapor was demonstrated in [103]. In addition, deep learning methods have also been applied to water vapor estimation by CMLs. Song et al. [104] trained an SVM model using prior data from RSL and water vapor density to mitigate the estimation error introduced by the process of extracting water vapor attenuation from RSL. Pu et al. [105] achieved high temporal resolution (5-min) water vapor retrieval based on E-band CMLs using an LSTM deep learning model. More studies using CMLs for water vapor estimation can be found in the literature [106,107,108,109]. In addition to these, CMLs have been shown to be valid in recognizing and measuring fog [110,111,112] and dew [113].
3.1.2. DSD Estimation
Assuming that the DSD follows a gamma distribution, Rincon et al. [21] and Berne et al. [114] estimated the average DSD over the path using dual-frequency and dual-polarized microwave links, respectively, which was in good agreement with the reference measurements. However, the above studies simplify the three-parameter model of DSD by setting a fixed shape parameter in the former and defining the slope parameter as a function of the shape parameter in the latter. This may lead to inherent errors in the algorithm. Therefore, a three-parameter estimation model for DSD based on dual-frequency, dual-polarized CMLs has been proposed in the literature [115]. Van Leth et al. [116] compared the three-parameter and two-parameter models for DSD estimation and found that the three-parameter model has limited superiority and slower retrieval.
3.1.3. Precipitation Type Identification
By analyzing the different attenuation patterns of snow and rainfall on microwaves, Holt et al. [117,118] suggested that dual-frequency CMLs could be used to distinguish between rainfall, snow and wet snow. Subsequently, Cherkassky et al. employed the attenuation dynamics from CMLs as a discriminant feature, and successively proposed Fisher-based linear [63] and kernel discriminant [56] methods to distinguish between rainfall and sleet. With the emergence of deep learning methods, Pu et al. [119] reported the success of utilizing the extreme learning machine algorithm to construct the hydrometeor identification model. The results show that the model performance improves as the input features and the overall frequency or frequency difference (in the case of dual- and tri-frequency) increase. The algorithm for classifying rainfall types can be found in [120], where the authors implemented the distinction between convective and stratiform rainfall by constructing deep learning models based on the differential attenuation rates of multi-frequency dual-polarization CMLs. Moreover, Ostrometzky et al. [121] derived total mixed cumulative precipitation containing rain, snow and sleet using at least three CMLs on the same path, and the results were in fair agreement with the rain gauge.
3.1.4. Monitoring Phenomena Related to Air Refractivity
Since local temperature and humidity variations due to turbulent eddies lead to fluctuations in air refractivity, which cause the microwave signal of CMLs to scintillate, the sensible and latent heat fluxes associated with the air refractivity can be estimated by CML signals. On the basis of this principle, Leijnse et al. [122] proposed a method for estimating the sensible and latent heat fluxes and, hence, the areal evaporation using CMLs with consideration of the surface energy budget constraints. In addition, since temperature inversions, which are the main cause of poor air quality, lead to multipath and ducting phenomena in electromagnetic waves, thereby relatively amplifying or attenuating RSLs, David et al. [123] utilized CMLs to detect temperature inversions and, thus, air pollution. Similarly, the literature [124] measured wildfire smoke particulate matter concentrations using CMLs and found a power–law relationship between RSL fluctuations and PM10/PM2.5 (particulate matter concentration less than 2.5/10 μm). In addition, given the relationship between pollutant washout and rainfall, CMLs have the potential to point out areas with improved air quality [125].
3.1.5. Dynamics of Rainfall and Wind
Based on a dense CML network, the spatial distribution of rainfall with high spatial and temporal resolution can be theoretically reconstructed [126,127]. According to the analysis of the spatiotemporal evolution of the rainfall field, the dynamics of precipitation, and thereby the dynamics of wind, can be retrieved [128]. Using a stochastic space-time model based on a rainfall advection and a nonlinear extended Kalman filter, Zinevich et al. [129] attempted to obtain rainfall dynamics information from CML observations. Subsequently, the wind dynamics can be obtained by calculating the speed and direction of rain cloud movement.
3.2. Hydrological Application
3.2.1. Cooperation with Dedicated Rain Sensors
As an additional source of precipitation information, rainfall estimates from CMLs can supplement or cooperate with dedicated rain sensors. Bianchi et al. [130] utilized CMLs for quality control of rain gauges and detected the occurrence error and quantification error separately. In contrast, Fencl et al. [131] proposed a method for adjusting rainfall estimates from CMLs using rain gauges, demonstrating that even distant rain gauges can reduce bias. Rain gauges are also most commonly used to reconstruct rainfall fields in conjunction with CMLs [85,92,93].
Due to uncertainties such as Z–R relationships, ground clutter and microwave attenuation, Radar QPE requires near-surface rainfall information for improvement. Krämer et al. [132] first suggested that microwave links could be used to improve rainfall estimates from X-band radars. In their procedure, microwave link measurements were used on the one hand for radar attenuation correction and on the other hand to calibrate the Z–R relationship. Shortly after, Rahimi et al. [133] proposed a backward iterative algorithm for the attenuation calibration of X-band radars via attenuation measurements of microwave links. The results show that the method is effective in recovering the reflectivity information, especially under heavy rainfall conditions. More studies focused on radar attenuation correction using CMLs can be found in [134,135,136,137]. In addition, Cummings et al. [138] proposed a mean-field bias adjustment method for a radar QPE based on CMLs, with similar results to a rain gauge-based adjusted QPE. Liberman et al. [139] then fused radar and CML rainfall observations to reconstruct accurate rainfall maps. Furthermore, CMLs can be combined with radar to invert the vertical profile of rainfall, which is of interest in semi-arid regions for studying the Virga phenomenon (evaporation of precipitation before reaching the ground) and improving the accuracy of near-surface rainfall estimates [140].
For meteorological satellites, Kumah et al. [50,51] improved rain area detection and rainfall estimation by combining signals from satellites and CMLs. In addition, they attempted to construct a random forest model to map the satellite-retrieved cloud top attributes to the ground rainfall by taking the rainfall estimates from CMLs as the true values [141]. The results show that the algorithm enables rainfall inversion with high spatial and temporal resolution. In addition, in regions where dedicated rain sensors are scarce, CMLs may be the most promising option to validate rainfall products from satellites [142].
There are also research groups that assimilate precipitation data from CMLs and multiple dedicated rain sensors to jointly reconstruct the rainfall field. Bianchi et al. [30] used variational and Gauss–Newton methods to invert rainfall fields from observations of rain gauges, radar and CMLs in Switzerland, which resulted in improvements over the raw radar QPE. In addition, as described in Section 2.1, dedicated rain sensors can also contribute to the dry and wet period classification of CMLs.
3.2.2. Hydrological Modeling
Accurate hydrological models, which are generally supported by rain gauge and radar data, are essential for water resource management, disaster warning and hydrological research. However, considering the limited spatial representativeness of rain gauges and the coarse spatial resolution of radar, as well as their unavailability in urban and mountainous areas, there is an urgent need for additional near-surface precipitation information for small- and medium-scale hydrological modeling in these regions. As early as 2005, Grum et al. [143] attempted to integrate rainfall measurements from microwave links into hydrological modeling. Fencl et al. [31] compared the urban drainage model derived from CMLs with that of rain gauges and found that the former can significantly improve pipe flow prediction. They also tried to input the rainfall measurements from CMLs and rain gauges into the runoff model at the same time [144]. The results showed that CMLs improve predictions of hydrograph dynamics compared to the model using only rain gauge data. Subsequently, in [145], they demonstrated that the performance of runoff prediction is related to the sensitivity of CMLs to rainfall and their location in the catchment. Moreover, as the bias in rainfall estimates from CMLs would propagate into hydrological models [146], they also made efforts to obtain unbiased rainfall estimates from CMLs to optimize hydrological modeling [147,148]. In addition to modeling urban drainage, CMLs have also been used for river runoff simulation [149,150,151] and disaster warning [152,153,154,155,156].
4. Challenges in Rainfall Estimation by CMLs
Despite extensive research within the past two decades, the CML-based rainfall estimation technique still confronts certain challenges (refer to Table 2), which will be described in detail in the remainder of this section.

Table 2.
Challenges faced by CML rainfall measurement techniques.
4.1. Data Acquisition
In general, CML data derives from the mobile network operator’s Network Management System (NMS), which typically records maximum and minimum TSLs and RSLs at a 15 min time resolution. Although NMS can work at higher frequencies, for the purpose of checking the quality of communications, a time step of 15 min is satisfactory for mobile network operators. However, for rainfall monitoring, such a coarse sampling frequency may miss important information given the high temporal variability of rainfall. In addition, the sampling strategy of recording only extreme values poses difficulties in deriving the average rain rate over a 15 min period [157]. One solution is to calculate the maximum and minimum rain rates using maximum and minimum attenuation, respectively, to obtain an unbiased estimate of the mean rain rate according to the local rain rate probability function [10]. Another common approach treats a simple weighted average of the maximum and minimum rain rates as the average rain rate [49]. The literature [162] provides an introduction and comparison of three methods for estimating parameters from extreme values. Moreover, deep learning methods may also be an alternative [163,164]. Leijnse et al. [70] compared three sampling strategies for CML data and found that the performance of rainfall estimation was, in descending order, continuous measurements, 15 min averages and 15 min instantaneous values. Pudashine et al. [165] further compared the sampling strategy of 15 min averages with 15 min maximum/minimum, demonstrating the slight advantage of the latter. In the Netherlands, rainfall estimation experiments using CMLs demonstrated that 15 min maximum/minimum sampling is superior to instantaneous sampling at the same time step because the former contains information over the entire time interval [166]. In addition, NMS records RSL values with a resolution of typically 0.1, 0.3 or even 1 dB. As shown in Figure 5, the coarse quantization resolution limits the precision of the CMLs in estimating the rain rate [64,167]. Although this phenomenon can be mitigated with an increasing frequency and path length, it introduces other problems such as high energy consumption for high-frequency signals and rainfall variability over long paths. Moreover, coarse quantization also limits the analysis of the pattern of signal variation.
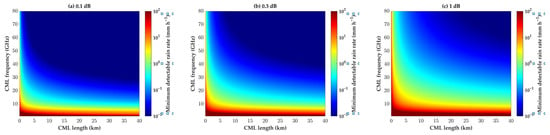
Figure 5.
Minimum detectable rain rate of CMLs at different quantization resolutions, path lengths and frequencies. Notably, the γ-R relation is referenced from the ITU-R model and the minimum detectable rain rate for most short CMLs below 10 GHz exceeds the upper limit of the color bar.
To ensure communication quality during rainfall, some CMLs are configured with automatic transmit power control (ATPC) to minimize RSL fluctuations. However, it can introduce additional errors, especially under low-temporal-resolution sampling conditions or with only RSL data available [158].
Currently, only a few research groups have shared their CML datasets [168,169,170], which may be related to the commercial confidentiality of mobile network operators. However, open access to the data may bring more insights.
Finally, in some developed countries, operators are planning to replace CMLs with fiber optic communications, which undoubtedly hurts the availability of CML data.
4.2. Baseline Estimates
The estimation of the baseline is of great importance in the operational flow of rainfall inversion by CMLs as it determines whether non-rain-induced attenuation can be accurately eliminated. As for baseline estimation approaches that require dry and wet period classification, though several methods based on different principles have been proposed for the classification of dry and wet periods, there remain difficulties in accurately determining whether rainfall exists along the path of CMLs at the current time. Since we only acquired RSL data (and in some cases TSL as well), it is difficult to determine what factors are responsible for the attenuation variations produced in the paths of the CMLs. Scintillation effects and multipath effects due to, for example, changes in the refractive index of air, may also lead to anomalous fluctuations in signal attenuation during dry periods, which may be incorrectly judged as wet periods. In addition, water films that accumulate on the antenna due to dew or after rainfall may produce false positives. Coarse RSL quantization also limits the ability of CMLs to detect light rain, especially for low-frequency short CMLs. These undoubtedly pose a negative impact on classification accuracy.
Moreover, for conventional empirical threshold-based classification methods, a priori information is required to make a comprehensive calibration of thresholds in order to obtain comparatively high dry and wet period detection capabilities simultaneously. Machine learning methods typically have a higher classification accuracy but require large, labeled datasets for training. However, on the one hand, it is not always the case that dedicated rain sensors exist in the vicinity of CMLs to provide rainfall data; on the other hand, due to the inhomogeneity of the rainfall distribution, the dataset is usually unbalanced (much fewer data in the wet period than in the dry period), which not only implies that it takes more time to collect enough wet period data, but also leads to the requirement of balancing the training set using undersampling or oversampling methods, which may contribute to overfitting or poorer performance of the model.
After dry and wet period classifications, the baseline will be determined by the dry period attenuation over a period of time around the rainfall event. In contrast, methods to estimate the baseline without dry and wet period information usually dynamically update the statistical values of attenuation in past time periods as the baseline. This may be a reasonable reference as the historical information on attenuation is able to reflect the classic state of CMLs working in the dry period. The problem is the fact that the baseline for the wet period will not remain constant but will vary with some regularity, and could possibly be quite different from the past dry period attenuation due to phenomena caused by rainfall such as increased water vapor, decreased temperatures, changes in the device conditions, etc. However, subject to the coarse sampling and quantization resolution of the RSL, most researchers have to ignore, to varying degrees, changes in the baseline during wet periods.
4.3. WAA Quantification
After the estimation of the baseline, another important source of error is the quantification of WAA. Undercompensation of WAA can lead to a systematic overestimation of rainfall. This phenomenon is especially exacerbated by higher WAA relative to rain-induced attenuation under short CML and light rain. Although a variety of empirical or semi-empirical WAA models have been developed, most of these studies have been derived from a few CMLs with limited frequency. In fact, WAA is highly correlated with the attributes of CML antennas, leading to the possibility that the properties of WAA found from different CMLs may be completely different: Schleiss et al. [29] reported antenna wetting times of up to 36 min, but other studies [46,73] have found wetting dynamics to be negligible. Additionally, contrary to common sense, hydrophobic antennas tend to form water beads on the antenna surface, which are more resistant to evaporation than the water film formed by hydrophilic antennas, prolonging the duration of the WAA’s impact after rainfall events end [159]. Therefore, the existing empirical WAA models may not be as portable for CMLs with different characteristics.
Another source of error is the way that WAA is calculated. In general, WAA values are obtained by measured attenuation minus the baseline and rain-induced attenuation, which is converted from rain rates measured by rain sensors near CMLs. However, as mentioned in Section 4.2, there is uncertainty in the estimation of the baseline, in which case the model may no longer simply compensate for WAA but include corrections for WAA and other unknown sources of bias. Furthermore, the number of antennas wetted during rainfall is also an important unknown factor, especially in the case of long CMLs and small-area rainfall.
Finally, in addition to rainfall, phenomena such as dew and fog may likewise wet the radome and produce WAA, which needs to be filtered out [126]. However, dew- and fog-induced WAA has still not been specifically studied for the properties of its dynamics and magnitude.
4.4. γ–R Relationship
As shown in Equations (6) and (7), accurate rainfall inversion can only be guaranteed if the γ-R relationship is close to linear or if rainfall is uniform on the path of CMLs. Although existing CMLs, most of which operate at 15 to 40 GHz, have a parameter b that can be approximated as 1, with the growing demand for bandwidth, higher-frequency CMLs will have to pay more attention to this problem [160], which will introduce considerable inherent errors into the rainfall estimation. This phenomenon is mitigated in the case of short CMLs because the variability of their path rainfall tends to be negligible.
Another source of uncertainty worth noting is the influence of DSD on the γ-R relationship. For CMLs outside of about 30 GHz, the dependence of the γ-R relationship on DSD is getting higher (Figure 4), i.e., the agreement between the scatter corresponding to γ-R and the fitted curve decreases, resulting in lower accuracy in rainfall estimation [18]. It has been shown that long-range spatial averaging of DSDs over the paths of CMLs can reduce rainfall estimation errors because the γ-R relationship over the paths becomes closer to the fitted power law as the path length increases [171,172]. In addition, considering different DSDs for stratiform and convective rainfall, the accuracy of rainfall inversion of the γ-R relationship for different rainfall types was analyzed by Pu et al. [160]. The results show that stratiform rainfall always exhibits a negative bias above 10 GHz, whereas convective rainfall exhibits a negative and positive bias below and above 50 GHz, respectively. Fitting power law relationships to different types of rainfall separately can provide more accurate rainfall estimates [47,84], but it requires additional information about the rainfall type.
4.5. Reconstruction of the Rainfall Spatial Distribution
In reconstructing the continuous spatial distribution of rainfall using sparse rainfall estimates from CMLs, uncertainties are inevitable. Although Gaona et al. [173] demonstrated that. In the Netherlands. the error in estimating rainfall by CMLs was greater compared to rainfall mapping, rainfall mapping is likely to be more critical over a larger area. The main sources of uncertainty in rainfall mapping include the representation of path-averaged rainfall estimates, systematic errors in mapping methods, and the density and distribution of CMLs. Firstly, the majority of studies simply treat the path-averaged rainfall estimates for CMLs as the rain rate at the midpoint of their path [45,126,127], which is feasible for short CMLs; but, for long CMLs, this undoubtedly ignores the spatial variability of rainfall on the path.
Secondly, mapping methods, regardless of geostatistical interpolation algorithms, tomographic reconstruction techniques, stochastic mixing or compressed sensing, each have their own limitations in their principles. When applying these methods, these limitations are, of course, reflected in the errors of the rainfall maps.
Thirdly, CMLs are not always distributed in high densities. Due to their purpose of communication, the density of CMLs in sparsely populated areas is usually much lower than in densely populated areas. This results in the poor ability of CMLs to capture the spatial distribution of rainfall in these areas. In addition, the unique topology of CML networks is not designed for measuring rainfall and does not facilitate rainfall mapping [161].
5. Future Work
Although CMLs, as opportunistic sensors, have the advantages of a low cost, high spatial and temporal resolution and wide coverage over traditional rain sensors, there is still a lot of room for improvement, as mentioned in Section 4. As shown in Table 3, the focus of our future work may need to concentrate on the following points, which are detailed in the remainder of this section.

Table 3.
Potential future work regarding rainfall measurement techniques based on CMLs.
5.1. Enhanced Collaboration with Mobile Network Operators
To advance the development of rainfall estimation techniques using CMLs, in the first place, we need to strengthen our collaboration with mobile network operators who are the maintainers and data providers of CMLs. Firstly, although the current sampling strategy for most CML data is not that satisfactory, it can be indeed improved. One solution is to install data loggers on cell towers, which can sample RSLs with free temporal resolution and accuracy [28]. However, the high expense of deploying and maintaining data loggers for a large number of CMLs undermines their low-cost advantage. In fact, some research groups [14,54] have already realized data acquisition with high temporal resolution via simple network management protocol (SNMP), which is a standard network management protocol widely used in TCP/IP networks. It is capable of supporting NMS for monitoring CMLs connected to the cellular network. Depending on the customized SNMP data acquisition software, RSL and TSL can be polled at a set sampling step as low as a few seconds. Despite the fact that the data quantization is still limited by the CML hardware, such CML data with high sampling frequencies are favorable for investigating variation patterns of signal attenuation. And, thanks to Chwala et al. [174], the related software has been open-sourced at GitHub. However, SNMP must be used only under the license of the mobile network operators as it requires access to their intranet. Therefore, trust between the research groups and the CML operators is a must.
Secondly, for commercial confidentiality reasons, mobile network operators usually permit the use of CML data only to the relevant research group; thus, CML data are generally not shared among different research groups. However, open access to high-quality CML data may be able to bring more insights into the issues. Researchers need to convince CML operators and guarantee that the data will be used without jeopardizing their interests.
Thirdly, the CML data now used for rainfall inversion are mainly signal strength information. In fact, many CMLs are configured with multiple sub-links due to communication needs, which may lead to additional opportunities for identifying hydrometeors [118], improving the accuracy of rainfall inversion [175] and humidity estimation [100] if phase information of microwave signal is available.
Finally, it is unrealistic for mobile network operators to provide CML data at no cost or for only researchers to pay for it. In fact, as operators provide CML data, hydrometeorological researchers can utilize expertise to assist operators in the design and real-time decision making of CML networks, as described in [176]. In addition, considering the practical value of CML rainfall measurement technology, researchers can help CML operators to operationalize and productize it for sale to fields such as agriculture, water resource management and meteorological research.
5.2. Improvement of Processing Procedures
Even though multiple procedures for processing CML data have been developed to date, they still have a lot of room for improvement. For dry and wet period classification, the WAA caused by antenna wetting by dew or fog, the WAA dynamics after rainfall and the drift of attenuation in the dry period induced by such factors as the occlusion of metallic objects in the path may produce false positives. In addition, due to the insensitivity of most existing CMLs to light rain, light rain events are often missed. However, limited by the availability of signal level data only and the similarity of the two types of phenomena, current classification algorithms are still unable to cope with these problems effectively. In the future, based on CML data with high temporal and quantization resolution, it may be possible to make a breakthrough by discovering the differences between the above phenomena.
For baseline determination, the baseline should not be constant during wet periods because of changes in the equipment conditions of the CMLs and in the environment along their paths. Existing methods more or less ignore this. With the rise of machine learning, time-series prediction algorithms based on recurrent neural networks, such as LSTM, may enable the estimation of wet period baselines [177].
For WAA correction, since WAA is highly dependent on antenna properties, the findings on WAA may vary from one research group to another. However, state-of-the-art WAA modeling is still limited to a small number of CMLs, which are usually from the same operators, and the mechanism of action between WAA and antenna properties remains unsystematically investigated. Although these models have been validated on large datasets, the errors may be masked in large-scale comparisons. In the future, investigating the effect of different antenna characteristic parameters on the WAA model by controlling variables may be a solution to achieve a more robust WAA quantization.
For rainfall inversion using the γ-R relationship, the power–law approximation introduces inherent errors due to the nonlinearity of the curve and the dependence on DSD. One possible solution is to utilize deep learning to substitute the γ-R relationship [188,189,190,191]. Habi et al. [178] have compared data-driven Recurrent Neural Network (RNN) algorithms with traditional power–law relations. The results show that the former has better performance but poorer robustness. Adding a temporal normalization layer can improve the robustness of the RNN algorithm, but at the same time compromise performance. In the future, perhaps an attempt can be made to combine deep learning with power–law relations to ensure excellent performance and robustness at the same time.
For rainfall mapping, most studies still use CML-based rainfall estimates as the rain rate at the midpoint of the path. This not only fails to take into account the spatial variability of rainfall on the path, but also ignores the advantage of CMLs in providing linear-integrated measurements. In addition, most rainfall mapping techniques directly follow the rainfall mapping methods of dedicated rain sensor networks. Future work could focus on improving rainfall mapping techniques by considering the unique topology and measurement characteristics of CMLs [179,180].
In addition, since the proposed CML processing procedures are usually applicable to different regions, open-source algorithms are not directly usable. While dedicated rainfall observations can be used to calibrate the algorithms to specific climates and CML networks [192], calibrating algorithms using only CML data remains a challenge in regions where rain sensors are not already available. Investigating low-cost but efficient calibration methods in these regions (such as utilizing other opportunistic rain sensors) may be a future direction of research.
5.3. Data Assimilation
One advantage of the use of CMLs for rainfall estimation is the availability of a sufficient network of virtual sensors; however, it is common that there may be more than one mobile network operator in a region. This means that their data need to be assimilated with each other because the sampling strategy and data format are quite likely to be different for different operators. Blettner et al. [181] recently reported the case of using CMLs from Germany and the Czech Republic to generate transboundary rainfall maps and found different anomalous behavior for heterogeneous datasets, emphasizing the importance of quality control algorithms. In addition, the situation is potentially improved in the future if access to the operator’s NMS is available as in Section 5.1.
In addition, in areas where dedicated precipitation observations exist, excessive focus should not be placed on discussing CML-only-based rainfall estimates. It may be more meaningful to assimilate CMLs with traditional rain sensors or even other opportunistic sensors [91] to complement the spatiotemporal resolution and accuracy of precipitation products.
5.4. Error Analysis of CMLs Applied to Mountainous Areas
A strength of the CML rainfall measurement technique, which has been widely mentioned in many literatures [41,42,43], is that it is available in mountainous areas where the deployment of radar and rain gauges is difficult. However, due to the unique topographic and climatic conditions of mountainous areas, the CML rainfall measurement technique may need to be adapted. First, the elevation angles of CMLs in mountainous areas are no longer negligible and can even reach tens of degrees [193]. Therefore, the calculation of the raindrop extinction cross-section needs to take into account the tilt angle of the raindrop with respect to microwave propagation, but little attention has been paid to this in the calibration of the γ-R relationship [28]. Second, the rainfall distribution on the inclined path is more heterogeneous because the variation of rainfall in the vertical direction needs to be considered in addition to the horizontal direction [194,195]. In order to validate that CMLs can substitute radar and rain gauges in mountainous areas and to promote the application of this technology, a systematic analysis of their performance on inclined paths must be performed based on experiments or simulations in the future.
5.5. Exploration of Other Applications of CMLs
In operation, CMLs are not only affected by the atmospheric environment but may also suffer from plant, animal and human activities. Moshe et al. [182] reported that the presence of birds along the path of CMLs causes additional attenuation and suggested the use of CMLs to monitor migratory birds. And, Hunt et al. [183] discovered that a cellular network signal strength of 2.4 GHz is related to the presence of vegetation in the path, and, if present, as well as to the water content of the vegetation and the distance the signal passes through the vegetation. Thus, the links between CMLs and arbitrary microwave receivers can be used to estimate vegetation characteristics. Furthermore, in [159], artificially caused occlusion of objects in the path was found to lead to a drift in the attenuation of the CMLs. It would be interesting to monitor these phenomena using CMLs. The variation character of the attenuation due to these phenomena could be studied in the future to enable the identification and observation of these phenomena.
5.6. Rainfall Prediction
After rainfall mapping, rainfall paths and intensities can be forecasted in the short term based on the variation of the spatial distribution of rainfall over time. Commonly, such short-term forecasts are supported by radar data. However, in economically backward developing countries or in areas unavailable to radar, rainfall maps based on CMLs may be an alternate option [196]. Imhoff et al. [185] constructed nowcasts for the first time in the Netherlands using country-wide rainfall maps based on CMLs and found that CMLs gave better results than radar in general. Recently, Zhang et al. [184] also carried out rainfall field nowcasting experiments based on CMLs in Jiangyin City, China, and found that the LSTM-based nowcasting algorithm has better performance for stratiform and mixed precipitation compared to convective precipitation. In addition, based on the assumption that atmospheric variables related to rainfall change prior to a rainfall event affect CMLs, CMLs can also directly predict whether and how much rain will fall in the future without the need for rainfall mapping [197]. Further research on techniques for predicting rainfall using CMLs could be useful for disaster prevention and control, especially in poor tropical regions where extreme events are common.
5.7. Application and Error Analysis of High-frequency CMLs
With fifth-generation (5G) and even sixth-generation (6G) wireless systems in operation, huge data throughput is forcing operators to design E-band CMLs at 71 to 86 GHz and replace older equipment. This may lead to new opportunities because these high-frequency CMLs are more sensitive to light rain and water vapor [47,198,199]. However, the increase in frequency also leads to nonlinearities in the γ-R relationship and increased dependence on DSD. In addition, high-frequency CMLs also suffer from more energy loss and, therefore, the path length is correspondingly shorter, which may lead to a more severe negative impact of WAA [186]. An error analysis of high-frequency CMLs could contribute to their future application in environmental monitoring.
5.8. Combination with Earth–Space Microwave Links
Similar to CMLs, microwave radiation from Earth–space links (ESLs), which connect satellites and ground receivers, will also be attenuated by rainfall [177,200,201]. Importantly, in contrast to CMLs, the downlink signal of ESLs can tilt through the rain area to obtain vertical information on precipitation [202,203,204]. Furthermore, with the development of satellite communications, a large number of satellites are expected to be launched in the near future [205]. Therefore, fusing opportunistic rainfall information from ESLs may be a topic for improving and expanding rainfall estimation based on CMLs [187,206,207]. However, most of the existing studies are still limited to examining rainfall measurement techniques based on CMLs and ESLs separately, and works on combining CMLs and ESLs have not yet been emphasized [208]. Future work could attempt the joint reconstruction of three-dimensional spatial rainfall fields using both ESLs and CMLs.
5.9. Attempts to Estimate Rainfall Using Cellphone Signals
As fiber optic communications are increasingly used in cellular communication networks, CMLs will become less available in certain areas. In this case, the large number of links between user terminals and cell towers (base stations) may be an alternative. These non-line-of-sight links typically operate at frequencies below 6 GHz and are, thus, theoretically insensitive to rainfall in the propagation path [209]. However, during rainfall, the wetting effect of obstacles in the path [210,211], reflective surfaces (walls, grounds, etc.) [212,213,214] and the transmitting antenna [215,216] may significantly affect the signal quality. Beritelli et al. [217] constructed a probabilistic neural network to distinguish rainfall classes using statistical features of 4G/Long Term Evolution (LTE) signals and achieved a classification accuracy of 96.7%. Subsequently, Song et al. [218] built a 2 GHz experimental link and used the C4.5 algorithm to implement the classification of dry and wet periods based on cellphone signals. In order to estimate the distance using low-frequency radio signals, Fang et al. [219] developed a path loss model considering rainfall attenuation effects, which achieved a satisfactory performance. Therefore, with distances between the receiving terminal and the cell tower known, the model should be able to provide accurate rainfall estimation. Recently, the literature [220] also reported cases of estimating rainfall using cellphone signals based on deep learning algorithms. Although preliminary studies on the use of cellphone signals to monitor rainfall have been conducted, the law of rainfall-induced comprehensive effects on signal propagation is still unclear and the generalization ability of the models proposed in the above studies is yet to be verified. Therefore, future explorations can attempt to model low-frequency non-line-of-sight signal transmissions to address the limitations in current studies of rainfall measurement by cellphone signals, especially in regions where the number of CMLs is decreasing.
6. Conclusions and Outlook
In this article, we provide a systematic overview of rainfall measurement techniques based on CMLs and summarize current challenges and possible future research directions. Compared to dedicated rain sensors, CMLs can economically provide near-surface precipitation information with a high spatial and temporal resolution and wide coverage, which can effectively complement dedicated precipitation observations. Within the past 20 years, scholars have comprehensively studied the processing flow of CML data and made great progress. However, the technology still faces some challenges [40,221,222]. Most importantly, breakthroughs must be made in data acquisition and CML data with high temporal and quantization resolutions may bring new insights into dry and wet period classification, baseline estimation and WAA correction. Encouragingly, a number of research groups have recently openly shared their high-quality datasets [169,170,223], making a critical contribution to the investigation of CML technology.
Another practical challenge is the gradual replacement of CMLs by fiber optic communication technologies. Due to the advantages of fiber optic transmission, such as high speed, low loss, high interference immunity and large information-carrying capacity, there is a tendency for the proportion of fiber optics to gradually increase in cellular communication networks. However, considering the difficulty and high cost of fiber deployment, developing countries, where CMLs have the greatest potential, will continue to rely on CMLs for a long time to come. Moreover, low-frequency non-line-of-sight links between cell towers and cellphone terminals have also shown potential to estimate precipitation, which could be an alternative in areas where the number of CMLs is decreasing.
As the demand for bandwidth continues to increase, the frequency of CMLs will expand towards higher frequencies in the future, which opens up the possibility of monitoring water vapor and improving the accuracy of light rain inversion. However, a systematic error analysis of rainfall inversion with high-frequency CMLs, especially for the γ-R relationship, is needed before application.
An additional issue that has not been widely investigated but is highly desirable is the productization and commercialization of rainfall estimates based on CMLs. While many studies have demonstrated that CMLs can provide reliable rainfall estimates or improve dedicated precipitation products, only a few operational precipitation products from CMLs have been reported so far [196]. On the one hand, rainfall inversion algorithms based on CMLs still face some challenges, as described in Section 4. On the other hand, and more importantly, in order to provide 24/7 real-time rainfall products, operators need to ensure reliable real-time availability of CML data, which entails additional costs and potential commercial confidentiality issues. Achieving this goal may be able to enhance collaboration between researchers and mobile network operators.
To conclude, we hope that our analysis and comments on the technique will help researchers recognize the current challenges and conduct further research.
Author Contributions
Conceptualization, P.Z. and X.L.; methodology, P.Z. and X.L.; validation, P.Z. and K.P.; formal analysis, P.Z. and K.P.; investigation, P.Z. and K.P.; resources, X.L.; writing—original draft preparation, P.Z.; writing—review and editing, X.L. and K.P.; visualization, P.Z. and K.P.; supervision, X.L.; project administration, X.L.; funding acquisition, X.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (Grant No. 42222505) and the Excellent Youth Scholars of Natural Science Foundation of Hunan Province of China (Grant No. 2021JJ20046).
Acknowledgments
The authors thank the editor and anonymous reviewers for providing helpful advice.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Getirana, A.; Kirschbaum, D.; Mandarino, F.; Ottoni, M.; Khan, S.; Arsenault, K. Potential of GPM IMERG Precipitation Estimates to Monitor Natural Disaster Triggers in Urban Areas: The Case of Rio de Janeiro, Brazil. Remote Sens. 2020, 12, 4095. [Google Scholar] [CrossRef]
- Berg, P.; Moseley, C.; Haerter, J.O. Strong increase in convective precipitation in response to higher temperatures. Nat. Geosci. 2013, 6, 181–185. [Google Scholar] [CrossRef]
- Nešpor, V.; Sevruk, B. Estimation of Wind-Induced Error of Rainfall Gauge Measurements Using a Numerical Simulation. J. Atmos. Ocean. Technol. 1999, 16, 450. [Google Scholar] [CrossRef]
- Ulbrich, C.W.; Lee, L.G. Rainfall Measurement Error by WSR-88D Radars due to Variations in Z–R Law Parameters and the Radar Constant. J. Atmos. Ocean. Technol. 1999, 16, 1017–1024. [Google Scholar] [CrossRef]
- Nikahd, A.; Hashim, M.; Nazemosadat, M.J. A Review of Uncertainty Sources on Weather Ground-Based Radar for Rainfall Estimation. Appl. Mech. Mater. 2016, 818, 254–271. [Google Scholar] [CrossRef]
- Hou, A.Y.; Kakar, R.K.; Neeck, S.; Azarbarzin, A.A.; Kummerow, C.D.; Kojima, M.; Oki, R.; Nakamura, K.; Iguchi, T. The Global Precipitation Measurement Mission. Bull. Am. Meteorol. Soc. 2014, 95, 701–722. [Google Scholar] [CrossRef]
- Meyer, H.; Kühnlein, M.; Appelhans, T.; Nauss, T. Comparison of four machine learning algorithms for their applicability in satellite-based optical rainfall retrievals. Atmos. Res. 2016, 169, 424–433. [Google Scholar] [CrossRef]
- Chen, R.; Bennartz, R. Rainfall Algorithms Using Oceanic Satellite Observations from MWHS-2. Adv. Atmos. Sci. 2021, 38, 1367–1378. [Google Scholar] [CrossRef]
- Stephens, C.M.; Pham, H.T.; Marshall, L.A.; Johnson, F.M. Which Rainfall Errors Can Hydrologic Models Handle? Implications for Using Satellite-Derived Products in Sparsely Gauged Catchments. Water Resour. Res. 2022, 58, e2020WR02933. [Google Scholar] [CrossRef]
- Messer, H.; Zinevich, A.; Alpert, P. Environmental monitoring by wireless communication networks. Science 2006, 312, 713. [Google Scholar] [CrossRef]
- de Vos, L.; Leijnse, H.; Overeem, A.; Uijlenhoet, R. The potential of urban rainfall monitoring with crowdsourced automatic weather stations in Amsterdam. Hydrol. Earth Syst. Sci. 2017, 21, 765–777. [Google Scholar] [CrossRef]
- Rabiei, E.; Haberlandt, U.; Sester, M.; Fitzner, D. Rainfall estimation using moving cars as rain gauges―Laboratory experiments. Hydrol. Earth Syst. Sci. 2013, 17, 4701–4712. [Google Scholar] [CrossRef]
- Jiang, S.; Babovic, V.; Zheng, Y.; Xiong, J. Advancing Opportunistic Sensing in Hydrology: A Novel Approach to Measuring Rainfall with Ordinary Surveillance Cameras. Water Resour. Res. 2019, 55, 3004–3027. [Google Scholar] [CrossRef]
- Fencl, M.; Rieckermann, J.; Sykora, P.; Stransky, D.; Bares, V. Commercial microwave links instead of rain gauges: Fiction or reality? Water Sci. Technol. 2015, 71, 31–37. [Google Scholar] [CrossRef] [PubMed]
- Gosset, M.; Kunstmann, H.; Zougmore, F.; Cazenave, F.; Leijnse, H.; Uijlenhoet, R.; Chwala, C.; Keis, F.; Doumounia, A.; Boubacar, B.; et al. Improving Rainfall Measurement in Gauge Poor Regions Thanks to Mobile Telecommunication Networks. Bull. Am. Meteorol. Soc. 2016, 97, 49–51. [Google Scholar] [CrossRef]
- de Vos, L.W.; Droste, A.M.; Zander, M.J.; Overeem, A.; Leijnse, H.; Heusinkveld, B.G.; Steeneveld, G.J.; Uijlenhoet, R. Hydrometeorological Monitoring Using Opportunistic Sensing Networks in the Amsterdam Metropolitan Area. Bull. Am. Meteorol. Soc. 2020, 101, 167–185. [Google Scholar] [CrossRef]
- Olsen, R.; Rogers, D.; Hodge, D. The aR b relation in the calculation of rain attenuation. IEEE Trans. Antennas Propag. 1978, 26, 318–329. [Google Scholar] [CrossRef]
- Atlas, D.; Ulbrich, C.W. Path- and Area-Integrated Rainfall Measurement by Microwave Attenuation in the 1–3 cm Band. J. Appl. Meteorol. Climatol. 1977, 16, 1322–1331. [Google Scholar] [CrossRef]
- Jameson, A.R. A Comparison of Microwave Techniques for Measuring Rainfall. J. Appl. Meteorol. Climatol. 1991, 30, 32–54. [Google Scholar] [CrossRef]
- Rincon, R.F.; Lang, R.H.; Thiele, O. Rain estimation using the NASA/TRMM microwave link. In Proceedings of the IEEE 1999 International Geoscience and Remote Sensing Symposium, IGARSS’99, Hamburg, Germany, 28 June–2 July 1999; pp. 2063–2065. [Google Scholar]
- Rincon, R.F.; Lang, R.H. Microwave link dual-wavelength measurements of path-average attenuation for the estimation of drop size distributions and rainfall. IEEE Trans. Geosci. Remote Sens. 2002, 40, 760–770. [Google Scholar] [CrossRef]
- Holt, A.R.; Goddard, J.W.F.; Upton, G.; Willis, M.J.; Rahimi, A.R.; Baxter, P.D.; Collier, C. Measurement of rainfall by dual-wavelength microwave attenuation. Electron. Lett. 2001, 36, 2099–2101. [Google Scholar] [CrossRef]
- Rahimi, A.R.; Holt, A.R.; Upton, G.J.G.; Cummings, R.J. Use of dual-frequency microwave links for measuring path-averaged rainfall. J. Geophys. Res. Atmos. 2003, 108, 4467. [Google Scholar] [CrossRef]
- Rahimi, A.R.; Upton, G.J.G.; Holt, A.R. Dual-frequency links—A complement to gauges and radar for the measurement of rain. J. Hydrol. 2004, 288, 3–12. [Google Scholar] [CrossRef]
- Chen, B.; Yang, J.; Pu, J. Statistical Characteristics of Raindrop Size Distribution in the Meiyu Season Observed in Eastern China. J. Meteorol. Soc. Japan. Ser. II 2013, 91, 215–227. [Google Scholar] [CrossRef]
- Leijnse, H.; Uijlenhoet, R.; Stricker, J.N.M. Rainfall measurement using radio links from cellular communication networks. Water Resour. Res. 2007, 43, W03201. [Google Scholar] [CrossRef]
- Schleiss, M.; Berne, A. Identification of Dry and Rainy Periods Using Telecommunication Microwave Links. IEEE Geosci. Remote Sens. Lett. 2010, 7, 611–615. [Google Scholar] [CrossRef]
- Chwala, C.; Gmeiner, A.; Qiu, W.; Hipp, S.; Nienaber, D.; Siart, U.; Eibert, T.; Pohl, M.; Seltmann, J.; Fritz, J.; et al. Precipitation observation using microwave backhaul links in the alpine and pre-alpine region of Southern Germany. Hydrol. Earth Syst. Sci. 2012, 16, 2647–2661. [Google Scholar] [CrossRef]
- Schleiss, M.; Rieckermann, J.; Berne, A. Quantification and Modeling of Wet-Antenna Attenuation for Commercial Microwave Links. IEEE Geosci. Remote Sens. Lett. 2013, 10, 1195–1199. [Google Scholar] [CrossRef]
- Bianchi, B.; Jan van Leeuwen, P.; Hogan, R.J.; Berne, A. A Variational Approach to Retrieve Rain Rate by Combining Information from Rain Gauges, Radars, and Microwave Links. J. Hydrometeorol. 2013, 14, 1897–1909. [Google Scholar] [CrossRef]
- Fencl, M.; Rieckermann, J.; Schleiss, M.; Stránský, D.; Bareš, V. Assessing the potential of using telecommunication microwave links in urban drainage modelling. Water Sci. Technol. 2013, 68, 1810–1818. [Google Scholar] [CrossRef]
- D’Amico, M.; Manzoni, A.; Solazzi, G.L. Use of Operational Microwave Link Measurements for the Tomographic Reconstruction of 2-D Maps of Accumulated Rainfall. IEEE Geosci. Remote Sens. Lett. 2016, 13, 1827–1831. [Google Scholar] [CrossRef]
- Rios Gaona, M.F.; Overeem, A.; Raupach, T.H.; Leijnse, H.; Uijlenhoet, R. Rainfall retrieval with commercial microwave links in São Paulo, Brazil. Atmos. Meas. Techn. 2018, 11, 4465–4476. [Google Scholar] [CrossRef]
- Song, K.; Liu, X.; Gao, T. Real-Time Rainfall Estimation Using Microwave Links: A Case Study in East China during the Plum Rain Season in 2020. Sensors 2021, 21, 858. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Zhao, K.; Zou, M.; Pu, K.; Song, K. Rainfall Monitoring Using a Microwave Links Network: A Long-Term Experiment in East China. Adv. Atmos. Sci. 2023, 40, 1567–1583. [Google Scholar] [CrossRef]
- Overeem, A.; Leijnse, H.; van Leth, T.C.; Bogerd, L.; Priebe, J.; Tricarico, D.; Droste, A.; Uijlenhoet, R. Tropical rainfall monitoring with commercial microwave links in Sri Lanka. Environ. Res. Lett. 2021, 16, 074058. [Google Scholar] [CrossRef]
- Turko, M.; Gosset, M.; Kacou, M.; Bouvier, C.; Chahinian, N.; Boone, A.; Alcoba, M. Rainfall Measurement from Commercial Microwave Links for Urban Hydrology in Africa: A Simulation Framework for Sensitivity Analysis. J. Hydrometeorol. 2021, 22, 1819–1834. [Google Scholar] [CrossRef]
- David, N.; Liu, Y.; Kumah, K.K.; Hoedjes, J.C.B.; Su, B.Z.; Gao, H.O. On the Power of Microwave Communication Data to Monitor Rain for Agricultural Needs in Africa. Water 2021, 13, 730. [Google Scholar] [CrossRef]
- Doumounia, A.; Gosset, M.; Cazenave, F.; Kacou, M.; François, Z. Rainfall Monitoring based on Microwave links from cellular telecommunication Networks: First Results from a West African Test Bed. Geophys. Res. Lett. 2014, 41, 6016–6022. [Google Scholar] [CrossRef]
- Messer, H.; Sendik, O. A New Approach to Precipitation Monitoring: A critical survey of existing technologies and challenges. IEEE Signal Process. Mag. 2015, 32, 110–122. [Google Scholar] [CrossRef]
- Uijlenhoet, R.; Overeem, A.; Leijnse, H. Opportunistic remote sensing of rainfall using microwave links from cellular communication networks. WIREs Water 2018, 5, e1289. [Google Scholar] [CrossRef]
- Chwala, C.; Kunstmann, H. Commercial microwave link networks for rainfall observation: Assessment of the current status and future challenges. WIREs Water 2019, 6, e1337. [Google Scholar] [CrossRef]
- Lian, B.; Wei, Z.; Sun, X.; Li, Z.; Zhao, J. A Review on Rainfall Measurement Based on Commercial Microwave Links in Wireless Cellular Networks. Sensors 2022, 22, 4395. [Google Scholar] [CrossRef]
- Leijnse, H.; Uijlenhoet, R.; Stricker, J.N.M. Hydrometeorological application of a microwave link: 2. Precipitation. Water Resour. Res. 2007, 43, W04417. [Google Scholar] [CrossRef]
- Overeem, A.; Leijnse, H.; Uijlenhoet, R. Retrieval algorithm for rainfall mapping from microwave links in a cellular communication network. Atmos. Meas. Tech. 2016, 9, 2425–2444. [Google Scholar] [CrossRef]
- Graf, M.; Chwala, C.; Polz, J.; Kunstmann, H. Rainfall estimation from a German-wide commercial microwave link network: Optimized processing and validation for 1 year of data. Hydrol. Earth Syst. Sci. 2020, 24, 2931–2950. [Google Scholar] [CrossRef]
- Fencl, M.; Dohnal, M.; Valtr, P.; Grabner, M.; Bareš, V. Atmospheric observations with E-band microwave links―challenges and opportunities. Atmos. Meas. Tech. 2020, 13, 6559–6578. [Google Scholar] [CrossRef]
- Upton, G.J.G.; Holt, A.R.; Cummings, R.J.; Rahimi, A.R.; Goddard, J.W.F. Microwave links: The future for urban rainfall measurement? Atmos. Res. 2005, 77, 300–312. [Google Scholar] [CrossRef]
- Overeem, A.; Leijnse, H.; Uijlenhoet, R. Measuring urban rainfall using microwave links from commercial cellular communication networks. Water Resour. Res. 2011, 47, W12505. [Google Scholar] [CrossRef]
- Kumah, K.K.; Hoedjes, J.C.B.; David, N.; Maathuis, B.H.P.; Gao, H.O.; Su, B.Z. Combining MWL and MSG SEVIRI Satellite Signals for Rainfall Detection and Estimation. Atmosphere 2020, 11, 884. [Google Scholar] [CrossRef]
- Kumah, K.K.; Hoedjes, J.C.B.; David, N.; Maathuis, B.H.P.; Gao, H.O.; Su, B.Z. The MSG Technique: Improving Commercial Microwave Link Rainfall Intensity by Using Rain Area Detection from Meteosat Second Generation. Remote Sens. 2021, 13, 3274. [Google Scholar] [CrossRef]
- Reller, C.; Loeliger, H.A.; Díaz, J.P.M. A model for quasi-periodic signals with application to rain estimation from microwave link gain. In Proceedings of the 2011 19th European Signal Processing Conference, Barcelona, Spain, 29 August–2 September 2011; pp. 971–975. [Google Scholar]
- Rayitsfeld, A.; Samuels, R.; Zinevich, A.; Hadar, U.; Alpert, P. Comparison of two methodologies for long term rainfall monitoring using a commercial microwave communication system. Atmos. Res. 2012, 104–105, 119–127. [Google Scholar] [CrossRef]
- Wang, Z.; Schleiss, M.; Jaffrain, J.; Berne, A.; Rieckermann, J. Using Markov switching models to infer dry and rainy periods from telecommunication microwave link signals. Atmos. Meas. Tech. 2012, 5, 1847–1859. [Google Scholar] [CrossRef]
- Harel, O.; Messer, H. Extension of the MFLRT to Detect an Unknown Deterministic Signal Using Multiple Sensors, Applied for Precipitation Detection. IEEE Signal Process. Lett. 2013, 20, 945–948. [Google Scholar] [CrossRef]
- Cherkassky, D.; Ostrometzky, J.; Messer, H. Precipitation Classification Using Measurements from Commercial Microwave Links. IEEE Trans. Geosci. Remote Sens. 2014, 52, 2350–2356. [Google Scholar] [CrossRef]
- Dordević, V.; Pronić-Rančić, O.; Marinkovic, Z.; Milijic, M.; Marković, V.; Siart, U.; Chwala, C.; Kunstmann, H. New method for detection of precipitation based on artificial neural networks. Microw. Rev. 2013, 19, 50–55. [Google Scholar]
- Habi, H.V.; Messer, H. Wet-dry classification using LSTM and commercial microwave links. In Proceedings of the 10th IEEE Sensor Array and Multichannel Signal Processing Workshop (SAM), Sheffield, UK, 8–11 July 2018; pp. 149–153. [Google Scholar]
- He, B.; Liu, X.; Hu, S.; Song, K.; Gao, T. Use of the C-Band Microwave Link to Distinguish between Rainy and Dry Periods. Adv. Meteorol. 2019, 2019, 3428786. [Google Scholar] [CrossRef]
- Song, K.; Liu, X.; Zou, M.; Zhou, D.; Wu, H.; Ji, F. Experimental Study of Detecting Rainfall Using Microwave Links: Classification of Wet and Dry Periods. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 5264–5271. [Google Scholar] [CrossRef]
- Polz, J.; Chwala, C.; Graf, M.; Kunstmann, H.; Kunstmann, H. Rain event detection in commercial microwave link attenuation data using convolutional neural networks. Atmos. Meas. Tech. 2020, 13, 3835–3853. [Google Scholar] [CrossRef]
- Kamtchoum, E.V.; Nzeukou Takougang, A.C.; Tayou Djamegni, C. A Machine Learning Approach for the Classification of Wet and Dry Periods Using Commercial Microwave Link Data. SN Comput. Sci. 2022, 3, 227. [Google Scholar] [CrossRef]
- Cherkassky, D.; Ostrometzky, J.; Messer, H. The Use of Linear Feature Projection for Precipitation Classification Using Measurements from Commercial Microwave Links. In Proceedings of the Latent Variable Analysis and Signal Separation, Tel Aviv, Israel, 12–15 March 2012; Springer: Berlin/Heidelberg, Germany, 2012; pp. 511–519. [Google Scholar]
- Zinevich, A.; Messer, H.; Alpert, P. Prediction of rainfall intensity measurement errors using commercial microwave communication links. Atmos. Meas. Tech. 2010, 3, 1385–1402. [Google Scholar] [CrossRef]
- Fenicia, F.; Pfister, L.; Kavetski, D.; Matgen, P.; Iffly, J.-F.; Hoffmann, L.; Uijlenhoet, R. Microwave links for rainfall estimation in an urban environment: Insights from an experimental setup in Luxembourg-City. J. Hydrol. 2012, 464–465, 69–78. [Google Scholar] [CrossRef]
- Ostrometzky, J.; Messer, H. Dynamic Determination of the Baseline Level in Microwave Links for Rain Monitoring from Minimum Attenuation Values. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 24–33. [Google Scholar] [CrossRef]
- Moroder, C.; Siart, U.; Chwala, C.; Kunstmann, H. Modeling of Wet Antenna Attenuation for Precipitation Estimation from Microwave Links. IEEE Geosci. Remote Sens. Lett. 2020, 17, 386–390. [Google Scholar] [CrossRef]
- Kharadly, M.M.Z.; Ross, R. Effect of wet antenna attenuation on propagation data statistics. IEEE Trans. Antennas Propag. 2001, 49, 1183–1191. [Google Scholar] [CrossRef]
- García-Rubia, J.M.; Riera, J.M.; Benarroch, A.; García-del-Pino, P. Estimation of Rain Attenuation from Experimental Drop Size Distributions. IEEE Antennas Wirel. Propag. Lett. 2011, 10, 839–842. [Google Scholar] [CrossRef]
- Leijnse, H.; Uijlenhoet, R.; Stricker, J.N.M. Microwave link rainfall estimation: Effects of link length and frequency, temporal sampling, power resolution, and wet antenna attenuation. Adv. Water. Resour. 2008, 31, 1481–1493. [Google Scholar] [CrossRef]
- Valtr, P.; Fencl, M.; Bares, V. Excess Attenuation Caused by Antenna Wetting of Terrestrial Microwave Links at 32 GHz. IEEE Antennas Wirel. Propag. Lett. 2019, 18, 1636–1640. [Google Scholar] [CrossRef]
- Minda, H.; Nakamura, K. High Temporal Resolution Path-Average Rain Gauge with 50-GHz Band Microwave. J. Atmos. Ocean. Technol. 2005, 22, 165–179. [Google Scholar] [CrossRef]
- Pastorek, J.; Fencl, M.; Rieckermann, J.; Bares, V. Precipitation Estimates from Commercial Microwave Links: Practical Approaches to Wet-Antenna Correction. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–9. [Google Scholar] [CrossRef]
- Fencl, M.; Valtr, P.; Kvicera, M.; Bares, V. Quantifying Wet Antenna Attenuation in 38-GHz Commercial Microwave Links of Cellular Backhaul. IEEE Geosci. Remote Sens. Lett. 2019, 16, 514–518. [Google Scholar] [CrossRef]
- Pu, K.; Liu, X.; He, H. Wet Antenna Attenuation Model of E-Band Microwave Links Based on the LSTM Algorithm. IEEE Antennas Wirel. Propag. Lett. 2020, 19, 1586–1590. [Google Scholar] [CrossRef]
- Moroder, C.; Siart, U.; Chwala, C.; Kunstmann, H. Microwave Instrument for Simultaneous Wet Antenna Attenuation and Precipitation Measurement. IEEE Trans. Instrum. Meas. 2020, 69, 5853–5861. [Google Scholar] [CrossRef]
- ITU. Specific attenuation model for rain for use in prediction methods. In Recommendation ITU-R P.838-3; ITU: Geneva, Switzerland, 2005. [Google Scholar]
- Kim, J.H.; Jung, M.-W.; Yoon, Y.K.; Chong, Y.J. The Measurements of Rain Attenuation for Terrestrial Link at millimeter Wave. In Proceedings of the 2013 International Conference on ICT Convergence (ICTC), Jeju Island, Republic of Korea, 14–16 October 2013. [Google Scholar]
- Halder, T.; Adhikari, A.; Maitra, A. Rain attenuation studies from radiometric and rain DSD measurements at two tropical locations. J. Atmos. Sol. -Terr. Phys. 2018, 170, 11–20. [Google Scholar] [CrossRef]
- Juttula, H.; Kokkoniemi, J.; Lehtomaki, J.; Makynen, A.; Juntti, M. Rain Induced Co-Channel Interference at 60 GHz and 300 GHz Frequencies. In Proceedings of the IEEE International Conference on Communications Workshops (ICC Workshops), Shanghai, China, 20–24 May 2019. [Google Scholar]
- Xichuan, L.I.U.; Mingzhong, Z.O.U.; Xuguang, Z. Analysis of Sensitive Parameters of 15~23 GHz Microwave Link Induced by Rain Attenuation. J. Electron. Inf. Technol. 2021, 43, 2007–2013. Available online: https://jeit.ac.cn/cn/article/doi/10.11999/JEIT200180 (accessed on 23 September 2023).
- Kim, M.-S.; Kwon, B. Rainfall Detection and Rainfall Rate Estimation Using Microwave Attenuation. Atmosphere 2018, 9, 287. [Google Scholar] [CrossRef]
- Song, K.; Liu, X.; Gao, T.; He, B. Rainfall estimation using a microwave link based on an improved rain-induced attenuation model. Remote Sens. Lett. 2019, 10, 1057–1066. [Google Scholar] [CrossRef]
- Han, C.; Feng, L.; Huo, J.; Deng, Z.; Zhang, G.; Ji, B.; Zhou, Y.; Bi, Y.; Duan, S.; Yuan, R. Characteristics of Rain-Induced Attenuation over Signal Links at Frequency Ranges of 25 and 38 GHz Observed in Beijing. Remote Sens. 2021, 13, 2156. [Google Scholar] [CrossRef]
- Goldshtein, O.; Messer, H.; Zinevich, A. Rain Rate Estimation Using Measurements from Commercial Telecommunications Links. IEEE Trans. Signal Process. 2009, 57, 1616–1625. [Google Scholar] [CrossRef]
- Eshel, A.; Ostrometzky, J.; Gat, S.; Alpert, P.; Messer, H. Spatial Reconstruction of Rain Fields from Wireless Telecommunication Networks—Scenario-Dependent Analysis of IDW-Based Algorithms. IEEE Geosci. Remote Sens. Lett. 2020, 17, 770–774. [Google Scholar] [CrossRef]
- Zheng, X.; Messer, H.; Wang, Q.; Xu, T.; Qin, Y.; Yang, T. On the potential of commercial microwave link networks for high spatial resolution rainfall monitoring in urban areas. Atmos. Res. 2022, 277, 106289. [Google Scholar] [CrossRef]
- Eshel, A.; Messer, H.; Kunstmann, H.; Alpert, P.; Chwala, C. Quantitative Analysis of the Performance of Spatial Interpolation Methods for Rainfall Estimation Using Commercial Microwave Links. J. Hydrometeorol. 2021, 22, 831–843. [Google Scholar] [CrossRef]
- Giuli, D.; Facheris, L.; Tanelli, S. Microwave tomographic inversion technique based on stochastic approach for rainfall fields monitoring. IEEE Trans. Geosci. Remote Sens. 1999, 37, 2536–2555. [Google Scholar] [CrossRef]
- Giuli, D.; Facheris, L.; Tanelli, S. A new microwave tomography approach for rainfall monitoring over limited areas. Phys. Chem. Earth 1997, 22, 265–273. [Google Scholar] [CrossRef]
- Graf, M.; El Hachem, A.; Eisele, M.; Seidel, J.; Chwala, C.; Kunstmann, H.; Bárdossy, A. Rainfall estimates from opportunistic sensors in Germany across spatio-temporal scales. J. Hydrol. Reg. Stud. 2021, 37, 100883. [Google Scholar] [CrossRef]
- Blettner, N.; Chwala, C.; Haese, B.; Hörning, S.; Kunstmann, H. Combining Commercial Microwave Link and Rain Gauge Observations to Estimate Countrywide Precipitation: A Stochastic Reconstruction and Pattern Analysis Approach. Water Resour. Res. 2022, 58, e2022WR032563. [Google Scholar] [CrossRef]
- Haese, B.; Hörning, S.; Chwala, C.; Bárdossy, A.; Schalge, B.; Kunstmann, H. Stochastic Reconstruction and Interpolation of Precipitation Fields Using Combined Information of Commercial Microwave Links and Rain Gauges. Water Resour. Res. 2017, 53, 10740–10756. [Google Scholar] [CrossRef]
- Gazit, L.; Messer, H. Sufficient Conditions for Reconstructing 2-D Rainfall Maps. IEEE Trans. Geosci. Remote Sens. 2018, 56, 6334–6343. [Google Scholar] [CrossRef]
- Abrajano, G.D.; Okada, M. Compressed sensing based detection of localized heavy rain using microwave network attenuation. In Proceedings of the 2013 7th European Conference on Antennas and Propagation (EuCAP), Gothenburg, Sweden, 8–12 April 2013; pp. 2383–2386. [Google Scholar]
- Roy, V.; Gishkori, S.; Leus, G. Dynamic rainfall monitoring using microwave links. EURASIP J. Adv. Signal Process. 2016, 2016, 77. [Google Scholar] [CrossRef]
- Abrajano, G.; Okada, M. Rainfall field reconstruction using rain attenuation of microwave mesh networks. ECTI Trans. Comput. Inf. Technol. 2013, 7, 117–125. [Google Scholar] [CrossRef]
- Eshel, A.; Alpert, P.; Messer, H. Estimating the Parameters of the Spatial Autocorrelation of Rainfall Fields by Measurements from Commercial Microwave Links. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–11. [Google Scholar] [CrossRef]
- David, N.; Alpert, P.; Messer, H. Technical Note: Novel method for water vapour monitoring using wireless communication networks measurements. Atmos. Chem. Phys. 2009, 9, 2413–2418. [Google Scholar] [CrossRef]
- Chwala, C.; Kunstmann, H.; Hipp, S.; Siart, U. A monostatic microwave transmission experiment for line integrated precipitation and humidity remote sensing. Atmos. Res. 2014, 144, 57–72. [Google Scholar] [CrossRef][Green Version]
- Montomoli, F.; Macelloni, G.; Facheris, L.; Cuccoli, F.; Del Bianco, S.; Gai, M.; Cortesi, U.; Di Natale, G.; Toccafondi, A.; Puggelli, F.; et al. Integrated Water Vapor Estimation Through Microwave Propagation Measurements: First Experiment on a Ground-to-Ground Radio Link. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–13. [Google Scholar] [CrossRef]
- Alpert, P.; Rubin, Y. First Daily Mapping of Surface Moisture from Cellular Network Data and Comparison with Both Observations/ECMWF Product. Geophys. Res. Lett. 2018, 45, 8619–8628. [Google Scholar] [CrossRef]
- Fencl, M.; Dohnal, M.; Bareš, V. Retrieving Water Vapor From an E-Band Microwave Link with an Empirical Model Not Requiring In Situ Calibration. Earth Space Sci. 2021, 8, e2021EA001911. [Google Scholar] [CrossRef]
- Song, K.; Liu, X.; Gao, T.; Zhang, P. Estimating Water Vapor Using Signals from Microwave Links below 25 GHz. Remote Sens. 2021, 13, 1409. [Google Scholar] [CrossRef]
- Pu, K.; Liu, X.; Liu, L.; Gao, T. Water Vapor Retrieval Using Commercial Microwave Links Based on the LSTM Network. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 4330–4338. [Google Scholar] [CrossRef]
- David, N.; Sendik, O.; Rubin, Y.; Messer, H.; Gao, H.O.; Rostkier-Edelstein, D.; Alpert, P. Analyzing the ability to reconstruct the moisture field using commercial microwave network data. Atmos. Res. 2019, 219, 213–222. [Google Scholar] [CrossRef]
- Rubin, Y.; Rostkier-Edelstein, D.; Chwala, C.; Alpert, P. Challenges in Diurnal Humidity Analysis from Cellular Microwave Links (CML) over Germany. Remote Sens. 2022, 14, 2353. [Google Scholar] [CrossRef]
- Han, C.; Su, G.; Bao, L.; Messer, H. Water Vapor Density Retrieval Studies Using Commercial Millimeter-Wave Links at 38 GHz and E-Band. Remote Sens. 2022, 14, 946. [Google Scholar] [CrossRef]
- Zheng, S.; Huo, J.; Cai, W.; Zhang, Y.; Li, P.; Zhang, G.; Ji, B.; Zhou, J.; Han, C. Water vapor estimation based on 1-year data of E-band millimeter wave link in North China. Atmos. Meas. Tech. 2022, 15, 1675–1687. [Google Scholar] [CrossRef]
- David, N.; Sendik, O.; Messer, H.; Alpert, P. Cellular Network Infrastructure: The Future of Fog Monitoring? Bull. Am. Meteorol. Soc. 2015, 96, 1687–1698. [Google Scholar] [CrossRef]
- David, N.; Alpert, P.; Messer, H. The potential of commercial microwave networks to monitor dense fog-feasibility study. J. Geophys. Res. Atmos. 2013, 118, 750–761. [Google Scholar] [CrossRef]
- David, N.; Gao, H.O. Using Cell-Phone Tower Signals for Detecting the Precursors of Fog. J. Geophys. Res. Atmos. 2018, 123, 1325–1338. [Google Scholar] [CrossRef]
- Harel, O.; David, N.; Alpert, P.; Messer, H. The Potential of Microwave Communication Networks to Detect Dew—Experimental Study. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 4396–4404. [Google Scholar] [CrossRef]
- Berne, A.; Schleiss, M. Retrieval of the rain drop size distribution using telecommunication dual-polarization microwave links. In Proceedings of the 34th Conference on Radar Meteorology, Williamsburg, VA, USA, 5–9 October 2009. [Google Scholar]
- Song, K.; Liu, X.; Gao, T.; He, B. Raindrop Size Distribution Retrieval Using Joint Dual-Frequency and Dual-Polarization Microwave Links. Adv. Meteorol. 2019, 2019, 7251870 . [Google Scholar] [CrossRef]
- van Leth, T.C.; Leijnse, H.; Overeem, A.; Uijlenhoet, R. Estimating raindrop size distributions using microwave link measurements: Potential and limitations. Atmos. Meas. Tech. 2020, 13, 1797–1815. [Google Scholar] [CrossRef]
- Upton, G.J.G.; Cummings, R.J.; Holt, A.R. Identification of melting snow using data from dual-frequency microwave links. IET Microw. Antennas Propag. 2007, 1, 282–288. [Google Scholar] [CrossRef]
- Upton, G.J.G.; Cummings, R.J.; Holt, A.R. The potential of microwave links for providing information concerning the amount and type of precipitation. In Proceedings of the 2008 IEEE International Conference Acoustic Speech Signal Process, Las Vegas, NV, USA, 31 March–4 April 2008; pp. 5153–5156. [Google Scholar]
- Pu, K.; Liu, X.; Hu, S.; Gao, T. Hydrometeor Identification Using Multiple-Frequency Microwave Links: A Numerical Simulation. Remote Sens. 2020, 12, 2158. [Google Scholar] [CrossRef]
- Pu, K.; Liu, X.; Xian, M.; Gao, T. Machine Learning Classification of Rainfall Types Based on the Differential Attenuation of Multiple Frequency Microwave Links. IEEE Trans. Geosci. Remote Sens. 2020, 58, 6888–6899. [Google Scholar] [CrossRef]
- Ostrometzky, J.; Cherkassky, D.; Messer, H. Accumulated Mixed Precipitation Estimation Using Measurements from Multiple Microwave Links. Adv. Meteorol. 2015, 2015, 707646. [Google Scholar] [CrossRef]
- Leijnse, H.; Uijlenhoet, R.; Stricker, J.N.M. Hydrometeorological application of a microwave link: 1. Evaporation. Water Resour. Res. 2007, 43, W04416. [Google Scholar] [CrossRef]
- David, N.; Gao, H.O. Using Cellular Communication Networks to Detect Air Pollution. Environ. Sci. Technol. 2016, 50, 9442–9451. [Google Scholar] [CrossRef] [PubMed]
- Guyot, A.; Pudashine, J.; Uijlenhoet, R.; Protat, A.; Pauwels, V.R.N.; Louf, V.; Walker, J.P. Wildfire Smoke Particulate Matter Concentration Measurements Using Radio Links from Cellular Communication Networks. AGU Adv. 2021, 2, e2020AV000258. [Google Scholar] [CrossRef]
- David, N.; Gao, H.O. A Data-Driven Approach for Studying the Washout Effects of Rain on Air Pollution. Int. J. Mar. Environ. Sci. 2020, 166, 264–268. [Google Scholar]
- Overeem, A.; Leijnse, H.; Uijlenhoet, R. Two and a half years of country-wide rainfall maps using radio links from commercial cellular telecommunication networks. Water Resour. Res. 2016, 52, 8039–8065. [Google Scholar] [CrossRef]
- Overeem, A.; Leijnse, H.; Uijlenhoet, R. Country-wide rainfall maps from cellular communication networks. Proc. Natl. Acad. Sci. USA 2013, 110, 2741–2745. [Google Scholar] [CrossRef]
- Messer, H.; Zinevich, A.; Alpert, P. Environmental sensor networks using existing wireless communication systems for rainfall and wind velocity measurements. IEEE Instrum. Meas. Mag. 2012, 15, 32–38. [Google Scholar] [CrossRef]
- Zinevich, A.; Messer, H.; Alpert, P. Frontal Rainfall Observation by a Commercial Microwave Communication Network. J. Appl. Meteorol. Climatol. 2009, 48, 1317–1334. [Google Scholar] [CrossRef]
- Bianchi, B.; Rieckermann, J.; Berne, A. Quality control of rain gauge measurements using telecommunication microwave links. J. Hydrol. 2013, 492, 15–23. [Google Scholar] [CrossRef]
- Fencl, M.; Dohnal, M.; Rieckermann, J.; Bareš, V. Gauge-adjusted rainfall estimates from commercial microwave links. Hydrol. Earth Syst. Sci. 2017, 21, 617–634. [Google Scholar] [CrossRef]
- Krämer, S.; Verworn, H.R.; Redder, A. Improvement of X-band radar rainfall estimates using a microwave link. Atmos. Res. 2005, 77, 278–299. [Google Scholar] [CrossRef]
- Rahimi, A.R.; Holt, A.R.; Upton, G.J.G. Attenuation Calibration of an X-Band Weather Radar Using a Microwave Link. J. Atmos. Ocean. Technol. 2006, 23, 395–405. [Google Scholar] [CrossRef]
- Kim, M.-S.; Kwon, B.H. Attenuation Correction of X-Band Radar Reflectivity Using Adjacent Multiple Microwave Links. Remote Sens. 2020, 12, 2133. [Google Scholar] [CrossRef]
- Xue, Y.; Liu, X.-c.; Gao, T.-c.; Yang, C.-y.; Song, K. Regional Attenuation Correction of Weather Radar Using a Distributed Microwave-Links Network. Adv. Meteorol. 2017, 2017, 8621239 . [Google Scholar] [CrossRef]
- Zhang, P.; Liu, X.; Li, Z.; Zhou, Z.; Song, K.; Yang, P. Attenuation Correction of Weather Radar Reflectivity with Arbitrary Oriented Microwave Link. Adv. Meteorol. 2017, 2017, 6124149. [Google Scholar] [CrossRef]
- Trömel, S.; Ziegert, M.; Ryzhkov, A.V.; Chwala, C.; Simmer, C. Using Microwave Backhaul Links to Optimize the Performance of Algorithms for Rainfall Estimation and Attenuation Correction. J. Atmos. Ocean. Technol. 2014, 31, 1748–1760. [Google Scholar] [CrossRef]
- Cummings, R.J.; Upton, G.J.G.; Holt, A.R.; Kitchen, M. Using microwave links to adjust the radar rainfall field. Adv. Water. Resour. 2009, 32, 1003–1010. [Google Scholar] [CrossRef]
- Liberman, Y.; Samuels, R.; Alpert, P.; Messer, H. New algorithm for integration between wireless microwave sensor network and radar for improved rainfall measurement and mapping. Atmos. Meas. Tech. 2014, 7, 3549–3563. [Google Scholar] [CrossRef]
- Raich, R.; Alpert, P.; Messer, H. Vertical Precipitation Estimation Using Microwave Links in Conjunction with Weather Radar. Environments 2018, 5, 74. [Google Scholar] [CrossRef]
- Kumah, K.K.; Maathuis, B.H.P.; Hoedjes, J.C.B.; Su, Z. Near real-time estimation of high spatiotemporal resolution rainfall from cloud top properties of the MSG satellite and commercial microwave link rainfall intensities. Atmos. Res. 2022, 279, 106357. [Google Scholar] [CrossRef]
- Rios Gaona, M.F.; Overeem, A.; Brasjen, A.M.; Meirink, J.F.; Leijnse, H.; Uijlenhoet, R. Evaluation of Rainfall Products Derived from Satellites and Microwave Links for The Netherlands. IEEE Trans. Geosci. Remote Sens. 2017, 55, 6849–6859. [Google Scholar] [CrossRef]
- Grum, M.; Kraemer, S.; Verworn, H.-R.; Redder, A. Combined use of point rain gauges, radar, microwave link and level measurements in urban hydrological modelling. Atmos. Res. 2005, 77, 313–321. [Google Scholar] [CrossRef]
- Stransky, D.; Fencl, M.; Bares, V. Runoff prediction using rainfall data from microwave links: Tabor case study. Water Sci. Technol. 2018, 2017, 351–359. [Google Scholar] [CrossRef] [PubMed]
- Pastorek, J.; Fencl, M.; Rieckermann, J.; Bareš, V. Commercial microwave links for urban drainage modelling: The effect of link characteristics and their position on runoff simulations. J. Environ. Manag. 2019, 251, 109522. [Google Scholar] [CrossRef] [PubMed]
- Turko, M.; Gosset, M.; Bouvier, C.; Chahinian, N.; Alcoba, M.; Kacou, M.; Yappi, A. Rainfall measurement from mobile telecommunication network and potential benefit for urban hydrology in Africa: A simulation framework for uncertainty propagation analysis. Proc. Int. Assoc. Hydrol. Sci. 2020, 383, 237–240. [Google Scholar] [CrossRef]
- Pastorek, J.; Fencl, M.; Rieckermann, J.; Bareš, V. Microwave link rainfall data for urban drainage modelling: Reducing the systematic errors under data-scarce conditions. In Proceedings of the 15th International Conference on Urban Drainage (ICUD 2021), Melbourne, Australia, 25–28 October 2021. [Google Scholar]
- Pastorek, J.; Fencl, M.; Bareš, V. Uncertainties in discharge predictions based on microwave link rainfall estimates in a small urban catchment. J. Hydrol. 2023, 617, 129051. [Google Scholar] [CrossRef]
- Cazzaniga, G.; De Michele, C.; D’Amico, M.; Deidda, C.; Ghezzi, A.; Nebuloni, R. Hydrological response of a peri-urban catchment exploiting conventional and unconventional rainfall observations: The case study of Lambro Catchment. Hydrol. Earth Syst. Sci. 2022, 26, 2093–2111. [Google Scholar] [CrossRef]
- Smiatek, G.; Keis, F.; Chwala, C.; Fersch, B.; Kunstmann, H. Potential of commercial microwave link network derived rainfall for river runoff simulations. Environ. Res. Lett. 2017, 12, 034026. [Google Scholar] [CrossRef]
- Brauer, C.C.; Overeem, A.; Leijnse, H.; Uijlenhoet, R. The effect of differences between rainfall measurement techniques on groundwater and discharge simulations in a lowland catchment. Hydrol. Process. 2016, 30, 3885–3900. [Google Scholar] [CrossRef]
- Hoedjes, J.C.B.; Kooiman, A.; Maathuis, B.H.P.; Said, M.Y.; Becht, R.; Limo, A.; Mumo, M.; Nduhiu-Mathenge, J.; Shaka, A.; Su, B. A Conceptual Flash Flood Early Warning System for Africa, Based on Terrestrial Microwave Links and Flash Flood Guidance. ISPRS Int. J. Geo-Inf. 2014, 3, 584–598. [Google Scholar] [CrossRef]
- Eshel, A.; Messer, H.; Ostrometzky, J.; Raich, R.; Alpert, P.; Laronne, J.B. On the Use of Measurements from a Commercial Microwave Link for Evaluation of Flash Floods in Arid Regions. Atmos. Chem. Phys. Discuss. 2017, 2017, 1–25. [Google Scholar] [CrossRef]
- David, N.; Alpert, P.; Messer, H. The potential of cellular network infrastructures for sudden rainfall monitoring in dry climate regions. Atmos. Res. 2013, 131, 13–21. [Google Scholar] [CrossRef]
- Gustilo, R.C. Design of Wireless Disaster Alarm System Using Microwave Links. J. Telecommun. Electron. Comput. Eng. 2018, 10, 103–108. [Google Scholar]
- Trömel, S.; Chwala, C.; Furusho-Percot, C.; Henken, C.C.; Polz, J.; Potthast, R.; Reinoso-Rondinel, R.; Simmer, C. Near-Realtime Quantitative Precipitation Estimation and Prediction (RealPEP). Bull. Am. Meteorol. Soc. 2021, 102, E1591–E1596. [Google Scholar] [CrossRef]
- Ostrometzky, J.; Eshel, A. Empirical Study of the Quantization Induced Bias in Commercial Microwave Links’ Min/Max Attenuation Measurements for Rain Monitoring. Environments 2018, 5, 80. [Google Scholar] [CrossRef]
- Roversi, G.; Alberoni, P.P.; Fornasiero, A.; Porcù, F. Commercial microwave links as a tool for operational rainfall monitoring in Northern Italy. Atmos. Meas. Tech. 2020, 13, 5779–5797. [Google Scholar] [CrossRef]
- van Leth, T.C.; Overeem, A.; Leijnse, H.; Uijlenhoet, R. A measurement campaign to assess sources of error in microwave link rainfall estimation. Atmos. Meas. Tech. 2018, 11, 4645–4669. [Google Scholar] [CrossRef]
- Pu, K.; Liu, X.; Sun, X.; Li, S. Error Analysis of Rainfall Inversion Based on Commercial Microwave Links With A–R Relationship Considering the Rainfall Features. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–12. [Google Scholar] [CrossRef]
- Zinevich, A.; Alpert, P.; Messer, H. Estimation of rainfall fields using commercial microwave communication networks of variable density. Adv. Water. Resour. 2008, 31, 1470–1480. [Google Scholar] [CrossRef]
- Ostrometzky, J.; Messer, H. Comparison of Different Methodologies of Parameter-Estimation from Extreme Values. IEEE Signal Process. Lett. 2017, 24, 1293–1297. [Google Scholar] [CrossRef]
- Pudashine, J.; Guyot, A.; Petitjean, F.; Pauwels, V.R.N.; Uijlenhoet, R.; Seed, A.; Prakash, M.; Walker, J.P. Deep Learning for an Improved Prediction of Rainfall Retrievals from Commercial Microwave Links. Water Resour. Res. 2020, 56, e2019WR026255. [Google Scholar] [CrossRef]
- Guerra-Moreno, I.; Navarro-Mesa, J.L.; García, A.G.; Suarez Araujo, C. On the Application of a Recurrent Neural Network for Rainfall Quantification Based on the Received Signal from Microwave Links. In Advances in Computational Intelligence; Springer International Publishing: Cham, Switzerland, 2019; pp. 39–51. [Google Scholar]
- Pudashine, J.; Guyot, A.; Overeem, A.; Pauwels, V.R.N.; Seed, A.; Uijlenhoet, R.; Prakash, M.; Walker, J.P. Rainfall retrieval using commercial microwave links: Effect of sampling strategy on retrieval accuracy. J. Hydrol. 2021, 603, 126909. [Google Scholar] [CrossRef]
- de Vos, L.W.; Overeem, A.; Leijnse, H.; Uijlenhoet, R. Rainfall Estimation Accuracy of a Nationwide Instantaneously Sampling Commercial Microwave Link Network: Error Dependency on Known Characteristics. J. Atmos. Ocean. Technol. 2019, 36, 1267–1283. [Google Scholar] [CrossRef]
- Messer, H. Rainfall Monitoring Using Cellular Networks [In the Spotlight]. IEEE Signal Process. Mag. 2007, 24, 142–144. [Google Scholar] [CrossRef]
- Fencl, M.; Dohnal, M.; Valtr, P.; Grabner, M.; Bareš, V. Data and code for the paper Atmospheric Observations with E-band Microwave Links—Challenges and Opportunities. Atmos. Meas. Tech. 2020, 13, 6559–6578. [Google Scholar] [CrossRef]
- Andersson, J.C.M.; Olsson, J.; van de Beek, R.; Hansryd, J. OpenMRG: Open data from Microwave links, Radar, and Gauges for rainfall quantification in Gothenburg, Sweden. Earth Syst. Sci. Data 2022, 14, 5411–5426. [Google Scholar] [CrossRef]
- Špačková, A.; Bareš, V.; Fencl, M.; Schleiss, M.; Jaffrain, J.; Berne, A.; Rieckermann, J. A year of attenuation data from a commercial dual-polarized duplex microwave link with concurrent disdrometer, rain gauge, and weather observations. Earth Syst. Sci. Data 2021, 13, 4219–4240. [Google Scholar] [CrossRef]
- Berne, A.; Uijlenhoet, R. Path-averaged rainfall estimation using microwave links: Uncertainty due to spatial rainfall variability. Geophys. Res. Lett. 2007, 34, L07403. [Google Scholar] [CrossRef]
- Uijlenhoet, R.; Leijnse, H.; Berne, A. Errors and Uncertainties in Microwave Link Rainfall Estimation Explored Using Drop Size Measurements and High-Resolution Radar Data. J. Hydrometeorol. 2010, 11, 1330–1344. [Google Scholar] [CrossRef]
- Gaona, M.F.R.; Overeem, A.; Leijnse, H.; Uijlenhoet, R. Measurement and interpolation uncertainties in rainfall maps from cellular communication networks. Hydrol. Earth Syst. Sci. 2015, 19, 3571–3584. [Google Scholar] [CrossRef]
- Chwala, C.; Keis, F.; Kunstmann, H. Real-time data acquisition of commercial microwave link networks for hydrometeorological applications. Atmos. Meas. Tech. 2016, 9, 991–999. [Google Scholar] [CrossRef]
- Holt, A.R.; Cummings, R.J.; Upton, G.J.G.; Bradford, W.J. Rain rates, drop size information, and precipitation type, obtained from one-way differential propagation phase and attenuation along a microwave link. Radio Sci. 2008, 43, 1–18. [Google Scholar] [CrossRef]
- Pudashine, J.; Velasco-Forero, C.; Curtis, M.; Guyot, A.; Pauwels, V.R.N.; Walker, J.P.; Seed, A. Probabilistic Attenuation Nowcasting for the 5G Telecommunication Networks. IEEE Antennas Wirel. Propag. Lett. 2021, 20, 973–977. [Google Scholar] [CrossRef]
- Xian, M.; Liu, X.; Yin, M.; Song, K.; Zhao, S.; Gao, T. Rainfall Monitoring Based on Machine Learning by Earth-Space Link in the Ku Band. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 3656–3668. [Google Scholar] [CrossRef]
- Habi, H.V.; Messer, H. Recurrent Neural Network for Rain Estimation Using Commercial Microwave Links. IEEE Trans. Geosci. Remote Sens. 2021, 59, 3672–3681. [Google Scholar] [CrossRef]
- Messer, H.; Eshel, A.; Habi, H.V.; Sagiv, S.; Zheng, X. Rain Field Retrieval by Ground-Level Sensors of Various Types. Front. Signal Process. 2022, 2, 877336. [Google Scholar] [CrossRef]
- Gazit, L.; Messer, H. Advancements in the Statistical Study, Modeling, and Simulation of Microwave-Links in Cellular Backhaul Networks. Environments 2018, 5, 75. [Google Scholar] [CrossRef]
- Blettner, N.; Fencl, M.; Bareš, V.; Kunstmann, H.; Chwala, C. Transboundary Rainfall Estimation Using Commercial Microwave Links. Earth Space Sci. 2023, 10, e2023EA002869. [Google Scholar] [CrossRef]
- Moshe, D.B.; Messer, H.; Nathan, R.; Sapir, N. Empirical Study on the Effect of Birds on Commercial Microwave Links. IEEE Access 2022, 10, 103819–103826. [Google Scholar] [CrossRef]
- Hunt, K.P.; Niemeier, J.J.; Cunha, L.K.d.; Kruger, A. Using Cellular Network Signal Strength to Monitor Vegetation Characteristics. IEEE Geosci. Remote Sens. Lett. 2011, 8, 346–349. [Google Scholar] [CrossRef]
- Zhang, P.; Liu, X.; Zou, M. Reconstructing and Nowcasting the Rainfall Field by a CML Network. Earth Space Sci. 2023, 10, e2023EA002909. [Google Scholar] [CrossRef]
- Imhoff, R.O.; Overeem, A.; Brauer, C.C.; Leijnse, H.; Weerts, A.H.; Uijlenhoet, R. Rainfall Nowcasting Using Commercial Microwave Links. Geophys. Res. Lett. 2020, 47, 1–10. [Google Scholar] [CrossRef]
- Ostrometzky, J.; Raich, R.; Bao, L.; Hansryd, J.; Messer, H. The Wet-Antenna Effect—A Factor to be Considered in Future Communication Networks. IEEE Trans. Antennas Propag. 2018, 66, 315–322. [Google Scholar] [CrossRef]
- Saggese, F.; Lottici, V.; Giannetti, F. Rainfall Map from Attenuation Data Fusion of Satellite Broadcast and Commercial Microwave Links. Sensors 2022, 22, 7019. [Google Scholar] [CrossRef]
- Janco, R.; Ostrometzky, J.; Messer, H. In-City Rain Mapping from Commercial Microwave Links—Challenges and Opportunities. Sensors 2023, 23, 4653. [Google Scholar] [CrossRef]
- Habi, H.V.; Messer, H. Uncertainties in Short Commercial Microwave Links Fading Due to Rain. In Proceedings of the ICASSP 2020 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Barcelona, Spain, 4–8 May 2020; pp. 9006–9010. [Google Scholar]
- Jacoby, D.; Ostrometzky, J.; Messer, H. Model-based vs. Data-driven Approaches for Predicting Rain-induced Attenuation in Commercial Microwave Links: A Comparative Empirical Study. In Proceedings of the ICASSP 2023–2023 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Rhodes Island, Greece, 4–10 June 2023; pp. 1–5. [Google Scholar]
- Daher, A.; Al Sakka, H.; Chaaban, A.K. Low complexity single-layer neural network for enhanced rainfall estimation using microwave links. J. Hydroinformatics 2023, 25, 101–112. [Google Scholar] [CrossRef]
- Wolff, W.; Overeem, A.; Leijnse, H.; Uijlenhoet, R. Rainfall retrieval algorithm for commercial microwave links: Stochastic calibration. Atmos. Meas. Tech. 2022, 15, 485–502. [Google Scholar] [CrossRef]
- Nebuloni, R.; Cazzaniga, G.; D’Amico, M.; Deidda, C.; De Michele, C. Comparison of CML Rainfall Data against Rain Gauges and Disdrometers in a Mountainous Environment. Sensors 2022, 22, 3218. [Google Scholar] [CrossRef]
- Peters, G.; Fischer, B.; Münster, H.; Clemens, M.; Wagner, A. Profiles of Raindrop Size Distributions as Retrieved by Microrain Radars. J. Appl. Meteorol. 2005, 44, 1930–1949. [Google Scholar] [CrossRef]
- Narayana Rao, T.; Kirankumar, N.V.P.; Radhakrishna, B.; Narayana Rao, D. On the variability of the shape-slope parameter relations of the gamma raindrop size distribution model. Geophys. Res. Lett. 2006, 33, L22809. [Google Scholar] [CrossRef]
- Tollefson, J. Mobile-phone signals bolster street-level rain forecasts. Nature 2017, 544, 146–147. [Google Scholar] [CrossRef]
- Kamtchoum, E.V.; Takougang, A.C.N.; Djamegni, C.T. Short-term rainfall prediction using MLA based on commercial microwave links of mobile telecommunication networks. Bull. Atmos. Sci. Technol. 2022, 3, 5. [Google Scholar] [CrossRef]
- Han, C.; Huo, J.; Gao, Q.; Su, G.; Wang, H. Rainfall Monitoring Based on Next-Generation Millimeter-Wave Backhaul Technologies in a Dense Urban Environment. Remote Sens. 2020, 12, 1045. [Google Scholar] [CrossRef]
- Zheng, S.; Han, C.; Huo, J.; Cai, W.; Zhang, Y.; Li, P.; Zhang, G.; Ji, B.; Zhou, J. Research on Rainfall Monitoring Based on E-Band Millimeter Wave Link in East China. Sensors 2021, 21, 1670. [Google Scholar] [CrossRef]
- Barthès, L.; Mallet, C. Rainfall measurement from the opportunistic use of an Earth–space link in the Ku band. Atmos. Meas. Tech. 2013, 6, 2181–2193. [Google Scholar] [CrossRef]
- Lu, C.S.; Zhao, Z.W.; Wu, Z.S.; Lin, L.K.; Thiennviboon, P.; Zhang, X.; Lv, Z.F. A New Rain Attenuation Prediction Model for the Earth-Space Links. IEEE Trans. Antennas Propag. 2018, 66, 5432–5442. [Google Scholar] [CrossRef]
- Xian, M.-H.; Liu, X.-C.; Yin, M.; Song, K.; Gao, T.-C. Inversion of vertical rainfall field based on earth-space links. Acta Phys. Sin. 2020, 69, 024301. [Google Scholar] [CrossRef]
- Shen, X.; Huang, D.D.; Song, B.; Vincent, C.; Togneri, R. 3-D Tomographic Reconstruction of Rain Field Using Microwave Signals from LEO Satellites: Principle and Simulation Results. IEEE Trans. Geosci. Remote Sens. 2019, 57, 5434–5446. [Google Scholar] [CrossRef]
- Defeng, H.; Lu, X.; Xuxiang, F.; Wanyu, W. A hypothesis of 3D rainfall tomography using satellite signals. J. Commun. Inf. Netw. 2016, 1, 134–142. [Google Scholar] [CrossRef]
- Levchenko, I.; Xu, S.; Wu, Y.-L.; Bazaka, K. Hopes and concerns for astronomy of satellite constellations. Nat. Astron. 2020, 4, 1012–1014. [Google Scholar] [CrossRef]
- Zhao, Y.; Liu, X.; Pu, K.; Ye, J.; Xian, M. Research on the Method of Rainfall Field Retrieval Based on the Combination of Earth–Space Links and Horizontal Microwave Links. Remote Sens. 2022, 14, 2220. [Google Scholar] [CrossRef]
- Saggese, F.; Giannetti, F.; Lottici, V. A Novel Approach to Rainfall Rate Estimation based on Fusing Measurements from Terrestrial Microwave and Satellite Links. In Proceedings of the 2020 XXXIIIrd General Assembly and Scientific Symposium of the International Union of Radio Science, Rome, Italy, 29 August–5 September 2020; pp. 1–4. [Google Scholar]
- Diba, F.D.; Samad, M.A.; Ghimire, J.; Choi, D.Y. Wireless Telecommunication Links for Rainfall Monitoring: Deep Learning Approach and Experimental Results. IEEE Access 2021, 9, 66769–66780. [Google Scholar] [CrossRef]
- Okamura, S.; Oguchi, T. Electromagnetic wave propagation in rain and polarization effects. Proc. Jpn. Academy. Ser. B Phys. Biol. Sci. 2010, 86, 539–562. [Google Scholar] [CrossRef]
- Dalip Kumar, V. Effect of environmental parameters on GSM and GPS. Indian J. Sci. Technol. 2014, 7, 1183–1188. [Google Scholar]
- Yadnya, M.; Sudiartha, I. Simulation of broadcast level signal mobile station 3G network rain condition in Mataram. In Proceedings of the 2016 Asia Pacific Conference on Multimedia and Broadcasting (APMediaCast), Bali, Indonesia, 17–19 November 2016; pp. 24–28. [Google Scholar]
- Helhel, S.; Göksu, H.; Ozen, S. Investigation of GSM signal variation: Dry and wet earth effects. Prog. Electromagn. Res. B 2008, 1, 147–157. [Google Scholar] [CrossRef]
- Geng, Y.; Edwards, R.M.; Davis, J.G.; Lepper, P.; Pattison, I.; Khouakhi, A.; Clark, B.; Diamantides, K.; Dai, C.; Kaczmarczyk, M.; et al. Impact of Heavy Rain on Signal Propagation in the UK and Mexican 4G and 5G Networks. In Proceedings of the 2019 13th European Conference on Antennas and Propagation (EuCAP), Krakow, Poland, 31 March–5 April 2019; pp. 1–5. [Google Scholar]
- Micheli, D.; Muratore, G.; Vannelli, A.; Scaloni, A.; Sgheiz, M.; Cirella, P. Rain Effect on 4G LTE In-Car Electromagnetic Propagation Analyzed Through MDT Radio Data Measurement Reported by Mobile Phones. IEEE Trans. Antennas Propag. 2021, 69, 8641–8651. [Google Scholar] [CrossRef]
- Blevis, B. Losses due to rain on radomes and antenna reflecting surfaces. IEEE Trans. Antennas Propag. 1965, 13, 175–176. [Google Scholar] [CrossRef]
- Cheah, J.Y.C. Wet antenna effect on VSAT rain margin. IEEE Trans. Commun. 1993, 41, 1238–1244. [Google Scholar] [CrossRef]
- Beritelli, F.; Capizzi, G.; Lo Sciuto, G.; Scaglione, F.; Połap, D.; Woźniak, M. A Neural Network Pattern Recognition Approach to Automatic Rainfall Classification by Using Signal Strength in LTE/4G Networks. In Proceedings of the International Joint Conference on Rough Sets, Olsztyn, Poland, 3–7 July 2017; pp. 505–512. [Google Scholar]
- Song, K.; Liu, X.; Gao, T.; Yin, M.; He, B. The Feasibility Analysis of Cellphone Signal to Detect the Rain: Experimental Study. IEEE Geosci. Remote Sens. Lett. 2020, 17, 1158–1162. [Google Scholar] [CrossRef]
- Fang, S.-H.; Cheng, Y.-C.; Chien, Y.-R. Exploiting Sensed Radio Strength and Precipitation for Improved Distance Estimation. IEEE Sens. J. 2018, 18, 6863–6873. [Google Scholar] [CrossRef]
- Liu, D.; Zhang, Y.; Zhang, J.; Xiong, L.; Liu, P.; Chen, H.; Yin, J. Rainfall estimation using measurement report data from time-division long term evolution networks. J. Hydrol. 2021, 600, 126530. [Google Scholar] [CrossRef]
- Christofilakis, V.; Tatsis, G.; Chronopoulos, S.K.; Sakkas, A.; Skrivanos, A.G.; Peppas, K.P.; Nistazakis, H.E.; Baldoumas, G.; Kostarakis, P. Earth-to-Earth Microwave Rain Attenuation Measurements: A Survey on the Recent Literature. Symmetry 2020, 12, 1440. [Google Scholar] [CrossRef]
- Messer, H. Capitalizing on Cellular Technology—Opportunities and Challenges for Near Ground Weather Monitoring. Environments 2018, 5, 73. [Google Scholar] [CrossRef]
- Fencl, M.; Dohnal, M.; Mudroch, M.; Bareš, V. Data and code for the paper Atmospheric Observations with E-band Microwave Links—Challenges and Opportunities. Atmos. Meas. Tech. 2020, 13, 6559–6578. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).