Applicability Assessment of GPM IMERG Satellite Heavy-Rainfall-Informed Reservoir Short-Term Inflow Forecast and Optimal Operation: A Case Study of Wan’an Reservoir in China
Abstract
:1. Introduction
2. Study Area and Materials
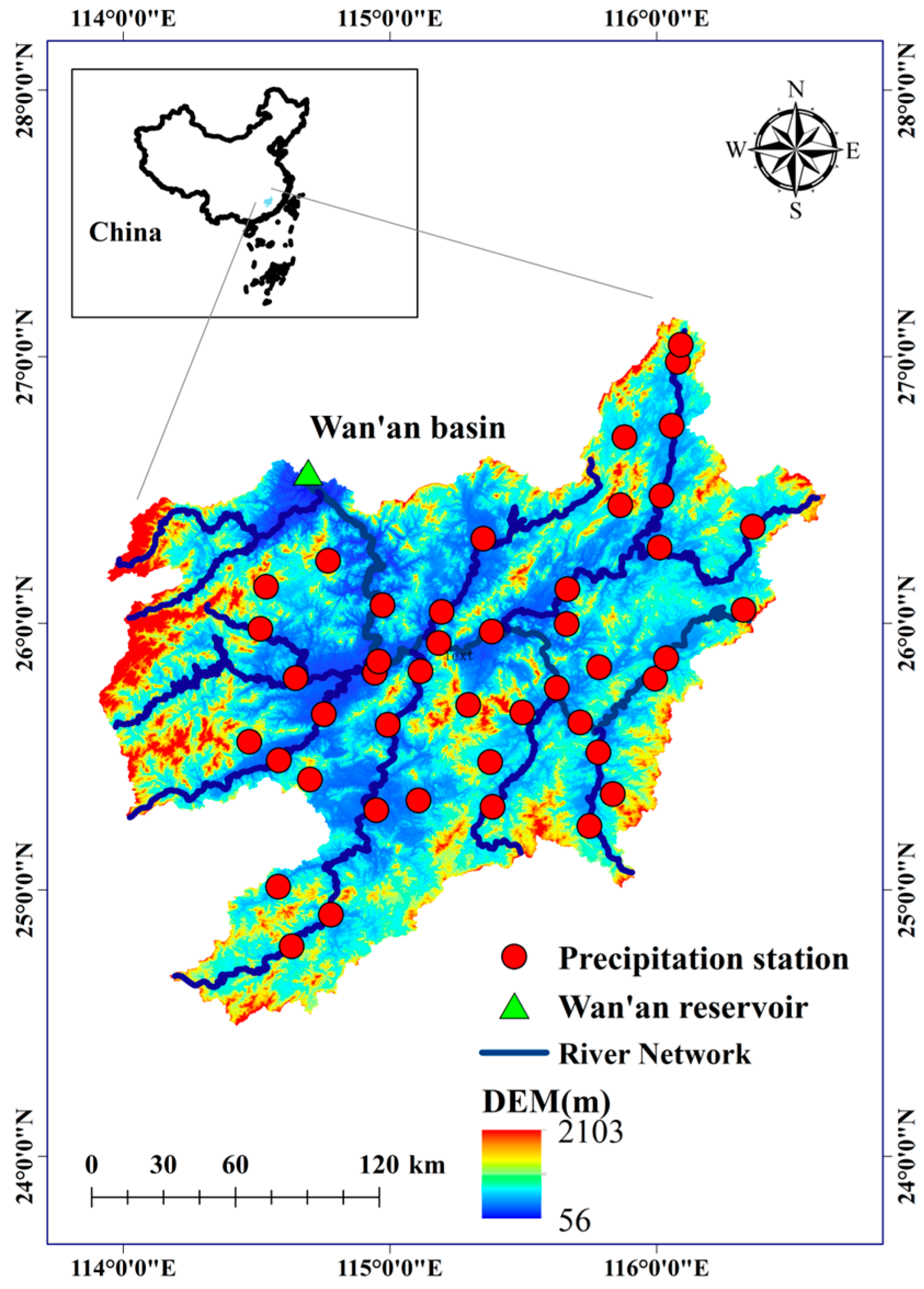
2.1. Study Area and Reservoir
2.2. Hydro-Meteorological Data
3. Methodology
3.1. Storm Stochastic Generator
3.2. Flood Forecasting Based on GR4H Model
3.3. Reservoir System Construction
3.3.1. Reservoir Optimal Operation Model
3.3.2. Robustness Criteria of Reservoir Operation Assessment
4. Results
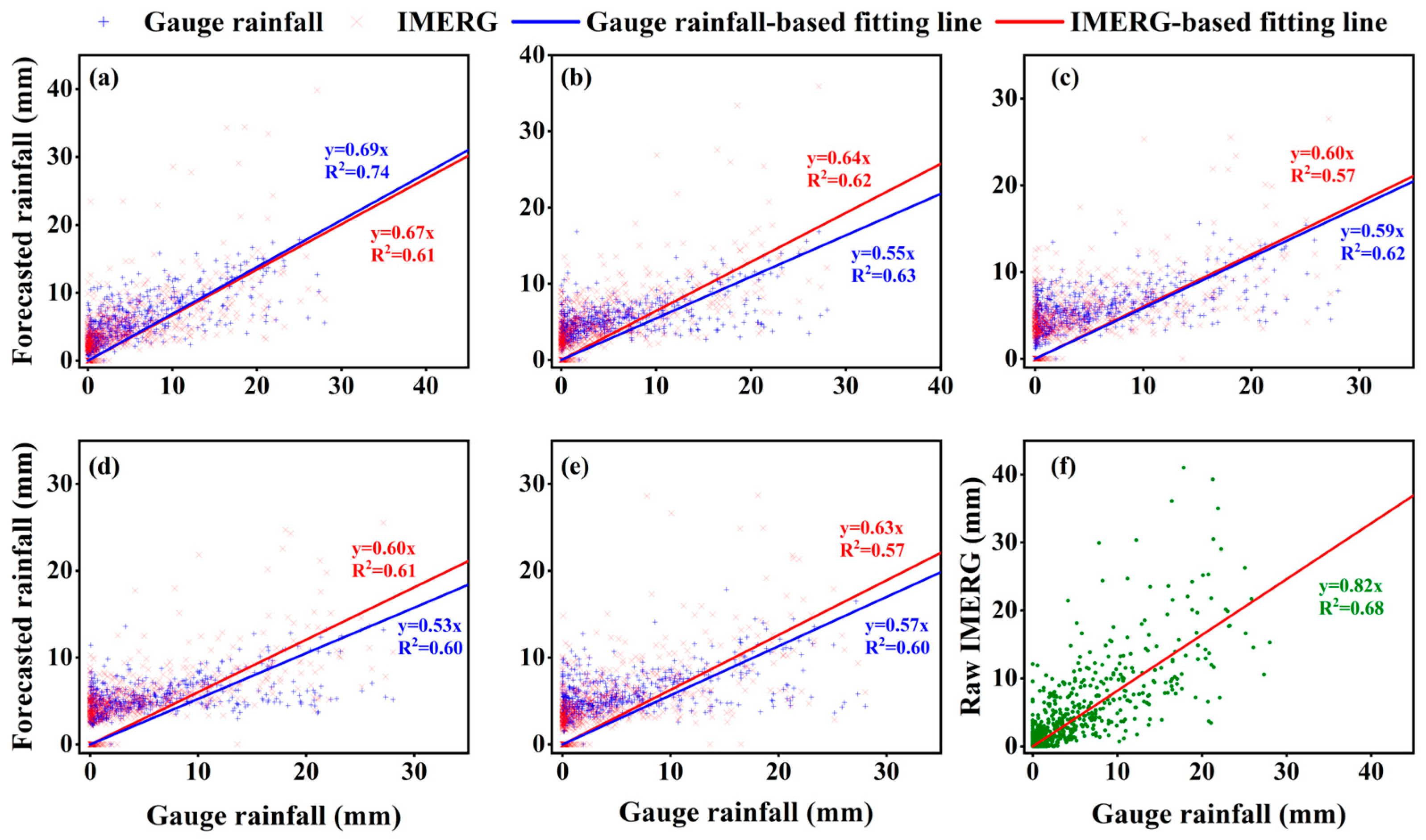
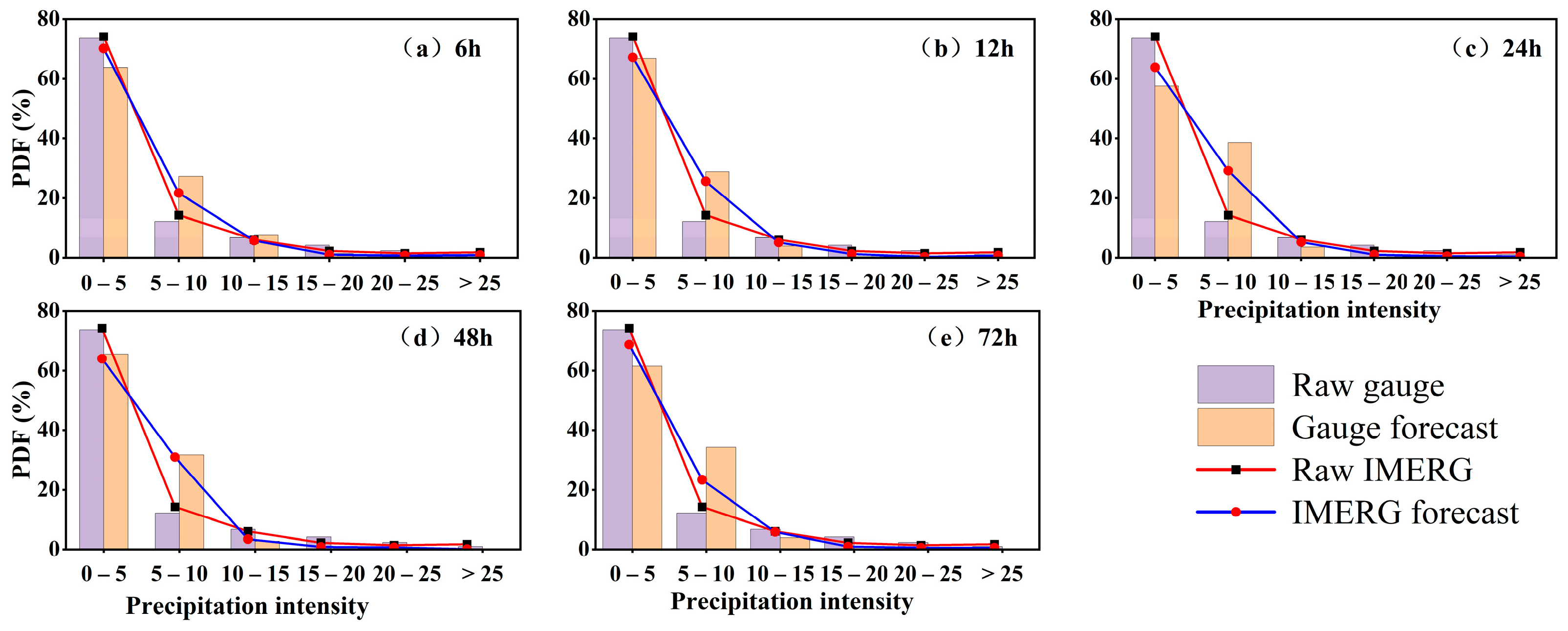
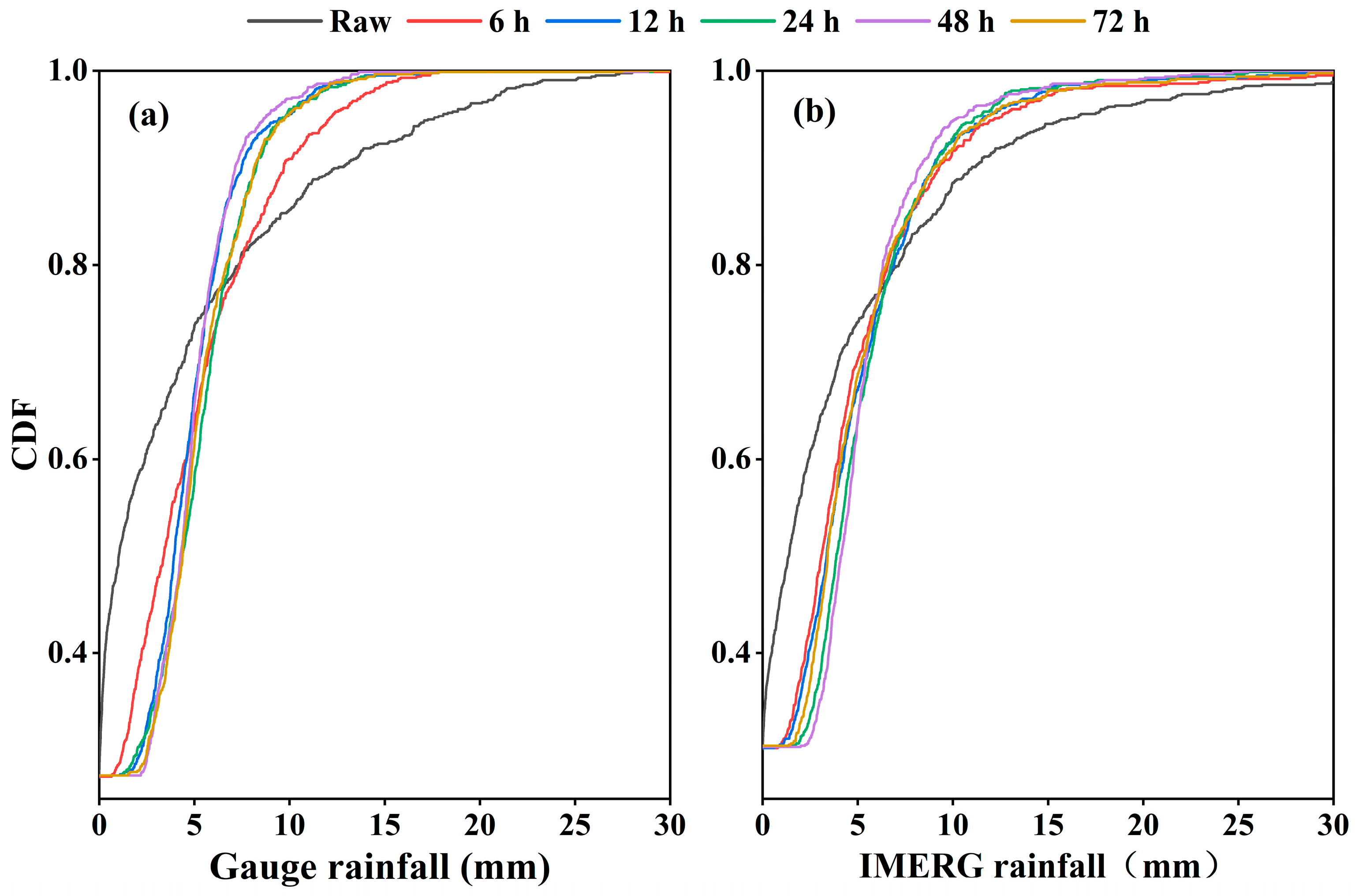
4.1. Forecasted IMERG Heavy Rainfall at Sub-Daily and Daily Lead Times
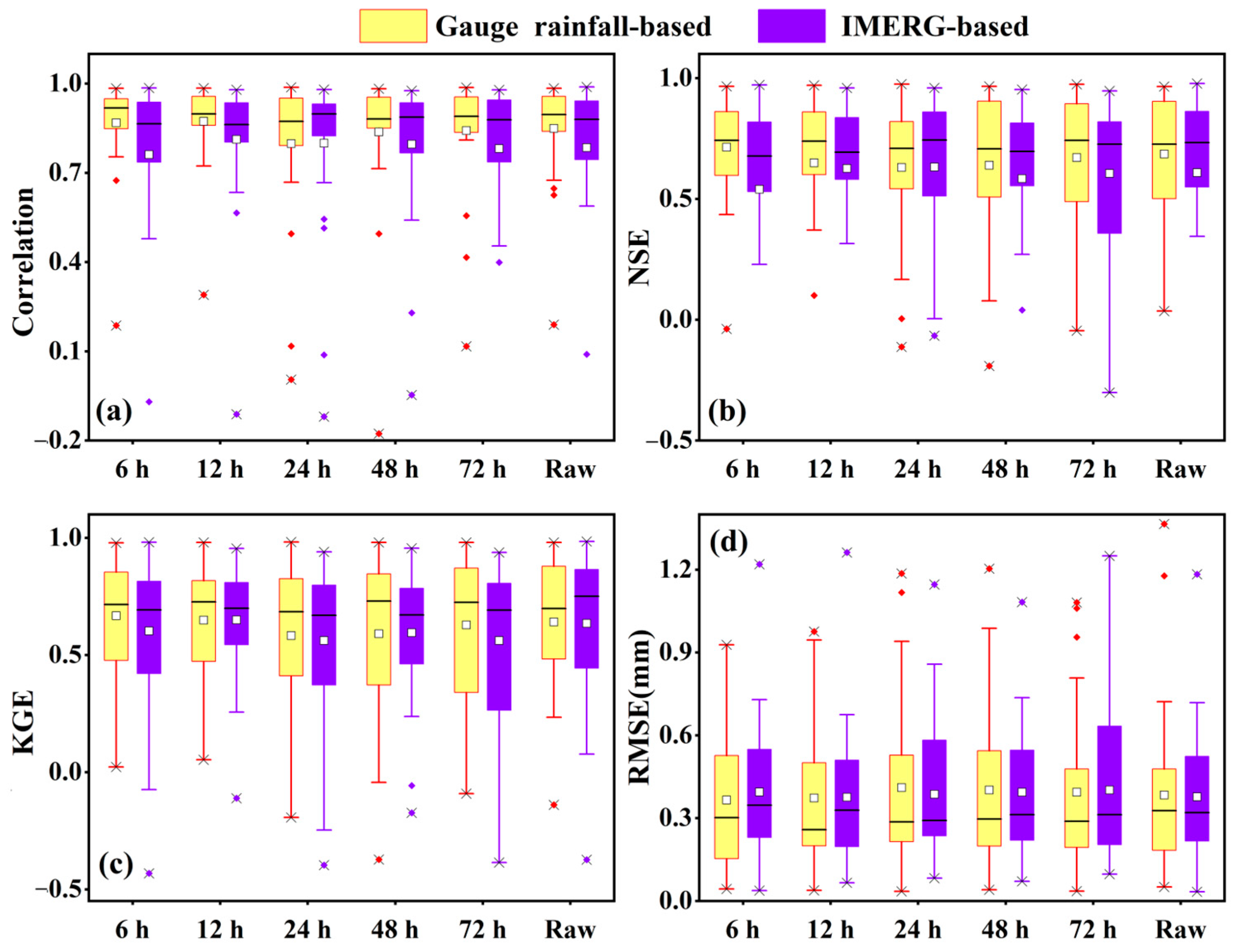
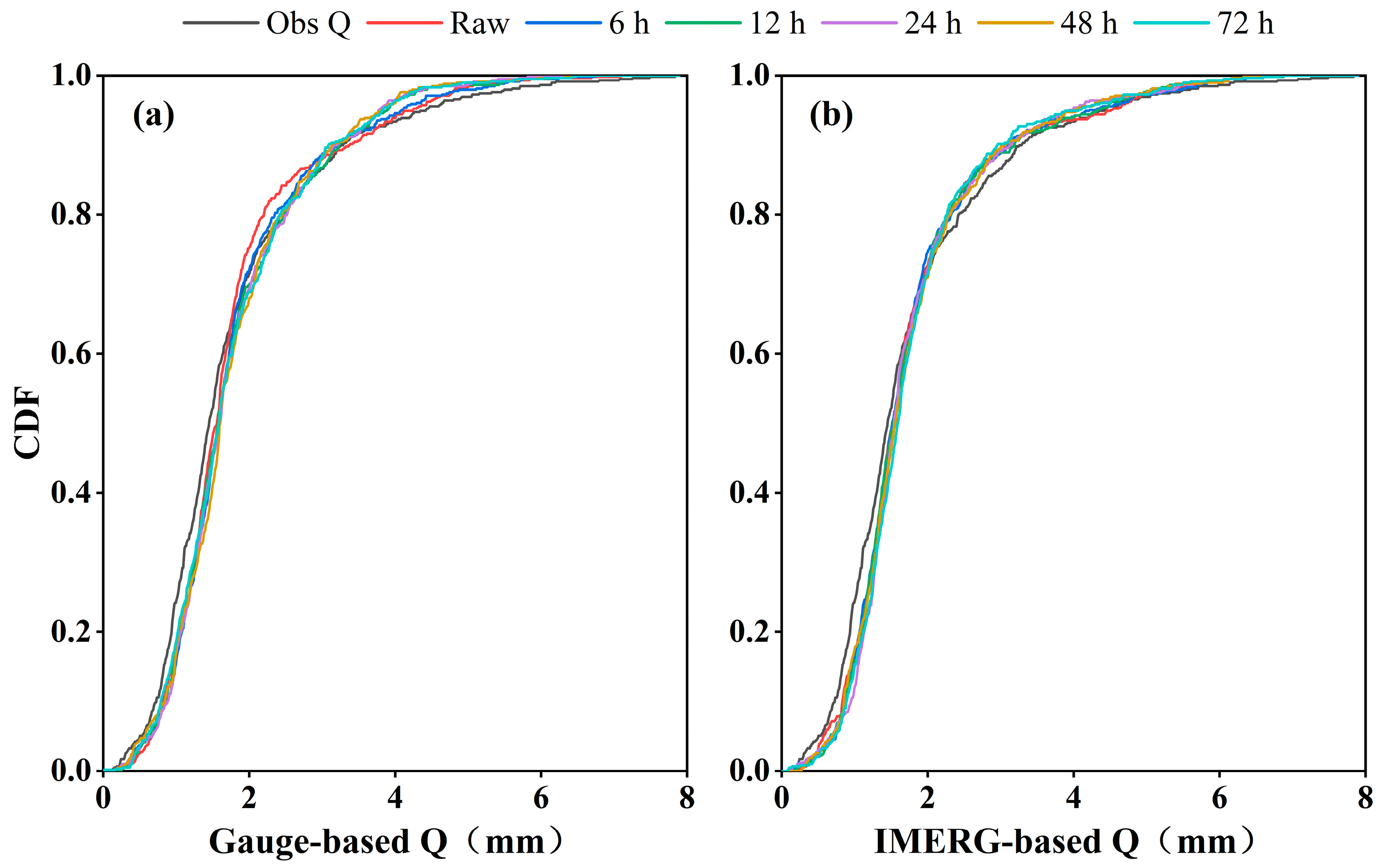
4.2. Event-Based Flood Forecast Analysis
4.3. Flood Inflow Forecast-Informed Reservoir Optimal Operation
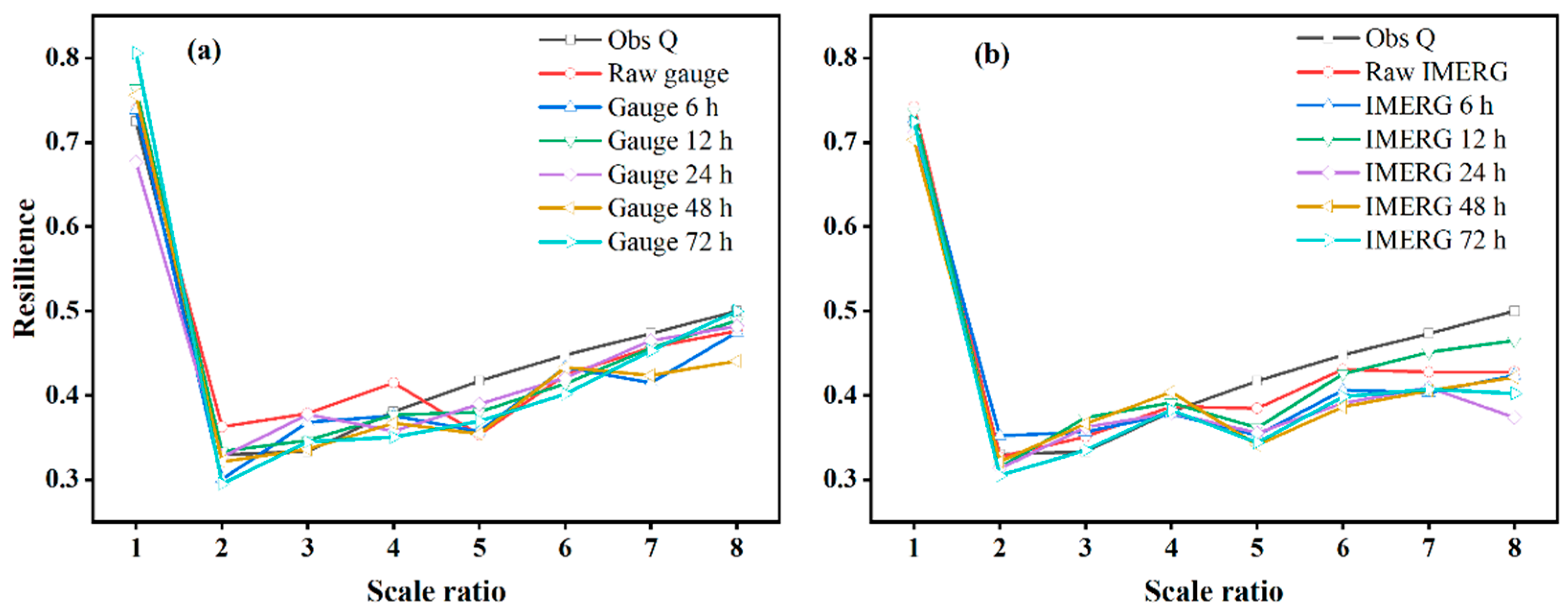
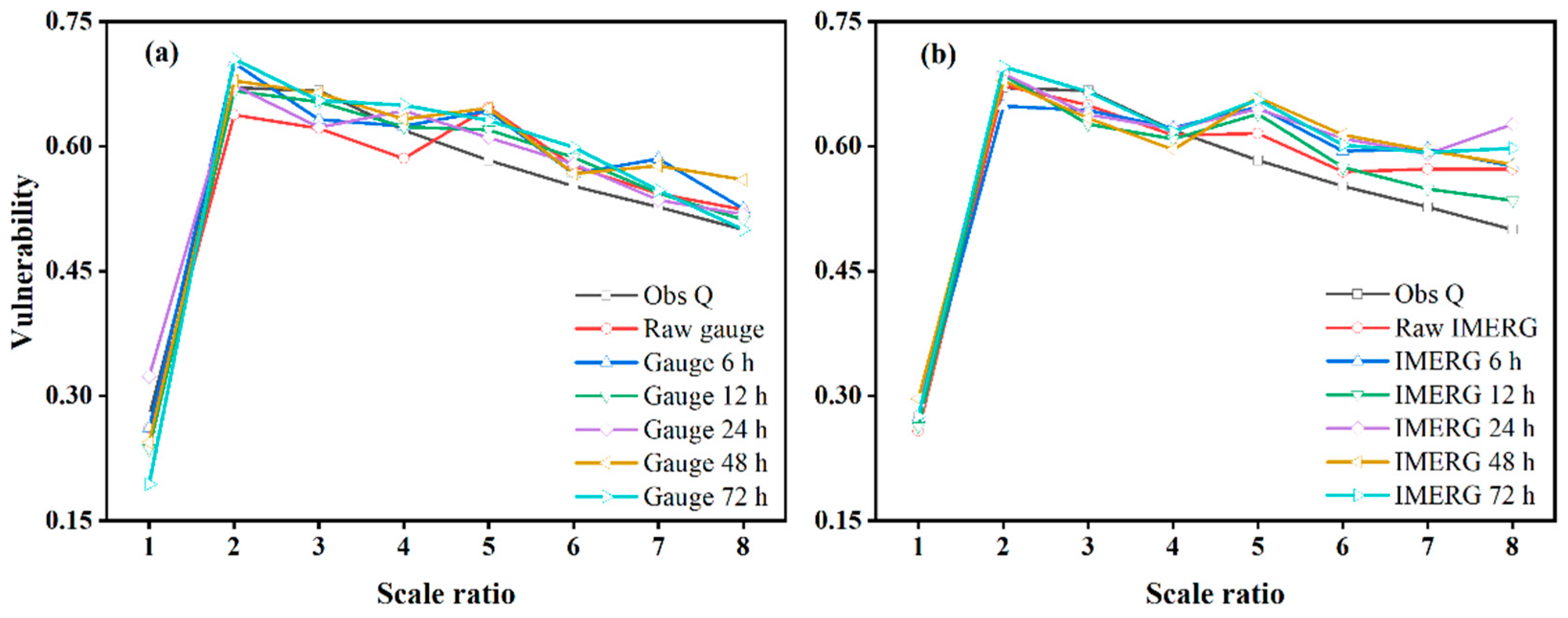
4.3.1. Analysis of rrv Indices
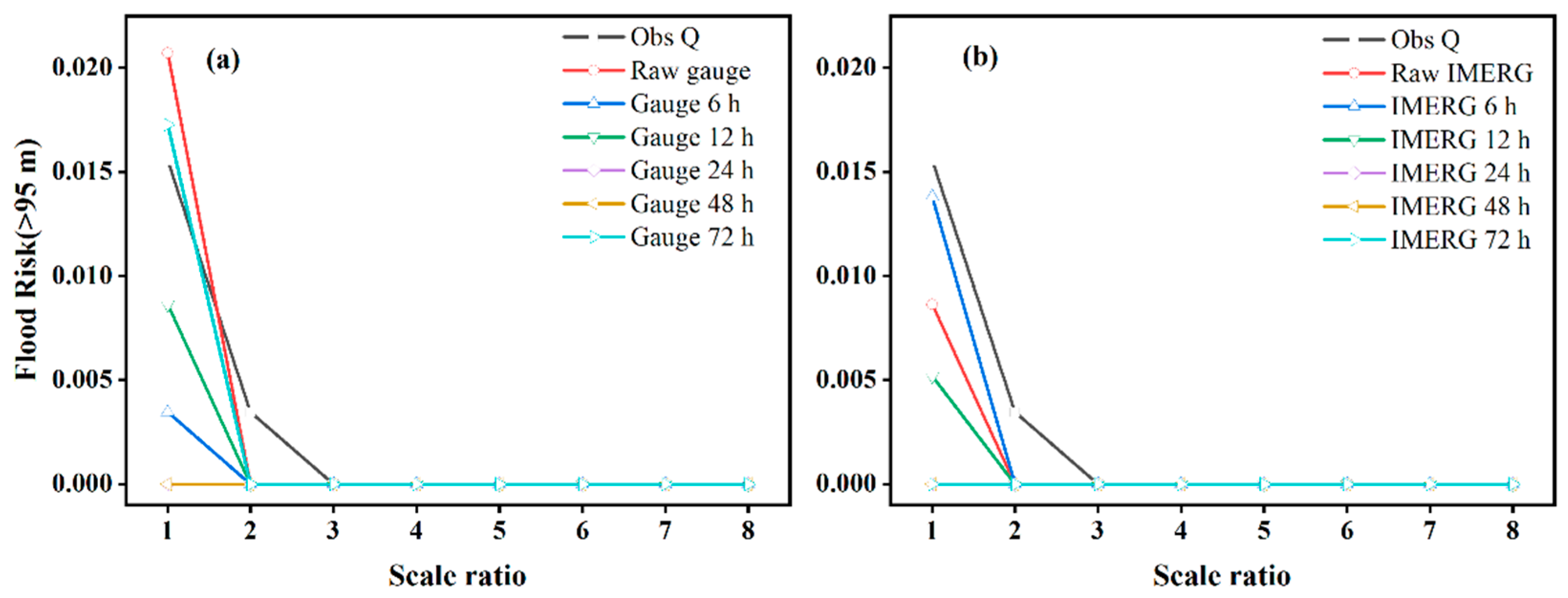
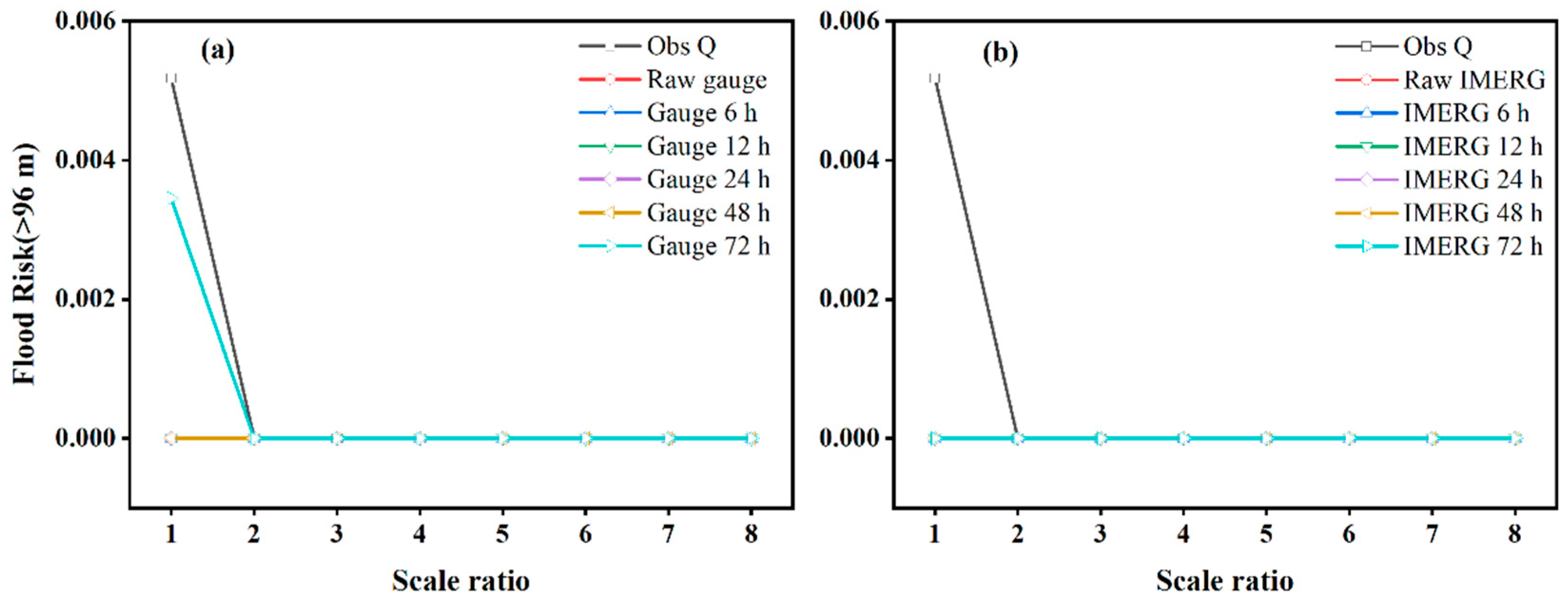
4.3.2. Analysis of Flood Risk Ratio Indices
5. Discussion
6. Conclusions
- (1)
- The flood forecast with GR4H forced with IMERG shows slightly lower accuracy than that driven by the gauge rainfall of the Wan’an basin with the median r, NSE, KGE, and RMSE values ranging from 0.86–0.91, 0.67–0.75, 0.68–0.73, and 0.29 mm–0.33 mm for IMERG, respectively, and 0.88–0.91, 0.72–0.74, 0.64–0.77, and 0.26 mm–0.32 mm for gauge measured rainfall, respectively, across varying lead times.
- (2)
- For a specific robustness index, its trends between IMERG and gauge rainfall inputs are comparable, while its magnitude depends on varying lead times and scale ratios (i.e., the reservoir scale). The rrv values are more sensitive to IMERG-related rainfall and inflow forecast uncertainty for the smaller reservoir scale.
- (3)
- The pattern of increasing forecast error in rainfall with the lead time increasing is changed in the resultant inflow forecast series and dynamics of four risk-based robustness indices of optimal operation decision, due to the rainfall–runoff model and reservoir operation system partly compensating the original heavy rainfall forecast errors in IMERG and gauge data.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Maggioni, V.; Massari, C. On the performance of satellite precipitation products in riverine flood modeling: A review. J. Hydrol. 2018, 558, 214–224. [Google Scholar] [CrossRef]
- Pradhan, R.K.; Markonis, Y.; Godoy, M.R.V.; Villalba-Pradas, A.; Andreadis, K.M.; Nikolopoulos, E.I.; Papalexiou, S.M.; Rahim, A.; Tapiador, F.J.; Hanel, M. Review of GPM IMERG performance: A global perspective. Remote Sens. Environ. 2022, 268, 112754. [Google Scholar] [CrossRef]
- Bitew, M.M.; Gebremichael, M. Assessment of satellite rainfall products for streamflow simulation in medium watersheds of the Ethiopian highlands. Hydrol. Earth. Syst. Sc. 2011, 15, 1147–1155. [Google Scholar] [CrossRef]
- Wu, H.; Kimball, J.S.; Li, H.; Huang, M.; Leung, L.R.; Adler, R.F. A new global river network database for macroscale hydrologic modeling. Water Resour. Res. 2012, 48, W09701. [Google Scholar] [CrossRef]
- Wang, Z.; Zhong, R.; Lai, C.; Chen, J. Evaluation of the GPM IMERG satellite-based precipitation products and the hydrological utility. Atmos. Res. 2017, 196, 151–163. [Google Scholar] [CrossRef]
- Wang, C.; Tang, G.; Han, Z.; Guo, X.; Hong, Y. Global intercomparison and regional evaluation of GPM IMERG Version-03, Version-04 and its latest Version-05 precipitation products: Similarity, difference and improvements. J. Hydrol. 2018, 564, 342–356. [Google Scholar] [CrossRef]
- Su, J.; Lü, H.; Zhu, Y.; Wang, X.; Wei, G. Component analysis of errors in four GPM-based precipitation estimations over Mainland China. Remote Sens. 2018, 10, 1420. [Google Scholar] [CrossRef]
- Sui, X.; Li, Z.; Ma, Z.; Xu, J.; Zhu, S.; Liu, H. Ground Validation and Error Sources Identification for GPM IMERG Product over the Southeast Coastal Regions of China. Remote Sens. 2020, 12, 4154. [Google Scholar] [CrossRef]
- Pradhan, R.K.; Markonis, Y. Performance evaluation of GPM IMERG precipitation products over the tropical oceans using Buoys. J. Hydrometeorol. 2023, in press. [CrossRef]
- Gentilucci, M.; Barbieri, M.; Pambianchi, G. Reliability of the IMERG product through reference rain gauges in Central Italy. Atmos. Res. 2022, 278, 106340. [Google Scholar] [CrossRef]
- Moazami, S.; Na, W.; Najafi, M.R.; de Souza, C. Spatiotemporal bias adjustment of IMERG satellite precipitation data across Canada. Adv. Water. Resour. 2022, 168, 104300. [Google Scholar] [CrossRef]
- Qi, W.; Zhang, C.; Fu, G.T.; Sweetapple, C.; Zhou, H.C. Evaluation of global fine-resolution precipitation products and their uncertainty quantification in ensemble discharge simulations. Hydrol. Earth. Syst. Sc. 2016, 20, 903–920. [Google Scholar] [CrossRef]
- Ali, M.; Amir, A.K. Capabilities of satellite precipitation datasets to estimate heavy precipitation rates at different temporal accumulations. Hydrol. Process. 2014, 28, 2262–2270. [Google Scholar]
- Sharifi, E.; Steinacker, R.; Saghafian, B. Multi time-scale evaluation of high-resolution satellite-based precipitation products over northeast of Austria. Atmos. Res. 2018, 206, 46–63. [Google Scholar] [CrossRef]
- Simanjuntak, F.; Jamaluddin, I.; Lin, T.-H.; Siahaan, H.A.W.; Chen, Y.-N. Rainfall Forecast Using Machine Learning with High Spatiotemporal Satellite Imagery Every 10 Minutes. Remote Sens. 2022, 14, 5950. [Google Scholar] [CrossRef]
- Yue, H.; Gebremichael, M.; Nourani, V. Performance of the Global Forecast System’s medium-range precipitation forecasts in the Niger river basin using multiple satellite-based products, Hydrol. Earth Syst. Sci. 2022, 26, 167–181. [Google Scholar] [CrossRef]
- Dobson, B.; Wagener, T.; Pianosi, F. An argument-driven classification and comparison of reservoir operation optimization methods. Adv. Water Resour. 2019, 128, 74–86. [Google Scholar] [CrossRef]
- Lu, Q.; Zhong, P.; Xu, B.; Zhu, F.; Ma, Y.; Wang, H.; Xu, S. Risk analysis for reservoir flood control operation considering two-dimensional uncertainties based on Bayesian network. J. Hydrol. 2020, 589, 125353. [Google Scholar] [CrossRef]
- Herbert, Z.C.; Asghar, Z.; Oroza, C.A. Long-term reservoir inflow forecasts: Enhanced water supply and inflow volume accuracy using deep learning. J. Hydrol. 2021, 601, 126676. [Google Scholar] [CrossRef]
- Ahmad, S.K.; Hossain, F. A generic data-driven technique for forecasting of reservoir inflow: Application for hydropower maximization. Environ. Modell. Softw. 2019, 119, 147–165. [Google Scholar] [CrossRef]
- Yang, S.; Yang, D.; Chen, J.; Zhao, B. Real-time reservoir operation using recurrent neural networks and inflow forecast from a distributed hydrological model. J. Hydrol. 2019, 579, 124229. [Google Scholar] [CrossRef]
- Meydani, A.; Dehghanipour, A.; Schoups, G.; Tajrishy, M. Daily reservoir inflow forecasting using weather forecast downscaling and rainfall-runoff modeling: Application to Urmia Lake basin, Iran. J. Hydrol. Reg. Stud. 2022, 44, 101228. [Google Scholar] [CrossRef]
- Prakash, S.; Mitra, A.K.; AghaKouchak, A.; Liu, Z.; Norouzi, H.; Pai, D.S. A preliminary assessment of GPM-based multi-satellite precipitation estimates over a monsoon dominated region. J. Hydrol. 2018, 556, 865–876. [Google Scholar] [CrossRef]
- Tang, G.; Clark, M.P.; Papalexiou, S.M.; Ma, Z.; Hong, Y. Have satellite precipitation products improved over last two decades? A comprehensive comparison of GPM IMERG with nine satellite and reanalysis datasets. Remote Sens. Environ. 2020, 240, 111697. [Google Scholar] [CrossRef]
- Huffman, G.J.; Bolvin, D.T.; Braithwaite, D.; Hsu, K.; Joyce, R.; Kidd, C.; Nelkin, E.J.; Sorooshian, S.; Tan, J.; Xie, P. NASA Global Precipitation Measurement (GPM) Integrated Multi-Satellite Retrievals for GPM (IMERG); Algorithm Theoretical Basis Document (ATBD) Version, 06; NASA/GSFC: Greenbelt, MD, USA, 2018; 39p. [Google Scholar]
- He, X.; Chaney, N.W.; Schleiss, M.; Sheffield, J. Spatial downscaling of precipitation using adaptable random forests. Water Resour. Res. 2016, 52, 8217–8237. [Google Scholar] [CrossRef]
- Van Esse, W.R.; Perrin, C.; Booij, M.J.; Augustijn, D.C.; Fenicia, F.; Kavetski, D.; Lobligeois, F. The influence of conceptual model structure on model performance: A comparative study for 237 French catchments. Hydrol. Earth Syst. Sci. 2013, 17, 4227–4239. [Google Scholar] [CrossRef]
- Perrin, C.; Michel, C.; Andréassian, V. Improvement of a parsimonious model for streamflow simulation. J. Hydrol. 2003, 279, 275–289. [Google Scholar] [CrossRef]
- Zhang, Y.; Vaze, J.; Chiew, F.H.; Teng, J.; Li, M. Predicting hydrological signatures in ungauged catchments using spatial interpolation, index model, and rainfall–runoff modelling. J. Hydrol. 2014, 517, 936–948. [Google Scholar] [CrossRef]
- Haruna, A.; Garambois, P.; Roux, H.; Javelle, P.; Jay-Allemand, M. Signature and sensitivity-based comparison of conceptual and process oriented models, GR4H, MARINE and SMASH, on French Mediterranean flash floods. Hydrol. Earth Syst. Sci. Discuss. 2021. preprint. [Google Scholar] [CrossRef]
- Basri, H.; Sidek, L.M.; Razad, A.Z.; Pokhrel, P. Hydrological Modelling of Surface Runoff for Temengor Reservoir Using GR4H Model. Int. J. Civ. Eng. Technol. 2019, 10, 22–28. [Google Scholar]
- Turner, S.W.; Galelli, S. Water supply sensitivity to climate change: An R package for implementing reservoir storage analysis in global and regional impact studies. Environ. Model. Softw. 2016, 76, 13–19. [Google Scholar] [CrossRef]


| Flood Inflow (Mm3) | Storage (Mm3) | Controlled Release (Mm3) | Regulated Water Level (m) | |||||
|---|---|---|---|---|---|---|---|---|
| Mean | Range | Mean | Range | Mean | Range | Mean | Range | |
| Obs Q | 66.14 | (4.97, 289.44) | 542.79 | (73.11, 1165.90) | 65.31 | (0, 317.09) | 87.46 | (69.52, 96.12) |
| Raw Gauge | 66.10 | (8.51, 262.32) | 553.70 | (96.98, 1115.16) | 65.44 | (0, 237.82) | 87.73 | (71.86, 95.62) |
| Gauge 6 h | 67.35 | (6.35, 248.59) | 554.13 | (54.53, 1061.21) | 66.95 | (0, 237.82) | 87.73 | (67.18, 95.06) |
| Gauge 12 h | 67.25 | (8.01, 236.85) | 556.53 | (61.95, 1071.52) | 66.81 | (0, 317.09) | 87.82 | (68.07, 95.17) |
| Gauge 24 h | 67.25 | (5.66, 222.97) | 557.72 | (79.49, 998.43) | 66.54 | (0, 237.82) | 87.82 | (70.21, 94.39) |
| Gauge 48 h | 67.14 | (0, 236.91) | 562.88 | (65.32, 980.98) | 66.54 | (0, 237.82) | 87.92 | (68.61, 94.19) |
| Gauge 72 h | 66.84 | (0, 239.33) | 564.71 | (93.23, 1130.52) | 66.27 | (0, 237.82) | 87.96 | (71.53, 95.77) |
| Raw IMERG | 66.58 | (6.15, 249.63) | 545.45 | (49.24, 1068.15) | 66.27 | (0, 237.82) | 87.52 | (66.38, 95.13) |
| IMERG 6 h | 66.63 | (4.98, 253.00) | 550.90 | (45.50, 1047.01) | 66.40 | (0, 237.82) | 87.61 | (65.77, 94.92) |
| IMERG 12 h | 66.90 | (6.49, 254.02) | 542.52 | (22.92, 1031.47) | 66.54 | (0, 237.82) | 87.44 | (60.70, 94.75) |
| IMERG 24 h | 67.08 | (4.41, 249.32) | 544.12 | (44.65, 978.26) | 67.09 | (0, 237.82) | 87.50 | 65.62, 94.16) |
| IMERG 48 h | 66.99 | (10.03, 243.42) | 551.56 | (57.03, 986.46) | 66.40 | (0, 237.82) | 87.64 | (67.53, 94.26) |
| IMERG 72 h | 67.12 | (3.22, 252.57) | 555.59 | (52.49, 948.99) | 66.95 | (0, 237.82) | 87.81 | (66.88, 93.83) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, Q.; Gui, X.; Xiong, B.; Li, R.; Yan, L. Applicability Assessment of GPM IMERG Satellite Heavy-Rainfall-Informed Reservoir Short-Term Inflow Forecast and Optimal Operation: A Case Study of Wan’an Reservoir in China. Remote Sens. 2023, 15, 4741. https://doi.org/10.3390/rs15194741
Ma Q, Gui X, Xiong B, Li R, Yan L. Applicability Assessment of GPM IMERG Satellite Heavy-Rainfall-Informed Reservoir Short-Term Inflow Forecast and Optimal Operation: A Case Study of Wan’an Reservoir in China. Remote Sensing. 2023; 15(19):4741. https://doi.org/10.3390/rs15194741
Chicago/Turabian StyleMa, Qiumei, Xu Gui, Bin Xiong, Rongrong Li, and Lei Yan. 2023. "Applicability Assessment of GPM IMERG Satellite Heavy-Rainfall-Informed Reservoir Short-Term Inflow Forecast and Optimal Operation: A Case Study of Wan’an Reservoir in China" Remote Sensing 15, no. 19: 4741. https://doi.org/10.3390/rs15194741
APA StyleMa, Q., Gui, X., Xiong, B., Li, R., & Yan, L. (2023). Applicability Assessment of GPM IMERG Satellite Heavy-Rainfall-Informed Reservoir Short-Term Inflow Forecast and Optimal Operation: A Case Study of Wan’an Reservoir in China. Remote Sensing, 15(19), 4741. https://doi.org/10.3390/rs15194741






