1. Introduction
Remote sensing imagery finds broad utility across diverse fields. It delivers high-resolution ground surface information, enabling researchers to classify, monitor, and forecast land use and cover types, while also facilitating the management and assessment of vital natural resources, including forests, grasslands, water bodies, and soil quality. Remote sensing images (RSIs) play a pivotal role in monitoring agricultural production conditions, encompassing factors, such as crop growth and pest infestation, thereby offering valuable insights for guiding agricultural decision making. Furthermore, these images are invaluable for tracking environmental concerns, including air pollution, water quality, soil contamination, as well as the occurrence and repercussions of natural disasters, such as floods and earthquakes. Moreover, RSIs hold significance in urban planning and management, spanning domains like traffic planning and community structure analysis. However, the efficacy of these visual applications crucially hinges upon the clarity and visibility of the input images. The degradation of RSIs arising from adverse atmospheric conditions can lead to a sharp decline in the algorithm performance of these downstream tasks, with haze emerging as the predominant atmospheric phenomenon among the various adverse conditions. To ensure the dependable operation of remote sensing vision systems, researchers have devoted substantial effort to solving the highly challenging problem of remote sensing haze image restoration.
The restoration of remote sensing haze images presents an inherently ill-posed problem, as it necessitates the simultaneous recovery of the dehazed image, the underlying atmospheric ambient light, and the depth-dependent transmission solely from a single hazy input. To tackle this challenge, researchers have endeavored to incorporate prior knowledge of haze images through observations, assumptions, and statistical methods [
1,
2,
3,
4,
5], serving as supplementary constraints to render the problem well defined. However, these algorithms all rely on a common assumption, specifically that the transmission within local image patches remains constant, which is feasible in areas with smooth depth but fails in areas with abrupt depth changes, such as the intersection between the foreground and background of an image and its edges. Hence, when constructing local image patches, it becomes imperative to fully account for the structural information of the image. Existing haze removal algorithms frequently regard fixed-size rectangular regions within the image as local blocks. This oversimplification undermines the assumption that transmission remains constant within the same image patch, leading to incorrect transmission estimations. Notably, this issue becomes more serious as the size of the patch increases.
Given the problems inherent in existing physical model-based haze removal algorithms, this paper introduces an enhanced local image patch partitioning method using superpixels. Evaluating the color and brightness similarities among pixels, it clusters pixels with similar features together to build a superpixel, which preserves the structure information of the image as much as possible. Therefore, the patches are partitioned with arbitrary shapes relevant to the image content rather than fixed-size rectangles. Within each superpixel patch, all constituent pixels exhibit similar physical properties, allowing the atmospheric light and transmission to be rationally treated as constants in this local region. Furthermore, considering that the imaging space of RSIs is significantly broader than that of outdoor images taken near the ground, we believe that modeling the atmospheric ambient light in RSIs as a non-uniform distribution is more appropriate than a globally uniform one. This is because the temperature, pressure, and aerosol motion in the atmosphere can generate fluctuations of the atmospheric environment in the imaging space, so a globally non-uniform ambient light more closely matches the real world. In addition, since the natural outdoor images taken near the ground often exhibit limited depth of the scene, the transmission is often approximated as equal in the red, green, and blue channels of the image, ignoring its wavelength-dependent properties to simplify the model calculations. However, in RSI imaging, the emergent light reflected by scene objects traverses an extremely long distance, rendering the treatment of transmission maps of the RGB channels as being equal inappropriate. Consequently, this paper proposes a channel-separated transmission map estimation algorithm, which computes the respective transmissions of the RGB channels separately.
The primary contributions of this paper can be succinctly outlined as follows:
Integration of Superpixel Technique for RSI Dehazing: We seamlessly incorporate the superpixel technique into the framework of RSI dehazing, thereby leveraging pixel clustering to preserve the intrinsic structural information of the original image in the estimation of local atmospheric light and transmission.
Nonuniform atmospheric light estimation: Exploiting the distinctive imaging characteristics inherent in remotely sensed imagery, this study introduces a global nonuniform atmospheric light prior and provides a superpixel-wise atmospheric light estimation method.
Channel-separated transmission estimation: Considering the distinct transmission abilities of different spectral wavelengths, this paper proposes a channel-separated transmission map estimation algorithm. This innovative approach independently computes the transmission maps of the RGB channels, leading to heightened accuracy in the estimation of transmission maps for RSIs.
Comprehensive experimental validation: We meticulously conducted an exhaustive array of experiments, including quantitative and qualitative evaluations on real-world and synthetic hazy RSIs. The experimental findings demonstrate the superior dehazing efficacy of the proposed method compared to several state-of-the-art algorithms.
2. Materials
2.1. Related Work
Extensive efforts have been dedicated to restoring degraded haze images over a significant period of time, resulting in the proposal of numerous remarkable algorithms one after another. In this section, we provide a concise overview of existing approaches for single image dehazing. It is important to acknowledge that many brilliant algorithms were originally designed for natural scenes, and it is only in recent years that dehazing techniques tailored for remote sensing scenes have been developed. The intrinsic disparities between remote sensing scenes and natural scenes render the dehazing algorithm designed for natural images ineffective when applied to RSIs.
2.1.1. Image Enhancement-Based Dehazing Methods
The image enhancement technique employed in dehazing methods fails to consider the physical degradation model of the hazy image. Instead, it focuses on enhancing the image quality by augmenting the image’s contrast and rectifying its color. To improve the visibility of degraded images affected by haze, Ancuti et al. [
6] proposed a fusion-based approach. This approach effectively combines two intermediate results derived from the original image, which undergoes white balance adjustment and contrast enhancement. The fusion strategy considers the image’s brightness, chromaticity, and saliency, resulting in a dehazed image that exhibits enhanced visibility. Galdran et al. [
7] introduced a novel variational image dehazing technique that incorporates a fusion scheme and energy functions. By minimizing the proposed variational formulation, the method achieves enhanced contrast and saturation of the input image. Retinex is a color vision model that simulates the human visual system’s ability to perceive scenes under varying illuminations. Galdran et al. [
8] theoretically demonstrated that Retinex at inverted intensities is a feasible solution for image dehazing tasks. Although three image enhancement techniques—white balance (WB), contrast enhancement (CE), and gamma correction (GC)—were utilized, Ren et al. [
9] innovatively adopted neural networks to learn how to fuse the results of these three enhancements rather than manually designing the fusion strategy to obtain clear haze-free images. Considering the dynamic range of the input image, Wang et al. [
10] proposed a multi-scale Retinex with color restoration (MSRCR)-based single-image dehazing method. Li et al. [
11] employed homomorphic filtering to enhance haze images on the basis of the observation that haze is highly correlated with the light component and is located mainly in the low-frequency part of the image. Note that the last two methods use the physical model of image degradation in addition to image enhancement techniques. Image enhancement-based dehazing algorithms sometimes suffer from over-enhancement, as they solely rely on the pixel information of the image and disregard the underlying physical degradation process of the haze images.
2.1.2. Physical Model-Based Dehazing Methods
The atmospheric scattering model that is widely used for hazy image restoration is an underdetermined optical model that describes the physical process of radiation propagation in the medium. In order to solve the model, existing studies [
1,
2,
3,
4,
5] have explored various haze-relevant priors through assumptions, observations, and statistics as complementary constraints to the atmospheric scattering model. However, these methods are based on priors of natural scene images, which are not well suited for RSIs. Therefore, researchers have attempted to uncover some latent priors of remote sensing hazy images to remove haze. Ning et al. [
12] proposed a RSI dehazing algorithm based on a light-dark channel prior, which first utilizes the dark channel prior to remove haze and then uses the light channel prior to remove shadows. As an alternative to the dark and bright channel prior, Han et al. [
13] proposed a RSI dehazing algorithm based on the local patchwise extremum prior and proved its feasibility and reliability. Zhu et al. [
14] used a linear model trained by differentiable functions to estimate the scene depth and find the atmospheric ambient light based on depth information, and subsequently generated a color-realistic and haze-free image from the remotely sensed data using the atmospheric scattering model. Pan et al. [
15] proposed a deformed haze imaging model by introducing a translation term and estimated the atmospheric light and transmission in the improved model through the dark channel, prior to achieving effective haze removal. Xu et al. [
16] introduced the concept of “virtual depth” into RSIs and proposed a dehazing method that combines patch-wise and pixel-wise dehazing operators, in which dehazing operators are executed iteratively to progressively remove haze. Liu et al. [
17] regarded haze as an additive veil, which can be represented by a haze thickness map, and proposed a haze distribution estimation algorithm to recover clear images effectively.
The dehazing algorithms based on the physical model try to solve the physical process of image degradation by haze, but the atmospheric scattering model is an ideal and simplified model that ignores the differences between the imaging environment of RSIs and natural outdoor images. Therefore, this paper attempts to integrate the characteristics of remote sensing imaging into the atmospheric scattering model.
2.1.3. Deep Learning-Based Dehazing Methods
With the significant breakthrough of deep neural network algorithms in various fields, an increasing number of deep learning-based haze removal algorithms have emerged. Ren et al. [
18] trained a multi-scale deep neural network on a synthetic dataset, which obtains the coarse transmission map by the coarse-scale subnet and then refines it by the fine-scale subnet. Following the coarse-to-fine strategy in [
18], Li et al. [
19] proposed FCTF-Net, a two-stage dehazing neural network that effectively removes irregularly distributed haze in RSIs by combining attention mechanisms and standard convolution operations. To reduce the error amplification caused by separately estimating atmospheric light and transmission, Li et al. [
20] reformulated the atmospheric scattering model and built an end-to-end lightweight neural network for efficient haze removal. By introducing an attention mechanism, Liu et al. [
21] proposed GridDehazeNet, a multi-scale deep neural network based on a grid network that effectively alleviates the bottleneck issue and achieves good dehazing results. For visible RSI dehazing, Chen et al. [
22] proposed a neural network with a nonuniform excitation module. It employs a dual attention block to extract locally enhanced features and deformable convolution to extract nonlocal features. The powerful feature extraction capability makes the network achieve a good dehazing effect. Chen et al. [
23] proposed a hybrid high-resolution haze removal network, whose high-resolution branch can obtain precise spatial features, while the multi-resolution convolution branch can output rich semantic features. Regarding the nonuniform distribution of haze in RSIs, Jiang et al. successively proposed a dehazing network combining wavelet transform [
24] and an asymmetric network with enhanced attention using k-means clustering and FFT [
25]. To adapt flexibly to the specific haze condition in each image, Nie et al. [
26] presented a haze-aware learning-based dynamic dehazing method using contrast learning, which can adaptively remove the diverse haze in RSIs. It is worth noting that deep learning-based and physics-based approaches are not completely separate, and some studies [
27,
28,
29] tried to embed physical prior knowledge in deep learning models and achieved significant progress.
Despite the promising results demonstrated by deep learning-based dehazing algorithms, they heavily rely on the availability of large-scale training datasets, which may be challenging to acquire, especially for remote sensing applications. Additionally, the deployment of deep learning models for real-time applications can be hindered by their hardware requirements and computational complexity.
2.1.4. Dehazing for Multispectral and Hyperspectral RSIs
The aforementioned algorithms are specifically developed for visible remote sensing hazy images, and numerous haze removal algorithms are also developed for multispectral RSIs. To alleviate the lack of real training data pairs for multispectral RSI dehazing, Guo et al. [
30] proposed a novel remote sensing hazy image simulation method to generate a realistic multispectral hazy image and presented their neural network model, RSDehazeNet, which enables the end-to-end restoration of multispectral hazy images through the introduced channel attention module. Similarly, Qin et al. [
31] employed the wavelength-dependent haze simulation method to generate a hyperspectral dataset with clear and hazy image pairs and utilized this dataset to train their proposed deep convolutional neural network with residual structure, which can perceive haze distribution by adaptive fusion and obtain clear images without haze. Because of the gap between hyperspectral RSIs and natural images, Kang et al. [
32] proposed a haze image degradation model suitable for hyperspectral data. By differentiating the average bands of the visible and infrared spectrum, they calculated the haze density map and transmission. And then, the high-quality hyperspectral images can be restored by solving the novel physical model. Considering the effect of both wavelength and haze atmospheric conditions, Guo et al. [
33] introduced an optimized atmospheric scattering model for Landsat-8 OLI multispectral image dehazing by estimating the haze transmission of each band. Facing the lack of hazy hyperspectral aerial image datasets, Mehta et al. [
34] proposed SkyGAN, an unsupervised dehazing algorithm, which utilizes conditional generative adversarial networks (cGANs) and consists of a domain-aware hazy-to-hyperspectral module and a multi-cue image-to-image translation module. Ma et al. [
35] designed a spectral grouping network (SG-Net), which can fully represent the interrelation between clear and haze images by leveraging the information in each spectral band to remove haze for hyperspectral images. Although these algorithms yield satisfactory results, they require additional spectral information and are not directly applicable to RGB images.
2.2. Atmospheric Scattering Model
The essence of image dehazing is to solve an underdetermined atmospheric scattering model [
36,
37] that describes the physical processes that occur as light traverses the medium to reach the imaging device, which is shown below:
where
and
denote the original scene radiance without degradation and the haze-contaminated image captured by the camera, respectively, while
x indicates the spatial position of the pixel in the image.
A is atmospheric ambient light, which describes the scattered light diffused in the atmosphere, and it is generally regarded as globally uniformly distributed for simplicity of calculation.
quantitatively describes the ability of radiation to penetrate the medium, and it is related to the wavelength and travel distance of the light, which can be formulated as
where
is the extinction coefficient related to the wavelength and
is the imaging distance, also known as the scene depth. The first term on the right of Equation (
1),
, represents the direct attenuation of light when it passes through the atmospheric medium, while
depicts the phenomenon of airlight, which represents the blend of the scene object’s irradiation and the ambient luminance reflected into the light path by the atmospheric medium.
The atmospheric scattering model described above is widely used in the dehazing task for natural scene images. However, most existing physical model-based algorithms (e.g., DCP [
1], CEP [
2], and CAP [
3]) are premised on the assumption that
A is globally homogeneous and
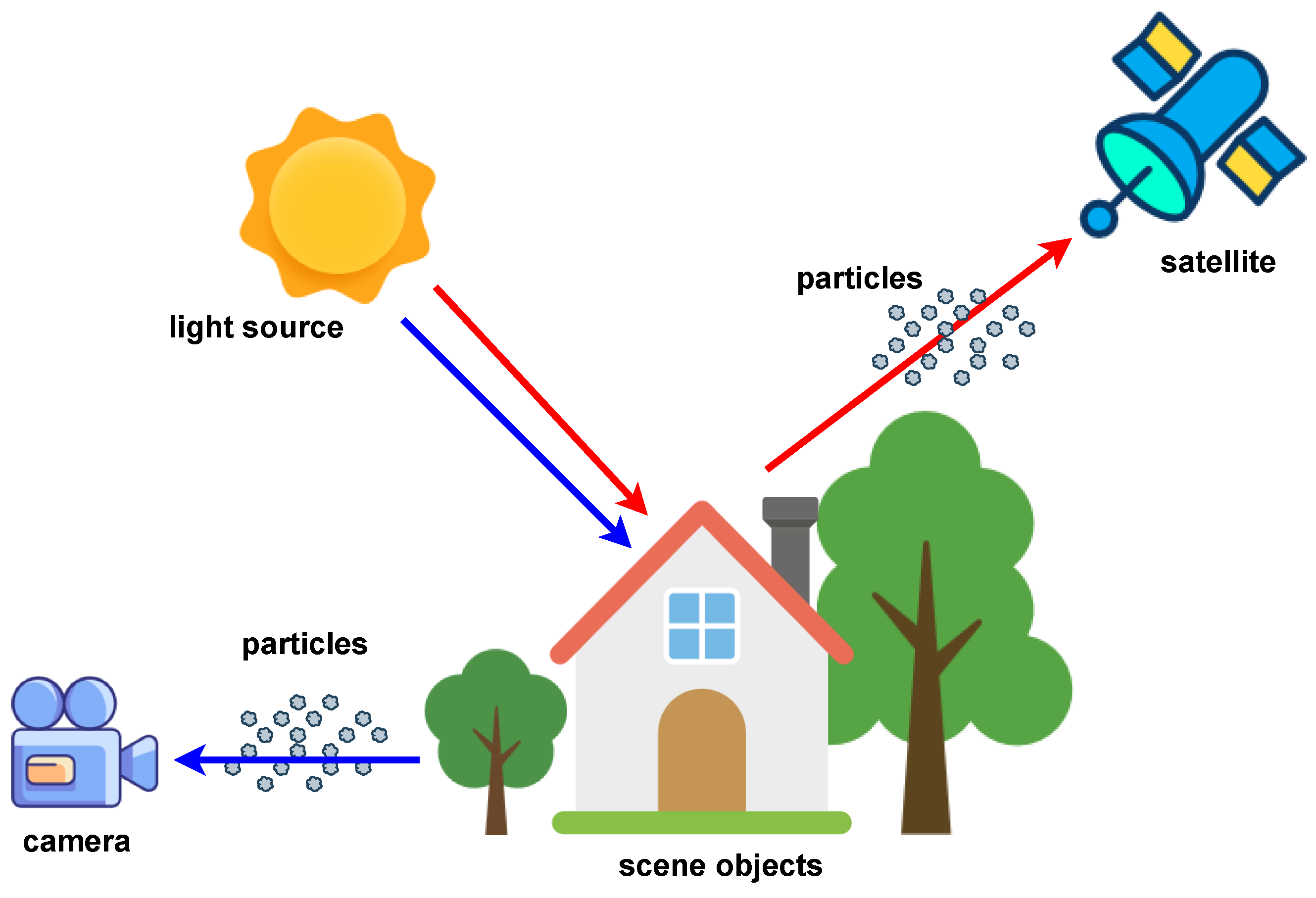
is locally equal. For natural outdoor images taken near the ground, this hypothesis can be used to add constraints to the atmospheric scattering model, making it easier to solve. However, there are significant differences in the imaging process between RSIs and natural scene images as shown in
Figure 1. For example, the spatial range of remote sensing imaging is much larger than that of natural outdoor images, and the imaging angle of RSIs is usually downward rather than horizontal. Therefore, the haze removal method for natural images cannot be directly applied to solve the degradation problem of remote sensing haze images. In this paper, we propose a RSI haze removal method based on superpixel segmentation, the non-uniform atmospheric light prior, and channel-separated transmission estimation, which is inspired by the imaging features of RSIs.
3. Methods
In this section, we first analyze the defects of the traditional dehazing algorithms in patch division for subsequent transmission estimation and propose an effective image patch extraction strategy by the superpixel. Secondly, considering that the imaging range of remote sensing images is very large, resulting in the atmospheric light in the whole imaging space being unable to be regarded as a global uniform distribution, we propose a heterogeneous atmospheric light estimation method by combining the superpixel segmentation technique with the maximum reflectance prior. Then, the imaging distance of remote sensing images is so long that the transmissions of scene radiation with different wavelengths cannot be regarded as equal, so we propose a channel-separated transmission map estimation algorithm. Finally, we restore the haze-free remote sensing images according to the obtained atmospheric light and transmission.
3.1. Content-Aware Patch Division by Superpixel
The haze image restoration algorithms based on the physical model usually adopt the atmospheric scattering model introduced in
Section 2.2. However, the atmospheric scattering model is an underdetermined equation, and
in the model is a variable related to spatial location. To simplify the calculation, most algorithms assume that the transmittance is equal in the local space, i.e.,
in an image patch is a constant, which is feasible in the smooth area of the image, but if the image patch contains both the foreground and the background (e.g., the edge area), it is obvious that the
in this local patch should not be equal according to Equation (
2). Therefore, the accuracy of the estimation of
is strongly correlated with the way to divide the image patches. Most existing algorithms [
1,
2,
3,
12,
13,
38] divide the haze image into rectangular patches with a fixed size, which makes the obtained transmission map inaccurate and loses the structural information of the image. To address this issue, we present a simple and effective image patch division strategy based on superpixels, which employ the clustering approach to merge adjacent pixels with similar attributes into the same block so that the transmission
as well as the atmospheric light
A within each patch can be regarded as locally identical.
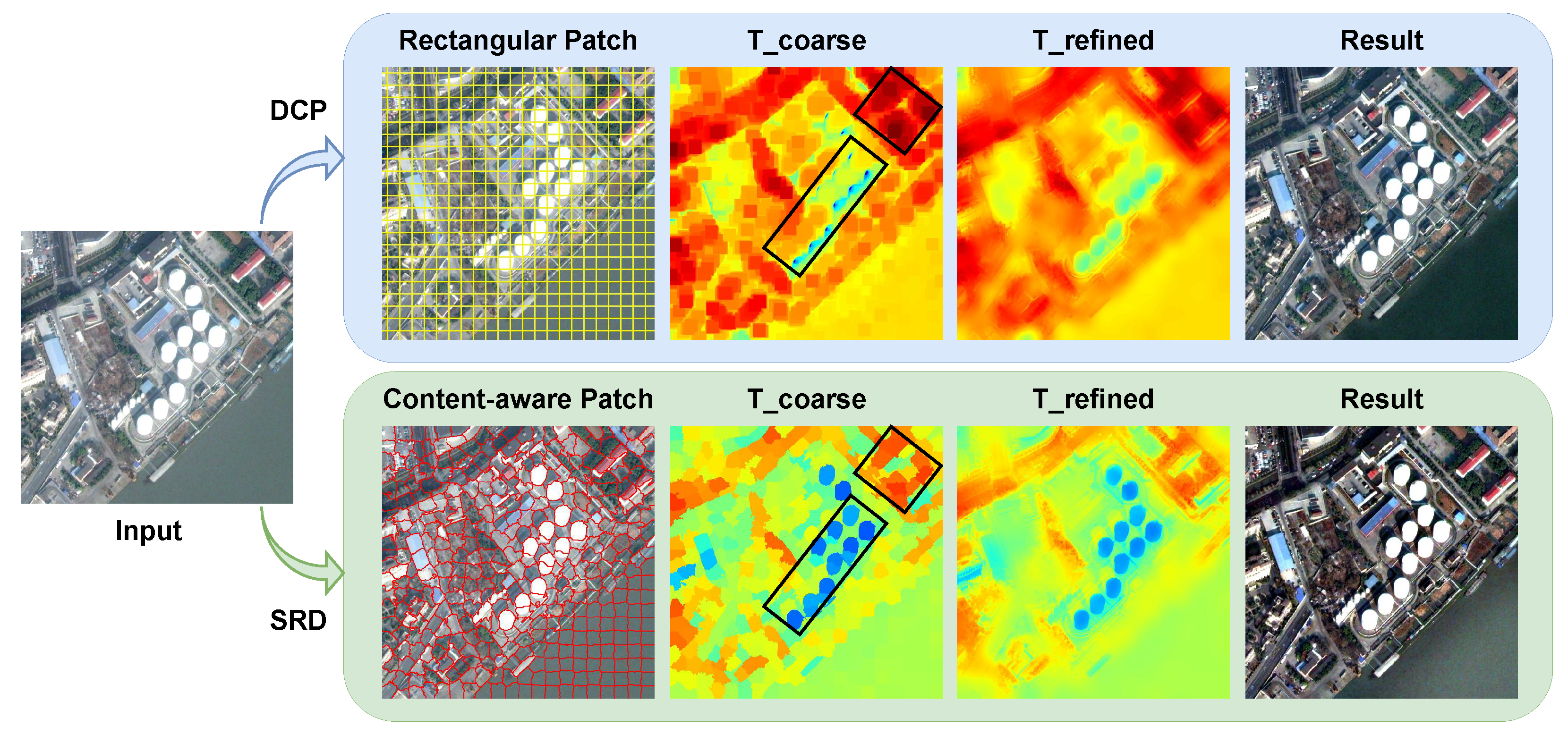
As shown in
Figure 2, the DCP method uses fixed-size rectangles to divide the haze image so that there are inevitably areas with discontinuous scene depth in the divided patches, resulting in errors and loss of edge information in the estimated transmission map, such as the region marked by the black box in the subfigure of “T_coarse” of the DCP method. In contrast, the SRD algorithm proposed in this paper adopts the super-pixel segmentation strategy for patch division, which can adaptively perceive the image content and obtain irregular blocks so that the calculated transmission map can retain more structural information of the image. It should be noted that most of the existing dehazing algorithms use a rectangular patch division scheme; for the convenience of visualization, we only take the DCP method as an example for comparison in
Figure 2. Moreover, although the coarse transmission maps will be subsequently refined, the transmission calculated using the fixed-size rectangular patch division approach irretrievably loses some image information.
A superpixel is a contiguous image area that contains some adjacent pixels with similar color and brightness. Superpixel is widely used in various vision tasks. We use the SLIC (simple linear iterative clustering) algorithm [
39] to extract the superpixels of haze images as local patches because it has very good execution efficiency, few parameters, and can identify image boundaries very well. The SLIC method first converts each pixel of the image into a five-dimensional vector
, where the
l,
a, and
b components denote the color in CIELAB space, and the
x and
y components represent the pixel’s position, respectively. Then, in order to determine which superpixel a certain unclustered pixel should be merged into, the SLIC measures the similar distance between the pixel and the average vectors of its adjacent superpixels by the following metric function:
where
,
, and
respectively indicate the color distance, spatial distance, and final distance to be evaluated between the two given vectors
i and
j.
S controls the interval between the superpixels and is formulated as
, where
N and
K denote the number of image pixels and the superpixels to be divided, respectively. The compactness of the superpixel is weighed by the parameter
m, which is usually regarded as a constant between 1 and 40, and the default value of
m is adopted in this paper. Therefore, the only variable parameter in this algorithm is
K, and the influence of parameter
K on the dehazing performance is discussed by experiments in
Section 5.1.
The proposed SRD algorithm can obtain content-aware image patches by SLIC, but this is only the first step of the entire dehazing framework. After that, we will calculate the transmission and atmospheric light within each local image patch, and the estimation methods for them will be described in detail in the following
Section 3.2 and
Section 3.3.
3.2. Non-Uniform Atmospheric Light Estimation
The accurate estimation of atmospheric light is a critical step in haze image restoration. The traditional atmospheric scattering model is premised on the uniform distribution of atmospheric light. However, this ideal model cannot fit the real-world atmospheric environment, which is dynamic and complex, so we model the atmospheric ambient light as a variable with a non-uniform distribution. In particular, the imaging space of remote sensing images is extremely large, and the non-homogeneity of the atmospheric light distribution is more prominent. Based on this prior, we improve the atmospheric scattering model as follows:
which simply modifies the constant
A into the position-dependent variable
compared to Equation (
1).
According to the imaging model, the image is the product of the illumination and the reflectance components. Following the existing work [
40], sunlight tends to be weak in hazy weather, so the main illumination of the scene is the atmospheric ambient light. Therefore, the original haze-free image can be expressed as
where
is the reflectance of the scene object. With Equations (
6) and (
7), the haze image can be represented as
Referring to the conclusion in the previous
Section 3.1, the atmospheric light and transmittance in each superpixel of the image can be regarded as constants. Therefore, for each image patch, Equation (
8) can be rewritten as
where
P denotes a local patch, and
and
denote the atmospheric light and transmittance in this path, respectively.
Zhang et al. proposed the maximum reflection prior [
41] based on the statistics on daytime haze-free images, i.e., the maximum reflection component in a local patch of a haze-free image tends to 1, which can be expressed as
Therefore, it can be derived from Equation (
9) that
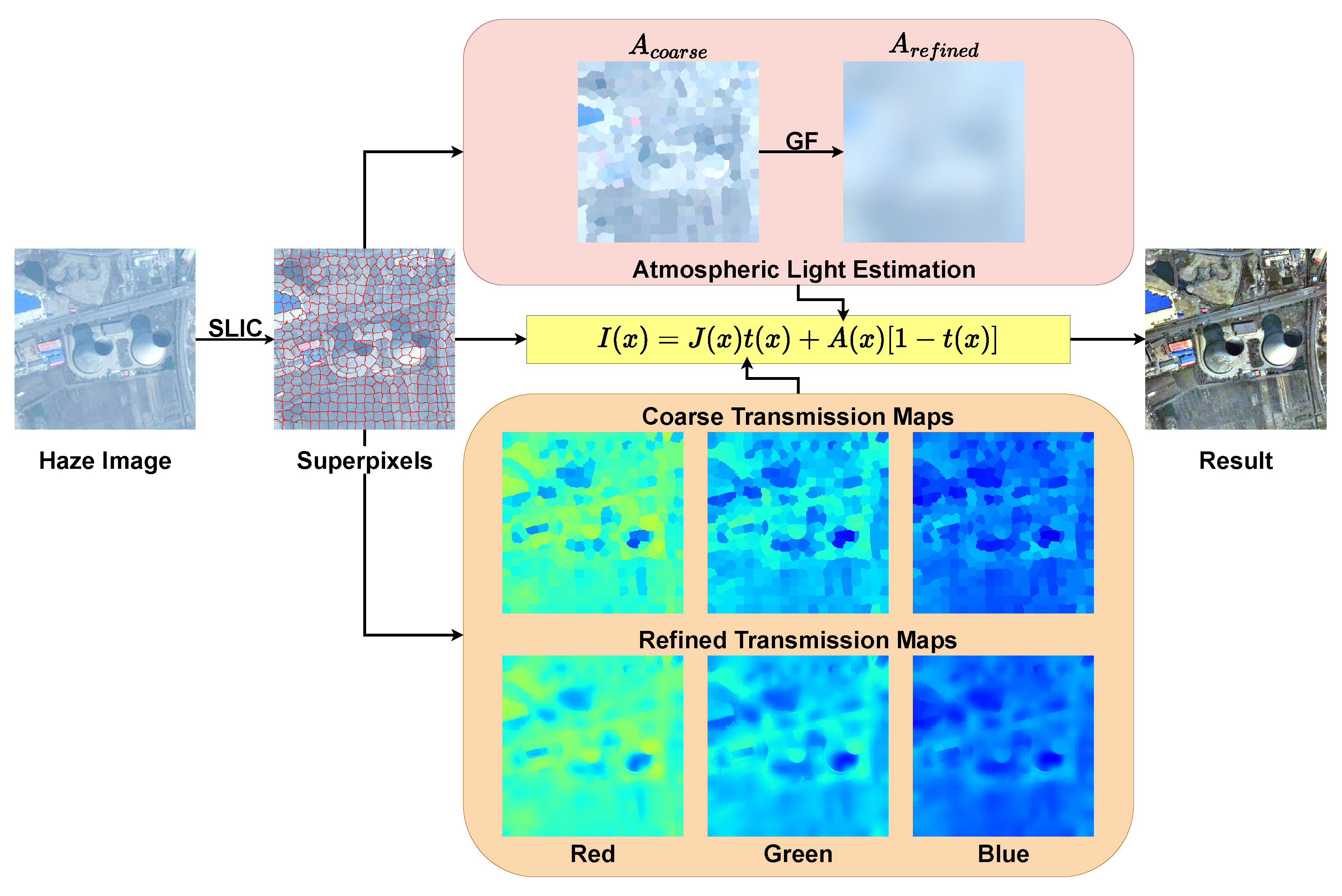
That is, the brightest pixel of a local patch can be approximated as the atmospheric light of the current patch. Accordingly, we can calculate the coarse non-uniform atmospheric light as shown in
Figure 3c. It should be noted that the patches used here are obtained using the superpixel technique introduced in
Section 3.1. Since the atmospheric light is spatially continuous, we employ the guided filter [
42] to smooth the coarse atmospheric light to suppress its blocking effects, and the results are shown in
Figure 3d. As a comparison, we also show the globally homogeneous atmospheric light computed by the DCP algorithm and the corresponding dehazed images in
Figure 3f,g, and it can be seen that the restored results of the DCP method are unnaturally dim due to its inaccurate estimation of the atmospheric light. To ensure that the refined atmospheric light is sufficiently smooth in the global space, the kernel radius r of the guided filter is set to 65, and the regularization parameter
to control the smoothness of the filtered result is set to 0.5.
3.3. Channel-Separated Transmission Estimation
In addition to atmospheric light, transmission also plays a critical role in image haze removal. According to the definition of the transmission (i.e., Equation (
2)), the extinction coefficient
is wavelength-dependent, and if the scene depth is given, the transmission of light with different wavelengths should be unequal. However, in order to simplify the computation, existing algorithms for natural scene outdoor image dehazing treat three transmissions of red, green, and blue channels (RGB) as equal. Since the scene radiation of a natural image traverses a very close distance through the atmospheric medium, this practice does not have a significant impact on the dehazing effect, while the imaging distance of a remote sensing image is extremely long, which will lead to a distinct difference in the transmission maps of the RGB three channels. Therefore, a transmission estimation approach based on channel separation is proposed in this paper, which calculates the transmission of each channel of a haze image independently.
According to Equations (
2) and (
8), we can deduce
and
. In hazy weather, the smaller the imaging distance, the greater the transmission of the scene radiation, the less the captured image is affected by haze, and the lower the intensity its pixels tend to have, so the scene object in the foreground has better visibility. Conversely, the larger the imaging distance, the smaller the transmission, and the higher the pixel values of the haze image (close to atmospheric light), which is consistent with the dark channel prior [
1]. Therefore, we approximate the coarse transmission with the local minimum brightness of the image patch, which can be expressed as
where
indicates the current channel, and
is the normalized image, which ranges from 0 to 1. We still use superpixels here as the image patch division method and follow the conclusion drawn in
Section 3.1 that the transmittances within a superpixel region are identical. Since we approximate the transmission by the minimum brightness of the local image patch, which may cause errors, we introduce an adjustable parameter
related to the content of the image, and we further discuss the effect of the parameter
on the dehazing results in
Section 5.2. Finally, we refine the obtained coarse transmission by a guided filter as shown in the orange area of
Figure 4.
3.4. Remote Sensing Image Dehazing
Once the non-uniform atmospheric light and the transmission are given, the remote sensing haze image can be easily restored using Equation (
6). However, a potential issue arises when the transmission
approaches zero, causing the direct attenuation term
to be very close to zero as well. Consequently, directly recovering the scene radiance
in such cases may lead to undesirable noise artifacts. To address this issue, we apply a constraint on the transmission
, imposing a lower bound denoted as
. For this study, the default value of t
is set to 0.1. The final scene radiance
is restored referring to the following equation:
The overall framework of the proposed SRD method is depicted in
Figure 4.
4. Results
In this section, we conduct a number of experiments to verify the effectiveness of the proposed SRD algorithm. First, we introduce the hardware configuration and software platform of the experiments, as well as the compared state-of-the-art algorithms. Then, we compare the dehazing effects of all algorithms on synthetic and real-world remote sensing images, respectively, and report the quantitative dehazing performance results.
4.1. Experimental Setup and Compared Algorithms
All experiments are performed on the same desktop computer equipped with Intel(R) Core(TM) i7-10700 CPU and 32 GB RAM. Our SRD method is implemented using Python 3.8 and executes in a Windows 10 operating system.
In order to comprehensively assess the efficacy of the proposed SRD algorithm, some comparison experiments are performed between SRD and several state-of-the-art techniques, including HL [
5], IDRLP [
43], GDN [
21], AOD [
20], PSD [
29], EVPM [
13], IDeRs [
16], HTM [
17], and SMIDCP [
11], where the first five algorithms are proposed for natural image haze removal, and the last four methods are designed specifically for remote sensing images. To ensure impartial evaluations, all source codes of the compared algorithms are collected directly from their respective authors and executed without any additional modifications. All test images are from published papers and publicly available datasets.
4.2. Qualitative Experiments on Real-World Remote Sensing Image Dehazing
To validate the dehazing ability of the SRD algorithm on remote sensing images, we compare and analyze the haze removal results of SRD and other state-of-the-art methods on real-world haze images. All test samples are from the Real-world Remote Sensing Haze Image Dataset (RRSHID) [
44], which contains 277 degraded images with haze, all of which are manually selected by the authors of RRSHID from two widely used remote sensing datasets, AID [
45] and DIOR [
46]. In this experiment, we employ three types of test samples for a more comprehensive assessment: (1) challenging samples with dense haze; (2) images with different color distributions; and (3) remote sensing haze images of various scenes.
Figure 5 shows the restored results of comparison methods for remote sensing images with dense haze. Among algorithms designed specifically for natural image dehazing, the results of the IDRLP algorithm are too dim with low contrast and color saturation as shown in samples (c) and (d). GDN is a data-driven algorithm based on deep learning, but due to the obvious domain gap between the training data and the test data, it cannot remove haze in remote sensing images well, so a lot of haze remains, a similar situation appearing in the results of the AOD algorithm. HL obtains clear images with good visuality on samples (b) and (d), while its results on samples (a) and (c) present color shifts and unnatural tones. The PSD algorithm greatly enhances the brightness of the image and improves its visibility, but it over-enhances the colors, resulting in unnatural colors in the results of (a)–(c). Among the algorithms designed for remote sensing haze images, IDeRs and SMIDCP produce unsatisfactory results with unreasonable colors. Similar to GDN, HTM cannot remove haze well, leaving a noticeable haze veil. Comparatively, EVPM and the proposed SRD algorithm obtain promising dehazing results, and especially for sample (a), the color recovered by SRD is more natural and realistic than that of EVPM.
The color distribution of the test image can significantly influence the robustness of dehazing algorithms. For instance, an image containing some white areas can render the dark channel prior [
1] invalid. Consequently, we conduct further experiments to assess the dehazing performance of various algorithms on remote sensing haze images exhibiting diverse color distributions as depicted in
Figure 6. The GDN, AOD, and HTM algorithms exhibit limited efficacy in removing haze for remote sensing images. Additionally, the results of the SMIDCP algorithm for samples (b)–(d) display inappropriate colors, which implies that the algorithm cannot adequately restore the original land cover. Both the PSD and IDeRs methods demonstrate an evident over-processing phenomenon, leading to excessively high color saturation in the restored images. The IDRLP and EVPM algorithms produce dim results in the local area of sample (a), leading to the loss of critical image details. However, the HL and SRD algorithms demonstrate superior performance in removing haze for remote sensing images with diverse color distributions and yield satisfactory restored results.
Furthermore, our investigation extends to various imaging scenes, and the results are presented in
Figure 7. Similar to the observations in
Figure 5 and
Figure 6, distinct degrees of algorithmic failure are observed for GDN, HTM, AOD, and SMIDCP. The IDeRs and PSD algorithms still produce over-saturated images, while the EVPM algorithm yields images with reduced intensity. Notably, HL exhibits perceptually unnatural results in samples (c) and (e). In contrast, the IDRLP and SRD algorithms demonstrate superior capability in effectively removing haze in remote sensing images captured in diverse imaging scenes.
4.3. Quantitative Experiments on Real-World Remote Sensing Image Dehazing
As a valuable complement to visual comparisons, the quantitative evaluation of the restored images dehazed by various algorithms on real-world remote sensing data is presented in this subsection. The previously mentioned RRSHID dataset is adopted here as the benchmark dataset. Three widely used no-reference image quality assessment (IQA) metrics are used to compute the average scores of 277 dehazed images by each compared algorithm, which are BRISQUE [
47], ILNIQE [
48], and DHQI [
49]. BRISQUE employs support vector regression to obtain a no-reference IQA score for a given image based on the statistical regularities presented by natural images in the spatial domain. ILNIQE fits the quality-aware features extracted from a large number of natural images to a multivariate Gaussian model, then performs the same operation on the test image, and finally calculates the distance between these two fitting parameters as the evaluation score. DHQI extracts and fuses the haze features, structure-preserving features, and over-enhancement features of a restored image to obtain the evaluation score. Note that BRISQUE and ILNIQE are tailored for assessing the naturalness of images and are commonly used in various image restoration tasks, such as denoising and deblurring. While DHQI is meticulously designed for image dehazing, it focuses on the assessment of residual haze levels within the restored image and also takes into account the potential occurrence of over-enhancement.
The no-reference assessment scores are shown in
Table 1. The SRD algorithm achieves the second-best ILNIQE score as well as the fourth-best BRISQUE score. At the same time, it also receives the second-highest DHQI evaluation value. These two types of no-reference IQA scores demonstrate that the restored images by the SRD algorithm have both good naturalness and less residual haze, which is consistent with the findings of the visual comparison experiments in
Section 4.2.
4.4. Experiments on Synthetic Remote Sensing Haze Image Datasets
It is usually difficult to obtain the corresponding haze-free images (as the ground truth for dehazing performance evaluation) for real-world remote sensing haze images. Therefore, some researchers synthesize the haze-contaminated image according to the clear remote sensing image with some prior knowledge. Such paired remote sensing haze image datasets can be used as an important tool for the evaluation of haze removal algorithms. The Haze1k [
50] dataset comprises 1200 remote sensing images without haze and their synthetic hazy counterparts. The haze-free images are collected from the GF-2 satellite, while the corresponding simulated ones are generated through the atmospheric scattering model. Haze1k consists of three subsets with different haze densities, namely, Haze1k-thin, Haze1k-moderate, and Haze1k-thick. Each of these subsets is subsequently further partitioned into a training set, a validation set, and a test set. In this experiment, we evaluate the dehazing performance of the compared algorithms using the test sets of these three sub-datasets. In addition, we use the RICE [
51] dataset, which contains 500 pairs of remote sensing images with and without haze, which are acquired by the authors through the Google Earth platform.
Since the original haze-free image and the dehazed image are given simultaneously, we can use full-reference IQAs to quantitatively compare the haze removal ability of each compared algorithm. Considering the visual perception similarity, peak signal-to-noise ratio, structural similarity, feature similarity, and color error, we adopt five commonly used full-reference image quality assessment metrics, which are LPIPS [
52] (learned perceptual image patch similarity), PSNR (peak signal-to-noise ratio), SSIM (structural similarity), FSIM [
53] (feature similarity), and CIEDE2000. LPIPS measures the difference between the two given images based on perceptual loss to obtain an evaluation score consistent with human visual perception. PSNR mathematically assesses the errors between the pixel pairs of the input and reference images. SSIM models the brightness difference, contrast difference, and structure difference between the target image and the reference, and calculates the score that matches the human observation. Similar to the SSIM index, FSIM is based on the human visual system and obtains a quality evaluation score from the low-level features of the image. We test each compared method on the four datasets mentioned above to obtain the corresponding restored images, and then employ these five evaluation metrics to calculate the average score of each algorithm on each dataset as shown in
Table 2,
Table 3,
Table 4 and
Table 5.
EVPM obtains some good full reference evaluation scores on the Haze1k dataset, but the results on RICE are not satisfactory, having the highest color error, showing its poor robustness in various scenes. The HL method usually overestimates the haze concentration, and thus, it achieves poor evaluation scores on the dataset with thin haze but performs well on challenging data. GDN and HTM often have residual haze in restored images, which leads to inferior assessment scores. IDeRS is prone to over-enhancement, resulting in poor evaluation scores of perception quality. The GDN, AOD, and PSD algorithms are all data-driven methods based on deep learning. Their effects are commonly closely related to training data, and their generalization performance results are often inconsistent across different datasets. For example, the AOD and the PSD algorithms achieve competitive assessment scores on the Haze1k-thin dataset but inferior scores on the other three test datasets. In contrast, the SRD algorithm proposed in this paper can restore clear images that conform to human visual perception and can recover the structures and texture details of the original image with little color distortion. Therefore, SRD achieves the best full-reference assessment scores on all four datasets, implying that it has good dehazing ability and excellent robustness.
5. Discussion
5.1. The Parameter K of the Superpixel Number in Patch Division
An important innovation of the proposed SRD method is the introduction of the superpixel technique into the haze removal task for remote sensing images and the accurate estimation of local atmospheric light and transmission using a superpixel-by-superpixel strategy. Therefore, there is a critical parameter, the number of superpixels, in the image patch division stage of the SRD algorithm, i.e., the parameter
K mentioned in
Section 3.1. If the parameter
K is too small, the divided patches are too rough, which defeats the purpose of the introduction of superpixels, i.e., to preserve the image structure information when dividing the image into local patches. In extreme cases, when
K is 1, the non-uniform atmospheric light estimation algorithm fails, and the global brightest pixel is crudely used as the atmospheric light. If
K is too large, it will also lead to an inaccurate estimation of atmospheric light, making the predicted coarse atmospheric light approximate the original input image. Moreover, dividing too many patches will increase the computational overhead of the subsequent estimation of the atmospheric light and transmission. Therefore, the default value of the parameter
K in this paper is 200, which is a trade-off between the dehazing effect and computation overhead through a large number of experiments.
Figure 8 depicts the dehazed results and the corresponding quantitative evaluations of the SRD algorithm with different parameters
K. When
, the restored image has significant residual haze, thus yielding the lowest PSNR score and the largest color error. With
K ranging from 100 to 500, the dehazing effect of SRD is satisfactory, and the results keep consistent and good visibility. The smallest color error and best PSNR score arise when
. As parameter
K increases further, SRD tends to obtain over-enhanced results.
5.2. The Parameter in Channel-Separated Transmission Estimation
In the stage of transmission estimation, we approximate the coarse transmission with the minimum brightness within each superpixel while introducing the parameter
to reduce the error as shown in Equation (
12).
is supposed to be related to image brightness. According to a lot of tests, we set
to 0.85 in this paper. The LPIPS and PSNR scores on the four widely used haze image datasets are shown in
Figure 9. The perceptual error of the restored image by the SRD algorithm is insensitive to the parameter
. When
changes within the range of 0.7 to 1.0, the LPIPS scores of the four datasets only vary by an amount between 0.01 and 0.03. And when
is 0.85, SRD obtains a better PSNR evaluation score.
5.3. The Analysis of the Channel-Separated Transmission Estimation Effectiveness
One important innovation of the proposed SRD algorithm is the channel-separated transmission estimation method, which is derived from two considerations. Firstly, remote sensing images are often captured at very long distances, and the attenuation of scene light in the atmosphere is related to both the distance and wavelength according to the imaging model, so we propose a strategy to estimate the transmission independently for each color channel. Secondly, for each channel, we assume that the minimum intensity within a local region can approximately represent the transmission of this channel in the local space. To validate the effectiveness of our method, we conduct two groups of interesting and meaningful experiments.
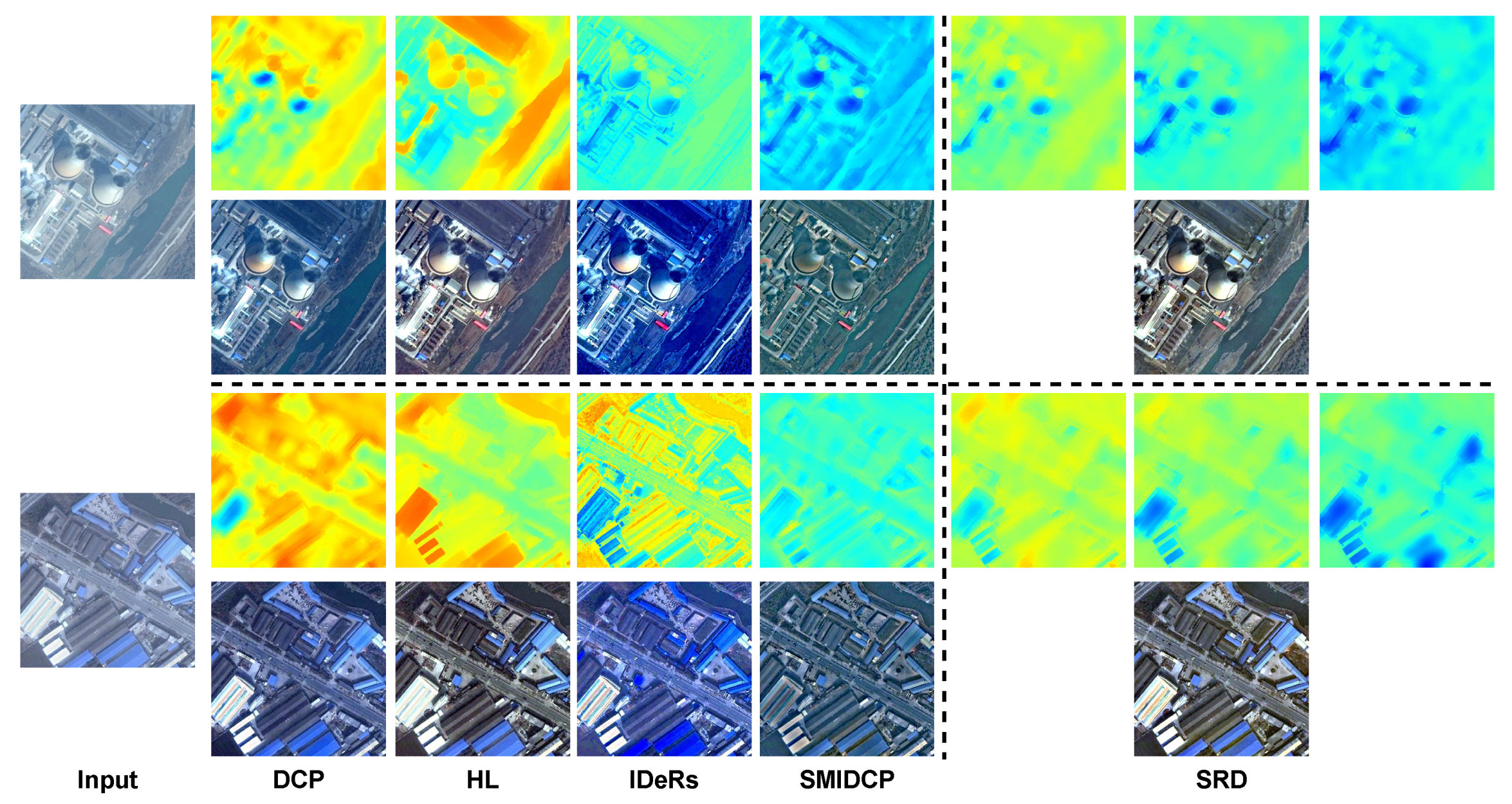
In
Figure 10, we visually compare the transmission maps estimated by various physical model-based dehazing algorithms and their corresponding dehazed results. The transmission maps of all the compared algorithms are a single channel (shown in pseudo-color for better visualization here), which implies that the transmittance of light with different wavelengths is assumed to be equivalent, resulting in color shifts in the final results. The transmission estimated by the SRD algorithm is consistent with the Rayleigh scattering model, wherein blue light with a shorter wavelength experiences greater energy attenuation during propagation, resulting in a lower transmittance compared to red light with a longer wavelength. For two different test samples in
Figure 10, it is obvious that the transmission of the blue channel predicted by SRD is smaller than that of the blue and red channels in turn. This reasonable strategy makes the images restored by SRD have natural and realistic colors.
To quantitatively assess the impact of the channel-separated transmission estimation strategy on the dehazing performance, we replace the transmission of the SRD algorithm with that estimated by the IDeRs algorithm, keeping the rest of the steps of the SRD algorithm unchanged. This produces a new algorithm variant, labeled as “M2” in
Figure 11, while “M1” and “M3” represent the original IDeRs algorithm and our SRD algorithm, respectively. During the replacement process, to avoid the influence of coding details, we directly save the IDeRs’ transmission map as a “.mat” file, and then load the corresponding transmission data in the SRD algorithm. Finally, we test the dehazing performance of variant method “M2” using the four test datasets adopted in
Section 4.4 and compare it with “M1” and “M3” using four full-reference IQAs: PSNR, SSIM, LPIPS, and FSIM. The results are shown in
Figure 11. They demonstrate that the channel-separated transmission estimation strategy can significantly improve the dehazing performance for RSIs.
5.4. Execution Efficiency
The execution efficiency of the algorithm determines its availability in various application scenarios. Here, we comprehensively compare the average processing time of various dehazing algorithms for input images with different resolutions. We randomly select 100 images from the RRSHID dataset [
44] mentioned in
Section 4.2 and resize them to three resolutions:
,
, and
, constituting three test sets. Then, we execute the SRD algorithm and each comparison method separately on the same computer (described in
Section 4.1) and calculate their average computing time on these three test sets. For the sake of fairness, we severally test the computation times of all three deep learning-based algorithms, GDN, AOD, and PSD, with and without acceleration by the GPU.
As shown in
Table 6, the computational overhead of the algorithms based on deep learning is very high and requires the computation acceleration by GPUs to obtain a satisfactory computing speed, which limits the application of the algorithm in various complex scenarios. It is important to note that the PSD algorithm has significant computational demands, which can lead to out-of-memory errors when processing a single image with
resolution on our computer equipped with a NVIDIA RTX 3090 GPU with 24 GB of graphics memory. The proposed SRD algorithm achieves a good dehazing effect with little increase in the computational overhead, and it demonstrates superior processing speed in comparison to the HL, HTM, and IDeRs algorithms when subjected to equivalent testing conditions. The time cost of the SRD algorithm is primarily devoted to the division of image patches by the superpixel technique, as well as to the calculation of the local maximum and minima within each patch to estimate the coarse atmospheric light and the channel-separated transmission. Fortunately, our method exhibits good parallelism because the computations within each superpixel patch are independent of each other and can be implemented concurrently. Moreover, within any given image patch, the operations of finding the maximum and minimum values can also be independently executed as well.
5.5. Dehazing for Natural Scene Images
Although SRD is a haze removal algorithm designed based on the imaging features of remote sensing images, it also has excellent performance in outdoor natural image haze removal because the atmospheric light estimated by the SRD algorithm is non-uniform, which can reduce the atmospheric light prediction errors caused by local bright pixels in the test image. We tested the SRD algorithm for four representative outdoor haze images, and the results are shown in
Figure 12. In the first sample, our algorithm restores the details of the hayrick in the near distance and the contours of the field ridge in the far distance very well. For the challenging samples with dense haze, such as the second and fourth images, SRD effectively recovers the structural information as well as the realistic and natural colors of the scene objects. The third image shows that SRD can still dehaze well for images of complex scenes captured at close range.
5.6. Limitations and Future Work
The SRD algorithm proposed in this paper has some limitations, which are shown in
Figure 13. (a) When there is a lot of noise in the hazy image, SRD will potentially fail due to inaccurate estimation of the atmospheric light and transmission map because our atmospheric light and transmission in each superpixel are calculated by local extreme values, which are highly disturbed by noise. The enlarged and colored areas of the images in
Figure 13a visually illustrate the adverse effects of noise. (b) There is extremely dense and unevenly distributed haze in the test sample, which will lead to some irretrievable loss of image information and render the SRD algorithm powerless for hazy image restoration. (c) The SRD algorithm does not work well for indoor images because it is proposed based on the imaging features of remote sensing images, which are quite different from those of indoor images. For example, the green box areas of the restored image in
Figure 13c show some obvious discordant and dark spots. In the future, we will explore more robust priors that can better deal with noisy haze images and design image dehazing algorithms combined with multi-sensor information, e.g., utilizing multi-spectral or hyperspectral data.
6. Conclusions
In this article, we present a novel haze removal algorithm specifically for RSIs, namely SRD, which is developed based on the distinctive imaging characteristics inherent to RSIs. Firstly, the imaging space of RSI is extremely large, so the assumption of globally uniform atmospheric light distribution is not tenable. To address this issue, we propose a global non-uniform atmospheric light estimation algorithm utilizing the maximum reflection prior. Secondly, the imaging distance of RSI is very far, which makes the transmissions of each color channel of the image unequal. Therefore, we introduce a channel-separated transmission estimation method. Our estimations of both atmospheric light and transmission are based on local image patches. However, existing dehazing algorithms divide the image into local patches using fixed-size rectangles, which tends to result in the loss of crucial structural information and undermines the availability of haze-relevant priors. Consequently, we introduce a superpixel-based patch division strategy, which can preserve the structure and color information of the input image, ensuring that pixels within each local patch exhibit similar imaging behavior. Furthermore, we validate the proposed SRD algorithm on a large number of real-world and synthetic haze RSIs, and the comparison experiments with existing state-of-the-art algorithms suggest that the dehazed images by SRD exhibit enhanced natural color fidelity, well-defined structural contours, and overall improved visual quality. The quantitative assessment based on both full-reference and no-reference IQAs demonstrates that SRD has superior dehazing performance. Moreover, our parameter analysis experiments affirm the robustness of the SRD method and its potential to yield promising dehazing results, even when applied to outdoor natural images.