Inundation–Desiccation State Prediction for Salt Pans in the Western Pannonian Basin Using Remote Sensing, Groundwater, and Meteorological Data
Abstract
:1. Introduction
2. Materials
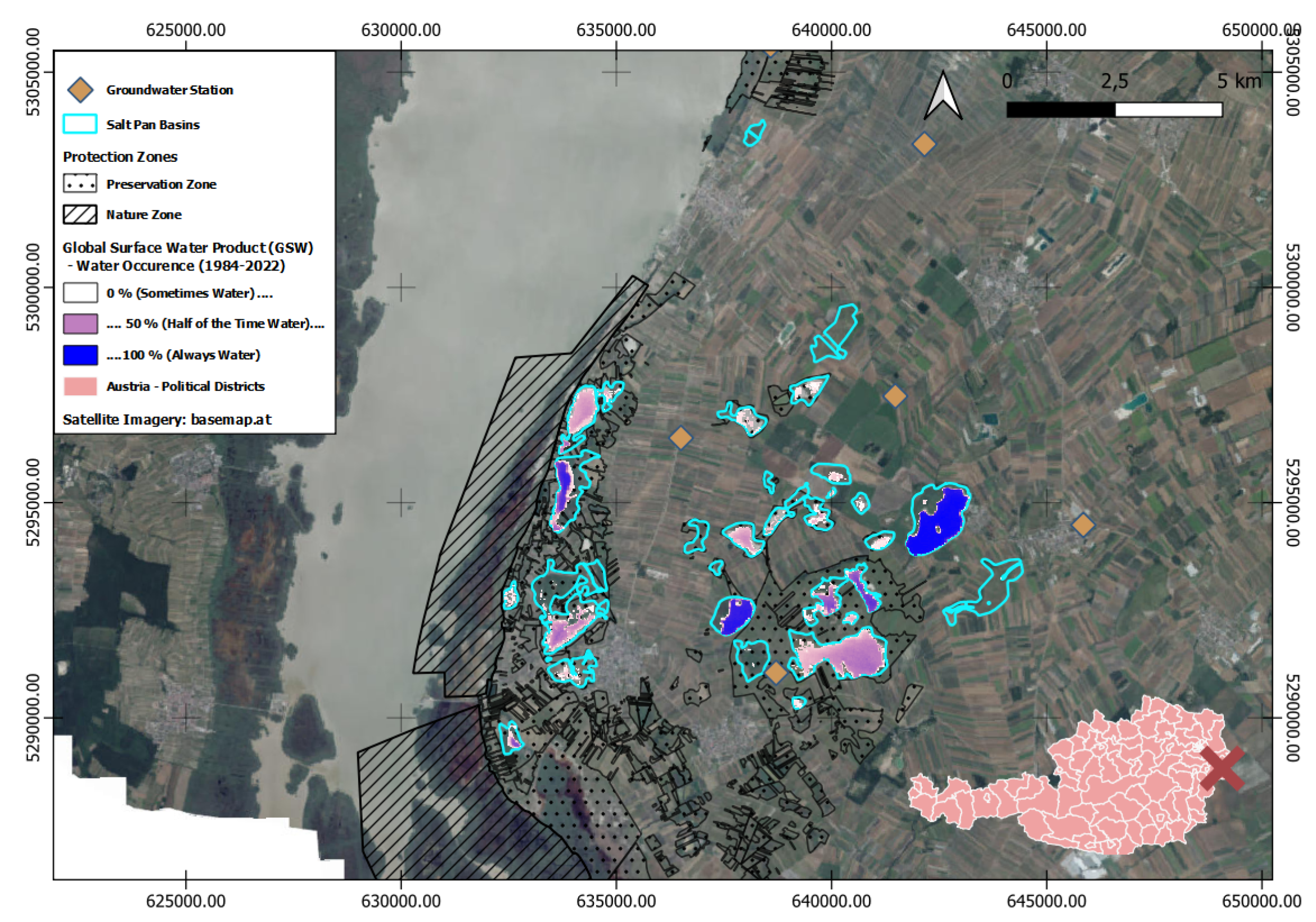
2.1. Study Area
2.2. Multispectral Satellite Imagery
2.3. Predictor Data
2.3.1. Predictor Selection
| Field | Variable [Unit] | Derived Predictor [Unit] (Abbrev.) | Integ. Period | Relation to Salt Pan Cycle | Data Source |
|---|---|---|---|---|---|
| Hydrology | Groundwater [m.a.s.l.] | Anomalies [unitless] (GW Anom.) | 12 m. | Groundwater is of key importance for salt pan water abundance in Seewinkel [21] Short-term and especially long-term groundwater depletion leads to salt pan degradation [114] | Austrian eHyd portal |
| SGI [unitless] (SGI) | Cont. | The Standardized Groundwater Index can serve as a robust estimation of groundwater drought [115,116] Groundwater drought in March influences the salt pan water extent in spring and therefore the inundation state in summer | |||
| Level ratio [unitless] (GW level ratio) | Oct./March (6 m.) | Fall-winter groundwater level ratio is closely connected to regional precipitation during that time [117] The level ratio stands in relation to salt pan water extent in spring [14] | |||
| Meteorology | Temperature [°C] | Anomalies [unitless] (T Anom.) | 12 m. | Higher temperature increases water temperature [21,118,119,120] Higher summer temperature increases evaporation and therefore the number of drying events [14] Higher temperatures in winter decrease spring water extent [20] | ERA5-Land [121], DOI: 10.24381/cds.68d2bb30 |
| Numb. of days above 25 °C [days] | 12 m. | The number of days above 25 °C is connected to heatwaves and extensive evaporation [122] | |||
| Evaporation [mm] | Anomalies [unitless] (Epot Anom.) | 12 m. | Evaporation leads to salt pan concentration and desiccation [1,123] | ||
| Precipitation [mm] | Anomalies [unitless] (P Anom.) | 12 m. | Precipitation leads to salt pan filling [1] Precipitation leads to eluviation of the saliferous horizon [20] Precipitation as observed over a 12-month period is related to hydrological drought [124] | ||
| SPI 6 [unitless] | 6 m. | Standardized Precipitation Index 6 is connected to medium-term precipitation patterns and agricultural drought [125,126] | |||
| SPI 24 [unitless] | 24 m. | Standardized Precipitation Index 24 is connected to long-term precipitation patterns and hydrological/socioeconomic drought [124,125,126,127] |
2.3.2. Groundwater Level
2.3.3. ERA5-Land Meteorology
3. Methods
3.1. Salt Pan Mapping
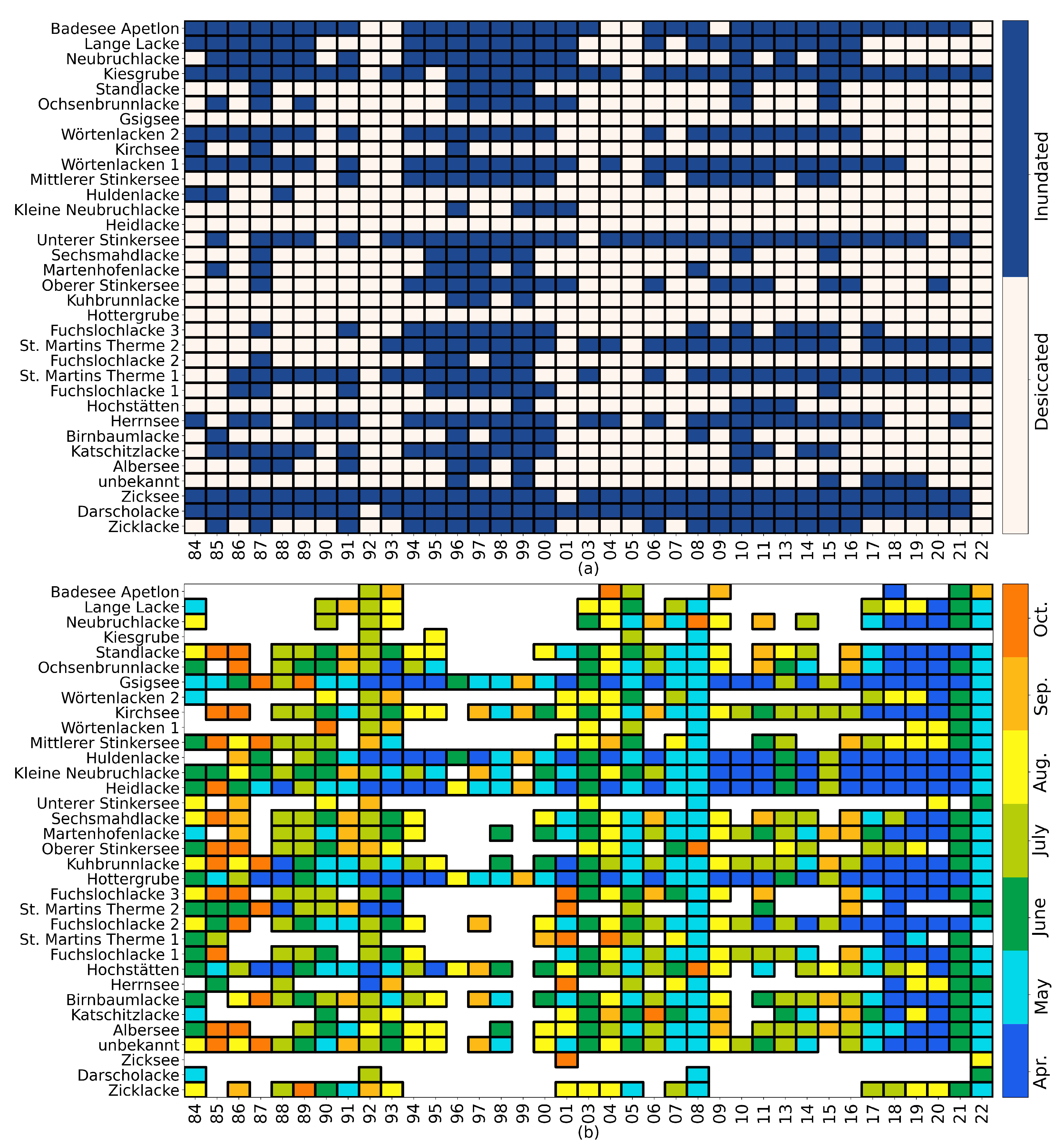
3.1.1. Derivation of Water Extent Time Series
3.1.2. Derivation of JASO Inundation State
3.2. Inundation State Prediction
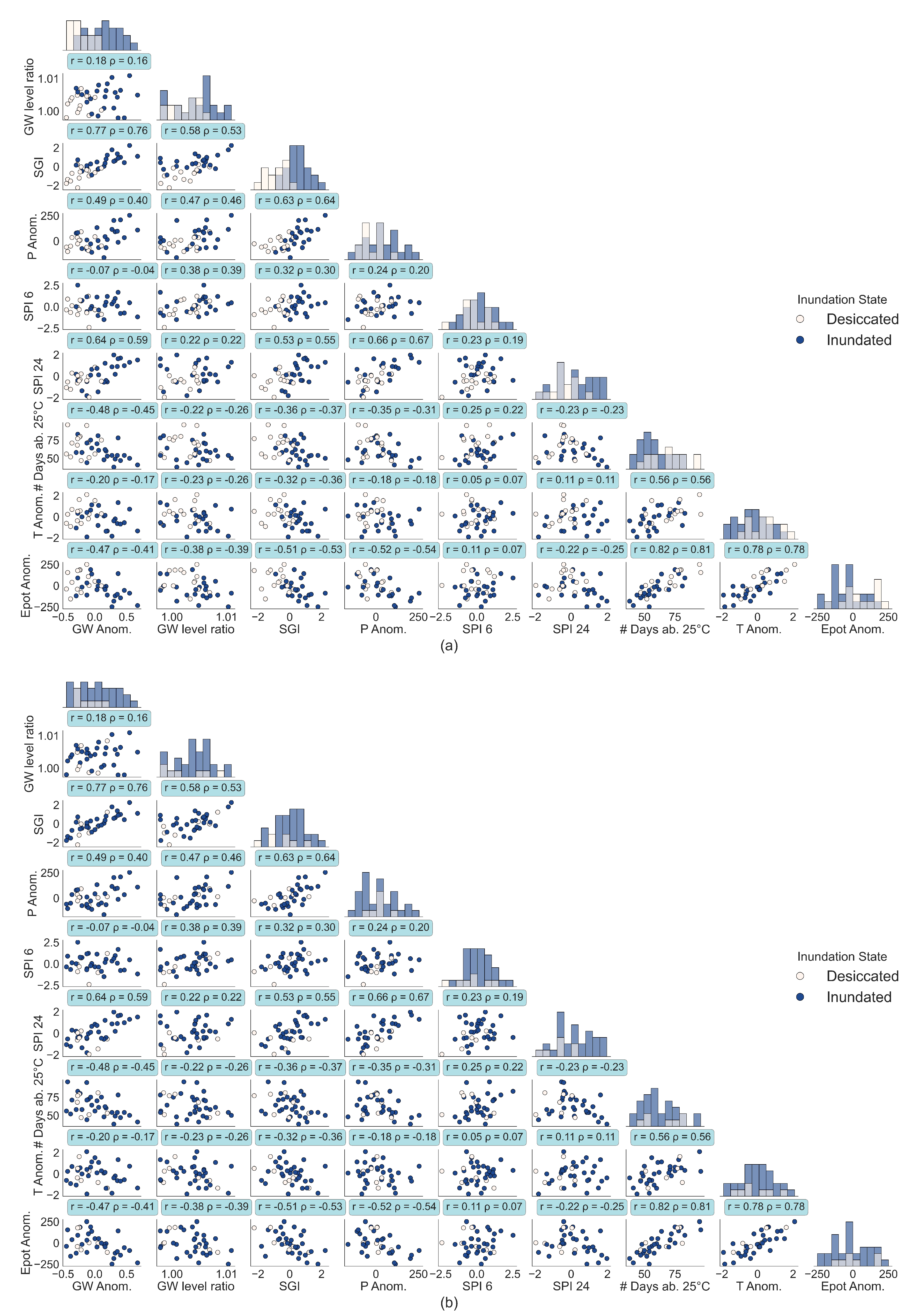
3.2.1. Exploratory Data Analysis: Separability and Correlation Analysis
3.2.2. Random Forests
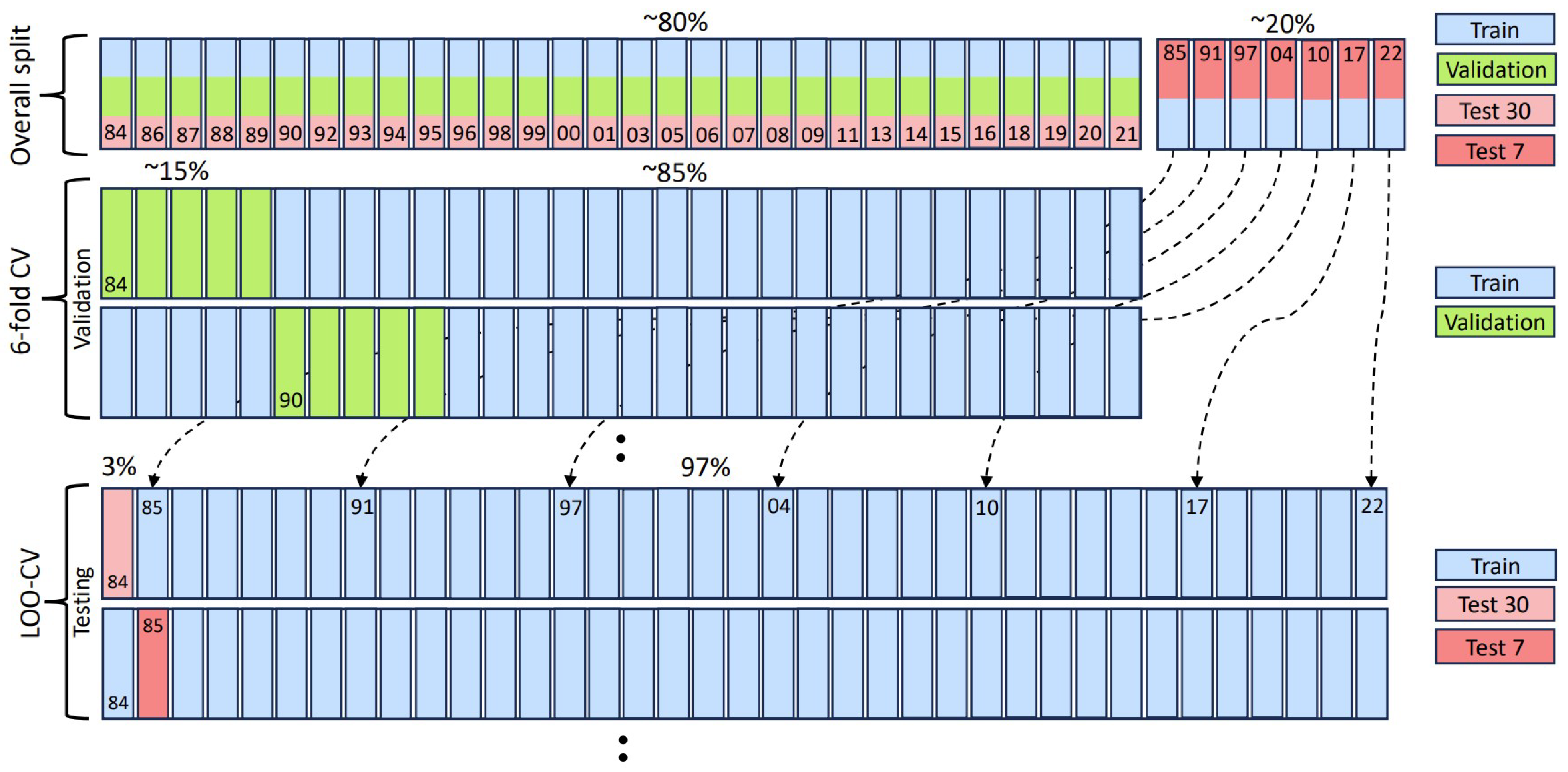
3.2.3. Model Setup
3.2.4. Model Testing
3.2.5. Model Validation
3.2.6. Evaluation Metrics
3.2.7. Feature Importance
4. Results
4.1. Salt Pan Mapping
4.2. Inundation State Prediction
4.2.1. Exploratory Data Analysis
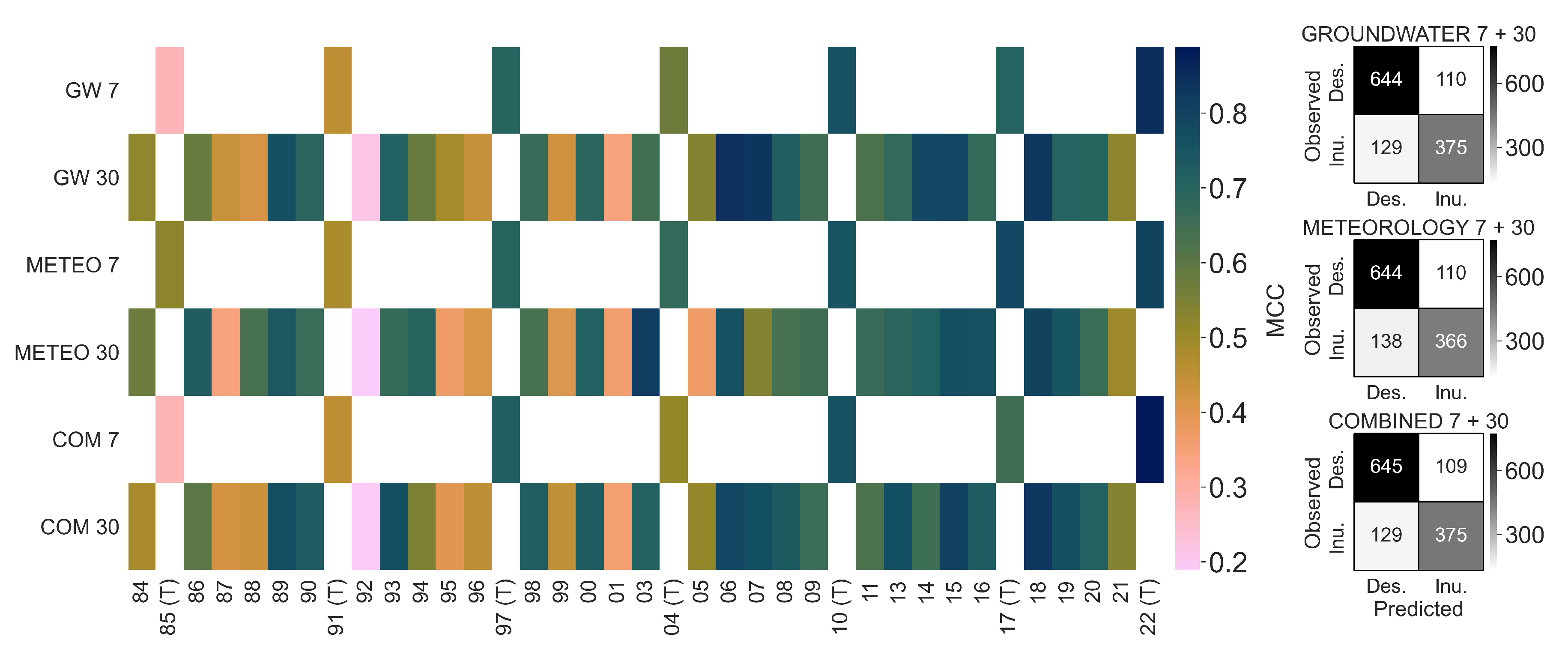
4.2.2. Average Prediction Skill
4.2.3. Detailed Analysis of Single LOOCV Model Runs
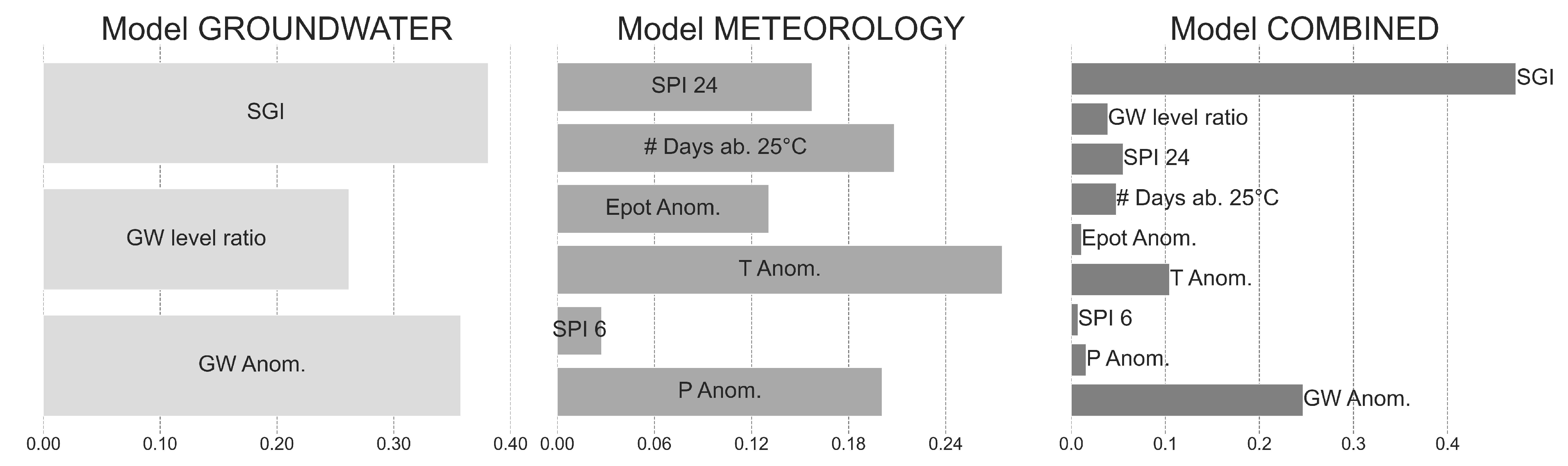
4.2.4. Feature Importance
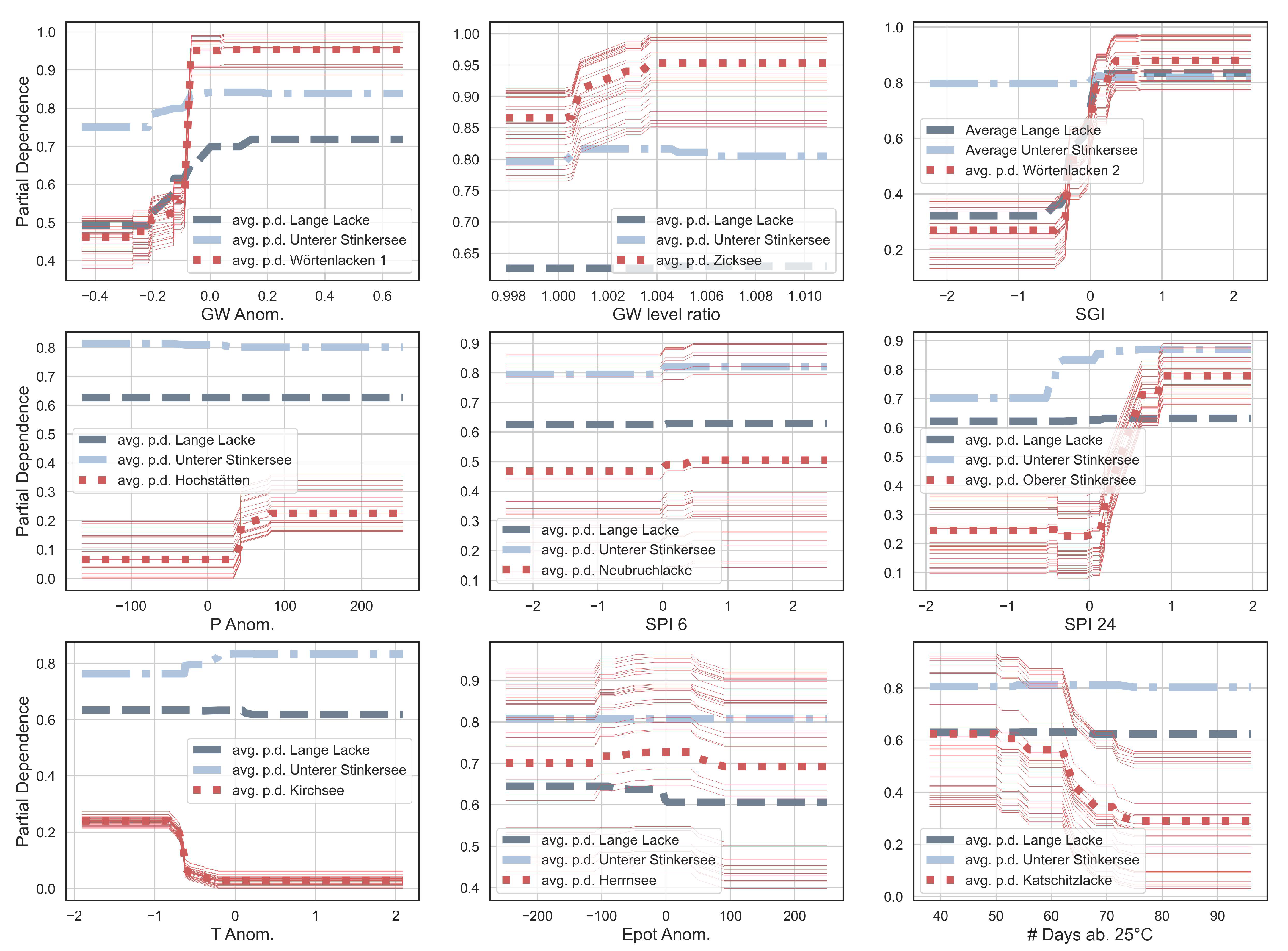
4.2.5. Partial Dependency
5. Discussion
5.1. Assumptions
5.2. Predictors
5.3. Target
5.4. Model Error
5.5. Model Transferability
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Predictor with Largest PDP Spread | Threshold for Predictor | |
|---|---|---|
| Badesee Apetlon | GW Anomal (0.18) | −0.09 |
| Lange Lacke | SGI (0.51) | −0.09 |
| Neubruchlacke | GW Anomal (0.43) | 0.1 |
| Kiesgrube | GW Anomal (0.12) | −0.12 |
| Standlacke | GW Anomal (0.25) | 0.14 |
| Ochsenbrunnlacke | GW Anomal (0.25) | 0.1 |
| Gsigsee | GW Anomal (0.0) | −0.45 |
| Wörtenlacken 2 | SGI (0.61) | −0.03 |
| Kirchsee | T Anomal (0.21) | −0.62 |
| Wörtenlacken 1 | GW Anomal (0.49) | −0.09 |
| Mittlerer Stinkersee | SPI 24 (0.28) | 0.09 |
| Huldenlacke | T Anomal (0.13) | −0.2 |
| Kleine Neubruchlacke | SPI 24 (0.21) | 0.29 |
| Heidlacke | GW Anomal (0.0) | −0.45 |
| Unterer Stinkersee | SPI 24 (0.17) | −0.41 |
| Sechsmahdlacke | GW Anomal (0.2) | 0.14 |
| Martenhofenlacke | SGI (0.22) | 0.09 |
| Oberer Stinkersee | SPI 24 (0.55) | 0.29 |
| Kuhbrunnlacke | GW Anomal (0.08) | 0.1 |
| Hottergrube | GW Anomal (0.0) | −0.45 |
| Fuchslochlacke 3 | SGI (0.32) | 0.09 |
| St. Martins Therme 2 | SPI 24 (0.23) | −0.47 |
| Fuchslochlacke 2 | SGI (0.12) | 0.09 |
| St. Martins Therme 1 | GW level ratio (0.15) | 1.0 |
| Fuchslochlacke 1 | GW Anomal (0.31) | 0.16 |
| Hochstätten | P Anomal (0.16) | 42.27 |
| Herrnsee | SGI (0.33) | −0.03 |
| Birnbaumlacke | SPI 24 (0.17) | 0.73 |
| Katschitzlacke | # Days ab. 25 °C (0.33) | 64.0 |
| Albersee | GW Anomal (0.21) | 0.14 |
| unbekannt | GW Anomal (0.08) | 0.06 |
| Zicksee | GW level ratio (0.09 ) | 1.0 |
| Darscholacke | GW Anomal (0.12) | −0.13 |
| Zicklacke | SGI (0.59) | −0.03 |
References
- Lowenstein, T.K.; Hardie, L.A. Criteria for the recognition of salt-pan evaporites. Sedimentology 1985, 32, 627–644. [Google Scholar] [CrossRef]
- Shaw, P.; Bryant, R. Pans, Playas and Salt Lakes. In Arid Zone Geomorphology; John Wiley and Sons, Ltd: Hoboken, NJ, USA, 2011; Chapter 15; pp. 373–401. [Google Scholar] [CrossRef]
- Leemans, R.; De Groot, R. Millennium Ecosystem Assessment: Ecosystems and Human Well-Being: A Framework for Assessment; Island Press: Washington, DC, USA, 2003. [Google Scholar]
- Wurtsbaugh, W.A.; Miller, C.; Null, S.E.; DeRose, R.J.; Wilcock, P.; Hahnenberger, M.; Howe, F.; Moore, J. Decline of the world’s saline lakes. Nat. Geosci. 2017, 10, 816–821. [Google Scholar] [CrossRef]
- Williams, W.D. Lakes in Arid Environments. In The Lakes Handbook; John Wiley & Sons, Ltd: Oxford, UK, 2004; Chapter 8; pp. 200–240. [Google Scholar] [CrossRef]
- Safaee, S.; Wang, J. Towards global mapping of salt pans and salt playas using Landsat imagery: A case study of western United States. Int. J. Remote Sens. 2020, 41, 8693–8716. [Google Scholar] [CrossRef]
- Wasserman, J.; Adams, J.B.; Lemley, D.A. Investigating the potential for saltpan restoration for the provision of multiple ecosystem services. Afr. J. Aquat. Sci. 2022, 47, 436–446. [Google Scholar] [CrossRef]
- Nayak, S.; Pandeya, A.; Gupta, M.; Trivedi, C.; Prasad, K.; Kadri, S. Application of Satellite Data for Monitoring Degradation of Tidal Wetlands of the Gulf of Kachchh, Western India. In Space and Humanity; Napolitano, L., Ed.; Pergamon: Oxford, UK, 1989; pp. 171–178. [Google Scholar] [CrossRef]
- Picado, A.; Dias, J.M.; Fortunato, A.B. Effect of flooding the salt pans in the Ria de Aveiro. J. Coast. Res. 2009, 2, 1395–1399. [Google Scholar]
- Da Silva, M.F.; Albuquerque, H.; Martins, F.; Buron, G. Salt pans: An Indissociable Natural and Cultural Heritage – A Comparative Study Between Aveiro, Portugal and Guérande, France. In Tourism Planning and Development in Western Europe; CABI, Ltd.: Hoboken, NJ, USA, 2022; pp. 65–79. [Google Scholar] [CrossRef]
- Herzig, A. Soda pans–jewels of the Nationalpark Neusiedler See-Seewinkel An opinion based on limnological data. Acta ZooBot Austria 2020, 157, 81–114. [Google Scholar]
- Boros, E.; Ecsedi, Z.; Oláh, J.; Szegedi, R.; Dunn, J. Ecology and Management of Soda Pans in the Carpathian Basin; Hortobágy Environmental Association: Hortobágy, Hungary, 2013. [Google Scholar]
- Albert, R.; Werner, V.; Popp, M.; Fischer, M.; Niklfeld, H. Botanische Kostbarkeiten vor unserer Haustür Die Salzpflanzen im Gebiet des Neusiedler Sees, Burgenland (Österreich). Acta ZooBot Austria 2020, 157, 115–143. [Google Scholar]
- Krachler, R.; Korner, I.; Dvorak, M.; Milazowszky, N.; Rabitsch, W.; Werba, F.; Zulka, P.; Kirschner, A. Die Salzlacken des Seewinkels: Erhebung des Aktuellen Oekologischen Zustandes Sowie Entwicklung Individueller LacKenerhaltungskonzepte Fuer Die Salzlacken des Seewinkels (2008–2011); Technical Report; Naturschutzbund Burgenland: Eisenstadt, Austria, 2012. [Google Scholar]
- Cabela, A.; Grillitsch, H.; Tiedemann, F. Atlas zur Verbreitung und Ökologie der Amphibien und Reptilien in Österreich: Auswertung der Herpetofaunistischen Datenbank der Herpetologischen Sammlung des Naturhistorischen Museums in Wien; Technical Report; Umweltbundesamt: Wien, Austria, 2001. [Google Scholar]
- Dvorak, M.; Landmann, A.; Teufelbauer, N.; Wichmann, G.; Berg, H.M.; Probst, R. The conservation status of the breeding birds of Austria: Red List (5th version) and Birds of Conservation Concern (1st version). Egretta 2017, 55, 6–42. [Google Scholar]
- Dvorak, M.; Laber, J.; Ranner, A.; Pellinger, A.; Tatai, S.; Hadarics, T.; Dorogman, C.; Lang, A. Artenliste der Avifauna des Neusiedler See—Gebiets; Technical Report; Nationalpark Neusiedler See—Seewinkel Fertő–Hanság Nemzeti Park BirdLife Österreich: Neusiedl, Österreich, 2020. [Google Scholar]
- Dvorak, M.; Bieringer, G.; Braun, B.; Grüll, A.; Karner-Ranner, E.; Kohler, B.; Korner, I.; Laber, J.; Nemeth, E.; Rauer, G.; et al. Population size, distribution and population trends of threatened and ecologically important bird species in the National Park Neusiedler See—Seewinkel: Results from the years 2001–2015. Egretta 2016, 54, 4–86. [Google Scholar]
- Boros, E.; V.-Balogh, K.; Vörös, L.; Horváth, Z. Multiple extreme environmental conditions of intermittent soda pans in the Carpathian Basin (Central Europe). Limnologica 2017, 62, 38–46. [Google Scholar] [CrossRef]
- Krachler, R.; Krachler, R.; Milleret, E.; Wesner, W. Limnochemische Untersuchungen zur aktuellen Situation der Salzlacken im burgenlaendischen Seewinkel. Burg. Heim. 2000, 62, 3–49. [Google Scholar]
- Zimmermann-Timm, H.; Teubner, K. Folgen der Grundwassersenkung am Beispiel des Neusiedlers See Seewinkel (Burgenland, Österreich). In Warnsignal Klima: Boden und Landnutzung; Lozán, J.L.S.-W., Breckle, H.G., Kasang, D., Eds.; Wissenschaftliche Auswertungen in Kooperation mit GEO: Oxford, UK, 2021; pp. 142–149. [Google Scholar]
- Horvath, Z.; Ptacnik, R.; Vad, C.; Chase, J. Habitat loss over six decades accelerates regional and local biodiversity loss via changing landscape connectance. Ecol. Lett. 2019, 22, 1019–1027. [Google Scholar] [CrossRef] [PubMed]
- Mitter, H.; Schmid, E. Informing groundwater policies in semi-arid agricultural production regions under stochastic climate scenario impacts. Ecol. Econ. 2021, 180, 106908. [Google Scholar] [CrossRef]
- Vanderhoof, M.K.; Lane, C.R.; McManus, M.G.; Alexander, L.C.; Christensen, J.R. Wetlands inform how climate extremes influence surface water expansion and contraction. Hydrol. Earth Syst. Sci. 2018, 22, 1851–1873. [Google Scholar] [CrossRef] [PubMed]
- Sharma, L.; Naik, R.; Pandey, P. A Focus on Reaggregation of Playa Wetlandscapes in the Face of Global Ecological Disconnectivity. In Advances in Remote Sensing for Natural Resource Monitoring; John Wiley & Sons: Hoboken, NJ, USA, 2021; pp. 366–387. [Google Scholar] [CrossRef]
- Williams, D.D. The Biology of Temporary Waters; Oxford University Press: Oxford, UK, 2006. [Google Scholar]
- Nhiwatiwa, T.; Dalu, T. Seasonal variation in pans in relation to limno-chemistry, size, hydroperiod, and river connectivity in a semi-arid subtropical region. Phys. Chem. Earth, Parts A/B/C 2017, 97, 37–45. [Google Scholar] [CrossRef]
- Turak, E.; Harrison, I.; Dudgeon, D.; Abell, R.; Bush, A.; Darwall, W.; Finlayson, C.M.; Ferrier, S.; Freyhof, J.; Hermoso, V.; et al. Essential Biodiversity Variables for measuring change in global freshwater biodiversity. Biol. Conserv. 2017, 213, 272–279. [Google Scholar] [CrossRef]
- Foti, R.; del Jesus, M.; Rinaldo, A.; Rodriguez-Iturbe, I. Hydroperiod regime controls the organization of plant species in wetlands. Proc. Natl. Acad. Sci. USA 2012, 109, 19596–19600. [Google Scholar] [CrossRef]
- Hess, L.L.; Melack, J.M.; Novo, E.M.; Barbosa, C.C.; Gastil, M. Dual-season mapping of wetland inundation and vegetation for the central Amazon basin. Remote Sens. Environ. 2003, 87, 404–428. [Google Scholar] [CrossRef]
- Reschke, J.; Bartsch, A.; Schlaffer, S.; Schepaschenko, D. Capability of C-Band SAR for Operational Wetland Monitoring at High Latitudes. Remote Sens. 2012, 4, 2923–2943. [Google Scholar] [CrossRef]
- Krzepek, K.; Schmidt, J.; Iwaszczuk, D. Fusion of SAR and Multi-spectral Time Series for Determination of Water Table Depth and Lake Area in Peatlands. PFG-Photogramm. Remote Sens. Geoinf. Sci. 2022, 90, 561–575. [Google Scholar] [CrossRef]
- Kseňak, Ľ.; Pukanská, K.; Bartoš, K.; Blišťan, P. Assessment of the Usability of SAR and Optical Satellite Data for Monitoring Spatio-Temporal Changes in Surface Water: Bodrog River Case Study. Water 2022, 14, 299. [Google Scholar] [CrossRef]
- Bartsch, A.; Trofaier, A.M.; Hayman, G.; Sabel, D.; Schlaffer, S.; Clark, D.B.; Blyth, E. Detection of open water dynamics with ENVISAT ASAR in support of land surface modelling at high latitudes. Biogeosciences 2012, 9, 703–714. [Google Scholar] [CrossRef]
- Schlaffer, S.; Chini, M.; Dorigo, W.; Plank, S. Monitoring surface water dynamics in the Prairie Pothole Region of North Dakota using dual-polarised Sentinel-1 synthetic aperture radar (SAR) time series. Hydrol. Earth Syst. Sci. 2022, 26, 841–860. [Google Scholar] [CrossRef]
- Prigent, C.; Papa, F.; Aires, F.; Rossow, W.B.; Matthews, E. Global inundation dynamics inferred from multiple satellite observations, 1993–2000. J. Geophys. Res. Atmos. 2007, 112, D12. [Google Scholar] [CrossRef]
- Justice, C.; Vermote, E.; Townshend, J.; Defries, R.; Roy, D.; Hall, D.; Salomonson, V.; Privette, J.; Riggs, G.; Strahler, A.; et al. The Moderate Resolution Imaging Spectroradiometer (MODIS): Land remote sensing for global change research. IEEE Trans. Geosci. Remote Sens. 1998, 36, 1228–1249. [Google Scholar] [CrossRef]
- Wulder, M.A.; Loveland, T.R.; Roy, D.P.; Crawford, C.J.; Masek, J.G.; Woodcock, C.E.; Allen, R.G.; Anderson, M.C.; Belward, A.S.; Cohen, W.B.; et al. Current status of Landsat program, science, and applications. Remote Sens. Environ. 2019, 225, 127–147. [Google Scholar] [CrossRef]
- Pekel, J.F.; Cottam, A.; Gorelick, N.; Belward, A. High-resolution mapping of global surface water and its long-term changes. Nature 2016, 540, 418–422. [Google Scholar] [CrossRef]
- Jones, J. Improved Automated Detection of Subpixel-Scale Inundation—Revised Dynamic Surface Water Extent (DSWE) Partial Surface Water Tests. Remote Sens. 2019, 11, 374. [Google Scholar] [CrossRef]
- Sheng, Y.; Song, C.; Wang, J.; Lyons, E.A.; Knox, B.R.; Cox, J.S.; Gao, F. Representative lake water extent mapping at continental scales using multi-temporal Landsat-8 imagery. Remote Sens. Environ. 2016, 185, 129–141. [Google Scholar] [CrossRef]
- Heintzman, L.; Starr, S.; Mulligan, K.; Barbato, L.; McIntyre, N. Using Satellite Imagery to Examine the Relationship between Surface-Water Dynamics of the Salt Lakes of Western Texas and Ogallala Aquifer Depletion. Wetlands 2017, 37, 1055–1065. [Google Scholar] [CrossRef]
- Lefebvre, G.; Davranche, A.; Willm, L.; Campagna, J.; Redmond, L.; Merle, C.; Guelmami, A.; Poulin, B. Introducing WIW for Detecting the Presence of Water in Wetlands with Landsat and Sentinel Satellites. Remote Sens. 2019, 11, 2210. [Google Scholar] [CrossRef]
- Castañeda, C.; Herrero, J.; Auxiliadora Casterad, M. Landsat monitoring of playa-lakes in the Spanish Monegros desert. J. Arid Environ. 2005, 63, 497–516. [Google Scholar] [CrossRef]
- Bowen, B.B.; Kipnis, E.L.; Raming, L.W. Temporal dynamics of flooding, evaporation, and desiccation cycles and observations of salt crust area change at the Bonneville Salt Flats, Utah. Geomorphology 2017, 299, 1–11. [Google Scholar] [CrossRef]
- Chiloane, C.; Dube, T.; Shoko, C. Monitoring and assessment of the seasonal and inter-annual pan inundation dynamics in the Kgalagadi Transfrontier Park, Southern Africa. Phys. Chem. Earth Parts A/B/C 2020, 118–119, 102905. [Google Scholar] [CrossRef]
- Bryant, R.; Rainey, M. Investigation of flood inundation on playas within the Zone of Chotts, using a time-series of AVHRR. Remote Sens. Environ. 2002, 82, 360–375. [Google Scholar] [CrossRef]
- Chew, C.; Small, E. Estimating inundation extent using CYGNSS data: A conceptual modeling study. Remote Sens. Environ. 2020, 246, 111869. [Google Scholar] [CrossRef]
- Li, H.; Mao, D.; Li, X.; Wang, Z.; Wang, C. Monitoring 40-Year Lake Area Changes of the Qaidam Basin, Tibetan Plateau, Using Landsat Time Series. Remote Sens. 2019, 11, 343. [Google Scholar] [CrossRef]
- Schlaffer, S.; Chini, M.; Dettmering, D.; Wagner, W. Mapping Wetlands in Zambia Using Seasonal Backscatter Signatures Derived from ENVISAT ASAR Time Series. Remote Sens. 2016, 8, 402. [Google Scholar] [CrossRef]
- Nationalpark Neusiedler See - Seewinkel. Salt pan basins, Unpublished own data. 2022.
- Jajarmizadeh, M. A Review on Theoretical Consideration and Types of Models in Hydrology. J. Environ. Sci. Technol. 2012, 5, 249–261. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, Y.; Xu, Z.; Duan, Q. Conceptual Hydrological Models. In Handbook of Hydrometeorological Ensemble Forecasting; Duan, Q., Pappenberger, F., Thielen, J., Wood, A., Cloke, H.L., Schaake, J.C., Eds.; Springer Berlin Heidelberg: Berlin/Heidelberg, Germany, 2017; pp. 1–23. [Google Scholar] [CrossRef]
- Liu, G.; Schwartz, F.W. An integrated observational and model-based analysis of the hydrologic response of prairie pothole systems to variability in climate. Water Resour. Res. 2011, 47, W02504. [Google Scholar] [CrossRef]
- Blöschl, G.; Sivapalan, M. Scale issues in hydrological modelling: A review. Hydrol. Process. 1995, 9, 251–290. [Google Scholar] [CrossRef]
- Patil, S.D.; Stieglitz, M. Comparing spatial and temporal transferability of hydrological model parameters. J. Hydrol. 2015, 525, 409–417. [Google Scholar] [CrossRef]
- Chouaib, W.; Alila, Y.; Caldwell, P.V. Parameter transferability within homogeneous regions and comparisons with predictions from a priori parameters in the eastern United States. J. Hydrol. 2018, 560, 24–38. [Google Scholar] [CrossRef]
- Li, C.Z.; Zhang, L.; Wang, H.; Zhang, Y.Q.; Yu, F.L.; Yan, D.H. The transferability of hydrological models under nonstationary climatic conditions. Hydrol. Earth Syst. Sci. 2012, 16, 1239–1254. [Google Scholar] [CrossRef]
- Yang, W.; Xia, R.; Chen, H.; Wang, M.; Xu, C.Y. The impact of calibration conditions on the transferability of conceptual hydrological models under stationary and nonstationary climatic conditions. J. Hydrol. 2022, 613, 128310. [Google Scholar] [CrossRef]
- Farmer, W.H.; Vogel, R.M. On the deterministic and stochastic use of hydrologic models. Water Resour. Res. 2016, 52, 5619–5633. [Google Scholar] [CrossRef]
- Shen, C.; Chen, X.; Laloy, E. Editorial: Broadening the Use of Machine Learning in Hydrology. Front. Water 2021, 3, 681023. [Google Scholar] [CrossRef]
- Nearing, G.S.; Kratzert, F.; Sampson, A.K.; Pelissier, C.S.; Klotz, D.; Frame, J.M.; Prieto, C.; Gupta, H.V. What Role Does Hydrological Science Play in the Age of Machine Learning? Water Resour. Res. 2021, 57, e2020WR028091. [Google Scholar] [CrossRef]
- Lange, H.; Sippel, S. Machine Learning Applications in Hydrology. For.-Water Interact. 2020, 240, 233–257. [Google Scholar] [CrossRef]
- Mosaffa, H.; Sadeghi, M.; Mallakpour, I.; Naghdyzadegan Jahromi, M.; Pourghasemi, H.R. Chapter 43—Application of machine learning algorithms in hydrology. In Computers in Earth and Environmental Sciences; Pourghasemi, H.R., Ed.; Elsevier: Amsterdam, The Netherlands, 2022; pp. 585–591. [Google Scholar] [CrossRef]
- Osman, A.I.A.; Ahmed, A.N.; Huang, Y.F.; Kumar, P.; Birima, A.H.; Sherif, M.; Sefelnasr, A.; Ebraheemand, A.A.; El-Shafie, A. Past, present and perspective methodology for groundwater modeling-based machine learning approaches. Arch. Comput. Methods Eng. 2022, 29, 3843–3859. [Google Scholar] [CrossRef]
- Afrifa, S.; Zhang, T.; Appiahene, P.; Varadarajan, V. Mathematical and Machine Learning Models for Groundwater Level Changes: A Systematic Review and Bibliographic Analysis. Fut. Internet 2022, 14, 259. [Google Scholar] [CrossRef]
- Ahmadi, A.; Olyaei, M.; Heydari, Z.; Emami, M.; Zeynolabedin, A.; Ghomlaghi, A.; Daccache, A.; Fogg, G.E.; Sadegh, M. Groundwater Level Modeling with Machine Learning: A Systematic Review and Meta-Analysis. Water 2022, 14, 949. [Google Scholar] [CrossRef]
- Ardabili, S.; Mosavi, A.; Dehghani, M.; Várkonyi-Kóczy, A.R. Deep learning and machine learning in hydrological processes climate change and earth systems a systematic review. In Proceedings of the Engineering for Sustainable Future: Selected papers of the 18th International Conference on Global Research and Education Inter-Academia–2019, Budapest, Hungary, 4–7 September 2019; Springer: Berlin/Heidelberg, Germany, 2020; pp. 52–62. [Google Scholar] [CrossRef]
- Zounemat-Kermani, M.; Batelaan, O.; Fadaee, M.; Hinkelmann, R. Ensemble machine learning paradigms in hydrology: A review. J. Hydrol. 2021, 598, 126266. [Google Scholar] [CrossRef]
- Xu, T.; Liang, F. Machine learning for hydrologic sciences: An introductory overview. WIREs Water 2021, 8, e1533. [Google Scholar] [CrossRef]
- Papacharalampous, G.; Tyralis, H. A review of machine learning concepts and methods for addressing challenges in probabilistic hydrological post-processing and forecasting. Front. Water 2022, 4, 961954. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Tyralis, H.; Papacharalampous, G.; Langousis, A. A Brief Review of Random Forests for Water Scientists and Practitioners and Their Recent History in Water Resources. Water 2019, 11, 910. [Google Scholar] [CrossRef]
- Kraft, B.; Jung, M.; Körner, M.; Koirala, S.; Reichstein, M. Towards hybrid modeling of the global hydrological cycle. Hydrol. Earth Syst. Sci. 2022, 26, 1579–1614. [Google Scholar] [CrossRef]
- Fahimi, F.; Yaseen, Z.M.; El-shafie, A. Application of soft computing based hybrid models in hydrological variables modeling: A comprehensive review. Theor. Appl. Climatol. 2017, 128, 875–903. [Google Scholar] [CrossRef]
- Nourani, V.; Hosseini Baghanam, A.; Adamowski, J.; Kisi, O. Applications of hybrid wavelet–Artificial Intelligence models in hydrology: A review. J. Hydrol. 2014, 514, 358–377. [Google Scholar] [CrossRef]
- Khandelwal, A.; Xu, S.; Li, X.; Jia, X.; Stienbach, M.; Duffy, C.; Nieber, J.; Kumar, V. Physics Guided Machine Learning Methods for Hydrology. arXiv 2020, arXiv:2012.02854. [Google Scholar]
- Sit, M.; Demiray, B.Z.; Xiang, Z.; Ewing, G.J.; Sermet, Y.; Demir, I. A comprehensive review of deep learning applications in hydrology and water resources. Water Sci. Technol. 2020, 82, 2635–2670. [Google Scholar] [CrossRef] [PubMed]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Chakraborty, S.; Tomsett, R.; Raghavendra, R.; Harborne, D.; Alzantot, M.; Cerutti, F.; Srivastava, M.; Preece, A.; Julier, S.; Rao, R.M.; et al. Interpretability of deep learning models: A survey of results. In Proceedings of the 2017 IEEE SmartWorld, Ubiquitous Intelligence & Computing, Advanced & Trusted Computed, Scalable Computing & Communications, Cloud & Big Data Computing, Internet of People and Smart City Innovation (SmartWorld/SCALCOM/UIC/ATC/CBDCom/IOP/SCI), San Francisco, CA, USA, 4–8 August 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Wee, W.J.; Zaini, N.B.; Ahmed, A.N.; El-Shafie, A. A review of models for water level forecasting based on machine learning. Earth Sci. Inform. 2021, 14, 1707–1728. [Google Scholar] [CrossRef]
- Hussaini, A.; Mahmud, M.R.; Wee, K.T.K.; Abubakar, A.G. A Review of Water Level Fluctuation Models and Modelling Initiatives. J. Comput. Theor. Nanosci. 2020, 17, 645–653. [Google Scholar] [CrossRef]
- Zhu, S.; Lu, H.; Ptak, M.; Dai, J.; Ji, Q. Lake water-level fluctuation forecasting using machine learning models: A systematic review. Environ. Sci. Pollut. Res. 2020, 27, 44807–44819. [Google Scholar] [CrossRef] [PubMed]
- Li, B.; Yang, G.; Wan, R.; Dai, X.; Zhang, Y. Comparison of random forests and other statistical methods for the prediction of lake water level: A case study of the Poyang Lake in China. Hydrol. Res. 2016, 47, 69–83. [Google Scholar] [CrossRef]
- Choi, C.; Kim, J.; Han, H.; Han, D.; Kim, H.S. Development of Water Level Prediction Models Using Machine Learning in Wetlands: A Case Study of Upo Wetland in South Korea. Water 2020, 12, 93. [Google Scholar] [CrossRef]
- Cartwright, J.; Morelli, T.L.; Grant, E.H.C. Identifying climate-resistant vernal pools: Hydrologic refugia for amphibian reproduction under droughts and climate change. Ecohydrology 2022, 15, e2354. [Google Scholar] [CrossRef]
- Riley, J.W.; Stillwell, C.C. Predicting Inundation Dynamics and Hydroperiods of Small, Isolated Wetlands Using a Machine Learning Approach. Wetlands 2023, 43, 63. [Google Scholar] [CrossRef]
- Dorigo, W.; Dietrich, S.; Aires, F.; Brocca, L.; Carter, S.; Cretaux, J.F.; Dunkerley, D.; Enomoto, H.; Forsberg, R.; Güntner, A.; et al. Closing the Water Cycle from Observations across Scales: Where Do We Stand? Bull. Am. Meteorol. Soc. 2021, 102, E1897–E1935. [Google Scholar] [CrossRef]
- Sogno, P.; Klein, I.; Kuenzer, C. Remote Sensing of Surface Water Dynamics in the Context of Global Change—A Review. Remote Sens. 2022, 14, 2475. [Google Scholar] [CrossRef]
- Solvik, K.; Bartuszevige, A.M.; Bogaerts, M.; Joseph, M.B. Predicting Playa Inundation Using a Long Short-Term Memory Neural Network. Water Resour. Res. 2021, 57, e2020WR029009. [Google Scholar] [CrossRef]
- Shaeri Karimi, S.; Saintilan, N.; Wen, L.; Valavi, R. Application of Machine Learning to Model Wetland Inundation Patterns Across a Large Semiarid Floodplain. Water Resour. Res. 2019, 55, 8765–8778. [Google Scholar] [CrossRef]
- Soltani, K.; Amiri, A.; Zeynoddin, M.; Ebtehaj, I.; Gharabaghi, B.; Bonakdari, H. Forecasting monthly fluctuations of lake surface areas using remote sensing techniques and novel Machine Learning Methods. Theor. Appl. Climatol. 2020, 143, 713–735. [Google Scholar] [CrossRef]
- Daniel, J.; Rooney, R.C.; Robinson, D.T. Climate, land cover and topography: Essential ingredients in predicting wetland permanence. Biogeosciences 2022, 19, 1547–1570. [Google Scholar] [CrossRef]
- Wulder, M.A.; White, J.C.; Loveland, T.R.; Woodcock, C.E.; Belward, A.S.; Cohen, W.B.; Fosnight, E.A.; Shaw, J.; Masek, J.G.; Roy, D.P. The global Landsat archive: Status, consolidation, and direction. Remote Sens. Environ. 2016, 185, 271–283. [Google Scholar] [CrossRef]
- Gunning, D.; Stefik, M.; Choi, J.; Miller, T.; Stumpf, S.; Yang, G.Z. XAI—Explainable artificial intelligence. Sci. Robot. 2019, 4, eaay7120. [Google Scholar] [CrossRef]
- Draganits, E.; Weißl, M.; Zámolyi, A.; Doneus, M. Lake Neusiedl area: A particular lakescape at the boundary between Alps and Pannonian Basin. In Landscapes and Landforms of Austria; Springer: Berlin/Heidelberg, Germany, 2022; pp. 207–222. [Google Scholar]
- Häusler, H. Erläuterungen zu den Blättern 79 Neusiedl am See 80 Ungarisch-Altenburg 109 Pamhagen. Geol. Kt. Der Repub. ÖSterreich 2007, 1, 145–157. [Google Scholar]
- Kirschner, A.; Krachler, R.; Krachler, R.; Korner, I. Renaturierung Ausgewählter Salzlacken des Burgenländischen Seewinkels; Technical Report; Naturschutzbund Burgenland: Eisenstadt, Austria, 2007. [Google Scholar]
- Häusler, H. Wie gelangte das Salz in die Salzlacken?–Zum Stand der Forschung über die Entstehung des “Salzführenden Horizontes” und der Salzböden des Seewinkels. Acta ZooBot Austria 2020, 157, 145–157. [Google Scholar]
- Köppen, W. The thermal zones of the Earth according to the duration of hot, moderate and cold periods and to the impact of heat on the organic world. Meteorol. Z. 2011, 20, 351–360. [Google Scholar] [CrossRef] [PubMed]
- Soja, G.; Züger, J.; Knoflacher, M.; Kinner, P.; Soja, A.M. Climate impacts on water balance of a shallow steppe lake in Eastern Austria (Lake Neusiedl). J. Hydrol. 2013, 480, 115–124. [Google Scholar] [CrossRef]
- Hackl, P.; Ledolter, J. A Statistical Analysis of the Water Levels at Lake Neusiedl. Austrian J. Stat. 2023, 52, 87–100. [Google Scholar] [CrossRef]
- Crocetti, L.; Forkel, M.; Fischer, M.; Jurecka, F.; Grlj, A.; Salentinig, A.; Trnka, M.; Anderson, M.; Ng, W.T.; Kokalj, Ž.; et al. Earth Observation for agricultural drought monitoring in the Pannonian Basin (southeastern Europe): Current state and future directions. Reg. Environ. Chang. 2020, 20, 123. [Google Scholar] [CrossRef]
- Tolotti, M.; Guella, G.; Herzig, A.; Rodeghiero, M.; Rose, N.L.; Soja, G.; Zechmeister, T.; Yang, H.; Teubner, K. Assessing the ecological vulnerability of the shallow steppe Lake Neusiedl (Austria-Hungary) to climate-driven hydrological changes using a palaeolimnological approach. J. Great Lakes Res. 2021, 47, 1327–1344. [Google Scholar] [CrossRef]
- Eitzinger, J.; Kubu, G.; Formayer, H.; Haas, P.; Gerersdorfer, T.; Kromp-Kolb, H. Auswirkungen einer Klimaänderung auf den Wasserhaushalt des Neusiedlersees; Technical Report; Endbericht im Auftrag der Burgenländischen Landesregierung vom: Land Burgenland, Austrian, 2005. [Google Scholar]
- Burgenland, L. Klimaszenarien für das Bundesland Burgenland BIS 2100. Technical report; Land Burgenland: Eisenstadt, Austria, 2016. [Google Scholar]
- Haslinger, K.; Schöner, W.; Abermann, J.; Laaha, G.; Andre, K.; Olefs, M.; Koch, R. Apparent contradiction in the projected climatic water balance for Austria: Wetter conditions on average versus higher probability of meteorological droughts. Nat. Hazards Earth Syst. Sci. 2023, 23, 2749–2768. [Google Scholar] [CrossRef]
- Wulder, M.A.; Roy, D.P.; Radeloff, V.C.; Loveland, T.R.; Anderson, M.C.; Johnson, D.M.; Healey, S.; Zhu, Z.; Scambos, T.A.; Pahlevan, N.; et al. Fifty years of Landsat science and impacts. Remote Sens. Environ. 2022, 280, 113195. [Google Scholar] [CrossRef]
- Gorelick, N.; Hancher, M.; Dixon, M.; Ilyushchenko, S.; Thau, D.; Moore, R. Google Earth Engine: Planetary-scale geospatial analysis for everyone. Remote Sens. Environ. 2017, 202, 18–27. [Google Scholar] [CrossRef]
- RH. Natonalpark Neusiedler See–Seewinkel Bericht des Rechnungshofes. Technical Report 29, Rechnungshofs Österreich. 2020.
- Hamed, K.H.; Rao, A.R. A modified Mann-Kendall trend test for autocorrelated data. J. Hydrol. 1998, 204, 182–196. [Google Scholar] [CrossRef]
- Jović, A.; Brkić, K.; Bogunović, N. A review of feature selection methods with applications. In Proceedings of the 2015 38th International Convention on Information and Communication Technology, Electronics and Microelectronics (MIPRO), Opatija, Croatia, 25–29 May 2015; pp. 1200–1205. [Google Scholar] [CrossRef]
- Sima, C.; Dougherty, E.R. What should be expected from feature selection in small-sample settings. Bioinformatics 2006, 22, 2430–2436. [Google Scholar] [CrossRef]
- Krachler, R. Renaturierung von Sodalacken im burgenländischen Seewinkel. PLUS LUCIS 2007, 1-2, 23–27. [Google Scholar]
- Bloomfield, J.P.; Marchant, B.P. Analysis of groundwater drought building on the standardised precipitation index approach. Hydrol. Earth Syst. Sci. 2013, 17, 4769–4787. [Google Scholar] [CrossRef]
- Turkeltaub, T.; Bel, G. The effects of rain and evapotranspiration statistics on groundwater recharge estimations for semi-arid environments. Hydrol. Earth Syst. Sci. 2023, 27, 289–302. [Google Scholar] [CrossRef]
- Hughes, A.; Mansour, M.; Ward, R.; Kieboom, N.; Allen, S.; Seccombe, D.; Charlton, M.; Prudhomme, C. The impact of climate change on groundwater recharge: National-scale assessment for the British mainland. J. Hydrol. 2021, 598, 126336. [Google Scholar] [CrossRef]
- Oroud, I. Temperature and evaporation dynamics of saline solutions. J. Hydrol. 1999, 226, 1–10. [Google Scholar] [CrossRef]
- Oroud, I. Dynamics of evaporation from saline water bodies. J. Geophys. Res. Atmos. 2001, 106, 4695–4701. [Google Scholar] [CrossRef]
- Liu, T.; Harman, C.J.; Kipnis, E.L.; Bowen, B.B. Modeling Episodic Ephemeral Brine Lake Evaporation and Salt Crystallization on the Bonneville Salt Flats, Utah. In Proceedings of the AGU Fall Meeting Abstracts, New Orleans, LA, USA, 11–15 December 2017; Volume 2017, p. EP11C-1568. [Google Scholar]
- Muñoz Sabater, J.; Dutra, E.; Agustí-Panareda, A.; Albergel, C.; Arduini, G.; Balsamo, G.; Boussetta, S.; Choulga, M.; Harrigan, S.; Hersbach, H.; et al. ERA5-Land: A state-of-the-art global reanalysis dataset for land applications. Earth Syst. Sci. Data 2021, 13, 4349–4383. [Google Scholar] [CrossRef]
- WMO. WMO Guidelines on the Calculation of Climate Normals; Technical Report; WMO: Geneva, Switzerland, 2017. [Google Scholar]
- Bloch, M.; Farkas, L.; Spiegler, K. Solar Evaporation of Salt Brines. Ind. Eng. Chem. 1951, 43, 1544–1553. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; Beguería, S.; López-Moreno, J.I. A Multiscalar Drought Index Sensitive to Global Warming: The Standardized Precipitation Evapotranspiration Index. J. Clim. 2010, 23, 1696–1718. [Google Scholar] [CrossRef]
- McKee, T.B.; Doesken, N.J.; Kleist, J. The relationship of drought frequency and duration to time scales. In Proceedings of the 8th Conference on Applied Climatology, Anaheim, CA, USA, 17–22 January 1993; Volume 17, pp. 179–183. [Google Scholar]
- Kumar, R.; Musuuza, J.L.; Van Loon, A.F.; Teuling, A.J.; Barthel, R.; Ten Broek, J.; Mai, J.; Samaniego, L.; Attinger, S. Multiscale evaluation of the Standardized Precipitation Index as a groundwater drought indicator. Hydrol. Earth Syst. Sci. 2016, 20, 1117–1131. [Google Scholar] [CrossRef]
- Secci, D.; Tanda, M.G.; D’Oria, M.; Todaro, V.; Fagandini, C. Impacts of climate change on groundwater droughts by means of standardized indices and regional climate models. J. Hydrol. 2021, 603, 127154. [Google Scholar] [CrossRef]
- Bueechi, E.; Fischer, M.; Crocetti, L.; Trnka, M.; Grlj, A.; Zappa, L.; Dorigo, W. Crop yield anomaly forecasting in the Pannonian basin using gradient boosting and its performance in years of severe drought. Agric. For. Meteorol. 2023, 340, 109596. [Google Scholar] [CrossRef]
- Papagiannopoulou, C.; Miralles, D.G.; Decubber, S.; Demuzere, M.; Verhoest, N.E.C.; Dorigo, W.A.; Waegeman, W. A non-linear Granger-causality framework to investigate climate–vegetation dynamics. Geosci. Model Dev. 2017, 10, 1945–1960. [Google Scholar] [CrossRef]
- Harris, C.R.; Millman, K.J.; Van Der Walt, S.J.; Gommers, R.; Virtanen, P.; Cournapeau, D.; Wieser, E.; Taylor, J.; Berg, S.; Smith, N.J.; et al. Array programming with NumPy. Nature 2020, 585, 357–362. [Google Scholar] [CrossRef] [PubMed]
- Pandas Development Team, T. Pandas-Dev/Pandas: Pandas. 2023. Available online: https://zenodo.org/record/8092754 (accessed on 10 August 2023).
- Collenteur, R.A.; Bakker, M.; Caljé, R.; Klop, S.A.; Schaars, F. Pastas: Open Source Software for the Analysis of Groundwater Time Series. Groundwater 2019, 57, 877–885. [Google Scholar] [CrossRef]
- Bandhauer, M.; Isotta, F.; Lakatos, M.; Lussana, C.; Båserud, L.; Izsák, B.; Szentes, O.; Tveito, O.E.; Frei, C. Evaluation of daily precipitation analyses in E-OBS (v19.0e) and ERA5 by comparison to regional high-resolution datasets in European regions. Int. J. Climatol. 2022, 42, 727–747. [Google Scholar] [CrossRef]
- Lavers, D.A.; Simmons, A.; Vamborg, F.; Rodwell, M.J. An evaluation of ERA5 precipitation for climate monitoring. Q. J. R. Meteorol. Soc. 2022, 148, 3152–3165. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Bell, B.; Hersbach, H.; Simmons, A.; Berrisford, P.; Dahlgren, P.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis: Preliminary extension to 1950. Q. J. R. Meteorol. Soc. 2021, 147, 4186–4227. [Google Scholar] [CrossRef]
- Nistor, M.M.; Cheval, S.; Gualtieri, A.F.; Dumitrescu, A.; Boţan, V.E.; Berni, A.; Hognogi, G.; Irimuş, I.A.; Porumb-Ghiurco, C.G. Crop evapotranspiration assessment under climate change in the Pannonian basin during 1991–2050. Meteorol. Appl. 2017, 24, 84–91. [Google Scholar] [CrossRef]
- Cheval, S. The standardized precipitation index–an overview. Rom. J. Meteorol 2015, 12, 17–64. [Google Scholar]
- Jensen, J. Remote Sensing of the Environment: An Earth Resource Perspective; Prentice Hall Series in Geographic Information Science; Pearson Prentice Hall: Upper Saddle River, NJ, USA, 2007. [Google Scholar]
- McFeeters, S.K. The use of the Normalized Difference Water Index (NDWI) in the delineation of open water features. Int. J. Remote Sens. 1996, 17, 1425–1432. [Google Scholar] [CrossRef]
- Xu, H. Modification of normalised difference water index (NDWI) to enhance open water features in remotely sensed imagery. Int. J. Remote Sens. 2006, 27, 3025–3033. [Google Scholar] [CrossRef]
- Hunter, J.D. Matplotlib: A 2D graphics environment. Comput. Sci. Eng. 2007, 9, 90–95. [Google Scholar] [CrossRef]
- Morgenthaler, S. Exploratory data analysis. WIREs Comput. Stat. 2009, 1, 33–44. [Google Scholar] [CrossRef]
- Waskom, M.L. seaborn: Statistical data visualization. J. Open Source Softw. 2021, 6, 3021. [Google Scholar] [CrossRef]
- Lorena, A.; Garcia, L.P.; Lehmann, J.; de Souto, M.; Ho, T. How Complex Is Your Classification Problem?: A Survey on Measuring Classification Complexity. ACM Comput. Surv. 2019, 52, 1–34. [Google Scholar] [CrossRef]
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; et al. SciPy 1.0: Fundamental Algorithms for Scientific Computing in Python. Nat. Methods 2020, 17, 261–272. [Google Scholar] [CrossRef]
- Belgiu, M.; Drăguţ, L. Random forest in remote sensing: A review of applications and future directions. ISPRS J. Photogramm. Remote Sens. 2016, 114, 24–31. [Google Scholar] [CrossRef]
- Dorigo, W.; Lucieer, A.; Podobnikar, T.; Čarni, A. Mapping invasive Fallopia japonica by combined spectral, spatial, and temporal analysis of digital orthophotos. Int. J. Appl. Earth Obs. Geoinf. 2012, 19, 185–195. [Google Scholar] [CrossRef]
- Linusson, H. Multi-Output Random Forests; University of Borås/School of Business and IT: Borås, Swedish, 2013. [Google Scholar]
- Faddoul, J.B.; Chidlovskii, B.; Gilleron, R.; Torre, F. Learning Multiple Tasks with Boosted Decision Trees. In Proceedings of the 2012th European Conference on Machine Learning and Knowledge Discovery in Databases—Volume Part I, Bristol, UK, 24–28 September 2012; Springer: Berlin/Heidelberg, Germany, 2012. ECMLPKDD’12. pp. 681–696. [Google Scholar]
- Probst, P.; Wright, M.N.; Boulesteix, A.L. Hyperparameters and tuning strategies for random forest. WIREs Data Min. Knowl. Discov. 2019, 9, e1301. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Joseph, V.R. Optimal ratio for data splitting. Stat. Anal. Data Mining: ASA Data Sci. J. 2022, 15, 531–538. [Google Scholar] [CrossRef]
- Xu, Y.; Goodacre, R. On splitting training and validation set: A comparative study of cross-validation, bootstrap and systematic sampling for estimating the generalization performance of supervised learning. J. Anal. Test. 2018, 2, 249–262. [Google Scholar] [CrossRef] [PubMed]
- Ripley, B.D. Pattern Recognition and Neural Networks; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Fukunaga, K.; Hummels, D. Leave-one-out procedures for nonparametric error estimates. IEEE Trans. Pattern Anal. Mach. Intell. 1989, 11, 421–423. [Google Scholar] [CrossRef]
- Wong, T.T. Performance evaluation of classification algorithms by k-fold and leave-one-out cross validation. Pattern Recognit. 2015, 48, 2839–2846. [Google Scholar] [CrossRef]
- Cerqueira, V.; Torgo, L.; Mozetič, I. Evaluating time series forecasting models: An empirical study on performance estimation methods. Mach. Learn. 2020, 109, 1997–2028. [Google Scholar] [CrossRef]
- Bergstra, J.; Bengio, Y. Random Search for Hyper-Parameter Optimization. J. Mach. Learn. Res. 2012, 13, 281–305. [Google Scholar]
- Buitinck, L.; Louppe, G.; Blondel, M.; Pedregosa, F.; Mueller, A.; Grisel, O.; Niculae, V.; Prettenhofer, P.; Gramfort, A.; Grobler, J.; et al. API design for machine learning software: Experiences from the scikit-learn project. arXiv 2013. [Google Scholar] [CrossRef]
- Opitz, J.; Burst, S. Macro f1 and macro f1. arXiv 2019. [Google Scholar] [CrossRef]
- Chicco, D.; Jurman, G. The advantages of the Matthews correlation coefficient (MCC) over F1 score and accuracy in binary classification evaluation. BMC Genom. 2020, 21, 6. [Google Scholar] [CrossRef] [PubMed]
- Zhu, Q. On the performance of Matthews correlation coefficient (MCC) for imbalanced dataset. Pattern Recognit. Lett. 2020, 136, 71–80. [Google Scholar] [CrossRef]
- Rebala, G.; Ravi, A.; Churiwala, S. An Introduction to Machine Learning; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar] [CrossRef]
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Goldstein, A.; Kapelner, A.; Bleich, J.; Pitkin, E. Peeking Inside the Black Box: Visualizing Statistical Learning With Plots of Individual Conditional Expectation. J. Comput. Graph. Stat. 2015, 24, 44–65. [Google Scholar] [CrossRef]
- Altmann, A.; Toloşi, L.; Sander, O.; Lengauer, T. Permutation importance: A corrected feature importance measure. Bioinformatics 2010, 26, 1340–1347. [Google Scholar] [CrossRef]
- Saarela, M.; Jauhiainen, S. Comparison of feature importance measures as explanations for classification models. SN Appl. Sci. 2021, 3, 1–12. [Google Scholar] [CrossRef]
- Molnar, C. Interpretable Machine Learning; Lulu.com: Morrisville, NC, USA, 2020. [Google Scholar]
- Sun, F.; Roderick, M.L.; Farquhar, G.D. Rainfall statistics, stationarity, and climate change. Proc. Natl. Acad. Sci. USA 2018, 115, 2305–2310. [Google Scholar] [CrossRef]
- Cancelliere, A.; Salas, J.D. Drought probabilities and return period for annual streamflows series. J. Hydrol. 2010, 391, 77–89. [Google Scholar] [CrossRef]
- Tallaksen, L.M.; Hisdal, H.; Lanen, H.A.V. Space–time modelling of catchment scale drought characteristics. J. Hydrol. 2009, 375, 363–372. [Google Scholar] [CrossRef]
- Miralles, D.G.; De Jeu, R.A.M.; Gash, J.H.; Holmes, T.R.H.; Dolman, A.J. Magnitude and variability of land evaporation and its components at the global scale. Hydrol. Earth Syst. Sci. 2011, 15, 967–981. [Google Scholar] [CrossRef]
- Vanderhoof, M.K.; Alexander, L.C.; Todd, M.J. Temporal and spatial patterns of wetland extent influence variability of surface water connectivity in the Prairie Pothole Region, United States. Landsc. Ecol. 2015, 31, 805–824. [Google Scholar] [CrossRef]

| Hyperparameter | GROUNDWATER (0.6 (0.15)/0.65 (0.03)) | METEOROLOGY (0.53 (0.12)/0.58 (0.02)) | COMBINED (0.58 (0.14)/0.65 (0.03)) | Tested Range by GridSearchCV | Default |
|---|---|---|---|---|---|
| n_estimators | 40 | 40 | 40 | 40, 100, 300 | 100 |
| max_feature | log2 | log2 | all | sqrt, log2, all | sqrt |
| max_depth | 2 | 4 | 2 | 1, 2, 3, 4 | ultd. |
| min_samples_leaf | 5 | 3 | 7 | 3, 5, 7, 9, 10 | 1 |
| min_samples_split | 10 | 17 | 10 | 6, 10, 13, 17 | 2 |
| max_leaf_nodes | 5 | 2 | 7 | 2, 3, 5, 7 | ultd. |
| Date Landsat | Date Reference | TPR | OA | Kappa |
|---|---|---|---|---|
| 28 May 2017 | 28 May 2017 | 0.90 | 0.95 | 0.90 |
| 29 April 2018 | 28 April 2018 | 0.50 | 0.75 | 0.50 |
| 12 June 2019 | 12 June 2019 | 0.53 | 0.81 | 0.58 |
| 8 August 2020 | 8 August 2020 | 0.88 | 0.94 | 0.88 |
| 9 September 2020 | 9 September 2020 | 0.86 | 0.93 | 0.86 |
| 22 July 2022 | 21 July 2022 | 0.82 | 0.91 | 0.82 |
| 17 October 2022 | 17 October 2022 | 0.61 | 0.81 | 0.62 |
| Model/Score | GROUND-WATER 7 | METEO-ROLOGY 7 | COMB-INED 7 | RAN-DOM 7 | GROUND-WATER 30 | METEO-ROLOGY 30 | COMB-INED 30 |
|---|---|---|---|---|---|---|---|
| -Test | 0.59 | 0.66 | 0.57 | 0.36 | 0.61 | 0.57 | 0.61 |
| -Train | 0.68 | 0.66 | 0.68 | 0.56 | 0.68 | 0.66 | 0.68 |
| F1-Macro Test | 0.79 | 0.83 | 0.78 | 0.68 | 0.80 | 0.79 | 0.81 |
| F1-Macro Train | 0.84 | 0.83 | 0.84 | 0.78 | 0.84 | 0.83 | 0.84 |
| Accuracy Test | 0.80 | 0.83 | 0.79 | 0.7 | 0.81 | 0.80 | 0.82 |
| Accuracy Train | 0.85 | 0.83 | 0.85 | 0.79 | 0.85 | 0.84 | 0.85 |
| Average MCC | Zicklacke | Katschitz-Lacke | Fuchsloch-Lacke 3 | Oberer Stinkersee | Mittlerer Stinkersee | Wörten-Lacken 2 | Neubruch-Lacke | Lange Lacke | Mean |
|---|---|---|---|---|---|---|---|---|---|
| Model GW | 0.46 | 0.51 | 0.13 | 0.5 | 0.15 | 0.6 | 0.57 | 0.6 | 0.44 |
| Model METEO | 0.2 | 0.34 | 0.37 | 0.51 | 0.49 | 0.13 | 0.19 | 0.11 | 0.29 |
| Model COM | 0.46 | 0.35 | 0.15 | 0.4 | 0.28 | 0.44 | 0.4 | 0.44 | 0.37 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schauer, H.; Schlaffer, S.; Bueechi, E.; Dorigo, W. Inundation–Desiccation State Prediction for Salt Pans in the Western Pannonian Basin Using Remote Sensing, Groundwater, and Meteorological Data. Remote Sens. 2023, 15, 4659. https://doi.org/10.3390/rs15194659
Schauer H, Schlaffer S, Bueechi E, Dorigo W. Inundation–Desiccation State Prediction for Salt Pans in the Western Pannonian Basin Using Remote Sensing, Groundwater, and Meteorological Data. Remote Sensing. 2023; 15(19):4659. https://doi.org/10.3390/rs15194659
Chicago/Turabian StyleSchauer, Henri, Stefan Schlaffer, Emanuel Bueechi, and Wouter Dorigo. 2023. "Inundation–Desiccation State Prediction for Salt Pans in the Western Pannonian Basin Using Remote Sensing, Groundwater, and Meteorological Data" Remote Sensing 15, no. 19: 4659. https://doi.org/10.3390/rs15194659
APA StyleSchauer, H., Schlaffer, S., Bueechi, E., & Dorigo, W. (2023). Inundation–Desiccation State Prediction for Salt Pans in the Western Pannonian Basin Using Remote Sensing, Groundwater, and Meteorological Data. Remote Sensing, 15(19), 4659. https://doi.org/10.3390/rs15194659






