Next Article in Journal
Estimation of Total Phosphorus Concentration in Lakes in the Yangtze-Huaihe Region Based on Sentinel-3/OLCI Images
Previous Article in Journal
Prediction of Sea Surface Chlorophyll-a Concentrations Based on Deep Learning and Time-Series Remote Sensing Data
Previous Article in Special Issue
Mean Seasonal Sea Surface Height Variations in and around the Makassar Strait
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Remote Sensing
Volume 15
Issue 18
10.3390/rs15184479
remotesensing-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Polar Ocean Tides—Revisited Using Cryosat-2

by
Ole Baltazar Andersen
1,*,
Stine Kildegaard Rose
1 and
Michael G. Hart-Davis
2
1
DTU Space, National Space Institute, Elektrovej 327/328, DK-2800 Kongens Lyngby, Denmark
2
Deutsches Geodätisches Forschungsinstitut, Technische Universitat Munchen, D-80333 Munich, Germany
*
Author to whom correspondence should be addressed.
Remote Sens. 2023, 15(18), 4479; https://doi.org/10.3390/rs15184479
Submission received: 3 July 2023 / Revised: 5 September 2023 / Accepted: 8 September 2023 / Published: 12 September 2023
(This article belongs to the Special Issue Advances in Satellite Altimetry)
Browse Figures
Review Reports Versions Notes

Abstract

:
With the availability of more than 9 years of Cryosat-2, it is possible to revisit polar ocean tides, which have traditionally been difficult to determine from satellite altimetry. The SAMOSA+ physical retracker is a stable retracker developed particularly for Cryosat-2. Being a physical retracker, it enables the determination of the sea state bias. Correcting for the sea state bias enables more reliable sea level estimates compared with traditional empirical retrackers used before. Cryosat-2 data have been analyzed for residual ocean tides to the FES2014 ocean tide model in the Arctic Ocean and Antarctic Ocean using the response formalism. We utilize data from the sub-cycle of Cryosat-2, which follows a repeating pattern of approximately 28.33 days. This sub-repeat period makes it an advantageous alias period for the majority of significant constituents. This allowed for the estimation and mapping of the major tidal constituents in the open ocean and also in floating ice shelves from data extracted from leads in the sea ice. A novel empirical ocean tide model designed specifically for the polar region, DTU22, is introduced. Our findings reveal substantial enhancements in semi-diurnal tides within the Arctic Ocean and improvement in diurnal constituents within the Southern Ocean. In the Southern Ocean, the diurnal constituents are particularly improved using the empirical model by more than a factor of two to around 3 cm for both constituents compared with FES2014b. These outcomes underscore the significance of incorporating the reprocessed and retracted Cryosat-2 data into tidal modeling, highlighting its pivotal role in advancing the field.

1. Introduction

The flood and ebb caused by ocean tides have fascinated humans for thousands of years, and understanding and modeling ocean tides are vital for numerous geophysical fields. The ocean tides are responsible for more than 70% of the ocean variability. When using satellite altimetry, precise knowledge of tides is important to unravel smaller sea level signals like ocean currents and sea level change.
Prior to satellite altimetry, tides were derived using information from tide gauges. Our knowledge about tides has improved dramatically with the launch of satellite altimetry three decades ago. Important papers on the evaluation and constant improvement in state-of-the-art tide models have been presented by [1,2], and today, satellite altimetry is fundamental for tidal science and has changed our understanding of both ocean and internal tides in the ocean [3,4].
In the open ocean, tides are known with an accuracy of 2 cm or better [2,5,6]; however, present-day models show large discrepancies compared to in situ observations in the coastal and high-latitude regions [2,7]. This is related to a combination of the fact that in shallow waters, tides have larger amplitudes and are considerably more complex, and the wavelength of the tides is scaled down in shallow water [6,8].
The orbits for the TOPEX/Poseidon, Jason’s, and recently the Sentinel-6a have all been selected to avoid aliasing of tidal variability into other oceanographic signals [9]. However, these satellites have an inclination of 66°, which means that they do not cover the Arctic Ocean as well as the coastal regions around Antarctica. Altimetry between 66° and 82° has until now mainly been available from the ERS1/ERS2/Envisat and SARAL/AltiKa missions. Unfortunately, these satellites were launched with sun-synchronous orbits, which are problematic for tidal studies [7]. Sun-synchronous orbit causes major solar constituent S2 to be aliased into zero frequency (hence, it appears as a mean value) and causes the major diurnal constituent K1 to be aliased into the annual signal [10]. In polar regions, another complication is due to the presence of sea ice, which frequently degrades satellite altimetry data. Finally, the accuracy of the bathymetric maps is problematic [11]. This means that the polar regions are today considered significantly less accurate compared with the global ocean [2], and hence, significant efforts have been put into improving polar oceans [12,13].
Cryosat-2 is different from most other radar altimeters in that it was designed for mapping the cryosphere [14], and hence, the satellite was launched with an inclination of 88° to map all of the Arctic to within 200 km of the North Pole. Cryosat-2 is also unique in the sense that it carries a Synthetic Aperture Radar/Interferometric Radar Altimeter (SIRAL-2), which can switch between three modes to optimize observations dependent on the surface type [15]. Low-resolution mode (LRM) is optimized for the open ocean and ice sheets. Synthetic Aperture Radar mode (SAR) is optimized for sea ice and SAR interferometry (SARIn or SIN in short) for regions of large topography and ice margins [15]. The recent version 5 of the mode mask is shown in Figure 1.
In polar regions, usable Sea Surface Height (SSH) observations from altimetry will generally come from either the open ocean or from water between ice-floes, also called sea ice leads. Conventional altimeter (e.g., ERS-1/2 or ENVISAT) has such a large footprint (>150 km2) that they have problems resolving SSH in leads [17]. A SAR altimeter has a much smaller footprint (~4 km2) due to multi-looking [14]. Hence, it can discriminate more accurately between the open ocean and leads.
The major advantage of Cryosat-2 for tidal prediction stems from the fact that Cryosat-2 is not sun-synchronous. It has a very long exact repeat period of 368.24 days, which intuitively seems very long for tidal modeling. However, the satellite was designed with 13 favorable sub-cycles of 28.33 days, which is a very good sampling period for tidal analysis. In each of the 13 sub-cycles, Cryosat-2 lays out a global homogenous track pattern with coarse resolution. For the exact repeat of 368.24 days, the track-to-track distance is 8 km, but the sub-cycle track-to-track distance is 104 km. This roughly decreased with cosine to the latitude, and at 70° latitude, the track-to-track distance for the sub-cycle is as low as 35 km. For each subsequent sub-cycle, the global track pattern is shifted 8 km to the west at the Equator. An example of the exact-repeat tracks and sub-cycle tracks can be found in [18], who developed a tide model for the Weddell Sea south of 60°S.
In this paper, we present both new tidal estimates and a new empirical ocean tide model from the Technical University of Denmark (DTU) called DTU22OT. This model is inspired by the work of Ed Zaron presented in [18]. However, we applied an improved retracked Cryosat-2 dataset for polar regions and a different tide prediction method which proved favorable for many tidal constituents.
The paper is organized as follows: The next section describes the data processing and retracking as well as the determination of tidal constituents. The following section deals with tide prediction, and the subsequent section with evaluation and comparison with in situ data.

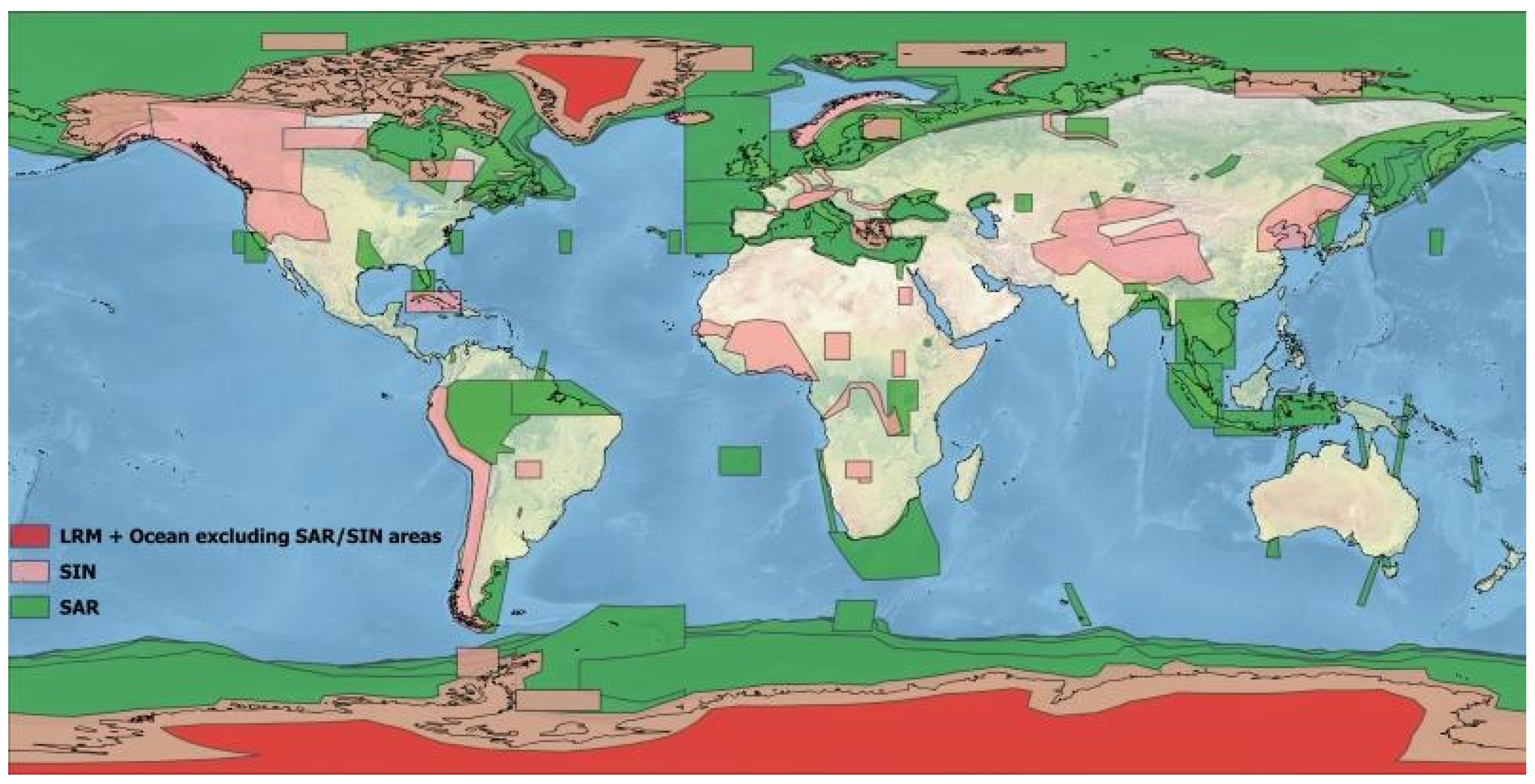
2. Data and Processing

With the assistance of the European Space Agency (ESA) Grid Processing On-Demand (GPOD) and Service Support (RSS) [19], we have processed Cryosat-2 SAR and SARin/SIN for both the Arctic and the Southern Ocean between October 2010 and October 2019. Observations over the sea ice/open ocean interface were removed in the processing, and only observations over sea ice leads were selected, similar to the work by [20].
Compared to the use of conventional 1-Hz altimetry, there are several advantages of reprocessing and retracking Cryosat-2 satellite altimetry for tidal modeling at 20-Hz in the polar regions. The advantages relate to increased spatio-temporal coverage and increased range precision, and we will demonstrate the advantages in the following subsections.

2.1. Retracking Cryosat-2 Using Physical Retracker

Retracking is performed by fitting a functional form to the returned radar power to the satellite. This can be empirical (threshold, peak, etc.) or based on physics. Generally, empirical retrackers are more robust over surfaces with highly varying terrain, such as coastal areas, inland waters, and ice sheets, and more data will be available. However, physical retrackers are always preferred over the oceans as they generally provide higher range precision important to residual tide modeling [5,20,21]. Furthermore, physical retrackers generally provide additional parameters enabling a correction for the sea state bias [9,22]. The returned power as a function of time (waveform) is radically changed by the presence of sea ice. Hence, the retracker must be able to handle this. Over oceans or sea ice, power is returned from a larger surface, and hence, the waveform becomes broader. Over the sea ice, the still water acts like a mirror, and the waveform becomes specular.
For the SAR and SARIn/SIN data, we applied the SAMOSA+ physical retracking [23]. SAMOSA+ adapts the SAMOSA retracking model [24] to operate over specular scattering surfaces as ice-covered polar oceans. SAMOSA and SAMOSA+ retracking has successfully been applied to determine sea-ice freeboard and polar ocean sea level from CryoSat-2 SAR data in [25,26] and recently also for mean sea surface determination [27].
Retracking 9 years of Cryosat-2 can be performed in a matter of hours using an empirical retracker, whereas retracking using the SAMOSA+ physical retracker takes many months. To illustrate the importance of applying the SAMOSA+ physical retracker, we compared it with a simpler 70% empirical threshold retracker from the DTU LARS retracking system [17]. We subsequently performed a simultaneous estimation of residual tides using near-identical Cryosat-2 data. The derived SAMOSA+ sea state bias was applied for the SAMOSA+ but not for the empirical threshold retracked data. The residual tide estimation procedure is described in detail in the subsequent section using remove/restore with the FES2014 ocean tide correction [28].
Figure 2 shows the estimated in-phase part of the residual M2 ocean tide on a scale from −5 to 5 cm estimated from SAMOSA+ physical retracking (left) and from 70% threshold retracking (right) using nearly the same amount of data. It is clear that the estimates using the empirical threshold data are far noisier compared with the physically retracked data. A close inspection of the Baffin Bay region between Greenland and Canada reveals that the two estimates roughly estimate the same 5 cm residual tidal signal. However, the noise of the threshold estimates is significantly higher, which calls for increased spatial smoothing in order for these to be useful.
After retracking the Cryosat-2 data, all geophysical and range corrections are performed to the 20-Hz data as described in [22]. This includes the correction for the sea state bias following [29]. Satellite altimetry observes the elastic ocean tide and not the real ocean tide. The elastic ocean tide is the sum of the ocean and loading tide. We subsequently removed known elastic ocean tides using the FES2014b elastic ocean tide model [27].
We finally remove the mean sea surface from the observations to create the sea surface height anomalies. We used the DTU21MSS [27,30]. This model is particularly well-suited for the current analysis as it is derived using the same Cryosat-2 data retracked using the SAMOSA+ retracker as is used here.

2.2. Data Binning and Ocean Tide Prediction

When using satellites to sample ocean tides, the tidal signal will always have a much higher frequency than the sampling of the satellite. Therefore, the tidal signal will be heavily subsampled and aliased into periods longer than the sampling of the satellite [6,30]. This aliasing period depends on the sampling rate by the satellites and the tidal frequency. Table 1 shows the alias periods for the four major diurnal and semi-diurnal constituents, as well as the largest shallow water constituent M4, when sampled using various satellite altimetry missions. It is seen that, in general, it is very problematic to use Envisat (35-day) and Sentinel3 (27-day) altimetry in the polar oceans due to the sun-synchronous orbits causing very problematic alias periods.
When designing tidal prediction using satellite altimetry, it is important to look both at the temporal and spatial sampling of the satellite to optimize the processing and extraction of the residual tides. For Cryosat-2, we have processed 9 years, equivalent to 3285 days of data. It would be impractical to solve for the tidal constituent using data from the exact repeat of 368.23 days mission. This is because a number of tidal constituents cannot be resolved within the measurement period of 3285 days, as the alias period is longer than this period.
The Cryosat-2 orbit design created a global uniform sub-grid every 28.331 days, which is slightly drifting, creating the next global uniform sub-grid shifted by roughly 8 km to the west. The Cryosat-2 sub-cycle repeat of 28.331 days is much more viable for tidal analysis. Here, all constituents have well-separated alias periods inside the length of the measurement period. The two constituents that, theoretically, can be slightly problematic to resolve are the M2 constituent and the K1 constituent. The problem with K1 is the fact that it has a very long alias period comparable to the duration of the observations. The problem with M2 is the fact that it has an alias period of 371 days, which is only 6 days from the annual variation of 365 days. A complete separation of the two would require 60 years, according to the Rayleigh criterion [6]. However, by simultaneously solving for both tidal parameters and the annual signal, we can separate these signals and find a reliable solution for the M2 constituent.
When using data from the sub-cycle, we will only be able to solve the tidal residuals at a coarser resolution as the observations are not taken at the same location. We decided to use a longitudinal bin size of 3° equivalent to 150 km at 60° and 75 km at 75° latitude. In the latitude direction, the bin size will be constant with latitude, and we decided to fix it at 0.5°, which corresponds to roughly 55 km.
For the tidal analysis in the polar regions, it is important to use 20-Hz observations directly rather than first computing 1-Hz, which is performed in the Radar Altimeter Database System (RADS) [31]. This stems from the nature of the leads being very small and scattered. Frequently, only a few scattered 20-Hz observations are available. Naturally, the 20-Hz observations will be noisier than the averaged 1 Hz observations, but as Figure 3 demonstrates, this approach retrieves more data and much better distribution in time and space, which clearly outperforms the higher noise on 20-Hz data.
Figure 3 illustrates all Cryosat-2 data in the Arctic Ocean and Southern Oceans for November 2010 retracked using the SAMOSA+ retracker (left panels) and RADS (right panels). It can be seen that the limits of the SAMOSA+ retracker are 55° in the Southern Hemisphere and 65° in the Northern Hemisphere.
The SAMOSA+ retracking was performed on the SAR data (blue region) and SARin/SIN data (green region). The LRM data were used directly from ESA 20-Hz GPD data (sand color). Notice that within the blue SAR zone in the lower left plot in Figure 2, there is a clear white zone where there is no data. This is exactly the transition zone from the open ocean where the SAMOSA+ retracker fails due to very noisy waveforms. It is very noticeable that around the perimeter.
It is also noticeable that RADS lacks data in large sections of the region. This stems from the fact that 1-Hz data in RADS are only computed when at least 16 out of the 20 possible 20-Hz observations within one second are available.
The processing of the data in this study was performed in the following way. Every time a satellite track crosses a bin, all 20-Hz observations are used to form the residual SLA observation used for the subsequent tidal analysis. The location of this bin average is taken as the average location of all data locations during the crossing of the bin. The use of an accurate mean sea surface is particularly important in this process as data are not taken at the same location but within a region of 3.0° × 0.5°. Subsequently, errors in the mean sea surface will add significantly to the nontidal noise of the measurements. Fortunately, the DTU21MSS used here is consistent with the retracked data used here, which minimizes this effect.
Within each 3.0° × 0.5° data bin, we computed the amount of crossing over the nine-year Cryosat-2 period, from which averaged sea surface height data could be computed for the tidal prediction. This is illustrated in Figure 4. In general, we have more than 500 sea surface height observations to determine the tides adequately.
The along-track sea level residuals have been analyzed using the response method [32] extended with the orthotide formalism by [6,33,34]. In this analysis, we have augmented the formalism with a simultaneous solution for the annual signal due to the 371-day M2 alias period. The formalism has previously proved very efficient in high-latitude polar regions where there were only sun-synchronous satellites available until the launch of Cryosat-2 in 2010 and in combination with a harmonic solution for shallow water tides [8,35].

2.3. Tide Gauges

In order to perform an independent and quantitative evaluation of the tidal estimates, the use of tide gauges is normally preferred. The tidal estimations in both the Antarctic and the Arctic Ocean were evaluated using in situ measurements obtained from a combination of tide gauges, ocean bottom pressure sensors, and GNSS-reflectometry (GNSS-IR) [36]. Existing global tidal constituent databases provide limited data in these regions; for example, TICON-3 [37] only provides 18 gauges below 60°S and 21 above 70°N. For the Arctic Ocean, a new tidal constituent dataset termed ArcTiCA is used [38]. This dataset was the result of a concerted effort to collect all available tide gauges, Ocean Bottom Pressure (OBP) buoys, and GNSS-IR measurements. Using the flagging provided within this dataset, we selected 68 M2, S2, O1, and K1 constituents above 65°N from a total of 1095 data. This dataset is shown in the right panel of Figure 5.
For the Antarctic, the in situ database published in [18] was used in this manuscript to provide a one-to-one comparison with the results presented in that study. A total of 27 measurements are used, which are mainly located around the Weddell Sea. Other tidal constituent databases do exist; especially notable is the Ant TG of [38], which contains over 100 measurements. However, for consistency purposes and to evaluate the results against previous literature, only the database of [18] is used in this manuscript. These tide gauges are shown in the left panel of Figure 5.

3. Results

To confirm the realistic estimations presented using the response method, an additional harmonic approach was performed for the exact same data in the Antarctic region following the methods described in [5] and is presented in Figure 6. The figure illustrates the raw and ungridded tidal estimates within each of the 3.0° × 0.5° bins defined earlier.
Differences between the response and harmonic approaches for the M2 amplitude are, on average 0.2 mm, with the only areas of larger differences being found in the Antarctic Circumpolar Current (ACC). The ACC is known for high levels of mesoscale activity, which have traditionally been areas where altimetry-derived estimations of ocean tides have struggled. Furthermore, the spatial separation of the Cryosat-2 orbit increases with lower latitudes, degrading tidal estimations. Therefore, it is no surprise that these two approaches differ in these regions.
To avoid the increased amount of oceanographic noise on the tidal estimates in the ACC, it was decided to add data from Jason-1/2/3 in each of the estimation cells above the 66°S parallel. This has been performed in the lower left panel. It is seen that the Jasons provides additional stability to the tidal estimates above the 66°S parallel, which is the turning latitude of these satellites.
To demonstrate the importance of retracking and using 20-Hz data, the residual M2 was derived from the 1 Hz Cryosat-2 data from RADS. As expected, these data are too sparse to resolve the tides in the Weddell Sea. It can also be seen that the RADS data are not processed for the SARIn data close to the coastline of Antarctica. The SARIn coastal mask is clearly seen in Figure 1.
The tidal constituents (in phase and in quadrature corresponding to cosine and sine) signals were subsequently optimally interpolated using a Gauss Markov covariance function with a half-length of 800 km onto the 1/16 degree grid similar to the resolution of the FES2014 model. Hereafter, they were added to the tidal constituents of FES2014 in order to derive the empirical tidal model called DTU22.
The M2 residual to FES2014b for the Arctic and Antarctic regions are shown in Figure 7, and the S2 and K1 residual to FES2014b for the Arctic and Antarctic regions in Figure 8. Significant tidal residuals are seen in large parts of the Arctic Ocean. Particularly, the M2 cosine has residuals of 1–2 cm across a large part of the central Arctic Ocean. In the Baffin Bay between Greenland and Canada, residuals in both M2 cosine and sine components between 5 and 10 cm are found. Similarly, tidal residuals up to 15 cm can be found in the Canadian Arctic Archipelago.
The S2 and K1 residuals to FES2014b for the Arctic and Antarctic regions in Figure 8 are generally smaller than the M2 residuals and shown with a color scale ranging between −3 cm and 3 cm. Significant tidal residuals are seen in somewhat similar regions to the M2 residuals in the Arctic Ocean. Significant S2 residuals are seen in both the cosine and sine components in the Barents Sea north of Norway and the northern part of the Atlantic Ocean with residuals of 2–3 cm. Residuals are also seen on the eastern section of the Russian Shelf between latitudes of 120°E and 150°E. Similarly significant tidal residuals up to 6–12 cm are again found in the Canadian Arctic Archipelago.
In the Southern Ocean, the largest tidal residuals are seen in the Weddell Sea, ranging up to 6 cm. Some significant tidal residual is also found close to the Amery Ice shelf, around 75°E, and close to the Ross Ice shelf, around 170°E–180°E.
The largest diurnal constituent, K1, has a particularly long alias period of more than 4 years or 1468 days when observed using Cryosat-2. Even though Cryosat-2 has been measuring for 9 years, it is expected that the constituent can be slightly more difficult to determine with Cryosat-2 due to the fact that the Cryosat-2 time series is far from complete in time and space. The two lower panels illustrate the cosine and sine residuals with respect to FES2014b. Significant tidal residuals are seen at very high latitudes towards the North Pole and in the eastern part of the Barents Sea, where residuals reach 2–3 cm. Residuals are also seen towards the Bering Strait. Once again, significant tidal residuals are found in the Canadian Arctic Archipelago, where they reach 5–10 cm.
In the Southern Ocean, the largest tidal residuals are seen in the Ross Sea with amplitudes up to 5 cm in both the sine and cosine components. Significant K1 residual is also found in the western part of the Weddell Sea close to the Larsen Ice shelves and the Graham land.

4. Evaluation against Tide Gauges

In order to perform an independent assessment of the tidal estimates, we used the tide gauges described in Section 2. When using the response formalism, a number of minor constituents can be inferred from the admittance parameter largely defined by the larger tidal constituents. Hence, it is important to evaluate the method’s ability to predict the larger constituents. This was initially performed by comparing the solution in the Southern Ocean against tide gauges with a harmonic solution, which is based on the exact same data and interpolation method.
The ocean tide model by Zaron [18] only covers the Weddell Sea. Hence, only 20 common tide gauges are involved in this comparison. For DTU22, the numbers in brackets are the comparison with the same 20 tide gauges. The numbers for the Zaron model are copied from [18]
The evaluation against 27 tide gauges around Antarctica is shown in Table 2 for the four major constituents as Mean Vector Differences (MVD), which include both cosine and sine differences. The table gives the comparison of the FES2014 model and the estimated empirical DTU22 model based on the response formalism as well as estimations based on harmonic constituents (Harmonic). The FES2014 ocean tide model does not include Cryosat-2 altimetry but assimilates a number of the tide gauges in the region. Additionally, the comparison with the model for the Weddell Sea by Zaron [18] is included in the table. The numbers in the bracket for DTU22 are a comparison with the same 20 tide gauges. Generally, the comparison is similar between DTU22 and Zaron [18] except for the comparison for the S2 constituents. The factor of two improvements for the S2 semi-diurnal constituent is largely attributed to the physical retracking of the data using the SAMOSA+ retracker in this study. In general, an MVD of 4–5 cm is seen for both semi-diurnal constituents for the FES2014b model, rising to 6–8 cm for the diurnal constituents. It is seen that the semi-diurnal constituents are improved to 2–4 cm using both the response and empirical analysis. The diurnal constituents are particularly improved using the empirical methods by more than a factor of two to around 3 cm for both constituents. A cross-comparison with the results by [18] indicates that the same improvements are found for the M2 and the diurnal constituents.
Table 3 presents a comparison with 67 tide gauges in the Arctic Ocean, as shown in Figure 5, taken from the ArcTiCA dataset [38], where the gauges in the Baltic have been excluded and only gauges recording sea level for longer than 1 year have been selected. The ArcTiCA database contains a number of repeated tide gauges where the repeated observations were also removed. Furthermore, gauges can be found in fjords or rivers where the tidal dynamics are extremely variable, and the altimetry approaches used in this study will not be able to capture them appropriately. Hence, we expect relatively large differences when comparing the data in this database with the numbers found using an edited set of tide gauges in [2], as the gauges are not removed from the analysis.
The comparison between bi-cubic interpolated values in the tide model and the 67 selected ArcTiCa tidal constituents is shown in Table 3. The table shows small improvements for all constituents but most significant for the larger semi-diurnal constituents with the DTU22 empirical ocean tide model. This is very different from the comparison in the Southern Ocean, where the largest improvements were seen for the diurnal constituents. However, the diurnal constituents are comparatively much smaller in the Arctic Ocean compared with the Southern Ocean.
It should be noted that a number of the ArcTiCa tide gauges are assimilated in the FES2014b model, which might mean the model better resolves the tides in the regions near the gauges and, this way, favors the FES2014b tide model.

5. Discussion and Conclusions

With the assistance of the European Space Agency (ESA) Grid Processing On-Demand (GPOD) and Service Support (SS), we have processed a total of 9 years of Cryosat-2 (October 2010 to October 2019) for both the Arctic and the Southern Ocean. This enabled us to revisit polar ocean tides following the pioneering work by [18] using data retracked using a physical retracker.
The SAMOSA+ physical retracker provides more stable sea level estimates compared with traditional empirical retrackers, which is very important in the determination of small residual tides. Cryosat-2 data have been analyzed for residual ocean tides to the FES2014 ocean tide model in the Arctic Ocean and Antarctic Ocean. We designed the tidal analysis to follow the near 28-day sub-cycle of Cryosat, which has an advantageous aliasing period for the majority of significant constituents. Using this information, the long wavelength corrections to FES2014 have been derived for the major astronomical constituents M2, S2, K2, N2, K1, O1, P1, and Q1 tides for both the ocean and floating ice shelves domains as data have been retracked into the leads in the ice.
The binned sea level residuals in 3° × 0.5° cells have been analyzed using both the response method extended with the orthotide formalism as well as the harmonic methods. Both methods deliver very similar results with differences on the mm scale. Compared with 27 tide gauges, we found these solutions superior to the FES2014b ocean tide model, which has been derived without using Cryosat-2 altimetry. Our findings reveal enhancements in mainly semi-diurnal tides within the Arctic Ocean and a reciprocal improvement in diurnal constituents within the Southern Ocean. In this region, the diurnal constituents are particularly improved using the empirical model by more than a factor of two to around 3 cm for both constituents compared with FES2014b. These outcomes underscore the significance of incorporating the reprocessed and retracted Cryosat-2 data into tidal modeling.

Author Contributions

Conceptualization, O.B.A.; methodology, O.B.A. and M.G.H.-D.; software, S.K.R.; validation, M.G.H.-D. and O.B.A.; formal analysis, O.B.A.; writing—original draft O.B.A.; writing—review and editing, M.G.H.-D. and S.K.R.; visualization, O.B.A. and M.G.H.-D. All authors have read and agreed to the published version of the manuscript.

Funding

We acknowledge the support of ESA to the Altimetry for Bathymetry and Tide Retrievals for the Southern Ocean, Sea ice, and ice shelves (ALBATROSS) funded under the EO4 Society (https://eo4society.esa.int/projects/albatross/ (accessed on 11 October 2022) through the ESA grant: 4000134597/21/I-NB.

Data Availability Statement

Data is available through data.dtu.dk. Both the gridded DTU22 ocean tide models, the estimated un-gridded tidal constituents, and the retracked Cryosat-2 sea level anomalies in each of the 0.5° × 1.5° bins have been made available. This way, users can apply the data to their various tidal estimations on the data.

Acknowledgments

We would like to acknowledge ESA-RSS (Research and Service Support for their assistance in processing the data with G-POD. This service is now hosted on the EarthConsole platform, https://earthconsole.eu (accessed on 1 July 2023), as a P-PRO service. We would like to acknowledge Ed Zaron for inspiration to the work. We acknowledge the work by M. Jensen and C. Bang-Hansen in preparing Figure 3.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Shum, C.; Woodworth, P.; Andersen, O.; Egbert, G.D.; Francis, O.; King, C.; Klosko, S.; Le Provost, C.; Li, X.; Molines, J.-M.; et al. Accuracy assessment of recent ocean tide models. J. Geophys. Res. Oceans 1997, 102, 25173–25194. [Google Scholar] [CrossRef]
  2. Stammer, D.; Ray, R.D.; Andersen, O.B.; Arbic, B.K.; Bosch, W.; Carrère, L.; Cheng, Y.; Chinn, D.S.; Dushaw, B.D.; Egbert, G.D.; et al. Accuracy assessment of global barotropic ocean tide models. Rev. Geophys. 2014, 52, 243–282. [Google Scholar] [CrossRef]
  3. Zaron, E.D. Mapping the non-stationary internal tide with satellite altimetry. J. Geophys. Res. 2017, 122, 539–554. [Google Scholar] [CrossRef]
  4. Ray, R.D. Precise comparisons of bottom-pressure and altimetric ocean tides. J. Geophys. Res. Ocean. 2013, 118, 4570–4584. [Google Scholar] [CrossRef]
  5. Hart-Davis, M.G.; Piccioni, G.; Dettmering, D.; Schwatke, C.; Passaro, M.; Seitz, F. EOT20: A global ocean tide model from multi-mission satellite altimetry. Earth Syst. Sci. Data 2021, 13, 3869–3884. [Google Scholar] [CrossRef]
  6. Andersen, O.B. Global Ocean tides from ERS-1 and TOPEX/POSEIDON altimeter. J. Geophys. Res. 1995, 100, 249–259. [Google Scholar] [CrossRef]
  7. Cheng, Y.; Andersen, O.B. Multimission empirical ocean tide modeling for shallow waters and polar seas. J. Geophys. Res. 2011, 116, C11001. [Google Scholar] [CrossRef]
  8. Andersen, O.B. Shallow water tides on the northwest European shelf from TOPEX/POSEIDON altimeter. J. Geophys. Res. 1999, 104, 7729–7741. [Google Scholar] [CrossRef]
  9. Fu, L.-L.; Cazenave, A. (Eds.) Satellite Altimetry and Earth Sciences: A Handbook of Techniques and Applications; Academic Press: San Diego, CA, USA, 2001; p. 463. [Google Scholar]
  10. Hart-Davis, M.G.; Dettmering, D.; Sulzbach, R.; Thomas, M.; Schwatke, C.; Seitz, F. Regional Evaluation of Minor Tidal Constituents for Improved Estimation of Ocean Tides. Remote Sens. 2021, 13, 3310. [Google Scholar] [CrossRef]
  11. Cancet, M.; Andersen, O.; Lyard, F.; Cotton, D.; Benveniste, J. Arctide2017, a high-resolution regional tidal model in the arctic ocean. Adv. Space Res. 2018, 62, 1324–1343. [Google Scholar] [CrossRef]
  12. Padman, L.; Fricker, H.A.; Coleman, R.; Howard, S.; Erofeeva, S. A new tidal model for the Antarctic ice shelves and seas. Ann. Glaciol. 2002, 34, 247–254. [Google Scholar] [CrossRef]
  13. Padman, L.; Erofeeva, S.Y.; Fricker, H.A. Improving Antarctic tide models by assimilation of ICESat laser altimetry over ice shelves. Geophys. Res. Lett. 2008, 35, L22504. [Google Scholar] [CrossRef]
  14. Wingham, D.; Francis, C.; Baker, S.; Bouzinac, C.; Brockley, D.; Cullen, R.; de Chateau-Thierry, P.; Laxon, S.; Mallow, U.; Mavrocordatos, C.; et al. CryoSat: A mission to determine the fluctuations in Earth’s land and marine ice fields. Adv. Space Res. 2006, 37, 841–871. [Google Scholar] [CrossRef]
  15. Boy, F.; Desjonquères, J.-D.; Picot, N.; Moreau, T.; Raynal, M. CryoSat-2 SAR-mode over oceans: Processing methods, global assessment, and benefits. IEEE Trans. Geosci. Remote Sens. 2017, 55, 148–158. [Google Scholar] [CrossRef]
  16. Cryosate-2 Mode Mask. Available online: https://earth.esa.int/eogateway/news/new-cryosat-geographical-mode-mask-v5-0-now-in-operation (accessed on 30 June 2023).
  17. Stenseng, L.; Andersen, O.B. Preliminary gravity recovery from CryoSat-2 data in Baffin Bay, Preliminary gravity recovery from CryoSat-2 data in the Baffin Bay. Adv. Space Res. 2015, 50, 1158–1163. [Google Scholar] [CrossRef]
  18. Zaron, E.D. Ocean and Ice Shelf Tides from Cryosat-2 Altimetry. Am. Meteorol. Soc. 2018, 48, 975–993. [Google Scholar] [CrossRef]
  19. Benveniste, J.; Dinardo, S.; Buchhaupt, C.; Scagliola, M.; Passaro, M.; Fenoglio-Marc, L.; Sabatino, G.; Ambrózio, A.; Restano, M. In Proceedings of the SAR, SARin, RDSAR and FF-SAR Altimetry Processing on Demand for CryoSat-2 and Sentinel-3 at ESA G-POD, EGU General Assembly 2021, Online, 19–30 April 2021; 2021. [CrossRef]
  20. Rose, S.K.; Andersen, O.B.; Passaro, M.; Ludwigsen, C.A.; Schwatke, C. Arctic Ocean Sea Level Record from the Complete Radar Altimetry Era 1991–2018. Rem. Sens. 2019, 11, 1672. [Google Scholar] [CrossRef]
  21. Piccioni, G.; Dettmering, D.; Passaro, M.; Schwatke, C.; Bosch, W.; Seitz, F. Coastal improvements for tide models: The impact of ALES retracker. Remote Sens. 2018, 10, 700. [Google Scholar] [CrossRef]
  22. Andersen, O.B.; Scharroo, R. Range and geophysical corrections in coastal regions: And implications for mean sea surface determination. In Coastal Altimetry; Vignudelli, S., Kostianoy, A.G., Cipollini, P., Benveniste, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; pp. 103–145. [Google Scholar]
  23. Dinardo, S.; Fenoglio-Marc, L.; Buchhaupt, C.; Becker, M.; Scharroo, R.; Fernandes, M.J.; Jérôme Benveniste, J. Coastal SAR and PLRM altimetry in German Bight and West Baltic Sea. Adv. Space Res. 2017, 62, 1371–1404. [Google Scholar] [CrossRef]
  24. Ray, C.; Martin-Puig, C.; Clarizia, M.P.; Runi, G.; Dinardo, S.; Gommenginger, C.; Benveniste, J. SAR altimeter backscattered waveform model. IEEE Trans. Geosci. Rem. Sens. 2015, 53, 911–919. [Google Scholar] [CrossRef]
  25. Laforge, A.; Fleury, S.; Dinardo, S.; Garnier, F.; Remy, F.; Benveniste, J.; Bouffard, J.; Verley, J. Toward improved sea ice freeboard observation with SAR altimetry using the physical retracker SAMOSA+. Adv. Space Res. 2021, 68, 732–745. [Google Scholar] [CrossRef]
  26. Fenoglio, L.; Dinardo, S.; Uebbing, B.; Buchhaupt, C.; Gärtner, M.; Staneva, J.; Becker, M.; Klos, A.; Kusche, J. Advances in NE-Atlantic coastal Sea Level Change Monitoring from Delay Doppler Altimetry. Adv. Space Res. 2021, 68, 571–592. [Google Scholar] [CrossRef]
  27. Andersen, O.B.; Rose, S.K.; Abulaitijiang, A.; Zhang, S.; Fleury, S. The DTU21 Global Mean Sea Surface and first evaluation in the Arctic Ocean. Earth Syst. Sci. Data, 2023; in press. [Google Scholar] [CrossRef]
  28. Lyard, F.H.; Allain, D.J.; Cancet, M.; Carrère, L.; Picot, N. Fes2014 global ocean tide atlas: Design and performance. Ocean Sci. 2021, 17, 615–649. [Google Scholar] [CrossRef]
  29. Tran, N.; Labroue, S.; Philipps, S.; Bronner, E. Picot Overview and update of the sea state bias corrections for the Jason-2, Jason-1 and TOPEX missions. Mar. Geod. 2010, 33 (Suppl. S1), 348–362. [Google Scholar] [CrossRef]
  30. Andersen, O.B.; Knudsen, P. DNSC08 mean sea surface and mean dynamic topography models. J. Geophys. Res. 2009, 114, C11001. [Google Scholar] [CrossRef]
  31. Scharroo, R.; Leuliette, E.W.; Lillibridge, J.L.; Byrne, D.; Naeije, M.C.; Mitchum, G.T. RADS: Consistent multi-mission products. In Proceedings of the Symposium on 20 Years of Progress in Radar Altimetry, Venice-Lido, Italy, 20–28 September 2012. [Google Scholar]
  32. Munk, W.H.; Cartwright, D.E. Tidal spectroscopy and prediction. Philos. Trans. R. Soc. Lond. Ser. A 1966, 259, 533–583. [Google Scholar]
  33. Cartwright, D.E.; Ray, R.D. Oceanic tides from Geosat altimetry. J. Geophys. Res. 1990, 95, 3069–3090. [Google Scholar] [CrossRef]
  34. Larson, K.M.; Ray, R.D.; Nievinski, F.G.; Freymueller, J.T. The accidental tide gauge: A GPS reflection case study from Kachemak Bay, Alaska. IEEE Geosci. Remote. Sens. Lett. 2013, 10, 1200–1204. [Google Scholar] [CrossRef]
  35. Andersen, O.B.; Egbert, G.D.; Erofeeva, S.Y.; Ray, R.D. Mapping nonlinear shallow-water tides: A look at the past and future. Ocean Dyn. 2006, 56, 416–429. [Google Scholar] [CrossRef]
  36. Hart-Davis, M.G.; Dettmering, D.; Seitz, F. TICON-3: Tidal Constants Based on GESLA-3 Sea-Level Records from Globally Distributed Tide Gauges Including Gauge Type Information (Data); PANGAEA: Bremen, Germany, 2022. [Google Scholar] [CrossRef]
  37. Hart-Davis, M.; Howard, S.; Ray, R.; Andersen, O.; Padman, L.; Nilsen, F.; Dettmering, D. Review. ArcTiCA: Arctic Tidal Constituents Atlas; Arctic Data Center: 2023. Available online: https://www.researchsquare.com/article/rs-3277941/v1 (accessed on 1 July 2023).
  38. Howard, S.L.; King, M.; Padman, L. Antarctic Tide Gauge Database, 1st ed.; U.S. Antarctic Program (USAP) Data Center: New York, NY, USA, 2020. [Google Scholar] [CrossRef]
Remotesensing 15 04479 g001
Figure 1. The Cryosat-2 Mode mask V5 operational since 1 May 2023. SAR mode is shown in green. SARin/SIN in purple and LRM in blue [16].
Figure 1. The Cryosat-2 Mode mask V5 operational since 1 May 2023. SAR mode is shown in green. SARin/SIN in purple and LRM in blue [16].
Remotesensing 15 04479 g001
Remotesensing 15 04479 g002
Figure 2. Residual M2 cosine ocean tide to FES2014b in the Arctic Ocean estimated from 9 years of Cryosat-2 using (left) SAMOSA+ physical retracker and (right) empirical 70% threshold retracker. The color scale ranges from −5 cm to 5 cm.
Figure 2. Residual M2 cosine ocean tide to FES2014b in the Arctic Ocean estimated from 9 years of Cryosat-2 using (left) SAMOSA+ physical retracker and (right) empirical 70% threshold retracker. The color scale ranges from −5 cm to 5 cm.
Remotesensing 15 04479 g002
Remotesensing 15 04479 g003
Figure 3. Cryosat-2 data in the Arctic and Southern Oceans for November 2010. The figure illustrates the different amounts of data when SAMOSA+ retracking is used (left panels) and when RADS data are used (right panels).
Figure 3. Cryosat-2 data in the Arctic and Southern Oceans for November 2010. The figure illustrates the different amounts of data when SAMOSA+ retracking is used (left panels) and when RADS data are used (right panels).
Remotesensing 15 04479 g003
Remotesensing 15 04479 g004
Figure 4. The amount of data points in each of the 3.0° × 0.5° bins used for the subsequent tidal analysis.
Figure 4. The amount of data points in each of the 3.0° × 0.5° bins used for the subsequent tidal analysis.
Remotesensing 15 04479 g004
Remotesensing 15 04479 g005
Figure 5. The M2 amplitude at the tide gauges used for comparison in the Antarctic and the Arctic Ocean [38].
Figure 5. The M2 amplitude at the tide gauges used for comparison in the Antarctic and the Arctic Ocean [38].
Remotesensing 15 04479 g005
Remotesensing 15 04479 g006
Figure 6. The M2 cosine component. (Upper left): Estimated from Cryosat-2 alone and using the response formalism. (Upper right): Estimated from Cryosat-2 alone using the harmonic method [5]. (Lower left): Estimated from Cryosat-2 below 66°S but from Cryosat-2 and Jason above 66°S. (Lower right): Estimated from 1 Hz RADS Cryosat-2 data. The color scale ranges from −5 cm to 5 cm.
Figure 6. The M2 cosine component. (Upper left): Estimated from Cryosat-2 alone and using the response formalism. (Upper right): Estimated from Cryosat-2 alone using the harmonic method [5]. (Lower left): Estimated from Cryosat-2 below 66°S but from Cryosat-2 and Jason above 66°S. (Lower right): Estimated from 1 Hz RADS Cryosat-2 data. The color scale ranges from −5 cm to 5 cm.
Remotesensing 15 04479 g006
Remotesensing 15 04479 g007
Figure 7. The M2 residual to FES2014b for the Arctic and Antarctic regions. (Upper row): M2 cosine. (Lower row): M2 sine. The color scale ranges from −5 to 5 cm.
Figure 7. The M2 residual to FES2014b for the Arctic and Antarctic regions. (Upper row): M2 cosine. (Lower row): M2 sine. The color scale ranges from −5 to 5 cm.
Remotesensing 15 04479 g007
Remotesensing 15 04479 g008
Figure 8. The S2 and K1 residual components to FES2014b for the Arctic and Antarctic regions. (Upper row). S2 cosine (Second row): S2 sine (Third row). K1 cosine and (bottom row): K1 sine. The color scale ranges from −3 cm to 3 cm.
Figure 8. The S2 and K1 residual components to FES2014b for the Arctic and Antarctic regions. (Upper row). S2 cosine (Second row): S2 sine (Third row). K1 cosine and (bottom row): K1 sine. The color scale ranges from −3 cm to 3 cm.
Remotesensing 15 04479 g008
Table 1. Alias period of major tidal constituents for various exact repeating satellites in days.
Table 1. Alias period of major tidal constituents for various exact repeating satellites in days.
Jason
(9.9156-day)		Envisat
(35-day)		Sentinel-3
(27-day)		Cryosat-2
(368.24-day)		Cryosat-2
Sub-Cycle
(28.331-day)
M262.10748094.486461157.537622800.070025379.709199
S258.741706InfiniteInfinite768.318394245.262712
K286.596122182.621095182.621095742.877694715.022170
N249.596177 97.392957140.9824832095.633360225.422047
K1173.192245365.242190365.2421901485.7553871430.044341
O145.714180132.806118277.0251361261.5526611294.393753
P188.890870365.242190365.2421901591.126753209.356579
Q169.364499132.806118229.6121395105.281211194.726710
M431.053740135.005529178.7688114633.024758185.354599
Table 2. Comparison against 27 Antarctica measurements. Mean Vector Differences (MVD), including errors in the cosine and sine differences, are given. The numbers in brackets are the comparison with the same 20 gauges used by Zaron [18] for the comparison in the Weddell Sea. The * indicates that this is a result of comparison with 20 gauges in [18].
Table 2. Comparison against 27 Antarctica measurements. Mean Vector Differences (MVD), including errors in the cosine and sine differences, are given. The numbers in brackets are the comparison with the same 20 gauges used by Zaron [18] for the comparison in the Weddell Sea. The * indicates that this is a result of comparison with 20 gauges in [18].
FES14bZaronDTU22Harmonic
M2 4.383.1 *4.01 (3.2)4.15
S2 4.316.6 *2.61 (3.8)2.65
K17.572.9 *3.26 (3.1)3.30
O16.522.0 *3.03 (2.0)2.88
Table 3. Comparison with 67 Arctic Ocean tide constituents taken from the ArcTiCA database [38]. The table gives Mean Vector Differences, including both cosine and sine differences.
Table 3. Comparison with 67 Arctic Ocean tide constituents taken from the ArcTiCA database [38]. The table gives Mean Vector Differences, including both cosine and sine differences.
FES14bDTU22
M29.867.58
S25.014.86
K1 4.784.75
O12.692.29
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Andersen, O.B.; Rose, S.K.; Hart-Davis, M.G. Polar Ocean Tides—Revisited Using Cryosat-2. Remote Sens. 2023, 15, 4479. https://doi.org/10.3390/rs15184479

AMA Style

Andersen OB, Rose SK, Hart-Davis MG. Polar Ocean Tides—Revisited Using Cryosat-2. Remote Sensing. 2023; 15(18):4479. https://doi.org/10.3390/rs15184479

Chicago/Turabian Style

Andersen, Ole Baltazar, Stine Kildegaard Rose, and Michael G. Hart-Davis. 2023. "Polar Ocean Tides—Revisited Using Cryosat-2" Remote Sensing 15, no. 18: 4479. https://doi.org/10.3390/rs15184479

APA Style

Andersen, O. B., Rose, S. K., & Hart-Davis, M. G. (2023). Polar Ocean Tides—Revisited Using Cryosat-2. Remote Sensing, 15(18), 4479. https://doi.org/10.3390/rs15184479

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop