Enhancing UAV-SfM Photogrammetry for Terrain Modeling from the Perspective of Spatial Structure of Errors
Abstract
:1. Introduction
2. Materials and Methods
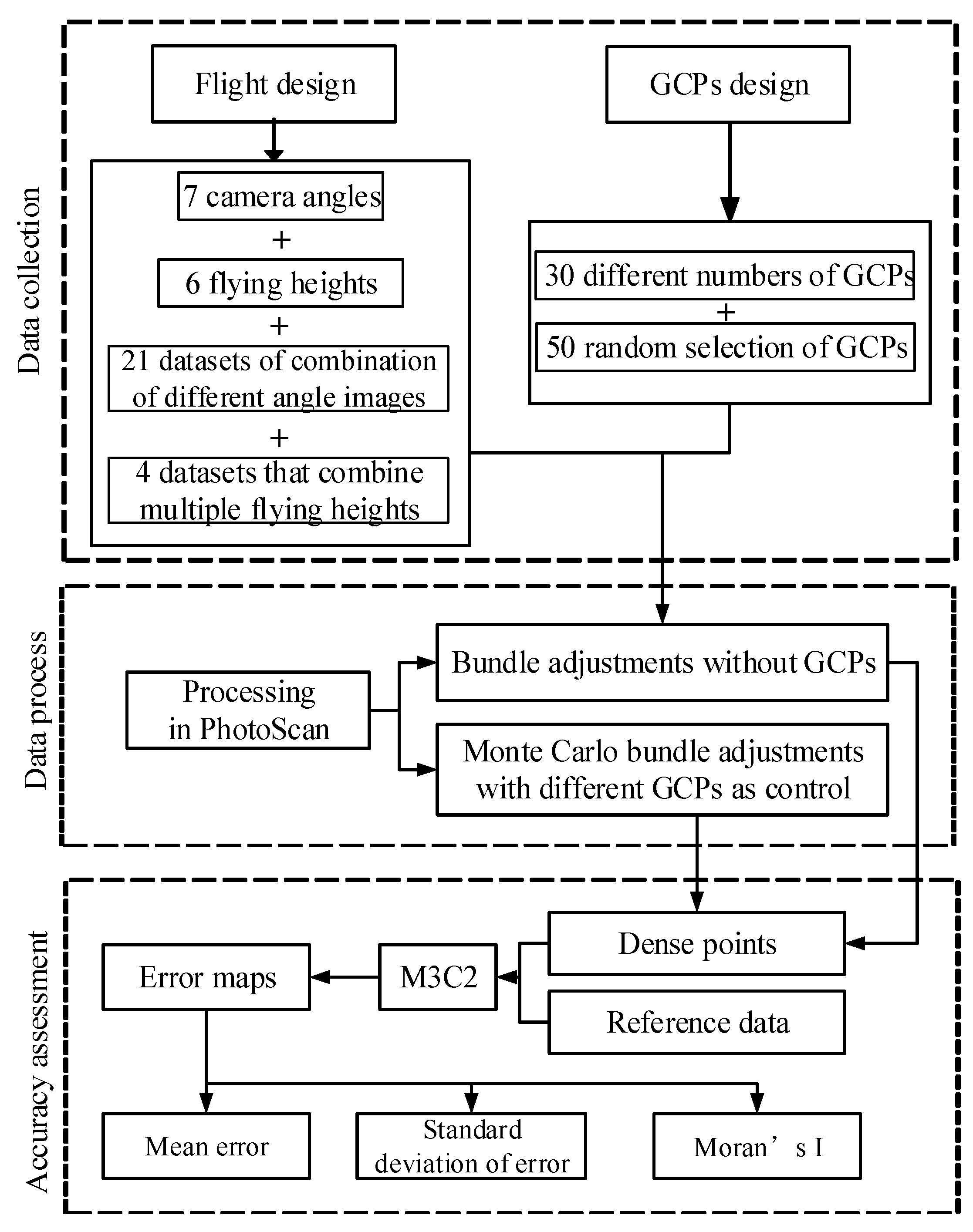
2.1. Overview
2.2. Image Data Collection
Study Areas
2.3. Image Collection
2.3.1. Camera Angle Design
2.3.2. Flying Height Design
2.4. Ground Control Points
2.4.1. Ground Control Design
2.4.2. The Number of GCPs
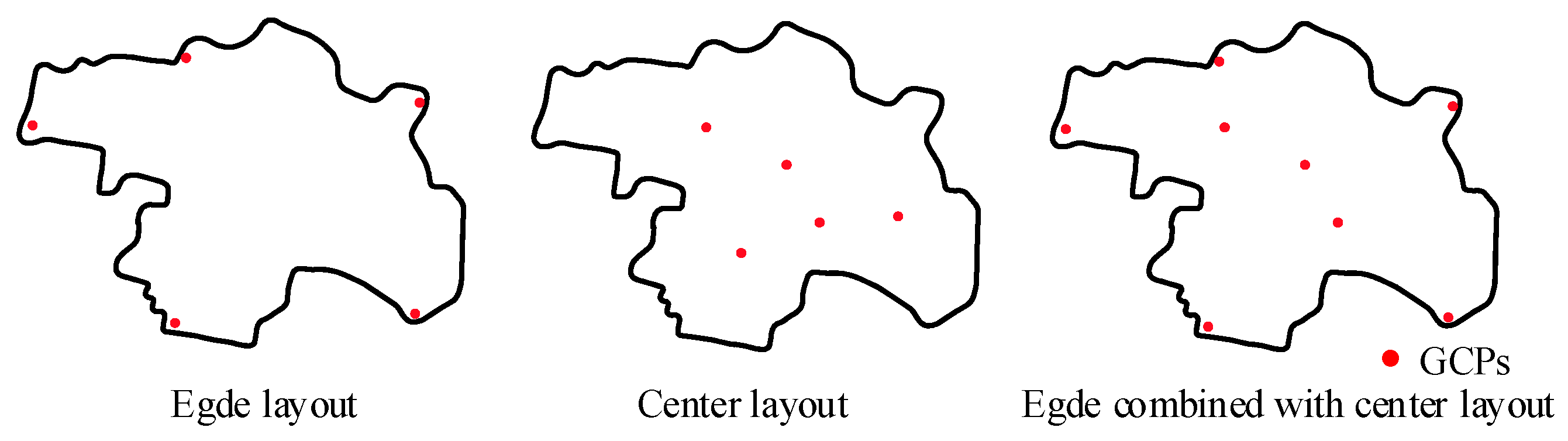
2.4.3. The Spatial Distribution of GCPs
2.5. Accuracy Evaluation
3. Results
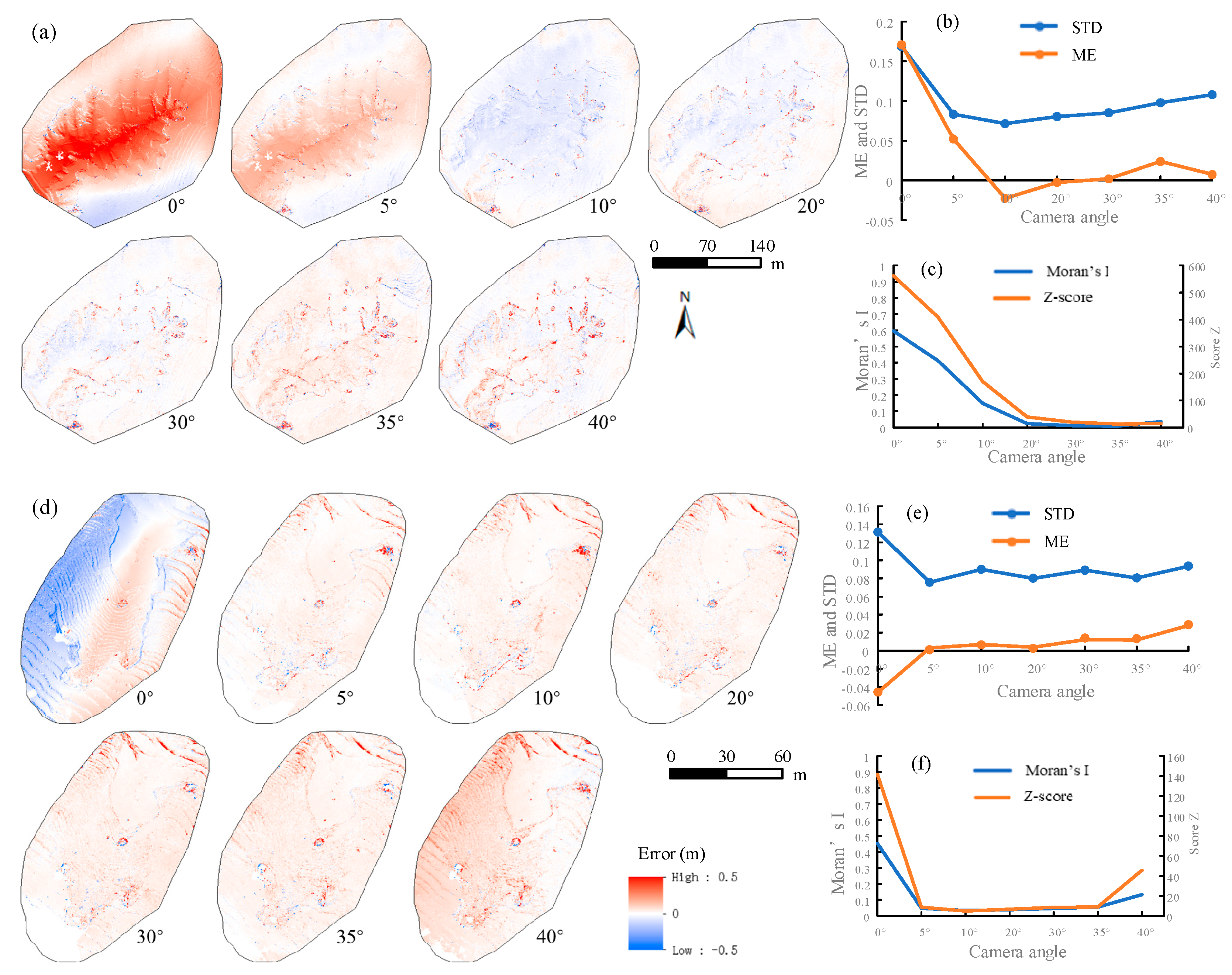
3.1. The Effects of Camera Angle
3.1.1. Single Camera Angle
3.1.2. Combination of Different Camera Angles
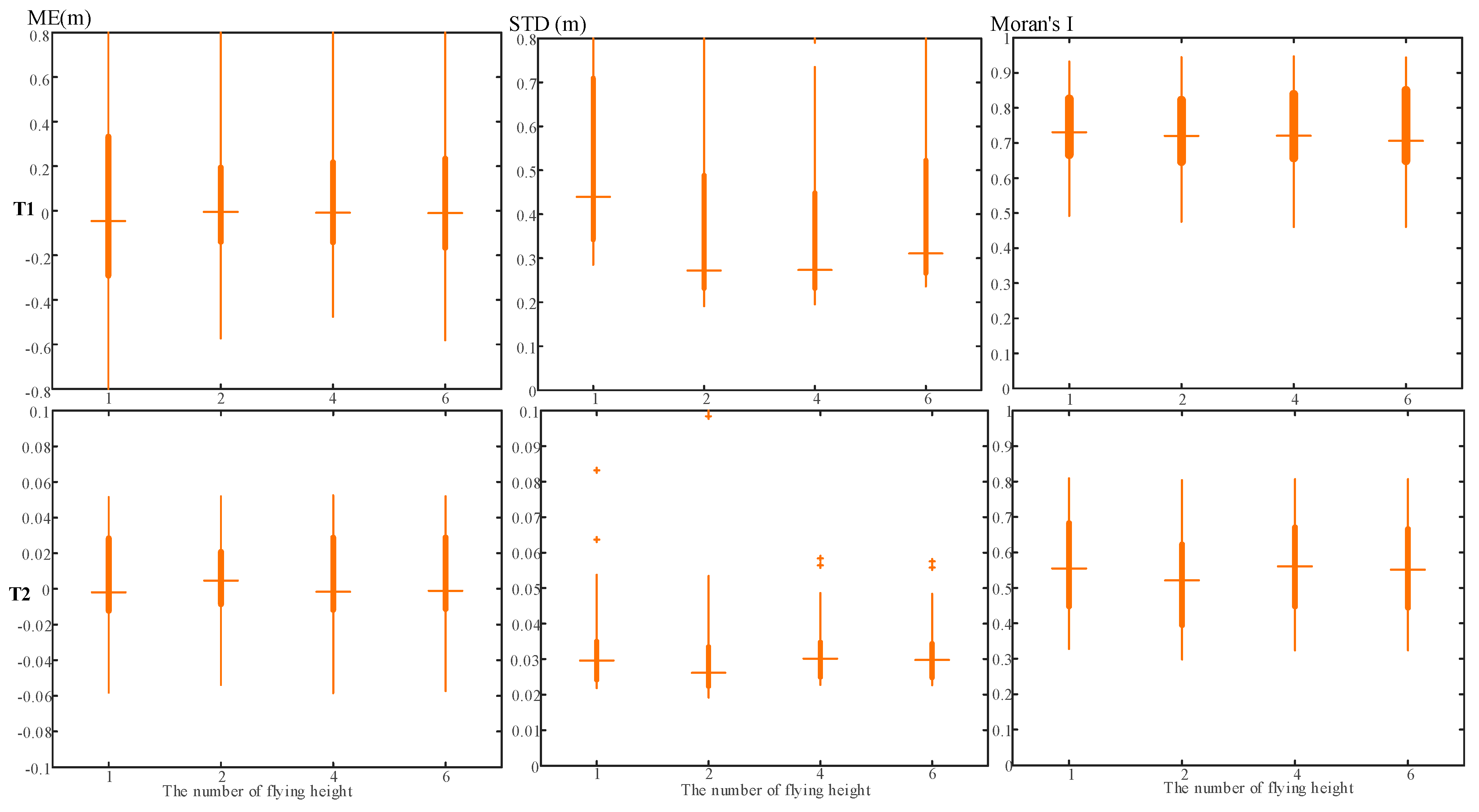
3.2. The Effects of Flying Height
3.2.1. Single Flying Height
3.2.2. Combination of Multiple Flying Heights
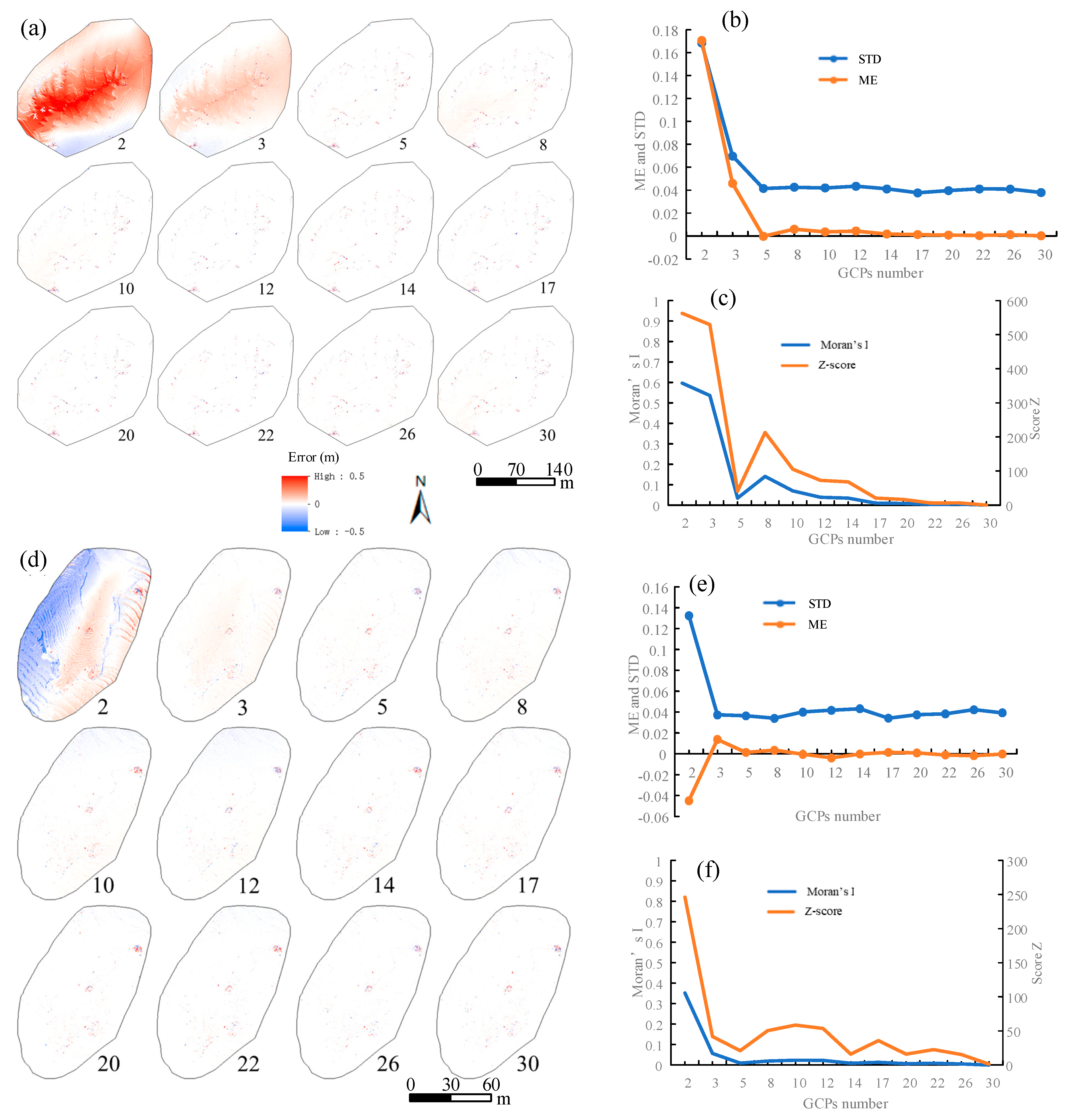
3.3. The Effects of GCPs
3.3.1. The Number of GCPs
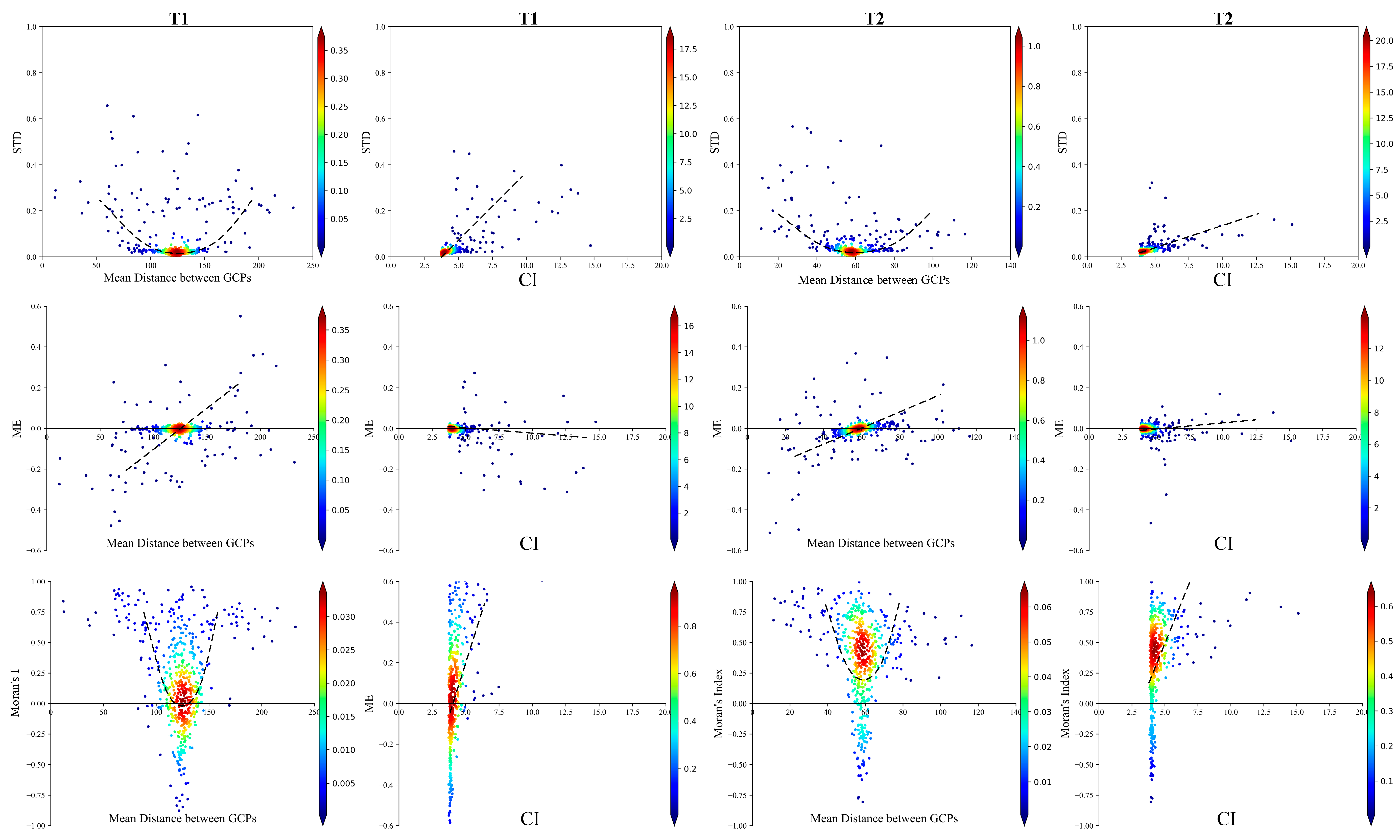
3.3.2. The Spatial Distribution of GCPs
4. Discussion
4.1. Camera Angle, Flying Height, and Combination Strategies
4.2. The Quantity and Spatial Distribution of GCPs
4.3. Other Factors
5. Conclusions
- A high camera inclination (20–40°) enhances UAV-SfM photogrammetry. This not only decreases the magnitude of errors, but also mitigates its spatial correlation (Moran’s I). Supplementing convergent images is valuable for reducing errors in a nadir camera block, but it is unnecessary when the image block is with a high camera angle.
- Flying height increases the magnitude of errors (ME and STD) but does not affect the spatial structure (Moran’s I). By contrast, the camera angle is more important than flying height for improving spatial pattern of errors. Moreover, the effect of flying height is nonlinear and could interact with the camera angle.
- A small number of GCPs rapidly improves the magnitude of errors (ME and STD), and a further increase in GCPs has a marginal effect. However, the structure of errors (Moran’s I) can be further improved with increasing GCPs.
- With the same number, the distribution of GCPs is critical for UAV-SfM photogrammetry. The edge distribution should be first considered, followed by the even distribution.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shahbazi, M.; Menard, P.; Sohn, G.; Theau, J. Unmanned aerial image dataset: Ready for 3D reconstruction. Data Brief 2019, 25, 103962. [Google Scholar] [CrossRef] [PubMed]
- Pierzchała, M.; Talbot, B.; Astrup, R. Estimating Soil Displacement from Timber Extraction Trails in Steep Terrain: Application of an Unmanned Aircraft for 3D Modelling. Forests 2014, 5, 1212–1223. [Google Scholar] [CrossRef]
- Chen, C.; Tian, B.; Wu, W.; Duan, Y.; Zhou, Y.; Zhang, C. UAV photogrammetry in intertidal mudflats: Accuracy, efficiency, and potential for integration with satellite imagery. Remote Sens. 2023, 15, 1814. [Google Scholar] [CrossRef]
- Gonçalves, J.A.; Henriques, R. UAV photogrammetry for topographic monitoring of coastal areas. ISPRS J. Photogramm. Remote Sens. 2015, 104, 101–111. [Google Scholar] [CrossRef]
- Jaud, M.; Bertin, S.; Beauverger, M.; Augereau, E.; Delacourt, C. RTK GNSS-Assisted Terrestrial SfM Photogrammetry without GCP: Application to Coastal Morphodynamics Monitoring. Remote Sens. 2020, 12, 1889. [Google Scholar] [CrossRef]
- Manfreda, S.; McCabe, M.; Miller, P.; Lucas, R.; Pajuelo Madrigal, V.; Mallinis, G.; Ben Dor, E.; Helman, D.; Estes, L.; Ciraolo, G.; et al. On the Use of Unmanned Aerial Systems for Environmental Monitoring. Remote Sens. 2018, 10, 641. [Google Scholar] [CrossRef]
- Cao, L.; Liu, H.; Fu, X.; Zhang, Z.; Shen, X.; Ruan, H. Comparison of UAV LiDAR and Digital Aerial Photogrammetry Point Clouds for Estimating Forest Structural Attributes in Subtropical Planted Forests. Forests 2019, 10, 145. [Google Scholar] [CrossRef]
- Candiago, S.; Remondino, F.; De Giglio, M.; Dubbini, M.; Gattelli, M. Evaluating Multispectral Images and Vegetation Indices for Precision Farming Applications from UAV Images. Remote Sens. 2015, 7, 4026–4047. [Google Scholar] [CrossRef]
- Bendig, J.; Yu, K.; Aasen, H.; Bolten, A.; Bennertz, S.; Broscheit, J.; Gnyp, M.L.; Bareth, G. Combining UAV-based plant height from crop surface models, visible, and near infrared vegetation indices for biomass monitoring in barley. Int. J. Appl. Earth Obs. Geoinf. 2015, 39, 79–87. [Google Scholar] [CrossRef]
- Tu, Y.-H.; Phinn, S.; Johansen, K.; Robson, A.; Wu, D. Optimising drone flight planning for measuring horticultural tree crop structure. ISPRS J. Photogramm. Remote Sens. 2020, 160, 83–96. [Google Scholar] [CrossRef]
- Swayze, N.C.; Tinkham, W.T.; Vogeler, J.C.; Hudak, A.T. Influence of flight parameters on UAS-based monitoring of tree height, diameter, and density. Remote Sens. Environ. 2021, 263, 112540. [Google Scholar] [CrossRef]
- Kameyama, S.; Sugiura, K. Effects of differences in structure from motion software on image processing of unmanned aerial vehicle photography and estimation of crown area and tree height in forests. Remote Sens. 2021, 13, 626. [Google Scholar] [CrossRef]
- Zhao, N.; Lu, W.; Sheng, M.; Chen, Y.; Tang, J.; Yu, F.R.; Wong, K.-K. UAV-Assisted Emergency Networks in Disasters. IEEE Wirel. Commun. 2019, 26, 45–51. [Google Scholar] [CrossRef]
- Erdelj, M.; Natalizio, E.; Chowdhury, K.R.; Akyildiz, I.F. Help from the Sky: Leveraging UAVs for Disaster Management. IEEE Pervasive Comput. 2017, 16, 24–32. [Google Scholar] [CrossRef]
- Tuna, G.; Nefzi, B.; Conte, G. Unmanned aerial vehicle-aided communications system for disaster recovery. J. Netw. Comput. Appl. 2014, 41, 27–36. [Google Scholar] [CrossRef]
- Westoby, M.J.; Brasington, J.; Glasser, N.F.; Hambrey, M.J.; Reynolds, J.M. ‘Structure-from-Motion’ photogrammetry: A low-cost, effective tool for geoscience applications. Geomorphology 2012, 179, 300–314. [Google Scholar] [CrossRef]
- Colomina, I.; Molina, P. Unmanned aerial systems for photogrammetry and remote sensing: A review. ISPRS J. Photogramm. Remote Sens. 2014, 92, 79–97. [Google Scholar] [CrossRef]
- Fonstad, M.A.; Dietrich, J.T.; Courville, B.C.; Jensen, J.L.; Carbonneau, P.E. Topographic structure from motion: A new development in photogrammetric measurement. Earth Surf. Process. Landf. 2013, 38, 421–430. [Google Scholar] [CrossRef]
- James, M.R.; Chandler, J.H.; Eltner, A.; Fraser, C.; Miller, P.E.; Mills, J.P.; Noble, T.; Robson, S.; Lane, S.N. Guidelines on the use of structure-from-motion photogrammetry in geomorphic research. Earth Surf. Process. Landf. 2019, 44, 2081–2084. [Google Scholar] [CrossRef]
- Štroner, M.; Urban, R.; Seidl, J.; Reindl, T.; Brouček, J. Photogrammetry Using UAV-Mounted GNSS RTK: Georeferencing Strategies without GCPs. Remote Sens. 2021, 13, 1336. [Google Scholar] [CrossRef]
- Ruzgienė, B.; Berteška, T.; Gečyte, S.; Jakubauskienė, E.; Aksamitauskas, V.Č. The surface modelling based on UAV Photogrammetry and qualitative estimation. Measurement 2015, 73, 619–627. [Google Scholar] [CrossRef]
- James, M.R.; Antoniazza, G.; Robson, S.; Lane, S.N. Mitigating systematic error in topographic models for geomorphic change detection: Accuracy, precision and considerations beyond off-nadir imagery. Earth Surf. Process. Landf. 2020, 45, 2251–2271. [Google Scholar] [CrossRef]
- Rossi, P.; Mancini, F.; Dubbini, M.; Mazzone, F.; Capra, A. Combining nadir and oblique UAV imagery to reconstruct quarry topography: Methodology and feasibility analysis. Eur. J. Remote Sens. 2017, 50, 211–221. [Google Scholar] [CrossRef]
- Nesbit, P.; Hugenholtz, C. Enhancing UAV–SfM 3D Model Accuracy in High-Relief Landscapes by Incorporating Oblique Images. Remote Sens. 2019, 11, 239. [Google Scholar] [CrossRef]
- Aguera-Vega, F.; Ferrer-Gonzalez, E.; Carvajal-Ramirez, F.; Martinez-Carricondo, P.; Rossi, P.; Mancini, F. Influence of AGL flight and off-nadir images on UAV-SfM accuracy in complex morphology terrains. Geocarto Int. 2022, 37, 12892–12912. [Google Scholar] [CrossRef]
- Martínez-Carricondo, P.; Agüera-Vega, F.; Carvajal-Ramírez, F.; Mesas-Carrascosa, F.-J.; García-Ferrer, A.; Pérez-Porras, F.-J. Assessment of UAV-photogrammetric mapping accuracy based on variation of ground control points. Int. J. Appl. Earth Obs. Geoinf. 2018, 72, 1–10. [Google Scholar] [CrossRef]
- Cabo, C.; Sanz-Ablanedo, E.; Roca-Pardinas, J.; Ordonez, C. Influence of the Number and Spatial Distribution of Ground Control Points in the Accuracy of UAV-SfM DEMs: An Approach Based on Generalized Additive Models. IEEE Trans. Geosci. Remote Sens. 2021, 59, 10618–10627. [Google Scholar] [CrossRef]
- Ferrer-González, E.; Agüera-Vega, F.; Carvajal-Ramírez, F.; Martínez-Carricondo, P. UAV Photogrammetry Accuracy Assessment for Corridor Mapping Based on the Number and Distribution of Ground Control Points. Remote Sens. 2020, 12, 2447. [Google Scholar] [CrossRef]
- James, M.R.; Robson, S.; d’Oleire-Oltmanns, S.; Niethammer, U. Optimising UAV topographic surveys processed with structure-from-motion: Ground control quality, quantity and bundle adjustment. Geomorphology 2017, 280, 51–66. [Google Scholar] [CrossRef]
- Sanz-Ablanedo, E.; Chandler, J.; Rodríguez-Pérez, J.; Ordóñez, C. Accuracy of Unmanned Aerial Vehicle (UAV) and SfM Photogrammetry Survey as a Function of the Number and Location of Ground Control Points Used. Remote Sens. 2018, 10, 1606. [Google Scholar] [CrossRef]
- Agüera-Vega, F.; Carvajal-Ramírez, F.; Martínez-Carricondo, P. Accuracy of Digital Surface Models and Orthophotos Derived from Unmanned Aerial Vehicle Photogrammetry. J. Surv. Eng. 2017, 143, 04016025. [Google Scholar] [CrossRef]
- Grau, J.; Liang, K.; Ogilvie, J.; Arp, P.; Li, S.; Robertson, B.; Meng, F.-R. Improved Accuracy of Riparian Zone Mapping Using Near Ground Unmanned Aerial Vehicle and Photogrammetry Method. Remote Sens. 2021, 13, 1997. [Google Scholar] [CrossRef]
- Jiménez-Jiménez, S.I.; Ojeda-Bustamante, W.; Marcial-Pablo, M.; Enciso, J. Digital Terrain Models Generated with Low-Cost UAV Photogrammetry: Methodology and Accuracy. ISPRS Int. J. Geo-Inf. 2021, 10, 285. [Google Scholar] [CrossRef]
- Dai, W.; Qian, W.; Liu, A.L.; Wang, C.; Yang, X.; Hu, G.H.; Tang, G.A. Monitoring and modeling sediment transport in space in small loess catchments using UAV-SfM photogrammetry. Catena 2022, 214, 106244. [Google Scholar] [CrossRef]
- James, M.R.; Robson, S.; Smith, M.W. 3-D uncertainty-based topographic change detection with structure-from-motion photogrammetry: Precision maps for ground control and directly georeferenced surveys. Earth Surf. Process. Landf. 2017, 42, 1769–1788. [Google Scholar] [CrossRef]
- Sanz-Ablanedo, E.; Chandler, J.H.; Ballesteros-Pérez, P.; Rodríguez-Pérez, J.R. Reducing systematic dome errors in digital elevation models through better UAV flight design. Earth Surf. Process. Landf. 2020, 45, 2134–2147. [Google Scholar] [CrossRef]
- Meinen, B.U.; Robinson, D.T. Mapping erosion and deposition in an agricultural landscape: Optimization of UAV image acquisition schemes for SfM-MVS. Remote Sens. Environ. 2020, 239, 111666. [Google Scholar] [CrossRef]
- James, M.R.; Robson, S. Mitigating systematic error in topographic models derived from UAV and ground-based image networks. Earth Surf. Process. Landf. 2014, 39, 1413–1420. [Google Scholar] [CrossRef]
- Moran, P.A. Notes on continuous stochastic phenomena. Biometrika 1950, 37, 17–23. [Google Scholar] [CrossRef]
- Smith, M.W.; Vericat, D. From experimental plots to experimental landscapes: Topography, erosion and deposition in sub-humid badlands from Structure-from-Motion photogrammetry. Earth Surf. Process. Landf. 2015, 40, 1656–1671. [Google Scholar] [CrossRef]
- Rupnik, E.; Nex, F.; Toschi, I.; Remondino, F. Aerial multi-camera systems: Accuracy and block triangulation issues. ISPRS J. Photogramm. Remote Sens. 2015, 101, 233–246. [Google Scholar] [CrossRef]
- Cucchiaro, S.; Cavalli, M.; Vericat, D.; Crema, S.; Llena, M.; Beinat, A.; Marchi, L.; Cazorzi, F. Monitoring topographic changes through 4D-structure-from-motion photogrammetry: Application to a debris-flow channel. Environ. Earth Sci. 2018, 77, 632. [Google Scholar] [CrossRef]
- Santos Santana, L.; Araújo E Silva Ferraz, G.; Bedin Marin, D.; Dienevam Souza Barbosa, B.; Mendes Dos Santos, L.; Ferreira Ponciano Ferraz, P.; Conti, L.; Camiciottoli, S.; Rossi, G. Influence of flight altitude and control points in the georeferencing of images obtained by unmanned aerial vehicle. Eur. J. Remote Sens. 2021, 54, 59–71. [Google Scholar] [CrossRef]
- Petrie, G. Systematic Oblique Aerial Photography Using Multiple Digital Cameras Oblique Photography -Introduction I -Multiple Oblique Photographs. Photogramm. Eng. Remote Sens. 2009, 75, 102–107. [Google Scholar]
- Jiang, S.; Jiang, C.; Jiang, W. Efficient structure from motion for large-scale UAV images: A review and a comparison of SfM tools. ISPRS J. Photogramm. Remote Sens. 2020, 167, 230–251. [Google Scholar]


| Study Area | Camera Angle (°) | Flying Height (m) | Flight Sorties | Ground Resolution (cm) |
|---|---|---|---|---|
| T1 | 0, 5, 10, 20, 30, 35, 40 | 100 | 7 | 2.7 |
| T2 | 0, 5, 10, 20, 30, 35, 40 | 70 | 7 | 1.9 |
| No. | Main Block (°) | Supplemented Images (°) | Combinations (Main + Supplement) |
|---|---|---|---|
| 1 | 0 | 5, 10, 20, 30, 35, or 40 | 0 + 5°, 0 + 10°, 0 + 20°, 0 + 30°, 0 + 35°, 0 + 40° |
| 2 | 5 | 10, 20, 30, 35, or 40 | 5 + 10°, 5 + 20°, 5 + 30°, 5 + 35°, 5 + 40° |
| 3 | 10 | 20, 30, 35, or 40 | 10 + 20°, 10 + 30°, 10 + 35°, 10 + 40° |
| 4 | 20 | 30, 35, or 40 | 20 + 30°, 20 + 35°, 20 + 40° |
| 5 | 30 | 35, or 40 | 30 + 35°, 30 + 40° |
| 6 | 35 | 40 | 35 + 40° |
| Study Area | Flying Height (m) | Camera Angle (°) | Flight Sorties | Average Ground Resolution (cm) |
|---|---|---|---|---|
| T1 | 60, 80, 100, 120, 140, 160 | 0 | 6 | 1.6–4.4 |
| T2 | 60, 80, 100, 120, 140, 160 | 15 | 6 | 1.6–4.4 |
| Study Area | Camera Angle (°) | No.1 Combination of Two Heights (m) | No.2 Combination of Four Heights (m) | No.3 Combination of Six Heights (m) |
|---|---|---|---|---|
| T1 | 0 | 100, 120 | 80, 100, 120, 140, | 60, 80, 100, 120, 140, 160 |
| T2 | 15 | 100, 120 | 80, 100, 120, 140, | 60, 80, 100, 120, 140, 160 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dai, W.; Qiu, R.; Wang, B.; Lu, W.; Zheng, G.; Amankwah, S.O.Y.; Wang, G. Enhancing UAV-SfM Photogrammetry for Terrain Modeling from the Perspective of Spatial Structure of Errors. Remote Sens. 2023, 15, 4305. https://doi.org/10.3390/rs15174305
Dai W, Qiu R, Wang B, Lu W, Zheng G, Amankwah SOY, Wang G. Enhancing UAV-SfM Photogrammetry for Terrain Modeling from the Perspective of Spatial Structure of Errors. Remote Sensing. 2023; 15(17):4305. https://doi.org/10.3390/rs15174305
Chicago/Turabian StyleDai, Wen, Ruibo Qiu, Bo Wang, Wangda Lu, Guanghui Zheng, Solomon Obiri Yeboah Amankwah, and Guojie Wang. 2023. "Enhancing UAV-SfM Photogrammetry for Terrain Modeling from the Perspective of Spatial Structure of Errors" Remote Sensing 15, no. 17: 4305. https://doi.org/10.3390/rs15174305
APA StyleDai, W., Qiu, R., Wang, B., Lu, W., Zheng, G., Amankwah, S. O. Y., & Wang, G. (2023). Enhancing UAV-SfM Photogrammetry for Terrain Modeling from the Perspective of Spatial Structure of Errors. Remote Sensing, 15(17), 4305. https://doi.org/10.3390/rs15174305










