Multi-Attention Multi-Image Super-Resolution Transformer (MAST) for Remote Sensing

Abstract

Deep-learning-driven multi-image super-resolution (MISR) reconstruction techniques have significant application value in the field of aerospace remote sensing. In particular, Transformer-based models have shown outstanding performance in super-resolution tasks. However, current MISR models have some deficiencies in the application of multi-scale information and the modeling of the attention mechanism, leading to an insufficient utilization of complementary information in multiple images. In this context, we innovatively propose a Multi-Attention Multi-Image Super-Resolution Transformer (MAST), which involves improvements in two main aspects. Firstly, we present a Multi-Scale and Mixed Attention Block (MMAB). With its multi-scale structure, the network is able to extract image features from different scales to obtain more contextual information. Additionally, the introduction of mixed attention allows the network to fully explore high-frequency features of the images in both channel and spatial dimensions. Secondly, we propose a Collaborative Attention Fusion Block (CAFB). By incorporating channel attention into the self-attention layer of the Transformer, we aim to better establish global correlations between multiple images. To improve the network’s perception ability of local detailed features, we introduce a Residual Local Attention Block (RLAB). With the aforementioned improvements, our model can better extract and utilize non-redundant information, achieving a superior restoration effect that balances the global structure and local details of the image. The results from the comparative experiments reveal that our approach demonstrated a notable enhancement in cPSNR, with improvements of 0.91 dB and 0.81 dB observed in the NIR and RED bands of the PROBA-V dataset, respectively, in comparison to the existing state-of-the-art methods. Extensive experiments demonstrate that the method proposed in this paper can provide a valuable reference for solving multi-image super-resolution tasks for remote sensing.

1. Introduction

Space optical remote sensing utilizes optical cameras in space to observe the Earth or space targets, capturing remote sensing images that reflect their reflection or the radiation information of the targets. It enables applications such as classification, identification, and comprehensive detection, serving as an important means of obtaining information for global change monitoring, regional surveillance, resource exploration, urban planning, and other fields [1]. The higher the geometric resolution of a space optical camera, the greater the precision in differentiating, identifying, and classifying targets.

Although increasing the optical aperture and focal length can directly improve the resolution, it significantly increases the cost, weight, volume, and development complexity of the camera. Additionally, regardless of the size, aperture, or focal length of the imaging system, the imaging resolution is inevitably limited by physical factors in the imaging chain. This leads to a decrease in the resolution index and is primarily caused by atmospheric blurring, optical aberrations and diffraction-induced blurring, aliasing due to an undersampling of CCD/CMOS detectors, and electronic noise [2].

Therefore, overcoming the physical limitations mentioned above and improving the resolution without changing the optical hardware is an important issue that needs to be addressed in space-based optical remote sensing. Image super-resolution reconstruction technology can overcome the limitations of traditional optical imaging and is an effective approach to solve the associated problems [3].

Image super-resolution reconstruction is the reconstruction of a high-resolution (HR) image from one or multiple low-resolution (LR) images. It possesses ill-posedness, falls within the realm of inverse problems, and represents a challenging research direction [4]. Since the problem was proposed by Harris [5] in 1964, scholars have proposed various super-resolution methods around the inverse convolution algorithm [6]. With the rapid development of deep learning technology, the use of neural networks to accomplish super-resolution reconstruction tasks has become a frontier approach in academic research, and a series of excellent super-resolution algorithms have emerged, often achieving state-of-the-art performance in various benchmarks of super-resolution [7]. In terms of network models, they can be divided into convolutional neural network algorithms [8,9,10], generative adversarial neural network algorithms [11,12,13], Transformer network algorithms [14,15,16,17], etc.

Single-image super-resolution aims to reconstruct an HR image from a noisy and low-quality LR image [18]. Multi-image super-resolution utilizes complementary information between multiple LR images of the same scene [19] to reconstruct an HR image through sub-pixel level information fusion [20,21]. Compared to single-image super-resolution algorithms, multi-image super-resolution (MISR) algorithms leverage complementary sub-pixel information [22], which can yield better reconstruction results [23].

The principle of the MISR algorithm is to extract and fuse sub-pixel features from multiple images to reconstruct the high-frequency information of the image and improve the resolution. It primarily focuses on three key aspects: (1) establishing a mechanism for extracting and fusing complementary sub-pixel features; (2) reducing the impact of registration errors between multiple images on the reconstruction; and (3) suppressing the influence of blurring and noise contamination on the reconstruction. In recent years, researchers in the field of remote sensing have conducted innovative research in high-frequency information feature extraction [24,25], registration error suppression [26,27,28], noise error suppression [29,30], and other aspects related to these three key aspects. However, there are still some issues that need to be addressed.

In terms of feature extraction, the existing algorithms are still inadequate in extracting the depth features that contribute to the super-resolution task in multiple images; the complementarity of features between each image is not sufficient, and features that do not contribute to the reconstruction task are also passed to the feature fusion step, which affects the reconstruction effect. In terms of feature fusion, the existing algorithms are still inadequate in terms of the local detail fusion mechanism, which leads to the fusion of sub-pixel features of multiple images while also fusing noise and blurred features, affecting the reconstruction effect. Finally, no optimization algorithm has been proposed that can comprehensively address the three abovementioned key aspects.

Based on the analysis of the limitations of the existing MISR methods for remote sensing, this paper innovatively proposes a synthetically improved Multi-Attention Multi-Image Super-Resolution Transformer (MAST). This network mitigates the issue of effective information loss that is present in existing methods by employing a multi-scale and multi-attention approach. Comparative experiments showed that the proposed algorithm achieved state-of-the-art super-resolution results in the NIR and RED bands of the PROBA-V MISR dataset, which can provide valuable references and insights for future studies in this field. In brief, the main contributions of this work are as follows:

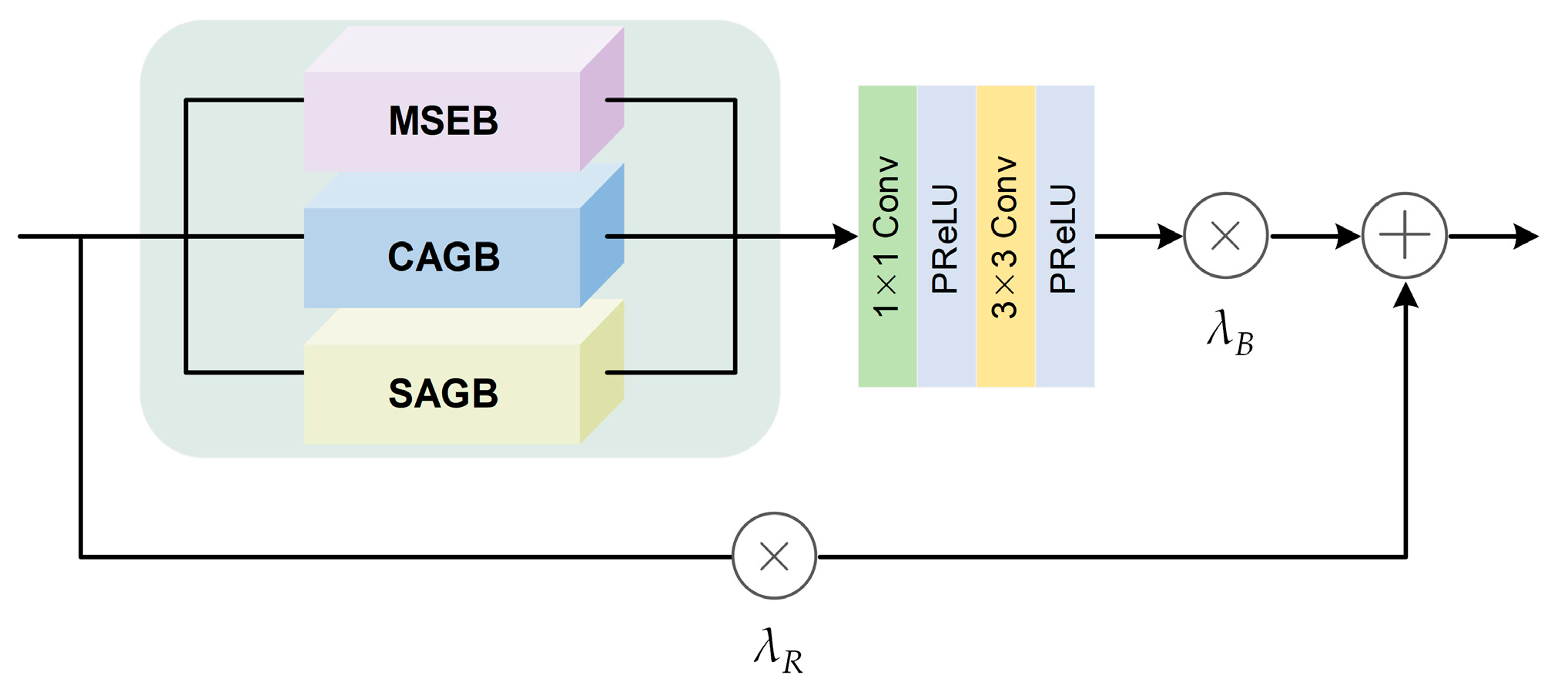
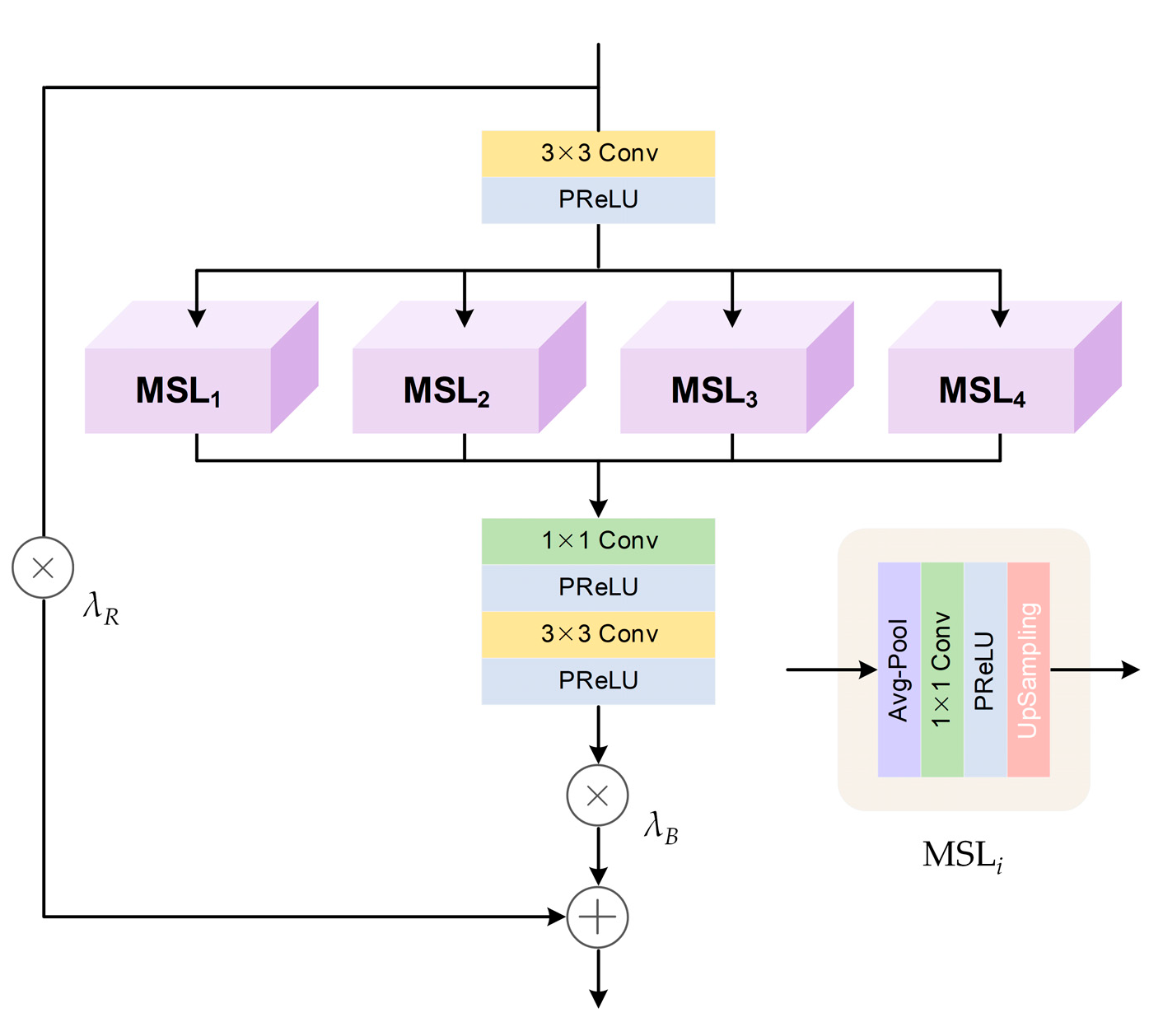
• We innovatively proposed a Multi-Scale and Mixed Attention Block (MMAB) that enabled a model to fully extract complementary information from multiple images. Specifically, we introduced a Multi-Scale Extraction Block (MSEB) to obtain more reference information and effectively suppress registration errors. We also presented a Channel Attention Guided Block (CAGB) and a Spatial Attention Guided Block (SAGB) to enhance the model’s perception of high-frequency features with high contributions to the super-resolution task in each image.
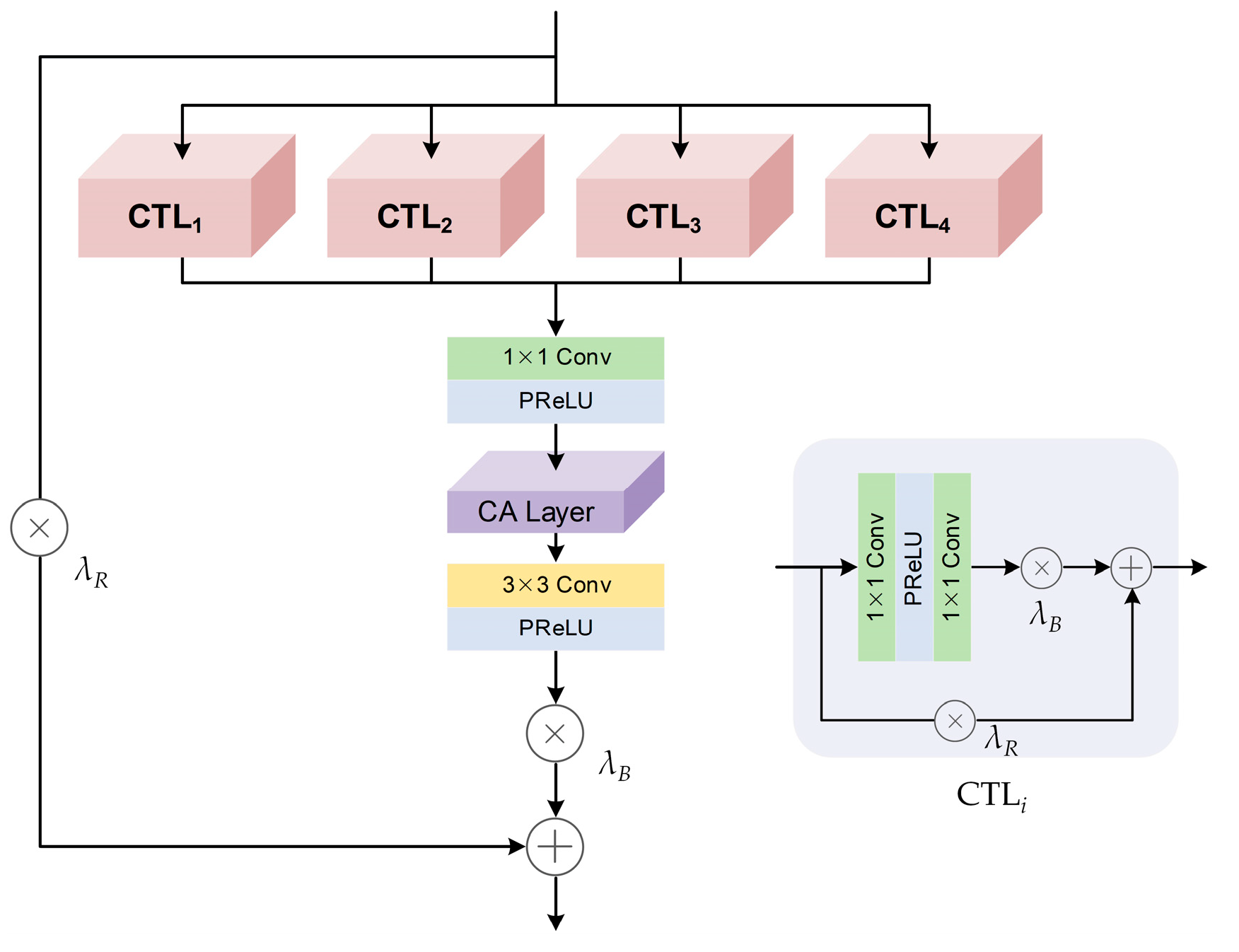
• We also presented a Collaborative Attention Fusion Block (CAFB) based on the Transformer, which constructed a more comprehensive feature fusion mechanism incorporating self-attention, channel attention, and local attention. The embedding of channel attention enhanced the advantage of the Transformer in establishing global correlations between multiple frames. The introduction of the Residual Local Attention Block (RLAB) largely broke through the limitations of the Transformer in capturing local high-frequency information, enabling the model to simultaneously restore the overall structure and local details of the image.

2. Related Work

2.1. Multi-Image Super-Resolution

The multi-image degradation model for the same scene imaged k times can be expressed as follows:

$${\mathit{y}}_{\mathit{k}}{=[\mathit{A} \otimes \mathit{H}}_{\mathit{k}}{ \otimes \mathit{C}}_{\mathit{k}}{] \otimes \mathit{x}+\mathit{n}}_{\mathit{k}}$$

(1)

where ${\mathit{y}}_{\mathit{k}}$ represents the k-th LR image, x represents the HR image, the symbol ⊗ denotes convolution, ${\mathit{n}}_{\mathit{k}}$ represents additive system noise, A represents the detector sampling coefficients, ${\mathit{H}}_{\mathit{k}}$ denotes the blur coefficients, and ${\mathit{C}}_{\mathit{k}}$ represents the inter-frame displacement relationship function. Multi-image super-resolution reconstruction involves solving for the HR image from this equation.

Tsai and Huang [31] first proposed the concept of multi-frame image super-resolution in 1984. They presented a frequency domain method that improves the spatial resolution of an image by utilizing the complementary information brought by the relative displacement between multiple LR images. However, the limitation of frequency domain methods is that they are restricted to global translational motion and linear space-invariant degradation models. Spatial domain methods, on the other hand, possess strong capabilities of incorporating prior constraints. These methods include iterative back-projection methods, convex set projection methods, maximum a posteriori methods, and more [32].

Although the deconvolution algorithm provides a solution for MISR, using it to address the multi-image super-resolution reconstruction problem involves solving an ill-posed problem that is inherently unstable. Registration errors and modeling errors are gradually amplified during the iterative process, making it difficult to effectively suppress them. With the continuous development of artificial intelligence technology, deep learning has provided a new approach to solve the multi-image super-resolution problem using deep neural networks. This approach avoids the instability caused by the ill-posed nature of deconvolution and provides a more effective solution.

2.2. Deep Learning for Multi-Image Super-Resolution

Deep learning methods have shown great potential in addressing multi-frame super-resolution problems [33,34,35,36,37]. Deudon et al. [22] proposed HighRes-net, which first utilizes deep learning to solve the multi-frame super-resolution task. They achieved implicit registration by setting a reference frame channel and recursively fused LR image pairs using a global fusion operator. Molini et al. [38] introduced the registration filter RegNet with feature learning capabilities in DeepSUM, integrating the image registration task into a CNN. They further incorporated non-local characteristics into the network using graph convolution methods in DeepSUM++. Arefin et al. [39] presented MISR-GRU, which employs the ConvGRU module to compute the hidden state of the feature representation generated by the encoder and utilizes global average pooling to obtain fusion features. Dorr et al. [40] introduced 3DWDSRNet, a 3D wide activation residual network that replaces 3D convolutions with wide activation blocks to enhance the spatio-temporal correlation of multiple images. They also employed frame permutation techniques for data augmentation.

By introducing attention mechanisms, the model’s perception and utilization of high-frequency features can be enhanced, leading to a better reconstruction of image details and further improving the performance of super-resolution tasks [41,42,43,44]. Salvetti et al. [45] introduced a 3D convolutional feature attention mechanism with embedded residual connections in the RAMS network, enabling the network to focus on extracting high-frequency information in both the temporal and spatial dimensions. Valsesia et al. [46] utilized self-attention mechanisms in the temporal dimension and studied the relationship between the uncertainty of super-resolution images and temporal variations. They constructed an MISR model, PIUnet, which possesses permutation invariance for temporal images. In the burst super-resolution task, Bhat et al. [47] aligned multiple frames using optical flow and employed attention-based adaptive weighting and fusion methods to generate denoised super-resolution RGB images.

2.3. Transformers for Multi-Image Super-Resolution

The Transformer model is a deep learning model based on the encoder–decoder architecture with a self-attention mechanism [48]. Compared to RNNs and CNNs, the Transformer model has two key advantages. Firstly, it enables fully parallel computation, which improves the efficiency of training and inference. Secondly, the Transformer has a global receptive field, which allows it to capture global information more effectively. Recently, significant progress has been made in image super-resolution research using the Transformer model [14,15,17,36,49].

An et al. [50] were the first to apply a Transformer to the remote sensing image MISR task, proposing TR-MISR, and through extensive experiments, they demonstrated the effectiveness of the Transformer model in multi-frame fusion and in improving the model’s robustness to noise. Luo et al. [36] reduced alignment errors by combining optical flow estimation and deformable convolution and proposed BSRT, utilizing blocks and groups based on the Swin Transformer as the backbone structure to more effectively extract global contextual information. Dudhane et al. [37] introduced Burstormer, a Transformer-based hierarchical model, for burst image restoration and enhancement tasks. This model improved feature alignment and fusion by introducing enhanced deformable alignment modules and reference-free feature enrichment modules, utilizing multi-scale local and non-local features.

3. Methodology

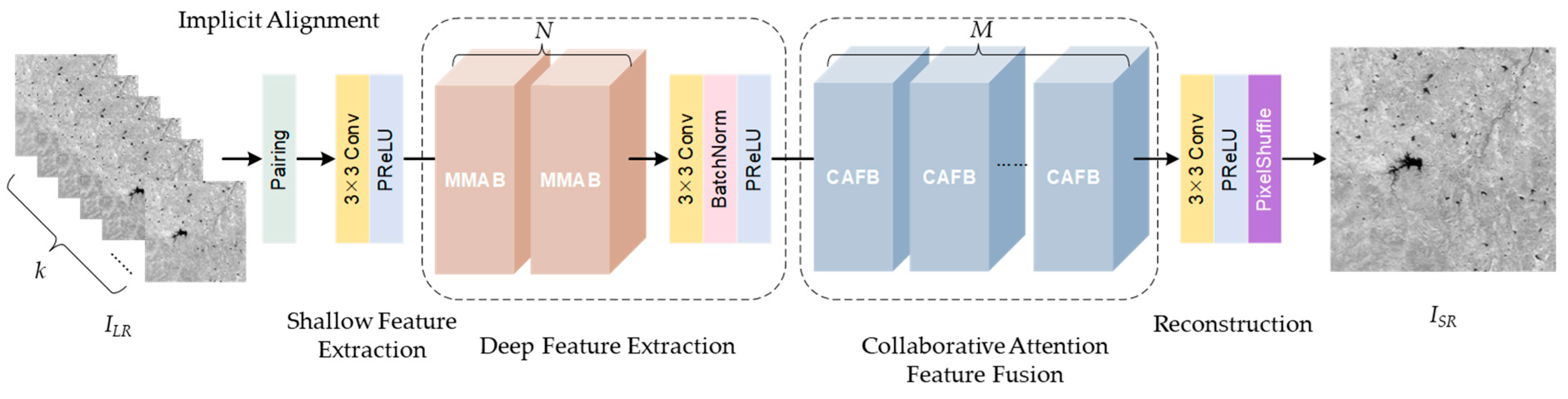
3.1. Network Architecture

The overall network of the Multi-Attention Multi-Image Super-Resolution Transformer (MAST) is illustrated in Figure 1, which consists of four parts: shallow feature extraction, deep feature extraction, collaborative attention feature fusion, and HR image reconstruction.

In particular, the MAST network takes I_LR as its input, which signifies a compilation of LR images captured from the identical scene. The shape of I_LR is H × W × k × C₀, with H, W, k, and C₀ denoting the image’s height, width, the number of LR images, and the channels per image, respectively. It is noteworthy that the value of C₀ is 1 in this context. To streamline our notation for simplicity, we abbreviate the shape of I_LR as H × W × k.

Initially, we determined the median image of the input image collection using the median operation. This step allowed us to establish a reference image, denoted as Ref, for each individual LR image. The process is illustrated below. In this context, x and y correspond to the pixel positions within the image, while i represents the index of the i-th among the initial 9 LR images.

$${\mathrm{Ref}[\mathit{x},\mathit{y}]=\mathrm{Median}(\mathit{I}}_{\mathit{LR}}[\mathit{x},\mathit{y},\mathit{i}]), \mathit{i}=1,2,\dots ,9$$

(2)

Following this, we proceeded to concatenate each LR image with its corresponding reference image along the channel dimension, leading to the generation of LR-Ref image pairs referred to as I_PR. These pairs possess a shape of H × W × 2k and are represented below. Here, j indicates the j-th LR image within the image set I_LR, while z signifies the channel of I_PR.

$${\mathit{I}}_{\mathit{PR}}[\mathit{x},\mathit{y},\mathit{z}]=\left\{\begin{array}{c}{\mathrm{LR}}_{\mathit{j}}[\mathit{x},\mathit{y},\mathit{z}], \mathit{z}[0,\mathit{k} - 1]\\ \mathrm{Ref}\left[\mathit{x},\mathit{y},\mathit{z}-\mathit{k}\right], \mathit{z}[\mathit{k},2\mathit{k} - 1]\end{array}\right., \mathit{j}=1,2,\dots ,\mathit{k}$$

(3)

This form of image pairing can be seen as an implicit initial image registration condition, and it exhibits a degree of resilience against challenges such as noise, distortion, or localized occlusion that are present in the images. It does not depend on explicit feature point matching or correspondence, thereby effectively mitigating some issues related to image misalignment.

The shallow feature extraction layer comprises a 3 × 3 convolutional layer, followed by a PReLU activation function layer. Through the process of feature extraction applied to the input LR images, we obtained the shallow feature F_S, which has the shape of H × W × C, where C (C > k) represents the channels of F_S.

$${\mathit{F}}_{\mathit{S}}{=\mathrm{PReLU}(\mathit{H}}_{3\times 3 \mathit{Conv}}{(\mathit{I}}_{\mathit{PR}}\left)\right)$$

(4)

Introducing convolutional layers into the Transformer model not only enhances the network’s training process, but also provides a more comprehensive feature representation for subsequent deep feature extraction and multi-frame information fusion [17]. Convolutional layers excel at capturing local patterns and structures in images, which are crucial for many visual tasks. Incorporating the convolutional layer into the Transformer model enhances the model’s ability to perceive these local features, resulting in a richer feature representation [51]. The important characteristics of convolutional layers are parameter sharing and local connectivity, which, to some extent, reduce the model’s parameter count, making it more amenable to training and optimization. Furthermore, convolutional layers can provide more stable gradient information during the early stages of training, aiding in accelerating the network’s convergence process [52].

Next, we proceeded to conduct deep feature extraction on the input feature, facilitating the network’s capacity to draw out additional complementary information through the integration of multi-scale and mixed attention guidance. This procedure resulted in a more intricate feature representation F_D, depicted as follows:

$$\begin{gathered} {\mathit{F}}_{\mathit{i}}{=\mathrm{MMAB}}_{\mathit{i}}{(\mathit{F}}_{\mathit{i} - 1}), \mathit{i}=1,2,\dots ,\mathit{N}, \\ {\mathit{F}}_{\mathit{D}}{=\mathrm{BN}(\mathit{H}}_{3\times 3 \mathit{Conv}}{(\mathit{F}}_{\mathit{N}}\left)\right) \end{gathered}$$

(5)

where F_i−1 and F_i indicate the input feature and output feature of i-th MMAB, respectively. BN represents the batch normalization operation.

By incorporating collaborative attention, the network in the fusion stage gains the ability to simultaneously grasp both global and local information within the image. This fosters a more comprehensive feature fusion, achieving a harmonious restoration of both the overall image structure and its intricate local details. F_M represents the fusion feature derived from the deep features, as demonstrated below. In this context, F_j−1 and F_j indicate the input and output features of the CAFB module, respectively.

$${\mathit{F}}_{\mathit{j}}{=\mathrm{CAFB}}_{\mathit{j}}{(\mathit{F}}_{\mathit{j}-1}), \mathit{j}=1,2,\dots ,\mathit{M},$$

(6)

The HR image reconstruction segment comprises a 3 × 3 convolutional layer, a PReLU layer (the two are denoted together as H_{3✕3 Conv}(·) below for brevity), and a pixel shuffle layer. Through this reconstruction process, we derived the super-resolution image I_SR, which can be represented as

$${\mathit{I}}_{\mathit{SR}}{=\mathrm{PixelShuffle}(\mathit{H}}_{3\times 3 \mathit{Conv}}{(\mathit{F}}_{\mathit{M}}\left)\right)$$

(7)

3.2. Deep Feature Extraction Module

The Multi-Scale and Mixed Attention Block (MMAB) serves as the pivotal module within the network’s deep feature extraction segment, with its structure illustrated in Figure 2. In our pursuit of effectively acquiring complementary high-frequency feature information, we harnessed three distinct mechanism-driven feature extraction modules: MESB, CAGB, and SAGB. Among these, MESB operates on the foundation of multi-scale feature extraction principles, CAGB amalgamates channel dimension compression and expansion techniques with channel attention mechanisms, and SAGB prioritizes the utilization of spatial attention for feature extraction.

By harmonizing the outputs of these three modules in a parallel fashion, our model can apprehend an expansive spectrum of complementary information across various frequencies during the feature extraction phase. This, in turn, enriches the contextual information available for image reconstruction. Additionally, existing research indicates that parallel fusion modules contribute to alleviating the adverse effects of motion blur on the outcomes, thereby enhancing the super-resolution capabilities of the model [53].

Moreover, we incorporated two learnable adaptive weight scaling parameters to dynamically fine-tune the weights of both the residual path and the backbone path [54]. λ_B signifies the weight assigned to the backbone path, whereas λ_R represents the weight attributed to the residual path. Throughout the entire training phase of the neural network, as the adaptive weights undergo continuous updates, they not only enhance the network’s focus on high-frequency features, but also improve the propagation of gradient information. This leads to an acceleration in the convergence of the network’s training process. The complete computational process of an MMAB can be succinctly described as follows:

$$\begin{gathered} {\mathit{G}}_1=\mathrm{MSEB}\left(\mathit{Y}\right){, \mathit{G}}_{2 }=\mathrm{CAGB}\left(\mathit{Y}\right){, \mathit{G}}_3=\mathrm{SAGB}\left(\mathit{Y}\right) \\ {\mathit{F}}_{\mathit{C}}[\mathit{x},\mathit{y},\mathit{z}]=\left\{\begin{array}{c}{\mathit{G}}_1[\mathit{x},\mathit{y},\mathit{z}], \mathit{z}\mathrm{\in }[0,\mathit{C}-1]\\ {\mathit{G}}_2[\mathit{x},\mathit{y},\mathit{z}-\mathit{C}], \mathit{z}\mathrm{\in }[\mathit{C},2\mathit{C}-1]\\ {\mathit{G}}_3[\mathit{x},\mathit{y},\mathit{z}-2\mathit{C}], \mathit{z}\mathrm{\in }[2\mathit{C},3\mathit{C}-1]\end{array}\right. \end{gathered}$$

(8)

$${\mathit{Z}=\mathsf{\lambda }}_{\mathit{R}}·{\mathit{Y}+\mathsf{\lambda }}_{\mathit{B}}·{\mathit{H}}_{3\times 3\mathit{Conv}}{(\mathit{H}}_{1\times 1\mathit{Conv}}{(\mathit{F}}_{\mathit{C}}\left)\right)$$

(9)

where MSEB(·), CAGB(·), and SAGB(·) correspond to the three sub-blocks present within the MMAB module. G₁, G₂, and G₃ denote the output features of the three modules. Y symbolizes the input feature. F_C indicates the concatenated output feature derived from the three branches, whereas Z signifies the resulting feature following adaptive weighting. The shapes of G₁, G₂, G₃, Y, and Z all maintain dimensions of H × W × C, while the shape of F_C adopts H × W × 3C. Additionally, H_{3✕3 Conv}(·) and H_{1✕1 Conv}(·) refer to the 3 × 3 and 1 × 1 convolution layers, respectively.

3.2.1. Multi-Scale Extraction Block (MSEB)

Objects exhibit different detailed characteristics at various scales. Multi-scale structures can capture contextual information at different scales through receptive fields of different sizes, thereby enhancing feature representation. Moreover, it was shown that the use of multi-scale structures in networks can help to suppress alignment errors [26,27,28]. We borrowed the idea of a Pyramid Pooling Module (PPM) [55] in our design and introduced adaptive weight scaling parameters to create a residual-structured multiscale feature extraction block (MSEB), the structure of which is shown in Figure 3. By incorporating the adaptive weight scaling parameter [54], the MSEB can dynamically fine-tune the feature contents within both the residual and backbone paths, enabling the model to extract complementary information more efficiently and optimize the network’s training process.

To elaborate, F₀ represents the input feature, and F_H signifies the features extracted via H_{3✕3 Conv}(·). MSL_i(·) denotes the feature extraction layer with varying pooling kernels. The specific procedure entails initiating average pooling to generate feature maps with sizes of 1 × 1, 2 × 2, 3 × 3, and 6 × 6. Among these, the 1 × 1 feature map encapsulates global information, while the remaining three encompass local details. Local features are employed to capture subtle local variations, while global features are utilized to maintain overall coherence. Subsequently, these feature maps are restored to their original sizes using bilinear interpolation. Concat(·) indicates the concatenation of feature maps of identical shape, following the same process as outlined in Equation (8). By fusing multi-scale contextual features, the adverse impacts of local noise and inaccuracies on the overall registration outcome can be effectively alleviated. F_A represents the fused multi-scale feature, while F_B signifies the output feature after the addition of residual connection. The overall calculation process is described as follows:

$${\mathit{F}}_{\mathit{A}}{=\mathit{H}}_{1\times 1 \mathit{Conv}}{\left(\mathrm{Concat}\right(\mathrm{MSL}}_1{\left({\mathit{F}}_{\mathit{H}}\right),\dots , \mathrm{MSL}}_4\left({\mathit{F}}_{\mathit{H}}\right)\left)\right)$$

(10)

$${\mathit{F}}_{\mathit{B}}{=\mathsf{\lambda }}_{\mathit{B}}·{\mathit{H}}_{3\times 3 \mathit{Conv}}{(\mathit{F}}_{\mathit{A}}{)+\mathsf{\lambda }}_{\mathit{R}}·{\mathit{F}}_0$$

(11)

3.2.2. Channel Attention Guided Block (CAGB)

The Channel Attention Guided Block (CAGB) is a sub-module of our proposed MMAB, the structure of which is shown in Figure 4, designed to direct the network to thoroughly harness high-frequency feature information within the channel dimension. By increasing the dimensionality, we can introduce a greater variety of distinct feature channels, enabling the model to comprehensively capture richer feature information [56]. Additionally, by reducing the dimensionality of the feature map in the channel dimension, the network can focus on more meaningful high-frequency features while reducing data redundancy [57].

Through the application of various dimension transformations, we obtained multi-level contextual information and performed information fusion to extract effective complementary information from the fused features. Furthermore, we introduced the channel attention mechanism, enabling the network to adaptively learn relationships between different feature channels, thus enhancing the perception of crucial high-frequency features.

In the depicted diagram, CTL_i denotes the channel attention layer. Among these, CTL₁(·) and CTL₂(·) indicate the channel expansion of input feature F₀, with expansion factors of 2 and 4, respectively, followed by a reduction to match the input channels. On the other hand, CTL₃(·) and CTL₄(·) signify the dimension reduction in F₀, with reduction factors of 1/2 and 1/4, respectively, followed by an expansion. F_K and F_Q represent the context-fused feature and the output feature after the addition of residual connection, respectively. H_CA(·) stands for the channel attention layer. The entire process unfolds as follows:

$${\mathit{F}}_{\mathit{K}}{=\mathit{H}}_{1\times 1 \mathit{Conv}}{\left(\mathrm{Concat}\right(\mathrm{CTL}}_1{\left({\mathit{F}}_0\right),\dots , \mathrm{CTL}}_4\left({\mathit{F}}_0\right)\left)\right)$$

(12)

$${\mathit{F}}_{\mathit{Q}}{=\mathsf{\lambda }}_{\mathit{B}}·{(\mathit{H}}_{3\times 3 \mathit{Conv}}{(\mathit{H}}_{\mathit{CA}}{(\mathit{F}}_{\mathit{K}}{\left)\right))+\mathsf{\lambda }}_{\mathit{R}}·{\mathit{F}}_0$$

(13)

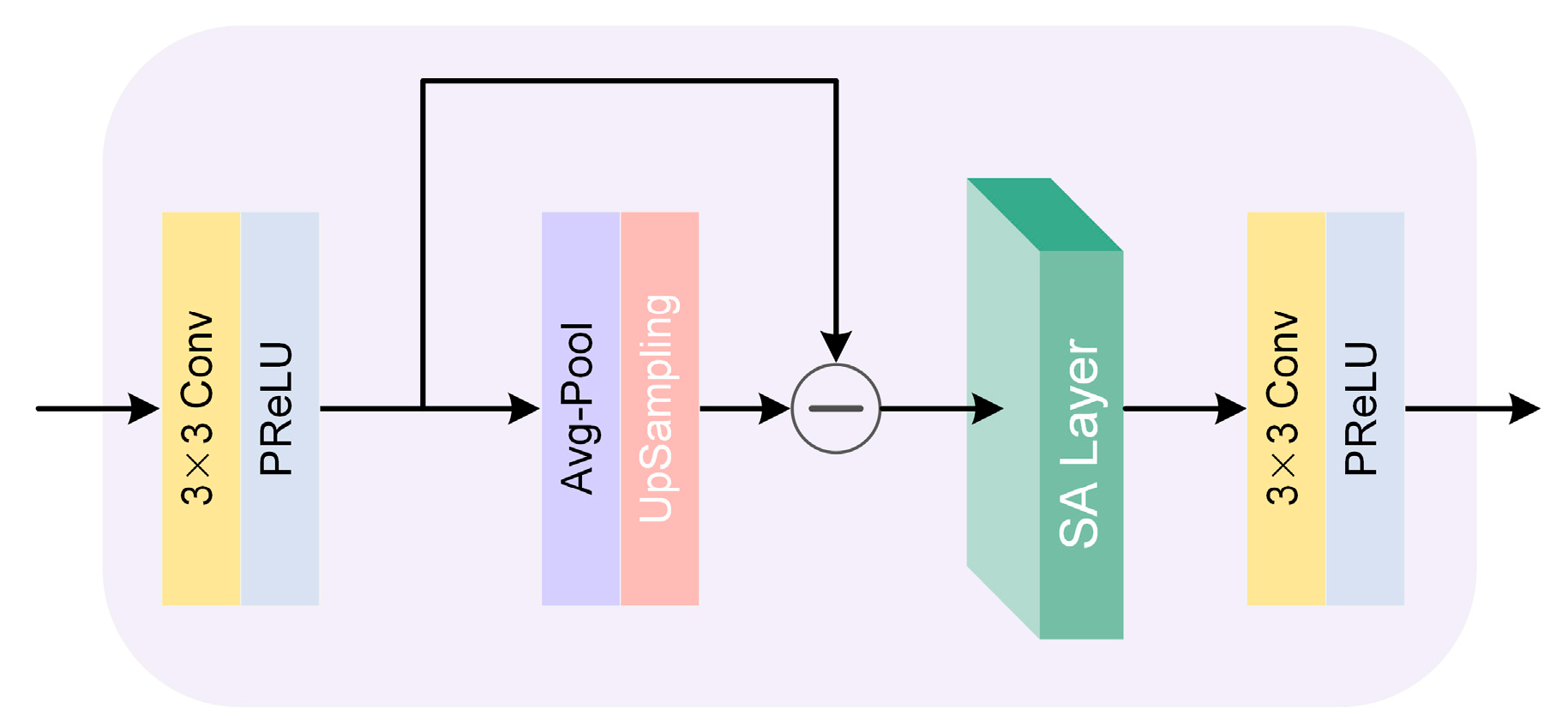
3.2.3. Spatial Attention Guided Block (SAGB)

The Spatial Attention Guided Block (SAGB) is another constituent of our proposed MMAB, the structure of which is shown in Figure 5, dedicated to delving more deeply into high-frequency feature information from the spatial dimension. By subtracting smoothed filtered feature maps from the original ones, we derived high-frequency filtered features. This process of enhancing high-frequency information can accentuate image details and edges. Subsequently, we applied computed spatial attention weights to the feature map. These weights prioritize different locations, thereby enhancing feature representation in significant image regions and subduing less important areas. This strategy effectively extracts high-frequency information. The computation process of the SAGB can be presented as follows:

$${\mathit{F}}_{\mathit{L}}{=\mathit{H}}_{\mathit{UP}}{(\mathit{H}}_{\mathit{Avg}}{(\mathit{F}}_{\mathit{G}}\left)\right)$$

(14)

$${\mathit{F}}_{\mathit{E}}{=\mathit{H}}_{3\times 3 \mathit{Conv}}{(\mathit{H}}_{\mathit{SA}}{(\mathit{F}}_{\mathit{G}}{ - \mathit{F}}_{\mathit{L}}\left)\right)$$

(15)

where F_G represents the feature obtained after H_{3×3 Conv} (·) with a size of H × W × C. F_L signifies the smoothed feature with a size of H/2 × W/2 × C. F_E denotes the output features. H_Avg(·) indicates the average pooling operation, while H_UP(·) represents bilinear interpolation. H_SA(·) represents the spatial attention layer, which adjusts the attention distribution in the spatial dimension, enabling the network to focus on high-frequency information regions.

3.3. Collaborative Attention Feature Fusion Module

The Collaborative Attention Fusion Block (CAFB) is the feature fusion module proposed by us based on the Transformer architecture, and its structure is illustrated in Figure 6. The reshaping process depicted in the figure below involves transforming the input feature map into a suitable format for the Transformer to process tokens. The Transformer model is suitable for multi-frame image processing as it is range-independent in computing attention weights and can capture distant dependencies throughout the input sequence. It demonstrates significant advantages in capturing correlation information between multiple images and enhancing robustness to noise. Our enhancement stems from the incorporation of both channel attention and residual local attention within the Transformer model. Compared to traditional attention mechanisms like CBAM, we adopted a parallel combination approach to simultaneously incorporate both global and local information.

By incorporating the channel attention mechanism to extract importance and correlation information from diverse channels and embedding this information into the Transformer, we further amplified the Transformer’s ability to capture comprehensive correlations among multi-frame information [58,59,60].

Meanwhile, the Residual Local Attention Block (RLAB) enhances the network’s ability to capture local high-frequency features. It does so by employing SimAM attention to extract the importance of neurons through the analytical solution of the energy function, directly inferring the 3D attention weights of the feature map [61]. Ultimately, through the application of weighted processing to the outputs of the two branches, an effective fusion of global and local information is accomplished. This empowers the super-resolution network to effectively restore both the overarching image structure and intricate details with proficiency during the reconstruction process. The complete computation process of CAFB unfolds as follows:

$${\mathit{X}}_{\mathit{M}}=\mathrm{MHA}\left(\mathrm{LN}\right(\mathit{X}\left)\right)+\alpha ·\mathrm{CA}\left(\mathrm{LN}\right(\mathit{X}\left)\right)+\mathit{X}$$

(16)

$${\mathit{X}}_{\mathit{N}}{=\mathrm{MLP}\left(\mathrm{LN}\right(\mathit{X}}_{\mathit{M}}{\left)\right)+\mathit{X}}_{\mathit{M}}$$

(17)

$${\mathit{X}}_{\mathit{U}}{=\mathit{X}}_{\mathit{N}}+\alpha ·{(\mathit{H}}_{3\times 3 \mathit{Conv}}\left(\mathrm{RLAB}\right(\mathit{X}\left)\right)+\mathit{X})$$

(18)

where X signifies the input of the CAFB module, constituting the feature acquired through deep extraction. X_U represents the resulting feature, incorporating insights from both the Transformer and RLAB. X_M and X_N correspond to the interim features derived during the processing stages. MHA corresponds to the standard multi-head attention, LN stands for the LayerNorm layer, and MLP represents the multi-layer perceptron.

To attain optimal fusion performance, we introduced the hyperparameter α. Through judicious weight allocation, we can harmonize the contributions of global structural information and local detail information. This allows for the extraction of comprehensive global structural insights while accentuating crucial local details, culminating in an enhanced feature representation. In the experimental context, we set α to a value of 0.01.

4. Experiments

In this section, we introduce the PROBA-V Kelvin Dataset, which is the MISR dataset used in the satellite imagery experiments. Furthermore, we delve into the exploration of evaluation metrics employed to gauge the quality of super-resolution images. Additionally, we offer a comprehensive introduction to both the data preprocessing process and the configurations of the model parameter settings.

4.1. PROBA-V Kelvin Dataset

The PROBA-V dataset is a real remote sensing image dataset provided by the PROBA-V satellite and serves as a benchmark dataset for multi-frame super-resolution tasks [62]. The dataset consists of satellite data collected from 74 manually selected regions worldwide. It includes imagery captured in two bands: NIR and RED. These images were acquired at different times. The dataset provides images with two different spatial resolutions. The LR images have a resolution of 300 m and a size of 128 × 128 pixels. The HR images, on the other hand, have a resolution of 100 m and a size of 384 × 384 pixels.

The dataset consists of a total of 1450 scenes, with 1160 scenes used for training and 290 scenes used for testing. Each scene includes an HR image and multiple LR images. The number of LR images in each scene ranges from 9 to 35. Since these images were acquired at different times and under different weather conditions, the occlusion of variable features such as clouds and snow may affect the results of the image alignment. The PROBA-V dataset provides a manually annotated quality map for each image in the scene. The quality map is encoded in binary format, using 0 to represent occluded pixels and using 1 to represent non-obscured pixels. Only non-obscured pixels are considered clear pixels, and we performed super-resolution reconstruction only for the portion of the image that is clear.

The PROBA-V dataset is a significant publicly available benchmark dataset that is currently used for remote sensing image tasks and multi-image super-resolution tasks. Several MISR algorithms have been trained on this dataset, providing reliable solutions to the tasks [22,45,46,50]. This dataset serves as compelling evidence to validate the superiority of our algorithms. In the future, we will actively strive to acquire more datasets to verify the generalizability of our model across various data distributions.

4.2. Evaluation Metric

In super-resolution tasks, PSNR and SSIM are commonly used to evaluate objective image quality metrics, but they may not be effective enough for evaluating the quality of super-resolution remote sensing images, especially when there are problems such as pixel shift and brightness bias in the images, and they have less reference value for assessing the quality of reconstructed images. To assess the reconstruction quality of remote sensing images more accurately, we introduced cPSNR and cSSIM, which are metrics that are used in the PROBA-V challenge. These metrics have been improved to address pixel offset, brightness deviation, and cloud-related factors that are present in remote sensing images.

The size of the LR in the validation set is 128 × 128 pixels, and the size of the super-resolution image SR is 384 × 384. As the acquisition of LR and HR images involves separate processes, there might be a slight misalignment at the pixel level between them. It was assumed that the maximum potential offset between the two images is 3 pixels. To account for the potential errors due to misalignment, a 3-pixel-wide strip along the edges of the SR was removed. This resulted in a cropped image denoted as ${\mathit{I}}_{3,3}^{\mathit{SR}}$, which has a size of 378 × 378 pixels. Subsequently, we proceeded to crop the HR image from the upper-left coordinate (u, v), resulting in a cropped image denoted as ${\mathit{I}}_{\mathit{u},\mathit{v}}^{\mathit{HR}}$ that is the same size as ${\mathit{I}}_{3,3}^{\mathit{SR}}$. The procedure for computing the brightness deviation between ${\mathit{I}}_{3,3}^{\mathit{SR}}$ and ${\mathit{I}}_{\mathit{u},\mathit{v}}^{\mathit{HR}}$ is outlined in Equation (19). In this equation, M_u,v represents a binary mask image. ‖·‖denotes the L₁ norm of the matrix. When calculating various metrics, we use the mask to restrict the range of statistics and only consider the results from clear pixels.

$${\mathit{b}}_{\mathit{u},\mathit{v}}=\frac{1}{\Vert {\mathit{M}}_{\mathit{u},\mathit{v}}\Vert }\sum {(\mathit{I}}_{\mathit{u},\mathit{v}}^{\mathit{HR}}{ - \mathit{I}}_{3,3}^{\mathit{SR}})·{\mathit{M}}_{\mathit{u},\mathit{v}}$$

(19)

In the experiments of this paper, we adopted negative cPSNR as the loss function for network training. The cPSNR and cSSIM are calculated as follows:

$$\mathrm{cMSE}=\underset{\mathit{u},\mathit{v}\left[0,6\right]}{\max }\frac{1}{\Vert {\mathit{M}}_{\mathit{u},\mathit{v}}\Vert }\sum {{[(\mathit{I}}_{\mathit{u},\mathit{v}}^{\mathit{HR}}{- \mathit{I}}_{3,3}^{\mathit{SR}})·{\mathit{M}}_{\mathit{u},\mathit{v}}{+\mathit{b}}_{\mathit{u},\mathit{v}}]}^2$$

(20)

$$\mathrm{cPSNR}=-10 \lg \left(\mathrm{cMSE}\right)$$

(21)

$$\mathrm{cSSIM}=\underset{\mathit{u},\mathit{v}\in \left[0,6\right]}{\max }{\mathrm{SSIM}(\mathit{I}}_{\mathit{u},\mathit{v}}^{\mathit{HR}}·{\mathit{M}}_{\mathit{u},\mathit{v}}{, \mathit{I}}_{\mathit{u},\mathit{v}}^{\mathit{SR}}·{\mathit{M}}_{\mathit{u},\mathit{v}})$$

(22)

4.3. Experimental Settings

4.3.1. Data Pre-Processing

We used 70% of the training set for model training, while the remaining 30% was used to validate the performance of the model. To obtain more image scenes, we used image cropping for data enhancement. By cropping, we could obtain more LR and HR image patches with sizes of 64 × 64 and 192 × 192 pixels, respectively. To ensure the quality of the reconstructed images and to maintain a balance of computational effort during the training process, we chose to use only the scenes with an average reliable pixel count higher than 85% to participate in the model training.

We sorted the images in the dataset from high to low based on the number of clear pixels in the LR images. For the experimental setup, the network took k LR images as the input. If there were more images in the scene than k, we selected the top k LR images with the highest number of clear pixels as the input for the network. If the number of LR images in the scene was less than k, we filled the missing images with zero matrices to meet the input requirements.

4.3.2. Parameter Settings

In the experiment, the input number of LR images k accepted by our network was 32. The LR images are grayscale images with a channel number C₀ of 1. The channels C for shallow feature F_S, deep feature F_D, and fusion feature F_M were all set to 64. In the MAST network, we set the number of the MMAB and CAFB to 2 and 6, respectively. The number of heads in the multi-head attention of the Transformer model was set to 8, and the dimension of the hidden layer in the MLP was set to 128.

We conducted experiments on the Ubuntu 18.04 system. The hardware setup included four Nvidia RTX A5000 GPUs (with a total memory of 96 GB) and an Intel Xeon (R) Gold 5320 CPU @ 2.20 GHz. The entire code framework was implemented using Python 3.7 and PyTorch 1.7.1. In the experiments, we set the batch size to 8 based on the computational capacity of the devices. For the optimizer, we used Adam with an initial learning rate of 5 × 10⁻⁴. The learning rate decay strategy employed cosine decay, with a minimum learning rate of 5 × 10⁻⁶. During the training process, we trained the model for a total of 400 epochs, which took approximately 76 h. Subsequently, we fine-tuned the model with a learning rate of 1 × 10⁻⁵ and performed 80 epochs of fine-tuning training. The model had a parameter count of 3.3 million.

5. Discussion

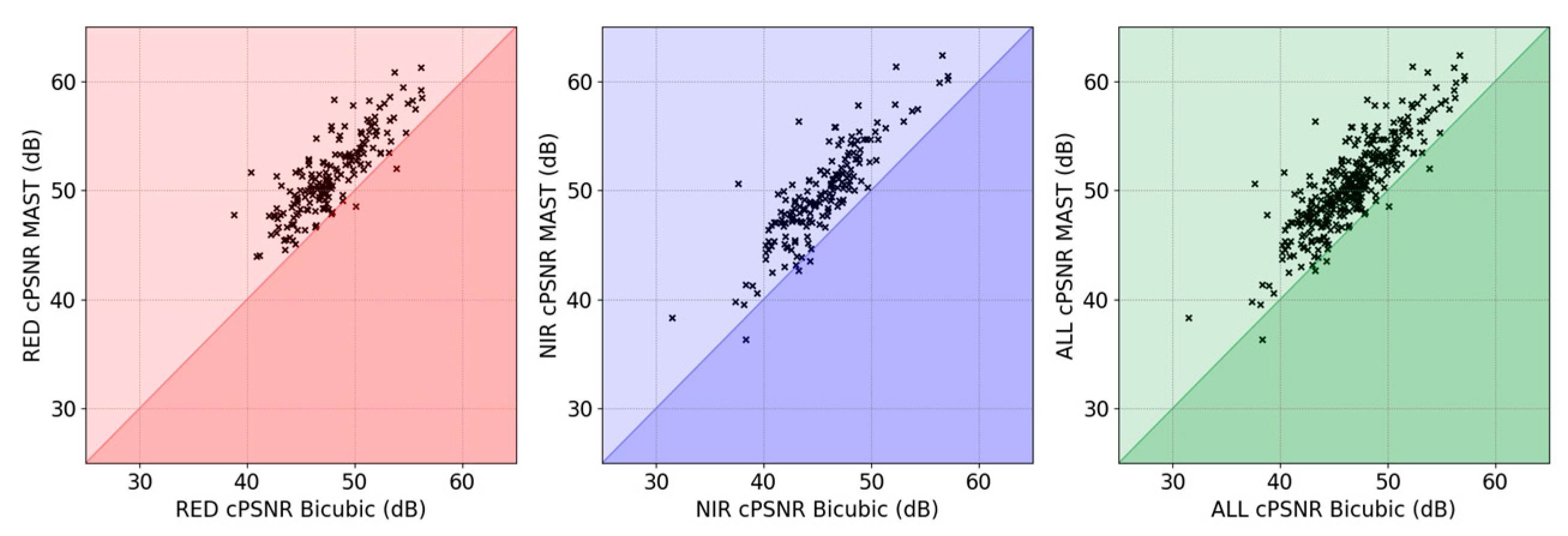
5.1. Comparison with State-of-the-Art Methods

We compared MAST with other existing MISR methods of remote sensing. Since the PROBA-V dataset did not provide ground-truth for the test set, we evaluated the reconstruction performance of different methods on the validation set using cPSNR and cSSIM as performance metrics to assess the quality of the reconstructed images.

Table 1. Quantitative comparison with different methods on the validation set.

Band	NIR		RED
Metric	cPSNR	cSSIM	cPSNR	cSSIM
Bicubic	45.44	0.9770	47.33	0.9840
BTV [63]	45.93	0.9794	48.12	0.9861
IBP [64]	45.96	0.9796	48.21	0.9965
RCAN [9]	45.66	0.9798	49.22	0.9870
VSR-DUF [65]	47.20	0.9850	49.59	0.9902
HighRes-net [22]	47.55	0.9855	49.75	0.9904
3DWDSRNet [40]	47.58	0.9856	49.90	0.9908
DeepSUM [38]	47.84	0.9858	50.00	0.9908
MISR-GRU [39]	47.88	0.9861	50.11	0.9910
DeepSUM++ [66]	47.93	0.9862	50.08	0.9912
RAMS [45]	48.23	0.9875	50.17	0.9913
RAMS+20 [45]	48.51	0.9880	50.44	0.9917
PIUnet [46]	48.72	0.9883	50.62	0.9921
TR-MISR [50]	48.54	0.9882	50.67	0.9921
MAST (this study)	49.63	0.9884	51.48	0.9924

presents the quantitative results obtained using various methods on the NIR and RED bands.

In Figure 7, we present a visual comparison of the test results between MAST and the baseline method using Bicubic interpolation in two bands: NIR and RED. The results show that MAST exhibited excellent reconstruction performance in almost all scenarios. Specifically, in 98.23% of the NIR band, the reconstruction performance of the MAST method surpassed that of the baseline method. Similarly, in the RED band, our MAST method outperformed the baseline method in as many as 98.86% of the scenarios in terms of reconstruction performance.

From the image regions shown in Figure 8 and Figure 9, it is visually apparent that our method significantly improved the preservation of textures and fine details, resulting in better visual results. These results further validate the excellent performance of the MAST method in the super-resolution task of multiple remote sensing images.

We used Bicubic interpolation as the baseline method for super-resolution reconstruction. For each scene, we applied Bicubic interpolation to the clearest image to obtain an HR image. The red boxes in the figures indicate the reconstructed regions we are comparing.

• Classical MISR Methods:

IBP obtains an initial image through Bicubic interpolation and performs registration using phase correlation. It gradually improves the estimation results by leveraging the image’s own information and reconstruction errors. BTV combines the characteristics of total variation regularization and bilateral filtering to solve the bilateral total variation minimization problem. This method can remove noise while preserving the edge information in the image.

2.

SISR Method:

RCAN learns the high-frequency details of images through residual learning and enhances the high-frequency features using the channel attention mechanism. The RCAN framework consists of five residual groups, each containing five residual channel attention blocks.

3.

Video Super-Resolution Method:

VSR-DUF utilizes dynamic upsampling filters to reconstruct HR images and enhances the image details by calculating residuals. We chose a base network consisting of 16 layers and used nine LR images as the input for the network.

4.

Deep Learning Super-Resolution Methods:

HighRes-net utilizes the reference frame for implicit alignment and recursively fuses multiple images. The experiments were conducted using the default framework, and training and testing were conducted with 16 LR images.

The 3DWDSRNet method utilizes 3D WDSR blocks instead of 3D convolutions to fuse multiple images, which helps to maintain lower GPU memory requirements. The experiments were conducted using seven LR images as the input.

DeepSUM introduces a dynamic registration subnetwork and utilizes 3D convolutions to fuse multiple images. The experiments were conducted using the clearest nine LR images to train the network. DeepSUM++ improves the non-local characteristics of the network by introducing graph convolutions.

MISR-GRU utilizes 24 LR images for implicit co-registration. It employs a fusion strategy based on ConvGRU and performs registration on super-resolution images using the ShiftNet network.

RAMS introduces an attention mechanism with 3D convolutions to better extract high-frequency features. The input consists of the clearest nine LR images. RAMS₊₂₀ improves upon the inference process by adopting a temporal self-ensemble strategy. It randomly permutes the input images 20 times and takes the average of the super-resolution results as the output.

PIUnet exhibits permutation invariance in the temporal dimension. However, it only performs well when the number of test images is close to the number of input images. Based on the parameter settings in the paper, we set the input to be nine LR images.

TR-MISR is currently the top-ranked algorithm in the leaderboard, and its network’s core is a fusion module based on a Transformer. In the experiments, we set the number of LR images to 32.

To address the issue of the insufficient utilization of complementary information from multiple frames in current MISR models, caused by a single scale and a single attention mechanism, this paper proposes an improved super-resolution network that combines multi-scale and multi-attention approaches. In terms of feature extraction, we introduce the Multi-Scale and Mixed Attention Block (MMAB) to enhance the extraction and utilization of complementary information from multiple images. Additionally, in the aspect of feature fusion, we propose the Collaborative Attention Fusion Block (CAFB) that simultaneously utilizes global and local information to achieve a balance between the restoration of the overall structure and the preservation of local details in the image.

Both the qualitative and quantitative results from the comparative experiments demonstrate that our method achieved state-of-the-art performance in the super-resolution reconstruction task on the PROBA-V dataset, further validating the effectiveness of our approach.

5.2. Analysis of Ablation Experiments

5.2.1. Effectiveness of Each Module

To validate the effectiveness of the two key modules, MMAB and CAFB, in the MAST network structure, we conducted a series of ablation experiments. We evaluated the contribution of each submodule to the overall performance, and the experimental results are recorded in

Table 2. Ablation results of individual components of MMAB on the validation set.

MMAB			NIR		RED
MSEB	SAGB	CAGB	cPSNR	cSSIM	cPSNR	cSSIM
√	×	×	48.93	0.9867	50.96	0.9916
√	√	×	48.98	0.9869	50.99	0.9919
√	√	√	50.99	0.9879	51.22	0.9921

and

Table 3. Ablation results of individual components of CAFB on the validation set.

CAFB			NIR		RED
Transformer	CA	RLAB	cPSNR	cSSIM	cPSNR	cSSIM
√	√	×	48.89	0.9874	50.84	0.9914
√	√	√	49.23	0.9881	51.19	0.9920

. The results of the ablation experiments intuitively demonstrate the importance of each submodule and provide guidance for further improvement and optimization of the network.

• Importance of MMAB

To evaluate the effectiveness of the MMAB in feature extraction, we conducted a series of ablation experiments with TR-MISR as the baseline. The feature extraction part of TR-MISR consists of two residual blocks. Apart from the differences in the feature extraction part, we maintained the same network structure as TR-MISR. In Table 2, we compare the cPSNR values of the models using three different versions of the feature extraction block on the validation set: (1) MSEB, (2) MSEB + SAGB, and (3) MSEB + SAGB + CAGB.

The multi-scale structure has a stronger ability to adapt to different scale feature information, allowing for more comprehensive feature extraction. The results in Table 2 show that when using only the MSEB for feature extraction, there was an average improvement of 0.2 dB on the validation set for both NIR and RED. The inclusion of attention mechanisms can guide the network to explore high-frequency information in the images and extract more complementary information from multiple images. The complete MMAB for feature extraction achieved cPSNR improvements of 0.52 dB and 0.55 dB on NIR and RED, respectively.

2.

Importance of CAFB

To evaluate the effectiveness of the CAFB, we conducted ablation experiments with TR-MISR as the baseline. Apart from the difference in the fusion module, we maintained the same network structure as TR-MISR. In Table 3, we compare the cPSNR values of the models using two different versions of the fusion module on the validation set: one with the Transformer + CA network and the other with the complete network (Transformer + CA + RLAB). Here, CA represents channel attention. RLAB represents the Residual Local Attention Block that we designed.

By incorporating channel attention, the ability of the Transformer model to capture more contextual features is effectively enhanced. Compared to the TR-MISR model that solely relies on the Transformer-based fusion block, our network achieved a surpassing improvement of 0.17 dB on both the NIR and RED validation sets when channel attention was added. Additionally, the inclusion of the local attention mechanism enables the model to focus more on high-frequency information. The complete fusion network showed a significant improvement in the model’s performance, with an average improvement of over 0.5 dB.

5.2.2. Analysis of the Effect of the Number of Input Images

In theory, as the number of input images increases, the MISR model can utilize more complementary information. However, it also introduces more noise and redundant information. The increase in noise can potentially degrade the quality of the reconstructed images. MISR utilizes complementary information between multiple images. If there is excessive redundant information in the network, it will increase the computational burden of the model and reduce the convergence speed of the network. The robustness of the model to noise has a significant impact on the quality of image reconstruction.

Table 4. Comparison of evaluation metrics on the validation dataset for different numbers of input LR images.

Band	NIR		RED
k	cPSNR	cSSIM	cPSNR	cSSIM
32	49.43	0.9883	51.36	0.9922
24	49.26	0.9884	51.27	0.9922
16	48.87	0.9879	51.02	0.9920
8	48.41	0.9865	50.64	0.9908

presents the cPSNR comparison results of our proposed method on the validation set using different numbers of input images (without fine-tuning). When the number of input images k was 16, our method achieved higher cPSNR in both the NIR and RED bands compared to the other comparative methods. As the number of input images increased to 32, the reconstruction performance of the model reached its best, significantly outperforming the current state-of-the-art MISR method. Specifically, in the NIR band, our method improved cPSNR by 0.71 dB, while in the RED band, it showed a relative improvement of 0.69 dB in cPSNR.

Figure 10 illustrate specific regions of the super-resolution images under different input conditions. It is visually evident that as the number of input images increased, the reconstructed images exhibited richer details and texture information. The experimental results strongly demonstrate that our proposed method can better utilize the complementary information from multiple images and exhibit improved robustness in handling noise. Our method achieved superior reconstruction performance on the PROBA-V dataset.

5.2.3. Impact of the Number of Blocks

To investigate the impact of the number of the proposed two main blocks on the model performance, we conducted a series of comparative experiments by varying the number of MMABs and CAFBs (denoted by N and M, respectively) in the network structure based on our current hardware configuration. The quantitative results obtained on the validation set are recorded in

Table 5. Comparison of evaluation metrics on the validation dataset for different numbers of modules.

Band		NIR		RED
NMMAB	NCAFB	cPSNR	cSSIM	cPSNR	cSSIM
2	6	49.43	0.9883	51.36	0.9922
2	4	49.21	0.9873	51.15	0.9918
2	2	48.96	0.9868	50.82	0.9912
3	4	49.30	0.9877	51.25	0.9923
1	6	48.50	0.9862	50.35	0.9908

.

The experimental results indicate that within a certain range, there was an improvement in the reconstruction performance as the number of blocks increased. It is noteworthy that the model achieved optimal reconstruction performance when N and M were set to 2 and 6, respectively. This implies that, in a fixed dataset size, appropriately increasing the number of modules can enhance the model’s capacity, leading to a better fitting of the input features and an improved performance in super-resolution reconstruction. The results further validate the effectiveness of the MMAB and CAFB modules.

5.2.4. Impact of the Size of the Training Images

The size of the input images often has an impact on the overall performance and speed of the model. To investigate the influence of image size in the training data on the super-resolution results, we conducted three sets of comparative experiments. Within the constraints of the computational conditions, we cropped the LR images in the training set to 64 × 64, 68 × 68, and 72 × 72, respectively. Correspondingly, the paired HR images were also cropped to three times the size of the corresponding LR images. The quantitative results of the validation set are reported in

Table 6. Comparison of evaluation metrics on the validation dataset for different input image sizes.

Band	NIR		RED
Size	cPSNR	cSSIM	cPSNR	cSSIM
64	49.63	0.9884	51.48	0.9924
68	49.68	0.9892	51.52	0.9925
72	49.77	0.9889	51.54	0.9925

.

Larger images usually contain more details and textures, which can provide more realistic information for the super-resolution algorithm and help to generate more accurate high-resolution details. The computational complexity of the Vision Transformer is proportional to the square of the image size, and it requires more computational resources and time to deal with larger images. Therefore, it is particularly important to select the appropriate image size in the model training.

6. Conclusions

In this article, we proposed a Multi-Attention Multi-Image Super-Resolution Transformer (MAST), a novel multi-image super-resolution network of remote sensing, which is innovative in two aspects. Firstly, we introduced the MMAB for deep feature extraction. Through the design of a multi-scale architecture, we enhanced the network’s ability to capture features at various scales. Additionally, we employed a method of mixed attention to guide the network in exploring high-frequency features across both channel and spatial dimensions. Through these improvements, the network’s capability to extract complementary high-frequency information from multiple images was elevated. Secondly, we presented the CAFB for feature fusion. By incorporating channel attention within the Transformer architecture, the MISR model gained the ability to effectively harness correlation information among multiple images. Furthermore, the introduction of RLAB enhanced the network’s capacity to discern local intricate features. These combined enhancements empowered the network to achieve a harmonious equilibrium between the utilization of local and global information during fusion. On the PROBA-V dataset, MAST achieved cPSNR values of 49.63 dB and 51.48 dB for the NIR and RED bands, respectively, along with cSSIM values of 0.9884 and 0.9924, demonstrating state-of-the-art super-resolution performance. The extensive experiments validated the superiority of MAST compared to other advanced methods. In the future, our work will focus on establishing more accurate registration mechanisms to further improve the super-resolution results of multiple images by reducing registration errors.