A Remote Sensing Image Quality Interpretation Scale Characterization Method Based on the TTP Criterion
Abstract
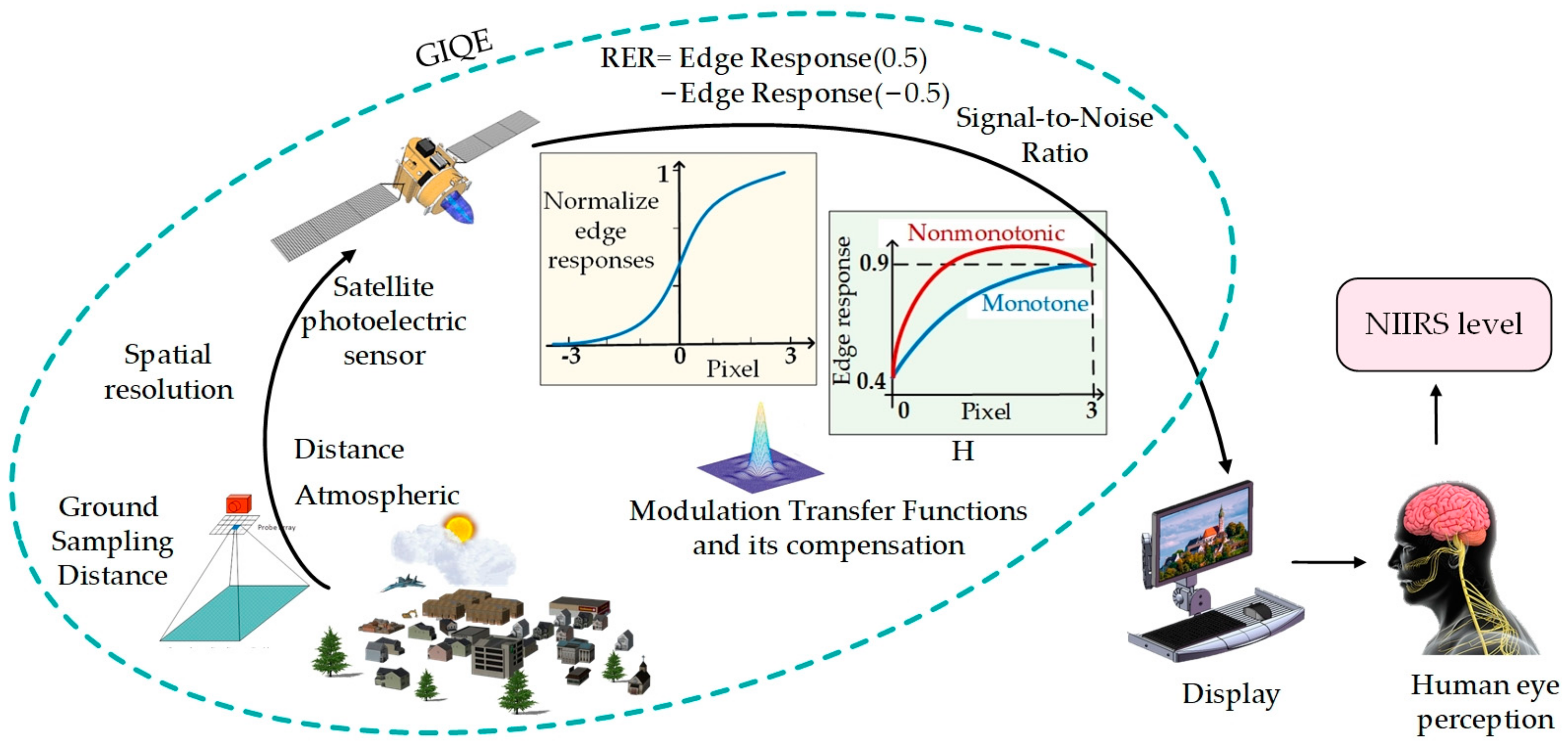
1. Introduction
2. Deficiencies of the GIQE
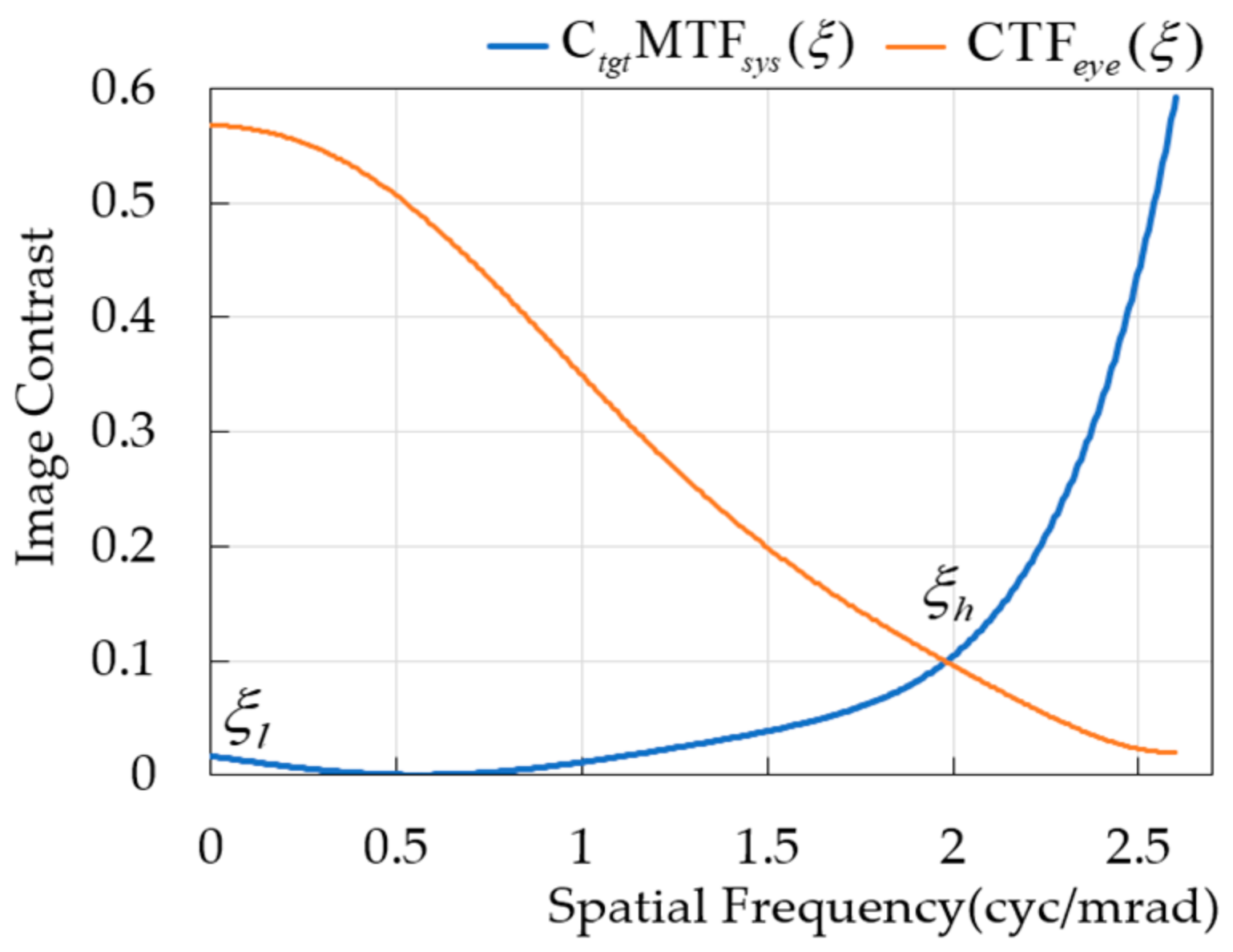
3. Theoretical Basis for the Introduction of the TTP Criterion
4. New Quality Equation for Remote Sensing Images
4.1. Construction of the New Model
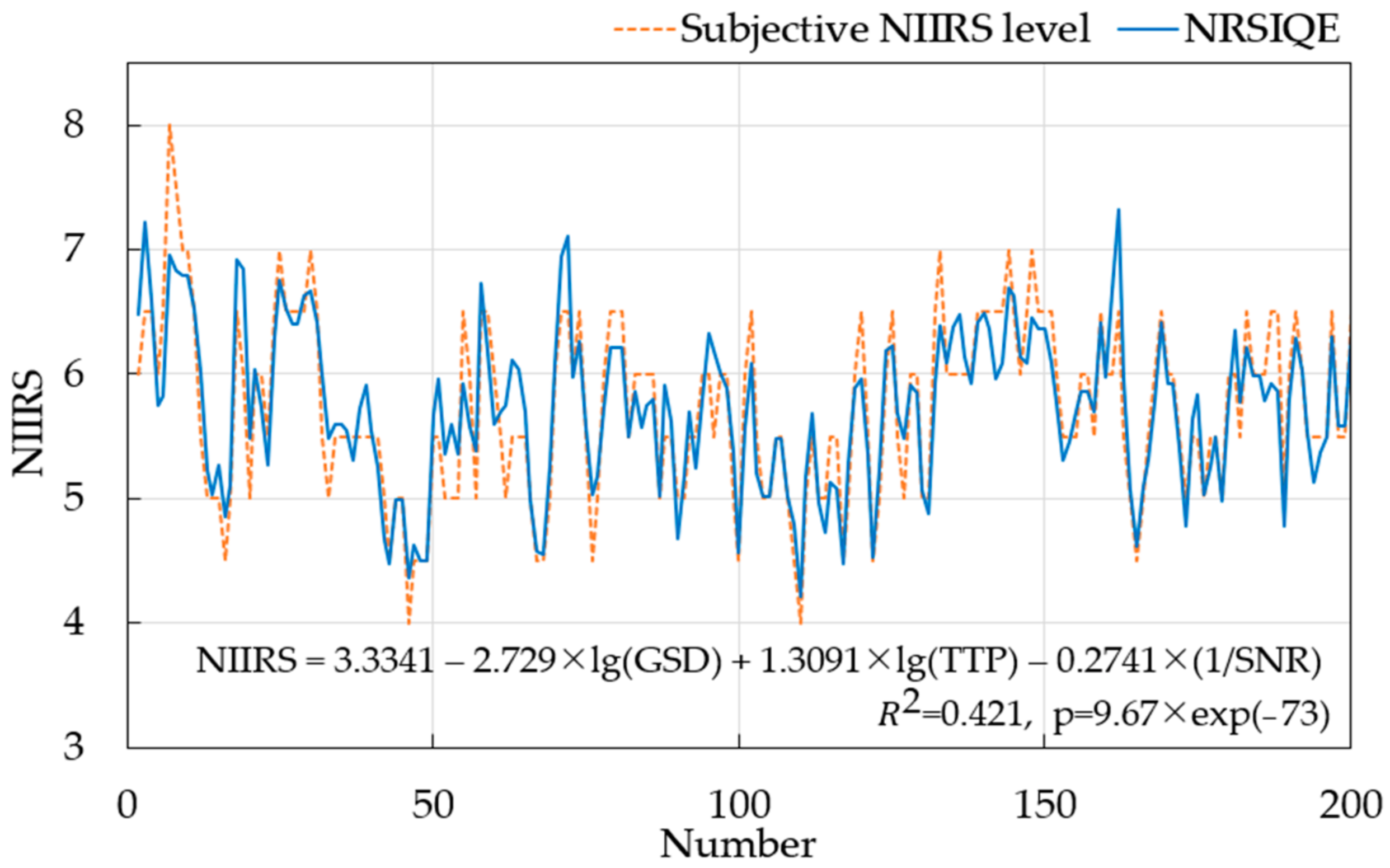
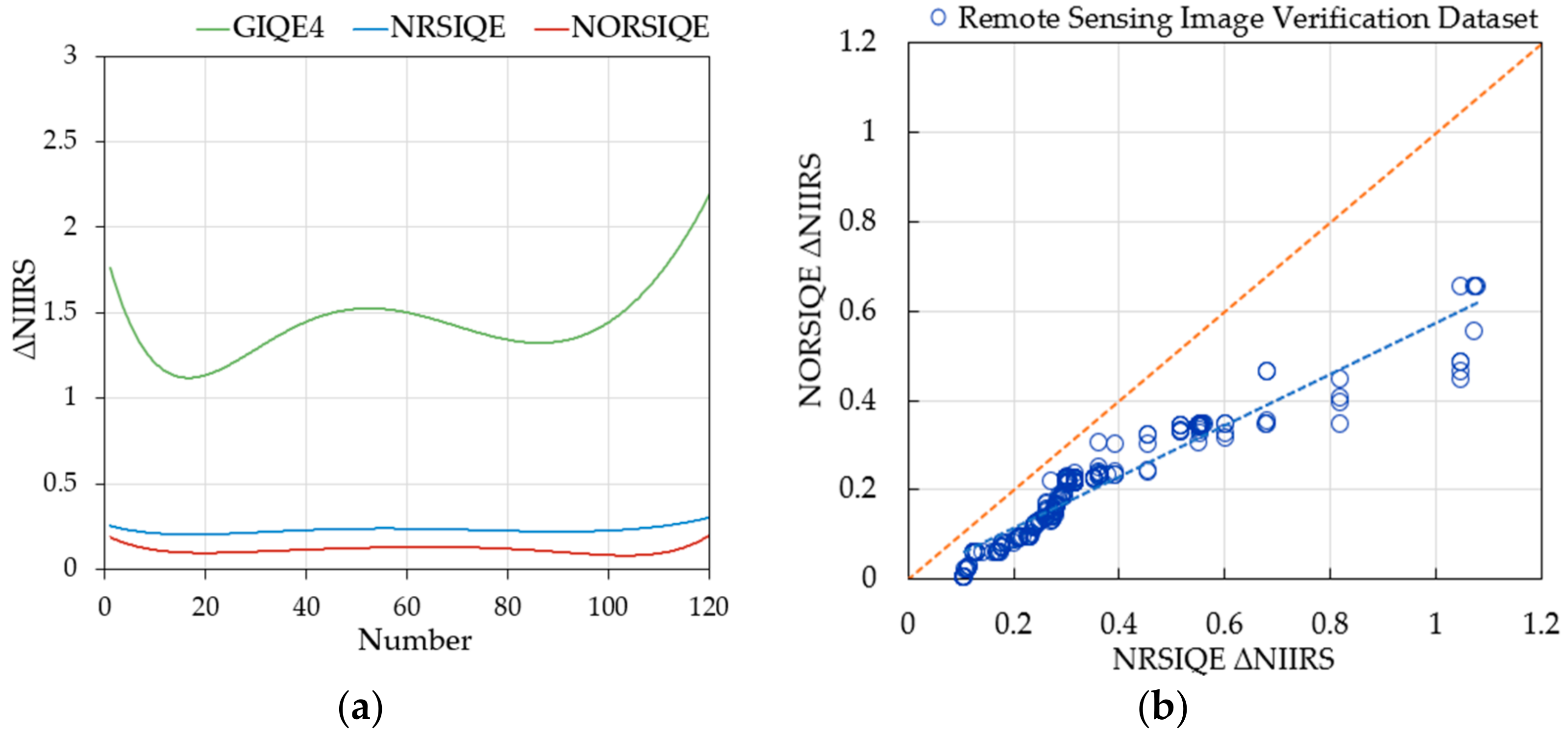
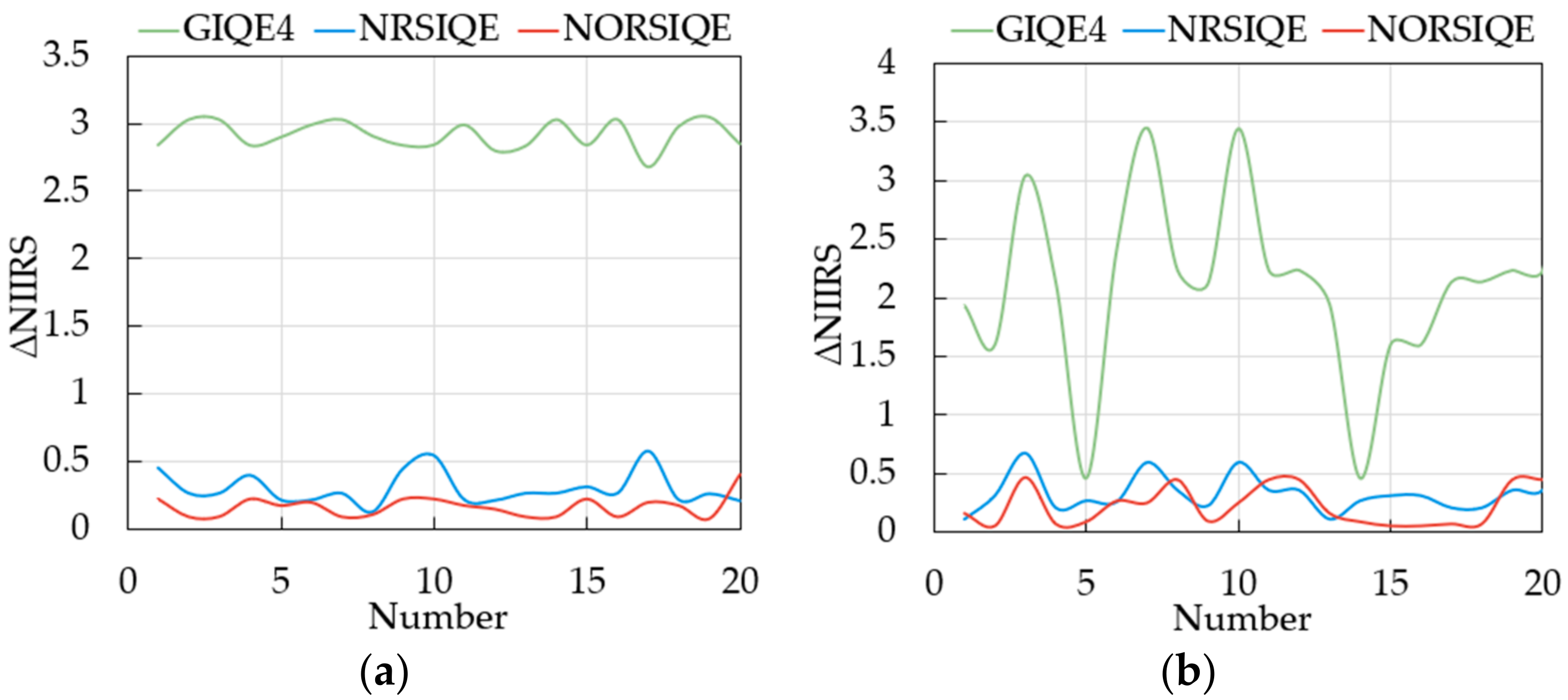
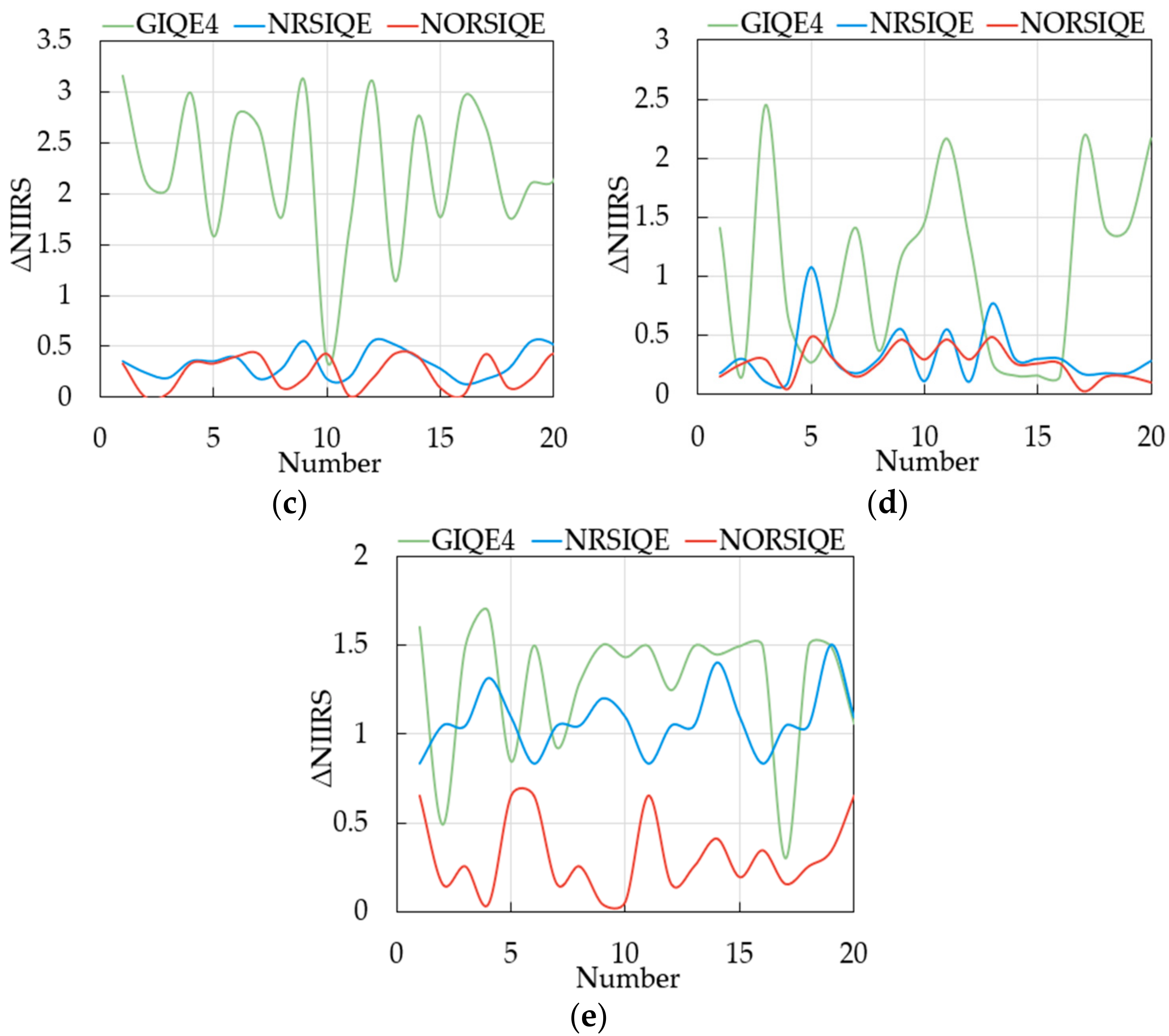
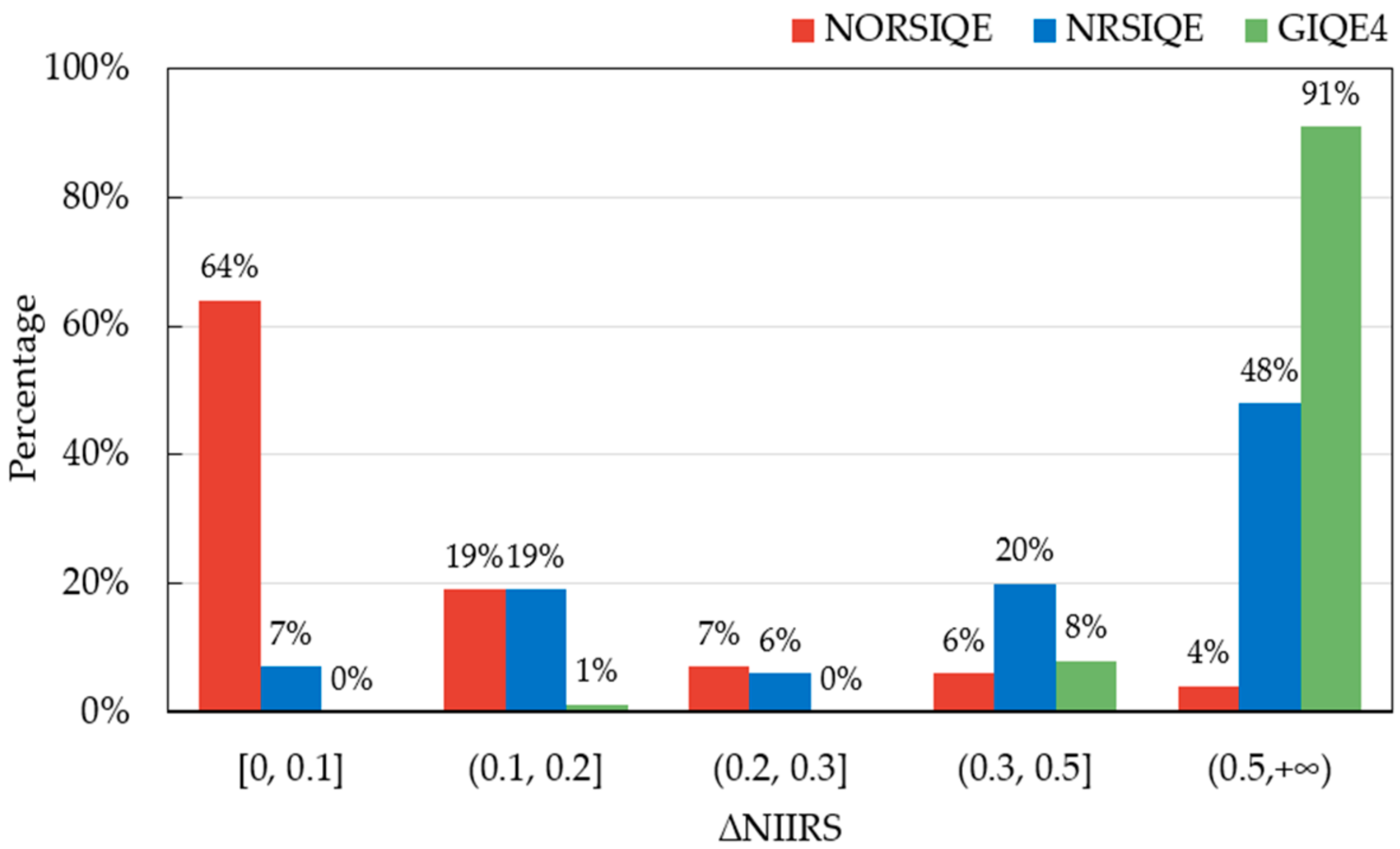
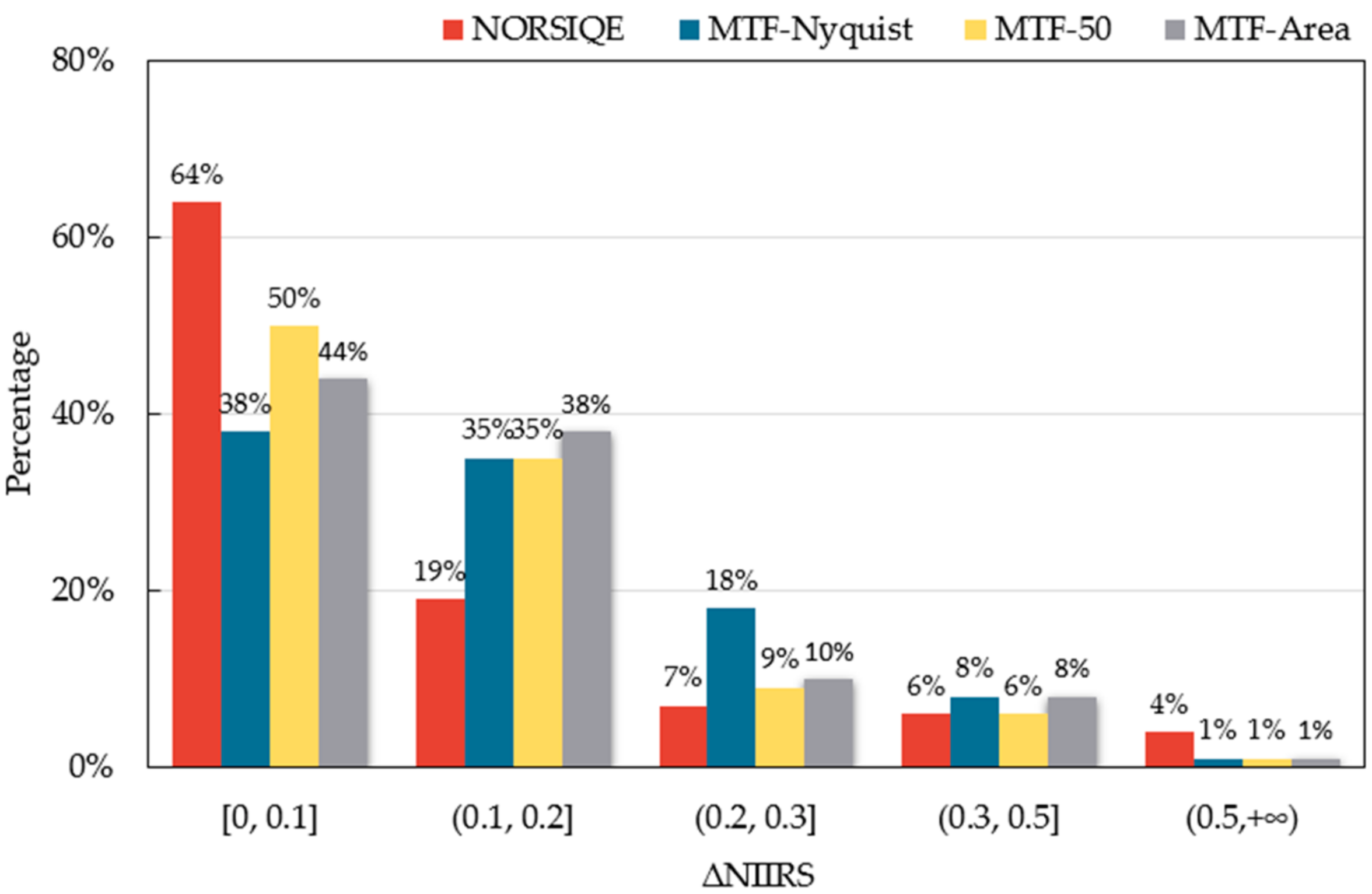
4.2. Verification of the New Model
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhou, J.; Ruwei, D.; Baihua, X. Overview of Research on Image Quality Evaluation. Comput. Sci. 2008, 35, 1–4. [Google Scholar]
- Lu, M. Research on Remote Sensing Image Quality Evaluation Methods; Harbin Institute of Technology: Harbin, China, 2013. [Google Scholar]
- Yin, L.Z.; Zhu, J.; Cai, G.L.; Wang, J.H. A review of remote sensing image quality evaluation methods. Mapp. Spat. Geogr. Inf. 2014, 37, 32–35+45. [Google Scholar]
- Zhang, W.; Wang, Y. High order statistics and evaluation of edge structure similarity image quality. J. Xi’an Univ. Technol. 2016, 36, 173–176. [Google Scholar]
- Qin, C.; Li, X. Color image quality evaluation algorithm based on frequency domain histogram and HVS. Telev. Technol. 2015, 39, 28–33. [Google Scholar]
- Liu, L.; Wang, Y.; Wu, Y. A Wavelet-Domain Structure Similarity for Image Quality Assessment. In Proceedings of the International Congress on Image and Signal Processing, Tianjin, China, 17–19 October 2009; IEEE: Piscataway, NJ, USA; pp. 1–5. [Google Scholar]
- Wei, X.; Li, J.; Chen, G. An image perception quality evaluation model. J. Comput. Aided Des. Graph. 2007, 19, 1540–1545. [Google Scholar]
- Liu, S.; Wu, L.; Gong, Y.; Liu, X. A review of image quality evaluation. China Sci. Technol. Pap. Online 2011, 6, 501–506+523. [Google Scholar]
- Jiang, G.; Huang, D.; Wang, X.; Yu, M. Research progress of image quality evaluation methods. J. Electron. Inf. 2010, 32, 219–226. [Google Scholar] [CrossRef]
- Leachtenauer, J.C.; Driggers, R.G. Surveillance and Reconnaissance Imaging System (Model and Performance Prediction); China Science and Technology Press: Beijing, China, 2007. [Google Scholar]
- Yang, F. Research on Radiation Quality Evaluation and Influencing Factors of High-Resolution Remote Sensing Images Based on Synchronous Observation; Wuhan University: Wuhan, China, 2016. [Google Scholar]
- Hu, A. Research on Subjective and Objective Consistency in Image Perception Quality Evaluation Methods; University of Science and Technology of China: Hefei, China, 2014. [Google Scholar]
- Li, L. Research on Remote Sensing Image Quality Evaluation Method Combining Subjective and Objective Methods; Nanjing University of Science and Technology: Nanjing, China, 2013. [Google Scholar]
- Liu, X.; Ren, X.; Zheng, Y.; Hu, T. Correlation analysis of subjective and objective evaluation of image fusion quality. J. Shenzhen Inst. Inf. Technol. 2011, 9, 23–30. [Google Scholar]
- Driggers, R.G.; Cox, P.; Kelley, M. National imagery interpretation rating system and the probabilities of detection, recognition, and identification. Opt. Eng. 1997, 36, 1952–1959. [Google Scholar] [CrossRef]
- Irvine, J.M. National imagery interpretability rating scales (NIIRS): Overview and methodology. In Airborne Reconnaissance XXI; SPIE: Cergy-Pontoise, France, 1997; Volume 3128, pp. 93–103. [Google Scholar]
- Shi, H.; Chen, S. A remote sensing image quality standard for user mission requirements-NIIRS. Space Return Remote Sens. 2003, 24, 30–35. [Google Scholar]
- Bai, H. Research on Image Quality Prediction and Evaluation Method of Remote Sensing System Based on NIIRS; Xi’an University of Electronic Science and Technology: Xi’an, China, 2010. [Google Scholar]
- Leachtenauer, J.C. Image Quality Equation and NIIRS. In Encyclopedia of Optical Engineering; CRC Press: Boca Raton, FL, USA, 2003; pp. 794–811. [Google Scholar]
- Leachtenauer, J.C.; Malila, W.; Irvine, J.; Colburn, L.; Salvaggio, N. General Image-Quality Equation: GIQE. Appl. Opt. 1997, 36, 8322–8328. [Google Scholar] [CrossRef] [PubMed]
- Thurman, S.T.; Fienup, J.R. Analysis of the general image quality equation. In Visual Information Processing XVI; SPIE: Cergy-Pontoise, France, 2008; Volume 6978, pp. 73350L-1–73350L-9. [Google Scholar]
- Irvine, J.M.; Nelson, E. Image quality and performance modeling for automated target detection. In Automatic Target Recognition XIX; SPIE: Cergy-Pontoise, France, 2009; Volume 7335, pp. 73350L-1–73350L-9. [Google Scholar]
- Cota, S.A.; Florio, C.J.; Duvall, D.J.; Leon, M.A. The Use of the General Image Quality Equation in the Design and Evaluation of Imaging Systems. In Remote Sensing System Engineering II; SPIE: Cergy-Pontoise, France, 2009; Volume 7458, pp. 74580H-1–74580H-20. [Google Scholar]
- Hindsley, R.; Rickard, L. The General Image Quality Equation and the structure of the modulation transfer function. In New Frontiers in Stellar Interferometry; SPIE: Cergy-Pontoise, France, 2004; Volume 5491, pp. 1557–1562. [Google Scholar]
- Harrington, L.; Blanchard, D.; Salacain, J.M.; Smith, S.J.; Amanik, P.S. General Image Quality Equation; GIQE Version 5; National Geospatial-Intelligence Agency: Springfield, VA, USA, 2015. [Google Scholar]
- Jason, M. Back-of-the-envelope image quality estimation using the national image interpretability rating scale: Erratum. Appl. Opt. 2019, 58, 8839. [Google Scholar]
- Lemaster Daniel, A. Airborne validation of the general image quality equation 5. Appl. Opt. 2020, 59, 9978–9984. [Google Scholar] [CrossRef] [PubMed]
- Valenzuela, A.Q.; Reyes, J.C.G. Comparative study of the different versions of the general image quality equation. SPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2019, IV–2/W5, 493–500. [Google Scholar] [CrossRef]
- Bai, J.; Sun, Y.; Chen, L.; Feng, Y.; Liu, J. EO Sensor Planning for UAV Engineering Reconnaissance Based on NIIRS and GIQE. Math. Probl. Eng. 2018, 2018, 6837014. [Google Scholar] [CrossRef]
- Lin, L.; Heng, L.; Haihong, Z. Estimation of the Image Interpretability of ZY-3 Sensor Corrected Panchromatic Nadir Data. Remote Sens. 2014, 6, 4409–4429. [Google Scholar] [CrossRef]
- Zhao, P. Evaluation of the Quality of Domestic High Resolution Images Based on GIQE. Master’s Thesis, Wuhan University, Wuhan, China, 2020. [Google Scholar]
- Vollmerhausen, R.H.; Jacobs, E. The Targeting Task Performance (TTP) Metric a New Model for Predicting Target Acquisition Performance; Technical Report AMSEL-NV-TR-230; US Army CERDEC: Fort Belvoir, VA, USA, 2004; p. 22060. [Google Scholar]
- Vollmerhausen, R.H.; Jacobs, E.; Driggers, R.G. New Metirc for Predicting Target Acquisition Performance. Opt. Eng. 2004, 43, 2806–2818. [Google Scholar] [CrossRef]
- He, L. Research on Target Mission Performance Evaluation Based on TTP Criteria; Xi’an University of Electronic Science and Technology: Xi’an, China, 2010. [Google Scholar]
- Bai, H.; Wang, X. A Quantitative Study on the Relationship between NIIRS and Target Task Performance Prediction. In Proceedings of 2011 Western Photonics Academic Conference Abstract Collection, San Francisco, CA, USA, 22–27 January 2011; Shaanxi Optical Society: Xi’an, China; High Speed Photography and Photonics Professional Committee of the Chinese Optical Society: Beijing, China, 2011; p. 22. [Google Scholar]
- Chen, Y.; Jin, W.; Zhao, L.; Zhao, L. A new method for infrared system evaluation based on target mission performance. Opt. Technol. 2008, 4, 555–559. [Google Scholar]
- Guo, L. Research on Performance Evaluation Technology of Infrared Imaging System Based on TTP Criteria; Harbin industrial University: Harbin, China, 2021. [Google Scholar]
- Barten Peter, G.J. The Square Root Integral (SQRI): A New Metric To Describe The Effect Of Various Display Parameters On Perceived Image Quality. In Human Vision, Visual Processing, and Digital Display; SPIE: Cergy-Pontoise, France, 1989; Volume 1077. [Google Scholar]

| Type | Date | Time | Location | Spatial Resolution | Subjective NIIRS Level |
|---|---|---|---|---|---|
| XX_1 | 2019.07.19 | 09:24:06 | E_118°07′14″, N_32°27′21″ | 6.80 inches | 4 |
| XX_1 | 2019.06.24 | 16:18:30 | E_119°46′41″, N_31°22′34″ | 25.78 inches | 5 |
| XX_2 | 2013.09.15 | 09:00:00 | E_117°12′17″, N_23°33′42″ | 6.99 inches | 7 |
| XX_2 | 2018.07.05 | 08:22:09 | E_117°39′45″, N_24°33′42″ | 7.22 inches | 7 |
| XX_2 | 2021.03.23 | 15:22:06 | E_120°06′07″, N_30°57′32″ | 2.72 inches | 7 |
| XX_3 | 2018.02.08 | 16:36:26 | E_120°06′07″, N_30°57′32″ | 3.27 inches | 5 |
| XX_3 | 2019.06.14 | 13:50:50 | E_120°06′04″, N_30°06′04″ | 1.46 inches | 6 |
| XX_3 | 2020.02.11 | 13:35:23 | E_123°03′01″, N_41°52′10″ | 4.20 inches | 6 |
| Equation | c1 | c2 | c3 | c4 f(x) | R2 | p | RMSE |
|---|---|---|---|---|---|---|---|
| NRSIQE | 3.3341 | −2.7291 | 1.3091 | −0.2741/SNR | 0.793 | 9.67 × 10−73 | 0.421 |
| NORSIQE | 4.6366 | −3.2058 | 0.5996 | 3.5611 lg(SNR) | 0.916 | 6.54 × 10−106 | 0.204 |
| Error Indicator | Subjective NIIRS Level | GIQE4 | NRSIQE | NORSIQE |
|---|---|---|---|---|
| RMSE | 4 | 2.919 | 0.302 | 0.164 |
| 5 | 2.205 | 0.340 | 0.234 | |
| 6 | 2.346 | 0.343 | 0.259 | |
| 7 | 1.315 | 0.379 | 0.271 | |
| 8 | 1.339 | 1.039 | 0.324 | |
| ---- | 2.025 | 0.481 | 0.250 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Wang, X.; Zhang, C. A Remote Sensing Image Quality Interpretation Scale Characterization Method Based on the TTP Criterion. Remote Sens. 2023, 15, 4121. https://doi.org/10.3390/rs15174121
Li Y, Wang X, Zhang C. A Remote Sensing Image Quality Interpretation Scale Characterization Method Based on the TTP Criterion. Remote Sensing. 2023; 15(17):4121. https://doi.org/10.3390/rs15174121
Chicago/Turabian StyleLi, Yue, Xiaorui Wang, and Chao Zhang. 2023. "A Remote Sensing Image Quality Interpretation Scale Characterization Method Based on the TTP Criterion" Remote Sensing 15, no. 17: 4121. https://doi.org/10.3390/rs15174121
APA StyleLi, Y., Wang, X., & Zhang, C. (2023). A Remote Sensing Image Quality Interpretation Scale Characterization Method Based on the TTP Criterion. Remote Sensing, 15(17), 4121. https://doi.org/10.3390/rs15174121






