Joint Direction of Arrival-Polarization Parameter Tracking Algorithm Based on Multi-Target Multi-Bernoulli Filter
Abstract
1. Introduction
- Investigation of joint DOA-polarization parameter estimation based on a uniform linear array. The proposed algorithm considers the variations of DOA and polarization parameters with the motion of the signal source carrier, establishing state models for the target’s state and a measurement model for the polarization-sensitive array.
- Introduction of a method for adaptive estimation of the number of sources using a polarization-sensitive array and MDL principle. This method effectively estimates the number of sources by incorporating the characteristics of the steering vector and provides prior information for subspace partitioning.
- Development of a SMC implementation of MeMBer filter for tracking the joint DOA-polarization parameters. The proposed method replaces the likelihood function with the joint parameters’ MUSIC spatial spectrum, which exhibits high spectral peaks when approaching the true state. By distinguishing different peak values, the approach approximates the target state.
2. Background
2.1. RFS Theory
2.2. Multi-Bernoulli Filter
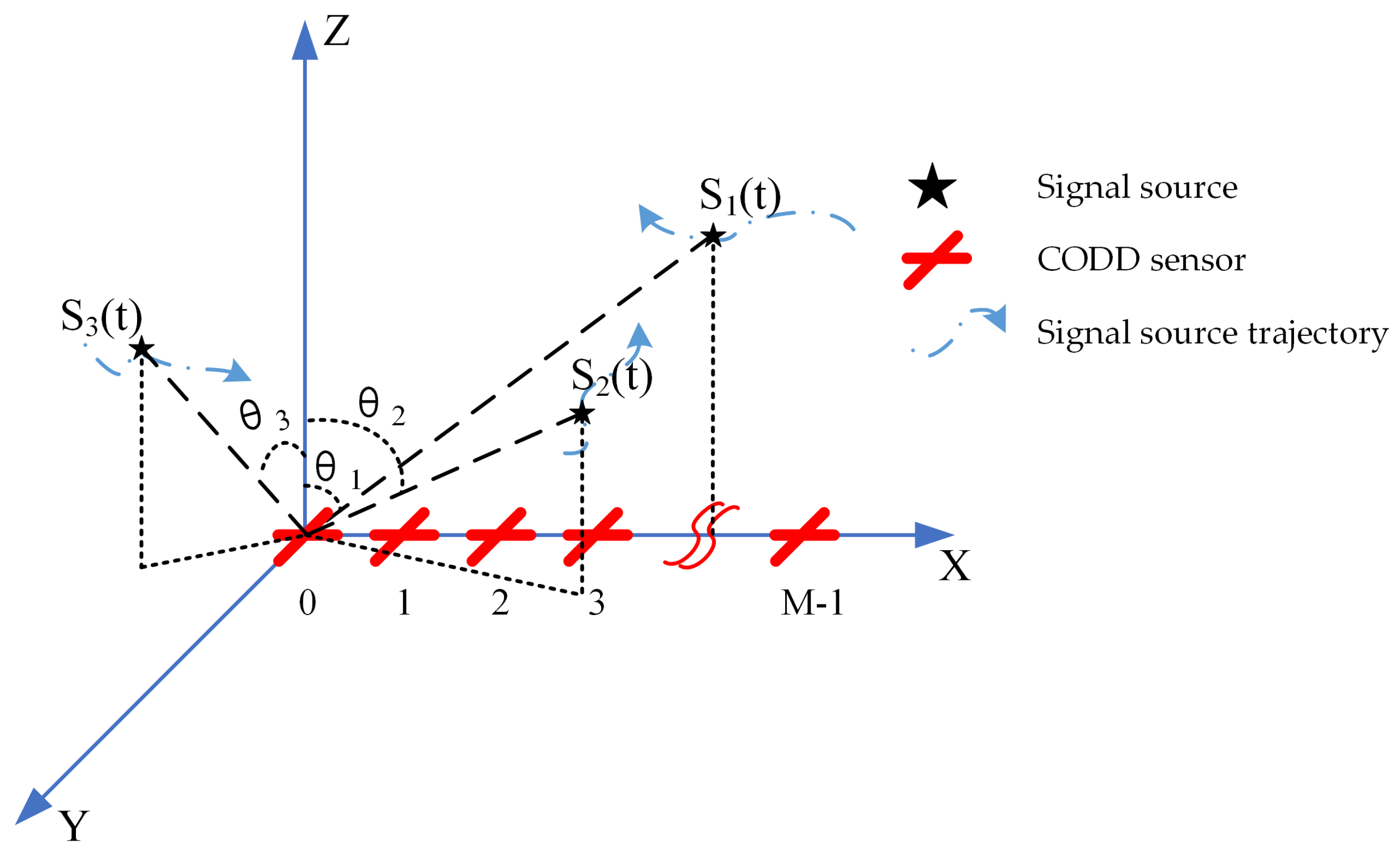
2.3. Signal and Array Models
3. Joint DOA-Polarization Parameter Tracking Algorithm Based on MeMBer
3.1. Estimation Algorithm of the Number of Sources
3.2. The Likelihood Function
3.3. SMC Implementation of MeMBer Joint DOA-Polarization Parameter Tracking
| Algorithm 1 MeMBer joint DOA-polarization parameters particle filter tracking algorithm |
| Input: Prediction
State extraction: Output: |
4. Simulation Analysis
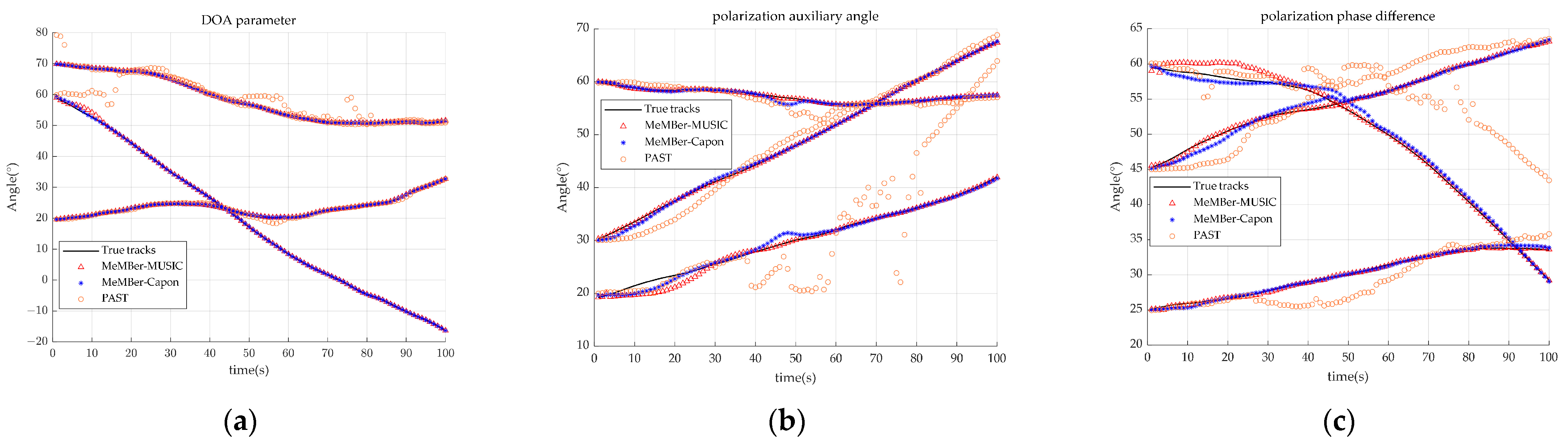
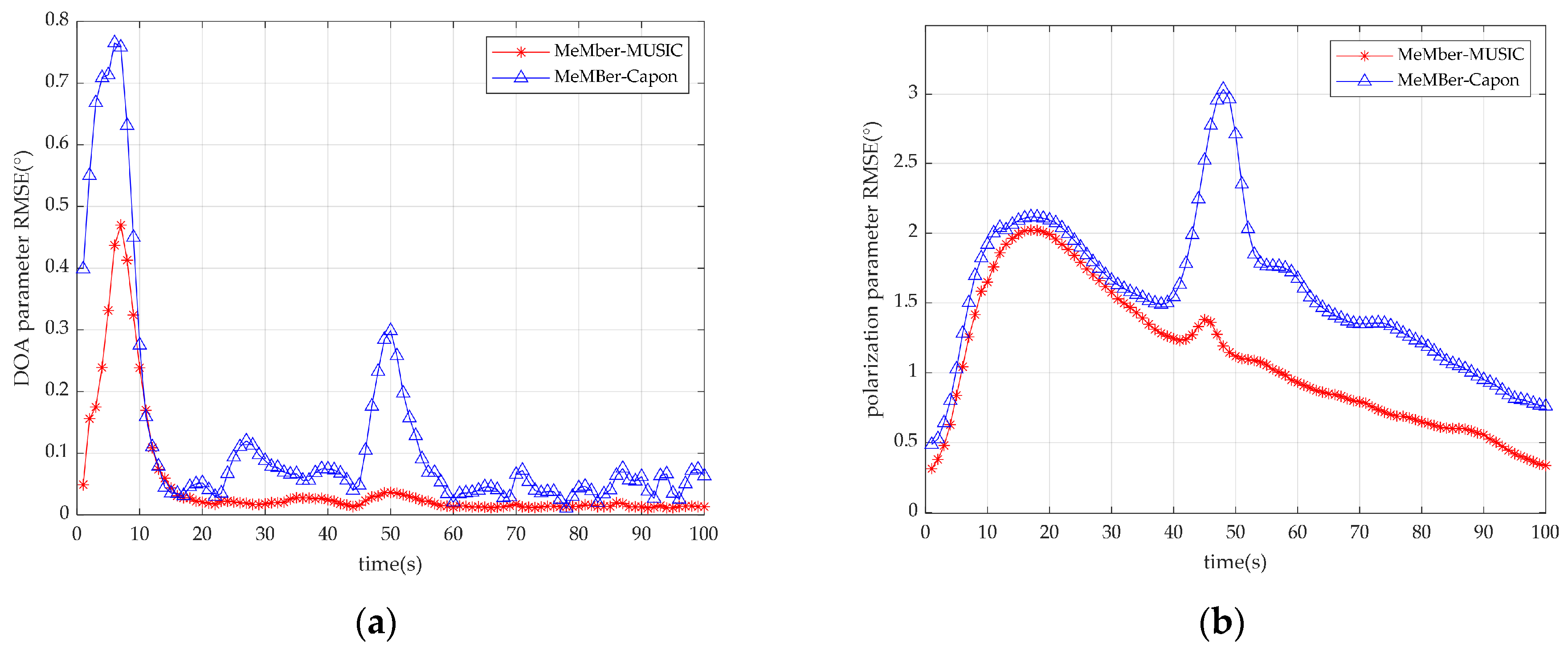
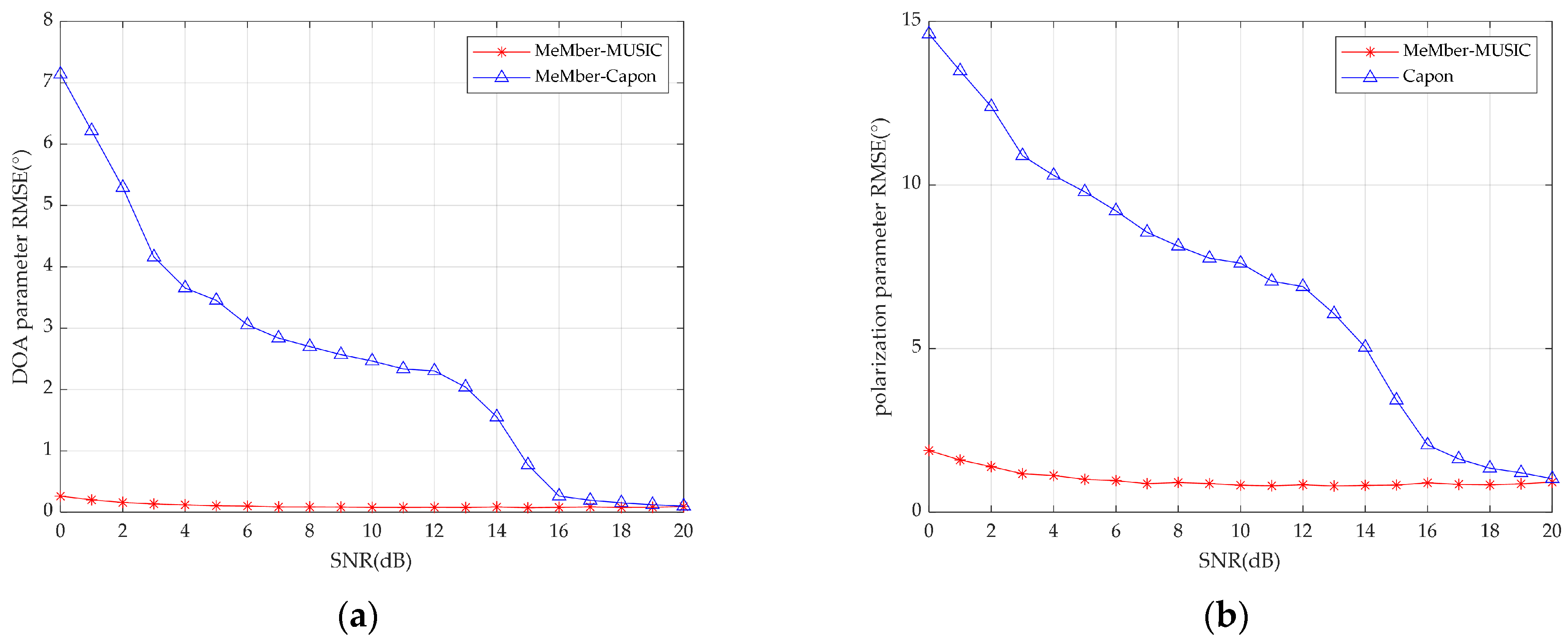
4.1. Joint DOA-Polarization Parameter Tracking with the Fixed Source Number
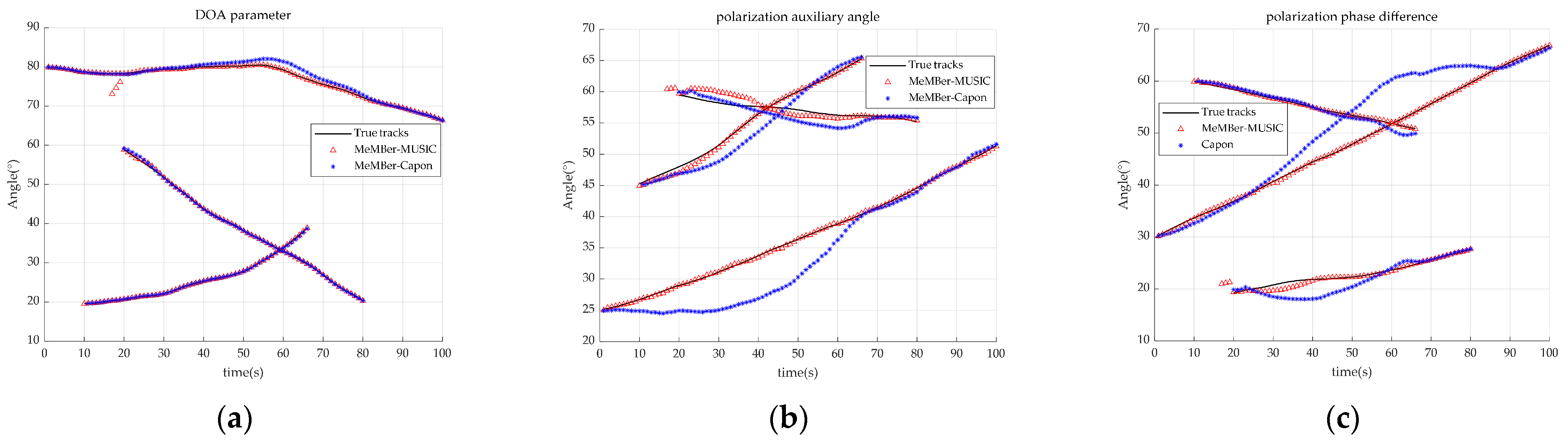
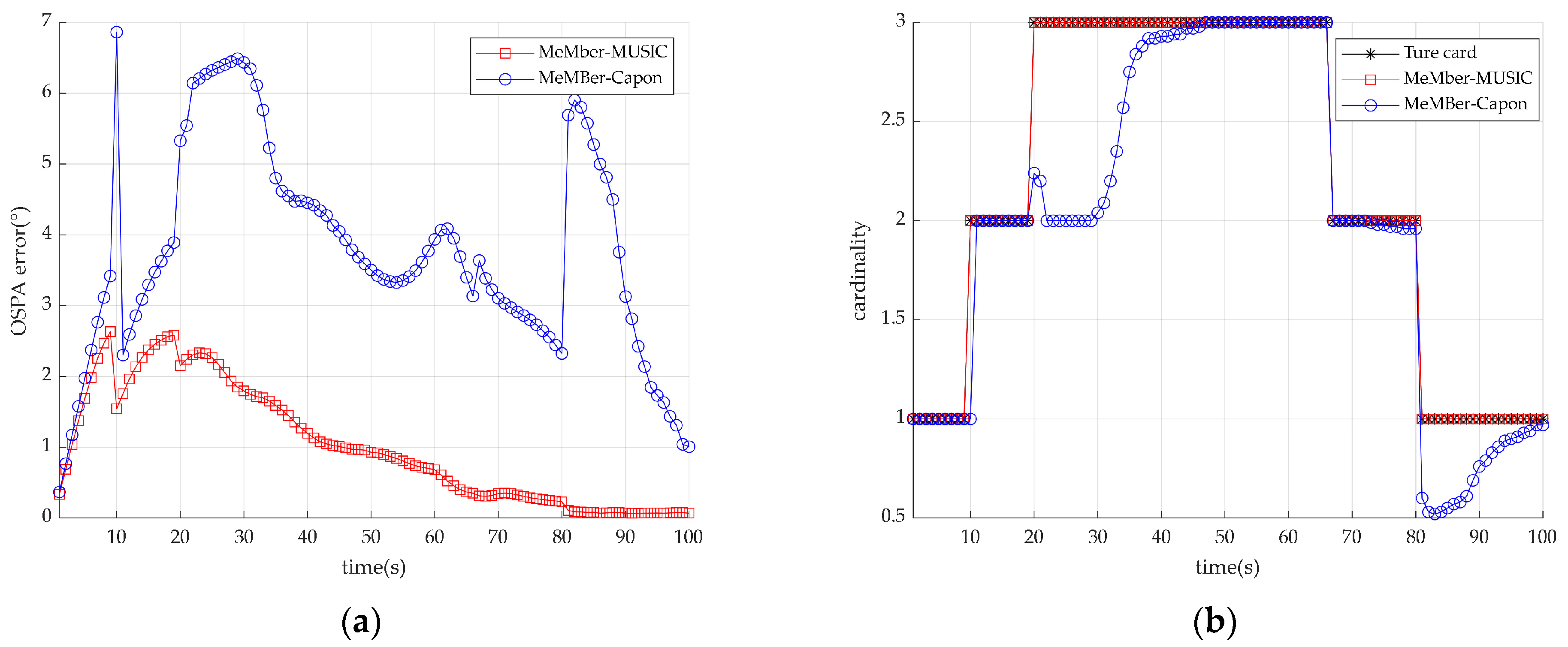
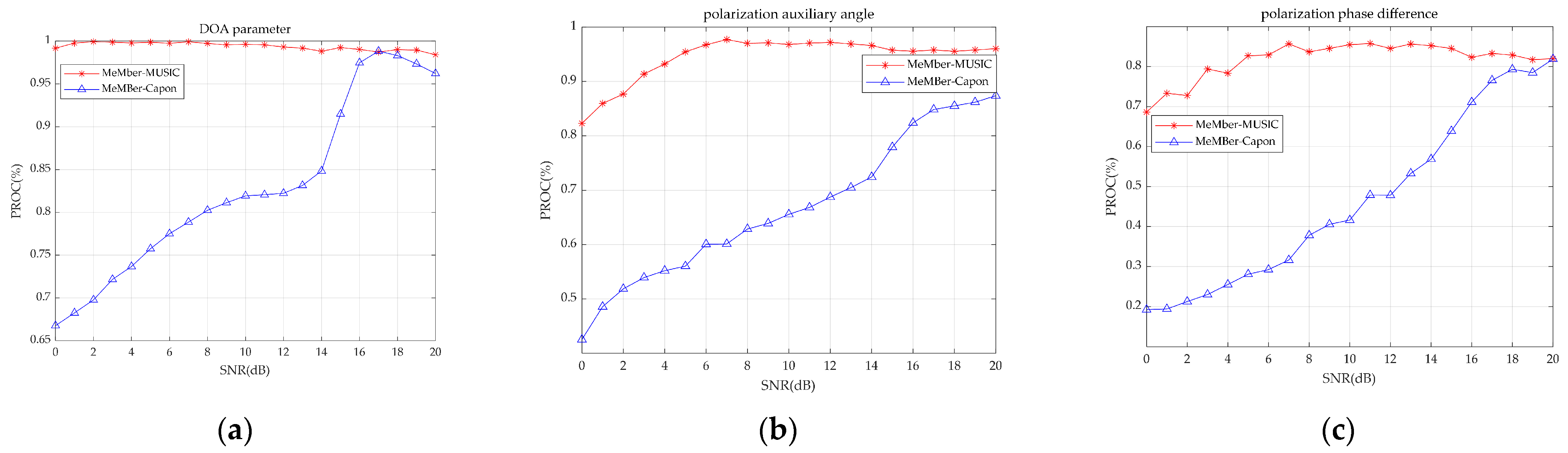
4.2. Joint DOA-Polarization Parameter Tracking with the Time-Varying Source Number
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Schmidt, R. Multiple emitter location and signal parameter estimation. IEEE Trans. Antennas Propag. 1986, 34, 1668–1676. [Google Scholar] [CrossRef]
- Ateşavcı, C.S.; Bahadırlar, Y.; Aldırmaz-Çolak, S. DoA Estimation in the Presence of Mutual Coupling Using Root-MUSIC Algorithm. In Proceedings of the 2021 8th International Conference on Electrical and Electronics Engineering (ICEEE), Antalya, Turkey, 9–11 April 2021. [Google Scholar]
- Yin, D.; Zhang, F. Uniform linear array MIMO radar unitary root MUSIC Angle estimation. In Proceedings of the 2020 Chinese Automation Congress (CAC), Shanghai, China, 6–8 November 2020. [Google Scholar]
- Li, J.; Li, D.; Jiang, D.; Zhang, X. Extended-Aperture Unitary Root MUSIC-Based DOA Estimation for Coprime Array. IEEE Commun. Lett. 2018, 22, 752–755. [Google Scholar] [CrossRef]
- Roy, R.; Kailath, T. ESPRIT-estimation of signal parameters via rotational invariance techniques. IEEE Trans. Acoust. Speech Signal Process. 1989, 37, 984–995. [Google Scholar] [CrossRef]
- Stoica, P.; Nehorai, A. MUSIC, maximum likelihood and Cramer-Rao bound. IEEE Trans. Acoust. Speech Signal Process. 1989, 37, 720–741. [Google Scholar] [CrossRef]
- Meng, D.; Wang, X.; Huang, M.; Wan, L.; Zhang, B. Robust Weighted Subspace Fitting for DOA Estimation via Block Sparse Recovery. IEEE Commun. Lett. 2020, 24, 563–567. [Google Scholar] [CrossRef]
- Tong, Y.; Zuo, W.; Xin, J.; Zheng, N.; Sano, A. Direction-of-Arrival and Range Estimation of Near-Field Sources Based on Subspace Fitting. In Proceedings of the 2021 China Automation Congress (CAC), Beijing, China, 22–24 October 2021. [Google Scholar]
- Yang, B. Projection approximation subspace tracking. IEEE Trans. Signal Process. 1995, 4, 95–107. [Google Scholar] [CrossRef]
- Orton, M.; Fitzgerald, W. A Bayesian approach to tracking multiple targets using sensor arrays and particle filters. IEEE Trans. Signal Process. 2002, 50, 216–223. [Google Scholar] [CrossRef]
- Mahler, R.P.S. Multitarget Bayes filtering via first-order multitarget moments. IEEE Trans. Aerosp. Electron. Syst. 2003, 39, 1152–1178. [Google Scholar] [CrossRef]
- Vo, B.T.; Vo, B.N. A random finite set conjugate prior and application to multi-target tracking. In Proceedings of the 2011 Seventh International Conference on Intelligent Sensors, Sensor Networks and Information Processing, Adelaide, SA, Australia, 6–9 December 2011. [Google Scholar]
- Vo, B.T.; Vo, B.N.; Cantoni, A. Analytic Implementations of the Cardinalized Probability Hypothesis Density Filter. IEEE Trans. Signal Process. 2007, 55, 3553–3567. [Google Scholar] [CrossRef]
- Nannuru, S.; Coates, M.; Mahler, R. Computationally-Tractable Approximate PHD and CPHD Filters for Superpositional Sensors. IEEE J. Sel. Top. Signal Process. 2013, 7, 410–420. [Google Scholar] [CrossRef]
- Saucan, A.A.; Chonavel, T.; Sintes, C. CPHD-DOA Tracking of Multiple Extended Sonar Targets in Impulsive Environments. IEEE Trans. Signal Process. 2016, 64, 1147–1160. [Google Scholar] [CrossRef]
- Choppala, P.B.; Teal, P.D.; Frean, M.R. Adapting the multi-Bernoulli filter to phased array observations using MUSIC as pseudo-likelihood. In Proceedings of the 17th International Conference on Information Fusion (FUSION), Salamanca, Spain, 7–10 July 2014. [Google Scholar]
- Wu, S.Y.; Zou, B.H.; Xue, Q.T. DOA tracking algorithm based on single snapshot spatial smoothing with multi-Bernoulli. Syst. Eng. Electron. 2021, 43, 2430–2438. [Google Scholar]
- Zhao, J.; Gui, R.; Dong, X.; Wu, S. Time-Varying DOA Tracking Algorithm Based on Generalized Labeled Multi-Bernoulli. IEEE Access 2021, 9, 5943–5950. [Google Scholar] [CrossRef]
- Zhao, J.; Gui, R.; Dong, X. A new measurement association mapping strategy for DOA tracking—ScienceDirect. Digit. Signal Process. 2021, 118, 103228. [Google Scholar] [CrossRef]
- Ferrara, E.; Parks, T. Direction finding with an array of antennas having diverse polarizations. IEEE Trans. Antennas Propag. 1983, 31, 231–236. [Google Scholar] [CrossRef]
- Wong, K.T.; Zoltowski, M.D. Self-initiating MUSIC-based direction finding and polarization estimation in spatio-polarizational beamspace. IEEE Trans. Antennas Propag. 2000, 48, 1235–1245. [Google Scholar]
- Yuan, Q.W.; Chen, Q.; Sawaya, K. MUSIC based DOA finding and polarization estimation using USV with polarization sensitive array antenna. In Proceedings of the 2006 IEEE Radio and Wireless Symposium, San Diego, CA, USA, 17–19 October 2006. [Google Scholar]
- Cheng, Q.; Hua, Y.B. Further study of the Pencil-MUSIC algorithm. IEEE Trans. Aerosp. Electron. Syst. 1996, 32, 284–299. [Google Scholar] [CrossRef]
- Wong, K.T.; Zoltowski, M.D. Polarization-beamspace self-initiating MUSIC for azimuth/elevation angle estimation. In Proceedings of the Radar 97 (Conference Publication Number 449), Edinburgh, UK, 14–16 October 1997. [Google Scholar]
- Li, J.; Compton, R.T. Angle estimation using a polarization sensitive array. In Proceedings of the Antennas and Propagation Society Symposium 1991 Digest, London, ON, Canada, 24–28 June 1991. [Google Scholar]
- Chen, F.J.; Kwong, S.; Kok, C.W. Two-dimensional angle and polarization estimation using ESPRIT without pairing. In Proceedings of the 2006 IEEE International Symposium on Circuits and Systems (ISCAS), Kos, Greece, 21–24 May 2006. [Google Scholar]
- Lin, C.H.; Fang, W.H.; Yang, W.S.; Line, J.D. SPS-ESPRIT for joint DOA and polarization estimation with a COLD array. In Proceedings of the 2007 IEEE Antennas and Propagation Society International Symposium, Honolulu, HI, USA, 9–15 June 2007. [Google Scholar]
- Picheral, J.; Piqueres, F. Joint angle/Delay/Polarization Estimation by esprit-like method for multipath channel identification. In Proceedings of the 2004 12th European Signal Processing Conference, Vienna, Austria, 6–10 September 2004. [Google Scholar]
- Sam, K.; Fei, J. Frequency and 2D Angle Estimation Based on a Sparse Uniform Array of Electromagnetic Vector Sensors. Eurasip J. Adv. Signal Process. 2006, 2006, 1–9. [Google Scholar]
- Friedlander, B.; Weiss, A.J. A direction finding algorithm for diversely polarized arrays. Digit. Signal Process. 2000, 2, 123–134. [Google Scholar] [CrossRef]
- Wong, K.T.; Li, L.S.; Zoltowski, M.D. Root-MUSIC-based direction-finding and polarization estimation using diversely polarized possibly collocated antennas. IEEE Antennas Wirel. Propag. Lett. 2004, 3, 129–132. [Google Scholar] [CrossRef]
- Belloni, F.; Richter, A.; Koivunen, V. Performance of root-MUSIC algorithm using real-world arrays. In Proceedings of the 2006 14th European Signal Processing Conference, Florence, Italy, 4–8 September 2006. [Google Scholar]
- Qiu, S.; Sheng, W.; Ma, X.; Kirubarajan, T. A Maximum Likelihood Method for Joint DOA and Polarization Estimation Based on Manifold Separation. IEEE Trans. Aerosp. Electron. Syst. 2021, 57, 2481–2500. [Google Scholar] [CrossRef]
- Chalise, B.K.; Zhang, Y.D.; Himed, B. Compressed Sensing based Joint Doa and Polarization Angle Estimation for Sparse Arrays with Dual-Polarized Antennas. In Proceedings of the 2018 IEEE Global Conference on Signal and Information Processing (GlobalSIP), Anaheim, CA, USA, 26–29 November 2018. [Google Scholar]
- Shao, S.; Liu, A.; Yu, C.J.; Zhao, Q.R. Polarization quaternion DOA estimation based on vector MISC array. J. Syst. Eng. Electron. 2021, 32, 764–778. [Google Scholar]
- Wang, J.; Du, Y.; Chen, L.; Han, D. Fast algorithm of joint polarization and DOA estimation for irregular array under coherent sources. In Proceedings of the IET International Radar Conference (IET IRC 2020), Online Conference, 4–6 November 2020. [Google Scholar]
- Yue, Y.; Zhang, Z.; Zhou, C.; Xing, F.; Shi, Z. Closed-form Two-dimensional DOA and Polarization Joint Estimation Using Parallel Non-collocated Sparse COLD Arrays. In Proceedings of the 2022 IEEE 12th Sensor Array and Multichannel Signal Processing Workshop (SAM), Trondheim, Norway, 20–23 June 2022. [Google Scholar]
- He, Z.; Tian, Z.; Zhou, M.; Li, Z.; Liu, K. DOA Estimation Method for Polarization Sensitive Circular Array Based on Reduced-Dimensional MUSIC. In Proceedings of the 2022 IEEE International Symposium on Antennas and Propagation and USNC-URSI Radio Science Meeting (AP-S/URSI), Denver, CO, USA, 10–15 July 2022. [Google Scholar]
- Wax, M.; Ziskind, I. Detection of the number of coherent signals by the MDL principle. IEEE Trans. Acoust. Speech Signal Process. 1989, 37, 1190–1196. [Google Scholar] [CrossRef]
- Zhang, G.P.; Zheng, C.; Sun, S.B. Joint Detection and DOA Tracking with a Bernoulli Filter Based on Information Theoretic Criteria. Sensors 2018, 18, 3473. [Google Scholar] [CrossRef] [PubMed]
- Cappe, O.; Godsill, S.J.; Moulines, E. An Overview of Existing Methods and Recent Advances in Sequential Monte Carlo. Proc. IEEE 2007, 95, 899–924. [Google Scholar] [CrossRef]
- Vo, B.T.; Clark, D.; Vo, B.N. Bernoulli Forward-Backward Smoothing for Joint Target Detection and Tracking. IEEE Trans. Signal Process. 2011, 59, 4473–4477. [Google Scholar] [CrossRef]

| Algorithms | Memory Usage | Average Processing Time per Time Instant |
|---|---|---|
| MeMBer—MUSIC | 1,860,180 Kb | 0.14884489 s |
| MeMBer—Capon | 1,838,996 Kb | 0.10783062 s |
| PAST | 1,981,908 Kb | 0.26529525 s |
| Target | Signal Source Joint DOA-Polarization Parameter Trajectory | ||
|---|---|---|---|
| State of Birth | Birth Time/s | Death Time/s | |
| Signal source 1 | 1 | 100 | |
| Signal source 2 | 10 | 66 | |
| Signal source3 | 20 | 80 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Z.; Wang, B.; Yang, R.; Lou, Y. Joint Direction of Arrival-Polarization Parameter Tracking Algorithm Based on Multi-Target Multi-Bernoulli Filter. Remote Sens. 2023, 15, 3929. https://doi.org/10.3390/rs15163929
Chen Z, Wang B, Yang R, Lou Y. Joint Direction of Arrival-Polarization Parameter Tracking Algorithm Based on Multi-Target Multi-Bernoulli Filter. Remote Sensing. 2023; 15(16):3929. https://doi.org/10.3390/rs15163929
Chicago/Turabian StyleChen, Zhikun, Bin’an Wang, Ruiheng Yang, and Yuchao Lou. 2023. "Joint Direction of Arrival-Polarization Parameter Tracking Algorithm Based on Multi-Target Multi-Bernoulli Filter" Remote Sensing 15, no. 16: 3929. https://doi.org/10.3390/rs15163929
APA StyleChen, Z., Wang, B., Yang, R., & Lou, Y. (2023). Joint Direction of Arrival-Polarization Parameter Tracking Algorithm Based on Multi-Target Multi-Bernoulli Filter. Remote Sensing, 15(16), 3929. https://doi.org/10.3390/rs15163929







