Synthesis of Synthetic Hyperspectral Images with Controllable Spectral Variability Using a Generative Adversarial Network
Abstract
1. Introduction
2. Materials and Methods
2.1. Generative Adversarial Networks
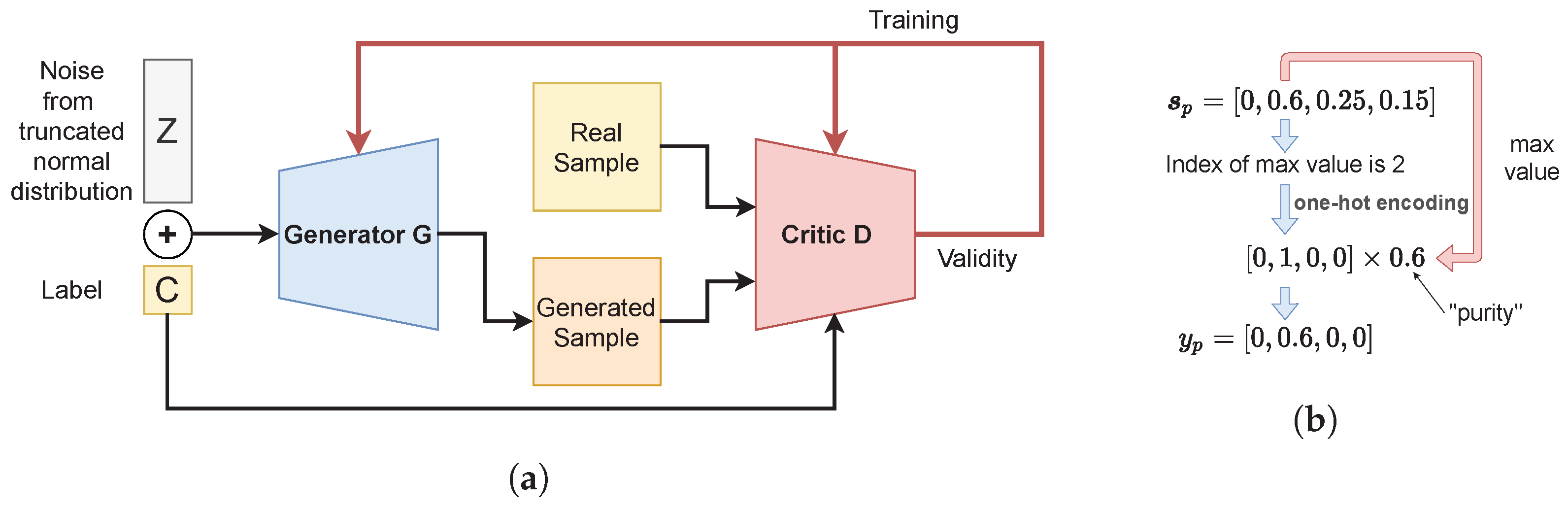
2.2. The Proposed Method
3. Experiments and Results
3.1. Experimental Set-Up
3.2. Evaluation
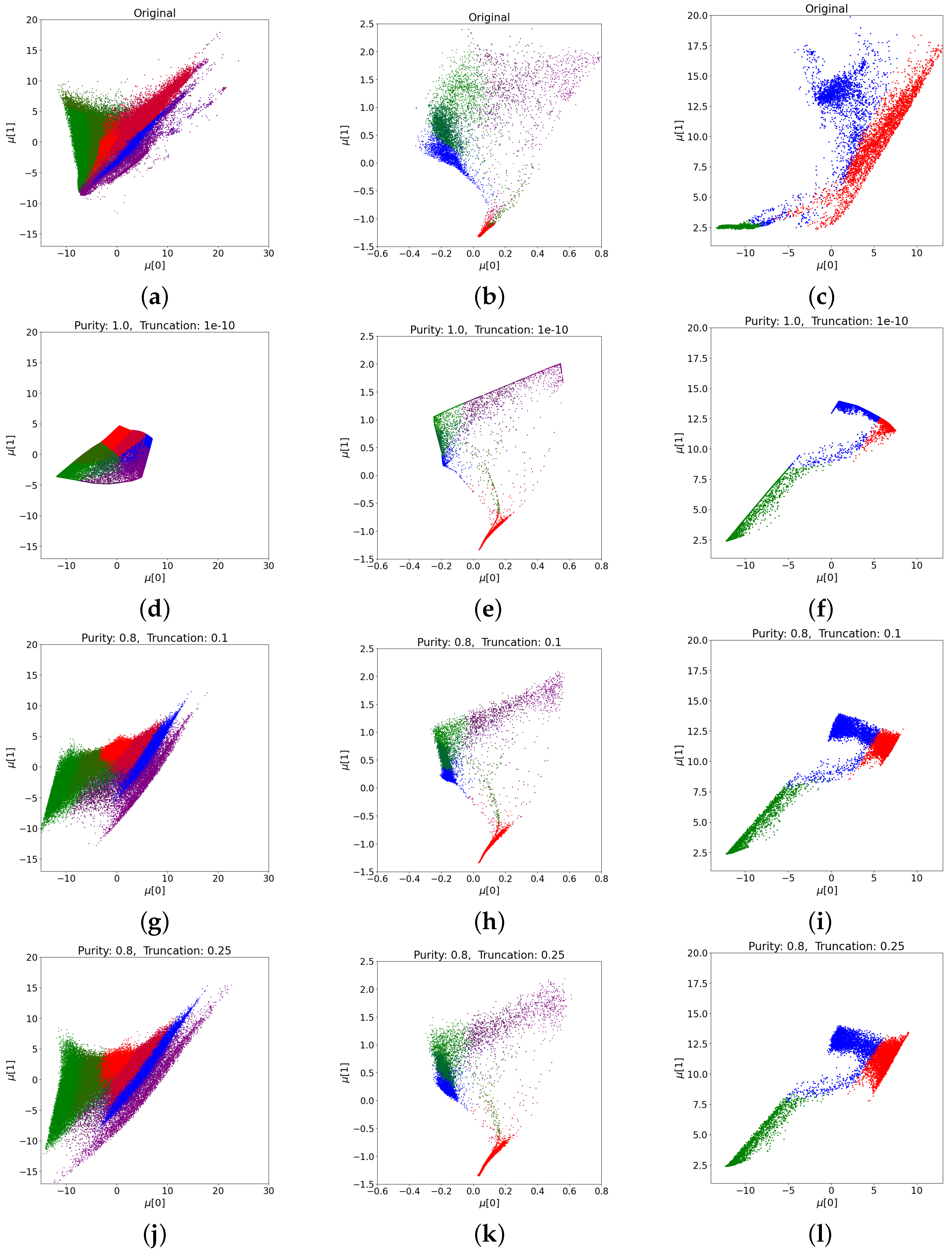
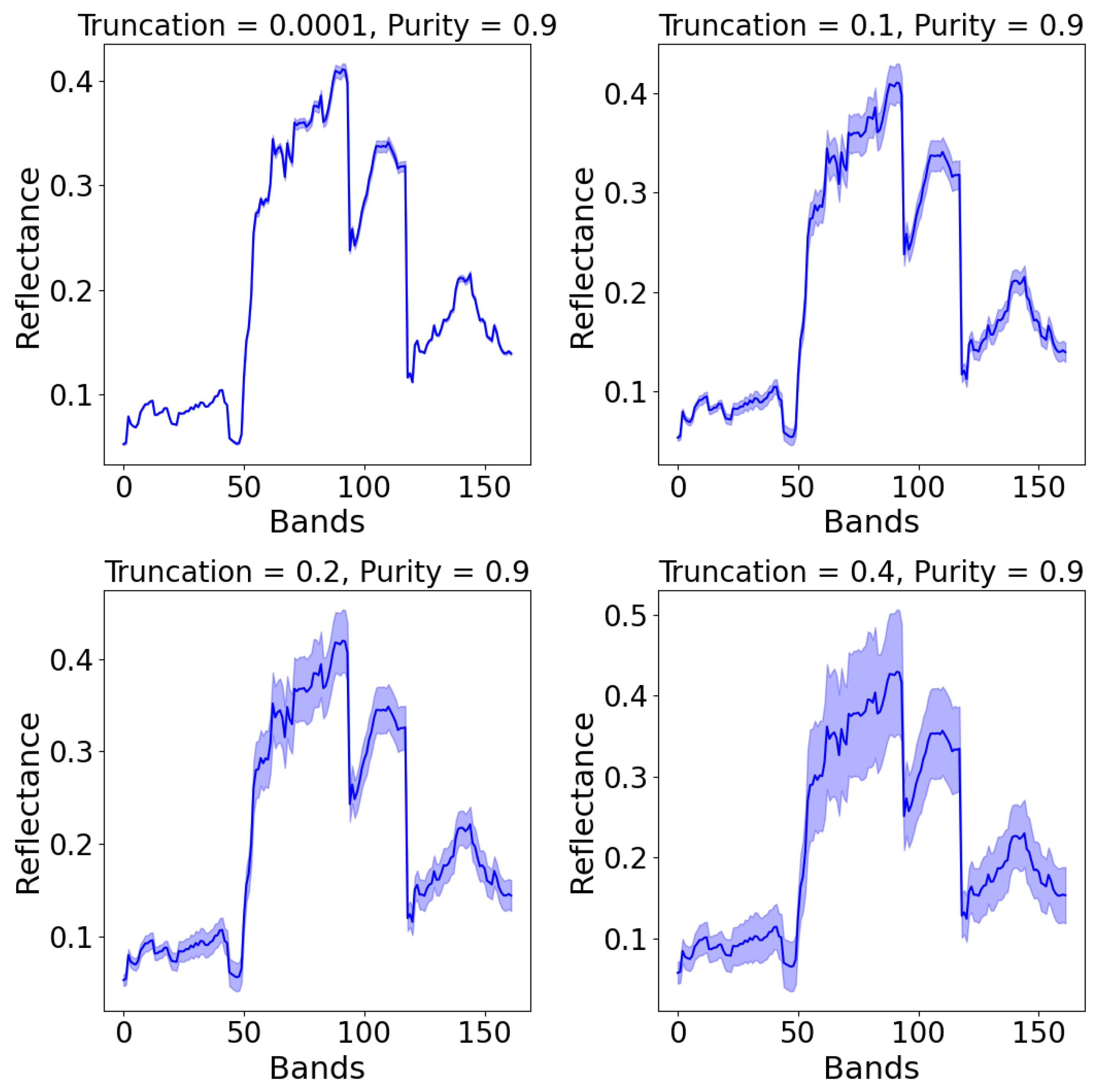
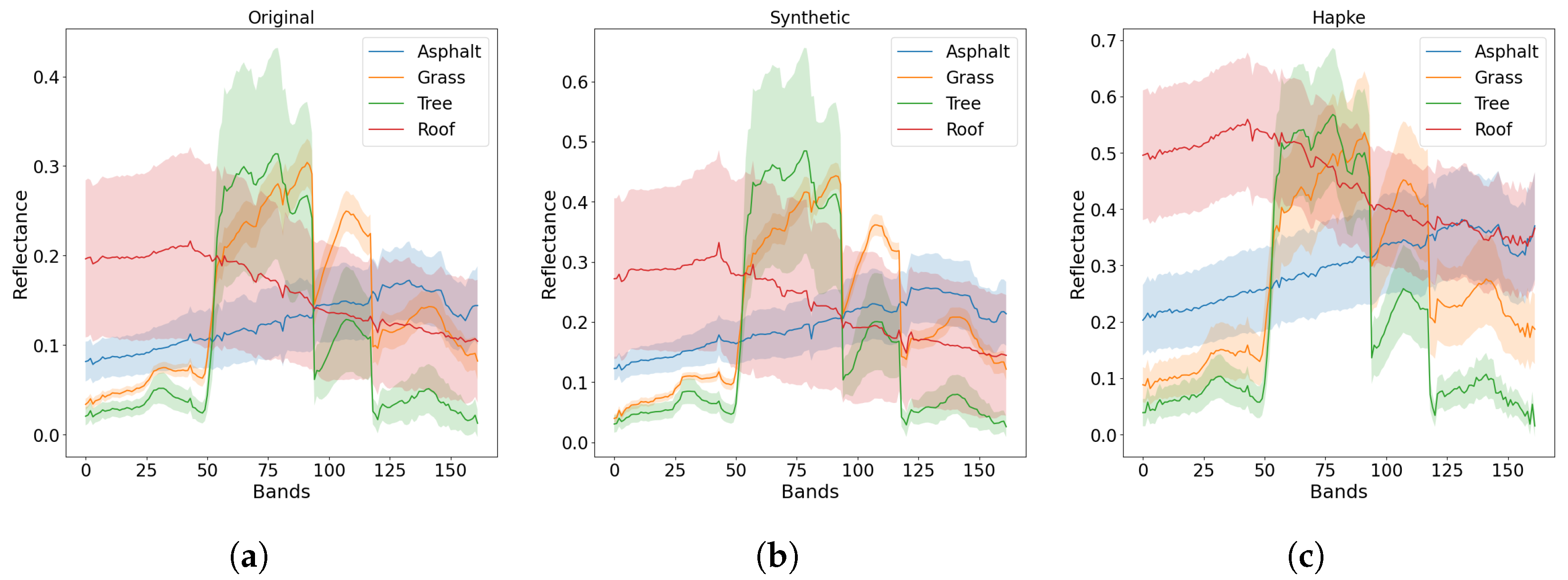
3.3. Results and Analysis
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Borsoi, R.; Imbiriba, T.; Bermudez, J.C.; Richard, C.; Chanussot, J.; Drumetz, L.; Tourneret, J.Y.; Zare, A.; Jutten, C. Spectral Variability in Hyperspectral Data Unmixing: A Comprehensive Review. IEEE Geosci. Remote Sens. Mag. 2021, 9, 223–270. [Google Scholar] [CrossRef]
- Uezato, T.; Fauvel, M.; Dobigeon, N. Hyperspectral Unmixing with Spectral Variability Using Adaptive Bundles and Double Sparsity. IEEE Trans. Geosci. Remote Sens. 2019, 57, 3980–3992. [Google Scholar] [CrossRef]
- Hong, D.; Yokoya, N.; Chanussot, J.; Zhu, X.X. An Augmented Linear Mixing Model to Address Spectral Variability for Hyperspectral Unmixing. IEEE Trans. Image Process. 2019, 28, 1923–1938. [Google Scholar] [CrossRef] [PubMed]
- Drumetz, L.; Veganzones, M.; Henrot, S.; Phlypo, R.; Chanussot, J.; Jutten, C. Blind Hyperspectral Unmixing Using an Extended Linear Mixing Model to Address Spectral Variability. IEEE Trans. Image Process. 2016, 25, 3890–3905. [Google Scholar] [CrossRef] [PubMed]
- Thouvenin, P.A.; Dobigeon, N.; Tourneret, J.Y. Hyperspectral Unmixing with Spectral Variability Using a Perturbed Linear Mixing Model. IEEE Trans. Signal Process. 2016, 64, 525–538. [Google Scholar] [CrossRef]
- Zhao, H.; Jiang, C.; Jia, G.; Tao, D. Simulation of hyperspectral radiance images with quantification of adjacency effects over rugged scenes. Meas. Sci. Technol. 2013, 24, 125405. [Google Scholar] [CrossRef]
- Liu, W.; You, J.; Lee, J. HSIGAN: A Conditional Hyperspectral Image Synthesis Method with Auxiliary Classifier. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 3330–3344. [Google Scholar] [CrossRef]
- Goodfellow, I.J.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative Adversarial Nets. In Proceedings of the 27th International Conference on Neural Information Processing Systems, Cambridge, MA, USA, 8–13 December 2014; Volume 2, pp. 2672–2680. [Google Scholar]
- Kingma, D.P.; Welling, M. Auto-Encoding Variational Bayes. Stat 2014, 1050, 10. [Google Scholar]
- Elbattah, M.; Loughnane, C.; Guérin, J.L.; Carette, R.; Cilia, F.; Dequen, G. Variational Autoencoder for Image-Based Augmentation of Eye-Tracking Data. J. Imaging 2021, 7, 83. [Google Scholar] [CrossRef]
- Peng, J.; Liu, D.; Xu, S.; Li, H. Generating Diverse Structure for Image Inpainting With Hierarchical VQ-VAE. In Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 19–25 June 2021; pp. 10770–10779. [Google Scholar] [CrossRef]
- Mak, H.W.L.; Han, R.; Yin, H.H.F. Application of Variational AutoEncoder (VAE) Model and Image Processing Approaches in Game Design. Sensors 2023, 23, 3457. [Google Scholar] [CrossRef] [PubMed]
- Palsson, B.; Ulfarsson, M.O.; Sveinsson, J.R. Synthetic Hyperspectral Images With Controllable Spectral Variability and Ground Truth. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Dhariwal, P.; Nichol, A. Diffusion models beat gans on image synthesis. Adv. Neural Inf. Process. Syst. 2021, 34, 8780–8794. [Google Scholar]
- Arjovsky, M.; Chintala, S.; Bottou, L. Wasserstein generative adversarial networks. In Proceedings of the International Conference on Machine Learning, PMLR, Sydney, Australia, 6–11 August 2017; pp. 214–223. [Google Scholar]
- Cobzaş, Ş.; Miculescu, R.; Nicolae, A. Lipschitz Functions; Springer: Berlin/Heidelberg, Germany, 2019; Volume 2241. [Google Scholar]
- Rudin, L.I.; Osher, S.; Fatemi, E. Nonlinear total variation based noise removal algorithms. Phys. D Nonlinear Phenom. 1992, 60, 259–268. [Google Scholar] [CrossRef]
- Brock, A.; Donahue, J.; Simonyan, K. Large scale GAN training for high fidelity natural image synthesis. arXiv 2018, arXiv:1809.11096. [Google Scholar]
- Higgins, I.; Matthey, L.; Pal, A.; Burgess, C.P.; Glorot, X.; Botvinick, M.M.; Mohamed, S.; Lerchner, A. beta-VAE: Learning Basic Visual Concepts with a Constrained Variational Framework. In Proceedings of the ICLR, 5th International Conference on Learning Representations, Toulon, France, 24–26 April 2017. [Google Scholar]
- Palsson, B.; Ulfarsson, M.O.; Sveinsson, J.R. Convolutional Autoencoder for Spectral–Spatial Hyperspectral Unmixing. IEEE Trans. Geosci. Remote Sens. 2021, 59, 535–549. [Google Scholar] [CrossRef]
- Qian, Y.; Jia, S.; Zhou, J.; Robles-Kelly, A. Hyperspectral Unmixing via L1/2 Sparsity-Constrained Nonnegative Matrix Factorization. IEEE Trans. Geosci. Remote Sens. 2011, 49, 4282–4297. [Google Scholar] [CrossRef]
- Hapke, B. Bidirectional reflectance spectroscopy: 1. Theory. J. Geophys. Res. Solid Earth 1981, 86, 3039–3054. [Google Scholar] [CrossRef]
- Magnusson, M.; Sigurdsson, J.; Armansson, S.E.; Ulfarsson, M.O.; Deborah, H.; Sveinsson, J.R. Creating RGB Images from Hyperspectral Images Using a Color Matching Function. In Proceedings of the IGARSS 2020—2020 IEEE International Geoscience and Remote Sensing Symposium, Waikoloa, HI, USA, 26 September–2 October 2020; pp. 2045–2048. [Google Scholar] [CrossRef]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Palsson, B.; Ulfarsson, M.O.; Sveinsson, J.R. Synthesis of Synthetic Hyperspectral Images with Controllable Spectral Variability Using a Generative Adversarial Network. Remote Sens. 2023, 15, 3919. https://doi.org/10.3390/rs15163919
Palsson B, Ulfarsson MO, Sveinsson JR. Synthesis of Synthetic Hyperspectral Images with Controllable Spectral Variability Using a Generative Adversarial Network. Remote Sensing. 2023; 15(16):3919. https://doi.org/10.3390/rs15163919
Chicago/Turabian StylePalsson, Burkni, Magnus O. Ulfarsson, and Johannes R. Sveinsson. 2023. "Synthesis of Synthetic Hyperspectral Images with Controllable Spectral Variability Using a Generative Adversarial Network" Remote Sensing 15, no. 16: 3919. https://doi.org/10.3390/rs15163919
APA StylePalsson, B., Ulfarsson, M. O., & Sveinsson, J. R. (2023). Synthesis of Synthetic Hyperspectral Images with Controllable Spectral Variability Using a Generative Adversarial Network. Remote Sensing, 15(16), 3919. https://doi.org/10.3390/rs15163919







