Modeling the Effects of Drivers on PM2.5 in the Yangtze River Delta with Geographically Weighted Random Forest
Abstract
1. Introduction
2. Materials and Methods
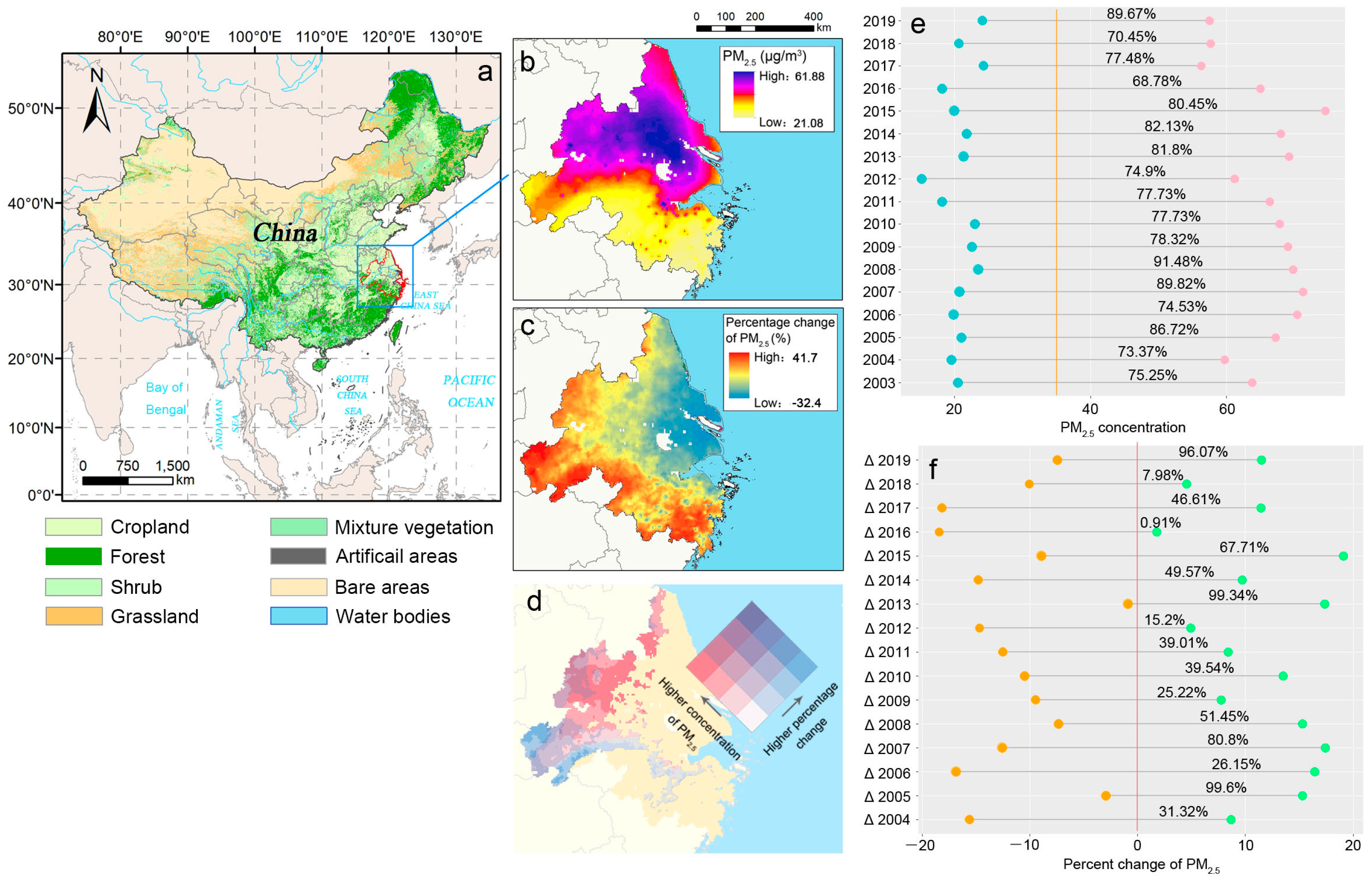
2.1. Research Area
2.2. Data Preparation
2.2.1. PM2.5 Raster Data
2.2.2. Explanatory Variable
Meteorological Variables
Vegetation Variables
Anthropogenic Variables
Fire Emission Variables
Scale and Datasets of Study Cell
2.3. Hot Spot Analysis
2.4. Predictive Model of PM2.5
2.4.1. Global Model Algorithms
Linear Regression Model (LM)
Gradient Boosting Machine (GBM)
Random Forest Regression (RF)
2.4.2. Local Model Algorithms
Geographically Weighted Regression (GWR)
Geographically Weighted Random Forest (GWRF)
2.4.3. Performance Evaluation of the Model
3. Results
3.1. Descriptive Statistics of Utilized Data
3.2. Spatio Patterns of PM2.5 Concentration and Change
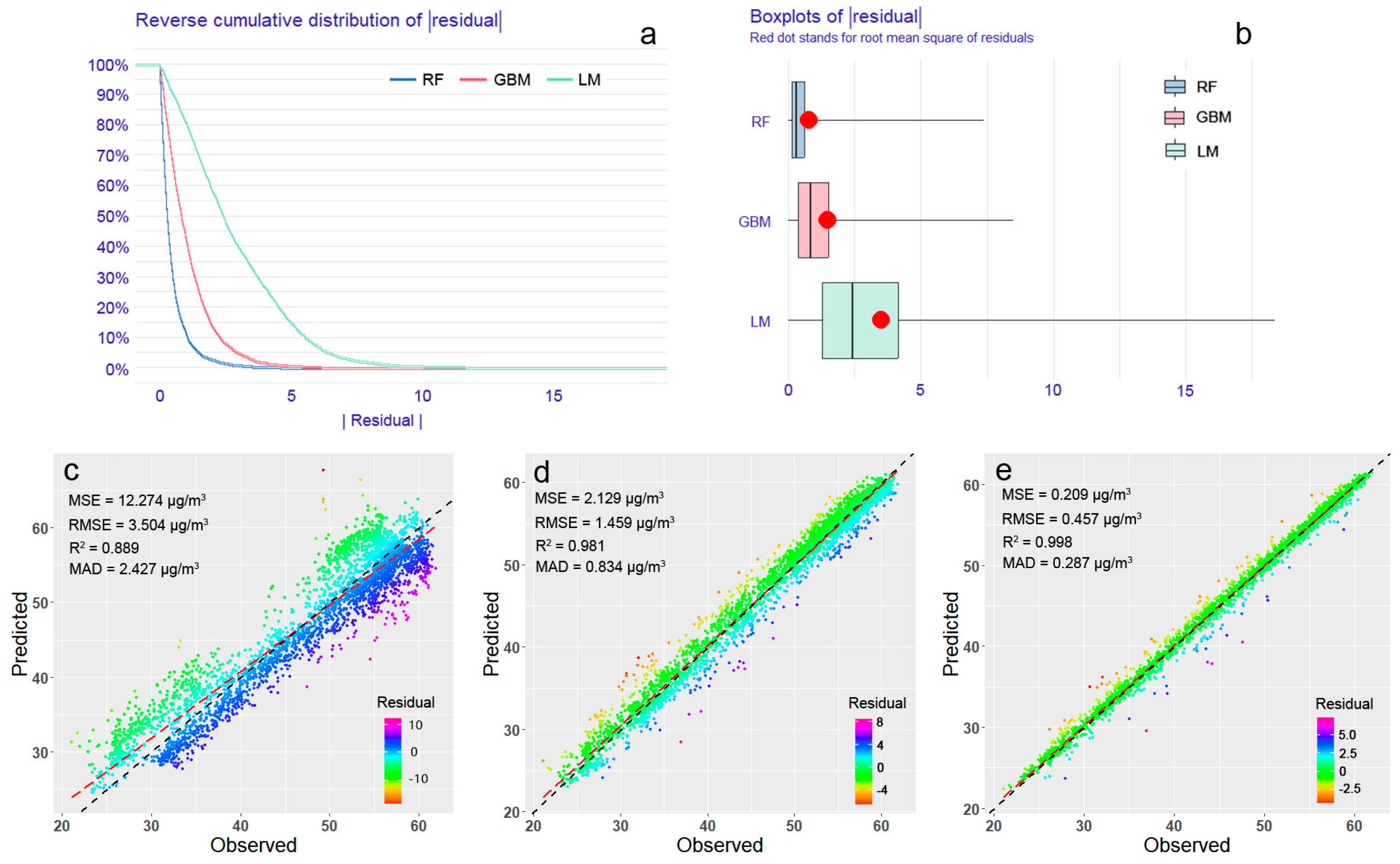
3.3. Evaluation of the Global Model
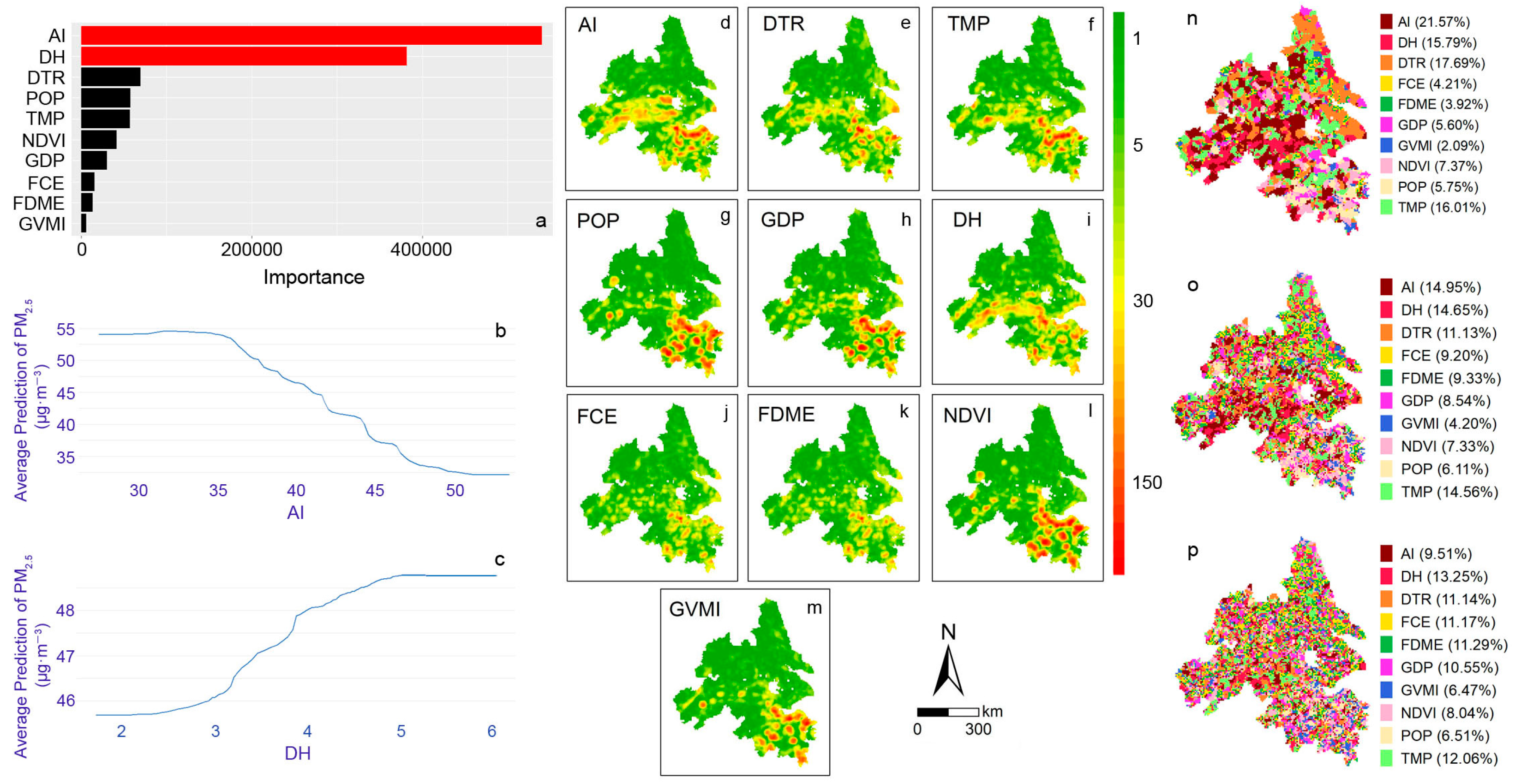
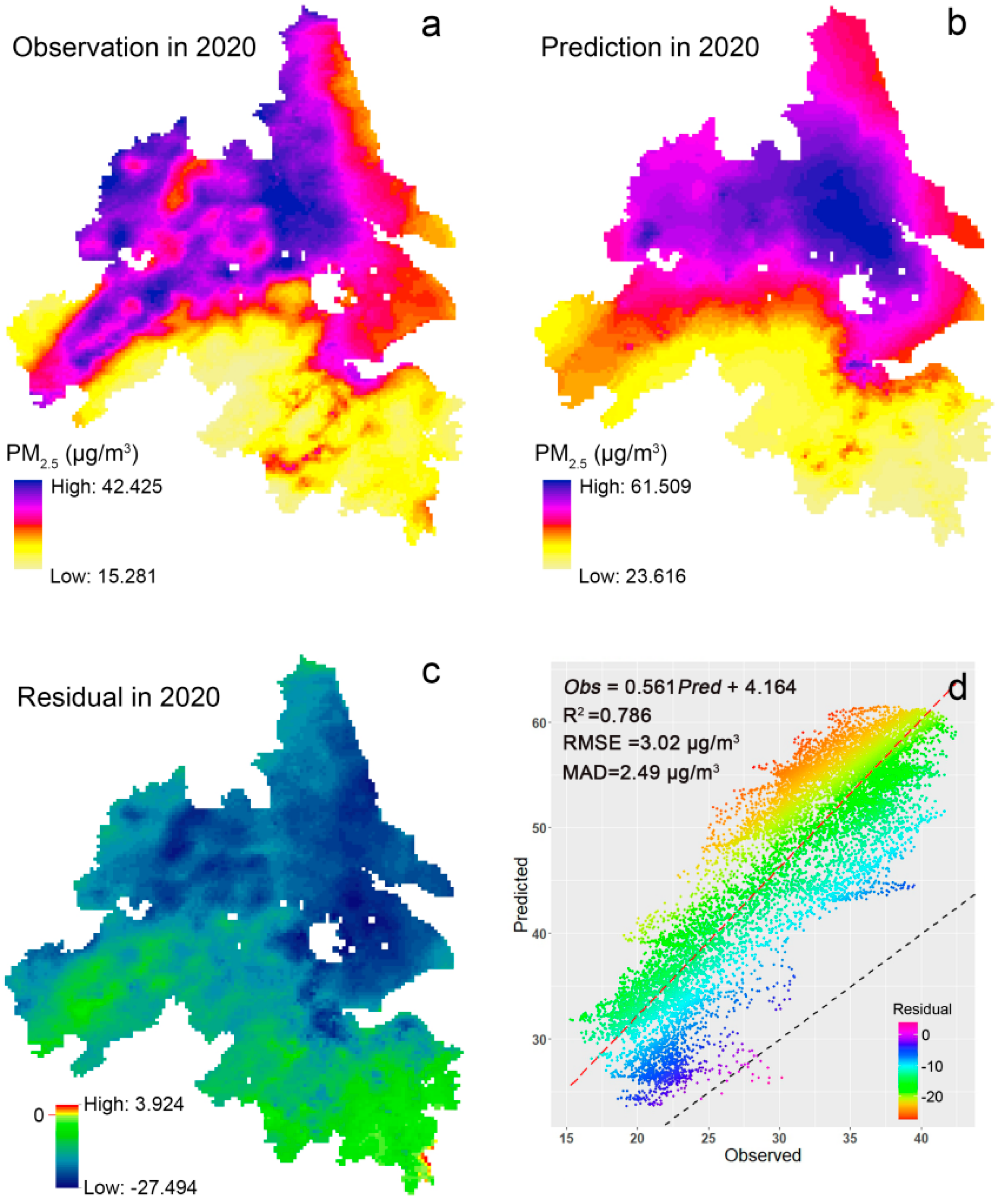
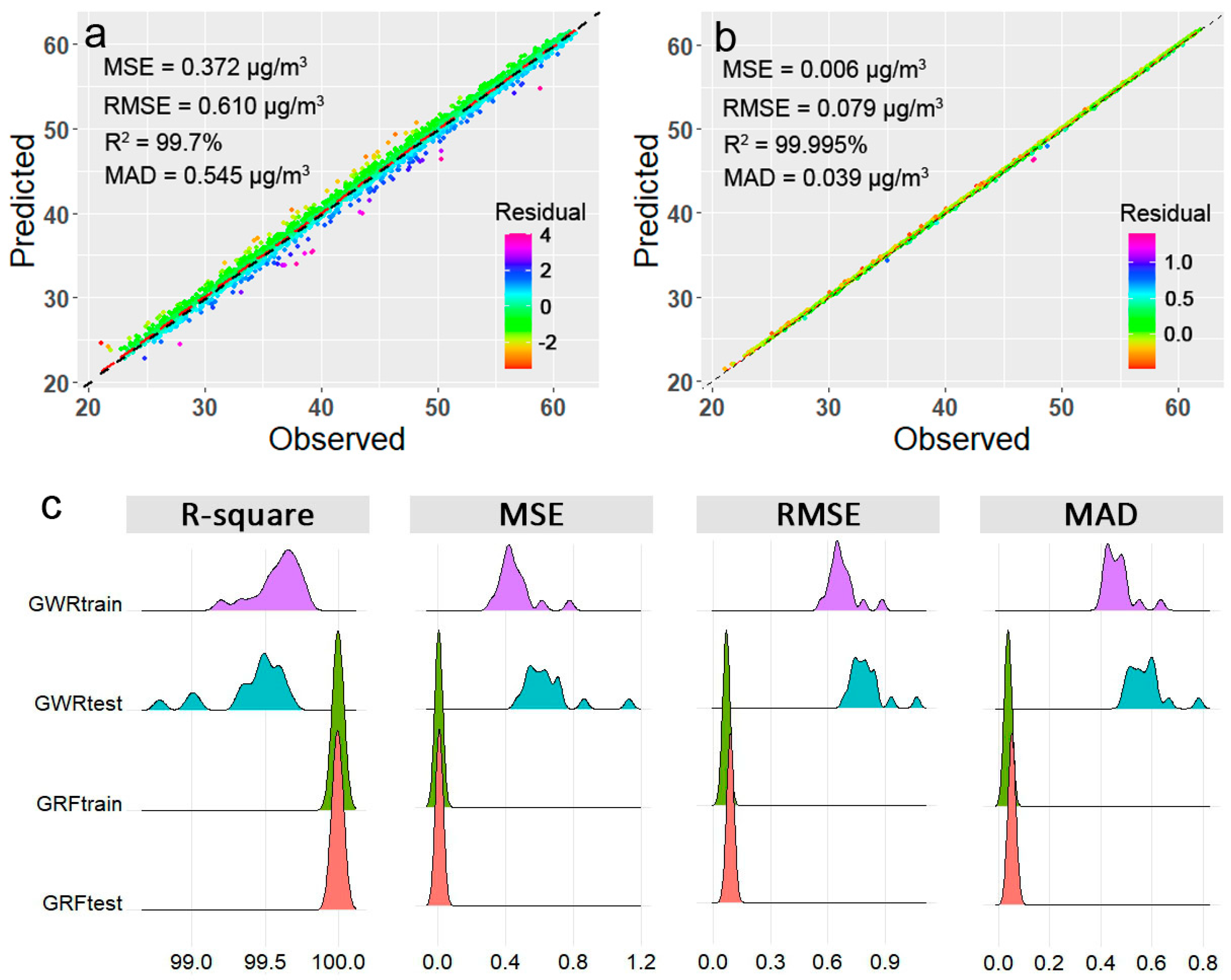
3.4. Evaluation of the Local Model
3.5. Comparison of Optimal Global and Local Models

4. Discussion
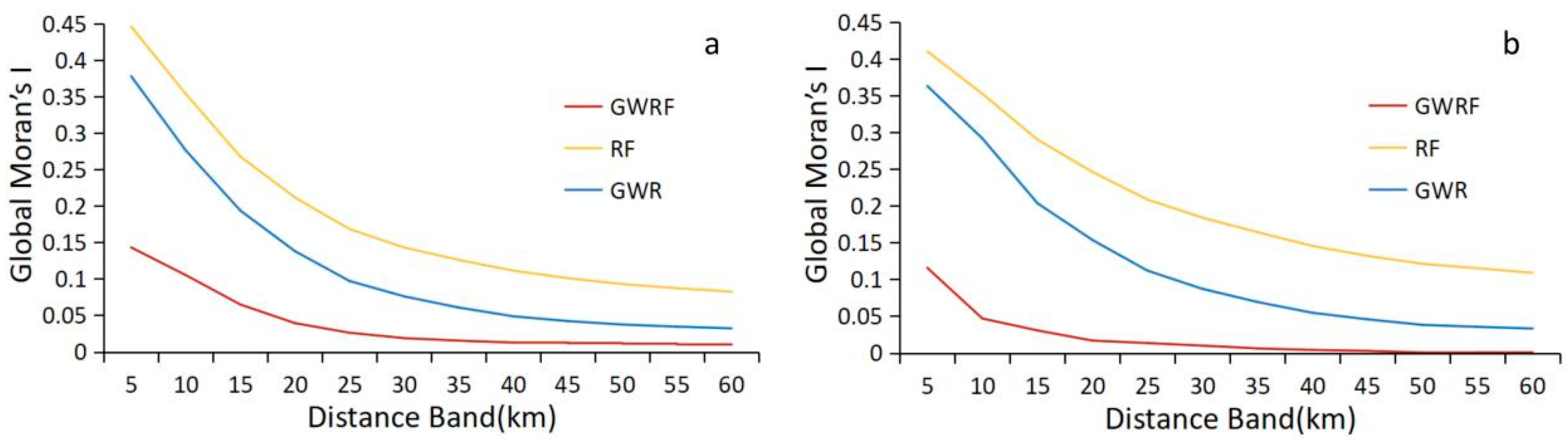
4.1. Spatial Distribution and Clustering of PM2.5
4.2. Comparison of PM2.5 Prediction Models
4.3. The Influencing Factors of PM2.5
4.4. Limitations
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Danesh Yazdi, M.; Kuang, Z.; Dimakopoulou, K.; Barratt, B.; Suel, E.; Amini, H.; Lyapustin, A.; Katsouyanni, K.; Schwartz, J. Predicting fine particulate matter (PM2.5) in the greater London area: An ensemble approach using machine learning methods. Remote Sens. 2020, 12, 914. [Google Scholar] [CrossRef]
- Luo, Y.; Teng, M.; Yang, K.; Zhu, Y.; Zhou, X.; Zhang, M.; Shi, Y. Research on PM2.5 estimation and prediction method and changing characteristics analysis under long temporal and large spatial scale—A case study in China typical regions. Sci. Total Environ. 2019, 696, 133983. [Google Scholar]
- Jin, H.; Zhong, R.; Liu, M.; Ye, C.; Chen, X. Spatiotemporal distribution characteristics of PM2.5 concentration in China from 2000 to 2018 and its impact on population. J. Environ. Manag. 2022, 323, 116273. [Google Scholar] [CrossRef] [PubMed]
- Bera, B.; Bhattacharjee, S.; Sengupta, N.; Saha, S. PM2.5 concentration prediction during COVID-19 lockdown over Kolkata metropolitan city, India using MLR and ANN models. Environ. Chall. 2021, 4, 100155. [Google Scholar] [CrossRef]
- He, W.; Meng, H.; Han, J.; Zhou, G.; Zheng, H.; Zhang, S. Spatiotemporal PM2.5 estimations in China from 2015 to 2020 using an improved gradient boosting decision tree. Chemosphere 2022, 296, 134003. [Google Scholar] [CrossRef]
- Yan, X.; Zang, Z.; Jiang, Y.; Shi, W.; Guo, Y.; Li, D.; Zhao, C.; Husi, L. A spatial-temporal interpretable deep learning model for improving interpretability and predictive accuracy of satellite-based PM2.5. Environ. Pollut. 2021, 273, 116459. [Google Scholar] [CrossRef]
- Yang, Z.; Zdanski, C.; Farkas, D.; Bang, J.; Williams, H. Evaluation of aerosol optical depth (AOD) and PM2.5 associations for air quality assessment. Remote Sens. Appl. 2020, 20, 100396. [Google Scholar] [CrossRef]
- Wei, J.; Huang, W.; Li, Z.; Xue, W.; Peng, Y.; Sun, L.; Cribb, M. Estimating 1-km-resolution PM2.5 concentrations across China using the space-time random forest approach. Remote Sens. Environ. 2019, 231, 111221. [Google Scholar] [CrossRef]
- Hu, X.; Belle, J.H.; Meng, X.; Wildani, A.; Waller, L.A.; Strickland, M.J.; Liu, Y. Estimating PM2.5 concentrations in the conterminous United States using the random forest approach. Environ. Sci. Technol. 2017, 51, 6936. [Google Scholar] [CrossRef]
- Liu, J.; Weng, F.; Li, Z. Satellite-based PM2.5 estimation directly from reflectance at the top of the atmosphere using a machine learning algorithm. Atmos. Environ. 2019, 208, 113–122. [Google Scholar] [CrossRef]
- van Donkelaar, A.; Martin, R.V.; Li, C.; Burnett, R.T. Regional estimates of chemical composition of fine particulate matter using a combined geosciencestatistical method with information from satellites, models, and monitors. Environ. Sci. Technol. 2019, 53, 2595–2611. [Google Scholar] [CrossRef]
- Su, Z.; Lin, L.; Chen, Y.; Hu, H. Understanding the distribution and drivers of PM2.5 concentrations in the Yangtze River Delta from 2015 to 2020 using Random Forest Regression. Environ. Monit. Assess. 2022, 94, 284. [Google Scholar] [CrossRef]
- Wang, X.; Sun, W. Meteorological parameters and gaseous pollutant concentrations as predictors of daily continuous PM2.5 concentrations using deep neural network in Beijing–Tianjin–Hebei, China. Atmos. Environ. 2019, 211, 128–137. [Google Scholar] [CrossRef]
- Kerckhoffs, J.; Hoek, G.; Portengen, L.; Brunekreef, B.; Vermeulen, R.C.H. Performance of prediction algorithms for modeling outdoor air pollution spatial surfaces. Environ. Sci. Technol. 2019, 53, 1413–1421. [Google Scholar] [CrossRef] [PubMed]
- Zhang, T.; He, W.; Zheng, H.; Cui, Y.; Song, H.; Fu, S. Satellite-based ground PM2.5 estimation using a gradient boosting decision tree. Chemosphere 2021, 268, 128801. [Google Scholar] [CrossRef]
- Zhang, P.; Ma, W.; Wen, F.; Liu, L.; Yang, L.; Song, J.; Wang, N.; Liu, Q. Estimating PM2.5 concentration using the machine learning GA-SVM method to improve the land use regression model in Shaanxi, China. Ecotox. Environ. Safe. 2021, 225, 112772. [Google Scholar] [CrossRef] [PubMed]
- Dai, H.; Huang, G.; Wang, J.; Zeng, H.; Zhou, F. Spatio-temporal characteristics of PM2.5 concentrations in china based on multiple sources of data and LUR-GBM during 2016–2021. Int. J. Environ. Res. Public Health 2022, 19, 6292. [Google Scholar] [CrossRef]
- Luo, Z.; Huang, F.; Liu, H. PM2.5 concentration estimation using convolutional neural network and gradient boosting machine. J. Environ. Sci. 2020, 98, 85–93. [Google Scholar] [CrossRef]
- Huang, G.; Li, X.; Zhang, B.; Ren, J. PM2.5 concentration forecasting at surface monitoring sites using GRU neural network based on empirical mode decomposition. Sci. Total Environ. 2021, 768, 144516. [Google Scholar] [CrossRef]
- Su, Z.; Xu, Z.; Lin, L.; Chen, Y.; Hu, H.; Wei, S.; Luo, S. Exploration of the Contribution of Fire Carbon Emissions to PM2.5 and Their Influencing Factors in Laotian Tropical Rainforests. Remote Sens. 2022, 14, 4052. [Google Scholar] [CrossRef]
- He, Q.; Huang, B. Satellite-based mapping of daily high-resolution ground PM2.5 in China via space-time regression modeling. Remote Sens. Environ. 2018, 206, 72–83. [Google Scholar] [CrossRef]
- Quiñones, S.; Goyal, A.; Ahmed, Z.U. Geographically weighted machine learning model for untangling spatial heterogeneity of type 2 diabetes mellitus (T2D) prevalence in the USA. Sci. Rep. 2021, 11, 6955. [Google Scholar] [CrossRef] [PubMed]
- Hengl, T.; Nussbaum, M.; Wright, M.N.; Heuvelink, G.B.M.; Gräler, B. Random Forest as a Generic Framework for Predictive Modeling of Spatial and Spatio-Temporal Variables. PeerJ 2018, 6, e5518. [Google Scholar] [CrossRef] [PubMed]
- Georganos, S.; Grippa, T.; Gadiaga, A.N.; Linard, C.; Lennert, M.; Vanhuysse, S.; Odhiambo Mboga, N.; Wolff, E.; Kalogirou, S. Geographical random forests: A spatial extension of the random forest algorithm to address spatial heterogeneity in remote sensing and population modelling. Geocarto Int. 2019, 36, 121–136. [Google Scholar] [CrossRef]
- Santos, F.; Graw, V.; Bonilla, S. A geographically weighted random forest approach for evaluate forest change drivers in the Northern Ecuadorian Amazon. PLoS ONE 2019, 14, e0226224. [Google Scholar] [CrossRef]
- Khan, S.N.; Li, D.; Maimaitijiang, M. A geographically weighted random forest approach to predict corn yield in the US corn belt. Remote Sens. 2022, 14, 2843. [Google Scholar] [CrossRef]
- Meng, X.; Hand, J.L.; Schichtel, B.A.; Liu, Y. Space-time trends of PM2.5 constituents in the conterminous United States estimated by a machine learning approach, 2005–2015. Environ. Int. 2018, 121, 1137–1147. [Google Scholar] [CrossRef]
- Kaur, M.; Nagpal, A.K. Evaluation of air pollution tolerance index and anticipated performance index of plants and their application in development of green space along the urban areas. Environ. Sci. Pollut. Res. 2017, 24, 18881–18895. [Google Scholar] [CrossRef]
- Hua, Y.; Cheng, Z.; Wang, S.; Jiang, J.; Chen, D.; Cai, S.; Fu, X.; Chen, C.; Xu, B.; Yu, J. Characteristics and source apportionment of PM2.5 during a fall heavy haze episode in the Yangtze River Delta of China. Atmos. Environ. 2015, 123, 380–391. [Google Scholar] [CrossRef]
- Zhang, Q.; Zheng, Y.; Tong, D.; Shao, M.; Hao, J. Drivers of improved PM2.5 air quality in China from 2013 to 2017. Proc. Natl. Acad. Sci. USA 2019, 116, 201907956. [Google Scholar] [CrossRef]
- Balogun, A.; Tella, A.; Baloo, L.; Adebisi, N. A review of the inter-correlation of climate change, air pollution and urban sustainability using novel machine learning algorithms and spatial information science. Urban Clim. 2021, 40, 100989. [Google Scholar] [CrossRef]
- Xue, T.; Zheng, Y.; Geng, G.; Zheng, B.; Jiang, X.; Zhang, Q.; He, K. Fusing observational, satellite remote sensing and air quality model simulated data to estimate spatiotemporal variations of PM2.5 exposure in China. Remote Sens. 2017, 9, 221. [Google Scholar] [CrossRef]
- Hammer, M.S.; van Donkelaar, A.; Li, C.; Lyapustin, A.; Sayer, A.M.; Hsu, N.C.; Levy, R.C.; Garay, M.J.; Kalashnikova, O.V.; Kahn, R.A.; et al. Global estimates and long-term trends of fine particulate matter concentrations (1998–2018). Environ. Sci. Technol. 2020, 54, 7879–7890. [Google Scholar] [CrossRef]
- Demetillo, M.A.G.; Anderson, J.F.; Geddes, J.A.; Yang, X.; Najacht, E.Y.; Herrera, S.A.; Kabasares, K.M.; Kotsakis, A.E.; Lerdau, M.T.; Pusede, S.E. Observing severe drought influences on ozone air pollution in California. Environ. Sci. Technol. 2019, 53, 4695–4706. [Google Scholar] [CrossRef] [PubMed]
- Berg, A.; McColl, K.A. No projected global drylands expansion under greenhouse warming. Nat. Clim. Chang. 2021, 11, 331–337. [Google Scholar] [CrossRef]
- Harris, I.; Osborn, T.J.; Jones, P.; Lister, D. Version 4 of the CRU TS monthly high-resolution gridded multivariate climate dataset. Sci. Data 2020, 7, 109. [Google Scholar] [CrossRef]
- Martinez, A.I.; Labib, S.M. Demystifying normalized difference vegetation index (NDVI) for greenness exposure assessments and policy interventions in urban greening. Environ. Res. 2023, 220, 115155. [Google Scholar] [CrossRef]
- Zubieta, R.; Ccanchi, Y.; Alejandra Martínez, A.; Saavedra, M.; Norabuena, E.; Alvarez, S.; Ilbay, M. The role of drought conditions on the recent increase in wildfire occurrence in the high Andean regions of Peru. Int. J. Wildland Fire 2023, 32, 531–544. [Google Scholar] [CrossRef]
- Du, X. Research on Vegetation Leaf Water Monitoring by Remote Sensing and Spatio-Temporai Character Analysis; Institute of Remote Sensing and Digital Earth Chinese Academy of Sciences: Beijing, China, 2006. (In Chinese) [Google Scholar]
- Su, Z.; Zheng, L.; Luo, S.; Tigabu, M.; Guo, F. Modeling wildfire drivers in Chinese tropical forest ecosystems using global logistic regression and geographically weighted logistic regression. Nat. Hazards 2021, 108, 1317–1345. [Google Scholar] [CrossRef]
- Zhang, X.; Brandt, M.; Tong, X.; Ciais, P.; Yue, Y.; Xiao, X.; Zhang, W.; Wang, K.; Fensholt, R. A large but transient carbon sink from urbanization and rural depopulation in China. Nat. Sustain. 2022, 5, 321–328. [Google Scholar] [CrossRef]
- Nethery, R.C.; Rushovich, T.; Peterson, E.; Chen, J.T.; Waterman, P.D.; Krieger, N.; Waller, L.; Coull, B.A. Comparing denominator sources for real-time disease incidence modeling: American Community Survey and WorldPop. SSM Popul. Health 2021, 14, 100786. [Google Scholar] [CrossRef] [PubMed]
- Guo, F.; Innes, L.J.; Wang, G.; Ma, X.; Sun, L.; Hu, H.; Su, Z. Historic distribution and driving factors of human-caused fires in the Chinese boreal forest between 1972 and 2005. J. Plant. Ecol. 2015, 8, 480–490. [Google Scholar] [CrossRef]
- Liu, S.; Liu, L.; Wu, X.; Hou, X.; Zhao, S.; Liu, G. Quantitative evaluation of human activity intensity on the regional ecological impact studies. Acta Ecol. Sin. 2018, 38, 6797–6809. (In Chinese) [Google Scholar]
- Beyhan, E.; Yarci, C.; Yilmaz, A. Investigation of hemeroby degree of vegetation in urban transport areas: The case of izmit (Kocaeli). Front. Life Sci. Relat. Technol. 2020, 1, 28–34. [Google Scholar]
- Prosperi, P.; Bloise, M.; Tubiello, F.N.; Conchedda, G.; Rossi, S.; Boschetti, L.; Salvatore, M.; Bernoux, M. New estimates of greenhouse gas emissions from biomass burning and peat fires using MODIS Collection 6 burned areas. Clim. Chang. 2020, 161, 415–432. [Google Scholar] [CrossRef]
- ESRI. ArcGIS Desktop, Release 10.6.1.; Environmental Systems Research Institute: Redlands, CA, USA, 2019. [Google Scholar]
- Ge, L.; Li, Y.; Wu, Y.; Fan, Z.; Song, Z. Differential Diagnosis of Rosacea Using Machine Learning and Dermoscopy. Clin. Cosmet. Inv. Derm. 2022, 15, 1465–1473. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Cutler, D.R.; Edwards, T.C.; Beard, K.H.; Cutler, A.; Hess, K.T.; Gibson, J. Random forests for classifcation in ecology. Ecology 2007, 88, 2783–2792. [Google Scholar] [CrossRef]
- Chen, Y.; Zheng, W.; Li, W.; Huang, Y. Large group activity security risk assessment and risk early warning based on random forest algorithm. Pattern. Recogn. Lett. 2021, 144, 1–5. [Google Scholar] [CrossRef]
- Zhan, Y.; Luo, Y.; Deng, X.; Zhang, K.; Zhang, M.; Grieneisen, M.L.; Di, B. Satellite-based estimates of daily NO2 exposure in China using hybrid random forest and spatiotemporal Kriging model. Environ. Sci. Technol. 2018, 52, 4180. [Google Scholar] [CrossRef]
- Zhang, B.; Tian, J.; Pei, S.; Chen, Y.; He, X.; Dong, Y.; Zhang, L.; Mo, X.; Huang, W.; Cong, S.; et al. Machine Learning-Assisted System for Thyroid Nodule Diagnosis. Thyroid 2019, 29, 858–867. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Seaborn, T.; Wang, Z.; Caudil, C.C.; Link, T.E. Modeling tree canopy height using machine learning over mixed vegetation landscapes. Int. J. Appl. Earth Obs. 2021, 101, 102353. [Google Scholar] [CrossRef]
- Rodrigues, M.; de la Riva, J.; Fotheringham, S. Modeling the spatial variation of the explanatory factors of human-caused wildfires in Spain using geographically weighted logistic regression. Appl. Geogr. 2014, 48, 52–63. [Google Scholar] [CrossRef]
- Yan, J.; Tao, F.; Zhang, S.; Lin, S.; Zhou, T. Spatiotemporal distribution characteristics and driving forces of PM2.5 in three urban agglomerations of the Yangtze River Economic Belt. Int. J. Environ. Res. Public Health 2021, 18, 2222. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Li, C.; Ristovski, Z.; Milic, A.; Gu, Y.; Islam, M.S.; Wang, S.; Hao, J.; Zhang, H.; He, C.; et al. A review of biomass burning: Emissions and impacts on air quality, health and climate in China. Sci. Total Environ. 2017, 579, 1000–1034. [Google Scholar] [CrossRef] [PubMed]
- She, Q.; Peng, X.; Xu, Q.; Long, L.; Wei, N.; Liu, M.; Jia, W.; Zhou, T.; Han, J.; Xiang, W. Air quality and its response to satellite-derived urban form in the Yangtze River Delta, China. Ecol. Indic. 2017, 75, 297–306. [Google Scholar] [CrossRef]
- Biancofiore, F.; Busilacchio, M.; Verdecchia, M.; Tomassetti, B.; Aruffo, E.; Bianco, S.; Di Tommaso, S.; Colangeli, C.; Rosatelli, G.; Di Carlo, P. Recursive neural network model for analysis and forecast of PM10 and PM2.5. Atmos. Pollut. Res. 2017, 8, 652–659. [Google Scholar] [CrossRef]
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Wei, J.; Li, Z.; Pinker, R.T.; Wang, J.; Sun, L.; Xue, W.; Li, R.; Cribb, M. Himawari-8-derived diurnal variations in ground-level PM2.5 pollution across China using the fast space-time Light Gradient Boosting Machine (LightGBM). Atmos. Chem. Phys. 2021, 21, 7863–7880. [Google Scholar] [CrossRef]
- Wang, Y.; Xie, Y.; Dong, W.; Ming, Y.; Wang, J.; Shen, L. Adverse effects of increasing drought on air quality via natural processes. Atmos. Chem. Phys. 2017, 17, 12827–12843. [Google Scholar] [CrossRef]
- Feng, X.; Wei, S.; Wang, S. Temperature inversions in the atmospheric boundary layer and lower troposphere over the Sichuan Basin, China: Climatology and impacts on air pollution. Sci. Total Environ. 2020, 726, 138579. [Google Scholar] [CrossRef] [PubMed]
- Geng, G.; Zhang, Q.; Martin, R.V.; van Donkelaar, A.; Huo, H.; Che, H.; Lin, J.; He, K. Estimating long-term PM2.5 concentrations in China using satellite-based aerosol optical depth and a chemical transport model. Remote Sens. Environ. 2015, 166, 262–270. [Google Scholar] [CrossRef]


| Variable | Variable Name | Code | Resolution/Unit | Source/Cite |
|---|---|---|---|---|
| PM2.5 | PM2.5 | PM2.5 | 0.01°/μg·m−3·yr−1 | Atmospheric Composition Analysis Group (ACAG) at the University of Washington (https://sites.wustl.edu/acag/datasets/surface-pm2–5/, accessed on 26 July 2023)/[3,11] |
| Climate | Average 2 m temperature | TMP | 0.5°/degrees Celsius | Version 4 of the CRUTS monthly high-resolution gridded multivariate climate dataset (https://crudata.uea.ac.uk/cru/data/hrg/, accessed on 26 July 2023)/[35,36] |
| Diurnal 2 m temperature range | DTR | 0.5°/degrees Celsius | ||
| Aridity index | AI | 0.5°/mm for Cumulative precipitation; 0.5°/mm for potential evapo-transpiration | ||
| Fire Emission | Fire carbon emission | FCE | 0.25°/gCm−2·month−1 | Global Fire Emissions Database (http://www.globalfiredata.org/, accessed on 14 September 2022)/[20] |
| Fire dry matter emission | FDME | 0.25°/gCm−2·month−1 | ||
| Vegetation | Normalized difference vegetation index | NDVI | 500 m/- | Geospatial Data Cloud (https://www.gscloud.cn, accessed on 26 July 2023)/[37,38,39,40] |
| Global vegetation Moisture Index | GVMI | 1 km/- | ||
| Anthropogenic | Density of population | POP | 1 km/person·km−2 | Population Density/Unconstrained individual countries 2000–2020 (https://hub.worldpop.org/, accessed on 26 July 2023)/[41,42] |
| Per capita GDP | GDP | 1 km/yuan·km−2 | Resource and Environment Science Data Center) (http://www.resdc.cn/doi, accessed on 26 July 2023)/[43] | |
| Degree of hemeroby | DH | 300 m/- | Copernicus Climate Change Service Data Platform (https://cds.climate.copernicus.eu/, accessed on 26 July 2023)/[12,44,45] |
| Min | 1st.QU | Median | Mean | 3st.QU | Max | |
|---|---|---|---|---|---|---|
| PM2.5 (μg·m−3·) | 21.0821 | 37.2647 | 50.5297 | 46.7770 | 55.48 | 61.8791 |
| DTR (°C) | 5.9026 | 7.7378 | 7.9709 | 7.9047 | 8.2065 | 8.7014 |
| TMP (°C) | 14.7459 | 16.1894 | 16.6688 | 16.5785 | 17.0441 | 17.9811 |
| AI | 27.4854 | 32.8977 | 37.0323 | 38.3146 | 43.8326 | 53.5153 |
| GDP (yuan·km−2) | 84.3036 | 852.106 | 1878.14 | 4881.0669 | 4502.17 | 692,855 |
| POP (person·km−2) | 2.2636 | 137.054 | 306.9 | 741.1342 | 615.775 | 45,627.3 |
| DH | 1.7262 | 3.09267 | 4.2747 | 3.9419 | 4.7646 | 6.0369 |
| FCE (gCm−2·month−1) | 0.2662 | 4.23712 | 9.1369 | 10.9016 | 14.6171 | 93.1017 |
| FDME (gCm−2·month−1) | 0.0006 | 0.0087 | 0.0189 | 0.0226 | 0.03024 | 0.1919 |
| NDVI | 0.0829 | 0.6998 | 0.7795 | 0.7402 | 0.8223 | 0.8844 |
| GVMI | 0.1553 | 0.246 | 0.2668 | 0.2674 | 0.2859 | 0.5819 |
| Min | 1st.QU | Median | Mean | 3st.QU | Max | |
|---|---|---|---|---|---|---|
| DTR | 0.0389 | 1.081 | 3.3355 | 10.2715 | 10.9743 | 337.5287 |
| TMP | 0.0328 | 1.1551 | 3.2694 | 11.2573 | 10.3566 | 323.7177 |
| AI | 0.0474 | 1.0467 | 3.614 | 12.7854 | 13.8376 | 342.0495 |
| GDP | 0.0217 | 0.751 | 2.2471 | 11.7726 | 7.4375 | 364.6094 |
| POP | 0.0237 | 0.4769 | 1.501 | 13.0538 | 6.3671 | 332.3118 |
| DH | 0.063 | 1.101 | 3.669 | 11.862 | 13.592 | 252.275 |
| FCE | 0.0328 | 0.9365 | 2.5774 | 6.5887 | 7.0685 | 264.5912 |
| FDME | 0.0327 | 0.9153 | 2.5478 | 6.5896 | 7.1617 | 268.7648 |
| NDVI | 0.0297 | 0.529 | 1.6525 | 14.4996 | 6.9073 | 424.704 |
| GVMI | 0.0357 | 0.5083 | 1.4760 | 9.2415 | 4.9289 | 272.4536 |
| Importance Ranking | DTR | TMP | AI | DH | POP | GDP | NDVI | GVMI | FCE | FDME |
|---|---|---|---|---|---|---|---|---|---|---|
| First | 17.69% | 16.01% | 21.57% | 15.79% | 5.75% | 5.60% | 7.37% | 2.09% | 4.21% | 3.92% |
| Second | 11.13% | 14.56% | 14.95% | 14.65% | 6.11% | 8.54% | 7.33% | 4.20% | 9.20% | 9.33% |
| Third | 11.14% | 12.06% | 9.51% | 13.25% | 6.51% | 10.55% | 8.04% | 6.47% | 11.17% | 11.29% |
| Fourth | 11.67% | 9.92% | 8.34% | 11.95% | 7.30% | 11.64% | 8.72% | 7.55% | 11.46% | 11.45% |
| Fifth | 8.92% | 9.38% | 8.38% | 10.59% | 8.51% | 12.25% | 9.24% | 9.50% | 11.65% | 11.59% |
| Sixth | 9.01% | 8.60% | 7.46% | 8.96% | 9.93% | 12.05% | 9.77% | 11.79% | 11.03% | 11.40% |
| Seventh | 8.85% | 7.72% | 8.02% | 8.01% | 12.07% | 11.21% | 10.83% | 12.94% | 9.95% | 10.41% |
| Eighth | 7.94% | 7.42% | 7.72% | 7.09% | 13.95% | 9.55% | 12.39% | 13.62% | 10.18% | 10.14% |
| Ninth | 6.87% | 6.94% | 6.98% | 5.00% | 13.84% | 9.43% | 12.46% | 13.76% | 12.47% | 12.26% |
| Tenth | 6.78% | 7.38% | 7.09% | 4.72% | 16.03% | 9.19% | 13.85% | 18.08% | 8.68% | 8.20% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Su, Z.; Lin, L.; Xu, Z.; Chen, Y.; Yang, L.; Hu, H.; Lin, Z.; Wei, S.; Luo, S. Modeling the Effects of Drivers on PM2.5 in the Yangtze River Delta with Geographically Weighted Random Forest. Remote Sens. 2023, 15, 3826. https://doi.org/10.3390/rs15153826
Su Z, Lin L, Xu Z, Chen Y, Yang L, Hu H, Lin Z, Wei S, Luo S. Modeling the Effects of Drivers on PM2.5 in the Yangtze River Delta with Geographically Weighted Random Forest. Remote Sensing. 2023; 15(15):3826. https://doi.org/10.3390/rs15153826
Chicago/Turabian StyleSu, Zhangwen, Lin Lin, Zhenhui Xu, Yimin Chen, Liming Yang, Honghao Hu, Zipeng Lin, Shujing Wei, and Sisheng Luo. 2023. "Modeling the Effects of Drivers on PM2.5 in the Yangtze River Delta with Geographically Weighted Random Forest" Remote Sensing 15, no. 15: 3826. https://doi.org/10.3390/rs15153826
APA StyleSu, Z., Lin, L., Xu, Z., Chen, Y., Yang, L., Hu, H., Lin, Z., Wei, S., & Luo, S. (2023). Modeling the Effects of Drivers on PM2.5 in the Yangtze River Delta with Geographically Weighted Random Forest. Remote Sensing, 15(15), 3826. https://doi.org/10.3390/rs15153826








