Adaptive Speckle Filter for Multi-Temporal PolSAR Image with Multi-Dimensional Information Fusion
Abstract
1. Introduction
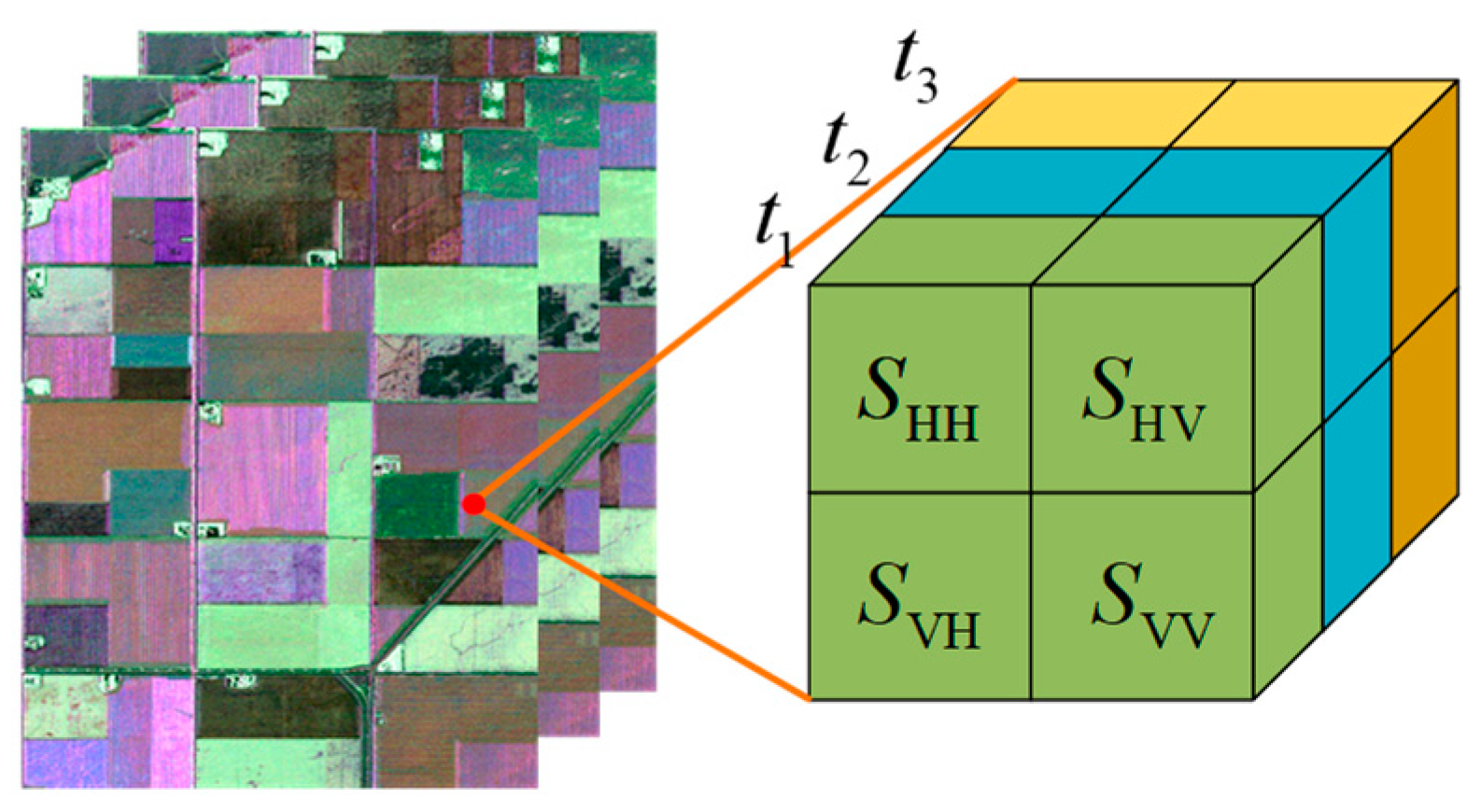
2. Multi-Temporal Polarimetric Covariance Matrix Formulation and Its Distribution
2.1. Multi-Temporal Polarimetric Covariance Matrix
2.2. Statistical Distribution
3. Adaptive Speckle Filter Development
3.1. Multi-Temporal Polarimetric Covariance Matrices Similarity Test
3.2. Similar Pixel Selection
3.3. Sensitivity Analysis and Demonstration
3.4. Proposed MTPCM Speckle Filter
4. Experimental Studies
4.1. Comparison with UAVSAR DATA
4.2. Comparison with ALOS/PALSAR Data
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lee, J.S.; Pottier, E. Polarimetric Radar Imaging: From Basics to Applications; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar]
- Chen, S.W.; Wang, X.S.; Xiao, S.P.; Sato, M. Target Scattering Mechanism in Polarimetric Synthetic Aperture Radar: Interpretation and Application; Springer: Singapore, 2018. [Google Scholar]
- Skriver, H. Crop Classification by Multitemporal C- and L-Band Single- and Dual-Polarization and Fully Polarimetric SAR. IEEE Trans. Geosci. Remote Sens. 2012, 50, 2138–2149. [Google Scholar] [CrossRef]
- Guo, J.; Wei, P.L.; Liu, J.; Jin, B.; Su, B.F.; Zhou, Z.S. Crop Classification Based on Differential Characteristics of H/α Scattering Parameters for Multitemporal Quad- and Dual-Polarization SAR Images. IEEE Trans. Geosci. Remote Sens. 2018, 56, 6111–6123. [Google Scholar] [CrossRef]
- Pirrone, D.; De, S.; Bhattacharya, A.; Bruzzone, L.; Bovolo, F. An Unsupervised Approach to Change Detection in Built-Up Areas by Multitemporal PolSAR Images. IEEE Geosci. Remote Sens. Lett. 2020, 17, 1914–1918. [Google Scholar] [CrossRef]
- Yu, X.; Yue, X. Similarity Matrix Entropy for Multitemporal Polarimetric SAR Change Detection. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Chen, S.W.; Sato, M. Tsunami Damage Investigation of Built-Up Areas Using Multitemporal Spaceborne Full Polarimetric SAR Images. IEEE Trans. Geosci. Remote Sens. 2013, 51, 1985–1997. [Google Scholar] [CrossRef]
- Chen, S.W.; Wang, X.S.; Sato, M. Urban Damage Level Mapping Based on Scattering Mechanism Investigation Using Fully Polarimetric SAR Data for the 3.11 East Japan Earthquake. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6919–6929. [Google Scholar] [CrossRef]
- Pirrone, D.; Bovolo, F.; Bruzzone, L. An Approach to Unsupervised Detection of Fully and Partially Destroyed Buildings in Multitemporal VHR SAR Images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 5938–5953. [Google Scholar] [CrossRef]
- Chen, S.W.; Wang, X.S.; Sato, M. PolInSAR Complex Coherence Estimation Based on Covariance Matrix Similarity Test. IEEE Trans. Geosci. Remote Sens. 2012, 50, 4699–4710. [Google Scholar] [CrossRef]
- Lê, T.T.; Atto, A.M.; Trouvé, E.; Nicolas, J.M. Adaptive Multitemporal SAR Image Filtering Based on the Change Detection Matrix. IEEE Geosci. Remote Sens. Lett. 2014, 11, 1826–1830. [Google Scholar] [CrossRef]
- Chierchia, G.; Gheche, M.E.; Scarpa, G.; Verdoliva, L. Multitemporal SAR Image Despeckling Based on Block-Matching and Collaborative Filtering. IEEE Trans. Geosci. Remote Sens. 2017, 55, 5467–5480. [Google Scholar] [CrossRef]
- Dong, J.; Liao, M.; Zhang, L.; Gong, J. A Unified Approach of Multitemporal SAR Data Filtering Through Adaptive Estimation of Complex Covariance Matrix. IEEE Trans. Geosci. Remote Sens. 2018, 56, 5320–5333. [Google Scholar] [CrossRef]
- Zhao, W.; Deledalle, C.A.; Denis, L.; Maître, H.; Nicolas, J.M.; Tupin, F. Ratio-Based Multitemporal SAR Images Denoising: RABASAR. IEEE Trans. Geosci. Remote Sens. 2019, 57, 3552–3565. [Google Scholar] [CrossRef]
- Ma, X.; Wang, C.; Yin, Z.; Wu, P. SAR Image Despeckling by Noisy Reference-Based Deep Learning Method. IEEE Trans. Geosci. Remote Sens. 2020, 58, 8807–8818. [Google Scholar] [CrossRef]
- Meraoumia, I.; Dalsasso, E.; Denis, L.; Abergel, R.; Tupin, F. Multitemporal Speckle Reduction With Self-Supervised Deep Neural Networks. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–14. [Google Scholar] [CrossRef]
- Lee, J.S. Refined Filtering of Image Noise Using Local Statistics. Comput. Graph. Image Process. 1981, 15, 380–389. [Google Scholar] [CrossRef]
- Lee, J.S.; Grunes, M.R.; Grandi, G.D. Polarimetric SAR Speckle Filtering and Its Implication for Classification. IEEE Trans. Geosci. Remote Sens. 1999, 37, 2363–2373. [Google Scholar] [CrossRef]
- Vasile, G.; Trouve, E.; Jong-Sen, L.; Buzuloiu, V. Intensity-Driven Adaptive-Neighborhood Technique for Polarimetric and Interferometric SAR Parameters Estimation. IEEE Trans. Geosci. Remote Sens. 2006, 44, 1609–1621. [Google Scholar] [CrossRef]
- Lee, J.S. Digital Image Enhancement and Noise Filtering by Use of Local Statistics. IEEE Trans. Pattern Anal. Mach. Intell. 1980, PAMI-2, 165–168. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.S.; Ainsworth, T.L.; Wang, Y.; Chen, K.S. Polarimetric SAR Speckle Filtering and the Extended Sigma Filter. IEEE Trans. Geosci. Remote Sens. 2015, 53, 1150–1160. [Google Scholar] [CrossRef]
- Nie, X.; Qiao, H.; Zhang, B.; Huang, X. A Nonlocal TV-Based Variational Method for PolSAR Data Speckle Reduction. IEEE Trans. Image Process. 2016, 25, 2620–2634. [Google Scholar] [CrossRef]
- Chen, J.; Chen, Y.; An, W.; Cui, Y.; Yang, J. Nonlocal Filtering for Polarimetric SAR Data: A Pretest Approach. IEEE Trans. Geosci. Remote Sens. 2011, 49, 1744–1754. [Google Scholar] [CrossRef]
- Lopez-Martinez, C.; Fabregas, X. Model-based polarimetric SAR speckle filter. IEEE Trans Geosci Remote Sens 2008, 46, 3894–3907. [Google Scholar] [CrossRef]
- Foucher, S.; López-Martínez, C. Analysis, Evaluation, and Comparison of Polarimetric SAR Speckle Filtering Techniques. IEEE Trans. Image Process. 2014, 23, 1751–1764. [Google Scholar] [CrossRef] [PubMed]
- Touzi, R. A Review of Speckle Filtering in the Context of Estimation Theory. IEEE Trans. Geosci. Remote Sens. 2002, 40, 2392–2404. [Google Scholar] [CrossRef]
- Velotto, D.; Nunziata, F.; Migliaccio, M.; Lehner, S. Dual-Polarimetric TerraSAR-X SAR Data for Target at Sea Observation. IEEE Geosci. Remote Sens. Lett. 2013, 10, 1114–1118. [Google Scholar] [CrossRef]
- Chen, S.W.; Wang, X.S.; Sato, M. Uniform Polarimetric Matrix Rotation Theory and Its Applications. IEEE Trans. Geosci. Remote Sens. 2014, 52, 4756–4770. [Google Scholar] [CrossRef]
- Li, H.L.; Li, M.D.; Cui, X.C.; Chen, S.W. Man-Made Target Structure Recognition with Polarimetric Correlation Pattern and Roll-Invariant Feature Coding. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Li, H.L.; Cui, X.C.; Chen, S.W. PolSAR Ship Detection with Optimal Polarimetric Rotation Domain Features and SVM. Remote Sens. 2021, 13, 3932. [Google Scholar] [CrossRef]
- Yang, Z.; Fang, L.; Shen, B.; Liu, T. PolSAR Ship Detection Based on Azimuth Sublook Polarimetric Covariance Matrix. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 8506–8518. [Google Scholar] [CrossRef]
- Chen, S.W.; Li, Y.Z.; Wang, X.S.; Xiao, S.P.; Sato, M. Modeling and Interpretation of Scattering Mechanisms in Polarimetric Synthetic Aperture Radar: Advances and perspectives. IEEE Signal Process. Mag. 2014, 31, 79–89. [Google Scholar] [CrossRef]
- Wu, G.Q.; Li, Y.Z.; Chen, S.W. Polarimetric Model-Based Decomposition with Refined Double-Bounce Orientation Angle and Scattering Model. Remote Sens. 2021, 13, 3070. [Google Scholar] [CrossRef]
- Lee, J.S.; Grunes, M.R.; Schuler, D.L.; Pottier, E.; Ferro-Famil, L. Scattering-Model-Based Speckle Filtering of Polarimetric SAR Data. IEEE Trans. Geosci. Remote Sens. 2006, 44, 176–187. [Google Scholar] [CrossRef]
- Zhao, F.; Mallorqui, J.J. SMF-POLOPT: An Adaptive Multitemporal Pol(DIn)SAR Filtering and Phase Optimization Algorithm for PSI Applications. IEEE Trans. Geosci. Remote Sens. 2019, 57, 7135–7147. [Google Scholar] [CrossRef]
- Conradsen, K.; Nielsen, A.A.; Schou, J.; Skriver, H. A Test Statistic in the Complex Wishart Distribution and Its Application to Change Detection in Polarimetric SAR Data. IEEE Trans. Geosci. Remote Sens. 2003, 41, 4–19. [Google Scholar] [CrossRef]
- Chen, S.W.; Wang, X.S.; Xiao, S.P. Polarimetric SAR Speckle Filtering Based on Similarity Test and Adaptive Clustering. IEEE Geosci. Remote Sens. Lett. 2021, 18, 702–706. [Google Scholar] [CrossRef]
- Salehi, M.; Mohammadzadeh, A.; Maghsoudi, Y. Adaptive Speckle Filtering for Time Series of Polarimetric SAR Images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 2841–2848. [Google Scholar] [CrossRef]
- Kumar, A.; Giusti, E.; Mancuso, F.; Ghio, S.; Lupidi, A.; Martorella, M. Three-Dimensional Polarimetric InISAR Imaging of Non-Cooperative Targets. IEEE Trans. Comput. Imaging 2023, 9, 210–223. [Google Scholar] [CrossRef]
- Lee, J.S.; Jen-Hung, W.; Ainsworth, T.L.; Kun-Shan, C.; Chen, A.J. Improved Sigma Filter for Speckle Filtering of SAR Imagery. IEEE Trans. Geosci. Remote Sens. 2009, 47, 202–213. [Google Scholar] [CrossRef]
- Argenti, F.; Lapini, A.; Bianchi, T.; Alparone, L. A Tutorial on Speckle Reduction in Synthetic Aperture Radar Images. IEEE Geosci. Remote Sens. Mag. 2013, 1, 6–35. [Google Scholar] [CrossRef]
- Touzi, R.; Lopes, A.; Bousquet, P. A Statistical and Geometrical Edge Detector for SAR Images. IEEE Trans. Geosci. Remote Sens. 1988, 26, 764–773. [Google Scholar] [CrossRef]
- McNairn, H.; Jackson, T.J.; Wiseman, G.; Belair, S.; Berg, A.; Bullock, P.; Colliander, A.; Cosh, M.H.; Kim, S.-B.; Magagi, R.; et al. The Soil Moisture Active Passive Validation Experiment 2012 (SMAPVEX12): Prelaunch Calibration and Validation of the SMAP Soil Moisture Algorithms. IEEE Trans. Geosci. Remote Sens. 2015, 53, 2784–2801. [Google Scholar] [CrossRef]




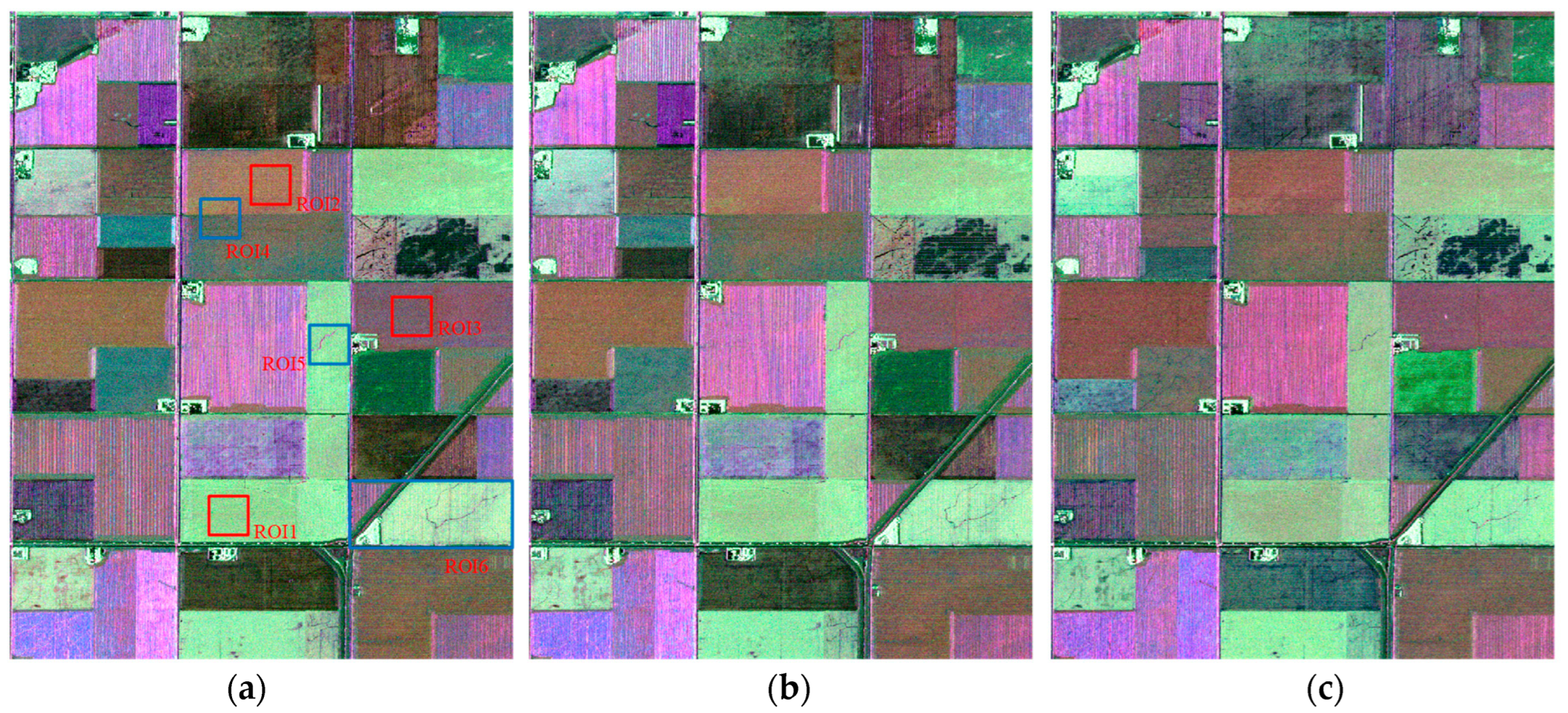







| Method | ENL | FOM | ||||
|---|---|---|---|---|---|---|
| ROI1 | ROI2 | ROI3 | ROI4 | ROI5 | ROI6 | |
| Original data | 20.62 | 16.23 | 20.54 | 0.10 | 0.12 | 0.34 |
| Boxcar | 440.42 | 385.80 | 430.27 | 0.62 | 0.03 | 0.45 |
| Refined Lee | 488.65 | 437.93 | 504.02 | 0.23 | 0.16 | 0.51 |
| Improved Sigma | 600.09 | 558.12 | 569.79 | 0.10 | 0.10 | 0.38 |
| IDAN | 455.03 | 398.33 | 445.50 | 0.59 | 0.16 | 0.39 |
| SimiTest | 963.75 | 841.82 | 906.04 | 0.82 | 0.54 | 0.60 |
| MTPCM | 966.15 | 854.95 | 905.82 | 0.83 | 0.81 | 0.70 |
| Method | ENL | FOM | ||||
|---|---|---|---|---|---|---|
| ROI1 | ROI2 | ROI3 | ROI4 | ROI5 | ROI6 | |
| Original data | 20.43 | 15.68 | 19.27 | 0.09 | 0.12 | 0.34 |
| Boxcar | 428.15 | 438.56 | 384.60 | 0.18 | 0.00 | 0.33 |
| Refined Lee | 368.65 | 345.58 | 351.25 | 0.21 | 0.16 | 0.52 |
| Improved Sigma | 428.13 | 438.56 | 384.61 | 0.27 | 0.11 | 0.38 |
| IDAN | 349.05 | 326.34 | 314.49 | 0.55 | 0.20 | 0.39 |
| SimiTest | 637.84 | 618.20 | 582.13 | 0.82 | 0.67 | 0.62 |
| MTPCM | 640.08 | 626.56 | 581.33 | 0.82 | 0.81 | 0.72 |
| Method | ENL | FOM | ||||
|---|---|---|---|---|---|---|
| ROI1 | ROI2 | ROI3 | ROI4 | ROI5 | ROI6 | |
| Original data | 18.13 | 16.45 | 19.25 | 0.06 | 0.12 | 0.37 |
| Boxcar | 544.05 | 324.30 | 529.98 | 0.09 | 0.00 | 0.30 |
| Refined Lee | 462.74 | 303.13 | 461.51 | 0.21 | 0.01 | 0.54 |
| Improved Sigma | 544.14 | 324.35 | 529.98 | 0.20 | 0.01 | 0.40 |
| IDAN | 408.89 | 270.30 | 413.73 | 0.56 | 0.20 | 0.38 |
| SimiTest | 838.76 | 423.43 | 898.69 | 0.83 | 0.39 | 0.61 |
| MTPCM | 851.84 | 438.95 | 903.51 | 0.84 | 0.53 | 0.68 |
| Number of Time Series | ENL | FOM | ||||
|---|---|---|---|---|---|---|
| ROI1 | ROI2 | ROI3 | ROI1 | ROI2 | ROI3 | |
| 1 | 963.75 | 841.82 | 906.04 | 0.82 | 0.54 | 0.60 |
| 2 | 965.62 | 854.23 | 905.59 | 0.83 | 0.76 | 0.67 |
| 3 | 966.15 | 854.95 | 905.82 | 0.83 | 0.81 | 0.70 |
| 4 | 962.81 | 851.05 | 898.71 | 0.81 | 0.80 | 0.69 |
| 5 | 950.80 | 848.12 | 891.08 | 0.78 | 0.73 | 0.61 |
| 7 | 916.81 | 795.54 | 806.64 | 0.67 | 0.41 | 0.45 |
| Combination of Time Series | ENL | FOM | ||||
|---|---|---|---|---|---|---|
| ROI1 | ROI2 | ROI3 | ROI1 | ROI2 | ROI3 | |
| 0622–0623 | 965.62 | 854.23 | 905.59 | 0.83 | 0.76 | 0.67 |
| 0622–0625 | 965.65 | 854.43 | 905.65 | 0.83 | 0.77 | 0.69 |
| 0622–0629 | 965.94 | 854.56 | 905.79 | 0.83 | 0.81 | 0.70 |
| 0622–0703 | 965.36 | 854.22 | 905.50 | 0.83 | 0.76 | 0.66 |
| 0622–0705 | 964.90 | 853.75 | 905.26 | 0.82 | 0.73 | 0.64 |
| 0622–0708 | 964.46 | 853.2 | 904.96 | 0.82 | 0.73 | 0.64 |
| Method | ROI1 | ROI2 | ROI3 | ROI4 | ROI5 | ROI6 |
|---|---|---|---|---|---|---|
| Original data | 5.38 | 4.83 | 5.66 | 3.61 | 3.39 | 1.93 |
| Boxcar | 97.45 | 85.24 | 107.34 | 74.56 | 41.61 | 12.86 |
| Refined Lee | 86.50 | 74.45 | 86.93 | 91.22 | 36.22 | 15.44 |
| Improved Sigma | 97.45 | 85.60 | 107.94 | 93.62 | 39.96 | 11.07 |
| IDAN | 74.81 | 61.18 | 80.22 | 74.58 | 35.47 | 13.58 |
| SimiTest | 104.93 | 98.17 | 118.34 | 98.15 | 64.32 | 21.51 |
| MTPCM | 134.84 | 138.27 | 148.68 | 104.36 | 69.09 | 21.68 |
| Method | ROI1 | ROI2 | ROI3 | ROI4 | ROI5 | ROI6 |
|---|---|---|---|---|---|---|
| Original data | 6.28 | 5.90 | 6.09 | 2.45 | 4.80 | 2.26 |
| Boxcar | 150.42 | 174.12 | 125.02 | 41.10 | 59.62 | 5.36 |
| Refined Lee | 110.02 | 137.55 | 114.78 | 65.78 | 58.83 | 30.16 |
| Improved Sigma | 150.03 | 174.00 | 125.99 | 63.17 | 61.93 | 7.51 |
| IDAN | 109.59 | 118.54 | 92.70 | 44.67 | 49.01 | 16.16 |
| SimiTest | 249.34 | 295.51 | 149.24 | 65.16 | 80.87 | 45.36 |
| MTPCM | 279.87 | 372.45 | 168.75 | 71.64 | 96.94 | 46.05 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, H.; Cui, X.; Li, M.; Deng, J.; Chen, S. Adaptive Speckle Filter for Multi-Temporal PolSAR Image with Multi-Dimensional Information Fusion. Remote Sens. 2023, 15, 3679. https://doi.org/10.3390/rs15143679
Li H, Cui X, Li M, Deng J, Chen S. Adaptive Speckle Filter for Multi-Temporal PolSAR Image with Multi-Dimensional Information Fusion. Remote Sensing. 2023; 15(14):3679. https://doi.org/10.3390/rs15143679
Chicago/Turabian StyleLi, Haoliang, Xingchao Cui, Mingdian Li, Junwu Deng, and Siwei Chen. 2023. "Adaptive Speckle Filter for Multi-Temporal PolSAR Image with Multi-Dimensional Information Fusion" Remote Sensing 15, no. 14: 3679. https://doi.org/10.3390/rs15143679
APA StyleLi, H., Cui, X., Li, M., Deng, J., & Chen, S. (2023). Adaptive Speckle Filter for Multi-Temporal PolSAR Image with Multi-Dimensional Information Fusion. Remote Sensing, 15(14), 3679. https://doi.org/10.3390/rs15143679








