Multi-Scale Feature Residual Feedback Network for Super-Resolution Reconstruction of the Vertical Structure of the Radar Echo
Abstract
1. Introduction
2. Related Work
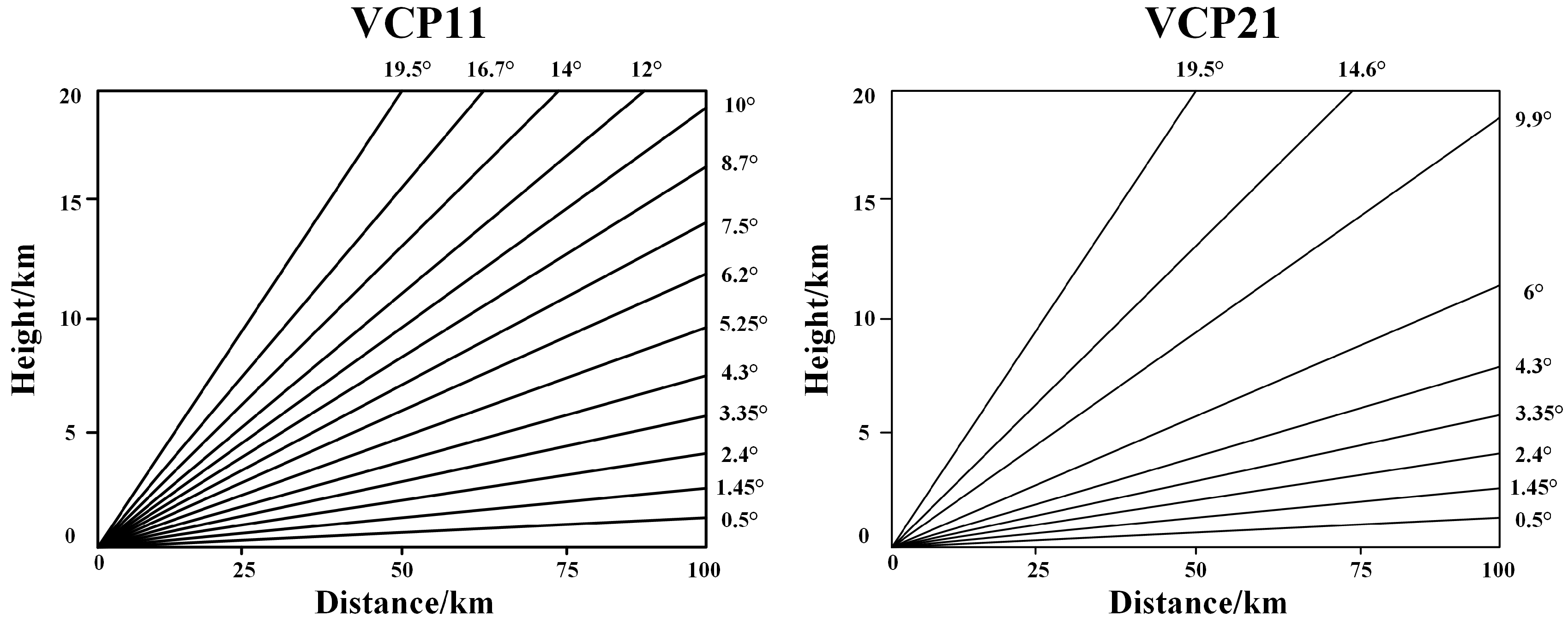
2.1. Radar Echo Based Resolution Improvement
2.2. Upsampling Block
3. Proposed Method
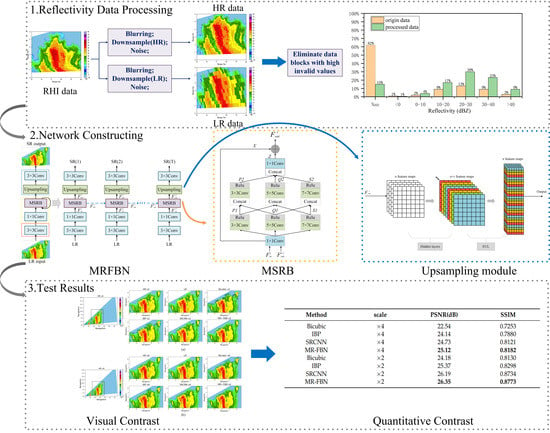
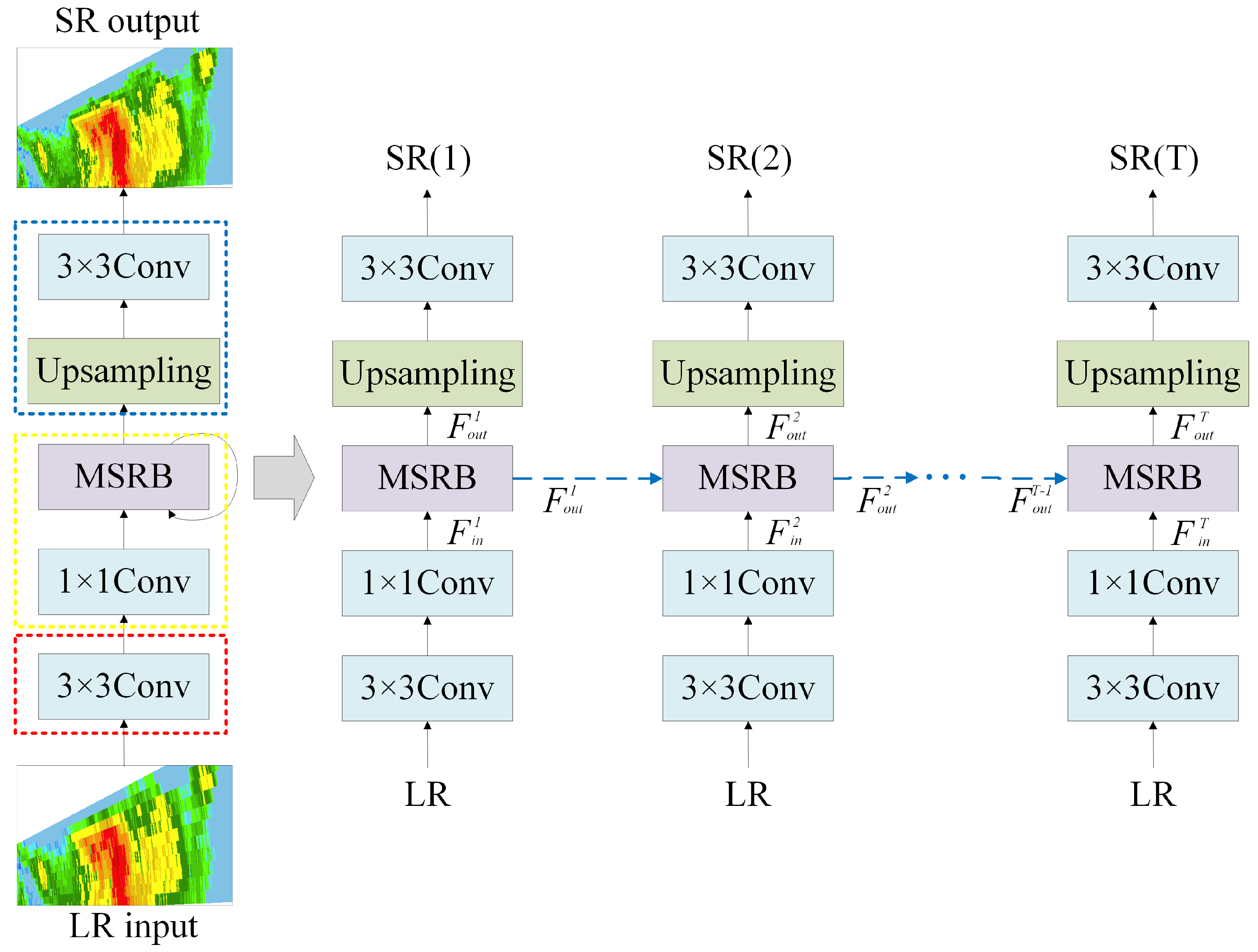
3.1. Network Structure
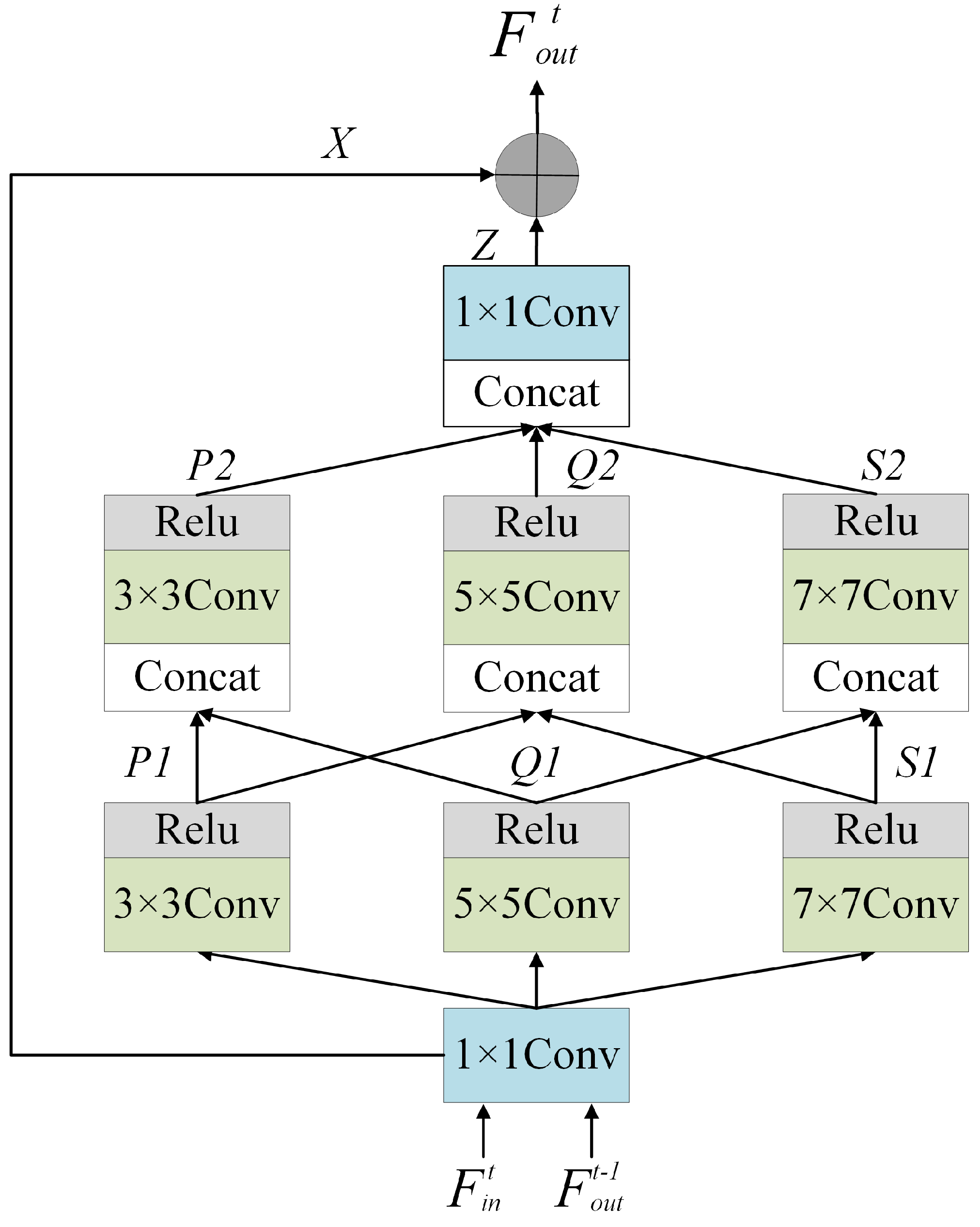
3.2. Multi-Scale Fusion Residual Block (MSRB)
3.3. Upsampling Module
4. Experiment
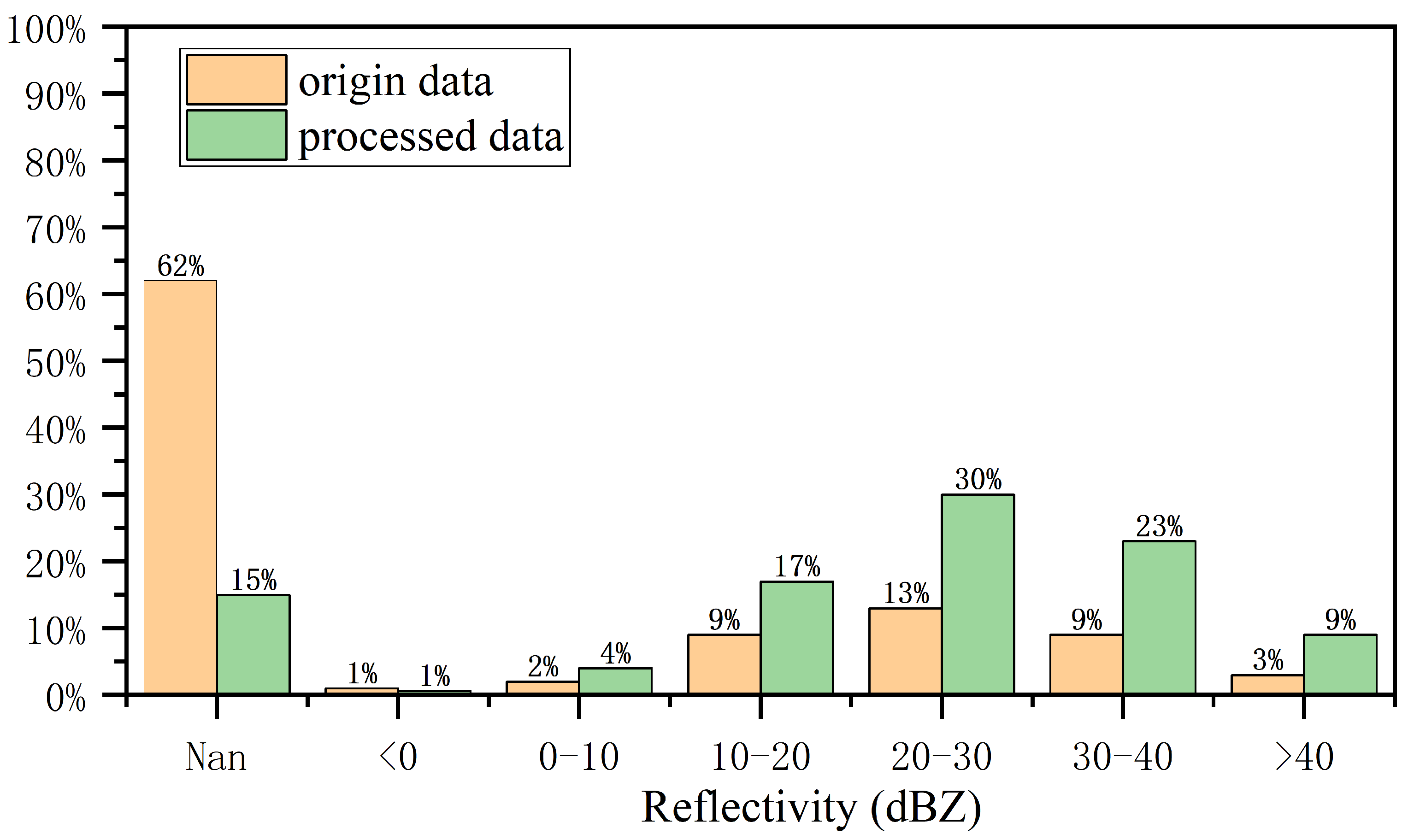
4.1. Datasets and Metrics
4.2. Implementation Details
4.3. Comparison with Existing Technology
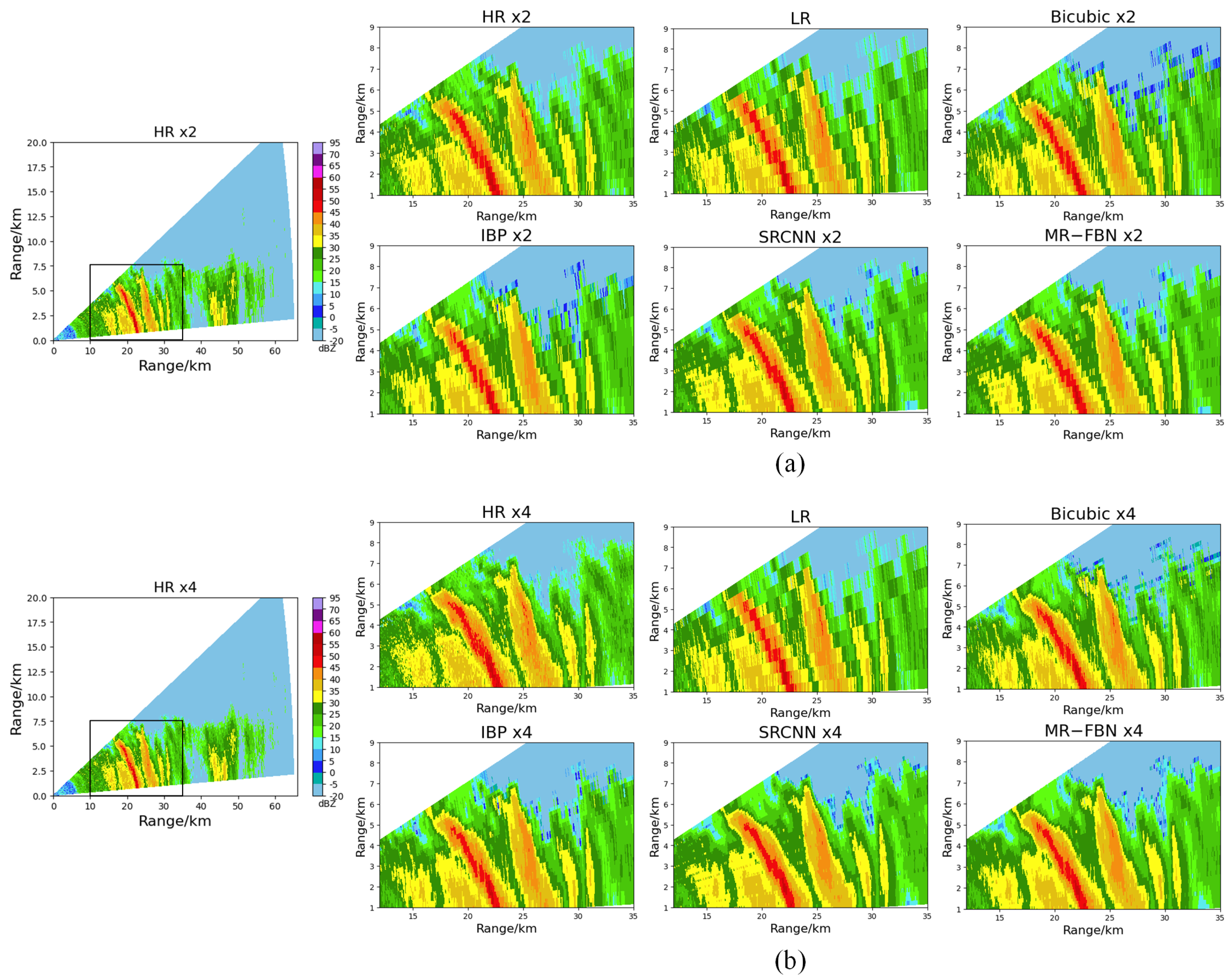
4.3.1. Visual Comparison
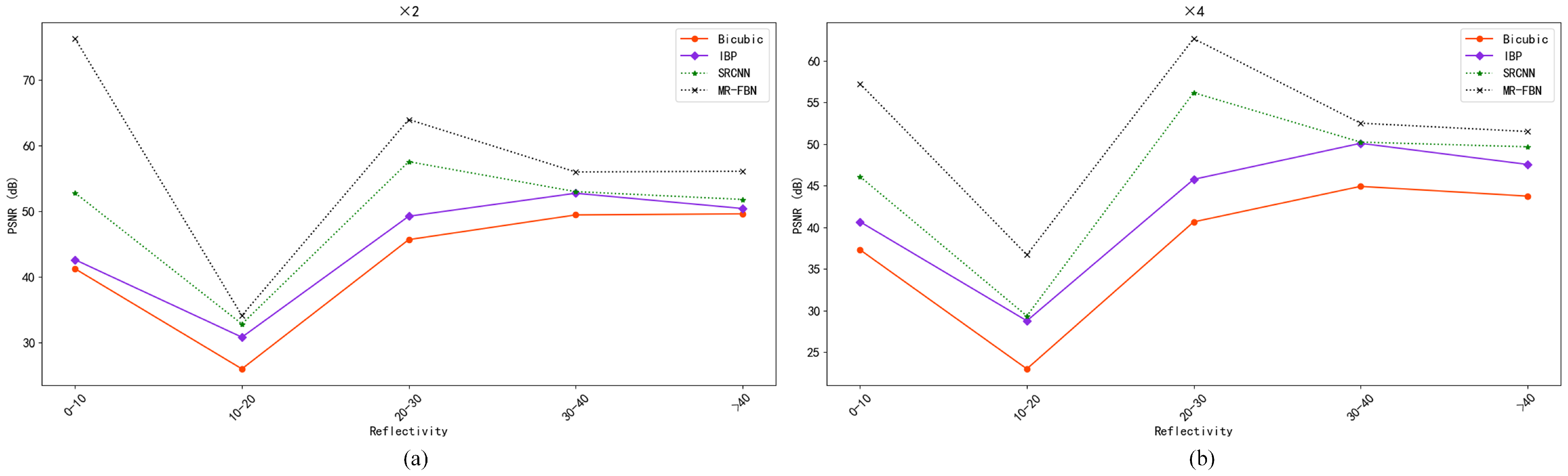
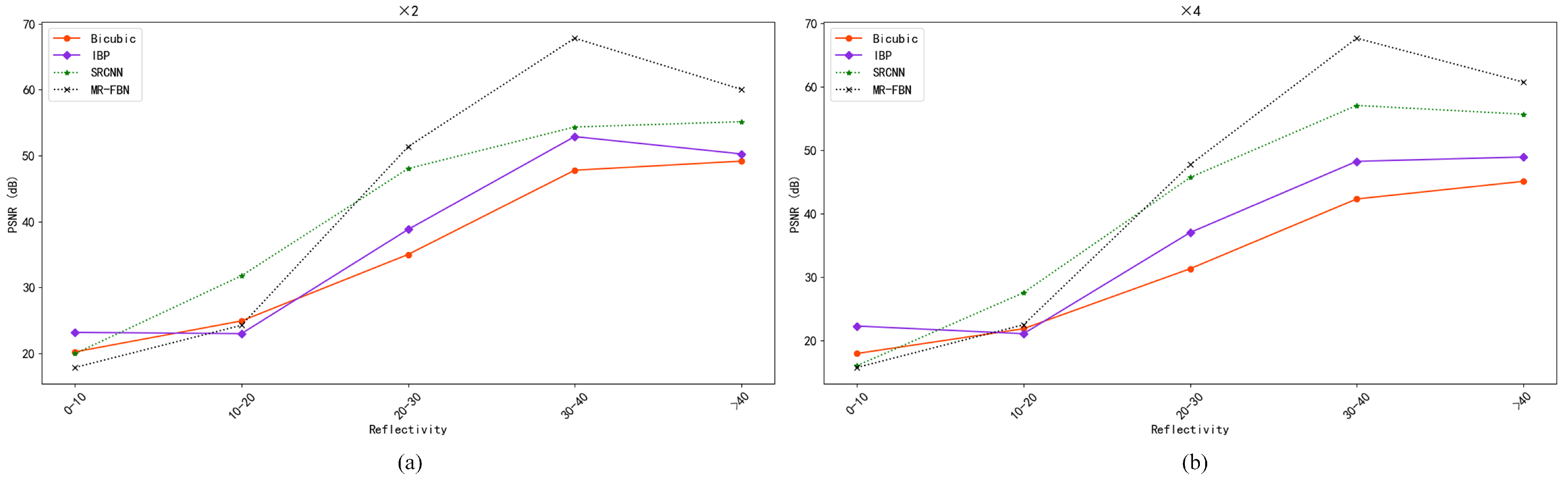
4.3.2. Quantitative Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| MR-FBN | Multi-Scale Residual Feedback Network |
| MSRB | Multi-Scale Feature Residual Blocks |
| EUL | Elevation Upsampling Layer |
| IBP | Interval Back-Projection |
| SRCNN | Super-Resolution Convolutional Neural Network |
| RHI | Range Height Indicator |
| VCP11 | Volume Coverage Pattern 11 |
| VCP21 | Volume Coverage Pattern 21 |
| CNN | Convolutional Neural Networks |
| LR | Low-Resolution |
| HR | High-Resolution |
| SR | Super-Resolution |
| PSNR | Peak Signal-to-Noise Ratio |
| SSIM | Structural Similarity Index |
| RNN | Recurrent Neural Networks |
| GAN | Generative Adversarial Networks |
References
- Liu, J.; Huang, X.; He, Y.; Wang, Z.; Wang, J. Comparison and Analysis of X-band Phased Array Weather Radar Echo Data. Plateau Meteorol. 2015, 34, 1167–1176. [Google Scholar]
- Lim, S.; Allabakash, S.; Jang, B.; Chandrasekar, V. Polarimetric radar signatures of a rare tornado event over South Korea. J. Atmos. Ocean. Technol. 2018, 35, 1977–1997. [Google Scholar] [CrossRef]
- Cho, J.Y.; Kurdzo, J.M. Weather radar network benefit model for tornadoes. J. Appl. Meteorol. Climatol. 2019, 58, 971–987. [Google Scholar] [CrossRef]
- Huang, C.; Zhang, A.; Chen, S.; Hu, B. Comparison of GPM Satellite and Ground Radar Estimation of Tornado Heavy Precipitation in Yancheng, Jiangsu. J. Atmos. Sci. 2020, 43, 370–380. [Google Scholar]
- Chen, D.; Chen, G.; Wu, Z. Combination RHI Automatic Realization Algorithm Based on Volume Scan Mode. Meteorological 2010, 36, 109–112. [Google Scholar]
- Liu, Y.; Gu, S.; Zhou, Y.; Zhang, S.; Dai, Z. Comparison and Analysis of Volume Scan Models of New Generation Weather Radar. Meteorological 2006, 32, 44–50. [Google Scholar]
- Zhang, Y.; Zhao, D.; Zhang, J.; Xiong, R.; Gao, W. Interpolation-dependent image downsampling. IEEE Trans. Image Process. 2011, 20, 3291–3296. [Google Scholar] [CrossRef]
- Thévenaz, P.; Blu, T.; Unser, M. Image interpolation and resampling. Handb. Med. Imaging Process. Anal. 2000, 1, 393–420. [Google Scholar]
- Qiu, D.; Zheng, L.; Zhu, J.; Huang, D. Multiple improved residual networks for medical image super-resolution. Future Gener. Comput. Syst. 2021, 116, 200–208. [Google Scholar] [CrossRef]
- Guo, K.; Guo, H.; Ren, S.; Zhang, J.; Li, X. Towards efficient motion-blurred public security video super-resolution based on back-projection networks. J. Netw. Comput. Appl. 2020, 166, 102691. [Google Scholar] [CrossRef]
- Huang, Y.; Shao, L.; Frangi, A.F. Simultaneous super-resolution and cross-modality synthesis of 3D medical images using weakly-supervised joint convolutional sparse coding. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 6070–6079. [Google Scholar]
- Dong, C.; Loy, C.C.; He, K.; Tang, X. Learning a deep convolutional network for image super-resolution. In Part IV 13, Proceedings of the Computer Vision–ECCV 2014: 13th European Conference, Zurich, Switzerland, 6–12 September 2014; Springer: New York, NY, USA, 2014; pp. 184–199. [Google Scholar]
- Torres, S.M.; Curtis, C.D. 5B. 10 Initial Implementation of Super-Resolution Data on the Nexrad Network. Available online: https://ams.confex.com/ams/87ANNUAL/techprogram/paper_116240.htm (accessed on 27 December 2022).
- Yao, H.; Wang, J.; Liu, X. Minimum Entropy Spectral Extrapolation Technique and Its Application in Radar Super-resolution. Mod. Radar 2005, 27, 18–19. [Google Scholar]
- Gallardo-Hernando, B.; Munoz-Ferreras, J.; Pérez-Martınez, F. Super-resolution techniques for wind turbine clutter spectrum enhancement in meteorological radars. IET Radar Sonar Navig. 2011, 5, 924–933. [Google Scholar] [CrossRef]
- He, J.; Ren, H.; Zeng, Q.; Li, X. Super-Resolution reconstruction algorithm of weather radar based on IBP. J. Sichuan Univ. (Nat. Sci. Ed.) 2014, 51, 415–418. [Google Scholar]
- Wu, Y.; Zhang, Y.; Zhang, Y.; Huang, Y.; Yang, J. TSVD with least squares optimization for scanning radar angular super-resolution. In Proceedings of the 2017 IEEE Radar Conference (RadarConf), Seattle, WA, USA, 8–12 May 2017; IEEE: New York, NY, USA, 2017; pp. 1450–1454. [Google Scholar]
- Tan, K.; Li, W.; Zhang, Q.; Huang, Y.; Wu, J.; Yang, J. Penalized maximum likelihood angular super-resolution method for scanning radar forward-looking imaging. Sensors 2018, 18, 912. [Google Scholar] [CrossRef]
- Zeng, Q.; He, J.; Shi, Z.; Li, X. Weather radar data compression based on spatial and temporal prediction. Atmosphere 2018, 9, 96. [Google Scholar] [CrossRef]
- Zhang, X.; He, J.; Zeng, Q.; Shi, Z. Weather radar echo super-resolution reconstruction based on nonlocal self-similarity sparse representation. Atmosphere 2019, 10, 254. [Google Scholar] [CrossRef]
- Yuan, H.; Zeng, Q.; He, J. Weather Radar Image Superresolution Using a Nonlocal Residual Network. J. Math. 2021, 2021, 4483907. [Google Scholar] [CrossRef]
- Zeiler, M.D.; Fergus, R. Visualizing and understanding convolutional networks. In Part I 13, Proceedings of the Computer Vision–ECCV 2014: 13th European Conference, Zurich, Switzerland, 6–12 September 2014; Springer: New York, NY, USA, 2014; pp. 818–833. [Google Scholar]
- Long, J.; Shelhamer, E.; Darrell, T. Fully convolutional networks for semantic segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 3431–3440. [Google Scholar]
- Dong, C.; Loy, C.C.; Tang, X. Accelerating the super-resolution convolutional neural network. In Part II 14, Proceedings of the Computer Vision–ECCV 2016: 14th European Conference, Amsterdam, The Netherlands, 11–14 October 2016; Springer: New York, NY, USA, 2016; pp. 391–407. [Google Scholar]
- Odena, A.; Dumoulin, V.; Olah, C. Deconvolution and checkerboard artifacts. Distill 2016, 1, e3. [Google Scholar] [CrossRef]
- Shi, W.; Caballero, J.; Huszár, F.; Totz, J.; Aitken, A.P.; Bishop, R.; Rueckert, D.; Wang, Z. Real-time single image and video super-resolution using an efficient sub-pixel convolutional neural network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 1874–1883. [Google Scholar]
- Wang, Z.; Chen, J.; Hoi, S.C. Deep learning for image super-resolution: A survey. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 43, 3365–3387. [Google Scholar] [CrossRef]
- Gao, H.; Yuan, H.; Wang, Z.; Ji, S. Pixel transposed convolutional networks. IEEE Trans. Pattern Anal. Mach. Intell. 2019, 42, 1218–1227. [Google Scholar] [CrossRef] [PubMed]
- Agarap, A.F. Deep learning using rectified linear units (relu). arXiv 2018, arXiv:1803.08375. [Google Scholar]
- Horé, A.; Ziou, D. Image Quality Metrics: PSNR vs. SSIM. In Proceedings of the 2010 20th International Conference on Pattern Recognition, Milan, Italy, 23–26 August 2010; pp. 2366–2369. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Wang, S.; Zhou, T.; Lu, Y.; Di, H. Contextual transformation network for lightweight remote-sensing image super-resolution. IEEE Trans. Geosci. Remote. Sens. 2021, 60, 1–13. [Google Scholar] [CrossRef]
- Li, Z.; Yang, J.; Liu, Z.; Yang, X.; Jeon, G.; Wu, W. Feedback network for image super-resolution. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 3867–3876. [Google Scholar]
- Paszke, A.; Gross, S.; Chintala, S.; Chanan, G.; Yang, E.; DeVito, Z.; Lin, Z.; Desmaison, A.; Antiga, L.; Lerer, A. Automatic Differentiation in Pytorch. 2017. Available online: https://openreview.net/forum?id=BJJsrmfCZ (accessed on 27 December 2022).





| Parameter | Min | Typ | Max | Unit |
|---|---|---|---|---|
| Frequency | 9380 | 9410 | 9440 | MHz |
| Peak Output Power | 18.0 | 18.5 | 25.0 | kW |
| Duty Cycle | 0.15 | 0.16 | % | |
| Pulse Width | 100 | 660 | 2000 | ns |
| Range sampling interval | 60 | m | ||
| Elevation angle interval | 0.1 | 0.3 | ° |
| Method | Scale | PSNR (dB) | SSIM |
|---|---|---|---|
| Bicubic | ×4 | 22.54 | 0.7253 |
| IBP | ×4 | 24.14 | 0.7880 |
| SRCNN | ×4 | 24.73 | 0.8121 |
| MR-FBN | ×4 | 25.12 | 0.8182 |
| Bicubic | ×2 | 24.18 | 0.8130 |
| IBP | ×2 | 25.37 | 0.8298 |
| SRCNN | ×2 | 26.19 | 0.8734 |
| MR-FBN | ×2 | 26.35 | 0.8773 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fu, X.; Zeng, Q.; Zhu, M.; Zhang, T.; Wang, H.; Chen, Q.; Yu, Q.; Xie, L. Multi-Scale Feature Residual Feedback Network for Super-Resolution Reconstruction of the Vertical Structure of the Radar Echo. Remote Sens. 2023, 15, 3676. https://doi.org/10.3390/rs15143676
Fu X, Zeng Q, Zhu M, Zhang T, Wang H, Chen Q, Yu Q, Xie L. Multi-Scale Feature Residual Feedback Network for Super-Resolution Reconstruction of the Vertical Structure of the Radar Echo. Remote Sensing. 2023; 15(14):3676. https://doi.org/10.3390/rs15143676
Chicago/Turabian StyleFu, Xiangyu, Qiangyu Zeng, Ming Zhu, Tao Zhang, Hao Wang, Qingqing Chen, Qiu Yu, and Linlin Xie. 2023. "Multi-Scale Feature Residual Feedback Network for Super-Resolution Reconstruction of the Vertical Structure of the Radar Echo" Remote Sensing 15, no. 14: 3676. https://doi.org/10.3390/rs15143676
APA StyleFu, X., Zeng, Q., Zhu, M., Zhang, T., Wang, H., Chen, Q., Yu, Q., & Xie, L. (2023). Multi-Scale Feature Residual Feedback Network for Super-Resolution Reconstruction of the Vertical Structure of the Radar Echo. Remote Sensing, 15(14), 3676. https://doi.org/10.3390/rs15143676