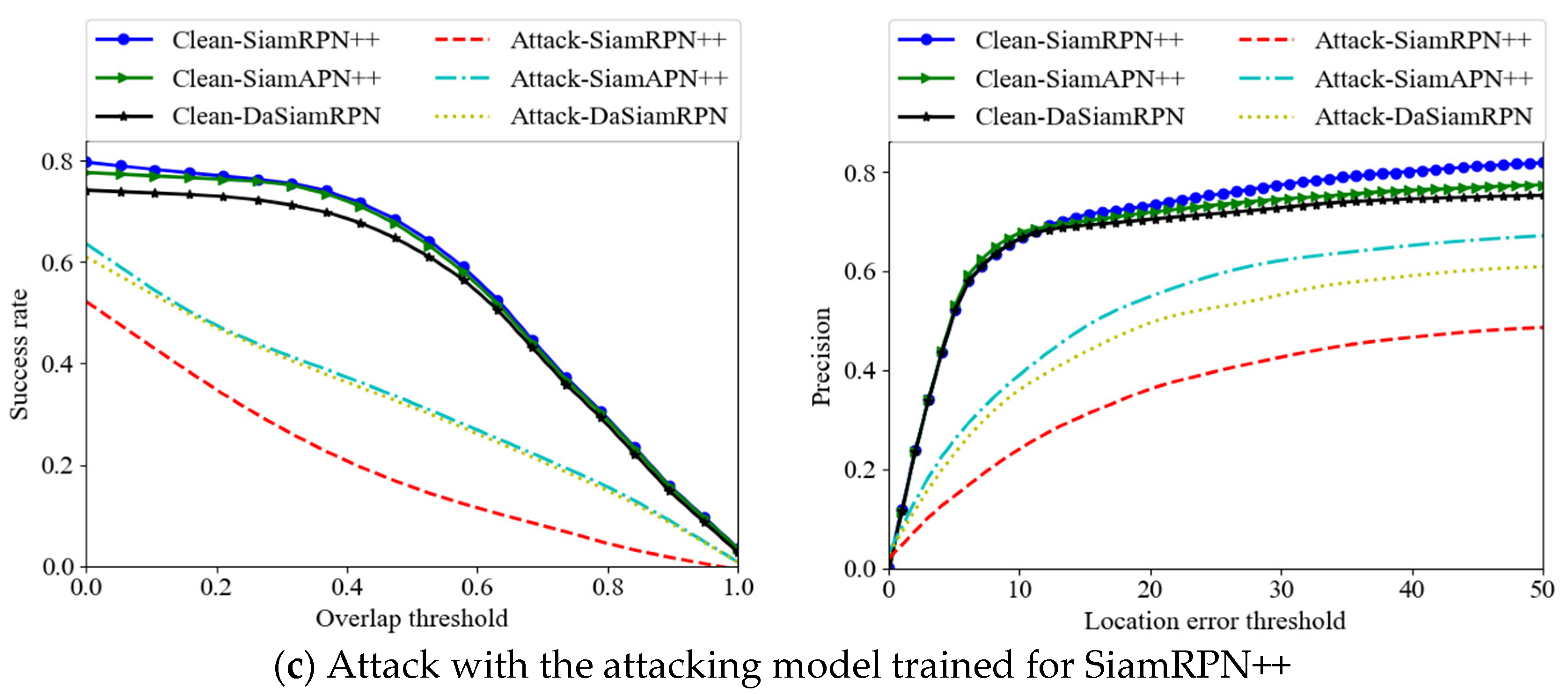
To effectively execute an adversarial attack on object tracking algorithms using adversarial patches, we have developed a patch-generating algorithm capable of generating distinct patches for both the template and search region. By introducing these patches, we aim to induce a mismatch in the tracked target, leading to a reduction in the bounding box size and an increase in the disparity of deep features between the search region and template.
3.1. Brief Description of SiamRPN++
The SiamRPN++ network improves upon the SiamRPN by introducing three key enhancements: a sampling strategy for increased spatial invariance, a feature aggregation strategy for improved representation, and a depth-wise separable correlation structure for enhanced cross-correlation operations. These improvements collectively contribute to the enhanced performance of the SiamRPN++ network in object-tracking tasks.
The SiamRPN++ object tracking network utilizes a modified ResNet-50 [
35] architecture as its Siamese network, extracting similar features from three levels for both the template and search regions. These features are then used in a cross-correlation operation, employing a depth-wise separable correlation structure and weighted sum operation to aggregate the outputs from the three levels.
Following the cross-correlation operation, the network generates two feature maps for prediction: the class score feature map and the regression feature map. The class score feature map is responsible for determining whether the regions correspond to the positive object, while the regression feature map is utilized to regress the exact location and size of the object based on anchor boxes.
During the inference phase, the proposal’s location and size are decoded based on the anchor boxes. The network then applies a cosine window and a scale change penalty to re-rank the proposals, selecting the highest-ranked proposals for further consideration. Finally, the Non-maximum Suppression (NMS) algorithm is employed to obtain the final tracking bounding box.
3.2. Patch Generating Network Structure
In Siamese network-based object tracking, the template branch plays a critical role in the tracking process for several reasons. Firstly, it provides an initial reference point for the tracker, enabling accurate localization of the target object. Secondly, the template branch is responsible for feature extraction and encoding, capturing appearance information and essential characteristics of the target, which forms a compact representation. Lastly, the template branch provides a template depth feature that is cross-correlated with the depth feature of the search region, facilitating the tracking process.
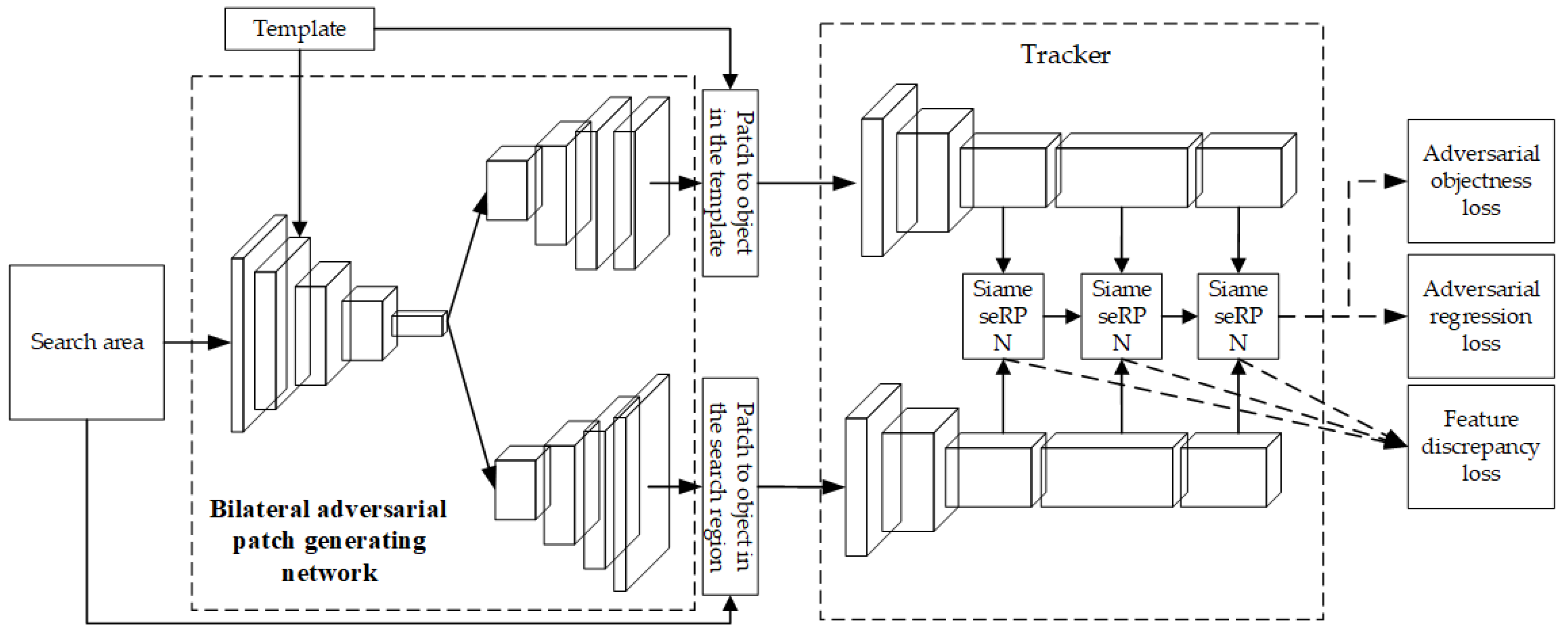
Based on the template branch’s importance and adversarial perturbations’ significant impact on deep features, we have devised BAPGNet, as depicted in
Figure 2. Our approach focuses on generating adversarial patches for both the template and search regions to enhance the discrepancy between them. Consequently, our patch-generating network takes both the search region and the template as inputs and produces two separate patches for each of them.
The overall structure of our network consists of three main components. Firstly, we employ a backbone architecture to extract features from both the template and search regions. This allows the network to capture relevant information from both inputs simultaneously. Secondly, we incorporate a branch specifically designed for generating an adversarial patch for the template region. This branch focuses on perturbing the template region while taking into account its unique characteristics. Thirdly, we include another branch dedicated to generating an adversarial patch for the search region. This branch focuses on influencing the search region while considering its distinctive attributes.
In the SiamRPN++ network, the search region is twice as large as the template, making it unsuitable for direct input to the network. To address this issue, we utilize the Focus operation from YOLOV5 [
36] to reduce the size of the search region by half. We then concatenate the half-sized search region with the template, creating the input for the network.
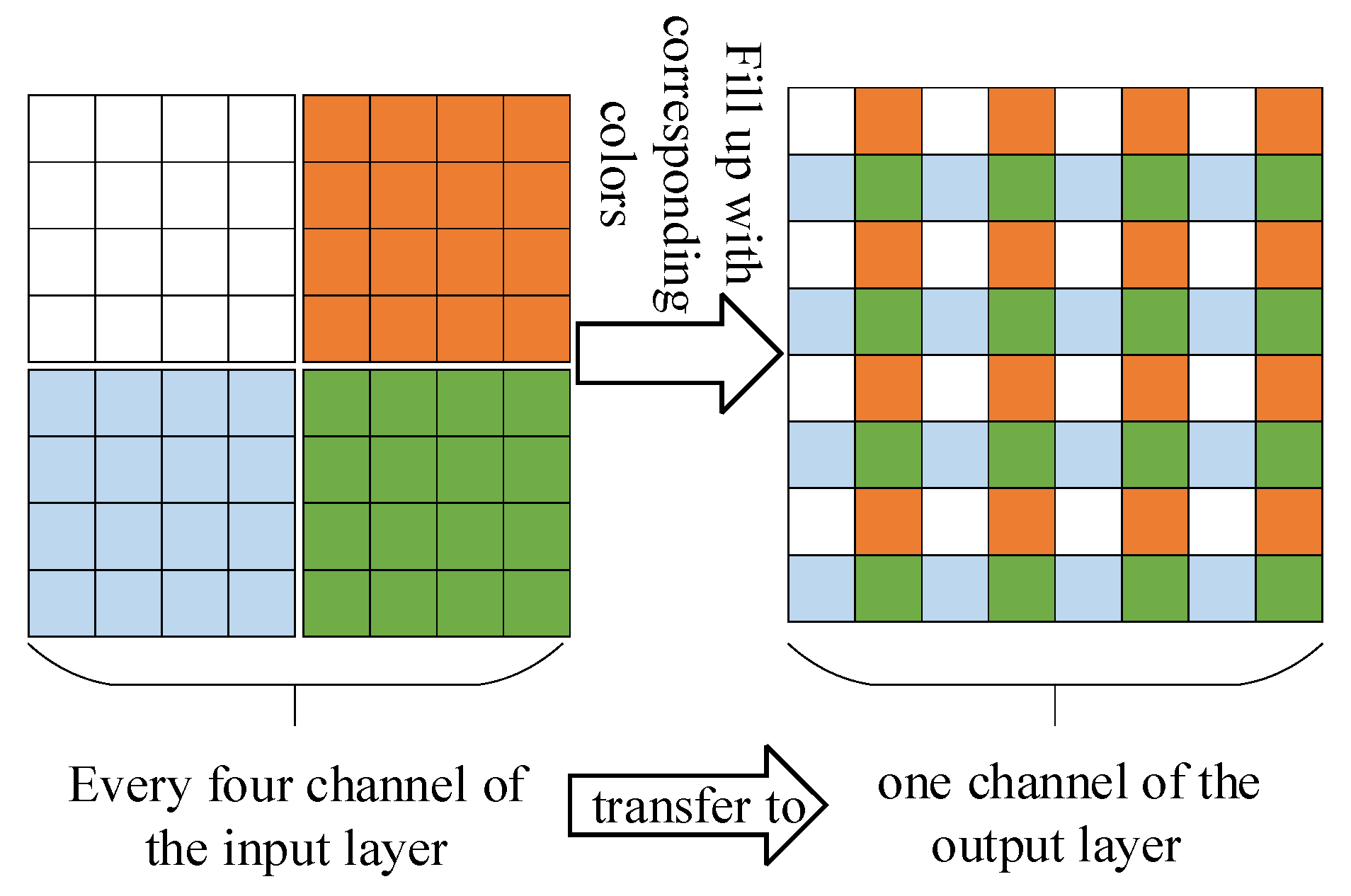
After extracting the features, we employ two branch networks to generate adversarial images separately for the template and search regions. The output size of the adversarial images matches the size of the template and search regions in the tracking network, respectively. To handle the size discrepancy between the template and search regions, we introduce the DeFocus model [
10] to the branch generating the adversarial image for the search region. The DeFocus operation effectively doubles the size of the feature map, ensuring compatibility. Furthermore, the DeFocus operation reduces the size of the preceding feature map, reducing computational complexity and improving operating speed. The DeFocus operation is depicted in
Figure 3.
The network’s direct output adversarial images in
Figure 2 cannot directly add to the tracker input. We use the ground truth to generate a mask
M for the objects in the template and search region, respectively. Then, use the mask
M to select the patch in the adversarial image and patch it to the corresponding location. The patch process is described as follows:
where the
Ip,
Ia,
I is the patched image (adversarial sample), adversarial image, and the clean input image, respectively. The
is the elementwise product operation. The
is the inverse of the mask
M.
The backbone used in this network is based on YOLOv5′s backbone, which has been proven to have strong feature extraction capabilities. To obtain adversarial images that have the same size as the inputs, we reversed the backbone as the decoder.
It is important to note that the search region size is not always exactly twice that of the template. We apply zero-padding to the template and search region to address this discrepancy. This ensures that the size of the search region is precisely twice that of the template. Subsequently, to restore the output to its original size, which matches the size of the search region and template in the tracking algorithm, we remove the pixels corresponding to the padded areas in the inputs. By doing so, we retain the consistency of the outputs with respect to the original input dimensions.
3.3. Loss Function
The network shown in
Figure 2 requires a specific training goal that aims to confuse the network instead of enabling it to locate a target within a search region accurately. To misguide the tracker, three approaches can be taken:
Introducing contrasts in the extracted features of the template and the search region before cross-correlation. These contrasts make it harder for the network to match the features of the template and the search region.
Leading the classification branch of the RPN to give the background a higher score than the tracking object. This approach makes the network more likely to identify background regions as potential targets.
Introducing deviations and shrink in the bounding box of the tracking object within the search region. This approach makes it more difficult for the network to precisely locate the object.
By implementing these three approaches during the training process, the network becomes more confused and less accurate in identifying and locating targets within a search region.
To specifically apply the first loss function, we utilize the maximum textural discrepancy loss [
14]. This loss function aims to maximize the discrepancy between the deep features of the search region and template, making their features unmatched. While this loss function helps to dampen the classification heat map of the RPN network to some extent, it does not directly deceive the tracking network alone. Therefore, to effectively fool the network, combining it with two other types of loss functions is necessary.
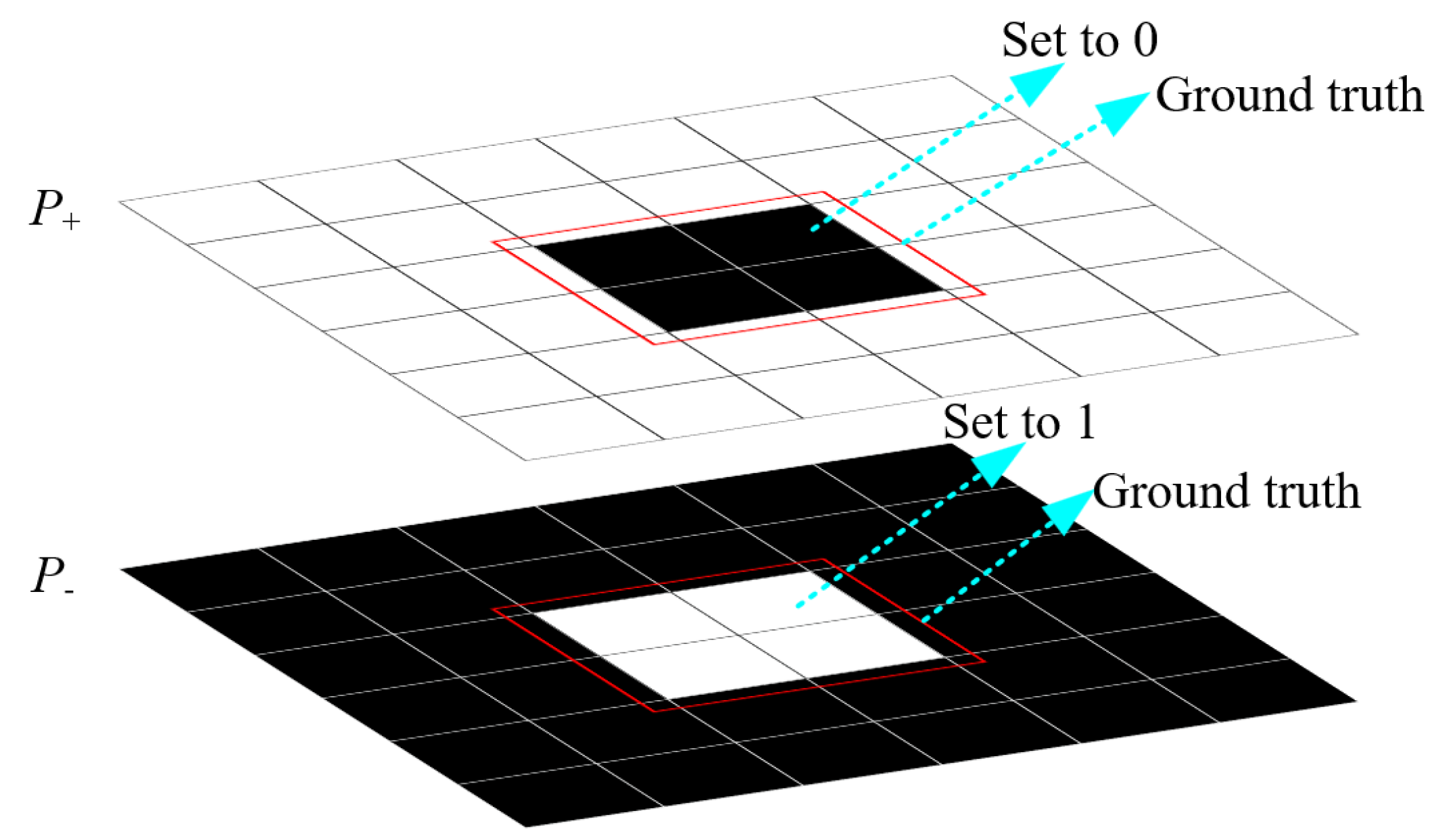
The second loss function leads the network to regard the background as the tracking object and vice versa. This can be achieved by attacking the classification branch of the RPN. Originally, the RPN assigns positive or negative labels to anchor boxes based on overlap with ground truth.
We reverse the label assignment method to lead the network to ignore the tracking object. In SiamRPN++, anchor boxes with an Intersection over Union (IoU) greater than 0.6 with the ground truth are assigned positive labels. To reverse the label assignment, we set
P+ to 0 and
P- to 1 when the anchor has an IoU greater than 0.2 with the ground truth and
P+ to 1 and
P- to 0 when the anchor has an IoU less than 0.2. This reversal in label assignment effectively leads the network to ignore the actual tracking object and treat the background as the target. The assignment process is illustrated in
Figure 4. Therefore, the second type of loss in this paper is designed as follows:
the
p+ and
p- are the positive and negative samples of ground truth, respectively. The
and
is the predicted result of the positive and negative samples.
N is the overall anchor in the network’s output. The loss function maximizes the probability of incorrect RPN classification predictions by reversing label assignments. It misleads the Region Proposal Network (RPN) into predicting high confidence scores for the background. This subtly misleads the SiamRPN++ tracker, causing it to lose the target.
For the third type of loss, we design an adversarial regression loss to attack the regression branch of the RPN. The RPN utilizes a regression branch to predict the offset of objects relative to corresponding anchor boxes. Specifically, it predicts four parameters (dx, dy, dw, and dh) that are used to calculate the bounding box coordinates of the object.
Mathematically, this can be expressed as:
where (
xan,
yan,
wan,
han) define the coordinates of the anchor box, and (
x,
y,
w,
h) represents the predicted bounding box of the tracking object. The
dx and
dy parameters denote the center offset, while
dw and
dh indicate the log-space width and height offsets. By regressing to offsets rather than directly predicting bounding box coordinates, the RPN is able to scale predictions to boxes of any size linearly. The exponential function used for width and height offsets further ensures that predicted boxes do not have excessively low or high aspect ratios. This formulation enables the RPN to propose anchor boxes and corresponding object-bounding boxes over a wide range of scales.
To effectively manipulate the RPN into generating incorrect predictions, we propose an adversarial attack strategy utilizing the Generalized Intersection over Union (GIoU) (GIoU) [
37] loss. This loss function is employed to subtly misguide and shrink the bounding box of the tracking object. In this attack, our objective is to modify the predicted bounding box offsets
dx,
dy,
dw, and
dh produced by the regression branch of the RPN. To carry out this attack, we define the coordinates of the ground truth bounding box as (
dx*,
dy*,
w*,
h*). The original predicted bounding box from the RPN regression branch is denoted as (
dx,
dy,
dw,
dh). With these definitions in place, the adversarial regression loss
Lareg used to misguide the RPN is formulated as follows:
where
represents the Generalized Intersection over Union operation applied to the ground truth bounding box
and predicted bounding box
. We calculate the GIoU on all anchor boxes. This is because the anchor boxes that do not intersect with the ground truth box will be selected as proposals according to the loss function
Laboj, and the anchor boxes that do intersect with the ground truth box have a possibility of being selected as proposals. Therefore, we need to set the ground truth (
dx*,
dy*,
w*,
h*) for all anchor boxes in order to mislead the network into generating incorrect predictions.
To manipulate the RPN to predict bounding boxes far from the true object, we categorize the anchor boxes into four groups based on the position of their center points relative to the object’s center point. These groups are (1) the upper left group (UL), (2) the upper right group (UR), (3) the bottom right group (BR), and (4) the bottom left group (BL). An anchor’s center point is denoted as (
xan,
yan), and the center point of the tracking object is denoted as (
xo,
yo). The anchor is assigned to one of the four groups based on the following conditions:
for each group of anchor boxes, we aim to optimize the loss function
Lareg to manipulate the predictions as far from the target object as possible. To achieve this, we set the ground truth values (
dx*,
dy*,
dw*,
dh*) for each group as follows:
in Equation (7), we set the (
w*,
h*) to (0, 0) to shrink the bounding boxes.
Finally, the adversarial loss is designed as follows:
where the
,
and
are the weights to balance the three types of loss. The three hyperparameters need to be set manually according to experimental results. In our paper, the
,
, and
are set to 50, 1, and 1, respectively.