Analysis of a Relative Offset between the North American and the Global Vertical Datum in Gravity Potential Space
Abstract
1. Introduction
2. Datasets
2.1. GNSS/Leveling Data
2.2. Terrestrial Gravity Data
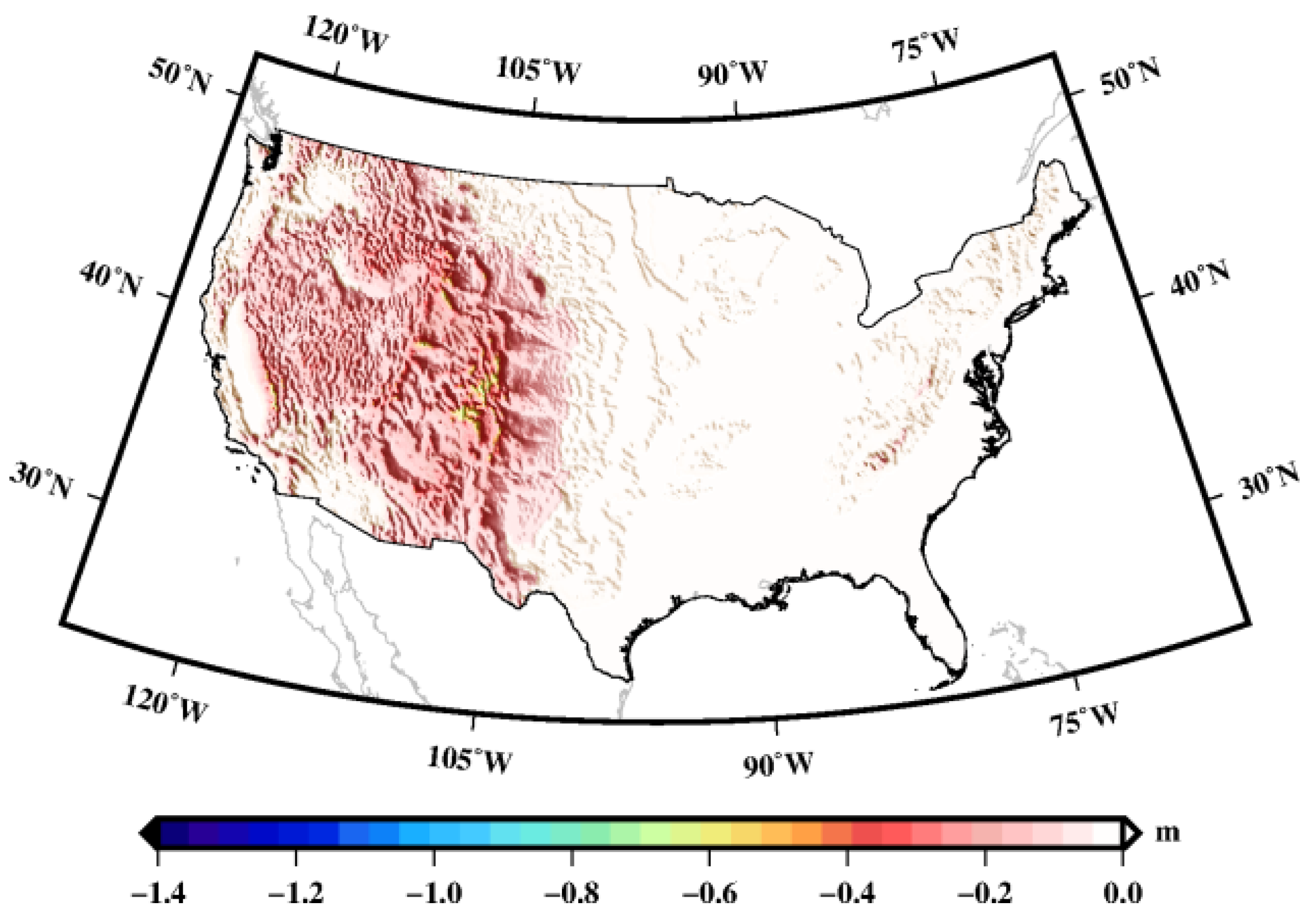
2.3. Topographic Data
2.4. GGMs
3. Methods to Determine Vertical Datum Offset
3.1. Geopotential Difference Approach
3.2. GBVP Approach
4. Some Issues Affecting LVD Offset Accuracy
4.1. Influence of the Ellipsoids
4.2. Gauss–Listing Geopotential Value
4.3. Parameter Transformations between the Ellipsoid and GGM
4.4. Contribution of the Zero-Order Term
4.5. Influence of the Tidal Effects
4.6. Treatment of Omission Error
4.7. Treatment of Systematic Errors
5. Results and Discussion
5.1. Results of Geopotential Difference Approach
5.2. Results of the GBVP Approach
6. Conclusions
- (1)
- The different methods for unifying the local and global vertical datums are explained. The datum offsets between different vertical datums are defined as the ratio of the geopotential difference to the mean gravity or mean normal gravity. The numerical results demonstrate that the discrepancy between the results obtained by different methods is negligible.
- (2)
- To estimate the vertical offset, it is necessary to consider the effects of the parameters of reference ellipsoids, the contribution of the zero-order term, the tide system, and the tilt error. Analysis shows that the effect caused only by the difference in geopotential values between GRS80 and the selected GGMs is approximately 93.8 cm. The difference in geoid heights related to the tide-free system and the mean-tide system reaches 9.7 cm at a latitude of 50°. In the presence of systematic effects and spatially correlated errors in height data, there is a significant northwest–southeast tilt in the differences between the GNSS/leveling data and gravimetric geoid heights, with an overall tilt of approximately 103 cm in the E–W direction and 69 cm in the N–S direction.
- (3)
- Theoretical derivation and numerical analysis indicate that the results of the vertical offsets as calculated through the geopotential approach and GBVP approach are consistent. When selecting the normal gravity geopotential of the geodetic reference system as the gravity geopotential of the global height datum , the NAVD is greater than the GVD by approximately 0.04 m with reference to the GRS80 ellipsoid and by about 0.97 m with reference to the WGS84 ellipsoid. When selecting the Gauss–Listing geopotential value as the gravity geopotential of the global height datum , the NAVD is approximately 1.45 m higher than the GVD with reference to the GRS80 reference ellipsoid and approximately 0.52 m with reference to the WGS84 ellipsoid.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Featherstone, W.E. Attempts to unify the Australian height datum between the Mainland and Tasmania. Vert. Ref. Syst. 2002, 124, 328–333. [Google Scholar]
- Filmer, M.S.; Hughes, C.W.; Woodworth, P.L.; Featherstone, W.E.; Bingham, R.J. Comparison between geodetic and oceanographic approaches to estimate mean dynamic topography for vertical datum unification: Evaluation at Australian tide gauges. J. Geod. 2018, 92, 1413–1437. [Google Scholar] [CrossRef]
- Slobbe, D.C.; Klees, R.; Verlaan, M.; Zijl, F.; Alberts, B.; Farahani, H.H. Height system connection between island and mainland using a hydrodynamic model: A case study connecting the Dutch Wadden islands to the Amsterdam ordnance datum (NAP). J. Geod. 2018, 92, 1439–1456. [Google Scholar] [CrossRef] [PubMed]
- Dilkoski, D.B. Results of the General Adjustment of the North American Vertical Datum of 1988. Surv. Land Inf. Syst. 1992, 52, 133–149. [Google Scholar]
- Smith, D.A.; Véronneau, M.; Roman, D.R.; Huang, J.; Sideris, M.G. Towards the Unification of the Vertical Datum Over the North American Continent; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Ardalan, A.A.; Safari, A. Global height datum unification: A new approach in gravity potential space. J. Geod. 2005, 79, 512–523. [Google Scholar] [CrossRef]
- Sánchez, L.; Dayoub, N.; Čunderlík, R.; Minarechová, Z.; Šíma, Z. W0 Estimates in the Frame of the GGOS Working Group on Vertical Datum Standardisation; Springer International Publishing: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Amin, H.; Sjoberg, L.E.; Bagherbandi, M. A global vertical datum defined by the conventional geoid potential and the Earth ellipsoid parameters. J. Geod. 2019, 93, 1943–1961. [Google Scholar] [CrossRef]
- Rummel, R. Global Integrated Geodetic and Geodynamic Observing System (GIGGOS). In Towards an Integrated Global Geodetic Observing System (IGGOS); Springer: Berlin/Heidelberg, Germany, 2000; Volume 120, pp. 253–260. [Google Scholar]
- Ihde, J.; Adam, J.; Gurtner, W.; Harsson, B.G.; Wppelmann, G. The Height Solution of the European Vertical Reference Network (EUVN). Veröff. Bayer. Komm. Für Die Internat. Erdmess. Astronom. Geod. Arb 2002, 61, 132–145. [Google Scholar]
- Rangelova, E.; Fotopoulos, G.; Sideris, M.G. Implementing a Dynamic Geoid as a Vertical Datum for Orthometric Heights in Canada. Gravity Geoid Earth Obs. 2010, 135, 295–302. [Google Scholar]
- Thompson, K.R.; Huang, J.; Véronneau, M.; Wright, D.G.; Lu, Y. Mean surface topography of the northwest Atlantic: Comparison of estimates based on satellite, terrestrial gravity, and oceanographic observations. J. Geophys. Res. 2009, 114. [Google Scholar] [CrossRef]
- Woodworth, P.L.; Hughes, C.W.; Bingham, R.J.; Gruber, T. Towards worldwide height system unification using ocean information. J. Geodetic Sci. 2011, 365, 2. [Google Scholar] [CrossRef]
- Bao, L.F.; Xu, H.Z.; Li, Z.C. Towards a 1 mGal accuracy and 1 min resolution altimetry gravity field. J. Geod. 2013, 87, 961–969. [Google Scholar] [CrossRef]
- Kotsakis, C.; Katsambalos, K.; Ampatzidis, D. Estimation of the zero-height geopotential level W0 LVDin a local vertical datum from inversion of co-located GPS, leveling and geoid heights: A case study in the Hellenic islands. J. Geod. 2012, 86, 423–439. [Google Scholar] [CrossRef]
- Tocho, C.; Vergos, G.S. Estimation of the Geopotential Value W0 for the Local Vertical Datum of Argentina Using EGM2008 and GPS/Levelling Data W0LVD. In IAG 150 Years; Springer: Berlin/Heidelberg, Germany, 2016; Volume 143, pp. 271–279. [Google Scholar]
- Bursa, M.; Kenyon, S.; Kouba, J.; Radej, K.; Vatrt, V.; Vojtiskova, M.; Simek, J. World height system specified by geopotential at tide gauge stations. Vert. Ref. Syst. 2002, 124, 291–296. [Google Scholar]
- Hayden, T.; Rangelova, E.; Sideris, M.G.; Véronneau, M. Evaluation of W0 in Canada using tide gauges and GOCE gravity field models. J. Geodetic Sci. 2012, 2, 290–301. [Google Scholar] [CrossRef]
- Grigoriadis, V.N.; Lambrou, E.; Vergos, G.S.; Tziavos, I.N. Assessment of the Greek Vertical Datum: A Case Study in Central Greece. In Proceedings of the International Symposium on Gravity, Geoid and Height Systems 2016: Proceedings Organized by IAG Commission 2 and the International Gravity Field Service, Thessaloniki, Greece, 19–23 September 2016; Springer International Publishing: Berlin/Heidelberg, Germany, 2019; pp. 185–191. [Google Scholar]
- Zhang, L.M.; Li, F.; Chen, W.; Zhang, C.Y. Height datum unification between Shenzhen and Hong Kong using the solution of the linearized fixed-gravimetric boundary value problem. J. Geod. 2009, 83, 411–417. [Google Scholar] [CrossRef]
- Gerlach, C.; Rummel, R. Global height system unification with GOCE: A simulation study on the indirect bias term in the GBVP approach. J. Geod. 2013, 87, 57–67. [Google Scholar] [CrossRef]
- Amjadiparvar, B.; Rangelova, E.; Sideris, M.G. The GBVP approach for vertical datum unification: Recent results in North America. J. Geod. 2016, 90, 45–63. [Google Scholar] [CrossRef]
- Shum, C.K.; Tapley, B.D.; Yuan, D.N.; Ries, J.C.; Schutz, B.E. An Improved Model for the Earth’s Gravity Field; The Ohio State University: Columbus, OH, USA, 1988. [Google Scholar]
- Denker, H. Evaluation of SRTM3 and GTOPO30 terrain data in Germany. In Gravity Geoid Space Mission; Springer: Berlin/Heidelberg, Germany, 2005; Volume 129, pp. 218–223. [Google Scholar]
- Pavlis, N.K.; Holmes, S.A.; Kenyon, S.C.; Factor, J.K. The development and evaluation of the Earth Gravitational Model 2008 (EGM2008). J. Geophys. Res.-Solid Earth 2012, 117. [Google Scholar] [CrossRef]
- Kosteleck, J.; Jaroslav, K.; Bucha, B.; Ale, B.; Frste, C. Evaluation of gravity field model EIGEN-6C4 by means of various functions of gravity potential, and by GNSS/levelling. Geoinformatics FCE CTU 2015, 14, 7. [Google Scholar] [CrossRef]
- Zingerle, P.; Pail, R.; Gruber, T.; Oikonomidou, X. The combined global gravity field model XGM2019e. J. Geod. 2020, 94, 66. [Google Scholar] [CrossRef]
- Grombein, T.; Seitz, K.; Heck, B. On High-Frequency Topography-Implied Gravity Signals for a Height System Unification Using GOCE-Based Global Geopotential Models. Surv. Geophys. 2017, 38, 443–477. [Google Scholar] [CrossRef]
- Turchette, Q.A.; Kielpinski, D.; King, B.E.; Leibfried, D.; Meekhof, D.M.; Myatt, C.J.; Rowe, M.A.; Sackett, C.A.; Wood, C.S.; Itano, W.M.; et al. Heating of trapped ions from the quantum ground state. Phys. Rev. A. 2000, 61, 063418. [Google Scholar] [CrossRef]
- Heiskanen, W.A.; Moritz, H. Physical Geodesy; W.H. Freeman and Company: San Francisco, CA, USA, 1967. [Google Scholar]
- Andersen, O.B.; Fotopolous, G.; Pavlis, N.K.; Sansò, F.; Tziavos, I.N. Geoid Determination: Theory and Methods; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Tenzer, R.; Vanicek, P.; Novak, P. Far-zone contributions to topographical effects in the Stokes-Helmert method of the geoid determination. Stud. Geophys. Geod. 2003, 47, 467–480. [Google Scholar] [CrossRef]
- Gatti, A.; Reguzzoni, M.; Venuti, G. The height datum problem and the role of satellite gravity models. J. Geod. 2013, 87, 15–22. [Google Scholar] [CrossRef]
- Sanso, F.; Venuti, G. The height datum/geodetic datum problem. Geophys. J. Int. 2002, 149, 768–775. [Google Scholar]
- Dayoub, N.; Edwards, S.J.; Moore, P. The Gauss–Listing geopotential value W0 and its rate from altimetric mean sea level and GRACE. J. Geod. 2012, 86, 681–694. [Google Scholar] [CrossRef]
- Heck, B. Problems in the Definition of Vertical Reference Frames. In V Hotine-Marussi Symposium on Mathematical Geodesy; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Sun, W.; Zhou, X.; Yang, L.; Zhou, D.; Li, F. Construction of the Mean Sea Surface Model Combined HY-2A With DTU18 MSS in the Antarctic Ocean. Front. Environ. Sci. 2021, 9, 697111. [Google Scholar] [CrossRef]
- Mäkinen, J. The permanent tide and the International Height Reference Frame IHRF. J. Geodesy. 2021, 95, 106. [Google Scholar] [CrossRef]
- Petit, G.; Luzum, B. IERS Conventions (2010); IERS Technical Note. US Naval Observatory: Washington, DC, USA, 2010. [Google Scholar]
- Rapp, R.H.; Wang, Y.M.; Pavlis, N.K. The Ohio State University Geopotential and sea Surface Topography Harmonic Coefficient Models; Department of Geodedic Sciences and Surveying, The Ohio State University: Columbus, OH, USA, 1991. [Google Scholar]
- Xiao, N.Y.; Xia, X.F. Love numbers calculated with PREM. Acta Geodaetica Et Cartographic Sinica. 1998, 27, 246–251. (In Chinese) [Google Scholar]
- Rülke, A.; Liebsch, G.; Sacher, M.; Schäfer, U.; Schirmer, U.; Ihde, J. Unification of European height system realizations. J. Geodetic Sci. 2012, 2, 343–354. [Google Scholar] [CrossRef]
- Hirt, C.; Marti, U.; Bürki, B.; Featherstone, W.E. Assessment of EGM2008 in Europe using accurate astrogeodetic vertical deflections and omission error estimates from SRTM/DTM2006.0 residual terrain model data. J. Geophys. Res. 2010, 115, B10404. [Google Scholar] [CrossRef]
- Hwang, C.; Hsu, H.J.; Featherstone, W.E.; Cheng, C.C.; Yang, M.; Huang, W.S.; Wang, C.Y.; Huang, J.F.; Chen, K.H.; Huang, C.H.; et al. New gravimetric-only and hybrid geoid models of Taiwan for height modernisation, cross-island datum connection and airborne LiDAR mapping. J. Geod. 2020, 94, 83. [Google Scholar] [CrossRef]
- Novák, P.; Kostelecký, J.; Klokočník, J. Testing global geopotential models through comparison of a local quasi-geoid model with GPS/leveling data. Stud. Geophys. Geod. 2009, 53, 39. [Google Scholar] [CrossRef]
- Burša, M.; Kouba, J.; Müller, A.; Raděj, K.; True, S.A.; Vatrt, V.; Vojtíšková, M. Determination of geopotential differences between local vertical datums and realization of a world height system. Stud. Geophys. Geod. 2001, 45, 127–132. [Google Scholar] [CrossRef]
- Amjadiparvar, B.; Rangelova, E.V.; Sideris, M.G.; Véronneau, M. North American height datums and their offsets: The effect of GOCE omission errors and systematic levelling effects. J. Appl. Geodesy. 2013, 7, 39–50. [Google Scholar] [CrossRef]
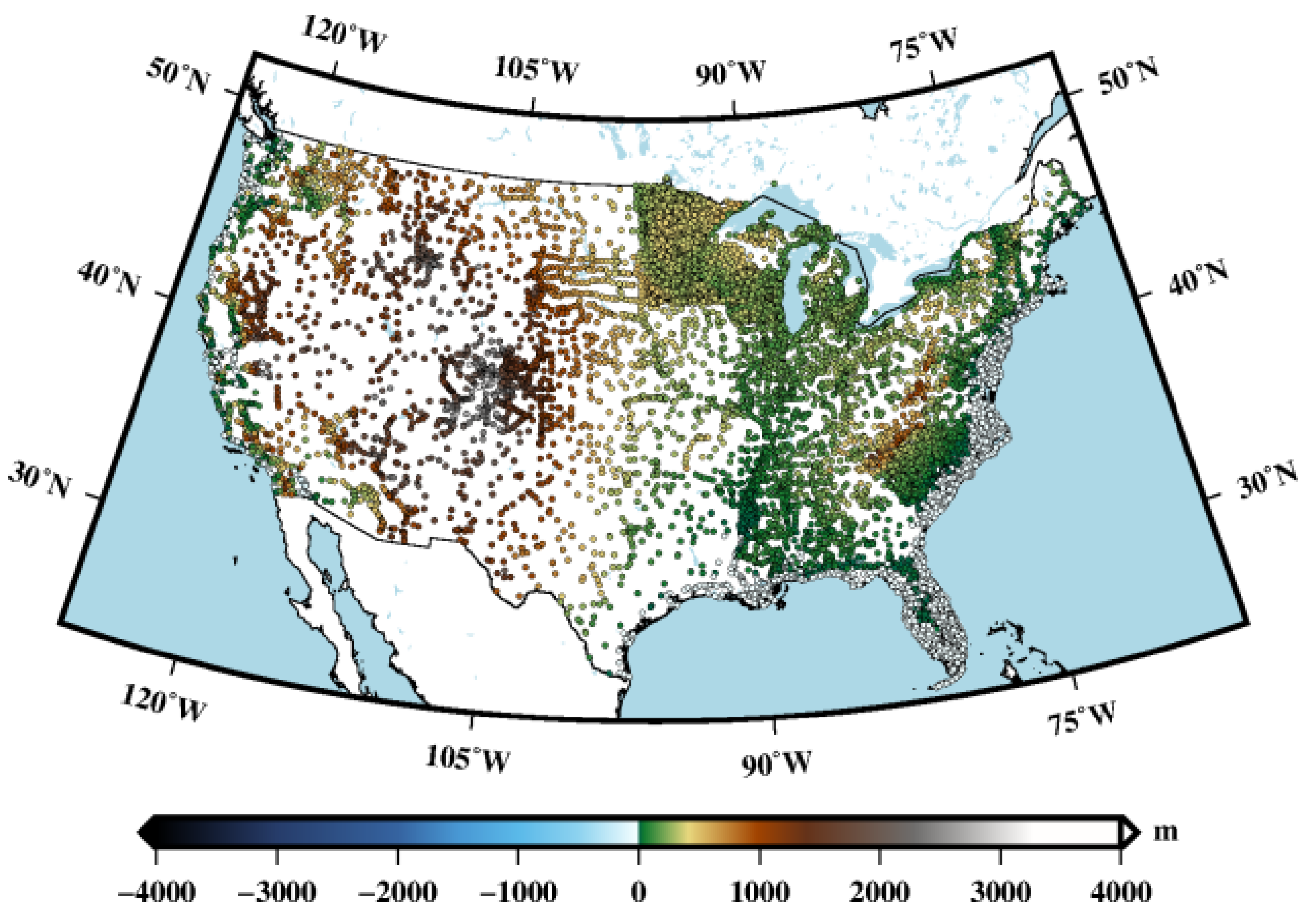
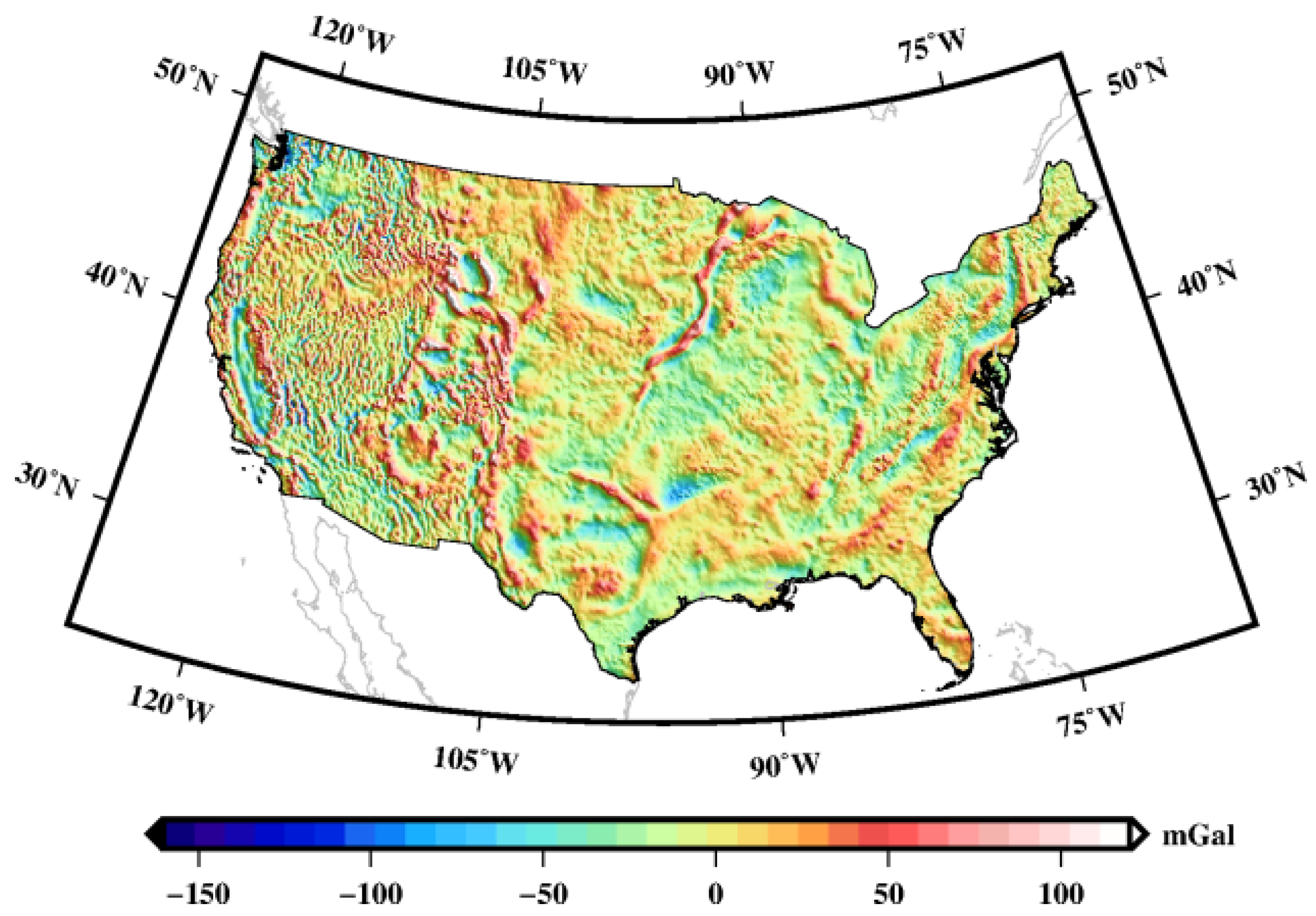

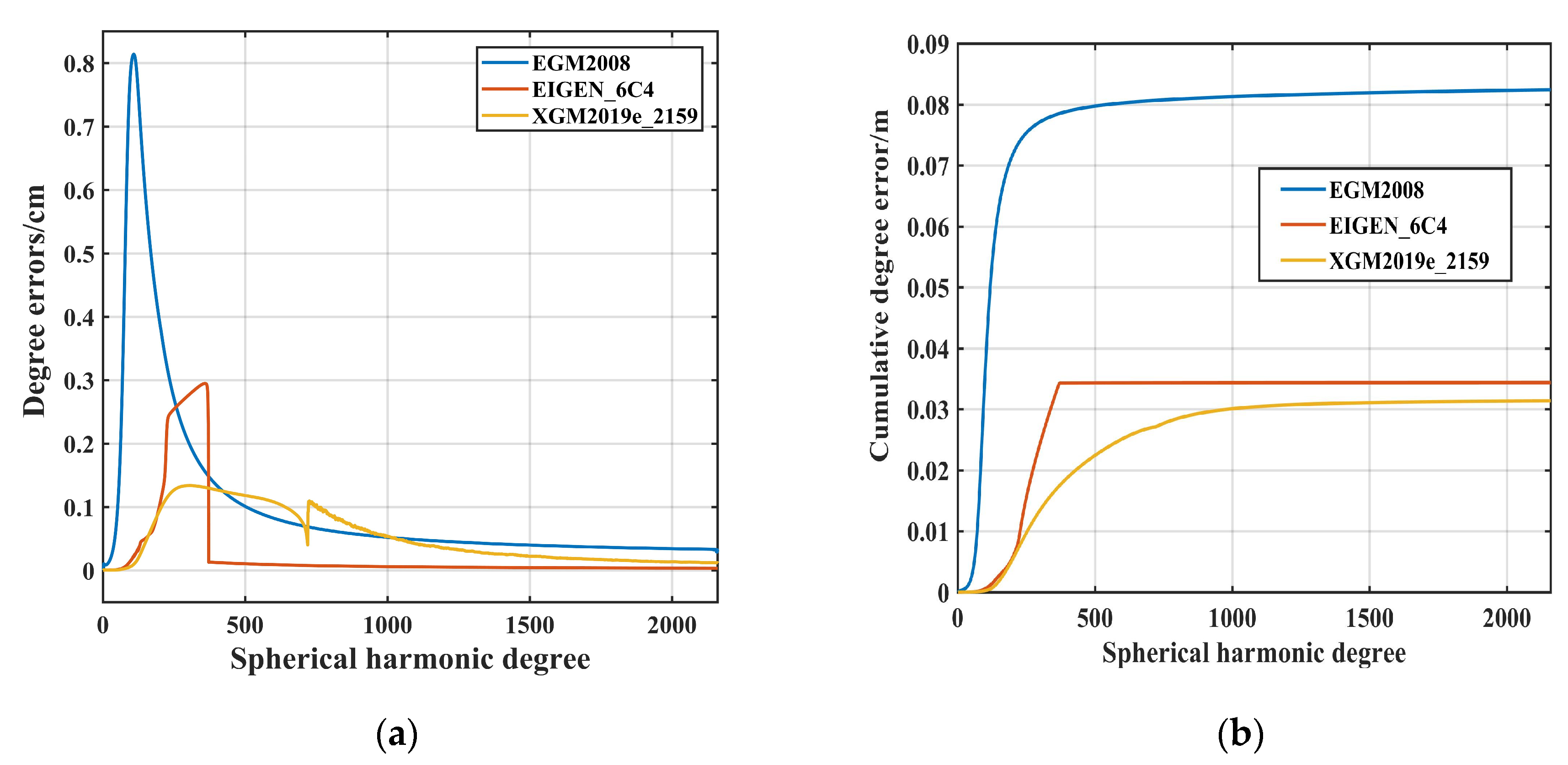



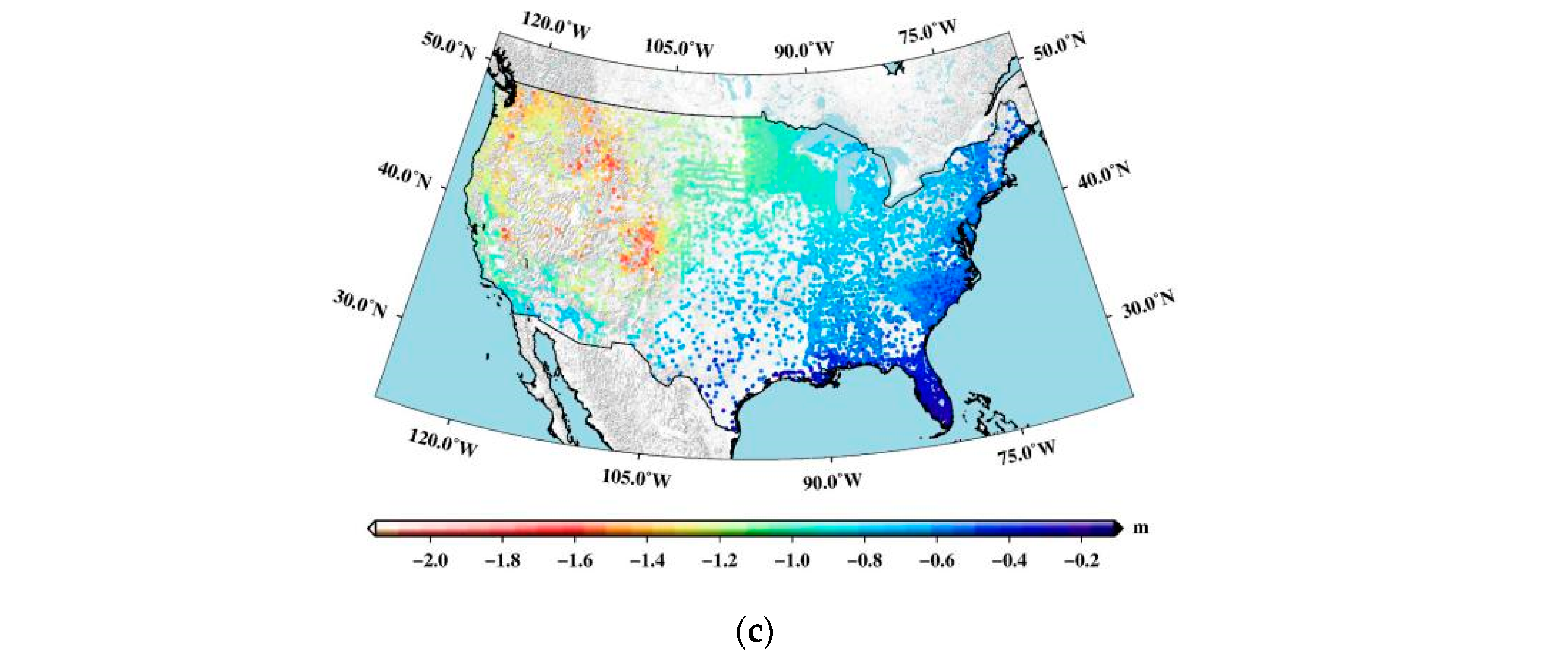

| Models | Max | Min | Mean | Std | |
|---|---|---|---|---|---|
| GNSS/leveling heights (m) | −7.45 | −38.96 | −27.63 | 6.07 | |
| SRTM (m) | 4276.21 | −484.52 | 777.69 | 728.08 | |
| DTM2006.0 (m) | 3807.24 | −622.36 | 779.83 | 722.11 | |
| terrestrial gravity (mGal) | 238.36 | −234.24 | −6.03 | 29.21 | |
| Gravity anomalies (mGal) | EGM2008 | 246.61 | −170.35 | 2.52 | 28.85 |
| EIGEN-6C4 | 248.59 | −170.87 | 2.53 | 28.89 | |
| XGM2019e_2159 | 252.42 | −175.26 | 2.52 | 28.42 | |
| Reference Systems | a/m | 1/f | GM/m3s−2 | U0/m2s−2 | J2/×10−3 |
|---|---|---|---|---|---|
| GRS80 | 6,378,137 | 298.257222101 | 3.986005000 × 1014 | 62,636,860.8500 | 0.484166854896119 |
| WGS84 | 6,378,137 | 298.257223563 | 3.986004418 × 1014 | 62,636,851.7146 | 0.484166774983522 |
| GGMs | a/m | Tide System | ||
|---|---|---|---|---|
| EGM2008 | 6,378,136.30 | −0.4841651437908150 × 10−3 | 3.986004415 × 1014 | tide-free |
| −0.4841693173669740 × 10−3 | zero-tide | |||
| EIGEN-6C4 | 6,378,136.46 | −0.4841652170610000 × 10−3 | 3.986004415 × 1014 | tide-free |
| XGM2019e_2159 | 6,378,136.30 | −0.4841694947475625 × 10−3 | 3.986004415 × 1014 | zero-tide |
| Reference Systems | EGM2008 | EIGEN-6C4 | XGM2019e_2159 |
|---|---|---|---|
| GRS80 | −0.938 | −0.938 | −0.938 |
| WGS84 | −0.005 | −0.005 | −0.005 |
| GGMs Used | Tilt Error in an E–W Direction (m/°) | Tilt Error in a N–S Direction (m/°) | Overall Tilt in an E–W Direction (m) | Overall Tilt in a N–S Direction (m) |
|---|---|---|---|---|
| EGM2008 | 0.028 | 0.018 | 1.03 | 0.69 |
| EIGEN-6C4 | 0.028 | 0.018 | 1.03 | 0.69 |
| XGM2019e_2159 | 0.026 | 0.018 | 1.03 | 0.64 |
| GGMs | Reference Systems | Geopotential Difference (m2s−2) | Vertical Offset (m) | |
|---|---|---|---|---|
| EGM2008 | GRS80 | 62,636,861.272 | −0.422 | −0.043 |
| WGS84 | 62,636,861.258 | −9.543 | −0.975 | |
| EIGEN-6C4 | GRS80 | 62,636,861.281 | −0.431 | −0.044 |
| WGS84 | 62,636,861.267 | −9.552 | −0.976 | |
| XGM2019e_2159 | GRS80 | 62,636,861.271 | −0.401 | −0.041 |
| WGS84 | 62,636,861.258 | −9.533 | −0.974 |
| GGMs | Reference Systems | Geopotential Difference (m2s−2) | Vertical Offset (m) |
|---|---|---|---|
| EGM2008 | GRS80 | −14.229 | −1.454 |
| WGS84 | −5.093 | −0.520 | |
| EIGEN-6C4 | GRS80 | −14.231 | −1.455 |
| WGS84 | −5.094 | −0.521 | |
| XGM2019e_2159 | GRS80 | −14.229 | −1.454 |
| WGS84 | −5.093 | −0.520 |
| GGMs | Reference Systems | Max | Min | Mean | Std |
|---|---|---|---|---|---|
| EGM2008 | GRS80 | 0.385 | −1.094 | −0.045 | 0.067 |
| WGS84 | −0.547 | −2.026 | −0.977 | 0.067 | |
| EIGEN-6C4 | GRS80 | 0.380 | −1.097 | −0.046 | 0.068 |
| WGS84 | −0.552 | −2.030 | −0.978 | 0.068 | |
| XGM2019e_2159 | GRS80 | 0.456 | −1.178 | −0.042 | 0.071 |
| WGS84 | −0.476 | −2.110 | −0.973 | 0.071 |
| GGMs | Reference Systems | (m2s−2) | Geopotential Difference (m2s−2) | Vertical Offset (m) |
|---|---|---|---|---|
| EGM2008 | GRS80 | 62,636,860.875 | −14.249 | −1.455 |
| WGS84 | 62,636,851.741 | −5.113 | −0.522 | |
| EIGEN-6C4 | GRS80 | 62,636,860.877 | −14.247 | −1.456 |
| WGS84 | 62,636,851.740 | −5.112 | −0.522 | |
| XGM2019e_2159 | GRS80 | 62,636,860.875 | −14.247 | −1.455 |
| WGS84 | 62,636,851.740 | −5.112 | −0.522 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, D.; Xue, Z. Analysis of a Relative Offset between the North American and the Global Vertical Datum in Gravity Potential Space. Remote Sens. 2023, 15, 3610. https://doi.org/10.3390/rs15143610
Guo D, Xue Z. Analysis of a Relative Offset between the North American and the Global Vertical Datum in Gravity Potential Space. Remote Sensing. 2023; 15(14):3610. https://doi.org/10.3390/rs15143610
Chicago/Turabian StyleGuo, Dongmei, and Zhixin Xue. 2023. "Analysis of a Relative Offset between the North American and the Global Vertical Datum in Gravity Potential Space" Remote Sensing 15, no. 14: 3610. https://doi.org/10.3390/rs15143610
APA StyleGuo, D., & Xue, Z. (2023). Analysis of a Relative Offset between the North American and the Global Vertical Datum in Gravity Potential Space. Remote Sensing, 15(14), 3610. https://doi.org/10.3390/rs15143610






