Abstract
Rock geochemical methods are effective for geological surveys, but typical sampling and laboratory-based analytical methods are time-consuming and costly. However, using visible–near-infrared spectroscopy to estimate the metal element content of rock is an alternative method. This study discussed the potential of hyperspectral estimation of Cu and its significant associated elemental content. Ninety-five rock samples were collected from the Kalatage Yudai copper–nickel deposit in Hami, Xinjiang. The effects of different spectral resolutions, spectral preprocessing, band indices, and characteristic band selection on the estimation of the element contents of Fe, Cu, Co, and Ti were investigated. The results show that when the spectral resolution is 5 nm, good results are obtained for all four metal elements, Fe, Cu, Co, and Ti, with the coefficients of determination R2 reaching 0.54, 0.59, 0.41, and 0.78, respectively. The best results are obtained for all transformed spectra with continuum removal, inverse transformation, continuum removal, and logarithmic transformation, respectively. In addition, the accuracy of the estimation models constructed by combining band indices and feature band selection was superior compared with full-band spectra for Fe (R2 = 0.654, MAE = 1.27%, and RPD = 1.498), Cu (R2 = 0.694, MAE = 20.509, and RPD = 1.711), Co (R2 = 0.805, MAE = 2.573, and RPD = 2.199), and Ti (R2 = 0.501, MAE = 0.04%, and RPD = 1.412). The results indicate that using band indices can provide a more accurate estimation of metal element content, providing a new technical method for the efficient acquisition of regional mineralization indicator element content distribution.
1. Introduction
The rock geochemical method is an essential tool for mineral exploration and is one of the most effective chemical exploration methods for finding occult deposits of hydrothermal origin [1,2,3,4,5,6]. A traditional rock geochemical survey is performed by collecting many rock samples in the field, analyzing them in the laboratory to determine the metal content, and then tracing the survey area based on geochemical anomalies. Although this method has high measurement accuracy, it is inefficient, costly, and problematic to obtain a continuous, large-area spatial distribution of elemental content [7,8,9]. Although it has been shown that handheld XRF can directly determine the essential content in the field, this method can only obtain sample point data and then get the regional elemental distribution according to the spatial interpolation method. The accuracy of the results is related to the number and spatial distribution of the test sample points [10,11]. The inability to obtain samples of areas where the natural environment is harsh and particularly inaccessible to humans will result in a lack of data in the area [12,13].
On the contrary, remote sensing technology has the advantages of a wide detection range, high efficiency, and low cost. The rapid development of hyperspectral remote sensing, which has hundreds of bands in the entire wavelength range, has enabled the technology to characterize the finer features of the target [14,15]. For example, soil organic matter and iron oxide have unique spectral absorption characteristics in the visible-NIR due to the presence of cations such as Fe2+, Fe3+, and Cr3+; overtone and combined vibrations of OH−, H2O, and CO32− and clay minerals have specific absorption characteristics in the shortwave infrared interval [16,17,18,19,20,21]. Additional studies have shown a quantitative relationship between elemental aluminum content and absorption position in the shortwave infrared gap [22]. However, metallic elements such as Cu, Pb, Zn, Ni, and Cr strongly correlate with these characteristic bands, providing a theoretical basis for the rapid and nondestructive estimation of metallic elemental content from hyperspectral data [23,24,25,26,27]. In recent years, many scholars have attempted to estimate the metal element content, soil organic matter content, and vegetation stress level using linear or nonlinear methods, such as partial least squares regression, stepwise regression, multiple regression, random forest, support vector machines, extreme machine learning, and neural networks, and they have achieved high estimation accuracy [28,29,30,31,32,33,34,35,36,37,38,39]. These results show that using hyperspectral techniques to estimate elemental content is feasible and practical.
However, the previous use of remote sensing technology to estimate elemental content has mostly been constrained to a single element; for mineral resource exploration, the formation process is more complex, and using only one fundamental content anomaly area to circle the exploration area will increase the uncertainty of mineral prediction [40,41,42]. Therefore, combining anomalous areas of mineralized elemental content and the abnormal regions of significantly related elements of mineralized elements for survey de-construction can make up for the shortcomings of single fundamental anomalies and thus improve the accuracy of mineral resource prediction [43,44]. Much research has been conducted on the factors affecting single-element estimation models, and an appropriate spectral resolution can reduce spectral redundancy and improve the model’s accuracy [45,46]. Appropriate preprocessing of the spectra before model construction, such as spectral smoothing and spectral transformation, can reduce the random noise and baseline drift generated by the instrument or external environment on the spectra, thus improving the prediction accuracy [39,47,48,49]. However, more research is required on whether estimating multiple elemental contents at the exact spectral resolution or with the same spectral transformation method has the same effect.
The greatest advantage of hyperspectral remote sensing is its high spectral resolution, but it also increases the redundancy of spectral information. Many studies have shown that the accuracy of models constructed by selecting feature bands is higher than that of models built using full bands, as features that introduce noise reduce model performance [50,51,52]. Furthermore, feature variable selection attempts to reduce the complexity of the model and improve its robustness. In feature variable selection, methods such as continuous projection algorithms (SPA), genetic algorithms (GA), stepwise regression (SRA), competing adaptive reweighting sampling (CARS), variable importance of projection (VIP), artificially introduced noise for uninformative variable elimination (NVE), and interval selection strategies are often used for optimal subset selection of spectra before the model constructed using the spectral subsets [53,54,55,56,57,58,59,60]. However, whether the models are built in a full band or feature interval bands, they are models constructed based on one-dimensional spectral data [61]. In practice, the quality of the spectral data strongly influences the model’s accuracy. Recent studies have shown that using multidimensional spectral data formed by combining multiple bands, such as two-band and three-band spectral indices, gives better results in terms of soil properties. These results not only improve the predictive power of the model but also enhance the robustness of the model [62,63,64,65]. The application of band indices has good potential for estimating the elemental content of a wide range of metals, which is a critical guideline for delineating mineral resource exploration areas.
Therefore, the objectives of this study were (1) to explore the best spectral resolution for estimating metals’ elemental content and the optimal spectral transformation method for different elemental content estimations; (2) to compare the performance of different three-band spectral indices for elemental content estimation; and (3) to determine whether it is possible to construct a multimetal elemental content estimation model with a simple model and good robustness using the characteristic indices selected from the three-band spectral indices.
2. Materials and Methods
2.1. Study Area and Sampling
The study area is located in Wubao Township, Hami City, Xinjiang, at the southern edge of the Tuha Basin in the Eastern Tianshan metallogenic belt, in the Kalatage area, about 140 km from Hami City. Study area: longitude 91°42′52.19″ to 91°47′4.60″E; latitude 42°41′3.03″ to 42°42′46.32″N. The study area is part of the Gobi Desert, with expansive valley hills, relatively flat terrain, and an average altitude of about 500–600 m [66]. The study area has a typical continental arid climate, with an average annual precipitation and temperature of 34.9 mm and 38 °C, respectively, and a maximum temperature of over 40 °C from June to August. The study area has no vegetation cover on the ground surface and is suitable for exploration work using remote-sensing techniques [67,68].
Ninety-five rock chip samples were collected from the study area on 18 September 2017 (Figure 1). Samples were collected and mixed into a sample bag (approximately 500 g) at five locations within a 1 m × 1 m area, while the coordinates of the sample centroid were recorded as the coordinates of the mixed sample point using a global positioning system (GPS). The collected samples were sent to the Xinjiang Nonferrous Geological Exploration Bureau Analysis and Testing Center for elemental content analysis. Before elemental content analysis, all samples were ground into powder with a particle diameter of less than 75 microns. The samples were then digested with nitric acid, hydrochloric acid, perchloric acid, and hydrofluoric acid, respectively; the Ti elemental content was measured using inductively coupled plasma emission spectrometry (ICP-OES), and the remaining elemental content was measured via inductively coupled plasma mass spectrometry (ICP-MS). Sample processing, analysis testing, and quality control were carried out by the “Specification for Geochemical Survey” (DZ/T0011-2010) and the “Quality Management Specification for Geological and Mineral Laboratories”.
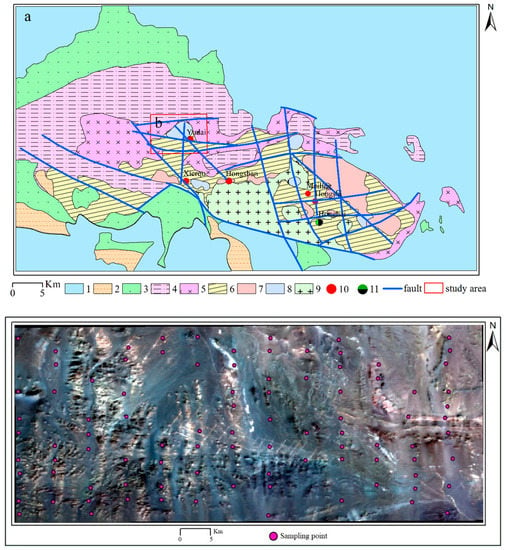
Figure 1.
Geological map of the study area and distribution of sampling points: (a). geological map of the Kalatage area (modified from [41]); (b). distribution of sampling points. 1—Cenozoic; 2—Shangonghe Formation; 3—Aqikebulake Formation; 4—Qishan Formation; 5—Dananhu Formation; 6—Kalatage group; 7—Huangcaopo group; 8—Late Paleozoic granitic intrusion; 9—Early Paleozoic granitic intrusion; 10—other volcanic hydrothermal/porphyry/skarn type deposits; 11—Honghai VMS-type deposit.
2.2. Spectral Measurements and Preprocessing
The sample spectra were measured in a laboratory darkroom environment using an Analytical Spectral Device (ASD) FieldSpec4 (Malvern Panalytical Ltd., Malvern, UK, formerly Analytical Spectral Devices Inc., Westborough, MA, USA) spectrometer. The spectrometer probe field of view was 25°, with a reflective domain of 350–2500 nm. From 350 to 1000 nm, the spectral sampling interval is 1.4 nm for a spectral resolution of 3 nm, and from 1000 to 2500 nm, the spectral sampling interval is 2 nm for a spectral resolution of 10 nm https://www.malvernpanalytical.com/en/products/product-range/asd-range (accessed on 14 July 2023). The probe is located 10 cm directly above the sample, and the reflectance output to users was resampled with ViewSpecPro (Version 6.20, Malvern Panalytical Ltd., Malvern, UK) to 1 nm for both spectral ranges, resulting in 2151 spectral bands. During the measurement process, it is difficult to hold the spectrometer probe stationary by hand, because when exploring, the shaking will unnecessarily increase spectral noise. Therefore, this experiment uses the stationary test platform shown in Figure 2. Five pieces of spectral data were collected for each sample, and the average of the remaining spectra was taken as the spectral data of the sample after removing the spectra with significant differences. The 350–400 nm spectral data with a low signal-to-noise ratio were excluded before data analysis. It was also shown that smoothing the spectra can reduce the effect of noise on the spectra [69]. Compared with other spectral smoothing methods, the Savitzky–Golay smoothing filter has apparent advantages for information noise removal; so, this study uses a Savitzky–Golay filter with a window of 7 for spectral smoothing [70].

Figure 2.
Test environment and spectrometer.
2.3. Spectral Preprocessing
Spectral preprocessing involves a series of enhanced preprocessing operations on the original spectrum to highlight the characteristic spectrum of a characterization target by reducing the effect of the background environment, illumination, and atmospheric scattering on the spectrum [71]. In this study, spectral preprocessing such as continuum removal, logarithmic, inverse, and derivative methods were used. Continuum removal can highlight absorption valleys and reflection peaks in the spectral profile, facilitating the extraction of characteristic bands between similar spectra [72,73,74]. Logarithmic transformation can reduce the effects of light variations by reducing the covariance and anisotropy between the data [40,75,76]. For discrete spectral data, difference techniques are often used to calculate spectral derivatives, with lower-order derivatives removing background noise and topographic shadows and higher-order derivatives removing atmospheric Rayleigh scattering [61,77,78].
where denotes the wavelength of the band i; and are the first- and second-order derivatives of wavelength , respectively; and ∆λ is the interval between two adjacent wavelengths.
2.4. Three-Band Index
Band indices are used to extract target spectral parameters by selecting characteristic bands for combination, and three-band index are used to determine three bands for combination to obtain parameters that can identify target features [20,62,79,80]. In this study, six band index methods were formed using combinations of bands (Table 1). Each band index calculation is obtained by traversing all band combinations and analyzing the correlation coefficient r between all band indices and elemental content, sorting the |r| values in descending order and extracting the band combination with the most significant |r| value for subsequent modeling. The optimal band combination algorithm is calculated in Python.

Table 1.
Calculation of band indices.
Where , , and are the spectral values at wavelengths a, b, and c, respectively, with a, b, and c taking values in the 400–2500 nm range, while a ≠ b ≠ c.
2.5. Stepwise Regression Analysis
Hyperspectral data have a strong correlation between adjacent bands, leading to a high information redundancy level [81]. The complexity of models constructed based on full-band spectral data is increased, thus reducing the robustness of the model [82]. Therefore, selecting a subset of characteristic spectra that can characterize the target from a large number of bands not only reduces the spectral dimensionality but also improves the computational efficiency and enhances the model’s generalization capability [51,83]. This study uses a stepwise regression analysis method to select the characteristic spectral bands. The stepwise regression analysis method adds bands to the model one by one from many bands, adding bands based on a p-value of 0.05 for the F-statistic and removing bands if the p-value is 0.1. After the new bands are added, an F-test is performed on all bands to remove bands with insignificant sums of squares for the partial regression. This process is repeated until no bands are added or removed [84,85].
2.6. Model Building and Validation
In this paper, in order to effectively analyze the relationship between the spectral estimation of the metal element content of rocks, the 95 sample data were sorted; 1 sample was taken every 2 samples at an interval from the 2nd sample onwards, and a total of 32 samples were taken for the validation set, and the remaining samples were used for the training set. A partial least squares regression model was developed using spectral reflectance (the independent variable) and metal element content (the dependent variable). Partial least squares is a multivariate regression model that combines multiple regression analysis, principal component analysis, and typical correlation analysis and has been successfully applied to remote sensing data to quantify vegetation characteristics and elemental content [19,86,87]. To avoid the degradation of model performance due to a low amount of training sample data, the model was constructed using leave-one-out cross-validation in the training set [61,88]. We use three statistical parameters—the coefficient of determination (R2), mean absolute error (MAE), and the ratio of the performance to deviation (RPD)—to evaluate the performance of the model. The closer the coefficient of determination is to 1, the smaller the MAE and the larger the RPD value, and the better the model performance. The range of RPD values can be divided into good models (RPD > 2.0), better models (2.0 > RPD > 1.4), and failed models (RPD < 1.4) [89,90]. This paper defines the best model performance as having a high coefficient of determination, a petite MAE, and a large RPD in the validation set.
3. Results
3.1. Elemental Correlation Analysis
The descriptive statistics of the content of the nine elements for all samples are shown in Table 2. With the exception of As and Ni, all the other seven elements have a wide range of content. The range of Fe content was the largest, with minimum and maximum values of 0.21% and 9.15%, respectively, and the range of As content was the smallest, with minimum and maximum values of 0.5 ppm and 12.45 ppm, respectively, indicating that there were significant gradients in the content of the nine elements, which provided primary data for the subsequent spectral estimation analysis.

Table 2.
Descriptive statistics for the content of each element (ppm).
At the same time, we aimed to identify abnormal areas for the mineralizing element Cu via remote sensing, where using a single element may result in information asymmetry or loss of information due to elemental imbalance effects [41]. For this reason, we propose to use multiple elemental combinations of anomalies to compensate for the lack of single elemental anomalies. The correlation between the content of nine elements (Table 3) was used to screen for elements significantly correlated with the mineralizing element Cu. The lower left part of Table 3 shows the correlation between the content of the two elements, and the upper right part shows the confidence ellipse between the content of the two elements. The results show that Fe, Mn, Ti, and Co are significantly correlated with Cu at the 0.05 level, with correlations of 0.72, 0.3, 0.61, and 0.73, respectively [44]. For this reason, we selected Fe, Ti, and Co, which are significantly correlated with Cu at the 0.05 level and have a correlation greater than 0.5, as the strange combination of elements. Thus, it is shown that the mineralized Cu elements are significantly correlated with these three elements [91].

Table 3.
Correlation and confidence ellipse for contents of 9 elements.
3.2. Element Content and Spectral Analysis
The mean content and CV of the total samples for the four elements Fe, Cu, Ti, and Co were 0.34% and 58%, 52.31 ppm and 96%, 0.28%, and 23%, and 11.58 ppm and 62%, respectively (Figure 3). The variation in the content of all three elements was significant, except for the relatively small variation in the content of Ti.
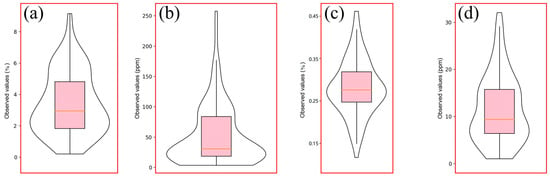
Figure 3.
Data densities and corresponding descriptive statistics for Fe, Cu, Ti, and Co: (a) Fe, (b) Cu, (c) Ti, and (d) Co.
The average spectral reflectance and continuum removal spectra for all sample sets are shown in Figure 4. The spectral reflectance increases gradually over the 0.4–2.5 μm, particularly over the range of 0.4–0.8 μm range, where the spectral value increases by 0.15. We can also see a clear reflection peak at 2.15 μm in the original spectra due to the absorption valleys at 1.9 μm and 2.2 μm, which are associated with the generalization of water absorption. After continuum removal, some absorption features are highlighted, such as absorption valleys at wavelengths of 0.43 μm, 0.49 μm, 0.7 μm, and 0.925 μm due to Fe electron leaps; absorption valleys at 0.58 μm, 1.04 μm, 1.12 μm, and 1.34 μm associated with organic matter; absorption valleys at 1.41 μm, 1.91 μm, and 2.22 μm associated with water oscillations; O-H stretching or Al-OH bending at 2.25 μm and 2.33 μm; and clay minerals associated with OH groups or carbonate at 2.25 μm and 2.33 μm [19,35,92]. In summary, these initial analyses of spectral reflectivity provide the basis for subsequent spectral modeling.
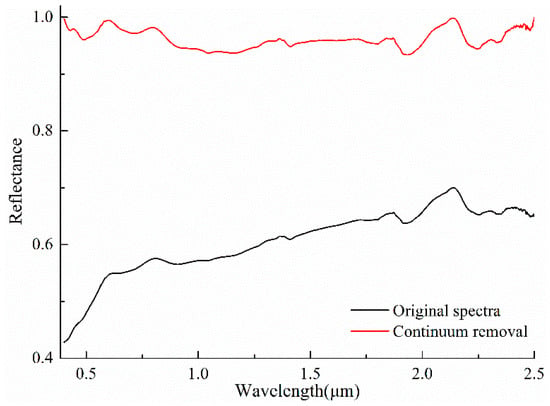
Figure 4.
Average and continuum removal spectra of all samples.
3.3. Effect of Spectral Resolution on the Accuracy of Elemental Content Estimation
In this study, 95 samples are divided into 63 training sets and 32 validation sets for model construction. In training the models, we used a leave-one-out cross-validation approach to avoid the problem of poor model performance due to the small number of samples, and we used the validation set to assess the accuracy of the models. PLSR models with different spectral resolutions were combined to relate the Fe, Cu, Ti, and Co contents to spectral reflectivity, resulting in 20 models (Table 4). It is evident in Table 4 that the estimation of the Fe, Cu, Ti, and Co content is relatively good when the spectral resolution is 1 nm, and the coefficients of determination in the validation set are all greater than 0.5; meanwhile, for Co, the coefficient of perseverance in the validation set is relatively low, only 0.44. The Fe, Cu, and Co element estimation accuracy at the spectral resolution of 1 nm, 5 nm, and 10 nm varies less and is more significant than 0.54. In particular, the accuracy of the estimation of Co content is the highest, reaching 0.78. However, the accuracy of the estimate of Ti is relatively low, reaching its highest at the spectral resolution of 1 nm and 5 nm (R2 = 0.41).

Table 4.
Accuracy of estimating elemental contents of Fe, Cu, Ti, and Co at different spectral resolutions.
We also found that the estimation accuracy of Fe, Cu, and Ti content decreased with a decreasing spectral resolution (Table 4). The coefficients determined in the validation set for the three elemental content estimates decrease by 0.07, 0.01, and 0.04, respectively, as the spectral resolution decreases from 1 nm to 20 nm. However, regarding the Co content, the model accuracy does not differ significantly across the five spectral resolutions, staying around 0.78. The results of previous studies have shown that as the spectral resolution increases, the more beneficial the observation of the fine spectral features contained in the segment becomes. Still, accordingly, it also increases the data’s redundancy, increasing the model’s complexity and reducing the efficiency of model training [93,94]. In Table 4, we find that when the spectral resolution is 5 nm, the model’s accuracy is close to that of the model with a spectral resolution of 1 nm, and both perform optimally or suboptimally. Combined with Figure 5, it can be seen that as the spectral resolution decreases, the spectral absorption features are also weakened. The continuum removal spectrograms for the corresponding intervals are shown below the rectangular boxes in Figure 5a–d. In Figure 5a–c, the absorption features at 1.38 μm, 1.85 μm, and 2.31 μm in the curve gradually disappear as the spectral resolution decreases (Figure 5). At the same time, the higher the spectral resolution, the more pronounced the “sawtooth” in the spectrum. The lower the spectral resolution, the smoother the spectrum is (Figure 5d). Combining Table 4 and Figure 5, we can see that when the spectral resolution is 5 nm, the spectral features are better represented, and the data redundancy is reduced, thus simplifying the complexity of the model while ensuring its accuracy.
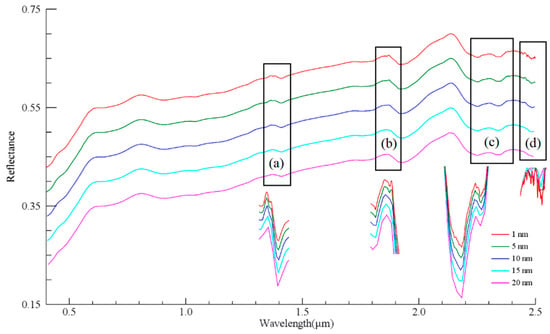
Figure 5.
Average spectra of all samples at different spectral resolutions (for comparative analysis, the spectral resolution is reduced by 5 nm, and the spectral values are correspondingly reduced by 0.05): (a). 1.38 μm; (b). 1.85 μm; (c). 2.31 μm; (d). 2.4–2.5 μm.
3.4. Estimation of Elemental Content by Full-Band Transform Spectroscopy
Table 5 shows the effect of transforming spectra with a spectral resolution of 5 nm for the estimation of different elemental contents. For the Fe content, the coefficients of determination of the original spectra are relatively high in the training and validation sets, 0.55 and 0.54, respectively. The overall accuracy of the seven transform spectra, except for the derivative spectra, is relatively high, with an R2 greater than 0.5 in the validation set. Still, the accuracy of the transform spectra decreases for the original spectra, except for the continuum removal spectra. Regarding the Cu content, the original spectra achieved better accuracy, with R2 reaching 0.59 in the validation set. The logarithmic, inverse, and square root spectra improved the accuracy of the Cu content estimation by 0.04, 0.06, and 0.03, respectively. The highest accuracy was achieved by the inverse spectrum, with a validation set accuracy of 0.65. The original spectrum could have been better regarding Ti content, achieving only 0.41. All six transformed spectra were improved, except for the first- and second-order derivative spectra, which were equivalent to the original spectrum with reduced accuracy. The best accuracy was achieved for the continuum removal spectra, with a validation set R2 of 0.63. The estimation of the Ti content by the original spectra was relatively average, only reaching 0.41. The estimation of the remaining six transformed spectra was improved, except for the first-order derivative and second-order derivative spectra, which were equivalent to the reduced estimation accuracy of the original spectra. The estimation accuracy of the original spectra for the Co content was significantly better than that of the remaining three elemental content estimations, and the R2 of the validation set could reach 0.78. Except for the continuum removal and second-order derivative spectra, which significantly reduced the estimation accuracy, the estimation accuracy of the remaining six spectra was relatively consistent, and the best estimation accuracy was achieved. The best estimation accuracy was obtained for the logarithmic spectrum (R2 = 0.8).

Table 5.
Accuracy of different transformation spectra for estimating elemental contents of Fe, Cu, Ti, and Co.
In Table 5, it can be found that the best spectral resolutions achieved for the estimation accuracy of Fe, Cu, Ti, and Co elements were the continuum removal spectra (R2 = 0.6), inverse spectra (R2 = 0.65), continuum removal spectra (R2 = 0.63), and logarithmic spectra (R2 = 0.8). From this, we conclude that for different elemental content estimates, different spectral preprocessing achieves different accuracies, in line with the results of previous studies [95,96,97]. The results suggest that in the future, studying one transformation formalism should not be used to estimate multiple elemental contents, as different elemental contents have other effects on the spectra, and different preprocessing has different effects on the extraction of feature information in the spectra. Therefore, highlighting the spectral features can be the research focus of future studies.
3.5. Estimation of Elemental Content via Optimal Band Combinations
Although better results were obtained for the estimation of the four elemental contents using the entire band (Table 5), since hyperspectral data possess thousands of bands, and the neighboring bands have high similarity; inputting all bands into the model for modeling will increase the redundancy of the model, which in turn increases the complexity of the model. For this reason, we propose a three-band indicator approach to construct an estimation model. Figure 6(a1–a6,b1–b6,c1–c6,d1–d6) shows the slice plots of the optimal band combinations with the highest correlation between the elemental contents of Fe, Cu, Ti, and Co for each band index, respectively, where the X, Y, and Z axes indicate the spectral ranges of bands b1, b2, and b3 at 400–2500 nm, respectively. Different band indices have different optimal slice positions (i.e., different band combinations) and different correlations (i.e., color changes). As shown in Figure 6, the band indices with the highest correlations with Fe, Cu, Ti, and Co elemental content are BI4, BI3, BI4, and BI3, with absolute correlation coefficients of 0.68, 0.82, 0.65, and 0.87, respectively.
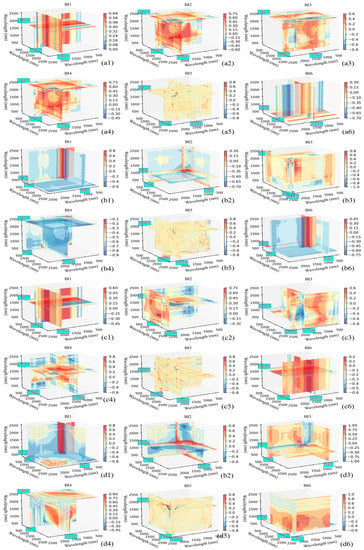
Figure 6.
Correlation between index spectra of different bands and contents of Fe, Cu, Ti, and Co: (a) Fe, (b) Cu, (c) Ti, and (d) Co.
In addition, we also analyzed the effect of each optimum band index on the estimation of Fe, Cu, Ti, and Co elemental contents (Table 6). In the validation set, BI6 had the highest coefficient of determination (R2 = 0.675) for estimating Fe elemental content in all band indices and in the whole band. However, the rest of the band indices are less effective than the full-band model for estimating the elemental content of Cu, Ti, and Co. The results show that spectral indices can improve the correlation between spectral parameters and elemental content. Still, it is difficult to better estimate fundamental rock content using only a single spectral parameter because stone is a complex object.

Table 6.
Quantitative analysis between the optimal band combinations of different BIs and the Fe, Cu, Ti, and Co elemental content.
To this end, six kinds of band indices were fed into the stepwise regression model to filter out the band indices that significantly improved the performance of each elemental content. The index with enhanced performance for Fe, Cu, Ti, and Co were BI1, BI5, and BI6; BI4, BI5, and BI6; BI1, BI3, and BI5; and BI1, BI3, and BI6. We then fed the screened indices into the PLS model to estimate the Fe, Cu, Ti, and Co content separately (Figure 7). Compared with the individual spectral index, using the combined band indices as input variables improved performance in both validation sets. The performance of the four elemental content estimates for Fe, Cu, Ti, and Co were R2 = 0.654, MAE = 1.27%, and RPD = 1.498; R2 = 0.694, MAE = 20.509, and RPD = 1.711; R2 = 0.501, MAE = 0.04%, and RPD = 1.412; and R2 = 0.805, MAE = 2.573, and RPD = 2.199. We also found that the model after feature band preferences had improved performance (Fe, Cu, and Co) or was similar (Ti) in the validation set compared with the model constructed in the full band. Using a small number of spectra gives overall better results and simplifies the complexity of the model.
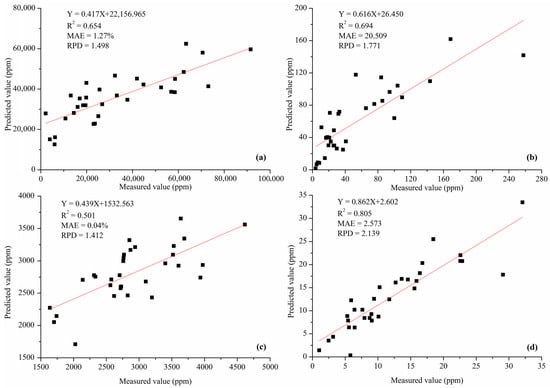
Figure 7.
Scatter plot between the tested values of Fe, Cu, Ti, and Co content and the predicted values obtained from the combination of the characteristic bands: (a) Fe, (b) Cu, (c) Ti, and (d) Co.
4. Discussion
Geochemical anomalies are vital in geological surveys, providing data to support the delineation of favorable mineralization zones in contrast to background areas [98,99]. However, combining information from multiple anomalies is essential to achieve better results and vice versa. Previous studies have shown that there is a significant bias in the trapping of favorable mineralization zones using only one anomaly or one elemental anomaly. This may be due to the migration of different elements due to external conditions, resulting in anomalies that deviate from the in situ information [100]. Therefore, using mineralized elemental anomalies and their significant correlations to define favorable mineralization zones will reduce the number of false anomalies caused by information imbalance [101]. In this study, we analyzed all measured elemental contents and found Fe, Mn, Ti, and Co to be significantly correlated with Cu at the 0.05 level. Porphyry copper ores, in previous studies, have also been shown to have significant correlations with these elements. This indicates the reliability of using standard anomalous zones for these elements to narrow the exploration area.
Spectral resolution plays an essential role in identifying diagnostic spectral features of a feature target, and studies have shown that a high spectral resolution can highlight diagnostic features that are not detected by multiple spectra [17]. As can be seen in Figure 5, the spectral profile absorption features gradually decrease as the spectral resolution decreases. The absorption feature at 1850 nm disappears when the spectral resolution is greater than 5 nm. Meanwhile, as seen in Table 4, the model performs poorly when the spectral resolution is low. This may be caused by weakening the diagnostic information of its features as the spectral resolution decreases. The best estimation of the four elemental contents of Fe, Cu, Ti, and Co was achieved at a spectral resolution of 5 nm, consistent with previous studies showing that the spectral resolution affects the model’s accuracy [102,103]. When the spectral resolution is chosen appropriately, it offers characteristic diagnostic features and reduces the redundancy between adjacent bands.
Previous studies have shown that models constructed using raw spectra often find it challenging to achieve the desired results [104]. Therefore, many researchers have used different spectral transformation techniques to preprocess the spectra to add spectral feature information while eliminating background noise [70]. The first- and second-order derivatives represent the slope and curvature of the spectra, respectively. The results of this paper show that the performance of the model constructed from the first-order derivative spectra is significantly better than that of the second-order derivative spectra, which is because although the derivatives can eliminate the baseline shift, the second-order derivatives may introduce more noise information and thus reduce the accuracy of the model, in line with the results of previous studies [61,105]. Furthermore, in this study, the estimation model constructed using envelope spectroscopy achieved optimal or suboptimal outcomes for the four metal elemental contents, since continuum removal normalizes the spectra to a consistent spectral background, thus effectively highlighting the absorption characteristics of the spectral profiles. The results of this study support the conclusion that previous work using continuum removal spectroscopy achieved better results in elemental estimation.
The spectral index is a simple and efficient method for extracting the spectral parameters of a feature [106]. In this paper, we obtained spectral parameters for all combinations of bands by traversing all bands, and we also found that the correlation between the spectral parameters obtained from spectral indices formed by different combinations of bands and the content of each element was distinct. Moreover, the correlation between the spectral parameters obtained by this algorithm and the elemental content was significantly improved compared with the original spectral values (Figure 6). Previous estimation models constructed based on spectral reflectance values or a single spectral index are not satisfactory in terms of model performance, as their spectral information is often saturated. Therefore, many scholars have proposed high-dimensional spectral indices and achieved better estimation results [107]. The results of many studies have shown that spectral indices constructed based on three wavelengths can provide better predictions of elemental content [62], and the same findings were obtained in this paper.
Although spectral indices can achieve good predictions, different spectral indices use various spectral bands that have other effects on the original content and thus achieve different results. Using all spectral indices as independent variables can reduce the model performance by introducing unnecessary variables [83]. In contrast, variable selection techniques can extract parameters significantly correlated with the original content, thereby improving the predictive accuracy of the model [108]. In this paper, the variables related to the content of four elements, Fe, Cu, Ti, and Co, were selected from six spectral indices for model construction using a stepwise regression technique, and better results were obtained. The coefficients of determination R2 for Fe, Cu, Ti, and Co in the validation set were improved by 0.112, 0.100, 0.087, and 0.023, respectively, compared with the model constructed in the whole band (Table 5 and Figure 7). However, the model performance was improved in all cases compared with individual spectral indices, thus indicating that the model constructed by combining the spectral index and band selection techniques has better predictive performance. The method can reduce the dimensionality of the hyperspectral data and extract favorable information from the spectra compared with the full-spectral data, thus improving the model’s accuracy (Figure 7). In addition, the bands in which the spectral indices selected by stepwise regression are located are significantly correlated with iron oxides (needle iron ore, hematite, water, iron, etc.) and anionic groups (OH, CO3, Al-OH, Mg-OH, C-O, etc.), indicating that the constructed model has some physical significance [109,110,111].
Although a combination of spectral transformation, spectral index, and characteristic band-selection techniques yielded promising results in estimating the elemental content of a wide range of metals, the accuracy was still significantly lower than that obtained from laboratory analysis [24,109]. This may be due to the difficulty of interpreting the variable rock properties using spectral data alone. Therefore, in future studies, multiple data sources can be combined to improve the prediction accuracy of the model, such as fusing VNIR-SWIR with data such as NIR spectra and magnetization or adding other environmental covariates (e.g., topographic data, PH values, and climate data) [112,113,114]. This work provides new technical means for extracting favorable information on mineralization from aerial or space imagery, enabling the efficient exploration and low-cost trapping of favorable mineralization zones.
5. Conclusions
This study discussed the potential of spectral resolution, spectral variability, band combination, and optimal band selection methods for multielement content estimation of Fe, Cu, Ti, and Co. The results obtained show the following:
(1) The spectral resolution is significant for the display of spectral diagnostic features and the model’s accuracy. When the spectral resolution is 5 nm, the spectral features can be better highlighted, and the estimation model constructed can also be obtained with higher accuracy.
(2) The accuracy of the model constructed using different transformed spectra is extra for other elemental contents. No singe spectral transformation is suitable for estimating multiple elemental contents; so, an appropriate transformation method can significantly improve the model’s accuracy.
(3) For the four elemental contents of Fe, Cu, Ti, and Co, the model constructed using a combination of the three-band index and the characteristic band selection method not only reduces the complexity of the model but also exhibits better accuracy than the model constructed using the entire band.
(4) The combination of spectral index and feature variable selection methods to estimate the mineralized elemental content and its significantly correlated elemental content has very high potential to improve the efficiency of a presurvey and reduce the uncertainty caused by the asymmetric information of single elemental anomalies, providing data support and technical reference for subsequent space or airborne remote sensing to detect regional elemental anomalies.
Author Contributions
Conceptualization, G.J. and X.C.; data curation, S.W., S.Z. and Y.B.; funding acquisition, H.Y.; investigation, T.L. and X.F.; methodology, G.J.; project administration, J.W. and K.M.; supervision, S.Z.; validation, G.J.; visualization, G.J.; writing—original draft, G.J.; writing—review and editing, S.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research is funded by the Open Project of Key Laboratory, Xinjiang Uygur Autonomous Region (No. 2020D04041), and Science and Technology Major Project of Xinjiang Uygur Autonomous Region, China (2021A03001-3), and National Natural Science Foundation of China (U2003107) and Institute of Resources and Ecology, Yili Normal University (YLNURE202212).
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare that they have no known competing financial interests or personal relationships that could have influenced the work reported in this study.
References
- Granier, C.; Hartley, J.; Michaud, J.C.; Troly, G. Contribution of 3-dimensional geochemical-exploration to the discovery of rxtensions of the thalanga polymetallic deposit under tertiary cover rocks (Queensland, Australia). J. Geochem. Explor. 1989, 32, 467–475. [Google Scholar] [CrossRef]
- Li, Q. Lithogeochemical anomaly evalue and reprospecting in Shiyingtan gold deposit in Xinjiang. Gold 2009, 30, 7–12. [Google Scholar]
- Jiao, B.Q.; Bai, R.J.; Sun, S.M.; Pan, Z.H.; Li, S.P. The application of geochemical zoning standardized method to the extraction of regional geochemical information. Geophys. Geochem. Explor. 2009, 165–169, 206, (In Chinese with English Abstract). [Google Scholar]
- Chen, J.; Li, Z.D.; Zhong, H.; Wu, M.G. Comparion of Multiple Methods to Determine the Geochemical Anomaly Threshold. Geol. Surv. Res. 2014, 37, 187–192, (In Chinese with English Abstract). [Google Scholar]
- Piercey, S.J.; Devine, M.C. Analysis of powdered reference materials and known samples with a benchtop, field portable X-ray fluorescence (pXRF) spectrometer: Evaluation of performance and potential applications for exploration lithogeochemistry. Geochem.-Explor. Environ. Anal. 2014, 14, 139–148. [Google Scholar] [CrossRef]
- Woguia, B.K.; Nono GD, K.; Tamfuh, P.A.; Embui, V.F.; Nforba, M.T.; Nzenti, J.P. Identifying multi-metal prospect using regional soil and stream sediment geochemical data in bidou, nyong series, north west of congo craton. Arab. J. Geosci. 2021, 14, 218. [Google Scholar] [CrossRef]
- Zhao, L.; Hu, Y.M.; Zhou, W.; Liu, Z.H.; Pan, Y.C.; Shi, Z.; Wang, L.; Wang, G.X. Estimation methods for soil mercury content using hyperspectral remote sensing. Sustainability 2018, 10, 2474. [Google Scholar] [CrossRef]
- Kopackova-Strnadova, V.; Rapprich, V.; McLemore, V.; Pour, O.; Magna, T. Quantitative estimation of rare earth element abundances in compositionally distinct carbonatites: Implications for proximal remote-sensing prospection of critical elements. Int. J. Appl. Earth Obs. Geoinf. 2021, 103, 102423. [Google Scholar] [CrossRef]
- Kasmaeeyazdi, S.; Dinelli, E.; Braga, R. Mapping Co-Cr-Cu and Fe occurrence in a legacy mining waste using geochemistry and satellite imagery analyses. Appl. Sci. 2022, 12, 1928. [Google Scholar] [CrossRef]
- Mancini, M.; Weindorf, D.C.; Chakraborty, S.; Silva, S.H.G.; Teixeira, A.F.D.; Guilherme, L.R.G.; Curi, N. Tracing tropical soil parent material analysis via portable X-ray fluorescence (pXRF) spectrometry in Brazilian Cerrado. Geoderma 2019, 337, 718–728. [Google Scholar] [CrossRef]
- Da Silva, A.C.; Triantafyllou, A.; Delmelle, N. Portable X-ray fluorescence calibrations: Workflow and guidelines for optimizing the analysis of geological samples. Chem. Geol. 2023, 623, 121395. [Google Scholar] [CrossRef]
- Ding, H.N.; Chen, Y.; Chen, Y.Z. Remote Sensing Inversion Method of Soil Iron Content in the Loess Plateau. Remote Sens. Technol. Appl. 2019, 34, 275–283, (In Chinese with English Abstract). [Google Scholar]
- Cui, S.C.; Zhou, K.F.; Ding, R.F.; Zhao, J.; Du, X.S.H. Comparing the effects of different spectral preprocessing on the estimation of the copper content of Seriphidium terrae-albae. J. Appl. Remote Sens. 2018, 12, 036003. [Google Scholar] [CrossRef]
- van der Meer, F.D.; van der Werff, H.M.A.; van Ruitenbeek, F.J.A.; Hecker, C.A.; Bakker, W.H.; Noomen, M.F.; van der Meijde, M.; Carranza, E.J.M.; de Smeth, J.B.; Woldai, T. Multi- and hyperspectral geologic remote sensing: A review. Int. J. Appl. Earth Obs. Geoinf. 2012, 14, 112–128. [Google Scholar] [CrossRef]
- Rasti, B.; Scheunders, P.; Ghamisi, P.; Licciardi, G.; Chanussot, J. Noise reduction in hyperspectral imagery: Overview and application. Remote Sens. 2018, 10, 482. [Google Scholar] [CrossRef]
- Hunt, G.R. Spectral signatures of particulate minerals in the visible and near-infrared. Geophysics 1997, 42, 501–513. [Google Scholar] [CrossRef]
- Clark, R.N. Spectroscopy of rocks and minerals, and principles of spectroscopy. Remote Sens. Earth Sci. 1999, 3, 3–58. [Google Scholar]
- Galvao, L.S.; Pizarro, M.A.; Epiphanio, J.C.N. Variations in reflectance of tropical soils: Spectral-chemical composition relationships from AVIRIS data. Remote Sens. Environ. 2001, 75, 245–255. [Google Scholar] [CrossRef]
- Rossel, V.R.A.; Behrens, T. Using data mining to model and interpret soil diffuse reflectance spectra. Geoderma 2010, 158, 46–54. [Google Scholar] [CrossRef]
- Shi, T.Z.; Chen, Y.Y.; Liu, Y.L.; Wu, G.F. Visible and near-infrared reflectance spectroscopy-An alternative for monitoring soil contamination by heavy metals. J. Hazard. Mater. 2014, 265, 166–176. [Google Scholar] [CrossRef]
- van der Meer, F.; Hecker, C.; van Ruitenbeek, F.; van der Werff, H.; de Wijkerslooth, C.; Wechsler, C. Geologic remote sensing for geothermal exploration: A review. Int. J. Appl. Earth Obs. Geoin-Mation 2014, 33, 255–269. [Google Scholar] [CrossRef]
- Clark, R.N.; King, T.V.V.; Klejwa, M.; Swayze, G.A.; Vergo, N. High spectral resolution reflectance spectroscopy of minerals. J. Geophys. Res. Solid Earth 1990, 95, 12653–12680. [Google Scholar] [CrossRef]
- Cheshire, M.V.; Dumat, C.; Fraser, A.R.; Hillier, S.; Staunton, S. The interaction between soil organic matter and soil clay minerals by selective removal and controlled addition of organic matter. Eur. J. Soil Sci. 2000, 51, 497–509. [Google Scholar] [CrossRef]
- Wang, J.J.; Cui, L.J.; Gao, W.X.; Shi, T.Z.; Chen, Y.Y.; Gao, Y. Prediction of low heavy metal concentrations in agricultural soils using visible and near-infrared reflectance spectroscopy. Geoderma 2014, 216, 1–9. [Google Scholar] [CrossRef]
- Zhou, W.; Yang, H.; Xie, L.J.; Li, H.R.; Huang, L.; Zhao, Y.P.; Yue, T.X. Hyperspectral inversion of soil heavy metals in three-river source region based on random forest model. Catena 2021, 202, 105222. [Google Scholar] [CrossRef]
- Han, C.; Lu, J.L.; Chen, S.B.; Xu, X.T.; Wang, Z.B.; Pei, Z.; Zhang, Y.; Li, F.X. Estimation of heavy metal (loid) contents in agricultural soil of the suzi river basin using optimal spectral indices. Sustainability 2021, 13, 12088. [Google Scholar] [CrossRef]
- Wang, Y.Y.; Zhao, Y.C.; Xu, S.X. Application of VNIR and machine learning technologies to predict heavy metals in soil and pollution indices in mining areas. J. Soils Sediments 2022, 22, 2777–2791. [Google Scholar] [CrossRef]
- Mouazen, A.M.; Kuang, B.; Baerdemaeker, J.D.; Ramon, H. Comparison among principal component, partial least squares and back propagation neural network analyses for accuracy of measurement of selected soil properties with visible and near infrared spectroscopy. Geoderma 2010, 158, 23–31. [Google Scholar] [CrossRef]
- Nickel, S.; Schroder, W.; Wosniok, W.; Harmens, H.; Frontasyeva, M.V.; Alber, R.; Aleksiayenak, J.; Barandovski, L.; Blum, O.; Danielsson, H.; et al. Modelling and mapping heavy metal and nitrogen concentrations in moss in 2010 throughout Europe by applying Random Forests models. Atmos. Environ. 2017, 156, 146–159. [Google Scholar] [CrossRef]
- Rumpf, T.; Mahlein, A.K.; Steiner, U.; Oerke, E.C.; Dehne, H.W.; Plumer, L. Early detection and classification of plant diseases with Support Vector Machines based on hyperspectral reflectance. Comput. Electron. Agric. 2010, 74, 91–99. [Google Scholar] [CrossRef]
- Zeng, F.R.; Ali, S.; Zhang, H.T.; Ouyang, Y.B.; Qiu, B.Y.; Wu, F.B.; Zhang, G.P. The influence of pH and organic matter content in paddy soil on heavy metal availability and their uptake by rice plants. Environ. Pollut. 2011, 159, 84–91. [Google Scholar] [CrossRef] [PubMed]
- Nawar, S.; Buddenbaum, H.; Hill, J.; Kozak, J.; Mouazen, A.M. Estimating the soil clay content and organic matter by means of different calibration methods of vis-NIR diffuse reflectance spectroscopy. Soil Tillage Res. 2016, 155, 510–522. [Google Scholar] [CrossRef]
- Ma, W.B.; Tan, K.; Li, H.D.; Yan, Q.W. Hyperspectral inversion of heavy metals in soil of a mining area using extreme learning machine. J. Ecol. Rural Environ. 2016, 32, 213–218, (In Chinese with English Abstract). [Google Scholar]
- Tu, Y.L.; Zou, B.; Jiang, X.L.; Tao, C.; Tang, Y.Q.; Feng, H.H. Hyperspectral remote sensing based modeling of cu content in mining soil. Spectrosc. Spectr. Anal. 2018, 38, 575–581. [Google Scholar]
- Hong, Y.S.; Shen, R.L.; Cheng, H.; Chen, Y.Y.; Zhang, Y.; Liu, Y.L.; Zhou, M.; Yu, L.; Liu, Y.; Liu, Y.F. Estimating lead and zinc concentrations in peri-urban agricultural soils through reflectance spectroscopy: Effects of fractional-order derivative and random forest. Sci. Total Environ. 2018, 651 Pt 2, 1969–1982. [Google Scholar] [CrossRef]
- Wang, J.Z.; Shi, T.Z.; Yu, D.L.; Teng, D.X.; Ge, X.Y.; Zhang, Z.P.; Yang, X.D.; Wang, H.X.; Wu, G.F. Ensemble machine-learning-based framework for estimating total nitrogen concentration in water using drone-borne hyperspectral imagery of emergent plants: A case study in an arid oasis, NW China. Environ. Pollut. 2020, 266, 115412. [Google Scholar] [CrossRef]
- Han, L.; Chen, R.; Zhu, H.L.; Zhao, Y.H.; Liu, Z.; Huo, H. Estimating soil arsenic content with visible and near-infrared hyperspectral reflectance. Sustainability 2020, 12, 1476. [Google Scholar] [CrossRef]
- Zhou, T.; Geng, Y.J.; Ji, C.; Xu, X.R.; Wang, H.; Pan, J.J.; Bumberger, J.; Haase, D.; Lausch, A. Prediction of soil organic carbon and the C:N ratio on a national scale using machine learning and satellite data: A comparison between Sentinel-2, Sentinel-3 and Landsat-8 images. Sci. Total Environ. 2021, 755, 142661. [Google Scholar] [CrossRef]
- Xu, X.T.; Chen, S.B.; Ren, L.G.; Han, C.; Lv, D.L.; Zhang, Y.F.; Ai, F.K. Estimation of heavy metals in agricultural soils using Vis-NIR spectroscopy with fractional-order derivative and generalized regression neural network. Remote Sens. 2021, 13, 2718. [Google Scholar] [CrossRef]
- Chen, J.L. The Recognition of Rock Geochemical Anomalies and Metallogenic Prognosis in Mawudigou Area, Wushan, Gansu Province; Lanzhou University: Lanzhou, China, 2014; (In Chinese with English Abstract). [Google Scholar]
- Mao, Y.J.; Qin, K.Z.; Tang, D.M.; Xue, S.C.; Feng, H.Y.; Tian, Y. Multiple stages of magma emplacement and mineralization of eastern Tianshan, Xingjiang: Examplified by the Huangshan Ni-Cu deposit. Acta Petrol. Sin. 2014, 30, 1575–1594. [Google Scholar]
- Chen, G.Q. The Research of the Meticulous Evaluation Methods of Mediumlatge Scale Geochemical Anomalies Combination; Jilin University: Jilin, China, 2017; (In Chinese with English Abstract). [Google Scholar]
- Cao, M.X.; Lu, L.J.; Chen, G.Q.; Ding, P.C. Distributiion of regional geochemical elements and combination anomaly method. Glob. Geol. 2012, 31, 515–521, (In Chinese with English Abstract). [Google Scholar]
- Yu, X.C.; Wang, S.C.; Wang, H.; Liang, Y.C.; Chen, S.Y.; Wu, K.; Yang, Z.Y.; Li, C.Y.; Chang, Y.Z.; Zhan, Y.; et al. Detection of geochemical element assemblage anomalies using a local correlation approach. J. Earth Sci. 2021, 32, 408–414. [Google Scholar] [CrossRef]
- Knox, N.M.; Skidmore, A.K.; Schlerf, M.; de Boer, W.F.; van Wieren, S.E.; van der Waal, C.; Prins HH, T.; Slotow, R. Nitrogen prediction in grasses: Effect of bandwidth and plant material state on absorption feature selection. Int. J. Remote Sens. 2010, 31, 691–704. [Google Scholar] [CrossRef]
- Castaldi, F.; Palombo, A.; Santini, F.; Pascucci, S.; Pignatti, S.; Casa, R. Evaluation of the potential of the current and forthcoming multispectral and hyperspectral imagers to estimate soil texture and organic carbon. Remote Sens. Environ. 2016, 179, 54–65. [Google Scholar] [CrossRef]
- Gong, P.; Pu, R.; Yu, B. Conifer species recognition: Effects of data transformation. Int. J. Remote Sens. 2001, 22, 3471–3481. [Google Scholar] [CrossRef]
- Zhang, Z.P.; Ding, J.L.; Zhu, C.M.; Wang, J.Z.; Ma, G.L.; Ge, X.Y.; Li, Z.S.; Han, L.J. Strategies for the efficient estimation of soil organic matter in salt-affected soils through Vis-NIR spectroscopy Optimal band combination algorithm and spectral degradation. Geoderma 2020, 382, 114729. [Google Scholar] [CrossRef]
- Zhang, Z.P.; Ding, J.L.; Zhu, C.M.; Wang, J.Z. Combination of efficient signal pre-processing and optimal band combination algorithm to predict soil organic matter through visible and near-infrared spectra. Spectrochim. Acta Part A-Mol. Biomol. Spectrosc. 2020, 240, 118553. [Google Scholar] [CrossRef]
- Norgaard, L.; Saudland, A.; Wagner, J.; Nielsen, J.P.; Engelsen, S.B. Interval partial least-squares regression (ipls): A comparative chemometric study with an example from near-infrared spectroscopy. Appl. Spectrosc. 2000, 54, 413–419. [Google Scholar] [CrossRef]
- Li, H.D.; Liang, Y.Z.; Xu, Q.S.; Cao, D.S. Key wavelengths screening using competitive adaptive reweighted sampling method for multivariate calibration. Anal. Chim. Acta 2009, 648, 77–84. [Google Scholar] [CrossRef]
- Li, B.; Xu, X.M.; Zhang, L.; Han, J.W.; Bian, C.S.; Li, G.C.; Liu, J.G.; Jin, L.P. Above-ground biomass estimation and yield prediction in potato by using UAV-based RGB and hyperspectral imaging. ISPRS J. Photogramm. Remote Sens. 2020, 162, 161–172. [Google Scholar] [CrossRef]
- Bangalore, A.S.; Shaffer, R.E.; Small, G.W.; Arnold, M.A. Genetic algorithm-based method for selecting wave-lengths and model size for use with partial least-squares regression: Application to near-infrared spectroscopy. Ana-Lytical Chem. 1996, 68, 4200–4212. [Google Scholar] [CrossRef] [PubMed]
- Leardi, R. Application of genetic algorithm-PLS for feature selection in spectral data sets. J. Chemom. 2000, 14, 643–655. [Google Scholar] [CrossRef]
- Ye, S.F.; Wang, D.; Min, S.G. Successive projections algorithm combined with uninformative variable elimination for spectral variable selection. Chemom. Intell. Lab. Syst. 2008, 91, 194–199. [Google Scholar] [CrossRef]
- Han, Q.J.; Wu, H.L.; Cai, C.B.; Xu, L.; Yu, R.Q. An ensemble of monte carlo uninformative variable elimination for wavelength selection. Anal. Chim. Acta 2008, 612, 121–125. [Google Scholar] [CrossRef] [PubMed]
- Soares SF, C.; Gomes, A.A.; Filho, A.R.G.; Araujo, M.; Galvo, R.K.H. The successive projections algorithm. TrAC Trends Anal. Chem. 2013, 42, 84–97. [Google Scholar] [CrossRef]
- Vohland, M.; Ludwig, M.; Thiele-Bruhn, S.; Ludwig, B. Determination of soil properties with visible to near- and mid-infrared spectroscopy: Effects of spectral variable selection. Geoderma 2014, 223–225, 88–96. [Google Scholar] [CrossRef]
- Farres, M.; Platikanov, S.; Tsakovski, S.; Tauler, R. Comparison of the variable importance in projection (VIP) and of the selectivity ratio (SR) methods for variable selection and interpretation. J. Chemom. 2015, 29, 528–536. [Google Scholar] [CrossRef]
- Wang, X.P.; Zhang, F.; Kung, H.T.; Johnson, V.C. New methods for improving the spectral estimation of soil organic matter content (SOMC) in the Ebinur Lake Wetland National Nature Reserve (ELWNNR) in northwest China. Remote Sens. Environ. 2018, 218, 104–118. [Google Scholar] [CrossRef]
- Hong, Y.S.; Guo, L.; Chen, S.C.; Linderman, M.; Mouazen, A.M.; Yu, L.; Chen, Y.Y.; Liu, Y.L.; Liu, Y.F.; Cheng, H.; et al. Exploring the potential of airborne hyperspectral image for estimating topsoil organic carbon: Effects of fractional-order derivative and optimal band combination algorithm. Geoderma 2020, 365, 114228. [Google Scholar] [CrossRef]
- Li, F.; Mistele, B.; Hu, Y.C.; Chen, X.P.; Schmidhalter, U. Optimising three-band spectral indices to assess aerial N concentration, N uptake and aboveground biomass of winter wheat remotely in China and Germany. ISPRS J. Photogramm. Remote Sens. 2014, 92, 112–123. [Google Scholar] [CrossRef]
- Wang, F.H.; Gao, J.; Zha, Y. Hyperspectral sensing of heavy metals in soil and vegetation: Feasibility and challenges. ISPRS J. Photogramm. Remote Sens. 2018, 136, 73–84. [Google Scholar] [CrossRef]
- Sawut, R.; Kasim, N.; Abliz, A.; Li, H.; Yalkun, A.; Maihemuti, B.; Shi, Q.D. Possibility of optimized indices for the assessment of heavy metal contents in soil around an open pit coal mine area. Int. J. Appl. Earth Obs. Geoinf. 2018, 73, 14–25. [Google Scholar] [CrossRef]
- Zhang, Z.P.; Ding, J.L.; Wang, J.Z.; Ge, X.Y. Prediction of soil organic matter in northwestern China using fractional-order derivative spectroscopy and modified normalized difference indices. Catena 2020, 185, 104257. [Google Scholar] [CrossRef]
- Xu, Y.X.; Qin, K.Z.; Ding, K.S.; Li, J.X.; Miao, Y.; Fang, T.H.; Xu, X.W.; Li, D.M.; Luo, X.Q. Geochronology evidence of Mesozoic metallogenesis and Cenozoic oxidation at Hongshan HS-epithermal Cu-Au deposit, Kalatage region, eastern Tianshan, and its tectonic and paleoclimatic significances. Acta Petrol. Sin. 2008, 24, 2371–2383. [Google Scholar]
- Zhang, S.L.; Fu, S.X.; Li, C.X. Application of remote sensing to prospecting of ore deposits in Kalatage, Xinjiang. Miner. Depos. 2002, 21, 1228–1231, (In Chinese with English Abstract). [Google Scholar]
- Feng, Y. The Metallogenic Prediction of Meiling-Hongshi-Honghai Cu-Zn Polymetallic Deposit, Xinjiang Province; China University of Geosciences: Beijing, China, 2014; (In Chinese with English Abstract). [Google Scholar]
- Rinnan, A.; van den Berg, F.; Engelsen, S.B. Review of the most common pre-processing techniques for near-infrared spectra. TrAC—Trends Anal. Chem. 2009, 29, 1201–1222. [Google Scholar] [CrossRef]
- Savitzky, A.; Golay, M.J.E. Golay Smoothing and differentiation of data by simplified least squares procedures. Anal. Chem. 1964, 36, 1627–1639. [Google Scholar] [CrossRef]
- Zhang, C.; Yu, Z.X.; Huang, T.; Zhang, Y.; Luo, H.C.; Niu, X.H. The study on fresh biomass estimation of zizania latifolia based on different spectral preprocessing of spectral reflectance. J. Southwest For. Univ. 2019, 39, 105–115, (In Chinese with English Abstract). [Google Scholar]
- Clark, R.N.; Roush, T.L. Reflectance spectroscopy: Quantitative analysis techniques for remote sensing applications. J. Geophys. Res. 1984, 89, 6329–6340. [Google Scholar] [CrossRef]
- Gomez, C.; Lagacherie, P.; Coulouma, G. Continuum removal versus plsr method for clay and calcium carbonate content estimation from laboratory and airborne hyperspectral measurements. Geoderma 2008, 148, 141–148. [Google Scholar] [CrossRef]
- Chen, C.; Jiang, Q.; Zhang, Z.; Shi, P.; Xu, Y.; Liu, B.; Xi, J.; Chang, S.Z. Hyperspectral inversion of petroleum hydrocarbon contents in soil based on continuum removal and wavelet packet decomposition. Sustainability 2020, 12, 4218. [Google Scholar] [CrossRef]
- Choe, E.; van der Meer, F.; van Ruitenbeek, F.; van der Werff, H.; de Smeth, B.; Kim, Y.W. Mapping of heavy metal pollution in stream sediments using combined geochemistry, field spectroscopy, and hyperspectral remote sensing: A case study of the Rodalquilar mining area, SE Spain. Remote Sens. Environ. 2008, 112, 3222–3233. [Google Scholar] [CrossRef]
- Liu, X.Y.; Zhang, J.L.; Yin, Y.F.; Yang, Y.; Wu, X.X. Underwater polarization image restoration based on logarithmic transformation and dark channel. Optoelectron. Lett. 2020, 16, 5. [Google Scholar] [CrossRef]
- Wang, C.Y. Earth Observation Technology and Fine Agriculture; Science Press: Beijing, China, 2001; (In Chinese with English Abstract). [Google Scholar]
- Sun, L.; Cheng, L.J. Analysis of spectral response of vegetation leaf biochemical components. Spectrosc. Spectr. Anal. 2010, 30, 3031–3035. [Google Scholar]
- Hu, C.M.; Lee, Z.; Franz, B. Chlorophyll a algorithms for oligotrophic oceans: A novel approach based on three-band reflectance difference. J. Geophys. Res.-Ocean. 2012, 117, C01011. [Google Scholar] [CrossRef]
- Wang, J.Z.; Ding, J.L.; Yu, D.L.; Ma, X.K.; Zhang, Z.P.; Ge, X.Y.; Teng, D.X.; Li, X.H.; Liang, J.; Lizag, A.; et al. Capability of Sentinel-2 MSI data for monitoring and mapping of soil salinity in dry and wet sea-sons in the Ebinur Lake region, Xinjiang, China. Geoderma 2019, 353, 172–187. [Google Scholar] [CrossRef]
- Zhao, B.; Gao, L.R.; Liao, W.Z.; Zhang, B. A new kernel method for hyperspectral image feature extraction. Geo-Spat. Inf. Sci. 2018, 20, 309–318. [Google Scholar] [CrossRef]
- Galvao, R.K.H.; Araujo, M.C.U.; Silva, E.C.; Jose, G.E.; Soares, S.F.C.; Paiva, H.M. Cross-validation for the se-lection of spectral variables using the successive projections algorithm. J. Braz. Chem. Soc. 2007, 18, 1580–1584. [Google Scholar] [CrossRef]
- Zou, X.B.; Zhao, J.W.; Povey, M.J.W.; Holmes, M.; Mao, H.P. Variables selection methods in near-infrared spectroscopy. Anal. Chim. Acta 2010, 667, 14–32. [Google Scholar]
- Chong, I.G.; Jun, C.H. Performance of some variable selection methods when multicollinearity is present. Chemom. Intell. Lab. Syst. 2005, 78, 103–112. [Google Scholar] [CrossRef]
- Liu, B.; Guo, S.; Wei, Y.H.; Zhan, Z.D. A fast independent component analysis algorithm for geochemical anomaly detection and its application to soil geochemistry data processing. J. Appl. Math. 2014, 2014, 319314. [Google Scholar] [CrossRef]
- Geladi, P.; Kowalski, B.R. Partial least-squares regression: A tutorial. Anal. Chim. Acta 1986, 185, 1–17. [Google Scholar] [CrossRef]
- Chin, W.W. The partial least squares approach to structural equation modeling. In Modern Methods for Business Research; Lawrence Erlbaum Associates, Inc., Publishers: Mahwah, NJ, USA, 1998; pp. 295–336. [Google Scholar]
- Fatehi, P.; Damm, A.; Schaepman, M.E.; Kneubuhler, M. Estimation of alpine forest structural variables from imaging spectrometer data. Remote Sens. 2016, 7, 15830. [Google Scholar] [CrossRef]
- Vohland, M.; Besold, J.; Hill, J.; Frund, H.C. Comparing different multivariate calibration methods for the determination of soil organic carbon pools with visible to near infrared spectroscopy. Geoderma 2011, 166, 198–205. [Google Scholar] [CrossRef]
- Hong, Y.S.; Shen, R.L.; Cheng, H.; Chen, S.C.; Chen, Y.Y.; Guo, L.; He, J.H.; Liu, Y.L.; Yu, L.; Liu, Y. Cadmium concentration estimation in pen-urban agricultural soils: Using reflectance spectroscopy, soil auxiliary information, or a combination of both? Geoderma 2019, 354, 113875. [Google Scholar] [CrossRef]
- Zhou, S.G.; Liao, S.B.; Zhou, K.F.; Wang, J.L.; Liu, Y.D. Application of portable X-ray fluorescence spectrometer in the analysis of rock samples. Rock Miner. Anal. 2018, 37, 56–63, (In Chinese with English Abstract). [Google Scholar]
- Knadel, M.; Viscarra Rossel, R.A.; Deng, F.; Thomsen, A.; Greve, M.H. Visible-near infraredspectra as a proxy for top-soil texture and glacial boundaries. Soil Sci. Soc. Am. J. 2013, 77, 568–579. [Google Scholar] [CrossRef]
- Zhao, W.Z.; Du, S.H. Spectral-spatial feature extraction for hyperspectral image classification: A dimension reduction and deep learning approach. IEEE Trans. Geosci. Remote Sens. 2016, 54, 4544–4554. [Google Scholar] [CrossRef]
- Gholizadeh, A.; Saberioon, M.; Ben-Dor, E.; Boruvka, L. Monitoring of selected soil contaminants using proximal and remote sensing techniques: Background, state-of-the-art and future perspectives. Crit. Rev. Environ. Sci. Technol. 2018, 48, 243–278. [Google Scholar] [CrossRef]
- Ren, H.E.; Zhuang, D.F.; Singh, A.N.; Pan, J.J.; Qiu, D.S.; Shi, R.H. Estimation of As and Cu contamination in agricultural soils around a mining area by reflectance spectroscopy: A case study. Pedosphere 2009, 19, 719–726. [Google Scholar] [CrossRef]
- Cui, S.C.; Zhou, K.F.; Ding, R.F.; Cheng, Y.Y.; Jiang, G. Estimation of soil copper content based on fractional-order derivative spectroscopy and spectral characteristic band selection. Spectrochim. Acta Part A Mol. Bio-Mol. Spectrosc. 2022, 275, 121190. [Google Scholar] [CrossRef] [PubMed]
- Xu, X.T.; Chen, S.B.; Xu, Z.Y.; Yu, Y.; Zhang, S.; Dai, R. Exploring appropriate preprocessing techniques for hyperspectral soil organic matter content estimation in black soil area. Remote Sens. 2020, 12, 3765. [Google Scholar] [CrossRef]
- Liu, D.; Sun, D.W.; Zeng, X.A. Recent advances in wavelength selection techniques for hyperspectral image processing in the food industry. Food Bioprocess Technol. 2014, 7, 307–323. [Google Scholar] [CrossRef]
- Chen, Z.; Chen, J.P.; Tian, S.F.; Penny, B. Application of fractal content-gradient method for delineating geochemical anomalies associated with copper occurrences in the Yangla ore field, China. Geosci. Front. 2017, 8, 189–197. [Google Scholar] [CrossRef]
- Lu, L.J.; Zhang, J.T.; Chen, G.Q.; Cao, M.X.; Yang, C. Preliminary study of geological space triple divided theory. J. Jinlin Univ. 2012, 42, 279–284. [Google Scholar]
- Nazarpour, A.; Paydar, G.R.; Carranza, E.J.M. Stepwise regression for recognition of geochemical anomalies: Case study in Takab area, NW Iran. J. Geochem. Explor. 2016, 168, 150–162. [Google Scholar] [CrossRef]
- Zhang, M.; Zhao, H.J.; Li, N. Analysis of the influence of hyperspectral spectral resolution on the mineral recognition. Infrared Laser Eng. 2006, 35, 493–498, (In Chinese with English Abstract). [Google Scholar]
- Liu, H.J.; Wu, B.F.; Zhao, C.J.; Zhao, Y.S. Effect of spectral resolution on black soil organic matter content predicting model based on laboratory reflectance. Spectrosc. Spectr. Anal. 2012, 32, 739–742. [Google Scholar]
- Nicola, B.M.; Beullens, K.; Bobelyn, E.; Peirs, A.; Saeys, W.; Theron, K.I.; Lammertyn, J. Nondestructive measurement of fruit and vegetable quality by means of nir spectroscopy: A review. Postharvest Biol. Technol. 2007, 46, 99–118. [Google Scholar] [CrossRef]
- Qiao, X.X.; Wang, C.; Feng, M.C.; Yang, W.D.; Ding, G.W.; Sun, H.; Liang, Z.Y.; Shi, C.C. Hyperspectral estimation of soil organic matter based on different spectral preprocessing techniques. Spectrosc. Lett. 2018, 50, 156–163. [Google Scholar] [CrossRef]
- Camps-Valls, G.; Campos-Taberner, M.; Moreno-Martinez, A.; Walther, S.; Duveiller, G.; Cescatti, A.; Mahecha, M.D.; Munoz-Mari, J.; Garcia-Haro, F.J.; Guanter, L.; et al. A unified vegetation index for quantifying the terrestrial biosphere. Sci. Adv. 2021, 7, eabc7447. [Google Scholar] [CrossRef] [PubMed]
- Bartholomew, H.M.; Schaepman, M.E.; Kooistra, L.; Stevens, A.; Pride, W.B.; Spaargaren, O.S.P. Spectral reflectance based indices for soil organic carbon quantification. Geoderma 2008, 145, 28–36. [Google Scholar] [CrossRef]
- Xu, H.; Liu, Z.C.; Cai, W.S.; Shao, X.G. A wavelength selection method based on randomization test for near-infrared spectral analysis. Chemom. Intell. Lab. Syst. 2009, 97, 189–193. [Google Scholar] [CrossRef]
- Malley, D.F.; Williams, P.C. Use of near-infrared reflectance spectroscopy in prediction of heavy metals in fresh-water sediment by their association with organic matter. Environ. Sci. Technol. 1997, 31, 3461–3467. [Google Scholar] [CrossRef]
- Hunt, G.R. Near-infrared (1.3–2.4 pm) Spectra of Alteration Minerals- Potential for use in Remote Sensing. Geophysics 1979, 44, 1974–1986. [Google Scholar] [CrossRef]
- Susan, J. Spectral reflectance of-carbonate minerals in the visible and near infrared (0.35–2.55 microns): Calcite, aragonite, and dolomite. Am. Mineral. 1986, 71, 151–162. [Google Scholar]
- Crowley, J.L. Principles and Techniques for Sensor Data Fusion. Signal Process. 1993, 32, 5–27. [Google Scholar] [CrossRef]
- Horta, A.; Malone, B.; Stockmann, U.; Minasny, B.; Bishop, T.F.A.; McBratney, A.B.; Pallasser, R.; Pozza, L. Potential of integrated field spectroscopy and spatial analysis for enhanced assessment of soil contamination: A prospective review. Geoderma 2015, 241–242, 180–209. [Google Scholar] [CrossRef]
- O’Rourke, S.M.; Stockmann, U.; Holden, N.M.; McBratney, A.B.; Minasny, B. An assessment of model averaging to improve predictive power of portable vis-NIR and XRF for the determination of agronomic soil properties. Geoderma 2016, 279, 31–44. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).



































