A Quantification of Heat Storage Change-Based Evaporation Behavior in Middle–Large-Sized Lakes in the Inland of the Tibetan Plateau and Their Temporal and Spatial Variations
Abstract
1. Introduction
2. Study Area and Data
2.1. Study Area
2.2. Data
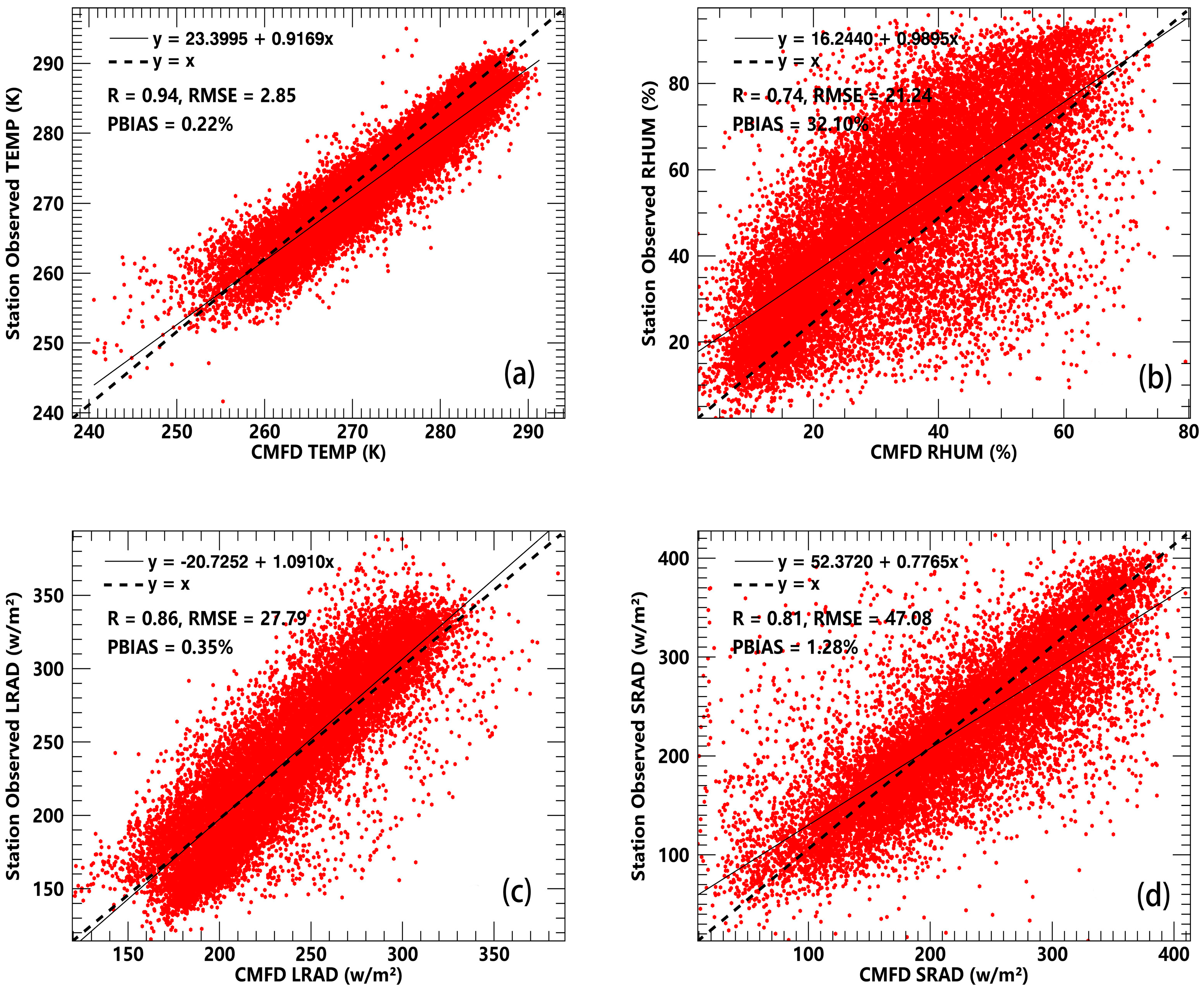
2.2.1. In Situ Meteorological Station Data
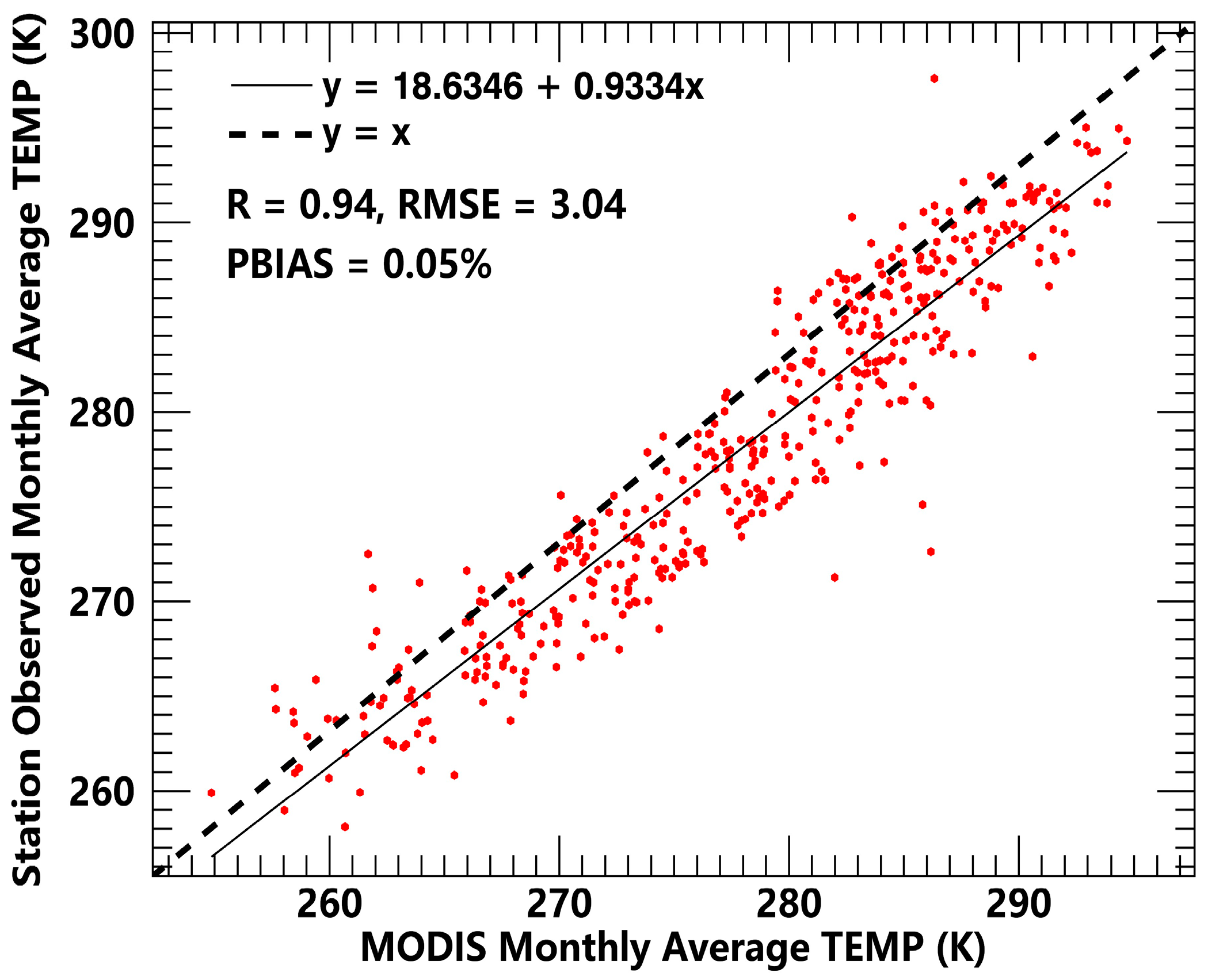
2.2.2. Lake Spatial Grid and Meteorological Datasets
2.2.3. Bathymetric Data of Lake
3. Methodology
3.1. Algorithm for Evaporation Rate
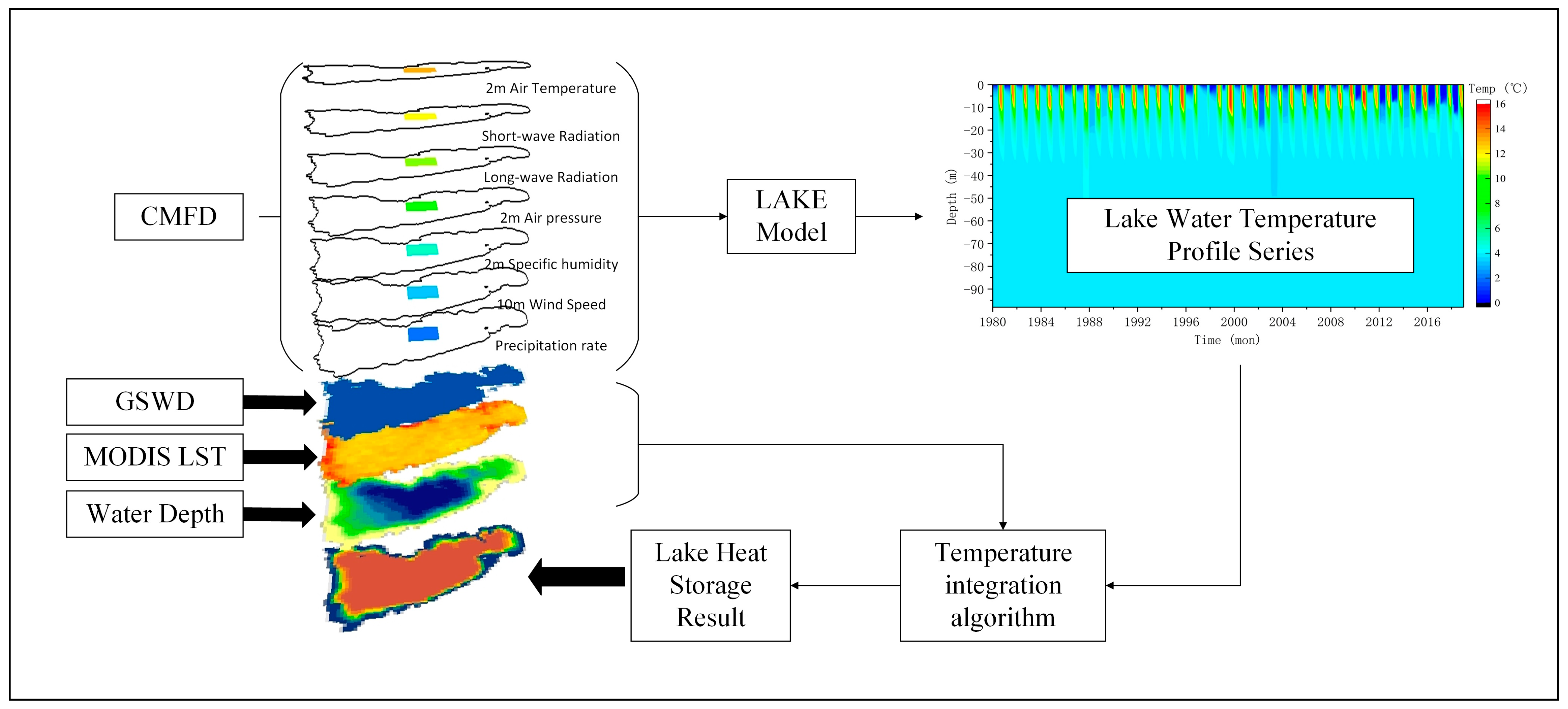
3.2. Algorithm for Lake Heat Storage Change
3.3. The One-Dimensional Numerical Lake Model
3.4. Empirical Formula Method for Lake Ice Sublimation
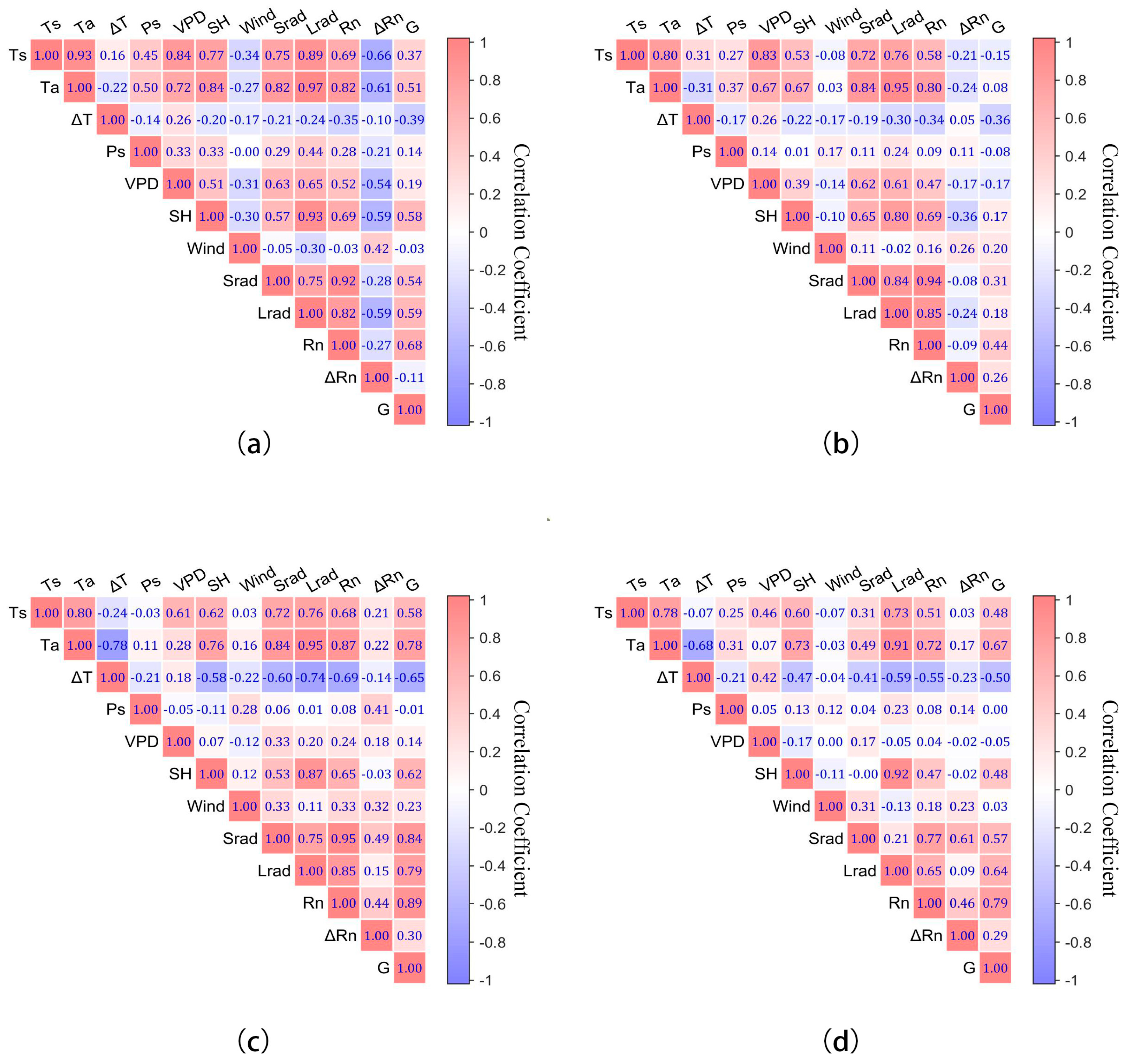
3.5. Attribution Analysis
4. Result
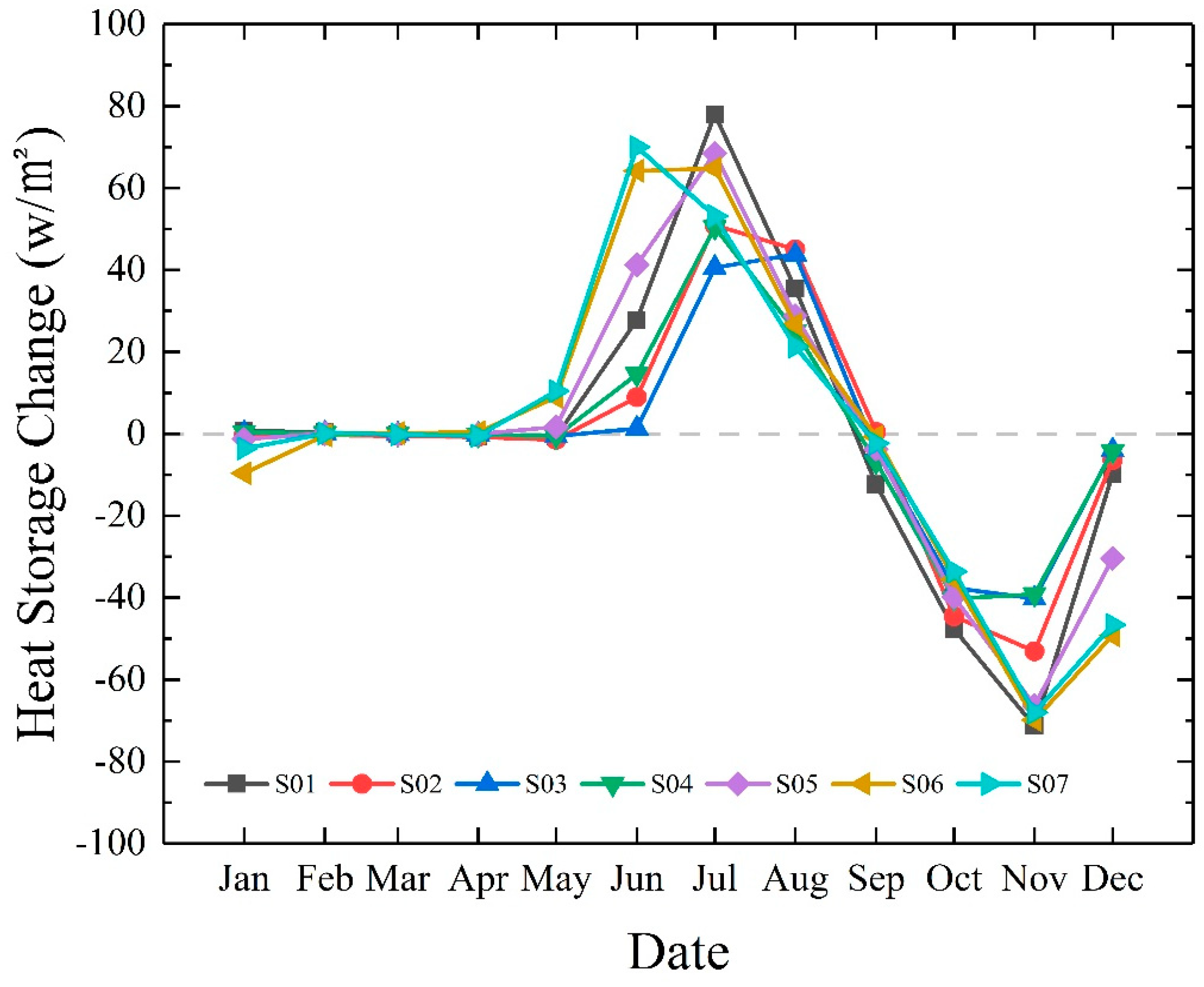
4.1. The Lake Heat Storage Change
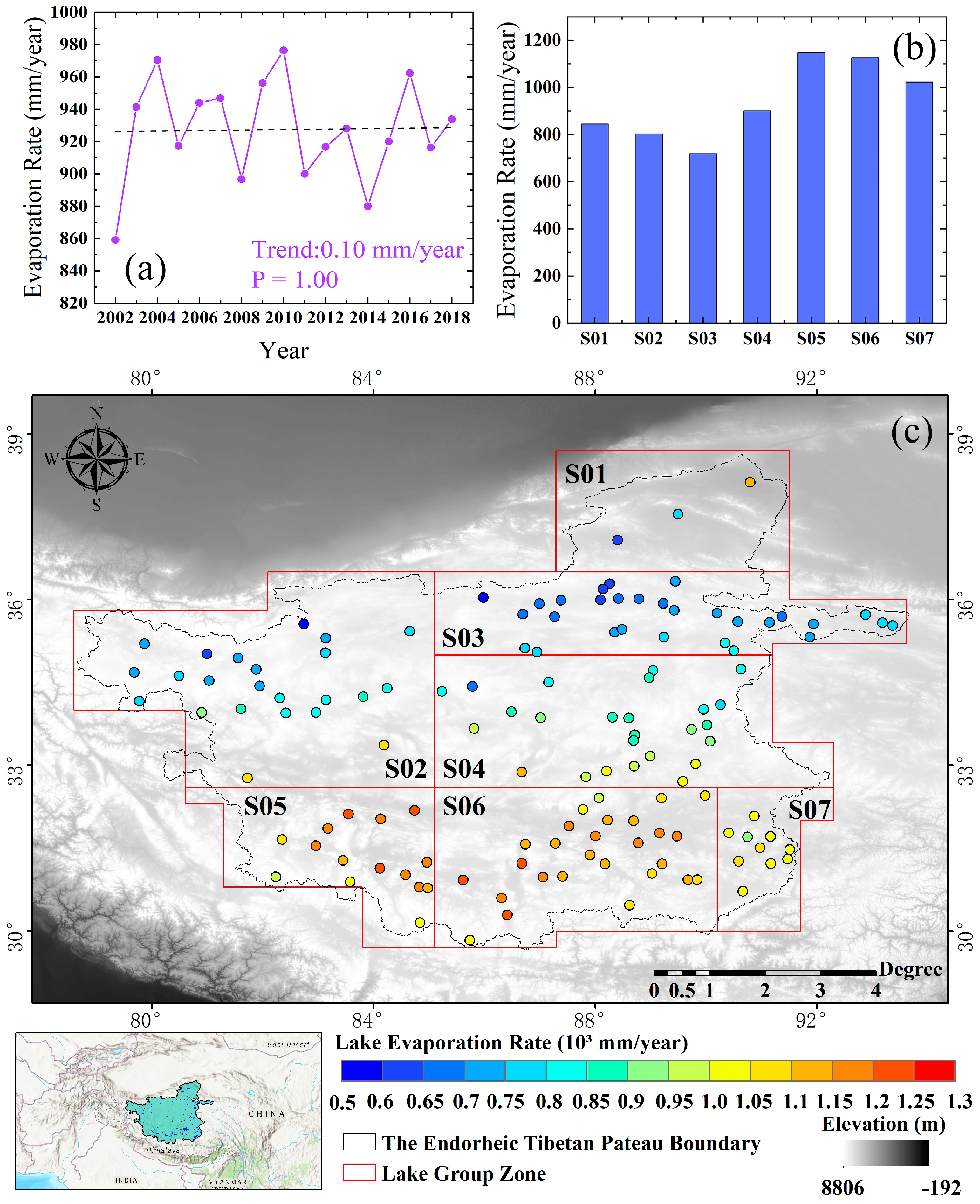
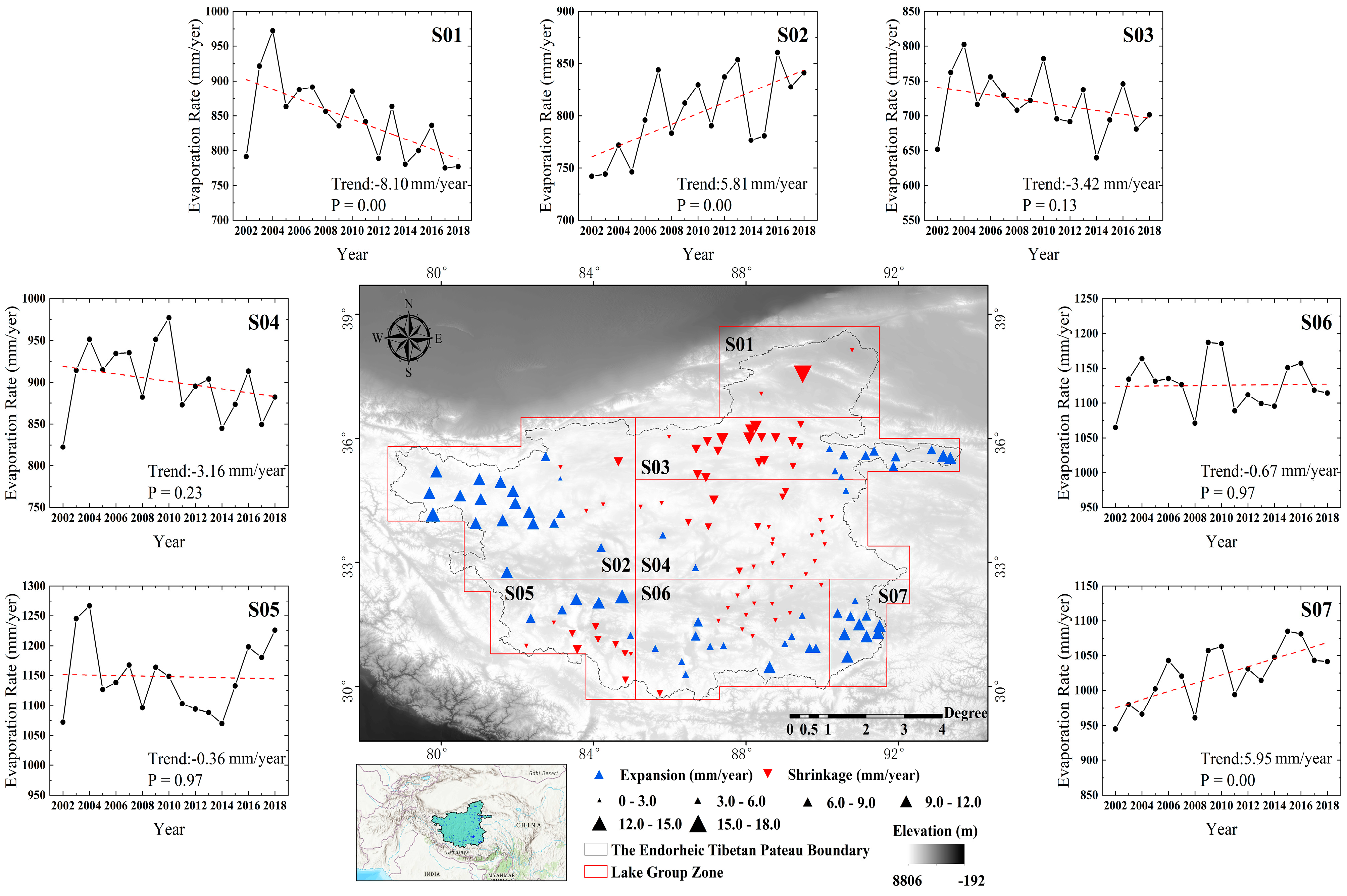
4.2. Spatial–Temporal Variations in the Lake Evaporation Rate
4.3. Spatial–Temporal Variations in the Lake Evaporation Volume
4.4. Magnitudes and Trends of Lake Evaporation
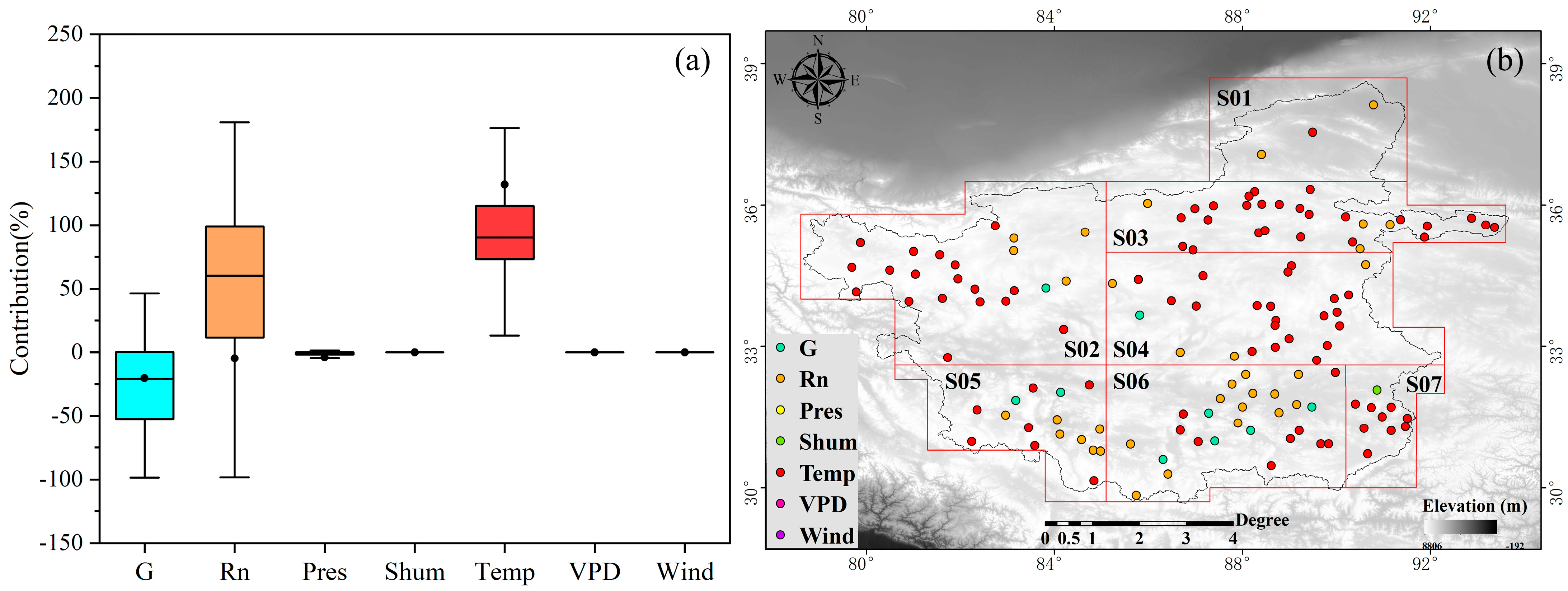
4.5. Attribution Analysis
5. Discussion
5.1. Comparison between Evaporation Rate in This Paper and Previous Studies
5.2. Uncertainty
6. Conclusions
- (1)
- The lake heat storage changes in lakes without available bathymetric data may be estimated by the regional regression model, which is established between the lake heat storage changes in lakes with available water depth and lake surface net radiation values.
- (2)
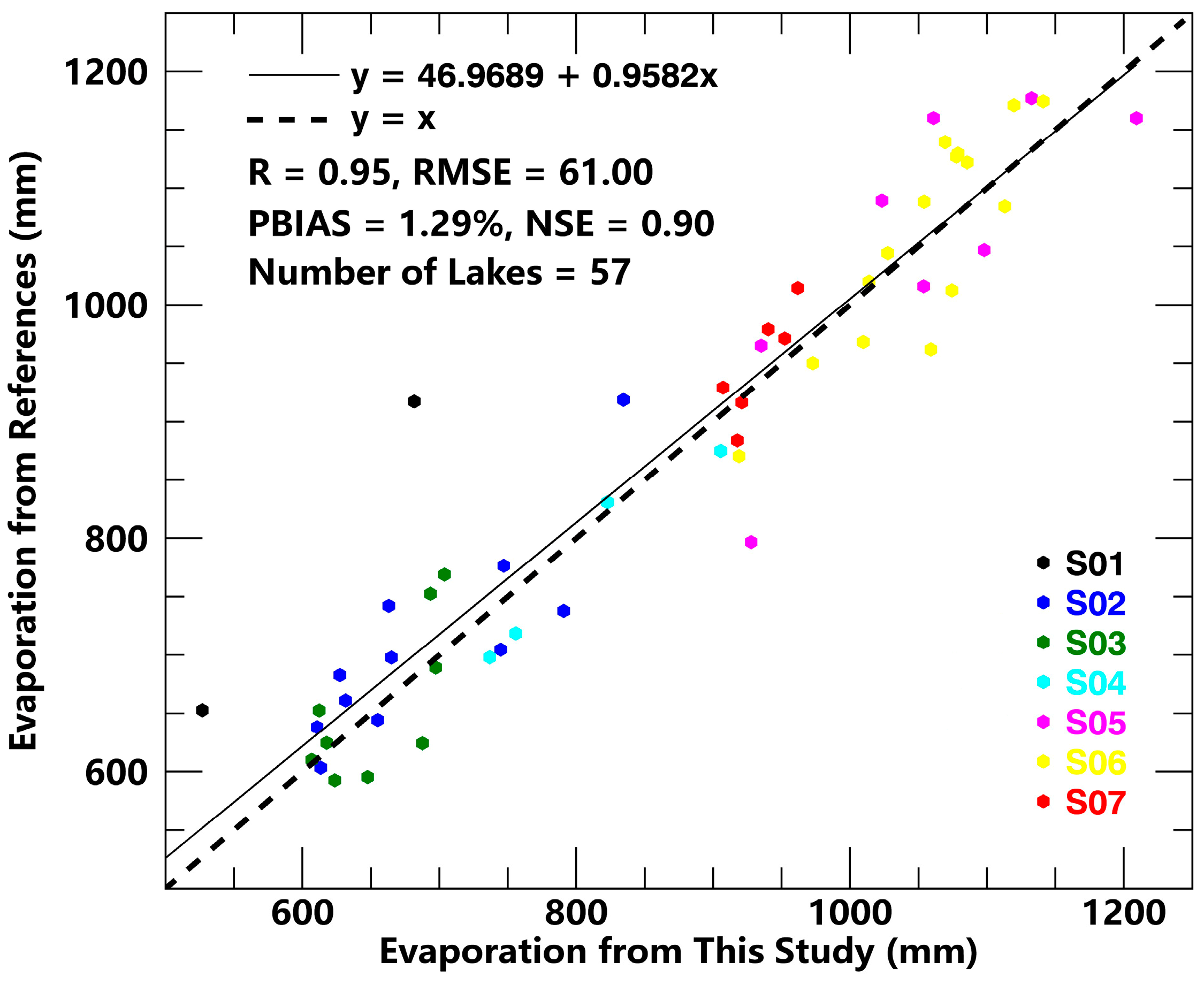
- There is a high degree of accordance of evaporation rates estimated by both the Bowen ratio and Penman methods in 57 middle–large-sized lakes. The correlation coefficient (R) is 0.95; the root mean square error (RMSE) is 61 mm; the percentage bias (PBIAS) is 1.29%; and the Nash–Sutcliffe efficiency (NSE) is 0.90. The good accuracy of the evaporation results make it abundantly clear that the heat storage change regression equations are credible.
- (3)
- From 2002 to 2018, the average annual evaporation rates of the 134 middle–large-sized lakes in the inland of the TP show an insignificant upward trend at about 0.10 mm/year but presented obvious spatial differences. The annual evaporation rate in the southern lakes was 1064.50 mm/year with an upward trend of about 0.62 mm/year, while that in the northern lakes was 750.09 mm/year with a downward trend of about −0.80 mm/year. Temperature is the main factor affecting the evaporation rate of 134 middle–large-sized lakes.
- (4)
- For the 134 middle–large-sized lakes we studied, the average annual evaporation volume from 2002 to 2018 was 25.02 km3 with an obvious upward trend of about 0.35 km3/year. The lake evaporation results did not show obvious spatial distribution differences; however, the total evaporation volume of different levels lakes showed obvious results. The results show that, from 2002 to 2018, the middle–large-sized lakes annual average evaporation volume contribution ratios were 14.04%, 44.46%, and 41.50% from 61 lakes with an area of 50–100 km2, 63 lakes with an area of 100–500 km2, and 10 lakes with an area greater than 500 km2, respectively. Lake area is the key influence factor of the total lake evaporation volume occurring in the inland area of the TP.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yao, T.; Bolch, T.; Chen, D.; Gao, J.; Immerzeel, W.; Piao, S.; Su, F.; Thompson, L.; Wada, Y.; Wang, L.; et al. The imbalance of the Asian water tower. Nat. Rev. Earth Environ. 2022, 3, 618–632. [Google Scholar] [CrossRef]
- Zhu, L.; Wang, J.; Ju, J.; Ma, N.; Zhang, Y.; Liu, C.; Han, B.; Liu, L.; Wang, M.; Ma, Q. Climatic and lake environmental changes in the Serling Co region of Tibet over a variety of timescales. Sci. Bull. 2019, 64, 422–424. [Google Scholar] [CrossRef]
- Zhu, L.; Lü, X.; Wang, J.; Peng, P.; Kasper, T.; Daut, G.; Haberzettl, T.; Frenzel, P.; Li, Q.; Yang, R.; et al. Climate change on the Tibetan Plateau in response to shifting atmospheric circulation since the LGM. Sci. Rep. 2015, 5, 13318. [Google Scholar] [CrossRef] [PubMed]
- Qiu, J. The Third Pole. Nature 2008, 454, 393–396. [Google Scholar] [CrossRef] [PubMed]
- Immerzeel, W.W.; Lutz, A.F.; Andrade, M.; Bahl, A.; Biemans, H.; Bolch, T.; Hyde, S.; Brumby, S.; Davies, B.J.; Elmore, A.C.; et al. Importance and vulnerability of the world’s water towers. Nature 2020, 577, 364–369. [Google Scholar] [CrossRef]
- Zhang, G.; Yao, T.; Shum, C.K.; Yi, S.; Yang, K.; Xie, H.; Feng, W.; Bolch, T.; Wang, L.; Behrangi, A.; et al. Lake volume and groundwater storage variations in Tibetan Plateau’s endorheic basin. Geophys. Res. Lett. 2017, 44, 5550–5560. [Google Scholar] [CrossRef]
- Yang, K.; Lu, H.; Yue, S.; Zhang, G.; Lei, Y.; La, Z.; Wang, W. Quantifying recent precipitation change and predicting lake expansion in the Inner Tibetan Plateau. Clim. Chang. 2017, 147, 149–163. [Google Scholar] [CrossRef]
- Zhang, G.; Bolch, T.; Allen, S.; Linsbauer, A.; Chen, W.; Wang, W. Glacial lake evolution and glacier–lake interactions in the Poiqu River basin, central Himalaya, 1964–2017. J. Glaciol. 2019, 65, 347–365. [Google Scholar] [CrossRef]
- Zhang, G.; Yao, T.; Xie, H.; Kang, S.; Lei, Y. Increased mass over the Tibetan Plateau: From lakes or glaciers? Geophys. Res. Lett. 2013, 40, 2125–2130. [Google Scholar] [CrossRef]
- Lei, Y.; Yao, T.; Yang, K.; Sheng, Y.; Kleinherenbrink, M.; Yi, S.; Bird, B.W.; Zhang, X.; Zhu, L.; Zhang, G. Lake seasonality across the Tibetan Plateau and their varying relationship with regional mass changes and local hydrology. Geophys. Res. Lett. 2017, 44, 892–900. [Google Scholar] [CrossRef]
- Zhang, G.; Chen, W.; Xie, H. Tibetan Plateau’s Lake Level and Volume Changes from NASA’s ICESat/ICESat-2 and Landsat Missions. Geophys. Res. Lett. 2019, 46, 13107–13118. [Google Scholar] [CrossRef]
- Zhang, G.; Yao, T.; Xie, H.; Yang, K.; Zhu, L.; Shum, C.; Bolch, T.; Yi, S.; Allen, S.; Jiang, L.; et al. Response of Tibetan Plateau lakes to climate change: Trends, patterns, and mechanisms. Earth-Sci. Rev. 2020, 208, 103269. [Google Scholar] [CrossRef]
- Zhang, G.; Chen, W.; Li, G.; Yang, W.; Yi, S.; Luo, W. Lake water and glacier mass gains in the northwestern Tibetan Plateau observed from multi-sensor remote sensing data: Implication of an enhanced hydrological cycle. Remote Sens. Environ. 2020, 237, 111554. [Google Scholar] [CrossRef]
- Han, C.; Ma, Y.; Wang, B.; Zhong, L.; Ma, W.; Chen, X.; Su, Z. Long term variations of actual evapotranspiration over the Tibetan Plateau. Earth Syst. Sci. Data 2021, 13, 3513–3524. [Google Scholar] [CrossRef]
- Yuan, L.; Ma, Y.; Chen, X.; Wang, Y.; Li, Z. An Enhanced MOD16 Evapotranspiration Model for the Tibetan Plateau During the Unfrozen Season. J. Geophys. Res. Atmos. 2021, 126, e2020JD032787. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, C.; Tang, Y.; Yang, Y. Trends in pan evaporation and reference and actual evapotranspiration across the Tibetan Plateau. J. Geophys. Res. 2007, 112, D12110. [Google Scholar] [CrossRef]
- Song, C.; Huang, B.; Ke, L.; Richards, K.S. Remote sensing of alpine lake water environment changes on the Tibetan Plateau and surroundings: A review. ISPRS J. Photogramm. Remote Sens. 2014, 92, 26–37. [Google Scholar] [CrossRef]
- Lin, S.; Wang, G.; Hu, Z.; Huang, K.; Sun, X.; Sun, J.; Luo, M.; Xiao, X. Dynamics of Evapotranspiration and Variations in Different Land-Cover Regions over the Tibetan Plateau during 1961–2014. J. Hydrometeorol. 2021, 22, 955–969. [Google Scholar] [CrossRef]
- Wang, B.; Ma, Y.; Wang, Y.; Su, Z.; Ma, W. Significant differences exist in lake-atmosphere interactions and the evaporation rates of high-elevation small and large lakes. J. Hydrol. 2019, 573, 220–234. [Google Scholar] [CrossRef]
- Li, W.; Pu, P. Estimates of Plateau Lake Evaporation: A Case Study of Zige Tangco. J. Lake Sci. 2001, 13, 227–232. (In Chinese) [Google Scholar]
- Li, X.-Y.; Xu, H.-Y.; Sun, Y.-L.; Zhang, D.-S.; Yang, Z.-P. Lake-Level Change and Water Balance Analysis at Lake Qinghai, West China during Recent Decades. Water Resour. Manag. 2006, 21, 1505–1516. [Google Scholar] [CrossRef]
- Zhu, L.; Xie, M.; Wu, Y. Quantitative analysis of lake area variations and the influence factors from 1971 to 2004 in the Nam Co basin of the Tibetan Plateau. Chin. Sci. Bull. 2010, 55, 1294–1303. [Google Scholar] [CrossRef]
- Zhang, B.; Wu, Y.; Zhu, L.; Wang, J.; Li, J.; Chen, D. Estimation and trend detection of water storage at Nam Co Lake, central Tibetan Plateau. J. Hydrol. 2011, 405, 161–170. [Google Scholar] [CrossRef]
- Huang, A.; Lazhu; Wang, J.; Dai, Y.; Yang, K.; Wei, N.; Wen, L.; Wu, Y.; Zhu, X.; Zhang, X.; et al. Evaluating and Improving the Performance of Three 1-D Lake Models in a Large Deep Lake of the Central Tibetan Plateau. J. Geophys. Res. Atmos. 2019, 124, 3143–3167. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Lyu, S.; Ao, Y.; Wen, L.; Zhao, L.; Wang, S. Long-term energy flux and radiation balance observations over Lake Ngoring, Tibetan Plateau. Atmos. Res. 2015, 155, 13–25. [Google Scholar] [CrossRef]
- Li, X.-Y.; Ma, Y.-J.; Huang, Y.-M.; Hu, X.; Wu, X.C.; Wang, P.; Li, G.Y.; Zhang, S.Y.; Wu, H.W.; Jiang, Z.Y.; et al. Evaporation and surface energy budget over the largest high-altitude saline lake on the Qinghai-Tibetan Plateau. J. Geophys. Res. Atmos. 2016, 121, 10, 410–470, 485. [Google Scholar] [CrossRef]
- Duan, Z.; Bastiaanssen, W.G.M. A new empirical procedure for estimating intra-annual heat storage changes in lakes and reservoirs: Review and analysis of 22 lakes. Remote Sens. Environ. 2015, 156, 143–156. [Google Scholar] [CrossRef]
- Hassan, M. Evaporation estimation for Lake Nasser based on remote sensing technology. Ain Shams Eng. J. 2013, 4, 593–604. [Google Scholar] [CrossRef]
- Lazhu, Y.K.; Wang, J.; Lei, Y.; Chen, Y.; Zhu, L.; Ding, B.; Qin, J. Quantifying evaporation and its decadal change for Lake Nam Co, central Tibetan Plateau. J. Geophys. Res. Atmos. 2016, 121, 7578–7591. [Google Scholar] [CrossRef]
- Ma, N.; Szilagyi, J.; Niu, G.-Y.; Zhang, Y.; Zhang, T.; Wang, B.; Wu, Y. Evaporation variability of Nam Co Lake in the Tibetan Plateau and its role in recent rapid lake expansion. J. Hydrol. 2016, 537, 27–35. [Google Scholar] [CrossRef]
- Wang, B.; Ma, Y.; Su, Z.; Wang, Y.; Ma, W. Quantifying the evaporation amounts of 75 high-elevation large dimictic lakes on the Tibetan Plateau. Sci. Adv. 2020, 6, eaay8558. [Google Scholar] [CrossRef]
- Wang, B.; Ma, Y.; Ma, W.; Su, B.; Dong, X. Evaluation of ten methods for estimating evaporation in a small high-elevation lake on the Tibetan Plateau. Theor. Appl. Climatol. 2018, 136, 1033–1045. [Google Scholar] [CrossRef]
- Qiao, B.; Zhu, L.; Wang, J.; Ju, J.; Ma, Q.; Huang, L.; Chen, H.; Liu, C.; Xu, T. Estimation of lake water storage and changes based on bathymetric data and altimetry data and the association with climate change in the central Tibetan Plateau. J. Hydrol. 2019, 578, 124052. [Google Scholar] [CrossRef]
- Qiao, B.; Zhu, L.; Yang, R. Temporal-spatial differences in lake water storage changes and their links to climate change throughout the Tibetan Plateau. Remote Sens. Environ. 2019, 222, 232–243. [Google Scholar] [CrossRef]
- Li, Y.; Su, F.; Chen, D.; Tang, Q. Atmospheric Water Transport to the Endorheic Tibetan Plateau and Its Effect on the Hydrological Status in the Region. J. Geophys. Res. Atmos. 2019, 124, 12864–12881. [Google Scholar] [CrossRef]
- Sun, J.; Yang, K.; Guo, W.; Wang, Y.; He, J.; Lu, H. Why Has the Inner Tibetan Plateau Become Wetter since the Mid-1990s? J. Clim. 2020, 33, 8507–8522. [Google Scholar] [CrossRef]
- Qiao, B.; Zhu, L. Difference and cause analysis of water storage changes for glacier-fed and non-glacier-fed lakes on the Tibetan Plateau. Sci. Total Environ. 2019, 693, 133399. [Google Scholar] [CrossRef]
- Cui, Y.; Zhang, X.; Liu, Y. Radiative and Aerodynamic Contribution to Evaporation: Eddy-Covariance Comparison Between a Plain and a Plateau Lake. Earth Space Sci. 2021, 8, e2021EA001913. [Google Scholar] [CrossRef]
- Zhang, R.; Zhu, L.; Ma, Q.; Chen, H.; Liu, C.; Zubaida, M. The consecutive lake group water storage variations and their dynamic response to climate change in the central Tibetan Plateau. J. Hydrol. 2021, 601, 126615. [Google Scholar] [CrossRef]
- Zhang, G.; Luo, W.; Chen, W.; Zheng, G. A robust but variable lake expansion on the Tibetan Plateau. Sci. Bull. 2019, 64, 1306–1309. [Google Scholar] [CrossRef] [PubMed]
- He, J.; Yang, K.; Tang, W.; Lu, H.; Qin, J.; Chen, Y.; Li, X. The first high-resolution meteorological forcing dataset for land process studies over China. Sci. Data 2020, 7, 25. [Google Scholar] [CrossRef]
- Zhao, G.; Gao, H.; Cai, X. Estimating lake temperature profile and evaporation losses by leveraging MODIS LST data. Remote Sens. Environ. 2020, 251, 112104. [Google Scholar] [CrossRef]
- Ma, Y.; Hu, Z.; Xie, Z.; Ma, W.; Wang, B.; Chen, X.; Li, M.; Zhong, L.; Sun, F.; Gu, L.; et al. A long-term (2005–2016) dataset of hourly integrated land–atmosphere interaction observations on the Tibetan Plateau. Earth Syst. Sci. Data 2020, 12, 2937–2957. [Google Scholar] [CrossRef]
- Wei, D.; Qi, Y.; Ma, Y.; Wang, X.; Ma, W.; Gao, T.; Huang, L.; Zhao, H.; Zhang, J.; Wang, X. Plant uptake of CO2 outpaces losses from permafrost and plant respiration on the Tibetan Plateau. Proc. Natl. Acad. Sci. USA 2021, 118, e2015283118. [Google Scholar] [CrossRef] [PubMed]
- Pekel, J.F.; Cottam, A.; Gorelick, N.; Belward, A.S. High-resolution mapping of global surface water and its long-term changes. Nature 2016, 540, 418–422. [Google Scholar] [CrossRef]
- Hutchinson, M.F. A new objective method for spatial interpolation of meteorological variables from irregular networks applied to the estimation of monthly mean solar radiation, temperature, precipitation and windrun. CSIRO Div. Water Resour. Tech. Memo 1989, 89, 95–104. [Google Scholar]
- Qiao, B.; Zhu, L.; Wang, J.; Ju, J.; Ma, Q.; Liu, C. Estimation of lakes water storage and their changes on the northwestern Tibetan Plateau based on bathymetric and Landsat data and driving force analyses. Quat. Int. 2017, 454, 56–67. [Google Scholar] [CrossRef]
- Tian, W.; Liu, X.; Wang, K.; Bai, P.; Liu, C. Estimation of reservoir evaporation losses for China. J. Hydrol. 2021, 596, 126142. [Google Scholar] [CrossRef]
- Wang, B.; Ma, Y.; Ma, W.; Su, Z. Physical controls on half-hourly, daily, and monthly turbulent flux and energy budget over a high-altitude small lake on the Tibetan Plateau. J. Geophys. Res. Atmos. 2017, 122, 2289–2303. [Google Scholar] [CrossRef]
- Lei, Y.; Yao, T.; Yang, K.; Ma, Y.; Bird, B.W. Contrasting hydrological and thermal intensities determine seasonal lake-level variations—A case study at Paiku Co on the southern Tibetan Plateau. Hydrol. Earth Syst. Sci. 2021, 25, 3163–3177. [Google Scholar] [CrossRef]
- Zhao, G.; Gao, H. Estimating reservoir evaporation losses for the United States: Fusing remote sensing and modeling approaches. Remote Sens. Environ. 2019, 226, 109–124. [Google Scholar] [CrossRef]
- Gan, G.; Liu, Y. Heat Storage Effect on Evaporation Estimates of China’s Largest Freshwater Lake. J. Geophys. Res. Atmos. 2020, 125, e2019JD032334. [Google Scholar] [CrossRef]
- Stepanenko, V.M.; Goyette, S.; Martynov, A.; Perroud, M.; Xing, F.; Mironov, D. First steps of a lake model intercomparison Project: LAKEMIP. Boreal Environ. Res. 2010, 15, 19. [Google Scholar]
- Stepanenko, V.M.; Martynov, A.; Jöhnk, K.D.; Subin, Z.M.; Perroud, M.; Fang, X.; Beyrich, F.; Mironov, D.; Goyette, S. A one-dimensional model intercomparison study of thermal regime of a shallow, turbid midlatitude lake. Geosci. Model Dev. 2013, 6, 1337–1352. [Google Scholar] [CrossRef]
- Thiery, W.I.M.; Stepanenko, V.M.; Fang, X.; Jöhnk, K.D.; Li, Z.; Martynov, A.; Perroud, M.; Subin, Z.M.; Darchambeau, F.; Mironov, D.; et al. LakeMIP Kivu: Evaluating the representation of a large, deep tropical lake by a set of one-dimensional lake models. Tellus A Dyn. Meteorol. Oceanogr. 2014, 66, 21390. [Google Scholar] [CrossRef]
- Stepanenko, V.; Mammarella, I.; Ojala, A.; Miettinen, H.; Lykosov, V.; Vesala, T. LAKE 2.0: A model for temperature, methane, carbon dioxide and oxygen dynamics in lakes. Geosci. Model Dev. 2016, 9, 1977–2006. [Google Scholar] [CrossRef]
- Hostetler, S.W.; Bartlein, P.J. Simulation of lake evaporation with application to modeling lake level variations of Harney-Malheur Lake, Oregon. Water Resour. Res. 1990, 10, 10. [Google Scholar]
- Hostetler, S.W.; Bates, G.T.; Giorgi, F. Interactive coupling of a lake thermal model with a regional climate model. J. Geophys. Res. 1993, 98, 5045–5057. [Google Scholar] [CrossRef]
- Fujii, Y.; Kusunoki, K. The role of sublimation and condensation in the formation of ice sheet surface at Mizuho Station, Antarctica. J. Geophys. Res. 1982, 87, 4293. [Google Scholar] [CrossRef]
- Mao, Y.; Nijssen, B.; Lettenmaier, D.P. Is climate change implicated in the 2013–2014 California drought? A hydrologic perspective. Geophys. Res. Lett. 2015, 42, 2805–2813. [Google Scholar] [CrossRef]
- Zhang, J.; Sun, F.; Xu, J.; Chen, Y.; Sang, Y.F.; Liu, C. Dependence of trends in and sensitivity of drought over China (1961–2013) on potential evaporation model. Geophys. Res. Lett. 2016, 43, 206–213. [Google Scholar] [CrossRef]
- Qiang, Y. The Effect of Heat Storage Changes on Lake Evaporation in Lakes on the Qinghai-Tibetan Plateau. Master’s Thesis, University of Chinese Academy Sciences, Beijing, China, 2021. (In Chinese). [Google Scholar]







| Zone | Proportion of Land-Cover Types | Elevation (m) | ||||
|---|---|---|---|---|---|---|
| Water | Open Shrublands | Grasslands | Snow and Ice | Barren Vegetated | ||
| S01 | 1.38% | 0.00% | 4.90% | 0.27% | 93.45% | 4020 |
| S02 | 1.06% | 0.24% | 4.47% | 2.50% | 91.74% | 5119 |
| S03 | 2.47% | 0.00% | 15.84% | 1.09% | 80.59% | 4979 |
| S04 | 2.14% | 0.27% | 62.90% | 0.89% | 33.80% | 5096 |
| S05 | 2.45% | 4.19% | 50.03% | 0.18% | 43.16% | 5056 |
| S06 | 5.19% | 0.23% | 86.01% | 0.02% | 8.55% | 4984 |
| S07 | 7.34% | 0.00% | 87.97% | 0.06% | 4.64% | 4847 |
| Site | Latitude, Longitude | Elevation (m) | Period | Land Cover | Variables (Units) | References |
|---|---|---|---|---|---|---|
| MAWORS | 38.42°N, 75.03°E | 3668 | 2005–2016 | Alpine desert | 2 m-Air temperature (°C) 0 m-Soil temperature (°C) 10 m-Wind speed (m/s) 2 m-Humidity (%)Radiations (w/m2) | Ma et al., 2020 [43] |
| NADORS | 33.39°N, 79.7°E | 4270 | 2005–2016 | Alpine desert | ||
| QOMS | 28.36°N, 86.95°E | 4298 | 2005–2016 | Alpine desert | ||
| NAMORS | 30.77°N, 90.96°E | 4730 | 2005–2016 | Alpine steppe | ||
| NAQU | 31.37°N, 91.9°E | 4509 | 2005–2016 | Alpine meadow | ||
| SETORS | 29.77°N, 94.74°E | 3327 | 2005–2016 | Alpine meadow | ||
| SHENZHA | 30.95°N, 88.7°E | 4750 | 2016–2018 | Wetland | Wei et al., 2021 [44] | |
| BATANG | 32.85°N, 96.95°E | 4003 | 2017–2018 | Meadow | ||
| DASHALONG | 38.84°N, 98.94°E | 3739 | 2015 | Wetland | ||
| AROU | 38.03°N, 100.45°E | 3033 | 2015 | Meadow | ||
| YAKOU | 38.01°N, 100.24°E | 4148 | 2015 | Meadow |
| Data Name | Spatial Resolution | Temporal Resolution | Purpose | Web Link |
|---|---|---|---|---|
| Lakes larger than 1 km2 in TP dataset [40] | Shapefile | 1–10 year | Lake mask | http://data.tpdc.ac.cn (accessed on 1 May 2023) |
| Global surface water dataset occurrence (GSWD) [45] | 30 m (resample to 0.01°) | Time invariant | Water area grid extraction and interpolation boundary | https://global-surface-water.appspot.com (accessed on 1 May 2023) |
| China Meteorological Forcing Dataset (CMFD) [41] | 0.1° | Daily | Driving lake and Penman models | http://data.tpdc.ac.cn (accessed on 1 May 2023) |
| MODIS Terra LST (MOD11A2) [42] | 1 km (resample to 0.01°) | 8 days | Water surface temperature and net radiation | https://search.earthdata.nasa.gov (accessed on 1 May 2023) |
| MODIS Aqua LST (MYD11A2) [42] | 1 km (resample to 0.01°) | 8 days | Water surface temperature and net radiation | https://search.earthdata.nasa.gov (accessed on 1 May 2023) |
| Lake Groups | No. Lakes with Measured Depth/No. Lakes without Measured Depth | No. of Data Pairs | G = a × Rn + b | Statistical Agreement | |||
|---|---|---|---|---|---|---|---|
| a | b (w/m2) | R2 | RMSE (w/m2) | NSE | |||
| S01 | 2/1 | 196 | 0.97 | −77.57 | 0.66 | 28.78 | 0.45 |
| S02 | 9/14 | 673 | 1.00 | −80.66 | 0.59 | 26.88 | 0.30 |
| S03 | 8/22 | 543 | 1.03 | −89.78 | 0.65 | 27.13 | 0.45 |
| S04 | 14/11 | 1275 | 0.85 | −84.75 | 0.51 | 29.13 | 0.30 |
| S05 | 8/8 | 968 | 1.02 | −107.84 | 0.62 | 31.25 | 0.40 |
| S06 | 19/8 | 2429 | 1.15 | −117.80 | 0.71 | 28.89 | 0.55 |
| S07 | 9/1 | 1178 | 1.09 | −107.28 | 0.77 | 23.43 | 0.52 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Du, B.; Zhu, L.; Ju, J.; Wang, J.; Ma, Q.; Kou, Q. A Quantification of Heat Storage Change-Based Evaporation Behavior in Middle–Large-Sized Lakes in the Inland of the Tibetan Plateau and Their Temporal and Spatial Variations. Remote Sens. 2023, 15, 3460. https://doi.org/10.3390/rs15143460
Du B, Zhu L, Ju J, Wang J, Ma Q, Kou Q. A Quantification of Heat Storage Change-Based Evaporation Behavior in Middle–Large-Sized Lakes in the Inland of the Tibetan Plateau and Their Temporal and Spatial Variations. Remote Sensing. 2023; 15(14):3460. https://doi.org/10.3390/rs15143460
Chicago/Turabian StyleDu, Baolong, Liping Zhu, Jianting Ju, Junbo Wang, Qingfeng Ma, and Qiangqiang Kou. 2023. "A Quantification of Heat Storage Change-Based Evaporation Behavior in Middle–Large-Sized Lakes in the Inland of the Tibetan Plateau and Their Temporal and Spatial Variations" Remote Sensing 15, no. 14: 3460. https://doi.org/10.3390/rs15143460
APA StyleDu, B., Zhu, L., Ju, J., Wang, J., Ma, Q., & Kou, Q. (2023). A Quantification of Heat Storage Change-Based Evaporation Behavior in Middle–Large-Sized Lakes in the Inland of the Tibetan Plateau and Their Temporal and Spatial Variations. Remote Sensing, 15(14), 3460. https://doi.org/10.3390/rs15143460






