Vision-Aided Hyperspectral Full-Waveform LiDAR System to Improve Detection Efficiency
Abstract
1. Introduction
2. Materials and Methods
2.1. System Configuration
2.2. Working Principle of the V-HSL System
2.2.1. Overview of the V-HSL System
- (1)
- Object detection in camera images. Select and train an object detection model with a dataset that contains annotated targets. The well-trained model should predict the classes, positions, and confidences of targets in the camera plane with high accuracy and speed, which is a prerequisite for the detection of the HSL subsystem;
- (2)
- Extrinsic parameters calibration. Select a camera with a high resolution and proper focus, then calibrate its intrinsic parameter first. Fix the camera and HSL system on the same platform, then carry out extrinsic parameters calibration between the camera coordinate system and the HSL coordinate system;
- (3)
- Target position estimation in the HSL system. This step has two objectives: (1) rotate the outgoing beam to make it point to the center of the target; and (2) determine the minimum imaging range that contains the detected target. Target depth in the camera coordinate system will be estimated by the methods we proposed. Then, the target position in the HSL coordinate system will be derived and combined with the results of step 1 and step 2;
- (4)
- Detection of the HSL subsystem. The HSL subsystem will acquire point clouds and spectra of the target synchronously. Then, the target will be extracted from the background based on spectral differences.
2.2.2. Object Detection Based on YOLOv5 Model
2.2.3. Extrinsic Parameters Calibration
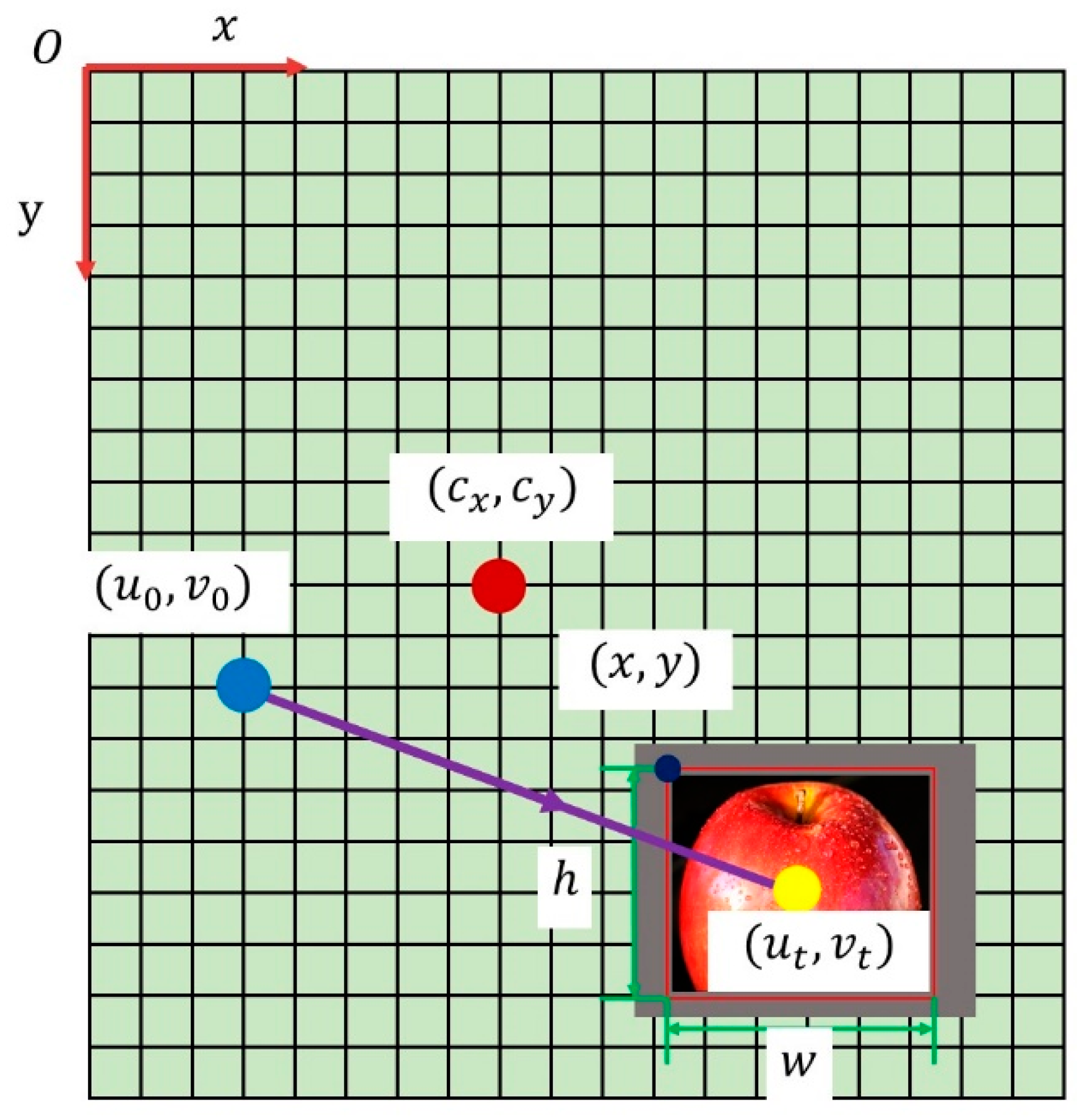
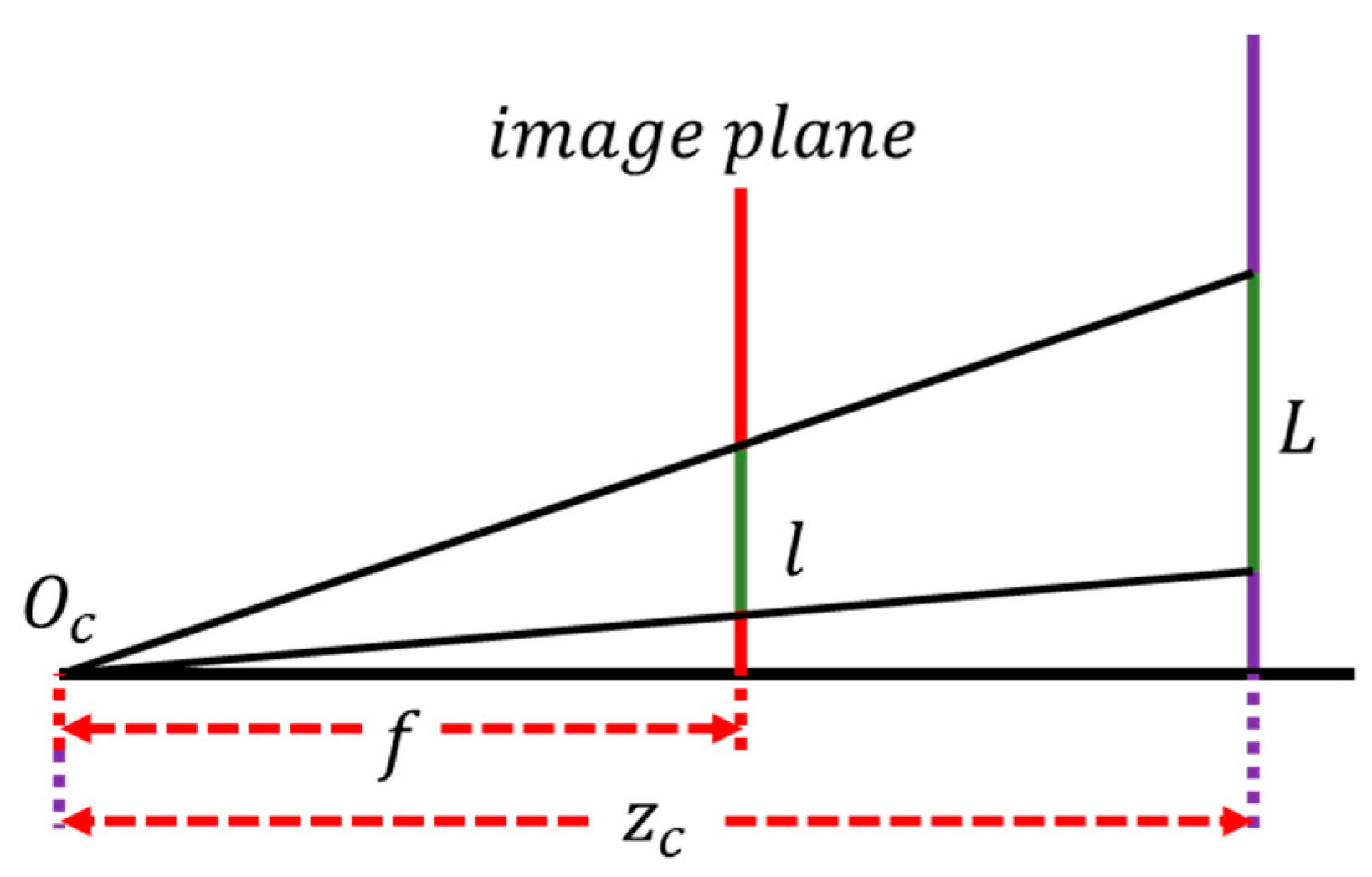
2.2.4. Target Position Estimation in the HSL System
- (1)
- Targets are close to the original footprint along the direction of the z-axis;
- (2)
- The angle between two optical axes of two subsystems is small.
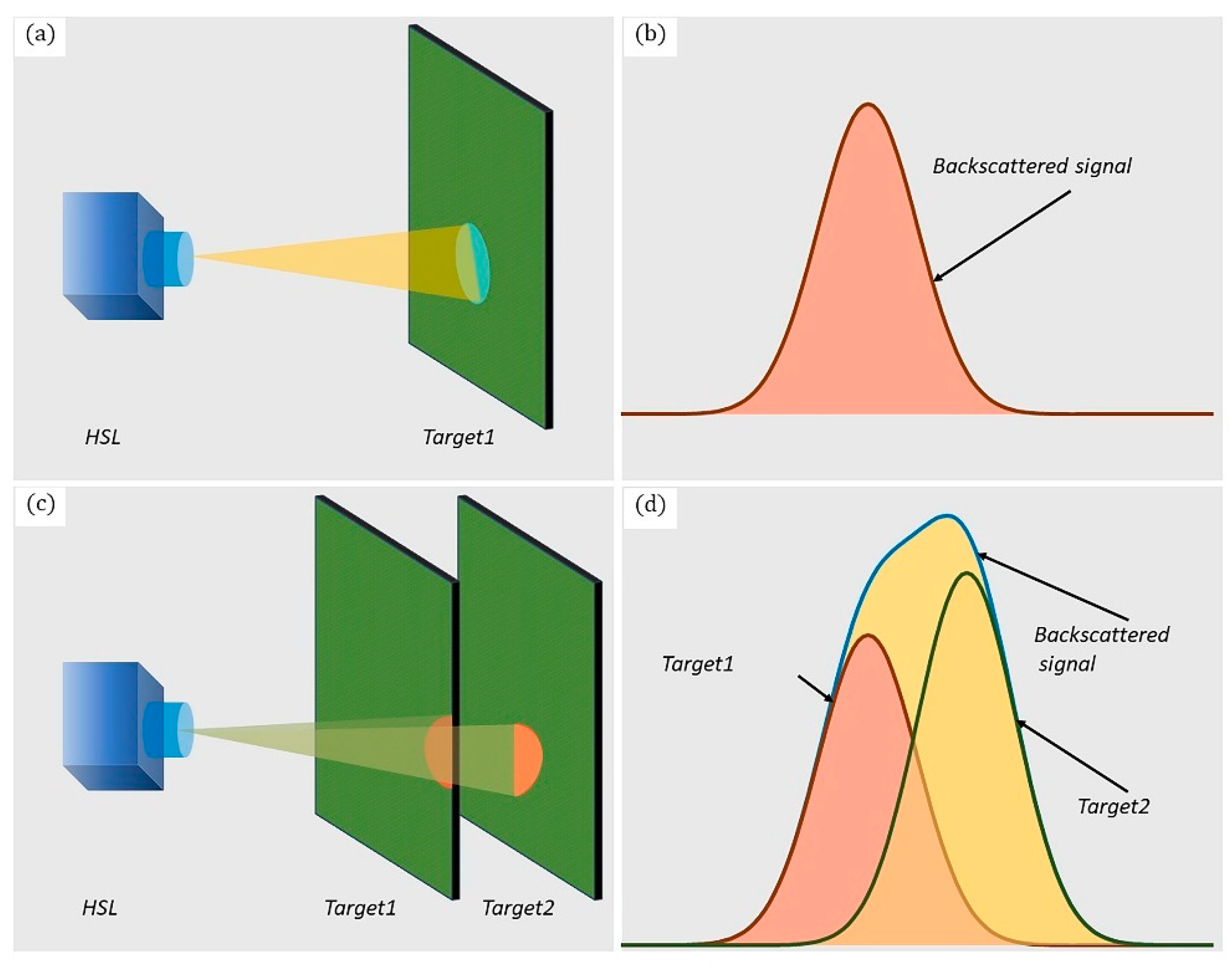
2.2.5. Detection of Spatial and Spectral Information Synchronously
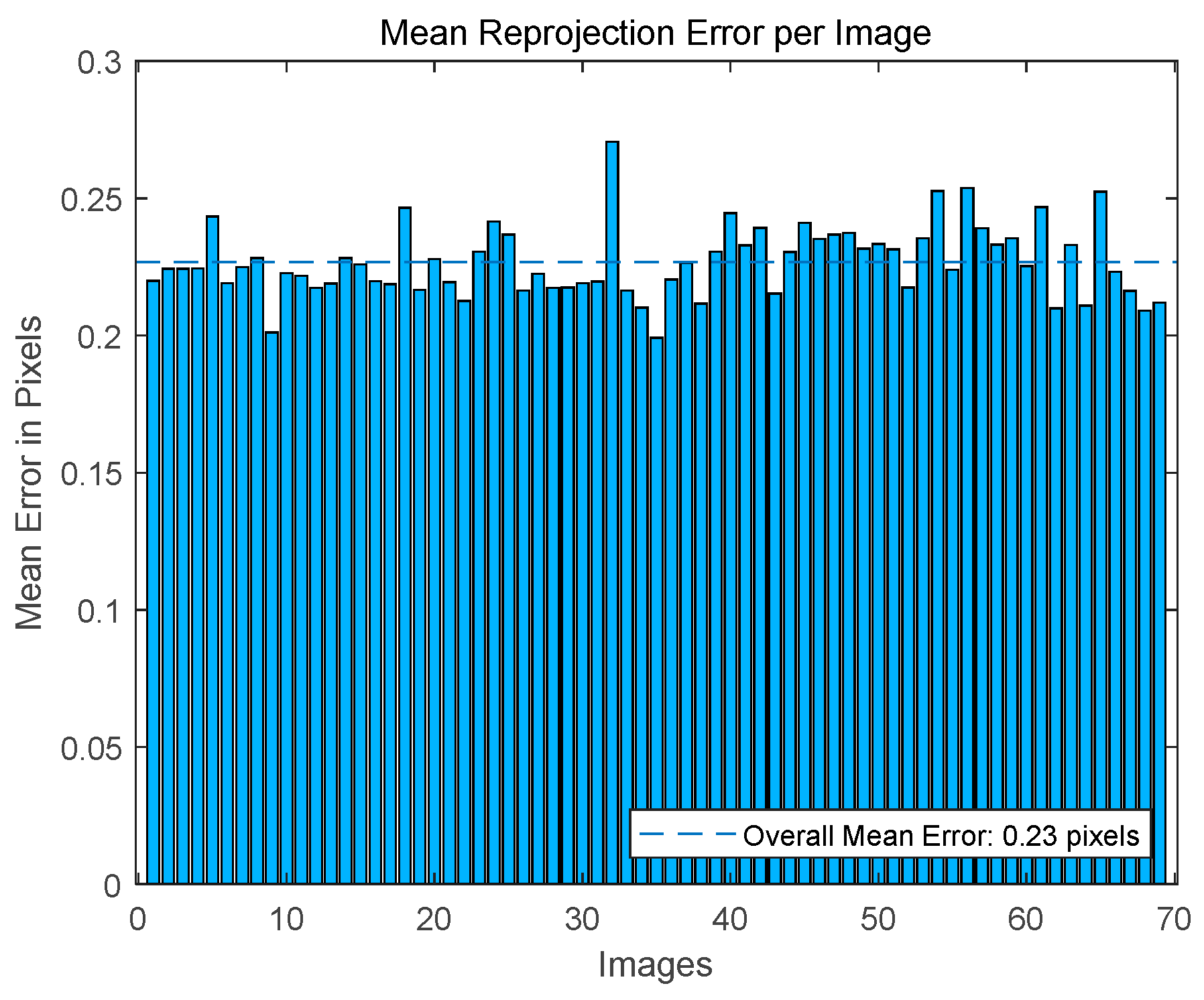
2.3. Performance Analysis and Evaluation
3. Experiment
3.1. Materials
3.2. Results
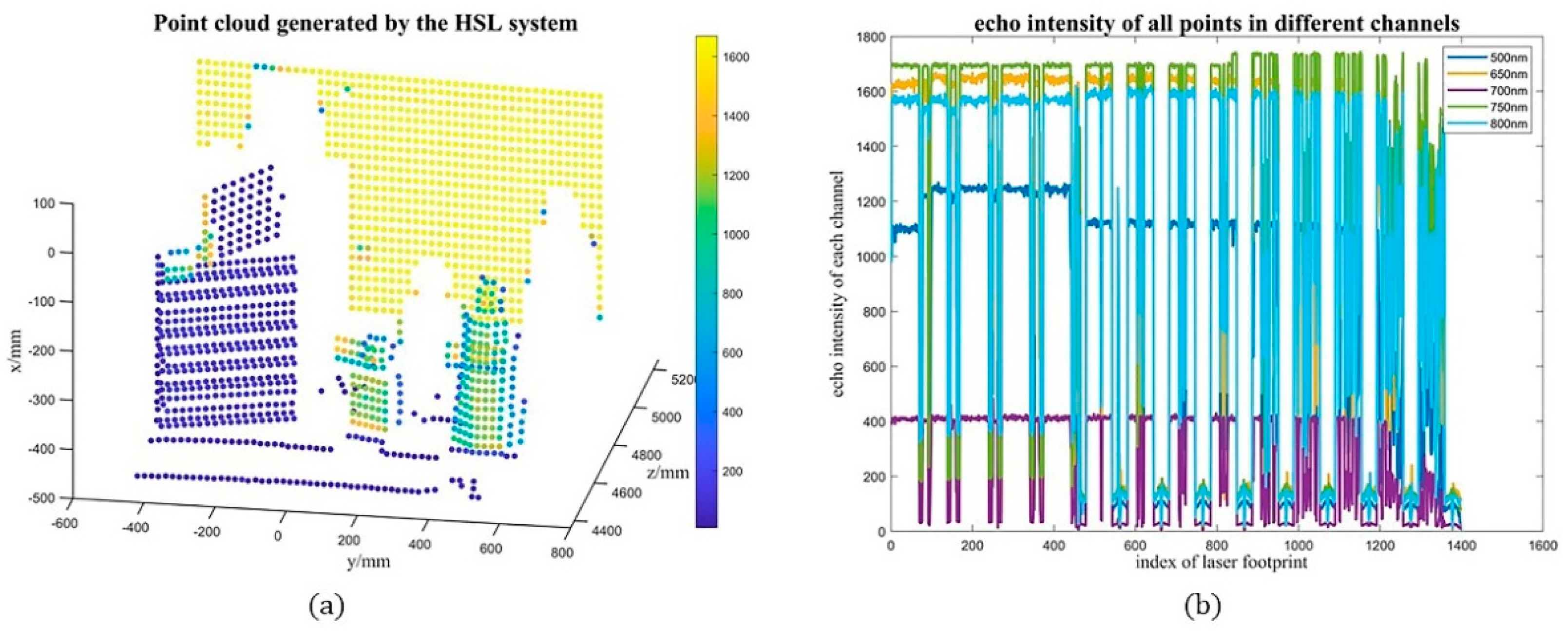
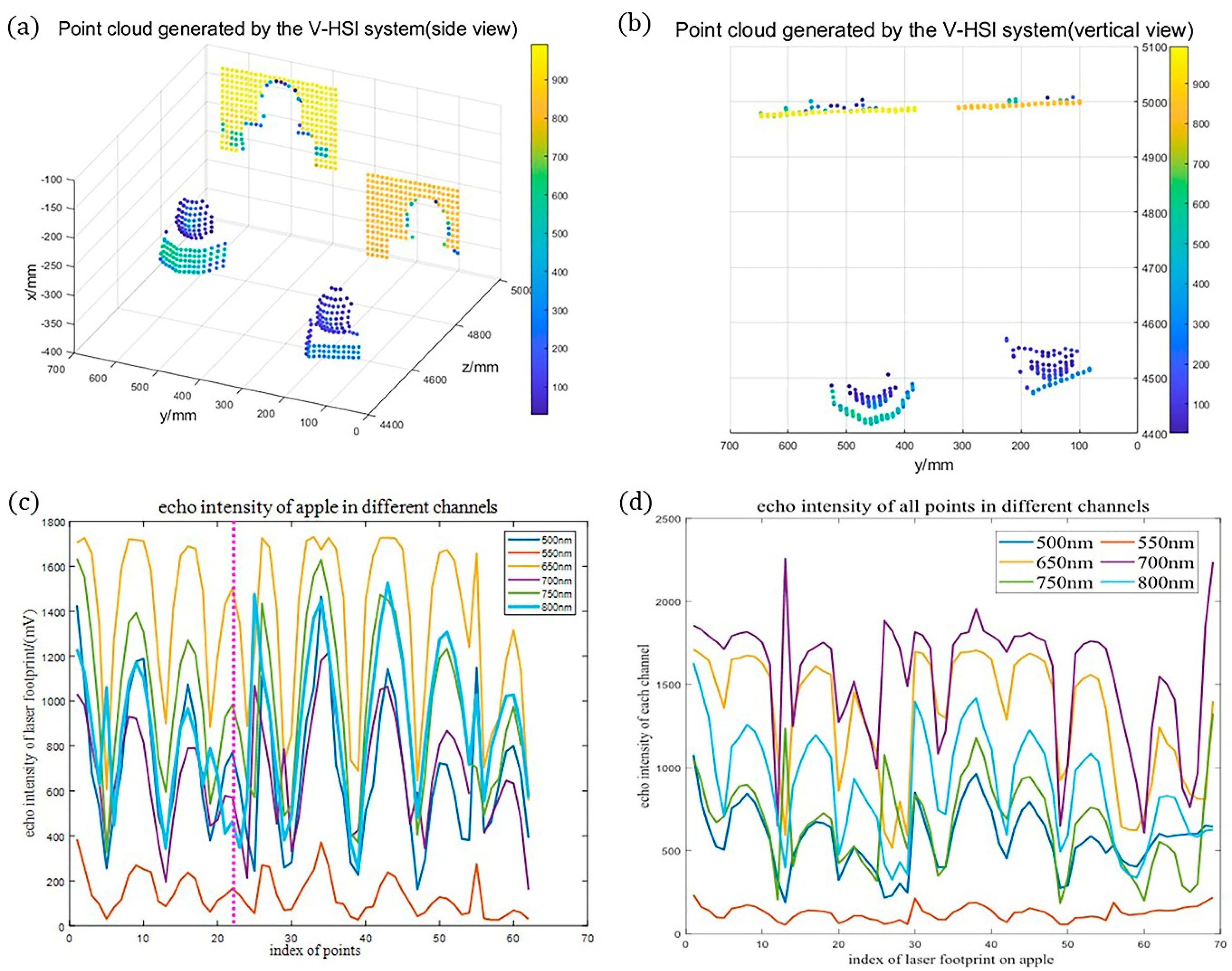
3.2.1. Detection of the HSL System
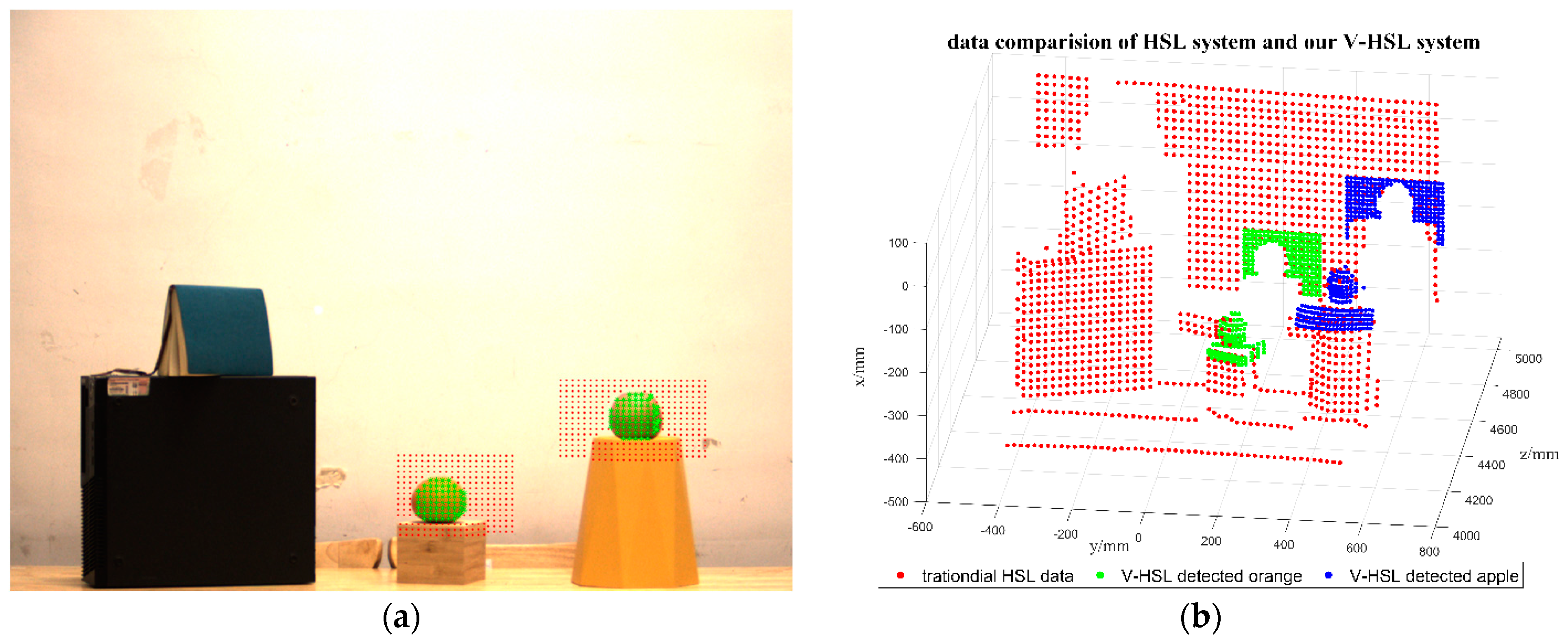
3.2.2. Detection of the V-HSL System
3.2.3. Evaluation of the V-HSL System
4. Discussion
4.1. Comparison of the V-HSL System with Reported Works
4.1.1. Comparison with the V-LiDAR System
4.1.2. Comparison with the HSL System
4.1.3. Comparison with the Single-Pixel Imaging LiDAR
4.2. Outlook
4.2.1. Improvements in Object Detection Model
4.2.2. Improvements in Extrinsic Parameter Calibration
4.2.3. Improvements in Target Position Estimation
4.2.4. Improvements in Detection of HSL Subsystem
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Royo, S.; Ballesta-Garcia, M. An Overview of Lidar Imaging Systems for Autonomous Vehicles. Appl. Sci. 2019, 9, 4093. [Google Scholar] [CrossRef]
- Li, Y.; Zhao, L.; Chen, Y.; Zhang, N.; Fan, H.; Zhang, Z. 3D LiDAR and multi-technology collaboration for preservation of built heritage in China: A review. Int. J. Appl. Earth Obs. Geoinf. 2023, 116, 103156. [Google Scholar] [CrossRef]
- Lv, W.; Wang, X. Overview of Hyperspectral Image Classification. J. Sens. 2020, 2020, 4817234. [Google Scholar] [CrossRef]
- Nardell, C.A.; Murchie, S.L.; Lucey, P.G.; Arvidson, R.E.; Bedini, P.; Yee, J.-H.; Garvin, J.B.; Beisser, K.; Bibring, J.-P.; Bishop, J.; et al. CRISM (Compact Reconnaissance Imaging Spectrometer for Mars) on MRO (Mars Reconnaissance Orbiter). In Proceedings of the Instruments, Science, and Methods for Geospace and Planetary Remote Sensing, Honolulu, HI, USA, 9–11 November 2004. [Google Scholar]
- Wang, C.; Liu, B.; Liu, L.; Zhu, Y.; Hou, J.; Liu, P.; Li, X. A review of deep learning used in the hyperspectral image analysis for agriculture. Artif. Intell. Rev. 2021, 54, 5205–5253. [Google Scholar] [CrossRef]
- Dalponte, M.; Bruzzone, L.; Gianelle, D. Fusion of Hyperspectral and LIDAR Remote Sensing Data for Classification of Complex Forest Areas. IEEE Trans. Geosci. Remote Sens. 2008, 46, 1416–1427. [Google Scholar] [CrossRef]
- Alonzo, M.; Bookhagen, B.; Roberts, D.A. Urban tree species mapping using hyperspectral and lidar data fusion. Remote Sens. Environ. 2014, 148, 70–83. [Google Scholar] [CrossRef]
- Gong, W.; Sun, J.; Shi, S.; Yang, J.; Du, L.; Zhu, B.; Song, S. Investigating the Potential of Using the Spatial and Spectral Information of Multispectral LiDAR for Object Classification. Sensors 2015, 15, 21989–22002. [Google Scholar] [CrossRef]
- Budylskii, S.S.D.; Tankoyeu, I.; Heremans, R. Fusion of lidar, hyperspectral and rgb datafor urban land use and land cover classification. In Proceedings of the IGARSS 2018, Valencia, Spain, 22–27 July 2018. [Google Scholar]
- Bauer, S.; Puente León, F. Spectral and geometric aspects of mineral identification by means of hyperspectral fluorescence imaging. tm-Tech. Mess. 2015, 82, 597–605. [Google Scholar] [CrossRef]
- Lu, X.; Hu, Y.; Trepte, C.; Zeng, S.; Churnside, J.H. Ocean subsurface studies with the CALIPSO spaceborne lidar. J. Geophys. Res. Ocean. 2014, 119, 4305–4317. [Google Scholar] [CrossRef]
- Zhou, Y.; Chen, Y.; Zhao, H.; Jamet, C.; Dionisi, D.; Chami, M.; Di Girolamo, P.; Churnside, J.H.; Malinka, A.; Zhao, H.; et al. Shipborne oceanic high-spectral-resolution lidar for accurate estimation of seawater depth-resolved optical properties. Light Sci. Appl. 2022, 11, 261. [Google Scholar] [CrossRef]
- Yu, S.; Liu, D.; Xu, J.; Wang, Z.; Wu, D.; Shan, Y.; Shao, J.; Mao, M.; Qian, L.; Wang, B.; et al. Optical properties and seasonal distribution of aerosol layers observed by lidar over Jinhua, southeast China. Atmos. Environ. 2021, 257, 118456. [Google Scholar] [CrossRef]
- Tan, S.; Narayanan, R.M. A Multiwavelength Airborne Polarimetric Lidar for Vegetation Remote Sensing: Instrumentation and Preliminary Test Results. IEEE Int. Geosci. Remote Sens. Symp. 2002, 5, 2675–2677. [Google Scholar] [CrossRef]
- Rall, J.A.R.; Knox, R.G. Spectral ratio biospheric lidar. In Proceedings of the Geoscience and Remote Sensing Symposium, Anchorage, AK, USA, 20–24 September 2004; Volume 1953, pp. 1951–1954. [Google Scholar]
- Gaulton, R.; Danson, F.M.; Ramirez, F.A.; Gunawan, O. The potential of dual-wavelength laser scanning for estimating vegetation moisture content. Remote Sens. Environ. 2013, 132, 32–39. [Google Scholar] [CrossRef]
- Sun, J.; Shi, S.; Yang, J.; Gong, W.; Qiu, F.; Wang, L.; Du, L.; Chen, B. Wavelength selection of the multispectral lidar system for estimating leaf chlorophyll and water contents through the PROSPECT model. Agric. For. Meteorol. 2019, 266–267, 43–52. [Google Scholar] [CrossRef]
- Wei, G.; Shalei, S.; Bo, Z.; Shuo, S.; Faquan, L.; Xuewu, C. Multi-wavelength canopy LiDAR for remote sensing of vegetation: Design and system performance. ISPRS J. Photogramm. Remote Sens. 2012, 69, 1–9. [Google Scholar] [CrossRef]
- Nantel, M.; Helmininack, G.A.; Gladysiewski, D.D.; Zhou, F.; Hershman, K.; Campbell, B.; Thomas, J. Supercontinuum generation in photonic crystal fibers for undergraduate laboratory. In Proceedings of the Tenth International Topical Meeting on Education and Training in Optics and Photonics, Ottawa, ON, Canada, 3–5 June 2007. [Google Scholar]
- Chen, Y.; Raikkonen, E.; Kaasalainen, S.; Suomalainen, J.; Hakala, T.; Hyyppa, J.; Chen, R. Two-channel hyperspectral LiDAR with a supercontinuum laser source. Sensors 2010, 10, 7057–7066. [Google Scholar] [CrossRef]
- Hakala, T.; Suomalainen, J.; Kaasalainen, S.; Chen, Y. Full waveform hyperspectral LiDAR for terrestrial laser scanning. Opt. Express 2012, 20, 7119–7127. [Google Scholar] [CrossRef]
- Kaasalainen, S.; Malkamaki, T. Potential of active multispectral lidar for detecting low reflectance targets. Opt. Express 2020, 28, 1408–1416. [Google Scholar] [CrossRef]
- Wang, Z.; Chen, Y. A Hyperspectral LiDAR with Eight Channels Covering from VIS to SWIR. In Proceedings of the IGARSS 2018—2018 IEEE International Geoscience and Remote Sensing, Valencia, Spain, 22–27 July 2018. [Google Scholar]
- Chen, Y.; Li, W.; Hyyppä, J.; Wang, N.; Jiang, C.; Meng, F.; Tang, L.; Puttonen, E.; Li, C. A 10-nm Spectral Resolution Hyperspectral LiDAR System Based on an Acousto-Optic Tunable Filter. Sensors 2019, 19, 1620. [Google Scholar] [CrossRef]
- Qian, L.; Wu, D.; Zhou, X.; Zhong, L.; Wei, W.; Wang, Y.; Shi, S.; Song, S.; Gong, W.; Liu, D. Optical system design for a hyperspectral imaging lidar using supercontinuum laser and its preliminary performance. Opt. Express 2021, 29, 17542–17553. [Google Scholar] [CrossRef]
- Powers, M.A.; Davis, C.C. Spectral LADAR: Active range-resolved threedimensional imaging spectroscopy. Appl. Opt. 2012, 51, 1468–1478. [Google Scholar] [CrossRef] [PubMed]
- Li, W.; Niu, Z.; Sun, G.; Gao, S.; Wu, M. Deriving backscatter reflective factors from 32-channel full-waveform LiDAR data for the estimation of leaf biochemical contents. Opt. Express 2016, 24, 4771–4785. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Jiang, C.; Hyyppa, J.; Qiu, S.; Wang, Z.; Tian, M.; Li, W.; Puttonen, E.; Zhou, H.; Feng, Z.; et al. Feasibility Study of Ore Classification Using Active Hyperspectral LiDAR. IEEE Geosci. Remote Sens. Lett. 2018, 15, 1785–1789. [Google Scholar] [CrossRef]
- Bi, K.; Gao, S.; Niu, Z.; Zhang, C.; Huang, N. Estimating leaf chlorophyll and nitrogen contents using active hyperspectral LiDAR and partial least square regression method. J. Appl. Remote Sens. 2019, 13, 034513. [Google Scholar] [CrossRef]
- Ilinca, J.; Kaasalainen, S.; Malkamaki, T.; Hakala, T. Improved waveform reconstruction and parameter accuracy retrieval for hyperspectral lidar data. Appl. Opt. 2019, 58, 9624–9633. [Google Scholar] [CrossRef]
- Chen, B.; Shi, S.; Gong, W.; Zhang, Q.; Yang, J.; Du, L.; Sun, J.; Zhang, Z.; Song, S. Multispectral LiDAR Point Cloud Classification: A Two-Step Approach. Remote Sens. 2017, 9, 373. [Google Scholar] [CrossRef]
- Chen, B.; Shi, S.; Sun, J.; Gong, W.; Yang, J.; Du, L.; Guo, K.; Wang, B.; Chen, B. Hyperspectral lidar point cloud segmentation based on geometric and spectral information. Opt. Express 2019, 27, 24043–24059. [Google Scholar] [CrossRef]
- Tang, Y.; Hu, Y.; Cui, J.; Liao, F.; Lao, M.; Lin, F.; Teo, R.S.H. Vision-Aided Multi-UAV Autonomous Flocking in GPS-Denied Environment. IEEE Trans. Ind. Electron. 2019, 66, 616–626. [Google Scholar] [CrossRef]
- Chen, X.; Phang, S.K.; Shan, M.; Chen, B.M. System Integration of a Vision-Guided UAV for Autonomous Landing on Moving Platform. In Proceedings of the 12th IEEE International Conference on Control & Automation, Kathmandu, Nepal, 1–3 June 2016. [Google Scholar]
- Chan, C.W.-H.; Leong, P.H.W.; So, H.K.-H. Vision Guided Crop Detection in Field Robots using FPGA-based Reconfigurable Computers. In Proceedings of the 2020 IEEE International Symposium on Circuits and Systems (ISCAS), Sevilla, Spain, 12–14 October 2020. [Google Scholar]
- Zou, Z.; Shi, Z.; Guo, Y.; Ye, J. Object Detection in 20 Years: A Survey. arXiv 2019. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. Adv. Neural Inf. Process. Syst. 2012, 60, 84–90. [Google Scholar] [CrossRef]
- Redmon, J.; Divvala, S.; Girshick, R.; Farhadi, A. You Only Look Once: Unified, Real-Time Object Detection. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 779–788. [Google Scholar]
- Jiang, P.; Ergu, D. A Review of Yolo Algorithm Developments. In Proceedings of the The 8th International Conference on Information Technology and Quantitative Management, Cambridge, UK, 25–27 March 2022; pp. 1066–1073. [Google Scholar]
- Park, Y.; Yun, S.; Won, C.S.; Cho, K.; Um, K.; Sim, S. Calibration between color camera and 3D LIDAR instruments with a polygonal planar board. Sensors 2014, 14, 5333–5353. [Google Scholar] [CrossRef] [PubMed]
- Pusztai, Z.; Hajder, L. Accurate Calibration of LiDAR-Camera Systems using Ordinary Boxes. In Proceedings of the 2017 IEEE International Conference on Computer Vision Workshops (ICCVW), Venice, Italy, 22–29 October 2017. [Google Scholar]
- Geiger, A.; Moosmann, F.; Car, O.; Schuster, B. Automatic Camera and Range Sensor Calibration using a single Shot. In Proceedings of the 2012 IEEE International Conference on Robotics and Automation (ICRA), RiverCentre, Saint Paul, MN, USA, 14–18 May 2012. [Google Scholar]
- Jocher, G.; Stoken, A.; Borovec, J.; Chaurasia, A.; Xie, T.; Liu, C.; Abhiram, V.; Laughing, T. ultralytics/yolov5: v5. 0-YOLOv5-P6 1280 models, AWS, Supervise.ly and YouTube Integrations. Zenodo 2021, 10, 4679653. [Google Scholar]
- Jing, Y.; Ren, Y.; Liu, Y.; Wang, D.; Yu, L. Automatic Extraction of Damaged Houses by Earthquake Based on Improved YOLOv5: A Case Study in Yangbi. Remote Sens. 2022, 14, 382. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. arXiv 2015. [Google Scholar] [CrossRef]
- Lin, T.-Y.; Maire, M.; Belongie, S.; Girshick, L.B.R.; Hays, J.; Perona, P.; Ramanan, D.; Dollár, C.L.Z.P. Microsoft COCO: Common Objects in Context. arXiv 2014. [Google Scholar] [CrossRef]
- Ultralytics. YOLOv5. Available online: https://github.com/ultralytics/yolov5 (accessed on 24 July 2020).
- Lv, S.; Tang, D.; Zhang, X.; Yang, D.; Deng, W.; Kemao, Q. Fringe projection profilometry method with high efficiency, precision, and convenience: Theoretical analysis and development. Opt. Express 2022, 30, 33515–33537. [Google Scholar] [CrossRef]
- Zhang, Z. A Flexible New Technique for Camera Calibration. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22, 1330–1334. [Google Scholar] [CrossRef]
- Hartley, R.; Zisserman, A. Multiple View Geometry in Computer Vision, 2nd ed.; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Wagner, W.; Ullrich, A.; Ducic, V.; Melzer, T.; Studnicka, N. Gaussian decomposition and calibration of a novel small-footprint full-waveform digitising airborne laser scanner. ISPRS J. Photogramm. Remote Sens. 2006, 60, 100–112. [Google Scholar] [CrossRef]
- Mountrakis, G. A linearly approximated iterative Gaussian decomposition method for aveform LiDAR processing. ISPRS J. Photogramm. Remote Sens. 2017, 129, 200–211. [Google Scholar] [CrossRef]
- Song, S.; Wang, B.; Gong, W.; Chen, Z.; Lin, X.; Sun, J.; Shi, S. A new waveform decomposition method for multispectral LiDAR. ISPRS J. Photogramm. Remote Sens. 2019, 149, 40–49. [Google Scholar] [CrossRef]
- Tian, W.; Tang, L.; Chen, Y.; Li, Z.; Zhu, J.; Jiang, C.; Hu, P.; He, W.; Wu, H.; Pan, M.; et al. Analysis and Radiometric Calibration for Backscatter Intensity of Hyperspectral LiDAR Caused by Incident Angle Effect. Sensors 2021, 21, 2960. [Google Scholar] [CrossRef] [PubMed]
- Wei, F.; Xianfeng, H.; Fan, Z.; Deren, L. Intensity Correction of Terrestrial Laser Scanning Data by Estimating Laser Transmission Function. IEEE Trans. Geosci. Remote Sens. 2015, 53, 942–951. [Google Scholar] [CrossRef]
- Qian, X.; Yang, J.; Shi, S.; Gong, W.; Du, L.; Chen, B.; Chen, B. Analyzing the effect of incident angle on echo intensity acquired by hyperspectral lidar based on the Lambert-Beckman model. Opt. Express 2021, 29, 11055–11069. [Google Scholar] [CrossRef] [PubMed]
- Suomalainen, J.; Hakala, T.; Kaartinen, H.; Räikkönen, E.; Kaasalainen, S. Demonstration of a virtual active hyperspectral LiDAR in automated point cloud classification. ISPRS J. Photogramm. Remote Sens. 2011, 66, 637–641. [Google Scholar] [CrossRef]
- Turner, M.D.; Kamerman, G.W.; Miller, C.I.; Thomas, J.J.; Kim, A.M.; Metcalf, J.P.; Olsen, R.C. Application of image classification techniques to multispectral lidar point cloud data. In Proceedings of the Laser Radar Technology and Applications XXI, Baltimore, MD, USA, 19–20 April 2016. [Google Scholar]
- Bi, K.; Xiao, S.; Gao, S.; Zhang, C.; Huang, N.; Niu, Z. Estimating Vertical Chlorophyll Concentrations in Maize in Different Health States Using Hyperspectral LiDAR. IEEE Trans. Geosci. Remote Sens. 2020, 58, 8125–8133. [Google Scholar] [CrossRef]
- Chen, B.; Shi, S.; Sun, J.; Chen, B.; Guo, K.; Du, L.; Yang, J.; Xu, Q.; Song, S.; Gong, W. Using HSI Color Space to Improve the Multispectral Lidar Classification Error Caused by Measurement Geometry. IEEE Trans. Geosci. Remote Sens. 2021, 59, 3567–3579. [Google Scholar] [CrossRef]
- Huang, J.; Li, Z.; Shi, D.; Chen, Y.; Yuan, K.; Hu, S.; Wang, Y. Scanning single-pixel imaging lidar. Opt. Express 2022, 30, 37484–37492. [Google Scholar] [CrossRef]
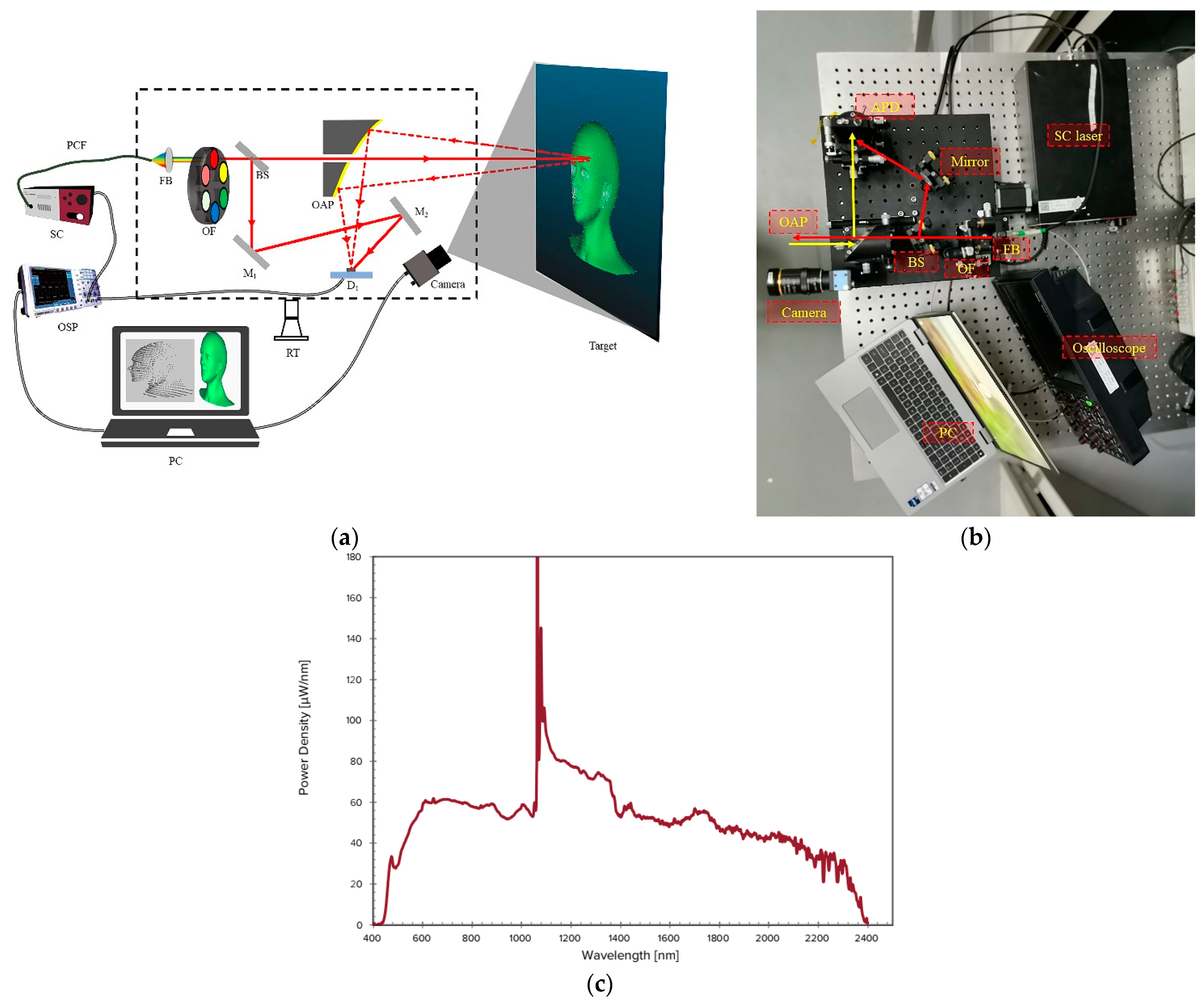
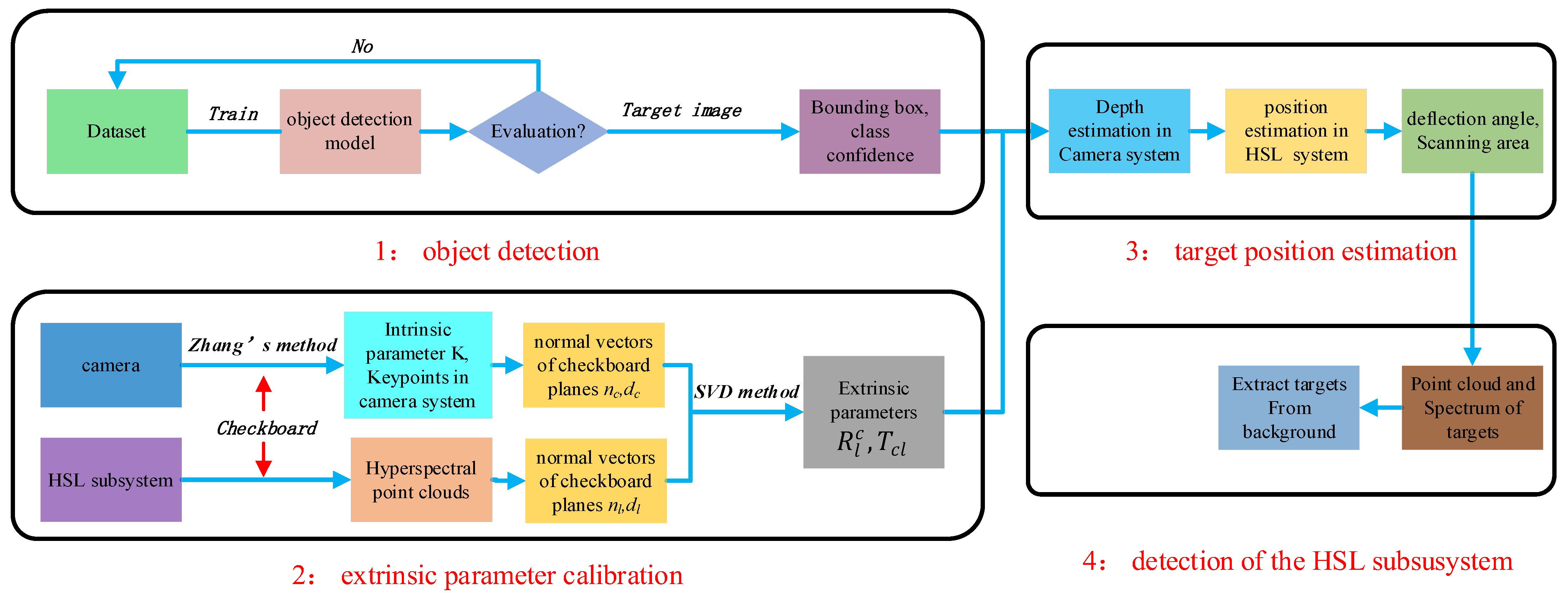
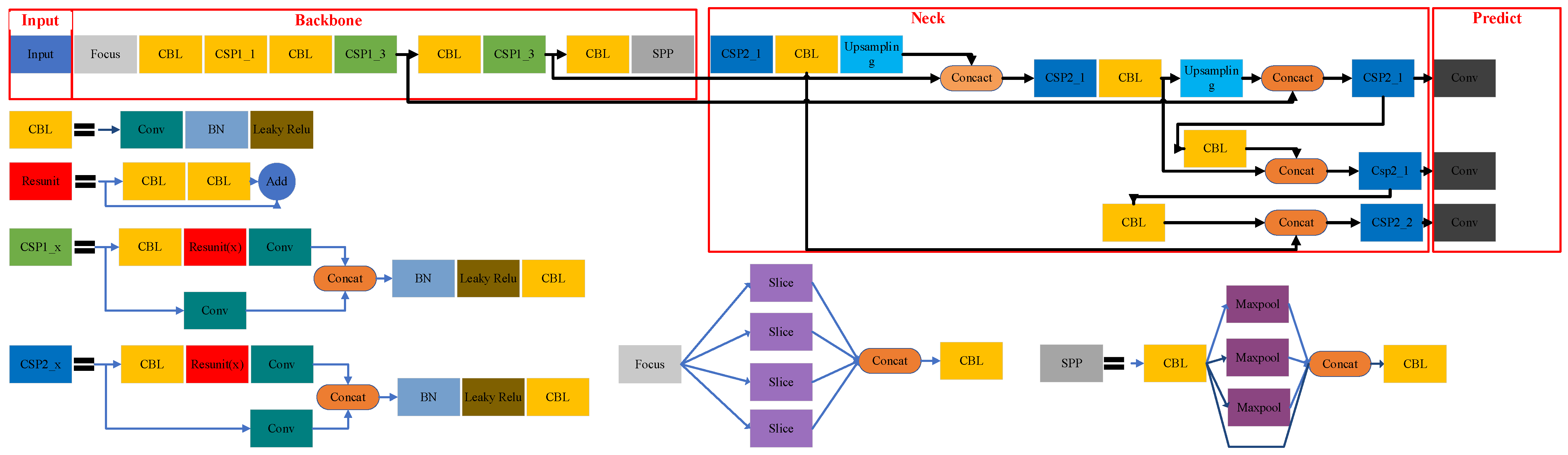
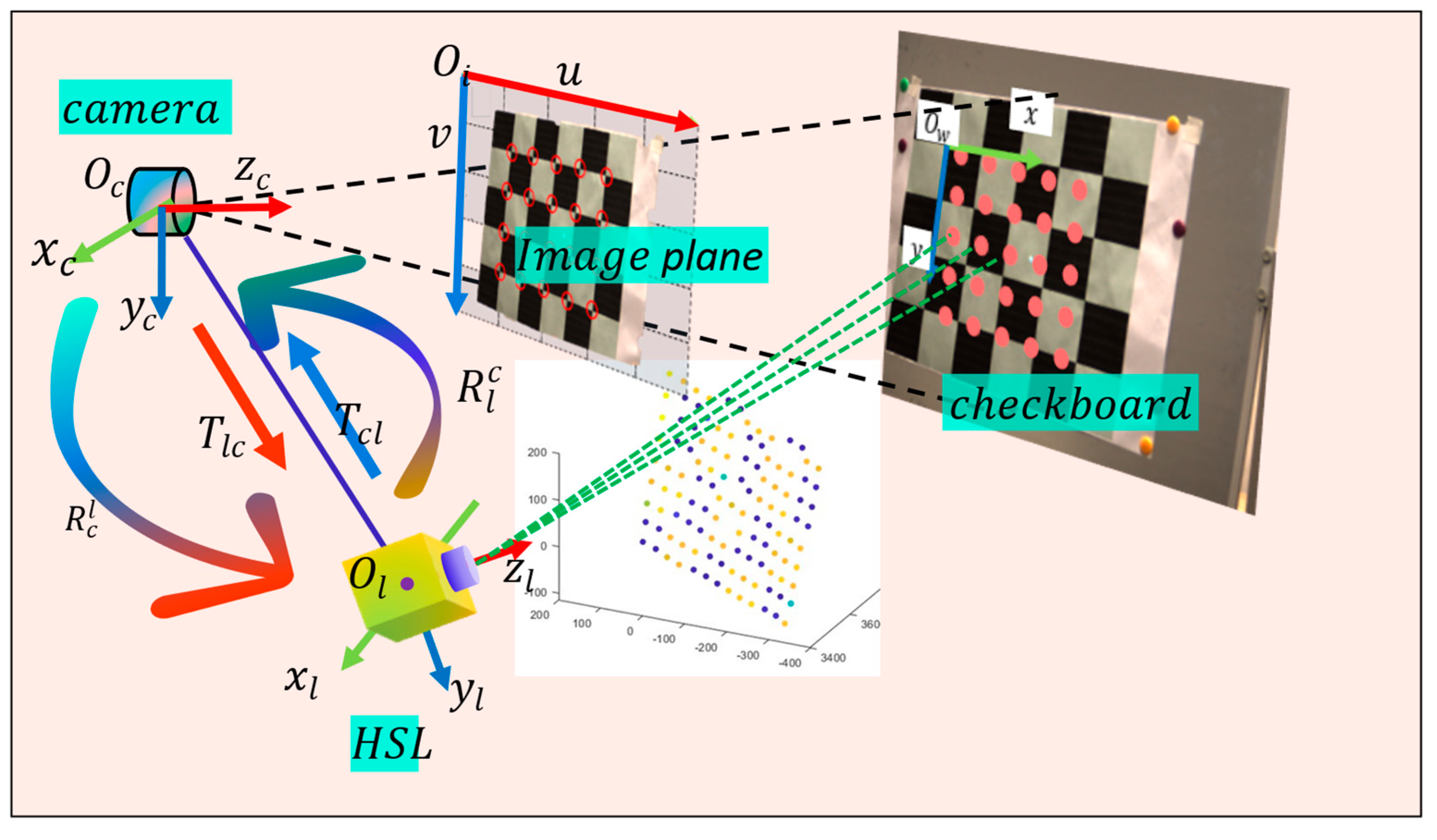





| Element | Parameter | Value |
|---|---|---|
| Filters in the filter wheel | channels | central wavelength/ spectral resolution |
| 1 | 500/30 nm | |
| 2 | 550/10 nm | |
| 3 | 650/10 nm | |
| 4 | 700/10 nm | |
| 5 | 750/10 nm | |
| 6 | 800/10 nm | |
| OAP | manufacturer | Thorlabs MPD269V-M03 |
| diameter | 2 inch | |
| back focus length | 6 inch | |
| Oscilloscope | manufacturer | RIGOL MSO8204 |
| bandwidth | 2 G | |
| sample frequency | 10 G/s (max), 5 G/s(used) | |
| APD | spectral range | 400–1000 nm |
| diameter | 0.5 mm | |
| bandwidth | 500 MHz | |
| Rotation stage | FOV | ±15 (vertical) |
| 360 (horizontal) | ||
| Camera | manufacturer | Daheng MER-161-61U3MC |
| image size | ||
| pixel size | 3.25 |
| Orange | Apple | |||
|---|---|---|---|---|
| Image position/pixel | 816 | 904 | 1186 | 751 |
| Estimate deflection angle/° | 2.909 | 4.05 | 7.07 | 2.3257 |
| Actual angle/° | 2.875 | 3.9375 | 6.75 | 2.1375 |
| Absolute error/° | 0.034 | 0.1125 | 0.32 | 0.3944 |
| Relative error/% | 1.18 | 2.86 | 4.74 | 8.8 |
| Target Point | Total Points | ||
|---|---|---|---|
| HSL system | 30 | 1500 | 1 |
| V-HSL system | 130 | 500 | 13 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, H.; Lin, C.; Li, C.; Zhang, J.; Gaoqu, Y.; Wang, S.; Wang, L.; Xue, H.; Sun, W.; Zheng, Y. Vision-Aided Hyperspectral Full-Waveform LiDAR System to Improve Detection Efficiency. Remote Sens. 2023, 15, 3448. https://doi.org/10.3390/rs15133448
Wu H, Lin C, Li C, Zhang J, Gaoqu Y, Wang S, Wang L, Xue H, Sun W, Zheng Y. Vision-Aided Hyperspectral Full-Waveform LiDAR System to Improve Detection Efficiency. Remote Sensing. 2023; 15(13):3448. https://doi.org/10.3390/rs15133448
Chicago/Turabian StyleWu, Hao, Chao Lin, Chengliang Li, Jialun Zhang, Youyang Gaoqu, Shuo Wang, Long Wang, Hao Xue, Wenqiang Sun, and Yuquan Zheng. 2023. "Vision-Aided Hyperspectral Full-Waveform LiDAR System to Improve Detection Efficiency" Remote Sensing 15, no. 13: 3448. https://doi.org/10.3390/rs15133448
APA StyleWu, H., Lin, C., Li, C., Zhang, J., Gaoqu, Y., Wang, S., Wang, L., Xue, H., Sun, W., & Zheng, Y. (2023). Vision-Aided Hyperspectral Full-Waveform LiDAR System to Improve Detection Efficiency. Remote Sensing, 15(13), 3448. https://doi.org/10.3390/rs15133448





