Designing CW Range-Resolved Environmental S-Lidars for Various Range Scales: From a Tabletop Test Bench to a 10 km Path
Abstract
1. Introduction: Specific Features of S-Lidar-Based Remote Sensing
2. Methods and Approaches
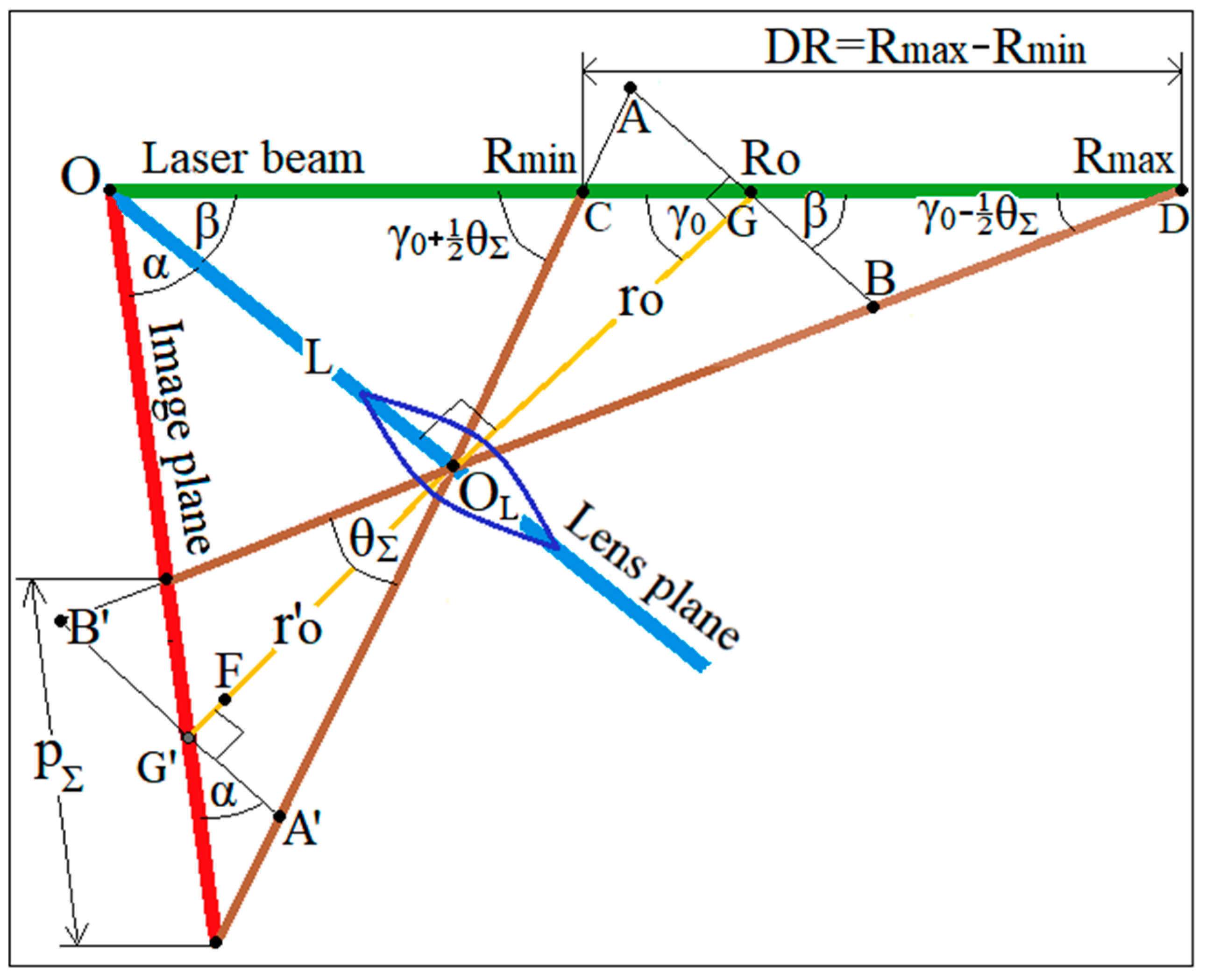
2.1. Problem Definition: Development of Methodology for Design of CW RR S-Lidars for Various Range Scales: From a 1 m Tabletop Test Bench to a 10 km Path
- -
- Tilt angle α of the image plane to the lens plane;
- -
- Tilt angle β of the lens plane to the plane of the sensing object (Figure 1);
- -
- Focal length f of the receiving optics;
- -
- Lidar base L as a distance from the lens center to the laser beam, measured in the lens plane;
- -
- Distance Ldet to the center of array detector;
- -
- Single pixel size p1,
- -
- Total number of pixels n of a linear array detector.
2.2. S-Lidar Alignment for the Desired Range: Eliminating Uncertainty When Choosing Tilt Angles of Receiving Optics and Detecting Array
2.2.1. Effect of Introduced S-Lidar-Specific Notions: Magnification M and Angular Function S(x)
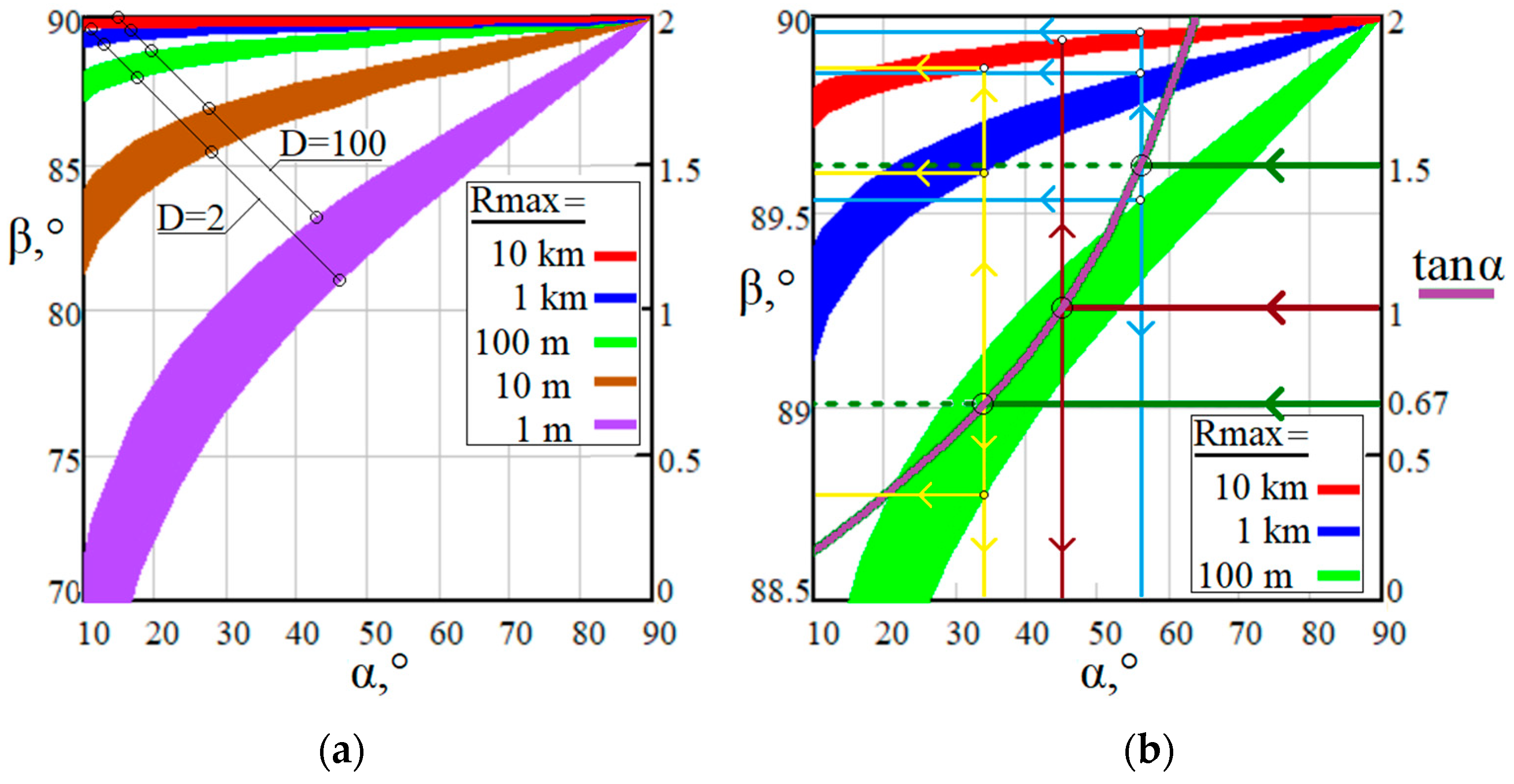
2.2.2. Sensitivity of Interdependent Tilt Angles α and β to Range–Domain Scales
2.2.3. A New “One and a Half” Criterion to Choose Proper Tilting Angles α and β
2.3. How to Select Suitable Hardware Parameters for S-Lidars with Different Range–Domain Scales from 1 m Up to 10 km
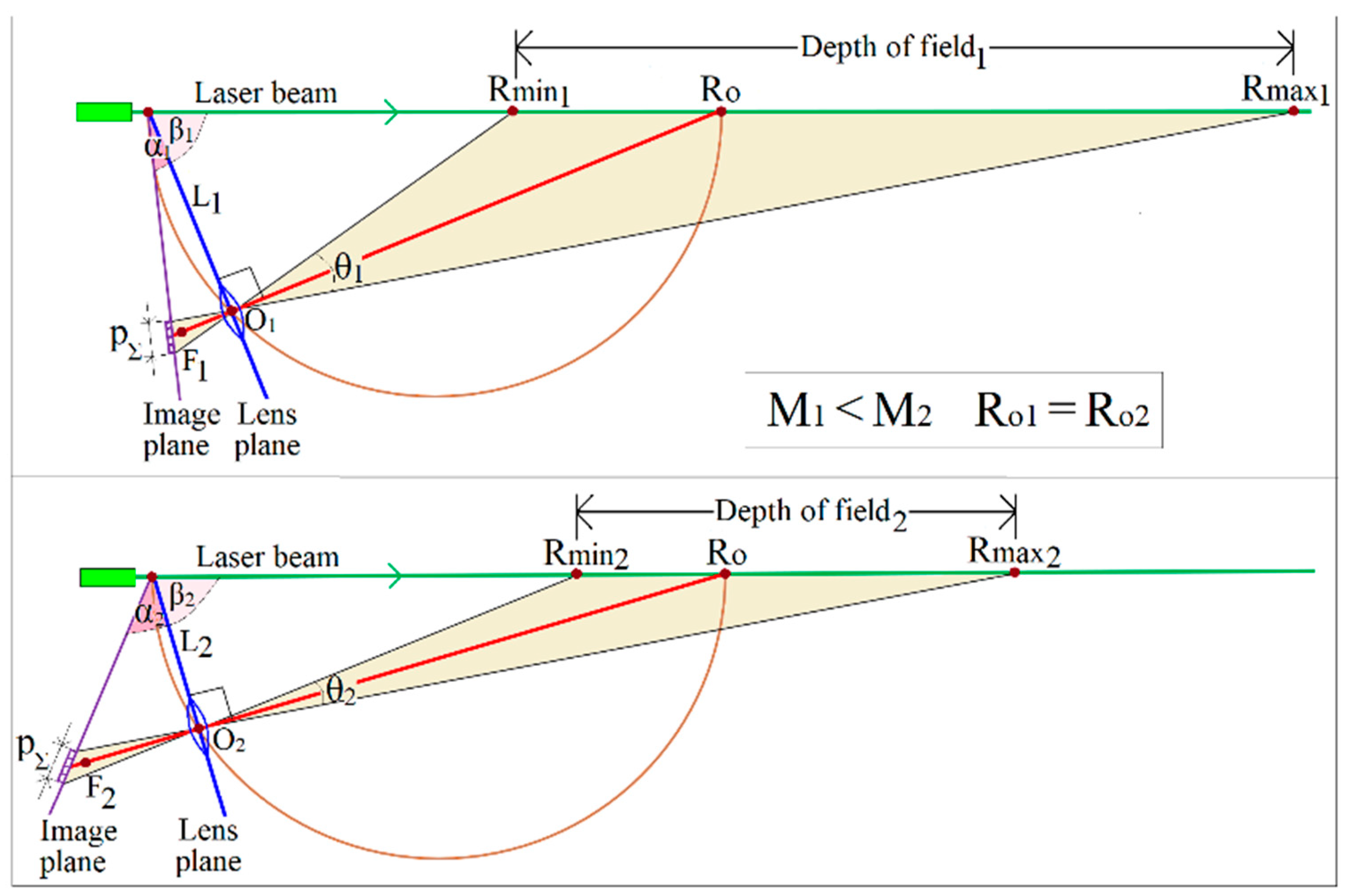
2.3.1. Adaptive Choice of Both Focal Length and Lidar Base to Specific Range–Domain Requirements
2.3.2. Examples of S-Sensors Design to Achieve Different Dynamic Ranges D
2.3.3. Receiving Field of View of S-Lidars: Adaptation to Depth of Field Required
3. Results and Discussions
3.1. Achievable Range Resolution and Its Variability Bounds in S-Lidars
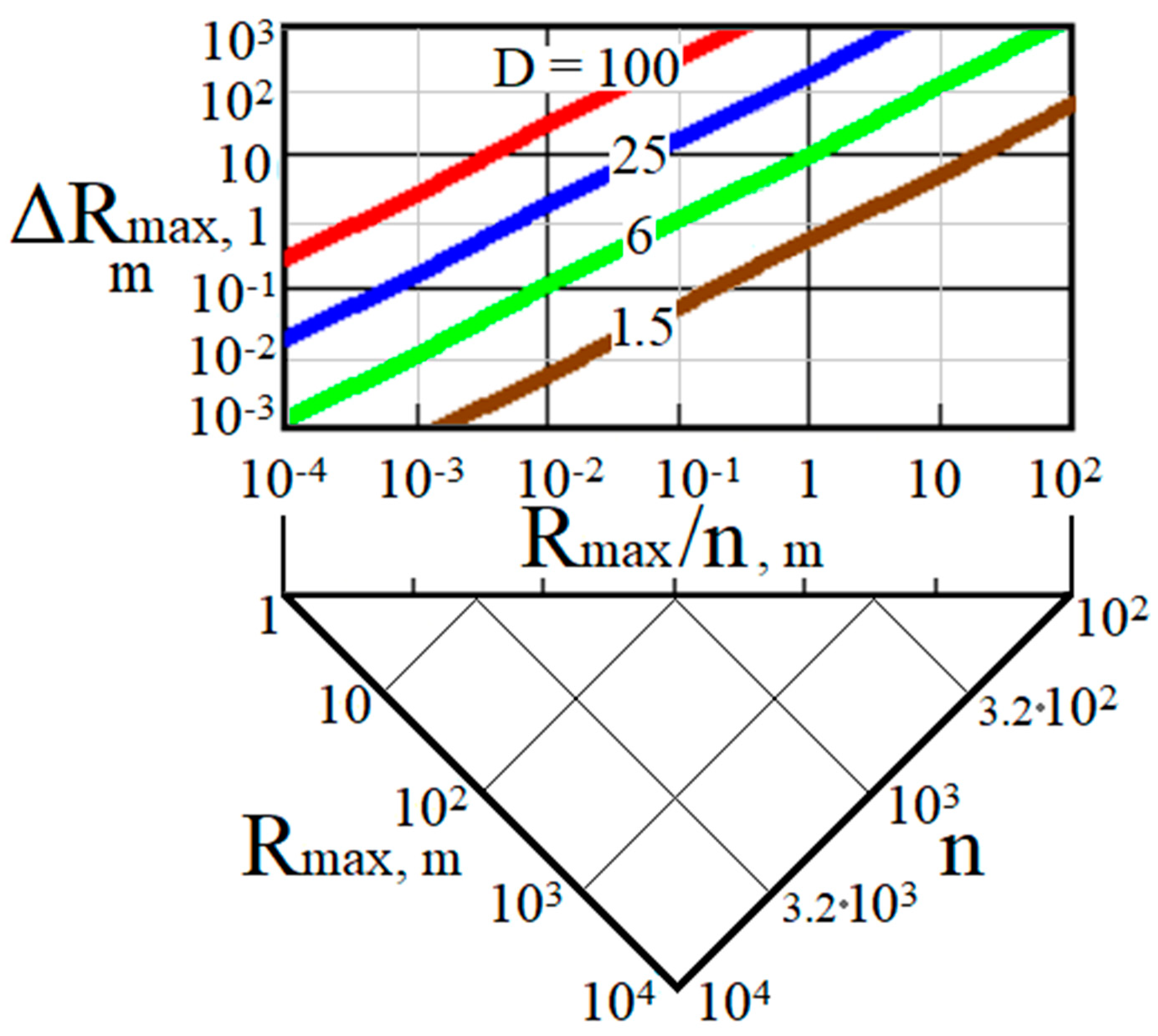
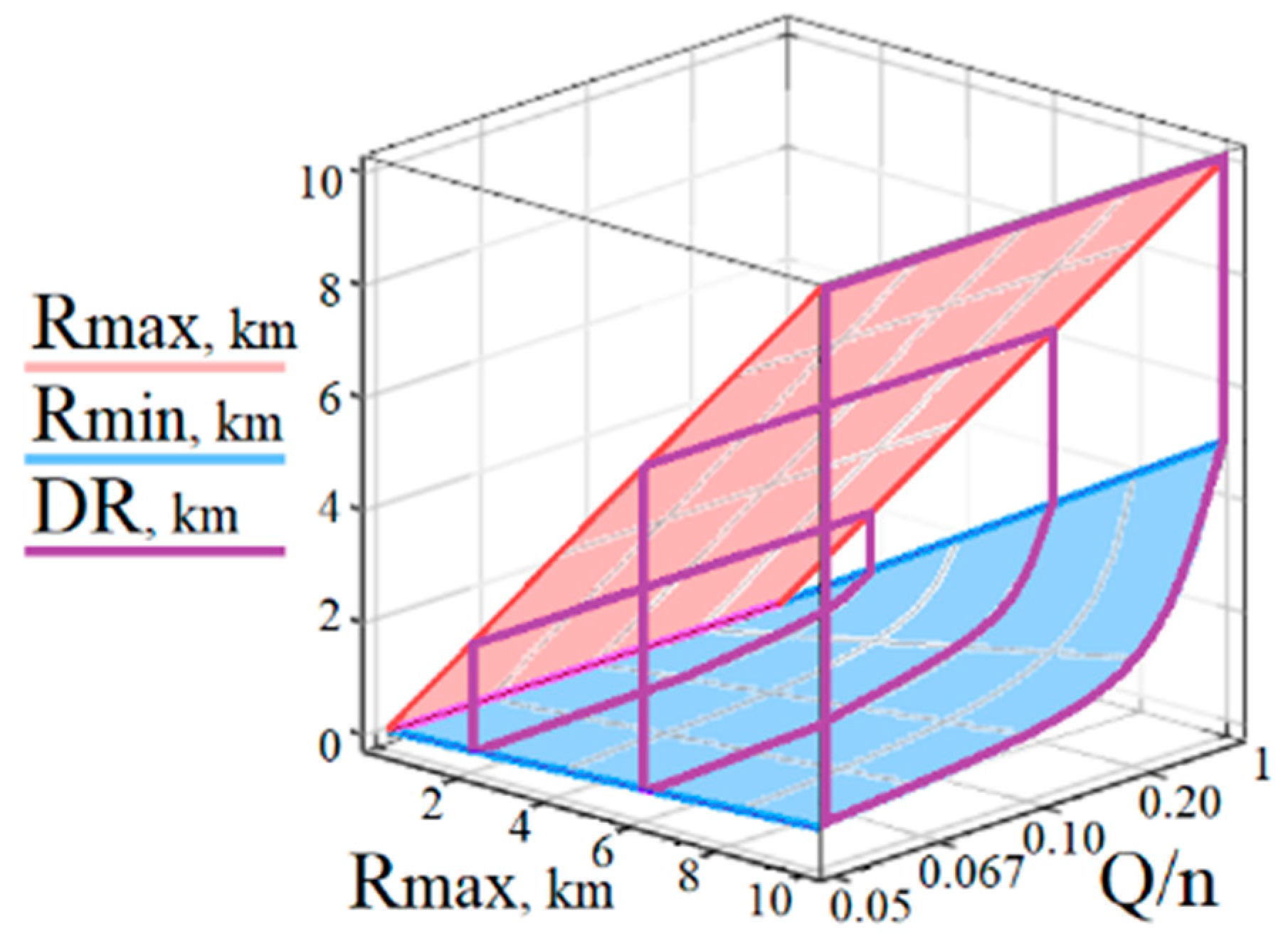
3.2. Distant Far Border and Wide Dynamic Range Vs. High-Range Resolution: Achieving Acceptable Trade-Offs
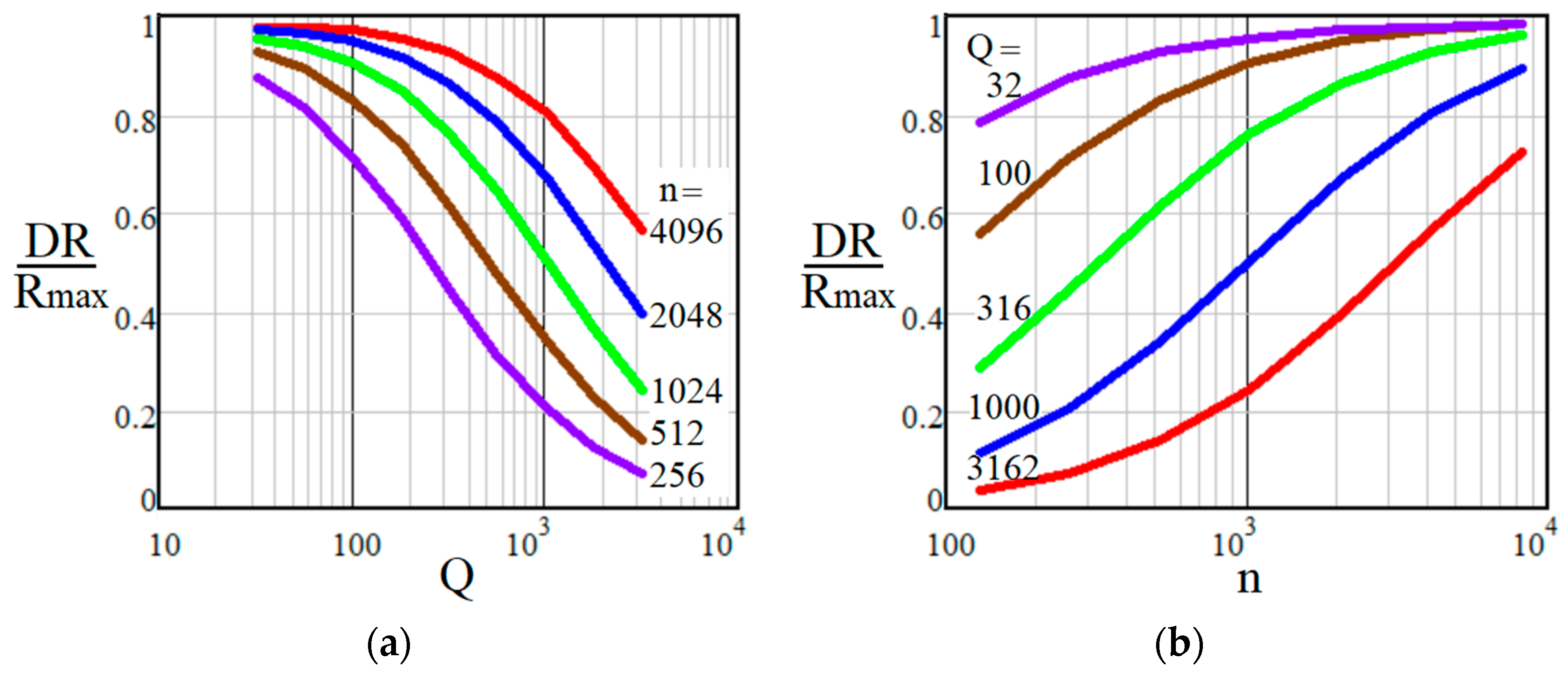
3.2.1. Prerequisites for Further Application of the Q-Factor
3.2.2. From i-th Pixel to i-th Layer at Distance Ri: A Simple Conversion Method
3.2.3. Formation of DoF as a Sequence of Spatially-Resolved Layers
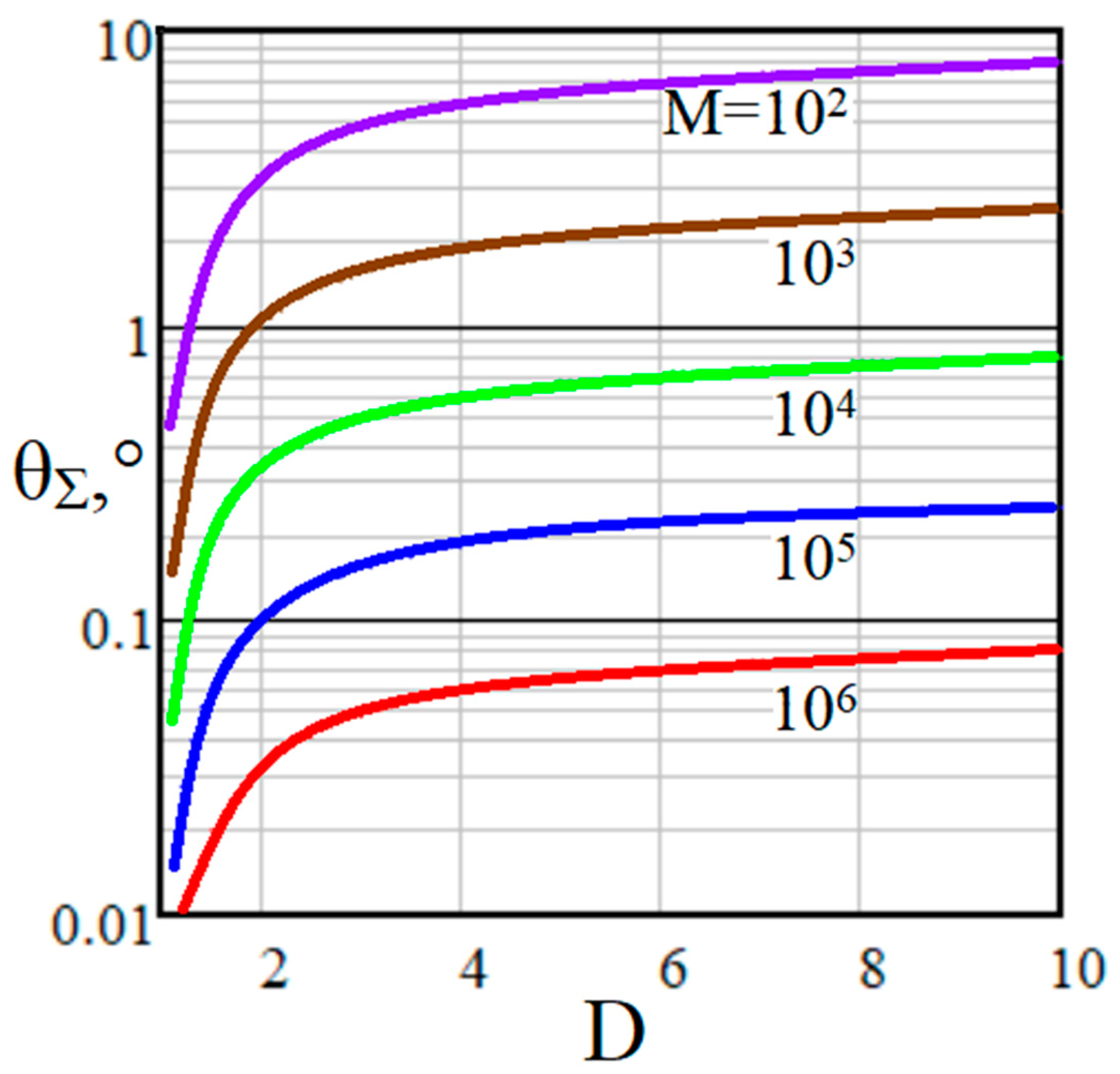
3.2.4. Trade-Off between Wide Dynamic Range D and High Spatial Resolution ΔR(Rmax)
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Measures, R. Laser Remote Sensing: Fundamentals and Applications; Springer: Berlin/Heidelberg, Germany, 1984; p. 320. [Google Scholar]
- Fujii, T.; Fukuchi, T. Laser Remote Sensing; CRC Press: Boca Raton, FL, USA, 2005; p. 240. [Google Scholar]
- Rees, W. Physical Principles of Remote Sensing; Cambridge University Press: Cambridge, UK, 2006; p. 470. [Google Scholar]
- Agishev, R. Laser Remote Sensing of the Environment: Methods and Techniques; PhysMathLit-Press: Moscow, Russia, 2019; p. 264. [Google Scholar]
- McManamon, P. Lidar Technologies and Systems; SPIE-Press: Bellingham, WA, USA, 2019; p. 520. [Google Scholar]
- Ball, J.; Anderson, D.; Chan, C. Comprehensive survey of deep learning in remote sensing: Theories, tools, and challenges for the community. J. Appl. Remote Sens. 2017, 11, 42609. [Google Scholar] [CrossRef]
- Chen, R.; Li, Y.; Xue, G.; Tao, Y.; Li, X. Laser triangulation measurement system with Scheimpflug calibration based on the Monte Carlo optimization strategy. Opt. Express 2022, 30, 25290. [Google Scholar] [CrossRef] [PubMed]
- Xing, L.; Dai, W.; Zhang, Y. Scheimpflug camera-based technique for multi-point displacement monitoring of bridges. Sensors 2022, 22, 4093. [Google Scholar] [CrossRef] [PubMed]
- Yi, S.; Min, S. Composition of sharp-focused image by rotation of Scheimpflug camera. Opt. Laser Technol. 2022, 155, 108406. [Google Scholar] [CrossRef]
- Gao, F.; Lin, H.; Chen, K.; Chen, X.; He, S. Light-sheet based two-dimensional Scheimpflug lidar system for profile measurements. Opt. Express 2018, 26, 338056. [Google Scholar] [CrossRef]
- Chen, X.; Jiang, Y.; Yao, Q.; Ji, J.; Evans, J.; He, S. Inelastic hyperspectral Scheimpflug lidar for microalgae classification and quantification. Appl. Opt. 2021, 60, 4778–4786. [Google Scholar] [CrossRef]
- Lin, H.; Zhang, Y.; Mei, L. Fluorescence Scheimpflug lidar developed for the three-dimension profiling of plants. Opt. Express 2020, 28, 9269–9279. [Google Scholar] [CrossRef]
- Zhao, G.; Malmqvist, E.; Rydhmer, K.; Strand, A.; Bianco, G.; Hansson, L.; Svanberg, S.; Brydegaard, M. Inelastic hyperspectral lidar for aquatic ecosystems monitoring and landscape plant scanning test. EPJ Web Conf. 2018, 176, 01003. [Google Scholar] [CrossRef]
- Duan, Z.; Li, Y.; Wang, X.; Wang, J. Drone-based fluorescence lidar systems for vegetation and marine environment monitoring. EPJ Web Conf. 2020, 237, 07013. [Google Scholar] [CrossRef]
- Ma, X.; Wang, Z.; Zhang, H.; Shan, H.; Han, J.; Zhao, S.; Wang, S.; Liu, D.; Wang, Y.; Tao, Z. Detecting aerosol backscattering coefficient across the whole troposphere by the side-scattering lidar system with three CCD cameras. Opt. Express 2022, 30, 29969–29978. [Google Scholar] [CrossRef]
- Kong, Z.; Yu, J.; Gong, Z.; Hua, D. Visible, near-infrared dual-polarization lidar based on polarization cameras: System design, evaluation and atmospheric measurements. Opt. Express 2022, 30, 28514–28533. [Google Scholar] [CrossRef]
- Mei, L.; Brydegaard, M. Atmospheric aerosol monitoring by an elastic Scheimpflug lidar system. Opt. Express 2015, 23, A1613–A1628. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.; Li, L.; Li, H. Preliminary Studies on Atmospheric Monitoring by Employing a Portable Unmanned Mie-Scattering Scheimpflug Lidar System. Remote Sens. 2019, 11, 837. [Google Scholar] [CrossRef]
- Larsson, J.; Bood, J.; Xu, C. Atmospheric CO2 sensing using Scheimpflug-lidar based on a 1.57-µm fiber source. Opt. Express 2019, 27, 17348–17358. [Google Scholar] [CrossRef]
- Zhou, B.; Zhang, S.; Xue, R.; Li, J.; Wang, S. A review of space-air-ground integrated remote sensing techniques. J. Environ. Sci. 2021, 123, 3–14. [Google Scholar] [CrossRef]
- Yang, Y.; Guan, P.; Mei, L. A scanning Scheimpflug lidar system developed for urban pollution monitoring. EPJ Web Conf. 2018, 176, 01013. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, Y.; Li, Z.; Liu, B.; Yin, B.; Wu, S. Small angle scattering intensity measurement by an improved ocean Scheimpflug lidar system. Remote Sens. 2021, 13, 2390. [Google Scholar] [CrossRef]
- Duan, Z.; Yuan, Y.; Lu, J. Underwater spatially, spectrally, and temporally resolved optical monitoring of aquatic fauna. Opt. Express 2020, 28, 2600–2610. [Google Scholar] [CrossRef]
- Gao, F.; Li, J.; Lin, H. Oil pollution discrimination by an inelastic hyperspectral Scheimpflug lidar system. Opt. Express 2017, 25, 515–522. [Google Scholar] [CrossRef]
- Wang, X.; Duan, Z.; Brydegaard, M.; Svanberg, S.; Zhao, G. Drone-based area scanning of vegetation fluorescence height profiles using a miniaturized hyperspectral lidar system. Appl. Phys. A 2018, 124, 207. [Google Scholar] [CrossRef]
- Malmqvist, E.; Brydegaard, M.; Aldén, M.; Bood, J. Scheimpflug lidar for combustion diagnostics. Opt. Express 2018, 26, 14842–14858. [Google Scholar] [CrossRef]
- Rydhmer, K.; Prangsma, J.; Brydegaard, M.; Smith, H. Scheimpfug lidar range profiling of bee activity patterns and spatial distributions. Anim. Biotelemetry 2022, 10, 14. [Google Scholar] [CrossRef]
- Heyworth, G.; Knox, K.; Boydston, K.; Zhu, Y. Multispectral Scheimpflug: Imaging degraded books that open less than 30 degrees. Arch. Conf. 2022, 19, 1–4. [Google Scholar] [CrossRef]
- Agishev, R. Environmental CW range-resolved S-lidars with Si/InGaAs arrays: Limitations and capabilities under sky background. Appl. Opt. 2022, 61, 8889–8897. [Google Scholar] [CrossRef]
- Agishev, R. Application of Imaging S-lidars: Functional and Diagnostic Capabilities for Remote Air Pollution Detection. Opt. Eng. 2021, 60, 084104. [Google Scholar] [CrossRef]
- Scheimpflug, T. Improved Method and Apparatus for the Systematic Alteration or Distortion of Plane Pictures and Images by Means of Lenses and Mirrors for Photography and for Other Purposes. GB Patent 1904, GB190401196A, 2 February 1904. [Google Scholar]
- Carpenter, J. Improvements in Enlarging or Like Cameras. GB Patent 1901, GB190101139A, 2 November 1901. [Google Scholar]
- Meki, K. Range-resolved bistatic imaging lidar for the measurement of the lower atmosphere. Opt. Lett. 1996, 21, 1318–1320. [Google Scholar] [CrossRef] [PubMed]
- Barnes, J.; Bronner, S.; Beck, R.; Parikh, N. Boundary layer scattering measurements with a charge-coupled device camera lidar. Appl. Opt. 2003, 42, 2647–2652. [Google Scholar] [CrossRef]
- Cilingiroglu, U.; Chen, S.; Cilingiroglu, E. Range sensing with a Scheimpflug camera and a CMOS sensor/processor chip. IEEE Sens. J. 2004, 4, 36–44. [Google Scholar] [CrossRef]
- Steger, C. A comprehensive and versatile camera model for cameras with tilt lenses. Intl. J. Comput. Vis. 2017, 123, 121–159. [Google Scholar] [CrossRef]
- Sun, C.; Liu, H.; Jia, M.; Chen, S. Review of Calibration Methods for Scheimpflug Camera. J. Sens. 2018, 2018, 3901431. [Google Scholar] [CrossRef]
- Agishev, R. CW range-resolved S-lidars: Capabilities and limitations in range domain. Opt. Lasers Eng. 2020, 134, 106260. [Google Scholar] [CrossRef]
- Agishev, R. Imaging S-lidars enhancement by optimizing range-domain characteristics. Opt. Eng. 2021, 60, 034110. [Google Scholar] [CrossRef]




| Given | To Be Determined | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Rmax | D | pΣ | α | β | f | L | Ldet | n | p1 | R0 | ΔR(R) | ΔR(Rmax) |
| tanα | D = Rmax/Rmin to Be Achieved | Far Borders Rmax for Different Application Types | Acceptable β Borders | ||||
|---|---|---|---|---|---|---|---|
| Open Path | Indoors | Table Top | |||||
| 10 km | 1 km | 100 m | 10 m | 1 m | |||
| 0.67…1.50 | 2 | 89.88° | 89.62° | 88.79° | 86.17° | 81.45° | βmin…βmax |
| 100 | 89.95° | 89.85° | 89.53° | 88.52° | 86.68° | ||
| 1 | 2 | 89.91° | 89.71° | 89.08° | 87.11° | 83.54° | |
| 100 | 89.93° | 89.79° | 89.35° | 89.94° | 85.41° | ||
| Given: | pΣ1 = pΣ1 | R01 = R02 | D1 > D2 | ||||
| Results: | M1 < M2 | α1 < α2 | β1 < β2 | L1 > L2 | f1 < f2 | ||
| Qmax = f (n, D) | |||
|---|---|---|---|
| n | D | ||
| 2 | 10 | 100 | |
| 256 | 256 | 29 | 2.6 |
| 1024 | 1024 | 114 | 19 |
| 4096 | 4096 | 455 | 41 |
| Range Scales | Test Bench | Indoors | Open Path | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Tactical and Hardware Parameters | ||||||||||
| Far border | Rmax | 1 m | 10 m | 100 m | 1 km | 3 km | 10 km | |||
| Dynamic range | D | 10 | 15 | 20 | 25 | 30 | 33 | |||
| Near border | Rmin = Rmax/D | 0.1 m | 0.67 m | 5 m | 40 m | 100 m | 300 m | |||
| Receiver setting | R0 = 2·Rmax/ (D + 1) | 0.18 m | 1.25 m | 9.5 m | 77 m | 194 m | 588 m | |||
| Quality required | Q | 50 | 100 | 150 | 200 | 400 | 200 | 400 | 200 | 400 |
| Range resolution | ∆R(Rmax) = Rmax/Q | 0.02 m | 0.1 m | 0.67 m | 5 m | 2.5 m | 15 m | 7.5 m | 50 m | 25 m |
| Cumulative factor | K1 = Rmax·Q | 50 m | 103 m | 1.5 × 104 m | 2 × 105 m | 4 × 105 m | 6 × 105 m | 1.2 × 106 m | 2 × 106 m | 4 × 106 m |
| Number of cells | nmin = (D − 1)·Q | 450 | 1400 | 2850 | 4800 | 9600 | 5800 | 11,600 | 6400 | 12,800 * |
| Single pixel size | p1 | 12.5 μm | 10 μm | 5 μm | 3 μm | 3 μm | 2 μm | 2 μm | 1 μm * | 1 μm * |
| Focal length and lidar base ** ** α = π/4 | 0.02 m | 0.084 m | 0.23 m | 0.65 m | 0.92 m | 0.92 m | 1.30 m | 1.19 m | 1.68 m | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Agishev, R.; Wang, Z.; Liu, D. Designing CW Range-Resolved Environmental S-Lidars for Various Range Scales: From a Tabletop Test Bench to a 10 km Path. Remote Sens. 2023, 15, 3426. https://doi.org/10.3390/rs15133426
Agishev R, Wang Z, Liu D. Designing CW Range-Resolved Environmental S-Lidars for Various Range Scales: From a Tabletop Test Bench to a 10 km Path. Remote Sensing. 2023; 15(13):3426. https://doi.org/10.3390/rs15133426
Chicago/Turabian StyleAgishev, Ravil, Zhenzhu Wang, and Dong Liu. 2023. "Designing CW Range-Resolved Environmental S-Lidars for Various Range Scales: From a Tabletop Test Bench to a 10 km Path" Remote Sensing 15, no. 13: 3426. https://doi.org/10.3390/rs15133426
APA StyleAgishev, R., Wang, Z., & Liu, D. (2023). Designing CW Range-Resolved Environmental S-Lidars for Various Range Scales: From a Tabletop Test Bench to a 10 km Path. Remote Sensing, 15(13), 3426. https://doi.org/10.3390/rs15133426








