Research on 4-D Imaging of Holographic SAR Differential Tomography
Abstract
1. Introduction
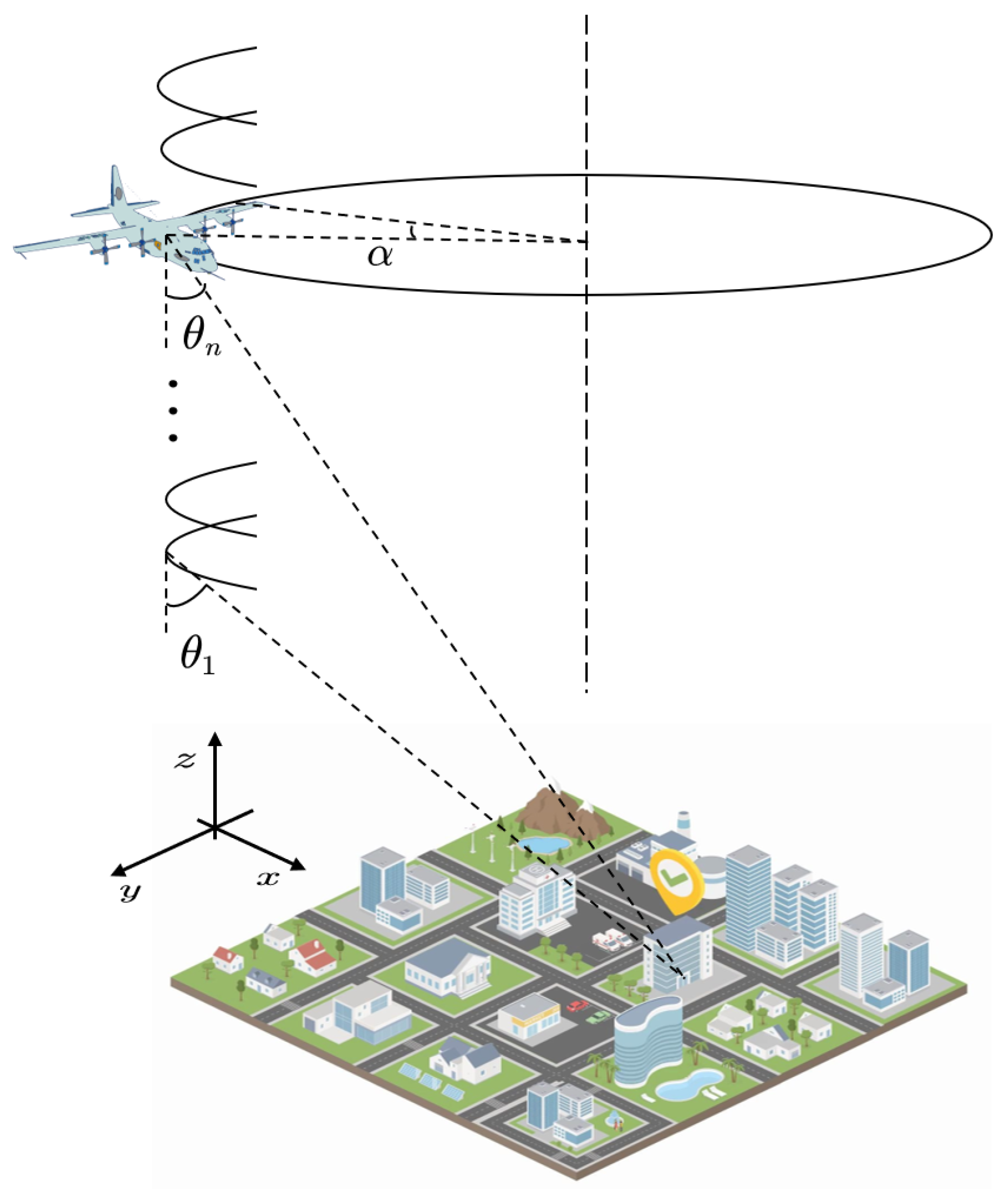
2. Imaging Model
2.1. TomoSAR Imaging Model
2.2. D-TomoSAR Imaging Model
2.3. Differential HoloSAR Imaging Model
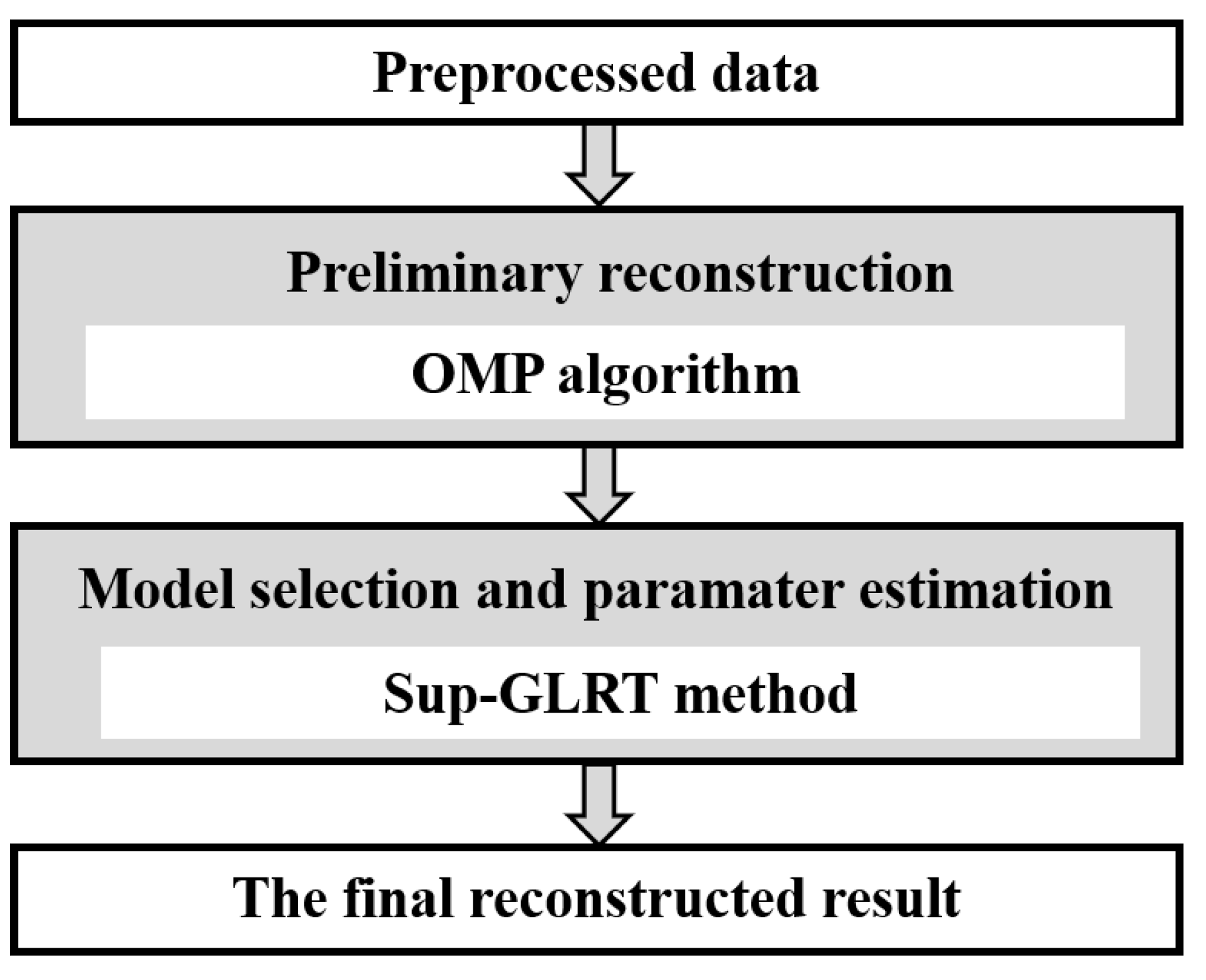
3. Imaging Method
3.1. Classical Spectral Estimation Method
3.2. OMP-Based CS Algorithm
3.3. The Proposed OMP Sup-GLRT Method
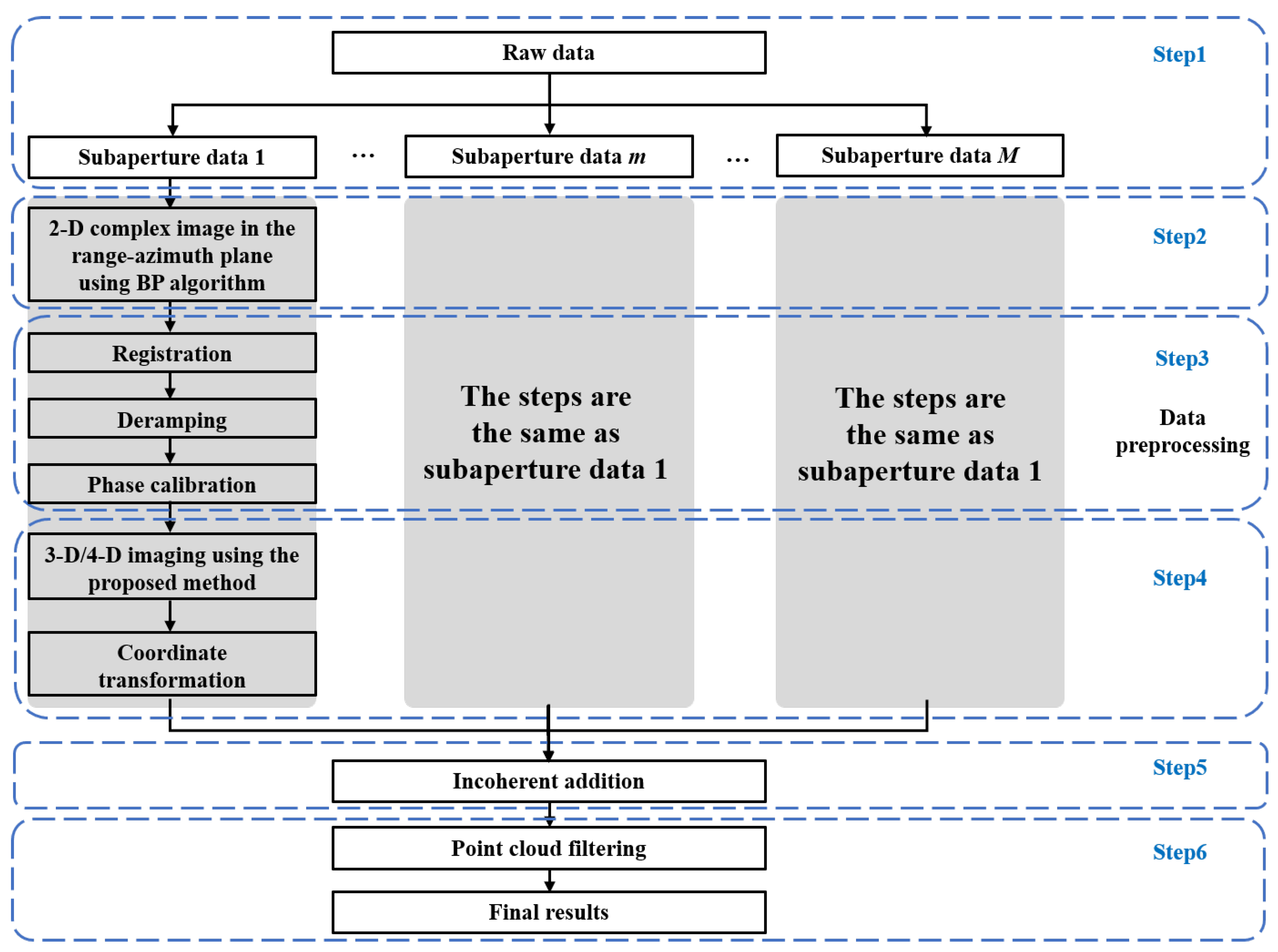
4. Processing Procedure of Differential HoloSAR
- Step 1: In order to ensure that the data of each sub-aperture is isotropic, the collected echo is divided into M non-overlapping sub-apertures according to a certain azimuth angle, and the corresponding acquisition time is also divided accordingly;
- Step 2: The inputs of 3-D and 4-D SAR imaging methods are multiple 2-D SAR images. Thus, we process the raw data in each sub-aperture to focus a 2-D complex image in the azimuth-range plane using the back-projection (BP) algorithm;
- Step 3: There are certain interference factors in the 2-D complex images, 3-D and 4-D imaging cannot be performed directly. A series of preprocessings are required, including image registration, deramping, and phase calibration;
- Step 4: Based on the 2-D complex images after preprocessing, we use the proposed method to perform HoloSAR 3-D imaging and differential HoloSAR 4-D imaging. Then, we carry out the coordinate transformation on the results, and convert it into the ground range coordinate;
- Step 5: For any one sub-aperture, each pixel unit contains the same number of scatterers; thus, the elevation scattering distributions of all pixel units are also consistent. In order to obtain omnidirectional observation results, it is necessary to perform an incoherent summation for the imaging results of all sub-apertures;
- Step 6: In order to remove unnecessary scatterers, point cloud filtering is performed to obtain the high-quality final result.
5. Results
5.1. Dataset
5.2. Experimental Results
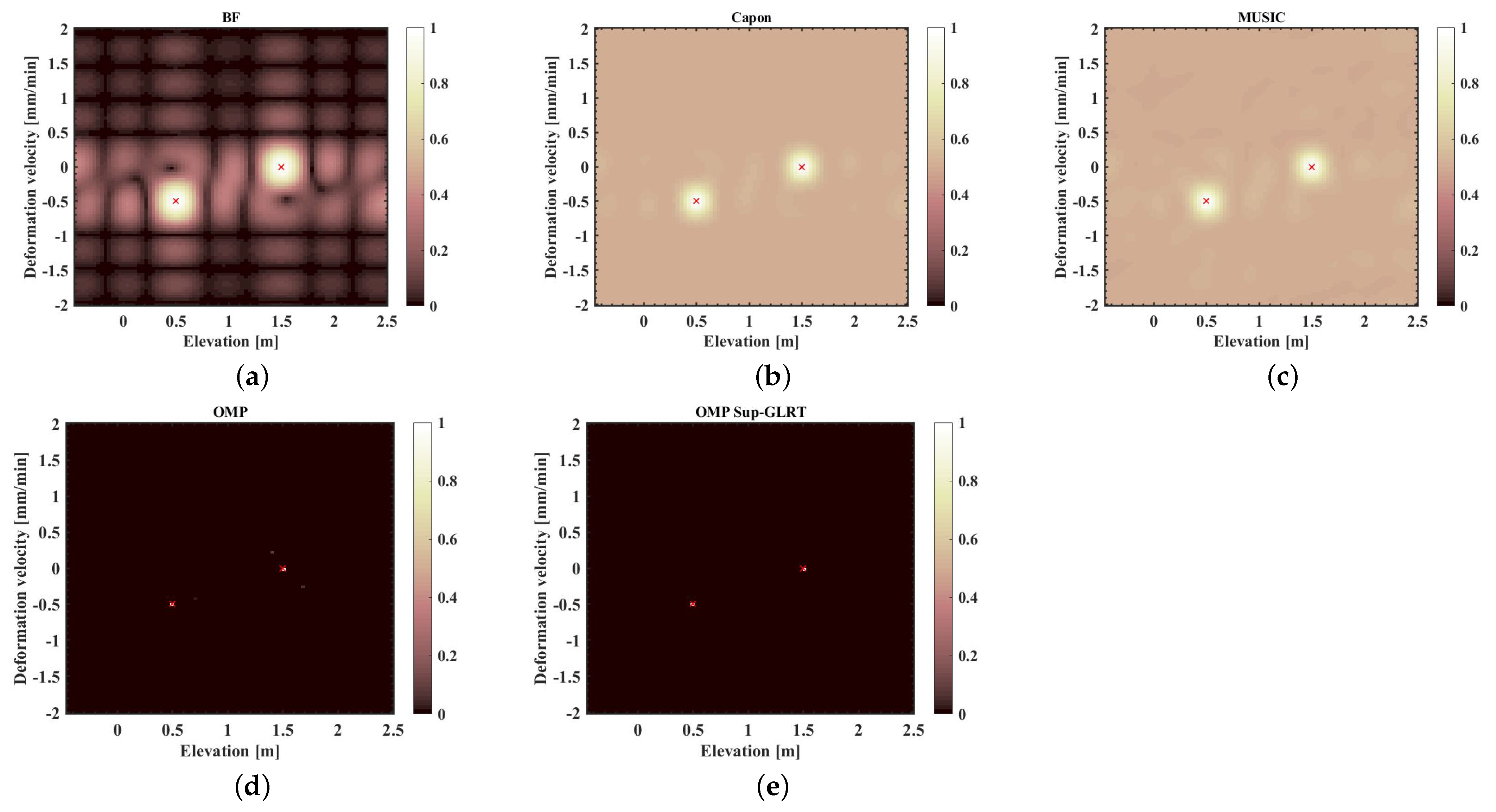
5.2.1. Simulation
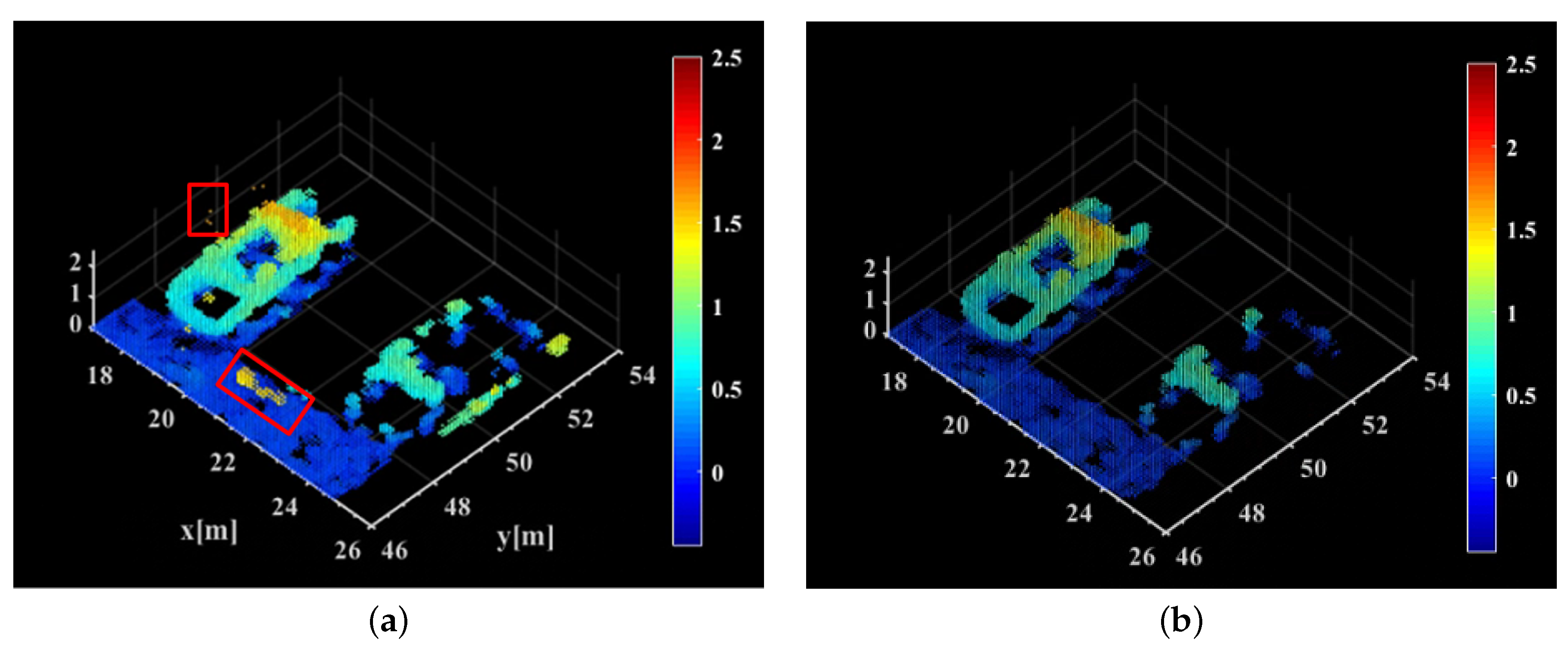
5.2.2. Point Cloud Filtering
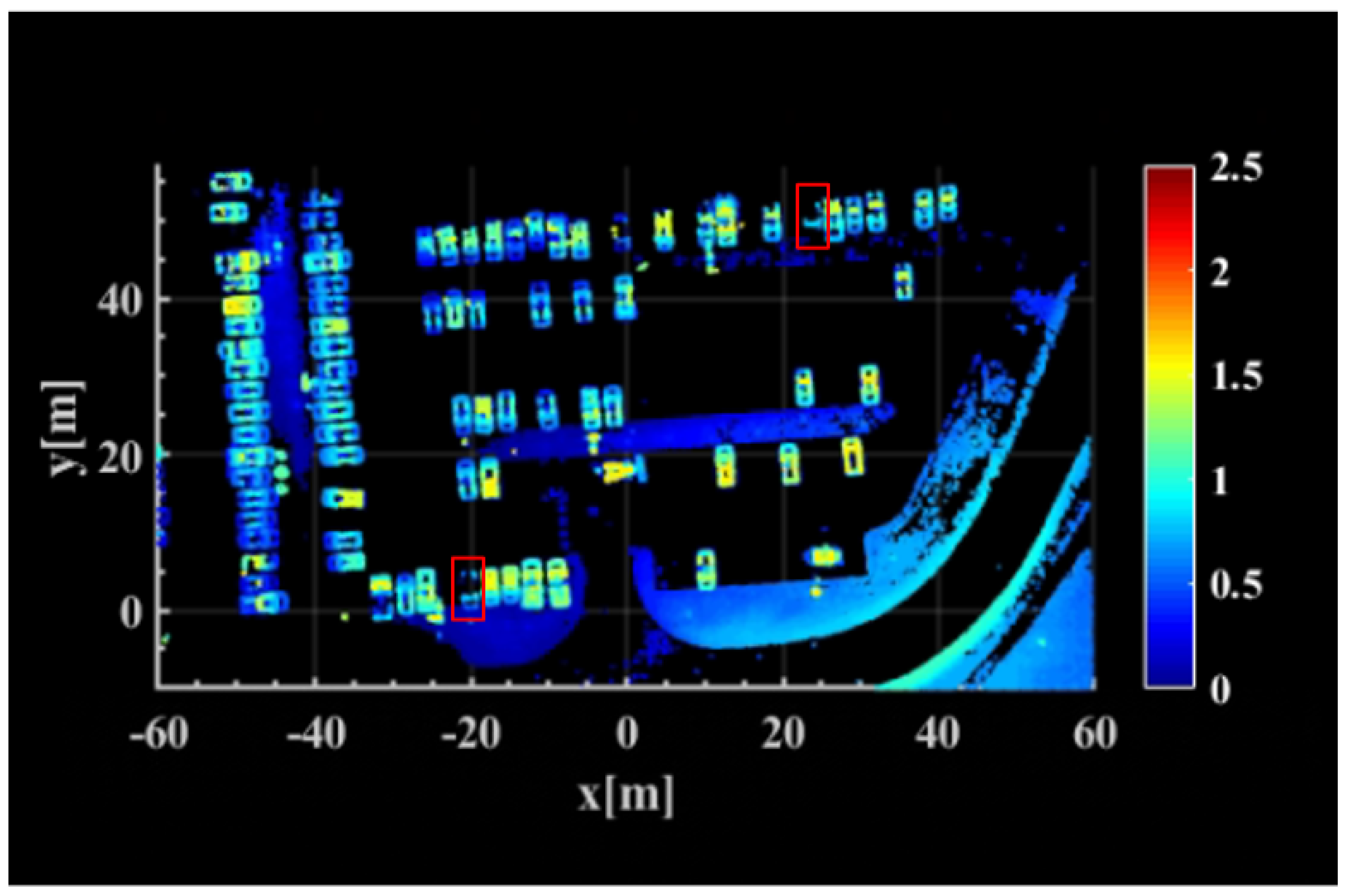
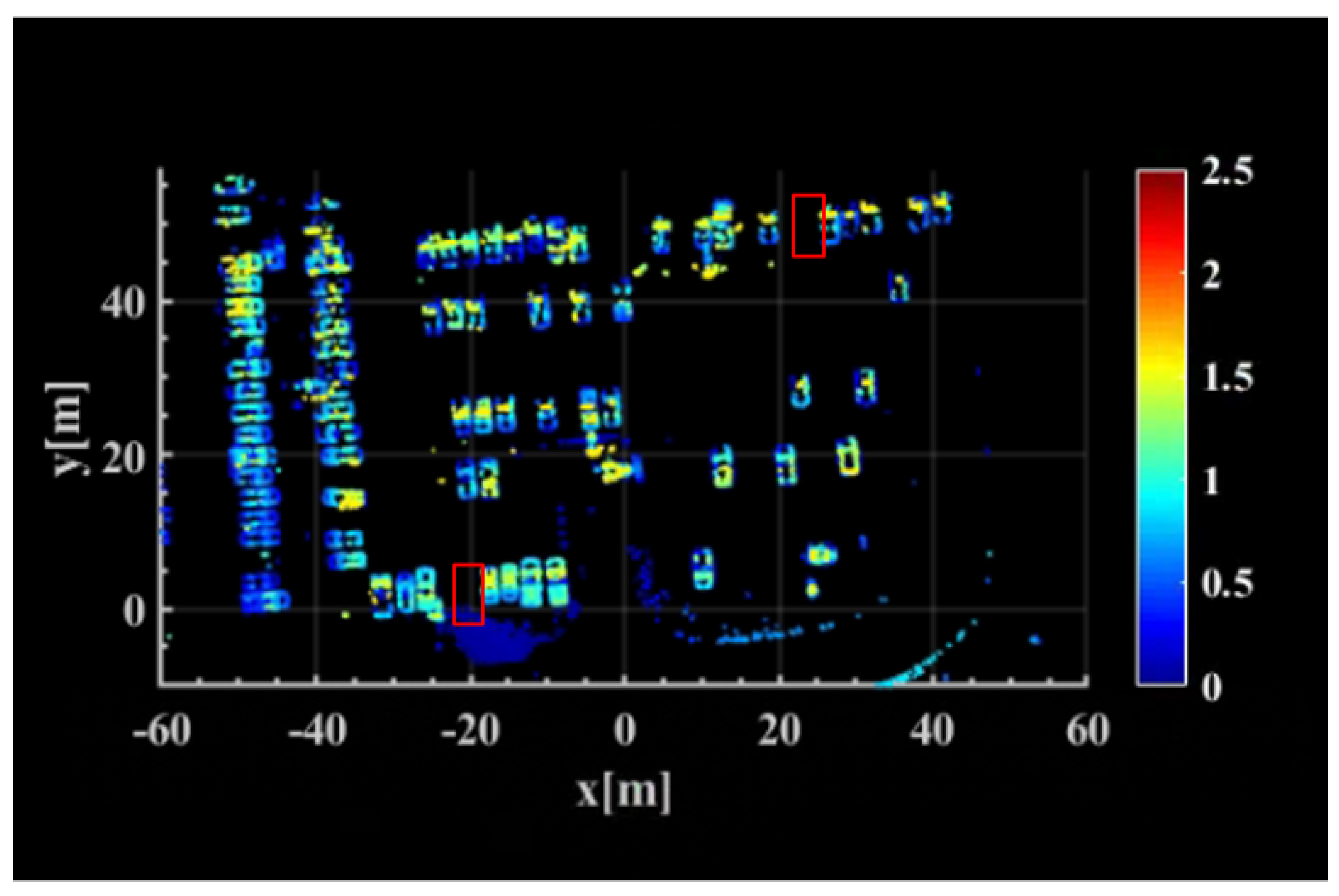
5.2.3. Real Data Experiment
6. Discussion
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| SAR | Synthetic Aperture Radar |
| CSAR | Circular Synthetic Aperture Radar |
| MCSAR | Multi-circular Synthetic Aperture Radar |
| 2-D | Two-dimensional |
| 3-D | Three-dimensional |
| 4-D | Four-dimensional |
| InSAR | Interference SAR |
| TomoSAR | SAR Tomography |
| D-TomoSAR | Differential SAR Tomography |
| CS | Compressive Sensing |
| HoloSAR | Holographic SAR Tomography |
| BF | Beamforming |
| Capon | Adaptive Beamforming |
| MUSIC | Multiple Signal Classification |
| OMP | Orthogonal Matching Pursuit |
| RIP | Restricted Isometric Property |
| GLRT | Generalized Likelihood Ratio Test |
| Sup-GLRT | Support Generalized Likelihood Ratio Test |
| CFAR | Constant False Alarm Rate |
| SOR | Statistical Outlier Removal |
| BIC | Bayesian Information Criterion |
| SNR | Signal-to-noise Ratio |
| BP | Back-projection |
References
- Soumekh, M. Reconnaissance with slant plane circular SAR imaging. IEEE Trans. Image Process. 1996, 5, 1252–1265. [Google Scholar] [CrossRef] [PubMed]
- Tsz-King, C.; Kuga, Y.; Ishimaru, A. Experimental studies on circular SAR imaging in clutter using angular correlation function technique. IEEE Trans. Geosci. Remote Sens. 1999, 37, 2192–2197. [Google Scholar] [CrossRef]
- Ponce, O.; Prats, P.; Scheiber, R.; Reigber, A.; Moreira, A. Multibaseline 3-D circular SAR imaging at L-band. In Proceedings of the 9th European Conference on Synthetic Aperture Radar, Nuremberg, Germany, 23–26 April 2012. [Google Scholar]
- Ponce, O.; Prats, P.; Scheiber, R.; Reigber, A.; Moreira, A. First demonstration of 3-D holographic tomography with fully polarimetric multi-circular SAR at L-band. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Melbourne, VIC, Australia, 21–26 July 2013. [Google Scholar]
- Ponce, O.; Prats-Iraola, P.; Pinheiro, M.; Rodriguez-Cassola, M.; Scheiber, R.; Reigber, A.; Moreira, A. Fully polarimetric high-resolution 3-D imaging with circular SAR at L-band. IEEE Trans. Geosci. Remote Sens. 2014, 52, 3074–3090. [Google Scholar] [CrossRef]
- Ponce, O.; Prats, P.; Scheiber, R.; Reigber, A.; Moreira, A. Study of the 3-D impulse response function of holographic SAR tomography with multi circular acquisitions. In Proceedings of the 10th European Conference on Synthetic Aperture Radar, Berlin, Germany, 3–5 June 2014. [Google Scholar]
- Bao, Q.; Lin, Y.; Hong, W.; Zhang, B. Multi-circular synthetic aperture radar imaging processing procedure based on compressive sensing. In Proceedings of the The 4th International Workshop on Compressed Sensing Theory and its Applications to Radar, Sonar and Remote Sensing, Aachen, Germany, 19–22 September 2016. [Google Scholar]
- Ponce, O.; Prats-Iraola, P.; Scheiber, R.; Reigber, A.; Moreira, A. First airborne demonstration of holographic SAR tomography with fully polarimetric multi circular acquisitions at L-band. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6170–6196. [Google Scholar] [CrossRef]
- Budillon, A.; Schirinzi, G. GLRT based on support estimation for multiple scatterers detection in SAR tomography. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 1086–1094. [Google Scholar] [CrossRef]
- Chen, L.; An, D.; Huang, X.; Zhou, Z. A 3D reconstruction strategy of vehicle outline based on single-pass single-polarization CSAR data. IEEE Trans. Image Process. 2017, 26, 5545–5554. [Google Scholar] [CrossRef] [PubMed]
- Bao, Q.; Lin, Y.; Hong, W.; Shen, W.; Zhao, Y.; Peng, X. Holographic SAR tomography image reconstruction by combination of adaptive imaging and sparse Bayesian inference. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1248–1252. [Google Scholar] [CrossRef]
- Feng, D.; An, D.; Huang, X.; Li, Y. A phase calibration method based on phase gradient autofocus for airborne holographic SAR imaging. IEEE Geosci. Remote Sens. Lett. 2019, 16, 864–1868. [Google Scholar] [CrossRef]
- Feng, D.; An, D.; Chen, L.; Huang, X. Holographic SAR tomography 3-D reconstruction based on iterative adaptive approach and generalized likelihood ratio test. IEEE Trans. Geosci. Remote Sens. 2021, 59, 305–315. [Google Scholar] [CrossRef]
- Wang, M.; Wei, S.; Zhou, Z.; Shi, J.; Zhang, X.; Guo, Y. CTV-Net: Complex-valued TV-driven network with nested topology for 3-D SAR imaging. IEEE Trans. Neural Netw. Learn. Syst. 2022, 1–15. [Google Scholar] [CrossRef]
- Smith, J.W.; Torlak, M. Deep learning-based multiband signal fusion for 3-D SAR super-resolution. IEEE Trans. Aerosp. Electron. Syst. 2023, 1–17. [Google Scholar] [CrossRef]
- Reigber, A.; Moreira, A.; Papathanassiou, K.P. First demonstration of airborne SAR tomography using multibaseline L-band data. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Hamburg, Germany, 28 June–2 July 1999. [Google Scholar]
- Reigber, A.; Moreira, A. First demonstration of airborne SAR tomography using multi baseline L-band data. IEEE Trans. Geosci. Remote Sens. 2000, 38, 2142–2152. [Google Scholar] [CrossRef]
- Lombardini, F. Differential tomography: A new framework for SAR interferometry. IEEE Trans. Geosci. Remote Sens. 2005, 43, 37–44. [Google Scholar] [CrossRef]
- Fornaro, G.; Serafino, F.; Reale, D. 4-D SAR imaging: The case study of Rome. IEEE Geosci. Remote Sens. Lett. 2010, 7, 236–240. [Google Scholar] [CrossRef]
- Reale, D.; Fornaro, G.; Pauciullo, A. Extension of 4-D SAR imaging to the monitoring of thermally dilating scatterers. IEEE Trans. Geosci. Remote Sens. 2013, 51, 5296–5306. [Google Scholar] [CrossRef]
- Lombardini, F.; Viviani, F. New developments of 4-D+ differential SAR tomography to probe complex dynamic scenes. In Proceedings of the IEEE Geoscience and Remote Sensing Symposium, Quebec City, QC, Canada, 13–18 July 2014. [Google Scholar]
- Jo, M.-J.; Jung, H.-S.; Chae, S.-H. Advances in three-dimensional deformation mapping from satellite radar observations: Application to the 2003 bam earthquake. Geomat. Nat. Hazards Risk 2018, 9, 678–690. [Google Scholar] [CrossRef]
- Chai, H.; Lv, X.; Yao, J.; Xue, F. Off-grid differential tomographic SAR and its application to railway monitoring. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 3999–4013. [Google Scholar] [CrossRef]
- Candès, E.J. Compressive sampling. Proc. Int. Congr. Math. 2006, 3, 1433–1452. [Google Scholar]
- Baraniuk, R.; Steeghs, P. Compressive radar imaging. In Proceedings of the IEEE Radar Conference, Waltham, MA, USA, 17–20 April 2007. [Google Scholar]
- Zhu, X.X.; Bamler, R. Super-resolution for 4-D SAR tomography via compressive sensing. In Proceedings of the 8th European Conference on Synthetic Aperture Radar, Aachen, Germany, 7–10 June 2010. [Google Scholar]
- Zhu, X.X.; Bamler, R. Superresolving SAR tomography for multidimensional imaging of urban areas: Compressive sensing-based TomoSAR inversion. IEEE Signal Process. Mag. 2014, 31, 51–58. [Google Scholar] [CrossRef]
- Wu, Y.Y.; Hong, W.; Zhang, B.C. Introduction to Sparse Microwave Imaging; Science Press: Beijing, China, 2018. [Google Scholar]
- Shi, Y.; Zhu, X.X.; Bamler, R. Nonlocal compressive sensing-based SAR tomography. IEEE Trans. Geosci. Remote Sens. 2019, 57, 3015–3024. [Google Scholar] [CrossRef]
- Chai, H.; Lv, X.; Xiao, P. Deformation monitoring using ground-based differential SAR tomography. IEEE Geosci. Remote Sens. Lett. 2020, 17, 993–997. [Google Scholar] [CrossRef]
- Lombardini, F.; Pardini, M. 3-D SAR tomography: The multibaseline sector interpolation approach. IEEE Geosci. Remote. Sens. Lett. 2008, 5, 630–634. [Google Scholar] [CrossRef]
- Zhu, X.X.; Bamler, R. Tomographic SAR inversion by L1-norm regularization—The compressive sensing approach. IEEE Trans. Geosci. Remote Sens. 2010, 48, 3839–3846. [Google Scholar] [CrossRef]
- Lin, Y.; Hong, W.; Tan, W.; Wang, Y.; Wu, Y. Interferometric circular SAR method for three-dimensional imaging. IEEE Geosci. Remote Sens. Lett. 2011, 8, 1026–1030. [Google Scholar] [CrossRef]
- Stoica, P.; Moses, R. Spectral Analysis of Signals; Pearson Prentice Hall: Upper Sadle River, NJ, USA, 2005. [Google Scholar]
- Capon, J. High-resolution frequency-wavenumber spectrum analysis. Proc. IEEE 1969, 57, 1408–1418. [Google Scholar] [CrossRef]
- Schmidt, R. Multiple emitter location and signal parameter estimation. IEEE Trans. Antennas Propag. 1979, 34, 276–280. [Google Scholar] [CrossRef]
- Stoica, P.; Arye, N. MUSIC, maximum likelihood, and Cramer-Rao bound. Acoust. Speech Signal Process. IEEE Trans. 1989, 37, 720–741. [Google Scholar] [CrossRef]
- Pati, Y.C.; Rezaiifar, R.; Krishnaprasad, P.S. Orthogonal matching pursuit: Recursive function approximation with applications to wavelet decomposition. In Proceedings of the 27th Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 1–3 November 1993; pp. 40–44. [Google Scholar]
- Tropp, J.A.; Gilbert, A.C. Signal recovery from random measurements via orthogonal matching pursuit. IEEE Trans. Inf. Theory 2007, 53, 4655–4666. [Google Scholar] [CrossRef]
- Luo, H.; Li, Z.; Dong, Z.; Yu, A.; Zhang, Y.; Zhu, X. Super-resolved multiple scatterers detection in SAR tomography based on compressive sensing generalized likelihood ratio test (CS-GLRT). Remote Sens. 2019, 11, 1930. [Google Scholar] [CrossRef]
- Casteel, C.H., Jr.; Gorham, L.A.; Minardi, M.J.; Scarborough, S.M.; Naidu, K.D.; Majumder, U.K. A challenge problem for 2D/3D imaging of targets from a volumetric data set in an urban environment. SPIE 2007, 6568, 97–103. [Google Scholar]
- Guo, J.; Feng, W.; Hao, T.; Wang, P.; Xia, S.; Mao, H. Denoising of a multi-station point cloud and 3D modeling accuracy for substation equipment based on statistical outlier removal. In Proceedings of the 2020 IEEE 4th Conference on Energy Internet and Energy System Integration, Wuhan, China, 30 October–1 November 2020; pp. 2793–2797. [Google Scholar]





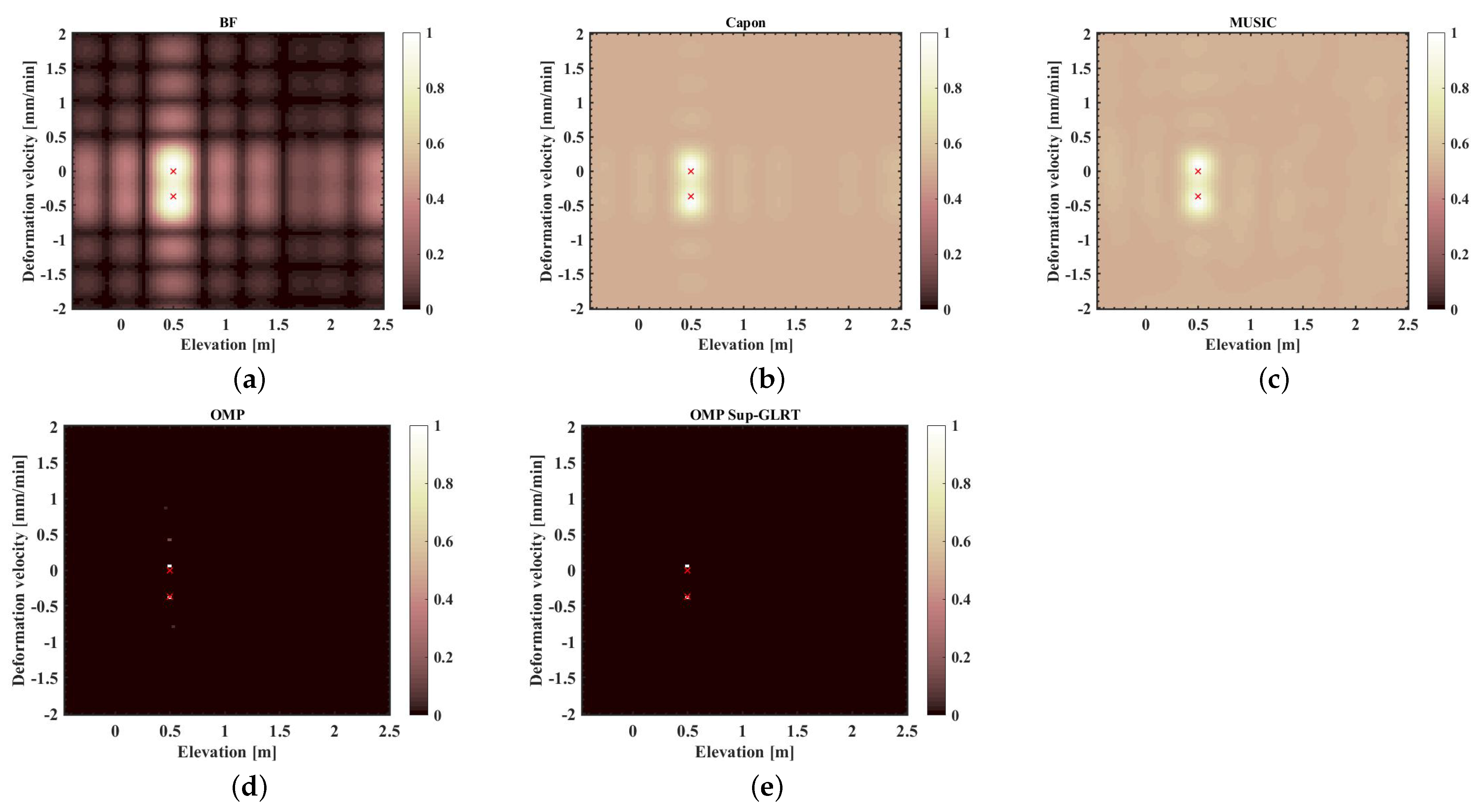






| OMP Algorithm |
|---|
|
| Model Selection-Sup-GLRT Algorithm |
|---|
|
| Wavelength | Average Slant Range | Average View Angle | Number of Data |
|---|---|---|---|
| 0.0313 m | 10,168.2 m | 44.3° | 8 |
| SAR Image ID | No.1 | No.2 | No.3 | No.4 | No.5 | No.6 | No.7 | No.8 (Master) |
|---|---|---|---|---|---|---|---|---|
| Temporal baseline | −28 min | −24 min | −20 min | −16 min | −12 min | −8 min | −4 min | 0 min |
| Elevation angle | 45.7485° | 45.5939° | 45.3287° | −45.0614° | 44.7775° | 44.4165° | 44.2241° | 44.0594° |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jin, S.; Bi, H.; Feng, J.; Xu, W.; Xu, J.; Zhang, J. Research on 4-D Imaging of Holographic SAR Differential Tomography. Remote Sens. 2023, 15, 3421. https://doi.org/10.3390/rs15133421
Jin S, Bi H, Feng J, Xu W, Xu J, Zhang J. Research on 4-D Imaging of Holographic SAR Differential Tomography. Remote Sensing. 2023; 15(13):3421. https://doi.org/10.3390/rs15133421
Chicago/Turabian StyleJin, Shuang, Hui Bi, Jing Feng, Weihao Xu, Jin Xu, and Jingjing Zhang. 2023. "Research on 4-D Imaging of Holographic SAR Differential Tomography" Remote Sensing 15, no. 13: 3421. https://doi.org/10.3390/rs15133421
APA StyleJin, S., Bi, H., Feng, J., Xu, W., Xu, J., & Zhang, J. (2023). Research on 4-D Imaging of Holographic SAR Differential Tomography. Remote Sensing, 15(13), 3421. https://doi.org/10.3390/rs15133421







