Hybrid Deep Learning and S2S Model for Improved Sub-Seasonal Surface and Root-Zone Soil Moisture Forecasting
Abstract
1. Introduction
2. Study Area and Data
2.1. Study Area
2.2. The ERA5 Reanalysis Data
2.3. The S2S Forecasting Data
2.4. Auxiliary Datasets
3. Methodology
3.1. The Machine Learning Forecasting Methods
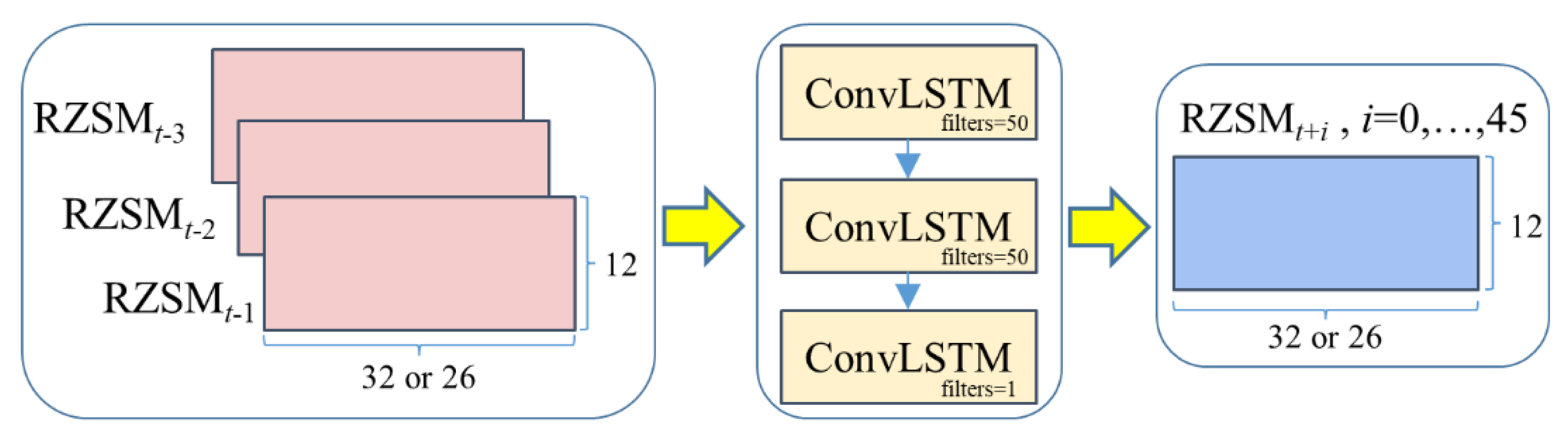
3.2. The Deep Learning Forecasting Model
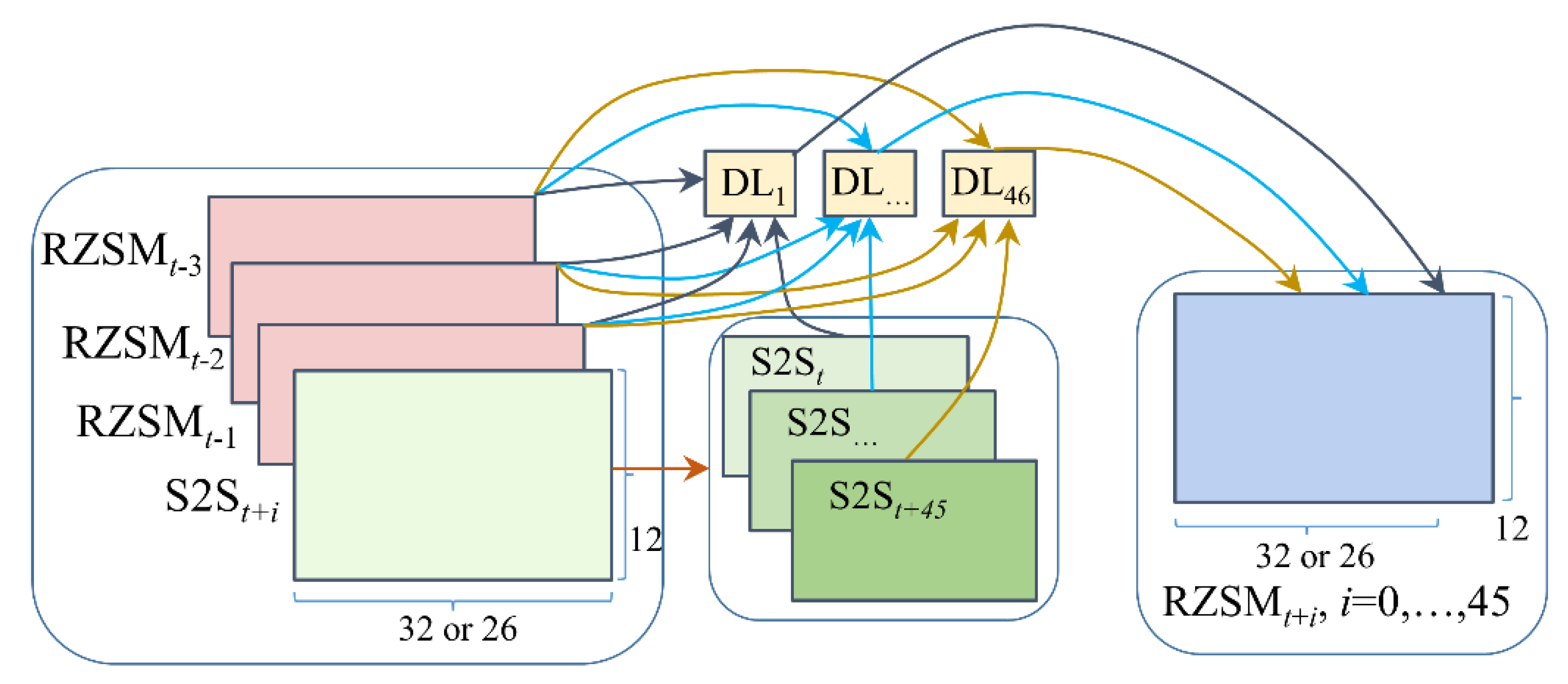
3.3. Hybrid Soil Moisture Forecasting Framework
3.4. Evaluation Metrics
4. Results and Discussion
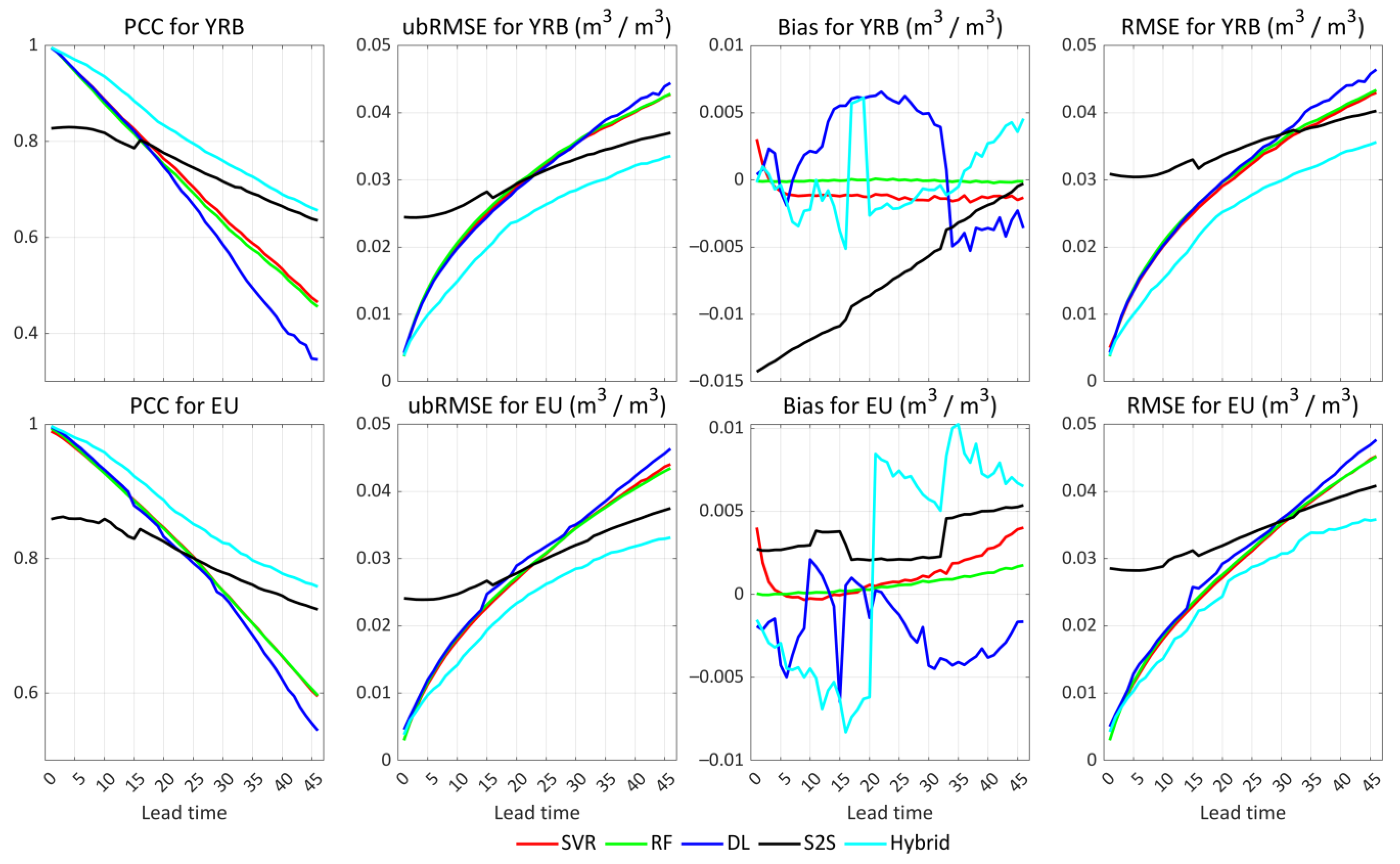
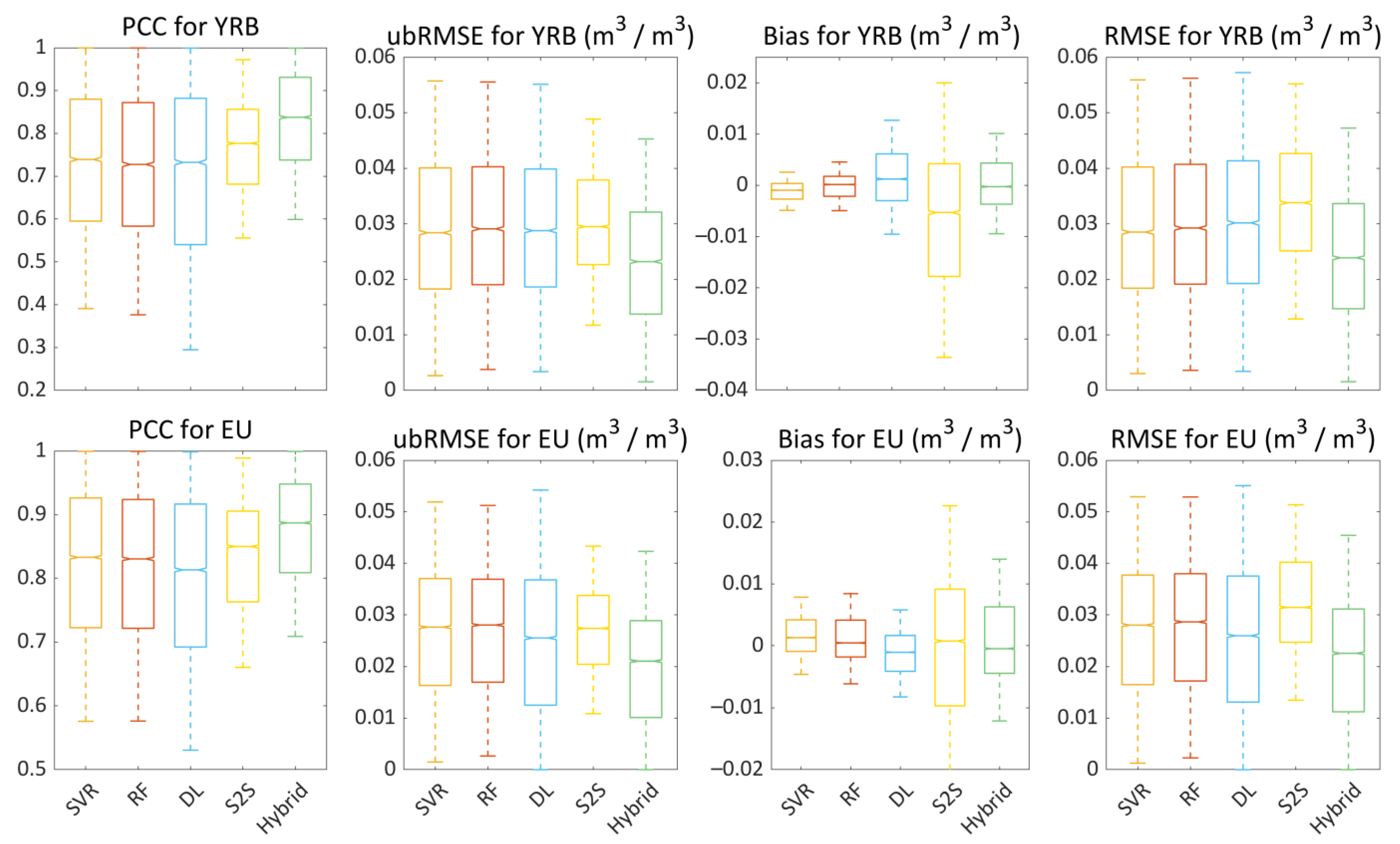
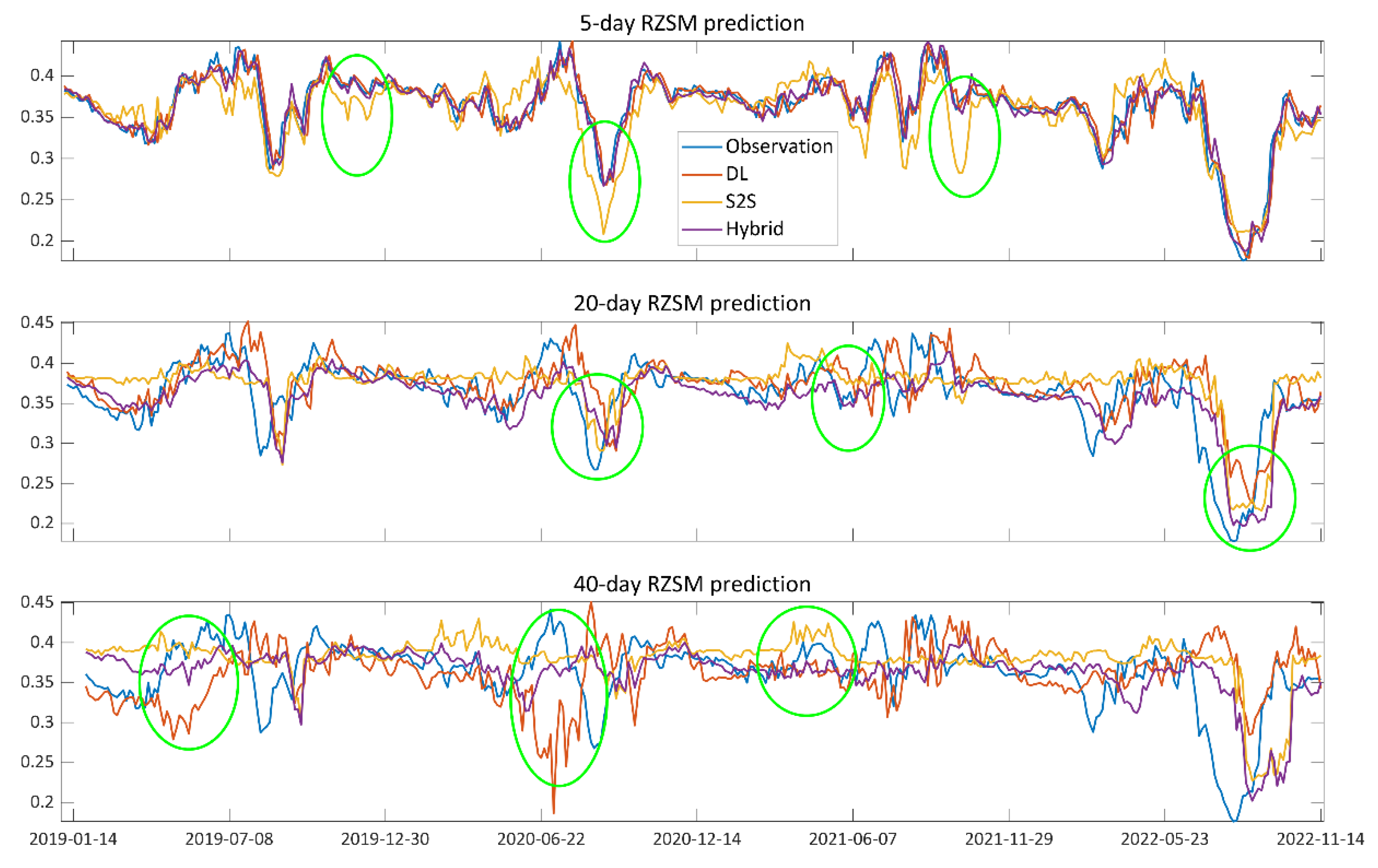
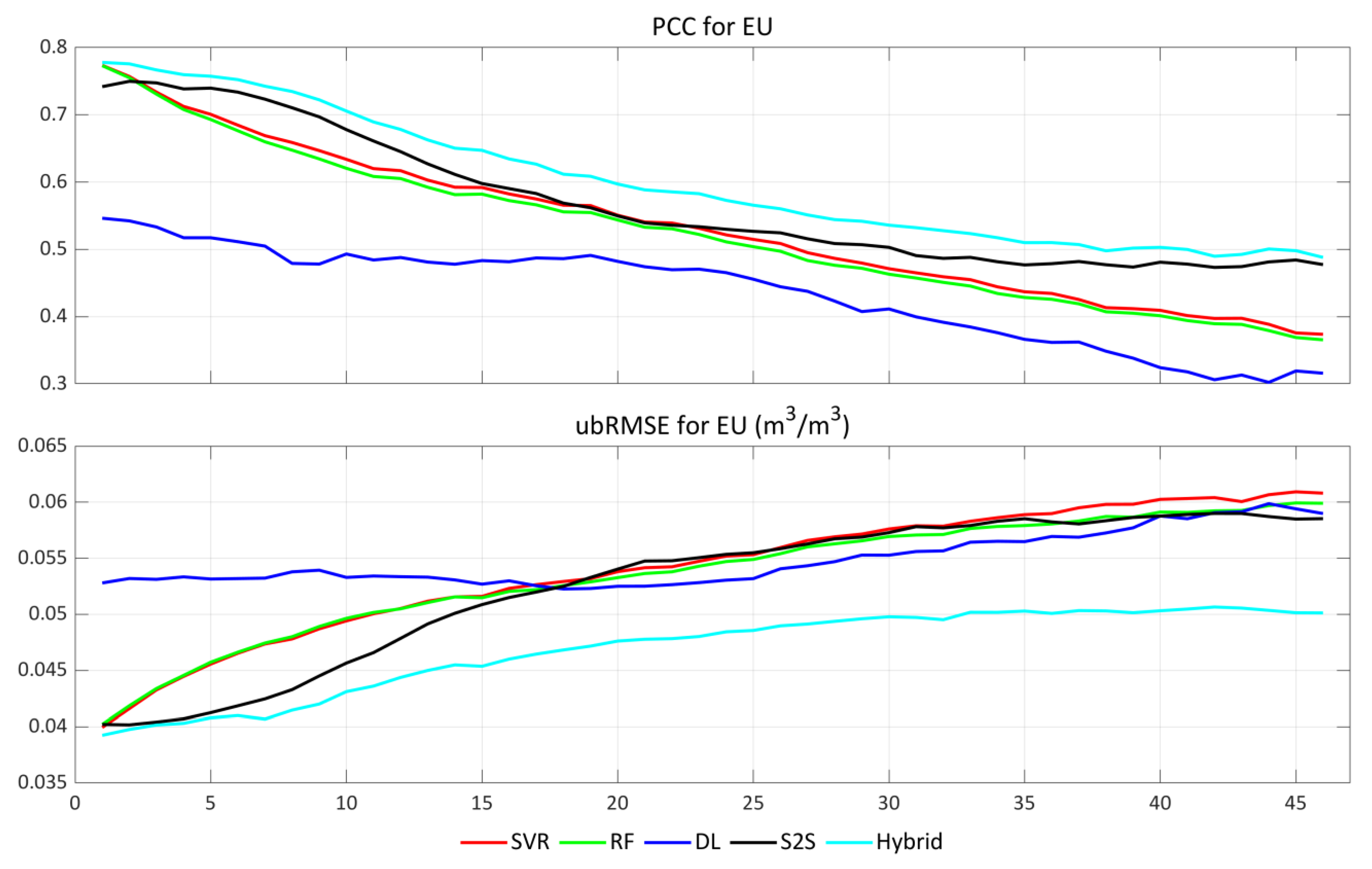
4.1. Overall Soil Moisture Forecasting Skill
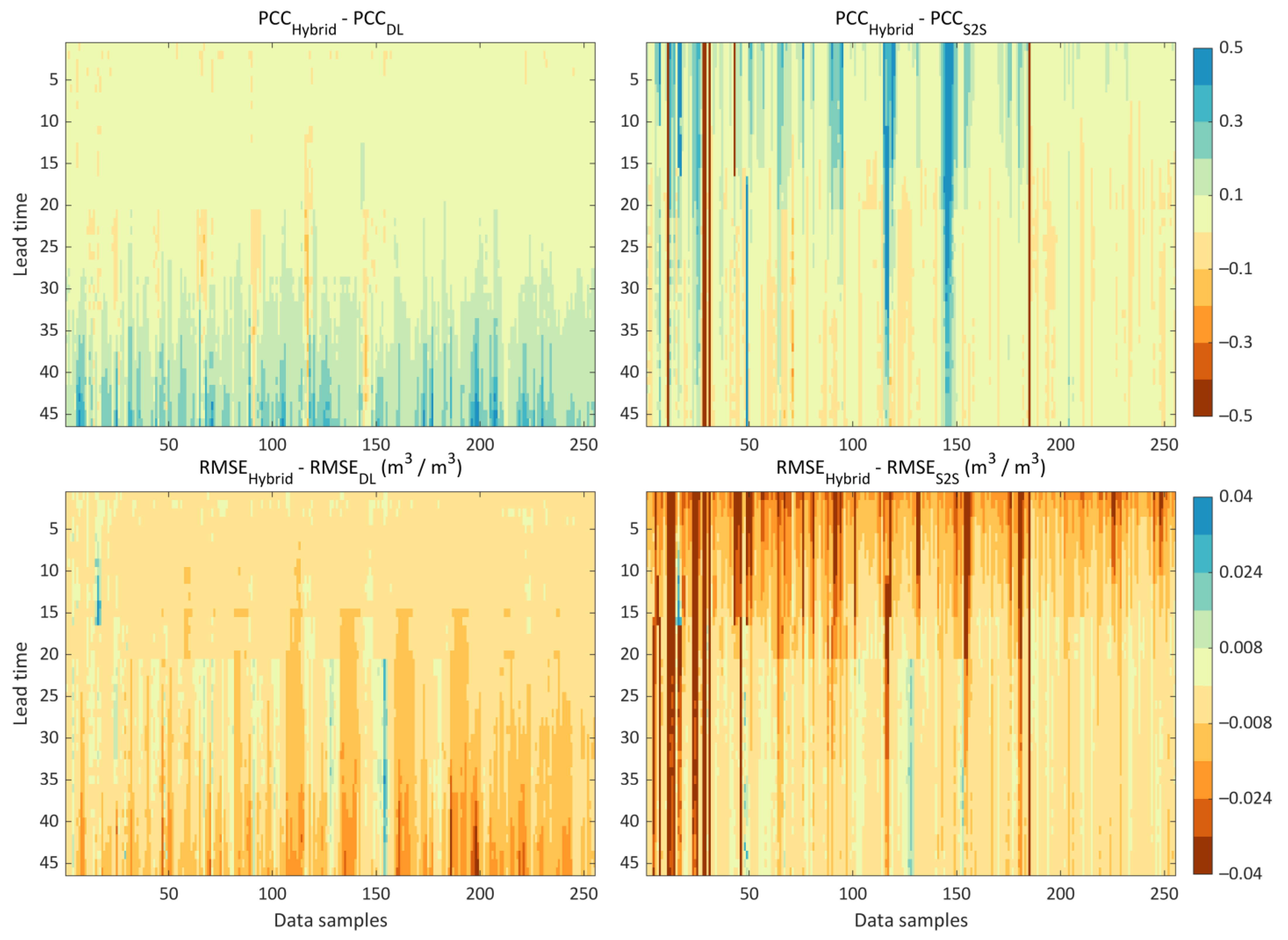
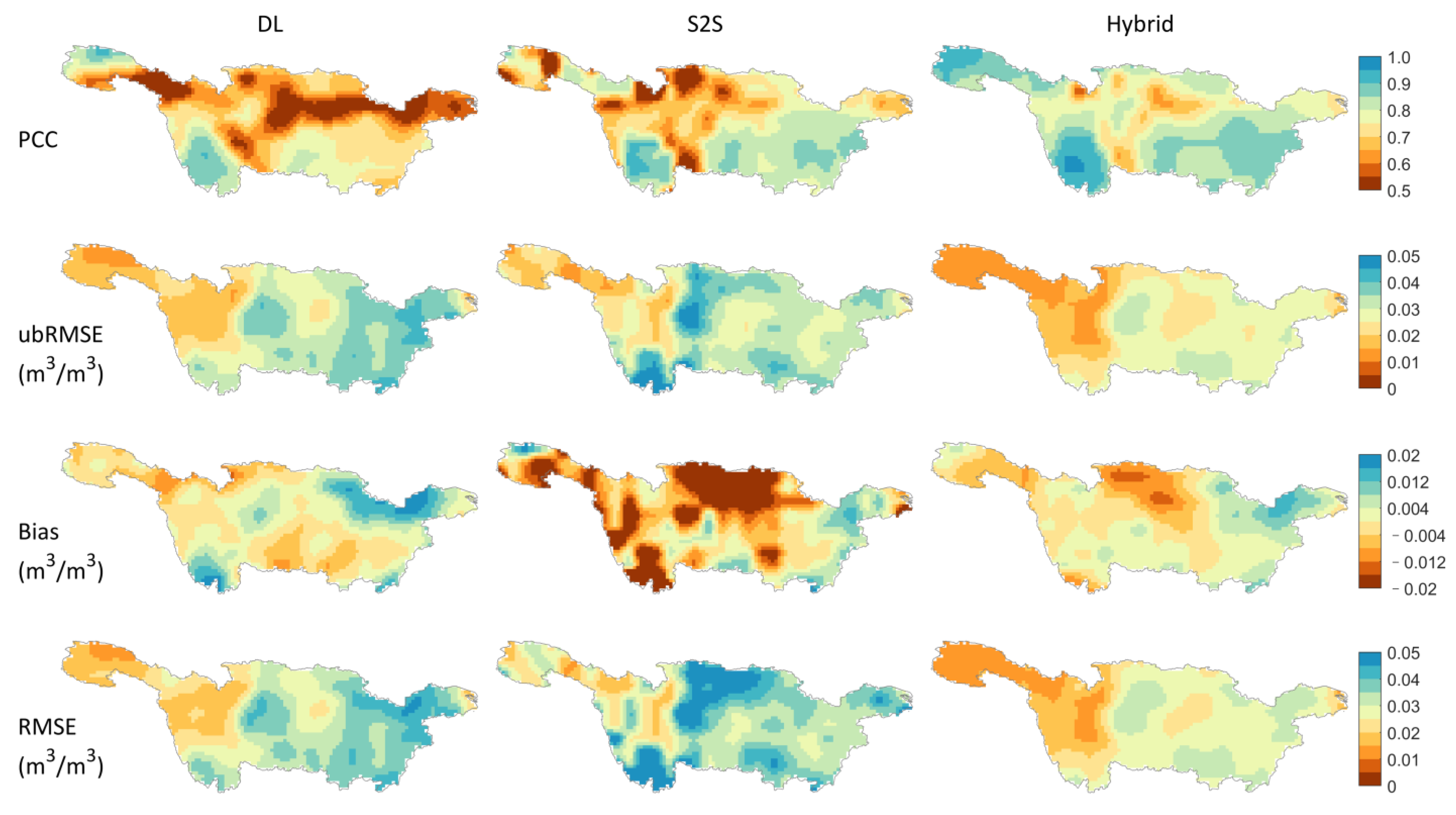
4.2. Spatiotemporal Patterns of Predictive Performance
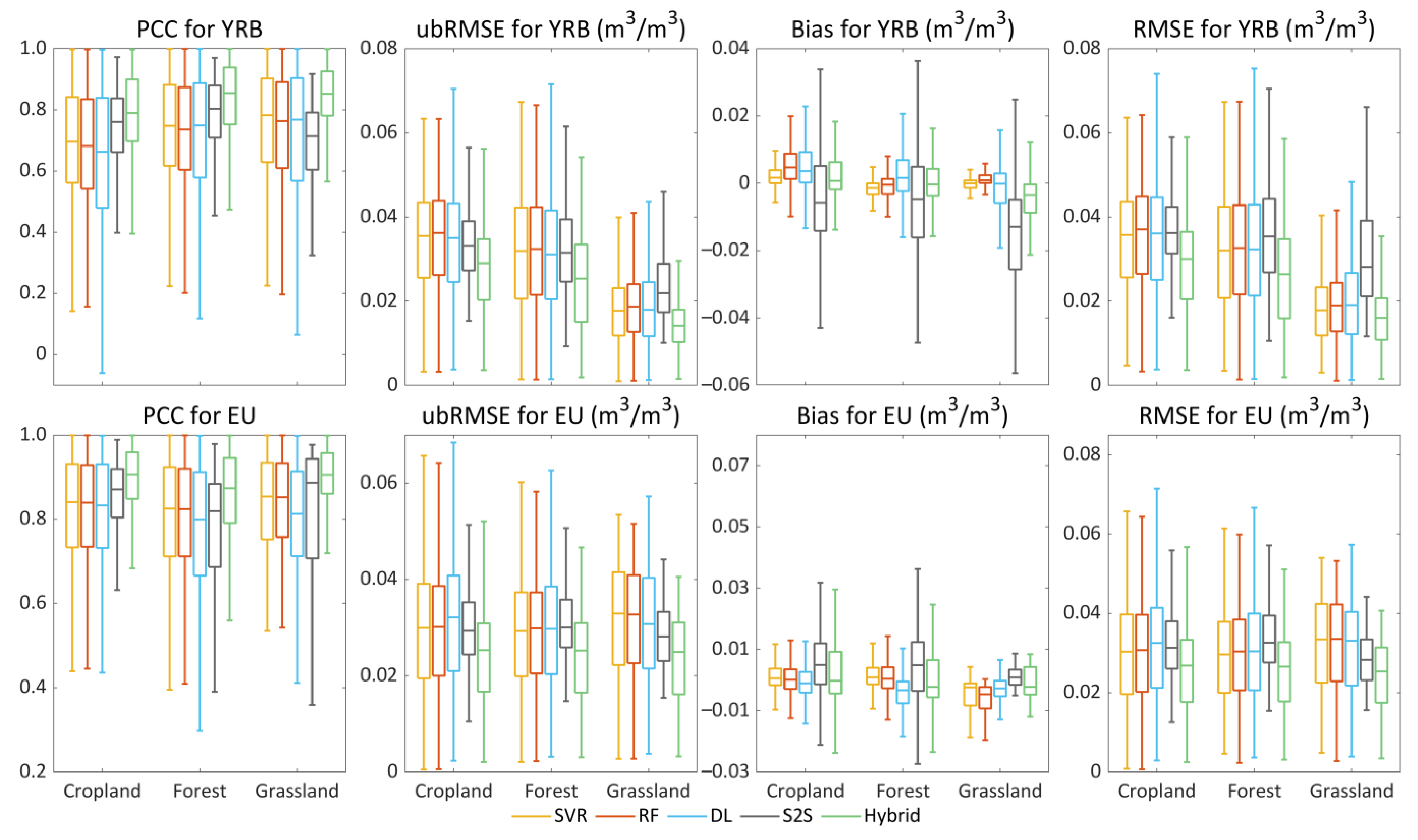
4.3. The Skill over Different Land Cover Types
4.4. In Situ Validation
4.5. Strengths and Limitations of the Hybrid Model
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Dirmeyer, P.A.; Cash, B.A.; Kinter, J.L., III; Stan, C.; Jung, T.; Marx, L.; Towers, P.; Wedi, N.; Adams, J.M.; Altshuler, E.L. Evidence for enhanced land–atmosphere feedback in a warming climate. J. Hydrometeorol. 2012, 13, 981–995. [Google Scholar] [CrossRef]
- Schumacher, D.L.; Keune, J.; Dirmeyer, P.; Miralles, D.G. Drought self-propagation in drylands due to land–atmosphere feedbacks. Nat. Geosci. 2022, 15, 262–268. [Google Scholar] [CrossRef] [PubMed]
- Zhou, S.; Williams, A.P.; Berg, A.M.; Cook, B.I.; Zhang, Y.; Hagemann, S.; Lorenz, R.; Seneviratne, S.I.; Gentine, P. Land–atmosphere feedbacks exacerbate concurrent soil drought and atmospheric aridity. Proc. Natl. Acad. Sci. USA 2019, 116, 18848–18853. [Google Scholar] [CrossRef] [PubMed]
- Koster, R.D.; Dirmeyer, P.A.; Guo, Z.; Bonan, G.; Chan, E.; Cox, P.; Gordon, C.; Kanae, S.; Kowalczyk, E.; Lawrence, D. Regions of strong coupling between soil moisture and precipitation. Science 2004, 305, 1138–1140. [Google Scholar] [CrossRef] [PubMed]
- Santanello, J.A., Jr.; Dirmeyer, P.A.; Ferguson, C.R.; Findell, K.L.; Tawfik, A.B.; Berg, A.; Ek, M.; Gentine, P.; Guillod, B.P.; Van Heerwaarden, C. Land–atmosphere interactions: The LoCo perspective. Bull. Am. Meteorol. Soc. 2018, 99, 1253–1272. [Google Scholar] [CrossRef]
- Seo, E.; Lee, M.-I.; Jeong, J.-H.; Koster, R.D.; Schubert, S.D.; Kim, H.-M.; Kim, D.; Kang, H.-S.; Kim, H.-K.; MacLachlan, C. Impact of soil moisture initialization on boreal summer subseasonal forecasts: Mid-latitude surface air temperature and heat wave events. Clim. Dynam. 2019, 52, 1695–1709. [Google Scholar] [CrossRef]
- Togneri, R.; dos Santos, D.F.; Camponogara, G.; Nagano, H.; Custódio, G.; Prati, R.; Fernandes, S.; Kamienski, C. Soil moisture forecast for smart irrigation: The primetime for machine learning. Expert Syst. Appl. 2022, 207, 117653. [Google Scholar] [CrossRef]
- Dubois, A.; Teytaud, F.; Verel, S. Short term soil moisture forecasts for potato crop farming: A machine learning approach. Comput. Electron. Agric. 2021, 180, 105902. [Google Scholar] [CrossRef]
- Esit, M.; Kumar, S.; Pandey, A.; Lawrence, D.M.; Rangwala, I.; Yeager, S. Seasonal to multi-year soil moisture drought forecasting. Npj Clim. Atmos. Sci. 2021, 4, 16. [Google Scholar] [CrossRef]
- Tian, S.; Van Dijk, A.I.; Tregoning, P.; Renzullo, L.J. Forecasting dryland vegetation condition months in advance through satellite data assimilation. Nat. Commun. 2019, 10, 469. [Google Scholar] [CrossRef]
- Dirmeyer, P.A.; Halder, S.; Bombardi, R. On the harvest of predictability from land states in a global forecast model. J. Geophys. Res. Atmos. 2018, 123, 13111–13127. [Google Scholar] [CrossRef]
- Ma, R.; Yuan, X. Sub-seasonal ensemble prediction of flash droughts over China. J. Hydrometeorol. 2023, 24, 897–910. [Google Scholar] [CrossRef]
- Entekhabi, D.; Njoku, E.G.; O’Neill, P.E.; Kellogg, K.H.; Crow, W.T.; Edelstein, W.N.; Entin, J.K.; Goodman, S.D.; Jackson, T.J.; Johnson, J. The soil moisture active passive (SMAP) mission. Proc. IEEE 2010, 98, 704–716. [Google Scholar] [CrossRef]
- Kerr, Y.H.; Waldteufel, P.; Wigneron, J.-P.; Delwart, S.; Cabot, F.; Boutin, J.; Escorihuela, M.-J.; Font, J.; Reul, N.; Gruhier, C. The SMOS mission: New tool for monitoring key elements ofthe global water cycle. Proc. IEEE 2010, 98, 666–687. [Google Scholar] [CrossRef]
- Chen, K.; English, S.; Bormann, N.; Zhu, J. Assessment of FY-3A and FY-3B MWHS observations. Weather Forecast. 2015, 30, 1280–1290. [Google Scholar] [CrossRef]
- Imaoka, K.; Maeda, T.; Kachi, M.; Kasahara, M.; Ito, N.; Nakagawa, K. Status of AMSR2 instrument on GCOM-W1. In Proceedings of the Earth Observing Missions and Sensors: Development, Implementation, and Characterization II, Kyoto, Japan, 9 November 2012; pp. 201–206. [Google Scholar]
- Dorigo, W.; Wagner, W.; Albergel, C.; Albrecht, F.; Balsamo, G.; Brocca, L.; Chung, D.; Ertl, M.; Forkel, M.; Gruber, A. ESA CCI Soil Moisture for improved Earth system understanding: State-of-the art and future directions. Remote Sens. Environ. 2017, 203, 185–215. [Google Scholar] [CrossRef]
- Xu, L.; Chen, N.; Zhang, X.; Moradkhani, H.; Zhang, C.; Hu, C. In-situ and triple-collocation based evaluations of eight global root zone soil moisture products. Remote Sens. Environ. 2021, 254, 112248. [Google Scholar] [CrossRef]
- Sabater, J.M.; Jarlan, L.; Calvet, J.-C.; Bouyssel, F.; De Rosnay, P. From near-surface to root-zone soil moisture using different assimilation techniques. J. Hydrometeorol. 2007, 8, 194–206. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D. The ERA5 global reanalysis. Q. J. R. Meteor. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Gelaro, R.; McCarty, W.; Suárez, M.J.; Todling, R.; Molod, A.; Takacs, L.; Randles, C.A.; Darmenov, A.; Bosilovich, M.G.; Reichle, R. The modern-era retrospective analysis for research and applications, version 2 (MERRA-2). J. Clim. 2017, 30, 5419–5454. [Google Scholar] [CrossRef]
- Rodell, M.; Houser, P.; Jambor, U.; Gottschalck, J.; Mitchell, K.; Meng, C.-J.; Arsenault, K.; Cosgrove, B.; Radakovich, J.; Bosilovich, M. The global land data assimilation system. Bull. Am. Meteorol. Soc. 2004, 85, 381–394. [Google Scholar] [CrossRef]
- Yang, S.; Zeng, J.; Fan, W.; Cui, Y. Evaluating Root-zone Soil Moisture Products from GLEAM, GLDAS, and ERA5 based on in Situ ObServations and Triple Collocation Method Over the Tibetan Plateau. J. Hydrometeorol. 2022, 23, 1861–1878. [Google Scholar] [CrossRef]
- Li, H.; Ye, A.; Zhang, Y.; Zhao, W. InterComparison and Evaluation of MultiSource Soil Moisture Products in China. Earth Space Sci. 2021, 8, e2021EA001845. [Google Scholar] [CrossRef]
- Shangguan, W.; Zhang, R.; Li, L.; Zhang, S.; Zhang, Y.; Huang, F.; Li, J.; Liu, W. Assessment of Agricultural Drought Based on Reanalysis Soil Moisture in Southern China. Land 2022, 11, 502. [Google Scholar] [CrossRef]
- Fan, L.; Xing, Z.; Lannoy, G.D.; Frappart, F.; Peng, J.; Zeng, J.; Li, X.; Yang, K.; Zhao, T.; Shi, J.; et al. Evaluation of satellite and reanalysis estimates of surface and root-zone soil moisture in croplands of Jiangsu Province, China. Remote Sens. Environ. 2022, 282, 113283. [Google Scholar] [CrossRef]
- Xu, L.; Abbaszadeh, P.; Moradkhani, H.; Chen, N.; Zhang, X. Continental drought monitoring using satellite soil moisture, data assimilation and an integrated drought index. Remote Sens. Environ. 2020, 250, 112028. [Google Scholar] [CrossRef]
- Xu, L.; Chen, N.; Chen, Z.; Zhang, C.; Yu, H. Spatiotemporal forecasting in earth system science: Methods, uncertainties, predictability and future directions. Earth-Sci. Rev. 2021, 222, 103828. [Google Scholar] [CrossRef]
- Singh, G.; Sharma, D.; Goap, A.; Sehgal, S.; Shukla, A.; Kumar, S. Machine Learning based soil moisture prediction for Internet of Things based Smart Irrigation System. In Proceedings of the 2019 5th International Conference on Signal Processing, Computing and Control (ISPCC), Solan, India, 10–12 October 2019; pp. 175–180. [Google Scholar]
- Becker, E.J.; Kirtman, B.P.; L’Heureux, M.; Muñoz, Á.G.; Pegion, K. A Decade of the North American Multimodel Ensemble (NMME): Research, Application, and Future Directions. Bull. Am. Meteorol. Soc. 2022, 103, E973–E995. [Google Scholar] [CrossRef]
- Cai, Y.; Zheng, W.; Zhang, X.; Zhangzhong, L.; Xue, X. Research on soil moisture prediction model based on deep learning. PLoS ONE 2019, 14, e0214508. [Google Scholar] [CrossRef]
- Prasad, R.; Deo, R.C.; Li, Y.; Maraseni, T. Soil moisture forecasting by a hybrid machine learning technique: ELM integrated with ensemble empirical mode decomposition. Geoderma 2018, 330, 136–161. [Google Scholar] [CrossRef]
- Li, Q.; Wang, Z.; Shangguan, W.; Li, L.; Yao, Y.; Yu, F. Improved daily SMAP satellite soil moisture prediction over China using deep learning model with transfer learning. J. Hydrol. 2021, 600, 126698. [Google Scholar] [CrossRef]
- ElSaadani, M.; Habib, E.; Abdelhameed, A.M.; Bayoumi, M. Assessment of a spatiotemporal deep learning approach for soil moisture prediction and filling the gaps in between soil moisture observations. Front. Artif. Intell. 2021, 4, 636234. [Google Scholar] [CrossRef]
- Tan, C.; Sun, F.; Kong, T.; Zhang, W.; Yang, C.; Liu, C. A survey on deep transfer learning. In Proceedings of the Artificial Neural Networks and Machine Learning–ICANN 2018: 27th International Conference on Artificial Neural Networks, Rhodes, Greece, 4–7 October 2018; pp. 270–279. [Google Scholar]
- McColl, K.A.; Alemohammad, S.H.; Akbar, R.; Konings, A.G.; Yueh, S.; Entekhabi, D. The global distribution and dynamics of surface soil moisture. Nat. Geosci. 2017, 10, 100–104. [Google Scholar] [CrossRef]
- McColl, K.A.; He, Q.; Lu, H.; Entekhabi, D. Short-term and long-term surface soil moisture memory time scales are spatially anticorrelated at global scales. J. Hydrometeorol. 2019, 20, 1165–1182. [Google Scholar] [CrossRef]
- Zhu, H.; Chen, H.; Zhou, Y.; Dong, X. Evaluation of the subseasonal forecast skill of surface soil moisture in the S2S database. Atmos. Ocean. Sci. Lett. 2019, 12, 467–474. [Google Scholar] [CrossRef]
- Gudoshava, M.; Wanzala, M.; Thompson, E.; Mwesigwa, J.; Endris, H.S.; Segele, Z.; Hirons, L.; Kipkogei, O.; Mumbua, C.; Njoka, W.; et al. Application of real time S2S forecasts over Eastern Africa in the co-production of climate services. Clim. Serv. 2022, 27, 100319. [Google Scholar] [CrossRef]
- AghaKouchak, A.; Pan, B.; Mazdiyasni, O.; Sadegh, M.; Jiwa, S.; Zhang, W.; Love, C.; Madadgar, S.; Papalexiou, S.; Davis, S. Status and prospects for drought forecasting: Opportunities in artificial intelligence and hybrid physical–statistical forecasting. Philos. Trans. R. Soc. A 2022, 380, 20210288. [Google Scholar] [CrossRef]
- Irrgang, C.; Boers, N.; Sonnewald, M.; Barnes, E.A.; Kadow, C.; Staneva, J.; Saynisch-Wagner, J. Towards neural Earth system modelling by integrating artificial intelligence in Earth system science. Nat. Mach. Intell. 2021, 3, 667–674. [Google Scholar] [CrossRef]
- Slater, L.; Arnal, L.; Boucher, M.-A.; Chang, A.Y.-Y.; Moulds, S.; Murphy, C.; Nearing, G.; Shalev, G.; Shen, C.; Speight, L. Hybrid forecasting: Using statistics and machine learning to integrate predictions from dynamical models. Hydrol. Earth Syst. Sci. Discuss. 2022, 1–35. [Google Scholar] [CrossRef]
- Han, Y.; Zhang, G.J.; Huang, X.; Wang, Y. A moist physics parameterization based on deep learning. J. Adv. Model. Earth Syst. 2020, 12, e2020MS002076. [Google Scholar] [CrossRef]
- Xu, L.; Chen, N.; Zhang, X.; Chen, Z. A data-driven multi-model ensemble for deterministic and probabilistic precipitation forecasting at seasonal scale. Clim. Dynam. 2020, 54, 3355–3374. [Google Scholar] [CrossRef]
- Vitart, F.; Ardilouze, C.; Bonet, A.; Brookshaw, A.; Chen, M.; Codorean, C.; Déqué, M.; Ferranti, L.; Fucile, E.; Fuentes, M. The subseasonal to seasonal (S2S) prediction project database. Bull. Am. Meteorol. Soc. 2017, 98, 163–173. [Google Scholar] [CrossRef]
- Kirtman, B.P.; Min, D.; Infanti, J.M.; Kinter, J.L.; Paolino, D.A.; Zhang, Q.; Van Den Dool, H.; Saha, S.; Mendez, M.P.; Becker, E. The North American multimodel ensemble: Phase-1 seasonal-to-interannual prediction; phase-2 toward developing intraseasonal prediction. Bull. Am. Meteorol. Soc. 2014, 95, 585–601. [Google Scholar] [CrossRef]
- Thober, S.; Kumar, R.; Sheffield, J.; Mai, J.; Schäfer, D.; Samaniego, L. Seasonal soil moisture drought prediction over Europe using the North American Multi-Model Ensemble (NMME). J. Hydrometeorol. 2015, 16, 2329–2344. [Google Scholar] [CrossRef]
- Yao, M.; Yuan, X. Superensemble seasonal forecasting of soil moisture by NMME. Int. J. Climatol. 2018, 38, 2565–2574. [Google Scholar] [CrossRef]
- Chevuturi, A.; Klingaman, N.P.; Guo, L.; Holloway, C.E.; Guimarães, B.S.; Coelho, C.A.S.; Kubota, P.Y.; Young, M.; Black, E.; Baker, J.C.A.; et al. Subseasonal prediction performance for South American land–atmosphere coupling in extended austral summer. Clim. Resil. Sustain. 2022, 1, e28. [Google Scholar] [CrossRef]
- Basak, A.; Schmidt, K.M.; Mengshoel, O.J. From data to interpretable models: Machine learning for soil moisture forecasting. Int. J. Data Sci. Anal. 2023, 15, 9–32. [Google Scholar] [CrossRef]
- Li, Q.; Zhu, Y.; Shangguan, W.; Wang, X.; Li, L.; Yu, F. An attention-aware LSTM model for soil moisture and soil temperature prediction. Geoderma 2022, 409, 115651. [Google Scholar] [CrossRef]
- Yu, J.; Zhang, X.; Xu, L.; Dong, J.; Zhangzhong, L. A hybrid CNN-GRU model for predicting soil moisture in maize root zone. Agric. Water Manag. 2021, 245, 106649. [Google Scholar] [CrossRef]
- Ahmed, A.M.; Deo, R.C.; Raj, N.; Ghahramani, A.; Feng, Q.; Yin, Z.; Yang, L. Deep learning forecasts of soil moisture: Convolutional neural network and gated recurrent unit models coupled with satellite-derived MODIS, observations and synoptic-scale climate index data. Remote Sens. 2021, 13, 554. [Google Scholar] [CrossRef]
- Ahmad, S.; Kalra, A.; Stephen, H. Estimating soil moisture using remote sensing data: A machine learning approach. Adv. Water Resour. 2010, 33, 69–80. [Google Scholar] [CrossRef]
- Jiang, W.; Wang, L.; Feng, L.; Zhang, M.; Yao, R. Drought characteristics and its impact on changes in surface vegetation from 1981 to 2015 in the Yangtze River Basin, China. Int. J. Climatol. 2020, 40, 3380–3397. [Google Scholar] [CrossRef]
- Zhang, D.; Zhang, Q.; Werner, A.D.; Liu, X. GRACE-based hydrological drought evaluation of the Yangtze River Basin, China. J. Hydrometeorol. 2016, 17, 811–828. [Google Scholar] [CrossRef]
- Xu, L.; Chen, N.; Zhang, X. Global drought trends under 1.5 and 2 C warming. Int. J. Climatol. 2019, 39, 2375–2385. [Google Scholar] [CrossRef]
- Spinoni, J.; Vogt, J.V.; Naumann, G.; Barbosa, P.; Dosio, A. Will drought events become more frequent and severe in Europe? Int. J. Climatol. 2018, 38, 1718–1736. [Google Scholar] [CrossRef]
- Naumann, G.; Cammalleri, C.; Mentaschi, L.; Feyen, L. Increased economic drought impacts in Europe with anthropogenic warming. Nat. Clim. Chang. 2021, 11, 485–491. [Google Scholar] [CrossRef]
- Dorigo, W.; Wagner, W.; Hohensinn, R.; Hahn, S.; Paulik, C.; Xaver, A.; Gruber, A.; Drusch, M.; Mecklenburg, S.; van Oevelen, P. The International Soil Moisture Network: A data hosting facility for global in situ soil moisture measurements. Hydrol. Earth Syst. Sci. 2011, 15, 1675–1698. [Google Scholar] [CrossRef]
- Dee, D.P.; Uppala, S.M.; Simmons, A.J.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.; Balsamo, G.; Bauer, P.; et al. The ERA-Interim reanalysis: Configuration and performance of the data assimilation system. Q. J. R. Meteor. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- Balsamo, G.; Boussetta, S.; Dutra, E.; Beljaars, A.; Viterbo, P.; Van den Hurk, B. Evolution of land surface processes in the IFS. ECMWF Newsl. 2011, 127, 78. [Google Scholar]
- Dataset: Resource and Environmental Science Data Registration and Publication System, Beijing, China. Available online: https://www.resdc.cn/DOI/doi.aspx?DOIid=54 (accessed on 6 December 2022).
- Dataset: Copernicus Climate Change Service. Available online: https://cds.climate.copernicus.eu/cdsapp#!/dataset/10.24381/cds.006f2c9a?tab=overview (accessed on 6 December 2022).
- Hong, Z.; Kalbarczyk, Z.; Iyer, R.K. A data-driven approach to soil moisture collection and prediction. In Proceedings of the 2016 IEEE International Conference on Smart Computing (SMARTCOMP), St. Louis, MO, USA, 18–20 May 2016; pp. 1–6. [Google Scholar]
- Prasad, R.; Deo, R.C.; Li, Y.; Maraseni, T. Weekly soil moisture forecasting with multivariate sequential, ensemble empirical mode decomposition and Boruta-random forest hybridizer algorithm approach. Catena 2019, 177, 149–166. [Google Scholar] [CrossRef]
- Vapnik, V. The Nature of Statistical Learning Theory; Springer Science & Business Media: New York, NY, USA, 1999. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Liaw, A.; Wiener, M. Classification and regression by randomForest. R News 2002, 2, 18–22. [Google Scholar]
- Oshiro, T.M.; Perez, P.S.; Baranauskas, J.A. How many trees in a random forest? In Proceedings of the Machine Learning and Data Mining in Pattern Recognition: 8th International Conference, MLDM 2012, Berlin, Germany, 13–20 July 2012; pp. 154–168. [Google Scholar]
- Adnan, M.N.; Islam, M.Z. Optimizing the number of trees in a decision forest to discover a subforest with high ensemble accuracy using a genetic algorithm. Knowl.-Based Syst. 2016, 110, 86–97. [Google Scholar] [CrossRef]
- Shi, X.; Chen, Z.; Wang, H.; Yeung, D.-Y.; Wong, W.-k.; Woo, W.-c. Convolutional LSTM network: A machine learning approach for precipitation nowcasting. Adv. Neural. Inf. Process. Syst. 2015, 28, 802–810. [Google Scholar]
- Robertson, D.E.; Wang, Q. A Bayesian approach to predictor selection for seasonal streamflow forecasting. J. Hydrometeorol. 2012, 13, 155–171. [Google Scholar] [CrossRef]
- Zhang, R.; Chen, Z.-Y.; Xu, L.-J.; Ou, C.-Q. Meteorological drought forecasting based on a statistical model with machine learning techniques in Shaanxi province, China. Sci. Total Environ. 2019, 665, 338–346. [Google Scholar] [CrossRef]
- Liu, T.; Schmitt, R.; Li, L. Global search for autumn-lead sea surface salinity predictors of winter precipitation in southwestern United States. Geophys. Res. Lett. 2018, 45, 8445–8454. [Google Scholar] [CrossRef]
- Reichstein, M.; Camps-Valls, G.; Stevens, B.; Jung, M.; Denzler, J.; Carvalhais, N. Deep learning and process understanding for data-driven Earth system science. Nature 2019, 566, 195–204. [Google Scholar] [CrossRef]
- Gruber, A.; De Lannoy, G.; Albergel, C.; Al-Yaari, A.; Brocca, L.; Calvet, J.-C.; Colliander, A.; Cosh, M.; Crow, W.; Dorigo, W. Validation practices for satellite soil moisture retrievals: What are (the) errors? Remote Sens. Environ. 2020, 244, 111806. [Google Scholar] [CrossRef]






Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, L.; Yu, H.; Chen, Z.; Du, W.; Chen, N.; Huang, M. Hybrid Deep Learning and S2S Model for Improved Sub-Seasonal Surface and Root-Zone Soil Moisture Forecasting. Remote Sens. 2023, 15, 3410. https://doi.org/10.3390/rs15133410
Xu L, Yu H, Chen Z, Du W, Chen N, Huang M. Hybrid Deep Learning and S2S Model for Improved Sub-Seasonal Surface and Root-Zone Soil Moisture Forecasting. Remote Sensing. 2023; 15(13):3410. https://doi.org/10.3390/rs15133410
Chicago/Turabian StyleXu, Lei, Hongchu Yu, Zeqiang Chen, Wenying Du, Nengcheng Chen, and Min Huang. 2023. "Hybrid Deep Learning and S2S Model for Improved Sub-Seasonal Surface and Root-Zone Soil Moisture Forecasting" Remote Sensing 15, no. 13: 3410. https://doi.org/10.3390/rs15133410
APA StyleXu, L., Yu, H., Chen, Z., Du, W., Chen, N., & Huang, M. (2023). Hybrid Deep Learning and S2S Model for Improved Sub-Seasonal Surface and Root-Zone Soil Moisture Forecasting. Remote Sensing, 15(13), 3410. https://doi.org/10.3390/rs15133410










