Cross-Domain Multi-Prototypes with Contradictory Structure Learning for Semi-Supervised Domain Adaptation Segmentation of Remote Sensing Images
Abstract
1. Introduction
- (1)
- A novel SSDA method for RSI semantic segmentation is proposed in this paper. To our knowledge, this is the first exploration of RSI SSDA, opening a new avenue for future work;
- (2)
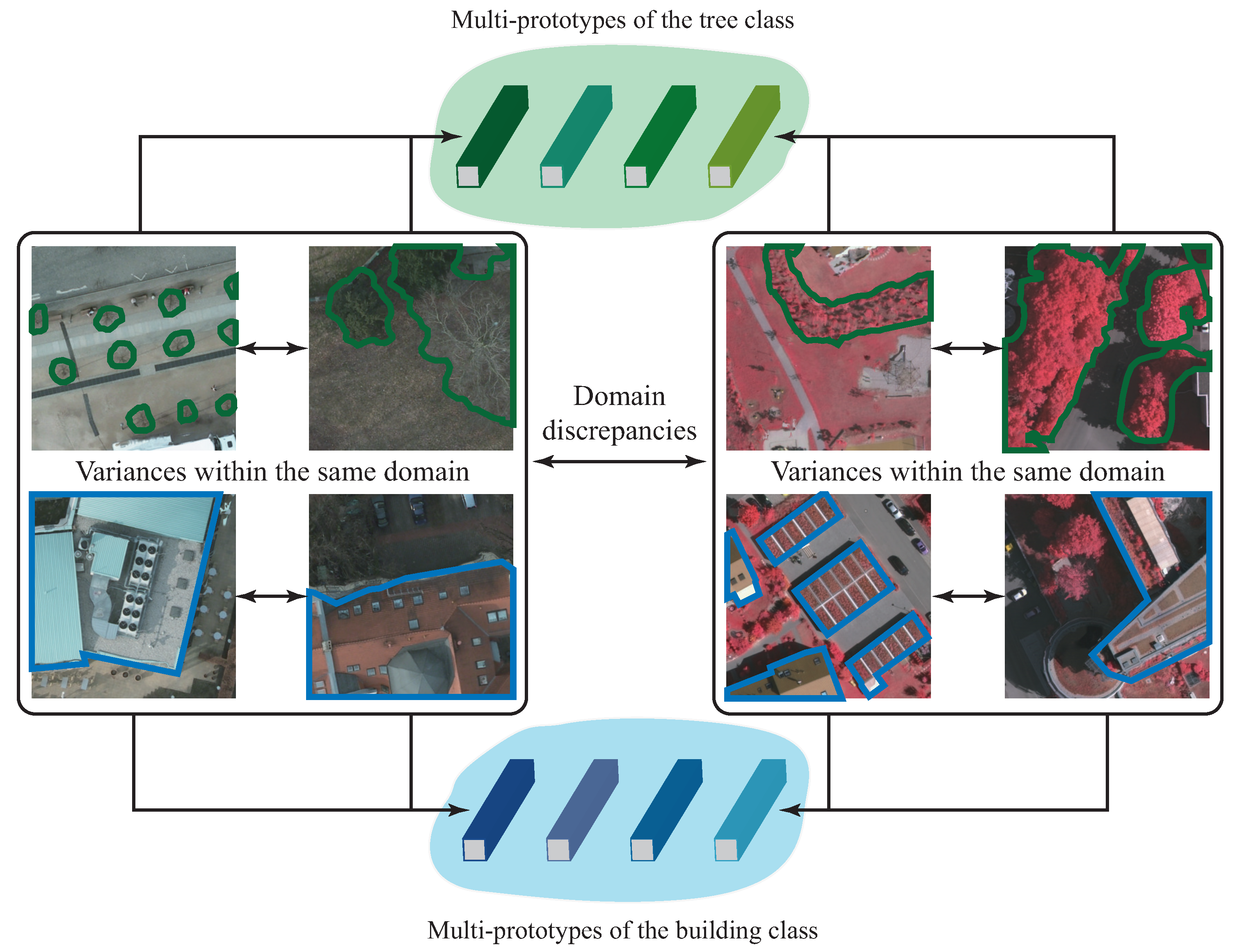
- A cross-domain multi-prototype constraint for RSI SSDA is proposed. On the one hand, the multiple sets of prototypes can better describe intra-class variances and inter-class discrepancies; on the other hand, the cooperation of source and target samples can effectively promote the utilization of the feature information in different RSI domains;
- (3)
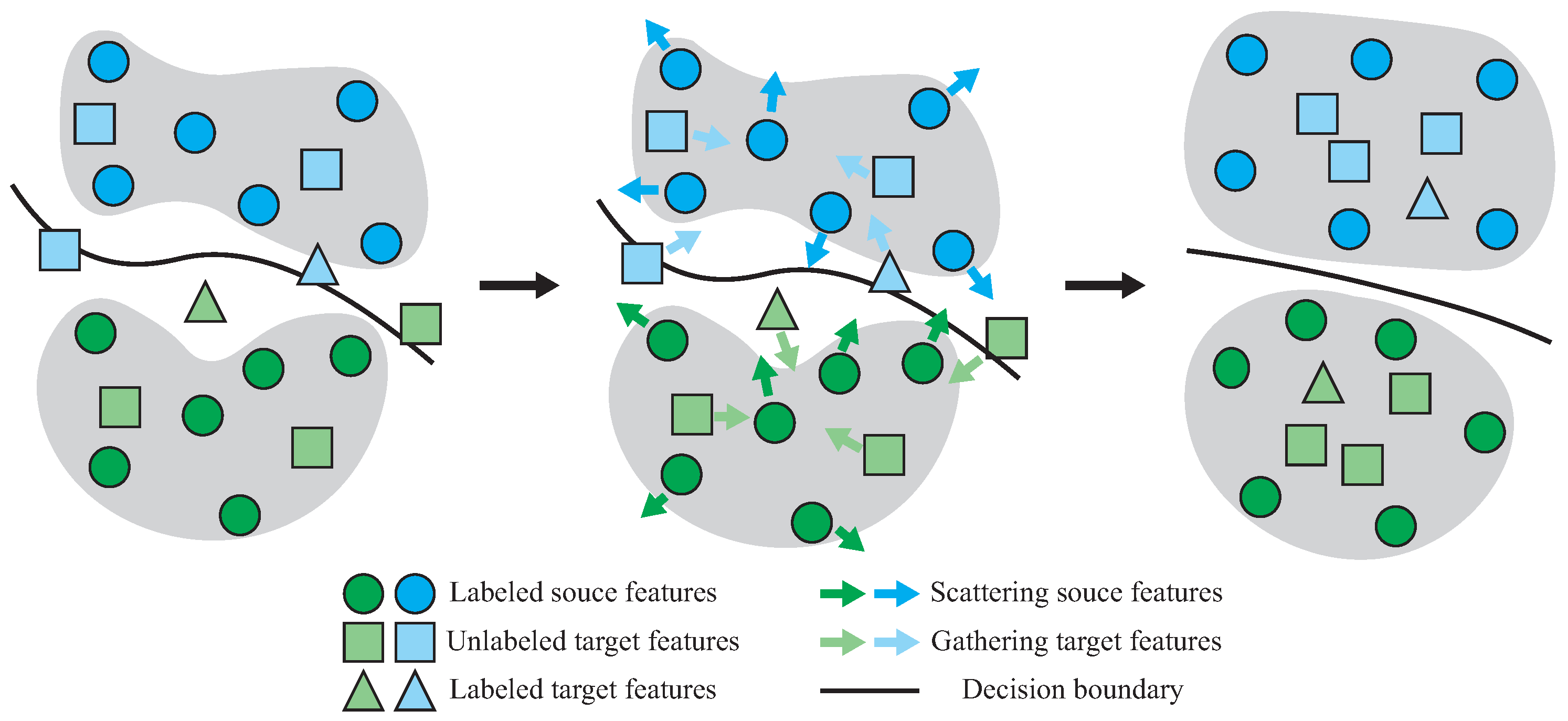
- A contradictory structure learning method is designed. Through gathering target features and scattering source features simultaneously, a better domain alignment with an enveloping form can be achieved;
- (4)
- Extensive experiments were carried out, and their statistics demonstrate that our method can, not only effectively improve the performance of SSDA segmentation of RSIs, but also significantly narrow the gap with supervised counterparts when only a few labeled target samples are available.
2. Related Work
2.1. RSI Semantic Segmentation
2.2. Semi-Supervised Domain Adaptation
3. Methodology
3.1. Problem Setting
3.2. Workflow
3.3. Cross-Domain Multi-Prototype Constraint
3.3.1. Multi-Prototype-Based Segmentation
3.3.2. Online Clustering and Momentum Updating
3.3.3. Contrastive Learning and Distance Optimization
3.4. Contradictory Structure Learning
3.5. Optimization Objective
| Algorithm 1 Proposed SSDA method for RSI segmentation |
|
4. Experimental Results
4.1. Dataset Description
4.2. Experimental Settings
4.3. Quantitative Results and Comparison
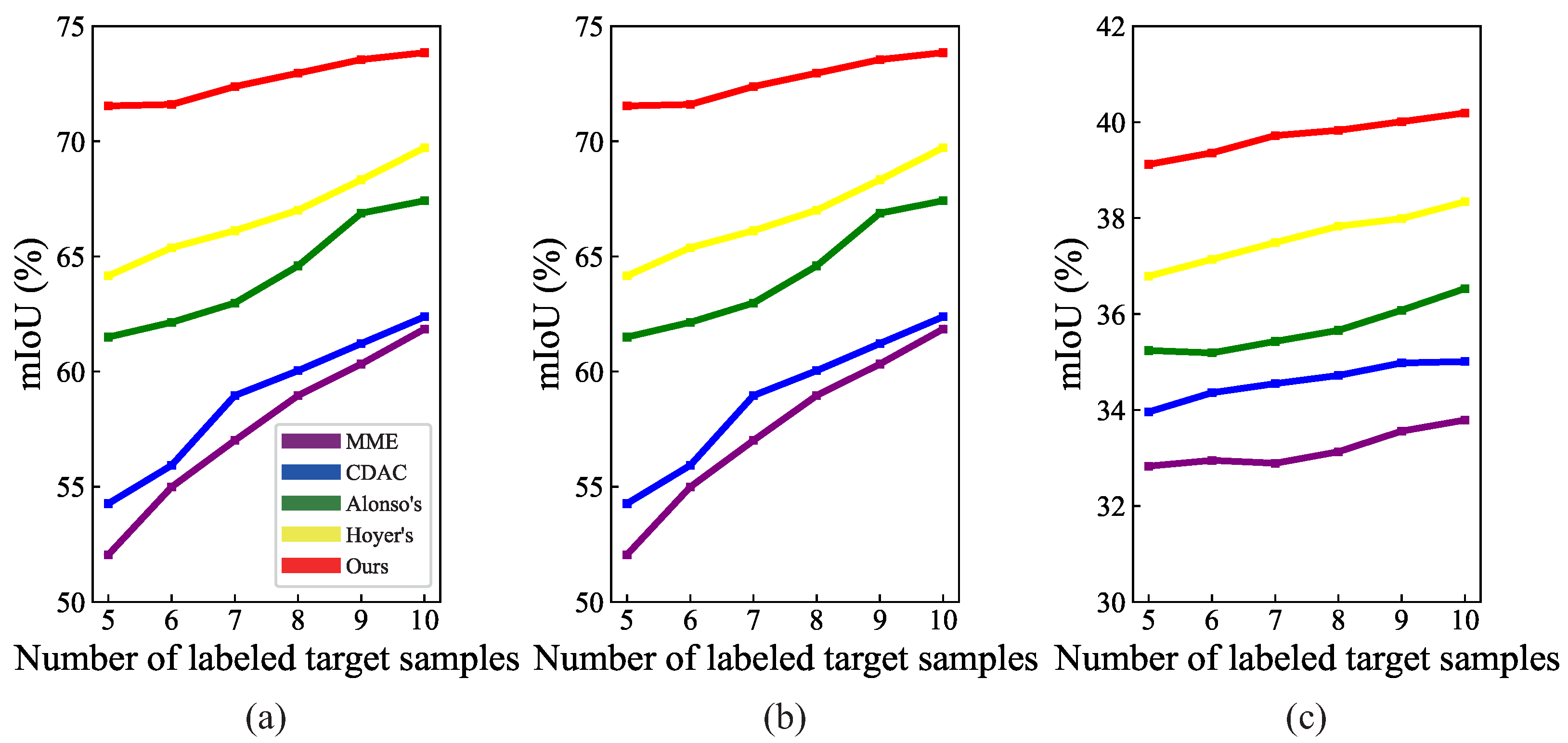
4.3.1. Comparison with SSDA Methods
- (1)
- The improvement in the segmentation performance for the target RSIs brought by the three extension SSDA methods was limited compared with the corresponding UDA methods. For example, the mIoU of Zheng’s (SSDA) in the three tasks increased by only 0.48%, 3.03%, and 0.90%, respectively. This indicates that simply extending the UDA methods to SSDA methods cannot obtain ideal results in SSDA segmentation of RSIs;
- (2)
- The two methods MME and CDAC could improve the segmentation performance for the target RSIs to a certain extent, and the mIoU increased by about 3.9%, 1.5%, and 0.3% on average, respectively, in the three tasks, compared with the three extension SSDA methods. In addition, the adaptive clustering strategy endowed CDAC with a better generalization ability, so its segmentation results were better than those of MME. However, both methods were originally designed for SSDA classification of natural images and are not suitable for dense prediction, so there is still a lot of room for performance improvement;
- (3)
- The two advanced SSDA methods for semantic segmentation, Alonso’s and Hoyer’s, could effectively improve the segmentation results by a large margin. Compared with CDAC, the mIoU of Alonso’s increased by 7.23%, 18.47%, and 1.28% in the three tasks, respectively, while the mIoU of Hoyer’s increased by 9.89%, 20.88%, and 2.83%, respectively. The network structures designed for semantic segmentation and advanced strategies tailored to SSDA enabled the two methods to better adapt to and generalize for the target RSIs;
- (4)
- The proposed method achieved the best segmentation results among all the SSDA methods, both in terms of overall metrics and individual classes. In the first task, the mIoU and PA of the proposed method were 7.38% and 4.41%,respectively, higher than those of the second-place method. In the second task, the mIoU and PA of the proposed method were 4.80% and 2.48%,respectively, higher than those of the second-place method. In the third task, the mIoU and PA of the proposed method were 2.33% and 1.49%, respectively, higher than those of the second-place method. Such improvements benefited from the ability of the proposed method to fully extract, fuse, and align the feature information in the source and target samples. Specifically, the representation abilities of multi-prototypes for inter- and intra-class relations, and the better domain alignment with an enveloping form, enabled the proposed method to better distinguish the classes with high inter-class similarity. For example, in the second task, the proposed method improved the IoU of the classes low vegetation and tree by 2.36% and 3.28%, respectively, compared with the second-place method. Meanwhile, the segmentation performance for challenging classes that were difficult to identify using the other methods was also greatly improved. For example, the proposed method increased the IoU of the car class by 11.13% and 14.19%, respectively, in the first two tasks, and increased the IoU of the agriculture class by 2.61% in the third task, over the second-place method.
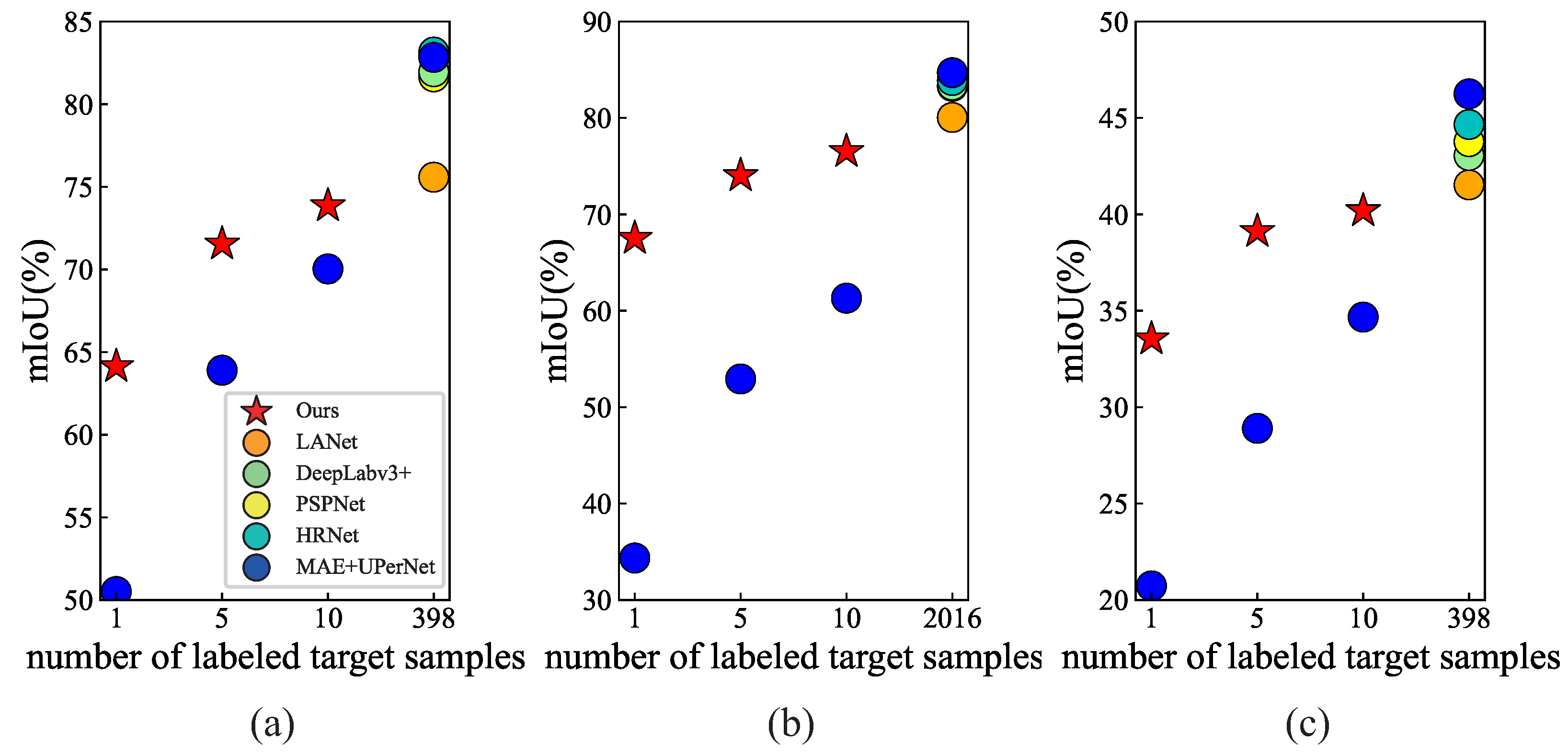
4.3.2. Comparison with UDA and SL Methods
- (1)
- Obviously, the segmentation performance of the UDA methods was far behind that of the SL methods on the target RSIs. In the first task, the highest mIoU obtained by the UDA method was 49.11%, which was at least 26.47% lower than that of the supervised counterparts. In the second task, this value rose to 34.06%. Such a large gap can be attributed to the lack of supervision information for the target RSIs, and this also indicates that only utilizing unlabeled target samples for RSI domain adaptation cannot achieve satisfactory segmentation results on target RSIs. The results in Table 5 reflect the same conclusions;
- (2)
- Compared with the UDA methods, the proposed method presented a significant improvement in segmentation results for target RSIs. In the three tasks, the mIoU of the proposed method was 22.43%, 28.02%, and 6.52% higher than that of the UDA methods with the best performance, respectively. Obviously, the proposed method significantly reduced the gap with its supervised counterparts. For example, in the PD→VH task, the proposed method narrowed the gap with LANet to 4.04% on the mIoU, while the gap on the PA was only 1.96%. It should be noted that, in the statistics of Table 3 and Table 4, the SL methods required a large number of labeled target samples, while the proposed method only utilized five labeled target samples for domain adaptation. Considering the segmentation performance and the required labeled samples, it can be seen that the proposed method was sample-efficient and cost-effective.
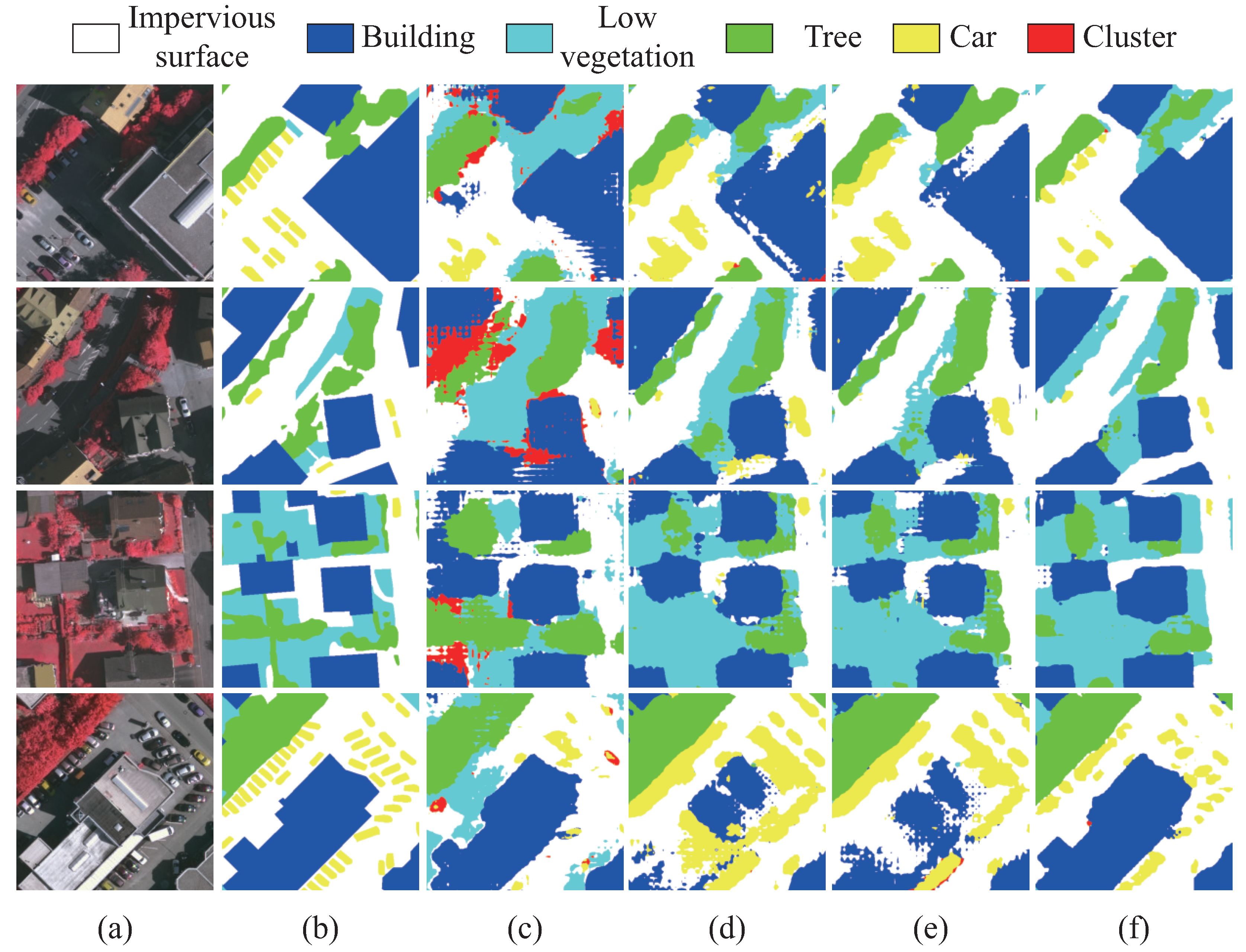
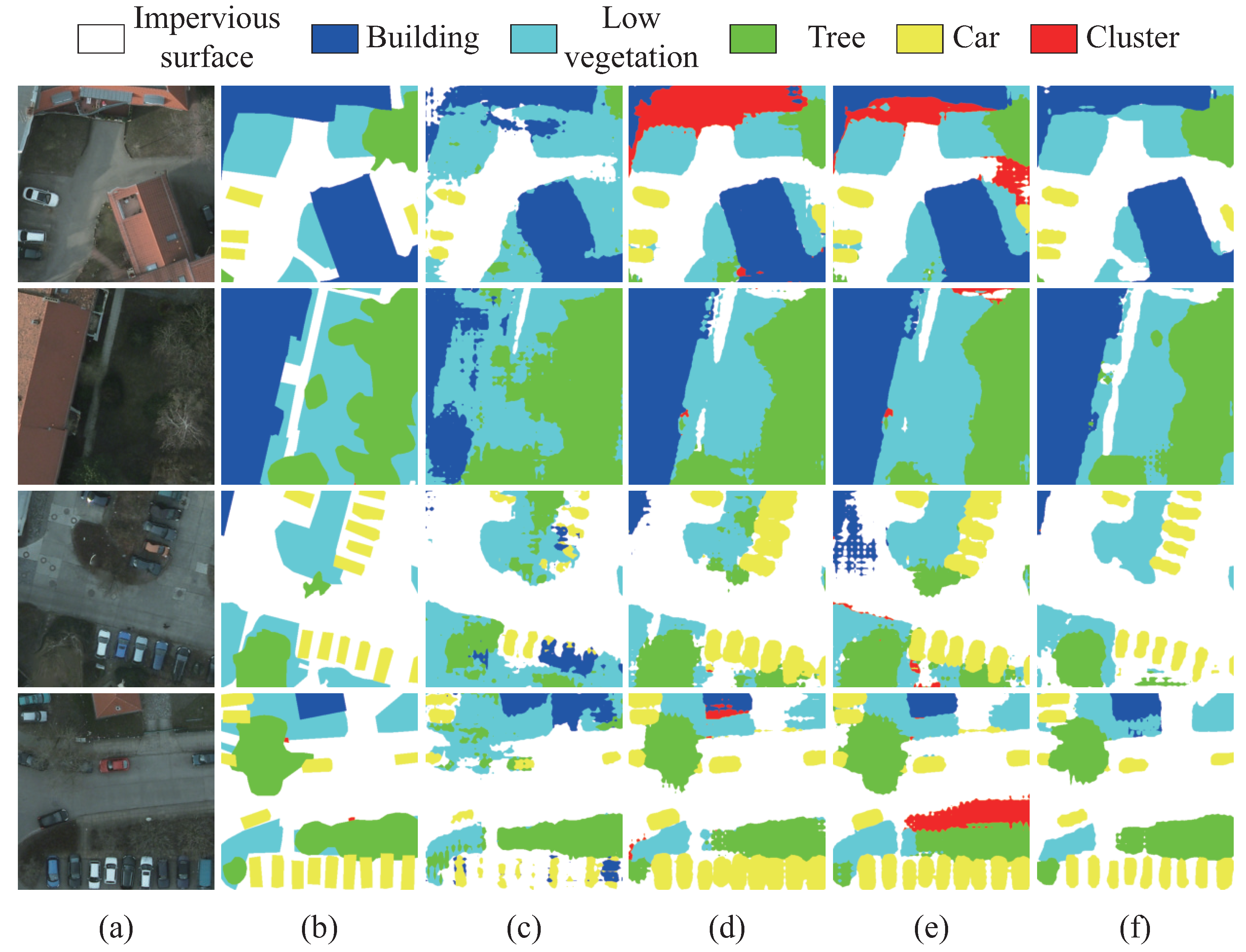
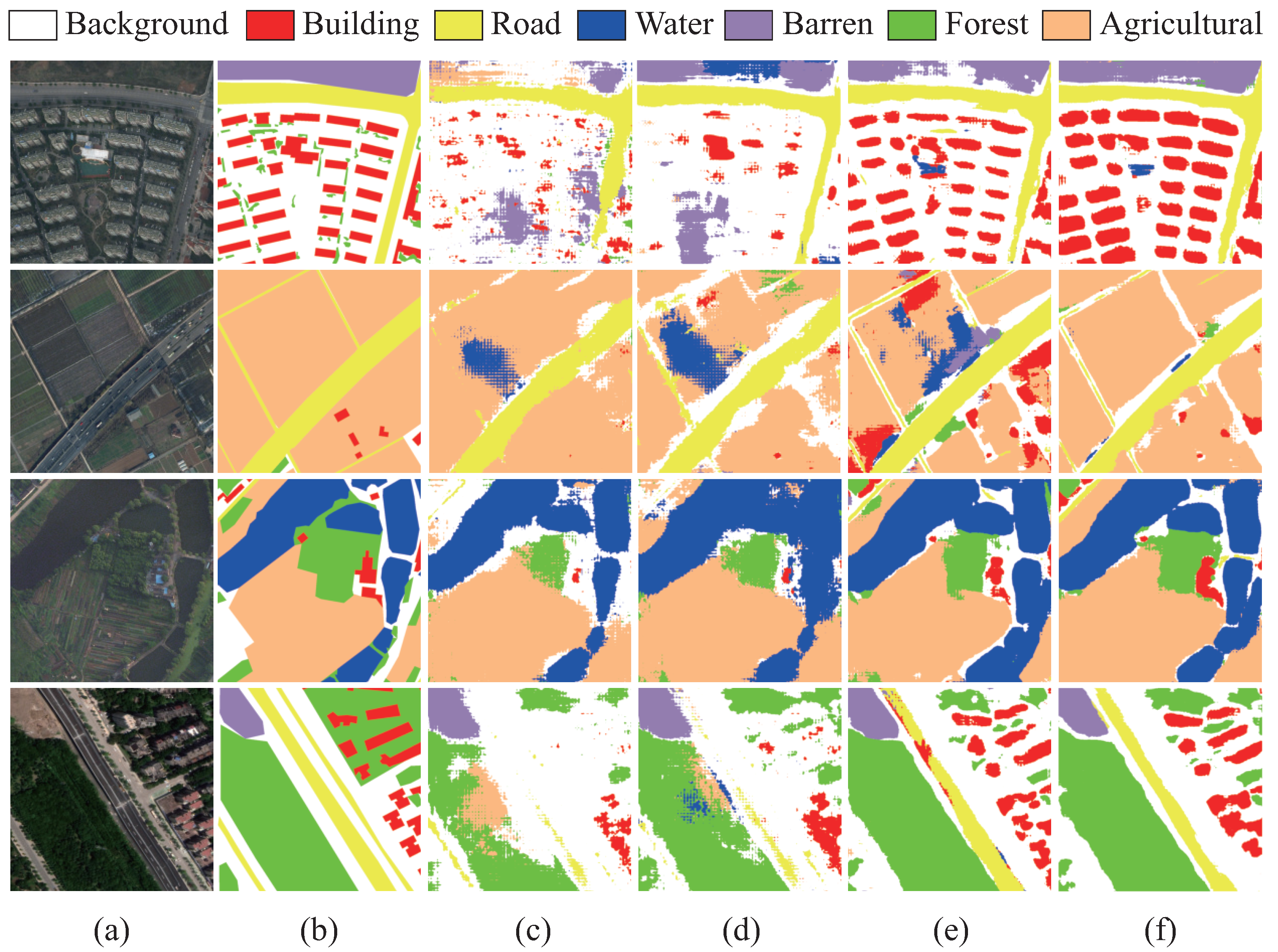
4.4. Qualitative Results and Comparison
5. Analysis and Discussion
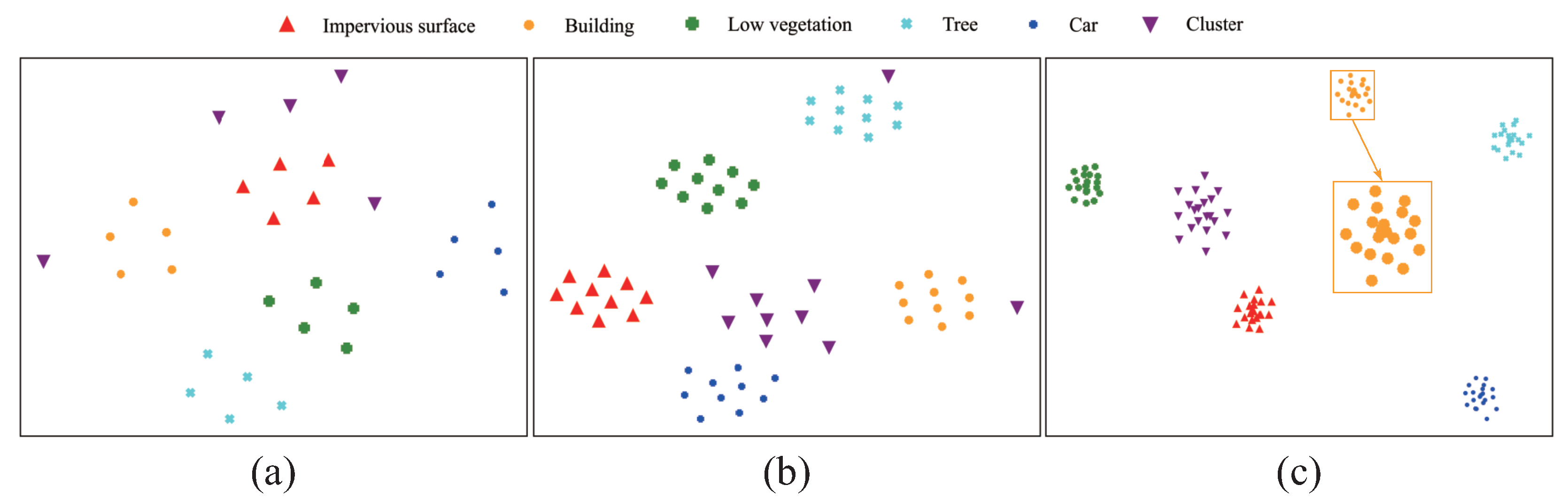
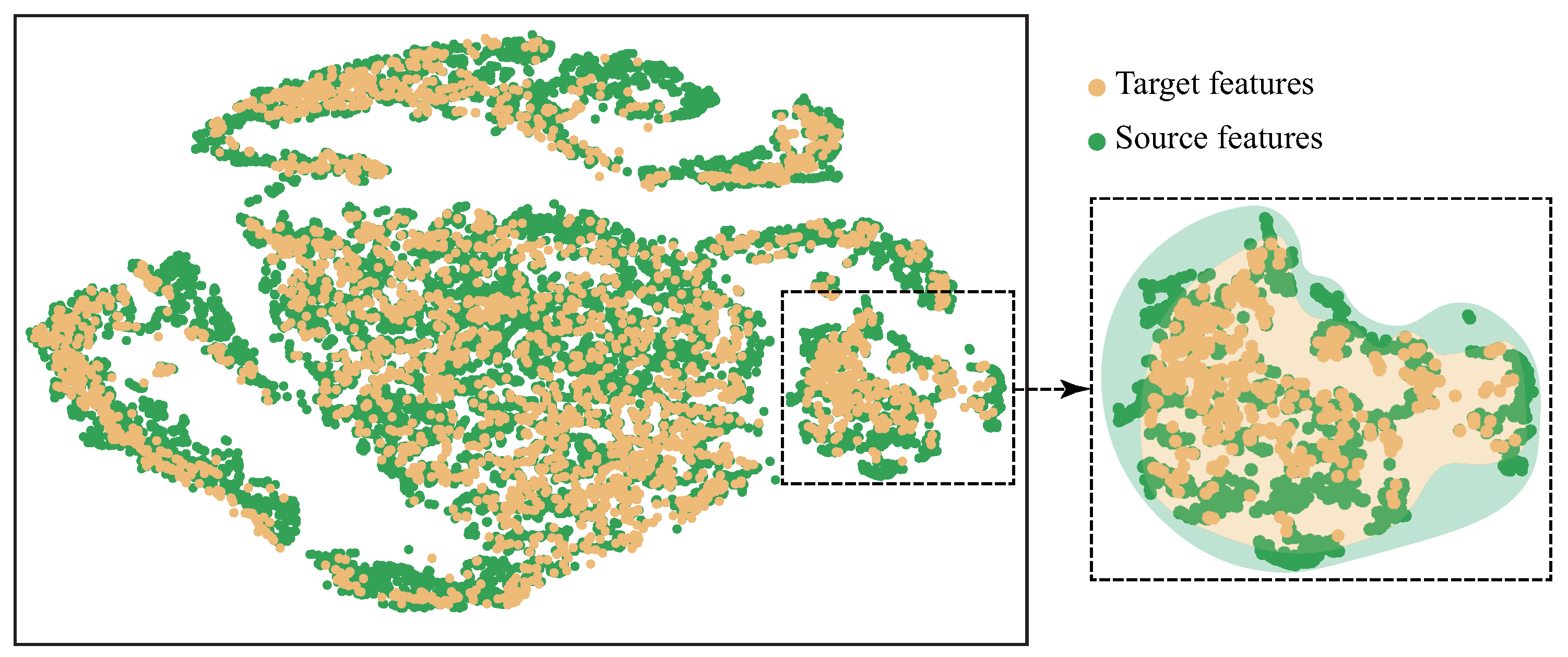
5.1. Visual Analysis
5.2. Ablation Studies
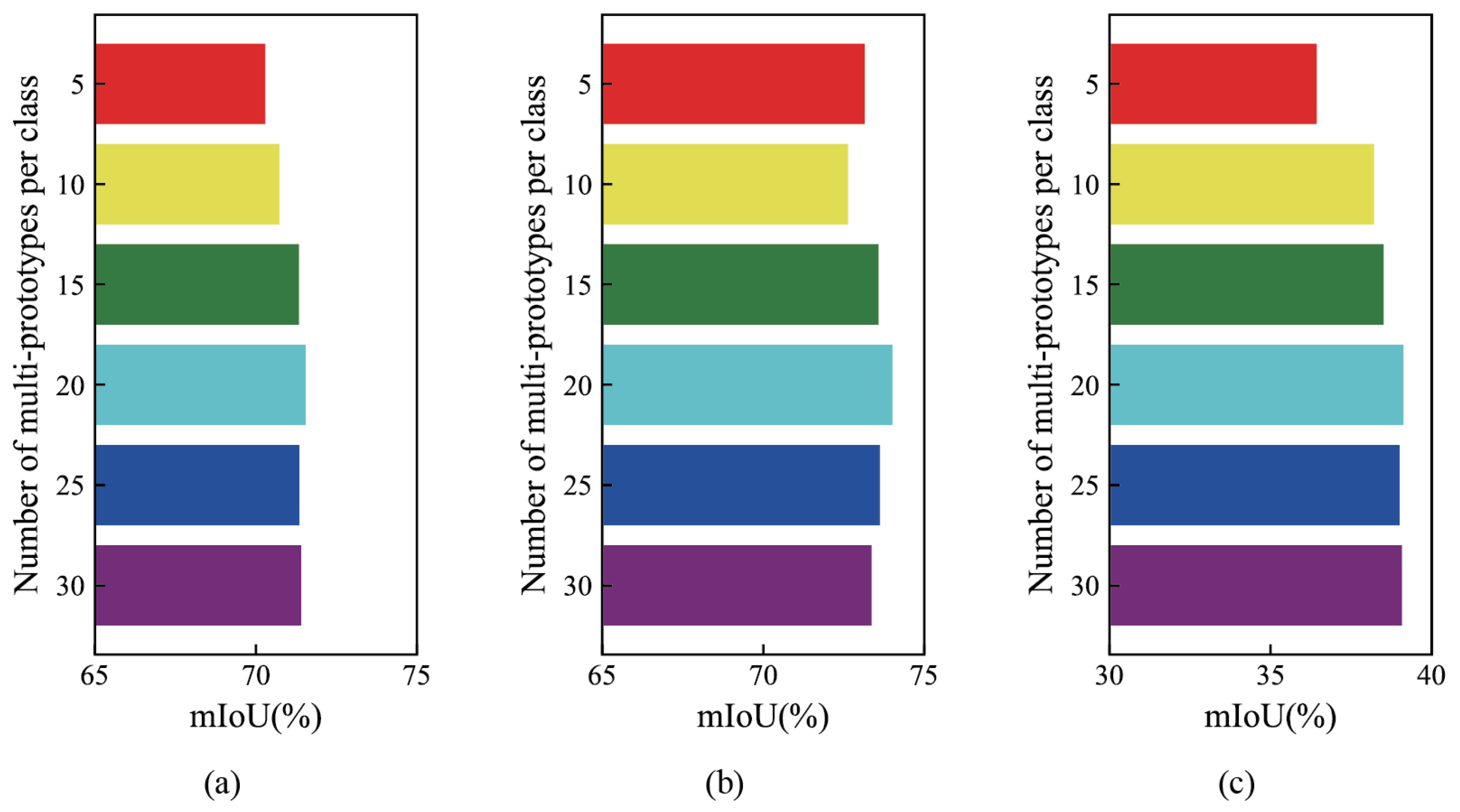
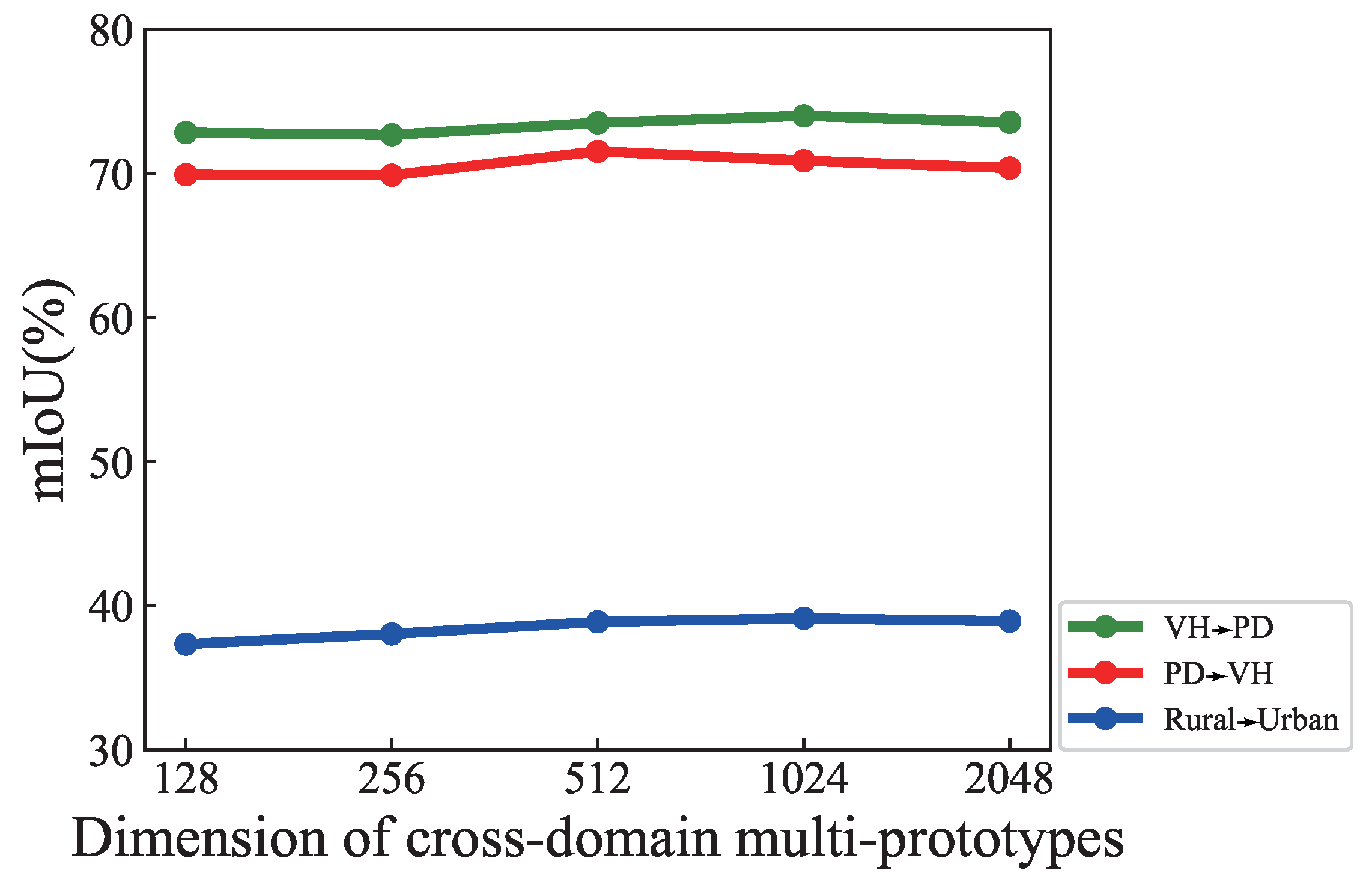
5.3. Hyperparameter Analysis
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Long, J.; Shelhamer, E.; Darrell, T. Fully convolutional networks for semantic segmentation. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 3431–3440. [Google Scholar] [CrossRef]
- Zhao, H.S.; Shi, J.P.; Qi, X.J.; Wang, X.G.; Jia, J.Y. Pyramid Scene Parsing Network. arXiv 2017, arXiv:1612.01105. [Google Scholar] [CrossRef]
- Xiao, T.T.; Liu, Y.C.; Zhou, B.L.; Jiang, Y.N.; Sun, J. Unified Perceptual Parsing for Scene Understanding. arXiv 2018, arXiv:1807.10221. [Google Scholar] [CrossRef]
- Ma, L.; Liu, Y.; Zhang, X.; Ye, Y.; Yin, G.; Johnson, B.A. Deep learning in remote sensing applications: A meta-analysis and review. ISPRS J. Photogramm. Remote Sens. 2019, 152, 166–177. [Google Scholar] [CrossRef]
- Gao, K.; Liu, B.; Yu, X.; Yu, A. Unsupervised Meta Learning With Multiview Constraints for Hyperspectral Image Small Sample set Classification. IEEE Trans. Image Process. 2022, 31, 3449–3462. [Google Scholar] [CrossRef] [PubMed]
- Kotaridis, I.; Lazaridou, M. Remote sensing image segmentation advances: A meta-analysis. ISPRS J. Photogramm. Remote Sens. 2021, 173, 309–322. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, L. Artificial Intelligence for Remote Sensing Data Analysis: A review of challenges and opportunities. IEEE Geosci. Remote Sens. Mag. 2022, 10, 270–294. [Google Scholar] [CrossRef]
- Luo, M.; Ji, S. Cross-spatiotemporal land-cover classification from VHR remote sensing images with deep learning based domain adaptation. ISPRS J. Photogramm. Remote Sens. 2022, 191, 105–128. [Google Scholar] [CrossRef]
- Zhao, S.; Yue, X.; Zhang, S.; Li, B.; Zhao, H.; Wu, B.; Krishna, R.; Gonzalez, J.E.; Sangiovanni-Vincentelli, A.L.; Seshia, S.A.; et al. A Review of Single-Source Deep Unsupervised Visual Domain Adaptation. IEEE Trans. Neural Netw. Learn. Syst. 2022, 33, 473–493. [Google Scholar] [CrossRef]
- Sun, X.; Wang, P.; Lu, W.; Zhu, Z.; Lu, X.; He, Q.; Li, J.; Rong, X.; Yang, Z.; Chang, H.; et al. RingMo: A Remote Sensing Foundation Model with Masked Image Modeling. IEEE Trans. Geosci. Remote Sens. 2022, 1. [Google Scholar] [CrossRef]
- Xu, Q.; Yuan, X.; Ouyang, C. Class-Aware Domain Adaptation for Semantic Segmentation of Remote Sensing Images. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–17. [Google Scholar] [CrossRef]
- Wang, J.; Zheng, Z.; Ma, A.; Lu, X.; Zhong, Y. LoveDA: A Remote Sensing Land-Cover Dataset for Domain Adaptive Semantic Segmentation. CoRR 2021, abs/2110.08733. Available online: http://xxx.lanl.gov/abs/2110.08733 (accessed on 1 July 2020.).
- Zheng, A.; Wang, M.; Li, C.; Tang, J.; Luo, B. Entropy Guided Adversarial Domain Adaptation for Aerial Image Semantic Segmentation. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–14. [Google Scholar] [CrossRef]
- Saito, K.; Kim, D.; Sclaroff, S.; Darrell, T.; Saenko, K. Semi-supervised Domain Adaptation via Minimax Entropy. arXiv 2019, arXiv:1904.06487. [Google Scholar] [CrossRef]
- Li, K.; Liu, C.; Zhao, H.D.; Zhang, Y.L.; Fu, Y.; IEEE. ECACL: A Holistic Framework for Semi-Supervised Domain Adaptation. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, QC, Canada, 10–17 October 2021. [Google Scholar] [CrossRef]
- Yan, Z.; Wu, Y.; Li, G.; Qin, Y.; Han, X.; Cui, S. Multi-level Consistency Learning for Semi-supervised Domain Adaptation. In Proceedings of the IJCAI, Vienna, Austria, 25 July 2022; pp. 1530–1536. [Google Scholar]
- Wang, Z.H.; Wei, Y.C.; Feris, R.; Xiong, J.J.; Hwu, W.M.; Huang, T.S.; Shi, H.H.; SOC, I.C. Alleviating Semantic-level Shift: A Semi-supervised Domain Adaptation Method for Semantic Segmentation. arXiv 2020, arXiv:2004.00794. [Google Scholar] [CrossRef]
- Alonso, I.; Sabater, A.; Ferstl, D.; Montesano, L.; Murillo, A.C.; IEEE. Semi-Supervised Semantic Segmentation with Pixel-Level Contrastive Learning from a Class-wise Memory Bank. arXiv 2021, arXiv:2104.13415. [Google Scholar] [CrossRef]
- Berthelot, D.; Roelofs, R.; Sohn, K.; Carlini, N.; Kurakin, A. AdaMatch: A Unified Approach to Semi-Supervised Learning and Domain Adaptation. In Proceedings of the International Conference on Learning Representations, Virtual Event, 25–29 April 2022. [Google Scholar]
- Jiang, X.; Zhou, N.; Li, X. Few-Shot Segmentation of Remote Sensing Images Using Deep Metric Learning. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Osco, L.P.; Marcato Junior, J.; Marques Ramos, A.P.; de Castro Jorge, L.A.; Fatholahi, S.N.; de Andrade Silva, J.; Matsubara, E.T.; Pistori, H.; Gonçalves, W.N.; Li, J. A review on deep learning in UAV remote sensing. Int. J. Appl. Earth Obs. Geoinf. 2021, 102, 102456. [Google Scholar] [CrossRef]
- Gao, K.; Liu, B.; Yu, X.; Qin, J.; Zhang, P.; Tan, X. Deep Relation Network for Hyperspectral Image Few-Shot Classification. Remote Sens. 2020, 12, 923. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. arXiv 2015, arXiv:1505.04597. [Google Scholar] [CrossRef]
- Diakogiannis, F.I.; Waldner, F.; Caccetta, P.; Wu, C. ResUNet-a: A deep learning framework for semantic segmentation of remotely sensed data. ISPRS J. Photogramm. Remote Sens. 2020, 162, 94–114. [Google Scholar] [CrossRef]
- Liu, Y.; Fan, B.; Wang, L.; Bai, J.; Xiang, S.; Pan, C. Semantic labeling in very high resolution images via a self-cascaded convolutional neural network. ISPRS J. Photogramm. Remote Sens. 2018, 145, 78–95. [Google Scholar] [CrossRef]
- Ding, L.; Tang, H.; Bruzzone, L. LANet: Local Attention Embedding to Improve the Semantic Segmentation of Remote Sensing Images. IEEE Trans. Geosci. Remote Sens. 2021, 59, 426–435. [Google Scholar] [CrossRef]
- Li, R.; Zheng, S.; Zhang, C.; Duan, C.; Su, J.; Wang, L.; Atkinson, P.M. Multiattention Network for Semantic Segmentation of Fine-Resolution Remote Sensing Images. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–13. [Google Scholar] [CrossRef]
- He, Q.; Sun, X.; Diao, W.; Yan, Z.; Yin, D.; Fu, K. Transformer-induced graph reasoning for multimodal semantic segmentation in remote sensing. ISPRS J. Photogramm. Remote Sens. 2022, 193, 90–103. [Google Scholar] [CrossRef]
- He, X.; Zhou, Y.; Zhao, J.; Zhang, D.; Yao, R.; Xue, Y. Swin Transformer Embedding UNet for Remote Sensing Image Semantic Segmentation. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–15. [Google Scholar] [CrossRef]
- Wang, L.; Li, R.; Zhang, C.; Fang, S.; Duan, C.; Meng, X.; Atkinson, P.M. UNetFormer: A UNet-like transformer for efficient semantic segmentation of remote sensing urban scene imagery. ISPRS J. Photogramm. Remote Sens. 2022, 190, 196–214. [Google Scholar] [CrossRef]
- Chen, Z.; Shang, Y.; Python, A.; Cai, Y.; Yin, J. DB-BlendMask: Decomposed Attention and Balanced BlendMask for Instance Segmentation of High-Resolution Remote Sensing Images. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–15. [Google Scholar] [CrossRef]
- Zhang, T.; Zhang, X.; Zhu, P.; Tang, X.; Li, C.; Jiao, L.; Zhou, H. Semantic Attention and Scale Complementary Network for Instance Segmentation in Remote Sensing Images. IEEE Trans. Cybern. 2022, 52, 10999–11013. [Google Scholar] [CrossRef]
- Ma, A.; Wang, J.; Zhong, Y.; Zheng, Z. FactSeg: Foreground Activation-Driven Small Object Semantic Segmentation in Large-Scale Remote Sensing Imagery. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–16. [Google Scholar] [CrossRef]
- Chen, X.; Pan, S.; Chong, Y. Unsupervised Domain Adaptation for Remote Sensing Image Semantic Segmentation Using Region and Category Adaptive Domain Discriminator. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–13. [Google Scholar] [CrossRef]
- Chen, J.; Zhu, J.; Guo, Y.; Sun, G.; Zhang, Y.; Deng, M. Unsupervised Domain Adaptation for Semantic Segmentation of High-Resolution Remote Sensing Imagery Driven by Category-Certainty Attention. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–15. [Google Scholar] [CrossRef]
- Chen, H.; Zhang, H.; Yang, G.; Li, S.; Zhang, L. A Mutual Information Domain Adaptation Network for Remotely Sensed Semantic Segmentation. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–16. [Google Scholar] [CrossRef]
- Gui, J.; Sun, Z.; Wen, Y.; Tao, D.; Ye, J. A Review on Generative Adversarial Networks: Algorithms, Theory, and Applications. IEEE Trans. Knowl. Data Eng. 2021, 35, 3313–3332. [Google Scholar] [CrossRef]
- Bai, L.; Du, S.; Zhang, X.; Wang, H.; Liu, B.; Ouyang, S. Domain Adaptation for Remote Sensing Image Semantic Segmentation: An Integrated Approach of Contrastive Learning and Adversarial Learning. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–13. [Google Scholar] [CrossRef]
- Wang, J.; Ma, A.; Zhong, Y.; Zheng, Z.; Zhang, L. Cross-sensor domain adaptation for high spatial resolution urban land-cover mapping: From airborne to spaceborne imagery. Remote Sens. Environ. 2022, 277, 113058. [Google Scholar] [CrossRef]
- Yan, L.; Fan, B.; Xiang, S.; Pan, C. CMT: Cross Mean Teacher Unsupervised Domain Adaptation for VHR Image Semantic Segmentation. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Li, Y.; Shi, T.; Zhang, Y.; Chen, W.; Wang, Z.; Li, H. Learning deep semantic segmentation network under multiple weakly-supervised constraints for cross-domain remote sensing image semantic segmentation. ISPRS J. Photogramm. Remote Sens. 2021, 175, 20–33. [Google Scholar] [CrossRef]
- Zhao, Y.; Gao, H.; Guo, P.; Sun, Z. ResiDualGAN: Resize-Residual DualGAN for Cross-Domain Remote Sensing Images Semantic Segmentation. CoRR 2022, abs/2201.11523. Available online: http://xxx.lanl.gov/abs/2201.11523 (accessed on 1 July 2020.).
- Tasar, O.; Happy, S.L.; Tarabalka, Y.; Alliez, P. ColorMapGAN: Unsupervised Domain Adaptation for Semantic Segmentation Using Color Mapping Generative Adversarial Networks. IEEE Trans. Geosci. Remote Sens. 2020, 58, 7178–7193. [Google Scholar] [CrossRef]
- Chen, S.; Jia, X.; He, J.; Shi, Y.; Liu, J. Semi-supervised Domain Adaptation based on Dual-level Domain Mixing for Semantic Segmentation. CoRR 2021, abs/2103.04705. [Google Scholar]
- Zhou, T.; Wang, W.; Konukoglu, E.; Van Goo, L. Rethinking Semantic Segmentation: A Prototype View. In Proceedings of the 2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), New Orleans, LA, USA, 18–24 June 2022; pp. 2572–2583. [Google Scholar] [CrossRef]
- Cuturi, M. Sinkhorn Distances: Lightspeed Computation of Optimal Transport. In Proceedings of the Advances in Neural Information Processing Systems; Burges, C., Bottou, L., Welling, M., Ghahramani, Z., Weinberger, K., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2013; Volume 26. [Google Scholar]
- Zhang, X.; Zhao, R.; Qiao, Y.; Li, H. RBF-Softmax: Learning Deep Representative Prototypes with Radial Basis Function Softmax. In Proceedings of the Computer Vision—ECCV 2020, Glasgow, UK, 23—28 August 2020; Vedaldi, A., Bischof, H., Brox, T., Frahm, J.M., Eds.; Springer International Publishing: Cham, Switzerkand, 2020; pp. 296–311. [Google Scholar]
- Qin, C.; Wang, L.; Ma, Q.; Yin, Y.; Wang, H.; Fu, Y. Semi-supervised Domain Adaptive Structure Learning. CoRR 2021, abs/2112.06161. Available online: http://xxx.lanl.gov/abs/2112.06161 (accessed on 1 July 2020.).
- Pan, X.; Ge, C.; Lu, R.; Song, S.; Chen, G.; Huang, Z.; Huang, G. On the Integration of Self-Attention and Convolution. In Proceedings of the 2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), New Orleans, LA, USA, 19–20 June 2022; pp. 805–815. [Google Scholar] [CrossRef]
- Fang, B.; Kou, R.; Pan, L.; Chen, P. Category-Sensitive Domain Adaptation for Land Cover Mapping in Aerial Scenes. Remote Sens. 2019, 11, 2631. [Google Scholar] [CrossRef]
- Loshchilov, I.; Hutter, F. Decoupled Weight Decay Regularization. In Proceedings of the 7th International Conference on Learning Representations, ICLR 2019, New Orleans, LA, USA, 6–9 May 2019. [Google Scholar]
- Tranheden, W.; Olsson, V.; Pinto, J.; Svensson, L. DACS: Domain Adaptation via Cross-domain Mixed Sampling. In Proceedings of the 2021 IEEE Winter Conference on Applications of Computer Vision (WACV), Waikoloa, HI, USA, 5–9 January 2021; pp. 1378–1388. [Google Scholar] [CrossRef]
- Zheng, Z.D.; Yang, Y. Unsupervised Scene Adaptation with Memory Regularization in vivo. arXiv 2020, arXiv:1912.11164. [Google Scholar]
- Vu, T.H.; Jain, H.; Bucher, M.; Cord, M.; Pérez, P. ADVENT: Adversarial Entropy Minimization for Domain Adaptation in Semantic Segmentation. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 2512–2521. [Google Scholar] [CrossRef]
- Zhao, Y.; Guo, P.; Gao, H.; Chen, X. Depth-Assisted ResiDualGAN for Cross-Domain Aerial Images Semantic Segmentation. CoRR 2022, abs/2208.09823. Available online: http://xxx.lanl.gov/abs/2208.09823 (accessed on 1 July 2020.). [CrossRef]
- Chen, L.C.E.; Zhu, Y.K.; Papandreou, G.; Schroff, F.; Adam, H. Encoder-Decoder with Atrous Separable Convolution for Semantic Image Segmentation. arXiv 2018, arXiv:1802.02611. [Google Scholar] [CrossRef]
- Wang, J.; Sun, K.; Cheng, T.; Jiang, B.; Deng, C.; Zhao, Y.; Liu, D.; Mu, Y.; Tan, M.; Wang, X.; et al. Deep High-Resolution Representation Learning for Visual Recognition. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 43, 3349–3364. [Google Scholar] [CrossRef] [PubMed]
- van der Maaten, L.; Hinton, G.E. Visualizing Data using t-SNE. J. Mach. Learn. Res. 2008, 9, 2579–2605. [Google Scholar]




| RSIs | Types | Coverage | Resolution | Bands |
|---|---|---|---|---|
| VH | Airborne | 1.38 km | 0.09 m | IRRG |
| PD | Airborne | 3.42 km | 0.05 m | RGB |
| LoveDA | Spaceborne | 536.15 km | 0.3 m | RGB |
| Tasks | S | T | ||
|---|---|---|---|---|
| PD→VH | 3456 | 398 | 5 | 344 |
| VH→PD | 344 | 2016 | 5 | 3456 |
| Rural→Urban | 1366 | 677 | 5 | 1156 |
| Types | Settings | Methods | PA | Impervious Surface | Building | Low Vegetation | Tree | Car | mIoU |
|---|---|---|---|---|---|---|---|---|---|
| UDA | training: S, without labels evaluating: | DACS | 62.27 | 58.09 | 80.63 | 16.26 | 41.70 | 43.48 | 48.03 |
| MRNet | 65.31 | 54.11 | 75.39 | 16.16 | 54.99 | 29.39 | 46.01 | ||
| Advent | 65.51 | 55.43 | 68.49 | 20.73 | 59.02 | 28.28 | 46.39 | ||
| Zheng’s | 67.50 | 55.06 | 72.73 | 31.54 | 55.40 | 21.73 | 47.29 | ||
| RDG | 66.44 | 53.88 | 74.22 | 22.52 | 58.11 | 29.89 | 47.72 | ||
| DRDG | 69.23 | 55.73 | 75.08 | 21.34 | 60.02 | 33.39 | 49.11 | ||
| SSDA | training: S, T, without labels evaluating: | DACS (SSDA) | 73.45 | 59.34 | 87.51 | 16.13 | 43.04 | 46.37 | 50.48 |
| Zheng’s (SSDA) | 69.27 | 57.25 | 74.64 | 23.77 | 59.43 | 23.76 | 47.77 | ||
| RDG (SSDA) | 71.34 | 56.33 | 76.12 | 23.60 | 59.13 | 32.24 | 49.48 | ||
| MME | 73.48 | 65.06 | 66.82 | 37.39 | 58.30 | 32.69 | 52.05 | ||
| CDAC | 76.75 | 70.38 | 72.54 | 36.36 | 63.46 | 28.59 | 54.27 | ||
| Alonso’s | 80.32 | 71.59 | 77.48 | 49.33 | 70.45 | 38.64 | 61.50 | ||
| Hoyer’s | 82.04 | 74.16 | 79.48 | 53.36 | 70.77 | 43.05 | 64.16 | ||
| Ours | 86.45 | 81.59 | 89.49 | 60.66 | 71.80 | 54.18 | 71.54 | ||
| SL | training: with labels evaluating: | LANet | 88.41 | 82.93 | 90.08 | 66.25 | 76.81 | 61.82 | 75.58 |
| PSPNet | 90.47 | 85.66 | 92.21 | 70.16 | 80.31 | 79.90 | 81.65 | ||
| DeepLabv3+ | 90.63 | 86.15 | 92.66 | 70.08 | 80.36 | 80.55 | 81.96 | ||
| HRNet | 91.05 | 87.21 | 93.23 | 71.09 | 80.58 | 83.64 | 83.15 | ||
| MAE+UPerNet | 91.57 | 87.61 | 93.92 | 72.66 | 81.66 | 78.28 | 82.83 |
| Types | Settings | Methods | PA | Impervious Surface | Building | Low Vegetation | Tree | Car | mIoU |
|---|---|---|---|---|---|---|---|---|---|
| UDA | training: S, without labels evaluating: | DACS | 57.19 | 45.76 | 51.88 | 39.01 | 15.61 | 43.62 | 39.18 |
| MRNet | 58.25 | 48.56 | 54.34 | 36.40 | 26.20 | 54.52 | 44.00 | ||
| Advent | 60.03 | 49.80 | 54.85 | 40.19 | 26.94 | 46.71 | 43.70 | ||
| Zheng’s | 60.89 | 47.63 | 48.77 | 34.92 | 41.17 | 51.58 | 44.81 | ||
| RDG | 60.63 | 52.17 | 48.00 | 40.01 | 37.69 | 44.47 | 44.47 | ||
| DRDG | 62.54 | 54.05 | 50.53 | 39.14 | 39.15 | 47.08 | 45.99 | ||
| SSDA | training: S, T, without labels evaluating: | DACS (SSDA) | 60.83 | 48.31 | 57.77 | 43.02 | 16.38 | 47.09 | 42.51 |
| Zheng’s (SSDA) | 62.96 | 53.63 | 52.48 | 42.14 | 38.17 | 52.26 | 47.84 | ||
| RDG (SSDA) | 61.98 | 51.35 | 48.45 | 43.04 | 40.43 | 53.91 | 47.44 | ||
| MME | 61.03 | 48.92 | 51.62 | 31.77 | 50.58 | 51.41 | 46.86 | ||
| CDAC | 64.71 | 60.03 | 61.47 | 20.01 | 44.32 | 55.82 | 48.33 | ||
| Alonso’s | 78.00 | 71.94 | 73.92 | 64.61 | 59.22 | 64.32 | 66.80 | ||
| Hoyer’s | 79.71 | 71.74 | 78.02 | 65.90 | 61.61 | 68.79 | 69.21 | ||
| Ours | 82.19 | 72.23 | 81.71 | 68.26 | 64.89 | 82.98 | 74.01 | ||
| SL | training: with labels evaluating: | LANet | 86.68 | 80.41 | 88.53 | 71.20 | 69.63 | 90.48 | 80.05 |
| PSPNet | 89.23 | 84.19 | 91.65 | 74.18 | 74.74 | 91.57 | 83.27 | ||
| DeepLabv3+ | 89.31 | 84.02 | 92.25 | 74.19 | 74.91 | 91.56 | 83.39 | ||
| HRNet | 89.69 | 85.16 | 92.89 | 74.76 | 75.10 | 91.51 | 83.88 | ||
| MAE+UPerNet | 90.20 | 85.95 | 93.25 | 76.33 | 76.08 | 91.82 | 84.69 |
| Types | Settings | Methods | PA | Background | Building | Road | Water | Barren | Forest | Agricultural | mIoU |
|---|---|---|---|---|---|---|---|---|---|---|---|
| UDA | training: S, without labels evaluating: | DACS | 53.85 | 46.33 | 37.87 | 32.39 | 35.61 | 21.33 | 21.42 | 14.79 | 29.96 |
| MRNet | 51.03 | 30.83 | 42.30 | 36.07 | 43.12 | 26.89 | 25.83 | 10.38 | 30.77 | ||
| Advent | 50.66 | 29.12 | 42.14 | 36.42 | 43.85 | 27.30 | 26.48 | 12.56 | 31.12 | ||
| Zheng’s | 52.69 | 43.73 | 37.23 | 32.22 | 48.92 | 21.26 | 26.65 | 10.97 | 31.57 | ||
| RDG | 53.85 | 49.58 | 36.17 | 36.58 | 55.73 | 19.07 | 15.68 | 15.37 | 32.60 | ||
| SSDA | training: S, T, without labels evaluating: | DACS (SSDA) | 54.13 | 47.93 | 38.02 | 34.03 | 37.43 | 20.94 | 22.06 | 15.39 | 30.83 |
| Zheng’s (SSDA) | 53.25 | 44.57 | 37.95 | 32.96 | 50.13 | 21.79 | 27.03 | 12.83 | 32.47 | ||
| RDG (SSDA) | 54.92 | 49.97 | 37.94 | 37.04 | 56.56 | 20.97 | 18.61 | 15.07 | 33.74 | ||
| MME | 53.96 | 41.12 | 40.98 | 33.65 | 53.90 | 27.06 | 20.54 | 12.59 | 32.83 | ||
| CDAC | 55.14 | 42.04 | 42.37 | 34.54 | 55.65 | 26.19 | 22.12 | 14.78 | 33.96 | ||
| Alonso’s | 56.97 | 50.06 | 46.11 | 39.05 | 42.24 | 22.63 | 31.09 | 15.52 | 35.24 | ||
| Hoyer’s | 57.43 | 43.26 | 44.40 | 38.70 | 53.20 | 32.28 | 33.17 | 12.53 | 36.79 | ||
| Ours | 58.92 | 44.44 | 47.70 | 38.90 | 62.98 | 29.39 | 32.29 | 18.13 | 39.12 | ||
| SL | training: with labels evaluating: | LANet | 62.22 | 43.99 | 45.77 | 49.22 | 64.96 | 29.95 | 31.91 | 24.90 | 41.53 |
| PSPNet | 64.45 | 51.59 | 51.32 | 53.34 | 71.07 | 24.77 | 22.29 | 32.02 | 43.77 | ||
| DeepLabv3+ | 62.61 | 50.21 | 45.21 | 46.73 | 67.06 | 29.45 | 31.42 | 31.27 | 43.05 | ||
| HRNet | 63.53 | 50.25 | 50.23 | 53.26 | 73.20 | 28.95 | 33.07 | 23.64 | 44.66 | ||
| MAE+UPerNet | 63.89 | 51.09 | 46.12 | 50.88 | 74.93 | 33.24 | 29.89 | 37.60 | 46.25 |
| Tasks | Cross-Domain Multi-Prototypes | Contradictory Structure Learning | Self-Supervised Learning | PA | mIoU |
|---|---|---|---|---|---|
| PD→VH | √ | √ | 84.59 | 69.14 | |
| √ | √ | 85.36 | 69.38 | ||
| √ | √ | 85.87 | 69.79 | ||
| √ | √ | √ | 86.45 | 71.54 | |
| VH→PD | √ | √ | 78.72 | 69.46 | |
| √ | √ | 80.11 | 71.25 | ||
| √ | √ | 81.08 | 72.10 | ||
| √ | √ | √ | 82.19 | 74.01 | |
| Rural→Urban | √ | √ | 56.04 | 36.37 | |
| √ | √ | 56.79 | 37.02 | ||
| √ | √ | 57.33 | 37.65 | ||
| √ | √ | √ | 58.92 | 39.12 |
| Tasks | ||||
|---|---|---|---|---|
| PD→VH | 70.72 | 71.19 | 71.54 | 70.60 |
| VH→PD | 71.46 | 73.25 | 74.01 | 72.33 |
| Rural→Urban | 37.97 | 38.64 | 39.12 | 38.03 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, K.; Yu, A.; You, X.; Qiu, C.; Liu, B.; Zhang, F. Cross-Domain Multi-Prototypes with Contradictory Structure Learning for Semi-Supervised Domain Adaptation Segmentation of Remote Sensing Images. Remote Sens. 2023, 15, 3398. https://doi.org/10.3390/rs15133398
Gao K, Yu A, You X, Qiu C, Liu B, Zhang F. Cross-Domain Multi-Prototypes with Contradictory Structure Learning for Semi-Supervised Domain Adaptation Segmentation of Remote Sensing Images. Remote Sensing. 2023; 15(13):3398. https://doi.org/10.3390/rs15133398
Chicago/Turabian StyleGao, Kuiliang, Anzhu Yu, Xiong You, Chunping Qiu, Bing Liu, and Fubing Zhang. 2023. "Cross-Domain Multi-Prototypes with Contradictory Structure Learning for Semi-Supervised Domain Adaptation Segmentation of Remote Sensing Images" Remote Sensing 15, no. 13: 3398. https://doi.org/10.3390/rs15133398
APA StyleGao, K., Yu, A., You, X., Qiu, C., Liu, B., & Zhang, F. (2023). Cross-Domain Multi-Prototypes with Contradictory Structure Learning for Semi-Supervised Domain Adaptation Segmentation of Remote Sensing Images. Remote Sensing, 15(13), 3398. https://doi.org/10.3390/rs15133398





