A Parallel Solution of Timing Synchronization in High-Speed Remote Sensing Data Transmission
Abstract
1. Introduction
2. Models and Methods
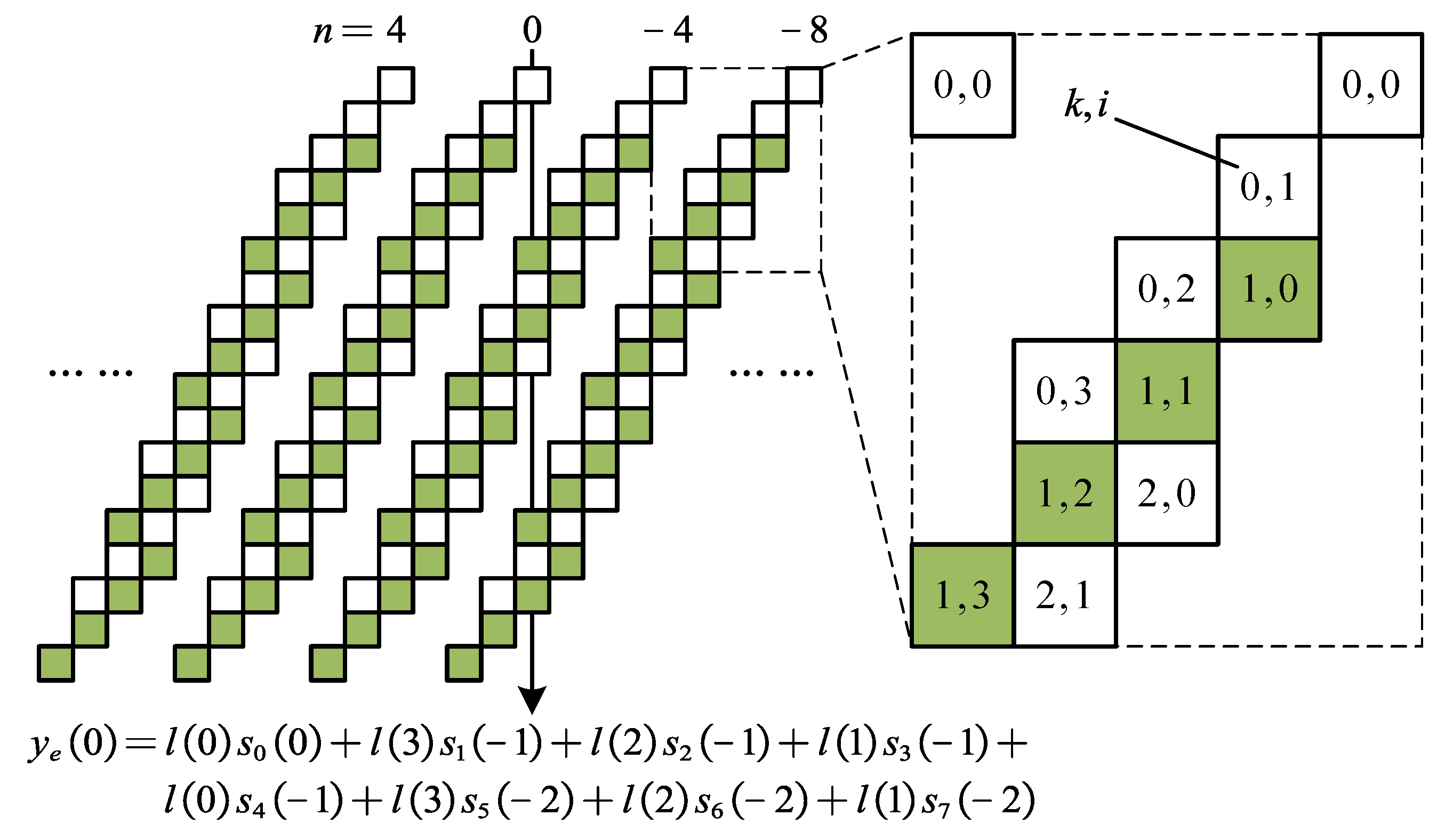
2.1. Parallel Structure Based on Polyphase DFT Filter Banks
2.2. Basic Principle of Feedforward Timing Error Estimation
2.2.1. Feedforward Timing Error Estimation Algorithm Based on Second-Order Statistics
2.2.2. Derivation of Feedforward Timing Estimation Algorithm Combining Second-Order and Fourth-Order Statistics
2.3. Parallel Design of Joint Second-Order and Fourth-Order Statistics Timing Estimation
2.4. Design of Parallel Timing Correction Scheme
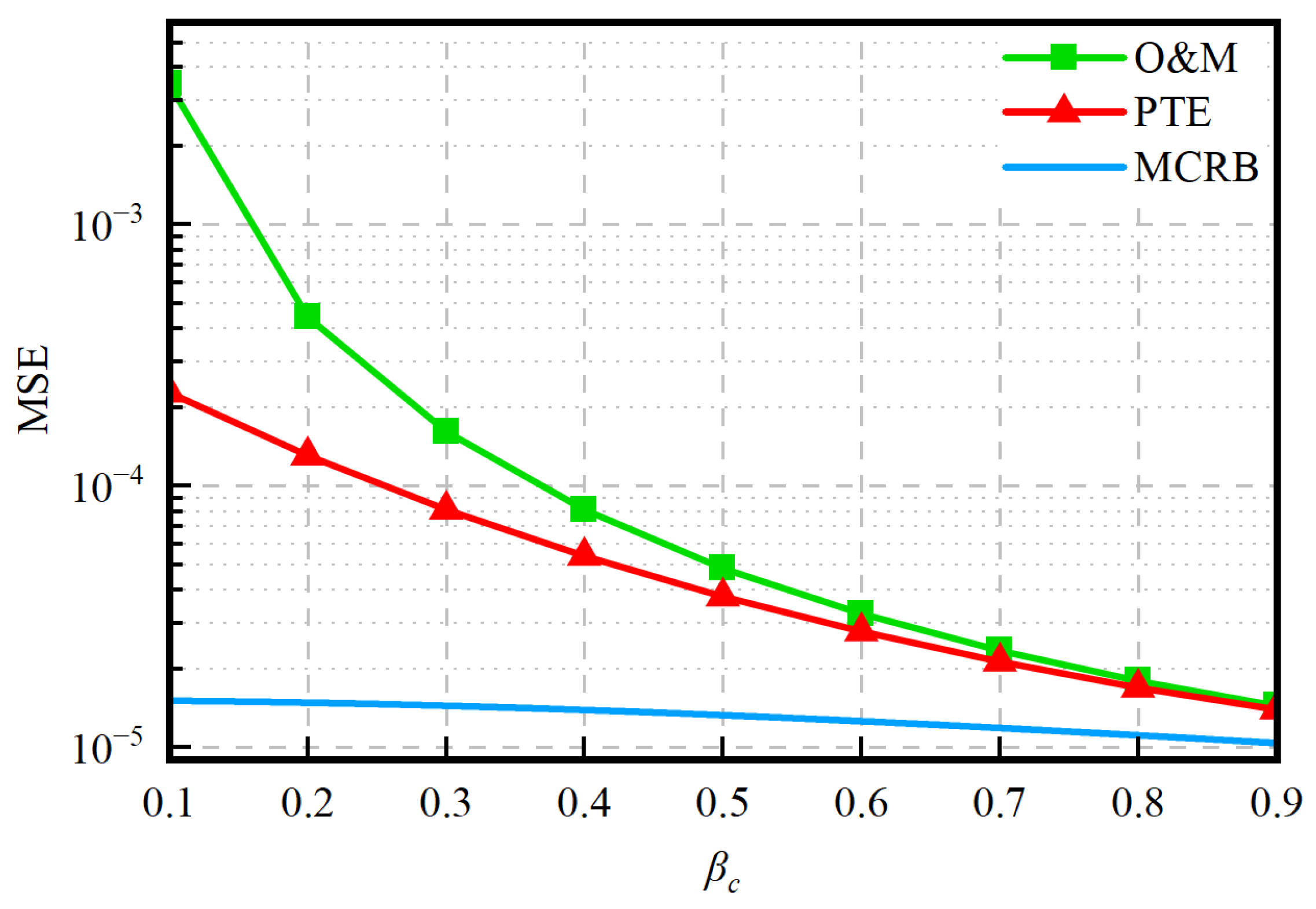
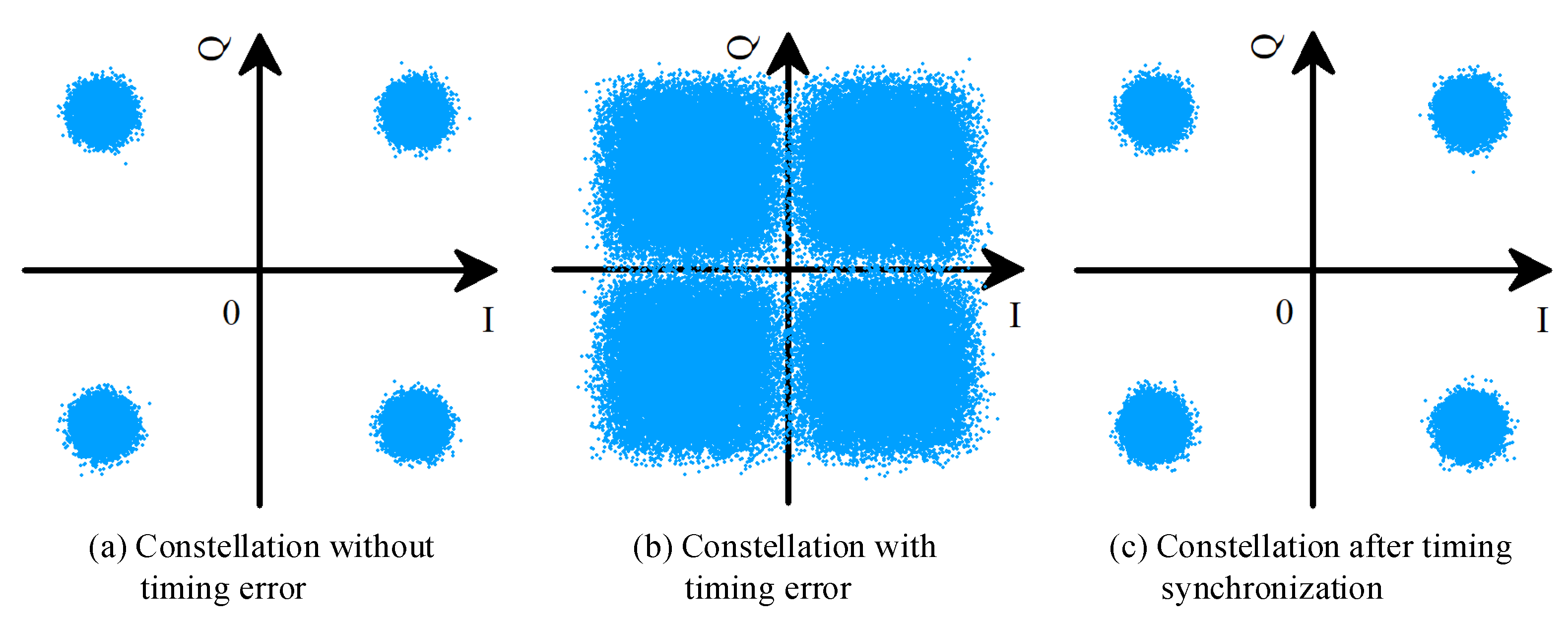
3. Results
4. Discussion
4.1. Analysis of Computational Complexity for Parallel Timing Error Estimation Algorithm
4.2. Analysis of Computational Complexity for Parallel Timing Correction Algorithm
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhou, Y. Discussion on the Development of Remote Sensing Satellite Data Transmission Technology. China Plant Eng. 2022, 2, 194–195. [Google Scholar]
- Wang, Q.; Li, W.; Yu, Z.; Abbasi, Q.; Imran, M.; Ansari, S.; Sambo, Y.; Wu, L.; Li, Q.; Zhu, T. An Overview of Emergency Communication Networks. Remote Sens. 2023, 15, 1595. [Google Scholar] [CrossRef]
- Srinivasan, M.; Chen, C.C.; Grebowsky, G.; Gray, A. An all-digital, high data-rate parallel receiver. Jpl Tda Prog. Rep. 1997, 42, 131. [Google Scholar]
- Ghuman, P.; Sheikh, S.; Koubek, S.; Hoy, S.; Gray, A. High Rate Digital Demodulator ASIC. In Proceedings of the 34th International Telemetering Conference, Town & Country Resort Hotel and Convention Center, San Diego, CA, USA, 26–29 October 1998. [Google Scholar]
- Gray, A.; Srinivasan, M.; Simon, M.; Yan, T.Y. Flexible all-digital receiver for bandwidth efficient modulations. In Proceedings of the 35th International Telemetering Conference, Riviera Hotel and Convention Center, Las Vegas, NA, USA, 25–28 October 1999. [Google Scholar]
- Springett, J.C. Achieving future space very long baseline interferometry gigabits-per-second data rates. In The Interplanetary Network Progress Report 42–149; NASA: Washington, DC, USA, 2002; pp. 1–26. Available online: https://ipnpr.jpl.nasa.gov (accessed on 27 March 2023).
- Liang, X. Research and Implementation of Matched Filtering and Timing Recovery for 800 Mbps High-Speed Data Transmission Receiver. Master’s Thesis, National University of Defense Technology, Changsha, China, 2007. [Google Scholar]
- Guo, X.F.; Zheng, X.F.; Lu, M.H.; Li, Y.H. Design and application of high-speed data transmission QAM demodulator. J. Telem. Track. Command. 2011, 32, 21–25. [Google Scholar]
- Lin, C.X. Research on Demodulation Technique and Its Implementation for 2 Gbps High Speed Communication. Ph.D. Thesis, Tsinghua University, Beijing, China, 2012. [Google Scholar]
- Zeng, H. Research on Demodulation Techniques Based on A Parallel All-digital Receiving Structure Named as APRX. Master’s Thesis, University of Electronic Science and Technology of China, Chengdu, China, 2013. [Google Scholar]
- Cui, L.B. Research on Parallel Timing Synchronization Technology in QAM Demodulation Data. Master’s Thesis, University of Electronic Science and Technology of China, Chengdu, China, 2018. [Google Scholar]
- Wang, Z.; Song, Y.; Li, Y. Ultra-Wideband Imaging via Frequency Diverse Array with Low Sampling Rate. Remote Sens. 2022, 14, 1271. [Google Scholar] [CrossRef]
- Chen, X.; Venosa, E.; Rao, B.D. Non-maximally decimated filter bank-based single-carrier receiver: A pathway to next-generation wideband communication. Eurasip J. Adv. Signal Process. 2014, 2014, 1–15. [Google Scholar] [CrossRef]
- Harris, F.J.; Rice, M. Multirate digital filters for symbol timing synchronization in software defined radios. IEEE J. Sel. Areas Commun. 2001, 19, 2346–2357. [Google Scholar] [CrossRef]
- Schmidt, D.; Lankl, B. Parallel architecture of an all digital timing recovery scheme for high speed receivers. In Proceedings of the 2010 7th International Symposium on Communication Systems, Networks & Digital Signal Processing (CSNDSP 2010), Newcastle Upon Tyne, UK, 21–23 July 2010; pp. 31–34. [Google Scholar]
- Xiao, L. Study and Implementation of Synchronization for Parallel High Data Rate Demodulation System. Master’s Thesis, University of Electronic Science and Technology of China, Chengdu, China, 2017. [Google Scholar]
- Wang, C.H. Design and Implementation of High Speed Parallel Interpolation Filter Based on FPGA. Master’s Thesis, Chengdu University of Technology, Chengdu, China, 2021. [Google Scholar]
- Li, Z. The research and Implementation of Symbol Variable Rate Timing Synchronization for Wideband Satellite. Master’s Thesis, Xidian University, Xi’an, China, 2022. [Google Scholar]
- Teng, F.; Jiao, Y.; Yang, W.; Yan, J.; Gao, Z.; Lu, Z. Multiphase Parallel Demodulation for Remote Sensing Satellite Data Transmission–Filter Bank Based on WOLA Structure. IEEE J. Sel. Top. Appl. Earth Obs. Remote. Sens. 2022, 15, 9556–9565. [Google Scholar] [CrossRef]
- Morge-Rollet, L.; Le Jeune, D.; Le Roy, F.; Canaff, C.; Gautier, R. From Modeling to Sensing of Micro-Doppler in Radio Communications. Remote Sens. 2022, 14, 6310. [Google Scholar] [CrossRef]
- Schlüter, M.; Dörpinghaus, M.; Fettweis, G.P. Bounds on phase, frequency, and timing synchronization in fully digital receivers with 1-bit quantization and oversampling. IEEE Trans. Commun. 2020, 68, 6499–6513. [Google Scholar] [CrossRef]
- Wang, Y.; Ciblat, P.; Serpedin, E.; Loubaton, P. Performance analysis of a class of nondata-aided frequency offset and symbol timing estimators for flat-fading channels. IEEE Trans. Signal Process. 2002, 50, 2295–2305. [Google Scholar] [CrossRef]
- Dandawate, A.V.; Giannakis, G.B. Asymptotic theory of mixed time averages and kth-order cyclic-moment and cumulant statistics. IEEE Trans. Inf. Theory 1995, 41, 216–232. [Google Scholar] [CrossRef]
- Gini, F.; Giannakis, G.B. Frequency offset and symbol timing recovery in flat-fading channels: A cyclostationary approach. IEEE Trans. Commun. 1998, 46, 400–411. [Google Scholar] [CrossRef]
- Wang, Y.; Serpedin, E.; Ciblat, P. Blind feedforward cyclostationarity-based timing estimation for linear modulations. IEEE Trans. Wirel. Commun. 2004, 3, 709–715. [Google Scholar] [CrossRef]
- Li, S.; Wang, S.; Zhao, C.; Cui, X.; Liu, J. A Non-Data-Aided Feedforward Timing Estimator Based on Multiple Cyclic Correlations for Short-Term Burst Signals. IEEE Commun. Lett. 2022, 26, 2166–2169. [Google Scholar] [CrossRef]
- Sirbu, G.; Leonardi, M. Fully Autonomous Orbit Determination and Synchronization for Satellite Navigation and Communication Systems in Halo Orbits. Remote Sens. 2023, 15, 1173. [Google Scholar] [CrossRef]
- Abd, M.H.; Al-Suhail, G.A.; Tahir, F.R.; Ali Ali, A.M.; Abbood, H.A.; Dashtipour, K.; Jamal, S.S.; Ahmad, J. Synchronization of Monostatic Radar Using a Time-Delayed Chaos-Based FM Waveform. Remote Sens. 2022, 14, 1984. [Google Scholar] [CrossRef]
- Zhou, Z.; Yang, Y.; Ma, M.; Jiao, B. Distortion reduction in fractional delay filters. IEEE Signal Process. Lett. 2021, 28, 588–592. [Google Scholar] [CrossRef]







| Modulation System | Oversampling Rate () | Roll off Factor () |
|---|---|---|
| QPSK | 4 | 0.2 |
| Timing Error | Observation Length | Number of Simulated Samples |
| 0.3/ | 100 |
| Evaluating indicator & Method | Traditional Method | Improved Method |
|---|---|---|
| Meansquare error of timing error estimation | (SNR = 0 dB) | (SNR = 0 dB) |
| (SNR = 10 dB) | (SNR = 10 dB) | |
| (SNR = 20 dB) | (SNR = 20 dB) | |
| comparatively large | reduced by 1–3 dB | |
| Demodulationerror rate after timing synchronization (SNR = 10 dB) | (reduced by 0.36 dB) | |
| Single channel data rate |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Teng, F.; Yang, W.; Yan, J.; Ma, H.; Jiao, Y.; Gao, Z. A Parallel Solution of Timing Synchronization in High-Speed Remote Sensing Data Transmission. Remote Sens. 2023, 15, 3347. https://doi.org/10.3390/rs15133347
Teng F, Yang W, Yan J, Ma H, Jiao Y, Gao Z. A Parallel Solution of Timing Synchronization in High-Speed Remote Sensing Data Transmission. Remote Sensing. 2023; 15(13):3347. https://doi.org/10.3390/rs15133347
Chicago/Turabian StyleTeng, Fei, Wenge Yang, Jining Yan, Hongbin Ma, Yiwen Jiao, and Zefu Gao. 2023. "A Parallel Solution of Timing Synchronization in High-Speed Remote Sensing Data Transmission" Remote Sensing 15, no. 13: 3347. https://doi.org/10.3390/rs15133347
APA StyleTeng, F., Yang, W., Yan, J., Ma, H., Jiao, Y., & Gao, Z. (2023). A Parallel Solution of Timing Synchronization in High-Speed Remote Sensing Data Transmission. Remote Sensing, 15(13), 3347. https://doi.org/10.3390/rs15133347








