Enhancing Remote Sensing Image Super-Resolution Guided by Bicubic-Downsampled Low-Resolution Image
Abstract
1. Introduction
2. Methodology
2.1. LR Image Transfer
2.2. Super-Resolution
2.3. Network Architecture
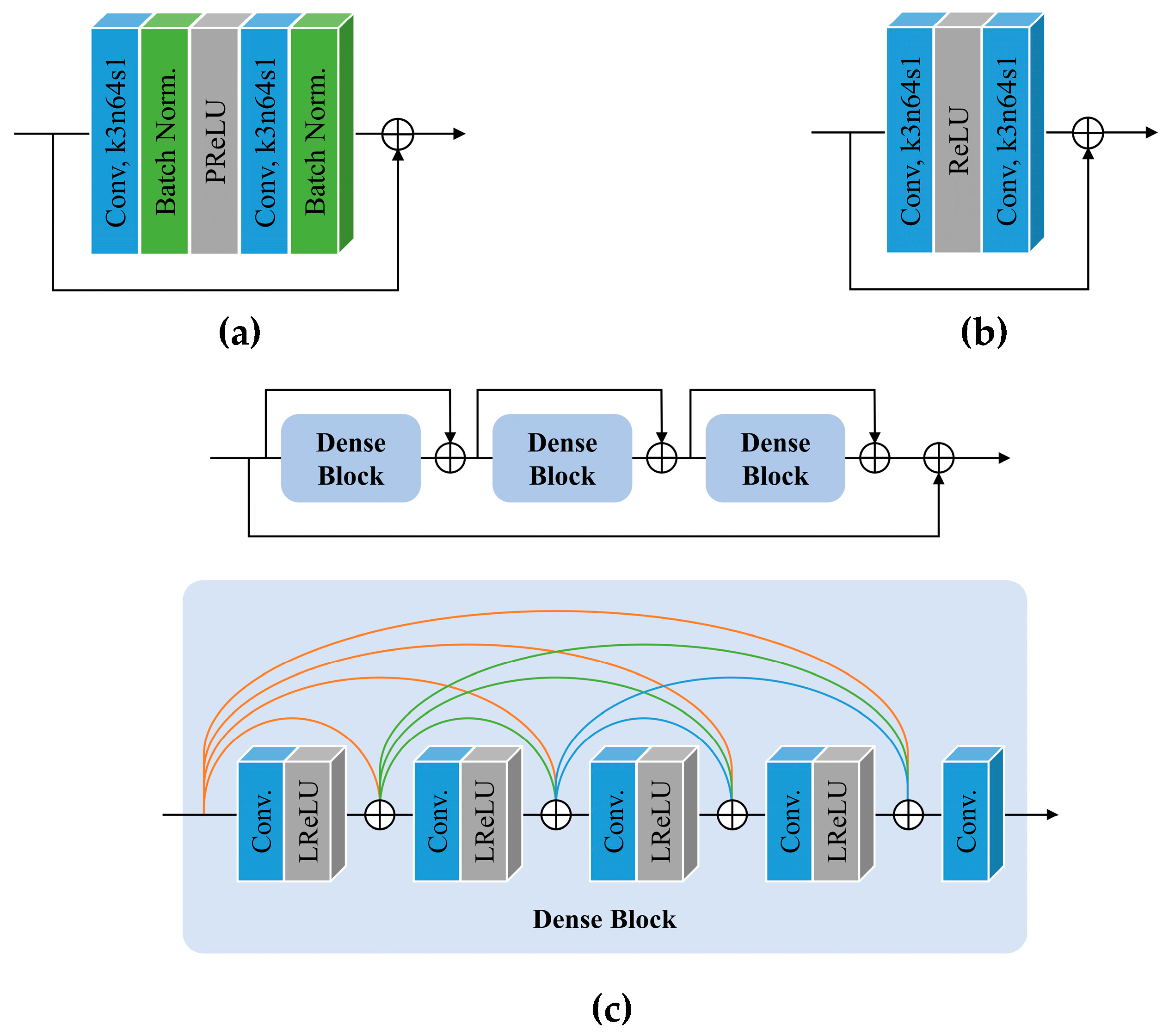
2.3.1. Generator
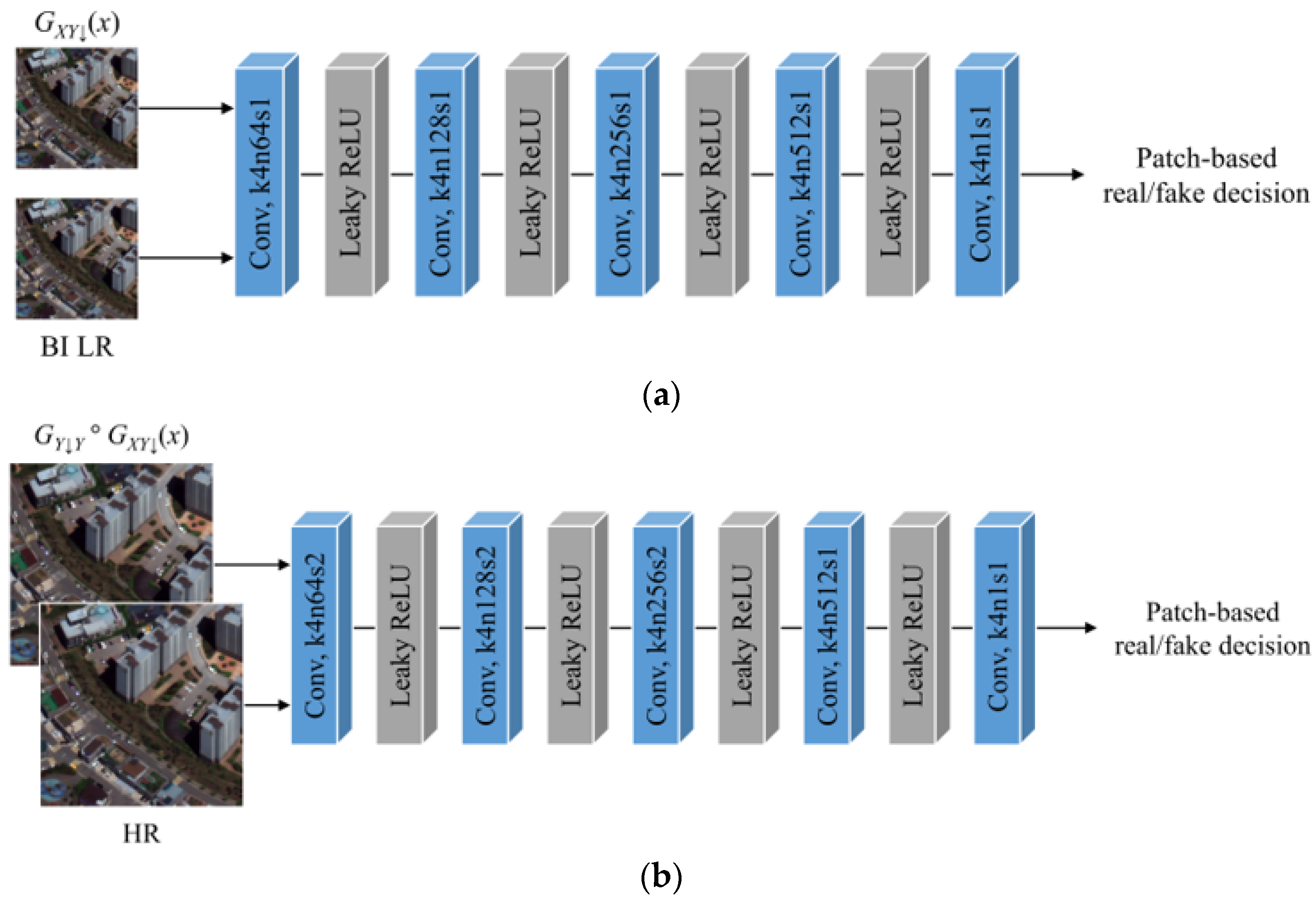
2.3.2. Discriminator
3. Experimental Results
3.1. Datasets
3.2. Quantitative Assessment Metrics
3.3. Implementation Details
3.4. Comparison with State-of-the-Art Methods
4. Discussion
4.1. Generator Architecture
4.2. Discriminator Architecture and GAN Loss
4.3. Perceptual Loss
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Method | PSNR | SSIM | SAM | ERGAS | UIQI | LPIPS | NIQE | |
|---|---|---|---|---|---|---|---|---|
| Bicubic | 32.8364 | 0.8846 | 0.0206 | 47.5450 | 0.6291 | 0.2757 | 6.6302 | |
| CNN-based | EDSR [11] | 34.3155 | 0.9103 | 0.0180 | 40.7123 | 0.6698 | 0.2300 | 7.8177 |
| D-DBPN [12] | 33.8119 | 0.9006 | 0.0204 | 42.8439 | 0.6423 | 0.2534 | 7.4990 | |
| RRDBNet [15] | 33.9596 | 0.9045 | 0.0200 | 42.2957 | 0.6514 | 0.2488 | 7.5386 | |
| RDN [14] | 34.5049 | 0.9134 | 0.0185 | 39.8893 | 0.6755 | 0.2197 | 7.6263 | |
| RCAN [13] | 34.2489 | 0.9094 | 0.0191 | 41.0236 | 0.6650 | 0.2294 | 7.4470 | |
| HAN [27] | 34.6353 | 0.9155 | 0.0182 | 39.3325 | 0.6814 | 0.2142 | 7.8436 | |
| DRN-L [48] | 34.4271 | 0.9123 | 0.0186 | 40.2755 | 0.6740 | 0.2236 | 7.6602 | |
| GAN-based | SRGAN [9] | 31.5388 | 0.8355 | 0.0525 | 56.1957 | 0.4871 | 0.2546 | 5.3869 |
| ESRGAN [15] | 31.4596 | 0.8467 | 0.0452 | 56.5095 | 0.5274 | 0.2290 | 5.2891 | |
| ESRGAN-FS [40] | 31.4043 | 0.8491 | 0.0426 | 57.9827 | 0.5370 | 0.2188 | 5.3988 | |
| EESRGAN [21] | 32.6946 | 0.8755 | 0.0305 | 48.9042 | 0.5939 | 0.2046 | 5.8502 | |
| SG-GAN [22] | 32.3234 | 0.8629 | 0.0356 | 51.0380 | 0.5435 | 0.2655 | 5.5719 | |
| Method | PSNR | SSIM | SAM | ERGAS | UIQI | LPIPS | NIQE | |
|---|---|---|---|---|---|---|---|---|
| Bicubic | 33.1650 | 0.8921 | 0.0185 | 38.7233 | 0.6612 | 0.2636 | 6.6402 | |
| CNN-based | EDSR [11] | 34.4422 | 0.9127 | 0.0168 | 33.6200 | 0.6912 | 0.2325 | 7.6672 |
| D-DBPN [12] | 34.0034 | 0.9046 | 0.0190 | 35.2938 | 0.6694 | 0.2509 | 7.2414 | |
| RRDBNet [15] | 34.1724 | 0.9090 | 0.0195 | 34.6322 | 0.6786 | 0.2435 | 7.1857 | |
| RDN [14] | 34.6515 | 0.9164 | 0.0172 | 32.8534 | 0.6982 | 0.2235 | 7.4615 | |
| RCAN [13] | 34.4469 | 0.9130 | 0.0176 | 33.6167 | 0.6911 | 0.2275 | 7.4895 | |
| HAN [27] | 34.8012 | 0.9188 | 0.0169 | 32.3318 | 0.7048 | 0.2174 | 7.4457 | |
| DRN-L [48] | 34.5861 | 0.9151 | 0.0173 | 33.0998 | 0.6972 | 0.2262 | 7.4913 | |
| GAN-based | SRGAN [9] | 31.3895 | 0.8367 | 0.0484 | 47.7144 | 0.5120 | 0.2661 | 5.4253 |
| ESRGAN [15] | 31.3861 | 0.8535 | 0.0418 | 47.9343 | 0.5639 | 0.2260 | 5.0752 | |
| ESRGAN-FS [40] | 31.6624 | 0.8567 | 0.0383 | 46.2197 | 0.5689 | 0.2183 | 5.4178 | |
| EESRGAN [21] | 33.0359 | 0.8793 | 0.0270 | 39.5130 | 0.6225 | 0.1987 | 5.6776 | |
| SG-GAN [22] | 33.8097 | 0.9038 | 0.0247 | 36.0339 | 0.6650 | 0.2388 | 7.1215 | |
Appendix B


References
- Freeman, W.T.; Pasztor, E.C.; Carmichael, O.T. Learning Low-Level Vision. Int. J. Comput. Vis. 2000, 40, 25–47. [Google Scholar] [CrossRef]
- Yue, L.; Shen, H.; Li, J.; Yuan, Q.; Zhang, H.; Zhang, L. Image Super-Resolution: The Techniques, Applications, and Future. Signal Process. 2016, 128, 389–408. [Google Scholar] [CrossRef]
- Freeman, W.T.; Jones, T.R.; Pasztor, E.C. Example-Based Super-Resolution. IEEE Comput. Graph. Appl. 2002, 22, 56–65. [Google Scholar] [CrossRef]
- Dong, C.; Loy, C.C.; He, K.; Tang, X. Image Super-Resolution Using Deep Convolutional Networks. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 38, 295–307. [Google Scholar] [CrossRef]
- Dong, C.; Loy, C.C.; Tang, X. Accelerating the Super-Resolution Convolutional Neural Network. In Proceedings of the European Conference on Computer Vision (ECCV), Amsterdam, The Netherlands, 11–14 October 2016; pp. 391–407. [Google Scholar]
- Kim, J.; Lee, J.K.; Lee, K.M. Accurate Image Super-Resolution Using Very Deep Convolutional Networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 1646–1654. [Google Scholar]
- Kim, J.; Lee, J.K.; Lee, K.M. Deeply-Recursive Convolutional Network for Image Super-Resolution. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 1637–1645. [Google Scholar]
- Tai, Y.; Yang, J.; Liu, X. Image Super-Resolution via Deep Recursive Residual Network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 3148–3155. [Google Scholar]
- Ledig, C.; Theis, L.; Huszár, F.; Caballero, J.; Cunningham, A.; Acosta, A.; Aitken, A.; Tejani, A.; Totz, J.; Wang, Z.; et al. Photo-Realistic Single Image Super-Resolution Using a Generative Adversarial Network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 105–114. [Google Scholar]
- Sajjadi, M.S.M.; Schölkopf, B.; Hirsch, M. EnhanceNet: Single Image Super-Resolution Through Automated Texture Synthesis. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 4491–4500. [Google Scholar]
- Lim, B.; Son, S.; Kim, H.; Nah, S.; Lee, K.M. Enhanced Deep Residual Networks for Single Image Super-Resolution. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Honolulu, HI, USA, 21–26 July 2017; pp. 1132–1140. [Google Scholar]
- Haris, M.; Shakhnarovich, G.; Ukita, N. Deep Back-Projection Networks for Super-Resolution. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–23 June 2018; pp. 1664–1673. [Google Scholar]
- Zhang, Y.; Li, K.; Li, K.; Wang, L.; Zhong, B.; Fu, Y. Image Super-Resolution Using Very Deep Residual Channel Attention Networks. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 294–310. [Google Scholar]
- Zhang, Y.; Tian, Y.; Kong, Y.; Zhong, B.; Fu, Y. Residual Dense Network for Image Super-Resolution. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–23 June 2018; pp. 2472–2481. [Google Scholar]
- Wang, X.; Yu, K.; Wu, S.; Gu, J.; Liu, Y.; Dong, C.; Qiao, Y.; Loy, C.C. ESRGAN: Enhanced Super-Resolution Generative Adversarial Networks. In Proceedings of the European Conference on Computer Vision Workshops (ECCVW), Munich, Germany, 8–14 September 2018; pp. 63–79. [Google Scholar]
- Ha, V.K.; Ren, J.-C.; Xu, X.-Y.; Zhao, S.; Xie, G.; Masero, V.; Hussain, A. Deep Learning Based Single Image Super-resolution: A Survey. Int. J. Autom. Comput. 2019, 16, 413–426. [Google Scholar] [CrossRef]
- Chen, H.; He, X.; Qing, L.; Wu, Y.; Ren, C.; Sheriff, R.E.; Zhu, C. Real-World Single Image Super-Resolution: A Brief Review. Inf. Fusion 2022, 79, 124–145. [Google Scholar] [CrossRef]
- Singla, K.; Pandey, R.; Ghanekar, U. A Review on Single Image Super Resolution Techniques Using Generative Adversarial Network. Optik 2022, 266, 169607. [Google Scholar] [CrossRef]
- Jozdani, S.; Chen, D.; Pouliot, D.; Johnson, B.A. A Review and Meta-Analysis of Generative Adversarial Networks and Their Applications in Remote Sensing. Int. J. Appl. Earth Obs. Geoinf. 2022, 108, 102734. [Google Scholar] [CrossRef]
- Jiang, K.; Wang, Z.; Yi, P.; Wang, G.; Lu, T.; Jiang, J. Edge-Enhanced GAN for Remote Sensing Image Superresolution. IEEE Trans. Geosci. Remote Sens. 2019, 57, 5799–5812. [Google Scholar] [CrossRef]
- Rabbi, J.; Ray, N.; Schubert, M.; Chowdhury, S.; Chao, D. Small-Object Detection in Remote Sensing Images with End-to-End Edge-Enhanced GAN and Object Detector Network. Remote Sens. 2020, 12, 1432. [Google Scholar] [CrossRef]
- Liu, B.; Zhao, L.; Li, J.; Zhao, H.; Liu, W.; Li, Y.; Wang, Y.; Chen, H.; Cao, W. Saliency-Guided Remote Sensing Image Super-Resolution. Remote Sens. 2021, 13, 5144. [Google Scholar] [CrossRef]
- Lai, W.-S.; Huang, J.-B.; Ahuja, N.; Yang, M.-H. Deep Laplacian Pyramid Networks for Fast and Accurate Super-Resolution. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 5835–5843. [Google Scholar]
- Zhang, K.; Zuo, W.; Gu, S.; Zhang, L. Learning Deep CNN Denoiser Prior for Image Restoration. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 2808–2817. [Google Scholar]
- Zhang, K.; Zuo, W.; Zhang, L. Learning a Single Convolutional Super-Resolution Network for Multiple Degradations. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Salt Lake City, UT, USA, 18–23 June 2018; pp. 3262–3271. [Google Scholar]
- Dai, T.; Cai, J.; Zhang, Y.; Xia, S.-T.; Zhang, L. Second-Order Attention Network for Single Image Super-Resolution. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 11057–11066. [Google Scholar]
- Niu, B.; Wen, W.; Ren, W.; Zhang, X.; Yang, L.; Wang, S.; Zhang, K.; Cao, X.; Shen, H. Single Image Super-Resolution via a Holistic Attention Network. In Proceedings of the European Conference on Computer Vision (ECCV), Glasgow, UK, 23–28 August 2020; pp. 191–207. [Google Scholar]
- Cai, J.; Zeng, H.; Yong, H.; Cao, Z.; Zhang, L. Toward Real-World Single Image Super-Resolution: A New Benchmark and a New Model. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Republic of Korea, 27 October–2 November 2019; pp. 3086–3095. [Google Scholar]
- Wei, P.; Xie, Z.; Lu, H.; Zhan, Z.; Ye, Q.; Zuo, W.; Lin, L. Component Divide-and-Conquer for Real-World Image Super-Resolution. In Proceedings of the European Conference on Computer Vision (ECCV), Glasgow, UK, 23–28 August 2020; pp. 101–117. [Google Scholar]
- Zhang, X.; Chen, Q.; Ng, R.; Koltun, V. Zoom to Learn, Learn to Zoom. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 3757–3765. [Google Scholar]
- Zhang, N.; Wang, Y.; Zhang, X.; Xu, D.; Wang, X.; Ben, G.; Zhao, Z.; Li, Z. A Multi-Degradation Aided Method for Unsupervised Remote Sensing Image Super Resolution With Convolution Neural Networks. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–14. [Google Scholar] [CrossRef]
- Zhang, J.; Xu, T.; Li, J.; Jiang, S.; Zhang, Y. Single-Image Super Resolution of Remote Sensing Images with Real-World Degradation Modeling. Remote Sens. 2022, 14, 2895. [Google Scholar] [CrossRef]
- Aiazzi, B.; Baronti, S.; Selva, M. Improving Component Substitution Pansharpening Through Multivariate Regression of MS+Pan Data. IEEE Trans. Geosci. Remote Sens. 2007, 45, 3230–3239. [Google Scholar] [CrossRef]
- Yuan, Y.; Liu, S.; Zhang, J.; Zhang, Y.; Dong, C.; Lin, L. Unsupervised Image Super-Resolution Using Cycle-in-Cycle Generative Adversarial Networks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Salt Lake City, UT, USA, 18–22 June 2018; pp. 814–823. [Google Scholar]
- Lugmayr, A.; Danelljan, M.; Timofte, R. Unsupervised Learning for Real-World Super-Resolution. In Proceedings of the IEEE/CVF International Conference on Computer Vision Workshop (ICCVW), Seoul, Republic of Korea, 27–28 October 2019; pp. 3408–3416. [Google Scholar]
- Maeda, S. Unpaired Image Super-Resolution Using Pseudo-Supervision. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 291–300. [Google Scholar]
- Mao, X.; Li, Q.; Xie, H.; Lau, R.Y.K.; Wang, Z.; Smolley, S.P. Least Squares Generative Adversarial Networks. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 2813–2821. [Google Scholar]
- Mao, X.; Li, Q.; Xie, H.; Lau, R.Y.K.; Wang, Z.; Smolley, S.P. On the Effectiveness of Least Squares Generative Adversarial Networks. IEEE Trans. Pattern Anal. Mach. Intell. 2019, 41, 2947–2960. [Google Scholar] [CrossRef]
- Zhang, R.; Isola, P.; Efros, A.A.; Shechtman, E.; Wang, O. The Unreasonable Effectiveness of Deep Features as a Perceptual Metric. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 586–595. [Google Scholar]
- Fritsche, M.; Gu, S.; Timofte, R. Frequency Separation for Real-World Super-Resolution. In Proceedings of the IEEE/CVF International Conference on Computer Vision Workshop (ICCVW), Seoul, Republic of Korea, 27–28 October 2019; pp. 3599–3608. [Google Scholar]
- Jo, Y.; Yang, S.; Kim, S.J. Investigating Loss Functions for Extreme Super-Resolution. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Seattle, WA, USA, 14–19 June 2020; pp. 1705–1712. [Google Scholar]
- Isola, P.; Zhu, J.-Y.; Zhou, T.; Efros, A.A. Image-to-Image Translation with Conditional Adversarial Networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 1125–1134. [Google Scholar]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image Quality Assessment: From Error Visibility to Structural Similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef]
- Yuhas, R.H.; Goetz, A.F.H.; Boardman, J.W. Discrimination among Semi-Arid Landscape Endmembers Using the Spectral Angle Mapper (SAM) Algorithm. In Proceedings of the Summaries of the Third Annu. JPL Airborne Geoscience Workshop, Pasadena, CA, USA, 1–5 June 1992; pp. 147–149. [Google Scholar]
- Liu, J.G. Smoothing Filter-based Intensity Modulation: A Spectral Preserve Image Fusion Technique for Improving Spatial Details. Int. J. Remote Sens. 2000, 21, 3461–3472. [Google Scholar] [CrossRef]
- Wang, Z.; Bovik, A.C. A Universal Image Quality Index. IEEE Signal Process. Lett. 2002, 9, 81–84. [Google Scholar] [CrossRef]
- Mittal, A.; Soundararajan, R.; Bovik, A.C. Making a “Completely Blind” Image Quality Analyzer. IEEE Signal Process. Lett. 2013, 20, 209–212. [Google Scholar] [CrossRef]
- Guo, Y.; Chen, J.; Wang, J.; Chen, Q.; Cao, J.; Deng, Z.; Xu, Y.; Tan, M. Closed-Loop Matters: Dual Regression Networks for Single Image Super-Resolution. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 5406–5415. [Google Scholar]
- Qin, X.; Zhang, Z.; Huang, C.; Gao, C.; Dehghan, M.; Jagersand, M. BASNet: Boundary-Aware Salient Object Detection. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 7471–7481. [Google Scholar]
- Lei, S.; Shi, Z.; Zou, Z. Coupled Adversarial Training for Remote Sensing Image Super-Resolution. IEEE Trans. Geosci. Remote Sens. 2020, 58, 3633–3643. [Google Scholar] [CrossRef]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative Adversarial Networks. Commun. ACM 2020, 63, 139–144. [Google Scholar] [CrossRef]
- Jolicoeur-Martineau, A. The Relativistic Discriminator: A Key Element Missing from Standard GAN. In Proceedings of the International Conference on Learning Representations (ICLR), New Orleans, LA, USA, 6–9 May 2019; pp. 1–26. [Google Scholar]
- Zhou, Y.; Deng, W.; Tong, T.; Gao, Q. Guided Frequency Separation Network for Real-World Super-Resolution. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Seattle, WA, USA, 14–19 June 2020; pp. 1722–1731. [Google Scholar]
- Choi, J.; Yu, K.; Kim, Y. A New Adaptive Component-Substitution-Based Satellite Image Fusion by Using Partial Replacement. IEEE Trans. Geosci. Remote Sens. 2011, 49, 295–309. [Google Scholar] [CrossRef]
- Choi, J.; Kim, G.; Park, N.; Park, H.; Choi, S. A Hybrid Pansharpening Algorithm of VHR Satellite Images that Employs Injection Gains Based on NDVI to Reduce Computational Costs. Remote Sens. 2017, 9, 976. [Google Scholar] [CrossRef]
- Chavez, P.; Sides, S.C.; Anderson, J.A. Comparison of Three Different Methods to Merge Multiresolution and Multispectral Data: Landsat TM and SPOT Panchromatic. Photogramm. Eng. Remote Sens. 1991, 57, 295–303. [Google Scholar]
- Otazu, X.; Gonzalez-Audicana, M.; Nunez, O.F.J. Introduction of Sensor Spectral Response into Image Fusion Methods. Application to Wavelet-Based Methods. IEEE Trans. Geosci. Remote Sens. 2005, 43, 2376–2385. [Google Scholar] [CrossRef]
- Vivone, G.; Restaino, R.; Mura, M.D.; Licciardi, G.; Chanussot, J. Contrast and Error-Based Fusion Schemes for Multispectral Image Pansharpening. IEEE Geosci. Remote Sens. Lett. 2014, 11, 930–934. [Google Scholar] [CrossRef]
- Venkatanath, N.; Praneeth, D.; Chandrasekhar, B.M.; Channappayya, S.S.; Medasani, S.S. Blind Image Quality Evaluation Using Perception Based Features. In Proceedings of the 21st National Conference on Communications (NCC), Mumbai, India, 27 February–1 March 2015; pp. 1–6. [Google Scholar]
- Mittal, A.; Moorthy, A.K.; Bovik, A.C. Blind/Referenceless Image Spatial Quality Evaluator. In Proceedings of the 45th Asilomar Conference on Signals, Systems and Computers (ASILOMAR), Pacific Grove, CA, USA, 6–9 November 2011; pp. 723–727. [Google Scholar]







| Method | PSNR | SSIM | SAM | ERGAS | UIQI | LPIPS | NIQE | |
|---|---|---|---|---|---|---|---|---|
| Bicubic | 30.2986 | 0.8173 | 0.0242 | 63.0769 | 0.4173 | 0.3545 | 7.2993 | |
| CNN-based | EDSR [11] | 31.9558 | 0.8586 | 0.0217 | 52.4538 | 0.4952 | 0.3247 | 7.3323 |
| D-DBPN [12] | 31.1050 | 0.8397 | 0.0248 | 57.6184 | 0.4528 | 0.3390 | 7.2362 | |
| RRDBNet [15] | 31.7101 | 0.8540 | 0.0238 | 53.9245 | 0.4855 | 0.3288 | 7.7258 | |
| RDN [14] | 32.5940 | 0.8704 | 0.0223 | 49.0862 | 0.5219 | 0.3092 | 7.3097 | |
| RCAN [13] | 32.1932 | 0.8626 | 0.0234 | 51.1209 | 0.5066 | 0.3107 | 7.2772 | |
| HAN [27] | 32.8207 | 0.8752 | 0.0215 | 47.8851 | 0.5359 | 0.2980 | 7.5154 | |
| DRN-L [48] | 32.0414 | 0.8615 | 0.0221 | 51.9685 | 0.5014 | 0.3222 | 7.7383 | |
| GAN-based | SRGAN [9] | 29.1961 | 0.7702 | 0.0560 | 72.4688 | 0.3420 | 0.3231 | 4.8997 |
| ESRGAN [15] | 29.2197 | 0.7892 | 0.0449 | 72.1651 | 0.3904 | 0.2870 | 5.0202 | |
| ESRGAN-FS [40] | 28.9710 | 0.7827 | 0.0504 | 74.3983 | 0.3881 | 0.2852 | 4.9360 | |
| EESRGAN [21] | 30.4883 | 0.8138 | 0.0350 | 62.1157 | 0.4329 | 0.2669 | 5.5291 | |
| SG-GAN [22] | 30.9505 | 0.8310 | 0.0293 | 58.6363 | 0.4378 | 0.3073 | 5.5822 | |
| BLG-GAN (1-stage) | 31.4131 | 0.8373 | 0.0272 | 55.8005 | 0.4557 | 0.2740 | 5.7224 | |
| BLG-GAN | 32.1416 | 0.8518 | 0.0247 | 51.8453 | 0.4883 | 0.2349 | 5.7999 | |
| Method | PSNR | SSIM | SAM | ERGAS | UIQI | LPIPS | NIQE | |
| Bicubic | 30.1314 | 0.8158 | 0.0246 | 54.9347 | 0.4392 | 0.3601 | 7.2807 | |
| CNN-based | EDSR [11] | 31.5149 | 0.8509 | 0.0244 | 47.0863 | 0.5032 | 0.3342 | 7.9368 |
| D-DBPN [12] | 31.1819 | 0.8423 | 0.0249 | 48.8536 | 0.4822 | 0.3444 | 7.9284 | |
| RRDBNet [15] | 31.2424 | 0.8463 | 0.0245 | 48.4882 | 0.4920 | 0.3424 | 8.2237 | |
| RDN [14] | 31.7136 | 0.8566 | 0.0248 | 46.0044 | 0.5136 | 0.3246 | 7.8459 | |
| RCAN [13] | 31.5306 | 0.8525 | 0.0235 | 46.8795 | 0.5048 | 0.3270 | 7.6668 | |
| HAN [27] | 31.8671 | 0.8612 | 0.0239 | 45.2343 | 0.5245 | 0.3151 | 7.9126 | |
| DRN-L [48] | 31.5219 | 0.8537 | 0.0231 | 46.9640 | 0.5080 | 0.3310 | 8.0392 | |
| GAN-based | SRGAN [9] | 28.9943 | 0.7653 | 0.0544 | 62.8320 | 0.3508 | 0.3301 | 5.1271 |
| ESRGAN [15] | 29.0857 | 0.7798 | 0.0582 | 62.1098 | 0.4006 | 0.3036 | 4.9066 | |
| ESRGAN-FS [40] | 29.2271 | 0.7899 | 0.0435 | 61.7939 | 0.4184 | 0.2894 | 5.1028 | |
| EESRGAN [21] | 30.3289 | 0.8076 | 0.0339 | 53.6708 | 0.4381 | 0.2781 | 5.3389 | |
| SG-GAN [22] | 30.4923 | 0.8200 | 0.0312 | 52.7853 | 0.4532 | 0.3181 | 5.4784 | |
| BLG-GAN (1-stage) | 30.8558 | 0.8267 | 0.0306 | 50.4641 | 0.4580 | 0.2858 | 5.5300 | |
| BLG-GAN | 31.1871 | 0.8331 | 0.0272 | 48.8193 | 0.4769 | 0.2493 | 5.6032 | |
| PSNR | SSIM | SAM | ERGAS | UIQI | LPIPS | NIQE | |
|---|---|---|---|---|---|---|---|
| Residual block with BN [9] | 31.5495 | 0.8392 | 0.0361 | 60.1968 | 0.4645 | 0.2966 | 5.5730 |
| Residual block without BN | 32.0368 | 0.8486 | 0.0257 | 52.3808 | 0.4740 | 0.2845 | 5.6019 |
| RRDB [15] | 32.1078 | 0.8516 | 0.0255 | 51.9306 | 0.4831 | 0.2775 | 5.2930 |
| RCAB [13] | 32.2062 | 0.8552 | 0.0242 | 51.4806 | 0.4927 | 0.2636 | 5.8955 |
| PSNR | SSIM | SAM | ERGAS | UIQI | LPIPS | NIQE | |
|---|---|---|---|---|---|---|---|
| Residual block with BN [9] | 30.8659 | 0.8255 | 0.0289 | 51.2175 | 0.4572 | 0.3057 | 5.4436 |
| Residual block without BN | 30.9909 | 0.8275 | 0.0269 | 49.7892 | 0.4620 | 0.3025 | 5.4305 |
| RRDB [15] | 31.1359 | 0.8308 | 0.0264 | 49.0844 | 0.4664 | 0.2953 | 5.1734 |
| RCAB [13] | 31.2822 | 0.8362 | 0.0255 | 48.2146 | 0.4806 | 0.2815 | 5.6038 |
| Type of Discriminator | Type of GAN Loss | PSNR | SSIM | SAM | ERGAS | UIQI | LPIPS | NIQE |
|---|---|---|---|---|---|---|---|---|
| SRGAN-D [9] | Standard [51] | 31.1322 | 0.8182 | 0.0345 | 58.0834 | 0.4363 | 0.2905 | 5.1780 |
| LSGAN [37] | 32.6198 | 0.8726 | 0.0219 | 48.9879 | 0.5287 | 0.2977 | 7.9888 | |
| RaGAN [52] | 30.7263 | 0.8099 | 0.0380 | 61.2168 | 0.4356 | 0.2923 | 5.1638 | |
| PatchGAN [42] | Standard [51] | 31.9389 | 0.8455 | 0.0255 | 53.1523 | 0.4805 | 0.2651 | 5.6226 |
| LSGAN [37] | 32.2062 | 0.8552 | 0.0242 | 51.4806 | 0.4927 | 0.2636 | 5.8955 |
| Type of Discriminator | Type of GAN Loss | PSNR | SSIM | SAM | ERGAS | UIQI | LPIPS | NIQE |
|---|---|---|---|---|---|---|---|---|
| SRGAN-D [9] | Standard [51] | 30.4062 | 0.8084 | 0.0341 | 53.2263 | 0.4388 | 0.3042 | 5.3235 |
| LSGAN [37] | 31.6627 | 0.8575 | 0.0233 | 46.2162 | 0.5163 | 0.3155 | 8.0493 | |
| RaGAN [52] | 30.5378 | 0.8237 | 0.0344 | 52.4700 | 0.4546 | 0.3233 | 5.6434 | |
| PatchGAN [42] | Standard [51] | 30.9809 | 0.8253 | 0.0271 | 49.9844 | 0.4666 | 0.2852 | 5.3255 |
| LSGAN [37] | 31.2822 | 0.8362 | 0.0255 | 48.2146 | 0.4806 | 0.2815 | 5.6038 |
| Type of Perceptual Loss | PSNR | SSIM | SAM | ERGAS | UIQI | LPIPS | NIQE |
|---|---|---|---|---|---|---|---|
| No perceptual loss | 32.2062 | 0.8552 | 0.0242 | 51.4806 | 0.4927 | 0.2636 | 5.8955 |
| LPIPS [39] | 32.1416 | 0.8518 | 0.0247 | 51.8453 | 0.4883 | 0.2349 | 5.7999 |
| VGG19-L1 | 32.0325 | 0.8474 | 0.0264 | 52.4761 | 0.4802 | 0.2451 | 6.0107 |
| VGG19-L2 | 31.9628 | 0.8440 | 0.0278 | 52.8709 | 0.4734 | 0.2459 | 5.7429 |
| Type of Perceptual Loss | PSNR | SSIM | SAM | ERGAS | UIQI | LPIPS | NIQE |
|---|---|---|---|---|---|---|---|
| No perceptual loss | 31.2822 | 0.8362 | 0.0255 | 48.2146 | 0.4806 | 0.2815 | 5.6038 |
| LPIPS [39] | 31.1871 | 0.8331 | 0.0272 | 48.8193 | 0.4769 | 0.2493 | 5.6032 |
| VGG19-L1 | 31.0858 | 0.8319 | 0.0272 | 49.2414 | 0.4714 | 0.2629 | 5.5312 |
| VGG19-L2 | 30.9904 | 0.8263 | 0.0293 | 49.8302 | 0.4617 | 0.2653 | 5.5133 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chung, M.; Jung, M.; Kim, Y. Enhancing Remote Sensing Image Super-Resolution Guided by Bicubic-Downsampled Low-Resolution Image. Remote Sens. 2023, 15, 3309. https://doi.org/10.3390/rs15133309
Chung M, Jung M, Kim Y. Enhancing Remote Sensing Image Super-Resolution Guided by Bicubic-Downsampled Low-Resolution Image. Remote Sensing. 2023; 15(13):3309. https://doi.org/10.3390/rs15133309
Chicago/Turabian StyleChung, Minkyung, Minyoung Jung, and Yongil Kim. 2023. "Enhancing Remote Sensing Image Super-Resolution Guided by Bicubic-Downsampled Low-Resolution Image" Remote Sensing 15, no. 13: 3309. https://doi.org/10.3390/rs15133309
APA StyleChung, M., Jung, M., & Kim, Y. (2023). Enhancing Remote Sensing Image Super-Resolution Guided by Bicubic-Downsampled Low-Resolution Image. Remote Sensing, 15(13), 3309. https://doi.org/10.3390/rs15133309






