CGC-Net: A Context-Guided Constrained Network for Remote-Sensing Image Super Resolution
Abstract
1. Introduction
- (1)
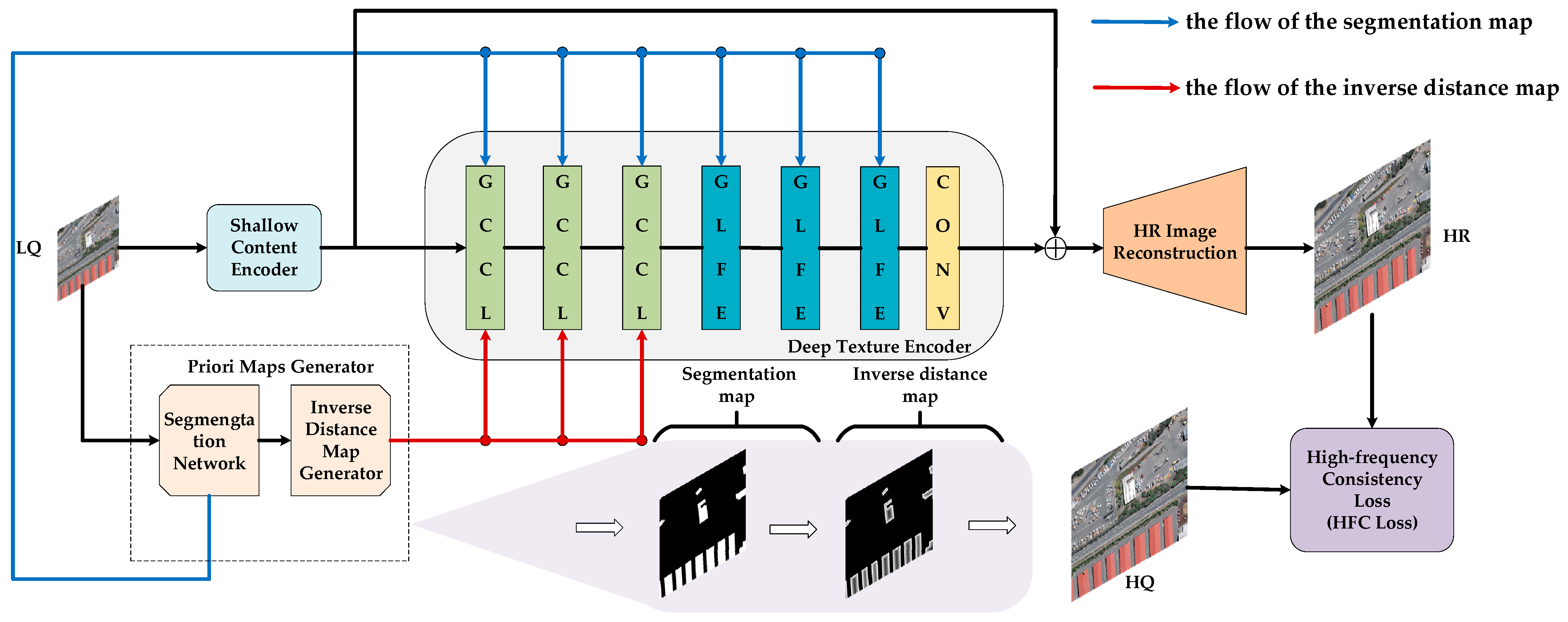
- Firstly, we design a prior map generator to generate the segmentation maps and the inverse distance maps. These two maps are applied as prior information for the proposed GCCL module and GLFE module.
- (2)
- We propose a global context-constrained layer (GCCL), which effectively utilizes the prior knowledge to model high-quality features with global context constraints.
- (3)
- To enhance the semantic feature with local details, we propose the guided local feature enhancement block (GLFE), which obtains features with local texture context via a learnable guided filter from deeper layers.
- (4)
- To enhance the gradient consistency between the reconstructed HR image and the original HQ image, we develop a novel high-frequency consistency loss (HFC loss) by training a three-layer convolution neural network to simulate the canny boundary detection operator [23]. Then, the trained network is used as the loss network to enhance the high-frequency details of the reconstructed HR image.
2. Related Work
2.1. Image Super-Resolution
2.2. Prior Knowledge-Based Image Super-Resolution
2.3. Perceptual Loss
3. Method
3.1. Overview of the Proposed Network
3.2. Prior Maps Generator
| Algorithm 1: Inverse Distance Map Generator |
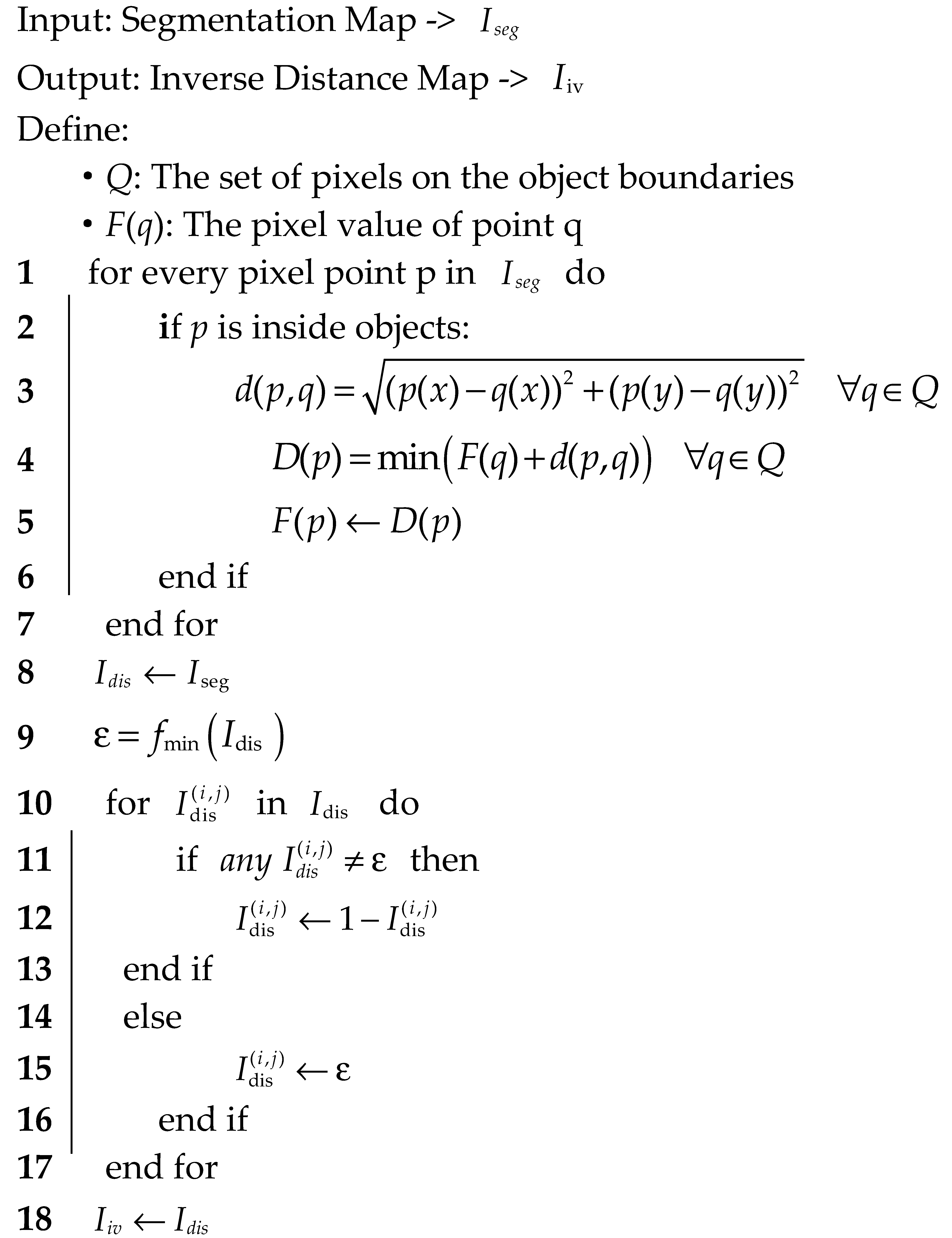 |
3.3. Global Contex-Constrained Layer (GCCL)
3.4. Guided Local Feature Enhancement Block (GLFE)
3.5. Loss Functions
4. Experiments and Analysis
4.1. Datasets and Implementation Details
4.1.1. Datasets
4.1.2. Implementation Details and Metrics
4.2. Comparison Experiments on the Inria Aerial Image Dataset
4.3. Comparison Experiments on the WHU Building Dataset
4.4. Comparison Experiments on the ISPRS Potsdam Dataset
4.5. Model Efficiency Analysis
4.6. Ablation Studies and Analysis
4.6.1. Hyperparameter Tuning of Weight Loss
4.6.2. The Influence of Using Different Images as Guided Images
4.6.3. Components Ablations
4.6.4. CGC-Net with Different Training Scales
4.6.5. Adaptability to Noise
4.6.6. Lower and Upper Boundaries of the Proposed CGC-Net
4.6.7. The Influence of Different Reconstructed HR Datasets on Segmentation Task
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sishodia, R.P.; Ray, R.L.; Singh, S.K. Applications of Remote Sensing in Precision Agriculture: A Review. Remote Sens. 2020, 12, 3136. [Google Scholar] [CrossRef]
- Majumdar, S. The Role of Remote Sensing and GIS in Military Strategy to Prevent Terror Attacks. Intell. Data Anal. Terror. Threat. Predict. Archit. Methodol. Tech. Appl. 2021, 14, 79–94. [Google Scholar]
- Yang, L.; Shi, L.; Sun, W.; Yang, J.; Li, P.; Li, D.; Liu, S.; Zhao, L. Radiometric and Polarimetric Quality Validation of Gaofen-3 over a Five-Year Operation Period. Remote Sens. 2023, 15, 1605. [Google Scholar] [CrossRef]
- Giovos, R.; Tassopoulos, D.; Kalivas, D.; Lougkos, N.; Priovol, A. Remote Sensing Vegetation Indices in Viticulture: A Critical Review. Agriculture 2021, 11, 457. [Google Scholar] [CrossRef]
- Shimoni, M.; Haelterman, R.; Perneel, C. Hypersectral Imaging for Military and Security Applications: Combining Myriad Processing and Sensing Techniques. IEEE Geosci. Remote Sens. Mag. 2019, 7, 101–117. [Google Scholar] [CrossRef]
- Zhu, Q.; Zhen, L.; Zhang, Y.; Guan, Q. Building Extraction from High Spatial Resolution Remote Sensing Images via Multiscale-Aware and Segmentation-Prior Conditional Random Fields. Remote Sens. 2020, 12, 3983. [Google Scholar] [CrossRef]
- Zhang, L.; Dong, R.; Yuan, S.; Li, W.; Zheng, J.; Fu, H. Making Low-Resolution Satellite Images Reborn: A Deep Learning Approach for Super-Resolution Building Extraction. Remote Sens. 2021, 13, 2872. [Google Scholar] [CrossRef]
- Schuegraf, P.; Bittner, K. Automatic Building Footprint Extraction from Multi-Resolution Remote Sensing Images Using a Hybrid FCN. ISPRS Int. J. Geo-Inf. 2019, 8, 191. [Google Scholar] [CrossRef]
- Zeng, Y.; Guo, Y.; Li, J. Recognition and extraction of high-resolution satellite remote sensing image buildings based on deep learning. Neural Comput. Appl. 2022, 34, 2691–2706. [Google Scholar] [CrossRef]
- Dong, Z.; Wang, M.; Wang, Y.; Zhu, Y.; Zhang, Z. Object Detection in High Resolution Remote Sensing Imagery Based on Convolutional Neural Networks With Suitable Object Scale Features. IEEE Trans. Geosci. Remote Sens. 2020, 58, 2104–2114. [Google Scholar] [CrossRef]
- Su, Y.; Wu, Y.; Wang, M.; Wang, F.; Cheng, J. Semantic Segmentation of High Resolution Remote Sensing Image Based on Batch-Attention Mechanism. In IEEE International Geoscience and Remote Sensing Symposium; IEEE: Piscataway, NJ, USA, 2019. [Google Scholar]
- Guo, Z.; Wu, G.; Song, X.; Yuan, W.; Chen, Q.; Zhang, H.; Shi, X.; Xu, M.; Xu, Y.; Shibasaki, R.; et al. Super-Resolution Integrated Building Semantic Segmentation for Multi-Source Remote Sensing Imagery. IEEE Access 2019, 7, 99381–99397. [Google Scholar] [CrossRef]
- Ding, Y.; Zhang, Z.; Zhao, X.; Cai, W.; Yang, N.; Hu, H.; Yuan, C.; Cai, W. Unsupervised Self-Correlated Learning Smoothy Enhanced Locality Preserving Graph Convolution Embedding Clustering for Hyperspectral Images. TGRS 2022, 60. [Google Scholar] [CrossRef]
- Zhang, J.; Xu, T.; Li, J.; Jiang, S.; Zhang, Y. Single-Image Super Resolution of Remote Sensing Images with Real-World Degradation Modeling. Remote Sens. 2022, 14, 2895. [Google Scholar] [CrossRef]
- Dong, C.; Loy, C.C.; He, K.; Tang, X. Image Super-Resolution Using Deep Convolutional Networks. IEEE Trans. Pattern Anal. Mach. Intell. 2014, 38, 295–307. [Google Scholar] [CrossRef]
- Liu, Z.; Lin, Y.; Cao, Y.; Hu, H.; Wei, Y.; Zhang, Z.; Lin, S.; Guo, B. Swin Transformer: Hierarchical Vision Transformer using Shifted Windows. arXiv 2021, arXiv:2103.14030. [Google Scholar]
- Liang, J.; Cao, J.; Sun, G.; Zhang, K.; Gool, L.V.; Timofte, R. SwinIR: Image Restoration Using Swin Transformer. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV) Workshops, Montreal, BC, Canada, 11–17 October 2021. [Google Scholar]
- Zamir, S.W.; Arora, A.; Khan, S.; Hayat, M.; Khan, F.S.; Yang, M.H. Restormer: Efficient Transformer for High-Resolution Image Restoration. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), New Orleans, LA, USA, 18–24 June 2022. [Google Scholar]
- Ding, Y.; Zhang, Z.; Zhao, X.; Hong, D.; Wei, C.; Yang, N.; Wang, B. Multi-scale receptive fields: Graph attention neural network for hyperspectral image classification. Expert Syst. Appl. 2023, 223, 119858. [Google Scholar] [CrossRef]
- Zhang, Z.; Ding, Y.; Zhao, X.; Siye, L.; Yang, N.; Cai, Y.; Zhan, Y. Multireceptive field: An adaptive path aggregation graph neural framework for hyperspectral image classification. Expert Syst. Appl. 2023, 217, 119508. [Google Scholar] [CrossRef]
- Zhang, D.; Shao, J.; Li, X.; Shen, H. Remote Sensing Image Super-Resolution via Mixed High-Order Attention Network. IEEE Trans. Geosci. Remote Sens. 2021, 59, 5183–5196. [Google Scholar] [CrossRef]
- Wang, J.; Shao, Z.; Huang, X.; Lu, T. From Artifact Removal to Super-Resolution. IEEE Trans. Geosci. Remote Sens. 2022, 60. [Google Scholar] [CrossRef]
- Canny, J. A Computational Approach to Edge Detection. IEEE Trans. Pattern Anal. Mach. Intell. 1987, PAMI-8, 679–698. [Google Scholar] [CrossRef]
- Yang, J.; Wright, J.; Huang, W.S.; Ma, Y. Image Super-Resolution Via Sparse Representation. IEEE Trans. Image Process. 2010, 19, 2861–2873. [Google Scholar] [CrossRef] [PubMed]
- Aharon, M.; Elad, M.; Bruckstein, A. K-SVD: An algorithm for designing overcomplete dictionaries for sparse representation. IEEE Trans. Signal Process. 2006, 54, 4311–4322. [Google Scholar] [CrossRef]
- Zhang, Y.; Sun, L.; Yan, C.; Ji, X.; Dai, Q. Adaptive Residual Networks for High-Quality Image Restoration. IEEE Trans. Image Process. 2018, 27, 3150–3163. [Google Scholar] [CrossRef] [PubMed]
- Dong, C.; Loy, C.; Tang, X. Accelerating the super-resolution convolutional neural network. In Proceedings of the Computer Vision–ECCV 2016: 14th European Conference, Amsterdam, The Netherlands, 11–14 October 2016. [Google Scholar]
- Shi, W.; Caballero, J.; Huszár, F.; Totz, J.; Aitken, A.P.; Bishop, R.; Rueckert, D.; Wang, Z. Real-Time Single Image and Video Super-Resolution Using an Efficient Sub-Pixel Convolutional Neural Network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016. [Google Scholar]
- BenGio, Y.; Simard, P.; Fransconi, P. Learning Long-Term Dependencies with Gradient Descent is Difficult. IEEE Trans. Neural Netw. 1994, 5, 157–166. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.; Lee, J.K.; Lee, K.M. Accurate Image Super-Resolution Using Very Deep Convolutional Networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 1646–1654. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016. [Google Scholar]
- Jung, Y.; Choi, Y.; Sim, J.; Kim, L. eSRCNN: A Framework for Optimizing Super-Resolution Tasks on Diverse Embedded CNN Accelerators. In Proceedings of the IEEE/ACM International Conference on Computer-Aided Design, Westminster, CO, USA, 4–7 November 2019. [Google Scholar]
- Lai, W.; Huang, J.; Ahuja, N.; Yang, M. Deep Laplacian Pyramid Networks for Fast and Accurate Super-Resolution. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–27 July 2017. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Lukasz, K.; Polosukhin, L. Attention Is All You Need. arXiv. Adv. Neural Inf. Process. Syst. 2017, 30. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, K.; Wang, L.; Zhong, B.; Fu, Y. Image Super-Resolution Using Very Deep Residual Channel Attention Networks. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018. [Google Scholar]
- Yang, F.; Yang, H.; Fu, J.; Lu, H.; Guo, B. Learning Texture Transformer Network for Image Super-Resolution. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020. [Google Scholar]
- Loshchilov, I.; Hutter, F. Decoupled Weight Decay Regularization. In Proceedings of the International Conference on Learning Representations (ICLR), Toulon, France, 24–26 April 2017. [Google Scholar]
- Liang, J.; Wang, J.; Zhou, S.; Gong, Y.; Zheng, N. Incorporating image priors with deep convolutional neural networks for image super-resolution. Neurocomputing 2016, 194, 340–347. [Google Scholar] [CrossRef]
- Kim, K.; Chun, S.Y. SREdgeNet: Edge Enhanced Single Image Super Resolution using Dense Edge Detection Network and Feature Merge Network. arXiv 2018, arXiv:1812.07174. [Google Scholar]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef]
- Johnson, J.; Alahi, A.; Li, F. Perceptual Losses for Real-Time Style Transfer and Super-Resolution. In Proceedings of the Computer Vision—ECCV 2016, Amsterdam, The Netherlands, 11–14 October 2016. [Google Scholar]
- Bruna, J.; Sprechmann, P.; LeCun, Y. Super-Resolution with Deep Convolutional Sufficient Statistics. arXiv 2016, arXiv:1511.05666. [Google Scholar]
- Li, C.; Wand, M. Precomputed Real-Time Texture Synthesis with Markovian Generative Adversarial Networks. In Proceedings of the Computer Vision—ECCV 2016, Amsterdam, The Netherlands, 11–14 October 2016. [Google Scholar]
- Li, C.; Wand, M. Combining Markov Random Fields and Convolutional Neural Networks for Image Synthesis. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016. [Google Scholar]
- Rad, M.S.; Bozorgtabar, B.; Marti, U.; Basler, M.; Ekenel, H.; Thiran, J. SROBB: Targeted Perceptual Loss for Single Image Super-Resolution. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Republic of Korea, 27 October–2 November 2019. [Google Scholar]
- Chen, Y.; Dapogny, A.; Cord, M. SEMEDA: Enhancing Segmentation Precision with Semantic Edge Aware Loss. Pattern Recognit. 2019, 108, 107557. [Google Scholar] [CrossRef]
- Chen, L.; Zhu, Y.; Papandreou, G.; Schoroff, F.; Adam, H. Encoder-Decoder with Atrous Separable Convolution for Semantic Image Segmentation. arXiv 2018, arXiv:1802.02611. [Google Scholar]
- Saha, S.; Obukhov, A.; Paudel, D.; Kanakis, M.; Chen, Y.; Georgoulis, S.; Gool, L. Learning to Relate Depth and Semantics for Unsupervised Domain Adaptation. arXiv 2021, arXiv:2105.07830. [Google Scholar]
- Liu, W.; Wen, Y.; Yu, Z.; Yang, M. Large-Margin Softmax Loss for Convolutional Neural Networks. arXiv 2016, arXiv:1612.02295. [Google Scholar]
- Schoenholz, S.S.; Gilmer, J.; Ganguli, S.; Sohl-Dickstein, J. Deep Information Propagation. arXiv 2016. [Google Scholar] [CrossRef]
- Zhang, Y.; Han, X.; Zhang, H.; Zhao, L. Edge detection algorithm of image fusion based on improved Sobel operator. In Proceedings of the IEEE 3rd Information Technology and Mechatronics Engineering Conference, Chongqing, China, 3–5 October 2017. [Google Scholar]
- He, K.; Sun, J.; Tang, X. Guided Image Filtering. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 35, 1397–1409. [Google Scholar] [CrossRef]
- Goodfellow, L.J.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative Adversarial Networks. IEEE Signal Process. Mag. 2018, 35, 53–65. [Google Scholar] [CrossRef]
- Maggiori, E.; Tarabalka, Y.; Charpiat, G.; Alliez, P. Can semantic labelling methods generalize to any city? The inria aerial image labelling benchmark. In Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017; pp. 3226–3229. [Google Scholar]
- Ji, S.; Wei, S.; Lu, M. Fully Convolutional Networks for Multisource Building Extraction From an Open Aerial and Satellite Imagery Data Set. IEEE Trans. Geosci. Remote Sens. 2018, 574, 574–586. [Google Scholar] [CrossRef]
- ISPRS Potsdam 2D Semantic Labeling Dataset. Available online: https://www.isprs.org/education/benchmarks/UrbanSemLab/2d-sem-label-potsdam.aspx (accessed on 15 December 2022).
- Lim, B.; Son, S.; Kim, H.; Nah, S.; Lee, K.M. Enhanced Deep Residual Networks for Single Image Super-Resolution. arXiv 2017, arXiv:1707.02921. [Google Scholar]
- Zhao, J.; Ma, Y.; Chenm, F.; Shang, E.; Yao, W.; Zhang, S.; Yang, J. SA-GAN: A Second Order Attention Generator Adversarial Network with Region Aware Strategy for Real Satellite Images Super Resolution Reconstruction. Remote Sens. 2023, 15, 1391. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, Z.; Lin, Z.L.; Qi, H. Image Super-Resolution by Neural Texture Transfer. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 7974–7983. [Google Scholar]
- Healy, D.J. Fast Fourier transforms for Nonequispaced Data. SIAM J. Sci. Comput. 1998, 19, 529–545. [Google Scholar]
- Mao, X.; Shen, C.; Yang, Y. Image Restoration Using Convolutional Auto-encoders with Symmetric Skip Connections. arXiv 2016, arXiv:1606.08921. [Google Scholar]
- Portilla, J.; Strela, V.; Wainwright, M.J.; Simoncelli, E.P. Imageenoising using scale mixtures of Gaussians in the wavelet domain. IEEE Trans. Image Process. 2003, 12, 1338–1351. [Google Scholar] [CrossRef] [PubMed]
- Xie, E.; Wang, W.; Yu, Z.; Anandkumar, A.; Alvarez, J.M.; Luo, P. SegFormer: Simple and Efficient Design for Semantic Segmentation with Transformers. Adv. Neural Inf. Process. Syst. 2021, 34, 12077–12090. [Google Scholar]













| Methods | Scales | PSNR↑ | SSIM↑ | LPIPS↓ |
|---|---|---|---|---|
| SRCNN [15] | 33.9729 | 0.8680 | 0.0963 | |
| VDSR [30] | 34.1635 | 0.8710 | 0.0880 | |
| EDSR [57] | 34.4402 | 0.8779 | 0.0800 | |
| RCAN [35] | 34.4525 | 0.8782 | 0.0776 | |
| SwinIR [17] | ×2 | 34.4400 | 0.8784 | 0.0831 |
| Restormer [18] | 34.4450 | 0.8787 | 0.0772 | |
| MHAN [21] | 34.3525 | 0.8774 | 0.0783 | |
| SA-GAN [58] | 34.3901 | 0.8777 | 0.0801 | |
| CGC-Net (Ours) | 34.8202 | 0.8886 | 0.0715 | |
| SRCNN [15] | 29.6069 | 0.7058 | 0.1787 | |
| VDSR [30] | 29.6957 | 0.7110 | 0.1592 | |
| EDSR [57] | 29.8370 | 0.7153 | 0.1401 | |
| RCAN [35] | 29.8044 | 0.7141 | 0.1431 | |
| SwinIR [17] | ×4 | 29.8411 | 0.7150 | 0.1409 |
| Restormer [18] | 29.8405 | 0.7009 | 0.1422 | |
| MHAN [21] | 29.8212 | 0.7121 | 0.1410 | |
| SA-GAN [58] | 29.8016 | 0.7119 | 0.1417 | |
| CGC-Net (Ours) | 30.1717 | 0.7249 | 0.1376 |
| Methods | Scales | PSNR↑ | SSIM↑ | LPIPS↓ |
|---|---|---|---|---|
| SRCNN [15] | 25.7705 | 0.7119 | 0.1326 | |
| VDSR [30] | 26.3692 | 0.7391 | 0.1124 | |
| EDSR [57] | 26.7306 | 0.7531 | 0.1031 | |
| RCAN [35] | 26.7347 | 0.7532 | 0.1030 | |
| SwinIR [17] | ×2 | 26.7504 | 0.7543 | 0.1023 |
| Restormer [18] | 26.6706 | 0.7510 | 0.1048 | |
| MHAN [21] | 26.7312 | 0.7533 | 0.1034 | |
| SA-GAN [58] | 26.6692 | 0.7507 | 0.1051 | |
| CGC-Net (Ours) | 27.0772 | 0.7615 | 0.1005 | |
| SRCNN [15] | 22.8173 | 0.4857 | 0.2252 | |
| VDSR [30] | 23.1390 | 0.5186 | 0.1932 | |
| EDSR [57] | 23.5048 | 0.5464 | 0.1824 | |
| RCAN [35] | 23.5346 | 0.5481 | 0.1818 | |
| SwinIR [17] | ×4 | 23.5216 | 0.5468 | 0.1820 |
| Restormer [18] | 23.5754 | 0.5522 | 0.1804 | |
| MHAN [21] | 23.5122 | 0.5466 | 0.1822 | |
| SA-GAN [58] | 23.4817 | 0.5452 | 0.1841 | |
| CGC-Net (Ours) | 24.0004 | 0.5626 | 0.1780 |
| Methods | Scales | PSNR↑ | SSIM↑ | LPIPS↓ |
|---|---|---|---|---|
| SRCNN [15] | 33.4417 | 0.8521 | 0.1206 | |
| VDSR [30] | 34.1902 | 0.8645 | 0.1056 | |
| EDSR [57] | 34.8442 | 0.8764 | 0.0944 | |
| RCAN [35] | 34.8863 | 0.8784 | 0.0947 | |
| SwinIR [17] | ×4 | 34.7476 | 0.8750 | 0.0951 |
| Restormer [18] | 34.8876 | 0.8789 | 0.0956 | |
| MHAN [21] | 34.8246 | 0.8762 | 0.0960 | |
| SA-GAN [58] | 34.6547 | 0.8709 | 0.0993 | |
| CGC-Net (Ours) | 34.9884 | 0.8802 | 0.0898 | |
| SRCNN [15] | 29.9821 | 0.7689 | 0.2151 | |
| VDSR [30] | 30.2869 | 0.7787 | 0.1894 | |
| EDSR [57] | 31.0672 | 0.7955 | 0.1727 | |
| RCAN [35] | 31.0507 | 0.7953 | 0.1734 | |
| SwinIR [17] | ×8 | 30.9103 | 0.7905 | 0.1751 |
| Restormer [18] | 31.0779 | 0.7994 | 0.1726 | |
| MHAN [21] | 31.0501 | 0.7954 | 0.1732 | |
| SA-GAN [58] | 31.0320 | 0.7948 | 0.1740 | |
| CGC-Net (Ours) | 31.1674 | 0.7985 | 0.1729 |
| Method | Param (M) | FLOPs (G) |
|---|---|---|
| SRCNN [15] | 0.06 | 0.26 |
| VDSR [30] | 0.67 | 1.53 |
| EDSR [57] | 40.72 | 4.75 |
| RCAN [35] | 15.44 | 35.36 |
| SwinIR [17] | 11.75 | 27.03 |
| Restormer [18] | 26.12 | 4.96 |
| MHAN [21] | 11.20 | 26.10 |
| SA-GAN [58] | 36.39 | 18.39 |
| CGC-Net (Ours) | 15.17 | 39.01 |
| λ1 | λ2 | λ3 | PSNR↑ | SSIM↑ |
|---|---|---|---|---|
| 1 | 0 | 0 | 26.7891 | 0.7557 |
| 1 | 0.1 | 0.04 | 26.9293 | 0.7602 |
| 1 | 0.2 | 0.02 | 26.8841 | 0.7577 |
| 1 | 0.2 | 0.04 | 27.0772 | 0.7615 |
| Guided Image | PSNR↑ | SSIM↑ |
|---|---|---|
| LQ image | 26.7858 | 0.7559 |
| the gradient map of LQ image | 26.7906 | 0.7561 |
| Segmentation map | 26.7379 | 0.7541 |
| the gradient map of the segmentation map | 27.0772 | 0.7615 |
| distance map | 26.7388 | 0.7543 |
| inverse distance map | 26.7440 | 0.7543 |
| Baseline | GCCL | GLFE | HFC Loss | GAN Loss | PSNR↑ | SSIM↑ |
|---|---|---|---|---|---|---|
| ✓ | ✗ | ✗ | ✗ | ✗ | 25.7745 | 0.7120 |
| ✓ | ✓ | ✗ | ✗ | ✗ | 26.5934 | 0.7480 |
| ✓ | ✓ | ✓ | ✗ | ✗ | 26.7891 | 0.7557 |
| ✓ | ✓ | ✓ | ✓ | ✗ | 26.9291 | 0.7600 |
| ✓ | ✓ | ✓ | ✓ | ✓ | 27.0772 | 0.7615 |
| Partition Ratio | Model | PSNR↑ | SSIM↑ |
|---|---|---|---|
| RCAN [35] | 26.6043 | 0.7530 | |
| training set/test set | MHAN [21] | 26.5778 | 0.7528 |
| (8:2) | SwinIR [17] | 26.6201 | 0.7532 |
| CGC-Net (Ours) | 26.9438 | 0.7591 | |
| RCAN [35] | 26.4044 | 0.7503 | |
| training set/test set | MHAN [21] | 26.4001 | 0.7493 |
| (5:5) | SwinIR [17] | 26.4079 | 0.7504 |
| CGC-Net (Ours) | 26.5021 | 0.7506 | |
| RCAN [35] | 26.2502 | 0.7394 | |
| training set/test set | MHAN [21] | 26.2379 | 0.7388 |
| (2:8) | SwinIR [17] | 26.2505 | 0.7396 |
| CGC-Net (Ours) | 26.3376 | 0.7401 |
| PSNR↑ | |||
| SRCNN [15] | 25.0205 | 22.8105 | 21.6805 |
| VDSR [30] | 25.6692 | 23.5392 | 22.4392 |
| EDSR [57] | 26.0402 | 23.9402 | 22.7402 |
| RCAN [35] | 25.9947 | 23.9647 | 22.7747 |
| SwinIR [17] | 26.0404 | 23.9104 | 22.7804 |
| Restormer [18] | 25.9606 | 23.7906 | 22.5906 |
| MHAN [21] | 26.0312 | 23.8812 | 22.7112 |
| SA-GAN [58] | 25.9392 | 23.8392 | 22.7092 |
| CGC-Net (Ours) | 26.3672 | 24.0672 | 22.9772 |
| SSIM↑ | |||
| SRCNN [15] | 0.6714 | 0.4851 | 0.3927 |
| VDSR [30] | 0.6944 | 0.5489 | 0.4197 |
| EDSR [57] | 0.7353 | 0.5900 | 0.4570 |
| RCAN [35] | 0.7352 | 0.5991 | 0.4569 |
| SwinIR [17] | 0.7359 | 0.5975 | 0.4591 |
| Restormer [18] | 0.7350 | 0.5910 | 0.4483 |
| MHAN [21] | 0.7354 | 0.5913 | 0.4585 |
| SA-GAN [58] | 0.7342 | 0.5879 | 0.4555 |
| CGC-Net (Ours) | 0.7442 | 0.6029 | 0.4665 |
| Prior Maps | PSNR↑ | SSIM↑ |
|---|---|---|
| Ground Truth | 27.1979 | 0.7619 |
| DeeplabV3+ [47] | 27.0772 | 0.7615 |
| Random noise map | 26.5379 | 0.7401 |
| Datasets | IoU (%) | Acc (%) | mIoU (%) | mAcc (%) | ||
|---|---|---|---|---|---|---|
| Building | Clutter | Building | Clutter | |||
| SRCNN (HR) [15] | 86.09 | 98.47 | 89.97 | 99.52 | 92.28 | 94.75 |
| VDSR (HR) [30] | 86.91 | 98.54 | 91.46 | 99.44 | 92.72 | 95.45 |
| EDSR (HR) [57] | 87.46 | 98.60 | 92.45 | 99.39 | 93.03 | 95.92 |
| RCAN (HR) [35] | 87.61 | 98.63 | 91.90 | 99.48 | 93.12 | 95.69 |
| SwinIR (HR) [17] | 88.18 | 98.69 | 92.21 | 99.51 | 93.44 | 95.86 |
| Restormer (HR) [18] | 87.89 | 98.66 | 92.21 | 99.48 | 93.27 | 95.84 |
| CGC-Net (Ours HR) | 89.47 | 98.83 | 93.84 | 99.48 | 94.15 | 96.66 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, P.; Jiang, J.; Zhang, Y.; Zeng, C.; Qin, C.; Li, Z. CGC-Net: A Context-Guided Constrained Network for Remote-Sensing Image Super Resolution. Remote Sens. 2023, 15, 3171. https://doi.org/10.3390/rs15123171
Zheng P, Jiang J, Zhang Y, Zeng C, Qin C, Li Z. CGC-Net: A Context-Guided Constrained Network for Remote-Sensing Image Super Resolution. Remote Sensing. 2023; 15(12):3171. https://doi.org/10.3390/rs15123171
Chicago/Turabian StyleZheng, Pengcheng, Jianan Jiang, Yan Zhang, Chengxiao Zeng, Chuanchuan Qin, and Zhenghao Li. 2023. "CGC-Net: A Context-Guided Constrained Network for Remote-Sensing Image Super Resolution" Remote Sensing 15, no. 12: 3171. https://doi.org/10.3390/rs15123171
APA StyleZheng, P., Jiang, J., Zhang, Y., Zeng, C., Qin, C., & Li, Z. (2023). CGC-Net: A Context-Guided Constrained Network for Remote-Sensing Image Super Resolution. Remote Sensing, 15(12), 3171. https://doi.org/10.3390/rs15123171






