A Proposal for Automatic Coastline Extraction from Landsat 8 OLI Images Combining Modified Optimum Index Factor (MOIF) and K-Means
Abstract
1. Introduction
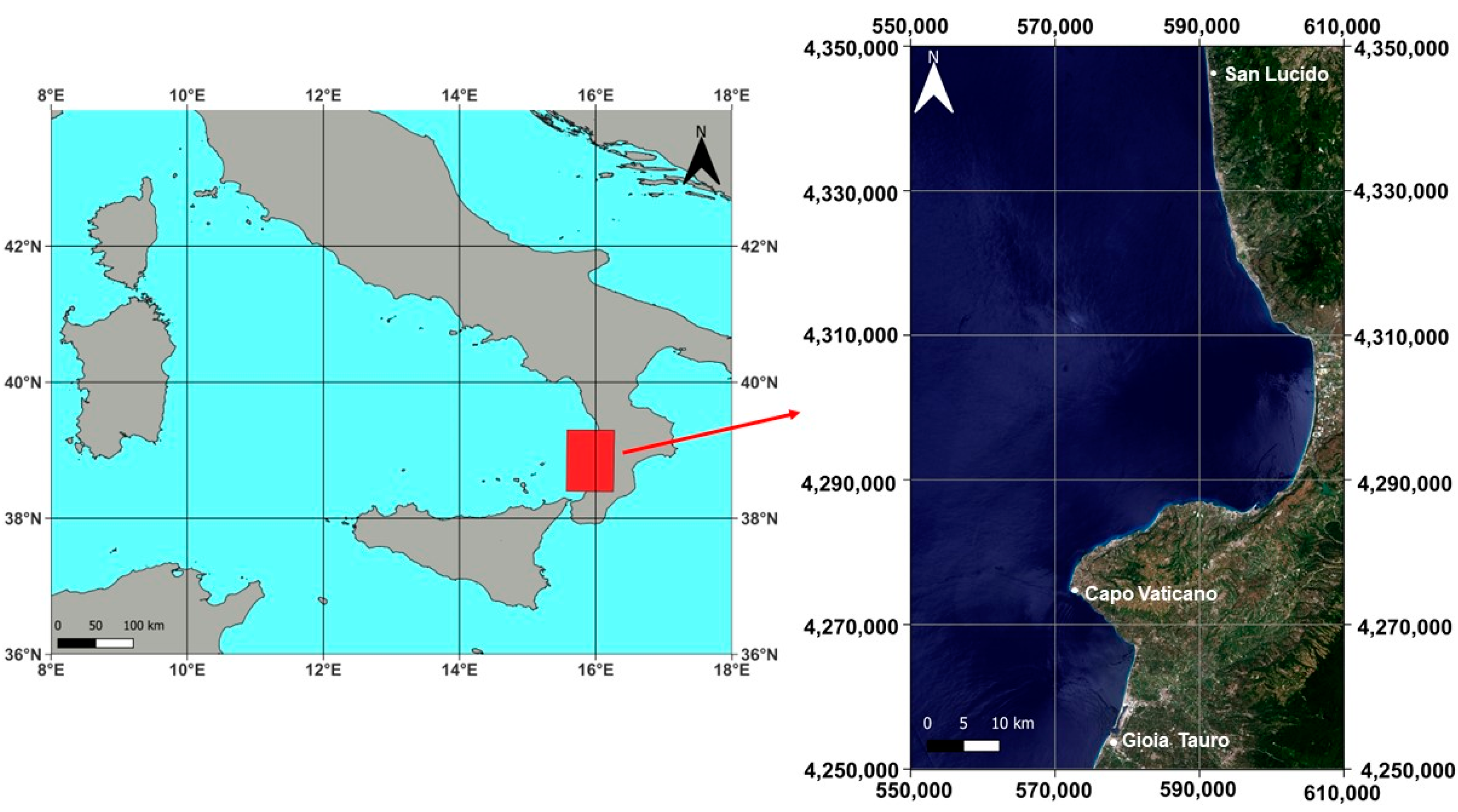
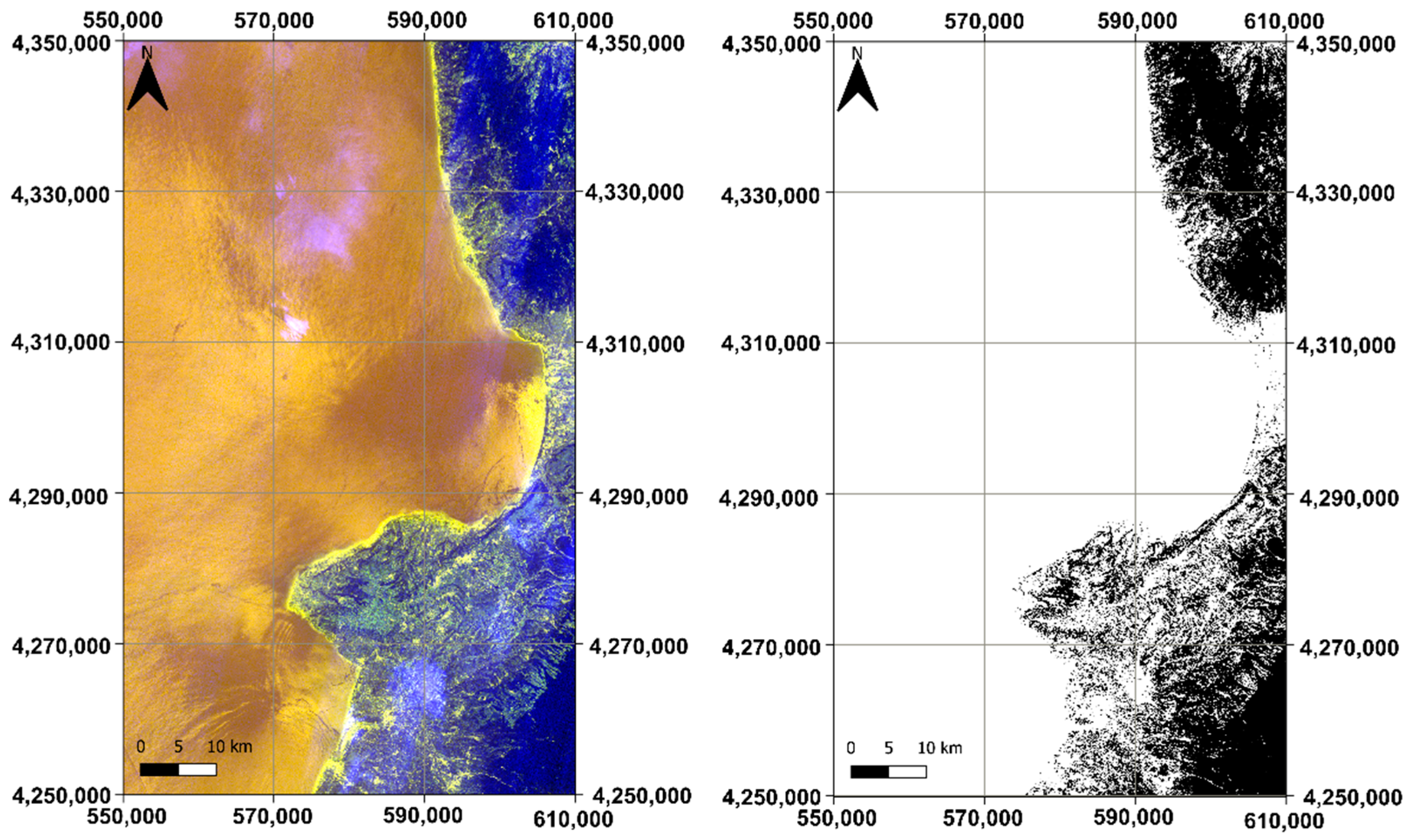
2. Study Area and Dataset
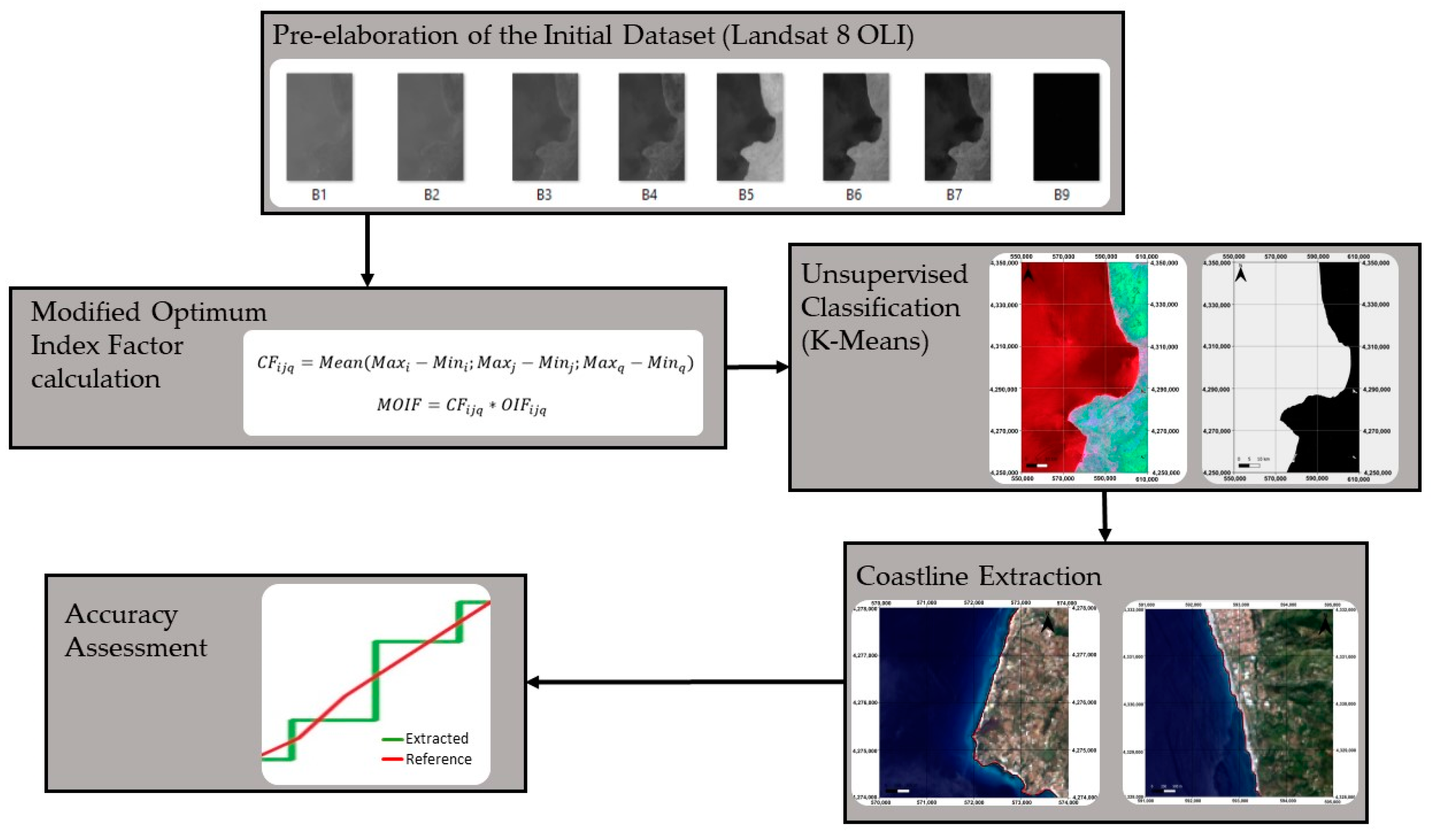
3. Methods
3.1. Landsat Data OLI Pre-Elaboration
3.2. Optimum Index Factor
3.3. Modified Optimum Index Factor
3.4. Image Classification Using K-Means
- Define k cluster and select k centroids from dataset randomly as initial clustering center;
- Calculate the Euclidean distance between k initial centroids and the data points of dataset and assign each data point to cluster with minimum distance;
- Calculate the average of data points that belongs to each cluster and reposition the new centroids;
- Repeat the second and third step until the centroids are not changing, which means the convergence point is reached, in order to obtain unchangeable cluster.
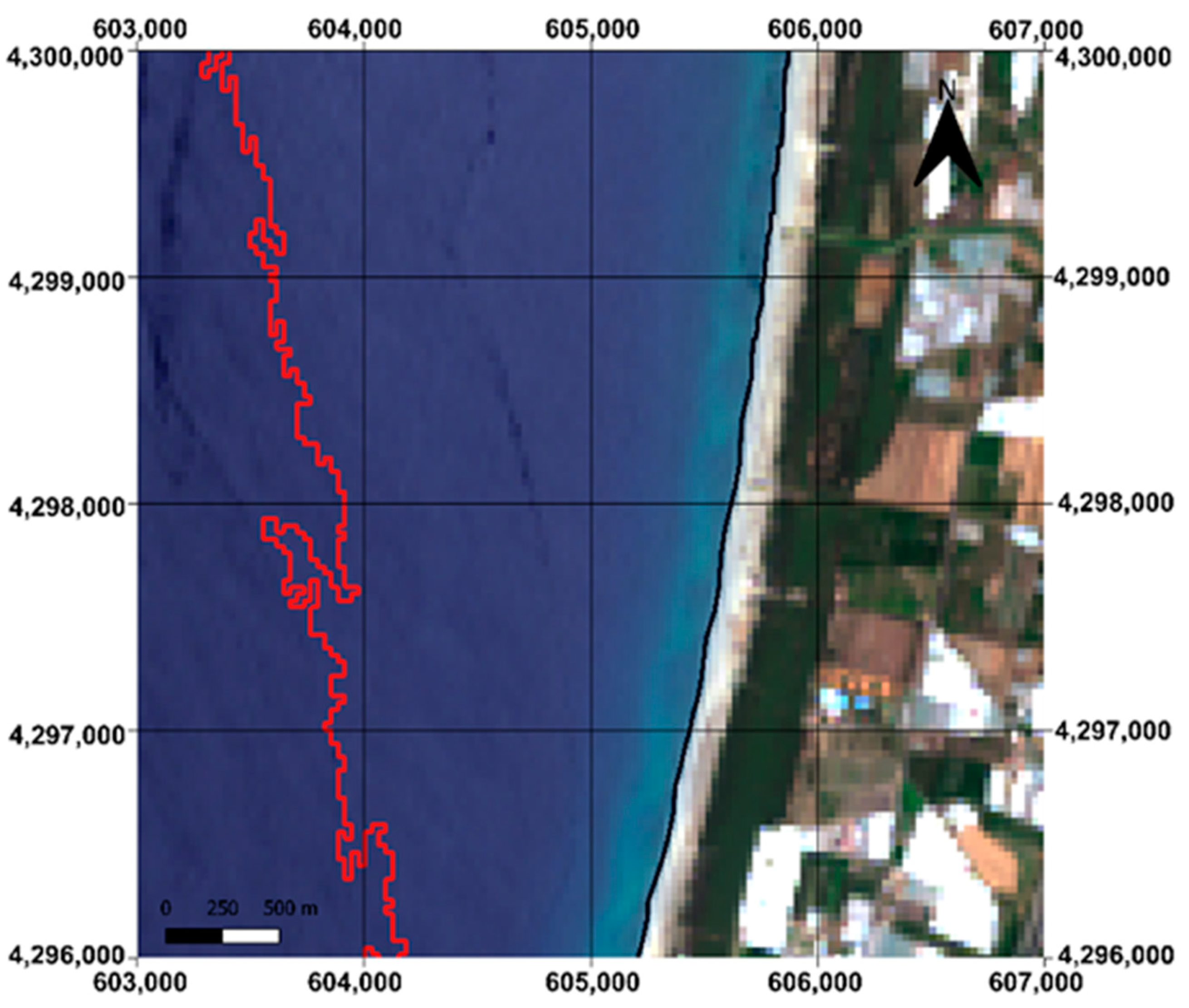
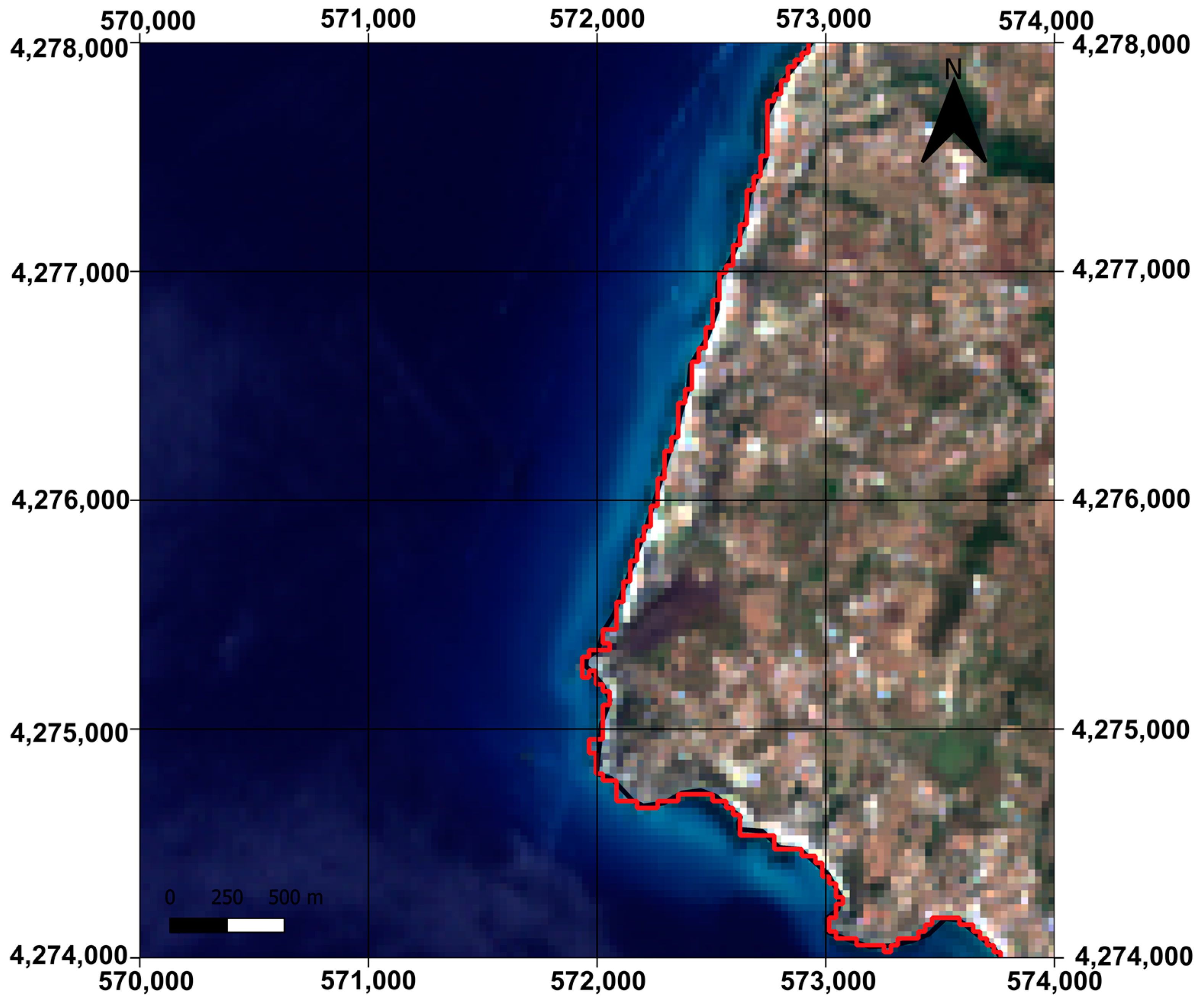
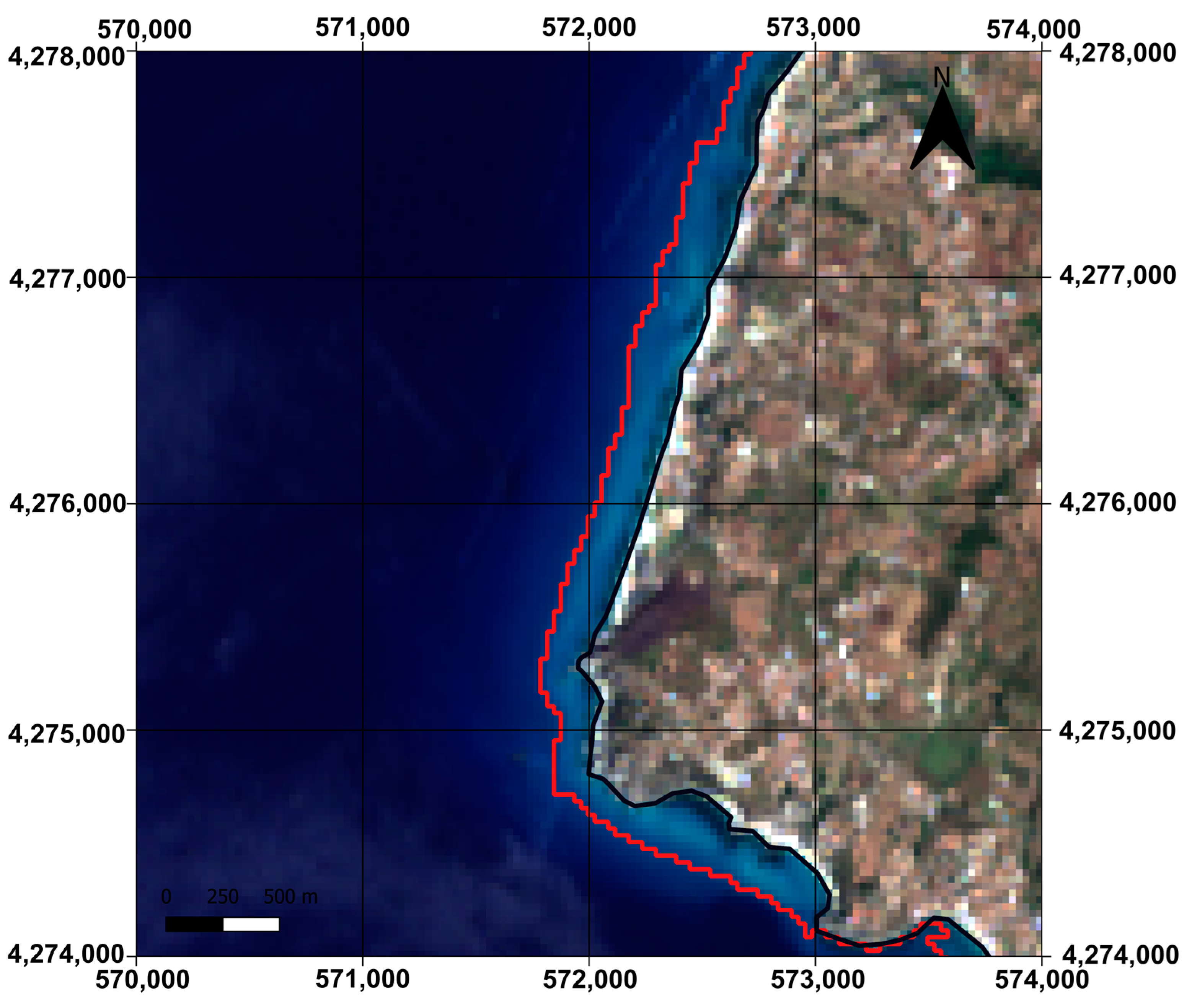
3.5. Accuracy Tests
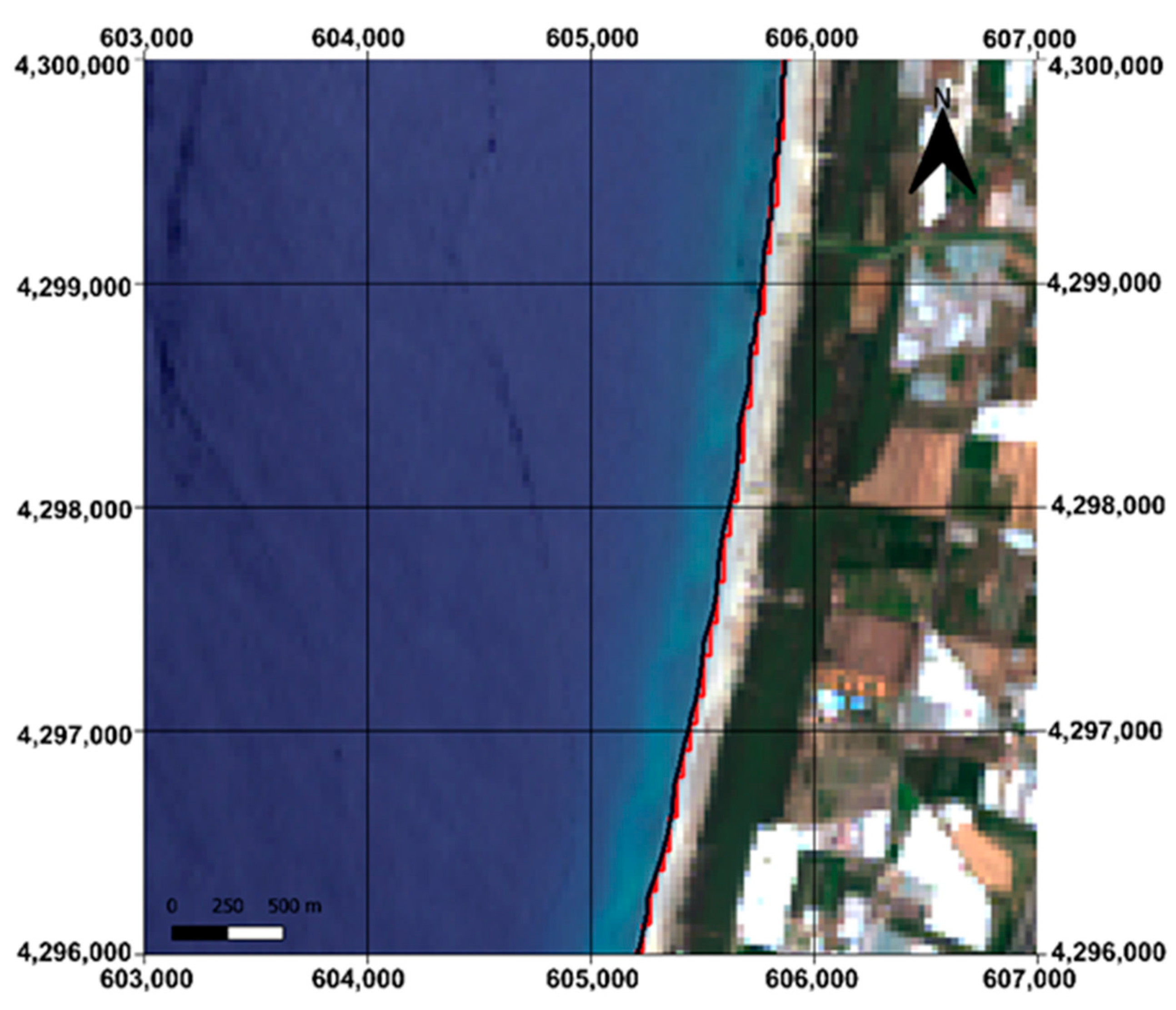
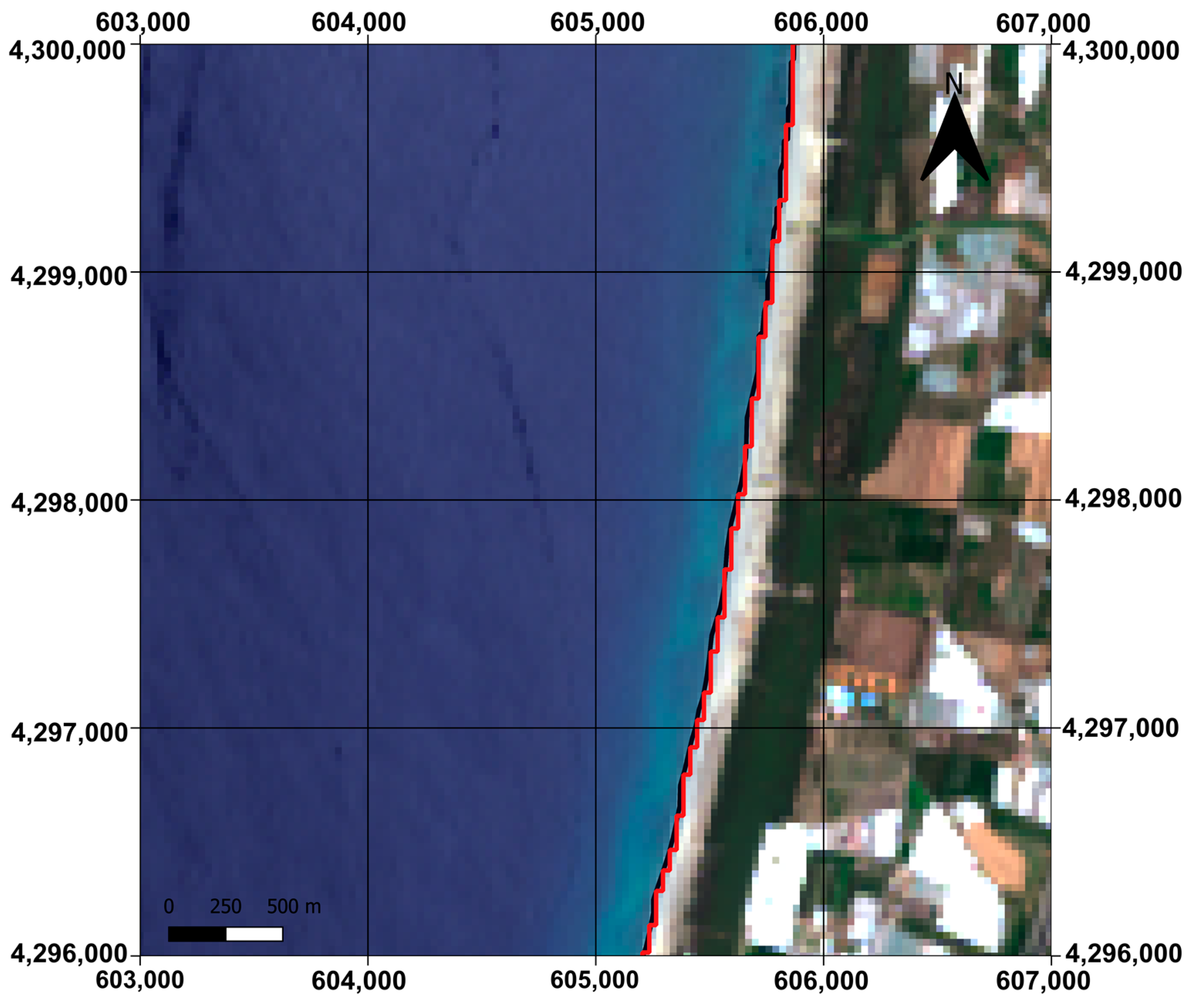
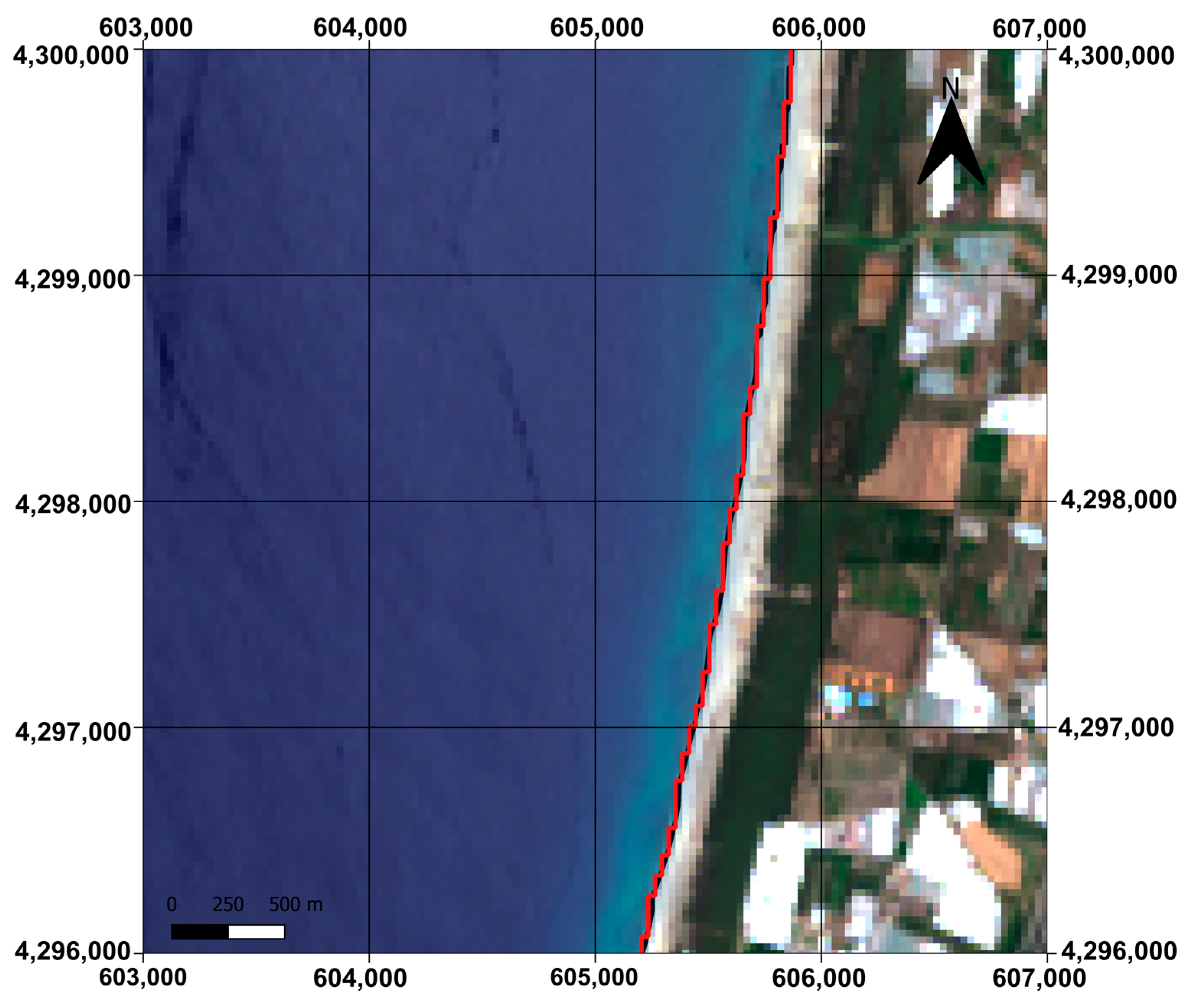
4. Results and Discussion
4.1. OIF and MOIF Results
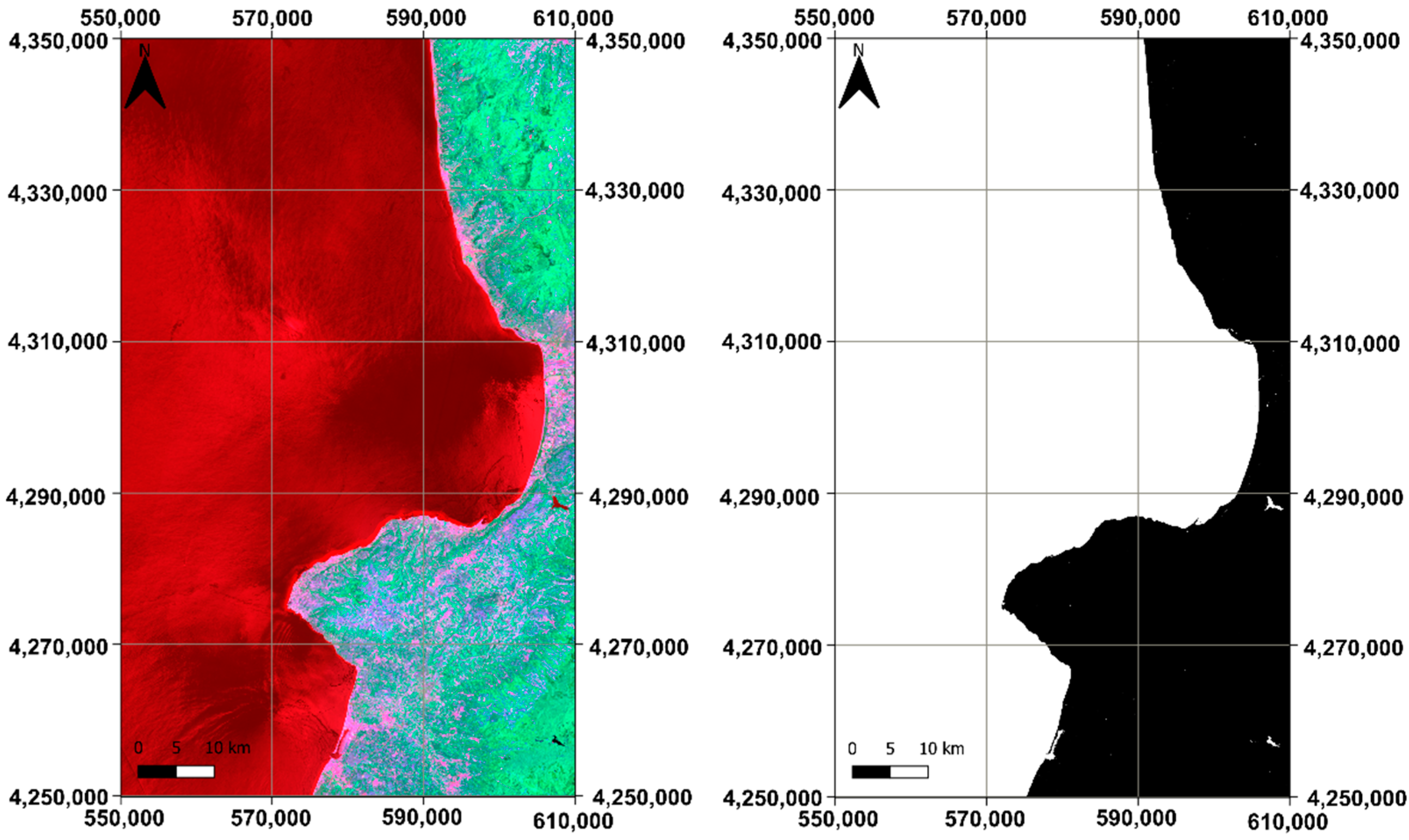
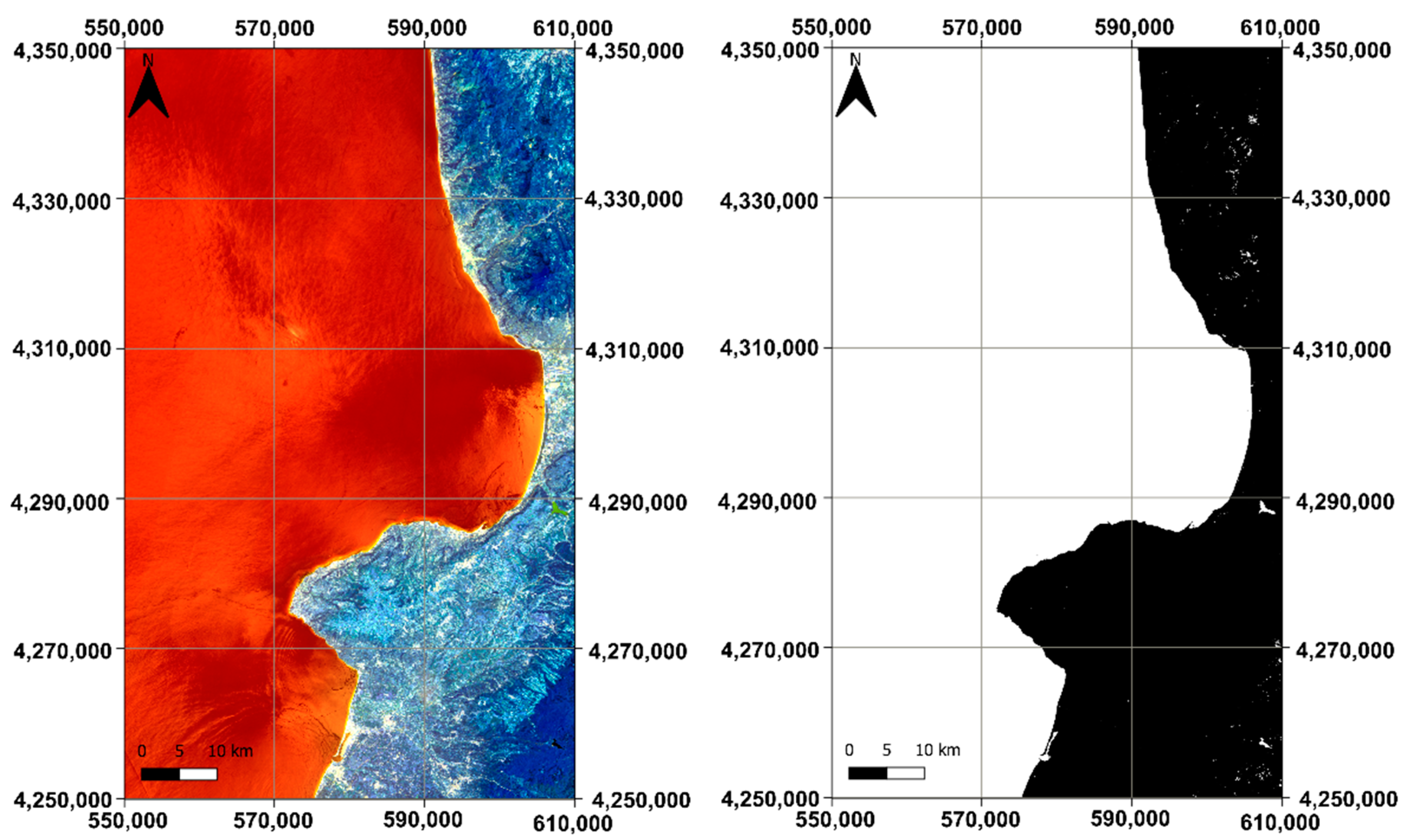
4.2. K-Means Application
4.3. DRI Evaluation
- The group including all Landsat OLI multispectral bands (B1, B2, B3, B4, B5, B6, B7, B9);
- The first three classified band composition given by MOIF (B2, B5, B6; B2, B5, B7; B5, B6, B7);
- Three classified respectively 12th, 21st and 26th given by the MOIF (B3 B5 B6; B2 B3 B5; B3 B4 B5);
- The two middle classified band composition given by MOIF (B2, B3 B6; B1 B3 B6);
- One classified 43rd given by the MOIF (B3 B4 B6)
- The last three classified given by MOIF (B2, B3, B9; B3, B4, B9; B1, B2, B9);
- The first two classified band composition given by OIF (B2, B5, B9; B4, B5, B9).
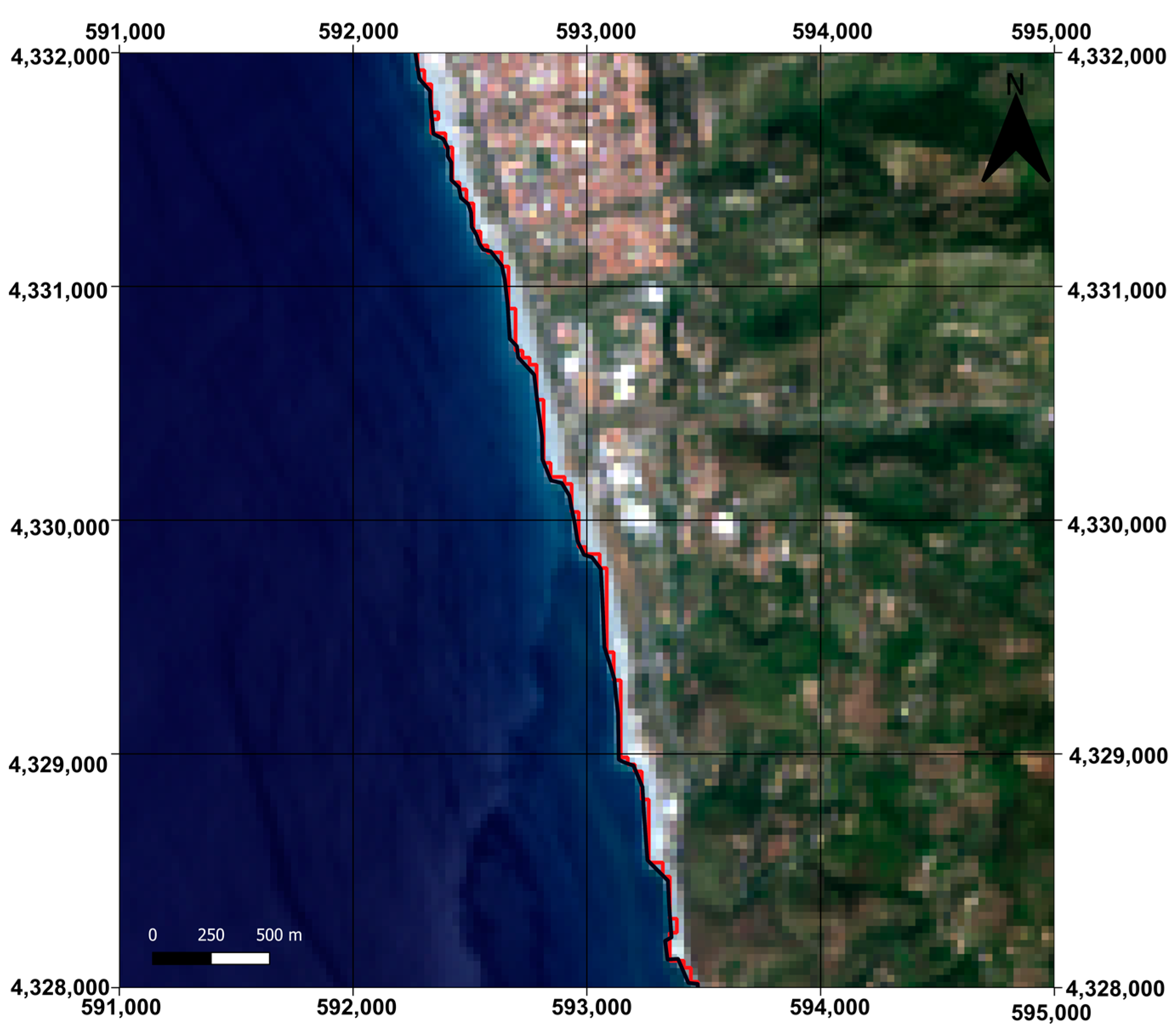
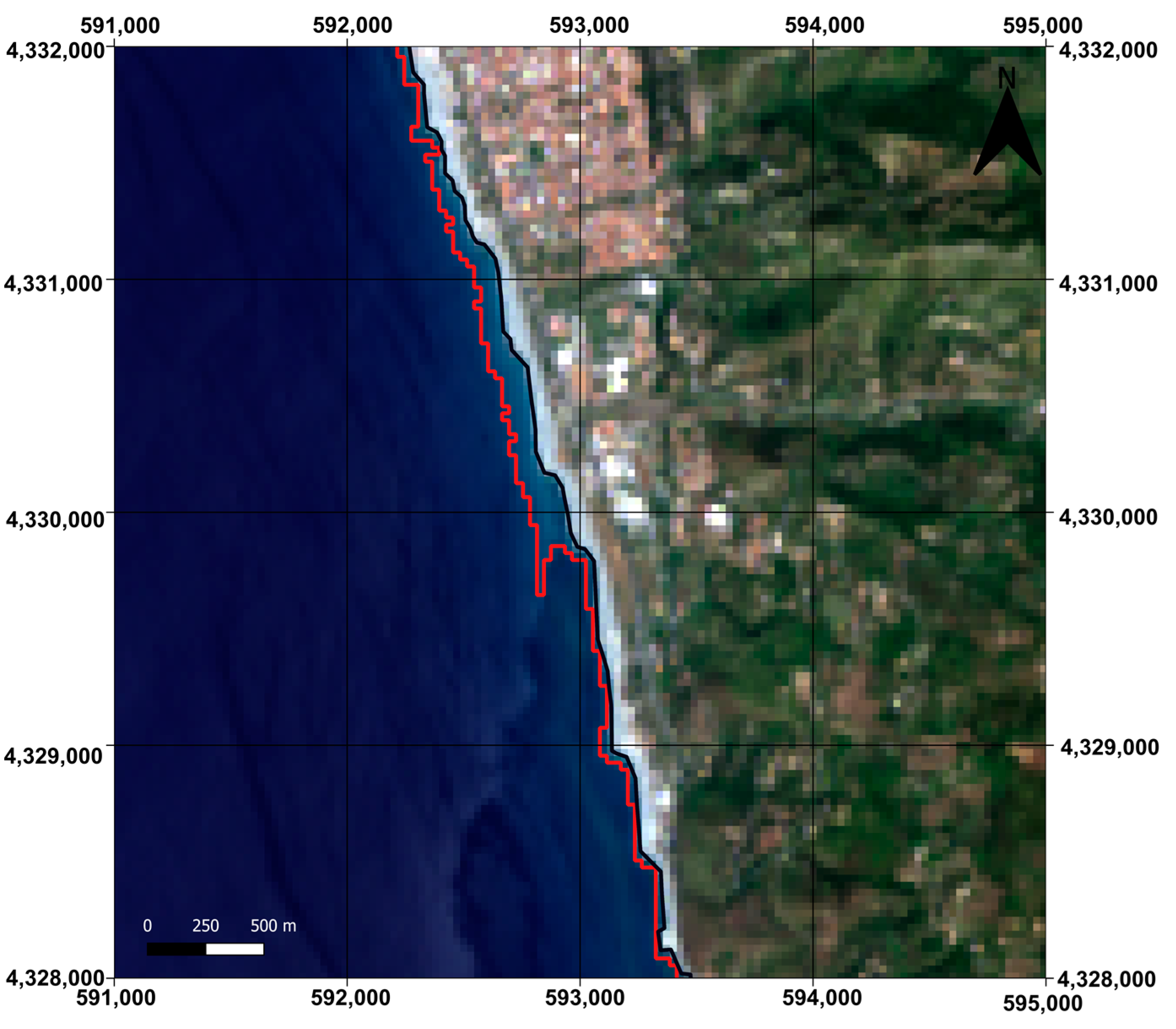
4.4. Classification Accuracy Evaluation
4.5. Comparison with Other Study Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- National Geographic, Coast. Available online: https://education.nationalgeographic.org/resource/coast/ (accessed on 14 April 2023).
- Maglione, P.; Parente, C.; Vallario, A. Coastline Extraction Using High Resolution WorldView-2 Satellite Imagery. Eur. J. Remote Sens. 2014, 47, 685–699. [Google Scholar] [CrossRef]
- Pepe, M.; Parente, C. Burned Area Recognition By Change Detection Analysis Using Images Derived From Sentinel-2 Satellite: The Case Study Of Sorrento Peninsula, Italy. J. Appl. Eng. Sci. 2018, 16, 225–232. [Google Scholar] [CrossRef]
- Seale, C.; Redfern, T.; Chatfield, P.; Luo, C.; Dempsey, K. Coastline Detection in Satellite Imagery: A Deep Learning Approach on New Benchmark Data. Remote Sens. Environ. 2022, 278, 113044. [Google Scholar] [CrossRef]
- Di, K.; Wang, J.; Ma, R.; Li, R. Automatic Shoreline Extraction from High Resolution IKONOS Satellite Imagery. In Proceedings of the ASPRS 2003 Annual Conference, Anchorage, Alaska, 5–9 May 2003. [Google Scholar]
- Duarte Viana, R.; Nicola Lima dos Reis, G.; Maria Gomes Velame, V.; Sehn Körting, T. Shoreline Extraction Using Unsupervised Classification On Sentinel-2 Imagery. In Proceedings of the 2019 Galoá Proceedings of XIX Brazilian Symposium on Remote Sensing, Santos, SP, Brazil, 14–17 April 2019; pp. 2422–2425. [Google Scholar]
- Toure, S.; Diop, O.; Kpalma, K.; Maiga, A.S. Shoreline Detection Using Optical Remote Sensing: A Review. ISPRS Int. J. Geo-Inf. 2019, 8, 75. [Google Scholar] [CrossRef]
- Dellepiane, S.; De Laurentiis, R.; Giordano, F. Coastline extraction from SAR images and a method for the evaluation of the coastline precision. Pattern Recognit. Lett. 2004, 25, 1461–1470. [Google Scholar] [CrossRef]
- Yu, S.; Mou, Y.; Xu, D.; You, X.; Zhou, L.; Zeng, W. A New Algorithm for Shoreline Extraction from Satellite Imagery with Non-Separable Wavelet and Level Set Method. IJMLC 2013, 3, 158–163. [Google Scholar] [CrossRef]
- Qiu, S.; Ye, H.; Liao, X. Coastline Recognition Algorithm Based on Multi-Feature Network Fusion of Multi-Spectral Remote Sensing Images. Remote Sens. 2022, 14, 5931. [Google Scholar] [CrossRef]
- Liu, H.; Jezek, K.C. Automated Extraction of Coastline from Satellite Imagery by Integrating Canny Edge Detection and Locally Adaptive Thresholding Methods. Int. J. Remote Sens. 2010, 25, 937–958. [Google Scholar] [CrossRef]
- Baud, I.; Kuffer, M.; Pfeffer, K.; Sliuzas, R.; Karuppannan, S. Understanding Heterogeneity in Metropolitan India: The Added Value of Remote Sensing Data for Analyzing Sub-Standard Residential Areas. Int. J. Appl. Earth Obs. Geoinf. 2010, 12, 359–374. [Google Scholar] [CrossRef]
- Forestier, G.; Wemmert, C.; Puissant, A. Coastal Image Interpretation Using Background Knowledge and Semantics. Comput. Geosci. 2013, 54, 88–96. [Google Scholar] [CrossRef]
- Kuenzer, C.; Ottinger, M.; Liu, G.; Sun, B.; Baumhauer, R.; Dech, S. Earth Observation-Based Coastal Zone Monitoring of the Yellow River Delta: Dynamics in China’s Second Largest Oil Producing Region over Four Decades. Appl. Geogr. 2014, 55, 92–107. [Google Scholar] [CrossRef]
- Alcaras, E.; Amoroso, P.P.; Baiocchi, V.; Falchi, U.; Parente, C. Unsupervised Classification Based Approach for Coastline Extraction from Sentinel-2 Imagery. In Proceedings of the 2021 International Workshop on Metrology for the Sea; Learning to Measure Sea Health Parameters (MetroSea), Reggio Calabria, Italy, 4–6 October 2021; pp. 423–427. [Google Scholar] [CrossRef]
- Nagendra, H.; Gadgil, M. Biodiversity Assessment at Multiple Scales: Linking Remotely Sensed Data with Field Information. Proc. Natl. Acad. Sci. USA 1999, 96, 9154–9158. [Google Scholar] [CrossRef] [PubMed]
- Maglione, P.; Parente, C.; Santamaria, R.; Vallario, A. Modelli Tematici 3D Della Copertura Del Suolo a Partire Da DTM e Immagini Telerilevate Ad Alta Risoluzione WorldView-2. Rend. Online Della Soc. Geol. Ital. 2014, 30, 33–40. [Google Scholar] [CrossRef]
- Alcaras, E.; Amoroso, P.P.; Figliomeni, F.G.; Parente, C.; Prezioso, G. Accuracy Evaluation of Coastline Extraction Methods In Remote Sensing: A Smart Procedure For Sentinel-2 Images. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2022. [Google Scholar] [CrossRef]
- Gao, Y.; Mas, J.F. A Comparison Of The Performance Of Pixel-Based And Object-Based Classifications Over Images with Various Spatial Resolutions. Online J. Earth Sci. 2008, 2, 27–35. [Google Scholar]
- Liu, D.; Xia, F. Assessing Object-Based Classification: Advantages and Limitations. Remote Sens. Lett. 2010, 1, 187–194. [Google Scholar] [CrossRef]
- Myint, S.W.; Gober, P.; Brazel, A.; Grossman-Clarke, S.; Weng, Q. Per-Pixel vs. Object-Based Classification of Urban Land Cover Extraction Using High Spatial Resolution Imagery. Remote Sens. Environ. 2011, 115, 1145–1161. [Google Scholar] [CrossRef]
- Zhang, T.; Yang, X.; Hu, S.; Su, F. Extraction of Coastline in Aquaculture Coast from Multispectral Remote Sensing Images: Object-Based Region Growing Integrating Edge Detection. Remote Sens. 2013, 5, 4470–4487. [Google Scholar] [CrossRef]
- Kalkan, K.; Bayram, B.; Maktav, D.; Sunar, F. Comparison Of Support Vector Machine And Object Based Classification Methods For Coastline Detection. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2013. [Google Scholar] [CrossRef]
- Basile Giannini, M.; Parente, C. An Object Based Approach for Coastline Extraction from Quickbird Multispectral Images. Int. J. Eng. Technol. 2015, 6, 2698–2704. [Google Scholar]
- Liu, Y.; Wang, X.; Ling, F.; Xu, S.; Wang, C. Analysis of Coastline Extraction from Landsat-8 OLI Imagery. Water 2017, 9, 816. [Google Scholar] [CrossRef]
- Mahlein, A.K.; Rumpf, T.; Welke, P.; Dehne, H.W.; Plümer, L.; Steiner, U.; Oerke, E.C. Development of Spectral Indices for Detecting and Identifying Plant Diseases. Remote Sens. Environ. 2013, 128, 21–30. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Merzlyak, M.N. Signature Analysis of Leaf Reflectance Spectra: Algorithm Development for Remote Sensing of Chlorophyll. J. Plant Physiol. 1996, 148, 494–500. [Google Scholar] [CrossRef]
- McFeeters, S.K. The Use of the Normalized Difference Water Index (NDWI) in the Delineation of Open Water Features. Int. J. Remote Sens. 1996, 17, 1425–1432. [Google Scholar] [CrossRef]
- Figliomeni, F.G.; Parente, C. Bathymetry from Satellite Images: A Proposal for Adapting the Band Ratio Approach to IKONOS Data. Appl. Geomat. 2022, 1, 1–17. [Google Scholar] [CrossRef]
- Dev Acharya, T.; Subedi, A.; Huang, H.; Lee, D.H. Application of Water Indices in Surface Water Change Detection Using Landsat Imagery in Nepal. Sens. Mater. 2019, 31, 1429–1447. [Google Scholar] [CrossRef]
- Ji, R.P.; Yu, W.Y.; Feng, R.; Wu, J.W.; Zhang, Y.S. The threshold determination methods of water body information extraction using GF-1 satellite image. In Proceedings of the IOP Conference Series: Materials Science and Engineering, International Conference on Manufacturing Technology, Materials and Chemical Engineering, Wuhan, China, 14–16 June 2019; Volume 592, p. 012088. [Google Scholar] [CrossRef]
- Alcaras, E.; Amoroso, P.P.; Parente, C.; Prezioso, G. Remotely Sensed Image Fast Classification And Smart Thematic Map Production. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2021, XLVI-4/W5, 43–50. [Google Scholar] [CrossRef]
- Tsiakos, C.A.D.; Chalkias, C. Use of Machine Learning and Remote Sensing Techniques for Shoreline Monitoring: A Review of Recent Literature. Appl. Sci. 2023, 13, 3268. [Google Scholar] [CrossRef]
- Dogan, A.; Birant, D. Machine Learning and Data Mining in Manufacturing. Expert Syst. Appl. 2021, 166, 114060. [Google Scholar] [CrossRef]
- Alcaras, E.; Falchi, U.; Parente, C.; Vallario, A. Accuracy Evaluation for Coastline Extraction from Pléiades Imagery Based on NDWI and IHS Pan-Sharpening Application. Appl. Geomat. 2022, 1, 1–11. [Google Scholar] [CrossRef]
- Lee, W.-M. Python Machine Learning; John Wiley & Sons, Inc.: Indianapolis, Indiana, 2019; p. 296. [Google Scholar]
- Widyantara, I.M.O.; Ary Esta Dewi Wirastuti, N.M.; Asana, I.M.D.P.; Adnyana, I.B.P. Gamma Correction-Based Image Enhancement and Canny Edge Detection for Shoreline Extraction from Coastal Imagery. In Proceedings of the 2017 1st International Conference on Informatics and Computational Sciences (ICICoS), Semarang, Indonesia, 15–16 November 2017; pp. 17–22. [Google Scholar] [CrossRef]
- Alcaras, E.; Amoroso, P.P.; Figliomeni, F.G.; Parente, C.; Vallario, A. Machine Learning Approaches for Coastline Extraction from Sentinel-2 Images: K-Means and K-Nearest Neighbour Algorithms in Comparison. In Communications in Computer and Information Science; Springer: Cham, Switzerland, 2022; Volume 1651, pp. 368–379. [Google Scholar] [CrossRef]
- Minghelli, A.; Spagnoli, J.; Lei, M.; Chami, M.; Charmasson, S. Shoreline Extraction from WorldView2 Satellite Data in the Presence of Foam Pixels Using Multispectral Classification Method. Remote Sens. 2020, 12, 2664. [Google Scholar] [CrossRef]
- Bengoufa, S.; Niculescu, S.; Mihoubi, M.K.; Belkessa, R.; Rami, A.; Rabehi, W.; Abbad, K. Machine Learning and Shoreline Monitoring Using Optical Satellite Images: Case Study of the Mostaganem Shoreline, Algeria. J. Appl. Remote Sens. 2021, 15, 026509. [Google Scholar] [CrossRef]
- Çelik, O.İ.; Gazioğlu, C. Coast Type Based Accuracy Assessment for Coastline Extraction from Satellite Image with Machine Learning Classifiers. Egypt. J. Remote Sens. Sp. Sci. 2022, 25, 289–299. [Google Scholar] [CrossRef]
- Bayram, B.; Erdem, F.; Akpinar, B.; Ince, A.K.; Bozkurt, S.; Catal Reis, H.; Seker, D.Z. The Efficiency Of Random Forest Method For Shoreline Extraction From Landsat-8 And Gokturk-2 Imageries. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2017, IV-4-W4, 141–145. [Google Scholar] [CrossRef]
- Bayram, B.; Ince, A. Integration Of Self-Organizing Map And Machine Learning Methods To Extract Shorelines From Landsat-8 Images. In Proceedings of the The 40th Asian Conference on Remote Sensing (ACRS 2019), Daejeon, Korea, 14–18 October 2019. [Google Scholar]
- Viaña-Borja, S.P.; Ortega-Sánchez, M. Automatic Methodology to Detect the Coastline from Landsat Images with a New Water Index Assessed on Three Different Spanish Mediterranean Deltas. Remote Sens. 2019, 11, 2186. [Google Scholar] [CrossRef]
- Schowengerdt, R.A. Thematic Classification. In Remote Sensing–Models and Methods for Image Processing; Academic Press: Cambridge, MA, USA, 2007; pp. 387–456. [Google Scholar] [CrossRef]
- Chavez, P.; Berlin, G.L.; Sowers, L.B. Statistical Method For Selecting Landsat Mss Ratios. Stat. Method Sel. Landsat Mss Ratios 1982, 8, 23–30. [Google Scholar]
- QGIS.org. QGIS Geographic Information System. QGIS Association. 2023. Available online: http://www.qgis.org (accessed on 3 May 2023).
- Byrnes, R.A. Landsat: A Global Land Imaging Program; Fact Sheet; Earth Resources Observation and Science (EROS) Center: Sioux Falls, SD, USA, 2012. [Google Scholar] [CrossRef]
- SVS—Landsat Orbit Swath. Available online: https://svs.gsfc.nasa.gov/11481 (accessed on 14 April 2023).
- USGS Fact Sheet 2013–3060: Landsat 8. Available online: https://pubs.usgs.gov/fs/2013/3060/ (accessed on 14 April 2023).
- Foti, G.; Barbaro, G.; Barillà, G.C.; Mancuso, P.; Puntorieri, P. Shoreline Erosion Due to Anthropogenic Pressure in Calabria (Italy). Eur. J. Remote Sens. 2022, 1–21. [Google Scholar] [CrossRef]
- Barillà, G.C.; Foti, G.; Barbaro, G.; Currò, F. Coastal Flood Hazard: A Quick Mapping Methodology. Case Study: Gioia Tauro (Italy). Smart Innov. Syst. Technol. 2021, 178, 1608–1617. [Google Scholar] [CrossRef]
- Modava, M.; Akbarizadeh, G.; Soroosh, M. Hierarchical coastline detection in SAR images based on spectral-textural features and global–local information. IET Radar Sonar Navig. 2019, 13, 2183–2195. [Google Scholar] [CrossRef]
- Zhang, Y.; Qiao, Q.; Liu, J.; Sang, H.; Yang, D.; Zhai, L.; Ning, L.; Yuan, X. Coastline changes in mainland China from 2000 to 2015. Int. J. Image Data Fusion 2022, 13, 95–112. [Google Scholar] [CrossRef]
- Aguilar, F.J.; Fernández, I.; Pérez, J.L.; López, A.; Aguilar, M.A.; Mozas, A.; Cardenal, J. Preliminary results on high accuracy estimation of shoreline change rate based on coastal elevation models. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2010, 33, 986–991. [Google Scholar]
- Young, N.E.; Anderson, R.S.; Chignell, S.M.; Vorster, A.G.; Lawrence, R.; Evangelista, P.H. A Survival Guide to Landsat Preprocessing. Ecology 2017, 98, 920–932. [Google Scholar] [CrossRef] [PubMed]
- Tomlin, C.D. Geographic Information Systems and Cartographic Modeliing; Prentice Hall: Englewood Cliffs, NJ, USA, 1990; Volume 249. [Google Scholar]
- DeMers, M.N. GIS Modeling in Raster; Wiley: Hoboken, NJ, USA, 2002. [Google Scholar]
- Kienast-Brown, S.; Boettinger, J.L. Applying the Optimum Index Factor to Multiple Data Types in Soil Survey. In Digital Soil Mapping; Springer: Dordrecht, The Netherlands, 2010; pp. 385–398. [Google Scholar] [CrossRef]
- Debdip, B.; Girls, C. Optimum Index Factor (OIF) for Landsat Data: A Case Study on Barasat Town, West Bengal, India. Int. J. Remote Sens. Geosci. 2013, 2, 11–17. [Google Scholar]
- Ehsani, A.; Quiel, F. Efficiency of Landsat ETM+ Thermal Band for Land Cover Classification of the Biosphere Reserve “Eastern Carpathians” (Central Europe) Using SMAP and ML Algorithms. Int. J. Environ. Res. 2010, 4, 741–750. [Google Scholar]
- Pan, Y.; Xing, S.; Liu, D. Partition optimal band selection method for hyperspectral image. J. Phys. Conf. Ser. 2021, 2005, 012054. [Google Scholar] [CrossRef]
- Julzarika, A.; Anggraini, N.; Adawiah, S.W. Detection of True Mangroves in Indonesia Using Satellite Remote Sensing. J. Environ. Anal. Progress 2019, 4, 157–167. [Google Scholar] [CrossRef]
- Sun, X.; Shen, X.; Pang, H.; Fu, X. Multiple Band Prioritization Criteria-Based Band Selection for Hyperspectral Imagery. Remote Sens. 2022, 14, 5679. [Google Scholar] [CrossRef]
- Richards, J.A. Remote Sensing Digital Image Analysis; Springer: New York, NY, USA, 2022; Volume 5. [Google Scholar]
- Xue, J.; Su, B. Significant remote sensing vegetation indices: A review of developments and applications. J. Sens. 2017, 2017, 1353691. [Google Scholar] [CrossRef]
- Xu, H. Modification of normalised difference water index (NDWI) to enhance open water features in remotely sensed imagery. Int. J. Remote Sens. 2006, 27, 3025–3033. [Google Scholar] [CrossRef]
- Feyisa, G.L.; Meilby, H.; Fensholt, R.; Proud, S.R. Automated water extraction index: A new technique for surface water mapping using Landsat imagery. Remote Sens. Environ. 2014, 140, 23–35. [Google Scholar] [CrossRef]
- Jin, Q.; Lin, N.; Zhang, Y. K-Means Clustering Algorithm Based on Chaotic Adaptive Artificial Bee Colony. Algorithms 2021, 14, 53. [Google Scholar] [CrossRef]
- Hamdan Ali, H.; Emad Kadhum, L. K-Means Clustering Algorithm Applications in Data Mining and Pattern Recognition. Int. J. Sci. Res. 2017, 6, 1577–1584. [Google Scholar] [CrossRef]
- Jin, X.; Han, J. Partitional Clustering. In Encyclopedia of Machine Learning and Data Mining; Springer: Boston, MA, USA, 2017; pp. 973–974. [Google Scholar] [CrossRef]
- MacQueen, J. Some Methods for Classification and Analysis of Multivariate Observations. In Berkeley Symposium on Mathematical Statistics and Probability June 21–July 18, 1965 and December 27, 7 January 1965; 1966|Statistical Laboratory of the University of California: Berkeley, CA, USA, 1967; Volume 5, pp. 281–297. [Google Scholar]
- Friedman, J.; Tibshirani, R.; Hastie, T. The Elements of Statistical Learning: Data Mining, Inference, and Prediction; Springer: Berlin/Heidelberg, Germany, 2009; ISBN 0387848584. [Google Scholar]
- An, M.; Sun, Q.; Hu, J.; Tang, Y.; Zhu, Z. Coastline detection with Gaofen-3 SAR images using an improved FCM method. Sensors 2018, 18, 1898. [Google Scholar] [CrossRef]
- Costantino, D.; Guastaferro, F.; Parente, C.; Pepe, M. Using images generated by sentinel-2 satellite optical sensor for burned area mapping. In R3 in Geomatics: Research, Results and Review. R3GEO 2019. Communications in Computer and Information Science; Springer: Cham, Switzerland, 2020; pp. 350–362. [Google Scholar]
- El Kafrawy, S.; Basiouny, M.; Ghanem, E.; Taha, A. Performance evaluation of shoreline extraction methods based on remote sensing data. J. Geogr. Environ. Earth Sci. Int. 2017, 11, 1–18. [Google Scholar] [CrossRef]
- Tuan, T.A.; Nguyet, N.T.A.; Hong, P.V.; Ngan, N.T.A.; Le Phuong, V. Interpretation of water indices for shoreline extraction from Landsat 8 OLI data on the southwest coast of Vietnam. Vietnam J. Mar. Sci. Technol. 2018, 18, 339–349. [Google Scholar] [CrossRef]
- Alcaras, E.; Errico, A.; Falchi, U.; Parente, C.; Vallario, A. Coastline extraction from optical satellite imagery and accuracy evaluation. In R3 in Geomatics: Research, Results and Review. R3GEO 2019. Communications in Computer and Information Science; Springer: Cham, Switzerland, 2020; pp. 336–349. [Google Scholar] [CrossRef]
- Budillon, F.; Amodio, S.; Contestabile, P.; Alberico, I.; Innangi, S.; Molisso, F. The present-day nearshore submarine depositional terraces off the Campania coast (South-eastern Tyrrhenian Sea): An analysis of their morpho-bathymetric variability. In Proceedings of the MetroSea 2020—TC19 International Workshop on Metrology for the Sea, Naples, Italy, 5–7 October 2020; pp. 132–138. [Google Scholar]




| Bands | Wavelength (Micrometers) | Resolution (Meters) |
|---|---|---|
| 1–Coastal aerosol | 0.43–0.45 | 30 |
| 2–Blue | 0.45–0.51 | 30 |
| 3–Green | 0.53–0.59 | 30 |
| 4–Red | 0.64–0.67 | 30 |
| 5–Near Infrared (NIR) | 0.85–0.88 | 30 |
| 6–Short-wave infrared (SWIR 1) | 1.57–1.65 | 30 |
| 7–Short-wave infrared (SWIR 2) | 2.11–2.29 | 30 |
| 9–Cirrus | 1.36–1.38 | 30 |
| Ranking | Composition | OIF | Ranking | Composition | OIF |
|---|---|---|---|---|---|
| 1 | B2 B5 B9 | 0.185793 | 29 | B1 B7 B9 | 0.084795 |
| 2 | B4 B5 B9 | 0.179868 | 30 | B2 B3 B6 | 0.083436 |
| 3 | B2 B5 B6 | 0.161869 | 32 | B6 B7 B9 | 0.081616 |
| 4 | B2 B5 B7 | 0.161682 | 33 | B4 B6 B9 | 0.079554 |
| 5 | B2 B6 B9 | 0.160785 | 31 | B1 B2 B5 | 0.083167 |
| 6 | B5 B6 B9 | 0.152709 | 34 | B3 B6 B9 | 0.068931 |
| 7 | B5 B7 B9 | 0.149738 | 35 | B1 B2 B6 | 0.068889 |
| 8 | B1 B4 B5 | 0.145300 | 36 | B1 B3 B7 | 0.067815 |
| 9 | B3 B5 B9 | 0.143396 | 37 | B1 B4 B7 | 0.066368 |
| 10 | B2 B4 B5 | 0.137307 | 38 | B1 B4 B9 | 0.065971 |
| 11 | B1 B3 B5 | 0.137066 | 39 | B1 B3 B9 | 0.064266 |
| 12 | B1 B5 B9 | 0.134586 | 40 | B4 B6 B7 | 0.059485 |
| 13 | B2 B7 B9 | 0.129449 | 41 | B1 B2 B7 | 0.058933 |
| 14 | B2 B3 B5 | 0.128051 | 42 | B2 B4 B7 | 0.058430 |
| 15 | B1 B5 B7 | 0.127501 | 43 | B2 B3 B7 | 0.058208 |
| 16 | B4 B5 B6 | 0.126693 | 44 | B3 B6 B7 | 0.055408 |
| 17 | B2 B6 B7 | 0.119407 | 45 | B4 B7 B9 | 0.050217 |
| 18 | B1 B5 B6 | 0.119198 | 46 | B3 B4 B6 | 0.049167 |
| 19 | B5 B6 B7 | 0.112271 | 47 | B1 B3 B4 | 0.049148 |
| 20 | B4 B5 B7 | 0.111690 | 48 | B2 B4 B9 | 0.047537 |
| 21 | B3 B5 B6 | 0.111136 | 49 | B3 B7 B9 | 0.044217 |
| 22 | B3 B4 B5 | 0.100531 | 50 | B2 B3 B9 | 0.043139 |
| 23 | B3 B5 B7 | 0.100150 | 51 | B1 B2 B3 | 0.033455 |
| 24 | B1 B6 B9 | 0.095998 | 52 | B3 B4 B7 | 0.032920 |
| 25 | B1 B4 B6 | 0.085985 | 53 | B1 B2 B4 | 0.032286 |
| 26 | B1 B6 B7 | 0.085925 | 54 | B2 B3 B4 | 0.030907 |
| 27 | B2 B4 B6 | 0.085484 | 55 | B3 B4 B9 | 0.028967 |
| 28 | B1 B3 B6 | 0.085092 | 56 | B1 B2 B9 | 0.022450 |
| Bands | Min | Max | Difference |
|---|---|---|---|
| B1 | 0.097669 | 0.483244 | 0.385575376 |
| B2 | 0.075677 | 0.521998 | 0.446321465 |
| B3 | 0.055101 | 0.576271 | 0.521169759 |
| B4 | 0.034242 | 0.642815 | 0.608572632 |
| B5 | 0.025000 | 0.818819 | 0.793818826 |
| B6 | 0.012838 | 1.319435 | 1.306597019 |
| B7 | 0.008784 | 1.314435 | 1.305651118 |
| B9 | 0.000000 | 0.069334 | 0.069333822 |
| Ranking | Composition | MOIF | Ranking | Composition | MOIF |
|---|---|---|---|---|---|
| 1 | B2 B5 B6 | 0.137412 | 29 | B1 B3 B6 | 0.062779 |
| 2 | B2 B5 B7 | 0.137202 | 30 | B3 B6 B7 | 0.057872 |
| 3 | B5 B6 B7 | 0.127468 | 31 | B1 B6 B9 | 0.056367 |
| 4 | B2 B6 B7 | 0.121738 | 32 | B1 B5 B9 | 0.056020 |
| 5 | B4 B5 B6 | 0.114403 | 33 | B4 B6 B9 | 0.052625 |
| 6 | B5 B6 B9 | 0.110446 | 34 | B1 B4 B7 | 0.050877 |
| 7 | B5 B7 B9 | 0.108250 | 35 | B1 B3 B7 | 0.050011 |
| 8 | B1 B5 B7 | 0.105615 | 36 | B1 B7 B9 | 0.049761 |
| 9 | B4 B5 B7 | 0.100820 | 37 | B1 B2 B6 | 0.049106 |
| 10 | B2 B6 B9 | 0.099729 | 38 | B2 B4 B7 | 0.045975 |
| 11 | B1 B5 B6 | 0.098775 | 39 | B1 B2 B5 | 0.045068 |
| 12 | B3 B5 B6 | 0.097117 | 40 | B2 B3 B7 | 0.044105 |
| 13 | B4 B5 B9 | 0.088238 | 41 | B3 B6 B9 | 0.043589 |
| 14 | B3 B5 B7 | 0.087485 | 42 | B1 B2 B7 | 0.041990 |
| 15 | B1 B4 B5 | 0.086597 | 43 | B3 B4 B6 | 0.039929 |
| 16 | B1 B6 B7 | 0.085862 | 44 | B4 B7 B9 | 0.033202 |
| 17 | B2 B4 B5 | 0.084613 | 45 | B3 B7 B9 | 0.027947 |
| 18 | B2 B5 B9 | 0.081097 | 46 | B3 B4 B7 | 0.026724 |
| 19 | B2 B7 B9 | 0.078588 | 47 | B1 B3 B4 | 0.024824 |
| 20 | B1 B3 B5 | 0.077696 | 48 | B1 B4 B9 | 0.023386 |
| 21 | B2 B3 B5 | 0.075179 | 49 | B1 B3 B9 | 0.020909 |
| 22 | B6 B7 B9 | 0.072953 | 50 | B2 B4 B9 | 0.017814 |
| 23 | B2 B4 B6 | 0.067290 | 51 | B2 B3 B4 | 0.016237 |
| 24 | B3 B5 B9 | 0.066168 | 52 | B1 B2 B4 | 0.015503 |
| 25 | B1 B4 B6 | 0.065943 | 53 | B1 B2 B3 | 0.015088 |
| 26 | B3 B4 B5 | 0.064459 | 54 | B2 B3 B9 | 0.014909 |
| 27 | B4 B6 B7 | 0.063863 | 55 | B3 B4 B9 | 0.011577 |
| 28 | B2 B3 B6 | 0.063246 | 56 | B1 B2 B9 | 0.006744 |
| Composition | MOIF Ranking | OIF Ranking | Min (m) | Max (m) | Mean (m) | Dev. ST. (m) | RMSE (m) |
|---|---|---|---|---|---|---|---|
| B1 B2 B3 B4 B5 B6 B7 B9 | - | - | 0.016 | 623.013 | 7.655 | 13.967 | 15.927 |
| B2 B5 B6 | 1 | 3 | 0.000 | 35.940 | 7.417 | 5.286 | 9.108 |
| B2 B5 B7 | 2 | 4 | 0.000 | 38.313 | 7.480 | 5.428 | 9.242 |
| B5 B6 B7 | 3 | 19 | 0.000 | 43.118 | 7.638 | 5.205 | 9.243 |
| B3 B5 B6 | 12 | 21 | 0.927 | 81.696 | 7.436 | 5.553 | 9.281 |
| B2 B3 B5 | 21 | 14 | 0.000 | 82.084 | 7.466 | 5.727 | 9.410 |
| B3 B4 B5 | 26 | 22 | 0.000 | 82.153 | 7.566 | 5.665 | 9.452 |
| B2 B3 B6 | 28 | 30 | 0.016 | 83.120 | 8.120 | 5.190 | 9.637 |
| B1 B3 B6 | 29 | 28 | 0.023 | 83.120 | 8.191 | 5.180 | 9.692 |
| B3 B4 B6 | 43 | 46 | 0.000 | 623.013 | 7.508 | 12.448 | 14.537 |
| B2 B3 B9 | 54 | 50 | 0.056 | 952.779 | 19.398 | 69.361 | 72.022 |
| B3 B4 B9 | 55 | 55 | 0.211 | 10,288.667 | 22.029 | 318.800 | 319.560 |
| B1 B2 B9 | 56 | 56 | 5.456 | 11,580.885 | 4280.705 | 3341.667 | 5430.578 |
| B2 B5 B9 | 18 | 1 | 0.000 | 63.827 | 7.264 | 6.309 | 9.621 |
| B4 B5 B9 | 13 | 2 | 0.000 | 53.103 | 7.611 | 5.814 | 9.577 |
| Composition | MOIF Ranking | OIF Ranking | Accuracy | Water | No-Water |
|---|---|---|---|---|---|
| B1 B2 B3 B4 B5 B6 B7 B9 | - | - | UA | 0.97832 | 0.96982 |
| PA | 0.96757 | 0.97984 | |||
| OA | 0.97389 | ||||
| B2 B5 B6 | 1 | 3 | UA | 0.98095 | 0.98108 |
| PA | 0.97986 | 0.98211 | |||
| OA | 0.98102 | ||||
| B2 B5 B7 | 2 | 4 | UA | 0.98131 | 0.97949 |
| PA | 0.97812 | 0.98248 | |||
| OA | 0.98037 | ||||
| B5 B6 B7 | 3 | 19 | UA | 0.97938 | 0.96533 |
| PA | 0.96253 | 0.98094 | |||
| OA | 0.97202 | ||||
| B3 B5 B6 | 12 | 21 | UA | 0.97983 | 0.96429 |
| PA | 0.96135 | 0.98139 | |||
| OA | 0.97168 | ||||
| B2 B3 B5 | 21 | 14 | UA | 0.98213 | 0.95876 |
| PA | 0.95500 | 0.98367 | |||
| OA | 0.96977 | ||||
| B3 B4 B5 | 26 | 22 | UA | 0.98019 | 0.96038 |
| PA | 0.95692 | 0.98182 | |||
| OA | 0.96975 | ||||
| B2 B3 B6 | 28 | 30 | UA | 0.96621 | 0.96840 |
| PA | 0.96639 | 0.96823 | |||
| OA | 0.96734 | ||||
| B1 B3 B6 | 29 | 28 | UA | 0.96634 | 0.96853 |
| PA | 0.96654 | 0.96834 | |||
| OA | 0.96747 | ||||
| B3 B4 B6 | 43 | 46 | UA | 0.80091 | 0.98911 |
| PA | 0.99100 | 0.76838 | |||
| OA | 0.87626 | ||||
| B2 B3 B9 | 54 | 50 | UA | 0.65335 | 0.99768 |
| PA | 0.99876 | 0.50178 | |||
| OA | 0.74261 | ||||
| B3 B4 B9 | 55 | 55 | UA | 0.75470 | 0.82372 |
| PA | 0.83013 | 0.74631 | |||
| OA | 0.78693 | ||||
| B1 B2 B9 | 56 | 56 | UA | 0.99286 | 0.52264 |
| PA | 0.02875 | 0.99981 | |||
| OA | 0.52924 | ||||
| B2 B5 B9 | 18 | 1 | UA | 0.98316 | 0.95884 |
| PA | 0.95504 | 0.98462 | |||
| OA | 0.97029 | ||||
| B4 B5 B9 | 13 | 2 | UA | 0.98154 | 0.96100 |
| PA | 0.95756 | 0.98306 | |||
| OA | 0.97071 | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Figliomeni, F.G.; Guastaferro, F.; Parente, C.; Vallario, A. A Proposal for Automatic Coastline Extraction from Landsat 8 OLI Images Combining Modified Optimum Index Factor (MOIF) and K-Means. Remote Sens. 2023, 15, 3181. https://doi.org/10.3390/rs15123181
Figliomeni FG, Guastaferro F, Parente C, Vallario A. A Proposal for Automatic Coastline Extraction from Landsat 8 OLI Images Combining Modified Optimum Index Factor (MOIF) and K-Means. Remote Sensing. 2023; 15(12):3181. https://doi.org/10.3390/rs15123181
Chicago/Turabian StyleFigliomeni, Francesco Giuseppe, Francesca Guastaferro, Claudio Parente, and Andrea Vallario. 2023. "A Proposal for Automatic Coastline Extraction from Landsat 8 OLI Images Combining Modified Optimum Index Factor (MOIF) and K-Means" Remote Sensing 15, no. 12: 3181. https://doi.org/10.3390/rs15123181
APA StyleFigliomeni, F. G., Guastaferro, F., Parente, C., & Vallario, A. (2023). A Proposal for Automatic Coastline Extraction from Landsat 8 OLI Images Combining Modified Optimum Index Factor (MOIF) and K-Means. Remote Sensing, 15(12), 3181. https://doi.org/10.3390/rs15123181







