Influence of On-Site Camera Calibration with Sub-Block of Images on the Accuracy of Spatial Data Obtained by PPK-Based UAS Photogrammetry
Abstract
1. Introduction
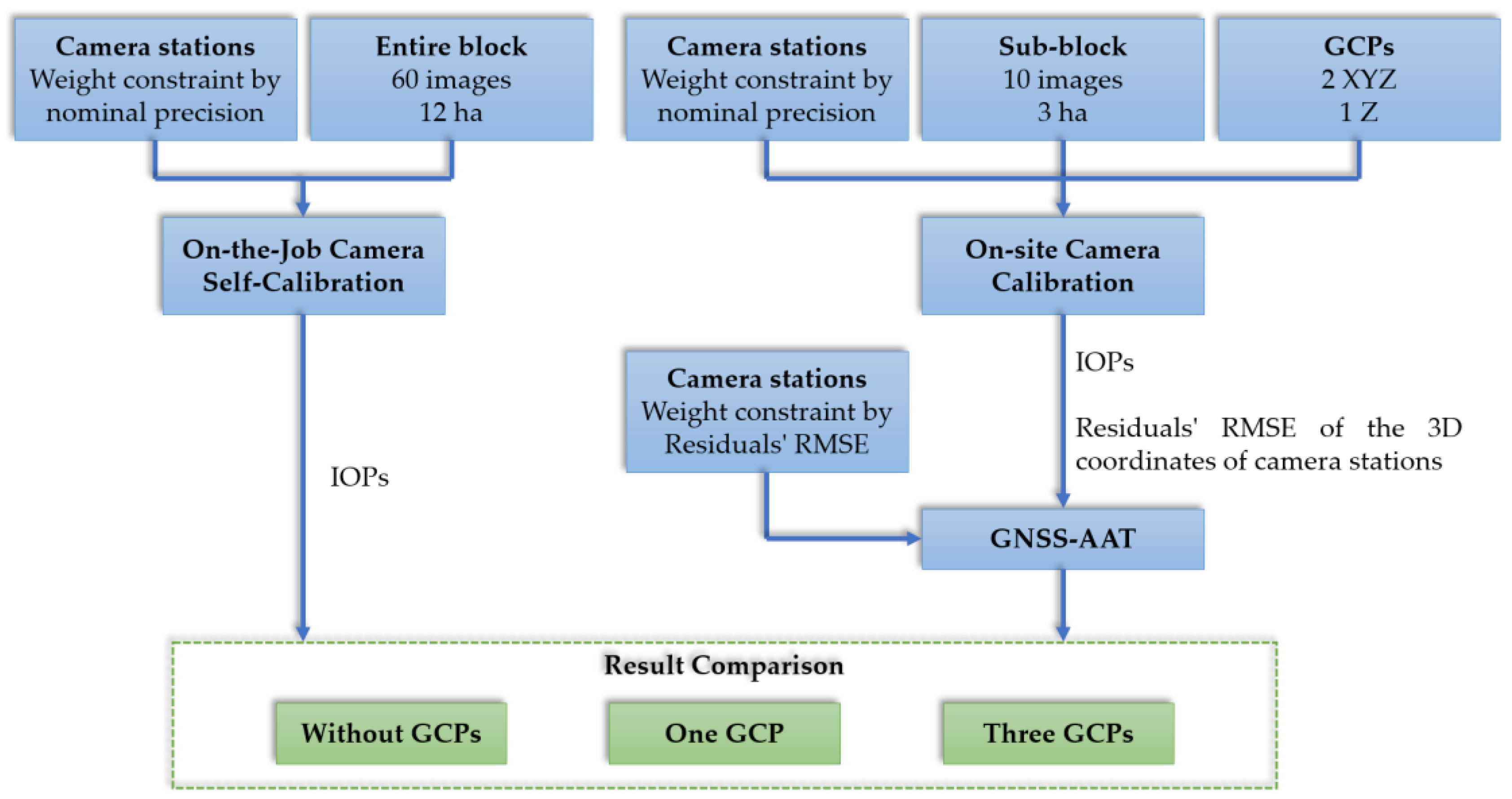
2. Materials and Methods
2.1. On-the-Job Camera Self-Calibration
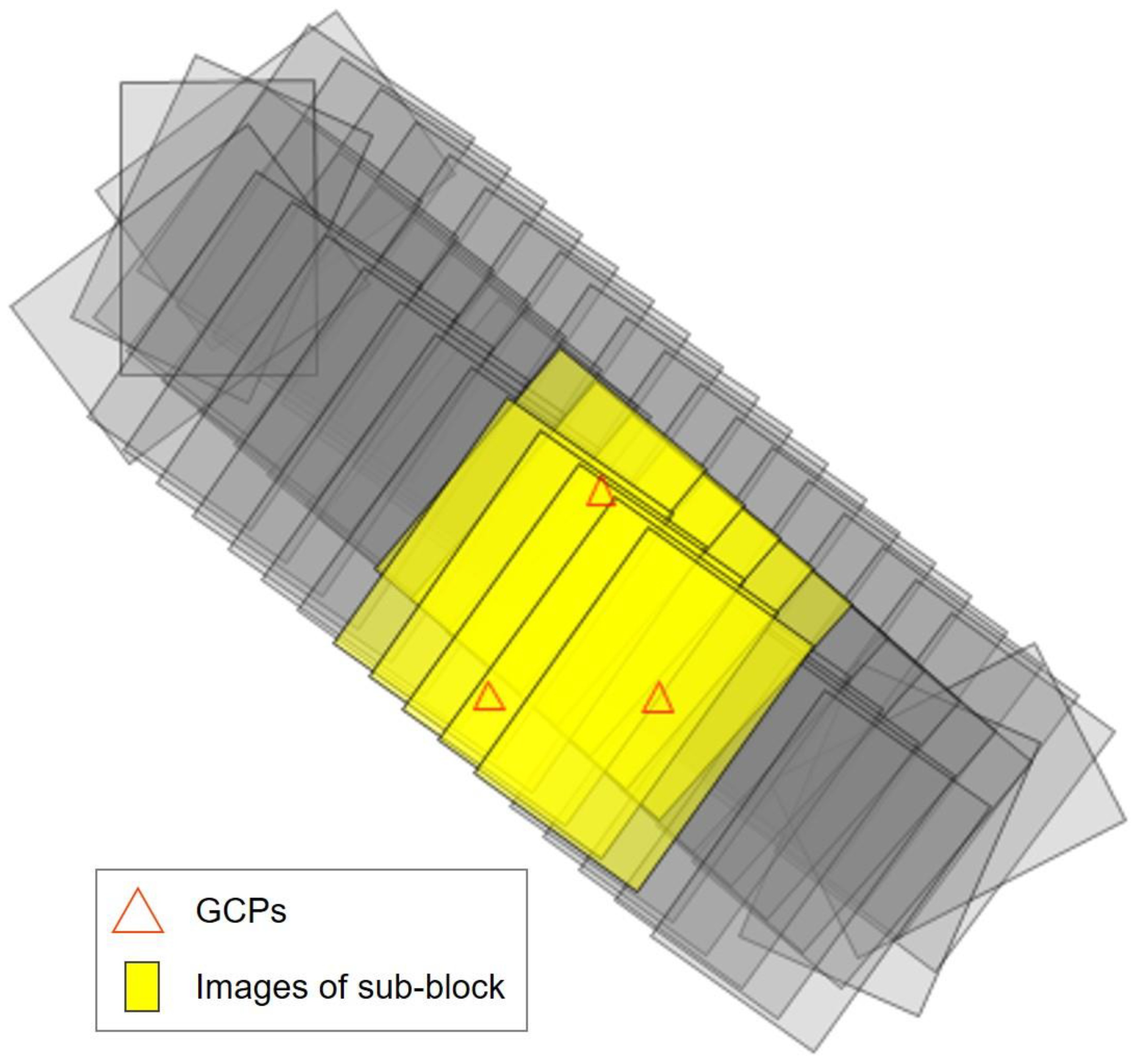
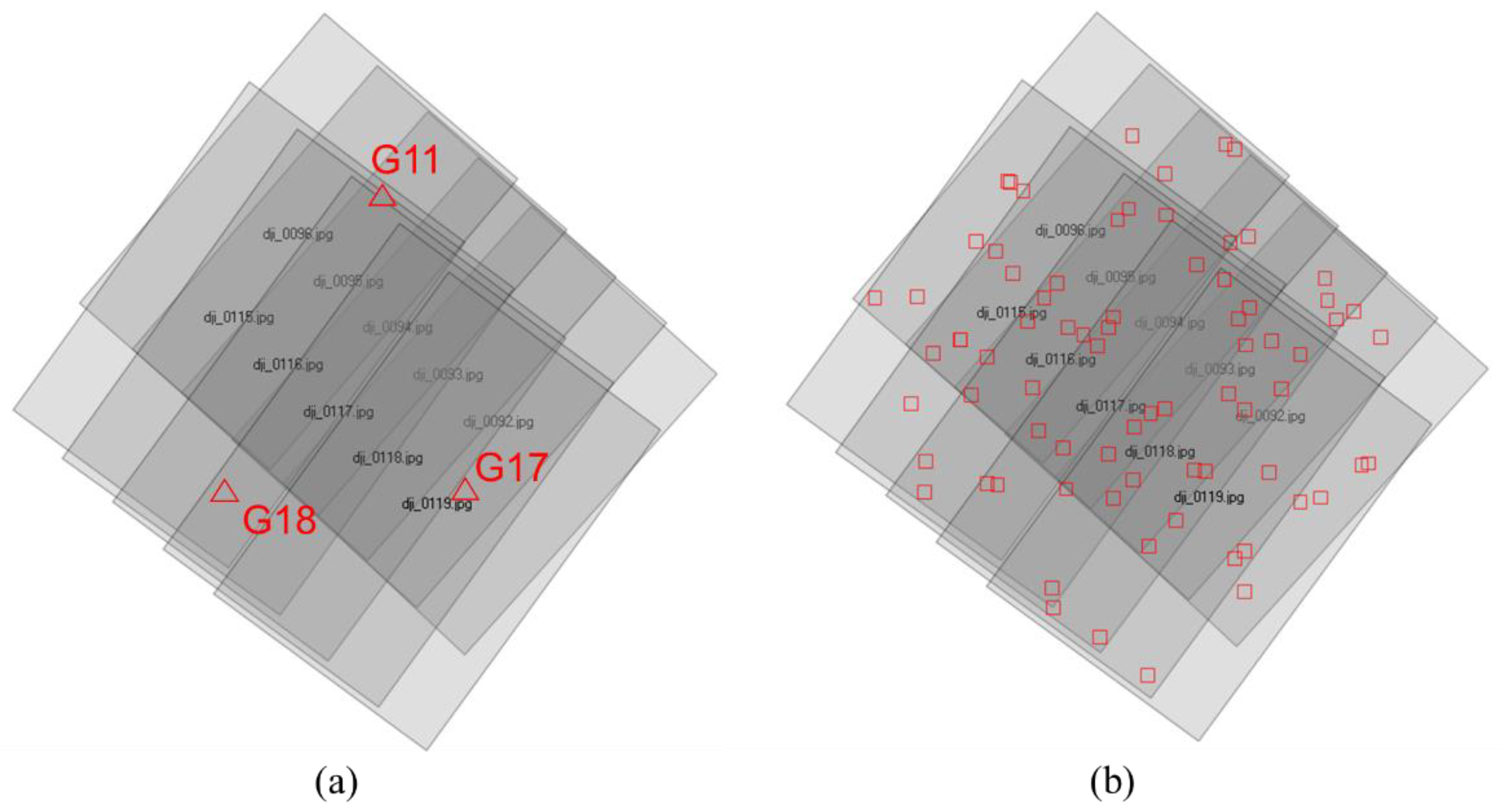
2.2. On-Site Camera Calibration Using Sub-Block of Images
- Null hypothesis (): ;
- Alternative hypothesis (): ;
2.3. GNSS-AAT Using IOPs from the On-Site Calibration
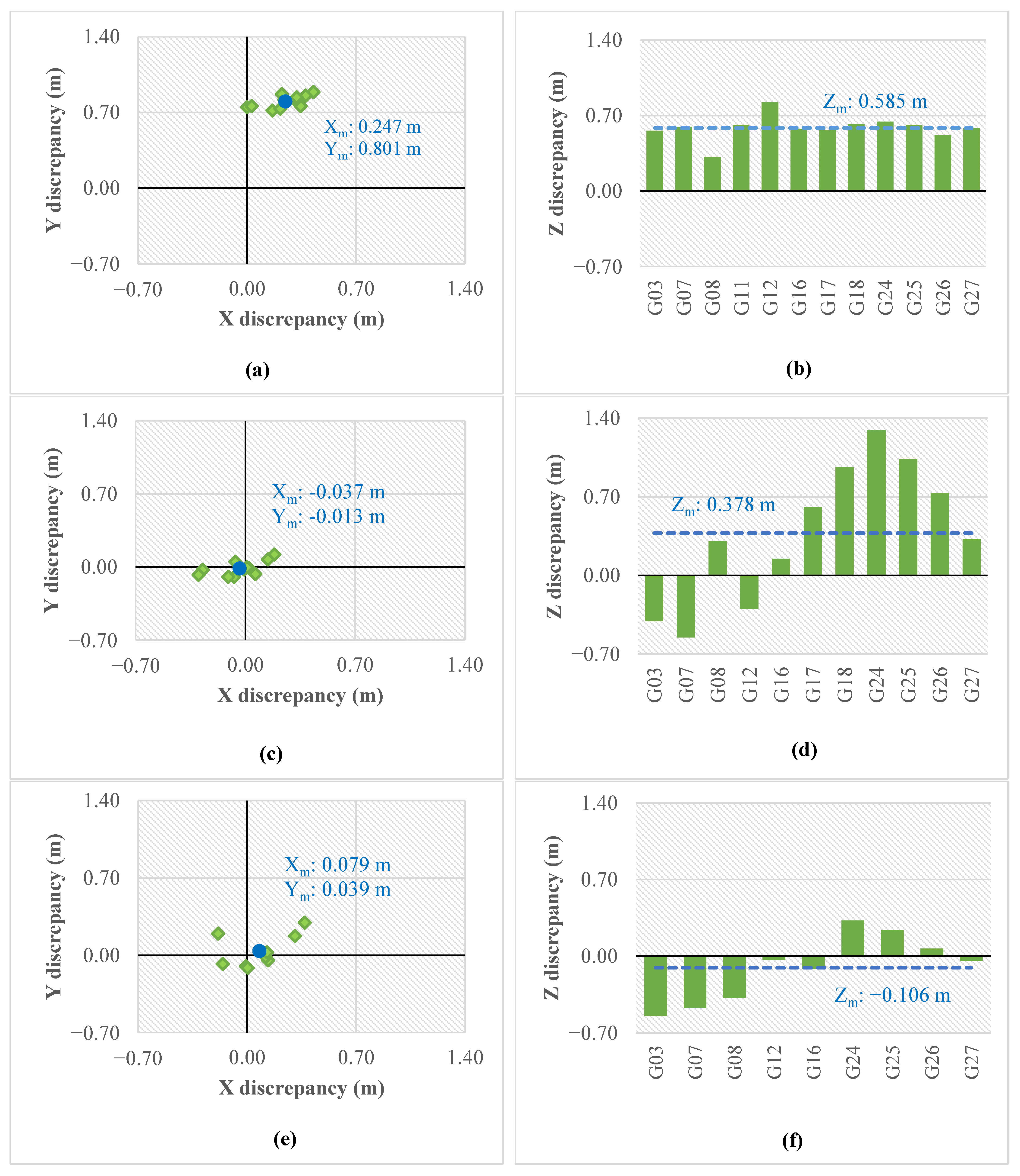
3. Results
3.1. On-the-Job Camera Self-Calibration
3.2. On-Site Camera Calibration
3.3. GNSS-AAT Using IOPs from the On-Site Calibration
4. Discussion
4.1. Influence of On-Site Camera Calibration with Sub-Block of Images
4.2. Influence of GCP Configuration
5. Conclusions
Limitations and Future Work
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Granshaw, S.I. RPV, UAV, UAS, RPAS … or Just Drone? Photogramm. Rec. 2018, 33, 160–170. [Google Scholar] [CrossRef]
- Tuffen, H.; James, M.R.; Castro, J.M.; Schipper, C.I. Exceptional Mobility of an Advancing Rhyolitic Obsidian Flow at Cordón Caulle Volcano in Chile. Nat. Commun. 2013, 4, 2709. [Google Scholar] [CrossRef]
- Civico, R.; Ricci, T.; Scarlato, P.; Andronico, D.; Cantarero, M.; Carr, B.B.; De Beni, E.; Del Bello, E.; Johnson, J.B.; Kueppers, U.; et al. Unoccupied Aircraft Systems (UASs) Reveal the Morphological Changes at Stromboli Volcano (Italy) before, between, and after the 3 July and 28 August 2019 Paroxysmal Eruptions. Remote Sens. 2021, 13, 2870. [Google Scholar] [CrossRef]
- Castillo, C.; Pérez, R.; James, M.R.; Quinton, J.N.; Taguas, E.V.; Gómez, J.A. Comparing the Accuracy of Several Field Methods for Measuring Gully Erosion. Soil Sci. Soc. Am. J. 2012, 76, 1319–1332. [Google Scholar] [CrossRef]
- Eltner, A.; Baumgart, P.; Maas, H.-G.; Faust, D. Multi-Temporal UAV Data for Automatic Measurement of Rill and Interrill Erosion on Loess Soil: Uav Data for Automatic Measurement Of Rill And Interrill Erosion. Earth Surf. Process. Landf. 2015, 40, 741–755. [Google Scholar] [CrossRef]
- James, M.R.; Robson, S.; Smith, M.W. 3-D Uncertainty-Based Topographic Change Detection with Structure-from-Motion Photogrammetry: Precision Maps for Ground Control and Directly Georeferenced Surveys: 3-D Uncertainty-Based Change Detection for SfM Surveys. Earth Surf. Process. Landf. 2017, 42, 1769–1788. [Google Scholar] [CrossRef]
- Niethammer, U.; James, M.R.; Rothmund, S.; Travelletti, J.; Joswig, M. UAV-Based Remote Sensing of the Super-Sauze Landslide: Evaluation and Results. Eng. Geol. 2012, 128, 2–11. [Google Scholar] [CrossRef]
- Lucieer, A.; de Jong, S.M.; Turner, D. Mapping Landslide Displacements Using Structure from Motion (SfM) and Image Correlation of Multi-Temporal UAV Photography. Prog. Phys. Geogr. Earth Environ. 2014, 38, 97–116. [Google Scholar] [CrossRef]
- Cho, J.; Lee, J.; Lee, B. Application of UAV Photogrammetry to Slope-Displacement Measurement. KSCE J. Civ. Eng. 2022, 26, 1904–1913. [Google Scholar] [CrossRef]
- Bemis, S.P.; Micklethwaite, S.; Turner, D.; James, M.R.; Akciz, S.; Thiele, S.T.; Bangash, H.A. Ground-Based and UAV-Based Photogrammetry: A Multi-Scale, High-Resolution Mapping Tool for Structural Geology and Paleoseismology. J. Struct. Geol. 2014, 69, 163–178. [Google Scholar] [CrossRef]
- Vasuki, Y.; Holden, E.-J.; Kovesi, P.; Micklethwaite, S. Semi-Automatic Mapping of Geological Structures Using UAV-Based Photogrammetric Data: An Image Analysis Approach. Comput. Geosci. 2014, 69, 22–32. [Google Scholar] [CrossRef]
- Ryan, J.C.; Hubbard, A.L.; Box, J.E.; Todd, J.; Christoffersen, P.; Carr, J.R.; Holt, T.O.; Snooke, N. UAV Photogrammetry and Structure from Motion to Assess Calving Dynamics at Store Glacier, a Large Outlet Draining the Greenland Ice Sheet. Cryosphere 2015, 9, 1–11. [Google Scholar] [CrossRef]
- Belloni, V.; Fugazza, D.; Di Rita, M. Uav-Based Glacier Monitoring: Gnss Kinematic Track Post-Processing and Direct Georeferencing for Accurate Reconstructions in Challenging Environments. Int. Arch. Photogramm. Remote Sens. Spatial Inf. Sci. 2022, XLIII-B1-2022, 367–373. [Google Scholar] [CrossRef]
- Deliry, S.I.; Avdan, U. Accuracy of Unmanned Aerial Systems Photogrammetry and Structure from Motion in Surveying and Mapping: A Review. J. Indian Soc. Remote Sens. 2021, 49, 1997–2017. [Google Scholar] [CrossRef]
- Liu, Y.; Han, K.; Rasdorf, W. Assessment and Prediction of Impact of Flight Configuration Factors on UAS-Based Photogrammetric Survey Accuracy. Remote Sens. 2022, 14, 4119. [Google Scholar] [CrossRef]
- Pargieła, K.; Rzonca, A. Determining Optimal Photogrammetric Adjustment of Images Obtained from a Fixed-wing UAV. Photogramm. Rec. 2021, 36, 285–302. [Google Scholar] [CrossRef]
- Sanz-Ablanedo, E.; Chandler, J.; Rodríguez-Pérez, J.; Ordóñez, C. Accuracy of Unmanned Aerial Vehicle (UAV) and SfM Photogrammetry Survey as a Function of the Number and Location of Ground Control Points Used. Remote Sens. 2018, 10, 1606. [Google Scholar] [CrossRef]
- Ferrer-González, E.; Agüera-Vega, F.; Carvajal-Ramírez, F.; Martínez-Carricondo, P. UAV Photogrammetry Accuracy Assessment for Corridor Mapping Based on the Number and Distribution of Ground Control Points. Remote Sens. 2020, 12, 2447. [Google Scholar] [CrossRef]
- Gomes Pessoa, G.; Caceres Carrilho, A.; Takahashi Miyoshi, G.; Amorim, A.; Galo, M. Assessment of UAV-Based Digital Surface Model and the Effects of Quantity and Distribution of Ground Control Points. Int. J. Remote Sens. 2021, 42, 65–83. [Google Scholar] [CrossRef]
- Liu, X.; Lian, X.; Yang, W.; Wang, F.; Han, Y.; Zhang, Y. Accuracy Assessment of a UAV Direct Georeferencing Method and Impact of the Configuration of Ground Control Points. Drones 2022, 6, 30. [Google Scholar] [CrossRef]
- Gerke, M.; Nex, F.; Remondino, F.; Jacobsen, K.; Kremer, J.; Karel, W.; Hu, H.; Ostrowski, W. Orientation of Oblique Airborne Image Sets &Ndash; Experiences from the Isprs/Eurosdr Benchmark on Multi-Platform Photogrammetry. Int. Arch. Photogramm. Remote Sens. Spatial Inf. Sci. 2016, XLI-B1, 185–191. [Google Scholar] [CrossRef]
- James, M.R.; Robson, S. Mitigating Systematic Error in Topographic Models Derived from UAV and Ground-Based Image Networks: Mitigating Systematic Error in Topographic Models. Earth Surf. Process. Landf. 2014, 39, 1413–1420. [Google Scholar] [CrossRef]
- Carbonneau, P.E.; Dietrich, J.T. Cost-Effective Non-Metric Photogrammetry from Consumer-Grade SUAS: Implications for Direct Georeferencing of Structure from Motion Photogrammetry: Cost-Effective Non-Metric Photogrammetry from Consumer-Grade SUAS. Earth Surf. Process. Landf. 2017, 42, 473–486. [Google Scholar] [CrossRef]
- Gerke, M.; Przybilla, H.-J. Accuracy Analysis of Photogrammetric UAV Image Blocks: Influence of Onboard RTK-GNSS and Cross Flight Patterns. Photogramm. Fernerkund. Geoinf. 2016, 2016, 17–30. [Google Scholar] [CrossRef]
- Štroner, M.; Urban, R.; Seidl, J.; Reindl, T.; Brouček, J. Photogrammetry Using UAV-Mounted GNSS RTK: Georeferencing Strategies without GCPs. Remote Sens. 2021, 13, 1336. [Google Scholar] [CrossRef]
- Stumpf, A.; Malet, J.-P.; Allemand, P.; Pierrot-Deseilligny, M.; Skupinski, G. Ground-Based Multi-View Photogrammetry for the Monitoring of Landslide Deformation and Erosion. Geomorphology 2015, 231, 130–145. [Google Scholar] [CrossRef]
- Kameyama, S.; Sugiura, K. Effects of Differences in Structure from Motion Software on Image Processing of Unmanned Aerial Vehicle Photography and Estimation of Crown Area and Tree Height in Forests. Remote Sens. 2021, 13, 626. [Google Scholar] [CrossRef]
- Jiang, S.; Jiang, C.; Jiang, W. Efficient Structure from Motion for Large-Scale UAV Images: A Review and a Comparison of SfM Tools. ISPRS J. Photogramm. Remote Sens. 2020, 167, 230–251. [Google Scholar] [CrossRef]
- Gonçalves, J.A.; Henriques, R. UAV Photogrammetry for Topographic Monitoring of Coastal Areas. ISPRS J. Photogramm. Remote Sens. 2015, 104, 101–111. [Google Scholar] [CrossRef]
- Grayson, B.; Penna, N.T.; Mills, J.P.; Grant, D.S. GPS Precise Point Positioning for UAV Photogrammetry. Photogramm. Rec. 2018, 33, 427–447. [Google Scholar] [CrossRef]
- Vericat, D.; Brasington, J.; Wheaton, J.; Cowie, M. Accuracy Assessment of Aerial Photographs Acquired Using Lighter-than-Air Blimps: Low-Cost Tools for Mapping River Corridors. River Res. Applic. 2009, 25, 985–1000. [Google Scholar] [CrossRef]
- Turner, D.; Lucieer, A.; Watson, C. An Automated Technique for Generating Georectified Mosaics from Ultra-High Resolution Unmanned Aerial Vehicle (UAV) Imagery, Based on Structure from Motion (SfM) Point Clouds. Remote Sens. 2012, 4, 1392–1410. [Google Scholar] [CrossRef]
- Chiabrando, F.; Giulio Tonolo, F.; Lingua, A. UAV Direct Georeferencing Approach in An Emergency Mapping Context. The 2016 Central Italy Earthquake Case Study. Int. Arch. Photogramm. Remote Sens. Spatial Inf. Sci. 2019, XLII-2/W13, 247–253. [Google Scholar] [CrossRef]
- Antoine, R.; Lopez, T.; Tanguy, M.; Lissak, C.; Gailler, L.; Labazuy, P.; Fauchard, C. Geoscientists in the Sky: Unmanned Aerial Vehicles Responding to Geohazards. Surv. Geophys. 2020, 41, 1285–1321. [Google Scholar] [CrossRef]
- Benjamin, A.R.; O’Brien, D.; Barnes, G.; Wilkinson, B.E.; Volkmann, W. Improving Data Acquisition Efficiency: Systematic Accuracy Evaluation of GNSS-Assisted Aerial Triangulation in UAS Operations. J. Surv. Eng. 2020, 146, 05019006. [Google Scholar] [CrossRef]
- Yastikli, N.; Jacobsen, K. Influence of System Calibration on Direct Sensor Orientation. Photogramm. Eng. Remote Sens. 2005, 71, 629–633. [Google Scholar] [CrossRef]
- Turner, D.; Lucieer, A.; Wallace, L. Direct Georeferencing of Ultrahigh-Resolution UAV Imagery. IEEE Trans. Geosci. Remote Sens. 2014, 52, 2738–2745. [Google Scholar] [CrossRef]
- Gabrlik, P. Boresight Calibration of a Multi-Sensor System for UAS Photogrammetry. ELEKTRO 2018, 1–6. [Google Scholar] [CrossRef]
- Wolf, P.R.; Dewitt, B.A.; Wilkinson, B.E. Elements of Photogrammetry with Applications in GIS, 4th ed.; McGraw-Hill Education: New York, NY, USA, 2014; ISBN 978-0-07-176112-3. [Google Scholar]
- Jacobsen, K. Direct/Integrated Sensor Orientation—Pros and Cons. Int. Arch. Photogramm. Remote Sens. 2004, 35, 829–835. [Google Scholar]
- Forlani, G.; Dall’Asta, E.; Diotri, F.; di Cella, U.M.; Roncella, R.; Santise, M. Quality Assessment of DSMs Produced from UAV Flights Georeferenced with On-Board RTK Positioning. Remote Sens. 2018, 10, 311. [Google Scholar] [CrossRef]
- Ip, A.; El-Sheimy, N.; Mostafa, M. Performance Analysis of Integrated Sensor Orientation. Photogramm. Eng. Remote Sens. 2007, 73, 89–97. [Google Scholar] [CrossRef]
- Habib, A.; Kersting, A.P.; Bang, K. Comparative Analysis of Different Approaches for The Incorporation of Position and Orientation Information in Integrated Sensor Orientation Procedures. In Proceedings of the Canadian Geomatics Conference 2010 and ISPRS Commision I Symposium, Calgary, AB, Canada, 15–18 June 2010; Volume AB. [Google Scholar]
- Heipke, C.; Jacobsen, K.; Wegmann, H.; Andersen, Ø.; Nilsen, B. Integrated Sensor Orientation—An Oeepe TEST. Int. Arch. Photogramm. Remote Sens. 2000, 33, 373–380. [Google Scholar]
- Kraus, K. Photogrammetry: Geometry from Images and Laser Scans; Walter de Gruyter: Berlin, Germany, 2007; ISBN 978-3-11-019007-6. [Google Scholar]
- Chiang, K.-W.; Tsai, M.-L.; Chu, C.-H. The Development of an UAV Borne Direct Georeferenced Photogrammetric Platform for Ground Control Point Free Applications. Sensors 2012, 12, 9161–9180. [Google Scholar] [CrossRef] [PubMed]
- Benassi, F.; Dall’Asta, E.; Diotri, F.; Forlani, G.; Morra di Cella, U.; Roncella, R.; Santise, M. Testing Accuracy and Repeatability of UAV Blocks Oriented with GNSS-Supported Aerial Triangulation. Remote Sens. 2017, 9, 172. [Google Scholar] [CrossRef]
- Zhou, Y.; Rupnik, E.; Faure, P.-H.; Pierrot-Deseilligny, M. GNSS-Assisted Integrated Sensor Orientation with Sensor Pre-Calibration for Accurate Corridor Mapping. Sensors 2018, 18, 2783. [Google Scholar] [CrossRef]
- Stöcker, C.; Nex, F.; Koeva, M.; Gerke, M. Quality Assessment of Combined Imu/Gnss Data For Direct Georeferencing in the Context of Uav-Based Mapping. Int. Arch. Photogramm. Remote Sens. Spatial Inf. Sci. 2017, XLII-2/W6, 355–361. [Google Scholar] [CrossRef]
- Przybilla, H.-J.; Bäumker, M.; Luhmann, T.; Hastedt, H.; Eilers, M. Interaction between Direct Georeferencing, Control Point Configuration and Camera Self-Calibration for Rtk-Based Uav Photogrammetry. Int. Arch. Photogramm. Remote Sens. Spatial Inf. Sci. 2020, XLIII-B1-2020, 485–492. [Google Scholar] [CrossRef]
- Zhou, Y.; Rupnik, E.; Meynard, C.; Thom, C.; Pierrot-Deseilligny, M. Simulation and Analysis of Photogrammetric UAV Image Blocks—Influence of Camera Calibration Error. Remote Sens. 2019, 12, 22. [Google Scholar] [CrossRef]
- Cledat, E.; Cucci, D.A.; Skaloud, J. Camera Calibration Models and Methods for Corridor Mapping with Uavs. ISPRS Ann. Photogramm. Remote Sens. Spatial Inf. Sci. 2020, V-1–2020, 231–238. [Google Scholar] [CrossRef]
- Mitishita, E.; Ercolin Filho, L.; Graça, N.; Centeno, J. Approach for Improving the Integrated Sensor Orientation. ISPRS Ann. Photogramm. Remote Sens. Spatial Inf. Sci. 2016, III–1, 33–39. [Google Scholar] [CrossRef]
- Costa, F.; Mitishita, E.; Martins, M. The Influence of Sub-Block Position on Performing Integrated Sensor Orientation Using In Situ Camera Calibration and Lidar Control Points. Remote Sens. 2018, 10, 260. [Google Scholar] [CrossRef]
- HiPer SR—Advanced, Ultra-Compact and Productive|Topcon Positioning. Available online: https://www.topconpositioning.com/gnss/gnss-receivers/hiper-sr#panel-product-specifications (accessed on 1 March 2023).
- Agisoft. Agisoft Metashape User Manual—Professional Edition, Version 1.5; Agisoft: St. Petersburg, Russia, 2019.
- Lowe, D.G. Distinctive Image Features from Scale-Invariant Keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Conrady, A.E. Decentred Lens-Systems. Mon. Not. R. Astron. Soc. 1919, 79, 384–390. [Google Scholar] [CrossRef]
- Brown, D.C. Close-Range Camera Calibration. Photogramm. Eng. 1971, 37, 855–866. [Google Scholar]
- Galo, M.; Maria, A.; Tommaselli, A.; Hasegawa, J.; De, P.; Camargo, O. Significance of Interior Orientation Parameters in Camera Calibration. In Proceedings of the II SIMGEO- Brazilian Symposium on Geodetic Sciences and Geoinformation Technologies, Recife, Brazil, 8–11 November 2008. [Google Scholar]
- Pasumansky, A. Definitive Help in How Photoscan Defines Its Yaw Pitch and Roll Angles. Available online: https://www.agisoft.com/forum/index.php?topic=6126.0 (accessed on 6 March 2023).
- Roncella, R.; Forlani, G. UAV Block Geometry Design and Camera Calibration: A Simulation Study. Sensors 2021, 21, 6090. [Google Scholar] [CrossRef]

| No. of GCP | RMSE in Camera Stations (m) | RMSE in GCP (m) | RMSE in Camera Stations (GSD) | RMSE in GCP (GSD) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Xs | Ys | Zs | X | Y | Z | Xs | Ys | Zs | X | Y | Z | |
| 0 | 0.131 | 0.104 | 0.017 | - | - | - | 4.6 | 3.7 | 0.6 | - | - | - |
| 1 | 0.152 | 0.140 | 0.394 | 0.012 | 0.014 | 0.000 | 5.3 | 4.9 | 13.9 | 0.4 | 0.5 | 0.0 |
| 3 | 0.156 | 0.468 | 0.220 | 0.019 | 0.036 | 0.058 | 5.5 | 16.5 | 7.7 | 0.7 | 1.3 | 2.1 |
| IOPs | 0 GCP | 1 GCP | 3 GCP | |||
|---|---|---|---|---|---|---|
| IOPs Values | Standard Deviation | IOPs Values | Standard Deviation | IOPs Values | Standard Deviation | |
| (mm) | 8.951 | 1.76 × 10−2 | 8.985 | 1.25 × 10−3 | 9.019 | 6.03 × 10−4 |
| (mm) | −0.001 | 1.25 × 10−4 | −0.001 | 1.25 × 10−4 | −0.002 | 1.37 × 10−4 |
| (mm) | 0.037 | 2.89 × 10−4 | 0.038 | 9.88 × 10−5 | 0.039 | 1.06 × 10−4 |
| (mm−2) | 1.019 × 10−5 | 1.253 × 10−7 | 1.025 × 10−5 | 1.205 × 10−7 | 1.105 × 10−5 | 1.085 × 10−7 |
| (mm−4) | −3.332 × 10−5 | 4.097 × 10−7 | −3.390 × 10−5 | 3.133 × 10−7 | −3.428 × 10−5 | 3.374 × 10−7 |
| (mm−6) | 3.588 × 10−5 | 5.061 × 10−7 | 3.677 × 10−5 | 2.892 × 10−7 | 3.717 × 10−5 | 3.374 × 10−7 |
| (mm−1) | 1.504 × 10−6 | 7.712 × 10−9 | 1.505 × 10−6 | 7.230 × 10−9 | 1.643 × 10−6 | 7.953 × 10−9 |
| (mm−1) | −5.941 × 10−7 | 6.025 × 10−9 | −5.805 × 10−7 | 6.025 × 10−9 | −5.760 × 10−7 | 6.748 × 10−9 |
| No. of GCP | RMSE (m) | RMSE (GSD) | ||||||
|---|---|---|---|---|---|---|---|---|
| X | Y | XY | Z | X | Y | XY | Z | |
| 0 | 0.277 | 0.803 | 0.849 | 0.595 | 9.7 | 28.3 | 29.9 | 20.9 |
| 1 | 0.149 | 0.068 | 0.164 | 0.699 | 5.2 | 2.4 | 5.8 | 24.6 |
| 3 | 0.194 | 0.145 | 0.242 | 0.308 | 6.8 | 5.1 | 8.5 | 10.8 |
| IOPs | Calib_1 | Calib_2 | Calib_3 | Calib_4 | Calib_5 | |
|---|---|---|---|---|---|---|
| (mm) | Value | 9.006 | 9.006 | 9.006 | 9.007 | 9.006 |
| Std. dev. | 0.006 | 0.006 | 0.007 | 0.006 | 0.006 | |
| 2,043,402.18 | 2,043,447.56 | 1,919,503.67 | 2,043,810.62 | 2,109,849.96 | ||
| (mm) | Value | −0.008 | −0.008 | −0.021 | −0.008 | −0.009 |
| Std. dev. | 0.004 | 0.004 | 0.003 | 0.004 | 0.004 | |
| 4.57 | 4.57 | 54.13 | 5.19 | 6.32 | ||
| (mm) | Value | −0.044 | −0.044 | −0.046 | −0.044 | −0.044 |
| Std. dev. | 0.003 | 0.002 | 0.002 | 0.002 | 0.002 | |
| 215.11 | 435.02 | 469.44 | 435.02 | 437.01 | ||
| (mm−2) | Value | 2.10 × 10−5 | 2.10 × 10−5 | 2.14 × 10−5 | 1.44 × 10−6 | 9.27 × 10−6 |
| Std. dev. | 1.69 × 10−5 | 1.69 × 10−5 | 1.74 × 10−5 | 9.22 × 10−6 | 5.57 × 10−6 | |
| 1.56 | 1.56 | 1.52 | 0.02 | 2.78 | ||
| (mm−4) | Value | −7.56 × 10−7 | −7.57 × 10−7 | −7.57 × 10−7 | 1.22 × 10−7 | 0.000 |
| Std. dev. | 6.43 × 10−7 | 6.43 × 10−7 | 6.62 × 10−7 | 1.06 × 10−7 | 0.000 | |
| 1.38 | 1.38 | 1.31 | 1.34 | - | ||
| (mm−6) | Value | 1.01 × 10−8 | 1.01 × 10−8 | 9.95 × 10−9 | 0.000 | 0.000 |
| Std. dev. | 7.32 × 10−9 | 7.32 × 10−9 | 7.55 × 10−9 | 0.000 | 0.000 | |
| 1.92 | 1.92 | 1.74 | - | - | ||
| (mm−1) | Value | 6.20 × 10−5 | 6.20 × 10−5 | 0.000 | 6.19 × 10−5 | 6.15 × 10−5 |
| Std. dev. | 1.13 × 10−5 | 1.13 × 10−5 | 0.000 | 1.13 × 10−5 | 1.13 × 10−5 | |
| 30.23 | 30.25 | - | 30.06 | 29.63 | ||
| (mm−1) | Value | −6.13 × 10−7 | 0.000 | 0.000 | 0.000 | 0.000 |
| Std. dev. | 8.94 × 10−6 | 0.000 | 0.000 | 0.000 | 0.000 | |
| 0.00 | - | - | - | - | ||
| Computed Chi-squared | 501.96 | 501.96 | 501.96 | 533.92 | 503.84 | |
| No. of GCP | RMSE in Camera Stations (m) | RMSE in GCP (m) | RMSE in Camera Stations (GSD) | RMSE in GCP (GSD) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Xs | Ys | Zs | X | Y | Z | Xs | Ys | Zs | X | Y | Z | |
| 0 | 0.137 | 0.118 | 0.049 | - | - | - | 4.8 | 4.2 | 1.7 | - | - | - |
| 1 | 0.145 | 0.364 | 0.188 | 0.003 | 0.007 | 0.003 | 5.1 | 12.8 | 6.6 | 0.1 | 0.3 | 0.1 |
| 3 | 0.150 | 0.579 | 0.089 | 0.015 | 0.016 | 0.007 | 5.3 | 20.4 | 3.1 | 0.5 | 0.6 | 0.3 |
| No. of GCP | RMSE (m) | RMSE (GSD) | ||||||
|---|---|---|---|---|---|---|---|---|
| X | Y | XY | Z | X | Y | XY | Z | |
| 0 | 0.290 | 0.806 | 0.857 | 0.103 | 10.2 | 28.4 | 30.2 | 3.6 |
| 1 | 0.165 | 0.075 | 0.181 | 0.373 | 5.8 | 2.6 | 6.4 | 13.1 |
| 3 | 0.157 | 0.157 | 0.222 | 0.154 | 5.5 | 5.5 | 7.8 | 5.4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pitombeira, K.; Mitishita, E. Influence of On-Site Camera Calibration with Sub-Block of Images on the Accuracy of Spatial Data Obtained by PPK-Based UAS Photogrammetry. Remote Sens. 2023, 15, 3126. https://doi.org/10.3390/rs15123126
Pitombeira K, Mitishita E. Influence of On-Site Camera Calibration with Sub-Block of Images on the Accuracy of Spatial Data Obtained by PPK-Based UAS Photogrammetry. Remote Sensing. 2023; 15(12):3126. https://doi.org/10.3390/rs15123126
Chicago/Turabian StylePitombeira, Kalima, and Edson Mitishita. 2023. "Influence of On-Site Camera Calibration with Sub-Block of Images on the Accuracy of Spatial Data Obtained by PPK-Based UAS Photogrammetry" Remote Sensing 15, no. 12: 3126. https://doi.org/10.3390/rs15123126
APA StylePitombeira, K., & Mitishita, E. (2023). Influence of On-Site Camera Calibration with Sub-Block of Images on the Accuracy of Spatial Data Obtained by PPK-Based UAS Photogrammetry. Remote Sensing, 15(12), 3126. https://doi.org/10.3390/rs15123126











